Translation Can Distort the Linguistic Parameters of Source Texts Written in Inflected Language. Case Study: Multidimensional Mathematical Analysis of “The Betrothed”, a Translation in English of “I Promessi Sposi” by A. Manzoni

1. Introduction

Translation is the replacement of a text in one language (source text) by an equivalent text in another language (target text). Most studies on translation report results not based on mathematical analysis of texts, as we do with our mathemartical/statistical theory on alphabetical languages developed in a series of papers [1,2,3,4,5,6,7,8]. When a mathematical approach is used [9,10,11,12,13], scholars neither consider Shannon’s communication theory [14] nor the fundamental connection linguistic variables have with reader’s reading skill and short–term memory, considered instead by our theory. Very often they refer only to one linguistic variable. The theory we have developed can be applied and unifies the study of any alphabetical language.

Of all types of translation, literary translation is maybe the most demanding and difficult because the language of literature is different from ordinary or technical language and involves many challenges on the syntactic, lexical, semantic and stylistic levels [15,16,17,18,19,20,21,22].

Often, in translation theory studies, especially of literary texts, scholars mention the concept of “equivalence” – or “sameness” - between the source text (to be translated) and the target text (translated text) [23,24,25]. This concept, however is loosely and never mathematically defined. On the contrary, our theory can mathematically “measure” how much texts differ from each other, with a multidimensional analysis [26], as we do also in the present paper.

Today, it is agreed that the translator of literary texts is an active role player and the intermediary between the source text and the target text [17,27].

In relation to the translator’s role, however, two main theories of translation are today discussed by scholars: “domestication” and “foreignization” [27]. Domestication is a translation method in which the translator tries to match the source text to the reader, mainly to reader’s reading skills. Foreignization is a method in which the translator tries to match the reader to the source text, essentially regardless of reader’s reading skills. In other words, domestication neglects the foreign reality, while foreignization retains the foreignness and cultural otherness of a foreign text.

In translation to English the dominant practice is mainly domestication [27] because very likely translation makes the target text more fluent. This is achieved, however, by erasing the linguistic and cultural difference of the foreign text, therefore, text fluency becomes the general criterion to judge a translation.

In this paper, as study case, we compare by means of a multidimensional mathematical analysis the text of a famous Italian novel, I promessi sposi (1840) written by Alessandro Manzoni (1785 – 1873), to the text of the most recent English translation, The Betrothed by Michael F. Moore [28], a masterful translation.

To avoid any misunderstanding, the mathematical theory, and its multidimensional application to texts, is not concerned with the efficacy and beauty of a text - in this case the target text - but merely with its mathematical underlying structure, compared, in this case, to the Italian original text. The discussion and conclusion we reach are meant to be valid only in this context. In other words, we try to measure the “equivalence” of the two texts mathematically, just like we have done with other, oftern unrelated, couples of texts in any language, even between different languages [4,5,6,7,8].

Alessandro Manzoni was an Italian poet and novelist. He is famous for the novel The Betrothed (In Italian: I promessi sposi), ranked among the masterpieces of world literature. He started to write the first version in 1821 after reading Ivanhoe by Walter Scott (1771-1832) in a French translation, and revised it in its final version in the years 1830s.

I promessi sposi is a symbol of the Italian Risorgimento – the Italian XIX century political renaissance movement which unified Italy as a country – both because of its patriotic message and because the novel was a fundamental milestone in developing the modern Italian language which Manzoni stabilized and ensured its unity throughout Italy. The novel is still today a required reading in Italian High Schools.

Of the two translation theories, domestication and foreignization, Moore clearly has chosen domestication. In fact, in his “Notes on the Translation” he writes [28]:

«Within the framework of fidelity to I promessi sposi, I felt adjustments were needed due to fundamental stylistic and grammatical differences between English and Italian conventions. For example, Manzoni often adopts the periodic structure for his sentences, stringing together clause after clause with a series of semicolons. Italian enables and even encourages this style, since as an inflected language, Italian embeds the person and number of the subject—the I, you, or we—in the verb. Subject pronouns are used minimally, so a series of clauses with the same subject can result in a sentence the length of a page. The period, or “full stop,” is regarded with barely concealed horror, as if it truncates an otherwise beautiful sentence. English is not as economical in its use of subject pronouns, and actually requires them, so rather than mimic the periodic style at full length, I broke his sentences up into smaller parcels, sometimes (but not always) using periods where he used semicolons, feeling that they do not impose the same sense of finality in English as they do in Italian.»

In the following of the paper, we will realize that the replacement of semicolons with periods has had a very large impact on the underlying mathematical structure of the translation. However, this is not the only change, because other linguistic parameters have been largely modified. The aim of the paper is to show what has been mathematically modified, to what extent and the impact it has on readers.

After this introductory section, Section 2 shows an example of translation (the incipt of the novel), Section 3 reports some total statistics, Section 4 reports an exploratory data analysis of linguistic variables, Section 5 defines deep-language variables, Section 6 defines a geometrical representation of texts and discusses the probability of confusing a text with another, Section 7 deals with the short-term memory of readers/writers, Section 8 deals with the fine-tuning analysis done with linguistic channels, Section 9 deals with a universal readability index and Section 10 summarizes the main results and draw a conclusion.

2. Example of Translation: Incipit

The beginning of I promessi sposi – the first sentence of Chapter 1: «Quel ramo del lago di Como…» - is the second most celebrated incipit in the Italian Literature, being Dante’s Inferno incipit – «Nel mezzo del cammin di nostra vita…» the first one. Generations of Italian High School students have memorized both and still do.

It is illuminating to read how the beginning paragraph was translated (the Italian and English paragraphs, for reader’s benefit, are reported in Appendix A). As mentioned in the introduction, here – and in the whole paper - we are not concerned with the meaning and beauty of words, with grammar and so on, but only with the statistics of the linguistic parameters, suitably defined. For this purpose, let us study how this paragraph was translated by calculating some statistics. These arid numbers, however, highlight some important changes done by the translator, which deeply affected the entire English version of the novel. Table 1 reports them.

The beginning paragraph was split in five. In the Italian paragraph, Manzoni describes Lake Como and its eastern branch, from north to south and down to the main town, Lecco. He describes coves, inlets, hills, mountains, ravines, steep inclines and flat terraces, cultivated fields, vineyards, towns, villages, roads and footpaths. Only when he introduces the first character, Don Abbondio walking along one of the footpaths, Manzoni starts a new paragraph, therefore after 682 words and 9 long sentences with 9 semicolons within them (Table 1).

He seems to act like a modern movie director who sets the stage for the movie first events and ends this introductory paragraph – hence, starts a new paragraph – when in the close-up on a particular footpath the first character appears, Don Abbondio.

Since a paragraph develops a single point, we understand that in Manzoni’s mind the single point was the detailed geographical setting of the beginning of his story. When the description is, in his plan, complete, then he starts a new paragraph.

This is not done by the translator. By splitting Manzoni’s setting in five paragraphs, he abbandons the original sequence/climax and breaks the flow and unity that Manzoni carefully planned in the entire novel [29,30,31,32,33]. By splitting the single paragraph in five, the translator automatically distinguishes and emphasises five points.

The interpunctions were drastically changed. The most striking change is the almost complete replacement of semicolons and colons with periods. In fact, the sum $9+9+5=23$ gives the number of periods in the translated version. The purpose of semicolons – to separate independent clauses while connecting them as related ideas, just like Manzoni amply does - seems no longer acceptable by modern writers/readers of English texts [34,35,36]. Of course, this agrees with the translation theory flaunted by the translator (domestication), explicitly stated in his Introduction to the novel, as recalled in Section 1. Consequently, the liguistic structure of the Italian original text is largely modified, therefore we should expect significant changes in the deep-language parameters.

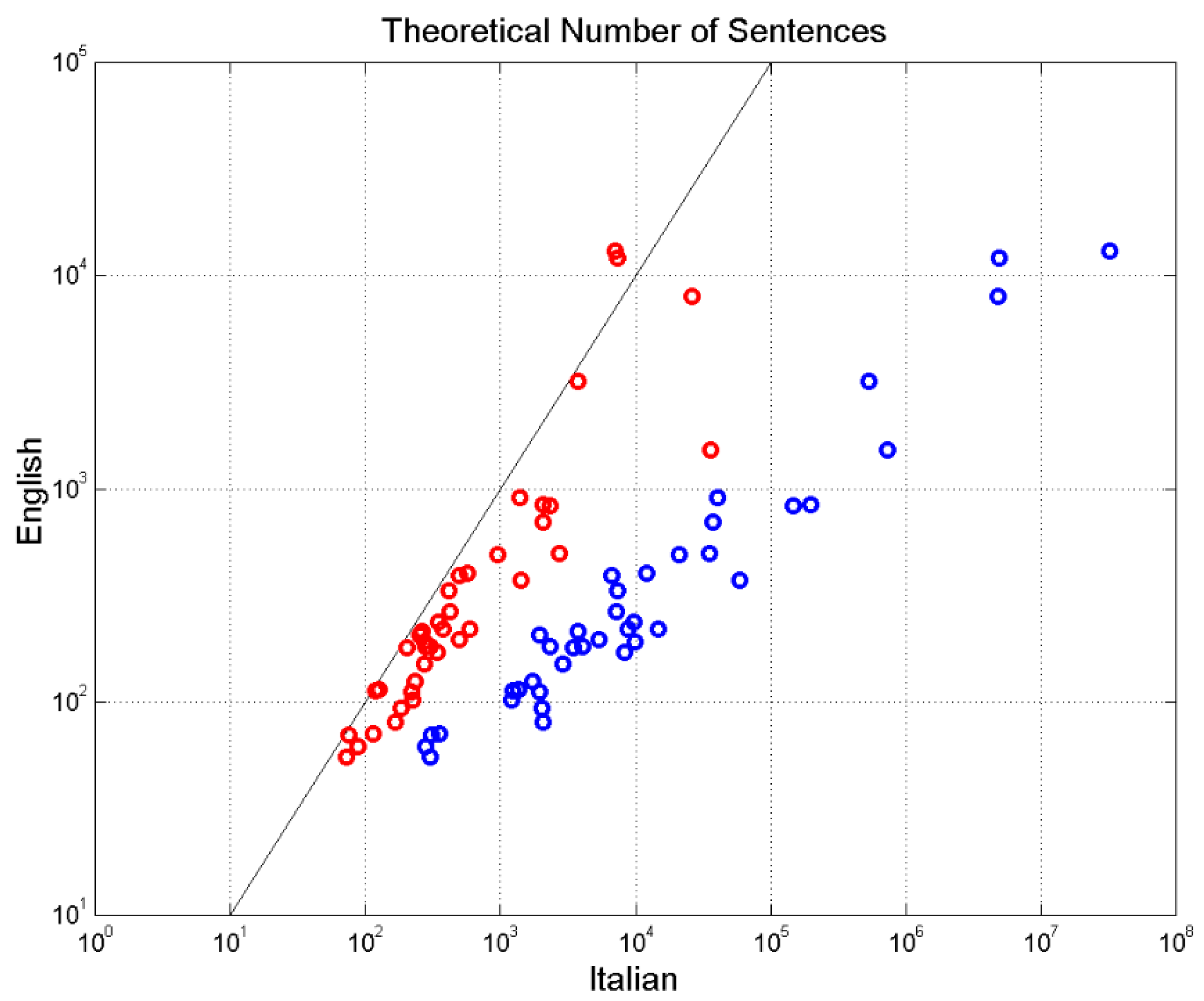
3. Total Statistics

In this section we report the overall total statistics of linguistic parameters. To calculate them, we have used the digital text (WinWord file) and counted, for each chapter, the number of characters, words, sentences and interpunctions (punctuation marks). Before doing so, we have deleted the titles, footnotes and other extraneous material present in the digital texts. The count is very simple, although time-consuming. Winword directly provides the number of characters and words. The number of sentences was calculated by using WinWord to replace every periods with periods (full stop): of course, this action does not change the text, but it gives the number of these substitutions and therefore the number of periods. The same procedure was repeated for question marks and exclamation marks. The sum of the three totals gives the total number of sentences. The same procedure gives the total number of commas, colons and semicolons. The sum of these latter values with the total number of sentences gives the total number of interpunctions.

Table 2 and Table 3 report these total statistics. In English, paragraphs, sentences and words are increased. The characters are fewer than in Italian, but not because the translator decided so, but because English words are, on the average, shorter than Italian words.

The text indicated with Italian-E refers to the Italian text in which $4020-263=3757$ periods replace semicolons in proportion to the number of words per chapter, to simulate a “reverse” domestication translation. In this case the number of sentences is about the same of the English text, 14676 against 14647, therefore the translator replaced semicolons with periods practically in the entire novel, and this replacement make the number of words per sentence very similar to that of Italian-E text, 16.0 against 15.3. English-I refers to the translation in which semicolons replace periods. In this latter case the number of sentences is smaller than in Italian.

In the next section we report an exploratory data analysis of the two texts. with the aim of visualing important relations between linguistic variables and further investigate the changes done by the translator.

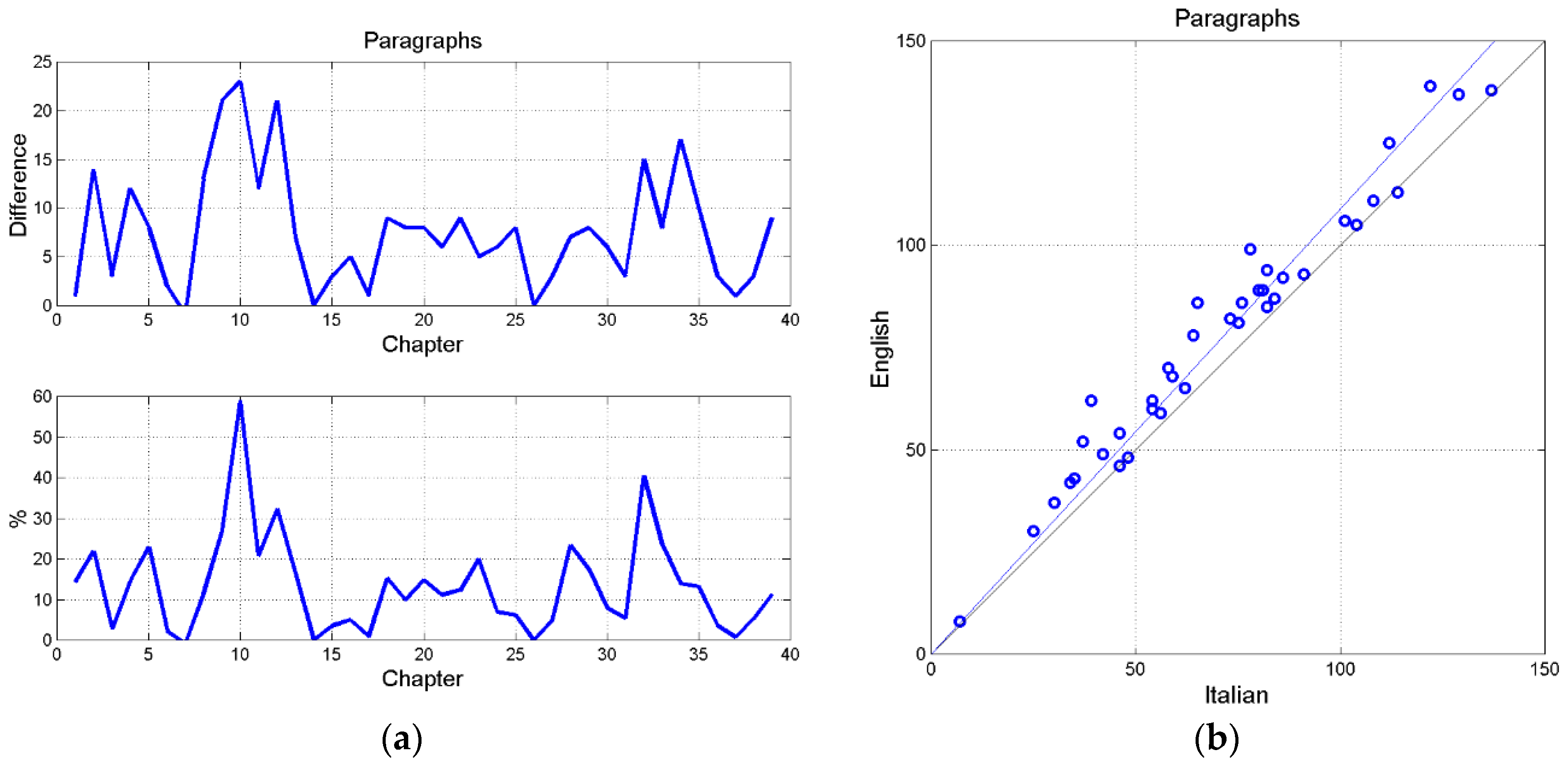
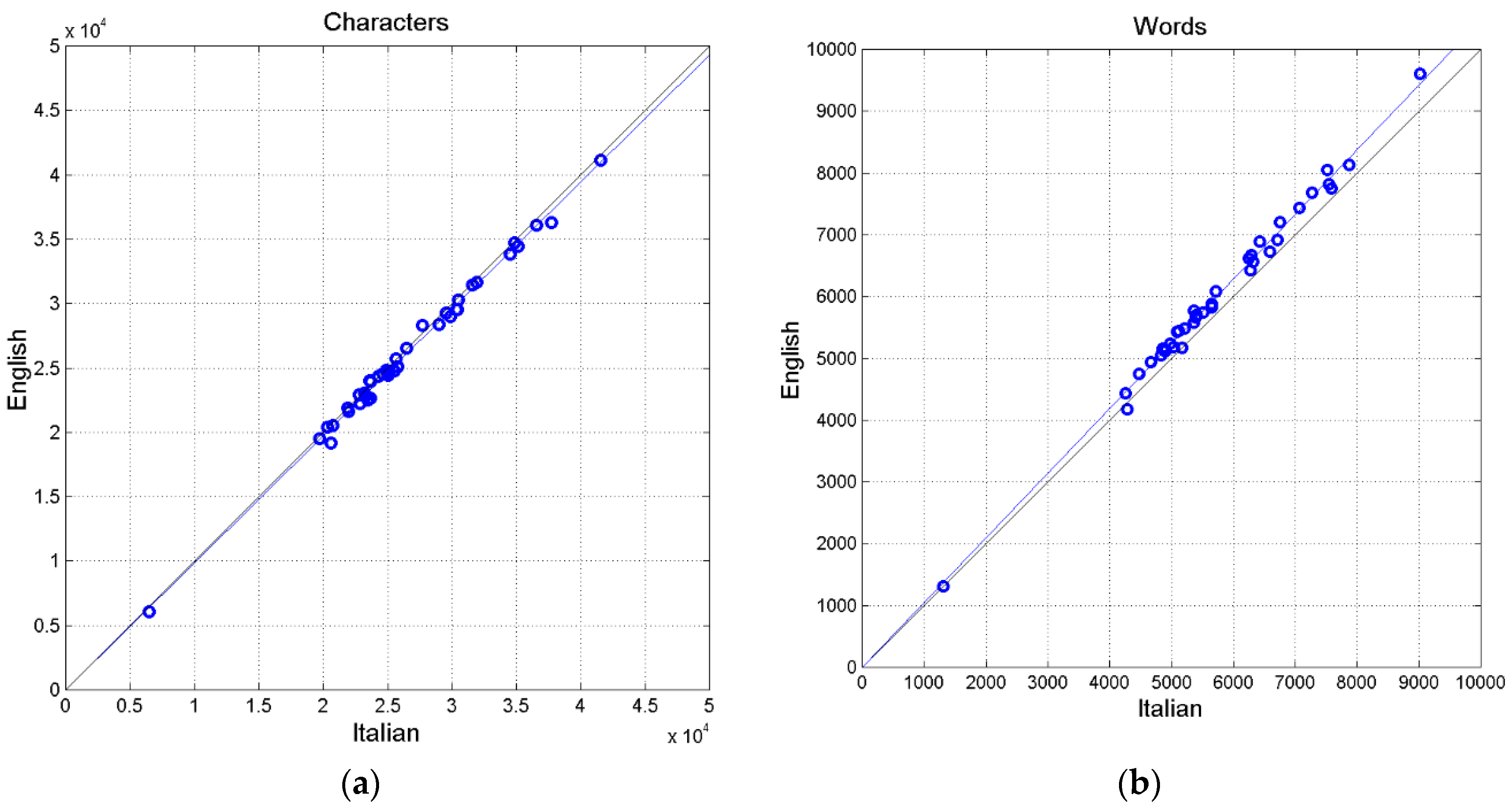
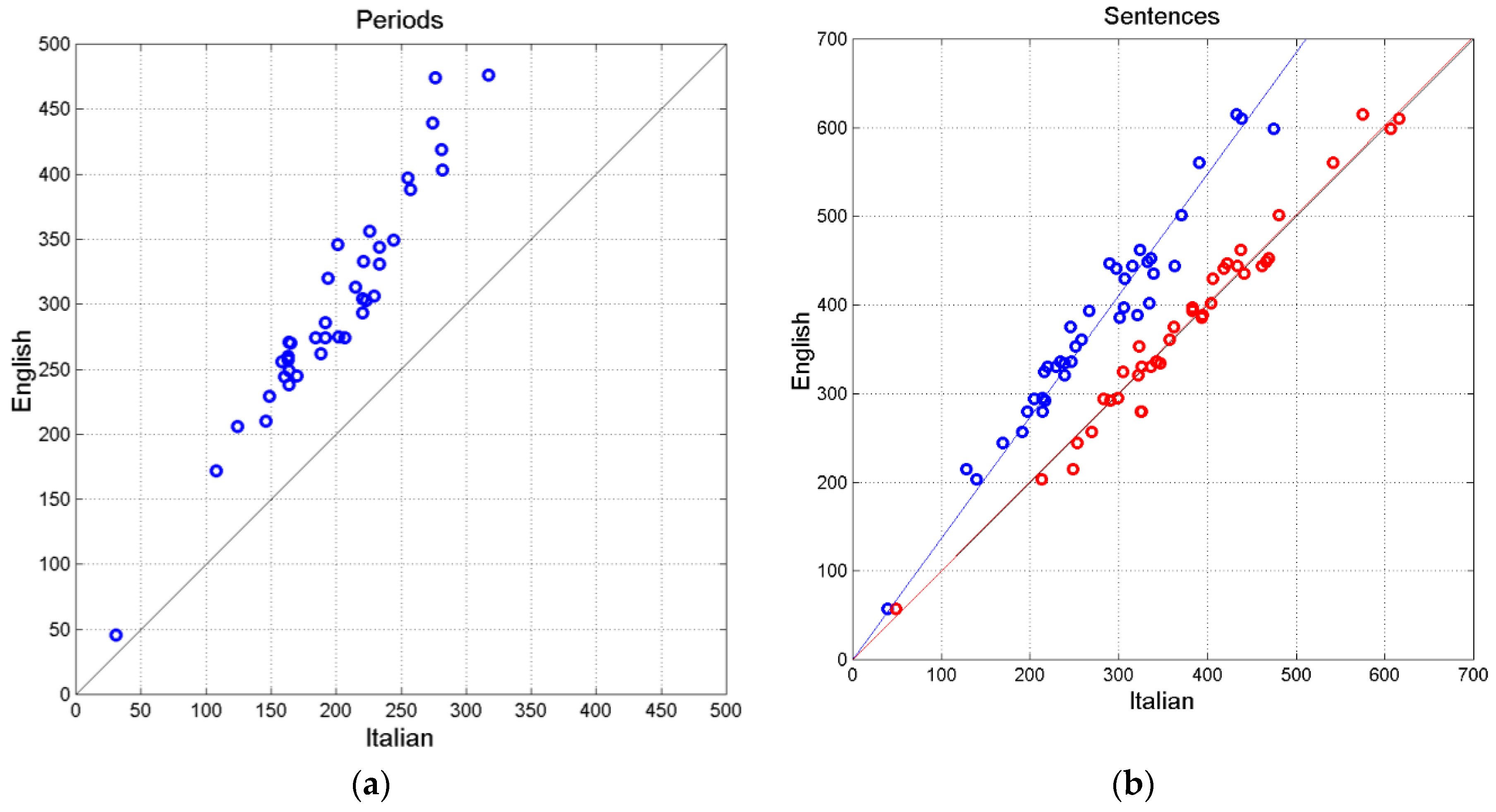
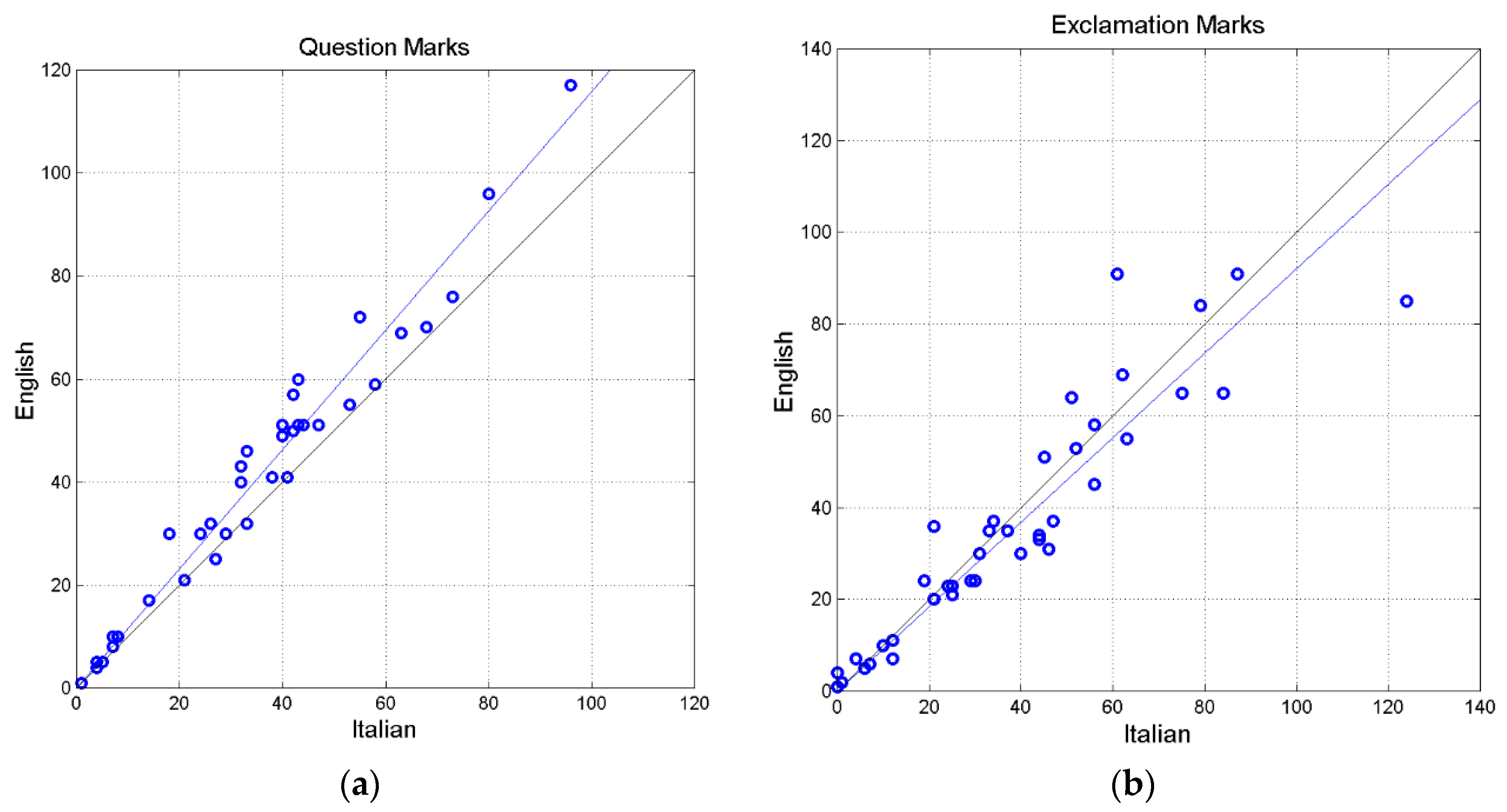
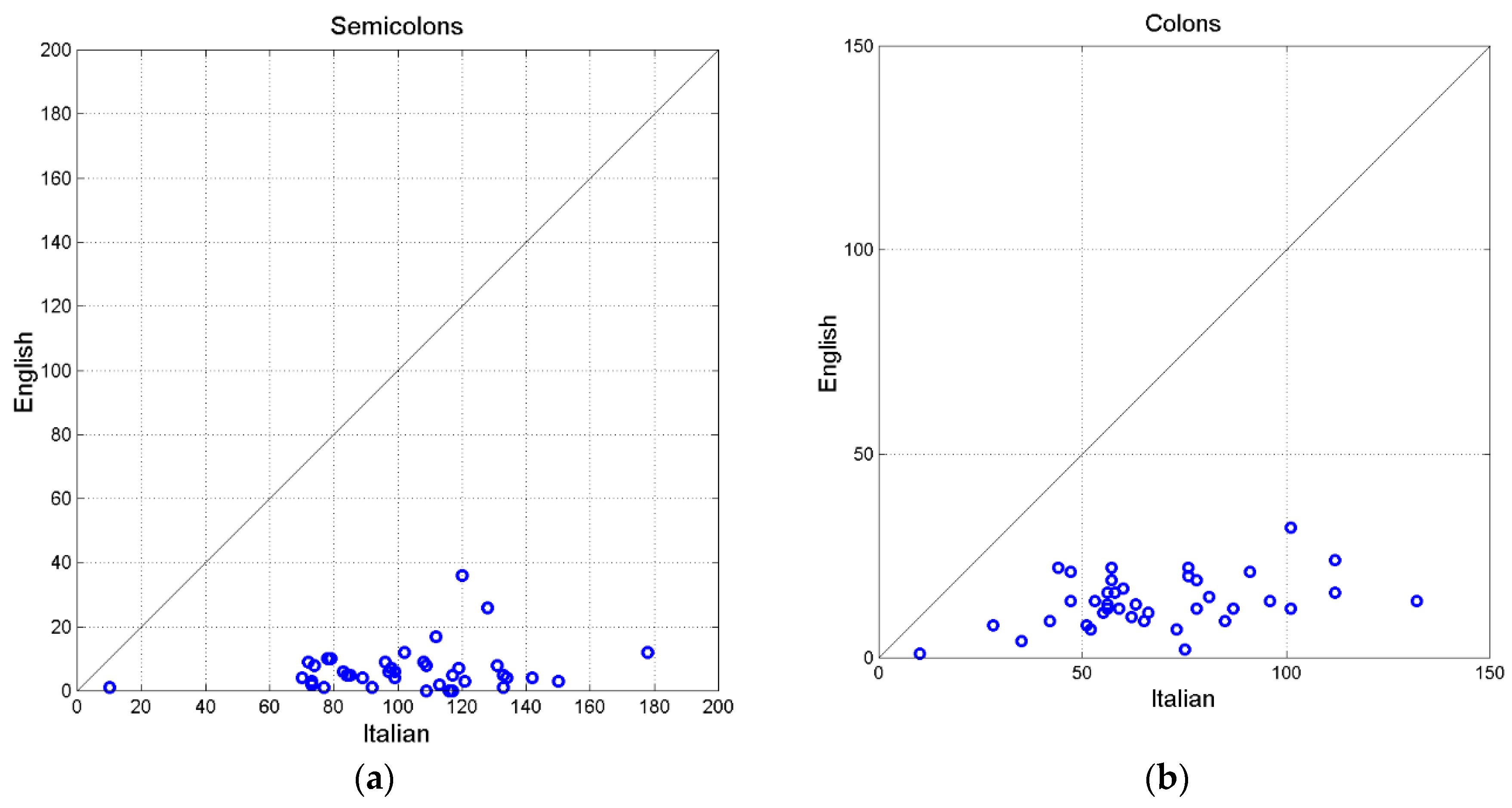
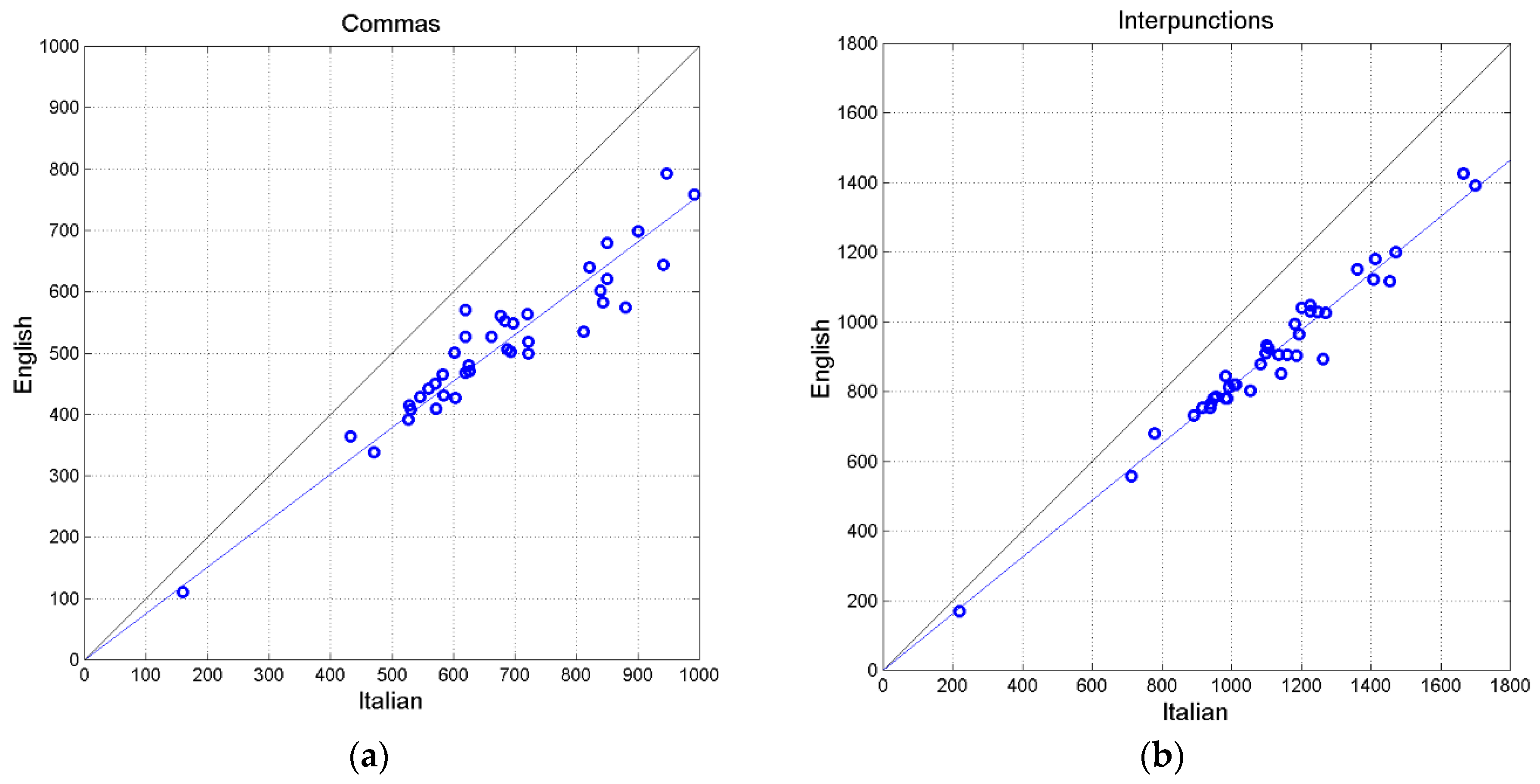
4. Exploratory Data Analysis: Relationships Between Italian and English Linguistic Variables

This section compares the linguistic variables per chapter of the English and Italian texts, 39 samples due to the Introduction (the one written by Manzoni) and 38 chapters of the novel. These scatterplots will be further studied in Section 8 according to the theory of linguistic channels.

Figure 1(a) shows the difference between the number of paragraphs per chapter in the two texts, $n_{par,Eng}-n_{par,Ita}$ and the percentage change $100\times (n_{par,Eng}-n_{par,Ita})/n_{par,Ita}$. We notice that the translator split the Italian paragraphs by increasing them up to 60%. Figure 1(b) shows the scatterplot between the number of paragraphs; it clearly shows that the data are all above the 45° line $y=x$. Table 4 reports the correlation coefficient and slope of the regression line for this scatterplot and also for the following ones.

Figurea 2(a) shows the scatterplot between characters and Figure 2(b) shows that between words. Both variables are very much correlated. In English the number of words is always larger than in Italian, therefore the translator needs more words to convey the original meaning. Characters and words are the most correlated variables.

Figure 3(a) shows the scatterplot between periods. The replacement of most semicolons with periods is clearly evidenced by being all samples above the 45° line $y=x$.

Figure 3(b) shows the scatterplot between sentences. The effect of replacing semicolons with periods is clearly evident in the blue circles and regression line. Since the Italian text contains many semicolons, sentences are quite long, therefore the regression line is far from the $y=x$ line. On the contrary, when in Italian the semicolons are counted as periods, then the agreement is very good, as the red circles and regression line show.

Figures 4(a) shows the scatterplot between question marks and Figure 4(b) between exclamation marks. It is surprising that both do not follow at all the Italian text (i.e. the 45° line), particularly the number of questions marks, which in English is larger than in Italian. Appendix C reports a short example in which question and exclamation marks are modified.

Figure 5(a) shows the scatterplot between semicolons and Figure 5(b) shows that between colons. The almost total cancellation in English of both interpunctions is clearly evident.

Figure 6(a) shows the scatterplot between commass. We notice that in English there are quite fewer commas than in Italian and this reduction, together with that in colons, semicolons, question and exclamation marks make the number of interpunctions quite smaller than in Italian, Figure 6(b).

In conclusion, the translator completely modified the underlying texture of interpunctions by distributing them quite differently from the original Italian text, therefore changing reader’s pauses and reader’s short-term memory load, as discussed in Section 7 below. A similar modification occurs also in the distribution of paragraphs.

Only characters, Fiogure 2(a), follow very strictly the 45° line, but this large agreement is not a translator’s choice but very likely due to two remarks: (a) both Italian and English are alphabetical languages with many similar words coming directly from Latin in Italian and indirectly, through French, in English; (b) alphabetical languages have very similar mean number of characters per word (see Table 1 of Ref.[37]).

In other terms, a blind comparison of the statistics concerning fundamental linguistic parameters would unlikely indicate these two texts refer to the same novel, altough written in different languages.

In the next section, we recall the deep-language variables which allow further studies.

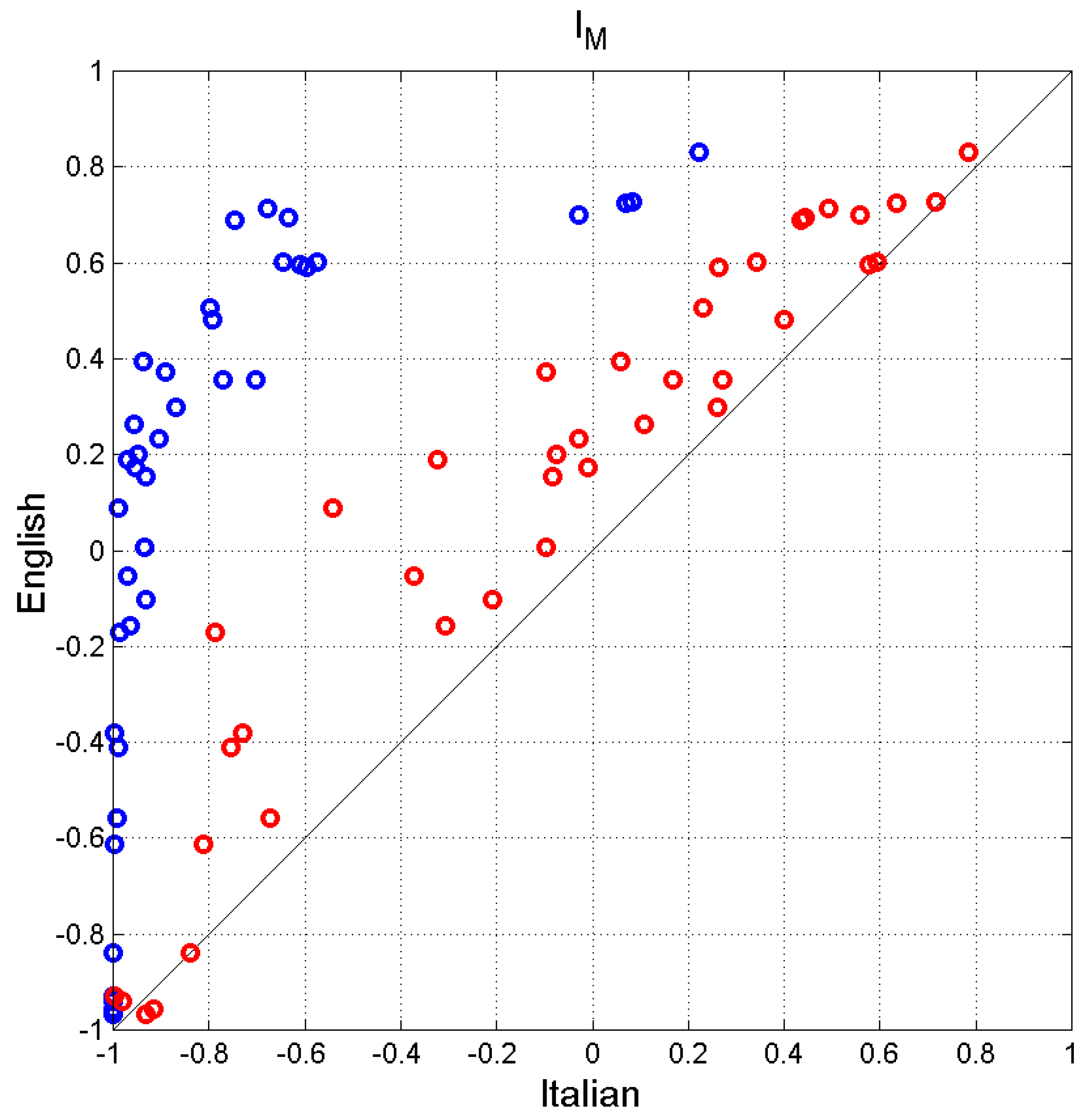
5. Deep–Language Variables

Let us recall four deep-language variables [1,2] which are not consciously managed by writers, therefore useful for assessing similarity of texts beyond writers’ awareness. To avoid possible misunderstanding, these variables refer to the “surface” structure of texts, not to the “deep” structure mentioned in cognitive theory.

Let $n_C$, $n_W$ and $n_I$ be respectively the number of characters, words and interpunctions (punctuation marks) calculated in disjoint blocks of texts, such as chapters (in this paper) or any other subdivisions, then we can define four deep–language variables (Appendix B lists the mathematical symbols used in the present paper):

The number of characters per word, $C_P$:

$${\mathit{C}}_{\mathit{P}}={\displaystyle \frac{{\mathit{n}}_{\mathit{C}}}{{\mathit{n}}_{\mathit{W}}}}$$

(1)

The number of words per sentence, $P_F$:

$${\mathit{P}}_{\mathit{F}}={\displaystyle \frac{{\mathit{n}}_{\mathit{W}}}{{\mathit{n}}_{\mathit{S}}}}$$

(2)

The number of interpunctions per word, referred to as the word interval, $I_P$:

$${\mathit{I}}_{\mathit{P}}={\displaystyle \frac{{\mathit{n}}_{\mathit{I}}}{{\mathit{n}}_{\mathit{W}}}}$$

(3)

The number of word intervals, $n_{I_P}$, per sentence, $M_F$:

$${\mathit{M}}_{\mathit{F}}={\displaystyle \frac{{\mathit{n}}_{{\mathit{I}}_{\mathit{P}}}}{{\mathit{n}}_{\mathit{S}}}}$$

(4)

Table 5 reports mean and standard deviation of these variables. These values have been calculated by weighing each text with its number of words to avoid that shorter texts weigh statistically as much as long ones. In other words, the statistical weight of a chapter is given by the ratio between the number of its words and the total number of words of the novel. Moreover, notice that the average values of these variables calculated from the totals, as done in Table 2 do not coincide with the arithmetic or statistical means (the ones reported in Table 5), as is proved in Appendix D.

From these statistical mean values, we notice:

a)

${<C}_p>$ is very similar in both languages, for the reason recalled in Section 4.

b)

${<P}_F>$ in Italian is, as expected, quite larger than in English. It becomes smaller and very similar to that in English only if semicolons are replaced by periods (Italian-E).

c)

${<I}_P>$ is significantly smaller in Italian than in English, due to the large number of interpunctions present in Italian. This parameter does not depend on the type of interpunctions, therefore it is the same also in Italian-E.

The mean values of Table 5 - or their minimum values directly calculated from the totals, as discussed in Appendix D - are useful for a first assessment of “similarity”of texts by defining linear combinations of deep–language parameters and then modeling them as vectors, a representation briefly recalled in the next section.

6. Geometrical Representation of Alphabetical Texts

The mean values of Table 5 can be used to model texts as vectors, representation discussed in detail in Refs.[1,2,3] and here briefly recalled. This geometrical representation allows also to calculate the probability that a text/author can be confused with another one, an extension in two dimensions of the problem discussed in Ref. [6]. The conditional probability can be considered an index indicating who influenced who, as shown in Ref.[26]. In our case it gives another indication on how much the translation differs from the original text.

6.1. Vector Representation of Texts

Let us consider the following six vectors of the indicated components of deep‒language variables$:$ $\overrightarrow{R_1}=({<C}_P>,{<P}_F>$), $\overrightarrow{R_2}=({<M}_F>,{<P}_F>$), $\overrightarrow{R_3}=(<I_P>,<P_F>$), $\overrightarrow{R_4}=({<C}_P>,{<M}_F>$), $\overrightarrow{R_5}=({<I}_P>,{<M}_F>$), $\overrightarrow{R_6}=({<I}_P>,<C_P>$) and their resulting vector sum:

$$\overrightarrow{R}={\sum }_{k=1}^6\overrightarrow{R_k}=x\overrightarrow{i}+y\overrightarrow{j}$$

(5)

The choice of which parameter represents the component in abscissa and ordinate axes is not important because, once the choice is made, the numerical results will depend on it, but not the relative comparisons and general conclusions.

In the first quadrant of the Cartesian coordinate plane two texts are likely mathematically connected ‒ they show close ending points of vector (5) ‒ if their relative Pythagorean distance is small.

To set the two texts here studied - especially the translated text - in the framework of the English Literature, we have considered the same Cartesian plane defined and discussed in Ref. [26], which reports the list of the English novels whose positions are reported in this figure.

By considering the vector components $x$ and $y$ of Eq. (5), we obtain the scatterplot shown in Figure 7 where $X$ and $Y$ are normalized coordinates calculated by setting Lord of the Rings at the origin $(X=0,Y=0)$ and Silmarillion at $(X=1,Y=1)$, according to the linear tranformations:

$$X={\displaystyle \frac{x-x_{Lord}}{x_{Silma}-x_{Lord}}}$$

(6)

$$X={\displaystyle \frac{y-y_{Lord}}{y_{Silma}-y_{Lord}}}$$

(7)

In Figure 7 we report the position of the Italian text (green diamond), its translation (blue diamond) and the position of Ivanohe - a novel that inspired Manzoni in writing his novel - with green $\text{×}.$Notice that since ${<C}_P>$ in the two languages is very similar (see Table 5), the position depends mainly on the other mean values.

We can notice that the translation (blue diamond) is well within the other English novels, in particular it almost concides with The Jungle Book. The Italian text is significantly displaced from most English novels.

Figure 8 shows a zoom. We can notice that if periods are replaced by semicolons in the translation (English-I, cyan diamond), then this text is located very near Ivanohe, which may indicate an indirect influence of Walter Scott on Manzoni’s writing. On the other hand, if semicolons are replaced by periods, Ivanohe gets closer to English (red $"\times "$). The red diamond refers to Italian-E, which falls well within the English texts reported in Figure 7.

These remarks refer to the display of vectors whose ending point depends only on mean values. The standard deviation of the four deep−language variables, reported in Table 5, do introduce data scattering, therefore in the next sub−section we study and discuss this issue by calculating the probability (called “error” probability) that a text may be mathematically confused with another one, as done in Ref. [26].

6.2. Error Probability

Besides the vector $\overrightarrow{R}$ of Eq. (5) - due to mean values - we can consider another vector $\overrightarrow{\rho }$, due to the standard deviation of the four deep−language variables, that adds to $\overrightarrow{R}$ [26]. In this case, the final random vector describing a text is given by:

$$\overrightarrow{T}=\overrightarrow{R}+\overrightarrow{\rho }$$

(8)

Now, to get some insight into this new description, we consider the area of a circle centered at the ending point of $\overrightarrow{R}$.

We fix the magnitude (radius)$\rho$ as follows. First, we add the variances of the deep−anguage variables that determine the components $x$ and $y$ of $\overrightarrow{R}$ − let them be ${\sigma }_x^2$, ${\sigma }_y^2$ − then we calculate the average value ${\sigma }_{\rho }^2=0.5\times ({\sigma }_x^2+{\sigma }_y^2)$ and finally we set:

$$\rho ={\sigma }_{\rho }$$

(9)

Now, since in calculating the coordinates $x$ and $y$ of $\overrightarrow{R}$ a deep−language variable can be summed twice or more, we add its standard deviation (referred to as sigma) twice or more times before squaring, as shown in [26].

Now, we can estimate the (conditional) probability that a text is confused with another by calculating ratios of areas. This procedure is correct if we assume that the bivariate density of the normalized coordinates ${\rho }_X,{\rho }_Y$, centred at $\overrightarrow{R}$, is uniform. By assuming this hypothesis, we can calculate probabilities as ratios of areas [38, 39]. As dicussed in [26], the hypothesis of substantial uniformity around $\overrightarrow{R}$ should be justified within 1-sigma bounds.

Now we can calculate the following probabilities. Let $A$ be the common area of two 1−sigma circles (i.e., the area proportional to the joint probability of two texts), let $A_1$ be the area of 1−sigma circle of text 1 and $A_2$ the area of 1−sigma circle of text 2. Now, since probabilities are proportional to areas, we get the following relationships:

$${\displaystyle \frac{A}{A_1}}={\displaystyle \frac{P(A_1,A_2)}{P\left(A_1\right)}}={\displaystyle \frac{P(A_2/A_1)P\left(A_1\right)}{P\left(A_1\right)}}=P(A_2/A_1)$$

(10)

$${\displaystyle \frac{A}{A_2}}={\displaystyle \frac{P(A_1,A_2)}{P\left(A_2\right)}}={\displaystyle \frac{P(A_1/A_2)P\left(A_2\right)}{P\left(A_2\right)}}=P(A_1/A_2)$$

(11)

Therefore, $A/A_1$gives the conditional probability $P(A_2/A_1)$ that part of text 2 can be confused (or “contained”) in text 1; $A/A_2$ gives the conditional probability $P(A_1/A_2)$that part of text 1 can be confused with text 2. $P(A_2/A_1)=1$ means [38,39$A=A_1$, therefore text 1 can be fully confused with text 2, and $P(A_1/A_2)=1$ means ${A=A}_2$, therefore text 2 can be fully confused with text 1.

Now, we can recall a synthetic parameter which highlights how much two texts can be erroneously confused with each other. The parameter is the average conditional probability:

$$p_e=P(A_2/A_1)P\left(A_1\right)+P(A_1/A_2)P\left(A_2\right)$$

(12)

Now, since in comparing two texts we can assume $P\left(A_1\right)=P\left(A_2\right)=0.5$, we get:

$$p_e=0.5\times \left[P\right(A_2/A_1)+P(A_1/A_2\left)\right]$$

(13)

If $p_e=0$, there is no intersection between the two 1−sigma circles, the two texts cannot be each other confused, therefore there is no mathematical connection involving the deep−language parameters. If $p_e=1$ the two texts can be totally confused, the two 1−sigma circles coincide.

In our exercise, assuming the Italian text as text 1 and its translation as text 2, we get $P(A_2/A_1)=0.225$ and $P(A_1/A_2)=0.339$, therefore $p_e=0.282$. Since this value is very low, there is little chance that the two texts can be each other confused. In conclusion, as already remarked, a blind analysis of the two texts will unlikely reveal their real relationship.

In the next section we study and discuss how the Italian text and its translation engage readers’ short-term memory.

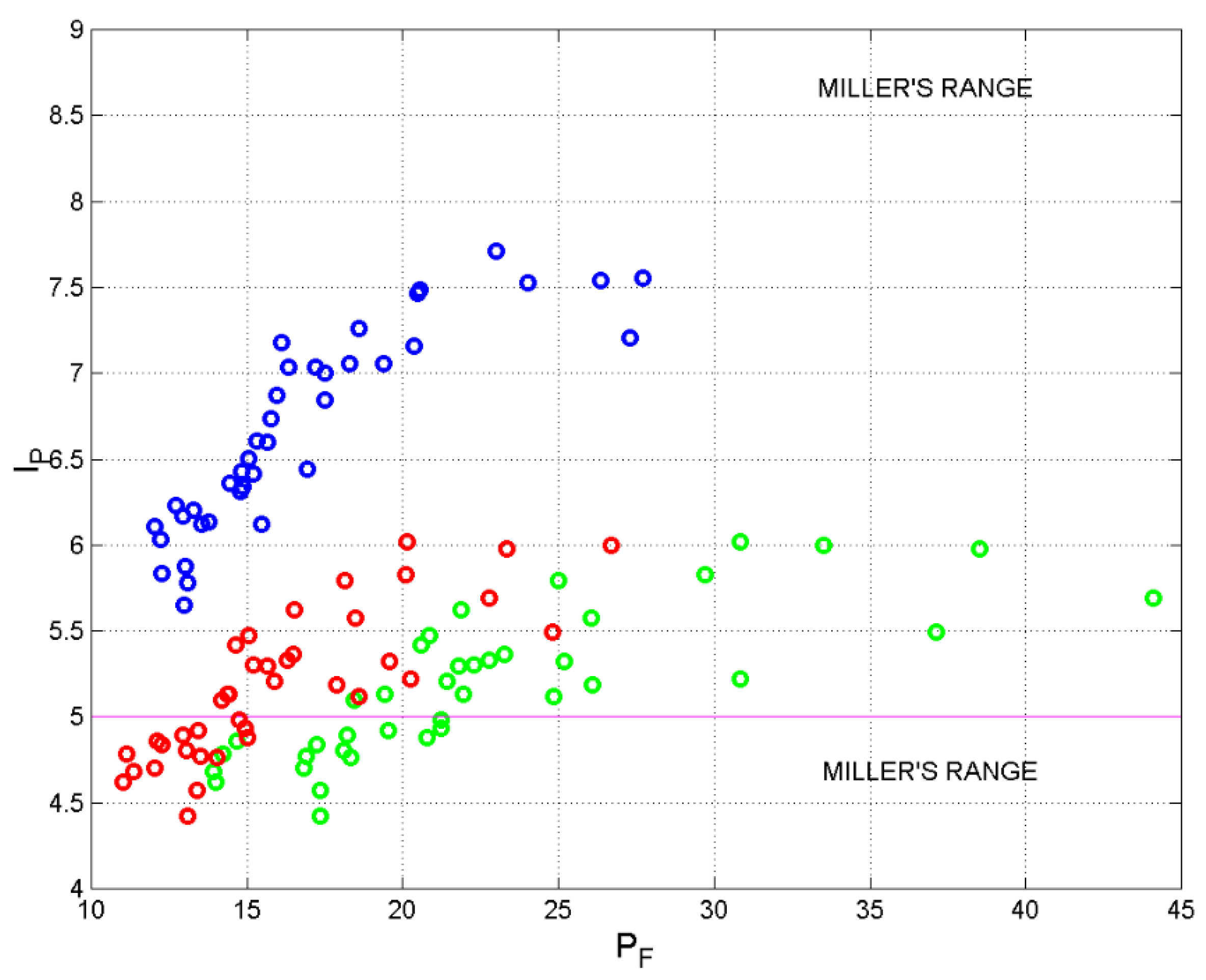
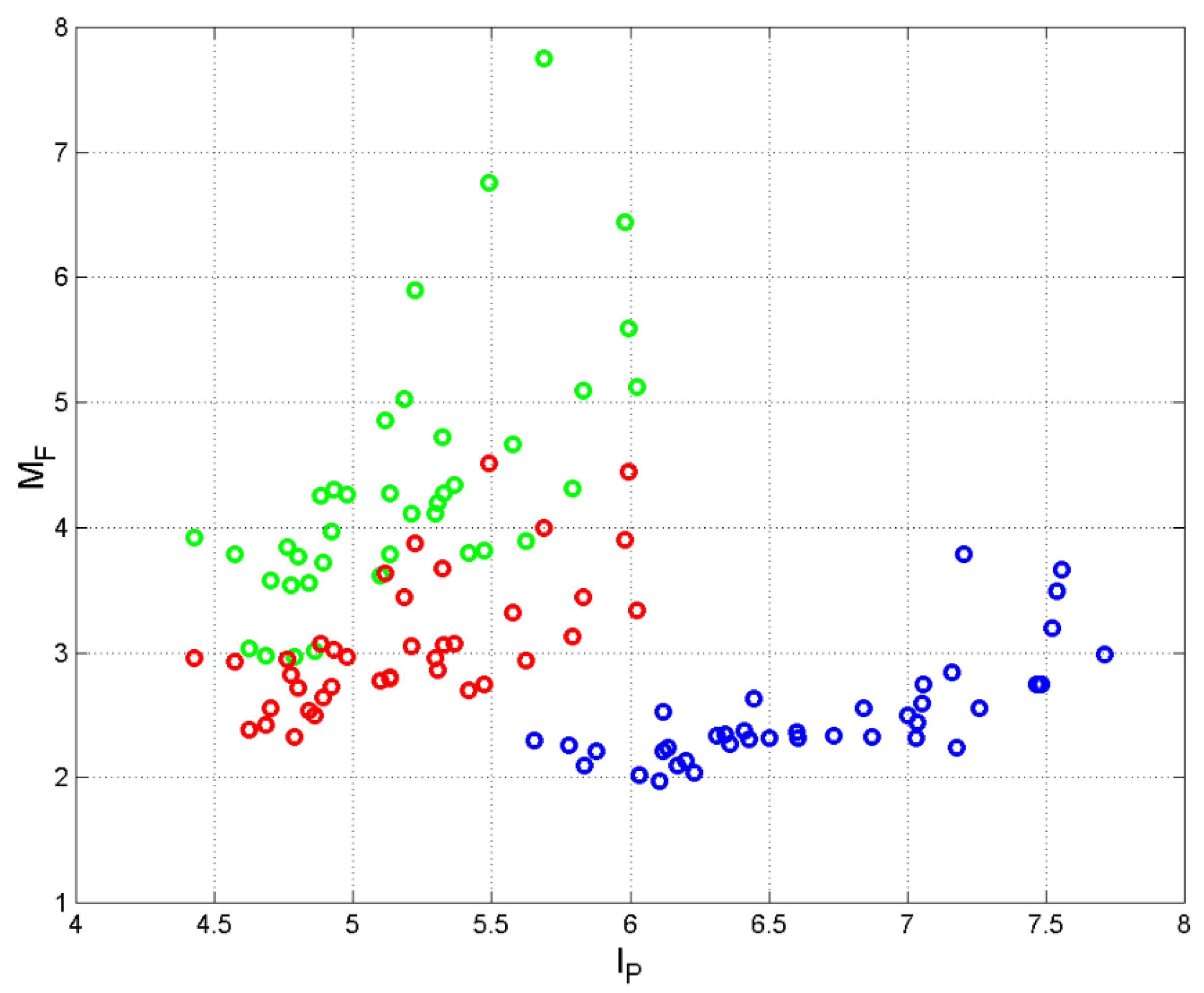
7. Short−Term Memory of Writers/Readers

The human short−term memory seems to be modelled by two practically independent variables, which apparently engage two short−term memory (STM) buffers in series [7,8]. The first buffer is modelled according to the number of words between two consecutive interpunctions - i.e., the variable $I_P$, the word interval -which follows Miller’s $7\pm 2$ law [40] (on the large literature on this topic, see the studies and remarks reported in [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63]). The second buffer is modelled according to the number of word intervals, the variable$M_F$, contained in a sentence, referred to as the extended short-term memory (E-STM).

As for the first buffer, Figure 9 shows $I_P$ versus $P_F$. Notice that the replacement of semicolons with periods is clearly evident (red circles). The trends shown are typical of alphabetical languages [1,2,3,4,5,6,7,8,26] and confirm two fundamental aspects:

a)

$I_P$ ranges approximately in Miller’s bounds.

b)

As the number of words in a sentence, $P_F,$increases, $I_P$ can increase but not linearly, because the first buffer cannot hold, approximately, a number of words larger than that empirically predicted by Miller’s Law, therefore saturation must occur. Scatterplots like that shown in Figure 9 give an insight into the short−term memory capacity engaged in reading/writing a text, because a writer is also a reader of his/her own text.

As for the second buffer, Figure 10 shows the scatterplot between $M_F$ and $I_P$. The effect of replacing semicolons with periods is clearly evident (red circles). Recall that $I_P$ is insensitive to this replacement because $n_I$ does not change.

More interestingly, in translation $M_F\approx 2.5=<M_F>$ (see Table 5) for a large range, while in Italian it varies more randomly. In other words, the effect of replacing semicolons with periods (English) has the effect of forcing the capacity of the second buffer to a constant value. Finally, Figure 10 shows that, for a large range $I_P$ and $M_F$ are uncorrelated, therefore independent, according to the log-normal probability modelling discussed in Ref. [26]. In other words, also the reading of these specific texts seem to require a STM made of two independent buffers in series.

In [8] we have studied the numerical patterns (due to combinations of $I_P$ and $M_F$) which give the number of sentences that theoretically can be recorded in the two STM buffers, regardless of their meaning. This number was compared with that of the sentences actually found in novels of Italian and English Literatures and found that most authors write for readers with small STM buffers and, consequently, are forced to reuse numerical patterns to convey multiple meanings.

Figure 11 shows the scatterplot between the theoretical number of sentences allowed in Italian and in English. In Italian this number is about two order of magnitude greater than in English, a find mainly due to the larger $M_F$ (see Figure 10). Only when semicolons are replaced by periods in the Italian text (red circles) the two variables agree more. In any case, in Italian the number of possible patterns is always larger than in English.

The ratio between the number of sentences in a novel and the number of sentences theoretically allowed by the two buffers concerning $I_P$ and $M_F$, referrred to as the multiplicity factor $\alpha$, can be used to compare two texts [8]. In the Italian and English Literatures we found that $\alpha >1$ is more likely than $\alpha <1$, and often $\alpha \gg 1$. In the latter case, writers reuse many times the same pattern of sentences.

In our present case, we study a text and its translation. Figure 12 shows $\alpha$ for the two texts. Differences are clearly evident and they depend, of course, on the finds reported in Figure 11, with very low values in Italian. Italian and English are clearly very different. In other words, Manzoni has potentially many patterns to use, according mainly to $M_F$, but he does not. These patterns are much reduced in English; only Italian-E (red circles) agrees more with English.

Another useful parameter is the mismatch index [8], which measures to what extent a writer uses the number of sentences theoretically available, defined by:

$$I_M={\displaystyle \frac{\alpha -1}{\alpha +1}}$$

(14)

$I_M=0$ if $\alpha =1$; in this case experimental and theoretical patterns are perfectly matched. They are over matched if $I_M>0$ ($\alpha >1)$and under matched if $I_M<0$ ($\alpha <1)$.

Figure 13 shows the scatterplot of $I_M$ between the two texts. Again there is a large difference between Italian and English (blue circes). Only Italian-E agrees with English (red circles).

In conclusion, in translation the STM reader’s buffers are so much diverse to make the two texts hardly recognizable as one the translation of the other. The two texts show significant correlation only if semicolons are replaced by periods in the Italian text, which indicates, as already noticed, that almost all semicolons were replaced with periods.

The next section recalls the theory of important linguistic channels.

8. Linguistic Channels

In this section, we first recall important linguistic channels present in alphabetical texts, which represent a “fine-tuning” analysis of linguistic variables; secondly the general theory of linear channels [3,6] concerning the joint processing of two experimental scatterplots; thirdly the theory applied to the particular case of processing a single scatterplot, and finally the application of the thoery to the two texts.

Notice that since the theory deals with linear regressions, it can be applied and be useful in any field in which linear relationhsips fit experimental data.

8.1. Linguistic Channels

In alpahabetical texts we can always define at least four linguistic linear channels [3,6], namely:

(a).

Sentence channel (S–channel)

(b).

Interpunctions channel (I–channel)

(c).

Word interval channel (WI–channel)

(d).

Characters channel (C–channel).

In S‒channels, the number of sentences of two texts is compared for the same number of words. From the two scatterplots relating $n_S$ to $n_W$ in two texts, we can relate $n_{S,j}$ of text $Y_j$ to $n_{S,k}$ of text $Y_k$ by setting $n_{W,j}=n_{W,k}$. These channels describe how many sentences the author of text $j$ writes, compared to the writer of text $k$ (reference text), by using the same number of words. Only the theory of linguistic channels allows this comparison. These channels are more linked to $P_F$ than to the other variables. Very likely they reflect the style of the writer.

In I‒channels, the number of word intervals, $M_F$, of two texts is compared for the same number of sentences. These channels describe how many short texts between two contiguous punctuation marks (of length $I_P$ words) two authors use. Since $M_F$ is connected to the E–STM, I‒channels are more related to the second buffer capacity than to the style of the writer.

In WI‒channels, the number of words contained in a word interval, (i.e., $I_P$) is compared for the same number of interpunctions, therefore WI‒channels are more related to the first buffer of the STM than to the style of the writer.

In C‒channels, the number of characters of two texts is compared for the same number of words. These channels are more related to the language used than to other variables.

8.2. General Theory of Linear Channels

In a scatterplot involving – in our case - linguistic variables, an independent (reference) variable x and a dependent variable $y$ can be related by a regression line (slope $m$) passing through the origin:

$$y=mx$$

(15)

However, Eq. (15) does not give the full relationship between $x$ and $y$ because it links only mean conditional values. For example, for two diverse texts $Y_k$ and $Y_j$, we can write Eq. (15) for the same variables $x$ and $y$.

More general linear relationships can be written by considering also the scattering of the data—measured in $Y_k$ and $Y_j$ by the correlation coefficients $r_k$ and $r_j$, not considered in Equation (12)—around the regression lines (slopes $m_k$ and $m_j$) in two scatterplots:

$$y_k=m_{k}x+n_k$$

(16)

$$y_j=m_{j}x+n_j$$

While Eq. (15) connects the dependent variable $y$ to the independent variable $x$only on the average, Eq. (16) introduces additive “noise” $n_k$ and $n_j$, with zero mean value. The noise, therefore, is due to the correlation coefficient $\left|r\right|\ne 1$.

The theory allows to compare two dependent variables $y_j$ and $y_k$ by eliminating $x$. We can calculate the slope and correlation coefficient of $y_j$ versus $y_k$ without knowing their scatterplot. For example, we can compare the number of sentences in two texts for an equal number of words by considering not only the two regression lines that link sentences to words – which would provide only the slope of the linear relationship between $y_j$ and $y_k$ - but also the scattering of the data. In this particular case, we refer to this linguistic channel as the “sentences channel” and to the channel processing as “fine tuning” because it deepens the analysis of the data and provides more insight into the relationship between two texts.

The mathematical theory is here briefly recalled (more details in Refs. [2,3]). Continuing the example of sentences, we can study the “sentences channel” that relates the sentences of the input text $Y_k$ to those of the output text $Y_j$ by eliminating $x$ (i.e., the variable words). From Eq. (16) we obtain the linear noisy relationship between the sentences in text $Y_k$ (reference, independent, channel input text) and the sentences in text $Y_j$ (dependent, channel output text):

$$y_j={\displaystyle \frac{m_j}{m_k}}{y}_k-{\displaystyle \frac{m_j}{m_k}}{n}_k+n_j$$

(17)

In Eq.(17) the slope of the regression line linking $y_j$ to $k$, $m_{jk}$, is given by:

$$m_{jk}={\displaystyle \frac{m_j}{m_k}}$$

(18)

The “regression noise–to–signal ratio”, $R_m$, due to $\left|m_{jk}\right|\ne 1$, of the channel is given by:

$$R_m={(m_{jk}-1)}^2$$

(19)

The unknown correlation coefficient $r_{jk}$ between $y_j$ and $y_k$ is given by [39]:

$$r_{jk}=\mathrm{c}\mathrm{o}\mathrm{s}\left|\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\left(r_j\right)-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\left(r_k\right)\right|$$

(20)

The “correlation noise–to–signal ratio”, $R_r$, due to $\left|r_{jk}\right|<1$, is given by:

$$R_r={\displaystyle \frac{1-r_{jk}^2}{r_{jk}^2}}{m}_{jk}^2$$

(21)

Because the two noise sources are disjoint, the total noise–to–signal ratio $R$of the channel connecting text $Y_k$ to text $Y_j$ is given by:

$$R={(m_{jk}-1)}^2+{\displaystyle \frac{1-r_{jk}^2}{r_{jk}^2}}{m}_{jk}^2$$

(22)

From Eq.(22) we obtain the signal-to-noise ratio γ (natural units) and Γ (dB)

$$\gamma ={\displaystyle \frac{1}{R}}$$

(23)

$$\mathsf{\Gamma }=10\times {\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\gamma$$

(24)

Notice that no channel can yield $\left|r_{jk}\right|=1$and $\left|m_{jk}\right|=1$ (i.e., $\gamma =\infty$), a case referred to as the ideal channel, unless a text is compared with itself (self–comparison, self–channel). In practice, we always find $\left|r_{jk}\right|<1$and $\left|m_{jk}\right|\ne 1$.

In summary, the slope $m_{jk}$ measures the multiplicative “bias” of the dependent variable compared to the independent variable; the correlation coefficient $r_{jk}$measures how “precise” the linear best fit is. The slope $m_{jk}$ is the source of the “regression noise” of the channel, the correlation coefficient $r_{jk}$is the source of the “correlation noise”.

Finally, notice that since the probability of jointly finding $\left|r\right|=1$ and $m=1$ is practically zero, all channels are always noisy.

8.3. The Channel with a Single Scatterplot: One–to–One Correspondence

To clarify what we mean by a single scatterplot and one–to–one correspondence, let us consider the translation of a text in which we draw a scatterplot for each linguistic variable. For example, we can display the number of words per chapter in the translated text versus that of the original text, as done in Figure 1 in which $m=1.047$ and $r=0.9967$. Now, if there were a perfect ideal translation, the translated text would have the same number of words per chapter of the original text, therefore $m=1$ and $r=1$ because the scatterplot would collapse to the deterministic $45°$ linear relationship between $x$ and $y$, giving the reelationship:

$$y_k=x$$

(25)

Let us show how the relationships of Section 8.2 change in this particular and ideal case. If $m_k=1$ and $n_k=0$, then $r_k=1$, therefore this is a special case of the general theory recalled in the previous sub-section, therefore we get the following expressions:

$$m_{jk}=m_j$$

(26)

$$R_m={(m_j-1)}^2$$

(27)

$$r_{jk}=\mathrm{c}\mathrm{o}\mathrm{s}\left|\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\left(r_j\right)-0)\right|=r_j$$

(28)

$$R_r={\displaystyle \frac{1-r_j^2}{r_j^2}}{m}_j^2$$

(29)

$$R={(m_j-1)}^2+{\displaystyle \frac{1-r_j^2}{r_j^2}}{m}_j^2$$

(30)

$$\gamma ={\displaystyle \frac{1}{R}}$$

(31)

In other words, by considering Eq. (25) we study how a determistic relationship, which describes a noiseless channel, is transformed into the experimental relationship of a noisy channel, $m_j\ne 1$ and $\left|r_{jk}\right|<1.$ In conclusion, we can study a single scatterplot with the tools of the general theory. Therefore, the signal-to-noise ratio $\gamma$ is still a single index that synthetically describes the relationship between $x$ and $y$.

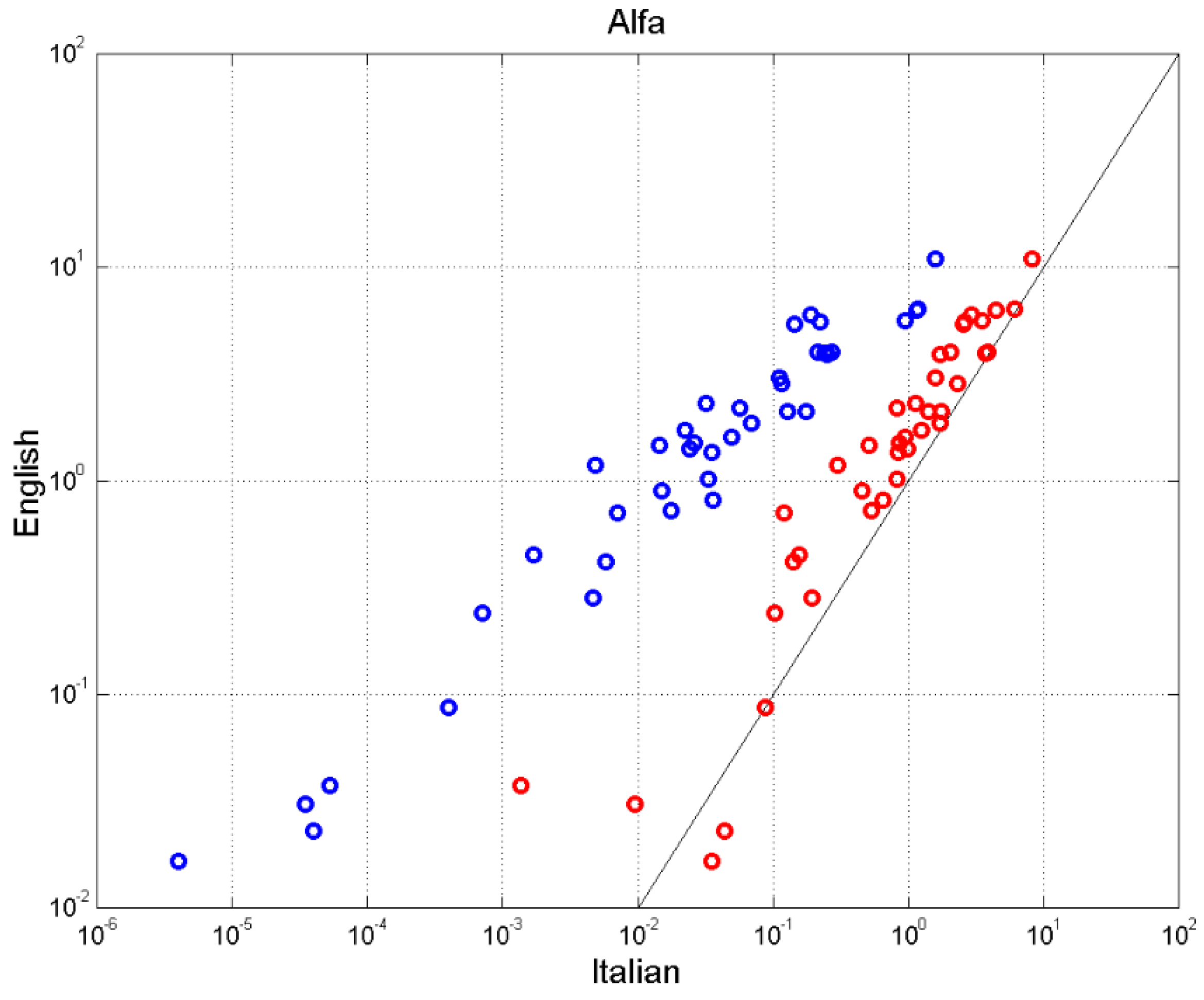
8.4. Performance of Linguistic Channels in Italian and in English

In this section we study the linguistic channels in Italian and in English. Table 6 reports the correlation and slope of the regression lines need to study the S–channel, I–channel, WI–channel and C–channel. Table 7 reports the signal-to-noise ratio in the channels.

It is very clear that the S–channel, I–channel and WI–channel between Italian (input) and English (output) are very noisy with very low signal-to-noise ratios. Only the S-Channel between Italian-E (input) and English (output) has a significant large $\mathsf{\Gamma }\approx 27$ dB ($\gamma \approx 500$), even larger that the expected large $\mathsf{\Gamma }\approx 24$ dB of the C–channel.

To study the single scatterplots (i.e. the scatterplot between same variables) we need the correlation and slope of the regression lines reported in Table 4. Table 8 reports the signal-to-noise ratio in the channels.

It is very clear that only the channels related to characters and words – both charatcters and words are very much correlated, see Figure 6(b) and Table 6 – show large signal-to-noie ratios, while the other channels (with the exception of the sentences in Italian-E) are very noisy.

The conclusion regarding the linguistic channels is the same as above: a blind comparison would unlikely indicate the two texts refer to the same novel.

In the next section, we consider a universal readability index. which measures the relative reading difficulty of texts.

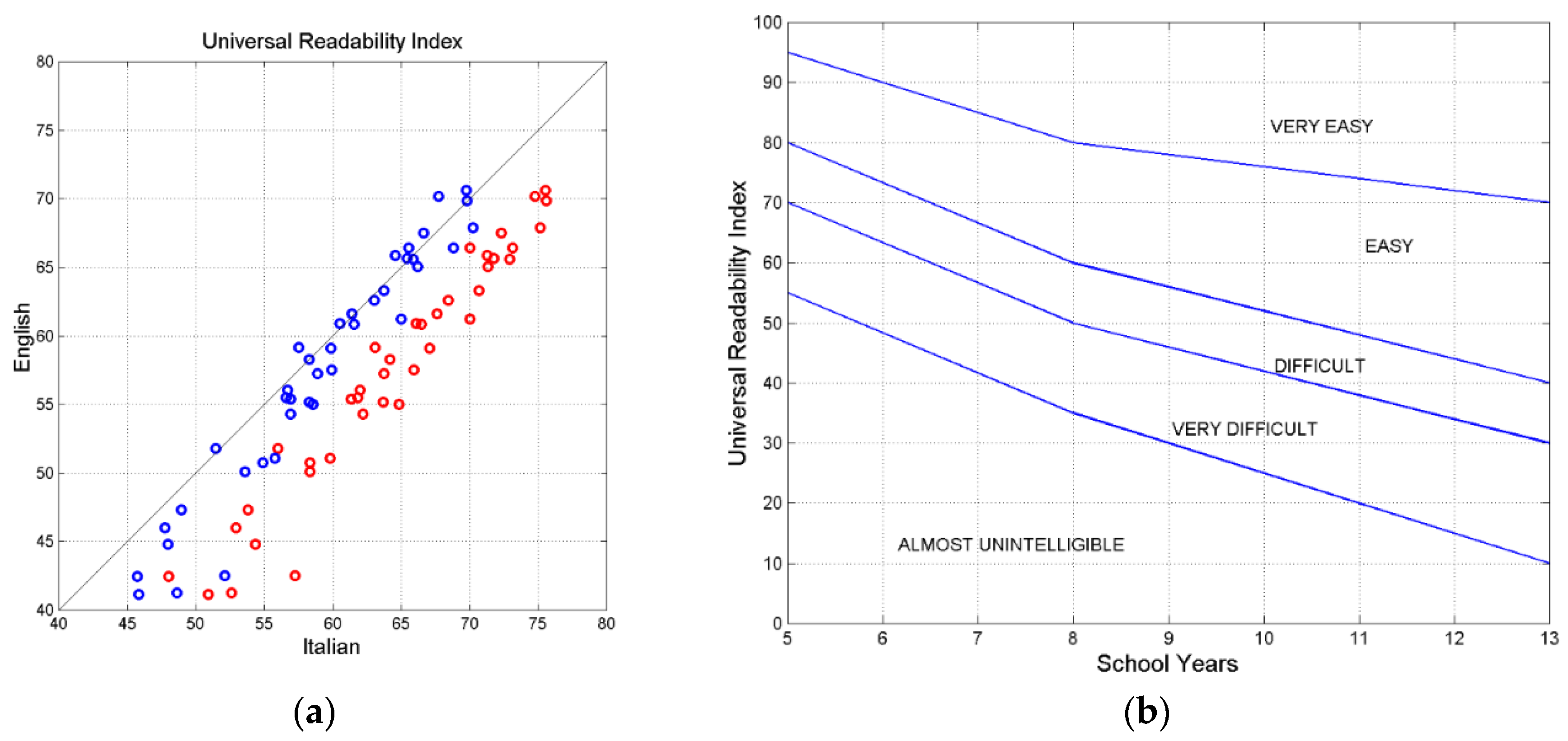
9. Universal Readability Index

The universal readability index $G_U$ – proposed in Ref. [64] - measures the relative reading difficulty of texts. It is underestood that readers are enough educated to understand the texts. It is given by:

$$G_U=89–10k{C}_P+300/P_F–6\left(I_P–6\right)$$

(32)

$$k=<C_{P,ITA}>/<C_{P,Lan}>$$

(33)

In the present paper ${<C}_{p,ITA}>=4.62$ refers to Italian, ${<C}_{p,Lan}>=4.36$ refers to English (see Table 5). By using Equations (22) and (33), the mean value ${<kC}_P>$ is forced to be equal to that found in Italian, namely $4.62$. The rationale for this choice is that $C_P$ is a parameter typical of a language/text which, if not scaled, would bias $G_U$ without really quantifying the reading difficulty of readers, who in their own language are used, on average, to read shorter or longer words than in Italian. This scaling, therefore, avoids changing $G_U$ only because a language has, on the average, words shorter (like English) than Italian. In any case, $C_p$ affects Equation (32) much less than $P_F$ or $I_P$.

Figure 14(a) shows the scatterplot of $G_U$ between Italian and English (blue circles) and Italian-E and English (red circles). We can notice two interesting facts:

a)

For $G_U<55$, the readability of English is less than Italian; for $G_U\gtrsim 55$ the two values agree more, they align more with the 45° line (in Italian, in this range, the lower values of $I_P$ balance in Eq. (32) the larger values of $P_F$).

b)

If semicolons are replaced by periods, the Italian-E text would be much more readable than English, becasue $P_F$ is noticeably reduced while $I_P$ does not change.

These values could be “decoded, for example, into the minimum number of school years $Y$necessary to assess that a text/author is “easy” to read, according to the modern Italian school system, assumed as a common reference, Figure 14(b) [64].

This assumption does not mean, of course, that English readers should attend school for the same number of years of the Italian readers, but it is only a way to do relative comparisons, otherwise difficult to assess from the mere values of $G_U$. In other words, we should consider $Y$ as an “equivalent” number of school years. We get, on the average, $Y\approx 9$ years for English, $Y\approx 8$ years for Italian and $Y\approx 7$ years for Italian-E.

10. Discussion and Conclusions

We have mathematically compared the text of a famous Italian novel, I promessi sposi written by Alessandro Manzoni, to the text of a well-received masterful English translation, The Betrothed by Michael F. Moore. To avoid any misunderstanding, the mathematical theory and its multidimensional application to this translation does not measure or judge its efficacy and beauty, but only its mathematical underlying structure. In other words, the discussion and conclusion we reach are meant to be valid only in this context. We have measured the “equivalence” of the source text and target text mathematically, just like we did with other unrelated couples of texts in any language, even different languages.

After the punctual discussion on the findings reported in each section, we can conclude that the translator largely modified the mathematical structure of the original Italian text. The translation theory he adopted was the “domestication” of the source text.

The almost total replacement of semicolons with periods was justified by stating that English is not as economical in its use of subject pronouns as Italian is. This was not the only change. Question and exclamation marks, and commas too, were also largely modified, with no clear justification due to an alleged “economy” of English. These modifications produce several consequences.

The short-term memory buffers required to the reader are significantly modified. The theoretical number of sentences allowed in Italian, i.e. the patterns of sentences available to Manzoni, is about two order of magnitude greater than in English, therefore the translator resused many times the same numerical pattern of words. Only when semicolons are replaced by periods in the Italian text, to simulate a reverse “domestication” translation, the two variables agree more.

The geometrical representation of texts and the related probability of error indicates that the two texts are practically disconnected and almost all linguistic channels are very noisy, with very poor signal-to-noise ratios, except the channel related to characters.

In conclusion, a blind comparison of the parameters of the multidemensional analysis on the two texts would unlikely indicate that the two texts refer to the same novel.