3. The Contradiction Phase
In this context, the "contradiction phase" refers to the historical conflict between quantum mechanics and special relativity in the field of physics. This disagreement, famously debated between Einstein and Bohr, continues to influence discussions today. The contradiction phase in psychological life describes a state where an individual's mental world has both quantum mechanical and relativistic aspects, leading to inherent conflicts and struggles.
To use Freud's terminology, during the contradiction phase, an individual's psychological life experiences a form of personality split between quantum mechanical and relativistic mental states. It is important to recognize that science is created by scientists; it is responsible for making ontological commitments to the physical world while being supported by the epistemological frameworks of physicists. While it is not appropriate to anthropomorphize physics itself, anthropomorphizing the field of physics is acceptable, thereby endowing it with psychological characteristics. Thus, in the psychological life of physics, a similar personality split may be observed.
During the contradiction phase of psychological life, individuals and society face each other with a mix of familiarity and estrangement, resembling a father-child dynamic with elements of an Oedipal complex. Individuals in this phase begin to question society philosophically, while society, in the role of a father, often lacks answers. At this stage, the individual starts to separate from the societal mother, shedding the "umbilical cord" and, metaphorically, becoming like a cell encased in a cell membrane. Inside this membrane, the language of DNA codes knowledge, while outside, RNA communicates with society. This process results in the creation of what is termed "protein-like knowledge."
3.1. Quantum Mechanical Mental States
In the contradiction phase, an individual’s mental world begins to form its own envelope, akin to having an internal space with intrinsic degrees of freedom, with dimensions that are not fixed. From this point on, the mental world becomes entirely the individual's, and it can only be registered as an individual entity, with society having no claim over it. The envelope of the mental internal space allows for self-rotation, with this rotational momentum referred to as spin. In quantum mechanics, particles have internal spaces, and spin is an intrinsic property of these particles; this concept has no counterpart in Newtonian mechanics. In this sense, the envelope of the individual’s mental space during the contradiction phase is quantum mechanical, differing from the Newtonian mechanical nature of the embrace phase’s mental state.
The mutual observation between individuals and society, as observed in empirical science, refers to a situation where both the individual and society become aware of each other’s complexities. The relationship between them becomes more intricate; what was once perceived as clear now becomes obscure. The intentions behind each other’s words and actions seem enigmatic, and the motives behind unsaid or undone actions appear ambiguous. This complexity and unpredictability in interactions can be described as quantum fluctuations.
An individual with independent thought navigating through society is often driven by a desire to find an ideal position within it. The relationship between this impulse and the ideal position is a categorical one. The question then arises: how strong must the motivation be, and how much effort is required to find this so-called ideal position? This is a dynamic process. When reflecting on this process, you might notice that the more definite the ideal position appears, the more uncertain the effort required to achieve it becomes, and vice versa. This phenomenon is akin to Heisenberg's uncertainty principle, reflecting the everyday experiences people have in social life.
In the embrace phase, whether one acts first or the other does, there was little difference in outcome, representing commutative relationships. Now, in the contradiction phase, society begins to resemble a jungle where the order of actions affects the outcome, signifying non-commutative relationships. This can be expressed with the following formula:
where [A, B] denotes the commutator of operators A and B, which in quantum mechanics represents the extent to which the order of operations affects the result.
3.2. Quantization and Regular Quantization
In this context, finding a non-commutative relationship means that this layer has been quantized, a process known as regular quantization. During the embrace phase, society is akin to a textbook: the more you learn, the more knowledge accumulates additively, satisfying the additive relationship. In this phase, knowledge accumulation is straightforward and additive.
In the contradiction phase, however, society is no longer a prescribed textbook but a reference book with multiple versions. When an individual reads a particular version of this reference book, understanding can vary in depth, recognition can differ in detail, and perspectives can vary. These differences mean that each piece of knowledge has different directional indicators, which can be described using vectors. These cognitive vectors no longer satisfy the additive relationship but only satisfy the superposition principle. Linear superposition is one of the fundamental assumptions in quantum mechanics.
In summary, the transition from an additive knowledge accumulation in the embrace phase to a superimposed knowledge understanding in the contradiction phase reflects a quantumization process, where the nature of knowledge and its interactions are characterized by the principles of quantum mechanics rather than classical mechanics.
In the contradiction period, individuals feel increasingly unclear about society. Behind many superficial phenomena are stories that are difficult to directly observe; in colloquial terms, it's said that "the water is very deep." In such situations, if you want to gather more information, what should you do? The only way is to use some statements or actions as probing stimuli to see how society responds. This is akin to playing a so-called "20 Questions" game with society. You ask a yes/no question, and the response provides some information. An individual with independent will discover that society is competitive because resources are limited.
For example, if two candidates are competing for one spot, and their ability levels are not directly observable, fairness requires an exam. In the exam, each question is a stimulus. The candidate’s performance is a response to the stimulus. Each question is given, and each candidate’s response is displayed; the candidate’s response is a function of the exam stimulus, referred to as the wave function in quantum mechanics. It is expressed in Dirac's bra-ket notation as follows:
Here, ψ represents an experiment, ai denotes a series of experimental tasks, and ϕ signifies the response to these tasks. This is called wave function syntax. The responses of two examinees, one recorded as a and the other as b, can be combined into a complex number . The squared modulus of this complex number is called the amplitude of the wave function. This amplitude represents the meaning of the wave function, also known as the amplitude semantics of the wave function. This complex number can be expressed in exponential form, with a phase in the exponent. When you give the two examinees another stimulus, you will get another amplitude and another phase. The phase difference between the two phases reflects the individual differences between the two individuals. Note that this complex amplitude has both a real part and an imaginary part, carrying a certain subjectivity. The imaginary number "i" has two meanings here: it represents the observer (I) and the information obtained by the observer (information). This description, which I learned from an article by the quantum physicist G. Ni from Fudan University, is quite vivid and I remembered it. The title of the collected works is "Quantum Mechanics: A Memento of the Past." For wave functions, there's a more vivid analogy. Imagine a distant iceberg, half submerged in water and half above water. When viewed from afar, the part above the water represents the real part, and the part below the water represents the imaginary part. Adding both together gives the complex number. This observation is well captured by the wave function. According to the Copenhagen interpretation of physical philosophy, the modulus squared of the wave function, also called its amplitude, can reveal the probability of the Titanic hitting the iceberg. The wave function represents the possibility of an observation outcome, and Dirac stated that the square of this possibility is the probability.
Quantum mechanics also has its weaknesses. Einstein couldn't stand quantum mechanics because it promised action at a distance in the ontological sense. He felt that this theory was somewhat like someone sitting in a teahouse chatting, with nothing they wouldn't brag about. No matter who in the world it is, regardless of distance or relationship, even those who are remotely connected, they all know each other in a roundabout way. No matter what happens in the world, they dare to chat about it, and everything can be related in some way. Since they dare to talk, it means they have a sense of connection in their hearts. Quantum mechanics gloriously calls this teahouse relationship "quantum entanglement." The amplitude of the wave function has a probabilistic interpretation by the Copenhagen school. So, there's nothing they wouldn't talk about, it's just a matter of probability. Want to buy the Great Wall in Beijing, or be on brotherly terms with Buffett, or comment on the world economic crisis as if they have an inextricable connection with it? Isn't it just a low probability event? Even if the probability is small, it's still a probability. Einstein thought this was akin to rolling dice, and angrily said, "God does not play dice." Saying this made him sound like a teacher, which annoyed quantum mechanics experts. They didn't listen much to the old man. A leader of the Copenhagen school named Bohr even argued and debated with him. The academic community called this academic debate. Such debates don't hurt harmony and belong to the realm of intellectual freedom, known as academic freedom. Academic freedom is the soul of academic life and the beacon of scientific progress.
The individual in the period of contradictions, with great ambitions for quantum mechanics, prepares to walk through society, make friends with heroes and great men, and achieve great feats. But he soon observes an inescapable, invisible shadow like a cone, blocking his way everywhere like a demon. This invisible cone shadow, in Einstein's special relativity [
2], is called the light cone.
3.3. Psychology of Special Relativity
The starting point of special relativity is the principle of the constancy of the speed of light. Light, being both wave-like and particle-like, is massless and the king of speed in the movement of all things in nature. Other things are called inertial systems, and whether their speed is a bit faster or slower, it makes little difference in the face of the speed of light. Through Lorentz transformations, they all exhibit the same submission to the sovereignty of light and share a common reverence, which is a symmetry relative to the king of light. The king of light, relying on its speed authority, behaves willfully and travels in straight lines, scattering in all directions, commonly known as radiating in all directions, which is what this means. When light starts from an excitation point, its scattering is cone-shaped; scattering downward forms a lower cone, and scattering upward forms an upper cone; the upper and lower cones meet at the excitation point and are collectively referred to as the light cone (see the diagram below).
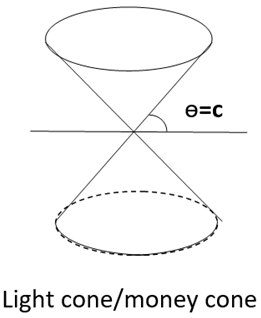
Later, Einstein discovered that under the influence of the gravitational field in general relativity, the path of light would also bend; however, the cone's body twists without losing its conical elegance.
As individuals navigate society during periods of contradiction, they quickly discover that society also possesses things with light-like properties, such as power in politics, money in economics, language in communication, and consciousness in the mind. In their respective domains, these elements are omnipresent. While you are training for a marathon, others are mastering the Great Shift of the Universe. Wherever you plan to go, it is already there, and that speed is incomparable. Light, power, money, language, and consciousness form a fivefold state of light-like properties. When the quintet plays, it is all melodious. Note, this is not a complete set of light-like states; for instance, the role of technology in social development is not discussed here. To borrow an old saying, all kings in the world are willful. Light has its light cone, and under the banner of light-like properties, there are corresponding cones of power, money, language, and consciousness in society. Thus, as individuals navigate society, they cannot avoid interacting with these four societal cones. These four cones compound and interlock, representing the reality individuals must face in society. Since there are four types of cones in society, the individual's relationship with each societal cone can only be in one of three states: within the cone, on the cone's surface, or outside the cone. How to determine which state it is in requires introducing the concept of "interval" in four-dimensional spacetime.
Special relativity [
2] speaks in the mathematical four-dimensional spacetime of Minkowski. Among the four dimensions, in addition to the three spatial dimensions, the other dimension is synthesized by multiplying time by the speed of light, called the energy axis. In four-dimensional spacetime, each point is called an event. To introduce a metric in spacetime as a mathematical space, it is (positive, negative, negative, negative). Thus, the displacement of an event can be characterized by the so-called interval, defined as follows:
According to the established metric, the interval is the differential of the displacement of energy minus the differentials of the displacements of the other three spatial dimensions. The interval of events on the cone surface is zero; the interval of events within the cone is greater than zero, called time-like events; the interval of events outside the cone is less than zero, called space-like events. The distinction between events inside and outside the cone corresponds to the difference between being worldly and otherworldly, describing the prosperity and decay of human affairs and the vicissitudes of life. Cone surface events are the fine balance maintained by the creator of the cone, perfectly balanced between the two realms.
When talking about the light cone, events within the cone have enough energy to support the displacement of the event; events outside the cone do not have enough energy to support the displacement of the event; events on the cone surface have just the right amount of energy to support the displacement of the event, no more, no less. Regarding the power cone, events within the cone fall within the scope of authority, and there is no problem handling the matter; events outside the cone exceed the scope of authority, and the matter cannot be handled; events on the cone surface have just enough authority to handle the matter, exactly on the line. Concerning the money cone, events within the cone fall within the budget surplus, and there is enough money to buy things; events outside the cone fall within the budget deficit, and there is not enough money to buy things; events on the cone surface fall within the "moonlight clan" who spend all they earn. Talking about the language cone, events within the cone mean strong language skills, and handling writing and speaking tasks with ease; events outside the cone mean weak language skills, with unclear expressions and off-topic writing. Events on the cone surface mean just enough language skill, with neither superfluous words nor missing points. Finally, talking about the consciousness cone, events within the cone mean awareness, and the matter is within the individual's consciousness; events outside the cone mean unpreparedness, with the matter not within the individual's consciousness; events on the cone surface mean just the right thought occurs at the right time.
The above descriptions all refer to social cones. Another important concept in special relativity is called "proper time". Proper time is registered by the individual and can reflect individual differences. Using proper time, one can generate an individual momentum cone. These are the topics for the next section on the psychological re-entry period, which will be skipped here.
The concept of the light cone is important because, as Einstein emphasized, it represents historical causality. Only events within the lower cone can cause the light source to be excited at the apex of the upper and lower cones, and only events within the upper cone are affected by the excited light source. A line starting from the lower cone, passing through the apex excitation point, and traversing the upper cone is called a world line. There are many world lines, each representing a historical causal relationship. Space-like events outside the cone are unrelated to causality and are marginalized. Similarly, in the various social cones, world lines passing through the upper and lower cones also reflect causal relationships in social life. Those outside the cones have no relevance to causality and are marginalized in society.
3.4. Psychological Conflict
As described above, during the period of contradictions, the mind experiences a state of split personality, with Einstein and Bohr clashing within. On one hand, under the guidance of a quantum mechanical mindset, who does not yearn for quantum entanglement with various ideals, even at the cost of living in a world full of uncertainties? On the other hand, driven by a mindset inclined toward special relativity, who does not want to ally with reality, striving to enter the various societal cones and become an elite within them? In mundane terms, within the cone lies abundant grain, beautiful companions, houses of gold, and carriages aplenty—comfort and success, fame and fortune. In more refined terms, within the cone, one can serve society, achieve brilliance, make great contributions, and repay the nation. Even if one falls outside the cone, there are many marginalized individuals who find contentment in an ordinary life, occasionally venting their frustrations, feeling envy and jealousy—such is life and reality.
Alas, Einstein or Bohr, how can my psyche not be split? Comedy or tragedy, it is indeed like a Shakespearean plot, serving two masters, yet being fulfilled and delighted. Traditional psychology calls this adolescent turmoil.
4. The Re-Entry Phase
The period of contradictions described above is both a tempering and a glory of psychological life. It is hard to imagine a psychologically healthy life that has not experienced a period of contradictions; this period is like a vaccine that protects psychological life. A psychological life that successfully navigates the period of contradictions feels reborn, like a phoenix rising from the ashes. When it re-enters society, it becomes mature and resilient. For the sake of convenience, we personify this psychological life entering the re-entry period as "Re-entry Lord." Re-entry Lord gradually understands the psychological version of quantum field theory in life, learning many things and understanding many principles. We know that quantum field theory is the integration of special relativity and quantum mechanics, which is the path out of the period of contradictions. Physics is thus, and so is psychology.
4.1. Proper Time and Individual Cones
There are no stories like "shedding the golden cicada skin" in psychology. So how does Re-entry Lord achieve a splendid transformation? During the phase of contradictions, this individual was worn out from trying to squeeze into various societal cones but did not lose heart. Suddenly, they saw Einstein, by the dim light, who introduced the notion of proper time.
Proper time is a concept in special relativity [
2]. A common example is the story of twin brothers, each carrying a clock. The elder brother travels into space on a fast spaceship; the younger brother stays on Earth, which moves at a slower speed. Years later, the elder brother returns to Earth, looking still young, while the younger brother appears aged. The reason is that speed equals distance divided by time, which here refers to absolute time. The faster the speed, the slower the clock time, in inverse proportion; this clock time is called proper time. Previously, we mentioned the concept of interval related to event displacement; the formula expressing the interval concept has four terms. Dividing each term by proper time defines four-dimensional momentum. With four-dimensional momentum, the momentum cone can be introduced.
Proper time is the clock time carried by an individual, so it is individualized, reflecting individual differences. For example, in an economic context, the market price of a commodity is the absolute price, but different individuals have their own proper prices. A new phone priced at $5,000 is the absolute price. For a wealthy person, $5,000 is nothing, quite cheap. For a poor person, $5,000 might be their entire monthly expense, too expensive. This is called the proper price, varying from person to person. Different personal economic conditions result in different proper prices psychologically. Cognitive economics refers to this as "individual mental accounts."
In economic mechanics, the concept of the individual momentum cone has been introduced [
16]. During the period of psychological contradictions, individuals encounter societal cones based on absolute costs given by society. Now, Re-entry Lord begins designing individual cones based on their proper costs. The cone can become wide and flat or tall and slender. Drawing a horizontal line through the apex of the upper and lower cones, the angle between this line and the cone is called the cone's phase. The flatter the cone, the smaller the phase; the taller the cone, the larger the phase. The width of the cone's top opening is called the "rush degree". The mechanism of cone shape change is that the smaller the proper cost, the smaller the phase, and the higher the rush degree, forming a wealthy cone. Conversely, the larger the proper cost, the larger the phase, and the lower the rush degree, forming a poor cone (see the diagram below). It can be seen that the proper cost is inversely proportional to the rush degree. In short, for an individual, the more expensive they feel an item is, the lower their psychological rush degree to purchase it, and vice versa.
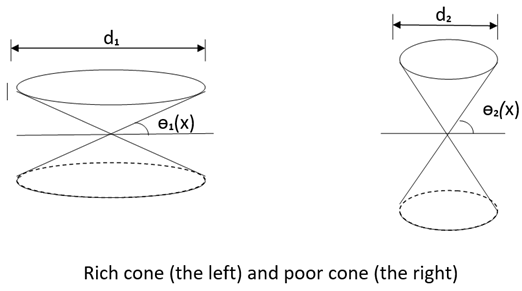
When Re-entry Lord designs their individualized power cone, they psychologically grasp the principle of doing what they can with their abilities—undertaking tasks that match their capability. When designing their individualized money cone, they adhere to the principle of spending within their means, managing expenses according to their budget. In designing their individualized language cone, they follow the principle of tailoring their communication to their abilities, speaking and writing based on their talent and capacity. When designing their individualized consciousness cone, they consider their own knowledge and experience, allowing the depth of their understanding to guide their thinking.
In this way, Re-entry Lord finds psychological confidence, no longer desperately trying to squeeze into various societal cones as they did during the period of contradictions. Re-entry Lord learns to continually adjust their psychological cone shapes, striving to reduce their proper costs and gradually increase their psychological rush degree. This approach allows Re-entry Lord to mature psychologically, earning praise from Einstein.
4.2. Suspension and Renormalization
Both physics and psychology are empirical sciences. Empirical science is not just about conducting experiments and writing reports; it places great emphasis on theory. Theory not only guides experimental design but also helps scientists understand the natural and social phenomena they observe. I am not fond of the so-called "anthropic principle" in physics, which suggests that nature is arranged according to human imagination. Theories in empirical sciences are always hypothetical and must be tested against experiments. However, people often conflate physics with physical phenomena, overlooking the distinction between natural phenomena (physics and psychology) and the theories created by physicists and psychologists. Natural phenomena have their inevitability, while scientific theories have their contingencies.
We sometimes describe a theorem as elegant or a theory as nearly perfect. These are expressions of admiration, although they come from genuine feelings. In reality, there is no perfect scientific theory; a perfect theory is called theology. Science is not theology, and scientists are not gods. Scientific theories, based on observation, undergo two processing steps by scientists: conceptualization and modeling, also known as conceptual and model processing. The term "processing" here is akin to the everyday use of "handling" a problem—it is not particularly mysterious.
One hallmark of Re-entry Lord’s psychological maturity is learning how to handle various matters. Different matters have different priorities, and Re-entry Lord differentiates accordingly. The approach to handling issues affects the outcomes, and Re-entry Lord is prepared to take responsibility for the consequences of different approaches. Classic decision theory considers preferences as mental states that can change overnight without cost. Contemporary decision theory, pioneered by Savage, introduces behavioral freedom, making preference relationships choices between two action functions. Actions have consequences, so choosing one action involves the opportunity cost of forgoing another. For example, if you are admitted to both Peking University and Tsinghua University and choose Peking University, you forgo Tsinghua University, which represents the opportunity cost. Psychologically, this is burdensome, and Re-entry Lord has the capacity to bear this psychological burden.
Another important feature of Re-entry Lord’s approach to handling issues is the establishment of the concept of "suspension"—learning to temporarily set aside challenges that are difficult to solve at the moment and revisiting them when conditions change in the future. According to Johnson-Laird's mental model theory, this means leaving a mental note. The suspension technique is also reflected in quantum field theory. For instance, inquiries about the physical background of the "renormalization" method have long been in a state of suspension. Quantum mechanics deals with particle physics at low energies and speeds, while special relativity addresses high energies and speeds. Integrating both in quantum field theory results in infinite quantities in calculations, which the theory cannot tolerate. For example, considering a particle with mass approaching or reaching the speed of light, according to Einstein’s mass-energy equivalence formula, would require infinite energy. The method of eliminating these infinite quantities is called renormalization.
Nobel laureate Richard Feynman reflected on the renormalization method, commenting that it is a crude technique, akin to hiding the infinities under the rug or sweeping the dirt under the rug. Physicists have become so adept at this that sometimes it seems not to be a serious problem. The crude technique Feynman refers to is essentially the idea of suspension. Renormalization is a crucial computational method in quantum field theory. It is evident that the creation of the renormalization technique by theoretical physicists is not only a result of good scientific training but also a product of psychological experience.
4.3. The Psychology of Scientists
It's often said that a person's psychological qualities can impact their career, and the field of science is no exception. The psychological state of scientists not only influences their individual academic paths but also affects the academic style of their fields. In my observation, contemporary theoretical physicists are among the most psychologically resilient scientists. Nature involves four fundamental forces: gravity, electromagnetism, the strong nuclear force, and the weak nuclear force. After establishing the theories of special and general relativity, Einstein pursued a unified field theory that would encompass all four fundamental forces. Although he did not complete this grand vision, the quest for a unified field theory remains a challenging scientific endeavor. Theoretical physicists have never abandoned the pursuit of a unified field theory, exhibiting the determination and spirit of great historical figures.
Each year, the Nobel Prize in Physics is celebrated, yet theoretical physics is a field rife with academic disputes. Criticism and skepticism about contemporary theoretical physics are constant. Theoretical physicists demonstrate a strong will to achieve a unified field theory, taking responsibility for criticism and exploring the unknown with courage, resilience, and perseverance.
Remarkably, theoretical physics is also a field where popular science outreach has excelled. Many outstanding theoretical physicists, such as Stephen Hawking, Brian Greene, Leonard Susskind, Roger Penrose, and Lisa Randall, have authored well-written, accessible books on advanced topics. Over the past decade, numerous publishers have excelled in introducing these works in China. Reading these popular science books not only provides a deeper and broader understanding of theoretical physics but also sheds light on how theoretical physicists create their knowledge. As a psychologist, I am also interested in the relationship between the psychological state of theoretical physicists and the theoretical frameworks they create. The intricacies are self-evident. Whenever I see a theoretical physicist describing their experience of "listening to the voice of nature," I feel a sense of sympathy and compassion. Achieving such profound knowledge is both thrilling and sorrowful, reflecting a heroic spirit that is both awe-inspiring and humbling.
Quantum field theory exemplifies the psychological characteristics of Re-entry phase. In his book,
Elementary Quantum Field Theory, physicist, Z. X. Wang [
12], mentions that physics has four levels: experimentation, phenomenological theory, fundamental theory, and mathematics. Experimental and phenomenological theories constitute experimental physics, phenomenological and fundamental theories make up theoretical physics, and fundamental theories and mathematics constitute mathematical physics. Quantum field theory, a fundamental theory of particle physics, represents our deepest understanding of the particle world and is a dynamic model of particle systems. It successfully integrates three of the four fundamental forces: electromagnetism, the strong nuclear force, and the weak nuclear force. This represents a significant advancement toward Einstein's unified field theory.
One of Re-entry Lord’s psychological characteristics is understanding that to achieve grand ideals, one must first compromise with reality. To reach strategic goals, flexible tactics must be employed. To realize personal ambitions and demonstrate value, one must align with society and synchronize with history. This may not be entirely intentional and might even be contrary to one's desires, but it is a necessary psychological function for maintaining balance. Achieving psychological self-consistency is crucial for mental health. This psychological trait is vividly demonstrated in quantum field theory, showing that theoretical physicists understand this principle. To build a tall building, one must first construct scaffolding, even though the scaffolding is not the building itself. To realize the grand vision of a unified field theory, quantum field theory inevitably becomes a vast theoretical system, requiring the introduction of non-physical parameters to ensure theoretical coherence.
In empirical science, observed phenomena are always fragmented, while the fundamental theories must be systematic. Therefore, to ensure theoretical coherence, sometimes non-phenomenological concepts are introduced as theoretical scaffolding. In quantum field theory, it is often necessary to introduce non-physical concepts and modeling techniques, resulting in numerous model parameters. For example, in quantum chromodynamics, quarks are confined, and only bound states of quarks can be observed experimentally. For instance, a proton is a bound state of two up quarks and one down quark held together by gluons. However, according to the Pauli exclusion principle, two up quarks, being identical particles, cannot occupy the same bound state. To resolve this theoretical contradiction, Gell-Mann introduced the concept of "color charge," allowing two up quarks to carry different color charges and thus logically coexist in the same proton bound state. The introduction of color charge is a theoretical scaffold, a non-physical concept introduced in physics theory without physical phenomenon support. Similarly, the concept of "ghost fields" in Feynman diagrams is still considered non-physical today.
In quantum field theory, the introduction of non-physical degrees of freedom demonstrates the wisdom of physicists. In psychological life, incorporating non-intentional, non-willing, or non-spontaneous psychological adjustment mechanisms also reflects the mature psychological traits of Re-entry Lord.
4.4. Life and Achievement
In the journey of psychological life, "life" and "achievement" stand as two prominent psychological pillars, central to one's existential reflection. Life is measured in terms of time, while achievement reflects one's position in society. In classical quantum mechanics, the dynamical equation is the Schrödinger equation. Position change is described by a second-order derivative (acceleration), while time is described by a first-order derivative (velocity). This difference in order represents a common psychological experience.
A notable example is the case of scientists who have passed away young, often portrayed as having worked relentlessly. However, this is not limited to these high-profile examples. Many people in their psychological lives, in their efforts to change their social position, consciously or unconsciously, actively or passively, push themselves to work with a second-order acceleration, treating life as a first-order uniform motion, as if life were inexhaustible and endowed with infinite endurance.
Quantum field theory changes this psychological state by modifying the fundamental theoretical framework. In the Dirac equation, the description of position change is adjusted from a second-order derivative to a first-order derivative, making the changes in position and time of the same order. This adjustment accurately reflects the psychological characteristic of Re-entry Lord, who views the continuity of life and career achievements as equally important. This represents a mark of psychological maturity, comprehensive mental health, and the nurturing of both life and career.
4.5. Creation and Annihilation
Psychological life exhibits a variety of mental states. The most fundamental state, known as the ground state, represents the ordinary mind or common rationality, as described by the Higgs field in quantum field theory. Quantum field theory posits that all particle states arise from excitations of the ground state. These excitations are not eternal; they have a finite existence, marked by a period of creation and annihilation. Hence, in quantum field theory, creation and annihilation operators are always present at the beginning and end of formulas, reminding particles to be active—life is finite.
Similarly, human psychological states, emotions, and dilemmas are also considered excitations. Re-entry Lord learns to master the creation and annihilation operators in their psychological life. One cannot remain in a single state of excitation indefinitely or be perpetually entangled in one emotional state. Regardless of the emotion or dilemma, it should have its time and duration. While emotional activation is inevitable, letting go of emotions is also a rational act. Re-entry Lord skillfully uses creation and annihilation operators to manage the rhythm of their psychological life, conducting the inner symphony.
Re-entry Lord understands a simple yet profound truth: humans need to eat and sleep, and to survive, many tasks must be accomplished. Psychological life, being life as well, cannot be overburdened or excessively strained. Psychological states also need rest and replenishment. Similar emotions and dilemmas may recur, reflecting a "creation-annihilation-recreation-re-annihilation" cycle in the psychological lifespan.
4.6. Positive and Negative Energy
Psychological life experiences ups and downs, and emotions can be either positive or negative. In contemporary language, cognitive discourse can convey positive or negative energy. These are common concepts in social discourse, but did you know that the concept of "negative energy" once caused a significant stir in the early development of quantum field theory?
Dirac, one of my idols in physics, is frequently mentioned in quantum field theory for his contributions to concepts, formulas, or equations. When Dirac's equation was first proposed, it faced substantial skepticism. The reason was that the equation involved taking the square root of the energy term, leading to both positive and negative solutions, which introduced the concept of negative energy. Traditionally, energy in physics is considered positive, so introducing negative energy raised significant questions. To address this, Dirac initially proposed the "Dirac Sea" theory. In the Dirac Sea, there are uniform ripples with depressions (negative energy) and elevations (positive energy). It was later understood that every particle has a corresponding antiparticle; particles themselves carry positive energy, while antiparticles carry negative energy. This concept has since become a standard part of physics textbooks.
Unlike the physical world, psychological life is subjective. Transforming negative energy into positive energy is a powerful psychological function of the Re-entry Lord.
4.7. The Four Steps of Experience
Since last summer, I have been appointed as the Director of the Graduate Program in my department, making me the youngest official on campus, a role that in American campus culture is known as "service," part of a professor's job. From January to April this year, I experienced the entire process of overseeing graduate admissions for the first time. My psychological journey through this process can be described in four stages, which correspond to the four stages of the concept of "field" in theoretical physics.
- (i)
Wave Function: At the beginning of the admissions process, I was not well-acquainted with the situation. I was unfamiliar with the entire admissions procedure, and the previous director and the department did not provide detailed explanations. Due to the pandemic, this year's admissions process was more complex. GRE scores became optional, the funding for doctoral scholarships was unclear due to financial constraints, and international students faced difficulties with visas. Additionally, I was unaware of the attitudes and thought processes of the faculty on the admissions committee. This situation was filled with uncertainty, with phenomena unclear and observational interference high. Initially, I could only proceed step by step, addressing each issue as it arose. This is akin to the concept of ‘wave functions’ in quantum mechanics, where uncertainty and lack of clear observation characterize the initial stage.
- (ii)
Field Theory: As I progressed, I gained an understanding of the candidates' materials, especially those on the shortlist, and of the thought processes of the admissions committee members. At this stage, each candidate and faculty member became part of a "field." In quantum field theory, fields interact through mutual interactions, which are considered ontological commitments. These interactions have causal effects, resolving issues like quantum entanglement and addressing Einstein's criticisms of quantum mechanics.
- (iii)
Operator: In the later stages of the admissions process, I became familiar with the entire procedure. The work of admissions became more of a routine operation for me, and I functioned more as an operator. In quantum field theory, a field is viewed as an operator, simplifying interactions and processes.
- (iv)
Operator Algebra: As the admissions process drew to a close, I gained a lot of experience and confidence. Looking back on this year and anticipating next year's admissions, I felt a deep understanding of the process. For me, it became like an operator algebra. In quantum field theory, transitioning from classical fields to quantum fields involves second quantization, where the classical field becomes a quantum field, adhering to specific commutation relations within Hilbert space.
This story illustrates that during the three-month admissions process, my psychological journey mirrored the stages of wave functions, fields, operators, and operator algebras in quantum field theory. In this sense, I evolved into a more mature version of myself, embodying the traits of a seasoned professional.
5. The Citizen Phase
If the previous stages—Nurturing, Conflict, and Re-entry—represent the endogenous and primary aspects of psychological life within the framework of Freudian personality theory, the process of becoming a citizen of psychological life extends beyond traditional Freudian frameworks. The rights and responsibilities of a citizen are defined by public matters and social structures, which are exogenous environmental structures or ecological structures. Thus, the process of psychological citizenship involves the internalization of this ecological environment. This leads us to discuss an important cognitive psychology school represented by German-American psychologist Ulric Neisser, known as the environmental school. This will be covered in section 5.1.
One might find it surprising to delineate a Citizen Phase in psychological life. However, there is no need to shy away from this; the psychological characteristics of citizenship are prominent, though often subconsciously overlooked. For example, if you have always been law-abiding, this refers to your behavior. Reflecting on your psychological activity when paying taxes on extra income will reveal the presence of a psychological Citizen Phase.
The psychological characteristics of the Citizen Phase have clear boundaries and scope. A citizen is a member of the state; thus, citizen psychology involves national consciousness. A citizen is also a member of society; hence, citizen psychology involves public awareness. A citizen is an individual with diverse backgrounds; therefore, citizen psychology addresses individual differences. Thus, while the boundaries and scope of citizen psychology are clear and complex, this complexity has a structured clarity. The concept of gauge theory in quantum field theory seems to fit this structure perfectly. Gauge theory is a central part of quantum field theory.
To understand the structure of citizen psychology within this gauge theory framework, it is helpful to know the five fundamental pairs of concepts, akin to five interconnected rings or five-tiered ladders. The next sections 5.2 to 5.7 will outline these five fundamental paths.
5.1. The Internalization of Citizenship in Psychological Life
I remember it was in the fall of 1990, when I had just transferred from the Department of Philosophy to the Department of Psychology. The department invited Professor Ulric Neisser from Emory University to give a lecture. After a dinner gathering at my advisor’s home, I had a brief one-on-one conversation with Professor Neisser. He asked me what research I was doing, and I mentioned that I was working on the "mind-body problem"—which, in China, is translated as the "embodiment of the mind." Professor Neisser immediately responded that everyone is studying the mind-body problem, but he wanted to know what specific topic I was working on. I then explained my thoughts on the complex nature of the mind and sought his advice. After a brief discussion, Professor Neisser suggested we change the topic. This left me somewhat disappointed. It wasn’t until later, after gaining more experience in psychology, especially experimental psychology, that I realized the different thinking approaches of psychologists and philosophers; my discussion with Professor Neisser had still been influenced by my philosophical background.
Neisser is sometimes referred to as the "father of cognitive psychology," largely because he was the first to use "Cognitive Psychology" as the title of his book. In my view, this is somewhat unfair. The cognitive revolution that emerged in the 1950s [
1] is generally considered to have produced three major schools. One is the Harvard School, led by linguist Noam Chomsky and psychologist George A. Miller, who were both young scholars at Harvard at the time. Another is the Carnegie Mellon School, also known as the Computational School, led by the renowned cognitive scientist Herbert Simon and computer scientist Allen Newell. The third is the Environmental School, represented by Neisser. Among these pioneers of cognitive science, I personally believe that Chomsky made the most significant and crucial contribution by breaking the constraints of the behaviorist research paradigm. Regardless of which school of thought has influenced your academic research more, when you read the works of these pioneers, you will be impressed by their profound theoretical knowledge, which reflects both their ability to construct extensive theoretical systems and their critical spirit essential for establishing new schools of thought. These aspects are necessary for reflection and revival in today’s academic world, where technical advancements have led to a widespread regression in basic theoretical research.
My doctoral training at New York University and postdoctoral training at Princeton University were both in experimental psychology, with research in the 1990s focusing mainly on psychology of reasoning and higher-order cognition. Higher-order cognitive experiments typically involved language tasks. Professor Miller, who was both a mentor and friend, and I would often discuss and drive him home after meetings, so I naturally felt a sense of camaraderie and closeness to the Harvard School.
I have always had respect for, but not admiration for, the Computational School, or Simulation School, within cognitive science. There is a well-known two-person game called "20 Questions." In this game, one person thinks of an object or concept, and the other person tries to guess what it is by asking yes/no questions. For example, if the object is an apple, questions might include, "Is it used for eating? Is it food? Is it meat? Is it a grain? Is it a fruit?" to narrow down the answer. The former Princeton theoretical physicist, Wigner, who was also a teacher to several Nobel laureates including Feynman, once said that quantum physics is like playing a 20 Questions game with nature. Similarly, my work today in economic mechanics and mental mechanics can also be seen as playing a 20 Questions game with the economic world and the mental world. However, Allen Newell of the Computational School argued that you cannot play a 20 Questions game with nature and win. Personally, I am more inclined toward Wigner’s idealistic scientific attitude compared to Newell’s realistic scientific view. It wasn’t until recently that I rekindled my interest in the P/NP problem in computational science, which changed my attitude towards the Computational School.
I had always neglected the Environmental School represented by Neisser. I thought its research path focused too much on perception and action, seeming more like a new bottle for traditional psychophysics, and too distant from higher-order cognition. One of Chomsky’s major theoretical contributions was distinguishing between "competence" and "performance." He proposed that although people’s ways of expressing language differ, they share an innate ability to acquire language. This ability is unique to the human species and is due to an innate learning device, a result of long-term evolution. This was a critical blow to the behaviorist paradigm during the cognitive revolution. Additionally, Neisser had actually been a student of Miller’s at Harvard. However, Neisser believed that the Harvard School's research perspective was too narrow.
Neisser introduced two key concepts in his theory. One is "environmental structure," which means that the environment has various structures. The other concept, translated into English as "affordance," is not clearly translatable into Chinese, but it refers to structures in the environment that can be psychologically acquired or internalized.
When I began writing this section on the Citizen Phase of psychological life, I encountered logical obstacles. I realized that the previously discussed phases—Nurturing, Conflict, and Re-entry—all had similar internal psychological paths that could be described within the frameworks of Freudian and Harvard School theories. However, the Citizen Phase has a distinct external-to-internal psychological path, which cannot be forced into the previous frameworks. After some struggle, I finally recalled Neisser and recognized the subtleties and effectiveness of the Environmental School. It turned out that it was I who had been narrow-minded.
5.2. Symmetries and the N
ether's Theorem
Symmetry is the essence of gauge field theory. For example, we often say that "everyone is equal before the law," which has two layers of meaning. First, the law is inviolable; it is neither tailored for any individual citizen nor can it be arbitrarily modified by any individual citizen. Here, "everyone" is used collectively as a universal quantifier meaning "all." Second, every citizen must adhere to the law, and the law has equal binding force on each citizen. Here, "every" is used in a specific enumerative sense. In fact, there is a third implied meaning: the laws and regulations constrain the actions of every citizen, not the psychological state of any citizen.
The use of universal quantifiers implies a symmetry among all citizens, meaning that every citizen and any citizen are in an equal position. This symmetry presupposes the inviolability or impartiality of the law. This presupposition, in logical terms, is called a sufficient condition. It is of the same nature as the inaccessibility of economic rationality and the opacity of the market's invisible hand, collectively referred to as non-observability in mathematical physics.
Why do we need this symmetry? Because symmetry implies conservation. For a physical system, a symmetry means some invariance, indicating that the system is a conservative system in this sense. The inaccessibility of economic rationality and the invisibility of the market's hand imply symmetry among all market participants, which is why the market can be a sustainable and conservative system. Consider if there were insider trading in the market, giving certain participants an information advantage and making them market winners; other participants would eventually withdraw, causing the market to lose its sustainability. Similarly, if there is bias in the legal and political system, it would damage the symmetry among citizens and, consequently, the symmetry of the public psychological system towards the legal and political system, harming the conservation of this psychological system. In common terms, this is detrimental to societal stability. Therefore, symmetry is the soul of citizen psychology, with a fundamental demand for fairness and justice in society.
These principles are common knowledge, but their theoretical depth is profound. Non-observability implies symmetry, and symmetry implies conservation. This is the famous Nöether's theorem in mathematical physics.
5.3. The Two-Tier Structure
The structure of gauge field theory is complex, but its basic framework is not. First, it is a two-tier structure, divided into global and local levels. Within each level, there is also a two-tier structure, consisting of gauge potential and gauge field strength.
As the external normative structure for citizens, the global level is independent of any individual citizen. The state represents the global gauge potential, while society represents the global gauge field strength. Logically, both the state and society are collective concepts with global significance. However, the state and society differ in terms of concepts and functions. The state has various functions, establishes various laws and regulations, and enacts policies. All these, before implementation, constitute the global gauge potential. Once policies and regulations are implemented, they impact society, which then reflects the global gauge field strength.
The local level involves individual differences among citizens. Each citizen has different intrinsic conditions, abilities, family backgrounds, educational backgrounds, economic conditions, surrounding environments, and knowledge accumulation. These factors contribute to individual differences among citizens. Regarding a policy or regulation, different states of individual citizens lead to different behaviors. The state of an individual citizen is the local gauge potential, and their behavior is the local gauge field strength.
There are many sensitive examples related to citizens' rights and obligations concerning the external normative structure. Generally, the social cone we discussed earlier belongs to the global level and uses absolute time, absolute prices, or absolute rights. The rotation of the social cone is unrelated to individuals. In contrast, the rotation of individual momentum cones can reflect individual differences, using inherent time, inherent prices, or inherent power. Here are a few non-sensitive examples to illustrate this.
The first example is market dynamics in economic mechanics. In this case, economic rationality represents the personification of a perfect competitive market, but there is a distinction between the two. At the global level, economic rationality is the gauge potential, while the market itself is the gauge field strength. At the local level, the budget of an individual market participant is the gauge potential, and actual consumption is the gauge field strength.
The second example is reasoning dynamics in cognitive mechanics. At the global level, logicians are the gauge potential, and the various logical systems they create are the gauge field strength. At the local level, a reasoner's reasoning ability is the gauge potential, and their reasoning performance is the gauge field strength.
The third example is standard educational testing dynamics. At the global level, the Educational Testing Service (ETS, Princeton) is the gauge potential, and a set of SAT questions is the gauge field strength. At the local level, a test-taker’s ability and preparation are the gauge potential, while their test performance and scores are the gauge field strength.
Using the concepts of mathematical set theory, the extension of a set refers to the many elements it contains, while its intension refers to the properties that these elements must satisfy. The relationship between a set and its subsets is an inclusion relationship, while the relationship between a set and its elements is a membership relationship. Inclusion is discussed at the global level, while membership is discussed at the local level. Confusing inclusion with membership can lead to the famous Russell's paradox. An individual citizen, by nature, is in a membership relationship with the state and society. However, if a citizen confuses membership and inclusion, they might mistakenly consider themselves a part of the state or society. This leads to various illegal behaviors, such as corruption, which stem from logical errors.
The described two-tier structure of the civic environment is entirely within human cognitive capabilities. That is to say, through this cognitive channel, the normative structure for citizens can be internalized by individuals. Note that internalization always refers to individual internalization, as the mental world is embodied in individuals, meaning that psychological accounts are registered with real names. So, how are the global and local levels connected, and how is symmetry manifested from gauge potential to gauge field strength?
5.4. Gauge Transformations
As mentioned earlier, in quantum mechanics, particles are characterized by their wave functions, while in quantum field theory, particles are characterized by the excitation states of fields. For convenience, we will use wave functions here, assuming the reader has some understanding of them. In this context, the wave function is a function with individual citizens as variables, covering all individuals. The change in the wave function represents the evolution of the particle's state.
When a particle transitions from one state to another, a linear transformation is applied, meaning that the gauge potential of the wave function in the new state is multiplied by a coefficient derived from the gauge potential of the original state. This coefficient is a complex number (or a complex matrix). This transformation is called a gauge transformation. Complex numbers have a natural exponential representation, where the imaginary part, multiplied by a phase, represents the phase difference of the wave function when transitioning from one state to another. With the concept of phase difference, the following discussion becomes more straightforward.
At the global level, this gauge transformation is independent of individuals, so the phase is not a function of individuals and is therefore a constant. At the global level, the wave function is continuously changing, so the phase can be any given constant. However, at the local level, things are more complicated. At this level, individual differences must be considered. The phase must vary for each individual, making it a function of individuals and thus called the phase function. In other words, when the wave function transitions from one state to a new state, the transformation coefficient (or matrix) itself becomes a function of individuals. Since the wave function itself is a function of individuals, when it transitions from one state to a new state, it can be expressed as the product of two functions, namely the wave function multiplied by a transformation function.
Next, let's introduce the concepts of gauge potential and gauge field strength. The most abstract yet simplest explanation involves calculus: gauge potential is the integral, and gauge field strength is the integrand. Consider an antiderivative, which is the indefinite integral of a function. The integral represents the potential of the antiderivative, and by differentiating this potential, it returns to the original function, which is the field strength. Note that the potential here is an indefinite integral, with an arbitrary constant term called gauge freedom. When differentiating to find the field strength, the constant term vanishes because the derivative of a constant is zero. Thus, the transformation from potential to field strength is a many-to-one mapping rather than a one-to-one mapping. This explanation was provided by Professor Z. J. Liu from Peking University (personal communicaton).
Gauge potentials cannot be directly compared. For example, the strength and preparation of two test-takers in a competitive standard educational test cannot be directly compared. What can be directly compared are the exam performances and scores, which represent the gauge field strength. The mathematics behind gauge field theory is based on the theory of fiber bundles in differential geometry. Simply put, at each point on the base manifold, there is a fiber extending, called the internal space of that point, or the potential space, or the preparation space. Points on the fiber can be called potential points. Potential points on one fiber cannot be compared to potential points on another fiber. However, each point on the base manifold has a small neighborhood, and the neighborhoods of two points have an overlapping part. There is a reversible mapping from the potential point on one fiber to the point on the overlapping part of the neighborhood. Suppose an exam is given in the overlapping part of the two points’ neighborhoods. The exam results are directly comparable; thus, the performance on this exam maps a potential point on one fiber to a point on the overlapping part of the neighborhood, and then from that point, it maps back to a potential point on the other fiber. In other words, an exam transforms a potential point on one fiber to a potential point on another fiber. This transformation is called a gauge transformation, and the exam is called a gauge function.
At the global level, gauge transformations are referred to as first-class gauge transformations, while at the local level, they are referred to as second-class gauge transformations. Gauge field theory requires both types of gauge transformations to be conformal to the transformation coefficients, as these coefficients represent a mathematical symmetry group. This is not a straightforward matter and requires introducing two new concepts: gauge fields and covariant derivatives.
This section using gauge field theory and fiber bundle theory tells us that citizens' thoughts and psychology cannot be directly compared, but only their speech and behavior can be directly compared. However, the latter can reflect the former. This is also why laws and regulations only regulate citizens' speech and behavior, as these involve public matters. At the same time, it tells us that thoughts and psychology, as gauge potentials, can influence citizens' speech and behavior and should not be neglected. Readers familiar with physics know that Maxwell, Bohm, and C. N. Yang have repeatedly emphasized the role of gauge potential. Similarly, Descartes, an earlier thinker on gauge potential ideas, expressed the thought "I think, therefore I am."
5.5. Gauge Fields and Covariant Derivatives
If symmetry is the soul of gauge field theory, then gauge fields are certainly the necessary path to achieving symmetry, meaning that gauge fields ensure the realization of symmetry. In this sense, the symmetry is referred to as gauge symmetry. For citizens, a gauge field is similar to a tax form from the tax bureau—balancing the accounts of overpayments and underpayments. It’s like a detailed record of debts and credits between people, with clear distinctions of obligations. In the market, it means that transactions are settled immediately—money is exchanged for goods. Symmetry, gauge fields, and covariant derivatives are all essential mechanisms for an ideal society.
The essence of gauge transformations lies in their conformality, meaning that the form of the equations remains unchanged before and after the transformation. This requires first transforming the gauge potential, and then differentiating the transformed gauge potential, which effectively transforms the gauge field strength as well. This field strength transformation must maintain the form of the gauge potential transformation. Specifically, when the wave function transitions from one state to another, a transformation coefficient, which is a complex number (or a complex matrix), is multiplied on the left side of the wave function. The conformality requirement of gauge transformations is that after differentiating the wave function with the transformation coefficient, the original transformation coefficient must remain independently multiplied on the left side of the derivative of the wave function. This transformation coefficient acts like a guard, first standing on the left side of the wave function and then on the left side of the derivative of the wave function, maintaining its position and appearance. This guard is called a symmetry group.
At the global level, the world is assumed to be flat and everyone is equal. Therefore, first-class gauge transformations do not require gauge fields. Recall that the transformation coefficient is a unit complex number, and its exponential representation with a phase is a constant, so this exponent is also a constant. When differentiating, according to differentiation rules, this constant coefficient is first factored out, followed by the derivative of the wave function, maintaining conformality as the classical derivative handles the job.
However, at the local level, the pursuit is of fair rules. The classical derivative loses its conformal property here. Since individual differences need to be reflected, the phase of the transformation coefficient is a function that varies with individual citizens, making the transformation coefficient itself a function. Consequently, the result of the gauge potential transformation is the product of two functions: the transformation function and the wave function. When applying classical differentiation, the chain rule is used, resulting in two terms. The first term treats the transformation function as a constant and factors it out, then multiplies it by the derivative of the wave function. The second term treats the wave function as a constant and factors it out, then multiplies it by the derivative of the transformation function. The first term is what we want, while the appearance of the second term disrupts conformality and must be eliminated.
Therefore, at the local level, when performing second-class gauge transformations, the concept of “covariant derivative” needs to be introduced, defined as follows:
The idea is that when differentiating the wave function, the changes must be coordinated across all individuals. To achieve this, the covariant derivative is defined as the classical differential operator plus a complex imaginary component, which is composed of the coupling constant and the gauge field. The gauge field is defined pointwise, and the formula is as follows:
The meaning is that the gauge field of the new state equals the gauge field of the original state minus an imaginary part. This imaginary part is given by the reciprocal of the coupling constant multiplied by the classical differential of the phase carried by the transformation coefficient function.
When performing a second-type gauge transformation at the local level, the covariant derivative is applied to the product of the transformation function and the wave function. The derivation process involves first expanding the covariant derivative, then expanding the gauge field. As a result, the transformation function stands as a guard on the left, and the covariant derivative of the wave function is on the right, achieving the requirement for conformal invariance. In mathematical terms, when the gauge potential transforms from one state to another, it is expressed as:
To calculate the gauge field strength, you need to perform the corresponding gauge transformation so that
Here, the covariant derivative is defined as , where the gauge field is defined as . We note that the transformation function Just like the previously mentioned guard, after performing the potential and field strength transformations, it remains at the front of the state, which is what conformality means. For a complete derivation of this gauge transformation, see the appendix at the end of this paper.
In summary, at the local level, to achieve local symmetry, the phase changes in the wave function caused by individual differences need to be balanced by the gauge field. From the definition of the gauge field, the difference between the gauge field at one point and another is exactly the classical derivative of the wave function phase change, that is, its rate of change. The wave function phase is the internal dynamical phase of the system, while the gauge field provides an external non-integrable factor, also known as the geometric phase. In the context of psychology, individual differences among citizens need to be compensated by society to balance the differences. This is an idealized state where local symmetry is a fairness demand under the assumption of equal conditions for all.
The covariant derivative and gauge field are frequently psychologicalized environmental structures. For example, when dividing housing units or evaluating job titles, you might reflect your family's specific difficulties and unique situation to the unit leader. This is discussing individual differences. You expect the leader to help resolve your issue, and this resolution is the gauge field. Your request is a fairness demand, with the expectation that your situation is treated equivalently to others, and the principle of equal opportunity used by the leader is the covariant derivative. Later, we will discuss from the perspective of welfare economics that the covariant derivative implies that the rate of common prosperity among people is coordinated. The gauge field signifies social compensation for individual differences. Social compensation comes at a cost and requires a fiscal budget, which is funded by taxes, and paying taxes is a citizen’s duty. This is a civic expression of the gauge field and covariant derivative.
In
Section 6 of this article, we will discuss the connection to general relativity, where it is assumed that the world is curved, meaning people are not born equal. We will introduce the Einstein equivalence principle, which describes the equivalence between conditions of inequality at birth and fairness achieved through individual effort.
The next section will introduce gauge symmetry groups and the gauge principles that describe the relationship between global and local symmetries.
5.6. Symmetry Groups and Gauge Principle
Group theory is crucial in quantum field theory because symmetries are characterized by group theory. If you don't know what a gauge symmetry group is, you won't understand what gauge theory is doing. A group is one of the simplest algebraic structures: easy to understand but not easy to remember. From a cognitive perspective, this is because the mathematics taught in primary and secondary school is relatively complex. Primary and secondary school mathematics makes us familiar with the concept of fields in mathematics, such as the field of natural numbers, the field of rational numbers, as well as the fields of real numbers and complex numbers. The definition of a field involves two operations. A field is a set where the elements are closed under both addition and multiplication, and each operation has an identity element, namely 0 for addition and 1 for multiplication; each element has an inverse. Additionally, both operations satisfy the commutative and associative laws. The definition of a group involves a single operation, multiplication, an identity element, and an inverse element; it only needs to satisfy the associative law, which makes it structurally half of a field. For example, This is a symmetry group with only one generator.
In 1987, I took a course in cognitive linguistics using a textbook that was newly published at the time by Professor George Lakoff, titled, Women, Fire, and Dangerous Things: What Categories Reveal About the Mind, published by the University of Chicago Press. The book proposed a cognitive semantic model that emphasizes the central function of metaphors. According to Lakoff, people acquire concepts not starting from the simplest or the most complex, but from typical concepts. We became familiar with the concept of domains in elementary and middle school, making it a typical concept in our minds about algebraic structures. Therefore, even though the definition of a group is simple, it can make the acquisition of the concept more difficult. Encouragingly, you have already learned complex mathematical structures like number domains in elementary and middle school. Remembering something as simple as a group, which is particularly useful, should be a leap you can easily make.
Earlier, we discussed the algebraic definition of a group; a geometric explanation might be more intuitive. Consider the unit circle in the complex plane, where each point is a unit complex number. All the points on this unit circle form a group, known as the unitary group. Each pair of unit complex numbers can be connected by two lines to the origin, and the angle between them is called the phase difference. Each unit complex number has its natural exponential representation, with the phase being the imaginary part of this representation. At the local level, as mentioned in
Section 4.5, this phase is a phase function. In the definition of a gauge field, the difference in gauge fields between two points is the classical derivative of this phase function's displacement.
Multiplying complex numbers is equivalent to adding their phase angles in the exponential representation. Since the phase angles add up and the result corresponds to a point still on the unit circle, multiplication is closed, and it naturally satisfies the group definition's associative law. Moreover, since exponentiation corresponds to adding phases, this unitary group also satisfies the commutative law, which is called an Abelian group. Groups that do not satisfy the commutative law of multiplication are called non-Abelian groups. Not all multiplications satisfy the commutative law; for example, matrix multiplication does not. When Heisenberg discovered the uncertainty principle, he found that position and momentum displacements did not satisfy commutation relations, and his mentor immediately realized this was matrix mechanics, the precursor to quantum mechanics.
In
Section 4.5, we went to great lengths to explain gauge transformations, especially the second type of gauge transformations at the local level, introducing gauge fields and covariant derivatives, all to ensure that gauge transformations are conformal. Conformal means ensuring that the gauge coefficient independently stands on the left of the wave function and then independently stands on the left of the wave function's covariant derivative. This gauge coefficient is naturally represented as a unit complex number. Why is the independence of this exponent so sensitive? Because it represents a symmetry that is expressed by a mathematical group called the gauge symmetry group.
There are many different groups in mathematics, forming a large family. The most commonly used group in gauge field theory is the unitary group, which is called the unitary group in physics. For example, quantum electrodynamics gauge theory satisfies the U(1) group, related to electromagnetic force. Quantum chromodynamics satisfies the SU(3) group, related to the strong force. Isospin dynamics satisfies the SU(2) group, related to the weak force. The electroweak model satisfies the U(1) group plus the SU(2) group, related to both electromagnetic and weak forces. The symbols and numbers of groups are used here; further explanation will follow.
SU refers to the special unitary group. To understand the concept of a group, two key concepts are foundational representation and generators. Generally speaking, in SU(n), the number n represents the number of basic representations; in physics, it refers to the number of charges.
For example, quantum electrodynamics has only one charge, and its gauge symmetry group is U(1). Quantum chromodynamics has three types of color charges, and its gauge symmetry group is SU(3). The number of generators is calculated from the number of basic representations. When n equals 1, there is only one generator. When n is greater than 1, the number of generators is equal to . For instance, SU(2) has three generators, and SU(3) has eight generators. The number of generators is crucial in gauge field theory because it determines the number of gauge fields needed. For example, isospin dynamics satisfies the SU(2) group and requires three gauge fields. Quantum chromodynamics satisfies the SU(3) group and requires eight gauge fields.
The famous Standard Model of particle physics satisfies the U(1) and SU(2) and SU(3) groups, unifying three of the four fundamental forces of nature: electromagnetic, strong, and weak forces, with only gravity remaining outside. In
Section 5 of this paper, when discussing the psychological phase of life, we will apply general relativity to introduce psychological gravity. Scientific development has a certain degree of randomness. I have a feeling that Einstein's ideal of a unified field theory might be realized in psychology before it is in physics. This idea will be explained in
Section 4.7.
While studying gauge field theory, I was puzzled. The second type of gauge transformation at the local level seems substantial and meaningful, while the first type of gauge transformation at the global level can be conformal using only classical differentiation, which seems somewhat thin. Why is it also considered a type of gauge transformation? The academic principle here is the gauge principle, which controls gauge field theory. The gauge principle states that without global symmetry, there is no local symmetry; in other words, if the first type of gauge transformation does not hold, then the second type of gauge transformation will not hold either. For example, in standard educational exams, if questions are leaked before the exam, global symmetry is lost. In such a case, no matter how the grading is done, local symmetry among the examinees cannot be achieved. Similarly, if there is insider trading in financial markets, global symmetry is lost. In such a case, no matter how the market is regulated, local symmetry among market participants cannot be established. In familiar terms, the gauge principle means: if the nation is not stable, how can the family be secure; if the great river has no water, the small rivers will surely dry up.
5.7. Psychological Pathways
Psychological life is not only a citizen of society but also a native of nature. When Huxley globally promoted Darwin’s theory, he frequently spoke about "the place of humans in the natural world." Citizenship is an important leap for psychological life. The characteristic of the psychological citizen period is the gradual acceptance of increasingly complex external environmental structures. This not only refers narrowly to structures in society and social sciences but also broadly includes structures in nature and natural sciences. Thus, psychological life in the citizen period involves not only primary instincts and psychological effects studied in traditional psychophysics but also a large amount of high-level cognitive psychological functions' stimulation and evolution. Absorbing complex structures is not only an interest of psychological life but also a necessity for survival. Configuring oneself with more complex social and natural structures to ensure survival of the fittest is a motive for making psychological life more vigorous.
The main thread of this section is the development of Neisser's academic thought, specifically how psychological life accepts and acquires external structures and transforms them into internal psychological structures. The formation of complex psychological structures is a characteristic of psychological development in the citizen period. Neisser’s theory is limited in its discussion of the psychologization process of external structures and selection pathways; this section makes essential improvements in that regard. The mental world is an extraordinarily complex and grand system, unparalleled in its reception and self-organizing functions. Particularly concerning scientific theoretical structures discovered and created by scientists, there are not only primary psychological perception and reception devices but also higher-order psychological language and bionic abilities.
This section provides a brief introduction to the normative field theory structure in physics. Quantum field theory contains many fascinating structures, such as path integrals, Lagrangians, and the principle of least action, which can generate a huge desire for internalization in psychological life, but the author prefers to leave these topics for future discussion. The psychological process is similar to copying a key: first creating a mold by referring to the original key, then using psychological language for conceptualization and structuring. This psychological function advantage can massively streamline scattered psychological effects and tightly structure scattered concepts. This was the original intention of cognitive psychology and the essence of cognitive science. Chaos entropy is a major taboo for mental health; structure and order are the pursuits of psychological life. Schrödinger, in "What Is Life," believed that life is a process of negative entropy. Similarly, science and social order are also negative entropy processes for physiological life. Abiding by laws and acting according to regulations are the true essence of psychological life citizenship. In terms of past popular terminology, this is called "raising awareness," being an enlightened citizen. As the saying goes, it is easy to be a citizen but difficult to be an enlightened citizen.
Below is a case that briefly explains the psychological pathway of the particle physics Standard Model structure mentioned earlier, using the language of mathematical category theory.
It is generally believed that the Standard Model of particle physics consists of three aforementioned symmetry groups plus the Higgs mechanism. The author develops these four structures into four categories. A category is defined by two classes: one for objects and one for morphisms.
The first category uses the U(1) symmetry group as the morphism method. In its object class, quantum electrodynamics is the domain, with market dynamics and reasoning dynamics as the co-domains. Market dynamics and reasoning dynamics are both constructed based on quantum electrodynamics, with a conceptual level fully parallel to quantum electrodynamics. All three are single-charge systems sharing the U(1) symmetry group. In market dynamics, intentionality carries market charge, cognitive field serves as the magnetic field, and value function acts as the gauge degree of freedom, and so on. In reasoning dynamics, intentionality carries logical charge, similarly with cognitive field as the magnetic field. This is a psychologization pathway for quantum electrodynamics.
The second category uses the SU(3) symmetry group as the morphism method. In its object class, quantum chromodynamics is the domain, with sub-economic dynamics and sub-cognitive dynamics as the co-domains. Sub-economic dynamics and sub-cognitive dynamics are both constructed based on quantum chromodynamics, with a conceptual level fully parallel to quantum chromodynamics. All three are three-charge dynamics systems sharing the SU(3) symmetry group. In the two co-domains, psychological impulses are depicted by quarks, achievement impulses and fear impulses are depicted by flavor charges, impulse levels are depicted by quark generations, and consciousness is depicted by gluons. In sub-economic dynamics, Freudian personality theory’s id, ego, and superego are introduced, depicted by three types of color charges. In sub-cognitive dynamics, Plato's three elements of knowledge acquisition—truth-seeking, belief-seeking, and verification-seeking—are also depicted by three types of color charges, and so on. These all outline the psychologization pathway for quantum chromodynamics.
The third category uses the SU(2) symmetry group as the morphism method. In its object class, isospin dynamics serves as the domain, with economic externality dynamics and learning externality dynamics as the co-domains. All three are weak force models and share the SU(2) symmetry group. Further explanation is needed here. Heisenberg discovered that protons and neutrons, as quark bound states, have the same binding mechanism, differing only in one quark. A proton is composed of two up quarks and one down quark, denoted as uud; a neutron is composed of two down quarks and one up quark, denoted as ddu. When a neutron decays into a proton (along with an electron and a neutrino), one of the down quarks (d) transforms into an up quark (u). The force that changes a down quark into an up quark, which means changing the flavor charge of a quark, is known as the weak force. The space where conversions occur between protons and neutrons due to the weak force is called isospin space, and its dynamics are known as isospin dynamics or weak force dynamics. In economic externality dynamics, an economic policy or external force can prompt conversion between achievement impulses and fear impulses. In learning externality dynamics, the importance of an exam or psychological counseling can similarly prompt conversions between achievement impulses and fear impulses. This conversion between two types of impulses is called psychological isospin, with economic externality and learning externality both characterized by the weak force. A notable concept in isospin dynamics is the neutrino, which naturally introduces the concept of "aftertaste" in the co-domains. For example, after buying something, one might feel it was either overpriced or a bargain; after an exam, one might feel the questions were either difficult or easy. These are familiar instances of aftertaste. The concept of aftertaste in the context of a chess move is a term used in Go. The above describes a psychologization pathway for the isospin weak force model.
The fourth category uses the Higgs mechanism as the morphism method. In the object class, the Higgs field interaction serves as the domain, with ordinary rationality as the co-domain. Further explanation is also needed here. The particle physics Standard Model is crafted from gauge field theory and symmetry group language. For over twenty years after Yang and Mills' pioneering paper, it did not attract much attention from theoretical physicists. This was because all the gauge particles defined in the Standard Model, including bosons and fermions, were massless, which was the original meaning of gauge symmetry. Later, Higgs proposed a method to give mass to gauge particles, causing spontaneous symmetry breaking; this method is called the Higgs mechanism. Ordinary rationality, proposed by Yang Yingrui, is entirely characterized by the Higgs mechanism.
Ordinary rationality consists of eight principles: the principle of high choice, the principle of subjective determinacy, the principle of empty decision, the principle of sunk cost, the principle of emotion, the principle of hesitation, the principle of face, and the principle of better life. Ordinary rationality shares three basic properties with the Higgs field. Property one is that it represents the state of lowest vacuum energy with a non-zero expectation value. Property two is that it is a complex scalar inertial system; T. D. Lee pointed out that inertial systems break all symmetries. Property three is that the Higgs field is a degenerate state, not isolatable by observation. Additionally, the Higgs field itself is characterized as a non-unit complex scalar. In its exponential representation, the coefficient is the true Higgs field, and the phase carried on the natural base is called the Goldstone field, which is the emotional field of an ordinary rational person.
Ordinary rationality has the function of causing spontaneous symmetry breaking. The success of any policy depends on the extent to which ordinary rational people accept and support it. The popularity of a new product in the market depends on the level of welcome from ordinary rational people. Here, the result is quality. The above outlines a psychologization pathway for the Higgs mechanism.
Additionally, the mathematics of gauge field theory is fiber bundle theory. In classical fiber theory, the principal bundle carries a symmetry group, and the associated bundle is equipped with an object domain. Current developments allow a category to be attached to the principal bundle, so that the associated bundle can simultaneously carry both an object domain and its co-domain. This is called higher-order gauge field theory. Within this framework, the particle physics Standard Model, economic dynamics, and mental dynamics form a complex unified structure.
To summarize, to argue that an external environmental structure can be formulated in a psychological state, describing its psychological pathway is essential, similar to proving in mathematics or logic, or providing evidence in empirical science. The case provided above is both specific and general, and I believe in its replicability, though the psychological pathways may differ.
6. The Sentiment Phase
What is sentiment? As Du Fu wrote in his poetry: "How I wish there were vast mansions for all to have, to shelter all the cold and weary under one roof, unmoved by the wind and rain, safe as a mountain. Alas! Seeing this solitary house before me, my humble abode alone is broken; if I freeze to death, it is enough!" This is what is called sentiment.
A problem is that the term sentiment seems to lack a direct English translation in dictionaries, relying on contextual interpretation for an appropriate translation. But can sentiment have a scientific definition? Let me whisper a secret: Newton defined physical gravity as acceleration, calling it an algebraic definition; Einstein defined physical gravity as curvature, calling it a geometric definition. The equivalence of these two definitions is the central idea of Einstein's General Theory of Relativity. Sentiment is psychological gravity, a harmonious blend of Newton and Einstein’s ideas, a synthesis of curvature and acceleration. The microcosm of Du Fu's words, focusing on the cold scholar’s dilapidated cottage, represents the geometric curvature of sentiment; the wish for vast mansions represents the algebraic acceleration of sentiment. This, of course, requires further explanation.
Below, 6.1 will explain the similarities and differences between General Relativity and Quantum Field Theory from the perspective of psychological perspectives, that is, the similarities and differences in their psychological pathways. This will also illustrate the similarities and differences between the sentiment period and the citizen period in psychological life. 6.2 provides a psychological pathway for the structure of General Relativity through welfare economics analysis. This content was previously presented in a separate paper. Applying it here will have an effect of efficiency. 6.3 introduces a direct psychological pathway for the structure of General Relativity. The key is to introduce the concept of psychological advantage, which considers psychological advantage as a scarce resource, and the pursuit of psychological advantage as one of the inherent natures of social beings, thus introducing a competitive mechanism into the psychological world. From an ethical perspective, sentiment is beautiful; from an economic perspective, sentiment is utilitarian; from a psychological perspective, sentiment is gravitational. There are two versions of the equivalence principle; we will see that the first version reflects Freud’s theory of complexes, while the second version reflects Yang’s theory of sentiment. The latter is an evolutionary cognition of the former.
6.1. The Curved World
Around the time of the global financial crisis in 2007, two bestsellers were published. Before that, the book was titled "The World is Flat" [
4]; after that, it was titled "The World is Curved" [
11]. I had read a Harvard physicist Lisa Randall's book, "Warped Passages" [
8], and was deeply impressed. The mathematics of Special Relativity is Minkowski space, which is a flat space. The mathematics of Quantum Mechanics is Hilbert space, which is also not a curved space. Quantum Field Theory, which integrates Special Relativity and Quantum Mechanics, has a mathematical background space that is either Minkowskian or Hilbertian, thus remaining smooth. In contrast, the mathematics of General Relativity is Riemannian space, which is a curved space. For the general reader, the specifics of these mathematical spaces are less important than what this means for psychological life theory. With a flat space as the backdrop, the theory presupposes that in the ideal social model, all psychological lives should be born equal—a very appealing ideal. With a curved space as the backdrop, the theory suggests that in social reality, psychological lives are, in fact, unequal—a stark reality. This distinction also roughly outlines the difference between the citizen phase and the sentiment phase in psychological life.
It is now generally believed that Quantum Field Theory and General Relativity are intricately connected. For example, Nobel laurate C. N. Yang made some insightful analogies [
13]: gauge field strength corresponds to curvature, gauge field corresponds to connection, and so on. Note that these analogies should not be extended indiscriminately; otherwise, Einstein's unified field theory would have been achieved long ago. Riemannian geometry is a part of differential geometry, so General Relativity is considered to embody Einstein's geometric program in theoretical physics. In gauge field theory, the role of the gauge field is to balance the phase changes within the phase space of the wave function. C. N. Yang [
13] discovered that the external phase compensation effect of gauge fields is a geometric phase, called a non-integrable phase factor. This idea was learned from Einstein, with some advancements, called the gauge field program. Some philosophers of science believe that Einstein's geometric program is a special case of the gauge field program. This statement should also not be extended indiscriminately, as it requires mathematical and physical technical support. From the perspective of psychological life, geometricization equals socialization. Concern for social issues and a willingness to work towards solving them represent the psychological state known as sentiment.
Whether in theoretical physics or social sciences, any dynamic theory has its pursuit, which is an ultimate goal, an invariant. In gauge field theory, why gauge transformations must be conformal is superficially about pursuing symmetry, but deeper reasons involve using conformal invariance of the Lagrangian to define the action by taking the minimum value of its integral. In General Relativity, this pursuit is the geodesic, the shortest path between two events in curved spacetime. Economics pursues efficiency, while psychological life theory pursues psychological advantage. The characteristic of the sentiment period is pursuit. This is different from the citizen period, where citizens are required to follow laws, but there is no requirement for citizens to have pursuits.
Princeton physicist John Wheeler once summarized, "Matter tells spacetime how to curve, and spacetime tells matter how to move." Many people do not realize that this is actually a statement of the equivalence principle. Its sentiment expression is that civilization progress leads to social inequality, meaning only a part of people can become rich first, and social inequality tells us to strive for social fairness and common prosperity. How the equivalence principle psychologizes into sentiment is the essence of this section. The commonly discussed patriotism, scientific sentiment, social sentiment, and even religious sentiment are all inherent to the topic.
In summary, gauge field theory is governed by the gauge principle, starting from global symmetry and then considering individual differences in reality, achieving individual welfare covariance through social compensation of the gauge field, thus realizing local symmetry. Accordingly, gauge transformations go from gauge potentials to gauge field strengths. This represents a romantic way of thinking. Li Bai is the immortal poet.
Similarly, General Relativity starts from the gauge field strength reflecting individual differences in reality, that is, curvature, and considers social connections between individuals in reality. Since the background space of society is assumed to be curved, i.e., universally unequal, Cartesian coordinate frameworks in flat spacetime, which extend infinitely, are no longer applicable, meaning that rights and obligations norms of the psychological life citizen period need to be transcended. In the sentiment period, one needs to realistically construct local frames in each individual’s small neighborhood and seek ways to connect between local frames. This is a realist thinking path. True sentiment is essentially realistic. Du Fu is the poet sage.
Li Bai, the Chinese immortal poet, expressed ideals in long and free-spirited poetry, representing the noble spirit. Du Fu, the Chinese poet sage, worried about the reality of life in his poetry, representing the commoner’s sentiment. I am a commoner and am more inclined toward the sentiment of the craftsman.
6.2. Economic Gravity
The economic path to the psychologization of General Relativity involves five key points, summarized as follows:
- (i)
Pareto Efficiency: In welfare economics, Pareto Efficiency is a foundational concept. It refers to a state where social welfare is at an ideal point, meaning no individual's welfare can be improved without reducing someone else's welfare. Pareto Efficiency is unrelated to fairness; in this state, individual welfare can vary widely, with the poor potentially becoming poorer and the rich richer. Considering individual differences, the background space must transition from a general flat space to a curved space, marking the starting point of the connection to General Relativity.
- (ii)
Pareto Path: If we connect all individual welfare levels under Pareto Efficiency in any manner, we get a curve (not unique). This curve is called the Pareto Path. At each point on the Pareto Path, the tangent vector reflects each individual's inclination to improve welfare. These tangent vectors generally point in different directions. However, due to the constraint of Pareto Efficiency, the length of each tangent vector can only be zero. These vectors are mathematically referred to as "iso-vectors." If all iso-vectors are approximately parallel, the Pareto Path becomes the shortest path, or geodesic. Thus, Pareto Efficiency in economics is described by the geodesic in General Relativity.
- (iii)
Pareto Improvement: Pareto Efficiency is an ideal state. In reality, each individual's welfare level will have fluctuation space, termed "Pareto Improvement" in economics. Pareto Improvement reflects the gap between actual welfare fluctuations and the Pareto Path, or geodesic. According to Feynman’s popular explanation, this gap is called "curvature." In General Relativity, gravity is defined by curvature, known as the geometric definition of gravity. Note that in Newtonian mechanics, gravity is defined by acceleration, known as the algebraic definition of gravity.
- (iv)
Equivalence Principle: One of the foundational concepts of General Relativity is Einstein's "Equivalence Principle," which has two layers of meaning. In Newtonian mechanics, there's a formula:
Roughly speaking, curvature here refers to the geometric description of gravitational field density. Einstein was initially troubled by this formula, unable to identify its error until one night before sleep when he realized that although inertial mass and gravitational mass are different, they are equivalent in everyday experience. This is the first layer of the equivalence principle, often illustrated with examples like elevators and free-fall in physics books. In Yang Yingrui’s theory of ordinary rationality, the difference between daily activities (acting) and null decisions (taking a null action) is hard to observe, though they are distinct. In economics, for example, if you take your child to the mall on a hot summer day and pretend to shop to enjoy the air conditioning, while another customer who actually intends to shop hesitates and leaves because of high prices, their mental states differ, but their behaviors appear equivalent.
The second layer of the equivalence principle is that since inertial mass and gravitational mass are equivalent, their ratio can be set to 1, thus eliminating the term in the formula's right-hand side. This achieved Einstein’s fame: acceleration = curvature, meaning the algebraic and geometric representations of gravity are equivalent. In economic terms, the effort to work harder (or less) due to being poor (or rich) reflects this equivalence. Here, poverty corresponds to positive curvature, wealth corresponds to negative curvature, and increased effort means positive acceleration, while reduced effort means negative acceleration.
- (v)
Welfare Space: Welfare space is not flat but curved. Inequality at birth is expressed mathematically as a curved space with irregularities, or in physical language, as an anisotropic physical field. In a curved space, we cannot use our familiar Cartesian coordinate systems or infinite extending flat coordinate axes. Instead, we need to establish local frames in each small neighborhood and explain how these local frames "connect" and "move parallel." This requires the further development of the concept of covariant derivatives, which is the mathematical basis of General Relativity, developed by Einstein over years of effort, known as Riemannian geometry.
Economic gravity, defined as the curvature-based Pareto Improvement, reflects the universal psychological pursuit of welfare improvement. Thus, the above describes a psychologization path of General Relativity.
6.3. Psychological Gravity
Various forms of social inequality, such as welfare structures, can be internalized into psychological life structures. This is an indirect path of psychologicalization. Various forms of social inequality can directly evolve into inequalities within the "social" of psychological life.
People have an inherent preference for pursuing psychological advantage, which is a pursuit of welfare in psychological life and a scarce resource. From international negotiations to interactions with friends, colleagues, and family, many misunderstandings and misjudgments arise from the pursuit of psychological advantage.
Imagine a society of psychological life. Inequalities in the real world reflect into this psychological society in various ways, leading to unequal levels of psychological advantage. Furthermore, suppose the efficiency requirements of social and economic changes are translated into efficiency tendencies within the psychological society. In this ideal condition, psychological advantage should approach a state of Pareto efficiency in psychological welfare, where improving the psychological advantage of one individual cannot be achieved without reducing the psychological advantage of others. This state of Pareto efficiency in the psychological society is unrelated to fairness; that is, some individuals' psychological advantages may become stronger while others' become weaker, leading to psychological inequality. Now, connecting all levels of psychological advantage into a line creates a curved, deformed curve known as the "Pareto Psychological Advantage Path," which is the geodesic of the psychological society.
Similar to the situation in the economic society, each psychological life has intentions to improve its own psychological advantage or welfare. The gap between this intention and the psychological society's geodesic is, in simple terms, the curvature of the curved psychological society, which is the geometric expression of psychological gravity.
As introduced in
Section 6.2, let's revisit the two versions of Einstein's equivalence principle. The first version, also known as the primary version, states that gravitational mass and inertial mass are equivalent. Freud argued that psychological habits, such as inferiority or superiority, dependency or defiance, fear or ambition, are mirror transformations of certain specific external stimuli in the subconscious. This equivalence is called the Freudian complex, such as the Oedipus complex or Electra complex.
The second version of the equivalence principle, which incorporates cognitive awareness, states that the geometric representation of gravity is equivalent to its algebraic representation, meaning curvature (i.e., gravitational field density) and acceleration are equivalent. Concern for social inequality and uneven development is a form of attention to the geometric curvature of society. Having the will to change certain social inequalities or development imbalances and diligently working towards it, whether through words or actions, is a contribution to social progress as an algebraic acceleration. These are two forms of psychological gravity, mutually equivalent. Together, they are referred to as sentiment. The sentiment phase is a time of intense and brilliant psychological life, a splendid chapter of psychological life.






