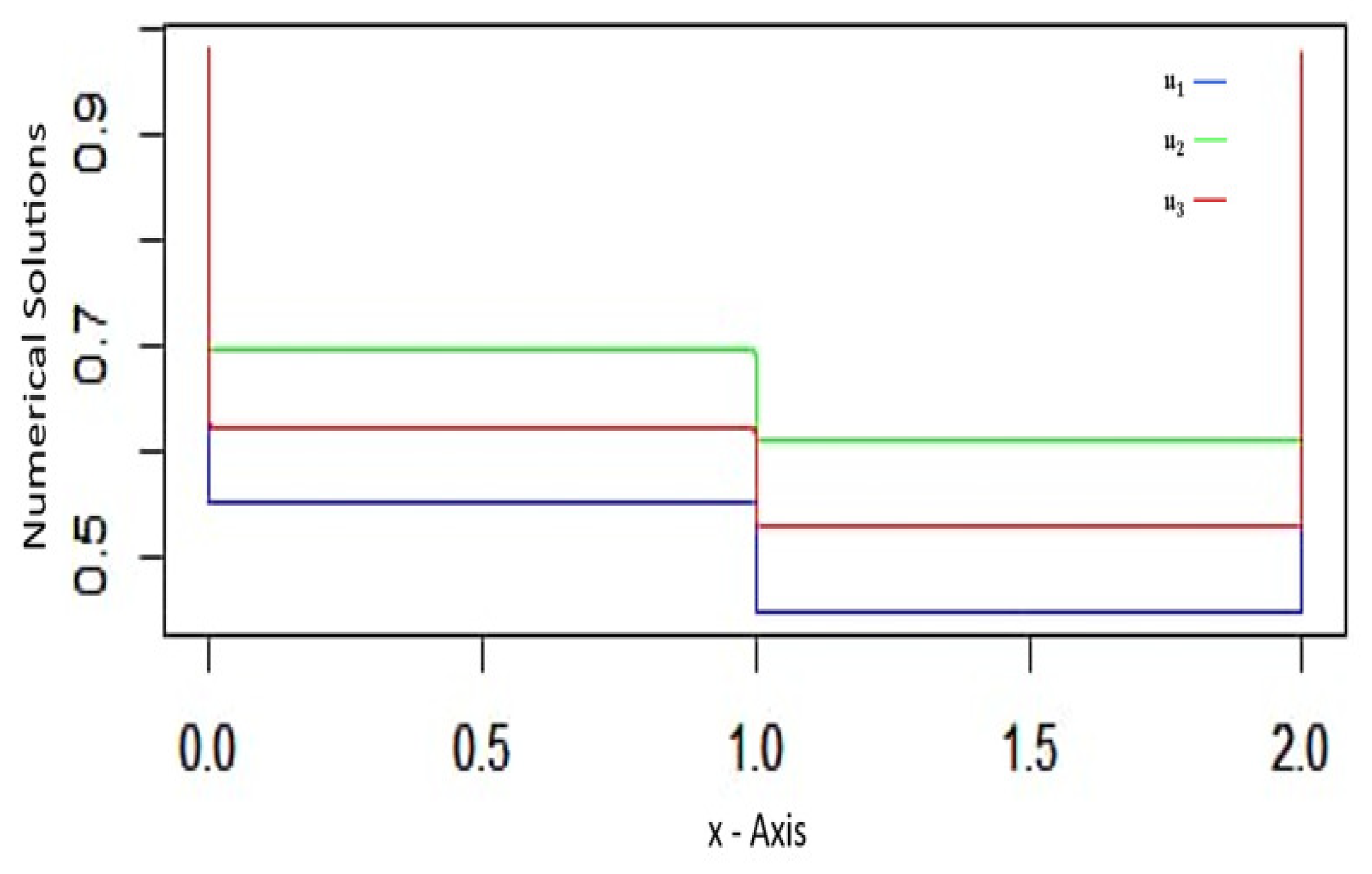
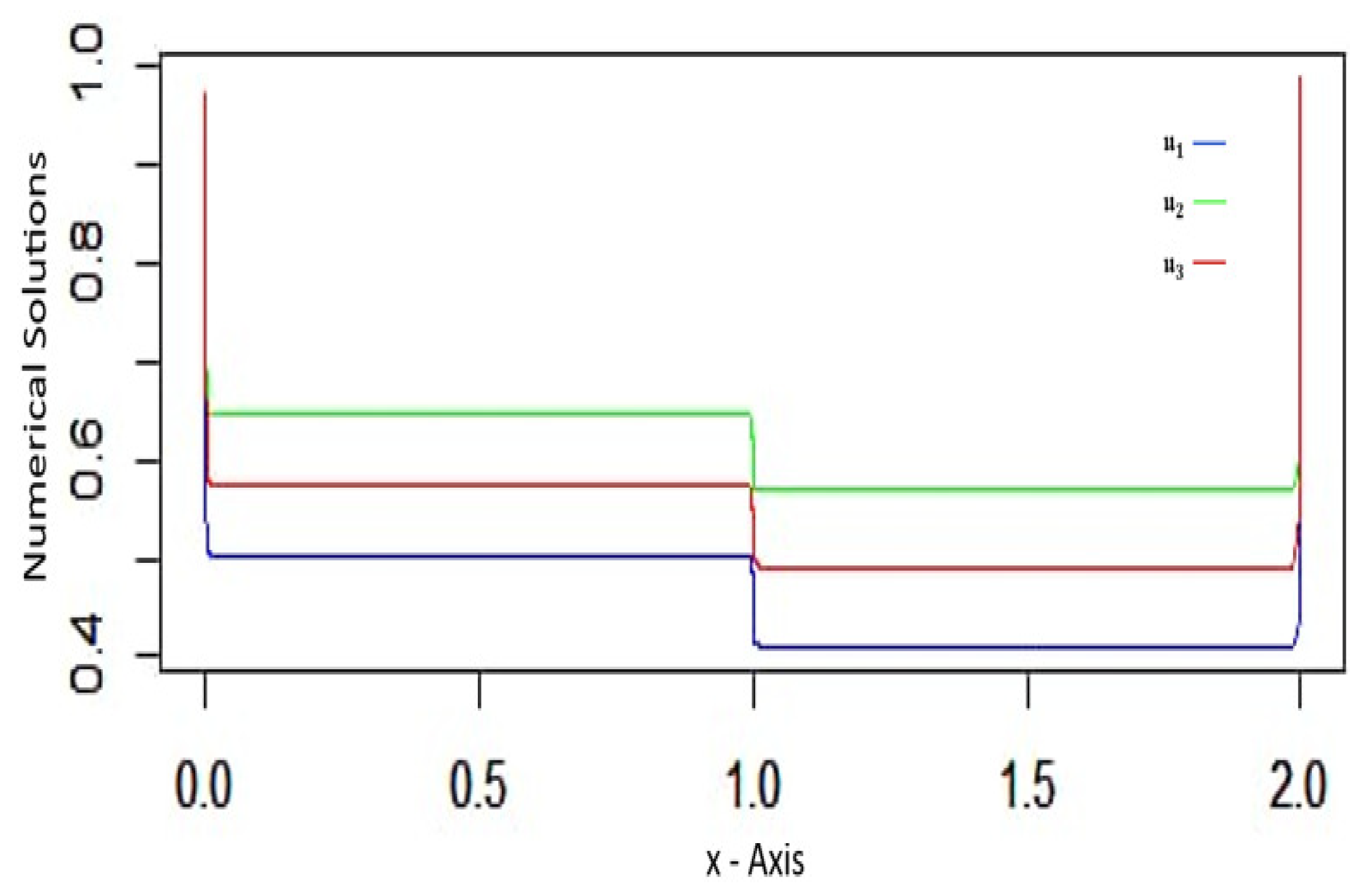
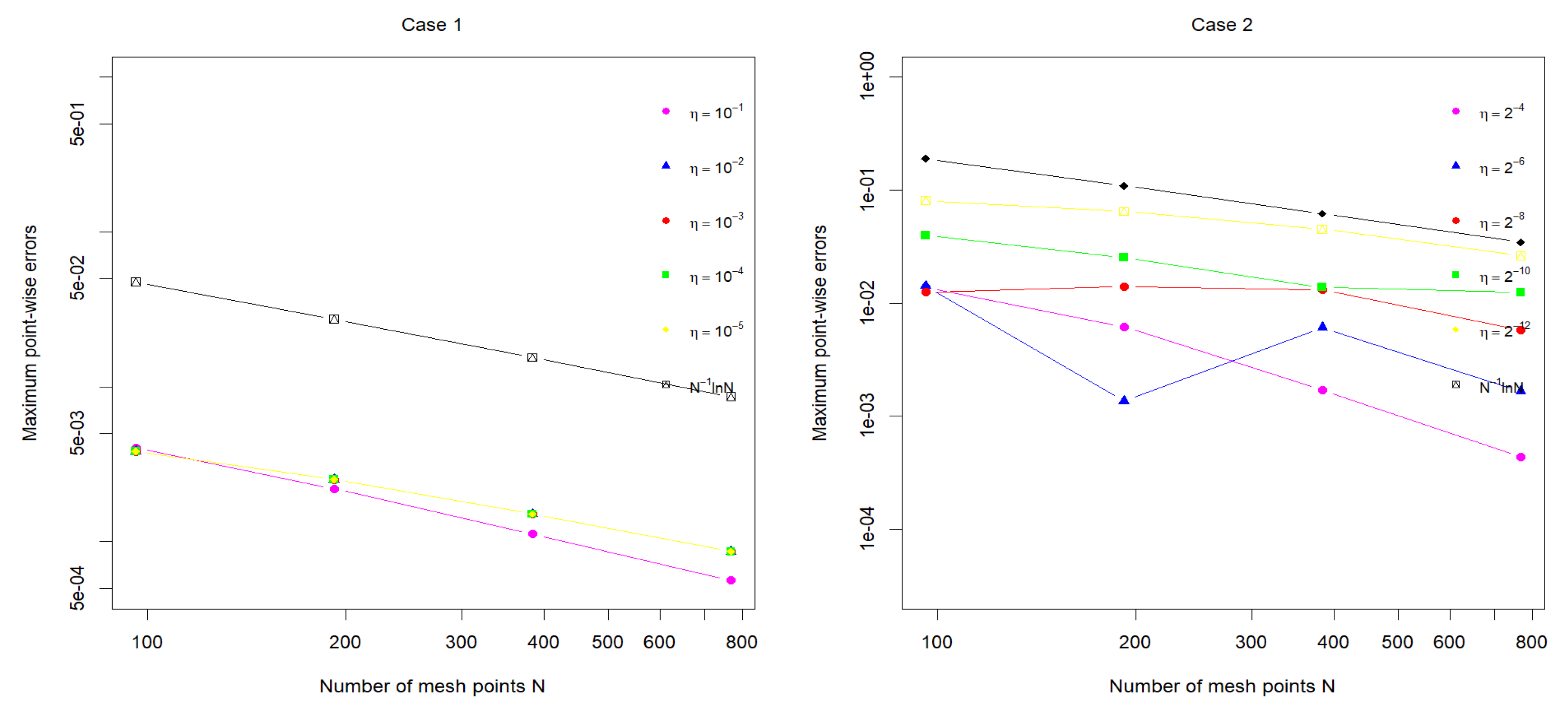
Proof.
Determining the local truncation error
for
. It is established that
. In this case
, from (
39) and (
42),
Using Lemma 11.2, consider the mesh functions,
Provided that the value of
C is sufficiently large, it follows that
Thus,
Similarly,
For the case
,
Similarly,
Thus,
The proof of the lemma is complete. □
The bounds on the error in the singular components
and
are estimated for the case
. These estimates are derived utilizing the mesh functions
, where
, which are defined over
,
Lemma 11.4.
For the case , the layer components and , satisfy the following bounds on ,
Proof. This result can be demonstrated by defining the appropriate mesh functions and and noticing that and . Furthermore, and . Consequently, the discrete minimum principle yields the expected result. The proof of the lemma is complete. □
Lemma 11.5.
Assume that , for . Let and satisfy (22), and satisfy (67) and (68). Then,
Proof. The local truncation error is given by
where
. Since
,the mesh
is uniform, then the value of
. In this instance,
and
.
similarly,
Let the barrier function
given by
on
, where
is a constant and it satisfies
,
The mesh functions described above is inspired by those constructed in [
14]. Now, that
,
,
,
and
. Then, define
. It is easy to observe that
and
. Hence, by applying minimum principle,
Simillarly,
The proof of the Lemma is complete. □
Lemma 11.6.
Let and satisfy (22) , and satisfy (67) and (68). Then,
Proof. The required result is established for each mesh point
by partitioning the interval
as shown in figure

for
. In each of these scenarios, first an estimate for the local truncation error is derived. This is followed by the formulation of a suitable barrier function, designed to capture the essential properties of the solution within a specified domain. By utilizing these barrier functions, the desired estimate is obtained.
Case (a):.
Clearly
. Then, utilizing the standard approach to local truncation through Taylor expansions, error estimates is obtained, which are valid for
and
,
Let the mesh functions be defined for
, where
and
,
Utilizing the minimum principle and barrier function , it has been established that similarly for the interval (1,2),
Case (b):.
The two scenarios considered are
Case (b1): and
Case (b2):.
Case (b1): , this case, the mesh is uniform within the interval
. Consequently, for any
, for
. Then,
Now for
and
, define,
Utilizing the minimum principle and barrier function
, it has been derived that
similarly for the interval (1,2),
Case (b2): , for this case,
, and hence for
, by utilizing the standard approach to local truncation errors in Taylor series expansions,
then,
Now using Lemma 8.1 , it is not hard to derive that
and for
,
Specify
and for
,
Case (c):.
Here are the three scenarios
Case (c1):
,
Case (c2): and
for some
q,
,
Case (c3):.
Case (c1): , since
and the mesh remains uniform over the interval
, it can be concluded that for
,
and hence
Utilizing the minimum principle and barrier function
, it has been derived that
similarly for the interval (1,2),
Case (c2): and
for some
q,
. In this case, since
, the region
, exhibits a uniform mesh points in this region satisfies
, for any point
. By utilizing the approach to local truncation is derived from Taylor expansions,
Now, utilizing Lemma 8.1, it is evident that for
,
and for
,
Now specify, for
,
and for
,
Case (c3):. In the previous arguments of the case (c2), replacing
q by
m and applying the inequality
, the estimates are valid for
. For
,
and for
,
For
, define
and for
,
Case (d):
There are three distinct cases to consider,
Case (d1): ,
Case (d2): and
for some
q,
and
Case (d3):.
Case (d1): . In this case, the mesh is uniformly distributed over the interval
. The corresponding result for this situation is derived in Lemma 11.5.
Case (d2): and
for some
q,
, for this scenario, based on the definition of
, it can be shown that
and by applying analogous arguments similar to Case (c2) lead to the estimates for
. For
,
and for
,
Now define, for
,
and for
,
respectively.
Case (d3): , let
be defined as
. Then, considering the interval
,
Hence,
Thus, for each of the cases, the barrier function is constructed and using minimum principle, it has been derived that
Therefore,
The proof of the lemma is complete.□
The bounds on the error in the singular components
and
are estimated for the case
. These estimates are derived utilizing the mesh functions
, where
, which are defined over
,
with
, for
, for
.
Lemma 11.7.
Let and satisfy (13), and satisfy (67) and (68). Then,
Proof. Assume that
, for
, the local truncation error is given by
where
. Since
, the mesh
is uniform, then the value of
. In this instance,
,
This is established for each mesh point
by partitioning the interval
as follows

for
. In each of these scenarios, first an estimate for the local truncation error. is derived. This is followed by the formulation of a suitable barrier function, designed to capture the essential properties of the solution within a specified domain. By utilizing these barrier functions, the desired estimate is obtained.
Case (a):.
Clearly
then, utilizing the approach to local truncation in Taylor expansions error estimates is obtained, which are valid for
and
,
Case (b):.
The two scenarios considered are
Case (b1): and
Case (b2):.
Case (b1): , this case, the mesh is uniform within the interval
. Consequently, for any
, for
. Then,
Case (b2):, for this case,
and hence for
, by utilizing the standard approach to local truncation errors in Taylor series expansions, the term
then, using Lemma 8.2
Case (c):.
Here are the three scenarios
Case (c1):
,
Case (c2): and
for some
q,
and
Case (c3):.
Case (c1): , since
and the mesh remains uniform over the interval
,it can be concluded that for
,
and hence
Case (c2): and
for some
q,
. Since
, the mesh is uniform in
, which implies that
, for
. By utilizing the approach to local truncation is derived from Taylor expansions, outlined in Lemma 8.2
Case (c3):. In the previous arguments of the case (c2), replacing
q by
m and applying the inequality
, the estimates are valid for
.
Case (d): There are three distinct cases to consider,
Case (d1): ,
Case (d2): and
for some
q,
and
Case (d3):.
Case (d1): . In this case, the mesh is uniformly distributed over the interval
. The corresponding result for this situation is derived in Lemma 11.5.
Case (d2): and
for some
q,
, for this scenario, based on the definition of
, it can be shown that
and by employing arguments analogous to Case (c2), it leads to the estimates for
.
Case (d3): . Let
be defined as
on the interval
. Hence,
and similarly,
. Therefore,
The proof of the lemma is complete.□
To establish the bounds on the error
, the mesh function is defined over
Lemma 11.8.
For the case , the layer components and , satisfy the following bounds on ,
Proof. This result can be demonstrated by defining the mesh functions and . Also, since , . Hence, . Also, for an appropriate choice of C, it follows that . Further, and . Hence, by the minimum principle , and , for . Hence, The proof of the lemma is complete.□
Lemma 11.9. At each point , , for the case .
Proof. The local truncation error is given by
where
. Consider the case
then,
. Hence,
Consider the case
. Hence,
for
, similarly like above
Examine the mesh region . It is known that , then, , For , The proof of the lemma is complete.□
Theorem 11.1.
Let be the solution of (1) and be the solution of (62)-(64). Then, for each mesh point ,
for both of the cases and .
Proof. The proof follows Lemmas 11.3, 11.5,11.7 and 11.9.
 for . In each of these scenarios, first an estimate for the local truncation error is derived. This is followed by the formulation of a suitable barrier function, designed to capture the essential properties of the solution within a specified domain. By utilizing these barrier functions, the desired estimate is obtained.
for . In each of these scenarios, first an estimate for the local truncation error is derived. This is followed by the formulation of a suitable barrier function, designed to capture the essential properties of the solution within a specified domain. By utilizing these barrier functions, the desired estimate is obtained. for . In each of these scenarios, first an estimate for the local truncation error. is derived. This is followed by the formulation of a suitable barrier function, designed to capture the essential properties of the solution within a specified domain. By utilizing these barrier functions, the desired estimate is obtained.
for . In each of these scenarios, first an estimate for the local truncation error. is derived. This is followed by the formulation of a suitable barrier function, designed to capture the essential properties of the solution within a specified domain. By utilizing these barrier functions, the desired estimate is obtained.