Submitted:
29 March 2025
Posted:
01 April 2025
You are already at the latest version
Abstract
Keywords:
Highlights
- Multipoint linear fitting is adopted, and the intersection of fitting lines is used as the cutoff point between the gentle and steep regions of the focusing curve.
- When designing evaluation metrics, considerations were given to the issues of accuracy and robustness of these metrics.
- The method proposed to determine the cutoff point between gentle and steep regions is relatively robust and can adapt to different shapes of focusing curves.
- Provides a theoretical foundation for selecting the optimal focus measure operator and the designing new focus measure operators.
1. Introduction
2. Design of Quantitative Metrics
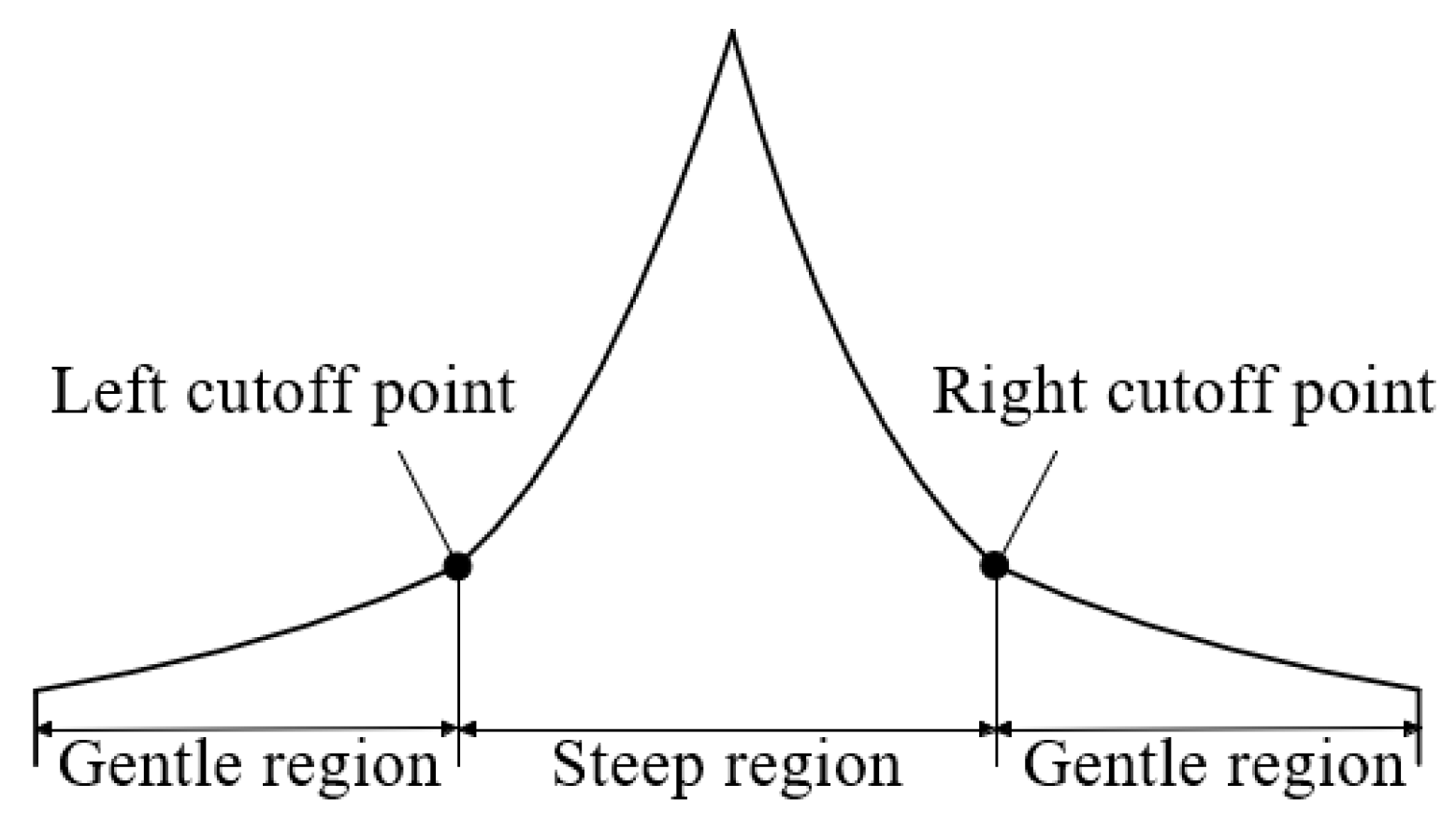
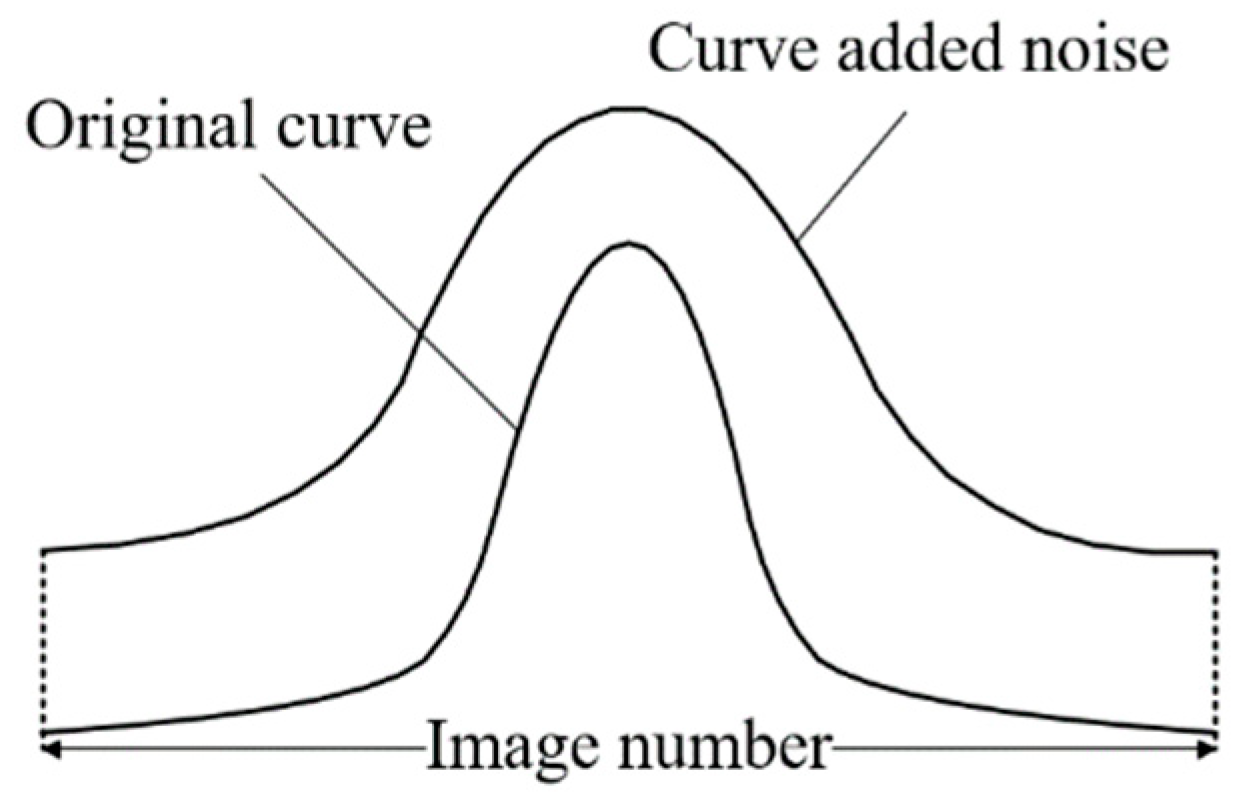
2.1. Selection of the Cutoff Point
2.2. Steep Region Width (Ws)

2.3. Steep to Gentle Ratio (Rsg)
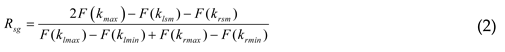
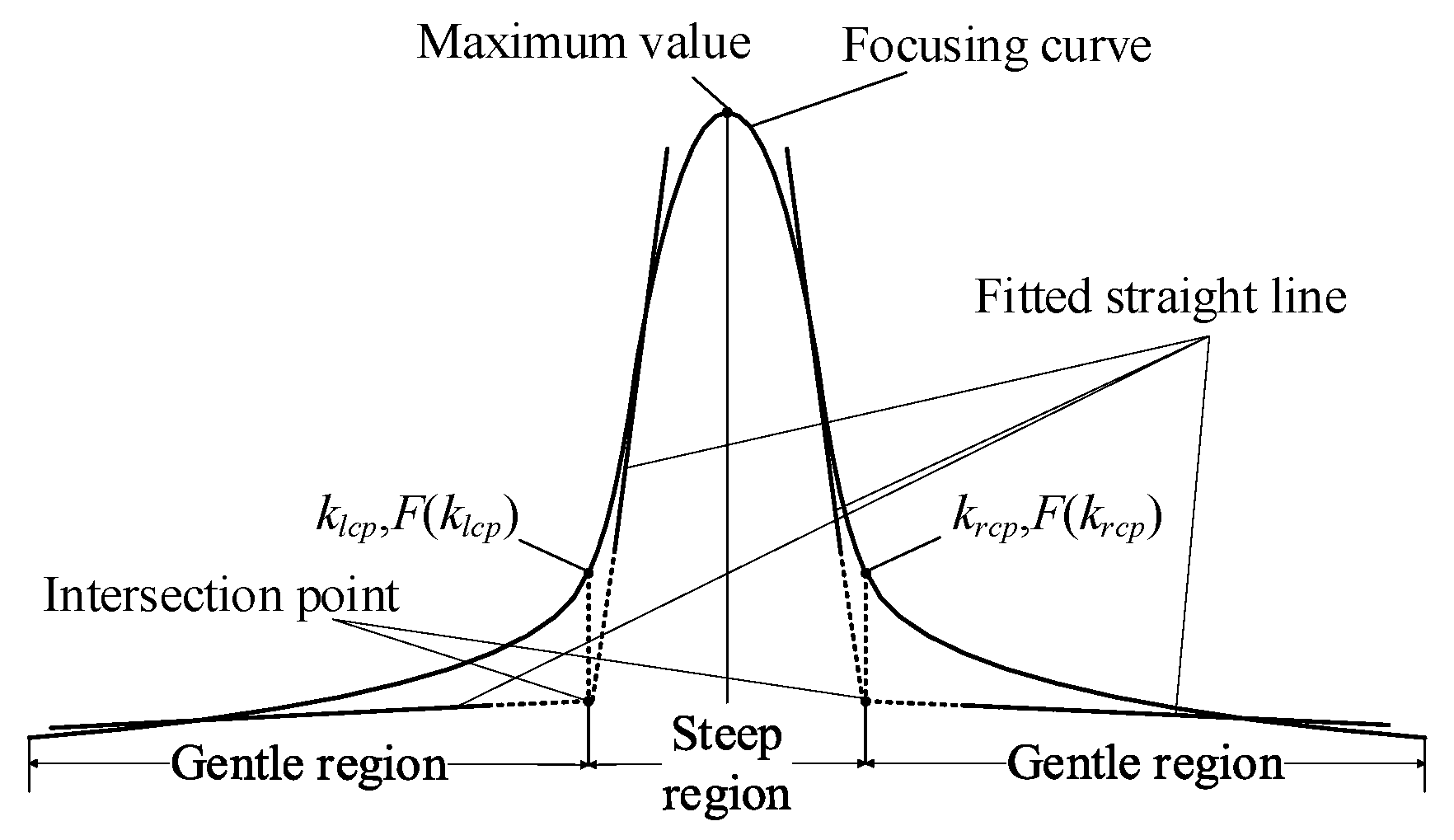
2.4. Curvature at Peak (Cp)

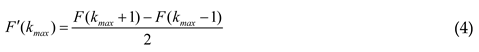
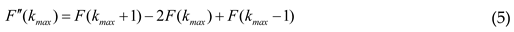
2.5. Relative Root Mean Square Error (RRMSE)
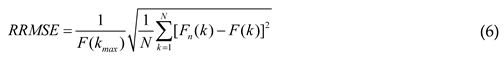
3. Focus Measure Operators
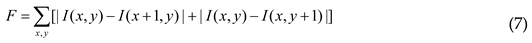
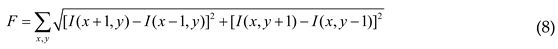




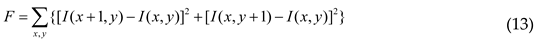
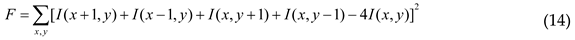
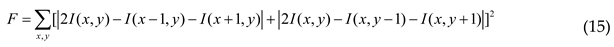

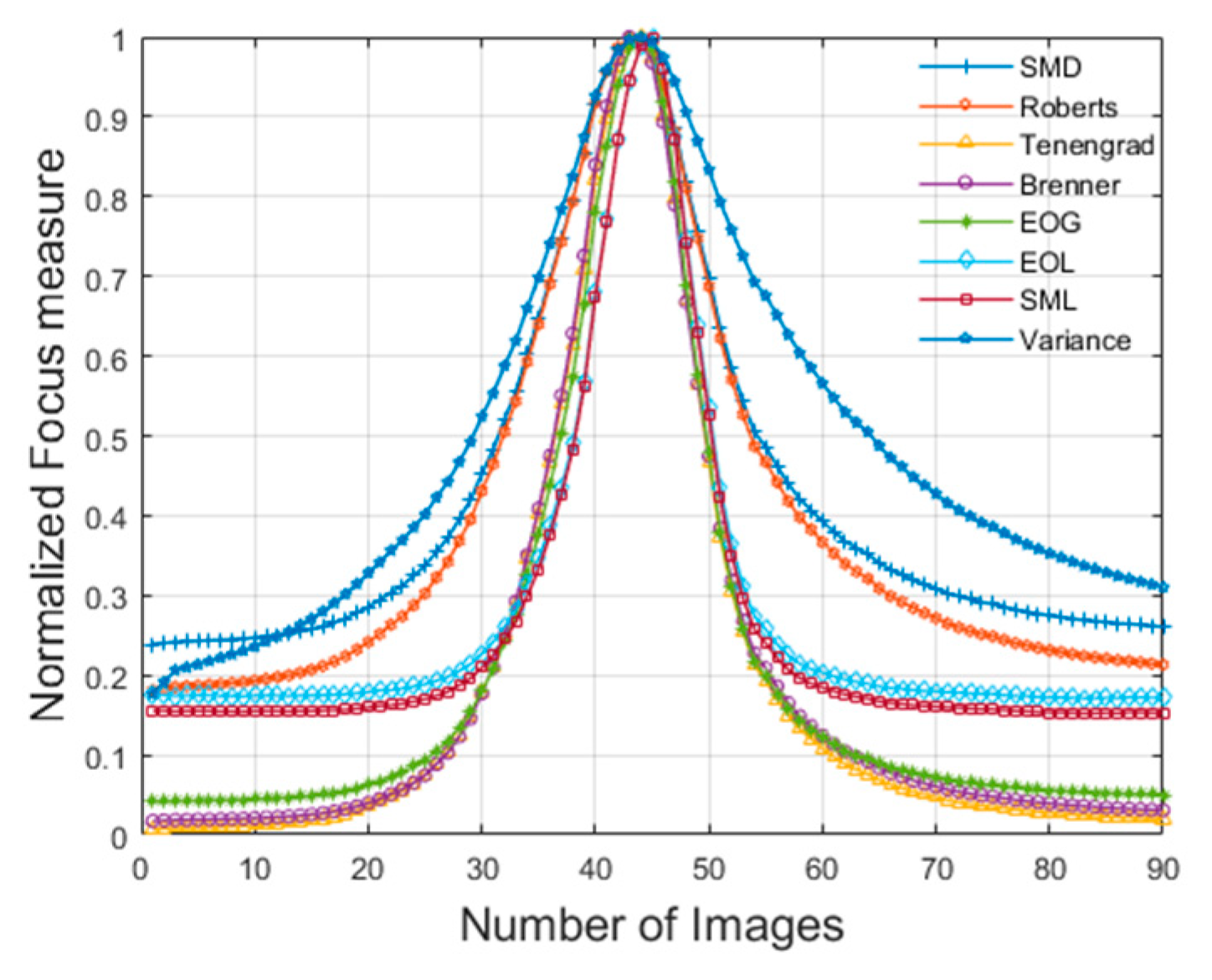
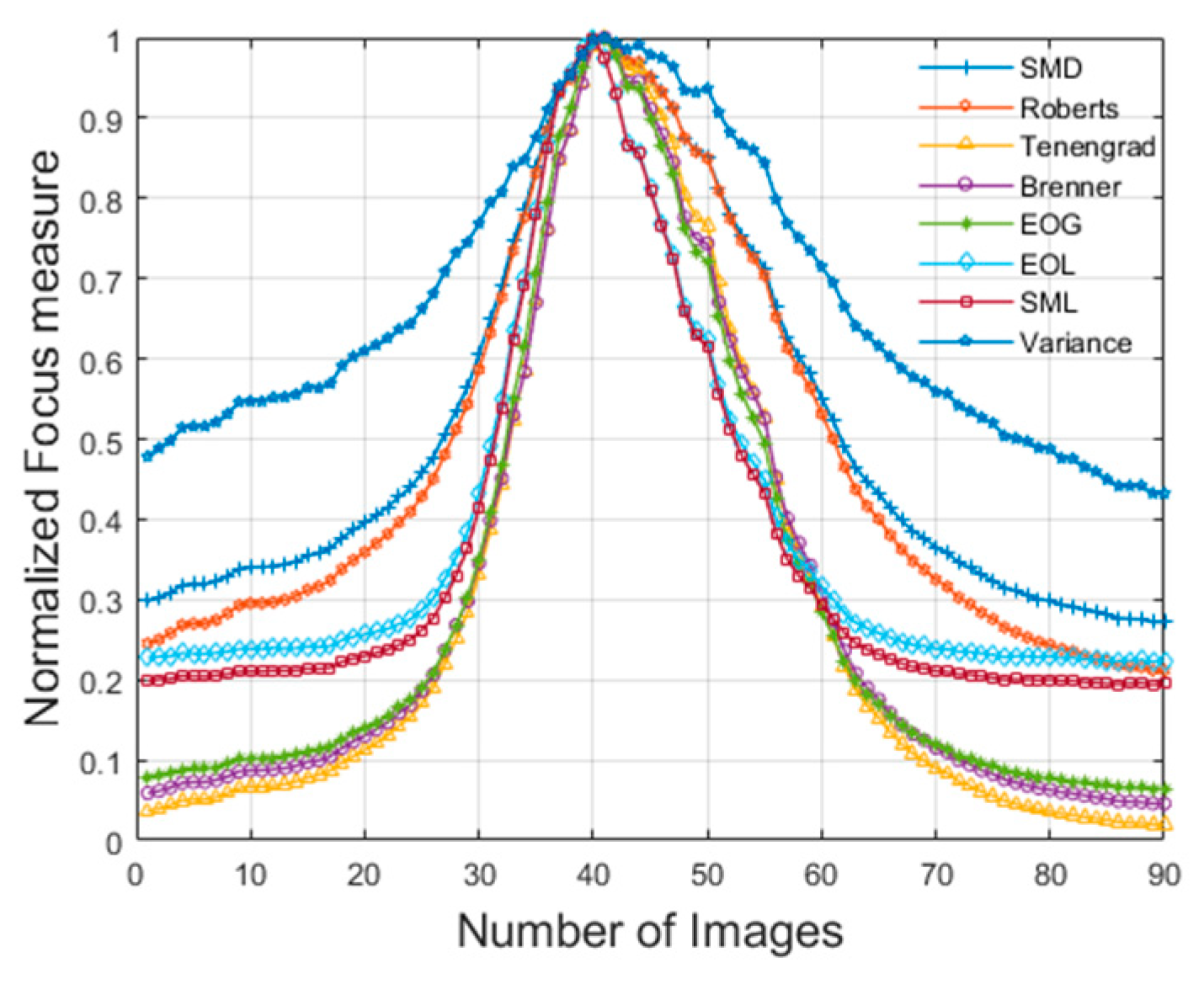
4. Experimental Analyses
4.1. Image Acquisition
4.2. Analysis of Results
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Nayar, S.K.; Nakagawa, Y.J.I.T.o.P.a.; intelligence, m. Shape from focus. 1994, 16, 824–831.
- Groen, F.C.; Young, I.T.; Ligthart, G. A comparison of different focus functions for use in autofocus algorithms. Cytometry 1985, 6, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Duthaler, S.; Nelson, B.J. Ieee. Autofocusing algorithm selection in computer microscopy. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, CANADA, 2005 Aug 02-06, 2005; pp. 419–425.
- Sun, J.; Yuan, Y.; Wang, C. Comparison and Analysis of Algorithms for Digital Image Processing in Autofocusing Criterion %J Acta optica sinica. 2007, 35-39.
- Zhai, Y.; Zhou, D.; Liu, Y.; Liu, S.; Peng, K. Design of Evaluation Index for Auto-Focusing Function and Optimal Function Selection %J Acta optica sinica. 2011, 31, 242–252.
- Pertuz, S.; Puig, D.; Angel Garcia, M. Analysis of focus measure operators for shape-from-focus. Pattern Recognition 2013, 46, 1415–1432. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, Y.; Yin, Y. An Improved Image Sharpness Assessment Method Based on Contrast Sensitivity. In Proceedings of the Conference on Applied Optics and Photonics (AOPC) - Image Processing and Analysis, Beijing, PEOPLES R CHINA, 2015 May 05-07, 2015.
- He, C.; Li, X.; Hu, Y.; Ye, Z.; Kang, H. Microscope images automatic focus algorithm based on eight-neighborhood operator and least square planar fitting. Optik 2020, 206. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, T. Focusing Algorithm of Automatic Control Microscope Based on Digital Image Processing. Journal of Sensors 2021, 2021. [Google Scholar] [CrossRef]
- Sha, X.; Wang, P.; Shan, P.; Li, H.; Li, Z. A fast autofocus sharpness function of microvision system based on the Robert function and Gauss fitting. Microscopy Research and Technique 2017, 80, 1096–1102. [Google Scholar] [CrossRef] [PubMed]
- Ko, P.; Li, D.; Hoenig, P.; Bailey, I.; Rempel, D. Effect of computer monitor distance on visual symptoms and changes in accommodation and binocular vision. In Proceedings of the Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 2009; pp. 1447–1451.
- Brenner, J.F.; Dew, B.S.; Horton, J.B.; King, T.; Neurath, P.W.; Selles, W.D. An automated microscope for cytologic research a preliminary evaluation. The journal of histochemistry and cytochemistry : official journal of the Histochemistry Society 1976, 24, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Dong, J.; Zhong, W.; Wang, G.; Liu, X.; Liu, Q.; Song, X. Motionless shape-from-focus depth measurement via high-speed axial optical scanning. Optics Communications 2023, 546. [Google Scholar] [CrossRef]
- Russell, M.J.; Douglas, T.S. Ieee. Evaluation of autofocus algorithms for tuberculosis microscopy. In Proceedings of the 29th Annual International Conference of the IEEE-Engineering-in-Medicine-and-Biology-Society, Lyon, FRANCE, 2007 Aug 22-26, 2007; pp. 3489–+.
- Fu, B.; He, R.; Yuan, Y.; Jia, W.; Yang, S.; Liu, F. Shape from focus using gradient of focus measure curve. Optics and Lasers in Engineering 2023, 160. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, H.; Jia, P.; Chen, K.; Zhang, X. A novel algorithm for three-dimensional shape reconstruction for microscopic objects based on shape from focus. Optics and Laser Technology 2024, 168. [Google Scholar] [CrossRef]


| SMD | Roberts | Tenengrad | Brenner | EOG | EOL | SML | Variance | |
|---|---|---|---|---|---|---|---|---|
| Ws | 30.18 | 31.82 | 32.19 | 24.44 | 23.92 | 21.21 | 21.34 | 35.83 |
| Rsg | 3.8391 | 3.4109 | 3.0901 | 4.6899 | 5.1242 | 6.6608 | 6.7004 | 2.2664 |
| Cp | 0.0159 | 0.0156 | 0.0153 | 0.0085 | 0.0307 | 0.0303 | 0.0489 | 0.0500 |
| RRMSE | 0.1679 | 0.0756 | 0.0400 | 0.0375 | 0.0949 | 0.4133 | 0.3687 | 0.0041 |
| SMD | Roberts | Tenengrad | Brenner | EOG | EOL | SML | Variance | |
|---|---|---|---|---|---|---|---|---|
| Ws | 40.00 | 40.90 | 41.20 | 36.75 | 36.00 | 31.53 | 31.75 | 41.73 |
| Rsg | 3.4043 | 2.8756 | 2.6686 | 4.7012 | 5.3235 | 6.3045 | 6.2466 | 2.2776 |
| Cp | 0.0123 | 0.0122 | 0.0121 | 0.0091 | 0.0250 | 0.0241 | 0.0381 | 0.0395 |
| RRMSE | 0.1278 | 0.0521 | 0.0247 | 0.0594 | 0.0991 | 0.3998 | 0.3505 | 0.0050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





