Submitted:
02 April 2025
Posted:
04 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theory and Results
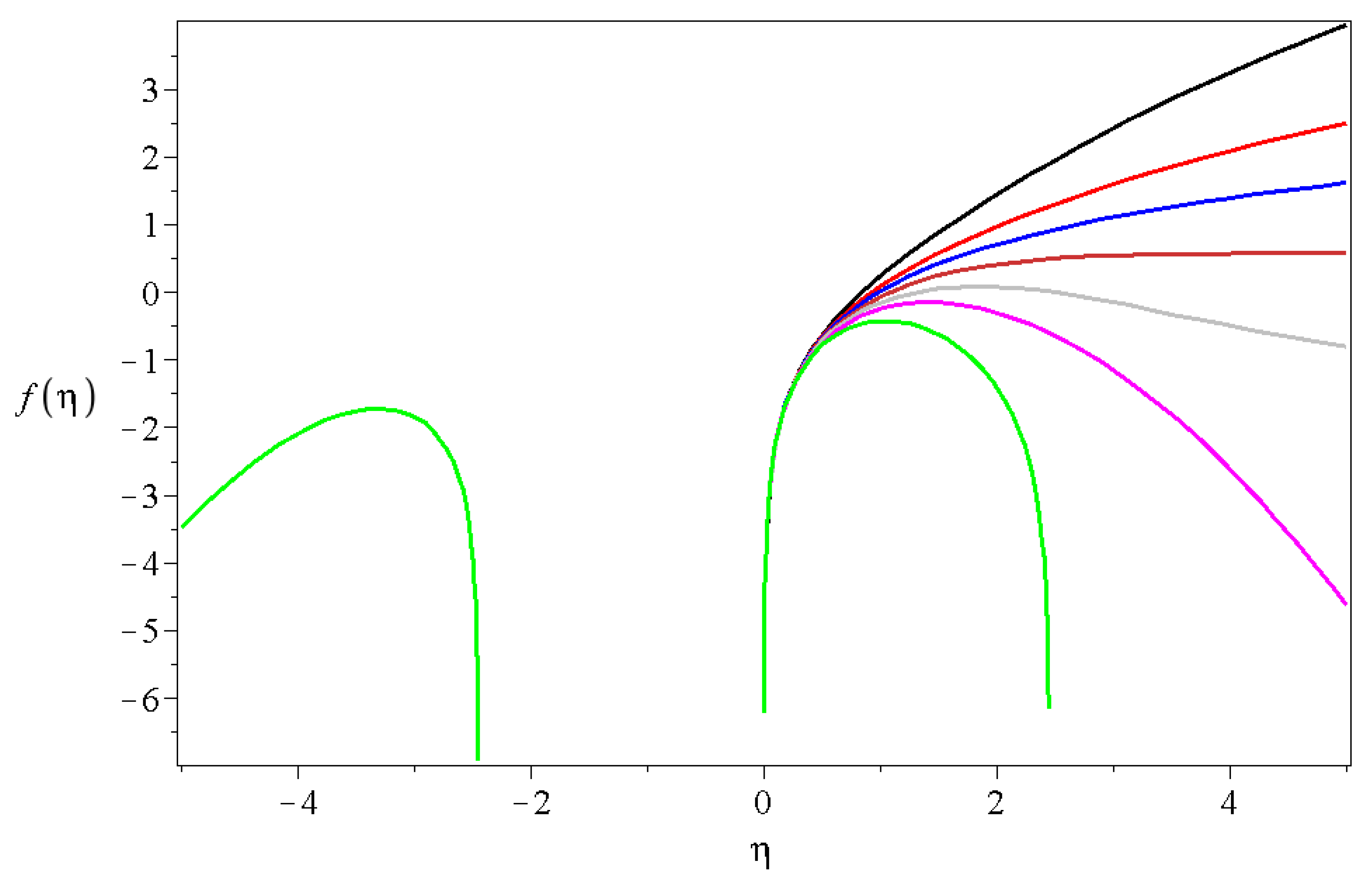
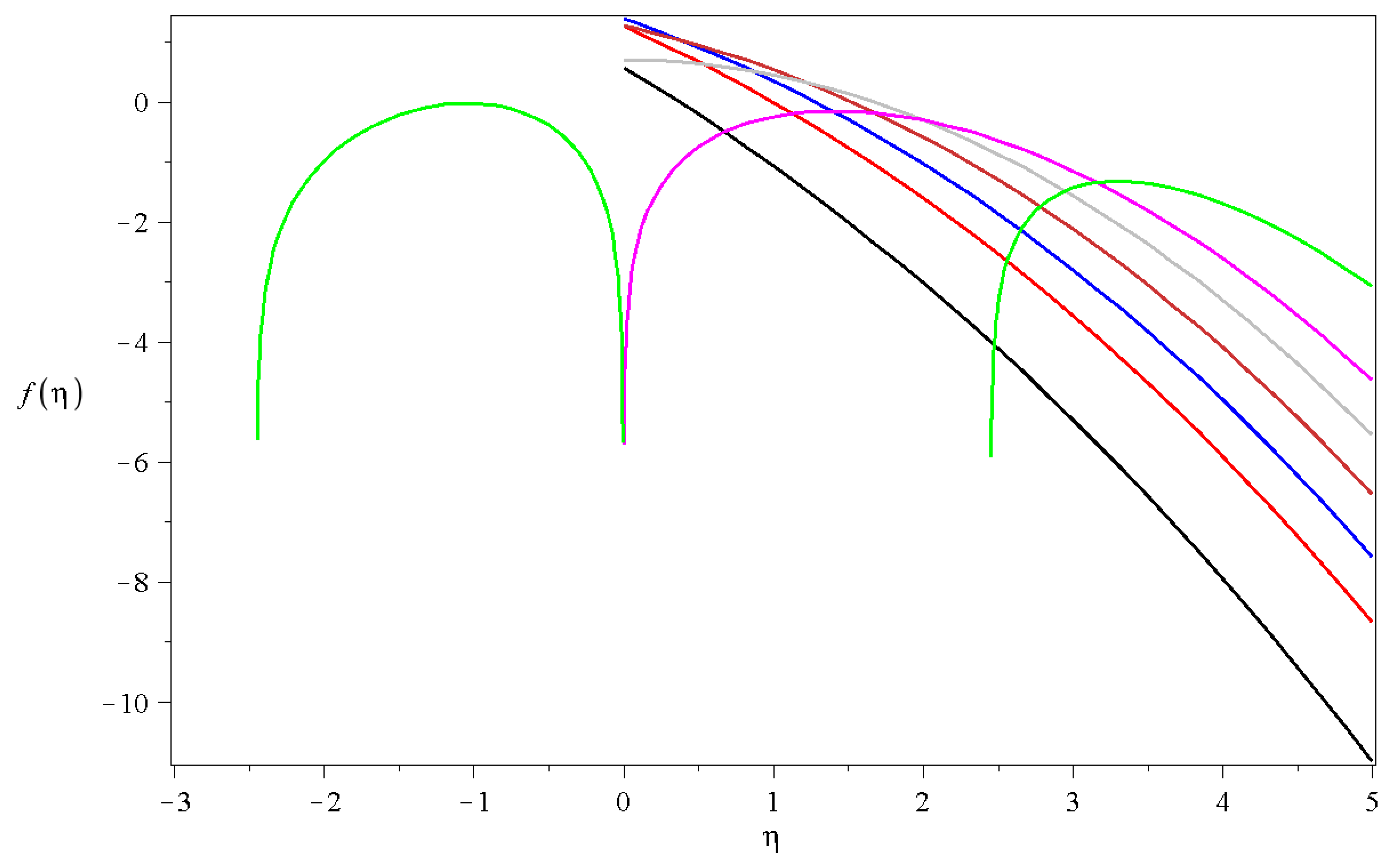
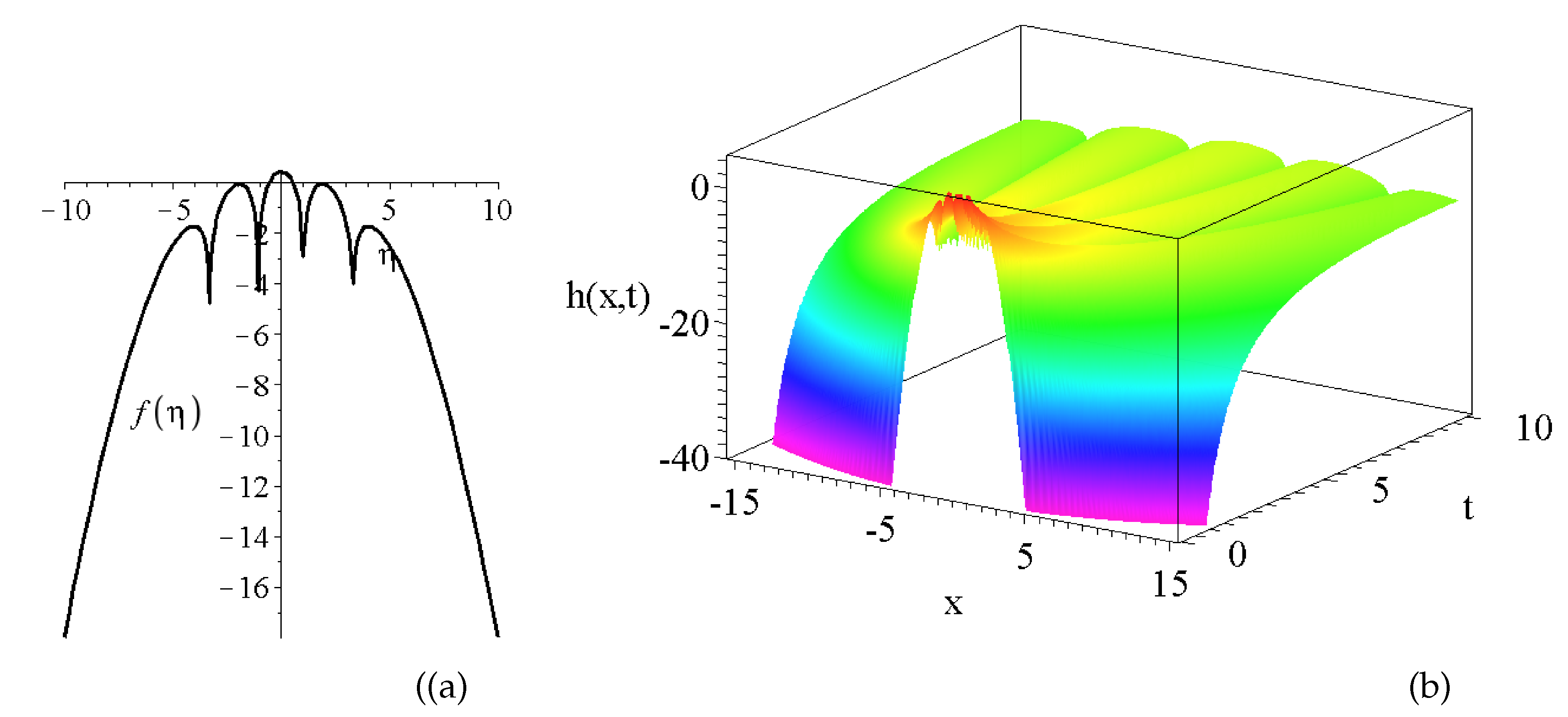
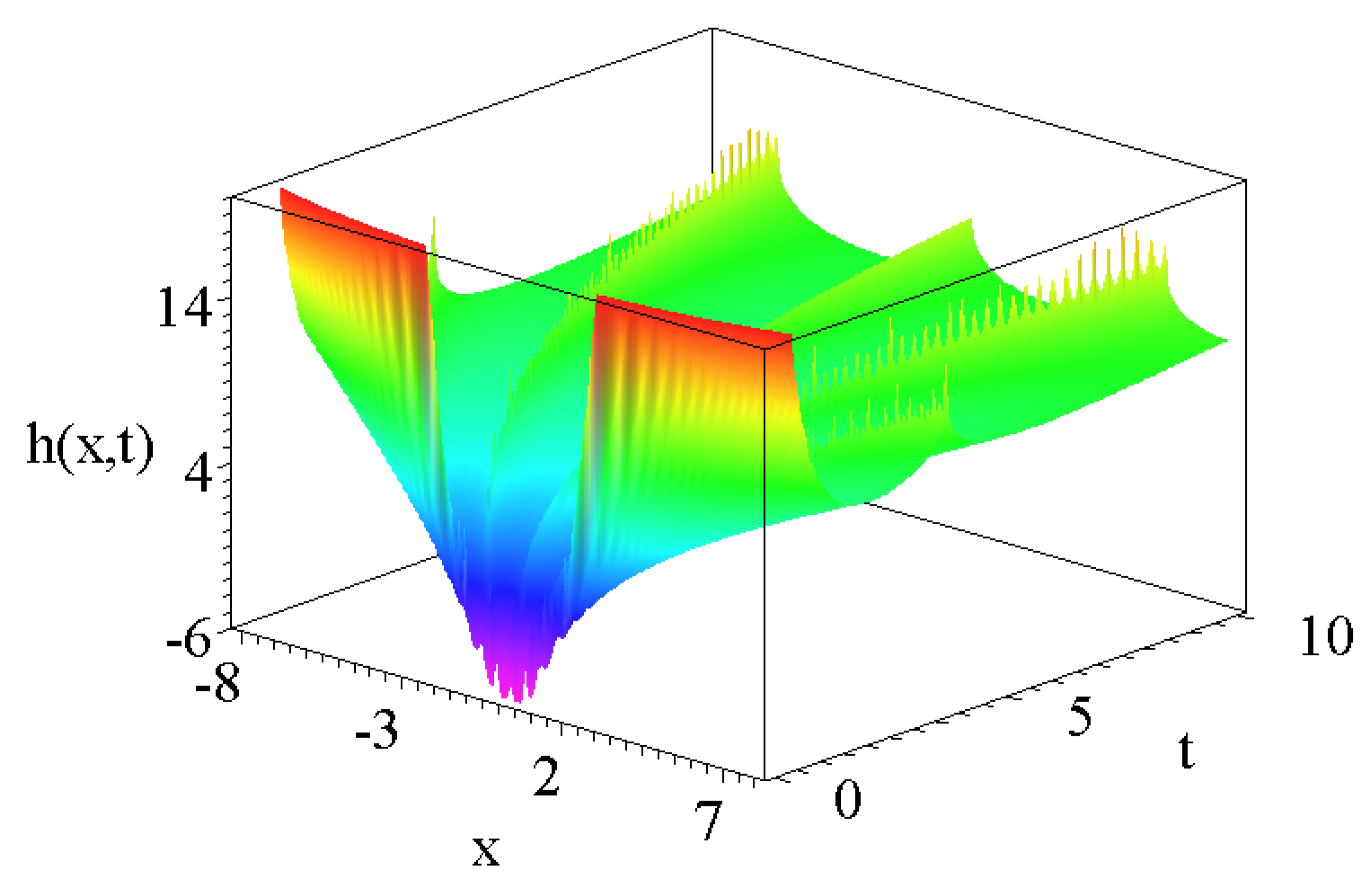
2.1. Self-Similar Solutions of the Diffusion Equation
- the M function is a finite polynomial if is integer and larger than two,
- the M function is constant, the decay of solutions are determined by the Gaussian term,
- the solutions have a local maxima and a decay to zero at large arguments,
- the solutions have oscillations proportional to the value of and have quicker and quicker decays to zero at larger values.
2.2. The Hopf-Cole Transformation
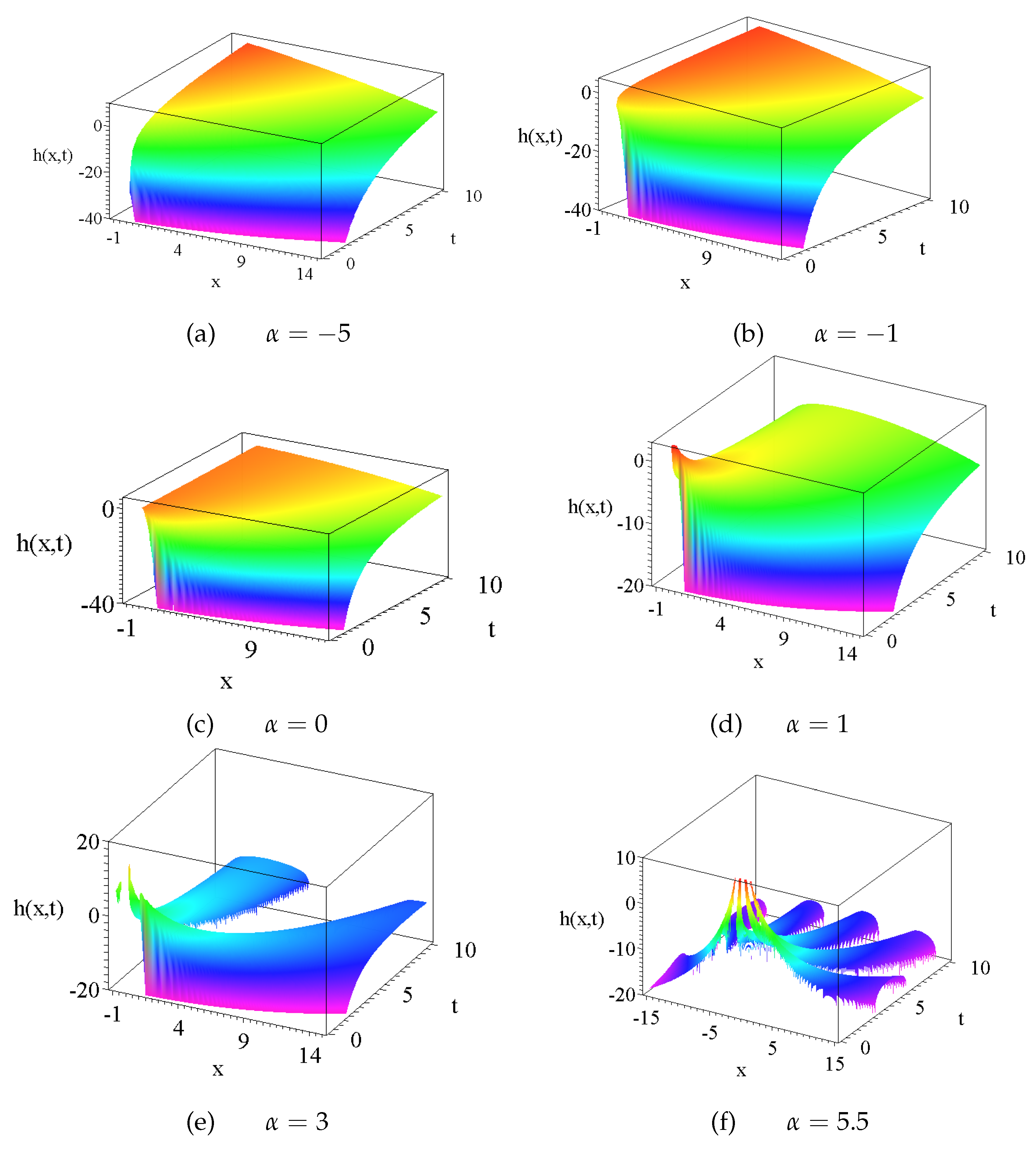
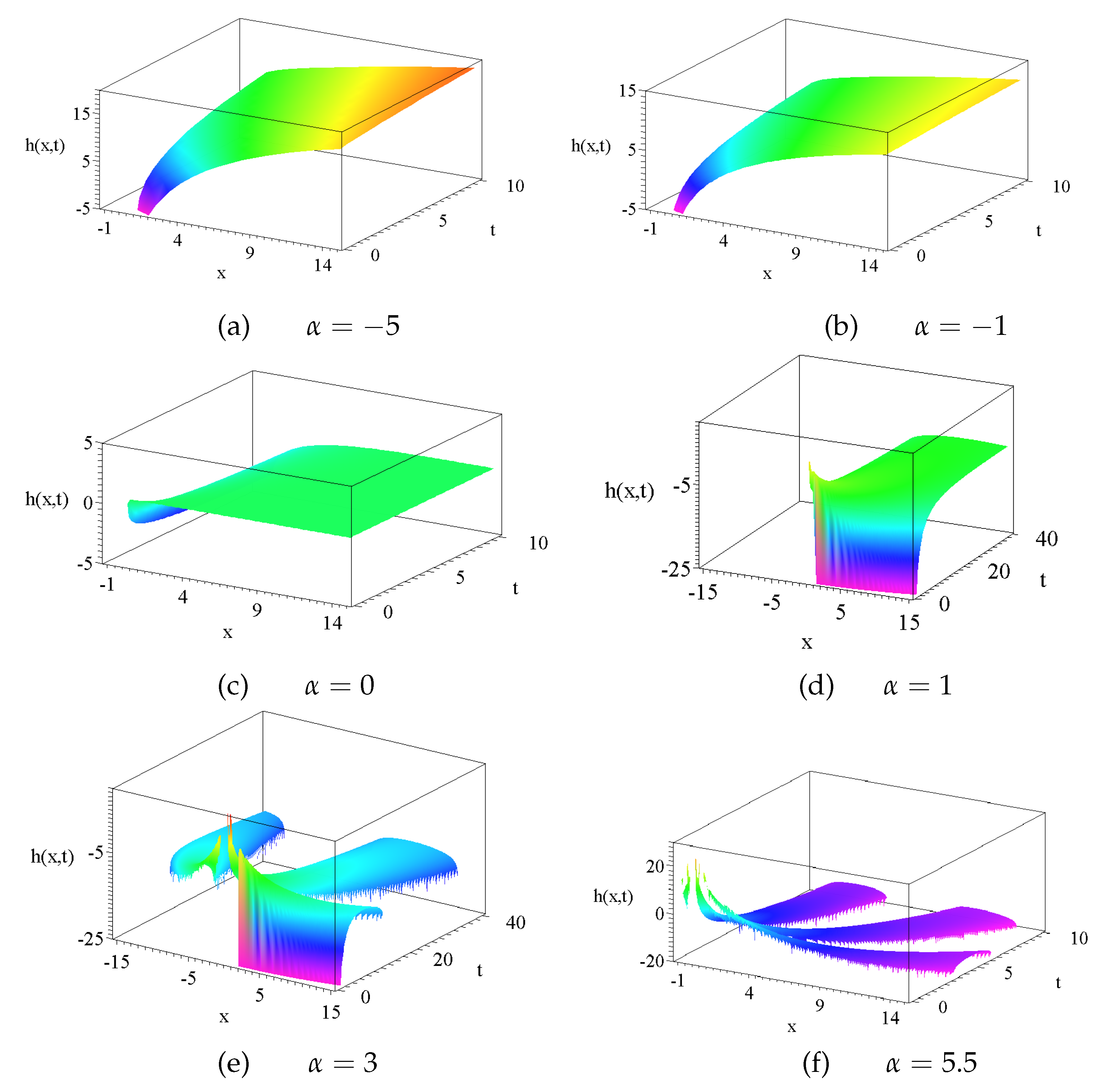
2.3. The New Solutions of the KPZ via the Hopf-Cole Transformation
2.4. The Question of Additional Source Terms in the Diffusion Equation
2.5. The Question of the Absolute Value
2.6. The Question of Surface Erosion
3. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crank, J. The Mathematics of Diffusion; Oxford, Clarendon Press, 1956.
- Z. Wu, J. Zhao, J.Y.; Li, H. Nonlinear Diffusion Equations; World Scientific, 2001.
- Favini, A.; Marinoschi, G. Degenerate Nonlinear Diffusion Equations; Springer, 2012.
- Pekalski, A.; Sznajd-Weron, K. Anomalous Diffusion; Springer, 1999.
- Bucur, C.; Valdinoci, E. Nonlocal Diffusion and Applications; Springer, 2016.
- Evangelista, L.; Lenzi, E. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press, 2018.
- Barabási, A.L. Fractal concepts in surface growth; Press Syndicate of the University of Cambridge, 1995.
- Saito, Y. Statistical Physics of Crystal Growth,; World Scientific Press, 1996.
- Pimpinelli, A.; Villain, J. Physics of Crystal Growth; Cambridge University Press,, 1998.
- Einax, M.; Dieterich, W.; Maass, P. Colloquium: Cluster growth on surfaces: Densities, size distributions, and morphologies. Rev. Mod. Phys. 2013, 85, 921–939. [CrossRef]
- Antczak, G.; Ehrlich, G. Surface Diffusion: Metals, Metal Atoms, and Clusters; Cambridge University Press,, 2010.
- Jackson, K.A. Kinetic Processes: Crystal Growth, Diffusion, and Phase Transitions in Materials; John Wiley & Sons, 2014.
- Tadahisa, F. Lectures on Random Interfaces; Springer Singapore, 2016.
- Calabrese, P.; Le Doussal, P. Exact Solution for the Kardar-Parisi-Zhang Equation with Flat Initial Conditions. Phys. Rev. Lett. 2011, 106, 250603. [CrossRef]
- Siegert, M.; Plischke, M. Instability in surface growth with diffusion. Phys. Rev. Lett. 1992, 68, 2035–2038. [CrossRef]
- Amar, J.G.; Lam, P.M.; Family, F. Groove instabilities in surface growth with diffusion. Phys. Rev. E 1993, 47, 3242–3245. [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889–892. [CrossRef]
- Woyczynski, W.A. Burgers-KPZ turbulence; Springer, 1998.
- Hopf, E. The partial differential equation ut + uux = xx. Communications on Pure and Applied Mathematics 1950, 3, 201–230. [CrossRef]
- Cole., J.D. On a quasi-linear parabolic equation occurring in aerodynamics. Quart. Appl. Math. 1951, 9, 225–236. [CrossRef]
- Hairer, M. Solving the KPZ equation. Ann. Math. 2013, 178, 559–664. [CrossRef]
- Wiese, K.J. On the Perturbation Expansion of the KPZ Equation. Journal of Statistical Physics 1998, 93, 143–154. [CrossRef]
- Hwa, T.; Frey, E. Exact scaling function of interface growth dynamics. Phys. Rev. A 1991, 44, R7873–R7876. [CrossRef]
- Frey, E.; Täuber, U.C.; Janssen, H.K. Scaling regimes and critical dimensions in the Kardar-Parisi-Zhang problem. Europhysics Letters 1999, 47, 14. [CrossRef]
- Kriecherbauer, T.; Krug, J. A pedestrian’s view on interacting particle systems, KPZ universality and random matrices. Journal of Physics A: Mathematical and Theoretical 2010, 43, 403001. [CrossRef]
- Lässig, M. On growth, disorder, and field theory. Journal of Physics: Condensed Matter 1998, 10, 9905. [CrossRef]
- Family, F.; Vicsek, T. Scaling of the active zone in the Eden process on percolation networks and the ballistic deposition model. Journal of Physics A: Mathematical and General 1985, 18, L75. [CrossRef]
- Gladkov, A. Self-similar blow-up solutions of the KPZ equation. International Journal of Differential Equations 2015, 2015, 572841. [CrossRef]
- Gladkov, A.; Guedda, M.; Kersner, R. A KPZ growth model with possibly unbounded data: correctness and blow-up. Nonlinear Analysis: Theory, Methods & Applications 2008, 68, 2079–2091. [CrossRef]
- Abdellaoui, B.; Peral, I.; Primo, A.; Soria, F. On the KPZ equation with fractional diffusion: Global regularity and existence results. Journal of Differential Equations 2022, 312, 65–147. [CrossRef]
- Kersner, R.; Vicsek, M. Travelling waves and dynamic scaling in a singular interface equation: analytic results. Journal of Physics A: Mathematical and General 1997, 30, 2457. [CrossRef]
- Kelling, J.; Ódor, G.; Gemming, S. Suppressing correlations in massively parallel simulations of lattice models. Comput. Phys. Commun. 2017, 220, 205–211. [CrossRef]
- Sasamoto, T. The 1D Kardar–Parisi–Zhang equation: Height distribution and universality. Progress of Theoretical and Experimental Physics 2016, 2016, 022A01. [CrossRef]
- Matsushita, M.; Wakita, J.; Itoh, H.; Rafols, I.; Matsuyama, T.; Sakaguchi, H.; Mimura, M. Interface growth and pattern formation in bacterial colonies. Physica A: Statistical Mechanics and its Applications 1998, 249, 517–524. [CrossRef]
- Kuramoto, Y.; Tsuzuki, T. Persistent Propagation of Concentration Waves in Dissipative Media Far from Thermal Equilibrium. Progress of Theoretical Physics 1976, 55, 356–369. [CrossRef]
- Gu, Y.; T. Komorowski, S. accepted in jan 20-. Stochastics and Partial Differential Equations: Analysis and Computations ( 2025, 55.
- Barna, I.F.; Mátyás, L. Advanced Analytic Self-Similar Solutions of Regular and Irregular Diffusion Equations. Mathematics 2022, 10, 3281. [CrossRef]
- Mátyás, L.; Barna, I.F. Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon. Universe 2023, 9, 264. [CrossRef]
- Mátyás, L.; Barna, I.F. Self-similar and traveling wave solutions of diffusion equations with concentration dependent diffusion coefficients. Romanian Journal of Physics 2024, 69, 106. [CrossRef]
- Kovács, E. New stable, explicit, first order method to solve the heat conduction equation. Journal of Computational and Applied Mechanics 2020, 15, 3–13. [CrossRef]
- Jalghaf, H.K.; Kovács, E.; Majár, J.; Nagy, A.; Askar, A.H. Explicit Stable Finite Difference Methods for Diffusion-Reaction Type Equations. Mathematics 2021, 9. [CrossRef]
- Barna, I.F.; Bognár, G.; Guedda, M.; Hriczó, K.; Mátyás, L. Analytic Self-Similar Solutions of the Kardar–Parisi–Zhang Interface Growing Equation with Various Noise Terms. Mathematical Modelling and Analysis 2020, 25, 241–256. [CrossRef]
- Barna, I.F.; Bognár, G.; Mátyás, L.; Guedda, M.; Hriczó, K. Travelling-wave solutions of the Kardar–Parisi–Zhang interface growing equation with different kind of noise terms. AIP Conference Proceedings 2020, 2293, 280005. [CrossRef]
- Kovács, E.; Barna, I.; Bognár, G.; Mátyás, L.; Hriczó, K. Analytical and numerical study of diffusion propelled surface growth phenomena. Partial Differential Equations in Applied Mathematics 2024, 11, 100798. [CrossRef]
- Sergi, D.; Camarano, A.; Molina, J.M.; Ortona, A.; Narciso, J. Surface growth for molten silicon infiltration into carbon millimeter-sized channels: Lattice–Boltzmann simulations, experiments and models. International Journal of Modern Physics C 2016, 27, 1650062. [CrossRef]
- Martynec, T.; Klapp, S.H.L. Impact of anisotropic interactions on nonequilibrium cluster growth at surfaces. Phys. Rev. E 2018, 98, 042801. [CrossRef]
- Mello, B.A. A random rule model of surface growth. Physica A: Statistical Mechanics and its Applications 2015, 419, 762–767. [CrossRef]
- Muravnik, A.B. On absence of global positive solutions of elliptic inequalities with KPZ-nonlinearities. Complex Variables and Elliptic Equations 2019, 64, 736–740. [CrossRef]
- Bluman, G.W.; Cole, J.D. The General Similarity Solution of the Heat Equation. J. Math. Mech. 1969, 18, 1025–1042. https://doi.org/https://personal.math.ubc.ca/bluman/jmm%20article%201969.pdf.
- Klages, R. Microscopic Chaos, Fractals and Transport in Nonequilibrium Statistical Mechanics; Advanced Series in Nonlinear Dynamics: Volume 24, 2007. [CrossRef]
- Pukach, P.; Chernukha, O.; Chernukha, Y.; Vovk, M. Three-Dimensional Mathematical Modeling and Simulation of the Impurity Diffusion Process Under the Given Statistics of Systems of Internal Point Mass Sources. Modelling 2025, 6. [CrossRef]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; CRC Press, 1993.
- Barna, I.F.; Bognár, G.; Mátyás, L.; Hriczó, K. Self-similar analysis of the time-dependent compressible and incompressible boundary layers including heat conduction. Journal of Thermal Analysis and Calorimetry 2022, 147, 13625–13632. [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W., Eds. NIST Handbook of Mathematical Functions; Cambridge University Press, 2010. https://doi.org/https://dlmf.nist.gov/.
- Yang, X.; Zhang, Y.; Li, W. Dynamics of rational and lump-soliton solutions to the reverse space-time nonlocal Hirota-Maccari system. Romanian Journal of Physics 2024, 69, 102. [CrossRef]
- Ur Rehman, M.I.; Chen, M.I.; Hamid, A. Multi-physics modeling of magnetohydrodynamic Carreau fluid flow with thermal radiation and Darcy-Forchheimer effects: a study on Soret and Dofour phenomena. Journal of Thermal Analysis and Calorimetry 2023, 148, 13883–13894. [CrossRef]
- Timofte, C. A bidomain model for calcium dynamics in living cells. Romanian Reports in Physics 2024, 76, 105. [CrossRef]
- Barna, I.F. Self-Similar Solutions of the G-Equation - Analytic Description of the Flame Surface. Journal of Generalized Lie Theory and Applications 2017, 11. [CrossRef]
- Lax, M. Classical Noise IV: Langevin Methods. Rev. Mod. Phys. 1966, 38, 541–566. [CrossRef]
- Pomeau, Y.; Piasecki, J. The Langevin equation. Comptes Rendus. Physique 2017, 18, 570–582. [CrossRef]
- Halpin-Healy, T.; Zhang, Y.C. Kinetic roughening phenomena, stochastic growth, directed polymers and all that. Aspects of multidisciplinary statistical mechanics. Physics Reports 1995, 254, 215–414. [CrossRef]
- Corwin, I. The Kardar–Parisi–Zhang Equation and Universality Class. Random Matrices: Theory and Applications 2012, 01, 1130001. [CrossRef]
- Konstantin Matetski, J.Q.a.R. The KPZ fixed point. Acta Math., 2021, 227, 15–203. [CrossRef]
- Alexander, G.; Sergei, N.; Alexander, V. KPZ scaling from the Krylov space. Journal of High Energy Physics 2024, 2024, 21. [CrossRef]
- Madelung, E. Eine anschauliche Deutung der Gleichung von Schrödinger. Naturwissenschaften 1926, 14, 1004–1004. [CrossRef]
- Simpao, V. Understanding The Schrödinger Equation: Some [Non]Linear Persectives; Nova Puplisher, 2020; chapter 6 I.F. Barna and L. Mátyás "Self-similar and Travelling-Wave Analysis of the Madelung Equations Obtained from the Free Schrödinger Equation.
- Bakirtaş, I.; Antar, N.; Horikis, D. Parabolic and rectangular self-similar evolution in saturable media. Romanian Reports in Physics 2023, 75, 4468. [CrossRef]
- Dearnley, P. Introduction to Surface Engineering; Cambridge University Press, 2017; chapter 6 Surface Degradation and Its Evaluatio.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




