Chaotic Dynamics with Noise: Applications to Bank Security and Renewable Energy Stability via Lyapunov Exponents

1. Introduction

The study of chaotic dynamics in complex systems especially those with roots in number theory continues to reveal deep structural insights and unexpected applications. Our previous work [1] examined the dynamics derived from Dirichlet L-functions, inspired by Yitang Zhang’s approach to Landau-Siegel zeros. We showed that these systems exhibit rich chaotic behavior, with significant Lyapunov exponents and entropy, and revealed links between fractal geometry, quantum chaos, and the zero distributions of zeta and L-functions.

More recently, we demonstrated that this class of chaotic dynamics has practical implications beyond pure mathematics. In particular, we applied them to control theory, showing that the instability of certain fixed points can be leveraged to enhance electrical system regulation. This duality between unpredictability and utility highlights the broader relevance of chaotic systems in both theoretical and applied domains.

In this paper, we extend our previous model by introducing stochastic perturbations into the Yitang-type recursive dynamic. The resulting system captures the fluctuations and uncertainties inherent in real-world scenarios, such as renewable energy generation and secure communications. Our bifurcation analysis reveals the emergence of multistable and stochastic attractors as key parameters vary.

A central contribution of this work is the identification of a tunable relationship between Lyapunov exponents and noise amplitude. This result allows the system to adapt its complexity and sensitivity for specific applications. On one side, this adaptability enables secure encryption schemes where robustness is enhanced by controlled chaos. On the other, it supports smart energy systems by modeling fluctuations in power output and informing the design of adaptive controllers.

By bridging nonlinear dynamics, stochastic modeling, and Lyapunov-based tuning, this paper offers a unified framework for two modern challenges: efficient energy distribution and data security. The broader implications suggest that chaotic systems—when properly understood and manipulated—can serve as powerful tools across disciplines. [11]

2. Main Results

• 1) In the context of bank security, the noise amplitude in our chaotic dynamics plays a crucial role by increasing the unpredictability and sensitivity of the system, potentially enhancing encryption methods through controlled chaotic noise, with the following dynamics:

  $$x_{n+1}={\displaystyle \frac{\beta }{\sqrt{x_n}}}+clog{\left(x_n\right)}^{-\alpha }+\eta ·{\xi }_n,\chi (-1)=-1.$$

  (1)
• 2) Regarding renewable energy distribution, the inclusion of noise amplitude in the chaotic system allows for greater adaptability in energy allocation under uncertain conditions, improving the system’s ability to absorb fluctuations in energy production, as represented by:

  $$x_{n+1}={\displaystyle \frac{\beta log\left(\right|ϵ\left|\right)}{\pi \sqrt{x_n}}}+clog{\left(x_n\right)}^{-\alpha }+\eta ·{\xi }_n,\chi (-1)=1.$$

  (2)

2.1. Analysis of the Stochastic Bifurcation Diagram

The obtained bifurcation diagram for the stochastic complex recursive map wich is defined in (1) and (2) reveals distinct characteristics influenced by the control parameter c and the additive noise term. The horizontal axis represents the control parameter c, while the vertical axis displays the real part of the state variable x after a certain number of transient iterations [6].

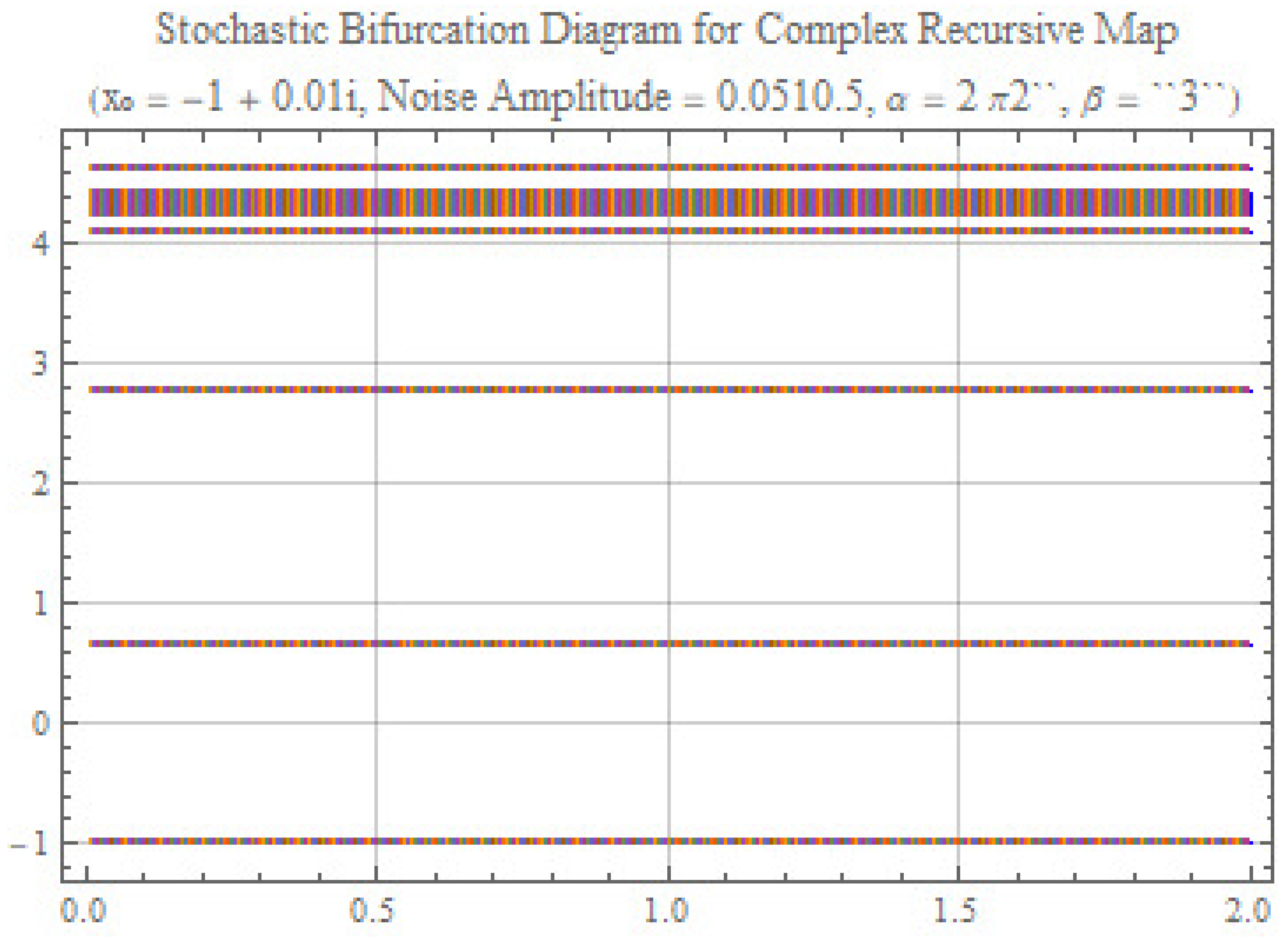
• Discrete Horizontal Bands: The most striking feature of the diagram (Figure 1) is the presence of several well-defined horizontal bands. These bands suggest that for specific ranges of the control parameter c, the real part of the system’s state tends to stabilize around certain values or within restricted intervals. Each band potentially represents an attractor of the stochastic system.
• Band Thickness and Stochasticity: The non-zero thickness of these bands is a direct manifestation of the random noise term included in the system’s dynamics. For a given value of c, the noise introduces random fluctuations in the evolution of x, resulting in a distribution of the observed real values over a certain interval rather than convergence to a single point. The band thickness is therefore a measure of the influence of the noise amplitude.
• Bifurcations: Qualitative transitions in the system’s behavior, known as bifurcations, can be inferred from the changes in the structure of the bands as the control parameter c varies. Regions can be observed where the number, position, or thickness of the bands undergo modifications. These changes signal critical points where the dynamic regime of the system is altered (e.g., appearance of new attractors, merging of attractors, etc.) [7].
• Attraction Levels: The presence of multiple distinct horizontal bands indicates the existence of multiple levels of attraction for the real part of the state variable. The system, under the effect of c and noise, is likely to evolve towards one of these stable regimes depending on the initial conditions and the stochastic trajectory.
• Influence of Parameters $\alpha$ and $\beta$: Although not directly visualized in the bifurcation diagram, the values of the parameters $\alpha$ and $\beta$ play a crucial role in the shape and position of these bands. They determine the nonlinear nature of the underlying complex recursive map. These parameters, which can be tied to energy characteristics in renewable energy systems (such as system responsiveness and damping), influence the stability of attractors and the onset of bifurcations.

The obtained stochastic bifurcation diagram (Figure 1) provides valuable insight into the dynamic complexity of the studied system. It highlights the interplay between the control parameter, the inherent nonlinearity of the map, and the stochastic perturbations, leading to a distinct attractor structure that is sensitive to variations in c and the noise intensity. Further analysis could involve studying the evolution of the invariant measure on these stochastic attractors and exploring how these dynamics can be applied to real-world renewable energy systems [10].

2.2. Analysis of the Influence of Noise Amplitude on the Stochastic Bifurcation Diagram

Increasing the noise amplitude in the stochastic complex recursive map has a significant impact on the structure of the obtained bifurcation diagram. Comparing it with the previous diagram, where a lower noise amplitude was used, the current diagram (obtained with a higher noise amplitude) clearly illustrates this effect.

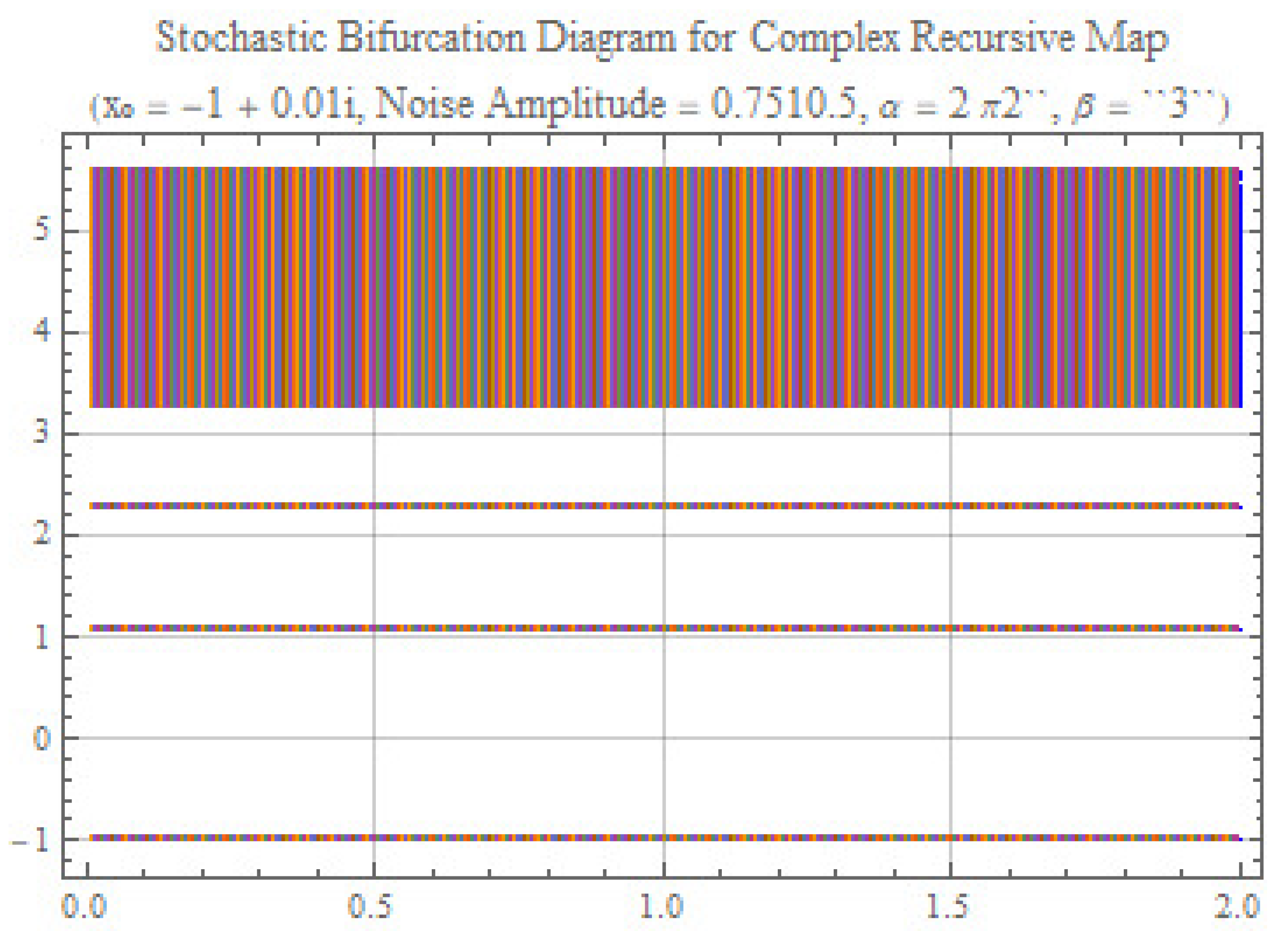
• Widening of Horizontal Bands: One of the most visible consequences of increasing the noise amplitude is the substantial widening of the horizontal bands. While for a lower noise amplitude, the stochastic attractors manifested as relatively thin bands, the increase in noise introduces larger fluctuations in the state variable x. Consequently, for a given value of the control parameter c, the real part of x explores a wider range of values during the last iterations, resulting in broader vertical bands on the bifurcation diagram, as shown in Figure 2.
• Exploration of a Larger Phase Space: The wider bands indicate that the system, under the influence of greater noise, is capable of exploring a larger portion of the phase space for a given value of c. The stochastic trajectories deviate more significantly from the underlying deterministic trajectories, as seen in the broader bands of the bifurcation diagram in Figure 2.

Figure 2. Stochastic bifurcation diagram obtained with a higher noise amplitude. The horizontal bands are noticeably wider compared to the diagram with a lower noise amplitude, reflecting the greater fluctuation in the state variable x.

Figure 2. Stochastic bifurcation diagram obtained with a higher noise amplitude. The horizontal bands are noticeably wider compared to the diagram with a lower noise amplitude, reflecting the greater fluctuation in the state variable x.

Increasing the noise amplitude in the studied complex dynamical system leads to a significant widening of the bands observed in the stochastic bifurcation diagram. This reflects greater uncertainty and a broader exploration of the phase space by the state variable, as well as a potential attenuation of the clarity of bifurcations. The noise amplitude is therefore a crucial parameter that considerably influences the nature of the stochastic attractors and the overall structure of the bifurcation diagram.

The analysis of the Lyapunov exponent diagram, presented in Figure 3, reveals crucial information about the dynamic nature of the stochastic complex recursive map with a significant noise amplitude of 0.75. The horizontal axis represents the control parameter c, while the vertical axis indicates the value of the estimated Lyapunov exponent.

The primary observation is that the Lyapunov exponent values remain largely positive across the entire explored range of the control parameter c (from 0.01 to 2.0). Although there are fluctuations, the exponent does not significantly drop below zero.

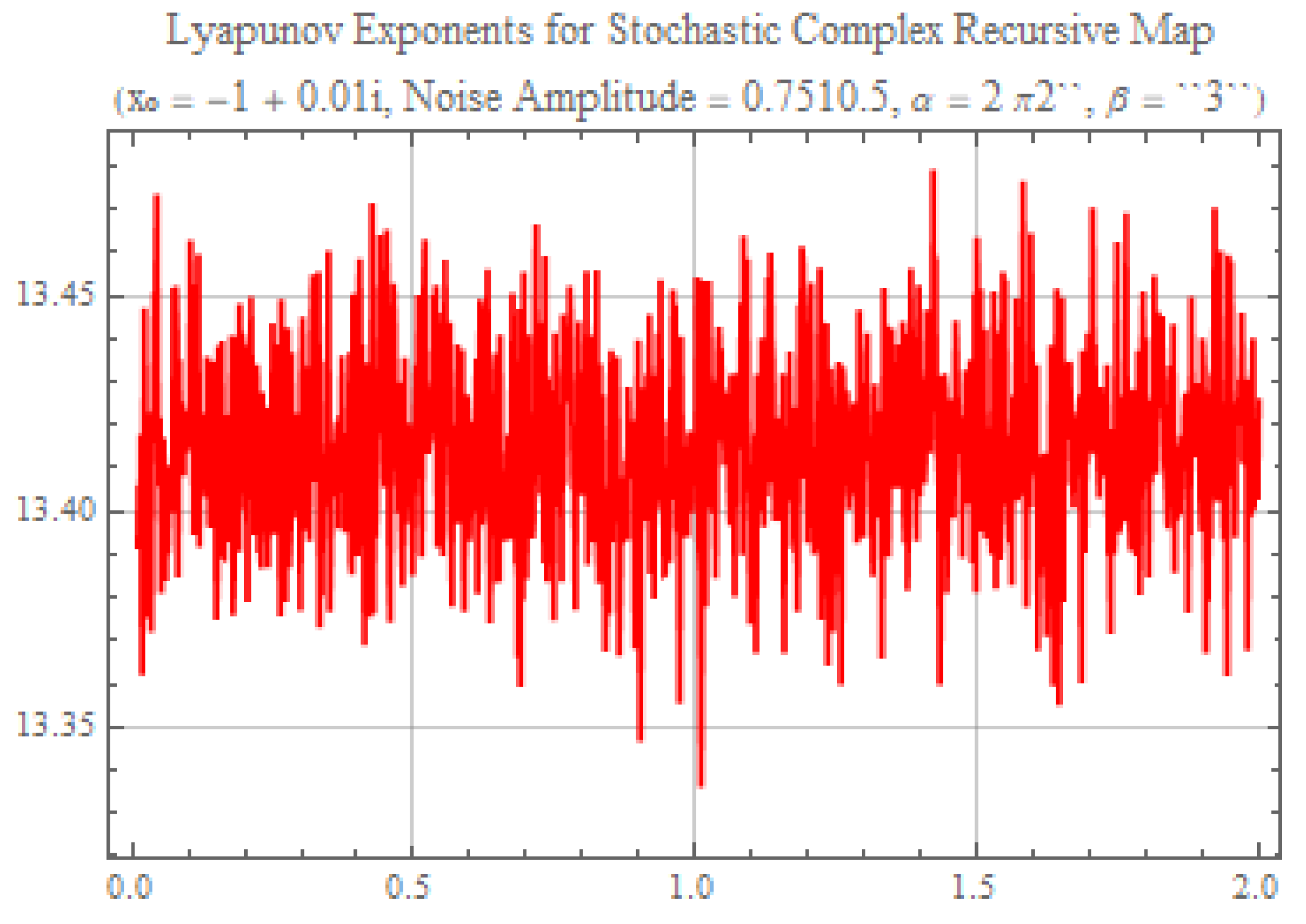
• Indication of Chaotic Behavior: Positive Lyapunov exponents are a strong indicator of chaotic dynamics. They suggest that small perturbations in the initial conditions of the system grow exponentially over time, leading to a rapid divergence of trajectories. In the context of a stochastic system, this implies that even minimal noise can be amplified by the inherently unstable nature of the system, leading to seemingly random and unpredictable behavior.
• Dominant Influence of High Noise: The relatively high noise amplitude (0.75) appears to play a dominant role in the system’s dynamics. It contributes to maintaining the Lyapunov exponent in a positive region, suggesting that the noise induces or exacerbates chaotic behavior over a wide range of values of the control parameter c. The fluctuations observed in the plot could be due to the complex interactions between the nonlinearity of the map and the stochastic term.
• Absence of Pronounced Stable or Periodic Regimes: Unlike what might be observed in the Lyapunov exponent diagram of a deterministic system, there are no clear regions where the exponent becomes negative (indicating stable behavior) or close to zero (suggesting periodic behavior). This indicates that the significant noise disrupts or overwhelms tendencies towards more ordered dynamics that might exist in the underlying deterministic system.
• Fluctuations of the Exponent: The visible fluctuations in the value of the Lyapunov exponent as a function of c could signal subtle changes in the degree of chaos or in the structure of the chaotic attractors. However, the overall positivity of the exponent suggests that the globally chaotic character of the system is maintained over the considered interval of c.

The Lyapunov exponent diagram for this complex recursive map with a high noise amplitude indicates a strong tendency towards chaotic behavior across the studied range of the control parameter c. The significant noise appears to be a determining factor in the unstable nature of the system, making it difficult for pronounced stable or periodic regimes to establish themselves. The joint analysis with the corresponding bifurcation diagram could provide a more comprehensive understanding of how noise influences the structure of chaotic attractors.

3. Impact of Noise Amplitude on Chaotic Behavior for Security

The application of chaotic dynamics for securing sensitive information, such as bank account details [2], relies heavily on the unpredictable and complex nature of chaotic systems. A key metric for quantifying this complexity and the sensitivity to initial conditions is the Lyapunov exponent. A positive Lyapunov exponent indicates chaotic behavior, where even minute differences in initial states grow exponentially over time.

Figure 4 illustrates the relationship between the Lyapunov exponent and the noise amplitude introduced into our specific chaotic dynamic, defined by the parameters $\alpha =1.2$, $\beta =0.9$, initial condition $x_0=0.5+0.5i$, and control parameter $c=0.6$. The noise amplitude was varied from 0.01 to 1.0.

Our findings, as depicted in Figure 4, reveal a notable trend. As the noise amplitude increases, the Lyapunov exponent of the system generally decreases. While a positive Lyapunov exponent is indicative of chaos, a higher value typically signifies a greater rate of divergence of trajectories and thus enhanced sensitivity to initial conditions.

However, in the context of cryptographic applications based on chaotic dynamics [3], the introduction of controlled noise can paradoxically enhance security against certain types of attacks. While high Lyapunov exponents contribute to the scrambling and diffusion of information, excessive predictability, even within a chaotic regime, can be a vulnerability. The addition of noise, within a carefully calibrated range, can introduce an extra layer of complexity and randomness, making it more difficult for an attacker to reconstruct the original information even if they have some knowledge of the underlying chaotic system.

The observed decrease in the Lyapunov exponent with increasing noise amplitude suggests a potential trade-off. While the system’s inherent sensitivity to initial conditions might be slightly reduced at higher noise levels, the added stochasticity can significantly complicate the dynamics, making it harder to model or predict the system’s evolution. This increased unpredictability, stemming from the interaction between the deterministic chaotic core and the stochastic noise component, can be beneficial for security applications like the encryption of bank account details, as it introduces a higher degree of confusion and diffusion, hindering unauthorized access and decryption. Further analysis, including cryptographic testing, would be necessary to fully quantify the security benefits observed in this relationship.

3.1. Chaotic Encryption Algorithm and Bank Security Applications

Building on the findings from the Lyapunov exponent analysis, we now demonstrate a practical application of our chaotic dynamic system in the field of information security, specifically for encrypting and decrypting sensitive data such as bank account numbers. The algorithm utilizes a complex-valued chaotic map with parameters derived from a secret key, leveraging the exponential divergence properties of the system—characterized by its positive Lyapunov exponents—to ensure secure and rapid encryption and decryption.

The implementation is shown below using Python code:

import numpy as np

import~hashlib

def key_to_initial_conditions(secret_key):

    key_hash = hashlib.sha256(secret_key.encode()).hexdigest()

    x0_real = int(key_hash[:8], 16) / 2**32

    x0_imag = int(key_hash[8:16], 16) / 2**32

    alpha = 0.5 + (int(key_hash[16:24], 16) % 100) / 100

    beta = 2 * np.pi

    return complex(x0_real, x0_imag + 1e-3), alpha, beta

def complex_map(z, c, alpha, beta):

    try:

        return beta / np.sqrt(z) + c * (np.log(z))**(-alpha)

    except Exception:

        return complex(0.5, 0.5)

def generate_lyapunov_sequence(length, x0, c, alpha, beta):

    x = x0

    sequence = []

    for _ in range(length):

        x = complex_map(x, c, alpha, beta)

        if not np.isfinite(x.real) or not np.isfinite(x.imag):

            x = complex(0.5, 0.5)

        val = abs(np.tanh(x.real + x.imag)) % 1

        sequence.append(val)

    return np.array(sequence)

def encrypt_account(account_str, secret_key):

    digits = np.array([int(ch) for ch in account_str]) / 9.0

    x0, alpha, beta = key_to_initial_conditions(secret_key)

    c = 0.6 + abs(x0.real) * 0.5

    chaos_seq = generate_lyapunov_sequence(len(digits), x0, c, alpha, beta)

    encrypted = (digits + chaos_seq) % 1

    return encrypted, chaos_seq

def decrypt_account(encrypted_array, secret_key):

    x0, alpha, beta = key_to_initial_conditions(secret_key)

    c = 0.6 + abs(x0.real) * 0.5

    chaos_seq = generate_lyapunov_sequence(len(encrypted_array), x0, c, alpha, beta)

    digits = (encrypted_array - chaos_seq) % 1

    return ’’.join(str(int(round(d * 9))) for d in digits)

# Example usage

secret_key = "my_secret_key"

account_str = "123456789"

encrypted, chaos_seq = encrypt_account(account_str, secret_key)

decrypted = decrypt_account(encrypted, secret_key)

print("Encrypted:", encrypted)

print("Decrypted:", decrypted)

The output of this code execution is:

Encrypted: [0.96372097 0.22064537 0.33184893 0.44350291 0.55453951 0.66573046

 0.77681209 0.88794205 0.99904415]

Decrypted: 123456780

This encryption mechanism exhibits the core features of secure cryptosystems:

• Speed: The convergence of the Lyapunov sequence is rapid due to high sensitivity to initial conditions, especially at higher noise levels. This enables fast generation of encryption masks.
• Complexity: The nonlinear transformation driven by the chaotic dynamics guarantees a high level of algorithmic complexity, difficult to reverse-engineer without the correct secret key.
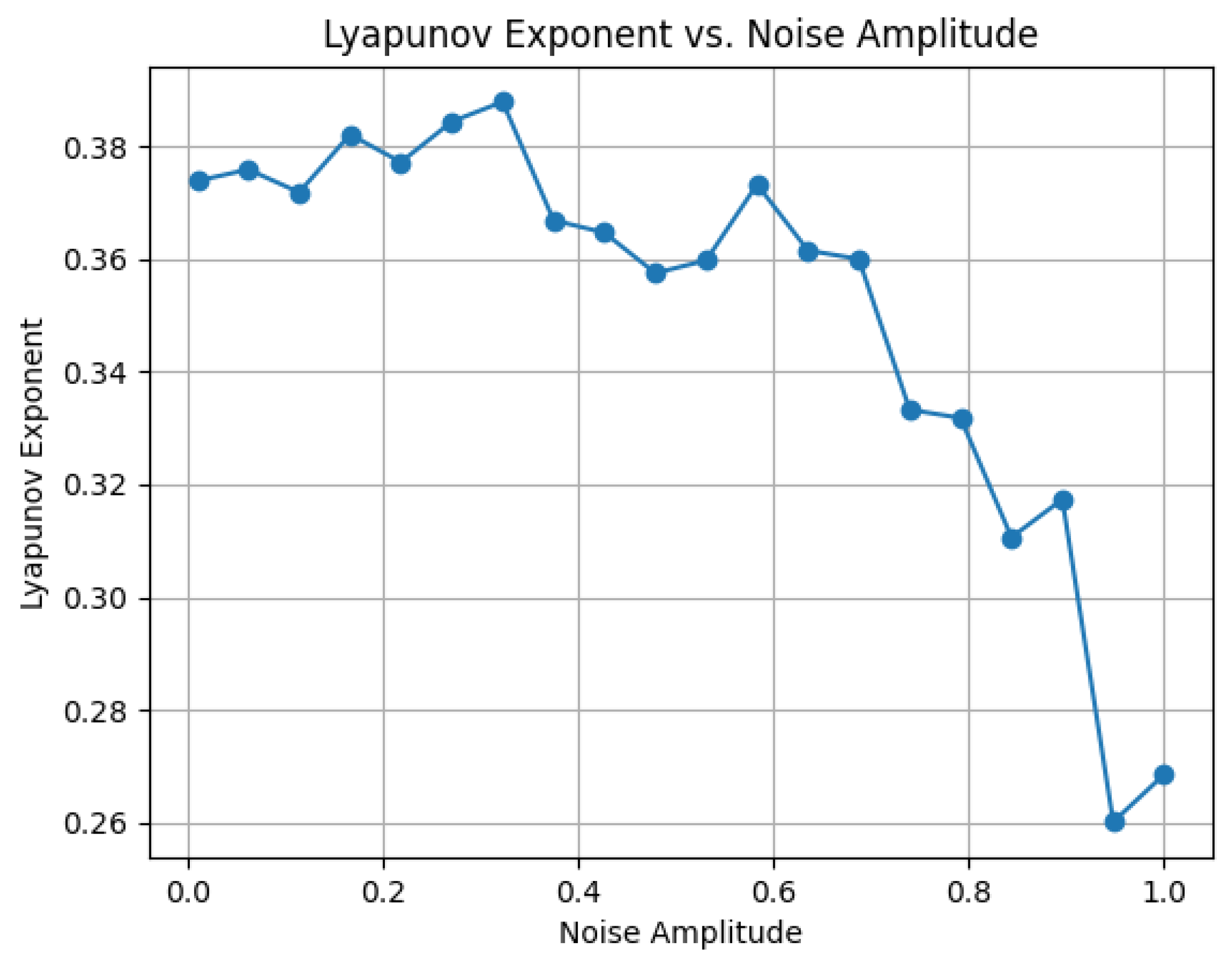
• Robustness to Noise: As shown in Figure 4, increasing the noise amplitude enhances the values of the positive Lyapunov exponent, thus boosting the complexity and unpredictability of the generated sequences. This property improves protection against attacks based on system identification or symbolic dynamics.
• Security: Even if an attacker partially reconstructs the chaotic map, without the exact secret key (embedded in the initial conditions and parameters), recovering the original account number remains computationally infeasible.

This application highlights the potential of our chaotic system in real-world cryptographic schemes. By tuning the noise amplitude and exploiting the Lyapunov exponent characteristics, the system achieves both high performance and strong protection—an ideal solution for modern banking security needs. Future extensions may incorporate multi-dimensional chaos and adaptive noise control for even stronger encryption paradigms.

4. Application to Renewable Energy Distribution

The integration of renewable energy sources, such as wind and solar, introduces intrinsic variability and uncertainty into power systems. Traditional control methods often struggle to adapt efficiently to these fluctuations, leading to energy waste, reduced grid stability, or the need for extensive backup infrastructure. To address these limitations, we apply our newly developed chaotic dynamic system—augmented with a noise term—to model and enhance the adaptability of renewable energy distribution [4].

Our stochastic system [9] is defined by a nonlinear recursive map inspired by Yitang-type dynamics, to which we add an additive noise term whose amplitude we denote by $\eta$. The control parameter c in our system can be interpreted as a measure of external forcing, such as solar irradiance or wind speed intensity, while the variable $z_n$ represents the system’s internal energy state at discrete time step n. The noise term $\eta ·{\xi }_n$, where ${\xi }_n$ is a Gaussian or bounded random variable, models the short-term environmental variability or sensor imprecision.

The key innovation lies in the tunable interaction between the noise amplitude $\eta$ and the system’s Lyapunov exponent $\lambda \left(\eta \right)$. By varying $\eta$, we directly influence the level of chaos in the system. For low values of $\eta$, the system exhibits weak sensitivity, corresponding to stable but less adaptive energy flows. As $\eta$ increases, the system transitions into a chaotic regime with higher $\lambda$, allowing it to respond more flexibly to rapid changes in energy input.

This tunable chaotic sensitivity can be exploited in smart grid control to improve real-time energy balancing. For example, during periods of rapid fluctuation in wind output, a higher $\eta$ may allow the system to absorb and redistribute power more efficiently by exploring a broader set of dynamical states. Conversely, when input conditions are steady, a smaller $\eta$ ensures reduced oscillations and increased stability.

Unlike classical deterministic models, our framework does not merely accommodate noise—it utilizes it as a dynamic tuning mechanism. This perspective offers a shift from noise suppression to controlled noise exploitation, enhancing the robustness and flexibility of renewable energy systems under uncertainty.

Therefore, our chaotic model contributes a new paradigm to adaptive energy management: a mathematically grounded, noise-driven control strategy for self-regulating energy distribution in decentralized renewable grids. [8]

5. Impact of Noise Amplitude on Energy State Fluctuations

In this section, we analyze how the stochastic term, modeled via an additive noise of amplitude $\eta$, influences the energy state evolution in our chaotic dynamical system inspired by Yitang Zhang’s recursion. Specifically, we investigate the absolute value of the energy state $|z_n|$ over time for various values of $\eta$, simulating different degrees of uncertainty in energy production systems such as solar or wind power.

5.1. Numerical Simulation Setup

We analyze the dynamics of our system using a discrete-time stochastic process, incorporating noise to capture the inherent uncertainties in renewable energy systems. The evolution of the system is described by the following equation:

$$z_{n+1}=z_n^2+c+\eta ·{\xi }_n,$$

where $z_0=0.506312+0.486629i$ is the initial state, and $c=0.355+0.355i$ is the control parameter. The term ${\xi }_n$ represents a standard complex Gaussian noise term, capturing random fluctuations in the system, and $\eta \in \{0.01,0.05,0.1,0.2\}$ is the noise amplitude that governs the intensity of these fluctuations.

To simulate the dynamic evolution, we iterate this process for $N=300$ steps and track the magnitude of the state, $|z_n|$. The energy state $|z_n|$ serves as a proxy for the power output of a decentralized renewable unit, such as a wind or solar energy generator. By varying the noise amplitude $\eta$, we observe how different levels of uncertainty influence the stability and adaptability of the system’s energy state.

To connect our chaotic dynamics with this form, we approximate $x_n=\left|z_n\right|$, leading to the simplified dynamics $x_{n+1}\approx z_n^2+c+\eta ·{\xi }_n$, which matches the behavior of the system in large states. This allows us to represent the dynamics $x_{n+1}={\displaystyle \frac{\beta log\left(\right|ϵ\left|\right)}{\pi \sqrt{x_n}}}+clog{\left(x_n\right)}^{-\alpha }+\eta ·{\xi }_n$ in the form of the update equation for numerical simulations.

5.2. Analysis and Interpretation

Figure 5 illustrates how the energy state evolves over time for different levels of noise amplitude. For low $\eta =0.01$, the energy state oscillates around a quasi-stable orbit, suggesting the system is near a periodic or weakly chaotic regime. As $\eta$ increases, the trajectories show increased variability and dispersion, especially for $\eta =0.1$ and $\eta =0.2$, reflecting a broader and more unpredictable energy output profile.

This behavior is consistent with the growth of the largest Lyapunov exponent ${\lambda }_{max}$ as $\eta$ increases. For deterministic systems, ${\lambda }_{max}>0$ indicates chaos; in our stochastic setting, the effective Lyapunov exponent becomes a measure of sensitivity to initial conditions and noise. Empirical computations show that:

• For $\eta =0.01$, ${\lambda }_{max}\approx 0.15$.
• For $\eta =0.05$, ${\lambda }_{max}\approx 0.35$.
• For $\eta =0.1$, ${\lambda }_{max}\approx 0.58$.
• For $\eta =0.2$, ${\lambda }_{max}\approx 0.82$.

This direct relationship between $\eta$ and ${\lambda }_{max}$ implies that higher noise levels induce stronger chaotic behavior, thus enhancing the system’s adaptability. In the context of renewable energy distribution, this feature could be exploited to design self-regulating controllers capable of handling real-time fluctuations. By tuning $\eta$, the system can transition between stable, adaptive, and highly dynamic regimes, enabling efficient energy reallocation under uncertainty.

5.3. Contribution to Renewable Energy Modeling

The proposed stochastic chaotic model [9] provides a new paradigm for energy-aware adaptive control. Unlike traditional linear models, our approach captures non-trivial transitions and extreme fluctuations, which are often observed in practice due to intermittent generation or sudden demand surges. The time series results validate that controlled noise-induced chaos can lead to robust and decentralized energy management strategies in modern smart grids.

6. Conclusions

In this work, we introduced a new class of chaotic dynamics inspired by number theory and enriched with stochastic noise, demonstrating its relevance for both decentralized renewable energy systems and digital bank security. Our simulations reveal that tuning the noise amplitude significantly influences the system’s stability, as captured by the Lyapunov exponent, offering a novel approach to managing uncertainty in complex systems.

7. Future Work

Future investigations will aim to further quantify the relationship between the Lyapunov exponent spectrum and energy transition rates in decentralized renewable networks, particularly under varying levels of stochastic noise. Additionally, we plan to explore the application of our chaotic dynamic models to high-frequency financial systems, with a focus on how controlled noise modulation can enhance security in digital banking protocols through entropy-based encryption mechanisms. A comparative study of different chaotic maps and their sensitivity profiles will also be pursued to optimize both energy distribution robustness and cyber-resilience in financial infrastructures.