Preprint
Article
Heat and Photon Energy Phenomena: Dealing with Matter at Atomic and Electronic Level
Altmetrics
Downloads
6865
Views
8852
Comments
1
This version is not peer-reviewed
Submitted:
18 April 2023
Posted:
19 April 2023
Read the latest preprint version here
Alerts
Abstract
There is a misconception about using the terms photon and electron. When the electron of the outer ring in the silicon atom executes interstate dynamics for only one cycle, it generates force and energy for the unit photon. The unit photon has a shape like Gaussian distribution in turned ends. When the photon of suitable length interacts with the side of the laterally orientated electron of a semisolid or solid atom, it converts into heat. Under the approximate angle of 90º, when a photon interacts with the tip of a laterally orientated electron, it divides into bits of energy having a shape like integral symbols. Solid or semisolid element atoms can reveal the phenomena of heat energy if their electrons deal with interactions of photons. In the neutral state silicon atom, the center acts as the reference point for electrons executing interstate dynamics, and the north-south tips of the electrons remain along the north-south poles. The energy shapes around the force tracing along the trajectory of electron dynamics. Under dynamics, two forces exert on the electron for one time, whereas two forces shape from opposite sides. In interstate dynamics, the electron of the outer ring first reaches the maximum limit point, where the one-bit energy shapes. In the remaining half cycle, that electron again shapes one-bit energy. When there is an uninterrupted supply of heat energy to the silicon atom, electron dynamics generate the photon having a shape-like wave. Path-independent but interstate-dependent forces take over the control of an electron. That electron executes dynamics nearly at the speed of light. In dynamics, the conservative forces exert on the position-acquiring electron. A photon can be in unending length if the electron dynamics remain uninterrupted. The changing aspect of the electron recalls the auxiliary moment of inertia at each point of turning. Atoms of suitable elements generate differently shaped photons when executing dynamics for the outer ring electrons. Thus, they can also reveal the phenomenon of photon energy.
Keywords:
Subject: Chemistry and Materials Science - Materials Science and Technology
1. Introduction
Technology is achieving its climax, but a basic understanding of science still awaits. The creation of Earth has benefited from heat and photon energy since its existence. Catching fire to different materials and burning various commodities are the usual phenomena under observation.
Many studies have been discussed in the literature studying the light-matter interaction, mainly covered under a phenomenon known as surface plasmons. The origin of plasmons has a long history of exploration [1,2,3,4].
The interaction of light or photons with matter recognizes by various terminologies, such as phonons, excitons, and plasmons. A study based on reviews discussed light-matter interaction considering the properties of polariton modes in two-dimensional materials [5].
In 1931, Frenkel proposed the concept of excitons or electron-hole pairs [6]. It deals with an excited state of the atom in a lattice traveling in a particle-like fashion without the net transfer of charge. Excitons can form due to photon absorption by a quantum dot [7], where the phonon is a collective excitation in the periodic arrangement of atoms or molecules.
Various studies dealing with different developing processes involve tiny-sized particles. The tiny-sized cluster is a simple chemical compound with various essential applications in diversified areas [8]. The unique nature of nanocrystals demands the fabrication of new materials having controlled features [9]. The development of nanoparticle technology is an obvious long-term benefit [10]. On the successful assembling of the tiny particles for a larger particle, tomorrow they can become the atoms and molecules of the materials [11]. Understanding the dynamics in the development of nanoparticles enables us to understand a bigger-sized particle [12].
Studying the surface features of nanoparticles can develop high-order materials [13]. Tiny-sized clusters possess molecule-shaped electronic and non-face-centered cubic geometric structures [14]. Geometric and distorted particles deal with different forces to amalgamate in solution [15]. The localized dynamics of the process contribute to developing the structure of gold [16,17,18,19], silver [19], and carbon [20,21] atoms.
Atomic elongation in the arrays of a tiny-shaped particle has been discussed elsewhere [22]. A solid atom elongates by stretching the energy knots uniformly [23].
Sir Isaac Newton explained gravity, which mainly covers by Newtonian Physics. Sir Albert Einstein discussed the theory of General Relativity. Bohr proposed electrons move around the allocated orbits, where they have fixed energy in the ground state. Generally, the discussions on the orbits and shells largely remained to describe the electronic structure of different element atoms. The description of atomic structure by quantum states also exists.
However, these studies and other related studies kept the researchers far from thinking about different atomic behaviors. The efforts put forth towards exploring fundamental science remained under less intention. A recent study discussed atomic structure differently from all previously discussed [24].
Under conservative forces, a study discussed the fundamental aspects of structural evolutions [25].
Fundamental aspects of binding different state carbon atoms have been discussed elsewhere [26]. The interaction of the photon with the clamped energy knot electron of any semisolid or solid atom is studied here. The electron dynamics of a silicon atom convert the heat energy into photons is discussed here.
Generating photons under the electron dynamics of suitable element atoms other than silicon atoms is also discussed in preliminary detail. Here, the matter at the atomic and electronic levels, which reveals the phenomena of heat and photon energy, is discussed.
2. Experimental Details
This work does not contain specific experimental detail. However, all those studies studying the photon-matter interaction, light-matter interaction, relation between electron and photon, heat energy, photon energy, fundamental forces, renewable energy, photovoltaics, bandgap, semiconductors, energy science, energy application, energy materials, physics and chemistry of materials may refer this study. This study also counters general physics and chemistry.
3. Models and Discussion
In the process of synergy, atoms of nanoparticles or particles deform under their different interactions [15]. A tiny-shaped particle develops due to elongating its atoms [22]. A photonic current is because of the propagation of featured photons rather than the flow of electrons or charged particles [23]. However, electrons of the suitable atoms can transform heat energy into photon energy when executing dynamics. The photonic current should relate to the propagation of featured photons in a suitable medium. The force and energy directly relate when solid atoms undertake transition states [24].
Different ground points of atoms executing the confined interstate electron dynamics are discussed [25]. Carbon atoms involve energy to form a structure, whereas engaging force [26].
Atoms of those elements, which generate the photons, need energy. Therefore, suitable element atoms can execute the electron dynamics to generate the photons.
A photon can diffract when it interacts with the side of clamped energy knot electron of a semisolid or solid atom. Photons can interact with the electronic tips at suitable angles to reflect also.
3.1. Heat Energy Phenomenon
By dissipating the heat in the air medium, photons travel in the air medium [23]. A long-length photon carries more heat energy than a short-length photon. Short and long-length photons can name overt photons. However, a very long-length or an unending-length photon is only a photon. When a photon dismantles into pieces under suitable interaction, it does not keep nodes and antinodes. The heat of the dismantled photon dissipates, and the force of the dismantled photon permeates the connected medium.
In a silicon atom, the execution of electron dynamics for one forward or reverse cycle generates the unit photon. Thus, the unit photon has the length of minimum conserved force and energy. In Figure 1, label (1) shows the minimum length photon. That photon is like the Gaussian distribution of upwardly turned ends.
The inverted unit photon having a shape like Gaussian distribution with downwardly turned ends is also shown by label (1) in Figure 1. When the unit photon interacts with an electron at a suitable angle, it divides into two equal parts. Each integral symbol relates to one bit of energy, as shown in labels (2) and (3) of Figure 1.
Figure 1.
(1) Unit photons shape like Gaussian distribution having turned ends, (2) division of unit photon in shape like integral symbol and (3) division of unit photon in shape like opposite integral symbol, (4) merged energy of unit photons and (5) broken pieces of unit photons.
Figure 1.
(1) Unit photons shape like Gaussian distribution having turned ends, (2) division of unit photon in shape like integral symbol and (3) division of unit photon in shape like opposite integral symbol, (4) merged energy of unit photons and (5) broken pieces of unit photons.
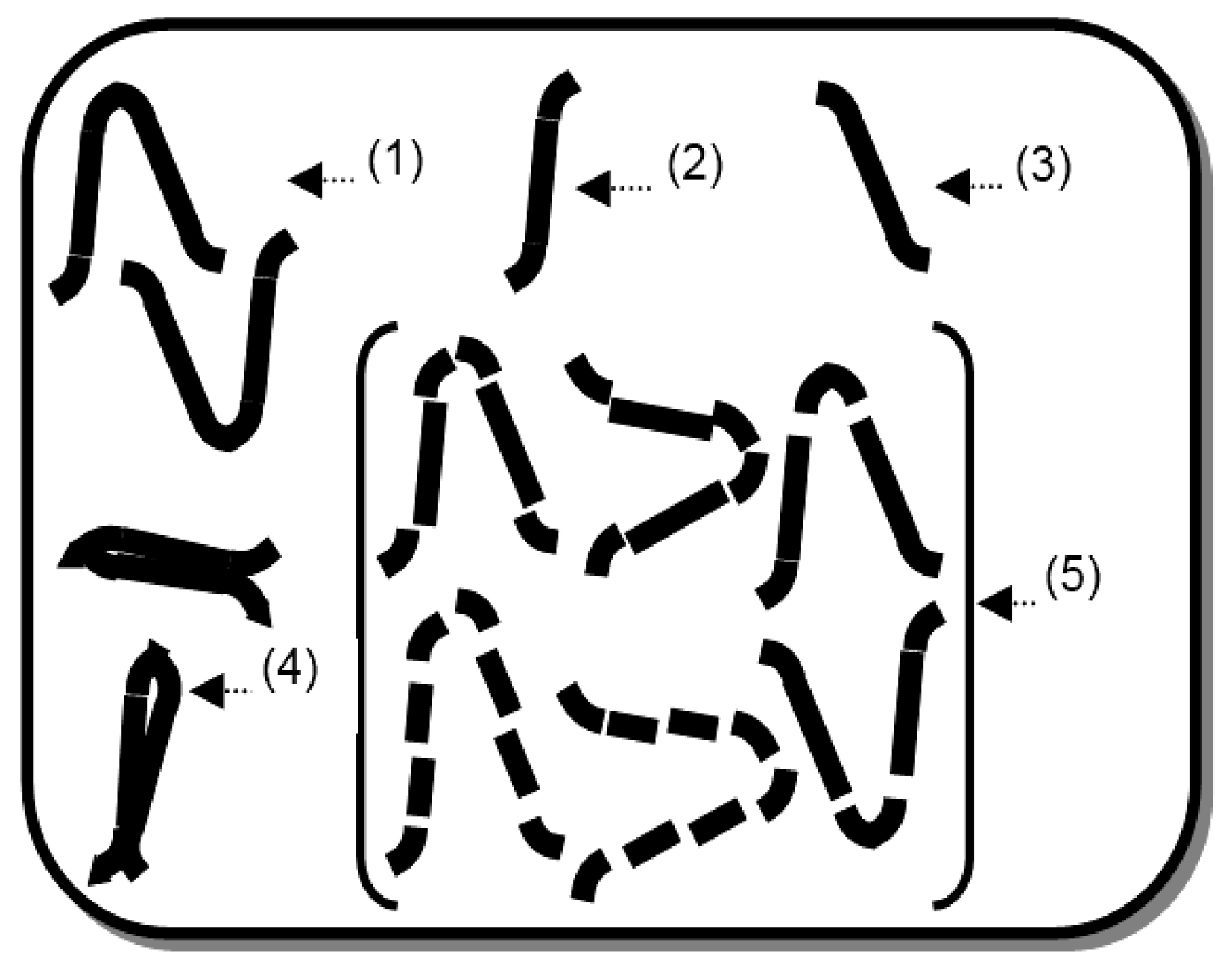
When a unit photon interacts with the electron of hypothesized semisolid or solid atom at a suitable incidence, the folded energy shaped as a fish can result. Label (4) in Figure 1 shows it. The folded energy of a unit photon is a bunch of the merging energy. A unit photon converts into many pieces when interacting with the electron’s side of the hypothesized semisolid or solid atom. Broken pieces of the unit photons relate to heat, as labeled by (5) in Figure 1. It is possible to validate these models from the experimental data. If not possible to validate, at least other arguments can present.
If the changing aspect of an electron within interstate executes uninterruptedly, then a photon of unending length results. A wave-shaped photon is labeled by (1) in Figure 2. That overt photon was generated by the three forward and reverse direction cycles of the electron of the silicon atom.
When a photon interacts with the side of the electron of the hypothesized semisolid or solid atom at a suitable incidence, it folds by the impact of absorption. Label (2) in Figure 2 indicates the incidence. That photon converts into many pieces of heat. Label (3) in Figure 2 shows many pieces. They are now related to only heat. By constructing the approximate angle of 90°, the photon interacts with the tip of the laterally orientated electron of the hypothesized semisolid or solid atom, dividing it into bits of energy. Label (4) in Figure 2 shows the incidence. In Figure 2, many energy bits shaped like integral symbols are labeled by (5). It is possible to validate these models from the experimental data, too. If not possible to validate, at least other arguments can present.
3.2. Photon Energy Phenomenon
In atoms of the semisolid elements, electrons keep half-length above and half-length below the middle of occupied energy knots [24]. Therefore, suitable electrons of the silicon atoms should deal with the forces of two poles for each time-changing aspect.
Electrons of the outer ring of a silicon atom systematically deal with conserved forces. The heat energy can trigger the interstate dynamics of the suitable electrons to convert into photon energy.
The forces exerted on the relevant poles of the electron introduce a moment of inertia, which is in an auxiliary manner at each point of turning that electron. When the suitable electron of the silicon atom executes dynamics for the first half-cycle, the energy of one bit engages along the tracing trajectory.
The energy of one bit also engages along the tracing trajectory of the electron in the second half-cycle. In a silicon atom, electrons of the zeroth ring and the first ring do not execute dynamics.
To execute interstate dynamics, forces from all four poles exert on the outer ring electron in a silicon atom. However, two forces exert at a time. From the poles of the remaining two forces, energy shapes around the force tracing along the electronic tip. In Figure 3a, a top left-sided electron of a silicon atom considers executing interstate dynamics. Figure 3b shows the conversion of heat energy into photon energy for the forwarding cycle of electron dynamics.
At the maximum limit point, the energy of one bit engages along the traced trajectory. Thus, one bit of energy shapes around the tracing force in the first half cycle.
The trajectory tracing by the electron for the first half cycle is up to the maximum limit point, as shown in Figure 3b. The turning of electrons deals with the auxiliary moment of inertia. In the second half cycle, another energy of one bit engages along the tracing trajectory of an electron to shape around the shaping force.
The tracing trajectory by the electron in the second half cycle is from the maximum limit point. The electron again deals with the auxiliary moment of inertia. Thus, a unit photon is due to the force and energy generated from one complete forward direction cycle of interstate electron dynamics. That electron recalls the moment of inertia at each point of turning, which is in an auxiliary manner. Figure 3b shows a complete forward cycle of confined interstate dynamics of the electron.
Figure 3.
(a) Neutral-state silicon atom: (1) targeted electron; (2) zeroth ring; (3) unfilled energy knot. (b) Electron dynamics in the forward cycle: (1) unfilled state; (2) interstate electron gap; (3) filled state; (4) one-bit energy shaping around the force tracing along the trajectory of an electron in the first half cycle; (5) maximum limit point; (6) one-bit energy shaping around the force tracing along the trajectory of an electron in the second half cycle. (c) Three forward cycles and three reverse cycles of interstate electron dynamics engaging the energy of twelve bits to generate the overt photon having a length equal to the lengths of unit photons in six.
Figure 3.
(a) Neutral-state silicon atom: (1) targeted electron; (2) zeroth ring; (3) unfilled energy knot. (b) Electron dynamics in the forward cycle: (1) unfilled state; (2) interstate electron gap; (3) filled state; (4) one-bit energy shaping around the force tracing along the trajectory of an electron in the first half cycle; (5) maximum limit point; (6) one-bit energy shaping around the force tracing along the trajectory of an electron in the second half cycle. (c) Three forward cycles and three reverse cycles of interstate electron dynamics engaging the energy of twelve bits to generate the overt photon having a length equal to the lengths of unit photons in six.
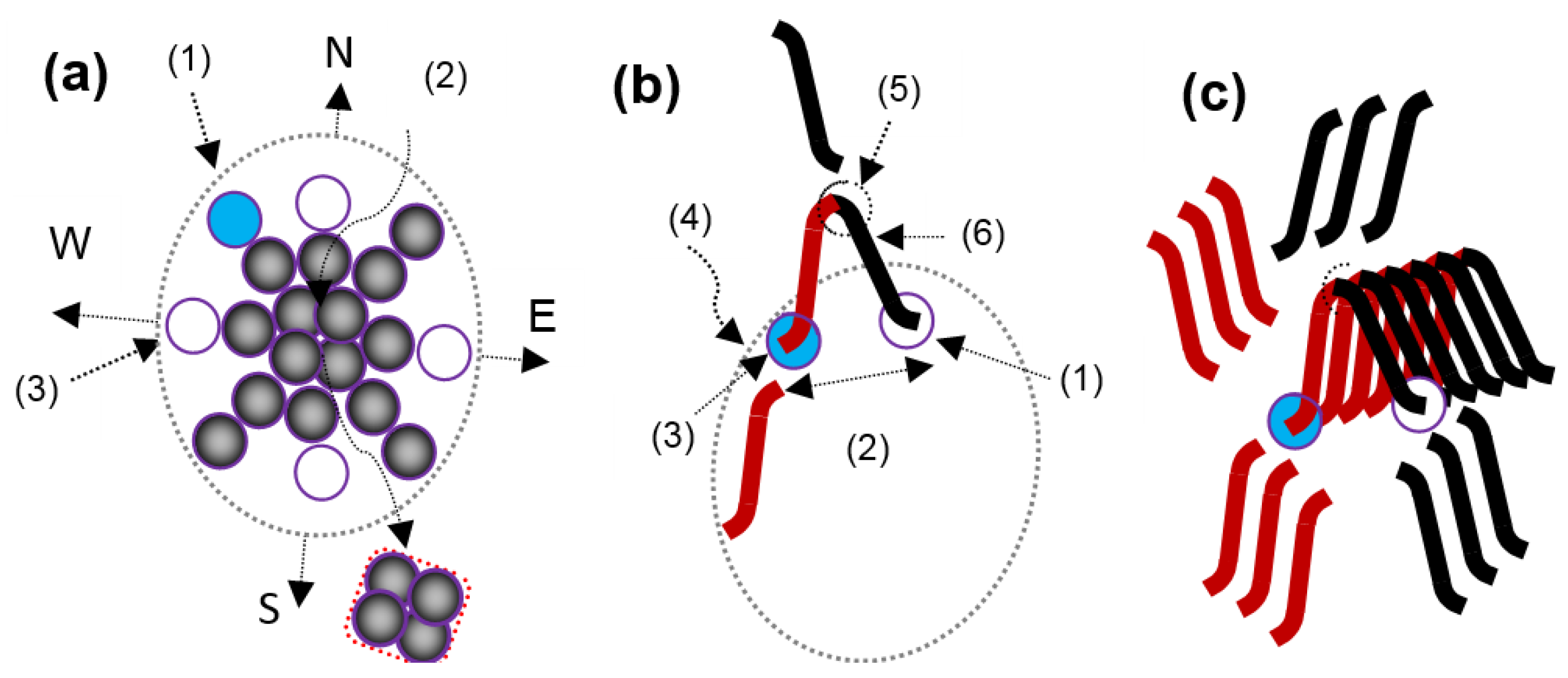
The turning positions of the electron under the auxiliary moment of inertia are responsible for forcing the energy of a photon from one point to another. The exerted forces on the electron remain path-independent. In Figure 3b, that electron executing confined interstate dynamics does not possess any other way to regain the state.
When the interstate electron dynamics of the silicon atom complete six cycles, three forward and three reverse directions, the energy of twelve bits forms a wave shape.
The electron does not touch the energy knot in the forward or reverse cycle. Hence, under uninterrupted forward and reverse cycles, the execution of interstate electron dynamics generates the force and energy to build an overt photon. The shape of energy engaged along the trajectory of electron dynamics for the first half cycle is like a straight integral symbol (ᶴ).
The shape of energy engaged along the trajectory of electron dynamics for the second half cycle is like the opposite integral symbol (ʅ). Figure 3c shows the energy bits of both shapes.
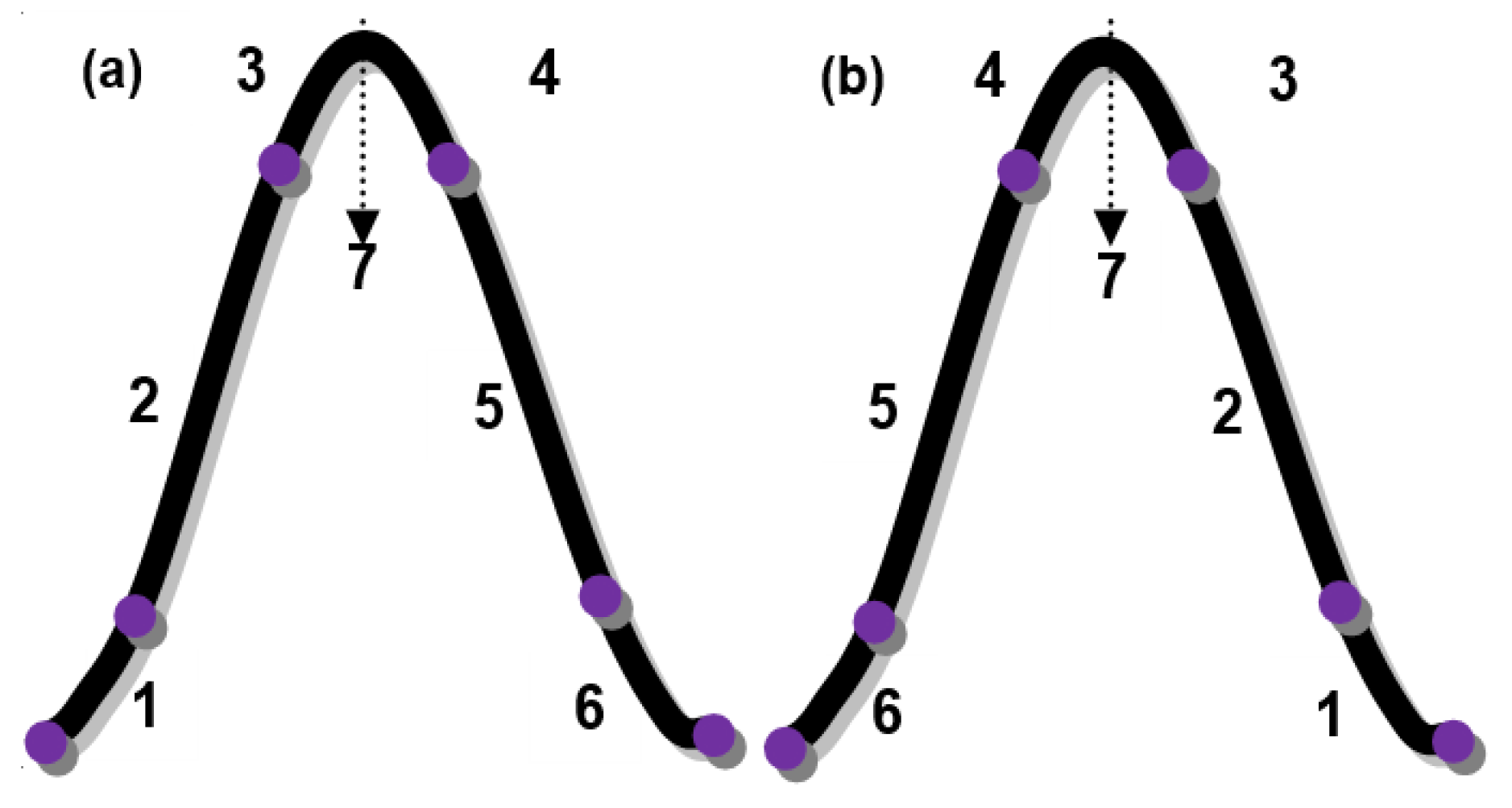
For the first-half and second-half forward cycles of electron dynamics, two shapes of integral symbols connect at the center of the maximum limit point resulting in the overall shape of force and energy shaped like Gaussian distribution in the turned ends, shown in Figure 4.
Figure 4a plots the relationship between force and energy in the forward cycle of the electron. Labels (1) to (6) denote different steps in Figure 4a. Figure 4b shows the reverse cycle of the electron and the relationship between force and energy. Labels 1, 2, 3, 4, 5, and 6 also show the different steps in Figure 4b. In Figure 4, label (7) denotes the maximum limit point. From that point, that electron turns towards the nearby unfilled state to occupy it due to the appearance of the opposite end exerted forces.
Figure 4.
Sections of the unit photon generated by electron dynamics of silicon atom in (a) forwarding and (b) reverse cycles; (7) maximum limit point connecting left and right half-cycles.
Figure 4.
Sections of the unit photon generated by electron dynamics of silicon atom in (a) forwarding and (b) reverse cycles; (7) maximum limit point connecting left and right half-cycles.
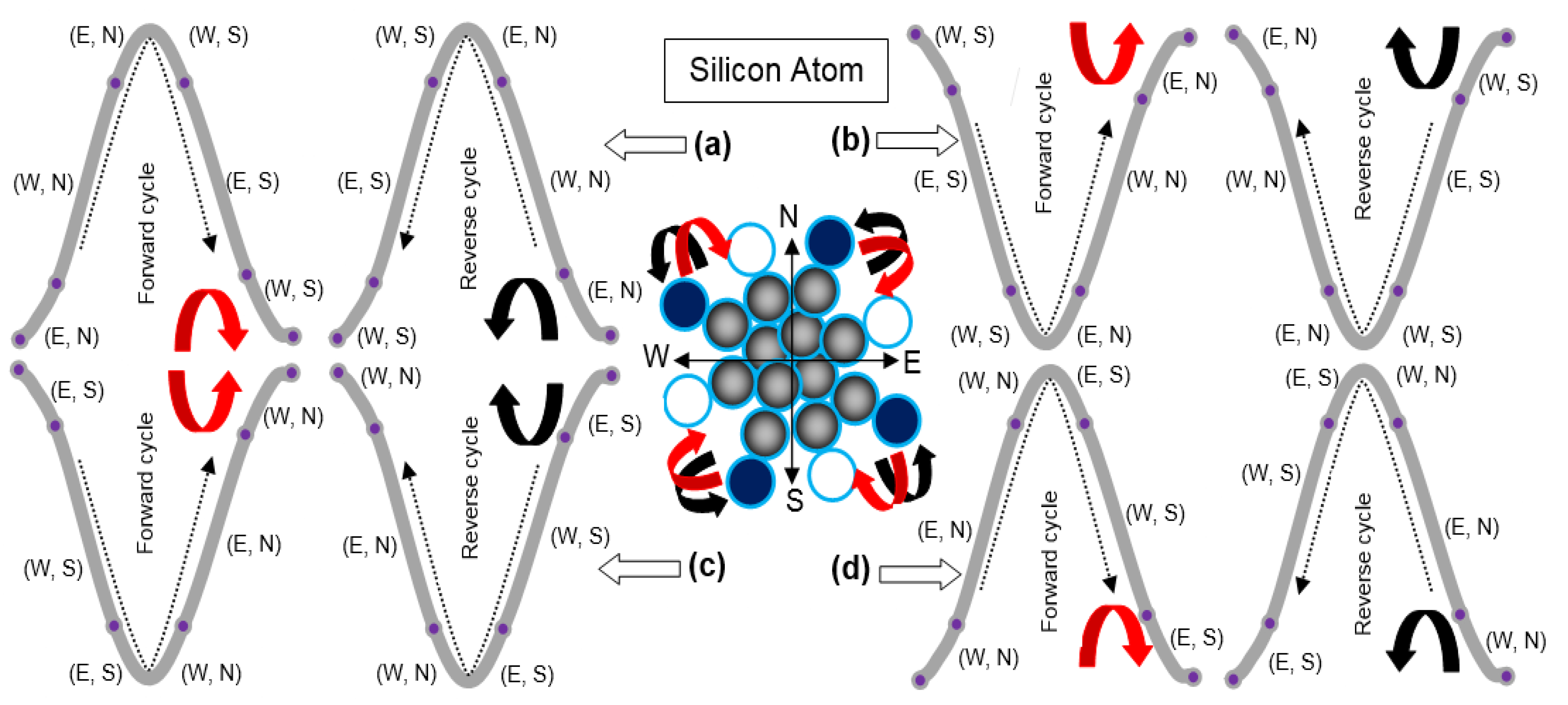
Therefore, by recalling the moment of inertia in an auxiliary manner, that electron deals with the following exerting forces. In each step of interstate electron dynamics, forces of two poles act together but from opposite sides, which causes that electron to turn. In Figure 5, electrons of four quadrants trace the trajectories of confined inter-state dynamics in both forward and reverse cycles. Figure 5a shows that an electron leaves the state from the rear side or tail and enters the nearby state from the front side or head while executing forward interstate dynamics. So, it will leave the state from the rear side or tail and enters the nearby state from the front side or head while executing reverse interstate dynamics.
The electron in Figure 5b oppositely executes dynamics to keep the equilibrium state of the atom. In Figure 5c, an electron leaves the state from the front or head and enters the nearby state from the rear side or tail while executing forward interstate dynamics. So, it will leave the state from the front side or head and enters the nearby state from the rear side or tail while executing reverse interstate dynamics.
In Figure 5, the electrons can also execute the dynamics in reverse order. Figure 5a–d shows forward and reverse cycles of electron dynamics in all quadrants of the silicon atom symbolically. Figure 5a–d also shows the forces exerted on the electron at each turning point.
Figure 5.
Electrons of four quadrants denoted by (a), (b), (c), and (d) deal with the east (E), west (W), north (N), and south (S) forces along the relevant poles while executing confined inter-state dynamics in forward (red-colored round arrows) and reverse (black colored round arrows) cycles.
Figure 5.
Electrons of four quadrants denoted by (a), (b), (c), and (d) deal with the east (E), west (W), north (N), and south (S) forces along the relevant poles while executing confined inter-state dynamics in forward (red-colored round arrows) and reverse (black colored round arrows) cycles.
In the atoms where conservative forces from three poles involve, interstate electron dynamics transform heat energy into photon energy shape like connected integral symbols. But it is pertinent to state here that an electron deals with the forces of only two poles at a time to execute interstate dynamics as indicated for a silicon atom in Figure 5.
In the atoms of those elements where conservative forces from only two poles exert, interstate electron dynamics transform heat energy into photon energy having a shape like connected tick symbols.
In the atoms of those elements where conservative forces from only three poles exert and an electron under dynamics attempts to cross the pole of its atom, heat energy converts into photon energy, having a shape like a connected L alphabet. However, an electron deals with the forces of only two poles at a time.
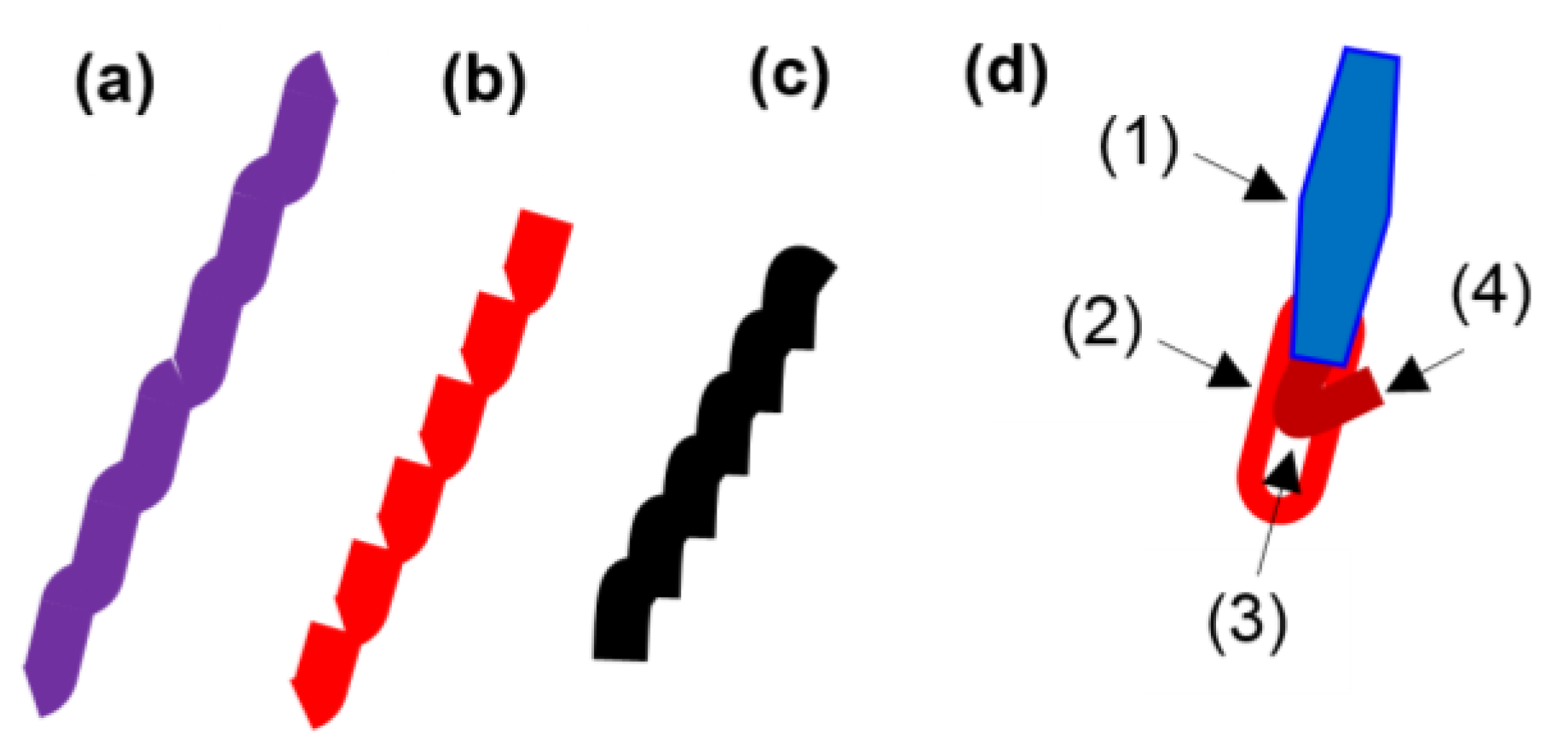
Figure 6a–c shows the shape of the photon-like connected integral symbols, tick symbols, and L-like symbols, respectively. In Figure 6d, a photon shows both portions of force and energy.
Suitable element atoms can generate photons of different characteristics. The generated photons with a different nature can open new areas of research.
3.3. General Discussion
Each silicon cell connected in the series in the solar panel adds up to the generating number of photons. As observed in solar panels, solar cells can generate maximum power when the setting is under the proper inclination.
The cycles of confined interstate electron dynamics of silicon atoms remain uninterrupted for an extended period, where titling the solar panel at a suitable angle concerning the base results in varying efficiency. Depositing silicon atoms for a few layers can generate high power.
It appears that one electron or three electrons of the outer ring cannot execute interstate dynamics. A generating photon by the confined interstate electron dynamics can also disturb the center of an atom, thus not providing the feasible conditions for one electron or three electrons to execute dynamics.
However, more work is required to depict the complete picture. Figure 5d shows that the electron oppositely executes dynamics under the equilibrium state of an atom.
When the featured photons interacted with the tips of laterally orientated electrons of elongated atoms, the reverted element of force prints the pattern [27]. The set modalities of photons depend on the origin of generation establishing the role set by the manufacturer. A structural design is crucial to introduce the specific application [28,29,30,31,32,33,34,35,36,37]. A structural shape is due to the controlled behavior of force and energy [17].
Where there is no specific interaction of a photon with the electron, it divides into pieces of heat. The heat of a divided photon dissipates in the structure of atoms. The conversion of energy from one form to another depends on structural characteristics.
The behaviors of force and energy are different in depositing carbon films [20,38]. The development of particles under predictor packing is also studied, where photons shaped as waves get converted into tuned pulses [39]. Measuring the temperature of such materials is an integral part of the research, and some studies have also shed light on it [40,41,42]. A study explained the role of van der Waals interactions in the isolated atoms by considering the induced dipoles [43]. Dispersion forces or van der Waals interactions attain when charge density fluctuations behave in a wave fashion [44].
4. Conclusion
A unit photon contains the energy of two bits, whereas a long-length photon has several bits. Two unit photons build the least length photon. When an overt photon interacts with the north-sided tip of the laterally orientated electron at approx. 90° angle, it gets divided into bits of energy. Bits of energy can further divide into pieces of heat.
When a photon interacts with the side of the electron of a semisolid or solid atom, it diffracts, dividing into pieces. Pieces of the dismantled photon dissipate the heat and permeate the force. When an outer ring electron of a silicon atom executes confined interstate dynamics, two forces exert at a time introducing an auxiliary moment of inertia. In a silicon atom, energy shapes around the force tracing along the trajectory of an electron. Energy in every electron dynamics shapes from the sides not dealing with the force exertion. When the interstate electron dynamics is for one forward or reverse cycle, a unit photon in shape like Gaussian distribution with turned ends generates.
The exerted forces on the electron change the aspects by restricting it in the interstate gap. The force and energy shaping along the trajectory of the electron remains preserved. The auxiliary moment of inertia recalls at each point of turning electron. In a silicon atom, a reference point of the electrons executing dynamics is the center of an atom. In the first stage, an electron lifts laterally. The forces exerting on the electron remain conserved within the interstate electron dynamics. Before crossing the maximum limit point, the electron examines by the opposite forces pulling it.
To return, it gets relief from the effect of first-half forces. So, to turn, opposite forces are exerted on the electron. Path-independent conservative forces exerted on the electron acquiring its lateral and adjacent positions are within the natural viability. The electron executes interstate dynamics at the speed of light. Electrons of the suitable atoms build a bandgap where photons propagate to define the photonic band gap. In the propagation of photons, force energy together transfers from one point to other.
Different atoms generate different shape photons depending on the built-in interstate gap of electron dynamics. So, suitable element atoms can generate photons other than a waveform depending on their built-in interstate electron gap. Such investigations open up new horizons in energy science and materials science.
Data Availability Statement
The work is related to the fundamental nature of science.
Acknowledgments
M. A. acknowledges this work to all the offices supported in his career.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bohm, D.; Pines, D. A Collective Description of Electron Interactions. I. Magnetic Interactions. Phys. Rev. 1951, 82, 625–634. [Google Scholar] [CrossRef]
- Pines, D.; Bohm, D. A Collective Description of Electron Interactions: II. Collective vs Individual Particle Aspects of the Interactions. Phys. Rev. 1952, 85, 338–353. [Google Scholar] [CrossRef]
- Ritchie, R.H. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Bohm, D.; Pines, D. A Collective Description of Electron Interactions: III. Coulomb Interactions in a Degenerate Electron Gas. Phys. Rev. 1957, 92, 609–625. [Google Scholar] [CrossRef]
- Low, T.; Chaves, A.; Caldwell, J.D.; Kumar, A.; Fang, N.X.; Avouris, P.; Heinz, T.F.; Guinea, F.; Martin-Moreno, L.; Koppens, F. Polaritons in layered two-dimensional materials. Nat. Mater. 2017, 16, 182–194. [Google Scholar] [CrossRef]
- Frenkel, J. On the Transformation of Light into Heat in Solid. I. Phys. Rev. 1931, 37, 17–44. [Google Scholar] [CrossRef]
- Couto, O.D.D., Jr.; Puebla, J.; Chekhovich, E.A.; Luxmoore, I.J.; Elliott, C.J.; Babazadeh, N.; Skolnick, M.S.; Tartakovskii, A.I.; Krysa, A.B. Charge control in InP/(Ga,In)P single quantum dots embedded in Schottky diodes. Phys. Rev. B 2011, 84, 125301-7. [Google Scholar] [CrossRef]
- Brust, M.; Walker, M.; Bethell, D.; Schiffrin, D.J.; Whyman, R. Synthesis of Thiol-derivatised Gold Nanoparticles in a Two-phase Liquid–Liquid System. J. Chem. Soc. Chem. Commun. 1994, 801–802. [Google Scholar] [CrossRef]
- Whetten, R.L.; Khoury, J.T.; Alvarez, M.M.; Murthy, S.; Vezmar, I.; Wang, Z.L.; Stephens, P.W.; Cleveland, C.L.; Luedtke, W.D.; Landman, U. Nanocrystal Gold Molecules. Adv. Mater. 1996, 8, 428–433. [Google Scholar] [CrossRef]
- Brust, M.; Kiely, C.J. Some recent advances in nanostructure preparation from gold and silver particles: a short topical review. Colloids and Surfaces A: Physicochem. Eng. Aspects. 2002, 202, 175–186. [Google Scholar] [CrossRef]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 2007, 6, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Link, S.; El-Sayed, M.A. Shape and size dependence of radiative, nonradiative and photothermal properties of gold nanocrystals. Int. Rev. Phys. Chem. 2000, 19, 409–453. [Google Scholar] [CrossRef]
- Shaw, C.P.; Fernig, D.G.; Lévy, R. Gold nanoparticles as advanced building blocks for nanoscale self-assembled systems. J. Mater. Chem. 2011, 21, 12181–12187. [Google Scholar] [CrossRef]
- Negishi, Y.; Nakazaki, T.; Malola, S.; Takano, S.; Niihori, Y.; Kurashige, W.; Yamazoe, S.; Tsukuda, T.; Häkkinen, H. A Critical Size for Emergence of Nonbulk Electronic and Geometric Structures in Dodecanethiolate-Protected Au Clusters. J. Am. Chem. Soc. 2015, 137, 1206–1212. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Lin, I.-N. Forces driving amalgamation of nanoparticles and particles in solution. Forces Mech. 2022, 7, 100076. [Google Scholar] [CrossRef]
- Ali, M.; Lin, I.-N. Development of Gold Tiny Particles and Particles in Different Sizes at Varying Precursor Concentration. Adv. Nat. Sci. Nanosci. Nanotechnol. 2020, 11, 015006. [Google Scholar] [CrossRef]
- Ali, M.; Lin, I.-N. Controlling morphology-structure of gold tiny particles, nanoparticles, and particles at different pulse rates and pulse polarity. Adv. Nat. Sci. Nanosci. Nanotechnol. 2019, 10, 025015. [Google Scholar] [CrossRef]
- Ali, M.; Lin, I.-N. Formation of tiny particles and their extended shapes: Origin of physics and chemistry of materials. Appl. Nanosci. 2019, 9, 1367–1382. [Google Scholar] [CrossRef]
- Ali, M.; Lin, I.-N.; Yeh, C.-J. Tapping Opportunity of Tiny-Shaped Particles and Role of Precursor in Developing Shaped Particles. Nano 2018, 13, 1850073. [Google Scholar] [CrossRef]
- Ali, M.; Lin, I.-N. Phase transitions and critical phenomena of tiny grains carbon films synthesized in microwave-based vapor deposition system. Surf. Interface Anal. 2019, 51, 389–399. [Google Scholar] [CrossRef]
- Ali, M.; Ürgen, M. Switching dynamics of morphology-structure in chemically deposited carbon films – A new insight. Carbon 2017, 122, 653–663. [Google Scholar] [CrossRef]
- Ali, M. Tiny-Shaped Particles Developing a Mono-Layer Shape Dealing with Localized Gravity and Levity at the Solution Surface. arXiv 2023. http://arxiv.org/abs/1609.08047v33.
- Ali, M. Atoms of None of the Elements Ionize While Atoms of Inert Behavior Split by Photonic Current. arXiv 2022. http://arxiv.org/abs/1611.05392v31.
- Ali, M. Atoms in Gaseous and Solid States and their Energy and Force Relationships under Transitional Behaviors. 2023. [Google Scholar] [CrossRef]
- Ali, M. Structure Evolutions in Atoms of the Elements Executing Confined Interstate Electron Dynamics. arXiv 2023. http://arxiv.org/abs/1611.01255v31.
- Ali, M. Atomic Structure and Binding of Carbon Atoms. 2023. https://www.preprints.org/manuscript/201801.0036/v16.
- Ali, M.; Lin, I.-N. Gold Nanostructures and Microstructures with Tunable Aspect Ratios for High-Speed Uni- and Multidirectional Photonic Applications. ACS Appl. Nano Mater. 2020, 3, 9410–9424. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, L. Structure Evolutions and Metallic Transitions in In2Se3 Under High Pressure. J. Phys. Chem. C 2014, 118, 5445–5452. [Google Scholar] [CrossRef]
- Manoharan, V.N. Colloidal matter: Packing, geometry, and entropy. Science 2015, 349, 1253751. [Google Scholar] [CrossRef]
- Park, J.; Elmlund, H.; Ercius, P.; Yuk, J.M.; Limmer, D.T.; Chen, Q.; Kim, K.; Han, S.H.; Weitz, D.A.; Zettl, A.; et al. 3D structure of individual nanocrystals in solution by electron microscopy. Science 2015, 349, 290–295. [Google Scholar] [CrossRef]
- Jacobsson, D.; Panciera, F.; Tersoff, J.; Reuter, M.C.; Lehmann, S.; Hofmann, S.; Dick, K.A.; Ross, F.M. Interface dynamics and crystal phase switching in GaAs nanowires. Nature 2016, 531, 317–322. [Google Scholar] [CrossRef]
- Tuma, T.; Pantazi, A.; Le Gallo, M.; Sebastian, A.; Eleftheriou, E. Stochastic phase-change neurons. Nat. Nanotechnol. 2016, 11, 693–699. [Google Scholar] [CrossRef]
- Rensberg, J.; Zhang, S.; Zhou, Y.; McLeod, A.S.; Schwarz, C.; Goldflam, M.; Liu, M.; Kerbusch, J.; Nawrodt, R.; Ramanathan, S.; et al. Active Optical Metasurfaces Based on Defect-Engineered Phase-Transition Materials. Nano Lett. 2016, 16, 1050–1055. [Google Scholar] [CrossRef]
- Suzuki, Y.; Cardone, G.; Restrepo, D.; Zavattieri, P.D.; Baker, T.S.; Tezcan, F.A. Self-assembly of coherently dynamic, auxetic, two-dimensional protein crystals. Nature 2016, 533, 369–373. [Google Scholar] [CrossRef]
- Evers, C.H.J.; Luiken, J.A.; Bolhuis, P.G.; Kegel, W.K. Self-assembly of microcapsules via colloidal bond hybridization and anisotropy. Nature 2016, 534, 364–368. [Google Scholar] [CrossRef]
- Epstein, I.R.; Xu, B. Reaction–diffusion processes at the nano- and microscales. Nat. Nanotechnol. 2016, 11, 312–319. [Google Scholar] [CrossRef]
- Azizi, A.; Wang, Y.; Lin, Z.; Wang, K.; Elias, A.L.; Terrones, M.; Crespi, V.H.; Alem, N. Spontaneous Formation of Atomically Thin Stripes in Transition Metal Dichalcogenide Monolayers. Nano Lett. 2016, 16, 6982–6987. [Google Scholar] [CrossRef] [PubMed]
- Ali, M. Etching of Photon Energy into Binding Energy in Depositing Carbon Films at Different Chamber Pressures. J. Mater. Sci. Mater. Electron. 2022. https://arxiv.org/abs/1802.00730v24. [CrossRef]
- Ali, M.; Lin, I.-N.; Yeh, C.-J. Predictor Packing in Developing Unprecedented Shaped Colloidal Particles. Nano 2018, 13, 1850109. [Google Scholar] [CrossRef]
- Mecklenburg, M.; Hubbard, W.A.; White, E.R.; Dhall, R.; Cronin, S.B.; Aloni, S.; Regan, B.C. Nanoscale temperature mapping in operating microelectronic devices. Science 2015, 347, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Hou, D.; Zheng, X.; Yan, Y.; Di Ventra, M. Local temperatures of strongly-correlated quantum dots out of equilibrium. Phys. Rev. B 2015, 91, 205106. [Google Scholar] [CrossRef]
- Menges, F.; Mensch, P.; Schmid, H.; Riel, H.; Stemmer, A.; Gotsmann, B. Temperature mapping of operating nanoscale devices by scanning probe thermometry. Nat. Commun. 2016, 7, 10874. [Google Scholar] [CrossRef] [PubMed]
- Kawai, S.; Foster, A.S.; Björkman, T.; Nowakowska, S.; Björk, J.; Canova, F.F.; Gade, L.H.; Jung, T.A.; Meyer, E. Van der Waals interactions and the limits of isolated atom models at interfaces. Nat. Commun. 2016, 7, 11559. [Google Scholar] [CrossRef] [PubMed]
- Ambrosetti, A.; Ferri, N.; DiStasio, R.A., Jr.; Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef]
Short Biography of Author
 |
In 1996, Mubarak Ali earned a B.Sc. degree in Physics and Mathematics. The University of the Punjab awarded him the degree. The M.Sc. degree in Materials Science got in 1998. Bahauddin Zakariya University Multan awarded him the degree of master with distinction. He completed his M.Sc. thesis at Quaid-i-Azam University Islamabad. He gained a Ph.D. in Mechanical Engineering from the Universiti Teknologi Malaysia under the award of the Malaysian Technical Cooperation Programme (MTCP;2004-07) and a postdoc in advanced surface technologies at Istanbul Technical University under the foreign fellowship of The Scientific and Technological Research Council of Turkey (TÜBİTAK, 2010). Dr. Mubarak completed another postdoc in nanotechnology at the Tamkang University Taipei, 2013-2014, sponsored by the National Science Council, now the Ministry of Science and Technology, Taiwan. He remained working as an Assistant Professor on the tenure track at COMSATS University Islamabad from May 2008 to June 2018, previously known as COMSATS Institute of Information Technology. His new position is in process. Before that, he remained a working assistant and deputy director at M/o Science & Technology, Pakistan Council of Renewable Energy Technologies, Islamabad, from January 2000 to May 2008. The Institute for Materials Research at Tohoku University Japan invited Dr. Mubarak to deliver a scientific talk. His scientific research remained a part of many conferences organized by renowned universities in many countries. His core area of research includes materials science, physics & nanotechnology. He also won a merit scholarship for Ph.D. study from the Higher Education Commission, Government of Pakistan. However, he did not avail the opportunity. He earned a diploma (in English) and a certificate (in the Japanese language) in 2000 and 2001, respectively, part-time from the National University of Modern Languages, Islamabad. He is the author of several articles available at the following links; https://www.researchgate.net/profile/Mubarak_Ali5 & https://scholar.google.com.pk/citations?hl=en&user=UYjvhDwAAAAJ. |
Figure 2.
(1) overt photon, (2) interaction of an overt photon with the side of laterally orientated electron of a hypothesized semisolid or solid atom, (3) pieces of heat, (4) interaction of an overt photon with the tip of laterally orientated electron of a hypothesized semisolid or solid atom and (5) bits of energy.
Figure 2.
(1) overt photon, (2) interaction of an overt photon with the side of laterally orientated electron of a hypothesized semisolid or solid atom, (3) pieces of heat, (4) interaction of an overt photon with the tip of laterally orientated electron of a hypothesized semisolid or solid atom and (5) bits of energy.
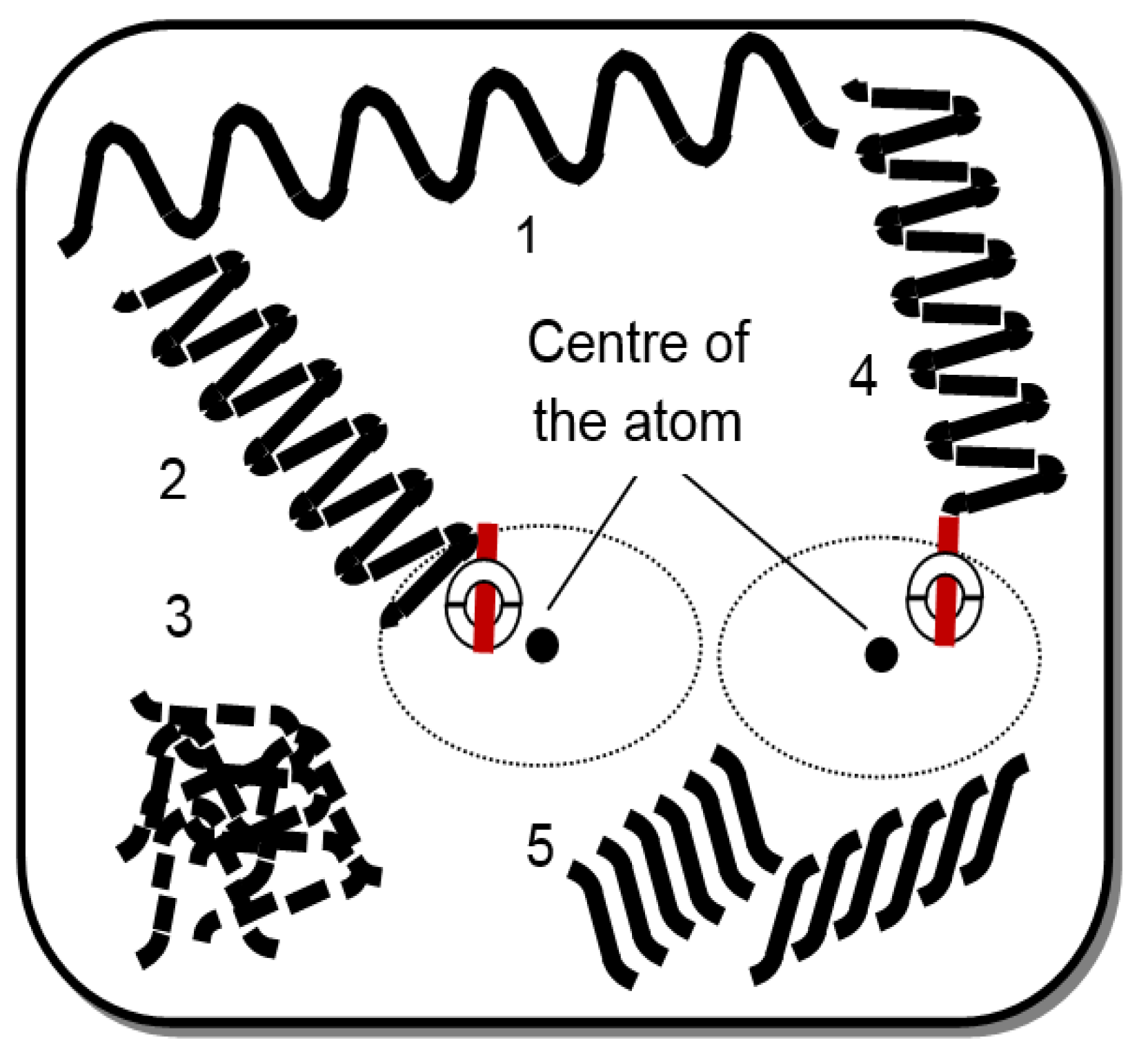
Figure 6.
Overt photon of connected (a) integral symbols, (b) tick symbols, (c) L-like symbols, and (d) shaping force and energy along the trajectory; (1) electron dynamics, (2) shaping energy, (3) shaping force, (4) the removed red-colored energy region showing the force in white color.
Figure 6.
Overt photon of connected (a) integral symbols, (b) tick symbols, (c) L-like symbols, and (d) shaping force and energy along the trajectory; (1) electron dynamics, (2) shaping energy, (3) shaping force, (4) the removed red-colored energy region showing the force in white color.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





