Prerpints.org logo
Preprint
Article

Atomic Structure and Binding of Carbon Atoms

Altmetrics

Downloads

4370

Views

5623

Comments

0

This version is not peer-reviewed

Submitted:

09 March 2024

Posted:

13 March 2024

You are already at the latest version

Alerts
Abstract
Carbon exhibits complex behavior due to several allotropes. Processing carbon precursors by different techniques and methods results in various carbon materials. However, the characterizations and analyses of processed carbon materials in any form do not keep up to the mark discussions. There are many uncertainties. First, there is a need to study each carbon allotropic form separately and then the binding of same-state atoms. Depending on the processing conditions of a carbon precursor, the state of the carbon atom changes. The conversion of the carbon atom from one state to another is due to the electron transfer mechanism. The bits of energy with shape-like dashes transfer electrons to nearby unfilled states during the state conversion of a carbon atom. The involved dash-shaped energy bit maintains partially conserved behavior. Atoms in the graphite state also study a one-dimensional structure under the execution of electron dynamics. There is a two-dimensional structure in nanotube atoms and a four-dimensional structure in fullerene atoms. If the diamond atoms bind, the outer ring electrons of the depositing diamond atom undertake an additional clamp of the outer ring energy knot of the deposited diamond atom. Binding in the diamond atoms occurs from the surface (east-west) to the south. Therefore, the growth of the diamond structure occurs from the south to the surface (east-west). Golf-stick-shaped energy bits bind the diamond, lonsdaleite, or graphene state atoms into their structures. In a glassy carbon structure, the layers of gaseous, graphitic, and lonsdaleite atoms bind simultaneously. The layers repeat in order during the growth process of glassy carbon. The hardness of the processed material in each state of carbon provides new insight. This study aimed to understand the fundamental and applied science of carbon atoms and their binding to structures.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1.0. Introduction

New strategies are needed to process and synthesize carbon materials. Characterizations and analyses of carbon materials can also help to explore new science at both the primary and applied levels. The forces exerted at the electron level should also explain the role of energy at the electron level, which is discussed in preliminary detail [1,2,3]. When structural formation in carbon atoms involves partial conservative energy at the electron level, there is also the engagement of partially conserved forces at the electron level. This can also be the case for the structural formation of graphite, nanotubes, and fullerene atoms.
However, in the structural formation of carbon atoms where the non-conserved energy is at the electron level, the non-conserved forces should also engage at the electron level.
Forces and energy can contribute together at the atomic level when a suitable state of carbon atoms amalgamates under attained dynamics. This can occur for graphite atoms when studying a two-dimensional or amorphous structure. The involvement of the energy at the electron level directs the forces to engage at the electron level. As a result, atoms bind to study their nanoscale or micro-sized grains. The outer ring electrons of carbons maintain a very close distance from the centers of their atoms. Overall, the nature of the involved energy should depend on the specific state of the carbon atom. In the literature, several studies have discussed the allotropic forms of carbon.
When conservative forces exist, an electron in a silicon atom executes uninterrupted dynamics to generate a photon of unending length [2]. This indicates that the built-in interstate gap of electron dynamics in the carbon atom differs from that in silicon. Both carbon and silicon atoms possess equal numbers of filled and unfilled states in the outer ring. However, the outer ring electrons of carbon and silicon maintain different distances from their atomic centers.
Gaseous and solid atoms deal with the transitions while undertaking the liquid state, where the electrons remain within the occupied energy knots [3]. The structures evolve in those atoms that execute confined interstate electron dynamics, as discussed elsewhere [4]. Atoms do not form ions [5]. The carbon film deposited in tiny grains is due to the synthetic protocol [6]. Carbon films with different morphologies were deposited under various process conditions [7].
At different chamber pressures, the deposited carbon films exhibit different morphologies and structures [8]. At different interwire distances, a carbon film was deposited in the diamond and graphitic phases [9]. This means that the electron transfer mechanism involves changing the chemical nature of an atom regardless of whether it belongs to the same element. The force entering from the north pole and leaving the ground surface for the south pole behaves differently than the forces exerted at the ground surface [10]. A recent study showed the transformation of graphene film into a diamond-like carbon film, where the elastic deformations and chemical natures were changed [11]. Wu et al. [12] reviewed the developments in Raman spectroscopy of graphene materials.
In the vapor deposition method, carbon nanofibers grow without a catalyst [13]. Different applications related to graphene hybrids have been reviewed [14]. Nitrogen-incorporated carbon dots were merged to modify a glassy carbon electrode [15]. A novel energy dissipation system was investigated by gathering the features of both carbon nanotubes and fullerenes [16]. Different carbon allotropes, in comparison, were studied for temperature dehydrogenation [17].
The exact position of the vacancies in a diamond crystal was also studied [18]. Liu et al. [19] presented an efficient strategy for fabricating a graphite-graphene Janus architecture. Some parameters under the optimized conditions of the process chosen to deposit the diamond [20]. Cheng and Zong [21] observed the structural evolution of damaged carbon atoms in a deep surface layer. Maruyama and Okada [22] investigated the electronic and magnetic structures of a two-dimensional network of carbon atoms. Narjabadifam et al. [23] studied carbon nanocones through molecular dynamics simulation. Levitated nanodiamonds burn in the air because of amorphous carbon [24]. The uncertainty in the temperature measurements of levitated nanodiamonds was removed [25].
Heat treatment improves the mechanical properties of carbon films deposited by magnetron sputtering [26]. A deposited carbon nanotube film shows enhanced electrode stability [27]. Carbon films are deposited in a pulse-based CVD system to improve tribological properties [28]. The electronic states of carbon-based materials control covalent bonding [29]. The relationships among the different parameters used for depositing carbon films have been discussed separately [30]. High negative bias voltages reduce the hydrogen content in deposited carbon films [31]. Carbon films deposited with an enhanced thickness are not beneficial for all purposes [32]. One study discussed the structure of carbon films deposited by the sputtering method [33]. The graphitic phase of deposited carbon films reduces the friction coefficient in a vacuum medium [34]. Carbon films have a decreased hydrogen content deposited by tuning the ratio of the graphitic and diamond phases [35].
The hardness of a single-walled carbon nanotube has been discussed separately [36]. Carbon nanotubes deposited by the floating catalyst CVD technique have potential applications [37]. Carbon nanotube films exhibit high thermal conductivity [38]. A recent study suggested the photochemical conversion of the graphitic phase into the diamond phase [39]. In the deposition of diamond-like carbon, the sp2 carbon or graphitic phase increases due to the introduction of titanium [40]. In deposited carbon films by HF-CVD, a structural and electrical relationship is established between amorphous carbon and graphene [41]. A recent study investigated porous carbon films for efficient electromagnetic applications [42]. Electrochemical sensor applications have been studied in vertical mesoporous carbon films [43]. The thermal stability and diffusion characteristics of ultrathin amorphous carbon films were investigated [44].
These studies and the ones not cited raise some fundamental questions. How do the different allotropes of carbon form? How do the same-state carbon atoms bind in the formation of a structure? How do energy and forces behave to convert one atomic state to another state? How do they function in the binding of same-state atoms in different carbon allotropes? How the structural formation of glassy carbon occurs is also relevant? Different carbon-based materials also discuss their hardness with new insight.

2.0. Experimental details

Many published studies on carbon films and other carbon-based materials have described the experimental details. Depositing carbon films has been extensively discussed in the literature. Several techniques in the literature have been used to analyze the deposition of carbon-based materials under different processing conditions. The purpose of this study was to explore the underlying mechanism of different carbon states rather than to provide additional details. A binding mechanism in the same-state carbon atoms is also a subject of this study.
The science discussed here is the central subject of every study considering the deposition of carbon materials in any form and by any technique. However, the experimental details can be found in those studies in which different carbon-based precursors and compounds were processed. This study explored the fundamental and applied science of carbon allotropes. According to published studies on carbon, models of its different allotropes can be drawn. This study also identified the kind of energy involved and the nature of the forces engaged in the binding of same-state carbon atoms. The present study also reports the Mohs hardnesses of different carbon materials.

3.0. Atomic structure in the carbon and electron transfer mechanism

3.1. Carbon lattice and structure of carbon allotropes or states

Different states of carbon atoms are extensively present in the literature. However, they do not show the electronic configuration for each state. The formation mechanism of the carbon lattice has also yet to be determined. Different-state carbon atoms rely on the same number of electrons. A carbon atom has a fixed number of filled and unfilled states for any state. Changing the position of the electrons gives rise to the new chemistry of that atom.
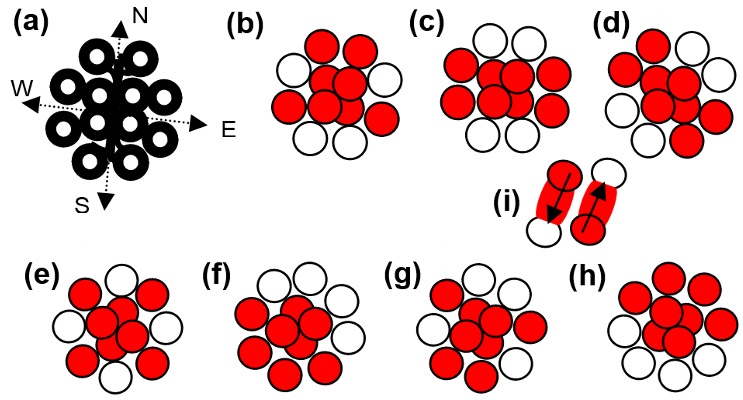
When overt (or long-length) photons intercross to build twelve energy knots, they shape the carbon lattice. In intercrossing, overt photons keep the centers of their lengths at a common point. Figure 1 (a) shows the lattice of a carbon atom. Two energy knots from each side of the center remained compressed from the neighboring states.
The lengths of the overt photons are such that their schedule crossing shapes the filled and unfilled states required to build the energy knot net of a carbon atom. The two pairs of overt photons intercross along the east and west sides. The remaining two pairs of photons intercross along the north and south sides. Figure 1 (a) shows this.
An overt photon maintains the conserved behaviors of force and energy [2]. As a reference, a separate study discussed the photonic current and the characteristics of photons [5]. The lattice of a carbon atom is also referred to as the energy-knot-net, as shown in Figure 1 (a). In the lattice, all the intercrossed overt photons maintain the positions of their mid-lengths at the same point. However, additional work is needed to understand the characteristics of photons at various wavelengths and impacts.
The outer ring of the carbon atom has four filled and four unfilled states. This order of states provides the option to study six different states of the carbon atom in addition to the gaseous state. Glassy carbon has a layered structure. It is part of a separate section.
The four electrons represent the zeroth ring of a carbon atom. Figure 1 shows the different states of a carbon atom where all the carbon states or allotropes contain four electrons in their central ring. The zeroth ring is related to the helium atom [3]. Figure 1 (b-h) shows the positions of electrons and energy knots for different states of a carbon atom.

3.2. Electron transfer mechanism in a carbon atom

To convert a carbon atom from one state to another, the etching of carbon precursors, carbon atoms, or methyl radicals has remained a hot topic. In a new investigation, this was not the case. The photon energy is etched into binding energy by the application of atomic hydrogen, as discussed elsewhere [8].
When the gaseous carbon atom converts into the graphite state, the engaged forces are mainly related to the surface and space formats. Here, a one-bit energy has a shape similar to a dash links to the left side, whereas the same shape of one-bit energy links to the right side.
The transferring electrons of the atom in the graphite state convert it into the lonsdaleite atom. A dash-shaped energy bit extends from west to south. The same-shaped energy bit also runs east to south. The forces exerted on the transferring electrons remain partially conserved. The exerted forces are related to the surface and grounded formats.
Two electrons are transferred to the nearby positioned unfilled states to convert into the diamond atom. As a result, the ground point in the diamond atom moves further below the ground surface. A carbon atom fully expands under its diamond state.
In the conversion, two bits of dash-shaped energy are involved, one along the left side and one along the right side of the carbon atom. Figure 1 (i) shows an electron transfer to the nearby unfilled state. Dash-shaped energy is like a pipe through which force can pass. From one end, the dash-shaped energy bit connects to the electronic tip.
From the opposite end, it connects to the nearby unfilled state. During transfer, the downward arrow in Figure 1 (i) indicates the increasing potential of the electron in terms of gravity. During transfer, the upward arrow in Figure 1 (i) indicates the decreasing potential of the electron in terms of gravity. Forces are only exerted on the two poles of an electron, as its two sides remain hidden during the transfer. An energy bit covers the transferring electron from both sides. An energy bit does not permit forces to influence an electron from those sides.
Therefore, during the transfer, only the forces of two poles are exerted on the left or right-sided electron of the carbon atom. An electron maintains the required potential to transfer in a lower or higher state. Upon transfer to the nearby state, the electron is fastened by the energy knot controlled from the center of its atom.

4.0. Structural formations in different state carbon atoms

Graphite material is famous for its layered or two-dimensional structure. As widely reported in the literature, carbon atoms in graphitic materials exhibit a sp2 hybridized state. An amorphous structure occurs when the arrangement of graphite atoms is not in order. A nanotube structure is famous for being a one-dimensional structure. In fullerene, a buckyball or cage-like structure results.
Diamonds are famous for their tetrahedral structure. In the diamond structure, the diamond atoms exhibit a sp3 hybridized configuration. A honeycomb-like structure is present in graphene. A glassy carbon is also known as a turbostratic structure. Lonsdaleite has a hexagonal structure. According to the published literature and because of differing opinions, there is additional information on the structures of carbon allotropes.
As discussed in the following sections, carbon atoms in the same state bind by studying the details of forces and energy at the electron level, except in the two-dimensional and amorphous structure of graphite. Furthermore, the structures of different carbon allotropes under electron dynamics have not been determined in the literature.
Earlier studies refer to only two-dimensional and amorphous structures of graphite, where the details of forces and energy at the atomic level are missing. Structural formation in graphite has also not yet been studied due to the electron dynamics of the atoms.

4.1. Structures of graphite atoms

In the literature, there are many studies on graphite structures. However, there is no difference in terms of the type of graphite structure. A graphite structure can be of three types. The type of graphite structure initially depends on the system’s limitations and processing parameters. When there is a graphite structure under the electron dynamics of atoms, it is a one-dimensional structure. Sub-section 4.1.1 discusses this.
The amalgamation of graphite atoms under uniform dynamics results in a two-dimensional structure. Sub-section 4.1.2 discusses this. When the amalgamation of graphite atoms occurs under non-uniform dynamics, an amorphous graphite structure is formed (or developed). Sub-section 4.1.3 discusses this.

4.1.1. Graphite structure under the electron dynamics of atoms

This section includes the graphite structural formation by the electron dynamics of the atoms. Figure 2 (a) shows the binding of the carbon atoms when in the graphite state. A carbon atom first converts into a graphite state before binding. Atom A binds to atom B by involving the dash-shaped energy of two bits.
A gaseous carbon atom is converted into a graphite state by involving the energy of two bits, as shown for each atom in Figure 2 (a). In Figure 2 (a), Atom C binds to Atom A from the opposite end by involving the dash-shaped energy of two bits. The forces exerted on each transferring electron remain in the partial conservative mode. Figure 2 (a) shows only the nucleation stage of the graphite. Further binding should be considered when studying the growth process of a graphite structure.
Under electron dynamics, a graphite structure should grow in one dimension. The binding graphite atoms can be from both X-axes. However, the electrons of the bound atoms are oriented along the same line, which is an adjacent orientation. The forces exerted on the electrons from the north-south poles are almost balanced. In tiny-grain carbon films, the atoms of arrays elongate and convert into smooth element structures [6].
The nucleated structure of graphite grows by further binding of graphite atoms. Figure 2 (a) also shows the layer of the graphite structure from the rear side. The dash-shaped energy bits are involved in binding the graphite state atoms. Graphite atoms bind under the same dash-shaped energy bits that are involved in transferring electrons to attain their states.
To transfer electrons from the left and right sides of the gaseous carbon atom while attaining the graphitic state, the potentials of the transferring electrons (from the upper states to lower states) increase. The transferring electrons maintain potential variation at the same level on both sides of the carbon atom. Thus, that atom maintains equilibrium during the conversion. To convert from a graphitic state to a gaseous state, transferred electrons change the potentials in an equalized manner [45]. A study given elsewhere [46] reported that a diamond structure changed to a graphite structure after laser irradiation.

4.1.2. Graphite structure under the attained dynamics of atoms

Graphite-state atoms first amalgamate under uniform dynamics to study a 2D structure. This means that carbon atoms do not execute electron dynamics during amalgamation. Therefore, energy bits shaped like dashes do not involve binding the graphite state atoms. A slight difference in the forces remains along the east and west poles of just amalgamated graphite state atoms.
A slight difference in the forces between graphite atoms keeps them binding as they were amalgamated only under the attained dynamics, which is shown in the arrays labeled (1), (2), and (3) in Figure 2 (b). Therefore, weak energy also remains in the binding of graphite atoms. Graphite atoms naturally follow two dimensions.
The forces and energy found among graphite atoms bind them from the east-west or west-east sides. However, further research is needed.
Forces and energy at the atomic level introduce weak application potential to preserve the graphite structure. Due to the same dynamics of the graphite atoms, they bind under uniform forces and energy. When the force energy is combined, there is a two-dimensional structure. This is the graphite structure when atoms do not execute electron dynamics during binding.

4.1.3. Amorphous graphite structure

An amorphous graphite structure occurs when the amalgamation of graphite atoms occurs under non-uniformly attained dynamics. The atoms are not positioned exactly from the east-west or west-east sides. Figure 2 (c) shows that the graphite atoms bind under non-uniformly attained dynamics where weak energy and forces also contribute. However, their contributions are non-uniform.
Graphitic atoms can also be used to study amorphous carbon structures when the ground surface is not flat. Due to the non-uniform amalgamation of graphite state atoms, the contributions of the forces and energy are non-uniform.
Due to the non-uniform dynamics of the graphite state atoms, an amorphous graphite structure is the case. Amalgamated graphite atoms also bind under non-uniform forces and energy. However, additional work is required to understand the complete picture.
The amalgamation of graphite atoms occurs under non-uniform dynamics. However, weak forces and energy contribute together non-uniformly. The atomic arrangement in amorphous carbon is a continuous random network, as discussed elsewhere [47].

4.2. Formation of nanotube and fullerene structures

The structure of a carbon nanotube nucleates when atoms in a nanotube state bind. A nanotube atom can be converted from the fullerene state atom before binding. In the state conversion, pieces of dash-shaped energy involve transferring electrons to unfilled states. Each transferring electron engages two forces. Each force represents its partially conserved behavior. The nanotube atoms bind by involving partial conservative energy.
Partially conserved forces related to the space and surface formats are exerted on the electron of one quadrant of the nanotube atom. The forces exerted on the electron of the opposite quadrant of the nanotube atom remain in the surface and grounded formats. In this manner, the binding carbon atom maintains equilibrium. Therefore, carbon atoms in a nanotube state can bind to the targeted or central atom in a nanotube state.
Figure 3 (a) shows atoms in the nanotube state bound to the targeted nanotube atom from both sides. This is the nucleation stage of the nanotube. The nucleation of a nanotube structure can occur under two options, as shown in Figure 3 (a). A carbon nanotube initially refers to a finite carbon structure shaped like a needle tube [48]. A straight carbon nanotube has superior mechanical properties to those of a wavy carbon nanotube [49].
The binding of nanotube atoms does not occur along the same axis. However, the binding occurs along the same axis for the graphite atoms. In the execution of electron dynamics, graphite atoms study one-dimensional structures. A nanotube structure is a two-dimensional structure. Here, the forces of the north-south poles also contribute.
A carbon atom is converted into a fullerene upon electron transfer at each dedicated position. The electrons of the outer ring involve an energy shape similar to a dash. The electron of each quadrant engages the forces in its transfer, which are partial in their conservative behavior.
For the transfer, each electron of the outer ring experiences two forces. The involved dash-shaped energy (at the electron level) binds fullerene state atoms for each quadrant of the centered fullerene state atom, as shown in Figure 3 (b). Figure 3 (b) shows the nucleation of the fullerene structure in two options.
When the structure is nucleated, the fullerene state atoms bind to all four quadrants of the centered fullerene state atom. The structure of fullerene atoms is four-dimensional. The exerting forces along the relevant poles of transferring electrons remain partially conserved. The dash-shaped energy bits involved for each electron also maintain partially conserved behavior. Both energy and forces, chemical in nature, behave in a partially conserved manner to study a fullerene structure. However, additional work is needed. In a pioneering work, a fullerene structure was shown to be similar to a football shape, as discussed elsewhere [50].

4.3. Formation of a diamond structure

Figure 4 (a) shows the lonsdaleite and diamond atoms. The lonsdaleite state atom keeps the ground point just below the ground surface. A lonsdaleite atom is converted into a diamond atom when electrons from the left and right sides are transferred to downward unfilled states. The lattice of the converted diamond atom also undergoes the same stretch level as the lattice of the deposited diamond atom.
Figure 4 (a) shows the expected point at which the diamond atoms bind. A diamond atom deals with the solid maximally. Therefore, the ground point of the diamond state atom remains below the ground point of the lonsdaleite state atom. A diamond-state atom is first deposited on a suitably treated substrate. Thus, the electrons of a deposited diamond state atom do not further gravitate. Again, due to the maximally achieved potential energy of the electrons, there is no additional stretching of their occupied energy knots.
By involving the golf-stick-shaped energy bit, each outer ring electron of the depositing diamond atom undertakes the clamp of each outer ring energy knot of the deposited diamond atom. Figure 4 (b) shows this. The outer ring electrons of a depositing atom experience forces related to the surface or east-west poles and grounded or south poles. Clamping each outer ring electron of the depositing diamond atom by each outer ring energy knot of the deposited diamond atom engages non-conservative forces.
To accommodate an additional clamp of an energy knot, an involved golf-stick-shaped energy bit for each electron maintains non-conserved behavior. The forces also exhibit non-conservative behavior. Therefore, by maintaining the maximum stretching of the energy knots, electrons (of a depositing diamond atom) orient from the east-west or surface to the south. Thus, two diamond atoms bind from the surface (east-west) to the south. This stage is the nucleation stage of a diamond. Figure 4 (b) also shows this. The orientation of the zeroth ring electrons adjusts accordingly.
Figure 4 (c) shows the growth trend of a diamond structure. During the growth of the diamond structure, the expansion and contraction of the depositing and deposited atoms mutually adjust. Figure 4 (c) also shows the electrons embedded in the substrate surface for the first deposited diamond atom. A diamond structure can grow with several faces. The different circles in Figure 4 (c) designate the filled and unfilled states.
In Figure 4 (c), the overlapping of the circles designates the additional clamping of the electrons. Upon binding two diamond-state atoms, the third diamond-state atom binds. Therefore, the growth of diamonds occurs from south to surface (east-west). However, the binding of diamond atoms occurs from the surface (east-west) to the south. The binding of diamond atoms occurs between the surface and grounded formats. Thus, the structural characteristics of a diamond are related to its topological structure.
Earlier studies discussed the diamond structure at the atomic level, which was not the case in this study. The current discussion is about electron-level understanding, which is practical and authentic. Again, the underlying mechanisms of nucleating and growing a diamond structure have largely not been addressed. However, preliminary details of the diamond structure studied from the X-ray usage are given elsewhere [51].
As discussed elsewhere [52], a diamond film also nucleates at low pressure. This might be due to the presence of the golf-stick-shaped energy bits discussed here. By choosing a suitable dopant, the band gap of the diamond can switch from indirect to direct [53]. However, a band gap is a photonic band gap under new insight [5]. A theoretical study provides insights into the transformation of graphite into diamonds [54]. For diamond crystals synthesized in a large-volume handling apparatus, increasing the pressure increased the crystallinity [55].

4.4. Lonsdaleite and graphene structures

The ground point at which the carbon atom is in a lonsdaleite state is slightly below the ground surface, as it exists below the ground point at which the graphite atom exists. Electrons in the lonsdaleite state maintain lower potential energy than electrons in the diamond state. Hence, the energy knots shaping the lattice of an atom are less stretchable. The lonsdaleite state atom is less expanded than the diamond state atom. Some historical facts about the lonsdaleite structure and its study under conventional insight are given elsewhere [56]. The lonsdaleite state atom also experiences non-conservative forces for two electrons with the involvement of non-conserved energy. Lonsdaleite atoms bind from east-west to slightly south, but their growth progresses from slightly south to surface (east-west). However, further studies are required to obtain better insight into this topic.
The single sheets of graphite are graphene, for which a detailed study is given elsewhere [57]. Under new insight, the ground point of the graphene state atom lies just above the ground surface. The binding of graphene atoms occurs through forces mainly at the surface and in space formats at the electron level. Therefore, the growth of the graphene structure occurs in the reverse manner as that of the diamond structure.
The involved energy and engaged forces at the electron level for the graphene state atoms function in a non-conserved manner. The growth of graphene occurs from the surface to the north. Principally, graphene atoms should grow with a topological structure. Adherence to only a few layers in the graphene structure is possible due to the limitations of the forces exerted on the electrons in the surface and space formats. However, additional work is needed.

4.5. Formation of glassy carbon structure

A study given elsewhere [58] reviewed the various aspects of glassy carbon based on conventional insights. However, given the fundamental science of glassy carbon, very different insights prevail in structural formation. In addition to the self-governing application, a study given elsewhere [59] discussed a new role of glassy carbon. This means that a glassy carbon material also holds high importance.
When nucleating a glassy carbon structure, three layers of carbon atoms in different states bind successively. By binding simultaneously, layers of gaseous carbon atoms, graphitic atoms, and lonsdaleite atoms nucleate the glassy carbon structure. For a glassy carbon structure, layers of gaseous, graphitic, and lonsdaleite atoms repeat in the same order. The energy bits having a golf stick or half-parabola shape are involved at the electron levels in binding different state carbon atoms arranged in the layers. Figure 5 shows the nucleation and growth of a glassy structure.
Layers of gaseous carbon atoms and graphitic atoms bind under the forces exerted in grounded and surface formats. The two upward-oriented outer ring electrons in each gaseous carbon atom undergo additional clamping of two downwardly positioned energy knots in the outer ring of each graphite atom. Electrons perform additional clamping of energy knots from the rear side. Figure 5 indicates these. Under new insight, binding the gaseous carbon atoms of each layer to the graphitic state atoms of each layer involves an inverted J-shaped energy (or golf-stick-shaped energy) at the electron level.
The clamping of an energy knot to an electron involves non-conserved energy. This process engages non-conservative forces. A clamp is nearly up to the half-length of an electron. Figure 5 shows the binding between the gaseous carbon atoms and graphitic state atoms labeled (1).
Layers of lonsdaleite and graphite atoms bind under the joint application of exerting forces in space and surface formats. The two downwardly orientated outer ring electrons in each lonsdaleite state atom perform clamping (or fastening) of two upwardly positioned energy knots in the outer ring in each graphite state atom. Electrons perform additional clamping of energy knots from the front side. Figure 5 also shows these findings.
Under new insight, binding the lonsdaleite state atoms of each layer to the graphite state atoms of each layer involves J-shaped energy (or golf-stick-shaped energy) at the electron level. The clamping of an electron by an energy knot is due to the involvement of non-conservative energy. As a result, non-conservative forces engage in the process of clamping an electron by an energy knot. A clamp is nearly up to the half-length of an electron. Figure 5 shows the binding between the lonsdaleite state and graphite state atoms. Label (2) shows this. In Figure 5, label (3) indicates the atomic expansion and contraction space between the layered structures.

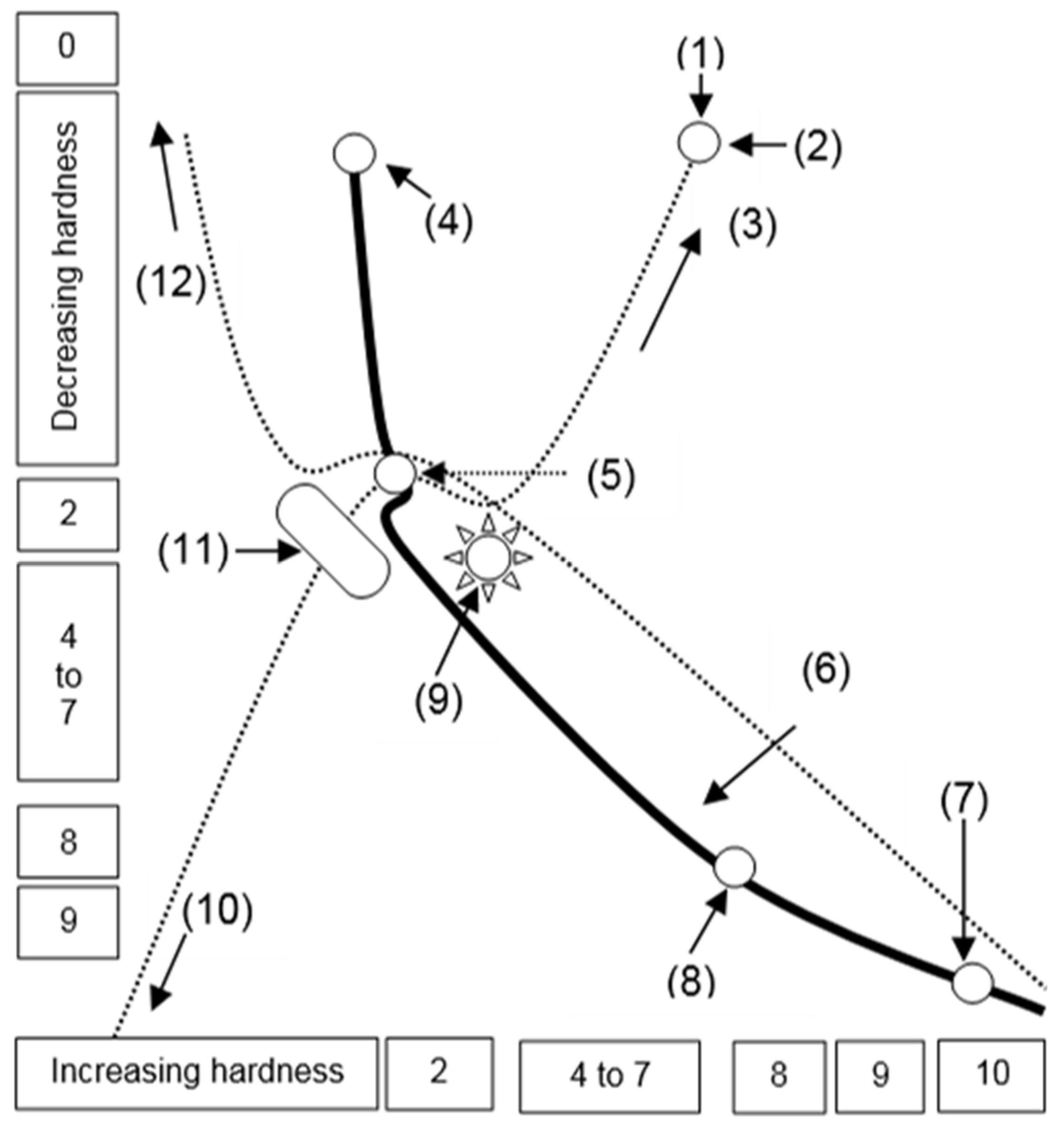
5.0. Estimated hardness of carbon-based materials at the Mohs scale

Figure 6 shows the hardness of the different carbon-based materials at the Mohs scale. Gaseous carbon maintains zero hardness at the Mohs scale. The plotted hardness in Figure 6 relies on the extracted data from published studies. However, the hardness of any carbon material depends on the details of chemical energy and forces. As graphite, nanotube, and fullerene structures maintain partially conserved energy and force details, they can exhibit average hardness. On the other hand, lonsdaleite, graphene, and glassy carbon structures maintain non-conserved energy and force details. Therefore, these structures maintain high hardness.
The extra high hardness of graphene and diamond structures is due to the involvement of golf-stick-shaped energy bits. In these materials, all oriented electrons of an outer ring undertake additional clamping of positioned energy knots by engaging non-conservative forces.
The high hardness of lonsdaleite and glassy carbon structures is also due to the involvement of golf-stick-shaped energy bits. However, in these materials, not all oriented electrons of an outer ring undertake additional clamping of positioned energy knots by engaging non-conservative forces. The hardness model shown in Figure 6 provides new insight into all kinds of carbon materials.
The hardness of carbon films depends on the nature of the forces and the kind of energy. Pieces of evidence from the published literature and the presented details also support the model.
The published data on hardness do not consider the details related to chemical energy and forces discussed here. Therefore, there is an actual need to re-investigate the hardness of different carbon-based materials. A recent study evaluated the hardness of diamond films by nanoindentation [60]. Another study discussed the full-scale structures of diamond and graphite phases in deposited carbon films and their hybrid application [61].
There is a need to investigate carbon films from the beginning. The hardness of different carbon-based materials also depends on the details of the forces and energy. These details can be found in the context of chemistry. Thus, all sorts of depositions and syntheses need to be re-visited.

6.0. Conclusion

Electrons are transferred from filled to nearby unfilled states during the state conversion of a carbon atom. A carbon atom converts from one state to another, where two dash-shaped energy bits are involved. The carbon atom maintains an equilibrium state during the electron transfer mechanism. The structure is one-dimensional when atoms in the graphite state execute electron dynamics. A structure is two-dimensional when graphite atoms bind under uniformly attained dynamics. Here, energy and forces contribute uniformly at the atomic level.
Atoms in the graphite state bind into a two-dimensional structure under weak forces and energy. The amorphous graphite structure is due to non-uniform energy and force contributions at the atomic level. The structural formation of nanotube atoms is two-dimensional under suitable electrons. In fullerene state atoms, the structure is four-dimensional. In fullerene, all four outer ring electrons of the atoms execute dynamics. In the structural formation of graphite in one dimension, nanotubes, and fullerenes, bits of partially conserved energy with a dashed shape are involved at the electron level by engaging the partially conserved forces.
Each outer ring electron of a depositing diamond atom undertakes an additional clamp of each outer ring energy knot of the deposited diamond atom. A bit of energy shaped like a golf stick involves transferring the electron nearly up to half-length to another energy knot. The binding of the diamond atoms occurs from the surface (east-west) to the south. The growth is from the south to the east-west. It has a tetra-electron topological structure. The binding of the lonsdaleite atoms occurs from the surface (east-west) to the slightly southern region, so the growth occurs from slightly south to east-west. It has a bi-electron topological structure.
In a glassy carbon structure, layers of gaseous, graphitic, and lonsdaleite atoms repeat in the same order. In glassy carbon, the orientated outer ring electrons of the gaseous and lonsdaleite atoms undergo additional clamping of the positioned energy knots (of the outer ring) of the graphite state atoms. In diamond, lonsdaleite, graphene, and glassy carbon structures, bits of non-conserved energy are involved at the electron level by engaging non-conserved forces. The hardness of carbon materials relates to the energy and force behaviors at the electronic level. The study of carbon atoms and their binding into structures opens new fields.

Data availability statement

All the data analyzed in this study are part of this article.

Acknowledgments

The author acknowledges the financial support of all the offices and countries. He also thanks whomever he learned from at any stage of his life.

Conflicts of interest

The author declares no conflicts of interest.

References

  1. Ali, M.; Lin, I.-N. Forces driving amalgamation of nanoparticles and particles in solution. Forces in Mech. 2022, 7, 100076. [Google Scholar] [CrossRef]
  2. Ali, M. Heat and Photon Energy Phenomena: Dealing with Matter at the Atomic and Electronic Levels. 2024. https://www.preprints.org/manuscript/201701. 0028. [Google Scholar]
  3. Ali, M. Atoms in Gaseous and Solid States and their Energy and Force Relationships under Transitional Behaviors. 2023. [CrossRef]
  4. Ali, M. Structure Evolutions in Atoms of the Elements Executing Confined Interstate Electron Dynamics. 2023. http://arxiv.org/abs/1611. 0125. [Google Scholar]
  5. Ali, M. Atoms of None of the Elements Ionize While Atoms of Inert Behavior Split by Photonic Current. 2024. http://arxiv.org/abs/1611. 0539. [Google Scholar]
  6. Ali, M.; Lin, I.-N. Phase transitions and critical phenomena of tiny grains carbon films synthesized in microwave-based vapor deposition system. Surf. Interface Anal. 2019, 51, 389–399. [Google Scholar] [CrossRef]
  7. Ali, M.; Ürgen, M. Switching dynamics of morphology-structure in chemically deposited carbon films –A new insight. Carbon 2017, 122, 653–663. [Google Scholar] [CrossRef]
  8. Ali, M. Etching of Photon Energy into Binding Energy in Depositing Carbon Films at Different Chamber Pressures. J. Mater. Sci. Mater. Electron. 2023, 34, 1209. [Google Scholar] [CrossRef]
  9. Ali, M.; Ürgen, M. Simultaneous growth of diamond and nanostructured graphite thin films by hot filament chemical vapor deposition. Solid State Sci. 2012, 14, 150–154. [Google Scholar] [CrossRef]
  10. Ali, M.; Lin, I.-N. Gold Nanostructures and Microstructures with Tunable Aspect Ratios for High-Speed Uni- and Multidirectional Photonic Applications. ACS Appl. Nano Mater. 2020, 3, 9410–9424. [Google Scholar]
  11. Gao, Y.; et al. Ultrahard carbon film from epitaxial two-layer graphene. Nature Nanotechnol. 2018, 13, 133–138. [Google Scholar] [CrossRef]
  12. Wu, J.-B.; Lin, M.L.; Cong, X.; Liu, H.N.; Tan, P.H. Raman spectroscopy of graphene-based materials and its applications in related devices. Chem. Soc. Rev. 2018, 47, 1822–1873. [Google Scholar] [CrossRef]
  13. Shoukat, R.; Khan, M.I. Synthesis of vertically aligned carbon nanofibers using inductively coupled plasma-enhanced chemical vapor deposition. Electr. Eng. 2018, 100, 997–1002. [Google Scholar] [CrossRef]
  14. Cao, M.S.; et al. Graphene nanohybrids: excellent electromagnetic properties for the absorbing and shielding of electromagnetic waves. J. Mater. Chem. C 2018, 6, 4586–4602. [Google Scholar] [CrossRef]
  15. Fu, L.; et al. A glassy carbon electrode modified with N-doped carbon dots for improved detection of hydrogen peroxide and paracetamol. Microchimica Acta 2018, 185, 87. [Google Scholar] [CrossRef] [PubMed]
  16. Hu, D.Y.; Hu, J.X.; Jiang, H.L.; Xu, J. A highly effective energy mitigation system combining carbon nanotube and buckyballs. Eur. Phys. J.-Spec. Top. 2018, 127, 155–166. [Google Scholar] [CrossRef]
  17. Hsu, C.P.; et al. Buckball-, carbon nanotube-, graphite-, and graphene-enhanced dehydrogenation of lithium. Chem. Commun. 2013, 49, 8845–8847. [Google Scholar] [CrossRef] [PubMed]
  18. Chen, C.Y.; et al. Laser writing of coherent colour centres in diamond. Nature Photonics 2017, 11, 77–80. [Google Scholar] [CrossRef]
  19. Z. Liu, et al. Graphite-graphene architecture stabilizing ultrafine Co3O4 nanoparticles for superior oxygen evolution. Carbon 2018, 140, 17–23. [Google Scholar] [CrossRef]
  20. Taylor, A.; et al. Precursor gas composition optimisation for large area boron doped nano-crystalline diamond growth by MW-LA-PECVD. Carbon 2018, 128, 164–171. [Google Scholar] [CrossRef]
  21. Cheng, X.; Zong, W.J. Anisotropic evolution of damaged carbons of a mechanically polished diamond surface in low-temperature annealing. Diam. Relat. Mater. 2018, 90, 7–17. [Google Scholar] [CrossRef]
  22. Maruyama, M.; Okada, S. Geometric and electronic structure of a two-dimensional covalent network of sp2 and sp3 carbon atoms. Diam. Relat. Mater. 2018, 81, 103–107. [Google Scholar] [CrossRef]
  23. Narjabadifam, F. Vakili-Tahami, M. Zehsaz, Elastic and failure properties of carbon nanocones using molecular dynamics simulation. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 777–789. [Google Scholar] [CrossRef]
  24. Rahman, A.T.M.A.; et al. Burning and graphitization of optically levitated nanodiamonds in vacuum. Sci. Rep. 2016, 6, 21633. [Google Scholar] [CrossRef]
  25. Frangeskou, A.C.; et al. Pure nanodiamonds for levitated optomechanics in vacuum. New, J. Phys. 2018, 20, 043016. [Google Scholar] [CrossRef]
  26. Yang, L.; et al. Effect of heat treatment on mechanical property of amorphous carbon films by magnetron sputtering. Diam. Relat. Mater. 2022, 129, 109328. [Google Scholar] [CrossRef]
  27. Huang, J.-Q.; et al. A freestanding hydroxylated carbon nanotube film boosting the stability of Zn metal anodes. Mater. Today Commun. 2022, 32, 103939. [Google Scholar] [CrossRef]
  28. Shi, J.; Zhao, R.; Ke, S.; Wang, W.; Wang, C. Probing the ultra-low friction mechanism of hydrogenated carbon films with controllable fullerene-like nanostructures grown with different bias voltage. Tribol. Int. 2022, 175, 107796. [Google Scholar] [CrossRef]
  29. Ishii, T.; Okuhara, D.; Kobayashi, R.; Ozaki, J.-I. Modulation of the electronic state of carbon thin films by inorganic substrates. Carbon 2022, 196, 313–319. [Google Scholar] [CrossRef]
  30. Shirani, A.; et al. Mechanochemically driven formation of protective carbon films from ethanol environment. Mater. Today Chem. 2022, 26, 101112. [Google Scholar] [CrossRef]
  31. Bae, H.; Sasai, K.; Suzuki, H.; Toyoda, H. High-speed deposition of graphite-like carbon film by Ar/C6H6 surface-wave plasma with high-voltage pulse biasing. Vacuum 2021, 192, 110429. [Google Scholar] [CrossRef]
  32. Thakur, B.; et al. Investigating the effect of thickness on the structural and magnetic properties of carbon thin film. Carbon 2022, 191, 205–214. [Google Scholar] [CrossRef]
  33. Jia, J.; et al. Structure and Electrochemical Properties of Carbon Films Prepared by an Electron Cyclotron Resonance Sputtering Method. Anal. Chem. 2007, 79, 98–105. [Google Scholar] [CrossRef]
  34. Wang, J.; et al. Alternative Friction Mechanism for Amorphous Carbon Films Sliding against Alumina. Ind. Eng. Chem. Res. 2019, 58, 4810–4817. [Google Scholar] [CrossRef]
  35. Kim, J.H.; et al. Tailored Hydrogen-Free Carbon Films by Tuning the sp2/sp3 Configuration. ACS Appl. Electron. Mater. 2021, 3, 1771–1779. [Google Scholar]
  36. Kato, Y.; et al. Indentation behavior of suspended single-walled carbon nanotube films. Carbon Trends 2021, 5, 100112. [Google Scholar] [CrossRef]
  37. Liao, Y.; et al. Single-Walled Carbon Nanotube Thin Film with High Semiconducting Purity by Aerosol Etching toward Thin-Film Transistors. ACS Appl. Nano Mater. 2021, 4, 9673–9679. [Google Scholar]
  38. Zhan, H.; et al. Highly aligned and densified carbon nanotube films with superior thermal conductivity and mechanical strength. Carbon 2022, 186, 205–214. [Google Scholar] [CrossRef]
  39. Larson, B.W.; et al. Arresting Photodegradation in Semiconducting Single-Walled Carbon Nanotube Thin Films. ACS Appl. Nano Mater. 2022, 5, 3502–3511. [Google Scholar]
  40. Zhang, M.; Xie, T.; Qian, X.; Zhu, Y.; Liu, X. Mechanical Properties and Biocompatibility of Ti-doped Diamond-like Carbon Films. ACS Omega 2020, 5, 22772–22777. [Google Scholar] [CrossRef]
  41. Zhai, Z.; Shen, H.; Chen, J.; Li, X.; Jiang, Y. Evolution of Structural and Electrical Properties of Carbon Films from Amorphous Carbon to Nanocrystalline Graphene on Quartz Glass by HFCVD. ACS Appl. Mater. Interfaces 2018, 10, 17427–17436. [Google Scholar] [CrossRef]
  42. Li, J.; et al. In Situ Fabrication of Magnetic and Hierarchically Porous Carbon Films for Efficient Electromagnetic Wave Shielding and Absorption. ACS Appl. Mater. Interfaces 2022, 14, 33675–33685. [Google Scholar] [CrossRef]
  43. Wang, R.; et al. Precisely Controlled Vertical Alignment in Mesostructured Carbon Thin Films for Efficient Electrochemical Sensing. ACS Nano 2021, 15, 7713–7721. [Google Scholar] [CrossRef]
  44. Wang, S.; Roy, A.; Komvopoulos, K. Thermal stability and diffusion characteristics of ultrathin amorphous carbon films grown on crystalline and nitrogenated silicon substrates by filtered cathodic vacuum arc deposition. Sci. Rep. 2021, 11, 13106. [Google Scholar] [CrossRef]
  45. Ali, M. Formation of CO and CO2 molecules under the tree roof and their dissociation. 2023. [CrossRef]
  46. Li, F.N.; Bao, H.W.; Li, Y.; Ma, F.; Wang, H.X. Laser-induced diamond/graphite structure for all-carbon deep-ultraviolet photodetector. Appl. Surf. Sci. 2023, 636, 157818. [Google Scholar] [CrossRef]
  47. Zachariasen, W.H. The atomic arrangement in glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. [Google Scholar] [CrossRef]
  48. Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
  49. Al Tahhan, A.B.; Alkhedher, M.; Mourad, A.-H.I.; Ramadan, M.; Nawash, J.M. Effect of induced vacancy defects on the mechanical behavior of wavy single-walled carbon nanotubes. Nano Trends 2023, 3, 100016. [Google Scholar] [CrossRef]
  50. Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
  51. Ali, M. Qualitative analyses of thin film-based materials validating new structures of atoms. Mater. Today Commun. 2023, 36, 106552. [Google Scholar] [CrossRef]
  52. Chen, Q. Investigation of Diamond Nucleation under Very Low Pressure in Chemical Vapor Deposition. 1997. arXiv:cond-mat/9708146.
  53. Cammarata, A.; Kaintz, M.; Polcar, T. Engineering width and directness of the band gap in diamond-based materials: An ab initio investigation towards electron-structure features control. Diam. Relat. Mater. 2022, 128, 109237. [Google Scholar] [CrossRef]
  54. Han, Q.; Luo, K.; Gao, Q.; Wu, Y.; He, J. Theoretical study on phase transition of various graphitic structures under high pressure. Diam. Related Mater. 2023, 33, 109725. [Google Scholar] [CrossRef]
  55. Li, M.; et al. Effect of pressure on large size diamond single crystal synthesized by temperature gradient method under low nitrogen condition. Int. J. Refract. Met. Hard Mater. 2023, 115, 106307. [Google Scholar] [CrossRef]
  56. Németh, P.; et al. Lonsdaleite is faulted and twinned cubic diamond and does not exist as a discrete material. Nat. Commun. 2014, 5, 5447. [Google Scholar] [CrossRef]
  57. Geim, K. Graphene prehistory. Phys. Scr. 2012, 2012, 014003. [Google Scholar] [CrossRef]
  58. Uskoković, V. A historical review of glassy carbon: Synthesis, structure, properties and applications. Carbon Trends 2021, 5, 100116. [Google Scholar] [CrossRef]
  59. Kim, G.; Noh, S.; Lee, S.; Lee, K.-S.; Kim, K.-J. In situ observation of an atomically modified glassy carbon surface: From synthesis of an Fe-N-C catalyst to intrinsic combined reactions of hydrogen dissociation and the oxygen reduction reaction. Diam. Relat. Mater. 2022, 130, 109464. [Google Scholar] [CrossRef]
  60. Xiong, J. et al.; et al. Mechanical properties evaluation of diamond films via nanoindentation. Diam. Relat. Mater. 2022, 130, 109403. [Google Scholar] [CrossRef]
  61. Ali, M. Structural analyses of carbon films deposited at different total mass rates in hot-filament CVD system. Mater. Adv. 2023, 4, 5361–5370. [Google Scholar] [CrossRef]

Bibliographic detail

Preprints 101010 i001
In 1996, Mubarak Ali earned a B.Sc. degree in Physics and Mathematics. The University of the Punjab awarded him a degree. His M.Sc. degree in Materials Science in 1998. Bahauddin Zakariya University Multan awarded him a master’s degree with distinction. He completed his thesis at Quaid-i-Azam University Islamabad. He gained a PhD in Mechanical Engineering from the Universiti Teknologi Malaysia under the award of the Malaysian Technical Cooperation Programme (MTCP;2004-07) and a postdoc in advanced surface technologies at Istanbul Technical University under the foreign fellowship of The Scientific and Technological Research Council of Turkey (TÜBİTAK, 2010). Dr Mubarak completed another postdoc in nanotechnology at Tamkang University Taipei, 2013-2014, sponsored by the National Science Council, now the Ministry of Science and Technology, Taiwan. He remained working as an Assistant Professor on the tenure track at COMSATS University Islamabad from May 2008 to June 2018, previously known as the COMSATS Institute of Information Technology. His new position is in process. He also worked as an assistant director and deputy director at M/o Science & Technology, Pakistan Council of Renewable Energy Technologies, Islamabad, from January 2000 to May 2008. The Institute for Materials Research at Tohoku University Japan invited Dr. Mubarak to deliver a scientific talk. His scientific research has been a part of many conferences organized by renowned universities in many countries. His core areas of research include materials science, physics, surface and coating technology, carbon-based materials, materials engineering, materials chemistry, physical chemistry, sustainability, energy science, and nanotechnology. He also won a merit scholarship for PhD studies from the Higher Education Commission, Government of Pakistan. However, he did not obtain this opportunity. He earned a diploma (in English) and a certificate (in the Japanese language) in 2000 and 2001, respectively, part-time from the National University of Modern Languages, Islamabad. He is the author of several articles. Please refer to the link https://www.researchgate.net/profile/Mubarak_Ali5 and the link https://scholar.google.com.pk/citations?hl=en&user=UYjvhDwAAAAJ
Preprints 101010 g001
Figure 1. (a) Lattice of a carbon atom. The atomic structure of the carbon atom in the (b) gaseous state, (c) graphitic state, (d) nanotube state, (e) fullerene state, (f) diamond state, (g) lonsdaleite state, (h) graphene state, and (i) electron transfer state (red circles indicate filled states and white circles indicate unfilled states).
Figure 1. (a) Lattice of a carbon atom. The atomic structure of the carbon atom in the (b) gaseous state, (c) graphitic state, (d) nanotube state, (e) fullerene state, (f) diamond state, (g) lonsdaleite state, (h) graphene state, and (i) electron transfer state (red circles indicate filled states and white circles indicate unfilled states).
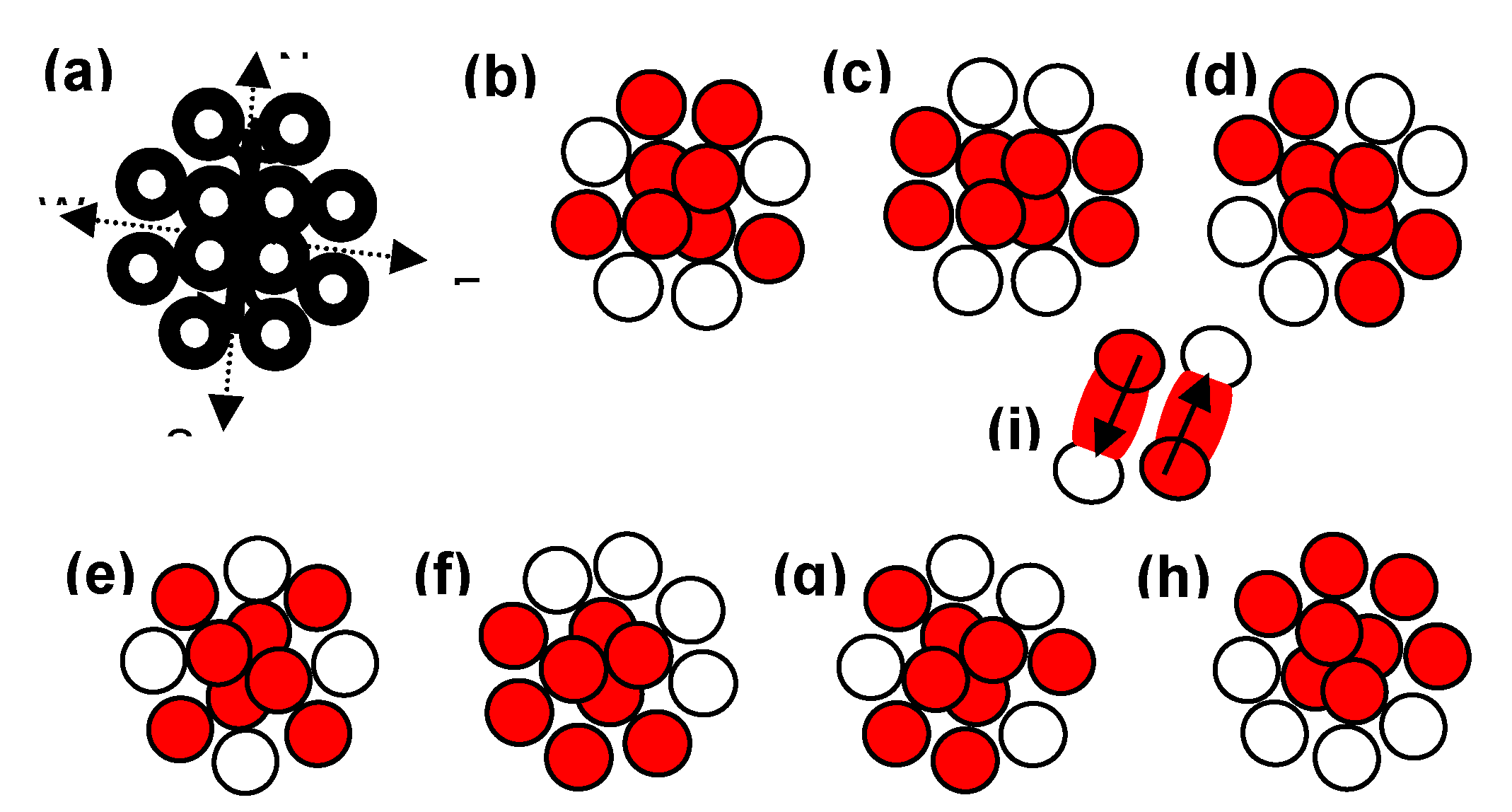
Preprints 101010 g001
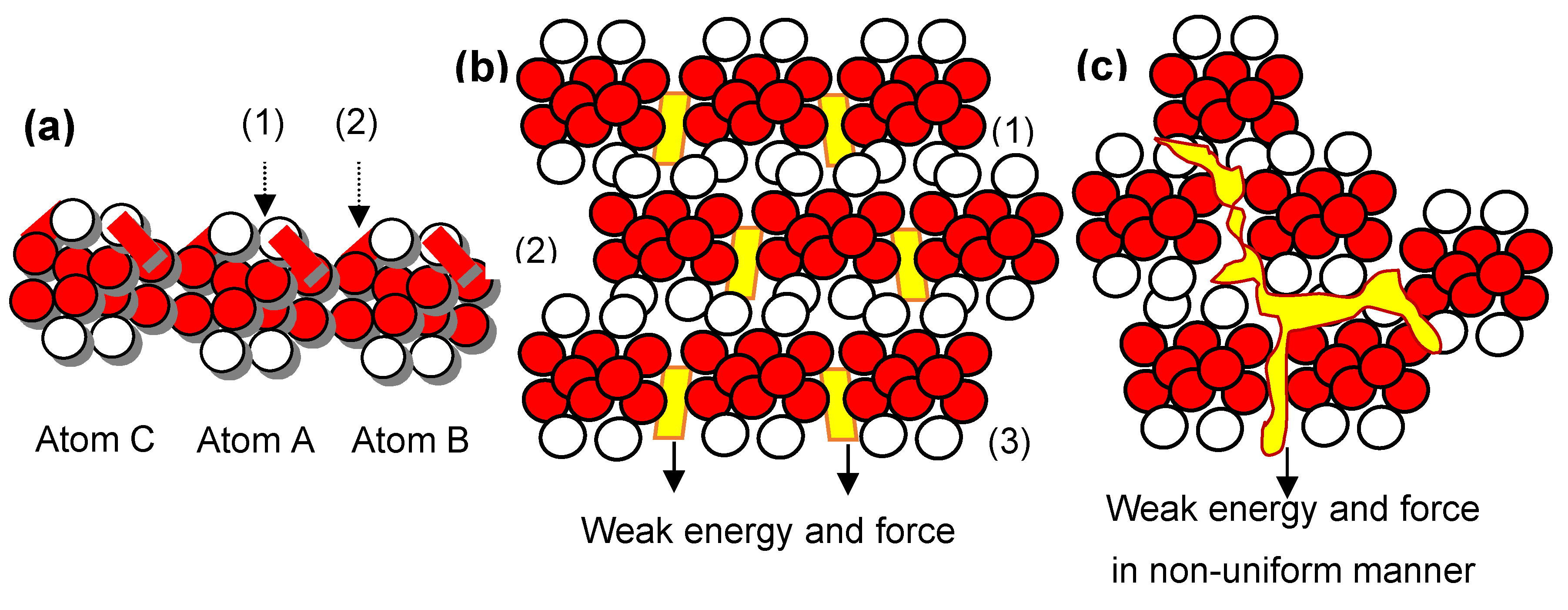
Preprints 101010 g002
Figure 2. (a) Formation of a graphite structure under interstate electron dynamics: (1) unfilled state of a transferred electron, (2) involved dash-shaped energy bit, (b) formation of a graphite structure when weak energy contributes to the uniformly attained dynamics of graphite atoms, and (c) amorphous graphite structure when weak energy contributes to the non-uniformly attained dynamics of graphite atoms.
Figure 2. (a) Formation of a graphite structure under interstate electron dynamics: (1) unfilled state of a transferred electron, (2) involved dash-shaped energy bit, (b) formation of a graphite structure when weak energy contributes to the uniformly attained dynamics of graphite atoms, and (c) amorphous graphite structure when weak energy contributes to the non-uniformly attained dynamics of graphite atoms.
Preprints 101010 g002
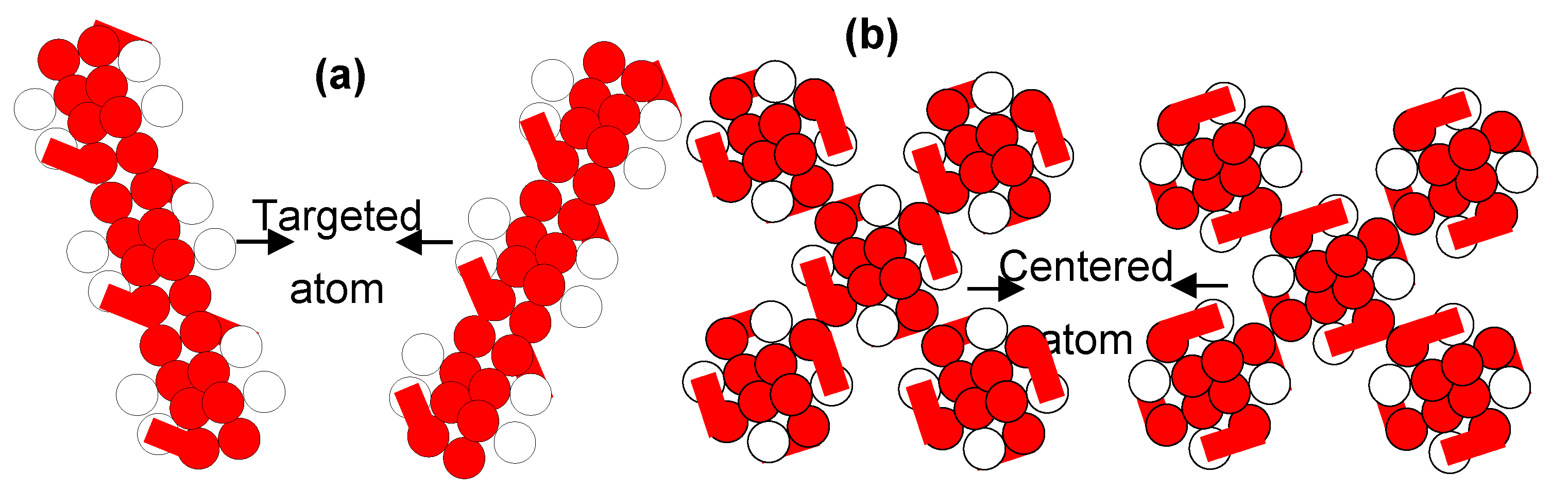
Preprints 101010 g003
Figure 3. (a) nanotubes with different structures and (b) different fullerene or buckyball structures.
Figure 3. (a) nanotubes with different structures and (b) different fullerene or buckyball structures.
Preprints 101010 g003
Preprints 101010 g004
Figure 4. (a) Lonsdaleite atom conversion into a diamond atom: (1) east-west poles, (2) ground point of a lonsdaleite atom, (3) expected binding point of two diamond atoms, and (4) ground point of a deposited diamond atom. (b) Binding of a depositing diamond atom with the deposited diamond atom: (1) zeroth ring of a deposited diamond atom, (2) outer ring of a deposited diamond atom, (3) substrate, (4) positioned outer ring energy knots of a deposited diamond atom, (5) involved golf-stick-shaped energy at the electron level, and (6) oriented outer ring electrons of a depositing diamond atom. (c) Growth: (1) diamond growth south to east-west and (2) embedded electrons of a deposited diamond atom.
Figure 4. (a) Lonsdaleite atom conversion into a diamond atom: (1) east-west poles, (2) ground point of a lonsdaleite atom, (3) expected binding point of two diamond atoms, and (4) ground point of a deposited diamond atom. (b) Binding of a depositing diamond atom with the deposited diamond atom: (1) zeroth ring of a deposited diamond atom, (2) outer ring of a deposited diamond atom, (3) substrate, (4) positioned outer ring energy knots of a deposited diamond atom, (5) involved golf-stick-shaped energy at the electron level, and (6) oriented outer ring electrons of a depositing diamond atom. (c) Growth: (1) diamond growth south to east-west and (2) embedded electrons of a deposited diamond atom.
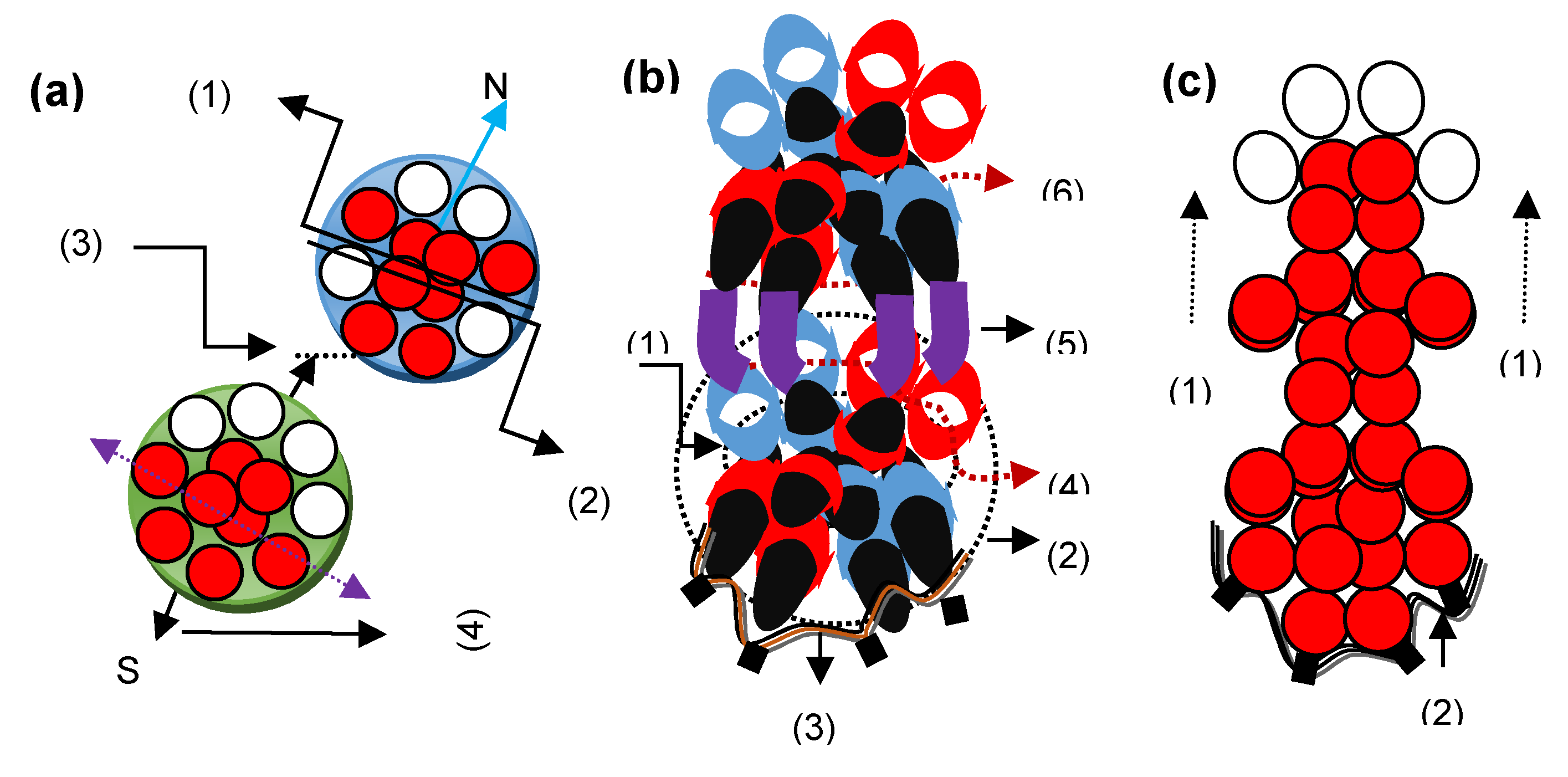
Preprints 101010 g004
Preprints 101010 g005
Figure 5. Formation of a glassy carbon structure where layers of gaseous carbon atoms, graphitic state atoms, and lonsdaleite state atoms bind successively.
Figure 5. Formation of a glassy carbon structure where layers of gaseous carbon atoms, graphitic state atoms, and lonsdaleite state atoms bind successively.
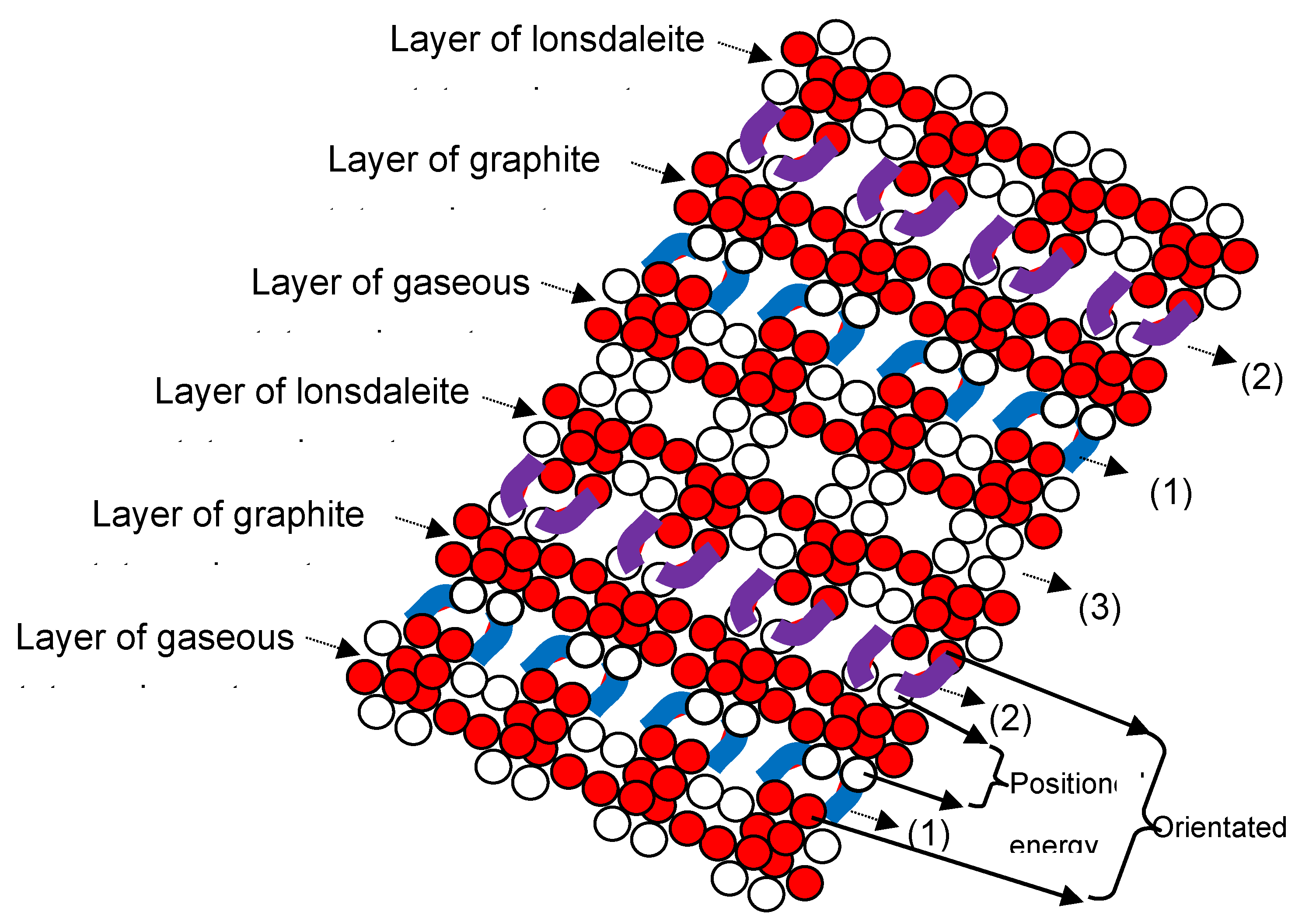
Preprints 101010 g005
Preprints 101010 g006
Figure 6. Plots of Mohs hardness and different carbon structures: (1) levitational force at the electron level, (2) graphene, (3) increasing levitational force, (4) gaseous carbon, (5) graphite, (6) increasing gravitational force, (7) diamond, (8) lonsdaleite, (9) fullerene, (10) maximum gravitational force, (11) nanotube, and (12) maximum levitational force.
Figure 6. Plots of Mohs hardness and different carbon structures: (1) levitational force at the electron level, (2) graphene, (3) increasing levitational force, (4) gaseous carbon, (5) graphite, (6) increasing gravitational force, (7) diamond, (8) lonsdaleite, (9) fullerene, (10) maximum gravitational force, (11) nanotube, and (12) maximum levitational force.
Preprints 101010 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated