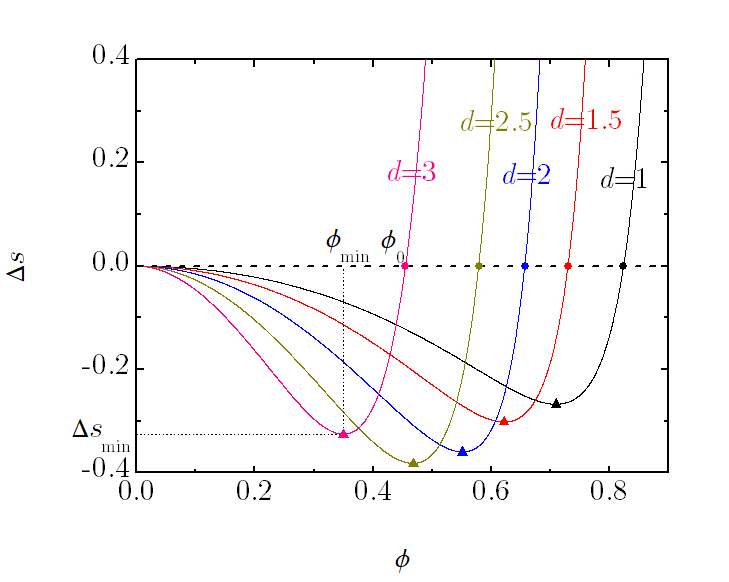
The residual multiparticle entropy (RMPE) of a fluid is defined as the difference, Δs, between the excess entropy per particle (relative to an ideal gas with the same temperature and density), s_ex, and the pair-correlation contribution, s₂. Thus, the RMPE represents the net contribution to s_ex due to spatial correlations involving three, four, or more particles. A heuristic “ordering” criterion identifies the vanishing of the RMPE as an underlying signature of an impending structural or thermodynamic transition of the system from a less ordered to a more spatially organized condition (freezing is a typical example). Regardless of this, the knowledge of the RMPE is important to assess the impact of non-pair multiparticle correlations on the entropy of the fluid. Recently, an accurate and simple proposal for the thermodynamic and structural properties of a hard-sphere fluid in fractional dimension 1 < d < 3 has been proposed [Santos, A.; López de Haro, M. Phys. Rev. E 2016, 93, 062126]. The aim of this work is to use this approach to evaluate the RMPE as a function of both d and the packing fraction ϕ. It is observed that, for any given dimensionality d, the RMPE takes negative values for small densities, reaches a negative minimum Δs_min at a packing fraction ϕ_min, and then rapidly increases, becoming positive beyond a certain packing fraction ϕ₀. Interestingly, while both ϕ_min and ϕ₀ monotonically decrease as dimensionality increases, the value of Δs_min exhibits a nonmonotonic behavior, reaching an absolute minimum at a fractional dimensionality d ≃ 2.38. A plot of the scaled RMPE Δs/|Δs_min| shows a quasiuniversal behavior in the region −0.14 ≲ ϕ − ϕ₀ ≲ 0.02.