Praks, P.; Brkić, D. One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials. Energies 2018, 11, 1825.
Praks, P.; Brkić, D. One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials. Energies 2018, 11, 1825.
Praks, P.; Brkić, D. One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials. Energies 2018, 11, 1825.
Praks, P.; Brkić, D. One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials. Energies 2018, 11, 1825.
Abstract
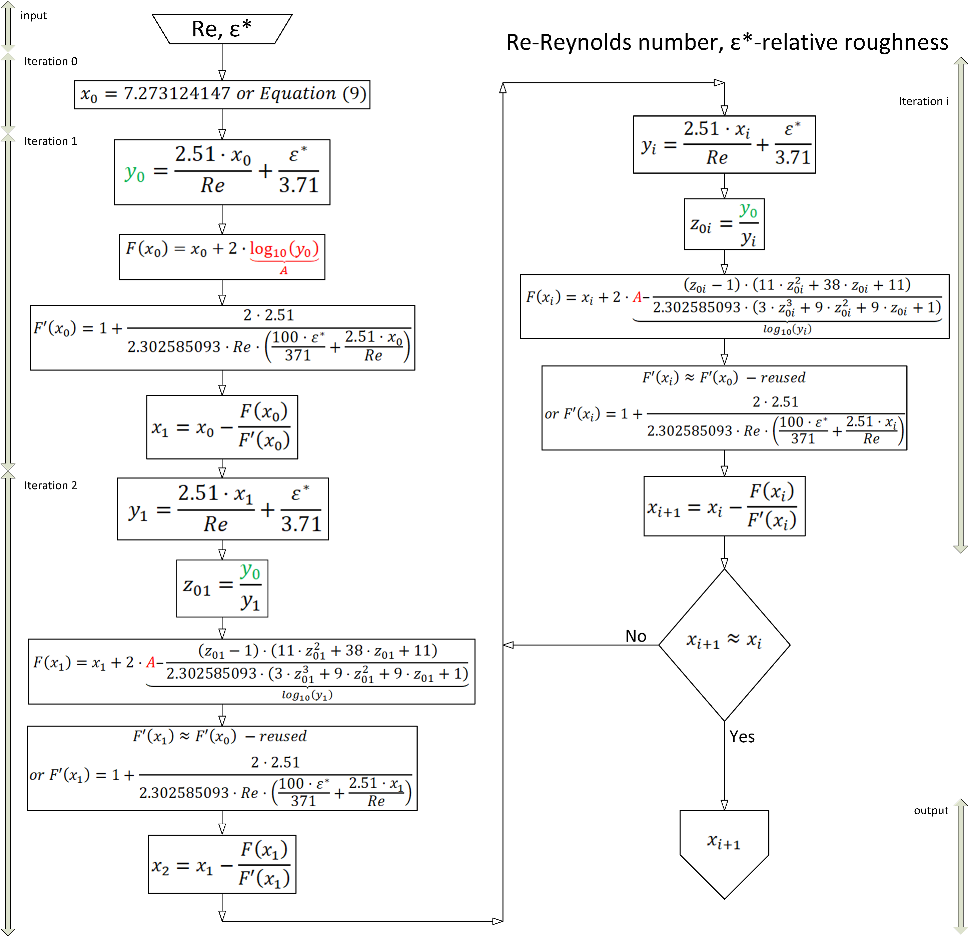
The eighty years old empirical Colebrook function widely used as an informal standard for hydraulic resistance relates implicitly the unknown flow friction factor , with the known Reynolds number and the known relative roughness of a pipe inner surface ; . It is based on logarithmic law in the form that captures the unknown flow friction factor in a way from which it cannot be extracted analytically. As an alternative to the explicit approximations or to the iterative procedures that require at least a few evaluations of computationally expensive logarithmic function or non-integer powers, this paper offers an accurate and computationally cheap iterative algorithm based on Padé polynomials with only one -call in total for the whole procedure (expensive -calls are substituted with Padé polynomials in each iteration with the exception of the first). The proposed modification is computationally less demanding compared with the standard approaches of engineering practice, but does not influence the accuracy or the number of iterations required to reach the final balanced solution.
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
