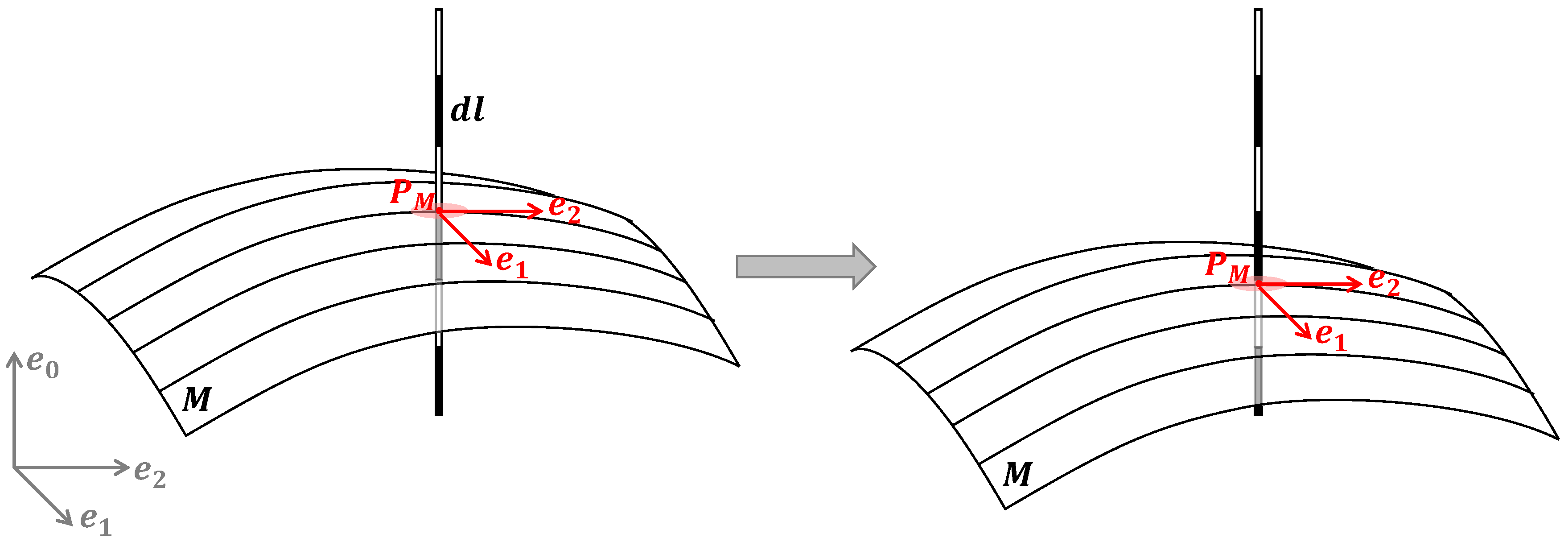
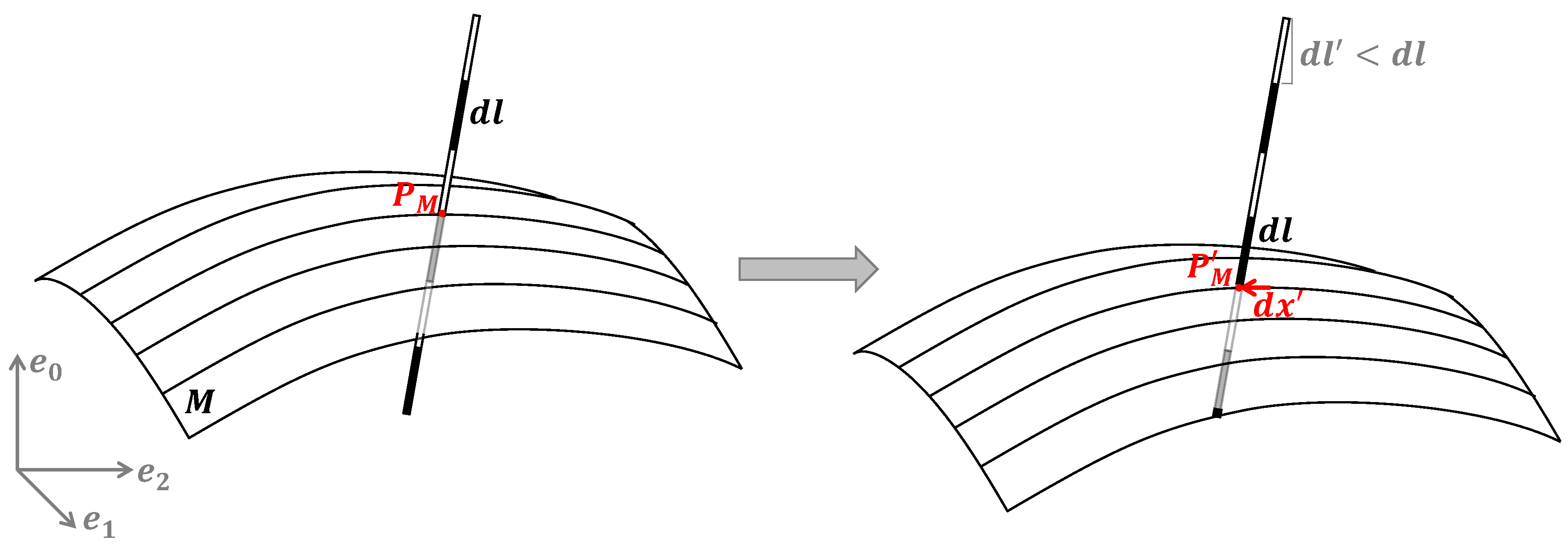
2.1. Basics and Notation
The following proof requires a precise notation for co- and contravariant transforming objects. Since there are different conventions, a brief summary of the nomenclature used in this article is given.
Co- and contravariant vectors are written in bold, second order tensors are written in bold and have capital letters; Greek indexes run from 0 to 3, Latin indexes from 1 to 3, unless otherwise noted.
Let
be a four-dimensional Euclidean vector space with states
. These states are expressed as a linear combination of a canonical basis
with elements from the dual space (orig. [
6], available at [
7]; introductions e.g. in [
8,
9]):
The scalar coefficients
are called the coordinates of state
with respect to the basis
. They can be summarized as a coordinate vector
(Eq.
2 last term). The coordinates are generated by the dual basis
, which is defined by the Euclidean metric tensor
:
Analogously, any dual state
can be expressed with respect to a canonical dual basis:
The coefficients
are called dual coordinates of the dual state
with respect to the dual basis
. They can be consolidated as a dual coordinate vector
(Eq.
4 last row). Thus, scalar and tensor products can be defined directly:
The state does not vary when there’s a change of basis. For this to be the case, the coordinates must change inversely to the basis.
Orientation preserving changes of orthonormal bases in four-dimensional Euclidean space are isomorphic to the Lie-group
, which can be represented by the special orthogonal matrices of fourth order
. Consider the change of basis from
to
. The elements of the new basis can be written as a linear combination of the elements of the old basis:
This translates into the following transformation rule for coordinate vectors (overall and componentwise):
which in the case of orthogonal bases becomes:
The transpose of matrix
is expressed by the index interchange in the last line of Eq.
8. The components of the transformation matrix and its inverse are:
It is said that the basis
transforms covariantly, whereas the coordinates
transform contravariantly. As required, the state
remains unchanged:
2.3. Proposition and Proof

Proof. Let be an Euclidean space with canonical basis and dual basis ; a Minkowski space with orthonormalized basis . It is to be shown that, upon a change of basis, the element of the dual Euclidean basis transforms like the element of the Minkowski basis.
The orientation preserving changes of basis in Euclidean space
can be expressed as an exponential series:
Where
t is the transformation parameter and
is a skew symmetric matrix (
). The skew symmetry of these matrices is what leads to the orthogonality of the finite transformations and the coordinate vectors to change with the transposed transformation rule (Eq.
8).
The matrices
build, together with the commutator
, the Lie-algebra
of the Lie-group
: the algebra that generates the infinitesimal orientation preserving coordinate transformations in
, which through exponential mapping span the whole Lie-group
(for introductions see e.g. [
10,
11]).
In the case of infinitesimal transformations (
) it is sufficient to only consider the first terms of the exponential series. The special role of the Lie-algebra is seen here:
The elements
of the Lie-algebra can once more be expressed as a linear combination of a basis, which in the case of
consists of six skew symmetrical matrices, e.g.:
and therefore
To apply a change of the mixed basis, a transformation rule has to be constructed which transforms the element
of the basis with the same coefficients that a normalized coordinate vector
is transformed with. Using transformation rule Eq.
7 and definition Eq.
14, the infinitesimal change of coordinate vector
can be written as follows:
The (pseudo-)inverse
denotes the inverse of
on the subspace spanned by
and
. In componentwise notation this reads:
Eq.
18 is rearranged to show the change
caused by the transformation. It holds for the individual components:
On the other hand, the transformation rule to obtain
is given by (from Eq.
6):
Rearrangement of Eq.
20 provides the change
induced by the transformation:
which results in component notation:
Sought is an infinitesimal basis transformation with which the individual entries of change
of the vector (Eq.
19) coincide with the entries of change
of the basis vector (Eq.
22). In order for this to be true for all transformations, the comparison of these two equations yields that the entries of the first row
of matrices
must be equal to the corresponding entries
of their inverted matrices
.
As expected, this condition cannot be fulfilled by regular (non-trivial) Euclidean transformations, since in this case the are skew symmetric and orthogonal, and thus . To nonetheless find a change of basis which has the same effect on as it has on , one must depart from changes of basis in the ordinary Euclidean sense and search for a new set of transformations.
In order for the new base transformations to be useful, they must again function as a Lie algebra, such that finite transformations can be generated from the infinitesimal transformations using the exponential map. The starting point is thus given by a new set of infinitesimal generators
(marked with a bar) of the same form as in Eq.
16:
According to the previous considerations, different elements
of the basis are sought, which are their own inverses in their spanned subspace:
Since this condition alone does not give a unique form for the matrices
, some additional requirements can be applied. The transformation of the other basis vectors should remain the same as before, thus the coefficients in columns
stay unchanged with respect to Eq.
14:
Furthermore, volume conservation can be preserved:
Considering conditions Eqs.
24,
25 and
26, the following new transformation matrices can be constructed:
The new elements retain the matrix form of the transformations, yet without orthogonality, since the skew symmetry of the Lie-algebra’s elements had to be abandoned. The generators Eq.
27 are inserted back into Eq.
23, which now describes the infinitesimal basis transformations between mixed bases according to Definition 2.
On the other hand, the unchanged matrices
(Eq.
13) build, together with the new matrices
(Eq.
27) and the commutator as a Lie bracket, the Lie-algebra
with elements
. By means of the exponential mapping this Lie-Algebra translates into the proper Lorentz group
, where:
Yet the elements of the proper Lorentz group
are defined as those orientation preserving changes of basis taking place in the Minkowski space
, with metric tensor
(see e.g. [
12]).
The determined infinitesimal transformation rule according to Eq.
23 for mixed bases in Euclidean space as specified in Definition 1 thus corresponds exactly to the infinitesimal transformation rule for a canonical base
of Minkowski space. Moreover, since only the basis vector
has been changed, the Euclidean space with mixed basis can be directly substituted by a Minkowski space with canonical basis:
transforms like the element of the Minkowski basis and vice versa, and the discovered transformation is equivalent to a regular change of basis in Minkowski space.