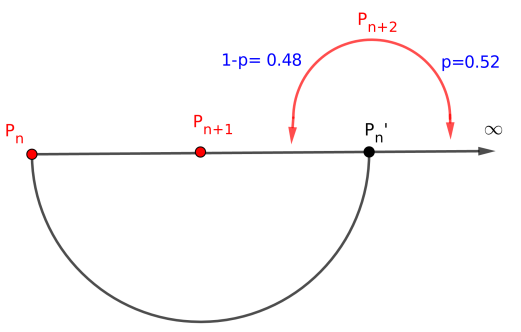
We talk about random when it is not possible to determine a pattern on the observed outcomes. A computer follows a sequence of fixed instructions to give any of its output, hence the difficulty of choosing numbers randomly from algorithmic approaches. However, some algorithms based on mathematical formulas like the Linear Congruential algorithm and the Lagged Fibonacci generator appear to produce "true" random sequences to anyone who does not know the secret initial input [1]. Up to now, we cannot rigorously answer the question on the randomness of prime numbers [2, page 1] and this highlights a connection between random number generator and the distribution of primes. From [3] and [4] one sees that it is quite naive to expect good random reproduction with prime numbers. We are, however, interested in the properties underlying the distribution of prime numbers, which emerge as sufficient or insufficient arguments to conclude a proof by contradiction which tends to show that prime numbers are not randomly distributed. To achieve this end, we use prime gap sequence variation. The algorithm that we produce makes possible to deduce, in the case of a binary choice, a uniform behavior in the individual consecutive occurrence of primes, and no uniformity trait when the occurrences are taken collectively.