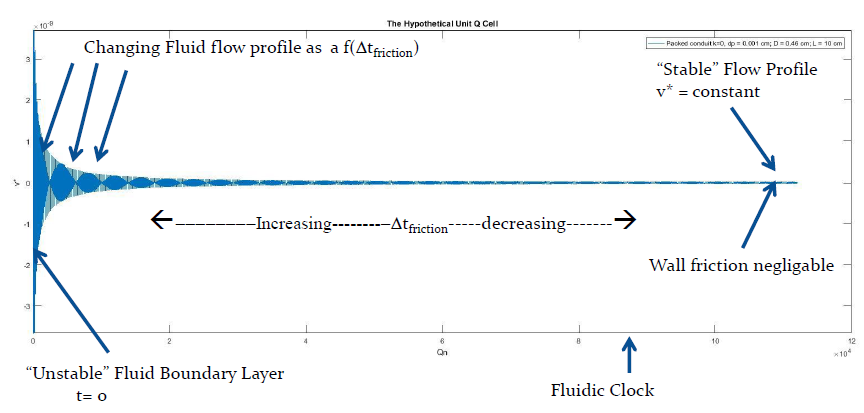
In this paper we develop from first principles a unique law pertaining to the flow of fluids through closed conduits. This law, which we call “Quinn’s Law”, may be described as follows: When fluids are forced to flow through closed conduits under the driving force of a pressure gradient, there is a linear relationship between the normalized dimensionless pressure gradient, P_Q, and the normalized dimensionless fluid current, C_Q. The relationship is expressed mathematically as: P_Q = k₁ +k₂C_Q. This linear relationship remains the same whether the conduit is filled with or devoid of solid obstacles. The law differentiates, however, between a packed and an empty conduit by virtue of the tortuosity of the fluid path, which is seamlessly accommodated within the normalization framework of the law itself. When movement of the fluid is very close to being at rest, i.e., very slow, this relationship has the unique minimum constant value of k₁, and as the fluid acceleration increases, it varies with a slope of k₂ as a function of normalized fluid current. Quinn’s Law is validated herein by applying it to the data from published classical studies of measured permeability in both packed and empty conduits, as well as to the data generated by home grown experiments performed in the author’s own laboratory.