Preprint
Article
A Unified Electro-Gravity Theory to Model Spiral Galaxies without Dark Matter
Altmetrics
Downloads
479
Views
727
Comments
1
This version is not peer-reviewed
Submitted:
20 July 2023
Posted:
20 July 2023
You are already at the latest version
Alerts
Abstract
A unified electro-gravity (UEG) theory, which has been successfully used for modeling an elementary particle, is applied in this paper to model gravitation in spiral galaxies. The new UEG model would explain the "flat rotation curves'' commonly observed in the spiral galaxies, without need for any hypothetical dark matter. The UEG theory is implemented in a somewhat different manner for a spiral galaxy, as compared to the simple application of the UEG theory to an elementary particle. This is because the spiral galaxy, unlike the elementary particle, is not spherically symmetric. The UEG constant $\gamma$, required in the new model to support the galaxies' flat rotation speeds, is estimated using measured data from a galaxy survey, as well as for a selected galaxy for illustration. The estimates are compared with the $\gamma$ derived from the UEG model of an elementary particle. The UEG model for the galaxy is shown to explain the empirical Tully-Fisher Relationship (TFR), is consistent with the Modified Newtonian Dynamics (MOND), and is also independently supported by measured trends of galaxy thickness with surface brightness and rotation speed. The UEG theory may similarly be extended to emulate the hypothetical dark matter in galaxy clusters as well as in cosmology.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Rotation curves of spiral galaxies [1] have been suspected not to confirm to gravitational forces due to galaxies’ visible mass as per the Newton’s Law of gravitation, which is known to work well in our day-to-day experience on earth as well for planetary orbits in our solar system. In order to explain the observed rotation curves, it has been proposed and long believed that there is significant amount of invisible “dark matter” surrounding almost all spiral galaxies. There was no other existing theory which could explain the rotation behavior in a satisfactory manner, although modification of the laws of Newtonian dynamics has been proposed [2]. Recently, a new unified electro-gravity (UEG) theory is established, which has been successfully applied to model an elementary particle and the Casimir Effect [3,4], where a new gravitational force proportional to electromagnetic energy density, is introduced. In this paper, the simple UEG theory of [3,4], applicable for the spherically symmetric structure of an elementary particle, would be extended for the non-spherical structure of a spiral galaxy. The energy density due to star lights in the galaxy would contribute to a new gravitational force, which could support the observed stellar rotation around the galaxy. A constant rotation speed beyond certain radial distance would require a -dependent gravitational acceleration, in the given region. When the UEG theory of [3,4] is properly modified for the non-spherical structure of a spiral galaxy, the required -dependent acceleration may result, although the stellar light radiation from the galaxy exhibit an approximate dependence, in the given region. This is possible, because the energy density of the actual light radiation may need to be redistributed, based on the physical asymmetry of the spiral galaxy. The UEG field may be defined in proportion to the redistributed, effective energy density.
The required UEG constant of proportionality, between the UEG field and the associated effective energy density, may be deduced from the new UEG model using measured data from galaxy survey as well as data for selected individual galaxies. The results may be compared with the UEG constant deduced from [3,4], for validation or verification of the new UEG model. The functional trends established from the new UEG model may be compared, for validation of the model, with those from the empirical Tully-Fisher Relation (TFR) [5] and the Modified Newtonian Dynamics (MOND) model [2,6]. The trends predicted from the UEG model would explicitly depend upon the spiral galaxy’s aspect ratio (ratio of the scale lengths in radius and thickness), because the new model is formulated based on the spherical asymmetry of the galaxy. This is distinct from the the MOND model, where there may not be such definitive interrelation between the galaxy’s aspect ratio and the rotation speed. The functional dependence of the galaxy’s aspect ratio on the surface brightness and rotation velocity, as required for the UEG galaxy model to reproduce the rotation curves, may be compared with available relevant measurements, for another independent validation of the basic UEG galaxy model.
As mentioned earlier, the galaxy’s UEG force field is to be defined in proportion to an effective distribution of energy density, not the actual energy density of stellar radiation as was the case in [3,4] for a spherical structure. The effective energy density may be obtained by suitable redistribution of the galaxy’s light radiation, in proportion to the distribution of the Newtonian gravitation potential of the galaxy, as discussed in the following section. The divergence of the resulting UEG force field surrounding the galaxy would be equivalent to having a fictitious “dark-matter” distribution [7], on the basis of the conventional Newtonian gravitation, which may be needed in order to explain the observed rotation behavior of the spiral galaxies, as well as formation and evolution of the galaxies. Beyond a sufficiently large radial distance from the galactic center, the galaxy would “look” like a point body with a spherically symmetric distribution of the Newtonian potential, and with a dependence of its light intensity. In this far region the radial UEG field would also be spherically symmetric, and therefore the field would be directly proportional to the -dependent light’s energy density, without any need for redistribution of the energy density as per the proposed model. This spherically symmetric, -dependent radial UEG field in the far region is associated with zero field divergence, and therefore with no dark matter. In contrast, the intermediate region where the conventional Newtonian potential exhibits strong spherical asymmetry, the UEG field (with the expected dependence) would be associated with a strong divergence, which would emulate heavy presence of the dark-matter in the region. The UEG field in the innermost region, where the spherical symmetry of the Newtonian potential is generally restored, would be associated with only minimal presence of the dark-matter, much smaller in magnitude than the intermediate region. The intermediate region of heavy dark-matter presence would at least include the smallest spherical region which encloses most of the galaxy’s mass and light sources, and may extend much farther.
Section 2 presents the theoretical concepts and an analytical formulation of the theory. The results for flat rotation velocity deduced from the model are validated with measured data for a galaxy survey as well as for an individual galaxy, in Section 3, Section 4. The Tully-Fisher Relation (TFR) and the Modified Newtonian Dynamics (MOND) model are studied in Section 5, in relation to the present UEG galaxy model, for further validation of the model. Possible extension of the theory to other astrophysical problems are discussed in Section 6, followed by general conclusion from the study in 7.
2. Theory
2.1. The UEG Theory of a Non-Spherical Radiating Body
As per the UEG theory, there exists a new gravitational force-field which is dependent on the electromagnetic energy density. This is in addition to the conventional Newtonian gravitation. For a simple spherical body, the new UEG field at any particular location is proportional to the energy density at the given location, and is directed toward the gravitational center of the body [3,4]. For completeness of understanding, a brief theory of [3,4] for an elementary particle is presented in the Appendix A, in order to introduce the new UEG theory and to estimate the required constant of proportionality between the UEG field and the energy density. The UEG theory of [3,4] has been successfully applied to model an electron, as well as predict the fine-structure constant and the Casimir effect, establishing significant confidence to the new theory. Therefore, in order to be scientifically consistent, a similar additional gravitational field must be included as well for a galaxy, dependent on the radiation energy density associated with the galaxy’s light distribution. However, the simple, direct relationship between the UEG field and the energy density, which is applicable for the spherically symmetric structure of an electron in [3,4], may not be valid in its simple form for the non-spherical structure of a galaxy.
Instead, the radial UEG field for the galaxy is expected to be proportional to a suitable distribution of an effective energy density, with the UEG constant [3,4] as the constant of proportionality. A reasonable proposition would be to define the effective energy density at any given location, by redistribution of the actual energy density of the galaxy’s stellar radiation on a spherical surface passing through the location, in proportion to the galaxy’s conventional Newtonian potential on the spherical surface. The redistribution would maintain the total integral of the actual and effective energy densities on the spherical surface to be equal, which is a definite measure of the equivalent UEG mass (dark-mass) enclosed inside the sphere. For the special case of a spherically symmetric body, the effective energy density would be equal to the actual energy density, in consistency with the simple UEG model [3,4] of an electron presented in the Appendix A.
2.2. Analytical Model for a Spiral Galaxy
The light radiation from a spherically distributed source, like a single isolated star for example, exhibits a dependence of its radiation energy density with radial distance r, external to the spherical source. Such dependence of radiation may also be seen for a non-spherical source, in an approximate form, outside of a spherical region of certain threshold radius. For a spiral galaxy, such a spherical region may be identified with a threshold radius equal to the galaxy’s scale radius R. This means, the radiation of the galaxy establishes an approximate spherical symmetry beyond the radius R.
A spherical source is defined by spherical equi-potential surfaces, which means all points on a spherical surface of radius r have the same potential. In contrast, the spiral galaxy may be represented as a thin disk of an average thickness , with the much smaller than its disk radius . The equi-potential surfaces (as per Newtonian gravity) for the disk structure would be thin disk-like surfaces in the vicinity enclosing the source disk (see Figure 1). Such equi-potential surfaces exhibit spherical asymmetry inherent in the disk structure, and such asymmetry in the Newtonian potential distribution may effectively extend well beyond the scale radius R. This is unlike the light’s energy density discussed above, which establishes a fairly spherical symmetry beyond the galaxy’s scale radius.
Now, consider a spherical surface of radius r, with a common center as the disk galaxy, as shown in Figure 1. The distribution of the Newtonian gravitational potential on this surface would in general be non-uniform, with stronger potential values near the plane of the disk over a constant thickness (independent of r), and weaker values in the rest of the spherical surface. As a first-order model, one may approximate the potential distribution to be uniform over its strong region of area Figure 1), and be negligible over the rest of the spherical surface. A uniform energy density of light radiation over the surface may be redistributed in proportion to the potential distribution, as approximated above, resulting in a stronger effective energy density near the galaxy plane. The radial UEG force is proposed to be proportional to this effective energy density , not the actual energy density . In accordance with the above principle, the two energy densities would in principle be equal if the potential was spherically symmetric, with a uniform value everywhere on the spherical surface of Figure 1.
The original energy density with a dependence would transform into an effective energy density with a dependence on the galaxy plane.
The gravitational potential distribution would exhibit closer spherical symmetry as one approaches towards the center, resulting in the effective density to be close to the actual energy density in the central region. Accordingly, as a first-order estimate, the effective and actual energy densities may be assumed to be equal to each other for . Based on this assumption and the above modeling (1), the effective and actual energy densities may be expressed as follows.
The energy density for may be approximated using the total luminosity L and the speed of light c, and assuming that the total light radiates in a spherically symmetric manner in the region, as if it radiates from a point source at the galaxy center. The total luminosity may be expressed using the surface density , which may be modeled with an exponential profile with amplitude and scale radius R.
The approximate energy density at can then be related to the light surface density at , with as the proportionality factor. For convenience of reference, the effective energy density function may be defined proportional to an equivalent effective surface density function , with the same above factor of proportionality. Using the relation (2) between the function and in the proposed definition, the effective surface density function may be related to the actual surface-density function .
The effective surface density function may be viewed as a -functional fit to the actual surface surface density function , such that they are equal to each other at . As mentioned above, the surface density function is modeled as an exponential distribution with an amplitude and a scale radius R. The amplitude b of the distribution may be related to the parameters and R. Consequently, the total luminosity L in (3) may be expressed in terms of the parameters b and R.
If the amplitude is maintained to be approximately constant, then b would be proportional to R, or equivalently the luminosity L would be proportional to . This may be the case for a large group of high surface brightness (HSB) galaxies, which were believed to confirm to the Freeman’s Law [8] of having an approximately constant central brightness .
The radial UEG field may now be expressed proportional to the equivalent energy density , with the constant of proportionality equal to the UEG constant . The potential function associated with the above radial field could be obtained by integrating the field in the radial variable r, from which the component of the field may also be derived (in principle) as the -derivative of the potential function. However, we are interested here only on the radial UEG field, which completely determines the orbital acceleration on the central plane of the galaxy, because the component of the UEG field on this plane would be zero. The magnitude of the radial UEG field on the central galaxy plane would be equal to the orbital acceleration . The (for ) is proportional to the effective surface density , having the same dependence as the orbital acceleration. Accordingly, the rotation velocity v would exhibit a “flat” behavior for , with proportional to the constant amplitude `b’.
Combining (7,5), the luminosity L may be expressed in terms of the velocity v, radius R, and the UEG constant .
Accordingly, the UEG constant may be estimated from (8) using measured values of the L, v and R, available from a galaxy survey [9]. Alternatively, the amplitude b for the effective surface density may be estimated directly from a measured surface-brightness profile for a selected individual galaxy, and then the be estimated using the b and the measured flat rotation velocity v, as per (7,4). The estimation directly using measured data of an individual galaxy would complement the estimation from the galaxy survey, providing an explicit illustration of the UEG model. However, the estimation using an averaged data from the galaxy survey can, in principle, be more reliable than that using data for individual galaxies. Inaccuracies from astronomical measurements of individual galaxy parameters, as well as uncertainty due to deviation of individual galaxy characteristics from any ideal theoretical assumptions, can often be significant. The resulting inaccuracy or uncertainty in the estimation of the is expected to be minimized by using an “average” or a central data point among a survey of large number of sample galaxies.
3. Estimation of Using Measured Data from Galaxy Survey
We first estimate the based on (8), using an average data point from the I-band measurement of the galaxy survey [9]. As suggested above, the data point is located approximately at the statistical center of the survey samples.
Similarly, we estimate the from the K-band measurement of [9]. Note that an effective radius, , is provided in [9] for the K-band measurements. The effective radius, defined as the radius of a sphere that encloses half of the total luminosity, would be times the scale radius R used in our modeling, assuming an exponential light profile.
Measurements in the K-band overestimates the luminosity and the energy density, leading to underestimation of the . On the other hand, measurements in the I-band underestimates the energy density, leading to overestimation of the . Accordingly, the above results estimate a useful range for the value of the , which is consistent with the value of the deduced from the UEG model [3,4] in the Appendix A for an elementary particle.
The best estimate for is assumed to be the average of the two estimates in the and bands.
The above estimate closely agrees with the from the particle model [3,4] in the Appendix A. Considering that we used a first-order approximation in the UEG modeling of (1,2), such agreement is remarkable. This means that the ideal conditions we assumed in the first-order UEG modeling of (1,2) are remarkably valid for the central data point of [9] used in our estimation.
4. Estimation of Using Measured Data of an Individual Galaxy
Measured data for the surface brightness distribution of a specific galaxy is first properly fitted with an exponential, and then an effective surface brightness distribution , as defined in (4). The data using mixed units, such as magnitude, arcsec, light-years, may be converted to suitable standard units. The distribution can then be related to the rotation velocity v using (7).
The UEG constant is deduced using the amplitude b, or its equivalent parameter , of the effective surface brightness distribution , the flat rotation velocity v and the distance d of the galaxy. Suitable correction factors may be needed to relate the K- and U-band measured magnitudes to a common reference of solar bolometric magnitude of . This assumes the solar magnitudes in the K- and U-bands are and , respectively.
Using the U-band (assumed ≃ U’-band) surface-brightness data [10] for the galaxy NGC-2403, presented in Figure 2, we estimate the amplitude parameter . This parameter, together with the galaxy’s distance MLyr [11] and flat rotation velocity m/s [12], would provide an estimate for the , using the above relation (14). Similarly, using the K-band data [13] for the same galaxy NGC-2403, presented in Figure 3, we estimate the amplitude parameter . This would provide an estimate for the , using (14). An average of these two estimates for the would lead to the best estimate for the from the available data for the galaxy NGC-2403. This is close to the deduced from the galaxy survey in (12) or the from particle model [3,4] in the Appendix A. Such remarkable agreement implies that any deviation from the basic model of (1-4) due to differences in the surface brightness (see Section 5)) of the individual galaxy NGC-2403 from the “average” galaxy used in the estimation (12), is minimal. The are estimated to be roughly equal to in both cases ([9], Figure 3), which is consistent with the above expectation.
5. The Tully-Fisher Relation (TFR) and the Modified Newtonian Dynamics (MOND) Model, Derived from the UEG Model
Combining (5,7) and assuming an approximately constant , a Tully-Fisher Relation (TFR) [5] may be deduced, where the total luminosity L would be proportional to the fourth power of the flat rotation velocity v. As mentioned before, the above condition of an approximately constant is satisfied by a large group of high surface brightness (HSB) galaxies that were believed to confirm to the Freeman’s Law [8].
However, the Freeman’s Law is no longer believed to be strictly valid, and galaxies are measured to exhibit a broad range of amplitudes covering variations among the HSB galaxies as well as extending to low surface brightness (LSB) galaxies with lower values of . For a general treatment to closely model the variation in the amplitude , we may introduce a new parameter for fitting the profile of with the exponential profile of in (4). The unit reference value of is expected to apply for an “average” HSB galaxy, as assumed in the basic model of (4) and in the estimations of (12,15). The may be adjusted to a smaller or larger value, relative to the , with a proportional adjustment of the parameter , which would represent a smaller or large value of the UEG force, respectively, as per (7).
The variable factor is accommodated in the gravitational potential model of (1,2), Figure 1, by recognizing the galaxy thickness to be an active variable, like the scale radius R or the surface brightness , for parametrization of galaxy characteristics. In the potential model of (1), an approximately uniform (spherically) potential would be established for all radial distances less than a variable threshold radius , dependent on a variable thickness , not less than the ideal fixed threshold radius assumed in (2). Accordingly, the effective energy density would match with the actual energy density for all the radial distances less than the variable threshold radius, not the ideal reference threshold assumed in (2). Consequently, the would no longer be equal to as ideally assumed in (2), but now be equal to , with the variable factor proportional to the normalized galaxy thickness .
Using the above revisions and (3), the relation (4) between the surface density and effective surface density , and the resulting expression for the luminosity L (5) using (7), may also be revised.
The TFR (16), which was established based on the simple assumption of an approximately constant , would still be valid for a range of different surface brightness , if in (18) is approximately a constant. This condition, of having a larger value of the for a lower , means there would be relatively more contribution from the UEG force as the surface brightness reduces. This trend better represents observed characteristics among the HSB galaxies, extending to LSB galaxies as well. The higher UEG contribution for a lower surface brightness would be equivalent to having relatively more “dark matter” contribution for a LSB galaxy [14], as per the current dark-matter paradigm.
The above TFR of having the luminosity proportional to the fourth power of the velocity v, is also consistent with prediction from an alternate model using a modified Newtonian dynamics (MOND) [2,6].
As derived in (17,18), the parameter , which proportionately represents the equivalent distribution or , is proportional to the normalized galaxy scale . Accordingly, the condition (19) of a constant factor , required for the validity of the TFR or MOND, would be satisfied if the normalized scale parameter is proportional to the square-root of the surface brightness . This general trend, of having the normalized galaxy thickness to be smaller for a lower surface brightness , may seem to be a sensible characteristic. The specific required relationship between the galaxy thickness and the surface brightness may be compared and verified with the measured data in [15].
Using the above required relationship (19) between the and the normalized scale in (18,7) would translate to another galaxy scaling relationship between the absolute thickness (not normalized to R) and the flat rotation velocity v.
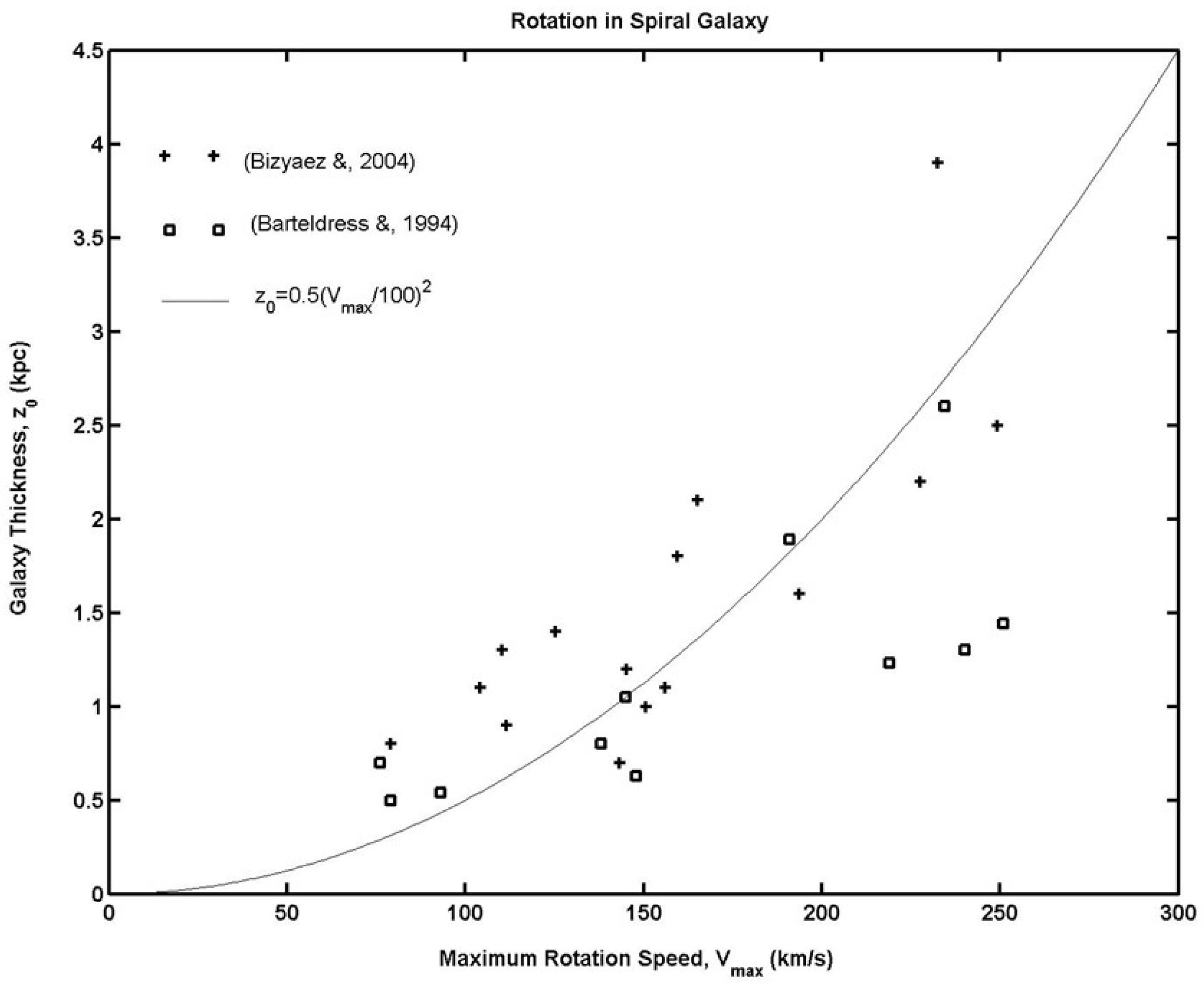
Accordingly, the galaxy thickness is required to be proportional to the square of the flat rotation velocity . This required relationship is clearly verified from the measured data of [15], as presented in the Figure 4. It is significant to note that the above two required relations (a) between the galaxy normalized thickness and the surface brightness , and (b) between the thickness and the flat rotation velocity v, are independently predicted from the UEG model of (17,18), based on the observed TFR (19,16), but could not have been anticipated either from the TFR of [5] or the MOND [2,6]. Verification of the above predictions from [15] is a significant development, which strongly validates the new UEG model of (1,17), as applied to the non-spherical structure of a galaxy.
5.1. Estimating the MOND Constant from the UEG Theory
The Modified Newtonian Dynamics (MOND) theory [2,6], which successfully models galaxy rotation without need for any hypothetical ”dark matter,” modifies the Newtonian gravitational acceleration due to the galaxy’s mass M into the actual rotational acceleration , for small values of . The threshold acceleration used in the MOND theory is believed to be a fundamental constant approximately equal to , valid for any galaxy modeling. However, the new Unified Electro-Gravity (UEG) theory presented here is expected to emulate the MOND theory, leading to consistent agreement of the UEG and MOND models with the Tully-Fisher Relationship (TFR) deduced in (19). In order to further strengthen the validity of the UEG theory, in consistency with the MOND theory, we would show that the empirical parameter can actually be derived from the UEG model, as estimated in the following using data from the galaxy survey [9] and the basic UEG relation (7,8).
The geometric mean values of the “central” data points from the and band survey [9] (see (9,10)) maybe used for luminosity L and radius R in the above expression, in order to find a reasonable estimate of the .
The gravitational constant , the UEG constant from [3,4] in Appendix A (see also (12.15)), and the standard values of solar mass and luminosity , are used in the above calculation. The estimated value of from (22) is in good agreement with its empirical value used in the MOND theory [2,6]. This is a significant finding, which suggests that the UEG theory is the actual fundamental basis behind the success of the empirical MOND theory.
The above estimation based on the formula (21) calculates the galaxy’s mass M, needed to find the Newtonian acceleration , from the galaxy’s measured luminosity L, by assuming that the mass-luminosity ratio of a galaxy, normalized to its standard solar reference value , is equal to unity. That is, , where , with the parameter assumed to be unity. The formula (21) also assumes that the parameter introduced earlier in (19,20), which relates the amplitude b of the effective profile to the surface brightness , to be unity. That is, . This led to expressing the UEG acceleration in (21) in terms of the luminosity , using (7,8), with the unit value of . That is, = = , with .
Accordingly, for a more accurate analysis, the expression of the MOND parameter in (21) needs to be multiplied with an extra factor , which is assumed to be unity for the central data points of the galaxy survey [9], for a reasonable estimate of the . For other galaxies with relatively lower (higher) surface-brightness , the parameter is established to be proportionately higher (lower) (see (20), remains constant), equivalently representing more (less) “dark matter,” while the other parameter is expected to be proportionately higher (lower), representing relatively larger (smaller) baryonic mass-to-light ratio. Therefore, the extra factor is expected to be approximately independent of any specific galaxy, so that the estimated value of in (21,22) would be applicable to all data points of the survey [9], and to all galaxies in general. This is a significant conclusion, which is consistent with the MOND hypothesis that the parameter remains a constant, uniformly applicable for all galaxy modeling.
5.2. Refinement in the Tully-Fisher Relation
Some refinement in the above TFR (19) may be needed, in order to confirm to the measured data [5,9] more accurately, where the luminosity seems to be proportional to a smaller exponent (than the ideal value of 4 in (19)) of the velocity v. This trend may be empirically established from (19) by having the factor to be weakly dependent on the velocity v (proportional to a relatively small exponent of v), instead of the ideal constant factor suggested above. This may be represented by suitable refinement in the required relation in (19) between the galaxy normalized thickness and the surface brightness .
However, this refined TFR does not confirm to the MOND, where the luminosity is definitively required to be proportional to the fourth power of the velocity v. It is not clear if the above refinement (23) is really fundamental or is simply due to selection bias in the measurements of [5,9], resulting in a limited range in the data over which the exponent d is estimated with a smaller value .
The total luminosity and surface brightness profile are usually proportional to the total baryonic mass and its mass distribution, respectively, in which case the TFR would work as well if the luminosity is interchanged with the baryonic mass. The proportionality between the baryonic mass and the luminosity may not, however, strictly extend to all LSB galaxies, having smaller luminosity and rotation velocity. In this case, the measured data follow a TFR more accurately, if the total baryonic mass is used in the relation (19,23), instead of the total luminosity L. The revised relation is referred to as the Baryonic Tully-Fisher Relation (BTFR) [16]. The baryonic mass would be proportional either to the fourth power or to a smaller exponent of the velocity, if the baronic mass substitutes the luminosity in the TFR versions (19) or (23), respectively. The former version of the BTFR is consistent with MOND which, to fundamentally begin with, relates the baryonic mass to the fourth power of the velocity v.
The deviation from the original TFR may be partly attributed to the larger contribution to the rotation velocity v from the Newtonian gravity due to the proportionately larger regular mass (baryonic), in the lower-luminosity LSB galaxies. More significantly, the revised trend may be empirically accommodated by properly adjusting the parameter in (18) to be dependent on both the surface brightness and an equivalent baryonic surface mass density of the galaxy. This would be consistent with the basic principles of the present UEG model in (1- 5,17), where the gravitational potential function that determines the redistribution of the energy density into the effective density (see Figure 1) may be recognized to depend upon both the Newtonian gravitation (related to mass profile) as well as the UEG field due to the light profile of a galaxy. However, more specific physical explanation behind such an empirical trend, leading to the preference of the baryonic mass over the luminosity in the BTFR, is at this point unclear, and is beyond the scope of the present work.
Accordingly, for a given surface luminosity , a larger value of the baryonic mass density is expected to result in a tighter confinement of the gravitational potential near the galaxy surface (smaller ), resulting in a larger . The two refinements (23,24) may need to be studied together, which may be associated with interdependent and/or mutually compensating physical effects.
6. Implication of the UEG theory for other Astrophysical Problems
The UEG theory for spiral galaxies is expected to be extended as well to model excess gravitational mass observed in galaxy clusters. The UEG acceleration produced due to the Cosmic Microwave Background (CMB) radiation surrounding a galaxy cluster could support the measured velocity dispersion and gravitational lensing in the galaxy cluster, emulating the effect of the hypothetical dark matter. For example, the effective gravitational mass of the Virgo cluster [17,18], measured at the outer boundary of the cluster of diameter (± 8 degrees, observed at the cluster’s average distance of Mpc) would be associated with an effective gravitational acceleration , where is the universal gravitational constant and is the reference solar mass. Assuming that the hypothetical dark matter content of the cluster is typically about of the total gravitational mass [19], the required non-Newtonian acceleration is about . This can be emulated by the UEG acceleration due to the energy density of the CMB radiation surrounding the cluster, where is the Stefan-Boltzman constant, the CMB temperature around the cluster with a red-shift , the current CMB temperature, the current Hubble constant, the UEG constant [3,4] from Appendix A, and the speed of light. The required non-Newtonian acceleration is quite close to the UEG acceleration within of difference, suggesting validity of the UEG theory. The small difference may, however, be accommodated by having the measured distance R (hence cluster diameter d) larger about (MPc). This is very likely, considering that the measurement of the distance R for the Virgo cluster, based on measurement of distance of individual galaxies in the cluster, has a significant spread [18].
Similarly, the effective gravitational mass of the Bullet cluster [20,21] would be associated with an effective gravitational acceleration , measured at a selected spherical boundary of diameter (expected to be somewhat larger than an estimated of the cluster’s 2-D gravitational-lensing boundary). The required non-Newtonian acceleration can be emulated by the UEG acceleration due to the energy density of the CMB radiation surrounding the cluster, with measured redshift . Like for the Virgo cluster, the required non-Newtonian acceleration for the Bullet cluster is reasonably emulated by the UEG acceleration , reconfirming the success of the UEG theory. Similar to the modeling for the spiral galaxies, the distribution of the UEG force, and equivalently of the gravitational mass for the non-spherical structure of the bullet cluster, is expected to be most concentrated around the region of strong Newtonian gravitation, which would clearly be confined around the radial axis connecting the Bullet sub-clusters. The analysis maybe followed further, based on a useful simplified model that the region of strong Newtonian potential due to the Bullet sub clusters constitute a cylindrical space enclosing the sub clusters, with the cylinder’s cross-sectional diameter close to the diameter of each sub cluster (assumed symmetrical), and the length of the cylinder extending somewhat beyond the axial ends of the clusters. The uniform UEG acceleration due to the uniform CMB radiation would be associated with equivalent gravitational mass, enclosed within in a spherical volume of a given radius, to increase with the square of the radius. This mass, to be concentrated in the cylindrical volume described above, as per the proposed UEG theory, would result in linearly increasing density of the gravitational mass in the cylinder, with increasing radial distance away from the center. This would result in the peak density towards the axial ends of the cylindrical region, which is radially offset away from the Newtonian mass centers of the sub clusters. This predicted offset of the gravitational mass concentration would be consistent with the gravitational lensing measurements of the Bullet cluster [22]. Any finer improvement of the analysis may involve proper modeling of the Newtonian potentials due to the separate gaseous and visible (galaxies) mass concentrations, as well as including additional contributions from any equivalent UEG gravitational mass outside of the idealized cylindrical region discussed above.
The above success of the UEG model for the Virgo and the Bullet clusters, is expected to extend as well to other galaxy clusters. Using median values of cluster mass ( to ) and diameter (2 to ) [19], the calculated acceleration at the outer boundary of a median cluster is lower than the UEG acceleration (assuming redshift , see calculations above). The difference between the accelerations a and would be reduced, with somewhat larger M and/or lower d. The calculations suggest there is adequate UEG acceleration to emulate the clusters’ gravitational effects, without any hypothetical dark matter.
The role of the hypothetical dark matter (possibly dark energy) in a cosmological model could also be similarly emulated by the UEG acceleration due to the CMB radiation (as well as current and future star lights). Specific details of the cosmological modeling based on the new UEG theory is beyond the scope of the present work, and is separately explored [23].
7. Conclusion
The estimate of the UEG constant from measured data from a galaxy survey [9], based on the new UEG model, agrees well with an accurate value derived from the UEG model in the Appendix A for an elementary particle [3,4]. This is based on a statistically average data point from the survey samples. Direct analysis of measured brightness profile and rotation curve of a specific selected galaxy is also illustrated to provide a similar estimate for the , that is consistent with the estimate from the galaxy survey. Further, the UEG galaxy model confirms to the TFR [5,16] for varying range of galaxy amplitudes, and is consistent with results from a modified Newtonian dynamics (MOND) [2,6] model. The required condition for the agreement between the UEG model, TFR and MOND is supported by measured relations of the galaxy thickness with the surface brightness and the rotation velocity [15], which may be considered as an independent validation of the UEG model. The above studies strongly support validity of the new UEG model, established for the non-spherical structure of a disk galaxy. The UEG theory is intended to serve as a theoretical substitute for the current “dark-matter” hypothesis. Further, the UEG model may similarly be applicable to model excess gravitation observed in galaxy clusters, as well as to model cosmological expansion of the universe.
The UEG theory, which is shown to be consistently applicable to model elementary particles [3,4] and spiral galaxies, and is extended as well to galaxy clusters and possibly for cosmological modeling, could provide a new unified theoretical paradigm for a broad range of physical concepts, covering both small and large size scales of nature, and spherically symmetric as well as asymmetric structures.
Appendix A. A Unified Electro-Gravity Theory, Applied to an Elementary Charged Particle
A Unified Electro-Gravity (UEG) theory is established based on the following basic principles:
(a) The mass m and its associated energy of a given body is assumed to be inversely proportional to the relative permittivity , or directly proportional to the inverse-relative permittivity , of the surrounding medium. This is in consistency with the energy of a spherical surface charge q of radius , placed in a medium with permittivity . The is the permittivity of an “ideal free-space” having an ideal unit relative permittivity , which is assumed to exist far away from any gravitating body .
Using the above concept of mass, a gravitational force at a given location , and its associated field defined as the gravitational force applied on a unit free-mass , may be modeled in terms of the gradient of the inverse-relative permittivity function .
(b) The gravitational field, conventionally defined by the Newton’s Law of gravitation, needs to be modified by adding a new part which is a function of the energy density associated with an electromagnetic field at a given location. As a simple first-order approximation, the new gravitational field , referred to as the UEG field, is assumed to be directly proportional to the energy density, with the proportionality constant referred to as the unified electro-gravity (UEG) constant. The proposed modification would maintain the Newtonian gravitational field as the total field for an electrically-neutral, non-radiating massive body (like planet earth), in the external region where the electromagnetic energy density is zero. It would, however, change the nature of gravitation for an electrically-charged body (like an electron), or a radiating body (like a star or galaxy), where the energy density associated with the electrical charge or light radiation is non-zero. Similarly, it would also change the nature of gravitation in the internal region of an electrically neutral body (like a neutron or neutrino,) which is assumed to consist of internal charged substructures. The modified theory may be alternately interpreted by not modifying the Newton’s Law of gravitation, but re-defining the energy density in an electromagnetic field, such that the total energy/mass of a neutral body remains unchanged.
The modified theory will fundamentally shape the physical structure of any charged particle, such as an electron. The new electro-gravitational field would determine the inverse-relative permittivity function around an electron, as per the relation (A1). We may further assume that the new gravitational field , directed toward the center along , is much stronger than the conventional Newtonian gravitational field, and therefore would essentially be equal to the total gravitational field .
Appendix A.1. Energy Density in a Non-Linear Medium
In the above unified electro-gravity (UEG) model, the permittivity distribution of the free-space is dependent upon the energy density distribution, which is dependent upon the source charge. This is unlike a linear dielectric medium where the permittivity function is independent of the field strength or the source charge. Having the permittivity distribution to be a function of the source charge, is equivalent to having the electric field distribution to be a non-linear function of the source charge. The energy density in such a non-linear medium needs to be properly modeled, using a general expression for the energy density.
The electric field and the electric flux density produced due to a spherical surface charge q of radius , at a distance r from the center of the charge, in the presence of a permittivity distribution , may be expressed using the Coulomb’s Law.
The total energy W and the associated mass of the charge may be calculated by integrating the energy density in its electric field over the spherical volume outside of the charge . The electric field, and the associated energy density, in the spherical region with would be zero. The may be expressed in (A4) in terms of the flux density due to the charge q, and its incremental value due to an incremental change of the charge. This expression of the energy density would be valid for a general non-linear medium, which may be simplified as for a linear medium.
In equivalency to a conventional definition of the energy density for a linear medium, it would be useful to define a new variable for a non-linear medium. The conventional expression of the energy density for a linear medium, with the inverse-permittivity for the linear medium simply substituted by the new equivalent variable , would be valid as well for a non-linear medium.
Appendix A.2. Series Solution for the Inverse-Relative Permittivity Function ϵ ̲ r (r ¯)
The inverse-relative permittivity function may be solved by expanding it as power-series of with unknown coefficients , , and then finding the coefficients in order to satisfy the above UEG relation (A5). This would be possible by establishing an iterative process, relating a coefficient with an increasingly higher index i to those with a lower index, starting with the known value for the lowest coefficient . In the limit of large distance r, the would approach unity, fixing the coefficients .
The governing relationship (A5) for would require the series solution with non-zero values of the coefficients only for . Accordingly, the series solution for the may be conveniently expressed as a power series of a normalized variable , with even powers of t. The normalization parameter is to be determined from (A5), which may be shown to be proportional to . We need not present the detailed steps, as prescribed above, to derive the individual coefficients for the series. The final solution for is expressed in (A6), which may simply be substituted in (A5) to verify its validity. The series (A6) may be recognized as the zeroth-order Bessel function .
Figure A1.
.
Appendix A.3. Particle Energy and Mass, as a Function of the Charge Radius
Once the inverse-relative permittivity function is solved, the energy density can be expressed in terms of the using (A4), which can then be integrated over the total volume outside the charge radius (there is no field inside the charge radius) to obtain the total energy or the equivalent mass of the particle.
The charge radius in (A7) is maintained as a general variable (=r). The general mass function in (A7) would also represent the equivalent energy (=) contained in the field external to a sphere of radius r, produced due to the charge placed at any radius less than r.
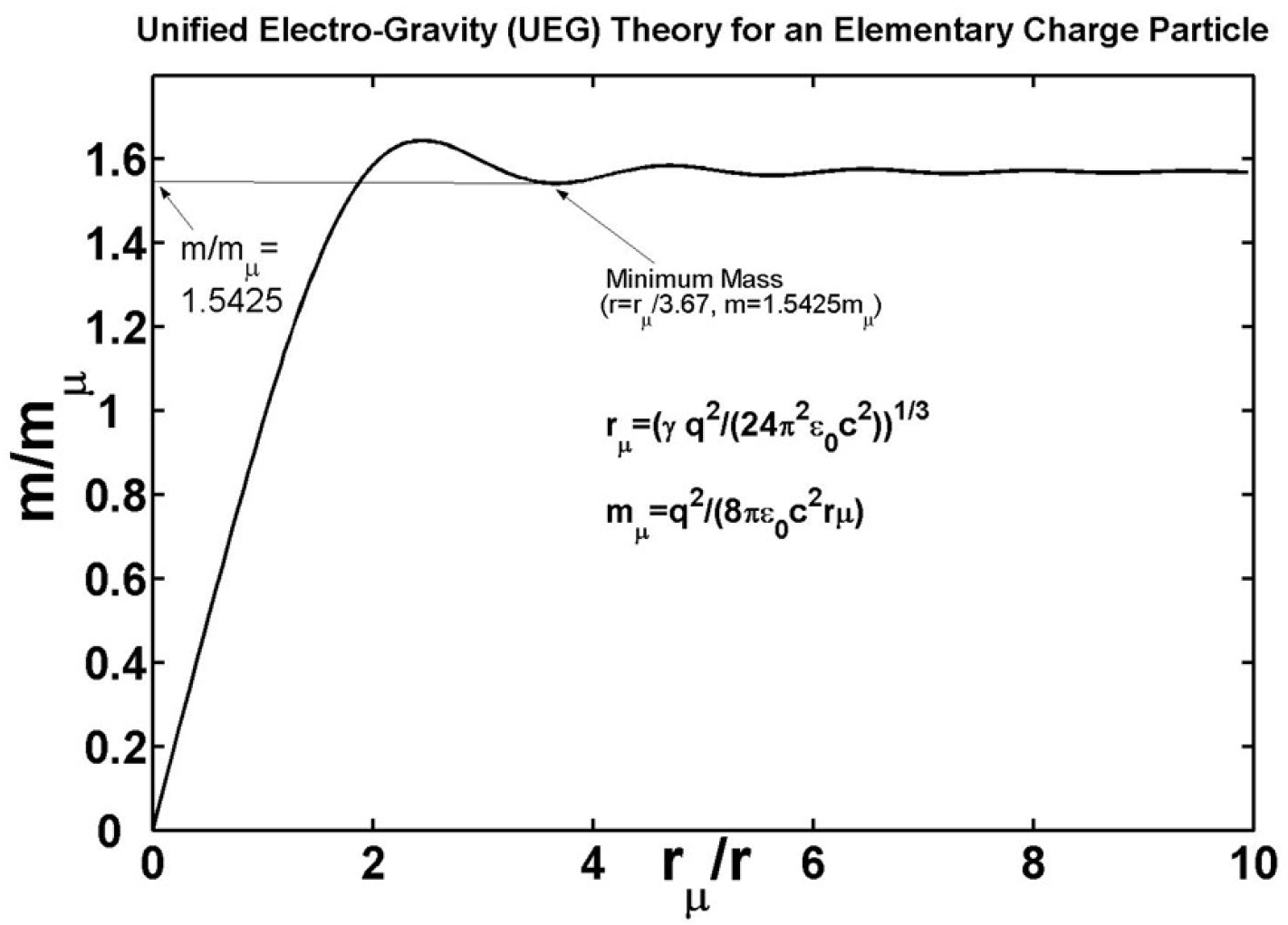
Figure A1 plots the normalized mass of (A7) as a function of the normalized radius , showing an oscillatory behavior of the mass function. Any of the minimum points of the mass function would correspond to a possible stable particle with the particular charge radius .
The smallest possible stable mass deduced from the oscillatory mass of (A7) Figure A1) is expected to be the mass of an electron (or a positron) without any spin. This is referred to as the static UEG mass of an electron. We will assume that the static UEG mass of an electron is about half of the total electron mass , that includes additional mass/energy due to the electron’s spin. This factor of about 2 between the and is suggested by recognizing that the electron’s spin g-factor is approximately equal to 2. The same conclusion may also be suggested by observing that the orbital magnetic moment of an atomic electron with an orbital angular momentum ℏ is approximately equal to the magnetic moment of a spinning electron with spin angular momentum .
With the assumption of for the minimum stable mass in Figure A1, the value of the normalization constant can be calculated, from which the value of the UEG constant is estimated.
As per the UEG theory of the electron, the constant is declared to be a new natural constant, which is equal to a new gravitational acceleration in toward the center of gravity, produced due to one of energy density.
Appendix A.4. General Relationship Between the UEG Constant γ, the Particle Mass and Classical Radius
The above estimate of the value of the UEG constant is associated the actual value of the UEG static mass of the electron, and carries a specific dimensional unit of . More fundamentally, a dimension-less relationship between the smallest stable UEG static mass of any elementary particle, the corresponding classical radius , and the UEG constant required to produce the mass , can be derived based on the expressions for the reference mass (A7) and reference radius (A6) used in the above analysis.
The value of the ratio from the Figure A1, for the smallest possible stable mass . Using this value, the , and may be related in term of a dimensionless constant.
If we simply assume the total mass of the elementary particle with spin to be twice the UEG mass , and the classical radius associated with half of that () with , the , and may be related using a new dimensionless constant, which would be eight times the above constant.
Notice that the above constant is close to twice the inverse-fine structure constant , and the earlier constant in (A10) is one fourth of the , with less than one percent of difference. The small difference may be due to lack of generality or rigor of the basic UEG static theory for the particle, presented in this paper with assumption of a simple UEG function in (A2), and without including the particle’s spin. The small difference may perhaps be related to the small difference between the actual value of the g-factor and its ideal value of 2 as discussed before. This may point to possible physical origin of the g-factor associated with the spin, governed by a more rigorous version of the new UEG theory.
Leaving aside any small difference due to lack of generality or rigor of the basic UEG model, the close relations of the above dimensionless constant (A10 or A11) to the fine-structure constant is intriguing. The very existence of a dimensionless constant based on the UEG theory, and its intriguing close numerological relationship with the known fine-structure constant , may strongly suggest certain fundamental basis and significance of the new UEG theory. The theory is further validated in [3,4] by successfully modeling the Casimir effect, and would be applied in this paper to model gravitation in spiral galaxies and reconfirm the estimate for the UEG constant .
References
- Rubin, V.; Thonard, N.; W. K. Ford, J. Rotational Properties of 21 Sc Galaxies with a Large Range of Luminosities and Radii from NGC 4605 (R=4kpc) to UGC 2885 (R=122kpc). Astrophysical Journal, Part 1 1980, 238, 471–487.
- Milgrom, M. A Modification of the Newtonian Dynamics as a Possible Alternative to the Hidden Mass Hypothesis. Astrophysical Journal, Part 1 1983, 270, 365–370.
- Das, N. A New Unified Electro-Gravity Theory for the Electron. Preprints, 2019070052 (https://doi.org/10.20944/preprints201907.0052.v2) 2019. [CrossRef]
- Das, N. A Unified Electro-Gravity Theory of a Spinning Electron, and the Fundamental Origins of the Fine Structure Constant and Quantum Concepts. American Physical Society April 2020 Meeting, Paper ID: Y15.00004 (https://meetings.aps.org/Meeting/APR20/Session/Y15.4) 2020.
- Tully, R.B.; Fisher, J.R. A New Method of Determining Distances to Galaxies. Astronomy and Astrophysics 1977, 54, 661–673.
- Milgrom, M. A Modification of the Newtonian Dynamics - Implications for Galaxies. Astrophysical Journal, Part 2 1983, 270, 371–389.
- Borriello, A.; Salucci, P. The Dark Matter Distribution in Disk Galaxies. Monthly Notices of the Royal Astronomical Society 2001, 323, 285–292. [CrossRef]
- Freeman, K.C. On the Disks of Spiral and SO Galaxies. Astrophysical Journal 1970, 160, 811–830.
- Courteau, S.; Dutton, A.A.; van den Bosch, F.C.; MacArthur, L.A.; Dekel, A.; McIntosh, D.H.; Dale, D.A. Scaling Relations of Spiral Galaxies. Astrophysical Journal 2007, 671, 203–225. [CrossRef]
- Weavers, B.M.H.R.; van der Kruit, P.C.; Allen, R.J. The Palomar-Westerbork Survey of Northern Spiral Galaxies. Astronomy and Astrophysics Supplement Series 1986, 66, 505–662.
- NED. Nasa Extragalactic Database, Results for NGC-2403. http://ned.ipac.caltech.edu, Retrieved February 2017, 2017.
- Begeman, K. HI Rotation Curves of Spiral Galaxies. PhD Thesis, University of Groningen, Netherlands 2006.
- Munoz-Mateos, J.; de Paz, A.G.; Boissier, S.; Zamorano, J.; Jarrett, T.; Gallego, J.; Madore, B.F. Specific Star Formation Rate Profiles in Nearby Spiral Galaxies: Quantifying the Inside-Out Formation of Disks. Astrophysical Journal 2007, 658, 1006–1026. [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S. The dark and Visible Matter Content of Low Surface Brightness Disc Galaxies. Monthly Notices of the Royal Astronomical Society 1997, 290, 533–552. [CrossRef]
- Bizyaev, D.; Kajsin, S. The Stellar Disk Thickness of Low Surface Brightness Galaxies. The Astrophysical Journal 2004, 613, 886–897. [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. The Astrophysical Journal 2000, 533, L99–L102. [CrossRef]
- Wikipedia. Virgo Cluster. http://en.wikipedia.org/wiki/Virgo_Cluster, Retrieved January 2020, 2020.
- Fouque, P.; Solanes, J.M.; Sanchis, T.; Balkowski, C. Structure, Mass and Distance of the Virgo Cluster from a Tolman-Bondi Model. Astronoly and Astrophysics 2001, 375, 770–780. [CrossRef]
- Wikipedia. Galaxy Cluster. http://en.wikipedia.org/wiki/Galaxy_cluster, Retrieved January 2020, 2020.
- Wikipedia. Bullet Cluster. http://en.wikipedia.org/wiki/Bullet_Cluster, Retrieved January 2020, 2020.
- Clowe, D.; Gonzalez, A.H.; Markevitch, M. Weak Lensing Mass Reconstruction of the Interacting Cluster 1E 0657-558: Direct Evidence for the Existence of Dark Matter. The Astrophysical Journal 2004, 6o4, 596–603. [CrossRef]
- Clowe, D.; Bradac, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Impirical Proof of the Dark Matter. The Astrophysical Journal Letters 2006, 648, 109–113. [CrossRef]
- Das, N. The Unified Electro-Gravity (UEG) Theory Applied to Cosmology. Paper #7, pp.74-86, in “A Unified Electro-Gravity (UEG) Theory of Nature," http://wp.nyu.edu/ueg, 2018.
Figure 1.
.
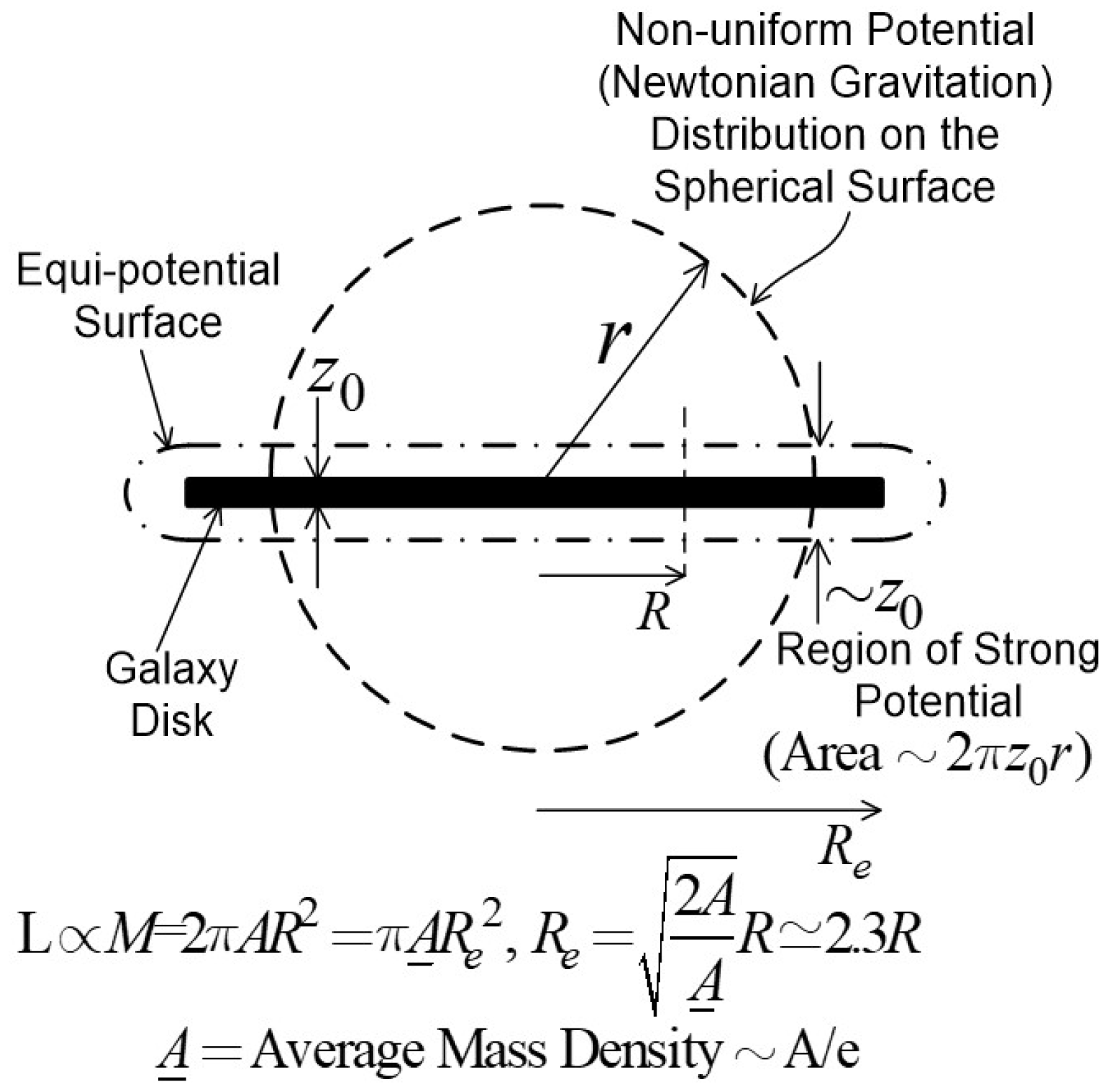
Figure 2.
.
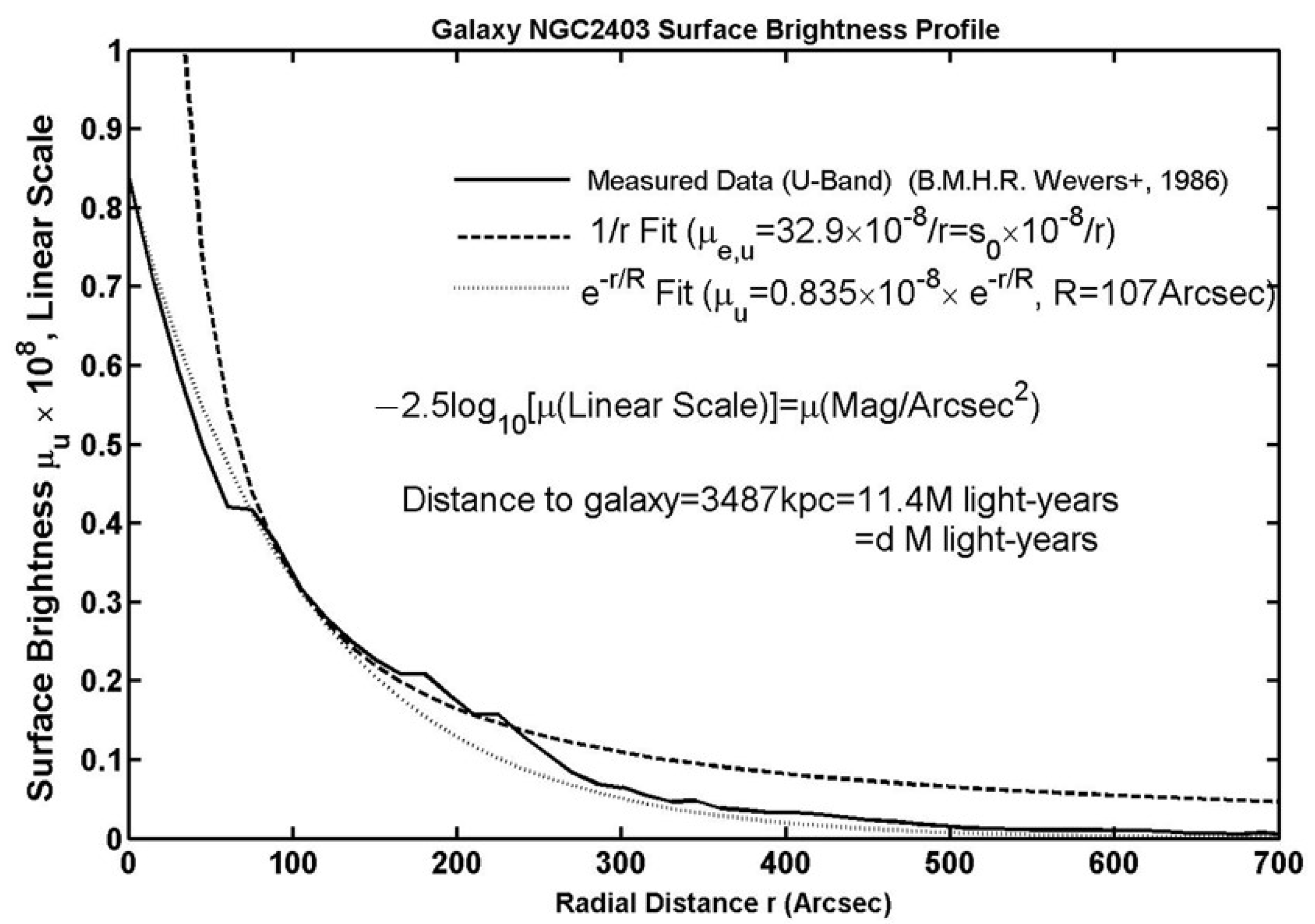
Figure 3.
.
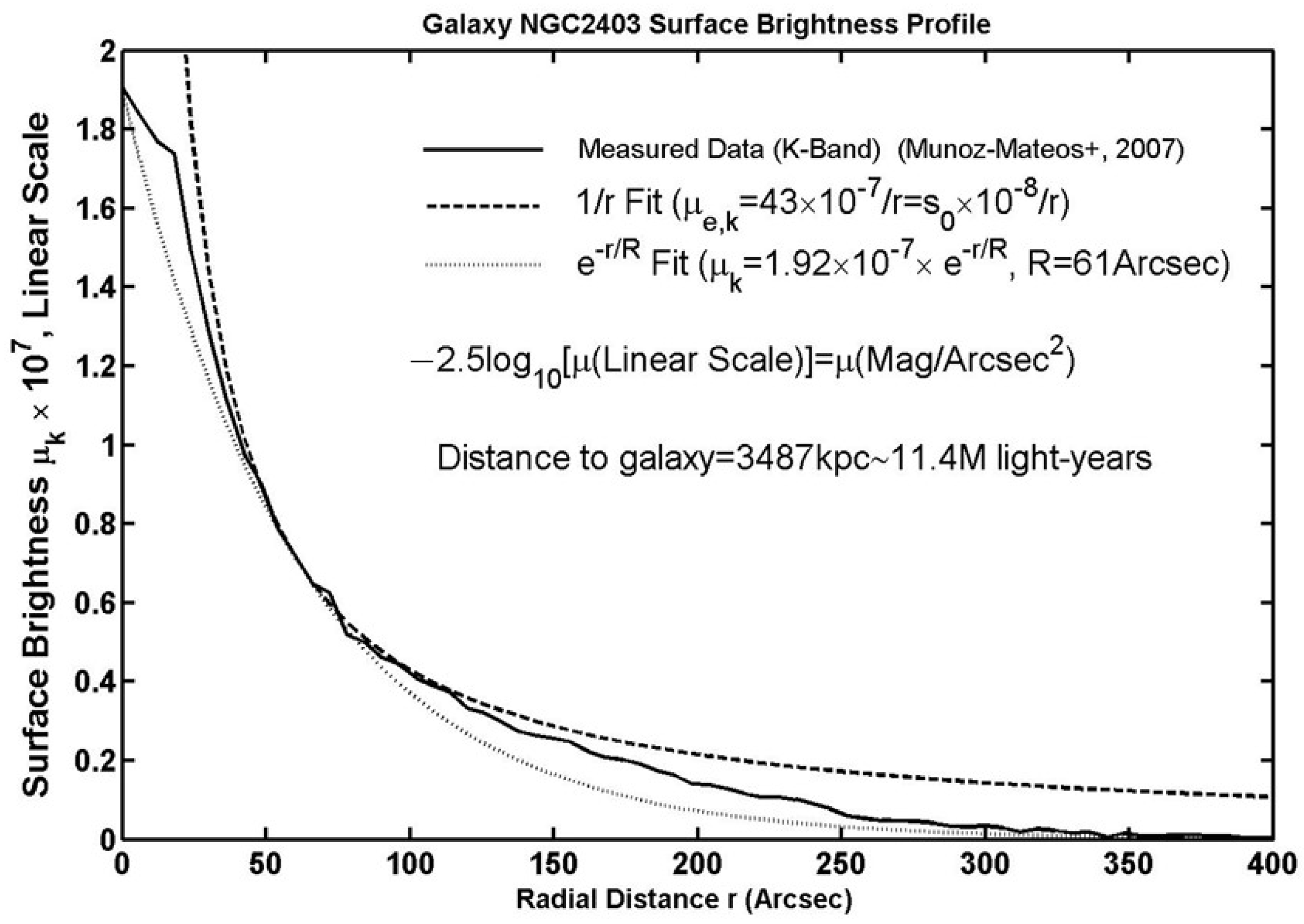
Figure 4.
.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




