Introduction
First of all, note that, as the abstract mentioned, the present paper is written under the condition that our previously published article [
1] was understood that describes the T
c-formula analytically. However, the present paper will provide the review sections.
Although several significant advancements have been presented, from the initial discovery of a superconductor, the most impressive discoveries are CuO
2-based superconductors (i.e., high-T
c cuprates) [
2]. This is because, prior to this result, superconductors generally require significantly high refrigeration because of their lower critical temperature (~20 K). However, because high-T
c cuprates have higher
Tc than LN
2, they received considerable attention and interests from condensed matter physics researchers and researchers in technologies. They demonstrated interest in the technical merits when applied to superconducting magnetic energy storage and energy transmission [
3,
4,
5]. Thus, initial results demonstrated that high-T
c cuprates involved researchers from many condensed matter physics and related technologies.
However, condensed matter physics researchers investigated high-T
c cuprates for much deeper reasons, i.e., they are the first case at which the standard band model and the Bardeen–Cooper–Schieffer (BCS) theory are not applied, which indicates that novel physical phenomena occurred. (Recent H-based superconductors [
6,
7,
8,
9] with extremely high pressures have high potentials to be applied to the BCS theory.) Note that it was considered that BCS theory could be applied to materials whose critical temperatures are up to around 30 K. Furthermore, crucially while BCS theory exhibits isotope effects, it was found that, in high-T
c cuprates, the normal isotope effects were not applied. Considering these facts, it is clear that the mechanism of the high-T
c cuprates differs from that of BCS theory, which gave this paper a motivation to make the mechanism be clear. Moreover, it is obvious that, similar to the BCS theory, the use of quantum field theory is not adequate because quantum field theory is extremely abstract and does not reflect the fact that a phenomenon in condensed matter physics involves many actual physical constants.
Furthermore, many claimed that it is related to many-body interactions [
10], which made many theoretical researchers’ approaches to the mechanism difficult. Thus, it is necessary to consider the mechanism of the cuprates with many-body interactions.
Moreover, while all researchers agree that the carrier is a Cooper pair, the origin is still unclear. Although multiple theories exist discussing the nature of the force to combine a Cooper pair and the origin of pseudo-gap using RVB model or Hubbard-like model, few theoretical articles analytically address and explain experiments data, in addition to the anomaly metal phase and the transition temperature T0 at which the anomaly metal phase appears. Thus, our paper needs to make clear the origin of attractive force to provide a Cooper pair.
Currently, there are many theories besides BCS theory. Here, let us consider why these existing theories are insufficient: Although many studies about the experiments have been reported [
11,
12,
13,
14,
15,
16], (in particular, STM and STS [
17,
18] experimental methods to date revealed many aspects in high-T
c cuprates,), no theory describes all of the experimental data.
These theories are divided to two methods: either Fermi-liquid model or resonating valence bond (RVB) model [
19,
20,
21,
22]. However, these theories have undetermined parameters, which inevitably leads to numerical or fitting methods. We must mention that they are insufficient because many related and actual physical parameters (i.e., physical constants) should be involved when the properties of high-T
c cuprates are considered.
For example, several researchers claim that, because of the existence of magnetic-field interactions, the natural force to combine a Cooper pair must be spin interactions. However, as will be mentioned in this study and our previous study [
1], magnetic-field interactions are not generally only the spin interactions. Furthermore, the spin-fluctuation [
22] model is a numerical one; in this sense, this model is similar to the Hubbard-like model [
23].
These models have multiple parameters to determine or to fit; thus, they do not reflect actual physical picture the high-T
c cuprates originally have. Moreover, if the interaction was defined as spin interactions, they could not explain why other multiple physical parameters such as phonons are related [
24,
25].
That is, thus far research-related challenges have been prevented from a complete investigation of the abovementioned issues. If the calculations can be analytically solved, condensed matter physics will make considerable progress in developing then methods for fabricating compounds with higher critical temperatures could be developed through condensed matter physics fields. Thus, uncovering the physical mechanics of high-Tc cuprates is urgently required, and has motivated the present study. We thus provide new answers to the above questions.
Briefly, the understanding of high-Tc cuprates requires
Analytical calculations of many-body interactions. Most theories use a numerical or fitting method; however, these approaches cannot clarify the physical picture in high-Tc cuprates.
To understand the nature of the force to combine a Cooper pair over long distance.
Combining with our previous study [
1], we will propose a concept of macroscopic Boson. This paper will describe the mechanism of high-T
c cuprates, using only this concept, with the consideration of many-body interactions. That is, basically, just only the existence of the macroscopic Boson will describe the mechanism of high-T
c cuprates.
As the contents of this paper, first we introduce a concept of macroscopic Boson, in which its mass and spin are described. Then using the partition function, the pseudo-gap energy is explained. Moreover, the method to handle many-body interaction will be introduced. Next, as the review of our previous article, we obtain the formula of
Tc [
1]. The calculations of obtaining formulas of
T* and
T0 are positioned, analyzing anomaly metal phases.
Section 3 is Method in which more concrete calculation methods are indicated. Then Result and Discussion sections are followed. Finally, the paper concludes the entire contents in section 6.
3. Results
As a general notation, for the comparisons between the experiments and the values of our theory, this paper cited the experimental literatures in each case. Overall, the agreements are good.
First,
Figure 7 shows the entire depictions of T
c, T
*, and T
0 on doping because of analytical calculations. Generally, the agreements with the experiments are good [e.g., 32]. Moreover, in
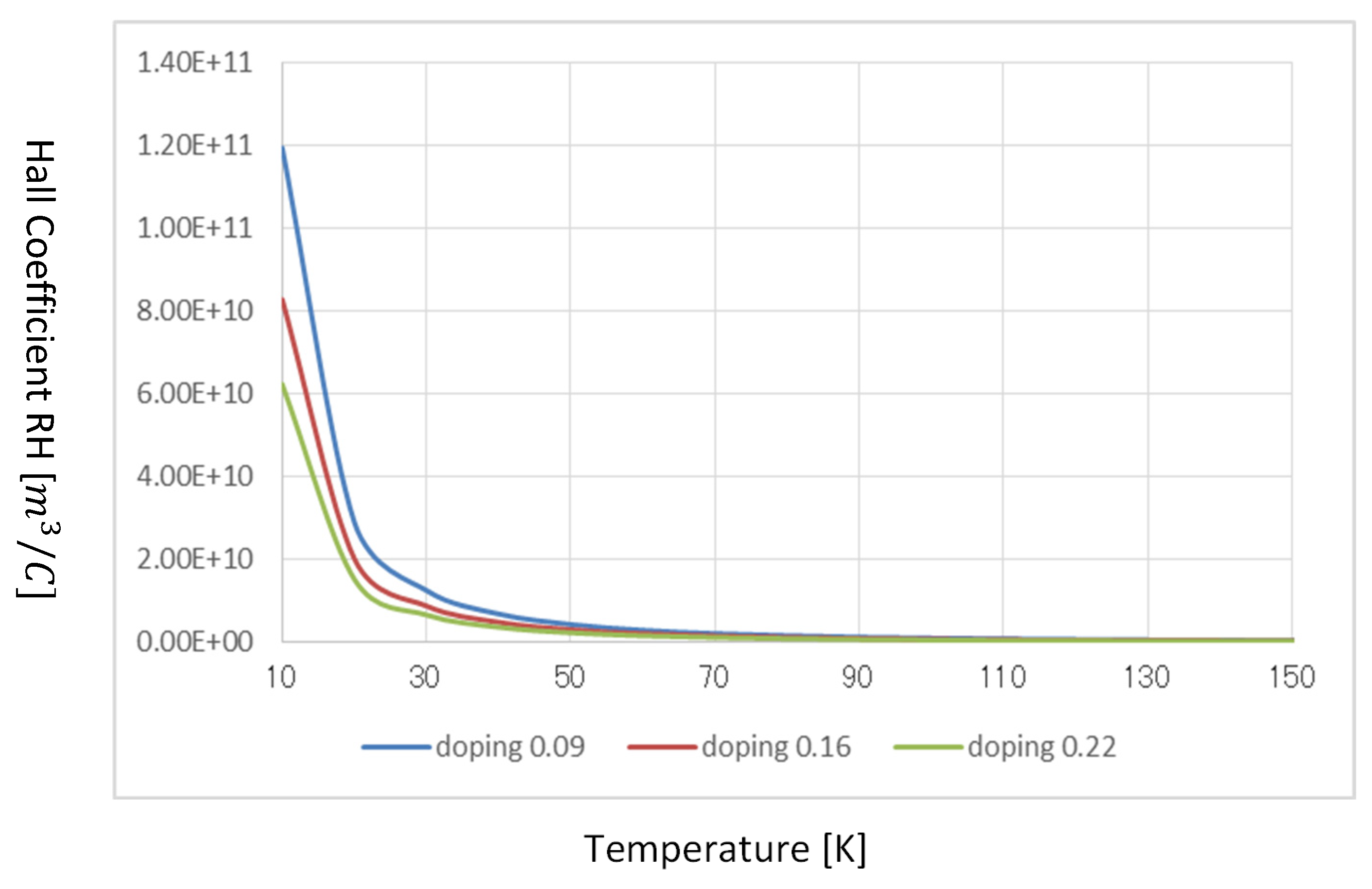
Figure 8, the result of theoretical calculations of the Hall coefficient RH is indicated. As shown, the lower doping, the higher RH, and the RH behave as non-linear on temperatures.
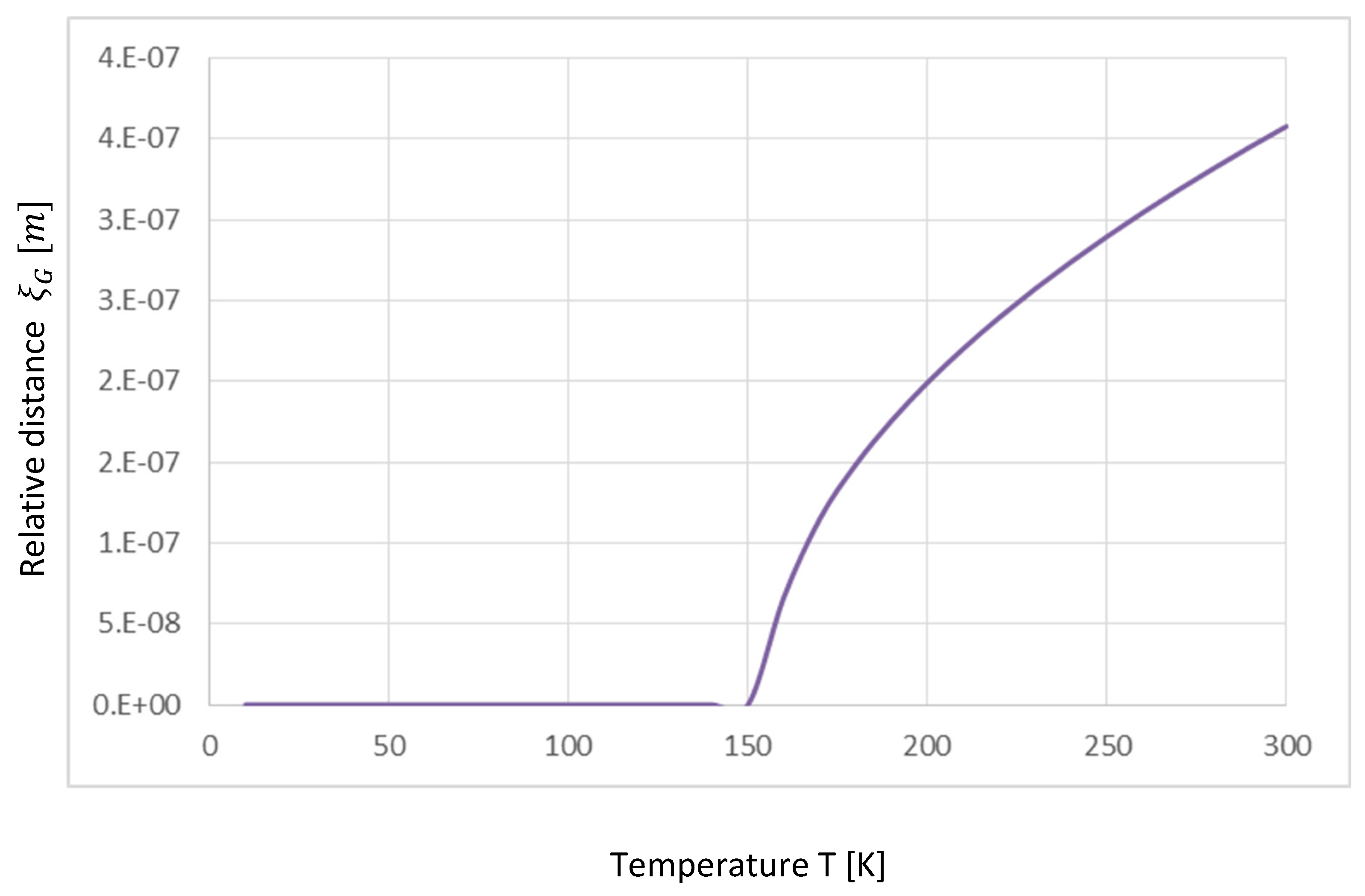
Because of the statistic equation for the many-body interactions,
Figure 10 shows superconductivity state up to a critical temperature ~140 K. In this figure, the state that relative distance
between two spherical shells (i.e., two macroscopic Bosons) is under 0 indicates the superconductivity state. From the further temperatures higher than this critical temperature, the relative distance
becomes much larger as a change of non-continuity. Obviously, a transition occurs at ~140 K. This result accurately agrees with the experiments such as [
34]. Importantly, in
Figure 10, the macroscopic Boson energy
UB (i.e., the magnetic field interaction Equation (29)), at optimum doping, is substituted in our statistic equation. Thus, the many-body interactions in terms of macroscopic Bosons are the reasons why high-T
c cuprates exhibit a considerably higher critical temperature.
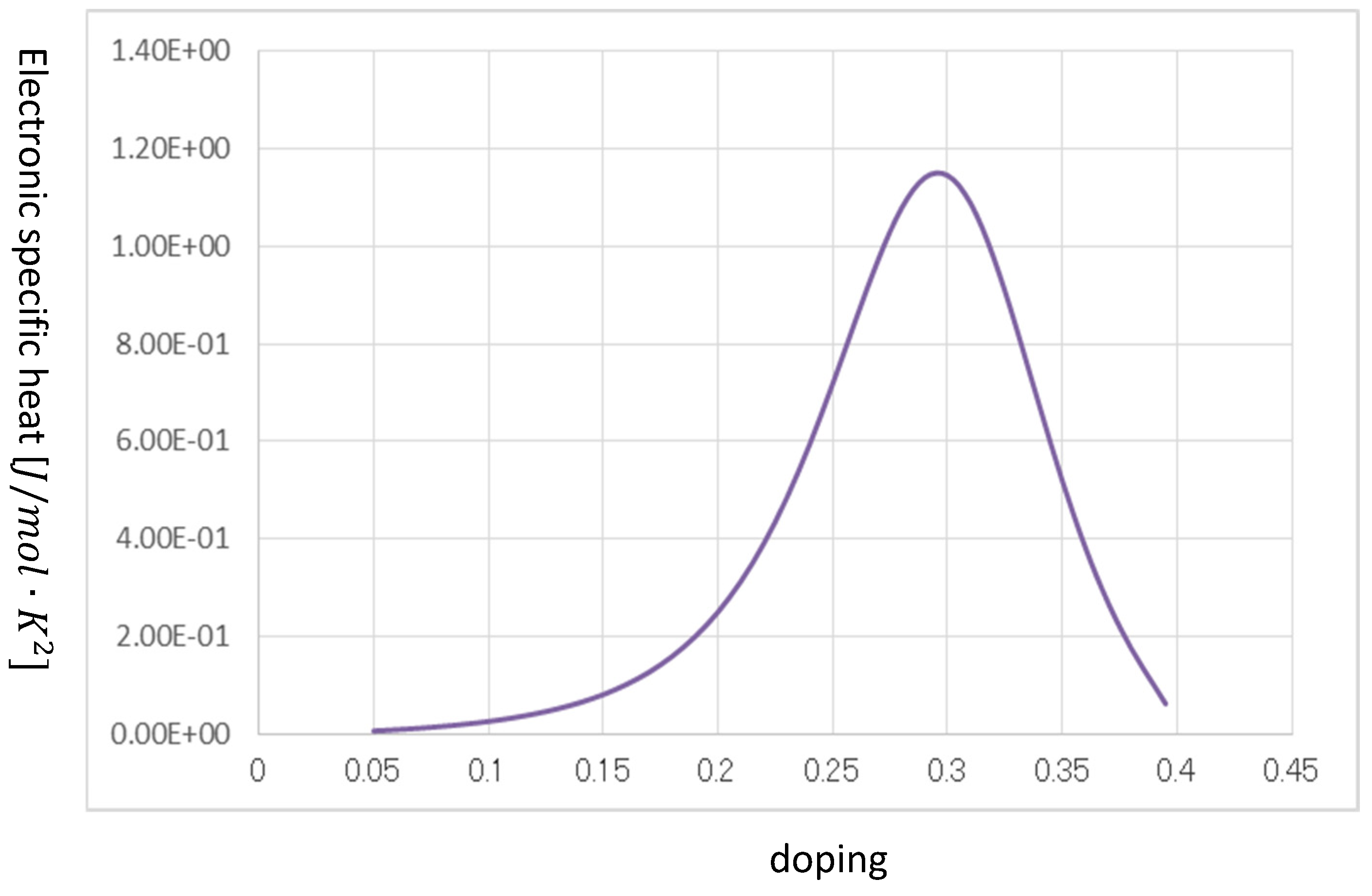
Furthermore,
Figure 9 shows a result of theoretical calculation for the electron specific heat coefficient. According to the experiments [
35,
36], the calculation values are valid; moreover, it takes a maximum at a higher doping.
5. Discussion
5.1. Macroscopic Boson and high-Tc Cuprates
We propose a particle describing high-Tc cuprates is not a normal hole but a macroscopic Boson, which is formed by the conservation of angular momentum in 2D and by rotational motion of a hole itself. The concept of a macroscopic Boson, as mentioned, provided a unique partition function; this partition function can explain every property in the anomaly metal phase. Moreover, the presence of this Boson gives substantial reason why high-Tc cuprates have significantly high critical temperature when considered with many-body interactions.
Let us consider how
Figure 7 relations each transition to the existence of a macroscopic Boson: In the equation of
Tc, considering that the coherence
ξ is essentially equal to the radius
η of a macroscopic Boson does relation the critical temperature
Tc to the macroscopic Boson. Furthermore, to the Equation (38) (
), substituting the energy of a macroscopic Boson results in the temperature
T*. Additionally, considering Equation (63) (
), the value of e
-1 provides the transition temperature
T0 (i.e., Equation (75)), which implies a creation of macroscopic Boson at that transition temperature.
5.2. Anomaly Metal Phase and Transition Temperature T0
Thus far, to understand the mechanism of a high-Tc cuprate, it was important to study the source of pseudo-gap energy. Although this is true, another important factor that should be understood is the source of the transition temperature T0, which defines the anomaly metal phase appearance. As mentioned, all equations that describe the anomaly metal phase have the parameter T0 and Tc.
5.3. Highlights of the Process for the Materials to Undergo Superconductivity
Let us review the process, which describes the mechanism from forming a macroscopic Bosons to undergoing BE condensation. First, high-Tc cuprate reaches the transition temperature T0 with a lower or no refrigeration. At this stage, because the wavelength of a hole along c-axis becomes longer than the width of a 2D CuO2 surface, the net 3D disappears and the conservation of angular momentum forms a macroscopic Boson, which indicates the rotation of a hole producing a magnetic field energy. Thus, this magnetic field energy gives a mass of macroscopic Boson.
By further refrigeration, our established statistic equation results in the following:
1. Many-body interactions, including the magnetic field energy of macroscopic Bosons and Coulomb interactions, result in very short relative distance of two holes (i.e., the net coherence of ~1 nm) as a result of two the sphere shells being superposed. Note that, at this stage, the paring of two macroscopic Bosons indicates the pairing of two holes.
2. Simultaneously, considering the short relative distance, two holes gain a strong combination of the Lorentz force when the relative kinetic energy among two holes becomes 0; note that all Cooper pairs take the identical energy and thus BE condensation is produced, which is the source of the Meissner effect.
Although the derivation of a macroscopic wave function inevitably results in the London equation using the GL equation [
37]; herein, let us review the reason why the Meissner effect is derived by another approach, thus stressing the converged and constant phase
.
Under an applied magnetic field
B (i.e., vector potential
A), we can derive the Aharonov–Bohm (AB) effect [
38] from the initial macroscopic wave function.
where
q,
j, and
denote the hole charge, imaginary unit and converged phase of the macroscopic wave function, respectively.
From Equation (89), it is derived that
where
n is the integer, and considering center-of-mass motion,
Substituting Equation (91) in Equation (90) and differentiating both sides of Equation (90), we obtain
The probability density flow is then defined as follows:
Substituting Equation (92) in Equation (93-1), we derive the following London equation:
This is the identical result from approaches by the GL equation.
5.4. The Reason Why High-Tc Cuprates Have Significantly High Critical Temperature
As mentioned, an attractive force is the Lorentz force when two charged particles have no relative kinetic energy. However, as shown in
Figure 11, this concept can be satisfied in s-wave pair and d-wave pair. Considering this schematic, the pair symmetry of high-T
c cuprates is not very important. Rather, it is crucial to focus on an irregular many-body interactions in high-T
c cuprates for an explanation of the significantly high critical temperature.
As per the model employed to handle many-body interactions in terms of charged particles, it is normally impossible for two particles to take their relative distance shorter than ~10-7 m. In this case, however, our employed equation in many-body interactions has magnetic field interaction in Equation (34) because of the presence of macroscopic Bosons (i.e., pseudo-gap energy) ad Coulomb interactions. Therefore, this fact renders relative distance between two macroscopic Bosons to be almost 0 up to a high temperature, which makes the net coherence of two holes become the order on the cell of a CuO2 surface (i.e., ~1 nm). This fact indicates that the combination energy becomes very strong.
This is demonstrated as shown in
Figure 10, which results in a critical temperature of ~140 K. Considering
in Equation (34) in our model equation to handle many-body interactions is pseudo-gap energy, Equation (24), which is essentially equal to the mass of a macroscopic Boson, the parameter
η [m] (i.e., radius of a Boson and order on a CuO
2 cell) determines the critical temperature. As per our derived statistic equation, the larger
UB is, the higher a critical temperature
Tc, and actual high-T
c indicates that
UB is sufficiently large, which is caused by the fact that the parameter
η [m] is sufficiently small, in addition to optimum doping.
In Equation (34), given the value of 0 for
, immediately the doping variable becomes fixed and the representative critical temperature
Tc, rep is derived;
where
indicates the pseudo-gap of Equation (24) for maximum doping. Thus,
Tc implies the representative critical temperature.
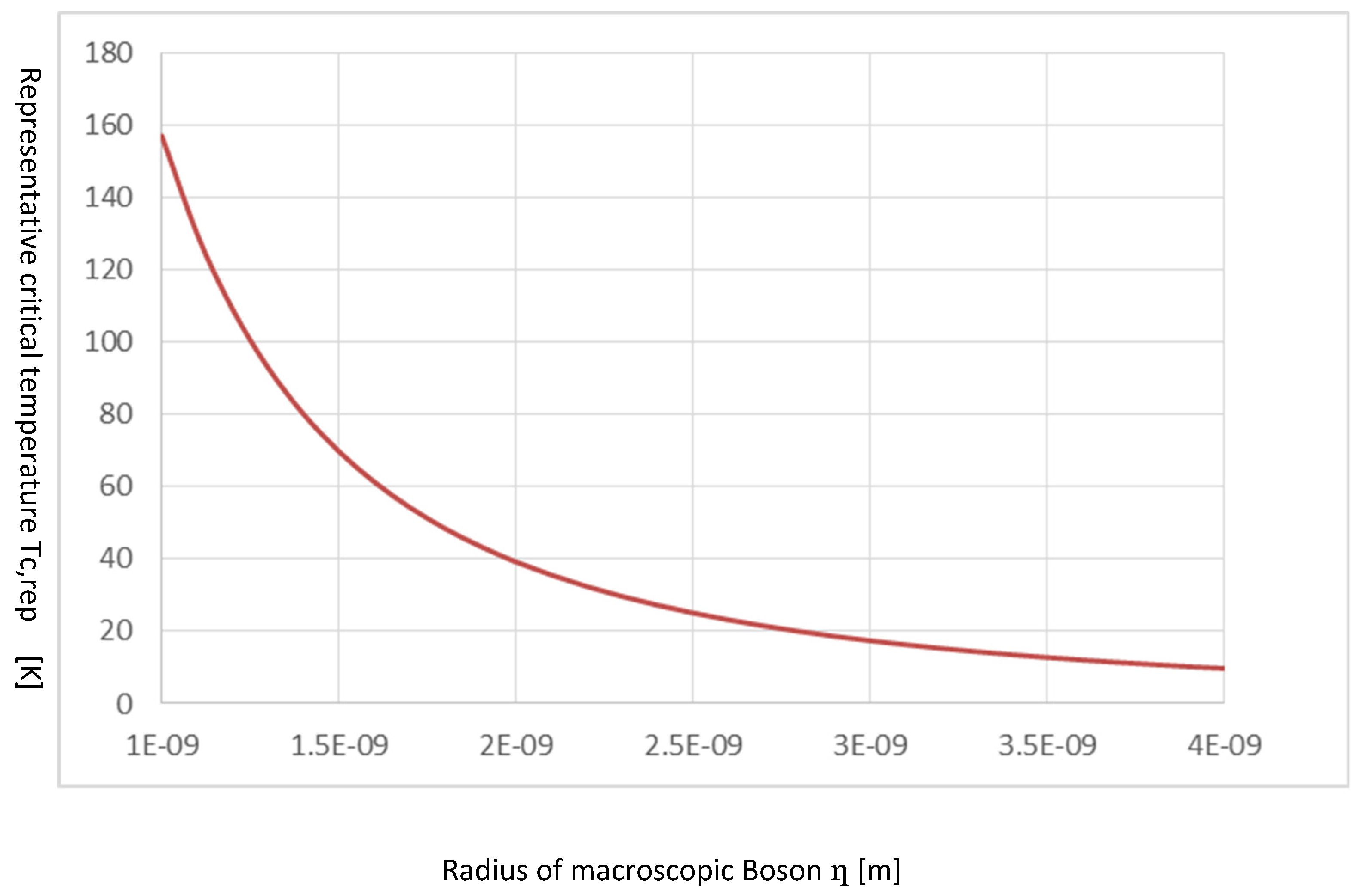
The calculation of quantities by Equation (95) is shown in
Figure 12. In this figure, the horizontal axis implies
η of the radius of a macroscopic Boson. This parameter indicates the unit cell order of the CuO
2 surface. An important point is that, considering the parameter
η is proportional to the lattice constant and although every high-T
c cuprate has macroscopic Bosons, differences in lattice constants render their critical temperature to be variable. Thus, if the type of material among the high-T
c cuprates differs, then the critical temperature is different.
To conclude, the existence of a macroscopic Boson indicates that:
- 1)
It causes the anomaly metal phase in high-Tc cuprates.
- 2)
Irregular many-body interactions are caused by it, which results in a high critical temperature higher than LN2.
Note that, if we consider electron-doping in a Mott insulator, carrier concentration dominates over the lattice concentration ni considering local electrons at each lattice in the Mott insulator; thus, the sign of the function ln in Equation (24) of pseudo-gap energy (i.e., UB in Equation (34)) is altered. Hence, the sign of UB in Equation (24) becomes the opposite, which makes electron-doping unable to have a high critical temperature because, on the contrary, UB would prevent the enhancement of critical temperatures Tc.
5.5. Image of Cooper Paring of Two Holes When
Figure 13 is an image that a hole on 2D of CuO
2 cell takes a circle, which implies a macroscopic Boson. When two macroscopic Bosons are close to each other and when the relative velocity between the two holes is zero, these two holes take the identical and rotational velocity and take the identical angular frequency as shown in
Figure 14. Therefore, when the attractive force principle is satisfied, in which the fact that relative velocity is zero is the source of an attractive force between them, the two holes take rotations, keeping the constant relative distance. This fact is represented in
Figure 15. That is, these holes take parallel motions. This corresponds to the d-wave pairing.
5.6. Consideration of Significances in This Paper
We believe that this study is significant because:
- 1)
It clarified why high-Tc cuprates have actual high critical temperature higher than LN2.
- 2)
It demonstrated that almost puzzles, including the properties of anomaly metal phase reported in previous articles, have been attributed to the presence of a macroscopic Boson.
To date, multiple theoretical investigations were reported to explain the mechanism of high-Tc cuprates but most of them used numerical computing or fitting methods; however, a general understanding of how the mechanism worked was largely unclear. Therefore, we proposed a detailed explanation of the mechanism that has been proposed for a comprehensive understanding of high-Tc cuprates.
Anticipated results and spillover effects:
- 1)
The analytical and physical understanding of high-Tc cuprates described in this study will promote the search for and synthesis of new materials exhibiting higher critical temperature near room temperature than standard materials at any given pressure.
- 2)
All fields of condensed matter physics rely on statistical methods. Therefore, pure analytical (not numerical) approaches can be applied to many-body interactions. Our model that handles many-body interactions will provide new results to unsolved problems in condensed matter physics. For example, the analysis of many-body interactions of magnetic quanta would solve the primary problems of physics and superconducting technologies such as analytical formulation of critical current density.
6. Conclusion
This study described theoretically high-Tc cuprate properties such as the transition temperatures on doping, Hall effect or electron specific heat coefficient on doping. Moreover, it established a novel model to handle general many-body interactions, which explained why the high-Tc cuprates exhibit a significantly high critical temperature.
In general, the derived resultant equations’ values accurately agree with data from experimental studies with no numerical calculations and fitting methods.
As discussed in the Discussion, consider the summary of significances in the present study.
- 1)
It has uncovered the source of mysteries in high-Tc cuprates, i.e., the presence of a macroscopic Boson.
- 2)
It has succeeded in describing the anomaly metal phase with a pure theory, which has no fitting or numerical calculations and which agrees with experiments.
- 3)
It has established a new model to handle general many-body interactions; using this model, this study has clarified why high-Tc cuprates have considerably high critical temperatures.
The resistivity on lower doping in the anomaly metal phase is not discussed in this study. However, an equation for conductivity, which takes linearly temperature dependence (i.e., non-linearly resistivity), was obtained in the theoretical section of this study because the carrier concentration in Equation (62), which lineally depends on temperatures, indicates the conductivity. However, this equation employs the critical temperature Tc and thus, over the lower doping, in which the resistivity appears, this equation is not available because, over the lower doping, critical temperatures are not defined. Thus, this will be a natural follow-up.
Moreover, the theory this paper presented seems not to describe electron doping cuprates. Furthermore, very recently, 2-dimentional CDW phases dependent on doping were measured. Thus, it is necessary to research these facts as follow-ups. However, in
Appendix B of this paper, a preliminary calculation of the 2-dimensional CDW will be presented.
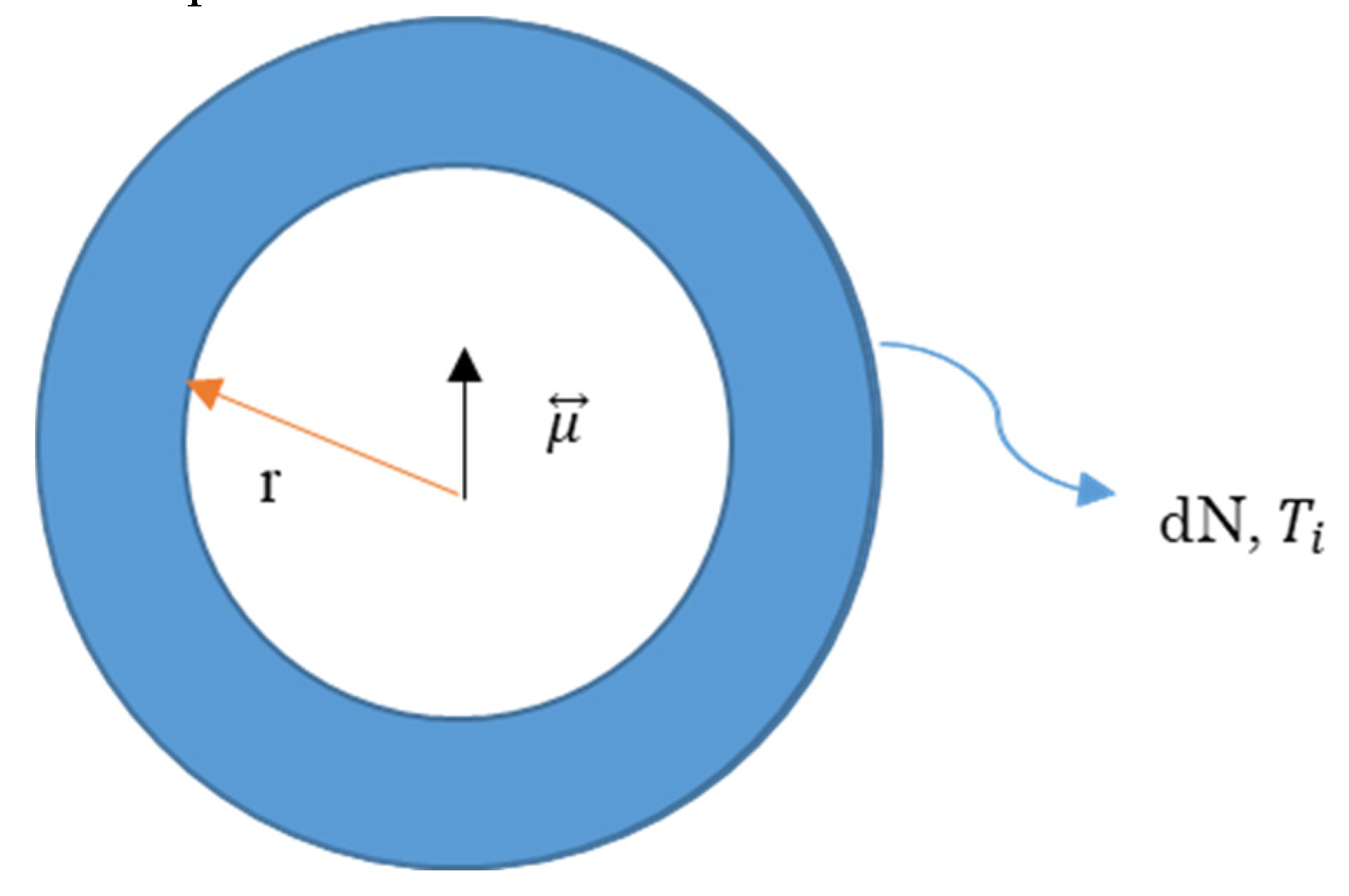
Figure 1.
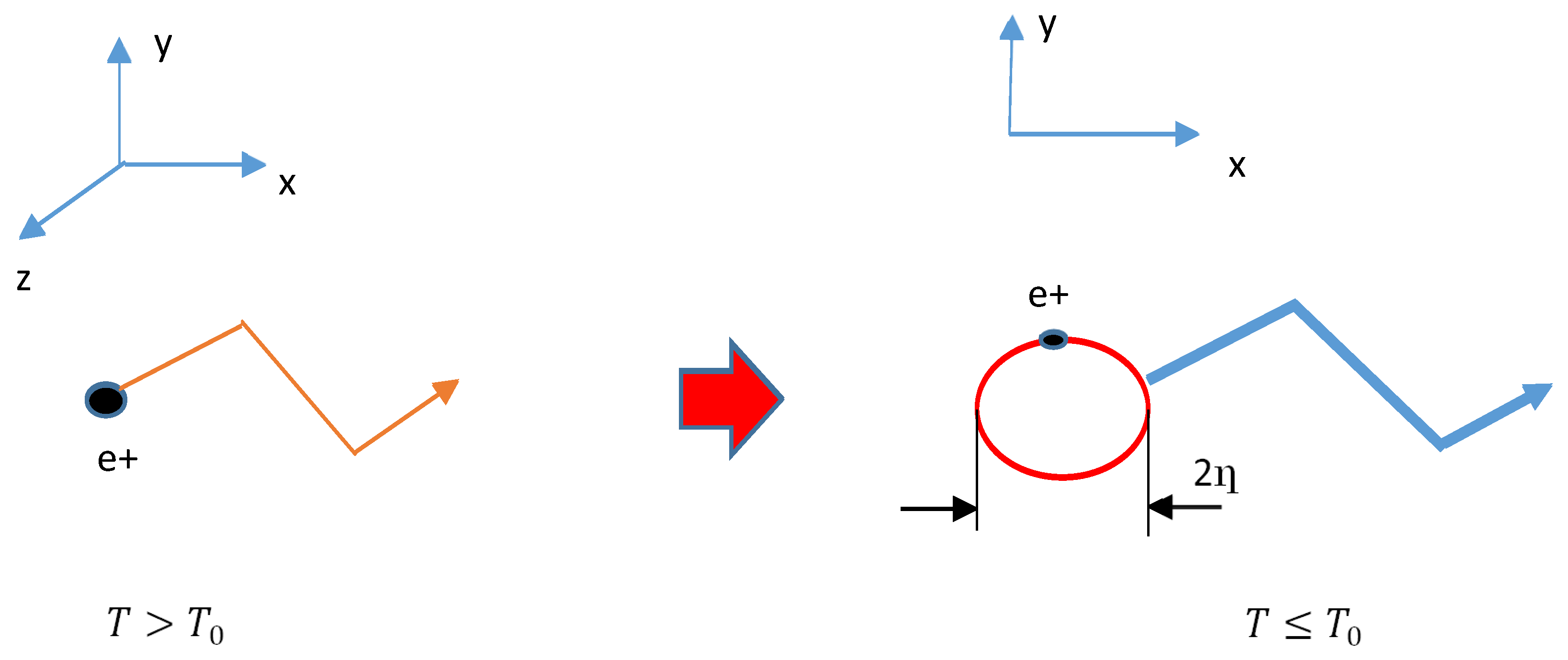
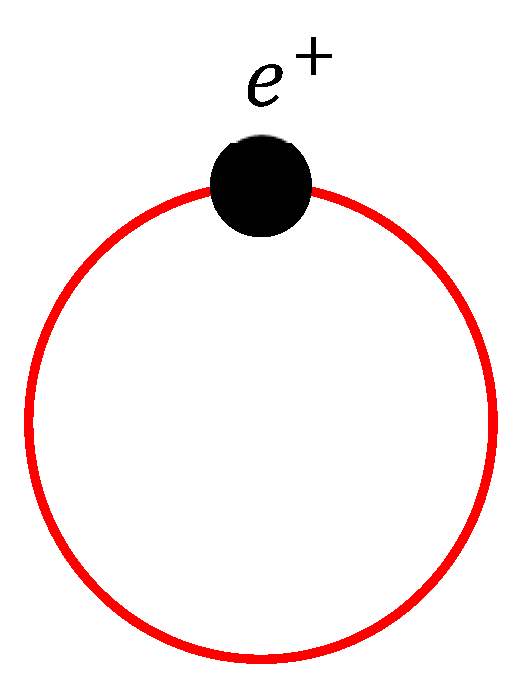
Schematic of a macroscopic Boson. Normally, holes move in 3D when their kinetic energy is high. However, when refrigeration reduces the momentum along z-direction, the complete x-y 2D motion is formed. Thus, a conservation of the angular momentum creates a rotation movement by a hole itself. This transition will be described later. Because a current circle by the rotation generates magnetic field energy, which determines the mass of this circle, this circle is essentially different from a normal hole. We will refer to this new particle as “a macroscopic Boson.” The radius η of a macroscopic Boson is assumed to be of the order of a CuO2 cell (i.e., ~1 nm).
Figure 1.
Schematic of a macroscopic Boson. Normally, holes move in 3D when their kinetic energy is high. However, when refrigeration reduces the momentum along z-direction, the complete x-y 2D motion is formed. Thus, a conservation of the angular momentum creates a rotation movement by a hole itself. This transition will be described later. Because a current circle by the rotation generates magnetic field energy, which determines the mass of this circle, this circle is essentially different from a normal hole. We will refer to this new particle as “a macroscopic Boson.” The radius η of a macroscopic Boson is assumed to be of the order of a CuO2 cell (i.e., ~1 nm).
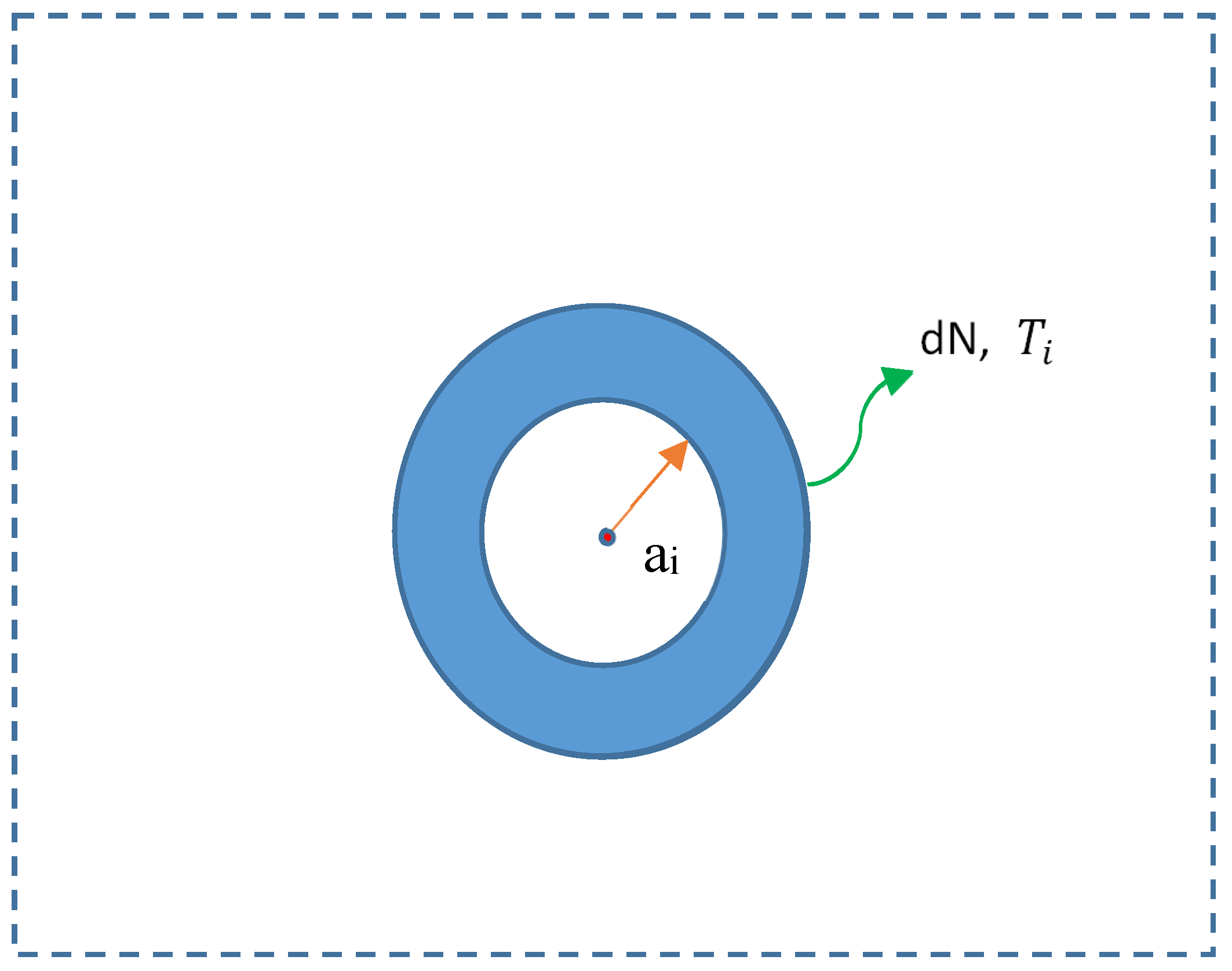
Figure 2.
Schematic of our established model to handle many-body interactions. Considering the nature of many-body interactions, note that temperatures are locally different. However, this model claims that in the differential number dN (a macroscopic Boson takes the center and dN takes a temperature ), a thermal equilibrium can be assumed. Therefore, a balance between force of expansion from Coulomb interactions, in addition to the magnetic field interactions from the Bosons and force of compression from immediate outer side, which is equal to the kinetic energies in dN (i.e., a temperature ), is formed. Calculating this balanced equation results in a new statistical equation.
Figure 2.
Schematic of our established model to handle many-body interactions. Considering the nature of many-body interactions, note that temperatures are locally different. However, this model claims that in the differential number dN (a macroscopic Boson takes the center and dN takes a temperature ), a thermal equilibrium can be assumed. Therefore, a balance between force of expansion from Coulomb interactions, in addition to the magnetic field interactions from the Bosons and force of compression from immediate outer side, which is equal to the kinetic energies in dN (i.e., a temperature ), is formed. Calculating this balanced equation results in a new statistical equation.
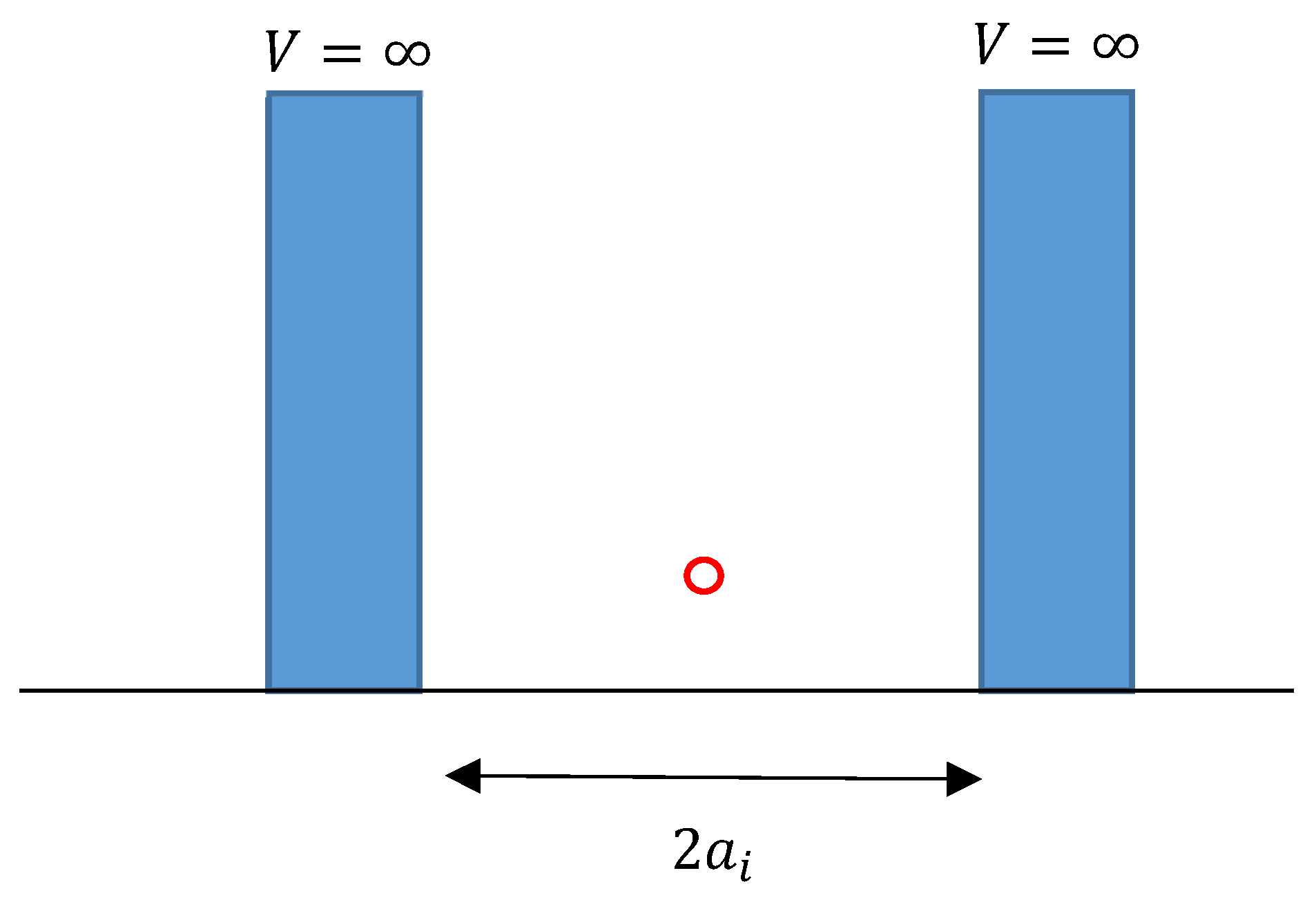
Figure 3.
A basic model of infinite well-potential. This model is directly related to the immediate prior figure model. The diameter 2 varies depending on a temperature . A macroscopic Boson in this well-potential forms a stationary wave, and its wave function and eigenvalue are presented in every basis textbook.
Figure 3.
A basic model of infinite well-potential. This model is directly related to the immediate prior figure model. The diameter 2 varies depending on a temperature . A macroscopic Boson in this well-potential forms a stationary wave, and its wave function and eigenvalue are presented in every basis textbook.
Figure 4.
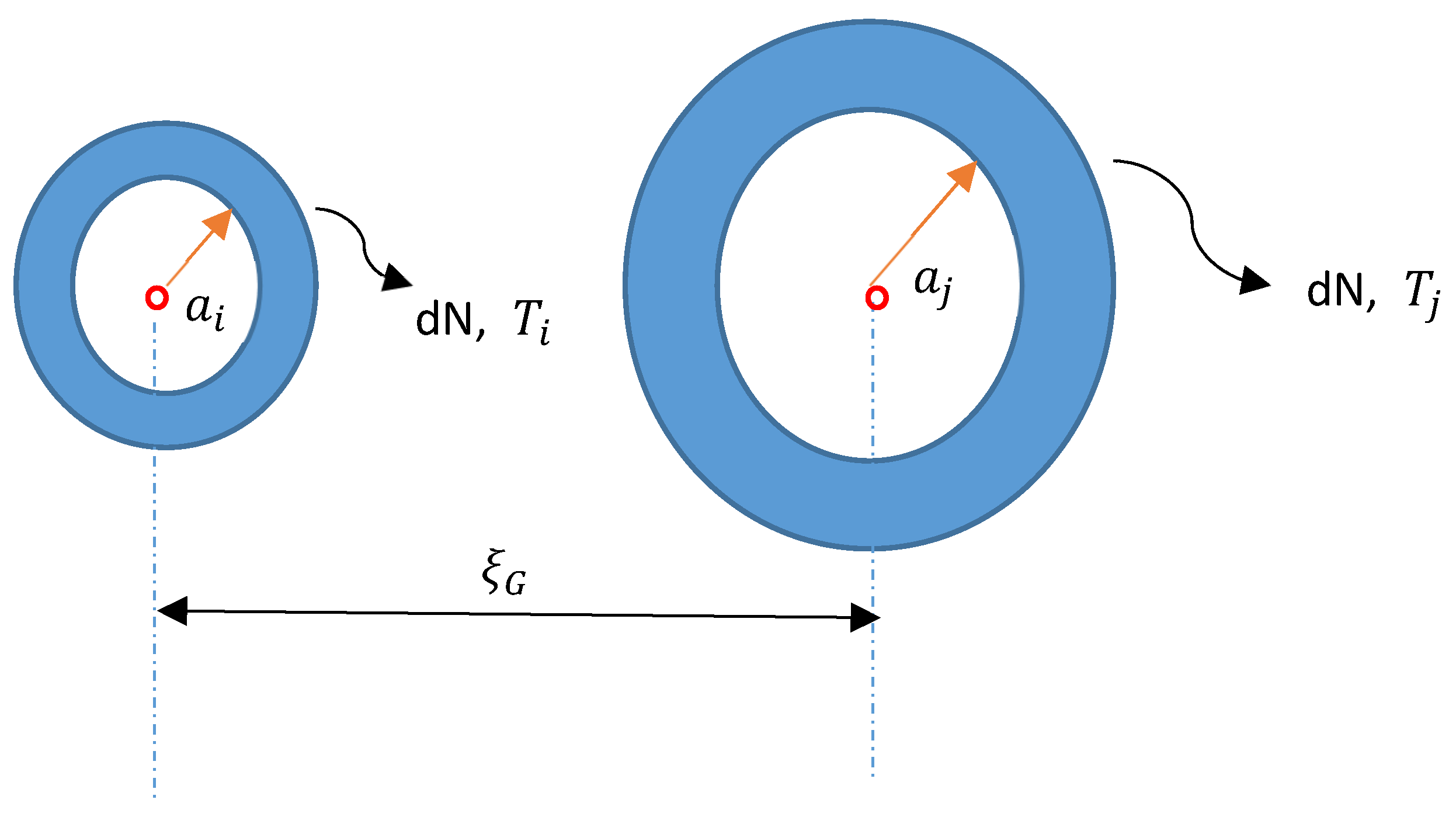
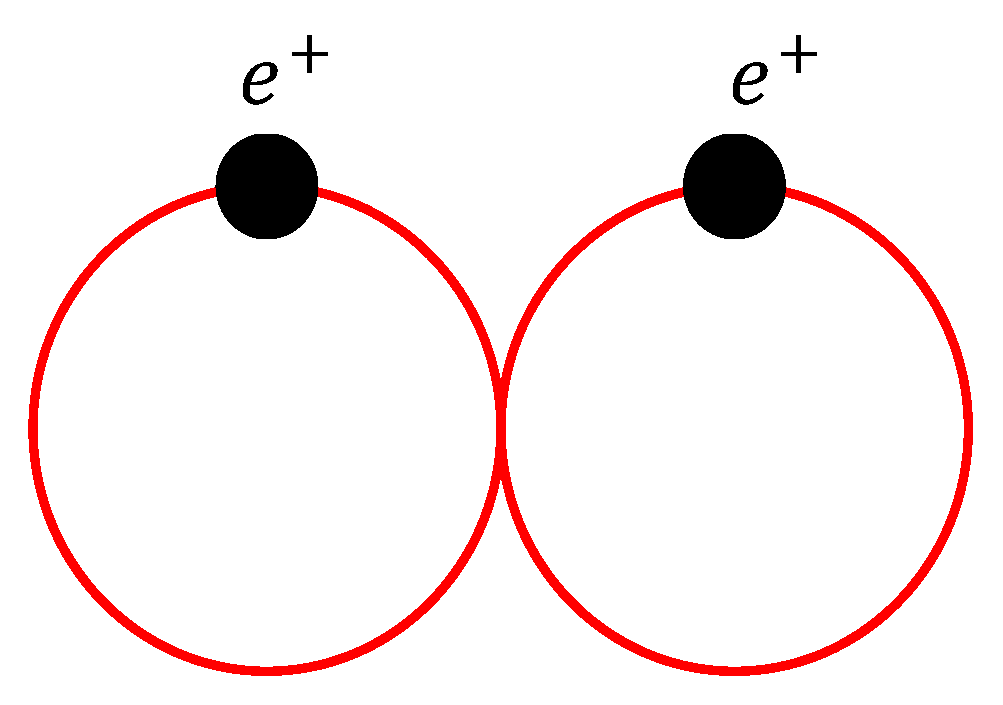
Schematic of two macroscopic Bosons having many-body interactions. The relative distance of indicates one between two macroscopic Bosons. When an attractive force F between them appears and because the relative kinetic energy becomes 0, indexes i and j take the same. Thus, a superposition between them occurs, rendering be 0. That is, two Bosons now combine to be a Cooper pair. Employing the statistic equations from our established model, we can predict this type of transition.
Figure 4.
Schematic of two macroscopic Bosons having many-body interactions. The relative distance of indicates one between two macroscopic Bosons. When an attractive force F between them appears and because the relative kinetic energy becomes 0, indexes i and j take the same. Thus, a superposition between them occurs, rendering be 0. That is, two Bosons now combine to be a Cooper pair. Employing the statistic equations from our established model, we can predict this type of transition.
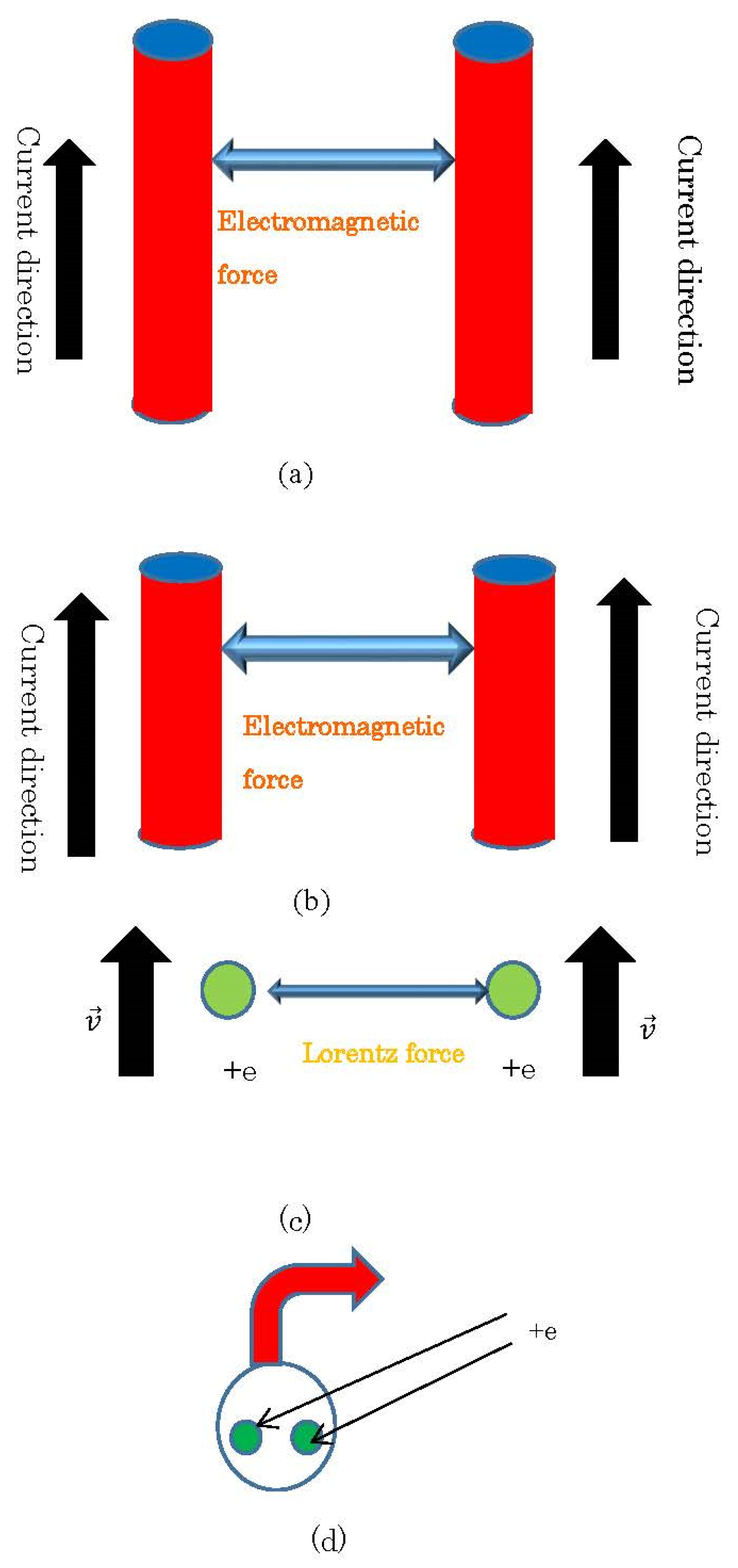
Figure 5.
(a) Currents in the same direction. (b) Shorter leads with currents in the same direction. (c) Holes with same direction and equal velocity. (d) Center-of-mass motion of Cooper pair.
Figure 5.
(a) Currents in the same direction. (b) Shorter leads with currents in the same direction. (c) Holes with same direction and equal velocity. (d) Center-of-mass motion of Cooper pair.
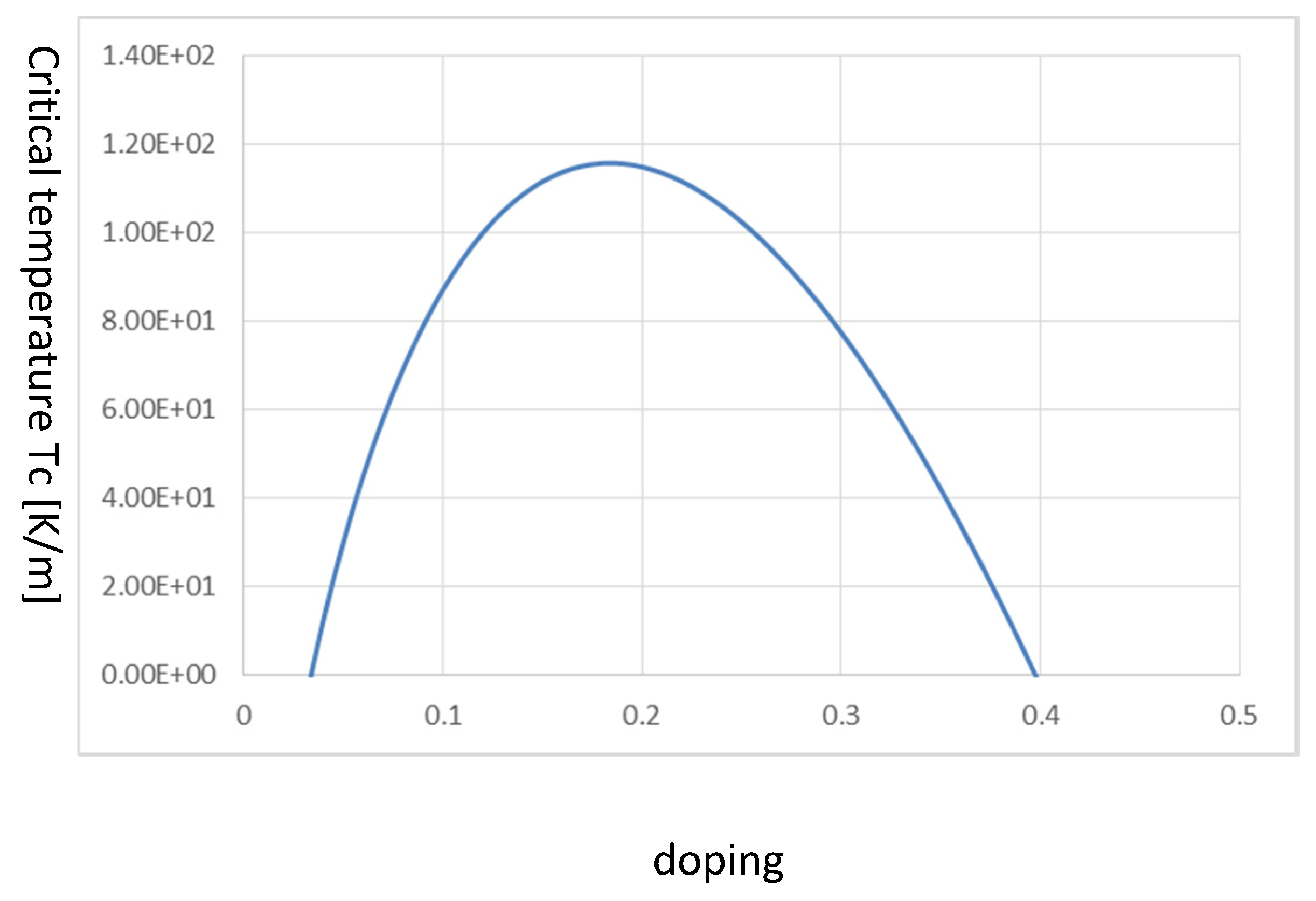
Figure 6.
A result of typical critical temperature on doping. This is derived from the equation by combining pseudo-gap energy (i.e., the general energy gap) and superconducting energy gap. At doping 0.16, the critical temperature reaches the maximum, which agrees with the experiments [e.g., [
32]] In calculations, no numerical calculations or fitting method are employed. The values of critical temperatures are relatively sensitive for Debye temperature and Fermi energy in our derived equation.
Figure 6.
A result of typical critical temperature on doping. This is derived from the equation by combining pseudo-gap energy (i.e., the general energy gap) and superconducting energy gap. At doping 0.16, the critical temperature reaches the maximum, which agrees with the experiments [e.g., [
32]] In calculations, no numerical calculations or fitting method are employed. The values of critical temperatures are relatively sensitive for Debye temperature and Fermi energy in our derived equation.
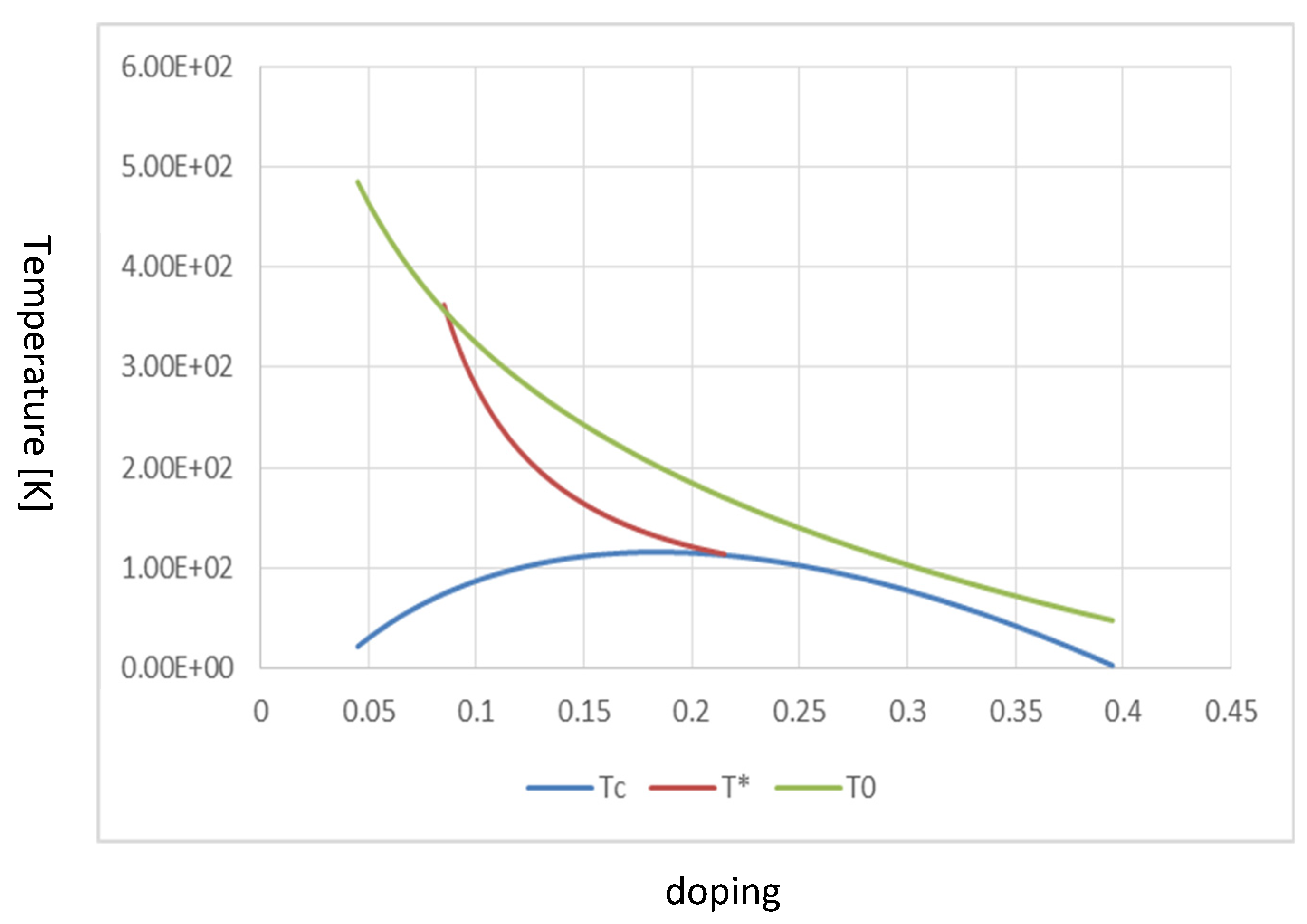
Figure 7.
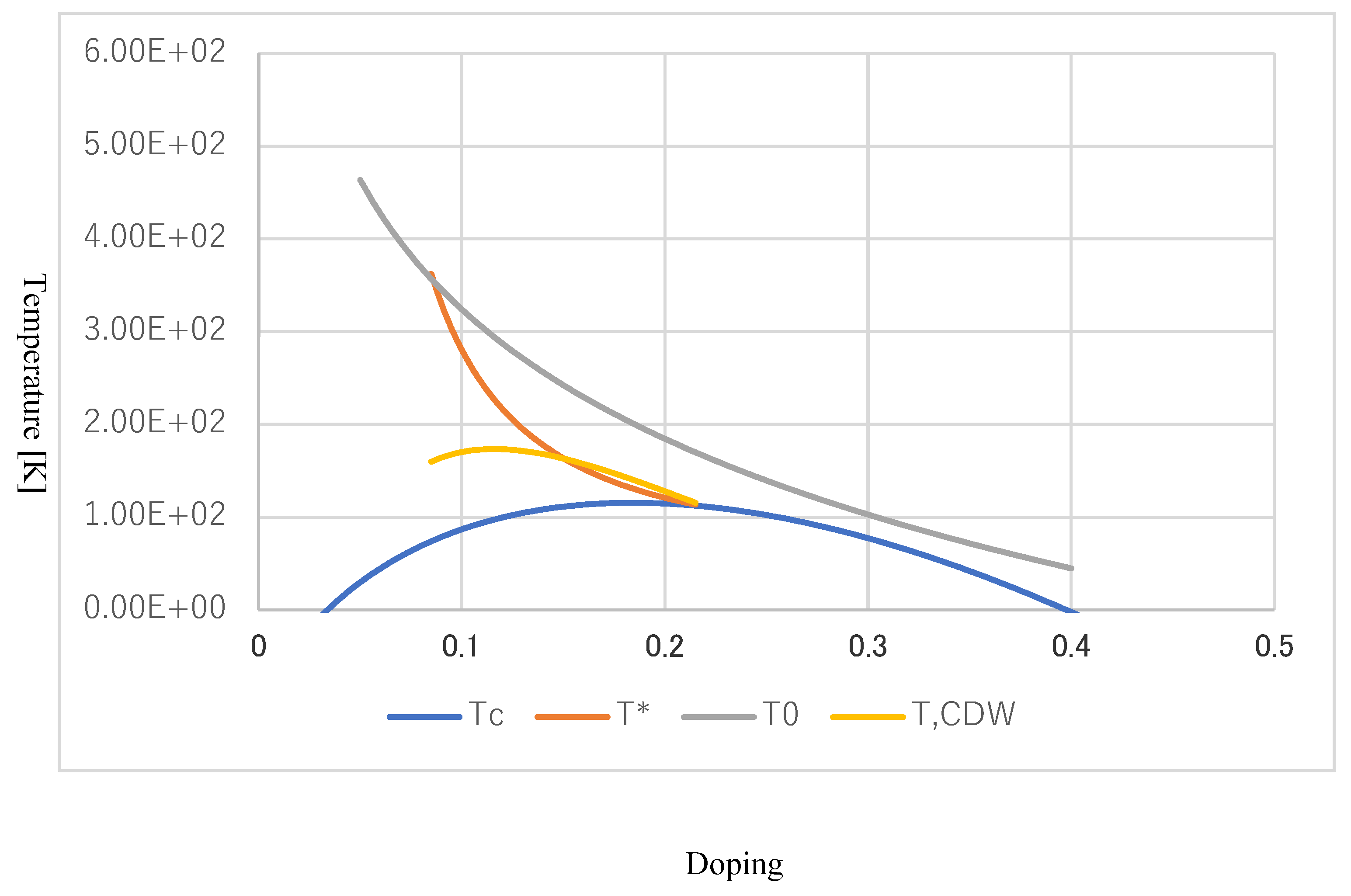
The complete depiction from theoretical calculations of Tc, T*, and T0 vs. doping. Note that the horizontal axis is . For the previous figure of Tc graph, T* and T0 are added. Note that T* is depicted on the understanding that it is smaller than T0. Moreover, T* has the gradual and easy minimum point on touching Tc- dome at the doping 0.21. Thus, it does not exist in the Tc-dome. As mentioned, no numerical calculations and fitting methods are employed. T0 begins with about 500 K and vanishes almost at the same doping at which Tc disappears. As mentioned in the main body, this transition temperature is important when considering the anomaly metal phase.
Figure 7.
The complete depiction from theoretical calculations of Tc, T*, and T0 vs. doping. Note that the horizontal axis is . For the previous figure of Tc graph, T* and T0 are added. Note that T* is depicted on the understanding that it is smaller than T0. Moreover, T* has the gradual and easy minimum point on touching Tc- dome at the doping 0.21. Thus, it does not exist in the Tc-dome. As mentioned, no numerical calculations and fitting methods are employed. T0 begins with about 500 K and vanishes almost at the same doping at which Tc disappears. As mentioned in the main body, this transition temperature is important when considering the anomaly metal phase.
Figure 8.
Hall-effect coefficient RH on both temperature and doping. As reported in many experimental papers, lowering the doping dose arises the RH. The calculated values generally agree with experiments (See Ref [
33] of the experiment as a reference).
Figure 8.
Hall-effect coefficient RH on both temperature and doping. As reported in many experimental papers, lowering the doping dose arises the RH. The calculated values generally agree with experiments (See Ref [
33] of the experiment as a reference).
Figure 9.
A theoretical result of electron specific heat coefficient on doping. At the relatively high doping, the curve takes the maximum, which agrees with the experiments. In other words, to both lower doping or higher doping from this the maximum, electron specific heat coefficient decreases.
Figure 9.
A theoretical result of electron specific heat coefficient on doping. At the relatively high doping, the curve takes the maximum, which agrees with the experiments. In other words, to both lower doping or higher doping from this the maximum, electron specific heat coefficient decreases.
Figure 10.
Relative distance between two macroscopic Bosons versus temperature. Because, up to about 140 K, relative distances s not defined according to our statistic equation to handle the many-body interactions, the net coherence of two holes is defined as about 1 nm, i.e., superconductivity state is maintained. However, at higher temperatures, relative distances suddenly becomes order. Obviously, a transition occurs at around 140 K. As an important notation, the macroscopic Boson energy UB is substituted at the optimum doping of 0.16. Thus, the many-body interaction in terms of macroscopic Bosons (not holes) is one of the reasons why high-Tc cuprates exhibit extremely high critical temperatures.
Figure 10.
Relative distance between two macroscopic Bosons versus temperature. Because, up to about 140 K, relative distances s not defined according to our statistic equation to handle the many-body interactions, the net coherence of two holes is defined as about 1 nm, i.e., superconductivity state is maintained. However, at higher temperatures, relative distances suddenly becomes order. Obviously, a transition occurs at around 140 K. As an important notation, the macroscopic Boson energy UB is substituted at the optimum doping of 0.16. Thus, the many-body interaction in terms of macroscopic Bosons (not holes) is one of the reasons why high-Tc cuprates exhibit extremely high critical temperatures.
Figure 11.
Schematic of paring symmetries. The principle to generate an attractive force between two charged particles is that relative momentum must be equal. That is, when this principle is satisfied and if outer macroscopic heat energy does not disturb, the two charged particles between a long distance are combined by the generated attractive force, which stems from the Lorentz force. The above figure illustrates this principle, i.e., s-wave and d-wave symmetries. This is why there is another irrelevant particle among force–experiencing two particles. This irrelevant charged particle with different momentum does not experience this attractive force. However, the Coulomb interactions does not have this characteristic.
Figure 11.
Schematic of paring symmetries. The principle to generate an attractive force between two charged particles is that relative momentum must be equal. That is, when this principle is satisfied and if outer macroscopic heat energy does not disturb, the two charged particles between a long distance are combined by the generated attractive force, which stems from the Lorentz force. The above figure illustrates this principle, i.e., s-wave and d-wave symmetries. This is why there is another irrelevant particle among force–experiencing two particles. This irrelevant charged particle with different momentum does not experience this attractive force. However, the Coulomb interactions does not have this characteristic.
Figure 12.
The representative Tc,rep for optimum doping vs. the radius of a macroscopic Boson η. Of note, the parameter η depends on a lattice constant. As shown, Tc,rep is very sensitive for parameters η. This indicates that, among high- Tc cuprates, varying substances renders their critical temperatures to be variable.
Figure 12.
The representative Tc,rep for optimum doping vs. the radius of a macroscopic Boson η. Of note, the parameter η depends on a lattice constant. As shown, Tc,rep is very sensitive for parameters η. This indicates that, among high- Tc cuprates, varying substances renders their critical temperatures to be variable.
Figure 13.
Schematic of a macroscopic Boson.
Figure 13.
Schematic of a macroscopic Boson.
Figure 14.
Schematic of paring of two macroscopic Bosons (i.e., the two holes).
Figure 14.
Schematic of paring of two macroscopic Bosons (i.e., the two holes).
Figure 15.
Translation of the aforementioned
Figure 14.
Figure 15.
Translation of the aforementioned
Figure 14.
Figure A2.
The phase diagram including the 2-dimentional CDW phase. The yellow curve is the transition. This figure was created on the basis of
Figure 7 in the man body.
Figure A2.
The phase diagram including the 2-dimentional CDW phase. The yellow curve is the transition. This figure was created on the basis of
Figure 7 in the man body.
Table 1.
Physical parameters in the equation of critical temperature.
Table 1.
Physical parameters in the equation of critical temperature.
| Debye temperature |
113.5 K |
| Coherence ξ |
1 nm |
| Fermi energy EF0
|
J |
| The number of layer nq
|
3 |
Table 2.
Physical constants in the obtained equations.
Table 2.
Physical constants in the obtained equations.