Working PaperArticleVersion 1This version is not peer-reviewed
Negative Effective Mass in Plasmonic Systems, II: Elucidating of Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation
Bormashenko, E.; Legchenkova, I.; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials2020, 13, 3512.
Bormashenko, E.; Legchenkova, I.; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials 2020, 13, 3512.
Bormashenko, E.; Legchenkova, I.; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials2020, 13, 3512.
Bormashenko, E.; Legchenkova, I.; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials 2020, 13, 3512.
Abstract
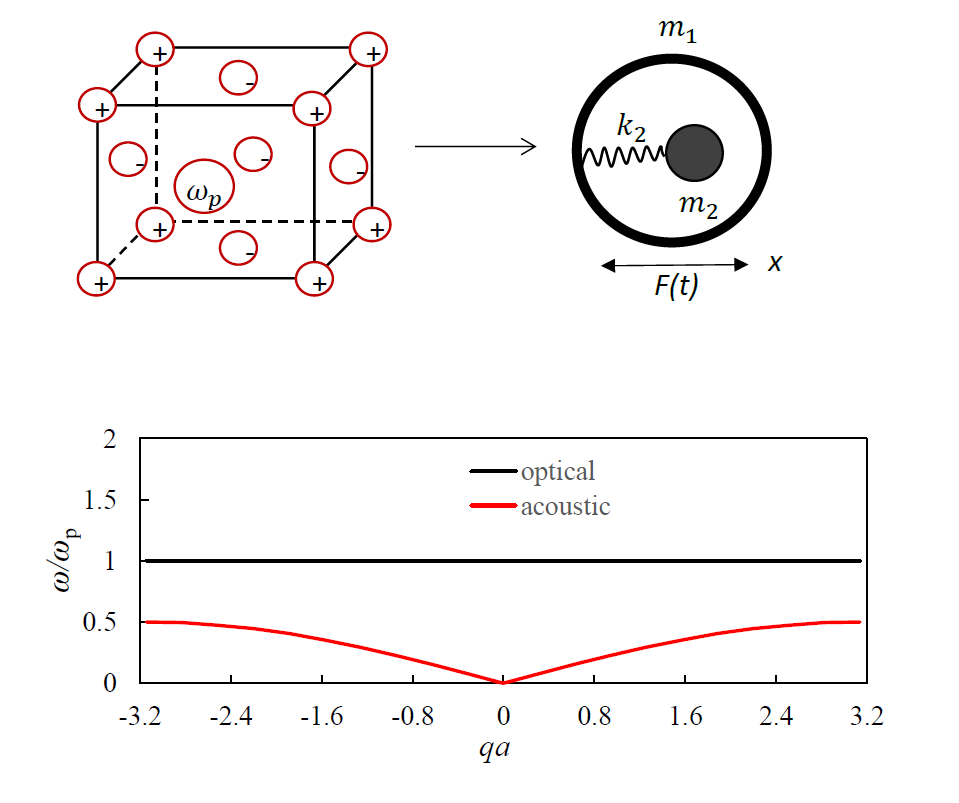
We report the negative effective mass metamaterials based on the electro-mechanical coupling exploiting plasma oscillations of a free electron gas. The negative mass appears as a result of vibration of a metallic particle with a frequency of ω which is close to the frequency of the plasma oscillations of the electron gas m_2 relatively to the ionic lattice m_1. The plasma oscillations are represented with the elastic spring k_2=ω_p^2 m_2, where ω_p is the plasma frequency. Thus, the metallic particle vibrated with the external frequency ω is described by the effective mass m_eff=m_1+(m_2 ω_p^2)/(ω_p^2-ω^2 ) , which is negative when the frequency ω approaches ω_p from above. The idea is exemplified with two conducting metals, namely Au and Li embedded into various matrices. The one-dimensional lattice built of the identical metallic micro-elements m_eff connected by ideal springs k_1 representing various media such as polydimethylsiloxane and soda-lime glass is treated. The optical and acoustical branches of longitudinal modes propagating through the lattice are elucidated for various ratios ω_1/ω_p . The 1D lattice built of the thin metallic wires giving rise to the low frequency plasmons is treated. The possibility of the anti-resonant propagation, strengthening the effect of the negative mass occurring under = p = 1 is addressed.
Keywords
metamaterials; negative effective mass; plasma oscillations; low frequency plasmons; optical and acoustical branches.
Subject
Chemistry and Materials Science, Materials Science and Technology
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
.png)
