Preprint
Article
Celestial and Quantum Propagation, Spinning, and Interaction as 4D Relativistic Cloud-Worlds Embedded in a 4D Conformal Bulk: From String to Cloud Theory
Altmetrics
Downloads
2614
Views
3061
Comments
0
This version is not peer-reviewed
Submitted:
18 July 2024
Posted:
18 July 2024
You are already at the latest version
Alerts
Abstract
Considerable efforts have been devoted to modifying gravity, which aim to elucidate the possible existence or nature of dark matter and energy, describe observational data more effectively, and formulate quantum gravity. In addition, despite the immense success of quantum field theory, the framework requires renormalization techniques and breaks down at high energies. Recently, the Planck legacy 2018 release confirmed the existence of an enhanced lensing amplitude in cosmic microwave background power spectra, which prefers that the early Universe had a positive curvature with a confidence level higher than 99%. This study considers the implied primordial curvature as the global curvature or curvature of “4D conformal bulk as a manifestation of vacuum energy” and distinguishes it from the localized curvature that is induced in the bulk by the presence of celestial objects that are regarded as ”4D relativistic cloud-worlds”. Analogously, because gravity appears to emerge owing to spacetime curvature and does not exhibit critical characteristics that are shared by other fields, it has been incorporated as the bulk’s local curvature affecting embedded quantum fields that are regarded as propagating “4D relativistic quantum clouds”. To consider the effects of the bulk on embedded clouds, this paper presents interaction field equations in terms of the brane-world modified gravity and perspective of geometrization of quantum mechanics; wherein gravity is manifested by the curvature of 4D conformal bulk as an indicator of the field strength of vacuum energy on the embedded 4D relativistic clouds in addition to the boundary interactions, which could eliminate the singularities and satisfy a conformal invariance theory. A visualization of the evolution of the 4D relativistic cloud-world over the conformal spacetime of the 4D bulk is presented. The standard said theories are recovered from the interaction field equations, whereas experimental conditions are recommended to directly falsify or provide confirmations to the derived equations.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
After the formulation of Einstein’s theory of General Relativity (GR) by utilizing 4D spacetime, Kaluza discovered in 1919 a potential field unification of electromagnetism and gravitation in 5D spacetime. To deal with the fifth dimension, Klein posited that it could be compactified. Nonetheless, these attempts and their expansions to higher dimensions have not culminated in testable predictions nor in the competence to elucidate observations yet. As an alternative to compactification, Gogberashvili, Randall, and Sundrum demonstrated in 1999 that the weak field of gravity could be explained by using a model of 4D spacetime that is embedded in a negatively curved and large fifth dimension; nevertheless, the model demanded massive gravitons [1,2,3].
On the other hand, to achieve an effective action for quantum corrections, several theories were formulated based on alterations of curvature terms and Lagrangian fields that included high-order curvature terms and non-minimally coupled scalar fields [4,5,6].
Moreover, although quantum anomalies can necessitate the use of a non-local Lagrangian, one of the major differences between GR and Quantum Field Theory (QFT) is that GR is background-independent, meaning it does not rely on the global structure, whereas QFT involves a background metric that in turn influences its predictions [7]. Recently, the Planck legacy 2018 (PL18) release confirmed the presence of an enhanced lensing amplitude in cosmic microwave background (CMB) power spectra, which prefers a positively curved early Universe with a confidence level higher than 99% [8,9], which is regarded in this study as curved global structure. In addition, the validity of combining CMB lensing and baryon acoustic oscillation data to recover the spatial flatness was challenged because the curvature parameter tension between these sets of data is 2.5 to 3σ [10]. On the other hand, the closed early Universe provides a physical justification for the anomalous lensing amplitude and is consistent with the low CMB anisotropy observations [8,11,12].
Based on this sign of a primordial global curvature and its feasible evolution over the conformal time into the present Universe spatial flatness, it is obvious that the background-independent theories, such as GR, do not consider the evolution in the background (global or bulk) curvature and regard celestial objects in the early Universe with a preferred curvature on equal footing with their counterparts in the present Universe of a spatially flat background; this shortcoming can be the cause of the dark matter problem.
A desirable gravity theory should consider metrics of both the celestial object and the bulk (background), and reduce to GR in a flat background. Moreover, concerning the wave-particle duality and the quantum interactions, a mutually harmonious geometrical formalism of quantum mechanics should be deemed to maintain the equivalence principle and count for the influence of gravity on the quantum systems. This is because gravity appears to emerge owing to spacetime curvature, imparting it with a geometrical nature, where it cancels out in free fall and cannot be shielded. This study aims to formulate interaction field equations that consider the global (including the background) curvature, signified as the 4D conformal bulk curvature, and its impact on celestial objects that are regarded as 4D relativistic cloud-worlds. It also aims to incorporate the impact of gravity, expressed by 4D conformal bulk curvature, on quantum fields that are regarded as 4D relativistic quantum clouds. This paper is organized as follows. Section 2 presents the electromagnetic-gravitational interaction field equations; Section 3 presents their visualizations; Section 4 incorporates quantum interactions and Section 5 reproduces quantum electrodynamics. Section 6 proposes a theory test. Finally, Section 7 concludes this work.
2. Electromagnetic and Gravitational Interaction Field Equations
The Sun flows in a nearly flat background, based on GR, where its induced curvature is proportional to its energy density and flux. Conversely, the Earth flows in a curved background (curved bulk) due to the Sun’s presence, where its own induced curvature is affected by the bulk curvature in addition to its energy density and flux. Moreover, the PL18 release preferred a positively curved early Universe that is a sign of a primordial global curvature or a curved conformal bulk where the evolution of conformal curvature is associated with the Universe scalar factor (Appendix A). To consider the bulk curvature and its evolution over conformal time into present spatial flatness, a modulus of spacetime deformation, , in terms of energy density is used based on the elasticity theory [13]. can be expressed in terms of the bulk’s resistance to localized curvature that is induced by celestial objects or in terms of the bulk field strength, , by using Lagrangian formalism of energy density existing in the bulk as a manifestation of the vacuum energy density as
where the stress is signified by the stress-energy tensor of trace while the strain is signified by the Ricci curvature tensor as the change in the curvature divided by the existing curvature as the background or bulk conformal curvature.
By incorporating the bulk influence, a nonlocal action is expressed as
where is the Ricci scalar denoting a localized curvature, which is induced in the bulk by a celestial object that is regarded as a 4D relativistic cloud-world of metric and Lagrangian density while is the scalar curvature of the 4D conformal bulk of metric and Lagrangian density as its internal stresses and momenta due to its curvature.
Because of the bulk modulus, , is constant with regards to the cloud-world action under the constant vacuum energy density condition; and by considering the expansion of the bulk over conformal time owing to the expansion of the Universe and its implication on the field strength of the bulk, a dual-action concerning the conservation of energy on global (bulk) and local (cloud-world) scales is introduced as follows
This action can be interpreted as describing an interactive flow of a 4D relativistic cloud-world through vacuum energy of field strength that is manifested by the 4D conformal bulk curvature. It implies eight-dimensional degrees of freedom as, where is the standard four dimensions of the Einstein–Hilbert action concerning a celestial object (conventional energy), is the four dimensions of the conformal bulk (vacuum energy) regarding the background curvature, and is a dimension-hierarchy factor. The bulk metric, , and the cloud-world metric, , are related by Weyl’s conformal transformation as , where is a conformal function [14]. The global-local action should hold for any variation as follows
where [15]. By considering the cloud-world’s boundary term, , the variation in the Ricci curvature tensor, , can be expressed in terms of the covariant derivative of the difference between two Levi-Civita connections, the Palatini identity, ; this variation with respect to the inverse metric, , can be obtained by using the metric compatibility of the covariant derivative, [15], as . Thus, the boundary term as a total derivative for any tensor density can be transformed based on Stokes theorem as
where the bulk scalar curvature, , is left outside the integral transformation as it only acts as a scalar. Besides, a second approach can be applied to the bulk’s boundary term as
where while resembles the Ricci flow in a normalized form, reflecting the conformal evolution in the boundary, which can be expressed as a function
based on Weyl’s transformation as .
By using the first approach of the boundary terms’ transformations given in Equation (5), the transformed boundary action, , is
where and are the traces of the cloud-world and the bulk extrinsic curvatures, respectively; and are the extrinsic traces of the Lagrangian density on the cloud-world and the bulk boundaries, respectively; and are the determinants of their induced metrics, respectively; and equals 1 when the normal is a spacelike entity and equals -1 when it is a timelike entity. is the 4D Lorentz force density. The boundary action should hold for any variation and, by considering the transformed cloud-world’s boundary term, , the variation is
where . By utilizing the Jacobi formula for the determinant differentiation, and the variation in the metric times the inverse metric, ; thus, the variation in the boundary term of the cloud-world is, as
where resembles the Ricci flow in a normalized form, reflecting the conformal distortion in the boundary over conformal time, which can be expressed as a function, according to Weyl’s conformal transformation [16], while the term . Thus, the boundary term is , where is the conformally transformed induced metric on the boundary of the cloud-world. The same is applied to the bulk and Lagrangian boundary terms. The variation in the whole action, by renaming the dummy indices, is
While the variation in the inverse metric, , can be omitted from both the curvature and Lagrangian sides of the local action, , (the standard action procedure), this is not the case with regards to the global action, . The outcome of the global action resembles the electromagnetic stress-energy tensor times the variation in inverse metric in addition to the boundary term: . By comparing Einstein field equations with Equations (1), (2) and (10); it reveals that , which is proportional to the fourth power of the speed of light that in turn is directly proportional to the frequency; this agrees with the frequency cut-off predictions of vacuum energy density in QFT [17,18]. Under the constant vacuum energy condition and by treating the boundary term as in Equation (6), which gives ; this shows changes in vacuum energy density metric in a region changes its boundary, i.e., the global action outcome is a constant representing vacuum energy density and corresponds to .
By applying the principle of stationary action for Equation (10), the field equations are
These interaction field equations can be interpreted as indicating that the induced curvature, , by the cloud-world over the bulk (background) curvature, , equals the ratio of the imposed energy density of the cloud-world and its flux, to the vacuum energy density of the bulk and its flux through the expanding/contracting Universe. The interaction field equations feature the following:
- is an extended conformal stress-energy tensor by including the cloud-world’s energy density and flux, , and the electromagnetic energy flux from its boundary, , over the conformal time.
- is a conformal electromagnetic stress-energy scalar representing vacuum energy density.
- The boundary term given by the extrinsic curvatures of the cloud-world, , and the bulk, , is only significant at high energies when the difference between the induced, , and background, , curvatures is significant.
The field equations include four contributions that come from the cloud-world’s intrinsic and extrinsic curvatures and bulk’s intrinsic and extrinsic curvatures. The field equations can be expressed in different forms depending on which contribution is required to be implicit or explicit. By applying the second approach in Equation (6) to the bulk boundary terms, the variation in the action with renaming the dummy indices is
By transforming intrinsic curvature of the bulk, , where the bulk’s metrics can be incorporated with cloud-world metric into a conformal metric. By applying the principle of stationary action, the simplified interaction field equations are
where , or can be expressed as , is the conformally transformed metric counting for contributions of cloud-world metric, , and bulk’s intrinsic and extrinsic curvatures based on and (intrinsic-equivalent to reflect external fields1) metrics, respectively, whereas Einstein spaces are a subclass of the conformal space [14]. Similarly, the conformally transformed induced metric on the cloud-world’s boundary is . The simplified equations feature:
- The implicit term is the background conformal curvature term, which reflects the cosmological ‘constant’ (parameter).
- is an effective Newtonian gravitational parameter that relies on the background curvature, which can accommodate the bulk curvature evolution over the conformal time against constant GR for a special flat spacetime case.
The field equations can remove singularities and satisfy a conformal invariance theory.
3. Evolution of the 4D Relativistic Cloud-World Traveling in the 4D Conformal Bulk
This section visualizes the evolution of the 4D relativistic cloud-worlds over the conformal space-time of the 4D bulk. Galaxy formation and evolution as a 4D relativistic cloud-world traveling in a curved 4D conformal bulk, as preferred by the PL18 release, is considered. The entire contribution comes from the boundary term when calculating the black hole entropy using the semiclassical approach [19,20]. This concept can be applied to the field equations in Equation (11) that are multiplied by the bulk curvature, , as
The field equations can describe the interaction between a 4D relativistic cloud-world of intrinsic and extrinsic curvatures with a stress-energy and the 4D bulk of intrinsic and extrinsic curvatures with a stress-energy . From Equation (14), the field equations yield
where , represents the bulk intrinsic curvature. The conformally transformed metric, , can be expressed as
where and are functions of the cloud-world curvature radius , while the conformal function is a function of the bulk curvature radius , which can be influenced by the cloud-world curvature radius. is a dimensionless conformal scale factor and is the metric on the two-sphere. The derivations of these functions in Appendix B are
where the conformal function relies on the gravitational potential of the bulk, while its influence is inversely proportional to the cloud-world potential.
In the case of PI18′s preferred early Universe positive curvature, the gravitational potential of the bulk can be expressed in terms of the early Universe plasma of mass, , while denotes the radius of the curvature of the bulk, where the bulk’s potential decreases with the Universe expansion and vanishes in the flat spacetime background (. The minus sign of reveals a spatial shrinking by evolving in the conformal time. Consequently, the conformally transformed metric tensor, , is
This nonlocal metric reduces to the Schwarzschild metric in a flat background (. The conformally transformed metric can be visualized by evolving in the conformal time by using Flamm’s approach as
where is a constant, and denotes less significant terms. Figure 1 shows this scenario, which reveals that a galaxy forms as a dual forced vortices due to the curvature of the background.
The visualization of Equation (19) as the scenario of the galaxy formation as a dual forced vortices due to the curvature of the background is shown in Figure 1, the evolution of the 4D cloud-world of metric through its travel and spin in the conformal space-time of the 4D bulk of metric .
4. Gravitational, Electromagnetic, and Quantum Interaction Field Equations
Regarding the wave-particle duality and analogous to the constant modulus of the bulk, , the curvature of the bulk, including both that which is conformal, , and induced by a celestial object, , can be considered constant regarding quantum fields, . Accordingly, the dual action in Equation (3) can be extended in terms of quantum waves, as follows
This action can be interpreted as conceptualizing that a 4D conformal bulk, as a manifestation of vacuum energy of a conformal time flow, embeds a 4D relativistic cloud-world representing a celestial object of a conventional time flow that in turns encapsulates 4D relativistic quantum clouds of a quantum time flow and so forth, where are Lagrangian densities of two entangled quantum fields of a metric tensor and four-momentum respectively, while, are the four-momentum of vacuum energy density of a Lagrangian density and is a proportionality constant.
By considering the induced curvature by the cloud-world in the bulk, the conceptual picture can be simplified to an interactive flow of 4D relativistic quantum clouds with the vacuum energy of a field strength that relies on the 4D conformal bulk curvature, which harmonizes the dual-action concept. The action should hold for any variation, as follows
By considering the boundary term of the quantum cloud, the variation in the four-momentum , i.e., the change in the total energy of the charged fields enclosed within the quantum cloud boundary , can represent the flow of the four-current through the cloud boundary , where multiplying this current by the four-potential that is generated by the current itself, , and that which is externally applied, , gives the following scalar: . This deduction is based on the gauge theory. However, the cloud’s volume and its boundary surface should be taken into consideration. The boundary term signifies the variation of two entangled quantum clouds, ; thus,
The variation in this transformed boundary term with relabeling as , yields
where is the induced metric on the boundary of the quantum cloud. The last two terms resemble the Ricci flow in a normalized form, reflecting the conformal distortion in the boundary, which can be expressed as a conformal function as
where , and is the conformal function.
On the other hand, the cloud-world’s boundary term can be transformed as
where while , which resembles normalized Ricci flow and represents the metric of the bulk regarding its extrinsic curvature. Accordingly, the variation in the whole action is
By applying the principle of stationary action while choosing ϵ as a time-like entity, the general form of the field equations is
where are the stress tensors, as shown in Figure 2, of the deformed configuration of two entangled quantum fields, whereas is the overall stress-energy scalar of the cloud-world and the bulk. The third term can be transformed as ; where is the metric of the parent-cloud regarding the intrinsic curvature. Consequently, the transformed term can be incorporated with the second term in a conformally transformed metric tensor counting for the contribution of the metric of the quantum cloud, and the contributions from the metric of the cloud-world, , regarding its intrinsic curvature.
By separating the two entangled quantum fields by renaming the dummy indices and utilizing the dimensional analysis,
where is the Planck constant and denotes the energy density and its flux of the quantum cloud and is the gravitational field strength of the parent cloud-world of mass and at radius .
In addition, by implementing the transformation approach of the bulk boundary term in Equation (25), the field equations can be simplified to
where is the conformally transformed metric tensor counting for the contribution of the quantum cloud’s metric, in addition to contributions from the intrinsic and extrinsic curvatures of the bulk based on its metrics and (intrinsic-equivalent). Similarly, is the conformally induced metric on the quantum cloud boundary. The equations in terms of operators are
where is the momentum operator and is the stress-energy (gravitational) operator. Because the gravitational field strength of the cloud-world of mass and at radius is , a plan/e wavefunction, , can be expressed by utilizing the Equation (30) as , consequently:
where are the Dirac matrices. Figure 2 shows the quantum cloud where is the traction vector on the inner surface and is the unit normal vector.
On the other hand, by using the explicit boundary term of the bulk in Equation (28), which could contribute towards the emergence of mass, the quantized equations are
where is the boundary interaction of the quantum cloud with electromagnetic field, represents the spin-spin correlation of the conventional, , and vacuum energy, , fields. While are two entangled fields denoting the momentum of vacuum energy (could be of total zero spin), can be conjectured as a single field of vacuum energy of a spin as an analog of a part of singlet Cooper pair of total zero spin. The spin-spin correlation times the bulk (vacuum energy) boundary term interaction, , contribute towards the emergence of mass.
5. Reproducing Concepts in Quantum Electrodynamics
The quantized field equations can be utilized to reproduce concepts in quantum electrodynamics by using an undeformed configuration of the quantum cloud given by the Minkowski metric, , of metric signature and using as the present gravitational parameter as
where the conformal metric is (using both background’s metrics in a flat form leads to cancelation of both while using only one flat background metric reverses the quantum metric signature). From Equation (33), the expected value of the quantum cloud’s volume is . This reveals that the quantum cloud’s volume is quantized and is reliant on gravitational strength. Thus, for a single electron of mass (deemed as having the same properties from all directions), the stress-energy tensor of the quantum cloud is then . Accordingly, the field equations are
By applying the same approach for the boundary term and choosing the quantum metric signature as , where the four-current density is , then
where the four-current density is , and is the charge of a single electron, thus, Equation (35) can be reformatted as
This resembles the Dirac equation and the interaction with the electromagnetic field, which the principal of quantum electrodynamics.
6. Experimental Tests of the Interaction Field Equations
The Newtonian gravitational ‘constant’ plays a crucial role in theoretical physics, astronomy, geophysics, and engineering. About three hundred experiments attempted to ascertain the value of up to date. However, the significant inconsistencies in their results have made it unfeasible to reach a consensus on an exact value. Many of them are precision measurements with a relative uncertainty of only 12 to 19 parts per million [21,22,23,24,25].
The achievement of such a low level of uncertainty can indicate that the margin of systematic errors in experiments is narrower than generally anticipated. At the same time, the significant inconsistencies among measurements’ outcomes imply that there could be phenomena that are not yet accounted for in the current framework of physics. From Equations (5) and (1), the Newtonian gravitational parameter is
where is the scalar curvature of the bulk. According to Equation (6), is proportional to and reflects the field strength of vacuum energy because any changes in the bulk’s metric, , changes the field strength of the bulk, , because of the constant modulus, . In addition, although the ground state of at the local present Universe appears to be spatially flat, it could have a small temporal curvature reflecting the present value of . The dependency of on the curvature of the bulk is discussed and visualized as follows.
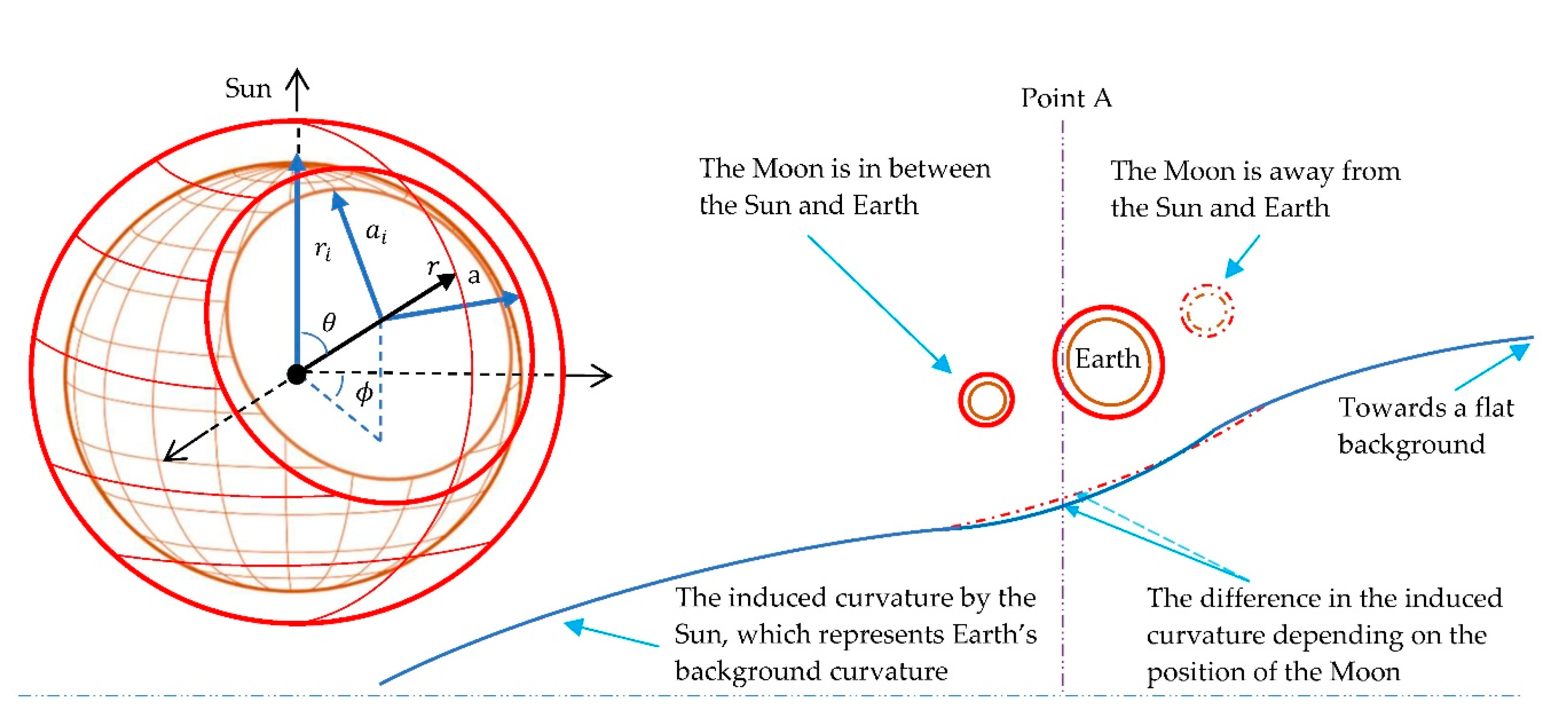
Regarding the Earth, Figure 3 shows the curvature of its background, the curved bulk owing to the Sun’s presence. In this curved background, both Earth and Moon are further inducing different curvature configurations depending on their positions. For instance, at Point A, the Earth’s background curvature is influenced by the Moon’s position as shown by the blue and red-dotted curves.
According to the Gauss's law, the flux of a field is stated as
To investigate the influence of the induced curvature by the Sun in the bulk (background) on the value, a positively curved metric, , of the Sun as a 4D relativistic cloud-world is utilized as
where is a dimensionless scale factor. According to the inverse square law, can be derived based on spherical symmetry. The changes in surface area in bulk can be modelled by changing its metric from spherical symmetry, which gives
As the background curvature has different values at point A in Figure 3, is predicted to have different values according to Equation (37). Based on this result, Equation (40) can be utilized to derive as follows:
where is the underline gravitational constant.
For general positive or negative curvatures, Figure 4 shows Sun’s induced curvature in the bulk:
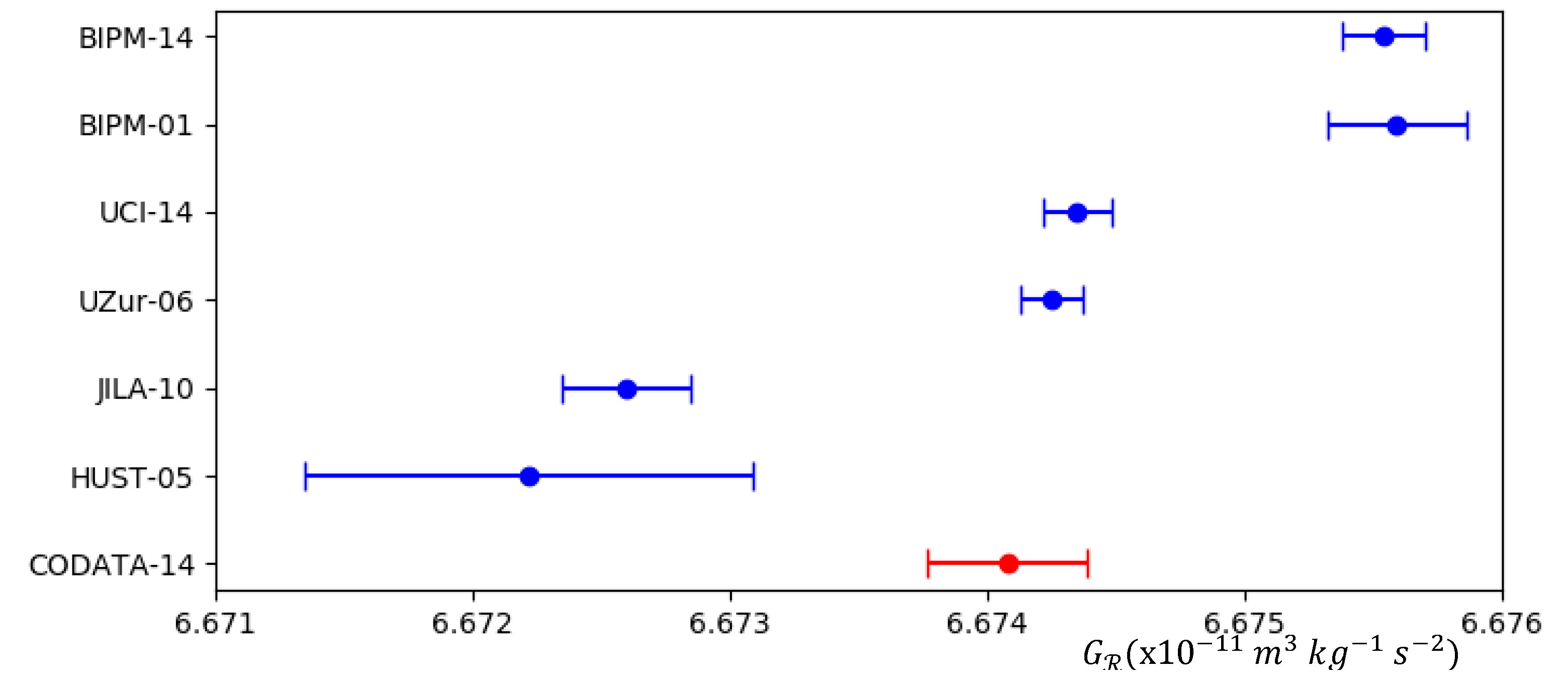
Figure 5 shows six of values by measurements: BIPM-14 [26], BIPM-01 [27], UCI-14 [28], UZur-06 [29], JILA-10 [30] and HUST-05 [31]. These values were among those adopted in the CODATA (Committee on Data for Science and Technology) 2014 of the recommended value of [32].
A one-way ANOVA test was performed on these precision measurements, resulting in an F-statistic of 302.089 and a p-value of 0.000, which indicates strong evidence against the null hypothesis. This signifies that there is a significant difference in the variances of these measurements. Despite the small relative uncertainty in the measurements, the significant differences in their outcomes that puzzled scientists [21] can be attributed to the differences in the curvature of the bulk at the time that the measurements were conducted, as stated in Equation (37), owing to varied positions of the Moon and other nearby planets.
7. Conclusions and Future Works
This study presented interaction field equations in terms of brane-world modified gravity and the perspective of geometrization of quantum mechanics. This study considered the implied curvature of the early Universe as the curvature of the background or 4D conformal bulk and distinguished it from the localized curvature that is induced into the bulk by the presence of celestial objects that are regarded as ‘relativistic 4D cloud-worlds’. Similarly, the quantum clouds are regarded as propagating ‘4D relativistic quantum clouds’ that are embedded in vacuum energy of a field strength that is reliant on the curvature of 4D conformal bulk. The derived interaction field equations are
The interaction field equations in Equation (42) can indicate that the general flow is of a wave nature where the collapse of the wave gives rise to the particle behavior or trapped waves, i.e., the wave particle duality, whereas the particle behavior is described by Equation (43). These equations can be interpreted as conceptualizing that a 4D conformal bulk, as a manifestation of vacuum energy of conformal time flow, embeds a 4D relativistic cloud-world representing a celestial object of conventional time flow that in turns encapsulates 4D relativistic quantum clouds of quantum time flow and so forth. By considering the induced curvature by the cloud-world in the bulk, the conceptual picture can be simplified to an interactive flow of the 4D relativistic clouds with vacuum energy of field strength that is reliant on the 4D conformal bulk curvature. The equations with explicit bulk term are
The interaction field equations can indicate that the induced curvature by the cloud-world over the bulk curvature equals the ratio of the imposed energy density of the cloud-world and its flux to the vacuum energy density of the bulk and its flux through the expanding/contracting Universe. They feature:
- An extended conformal stress-energy tensor by including the cloud-world’s energy density and flux and the electromagnetic energy flux from its boundary, over the conformal time.
- A conformal electromagnetic stress-energy tensor as vacuum energy density and flux, and counting for the conformal evolution in the bulk’s extrinsic curvature.
- The boundary term given by the extrinsic curvatures of the cloud-world and the bulk is only significant at high energies when the difference between the induced and background curvatures is significant.
- A background conformal curvature term reflecting the cosmological parameter.
- is an effective Newtonian gravitational parameter that relies on the background curvature, which can accommodate the bulk curvature evolution over the conformal time against constant for a special flat spacetime case.
Finally, to achieve consistent measurements, it is necessary to consider the positions of the Moon and other nearby planets, as they can influence the curvature of the background. Variations in background curvature can significantly contribute to observed differences in the precision measurements according to the derived interaction field equations, and it is essential to determine the extent of their impact on measurement variability. Future precision experiments should aim to address this issue of inconsistent measurements by accounting for the influence of these celestial bodies. One simple approach could be to conduct measurements twice, with one set taken when the Moon is on the horizon and another set taken when it is on the opposite side of the Earth. Finally, to ensure higher consistency, the positions of nearby planets can also be considered as well as the influence of changes in the background curvature on the field strength of vacuum energy and hence the emergent values of the experiment’s test masses. The standard theories are recovered from the interaction field equations, whereas the equations could remove the singularities and satisfy a conformal invariance theory.
| 1 |
1 The field equations can be expressed as based on the eight-dimensional metric according to the action in Equation (3), where the bulk boundary term seems to resemble an analogue to the Higgs mechanism as external fields exerted on galaxies, where an example as discussed in the next section. |
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
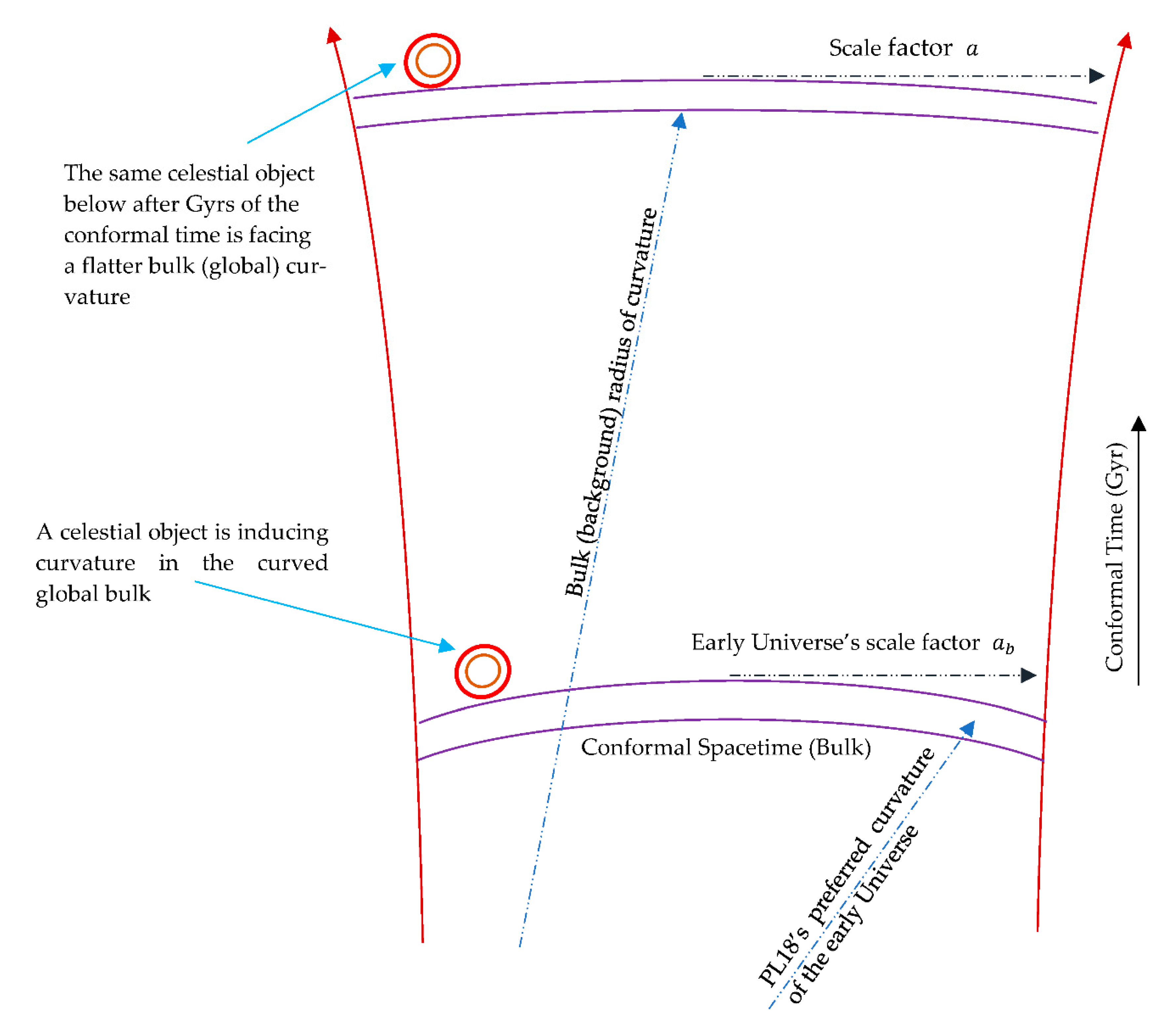
The conformal time is associated with the scale factor, , as . As shown is Figure A1, the radius of curvature increases through the conformal time as well as the scale factor where this curvature can be expressed as the background curvature or the curvature of the 4D conformal bulk.
Figure A1.
The evolution of the conformal curvature based on the scale factor.
Appendix B
The conformally transformed metric, , is
By performing the coordinate transformation as follows
The Christoffel symbols of this metric are
(A3)
The Ricci tensor components are
By substituting Ricci tensor components in Equation (27) gives
Equation (B8) yields
where for the conformal metric by considering the bulk curvature.
By applying the weak-field limit: , as follows
where is the Newtonian gravitational potential. By integrating both sides
where is the gravitational potential of the cloud-world’s spherical mass and that arises from the integration can be interpreted as the gravitational potential resulting from the bulk curvature, which can be expressed, using the same Newtonian analogue, in terms of the mass of the early Universe plasma of preferred positive curvature, , and the bulk curvature radius as . The metric should yield only the gravitational potential of the cloud-world when there is no bulk curvature and (; hence, ; thus, the conformal function is . By combining Equations (B9 - 11) yield
where the conformal function relies on the gravitational potential of the bulk while its influence is inversely proportional to cloud-world potential.
Appendix C
The referenced metric in Equation (A1) is inversed as follows
The inverse as follows
The Ricci curvature tensor is solved using the Christoffel symbols of the second kind which is given by for the referenced metric . The non-zero Christoffel symbols are
(A15)
(A16)
(A17)
(A18)
(A19)
(A20)
(A21)
(A22)
The Ricci curvature tensor given by .
The non-zero components are solved as follows. The component is
(A26)
The component of the Ricci tensor is
(A28)
(A29)
(A30)
The component is
(A31)
(A32)
(A33)
(A34)
(A35)
The component is
(A37)
(A38)
The Ricci scalar curvature is
(A41)
where the dotes are time derivatives.
(A42)
where are non-abelian Lagrangian densities of two entangled quantum fields. Analogous to the extending of quantum electrodynamics into chromodynamics, the quantized field equations in Equation (20) could be generalized to
where is the quark field. The boundary term, , indicates the energy flux from the boundary, which could represent Electroweak interactions.
Appendix D
The action in Equation (20) can be expanded to the non-abelian group as
References
- Randall L and Sundrum R 1999 An alternative to compactification Phys. Rev. Lett. 83 4690–3.
- Gogberashvili M 1999 Four Dimensionality in Non-compact Kaluza-Klein Model Mod. Phys. Lett. A 14 2025–31.
- Randall L and Sundrum R 1999 Large Mass Hierarchy from a Small Extra Dimension Phys. Rev. Lett. 83 3370.
- Vilkovisky G A 1992 Effective action in quantum gravity Class. Quantum Gravity 9 895–903.
- Capozziello S and Lambiase G 2000 Higher-order corrections to the effective gravitational action from Noether symmetry approach Gen. Relativ. Gravit. 32 295–311.
- Garattini R 2013 Distorting general relativity: Gravity’s rainbow and f(R) theories at work J. Cosmol. Astropart. Phys. 2013 017.
- Rickles D 2008 Chapter 7 Who’s Afraid of Background Independence? Philos. Found. Phys. 4 133–52.
- Di Valentino E, Melchiorri A and Silk J 2020 Planck evidence for a closed Universe and a possible crisis for cosmology Nat. Astron. 4 196–203.
- Mokeddem R, Hipólito-Ricaldi W S and Bernui A 2022 Excess of lensing amplitude in the Planck CMB power spectrum MNRAS 000.
- Handley W 2021 Curvature tension: Evidence for a closed universe Phys. Rev. D 103 L041301.
- Linde A 2003 Can we have inflation with Omega > 1? J. Cosmol. Astropart. Phys. 2003 002–002.
- Efstathiou G 2003 Is the Low CMB Quadrupole a Signature of Spatial Curvature? Mon. Not. R. Astron. Soc. 343 0–000.
- Landau L D 1986 Theory of Elasticity (Elsevier).
- Kozameh C, Newman E and TOD K P 1985 Conformal Einstein spaces Springer.
- S. M. Carroll 2003 Spacetime and Geometry: An Introduction to General Relativity.
- Straub W O 2006 Simple Derivation of the Weyl Conformal Tensor.
- Rugh S E and Zinkernagel H 2000 The Quantum Vacuum and the Cosmological Constant Problem Stud. Hist. Philos. Sci. Part B - Stud. Hist. Philos. Mod. Phys. 33 663–705.
- Gómez-Valent A 2017 VACUUM ENERGY IN QUANTUM FIELD THEORY AND COSMOLOGY.
- Dyer E and Hinterbichler K 2009 Boundary terms, variational principles, and higher derivative modified gravity Phys. Rev. D - Part. Fields, Gravit. Cosmol. 79.
- Brown J D and York J W 1993 Microcanonical functional integral for the gravitational field Phys. Rev. D 47 1420–31.
- Xue C, Liu J P, Li Q, Wu J F, Yang S Q, Liu Q, Shao C G, Tu L C, Hu Z K and Luo J 2020 Precision measurement of the Newtonian gravitational constant Natl. Sci. Rev. 7 1803–17.
- Rosi G, Sorrentino F, Cacciapuoti L, Prevedelli M and Tino G M 2014 Precision measurement of the Newtonian gravitational constant using cold atoms Nat. 2014 5107506 510 518–21.
- Schlamminger S 2018 Gravity measured with record precision Nat. 2021 5607720 560 562–3.
- Gibney E 2014 Rivals join forces to nail down Big G. Metrologists meet to design the ultimate gravitational-constant experiment Nature 514 150–1.
- Schlamminger S 2014 Fundamental constants: a cool way to measure big G Nature 510 478–80.
- Quinn T, Parks H, Speake C and Davis R 2013 Improved determination of G using two methods Phys. Rev. Lett. 111 101102.
- Quinn T J, Speake C C, Richman S J, Davis R S and Picard A 2001 A New Determination of G Using Two Methods Phys. Rev. Lett. 87 111101. =.
- Newman R, Bantel M, Berg E and Cross W 2014 A measurement of G with a cryogenic torsion pendulum Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 372.
- Schlamminger S, Holzschuh E, Kündig W, Nolting F, Pixley R E, Schurr J and Straumann U 2006 Measurement of Newton’s gravitational constant Phys. Rev. D - Part. Fields, Gravit. Cosmol. 74 082001.
- Parks H V. and Faller J E 2010 Simple pendulum determination of the gravitational constant Phys. Rev. Lett. 105 110801.
- Hu Z K, Guo J Q and Luo J 2005 Correction of source mass effects in the HUST-99 measurement of G Phys. Rev. D - Part. Fields, Gravit. Cosmol. 71 127505.
- Mohr P J, Newell D B and Taylor B N 2016 CODATA recommended values of the fundamental physical constants: 2014 Rev. Mod. Phys. 88 035009.
Figure 1.
The hypersphere of a compact core of a galaxy (the red–orange 4D cloud-world) along with its travel and spin through the conformal spacetime (the blue–purple 4D bulk) representing the bulk of distinctive curvature evolving over the conformal time.
Figure 1.
The hypersphere of a compact core of a galaxy (the red–orange 4D cloud-world) along with its travel and spin through the conformal spacetime (the blue–purple 4D bulk) representing the bulk of distinctive curvature evolving over the conformal time.
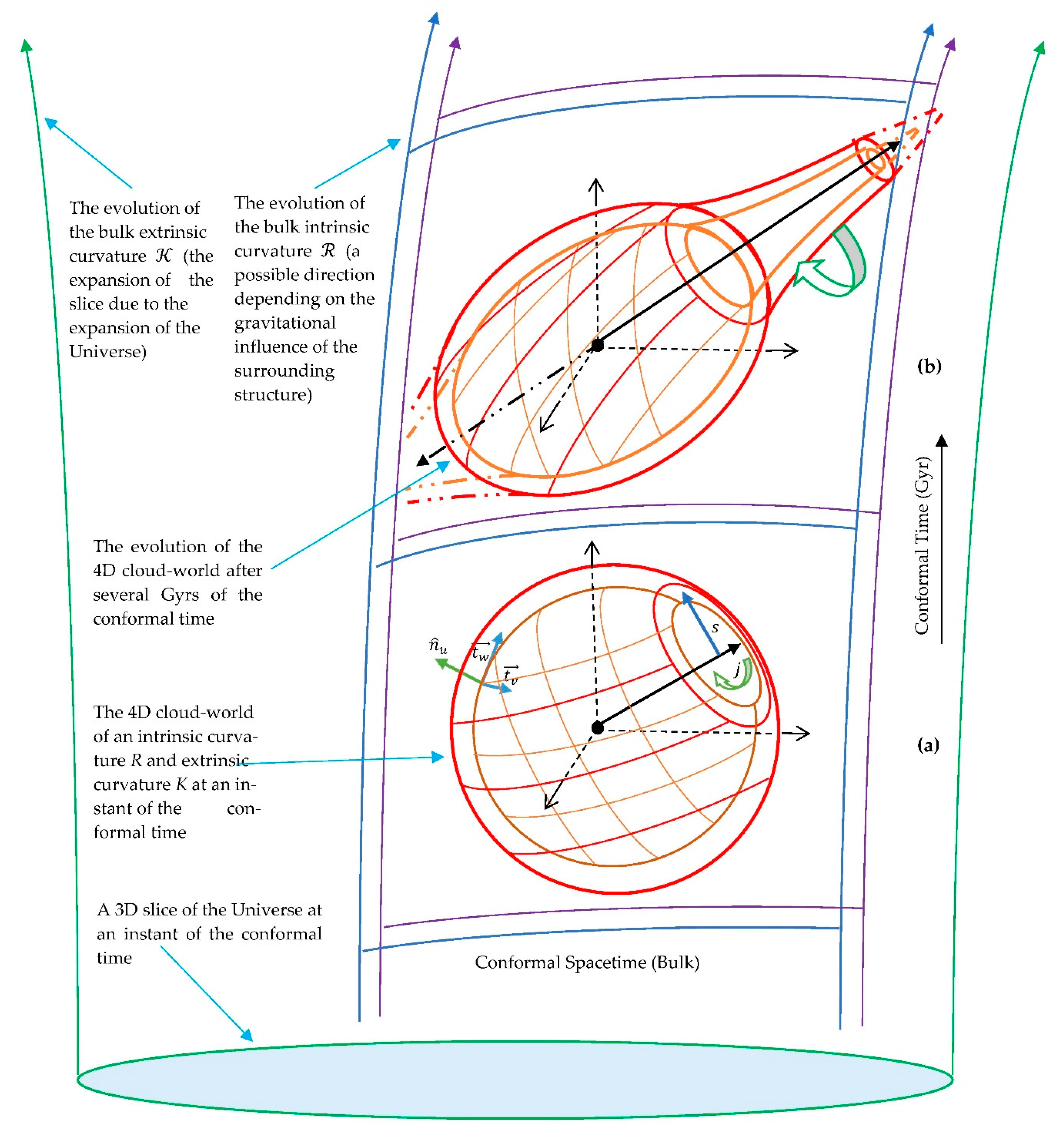
Figure 2.
The deformed configuration of the 4D relativistic quantum cloud of metric along its travel and spin though the curved background (bulk) of metric . The configuration is given by, , the inner surface of the quantum cloud that separates its continuum into two portions and encloses an arbitrary inner volume while is the outer surface of the cloud’s boundary.
Figure 2.
The deformed configuration of the 4D relativistic quantum cloud of metric along its travel and spin though the curved background (bulk) of metric . The configuration is given by, , the inner surface of the quantum cloud that separates its continuum into two portions and encloses an arbitrary inner volume while is the outer surface of the cloud’s boundary.
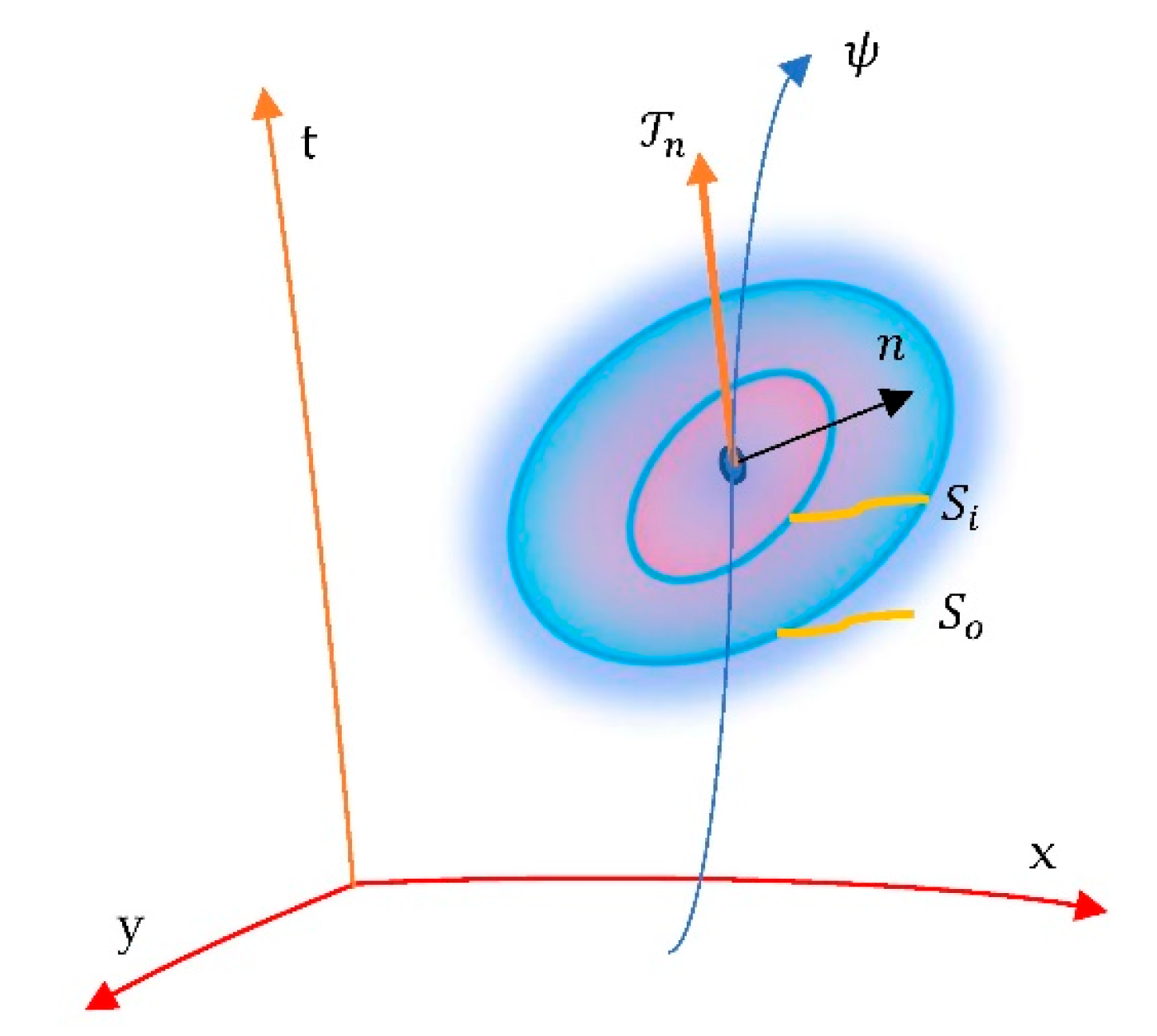
Figure 3.
The blue curve represents the Sun’s induced curvature in the bulk, which reduces and then vanishes far away from the Sun. The red and orange curves represent negative and flat cases respectively.
Figure 3.
The blue curve represents the Sun’s induced curvature in the bulk, which reduces and then vanishes far away from the Sun. The red and orange curves represent negative and flat cases respectively.

Figure 4.
The blue curve represents the Sun’s induced curvature in the bulk, which reduces and then vanishes far away from the Sun. The red and orange curves represent negative and flat cases respectively.
Figure 4.
The blue curve represents the Sun’s induced curvature in the bulk, which reduces and then vanishes far away from the Sun. The red and orange curves represent negative and flat cases respectively.
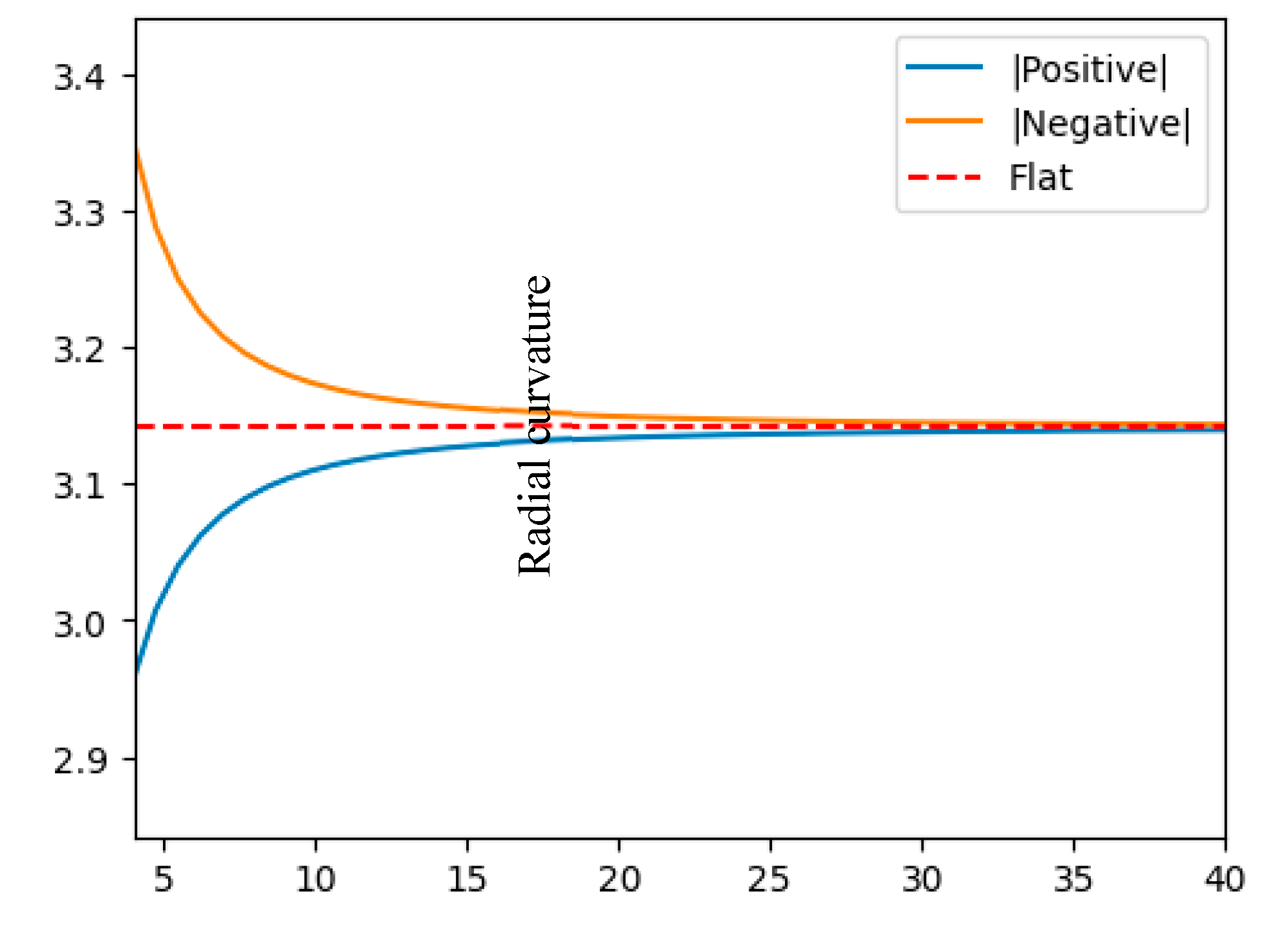
Figure 5.
Six of values among those that were adopted in the CODATA 2014 recommended value.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





