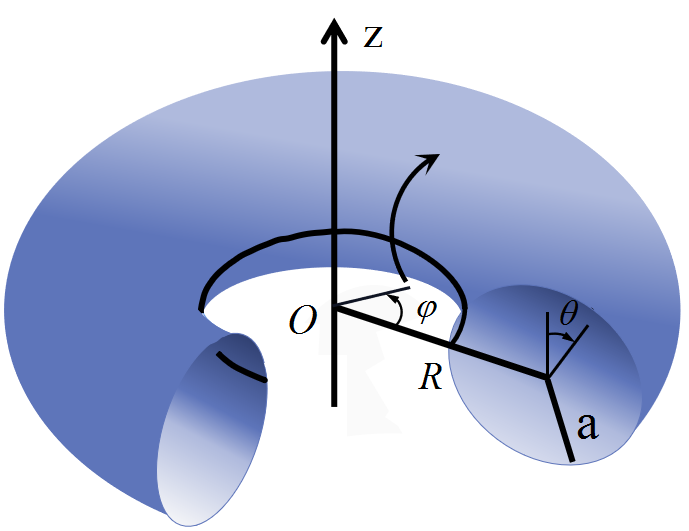
By introducing a variable transformation $\xi=\frac{1}{2}(\sin \theta+1)$, a complex-form ordinary differential equation (ODE) for the small symmetrical deformation of an elastic torus is successfully transformed into the well-known Heun's ODE, whose exact solution is obtained in terms of Heun's functions. To overcome the computational difficulties of the complex-form ODE in dealing with boundary conditions, a real-form ODE system is proposed. A general code of numerical solution of the real-form ODE is written by using Maple. Some numerical studies are carried out and verified by both finite element analysis and H. Reissner's formulation. Our investigations show that both deformation and stress response of an elastic torus are sensitive to the radius ratio, and suggest that the analysis of a torus should be done by using the bending theory of a shell.