Preprint

Article

On the Fundamental Particles and Reactions of Nature

Altmetrics

Downloads

673

Views

913

Comments

This version is not peer-reviewed

Submitted:

31 December 2022

Posted:

04 January 2023

You are already at the latest version

Alerts

Abstract

There are unsolved problems related to inflation, gravity, dark matter, dark energy, missing antimatter, and the birth of the universe. Some of them can be better answered by assuming the existence of aether and hypoatoms. Both were created during the inflation in the very early universe. While aether forms vacuum, hypoatoms, composed of both matter and antimatter and believed to be neutrinos, form all observable matter. In vacuum, aether exists between the particle-antiparticle dark matter form and the dark energy form in a dynamic equilibrium: A + A-bar = gamma + gamma. The same reaction stabilizes hypoatoms and generates a 3-dimensional sink flow of aether that causes gravity. Based on the hypoatom structure, the singularity does not exist inside a black hole; the core of the black hole is a hypoatom star or neutrino star. By gaining enough mass, ca. 3 X 10²² M_sun, to exceed neutrino degeneracy pressure, the black hole collapses or annihilates into the singularity, thus turning itself into a white hole or a Big Bang. The universe is anisotropic. Its center, or where the Big Bang happened, is at 0.66^+0.03_-0.01 times the radius of the observable universe at Galactic coordinates (l, b) = (286⁺¹⁰_-10, -43⁺⁷_-6). If we look from the Local Group to the center of the universe, the universe is rotating clockwise.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

I. INTRODUCTION

For the Schwarzschild metric:

d s^{2} = - (1 - \frac{2 G M}{r c^{2}}) c^{2} d t^{2} + {(1 - \frac{2 G M}{r c^{2}})}^{- 1} d r^{2} + r^{2} d Ω^{2}

(1)

if we define speed

v = \sqrt{2 G M / r}

(2)

we have

d s^{2} = - (1 - \frac{v^{2}}{c^{2}}) c^{2} d t^{2} + {(1 - \frac{v^{2}}{c^{2}})}^{- 1} d r^{2} + r^{2} d Ω^{2}

(3)

on the right of which, the first term shows the time dilation effect, and the second term shows the length contraction effect. This unequivocally indicates that the stationary objects in a gravitational field are in motion. The length contraction effect in equation (3) even says that the direction of motion is radial and the speed

v

of motion is equal to the escape speed

v_{esc} = \sqrt{2 G M / r}

. Since motion is always relative to a frame of reference, we can make the stationary objects move by finding the reference frame that is moving in the gravitational field. We therefore believe that there exist fundamental particles. Einstein once stated¹: “according to the general theory of relativity, space without aether is unthinkable.” We then use the term aether to name the fundamental particles.

II. BASIC THEORY

2.1. Creation of fundamental particles

To know what aether could be, we start with the idea of the inflation that was proposed to resolve the horizon, flatness, and magnetic monopole problems². Although the physical mechanism underlying inflation is still uncertain, it is often believed to be the result of a scalar field rolling down from the false vacuum to the true vacuum^3,4. We study the inflation by proposing the following reactions in the very early universe:

E \to A + \bar{A}

(I)

i A + i \bar{A} \to E (i \in N, i < n)

(II)

n A + n \bar{A} \to γ + γ

(III)

γ + γ \to B + \bar{B}

(IV)

B + \bar{B} \to γ + γ

(V)

B + n \bar{A} \to γ + γ

(VI)

\bar{B} + n A \to γ + γ

(VII)

Reaction (I) was the first phase transition in the universe, converting the pure energy (E) of the singularity universe into the particles (A) and antiparticles (

\bar{A}

) that are aether (Figure 1). This reaction fits in the current inflation theory well. As will be discussed below, the energy of the singularity can be regarded as photons whose wavelength is asymptote to zero. Therefore, the singularity universe was a false vacuum. As its energy was converted into aether particles, the universe became a true vacuum. According to Einstein’s mass-energy equivalence principle, matter and antimatter pairs are the only possible products from energy. As Planck taught us that energy is quantized, what the supercooled universe could first create could only be the most fundamental quanta, even though it had sufficient energy to create any complicated particles. The fundamental aether particles A and

\bar{A}

settled at the lowest mass and in the smallest size with the highest stability possible for them to survive in the hot and dense primeval universe. As the reaction finished, the universe became a globe of aether particles A and

\bar{A}

; the volume of the universe increased exponentially. As the energy of the universe was used up, the temperature of the universe dropped significantly, and the inflation ended naturally.

Right after the creation, aether particles A and

\bar{A}

were annihilated, raising the temperature of the universe back to what the adiabatic standard cosmology describes (Figure 1). This is known as the reheating process. In this work, we postulate: annihilation only happens if an equal amount of matter and antimatter particles are in contact with each other. Therefore, numerous annihilations initiated simultaneously across the globe of the universe, competing for the remaining aether particles A and

\bar{A}

, and finished together when there were no more A and

\bar{A}

left in contact. While a pair or a small number (i < n) of pairs of A and

\bar{A}

particles were annihilated to energy (reaction II) due to the wavelengths of products being larger than the size of the universe at that moment, n pairs of aether particles were annihilated to produce photons with a wavelength the size of the universe (reaction III). It is reaction (III) that allowed the universe to deviate from energy and create more complicated particles (discussed below). Of course, the annihilations were impossible to be 100% complete. Some aether particles were left along and therefore survived.

The formed photons then collided to create particles B and antiparticles

\bar{B}

(Figure 1) by the Breit-Wheeler pair production process (reaction IV). This phase transition has been regarded as the second episode of inflation^5,6, though the universe would not experience a significant change of volume as it was already large. Immediately followed were three possible annihilations to reheat the universe: 1) B and

\bar{B}

(reaction V); 2) n

\bar{A}

’s with a B (reaction VI, the total amount of matter must be equal to that of antimatter:

n ε_{\bar{A}} = ε_{B}

); and 3) n A’s with a

\bar{B}

(reaction VII,

n ε_{A} = ε_{\bar{B}}

). Because the primeval universe was dense enough to allow multiple

\bar{A}

’s to contact with a B simultaneously and multiple A’s to contact with a

\bar{B}

simultaneously for annihilation, both reactions (VI) and (VII) were possible, but their reaction rates did not have to be equal.

Although the reaction parameters are difficult to know, these proposed reactions provide a possible mechanism of the inflation and reheating. More importantly, it is the products of these reactions that formed the observable universe.

2.2. Fabric of space

Aether particles, as the fundamental units, formed vacuum⁷, or the fabric of space (Figure 2). Since they are undetectable dark matter, the nature of interparticle interaction is unknown. However, it is safe to assume that their pairs are bosons and the interaction between A and

\bar{A}

is attractive. As it has expanded for a long time after the Big Bang, the universe cooled down to a temperature of 2.7 K. Aether particles are much lighter than atoms, corresponding to a much higher transition temperature⁸, so the fabric of space has already become a Bose-Einstein condensate (BEC).

An atomic BEC could become unstable and make particles clump together⁸, if the interparticle interaction is attractive. The fabric of space is different. Once a pair of A and

\bar{A}

attract to clump or contact, the following annihilation happens:

A + \bar{A} ⇌ γ + γ

(VIII)

Since aether is the lightest particle in the universe, the generated photons are dark photons, having an ultralong wavelength, say, a light year. For reference, a reported mass⁹,

8.1 \times 10^{- 23} eV

, as well as other ultralight dark matter, could be a candidate of aether. The photons can penetrate across the universe, or trigger the further annihilation of other aether particles to form photons with higher energy. All these reactions are in nature the same as reaction (II); the products here are photons under the Planck distribution, which appear as the vacuum energy or dark energy. This process can be reversed to create aether particles A and

\bar{A}

(represented as the reverse of reaction VIII).

Due to reaction (VIII), as well as the induced collective oscillations of aether particles, the velocity of a specific aether particle in the fabric of space, as Dirac has foreseen, can no longer be well defined¹⁰. Absolute vacuum, or the pure fabric of space, is a dynamic equilibrium system, with an equal rate of annihilation and creation of aether particles:

R_{a} = R_{c}

(4)

Note that the rate

R_{a}

of the annihilation is controlled by the local concentration of aether particles, while the rate

R_{c}

of the creation is determined by the energy density of the whole fabric of space, i.e. the dark energy density.

2.3. Hypoatoms

The

\bar{B}

particles that survived from the reactions in the early universe recombined with aether particles A to form a species

\bar{B}

A_n:

\bar{B} + n A \to \bar{B} A_{n}

(IX)

With the structure of an atom in mind, we believe that the

\bar{B}

is a nucleus and that n A’s surround the

\bar{B}

(Figure 2). We call

\bar{B}

A_n a hypoatom. Note that this name does not mean that hypoatoms have the same structure as atoms. According to the particle-in-a-box model:

E_{n} = \frac{n^{2} h^{2}}{8 m l^{2}}, n \in N

, a hypoatom cannot exist as an atom, because it is impossible for the size l of a hypoatom to be much smaller than that of an atom, while the mass m and energy

E_{n}

of an aether particle are much smaller than those of an electron. Therefore, unlike the electron in an atom, the aether particle is not a standing wave in a hypoatom.

Instead, there exists a reaction on hypoatoms. An aether antiparticle

\bar{A}

oscillating with the dark energy in the fabric of space annihilates with one of the n aether particles A of a hypoatom

\bar{B}

A_n (step 1, Figure 2):

\bar{B} A_{n} + \bar{A} \to [\bar{B} A_{n - 1}] + γ + γ

(X)

The vacancy left in the hypoatom will then be filled by a particle A from the fabric of space (step 2, Figure 2):

[\bar{B} A_{n - 1}] + A \to \bar{B} A_{n}

(XI)

Therefore, hypoatoms

\bar{B}

A_n constantly consume the aether particles in the fabric of space:

A + \bar{A} \to γ + γ

(XII)

which is the forward of reaction (VIII), and, in nature, reaction (II). With that, the aether in a hypoatom can be regarded as a standing wave with an ultralong wavelength; hypoatoms are stabilized. Therefore, a hypoatom is not a small, localized particle. Instead, it can be regarded as an ultralarge, nonlocalized particle: a small core

\bar{B}

A_n tied up by the aether particles in the fabric of space. The size of a hypoatom can be considered as the same as the wavelength of a dark photon, or even the same as the size of the universe.

Similarly, particles B, if survived, would recombine with aether particles

\bar{A}

to form an antihypoatom B

\bar{A}

_n:

B + n \bar{A} \to B {\bar{A}}_{n}

(XIII)

Like hypoatoms, antihypoatoms could also exist stably in a dynamic equilibrium with the fabric of space.

2.4. Dark energy

Based on reaction (VIII), though the interaction between A and

\bar{A}

is attractive, the effective interaction⁸ is repulsive, and hence, the fabric of space is a stable system. Compared to the momenta of the oscillations under the dark energy, the mass of an A or

\bar{A}

is negligible:

m_{A} ≪ q ℏ / c

, therefore the Bogoliubov dispersion relation is simplified¹¹:

ω = q c

(5)

where q,

ℏ

, c,

ω

are wave vector, reduced Planck constant, speed of light, and angular frequency, respectively. Based on the Planck distribution, almost all of the oscillations occupy the ground state:

ϵ_{0} = \frac{1}{2} ℏ ω

(6)

Since the density of states is:

g (ω) = V q^{2} / 2 π^{2} c

, by summing up all frequencies from reactions (II) and (III), we have the dark energy density:

ε_{vac} = \frac{1}{V} \int_{0}^{ω_{A, m}} g (ω) ϵ_{0} d ω = \frac{ℏ ω_{A, m}^{4}}{{16 π}^{2} c^{3}}

(7)

where

ω_{A, m}

is the maximum angular frequency. As aether particles are oscillating in equilibrium with hypoatoms:

ℏ^{2} ω_{A, m}^{2} = m_{\bar{B} A n}^{2} c^{4} + q_{\bar{B} A n}^{2} c^{2} ℏ^{2} ≳ m_{\bar{B} A n}^{2} c^{4}

(8)

the dark energy density is

ε_{vac} ≳ \frac{m_{\bar{B} A_{n}}^{4} c^{5}}{{16 π}^{2} ℏ^{3}}

(9)

According to the Planck 2018 results¹², Hubble constant

H_{0} = 67.66 \pm 0.42 k m s^{- 1} {Mpc}^{- 1}

, the density parameter for dark energy

Ω_{Λ} = 0.6889 \pm 0.0056

, so the dark energy density is 5.92×10^-27 kg/m³. Therefore, the upper limit of the mass of the hypoatom is ca. 8 meV. This mass is close to that of a neutrino.

2.5. An earlier inflation

Although a wider range was proposed¹³, the inflation is generally assumed in the context of the Grand Unified Theory (GUT)^{2-4, 14}. However, based on the following factors: a) reaction (I) converted the pure energy of the singularity into aether particles A and

\bar{A}

; b) aether particles A and

\bar{A}

are not included in the GUT; c) it is widely accepted that gravity begins to differentiate from the other three forces at the Planck time (discussed below), there should have been an inflation that started as early as the Planck time if not earlier (Table 1).

At the Planck time,

5.4 \times 10^{- 44}

sec, the energy density of the false vacuum was

1.2 \times 10^{19}

GeV, equivalent to the mass density of

ρ_{f} = 5.2 \times 10^{96}

kg/cm³. The inflation started at a patch size of the Planck length,

l_{Pl} = {1.6 \times 10}^{- 35} m

. From the first-order Friedman equation:

{(\frac{\dot{a}}{a})}^{2} = \frac{8 π G ρ_{f}}{3}

, we have the size of the universe exponentially increase in the function of

a = Constant \cdot \exp (χ t)

, where

χ = \sqrt{\frac{8 π G ρ_{f}}{3}} = \sqrt{\frac{8 π c^{5}}{3 ℏ G}} = 5.4 \times 10^{43}

sec^-1. The universe after the first episode of the inflation and reheating (reactions I ~ III) would at least be as large as one half the wavelength of the B particle:

a \approx λ_{B} / 2 = \frac{h c}{E_{\bar{B} A_{n}}} ≳ \frac{h c}{8 meV} = 0.16 mm

(10)

Thus the size of the present universe:

a_{0} ≳ \frac{{1.2 \times 10}^{18} GeV}{k_{B} \times 2.7 K} \times 0.16 mm = 9.0 \times 10^{10} light years

(11)

which is in agreement with the inflationary theory¹⁴.

2.6. Neutrinos

The next to be created, after aether particles, in the second episode of inflation and reheating were

\bar{B}

particles (for simplicity, B particles will not be discussed). On the other hand, based on the inflationary theory^{2-6, 13, 14}, at ca. 10^-34 ~ 10^-32 sec or 10¹⁵ ~ 10¹⁴ GeV there was supposed to be a phase transition for the formation of a GUT particle (Table 1). To resonantly produce intermediate Z-bosons^{15, 16}:

ν + \bar{ν} \to Z

(XIV)

if a neutrino mass eigenstate is a hypoatom:

m_{ν} = m_{\bar{B} A_{n}} ≲ 8 meV

, then the required energy is:

E_{ν} = \frac{M_{Z}^{2}}{2 m_{ν}} ≳ 5 \times 10^{14} GeV

(12)

These neutrinos at the GUT energy scale are called ultrahigh-energy (UHE) neutrinos. Therefore, UHE neutrinos and

\bar{B}

particles were created at the same time. In addition, they both have a unique characteristic property. The neutrino cross section increases with energy^{17, 18}. If we recognize each created

\bar{B}

particle, with A particles nearby, as an ultralarge hypoatom

\bar{B}

A_n, then when the universe was cooled down, the hypoatom energy decreased with cross section.

This can further be confirmed by the phase transitions that happened in the early universe (Table 1). Up-quarks, down-quarks and electrons were created at ca 10^-12 ~ 10^-6 sec, nuclei at ca 1 ~ 10² sec, and then nuclei and electrons recombined to form atoms at ca 10¹³ sec. Aether particles were created at ca 10^-44 ~ 10^-42 sec, and

\bar{B}

particles at ca 10^-34 ~ 10^-32 sec. All these time slots are about 10¹⁰ ~ 10¹¹ times apart, so if there were a phase transition similar to the recombination of atoms, it would be at the next time slot near 10^-22 sec or 10⁸ GeV (Table 1). However, no stable particles were created in the period of 10^-32 ~ 10^-12 sec or 10¹⁴ ~ 10² GeV, which is called the gauge desert¹³. This matches our assumption: no recombination process was required to form hypoatoms; hypoatoms are neutrinos. Note that if the Z bosons decayed into photons, reaction (XIV) is equivalent to reaction (V), another agreement of our model with particle physics.

Of course the gauge desert was not truly quiet; various intermediates were formed in this period from the lepton asymmetry to the baryon asymmetry. Although the mechanism has not been fully understood, it is well accepted that flavor matters in this process. First, the third generation Yukawa couplings presented at ca 10¹² GeV, then decayed into the second generation (ca 10⁹ GeV) and finally into the first generation (ca 10⁵ GeV)^{19, 20}. This is understandable, because while the cross section reduced with temperature, the stability of hypoatoms that are composed of both matter and antimatter could be challenged. 10^-32 ~ 10^-12 sec can therefore be considered as the period that nature explored the stable states. Stabilized particles, which are up-quarks, down-quarks and electrons, then formed atoms. Thus our model fits in the baryogenesis-through-leptogenesis theory^{19, 20}.

2.7. Stability of hypoatoms

One might wonder how a particle composed of matter and antimatter could be stable. We will therefore discuss the lifetime of hypoatoms before any further discussion.

Known particles closest to hypoatoms

\bar{B}

A_n are the pseudoscalar mesons that have the same amount of matter and antimatter. Based on Sargent’s rule, the lifetime of a type of particle, including mesons, is directly proportional to the reciprocal of the mass to the fifth-power²¹:

τ \propto 1 / m^{5}

. Figure 3 plots the lifetimes of the pseudoscalar mesons

q \bar{q}

composed of symmetric quark q and antiquark

\bar{q}

versus their masses²². If we extrapolate the line: log(τ/sec) = -5.2123 - 5.0000 log(m/GeV) to the upper limit of the mass of a hypoatom, then the lifetime of a meson-like particle with the mass of 8 meV will be ca

2 \times 10^{35}

sec. Based on our postulate, annihilation only happens if all of the n+1 bodies that form a hypoatom contact simultaneously. Even if some of the n particles A settle on the particle

\bar{B}

, annihilation will not happen. Therefore, the lifetime of a hypoatom should be much longer than

2 \times 10^{35}

sec, which is projected for a 2-body meson-like particle. For comparison, the theoretical lifetime of an electron²³ is

2.1 \times 10^{36}

sec, and that of a proton²⁴ is in the range of

10^{35} ~ 10^{43}

sec.

It is interesting to note that based on the above calculation, a Majorana neutrino would stably exist in a structure as [(

\bar{B}

A_n)(B

\bar{A}

_n)], with an estimated lifetime of ca.

6 \times 10^{33}

sec.

2.8. Creation strategy

The matching lifetimes are not an accident. While using a type of matter particle and antimatter particle, such as A and

\bar{A}

, no stable systems would be created, using two types of matter particles and antimatter particles with significantly different masses, such as A and

\bar{B}

\bar{A}

and B, stable hypoatoms

\bar{B}

A_n and antihypoatoms B

\bar{A}

_n would be created (more hypoatoms would be created, see section 3.5). Nature uses this strategy of the asymmetric structure of hypoatoms and antihypoatoms to create this world.

Now we have a sketch of the universe: a) the fabric of space, or vacuum, is formed by aether particles A and

\bar{A}

and their energy form; b) all observable matter particles are composed of hypoatoms

\bar{B}

A_n (neutrinos) and antihypoatoms B

\bar{A}

_n (antineutrinos), the enigma of missing antimatter does not exist!

It is of interest to note from its composition that a hypoatom

\bar{B}

A_n does own the energy that Einstein taught us:

E = m_{\bar{B} A_{n}} c^{2}

, and it can be released once annihilated. A typical example is the nuclear energy that is released when some hypoatoms or neutrinos are annihilated in nuclear reactions.

III. DISCUSSION

3.1. General theory of relativity

In the general theory of relativity, the pure fabric of space is regarded as flat spacetime (equation 4 is valid):

d s^{2} = - c^{2} d t^{2} + d r^{2} + r^{2} d Ω^{2}

(13)

Based on our proposed model, the annihilation and creation of aether are in equilibrium (reaction VIII). Therefore, there is no net flow of aether particles (equation 4), and hence, aether has no observable mass in the pure fabric of space.

Now if a massive object is introduced, the rate R_a of annihilation rises dramatically. This annihilation generates a 3-dimensional sink flow of aether particles towards the center of the massive object. It is this sink flow that warps the spacetime in the vicinity of the massive object! Because of this flow, the time term of equation (13) needs to be rewritten with the time-dilation expression:

\sqrt{1 - v^{2} / c^{2}} d t

and its radial term with the length-contraction expression:

\frac{d r}{\sqrt{1 - v^{2} / c^{2}}}

, while the last term on the right stays correct²⁵. Considering equation (2), we have the Schwarzschild metric (equation 1). To the best of our knowledge, this is the first derivation of the general theory of relativity, the greatest law of nature. If the speed of the sink flow is small, the relativistic effect is negligible; we then have Gauss’s law or Poisson’s equation for gravity:

\nabla^{2} ϕ = 4 π G ρ

, equivalent to Newton’s law of universal gravitation.

In the above analysis, the creation of aether particles (the reverse of reaction VIII), which reduces the sink flow a bit, has not been considered, because compared to that of the annihilation, the rate of the creation is negligible:

R_{a} - R_{c} \approx R_{a}

(14)

If it is considered, then Einstein’s field equation should be written with the addition of the

Λ

term, and Newton’s law is:

\nabla^{2} ϕ = 4 π G ρ - Λ c^{2}

With the existence of the sink flow, aether particles in the fabric of space are in fact oscillating in quasi-equilibrium with hypoatoms (equation 8). It is time to note that this quasi-equilibrium is natural: if the dark energy density were higher, then more aether particles would be annihilated at hypoatoms, equivalent to a higher flowrate of the sink flow, thus resulting in a larger hypoatom mass and vice versa.

Based on the Landau criterion, within the limit of the speed of light (equation 5), the fabric of space is a superfluid⁷. Therefore, the sink flow only generates the curvature of spacetime, but does not pull or push objects directly.

Interestingly, our model does show that the fabric of space has the character of negative pressure that is vital to Einstein’s field equation. Think about an adiabatic cylinder-piston system. When A and

\bar{A}

are created (the reverse of reaction VIII), the change of internal energy is:

∆ U = m c^{2}

, where

m

is the mass of aether particles A and

\bar{A}

created. The creation of aether particles increases the volume of the system, so the system does work:

W = p ∆ V

. According to the first law of thermodynamics, we have

m c^{2} = - p ∆ V

p = - ρ c^{2}

. When A and

\bar{A}

are annihilated (the forward of reaction VIII), the character is identical. The negative pressure can also be understood in a different way. Each time when an

\bar{A}

from the fabric of space annihilates with an aether particle A of a hypoatom (reaction X), the hypoatom temporarily loses, not gains, the momentum of the annihilated aether particle A. Therefore, the hypoatom experiences negative pressure.

Einstein taught us that the curvature of spacetime causes gravity, but did not mention why. Using the character of negative pressure, it is not difficult to understand gravity. For an object m under the curvature of spacetime generated by an object M, the annihilation rate on the side near M is higher than that on the far side. In other words, the force on the near side (pointing towards M) is larger than that on the far side (pointing away from M). Therefore, m experiences an attractive force, which is gravity.

Newton taught us that gravity is universal. Indeed it is, because all matter is made of hypoatoms. For the same reason, gravity cannot be shielded by any objects. The objects in the gravitational field do nothing but result in reaction (XII), further warping spacetime. This is also true for energy, which enhances the annihilation of aether particles and generates gravity, in agreement with the general theory of relativity.

The difficulty of unifying four fundamental forces is well known. Based on our model, gravity, in fact, is a collective property of aether particles in the fabric of space, while the other three forces are just interactions of the interested particles or objects.

3.2. Dark matter

For a uniform sphere M of radius r_M and density

ρ_{M}

, the rate R_a of annihilation can be calculated by the flowrate of the sink flow across the sphere of radius r:

R_{a} = 4 π r^{2} v_{esc} ρ_{A}

(15)

where

ρ_{A}

is the density of the aether particles. The rate of annihilation is also proportional to mass:

R_{a} = k (M + A)

(16)

where A is the mass of the aether particles within the sphere of radius r, and k the proportional constant, then we have

d A = ρ_{A} \cdot 4 π r^{2} d r = {(\frac{k^{2}}{2 G})}^{\frac{1}{2}} {(M + A)}^{\frac{1}{2}} r^{\frac{1}{2}} d r

(17)

By integration, the mass of aether is

A = {(\frac{2 k^{2} M}{9 G})}^{\frac{1}{2}} r^{\frac{3}{2}} + \frac{k^{2}}{18 G} r^{3}

(18)

and the density of aether is

ρ_{A} = {(\frac{k^{2} M}{32 π^{2} G})}^{\frac{1}{2}} r^{- \frac{3}{2}} + \frac{k^{2}}{24 π G}

(19)

The last term on the right is the density at infinite distance (

r \to \infty

ρ_{A, \infty} \equiv \frac{k^{2}}{24 π G}

, which is also the density in the pure fabric of space. By subtracting it, the density

ρ_{D}

of dark matter is

ρ_{D} = ρ_{A} - ρ_{A, \infty} = {(ρ_{M} ρ_{A, \infty})}^{\frac{1}{2}} {(\frac{r_{M}}{r})}^{\frac{3}{2}}

(20)

The mass D of dark matter in the vicinity of M is

D = {2 (\frac{4}{3} π r^{3} ρ_{A, \infty} M)}^{\frac{1}{2}}

(21)

which is divergent. This indicates that all the halos in the universe are overlapping, which is correct as gravity is infinite.

To estimate the amount of dark matter, we need to choose a cutoff radius. From

- \frac{G M}{r} + \frac{1}{6} Λ c^{2} r^{2} = 0

, where

Λ = 8 π G ρ_{v a c} / c^{2}

, and

ρ_{v a c}

is the density of dark energy, we have

r_{cut - off}^{3} = \frac{6 G M}{Λ c^{2}} = \frac{M}{\frac{4}{3} π ρ_{v a c}}

(22)

The mass of dark matter in the vicinity of M, at least, is

D_{\min} = 2 {(\frac{ρ_{A, \infty}}{ρ_{v a c}})}^{\frac{1}{2}} M

(23)

The most important piece of information here is that every massive object in the universe has a dark matter halo whose mass is proportional to its own mass. Because the ratio

{ρ_{v a c} / ρ}_{A, \infty}

or the equilibrium constant of reaction (VIII) is unknown, we cannot compare

D_{\min} / M

with the ratio of dark matter to ordinary matter from cosmological observation. Given the fact that most popular stellar systems are galaxies composed of stars, this proportional relation allows us to estimate the mass of the dark matter halo for a galaxy by simply summing up all the masses in the galaxy. Because stars are distributed in the galaxy, the density will reduce along the radial direction a little slower than that of an isolated object (

r^{- 1.5}

, equation 20). For comparison, a profile²⁶ of dark matter obtained from cosmological N-body simulations has an asymptotic slope of

r^{- 1.4}

. Therefore, aether is a major contributor to dark matter.

It is of interest to note that as the universe expands, the mass ratio of dark matter to ordinary matter almost stays the same (equations 21 and 23), while the mass ratio of dark energy to matter increases with the expansion because the density of dark energy is a constant. This is in agreement with the results of cosmological observation.

3.3. Quantum mechanics

Based on our model, quantum mechanics can be understood relatively easily. Here are a couple of examples.

Because all particles are in the fabric of space and the fabric of space is a constantly oscillating dynamic system, the wave-particle duality is natural.

The zero-point vibration of aether particles (equation 6) is equivalent to Heisenberg’s uncertainty principle.

In theory, particles heavier than aether could be created by multiple ultralong-wavelength photons. Of course, the heavier the particles, the lower the chance of creation, corresponding to a shorter lifetime in the quantum field theory.

The wave function of a particle from the Schrodinger equation is the superposition of wave vectors from the local interactions and the creation and annihilation (reaction VIII) of aether particles in the fabric of space, not a property of only the interested particle itself. This is why Lorentz invariance is violated for Schrodinger’s wave functions.

For the double-slit interference experiment, the interference pattern of electrons (or photons) is obtained because the oscillation of the local fabric of space is interfered by the slits. When they are observed, the light of observation overwrites the interfered fabric of space, or the so-called wave function collapse occurs, hence the interference pattern no longer exists.

In order for the system of an object that is held by our hand, as well as our arm, to return to its original state, the system must rotate two cycles (i.e. 720°). Similarly, hypoatoms are held by the fabric of space (Figure 2) and have to rotate two cycles to return to the original quantum state. Therefore, it is natural that hypoatoms are spin-1/2 particles. When they have additional symmetry, particles made from hypoatoms would have different spin characters.

As shown in Figure 2, reaction (XII) is also the origin of the angular momenta of hypoatoms. Since reaction (XII) always exists, hypoatoms rotate constantly. The angular momentum will never disappear and hence becomes the intrinsic property of a hypoatom.

Furthermore, standing waves of aether can exist between hypoatoms, which leads to the entanglement of particles (Figure 4). Once one of the particles is observed, the standing wave between them is overwritten. Therefore, the entangled system collapses into a pair of particles that are spinning in opposite directions. The inflations in the very early universe and the falling fabric of space within a black hole (discussed below) indicate that there is no speed limit on the motion of aether. We thus suspect that there would be no speed limit on the collapse of an entangled system.

The Stern-Gerlach experiment can also be understood easily. Under the external magnetic field in a Stern-Gerlach apparatus, hypoatoms or those made from them are forced to spin either up (+) or down (-). We can understand this by imagining that when it is placed on a watershed, water flows down either towards the north or the south. For an apparatus S, 50% of the hypoatoms will go through

{\{\binom{+}{-|}\}}_{S}

{\{\binom{+|}{-}\}}_{S}

(Feynman’s symbol, ref.²⁷).

If we have two apparatuses S in succession

{\{\binom{+}{-|}\}}_{S} {\{\binom{+}{-|}\}}_{S}

, 100% of the hypoatoms that go through the first go through the second. If we have

{\{\binom{+}{-|}\}}_{S} {\{\binom{+|}{-}\}}_{S}

, none of the hypoatoms that go through the first can go through the second.

If we tilt the second apparatus T by 90° (ref.²⁷), then when the hypoatoms that go through the first reach the second, they are in fact, once again, placed in a watershed-like potential field and forced to spin either left (+) or right (-), just like when they encountered the first apparatus. Therefore, for either the experiment

{\{\binom{+}{-|}\}}_{S} {\{\binom{+}{-|}\}}_{T}

{\{\binom{+}{-|}\}}_{S} {\{\binom{+|}{-}\}}_{T}

, only 50% of the hypoatoms that go through the first can go through the second.

Similarly, for the experiment

{\{\binom{+}{-|}\}}_{S} {\{\binom{+}{-|}\}}_{T} {\{\binom{+}{-|}\}}_{S}

, the hypoatoms are placed in a watershed-like potential field at the third apparatus. The hypoatoms spinning left (+) that pass the second are forced to spin either up (+) or down (-) again. There is no reason that they should remember their spin directions when they pass the first apparatus. They do not remember any history, thus only 50% of those passing the second can go through the third.

Because hypoatoms are the fundamental building blocks, particles made from them can also have properties discussed as above.

Another unsolved problem is the conflict between the general theory of relativity and quantum mechanics. For a massive object, as the size goes down, for example, to the Schwarzschild radius, quantum effects from the dynamic fabric of space become negligible. Therefore, the general theory of relativity and quantum mechanics are compatible.

3.4. Black hole

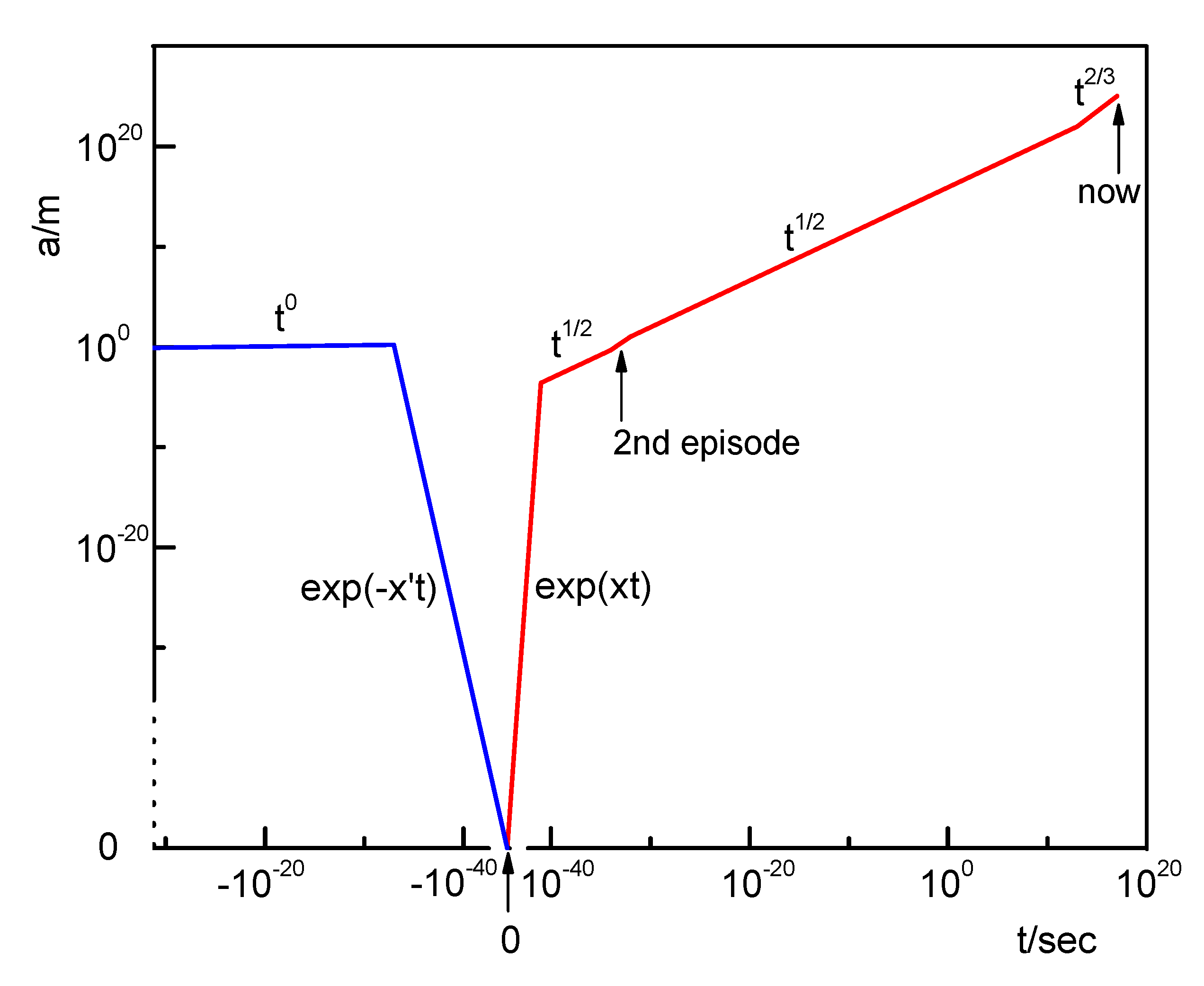
The most condensed star that can be directly observed is a neutron star. If its mass further increases, it collapses into a black hole. Within a black hole, it is generally believed to form a singularity. However, based on the proposed hypoatom structure, hypoatom degeneracy pressure can provide new support to prevent the collapse. In other words, the core of a black hole within the event horizon would be a hypoatom star or a neutrino star.

Outside its event horizon, a rotating black hole usually has an accretion disk perpendicular to the axis of rotation. As we have known, the accretion plane is the primary direction that matter falls into the black hole. Although we do not exactly know the physical law inside the event horizon, it is reasonable to assume that matter from the accretion disk would continue to fall (faster than the speed of light) into the core of the black hole in spiral flows V_s. Figure 5 illustrates the structure of a black hole. As the falling fabric of space passes through the event horizon, the photons from the annihilation of aether could no longer escape. The dark energy density inside the event horizon would thus be increased; there would exist a fireball. This annihilation process would easily become a nonlinear system, leading to pulsations or the so-called quasi-periodic oscillation²⁸.

The raised dark energy density would break the equilibrium with hypoatoms (equation 8). Therefore, it would initiate reaction (IV), creating B particles or, in consequence, hypoatoms. Together with the falling matter, if it exists, this process makes the mass of the hypoatom star increase or the black hole grow. The creation of hypoatoms or neutrinos would be the primary ability of black holes in the evolution of nature. This mechanism to create hypoatoms within black holes would be identical to the particle creation mechanism in the early universe, i.e. reactions (III) ~ (VII).

At the Big Bang, the universe was only able to convert part of its energy into matter by zigzagging inflation and reheating processes (reactions I ~ VII, IX and XIII). Therefore, it is reasonable to assume that in a much milder process on the course of the growth of black holes, not all aether falling into black holes would immediately be converted into hypoatoms and immobilized at the core. The energy that is not immobilized would temporarily escape from the core as emission beams V_b along the magnetic axis of the core (Figure 5). Of course nothing would be able to escape beyond the event horizon; the V_b would fall back as back falling flows V_f for further conversion and immobilization. The V_f would exist in two ways: a) immediately surrounding the V_b, and b) eventually falling into the V_s plane (Figure 5). This scene of a neutrino star inside a black hole would be similar to that of a pulsar, its less dense counterpart²⁹.

3.4.1. Birth of the universe

Analogous to the Tolman-Oppenheimer-Volkoff limit for neutron stars, we can estimate a mass limit for a neutrino star or a black hole:

M \approx {(\frac{m_{n}}{m_{ν}})}^{2} M_{n} ≳ {(\frac{939.6 MeV}{8 meV})}^{2} \times 2.2 M_{⊙} = 3 \times 10^{22} M_{⊙}

(24)

where m_n is the mass of a neutron,

m_{ν}

the mass of a neutrino, M_n the mass limit of a neutron star, and

M_{⊙}

the mass of the sun. Another method to estimate the mass limit for a neutrino star is to calculate the Jeans mass of the neutrino³⁰:

M = \frac{{1.8 M}_{Pl}^{3}}{m_{ν}^{2}} ≳ \frac{{1.8 \times (1.22 \times 10^{19} GeV)}^{3}}{{(8 meV)}^{2}} = 5 \times 10^{22} M_{⊙}

(25)

where M_Pl is the Planck mass. Without considering a potential addition due to the rotation of the black hole, both lowermost values estimated from the uppermost mass of neutrino are very close to the accepted mass of the observable universe, ca.

{10^{23} M}_{⊙}

. If the mass of a black hole exceeds this limit, the structure of the hypoatoms cannot withhold and thus the black hole or neutrino star collapses. In result, all particles annihilate to become the pure energy that is named as a singularity, in which the wavelength of photons is asymptote to zero. Thus the black hole turns into a white hole, producing the Big Bang (Figure 6).

The lowest cross section of neutrinos experimentally measured³¹ is about 10^-56 cm². If we use it to estimate the density of the hypoatoms:

ρ_{ν} = 8 meV / (10^{- 30} m)^{3} ~ 10^{52} kg / m^{3}

, then the minimum size of the cores of black holes right before the collapse can be estimated:

a ~ \sqrt[3]{M / ρ_{ν}} ≳ \sqrt[3]{3 \times 10^{22} M_{⊙} / 10^{52}} = 2 m

. This collapse before the Big Bang can almost be regarded as the reverse process of the inflation after the Big Bang (Figure 6).

Interestingly, the first episode of the inflation (reaction I) was a process to create, not consume, aether particles A and

\bar{A}

. Therefore, the gravity during the inflation appeared as a repulsive force! Although producing an attractive gravity later on, A and

\bar{A}

in the inflation were a repulsive-gravity material. Based on earlier discussion, this process did produce negative pressure. This mechanism is in agreement with the inflationary theory¹⁴. On the other hand, gravity indeed is the first force separated with the GUT force or from the universal forces, because once reaction (I) occurred, gravity existed. While they formed the matter of the universe, created B particles reduced the gravity of the universe, such that the universe would not collapse back to a black hole.

3.4.2. Where we are

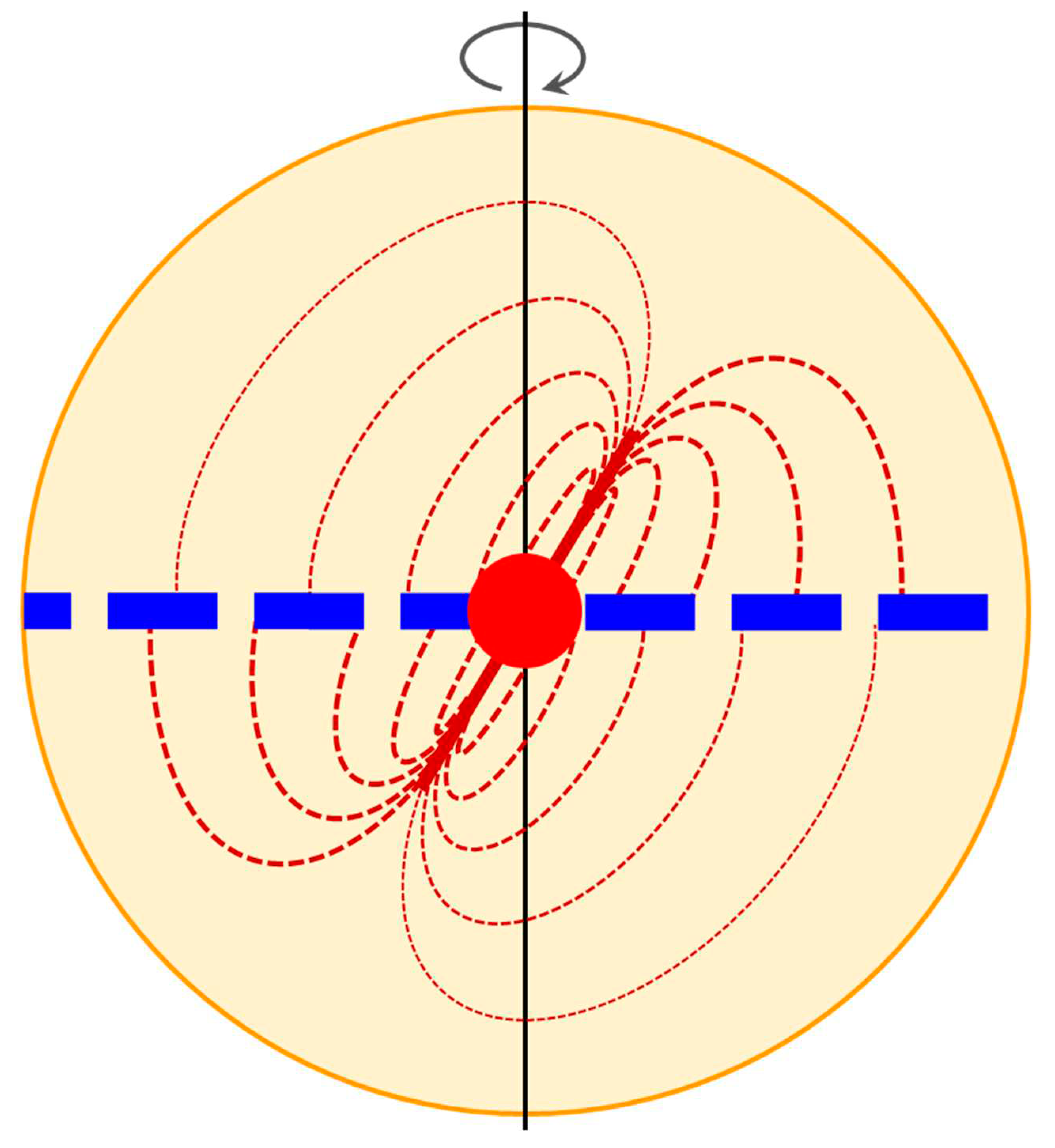
Based on our model, right before the Big Bang, the precursor black hole of our universe, a hypoatom star or neutrino star, collapsed into a singularity that can be regarded as photons whose wavelength is asymptote to zero. The singularity then turned into a white hole, emitting matter and energy at the speed of light or higher, which is the Big Bang. 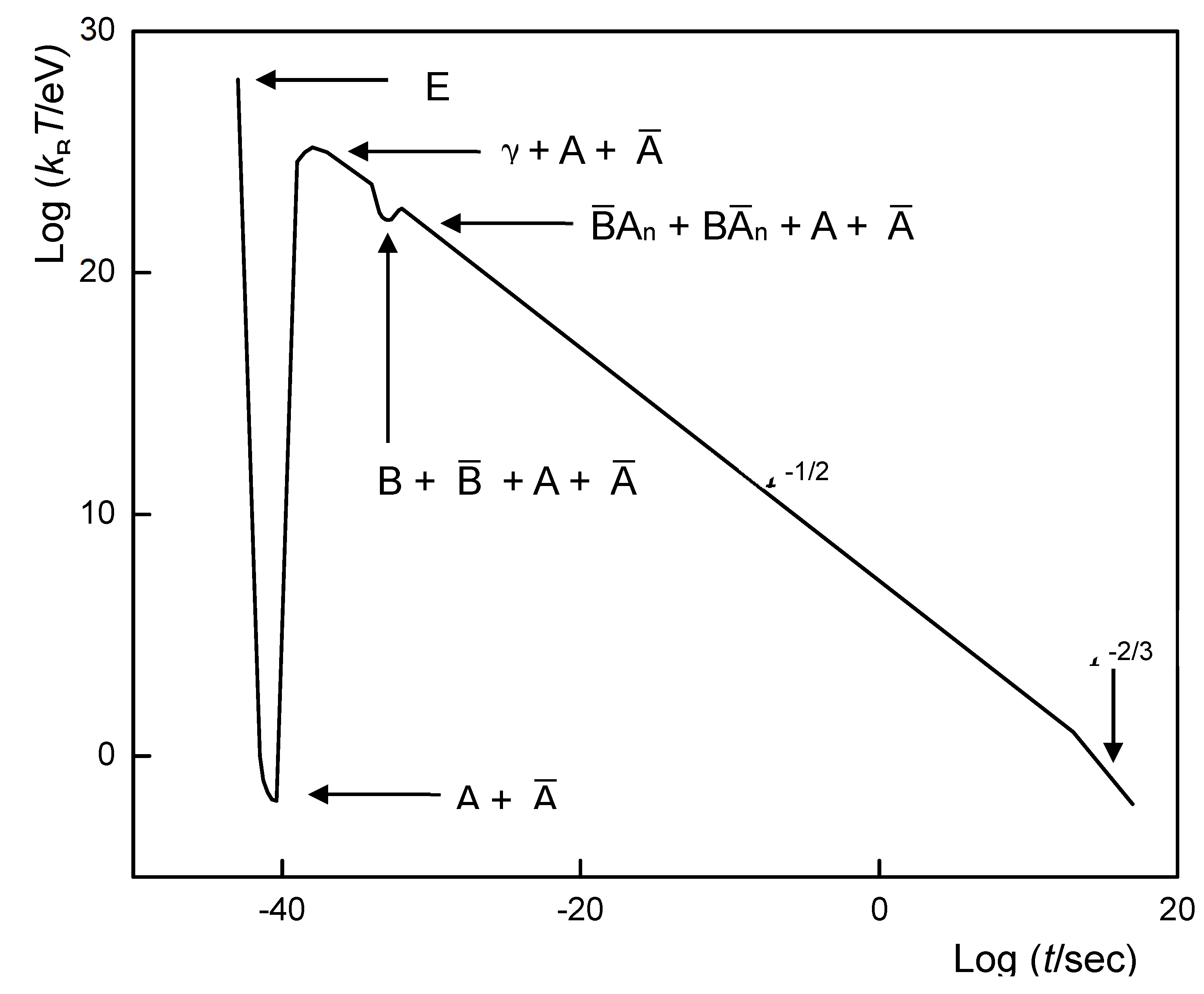We have known that before the collapse, besides the falling fabric of space, there existed the falling spiral flows V_s, the emission beams V_b and the back falling flows V_f around the core of the precursor black hole (Figure 5). These flows would be essential for the precursor neutrino star to grow and reach the mass limit for the Big Bang at ca. 10^-34 ~ 10^-32 sec before the Big Bang (Figure 6). Although their generations would be interrupted during the short emitting moment of the white hole, the V_s and V_f flows would exist after the Big Bang, so would the V_b beams due to the momenta they had in the precursor black hole. All of these flows would certainly interact with the powerful radial expansion waves V_BB of the Big Bang (Figure 7).

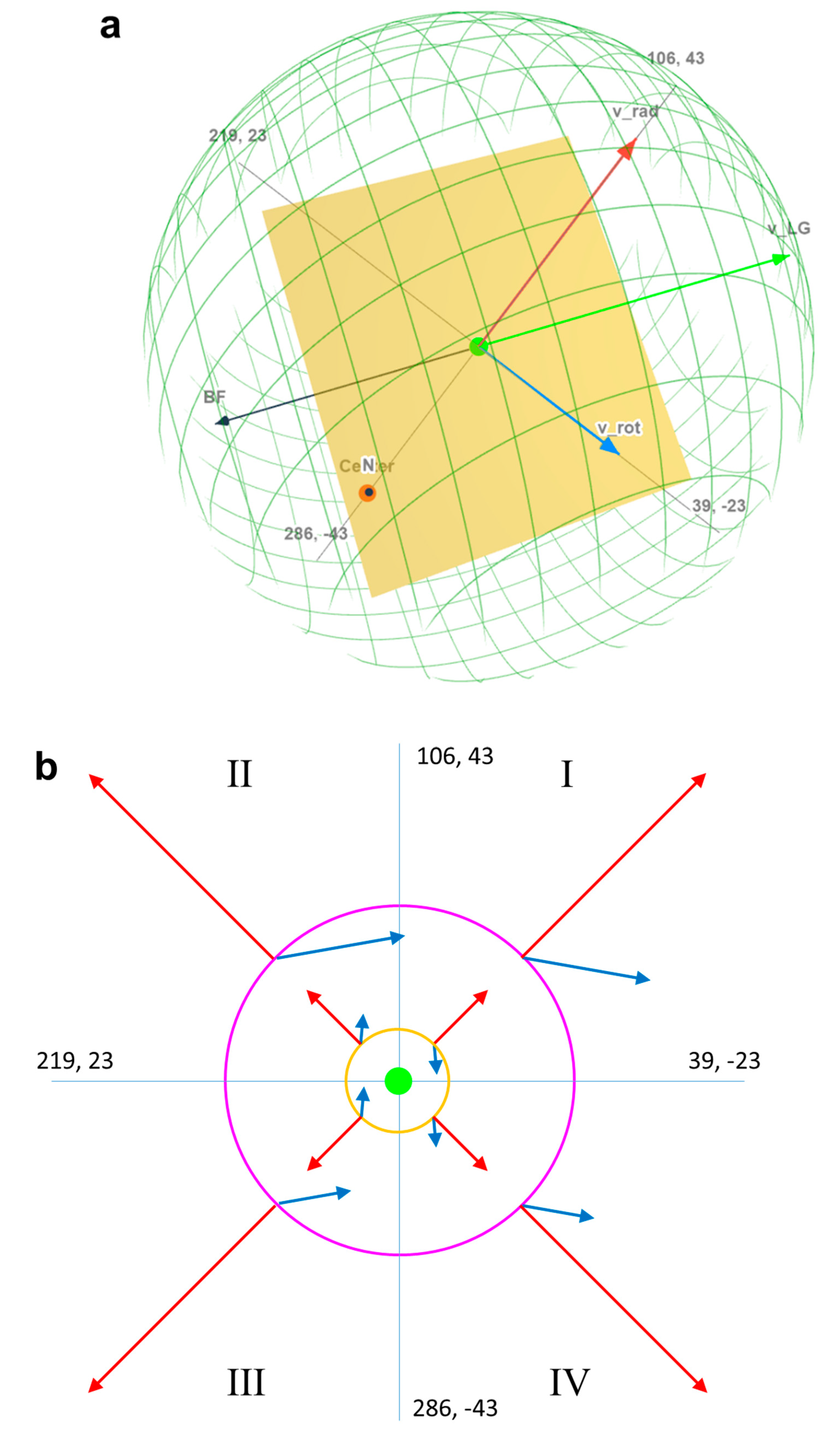
Because the V_s flows were perpendicular to the V_BB, they collided, resulting in hot spirals in the infant universe, even though the momenta of the V_s were small compared to that of the V_BB. The hot spirals intersected with the surface of last scattering (SLS) generating a hot ring in the cosmic microwave background (CMB). Half of the hot ring is easily noticeable in the range from Galactic coordinates

(l, b) ~ (265 °, 20 °) to (100 °, - 15 °)

in the CMB³², which is often related to the Axis of Evil. The hot ring is super thick, with an open angle larger than

30 °

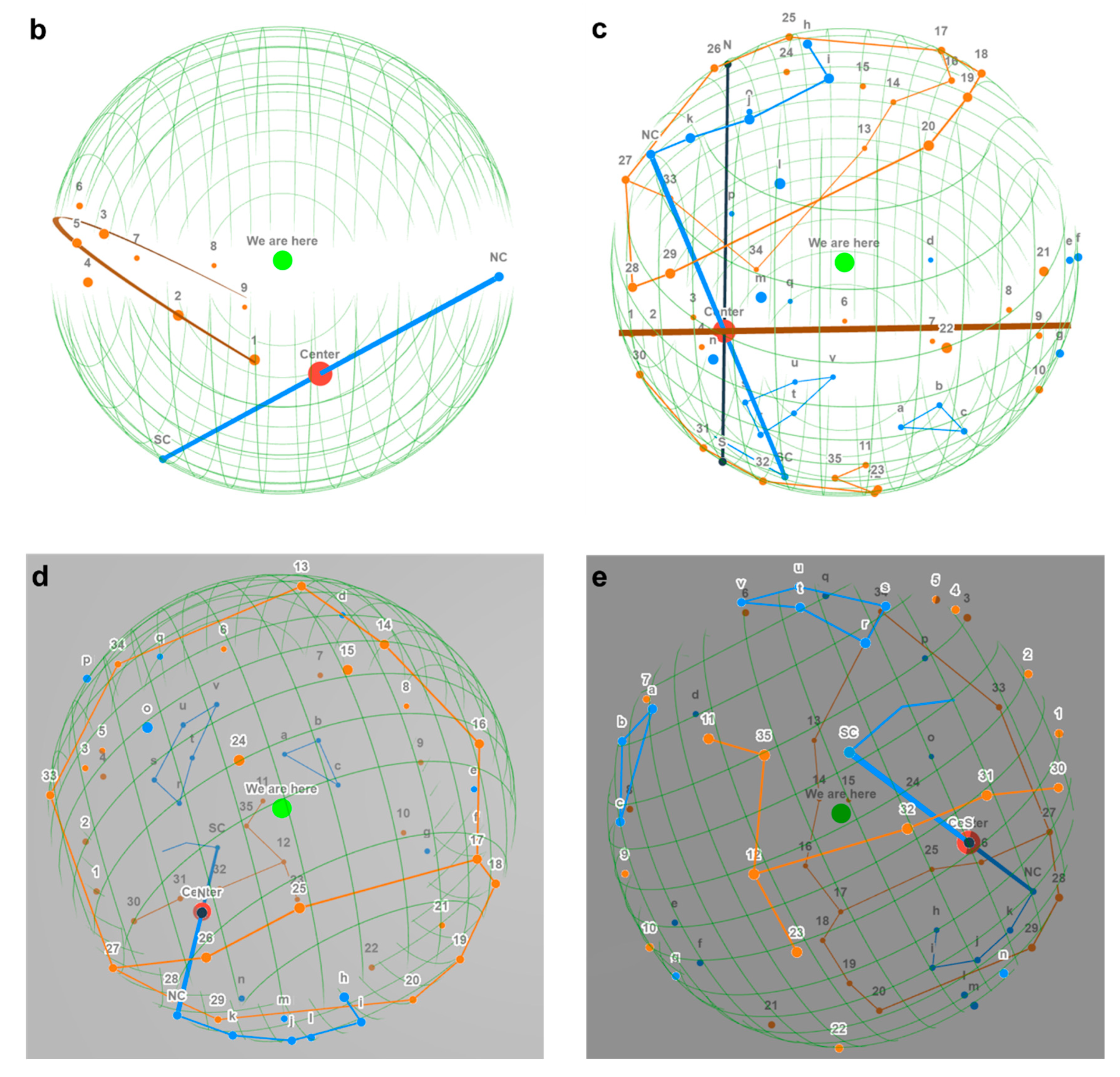
in the CMB, but is not always continuous, which is reasonable as it originated from the V_s. The hottest points in the middle of the ring, labelled as 1 to 9 (Figure 7a), are taken to define the V_s plane. The standard deviations of reading the Galactic coordinates from multiple Planck CMB maps³²: SMICA, Commander, NILC, SEVEM, SMICA-NOSZ, and Fgsub-sevem, are less than

1 °

. If we convert the Galactic coordinates into the Cartesian coordinates, then the best-fit V_s plane that can best represent the hot ring is:

z = (- 0.58 \pm 0.10) x + (0.03 \pm 0.03) y - (0.36 \pm 0.06) r_{SLS}

(26)

where

r_{SLS}

is the radius of the SLS.

Because the V_b had the same direction as the V_BB, compared to other regions (with the falling vacuum), less collisions happened, leading to a lower temperature where the V_b passed through. Therefore, two cold spots are observed in the CMB: SC, at

(l, b) = (208 °, - 56 °)

, on the South³³ of the V_s plane, and NC, at

(l, b) = (318 °, - 5 °)

, on the North (Figure 7a).

We therefore have the following important results:

The V_s plane of the hot ring and the V_b axis determined by the cold spots intersected at

(l, b) = (286 ° \pm 10 °, {- 43 °}_{- 6 °}^{+ 7 °})

and at a distance

({0.66}_{- 0.01}^{+ 0.03}) r_{SLS}

away from where we are (hereafter represented by the Local Group). This intersection is the point where the Big Bang happened or the center of the universe (Figure 7b). Since the comoving radius of the SLS is 14 Gpc (ref.³⁴), the center of the universe is 9.3 Gpc or 30 billion light years away from the Local Group.

Only half of the hot ring is observed, while the other half is hardly visible (Figure 7a). This is due to the Doppler effect and the Doppler beaming: if we look from the Local Group, the V_s flows were spiraling clockwise into the precursor core of the universe. Due to the frame-dragging effect, the core also rotated clockwise. We therefore know that: a) if we look from the Local Group to the center of the universe, the universe is rotating or spinning clockwise; b) the plane of the hot ring is the plane of the equator of the universe (equation 26); c) the angle between the equatorial plane of the universe and the Galactic plane is

30 ° \pm 5 °

; d) the North half-ball, or more accurately, the North half-ellipsoid, of the observable universe is bigger than the South half; e) the Local Group is inside the North half-ball; f) the axis of spin of the universe, perpendicular to the equatorial plane, is:

(x, y, z) = (0.13 r_{SLS}, - 0.47 r_{SLS}, - 0.45 r_{SLS}) + (0.58, - 0.03, 1.00) t

(27)

g) the spin axis intersects with the SLS at

(l, b) = (325 °, 31 °)

on the North end and

(l, b) = (256 °, - 62 °)

on the South end.

This clockwise spin is confirmed by the cold spots and a tail in the CMB. The angle between the V_s plane and the V_b axis is

58 ° \pm 6 °

. With this angle, the rotating precursor core dragged the beams to sweep the inner space within the event horizon, just like a pulsar sweeps through space. Therefore, a low-temperature tail spreading in a wide range is observed following the NC in the CMB (NC-k-j-i-h, Figure 7c). A similar tail should also exist following the SC. However, the regions of the SLS that the two beams were sweeping are very different. As the Northern beam swept from h to i, j, k, and NC, the distance to the universe center reduced (Figure 7c). This is very suitable for the tail to be observed, because the sweeping beam arrived at the SLS at almost the same time. On the contrary, as the Southern beam swept, the distance of the SLS to the universe center increased quickly (Figure 7c). Any potential tail would thus fly beyond the SLS. In addition, the potential tail, even if it existed, would be very much overshadowed by the high temperature near the universe center and the equator.

Finally, almost all the other characters in the CMB can be explained by our mechanism. The regions immediately surrounding the V_b show higher temperatures (the Northern: 29-28-27-26-25-17-18-19-20, Figs. 7c and 7d; the Southern: 35(11)-12(23)-32-31-30, Figure 7e), due to the V_f surrounding the V_b. Other regions that show higher temperatures are close to the edge of the Northern hemisphere (33-34-13-14-16, Figure 7d), due to the V_f falling towards the equatorial plane. Geometrically, the V_f flows also look longer and hence brighter on the edge. On the contrary, due to the lack of the V_f, the vast region below 20-19-18-17-16-14-13-34 (Figure 7c) is very uniform. The temperatures are lower for those close to the axis of spin rotating faster in the front, such as the l, m, and n regions (Figure 7c), and for those rotating slower in behind, such as the r-s-u-v-t and a-b-c regions (Figure 7e), due to the Doppler effect. For the regions immediately close to the equator from the South side (a-b-c and r-s-u-v-t), there existed an additional effect: the super thick spirals that originated from the V_s at the equator decoupled later because they were hotter, and hence were not as transparent as other regions.

It should be emphasized that since the universe spins, the cold spots that are used to define the V_b axis and, consequently, the center of the universe must be synchronous. Without the parameters inside the precursor black hole, the traditional method of using physical laws to deduce the properties of interest is invalid. We checked the distances from the cold spots to the center of the universe and found that they are the same:

(0.74 \pm 0.12) r_{SLS}

for the NC versus

(0.76 \pm 0.12) r_{SLS}

for the SC, therefore our results are reasonable. The Eridanus supervoid is generally believed to be insufficient to cause the temperature depression at the cold spot SC, though a recent Dark Energy Survey reported a much stronger Integrated Sachs-Wolfe imprint³⁵. Our neutrino star mechanism provides an additional explanation on the temperature depression.

Based on the Gödel metric, an exact solution of the Einstein field equations, matter in the universe rotates with the angular velocity:

ω = 2 {(π G ρ)}^{\frac{1}{2}}

, where

ρ

is the density of matter and G Newton’s gravitational constant^36,37. However, as Hawking emphasized, a velocity like this is a very high limit, corresponding to the order of the speed of light at a distance of the Hubble radius³⁸. If the universe spun at this high angular velocity, the required centripetal force would be comparable at the present time to gravity³⁸. Our neutrino star mechanism does not provide any real structures with heavy mass at the center of the universe after the Big Bang (for comparison, the precursor black hole had a heavy neutrino star core before the Big Bang). Without having sufficient centripetal force, matter has been flying away from the axis of spin. While the angular momentum is conserved, the energy of rotation has been gradually converted into that of rotationally radial expansion. Of course the dominating expansion has been accelerating (driven by the vacuum energy) in the Big Bang radial direction from the center of the universe. Therefore, we conclude that matter in the universe has been expanding in spiral trajectories.

The Local Group rotates about the axis of spin (equation 27) on the plane parallel to the equator:

z = - 0.58 x + 0.03 y

, thus the tangential velocity component of rotation points towards

(l, b) = (39 °, - 23 °)

. The velocity component in the rotationally radial direction

(l, b) = (121 °, 18 °)

is close (with an angle of 26°) to the Big Bang radial direction

(l, b) = (106 °, 43 °)

, and hence can be contributed to the Big Bang radial expansion.

3.4.3. Anisotropic universe

While Lamaître and Hubble discovered an expanding universe^39,40 in the 1920s, Gamow⁴¹ and Gödel^36,37 suspected that the universe is rotating in the 1940s. To date, the universe is generally believed to be isotropic and homogeneous; questions like where the Big Bang happened are meaningless. There has been little knowledge on whether the universe is truly rotating³⁸ or what the universe is rotating about.

It is important to note that the universe was born to be isotropic and homogeneous (except for its edge, of course), as it was a uniform globe of aether particles (reaction I) or hypoatoms (reactions IX and XIII). For the infant universe at ca. 380,000 years after the Big Bang, the deviation from the isotropy was insignificant. This is why the CMB looks nearly isotropic and homogeneous. As it expands, the universe has been becoming more anisotropic and nonhomogeneous, due to the vacuum energy from the edge of the universe and the spin of the universe.

We will provide multiple independent evidence from cosmological observations. The first evidence is about the spin of the universe. Other than Gödel’s^36,37 and Hawking’s³⁸ theoretical work, Longo⁴² focused on spiral galaxies, an idea closer to Gamow’s⁴¹. By counting the numbers, he found more left-handed spirals than right-handed ones, and thus believed that there is a parity violating asymmetry in the universe⁴². The axis of the dipole asymmetry was reported at

(l, b) = (52 °, 68.5 °)

, with an angle of 24° to equation (27), but the direction of rotation was not discussed. Shamir also found a similar asymmetry of spiral galaxies⁴³. By studying quasar polarization vectors, Hutsemékers et al. found that the polarization angle is rotating clockwise with increasing redshift in the North Galactic hemisphere and counterclockwise in the South one, which could be interpreted by the rotation of the universe⁴⁴.

The second evidence is about the existence of the bulk flow of the local universe^45,46. If the isotropic Hubble flow is not considered, then the local galaxy groups and clusters are moving with the Local Group. However, what we detect are their velocities in the past. Since the universe has been expanding in acceleration, the past local galaxy groups and clusters were moving slower than the current Local Group. Therefore, relative to the Local Group, the local galaxy groups and clusters appear to move backwards, which is observed as the bulk flow or dark flow. Cosmological observations are performed in the existence of the Hubble flow. The velocity components of the galaxy groups and clusters in the transverse direction (centered at the Local Group) are difficult to detect³⁸ and hence insignificant to the direction of the bulk flow. After the Hubble flow is removed from the cosmological results, the observed anisotropic motion of the Local Group becomes further away from the Big Bang radial direction, and the observed bulk flow is about the opposite direction, such as

(l, b) = (254 °, - 19 °)

(Figure 8a). Due to different relative positions to the Local Group, the observed direction (and magnitude) of the bulk flow must be relatively scattered, consistent with previous studies (e.g. fig. 3 in ref.⁴⁵, and fig. 13 in ref.⁴⁷).

The ΛCDM model predicts that the bulk flow exists with a reducing speed as the distance increases, which becomes negligible farther than 400 Mpc (refs.^46,48). Our mechanism predicts that the speed of the bulk flow increases as time goes further back, or the distance r to the Local Group increases:

|v_{BF}| = C_{BF} r

, where C_BF can be a constant in the local universe. The observed speed of the bulk flow is about 800-1000 km/s at 400 Mpc (refs.^46,49), corresponding to a constant

C_{BF} = 2.0 - 2.5 km s^{- 1} {Mpc}^{- 1}

. It is also worthy to note that based on our mechanism, the observed bulk flow does not mean that the local galaxy groups and clusters are truly departing from us (of course the Hubble flow still exists). This is probably why some reports reported no bulk flow^48,50.

The third evidence is about the anisotropy of the Hubble constant^47,51. For convenience of discussion, space can be divided into four quadrants by the line between the Local Group and the center of the universe, and the tangential direction of rotation of the Local Group (Figure 8b). The velocity of the Local Group, as well as the galaxy groups and clusters, is:

v = u_{rad} + v_{rot}

, where

v_{rot}

is the decelerating tangential velocity component of rotation. The accelerating radial velocity component

u_{rad}

is the sum of the isotropic velocity component

v_{iso}

and the accelerating radial velocity component

v_{rad}

u_{rad} = v_{iso} + v_{rad}

. The typical velocity components of the galaxy groups and clusters:

{∆ u}_{rad} = u_{rad, GG} - u_{rad, LG}

and

{∆ v}_{rot} = v_{rot, GG} - v_{rot, LG}

, are shown relative to the motion of the Local Group. For the galaxy groups and clusters in the local universe (

z \leq 0.1

), the speeds (not the direction) of rotation can be considered approximately the same as that of the Local Group:

|v_{rot, GG}| \approx |v_{rot, LG}|

(alternatively, the momenta of rotation or the angular velocities can be considered approximately the same). Therefore, the anisotropy of the Hubble constant has a quadrupole character: quadrants III and I host lower Hubble constants, while quadrants IV and II host higher Hubble constants (Figure 8b, the inner yellow circle). This quadrupole anisotropy matches what was observed by Migkas et al. (e.g. figs. 6 and 21 in ref.⁵¹). For the galaxy groups and clusters far away from the Local Group, their velocity components

v_{rot, GG}

of rotation were higher (pointing more to the right in Figure 8b, the outer pink circle) in the past. Therefore, the Hubble constants in quadrant I increase and those in quadrupole II decrease. The anisotropy shows more dipolar character at higher z, matching the observed results⁴⁷.

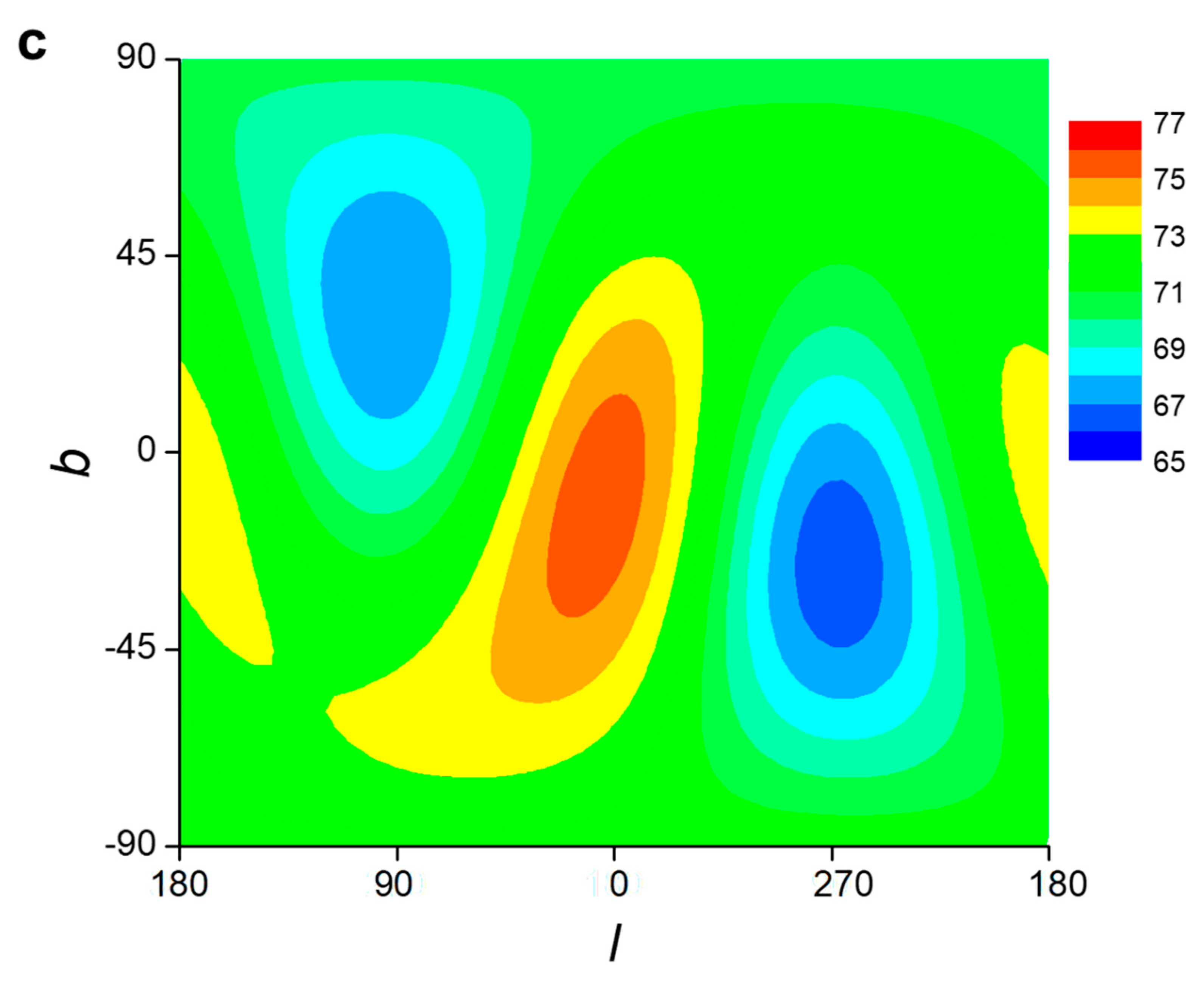
For further comparison, we performed a proof-of-concept simulation (see Methods) on the anisotropy of the Hubble constant in the local universe (

z \leq 0.1

). Since the distance R to the center of the universe ascends more rapidly than the

v_{rad} (R)

, the Hubble constant

H_{0} = u_{rad} (R)

/R always descends and will be asymptote to a constant. The Hubble law can be written as:

u_{r a d} (R) = H_{0, iso} R + v_{rad} (R)

(28)

where

H_{0, iso}

is the Hubble constant that represents the isotropic expansion. For the rotation about the axis of spin (equation 27), since what we detect are the past galaxy groups and clusters, we need to add a distance term:

|v_{rot, GG}| \approx |v_{rot, LG}| + C_{rot} r

(29)

where

C_{rot}

is the proportional constant for the velocity component of rotation. For the simulation of the Hubble constant in the local universe (

z = 0.1

), we assume the minimum number of parameters:

H_{0, iso} = 67.4 km s^{- 1} {Mpc}^{- 1}

v_{rad} = 53,000 km s^{- 1}

v_{rot} = 38,000 km s^{- 1}

(equivalent to an angular velocity

ω = 1.5 \times 10^{- 19} s^{- 1}

, which is about one order of magnitude less than that from the Gödel metric^36,37), and

C_{rot} = 1.25 km s^{- 1} {Mpc}^{- 1}

(equivalent to a speed of 500 km/s at 400 Mpc, which is less than

C_{BF}

and hence reasonable). The simulated map is shown in Figure 8c, impressively close to Migkas et al.’s observations in the local universe (fig. 21 in ref.⁵¹). Some key results are: the lowest

H_{0} = 66.3 km s^{- 1} {Mpc}^{- 1}

(l, b) = (267 °, - 26 °)

; and the highest

H_{0} = 75.6 km s^{- 1} {Mpc}^{- 1}

(l, b) = (6 °, - 12 °)

. For comparison, Migkas et al.’s results⁵¹ are: the lowest

H_{0} = 66.20 \pm 1.72 km s^{- 1} {Mpc}^{- 1}

(l, b) = (274 °, - 22 °)

; and the highest

H_{0} = 75.17 \pm 1.81 km s^{- 1} {Mpc}^{- 1}

(l, b) = (17 °, - 9 °)

. It is important to note that as long as the center and the rotation are applied to the simulation, similar patterns of the anisotropy can always be obtained even if the parameters are assumed differently in reasonable ranges (meaning that the best results may not have been obtained yet), which strongly supports our finding.

Another interesting point would be the constants that we assumed for the simulation. The Hubble constant representing the isotropic expansion,

H_{0, iso} = 67.4 km s^{- 1} {Mpc}^{- 1}

, is the same as that from the CMB¹². If we calculate it at the Local Group,

H_{0} = (67.4 + \frac{53,000}{9.3 \times 10^{3}}) km s^{- 1} {Mpc}^{- 1} = 73.1 km s^{- 1} {Mpc}^{- 1}

, which is the same as what Riess et al. observed in the local universe⁵². We therefore wonder if the Hubble tension^52,53 could be related to the anisotropic expansion of the universe⁵⁴. For the infant universe when it emitted the CMB, though it spun much faster, the contribution on the Hubble constant from the spinning (as well as the vacuum energy) was insignificant. Other observations such as the sigma-8 tension⁵⁵ would be due to the same reason.

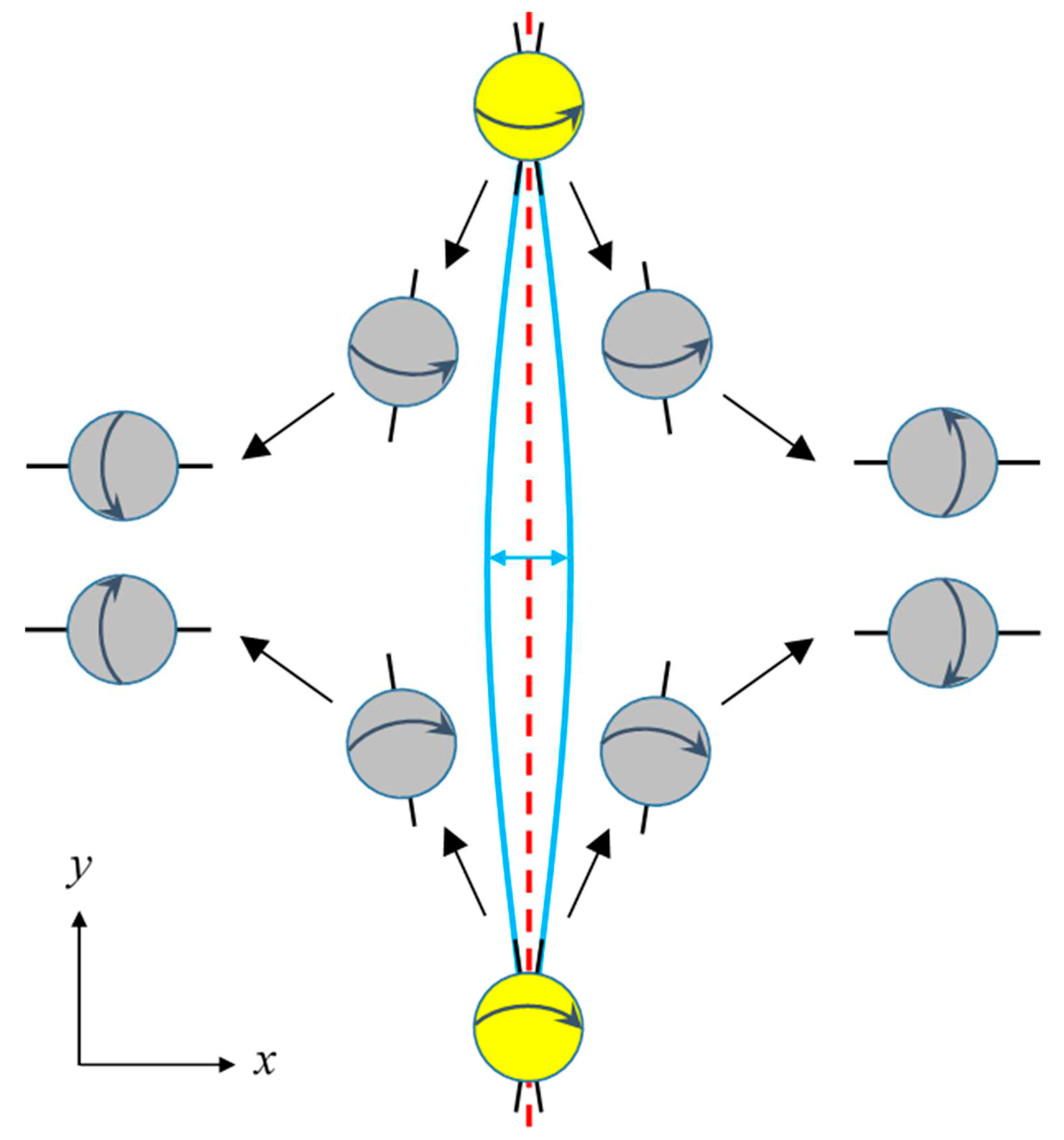
The fourth evidence is about the nucleation centers from the precursor. The emission beams V_b, the back falling flows V_f, and the falling spiral flows V_s around the core of the precursor black hole, a hypoatom star or neutrino star, would act as nucleation centers or seeds for the formation of the astronomical objects in our universe.

As discussed above, the falling spiral flows V_s were not continuous (Figure 5). The precursor core before the Big Bang was so small in diameter (only ca. 2 m), so the emission beams V_b and the back falling flows V_f (Figure 5) would sweep in a high angular speed, producing discontinuous clumps of high-density energy and/or matter across the space within the event horizon of the precursor black hole. During the early expansion of the Big Bang, these flows would collide with the powerful radial expansion waves V_BB of the Big Bang, resulting in more clumps and debris as nucleation centers for the new universe. Compared to the ΛCDM model in which nucleation centers were generated by quantum fluctuations, our model provides a mechanism to have nucleation centers much earlier, and hence explains multiple extraordinary astronomical facts.

As the universe cools down, the clumps of high-density energy and/or matter would collapse into primordial supermassive black holes, while attracting surrounding matter to form the first galaxies. Small debris would also form directly into the first stars while being attracted by nearby galaxies.

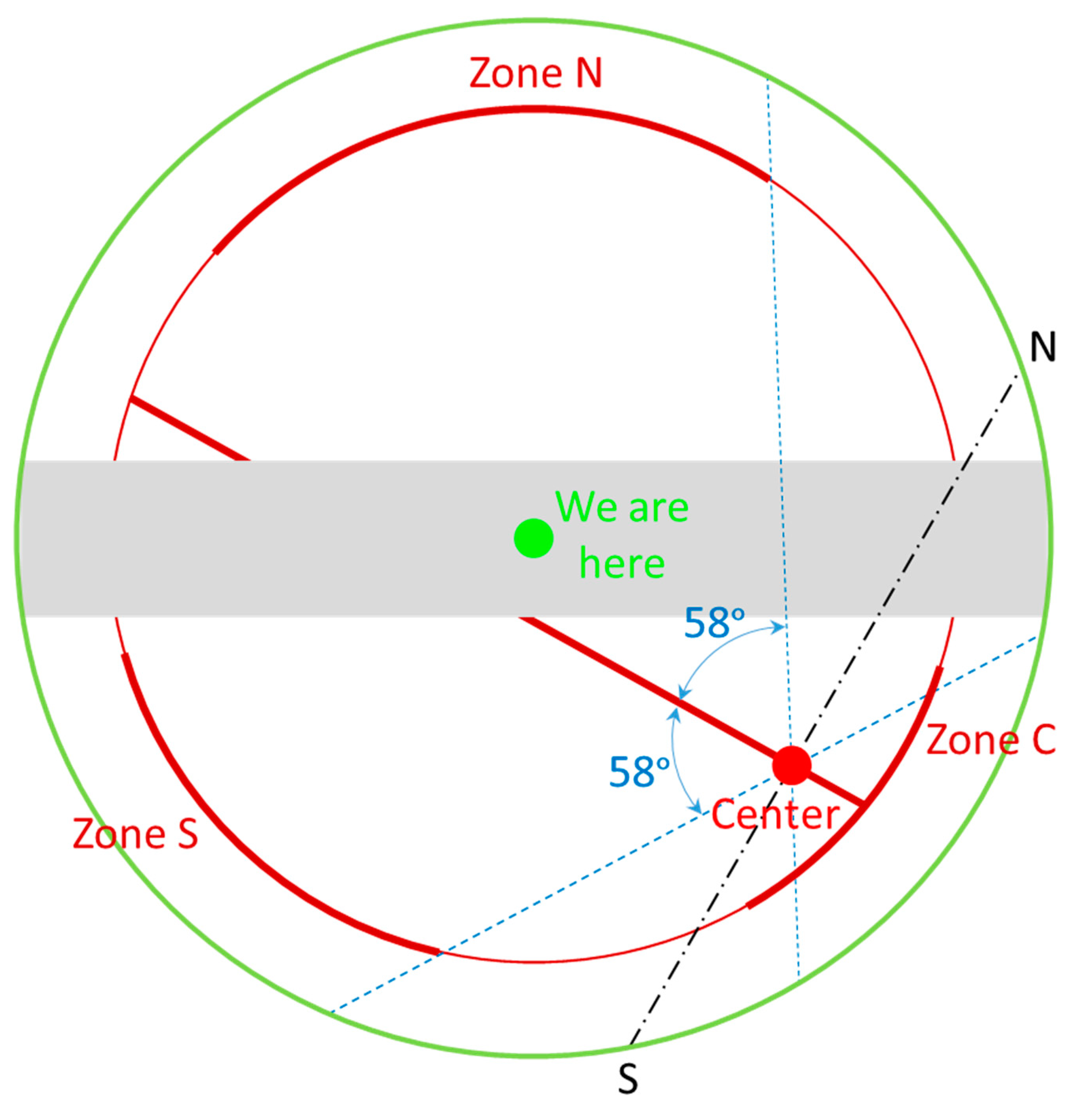
Primordial supermassive black holes and the first galaxies would be formed anywhere across the sky, because the clumps of high-density energy and/or matter would be sprayed anywhere within the event horizon (Figure 5 and Figure 9). However, the distribution would not be isotropic or homogeneous; some sky zones would have higher densities. The first would be Zone C, surrounding the center of the universe (Figure 9). As all the flows were either falling into or emitting to the core, a high density of the nucleation centers would be produced nearby. Therefore, a high density of supermassive black holes and the first galaxies would be observed in the direction of the center of the universe. The equatorial plane would have higher densities, though a large part of it would be in the Zone of Avoidance. Zone N in the North half-ball and Zone S in the South half-ball, which have a latitude viewing from the center, i.e. the angle with the equator, lower than 58° (Figure 9), would be two large high-density zones, if the emission beams V_b is assumed to fall into the equatorial plane more directly (Figure 5).

Of all these zones, Zone C would have the highest number and mass density of the first galaxies. However, because the collisions near the center are the strongest, the debris or seeds would be formed with relatively smaller masses. Therefore, individuals of black holes and the first galaxies would not have masses as high as those formed in other zones.

Note that the energy density of the universe was distributed almost uniformly because the V_BB was dominating. Compared to that from the Big Bang, the energy or mass that the nucleation centers carried from the precursor black hole would be negligible. Even the distribution of the seeds was not homogeneous in the infant universe. As the universe grows, an almost homogeneous distribution of the galaxies has been observed.

The James Webb Space Telescope (JWST) has shown its power to observe the first galaxies. The primary results indicate that there are lots of distant, complex galaxies^56,57. These results perfectly match our model. With the existence of the nucleation centers or seeds from the precursor black hole, the formation process of the first galaxies would be much faster than predicted by the ΛCDM model or the cosmological principle. We believe that the first galaxies would be formed even earlier than 250 million years after the Big Bang. Figure 9 was prepared at a radius where the universe was 100 million years after the Big Bang. The seeds would also speed up the growth of the galaxies and develop more complex galaxies, such as disk-shaped galaxies. The large number of debris from the collisions of the flows would result in so many distant galaxies observed by the JWST.

Other than black holes and galaxies, the nucleation centers would also generate other large cosmic structures or objects. One category is extraordinarily large great walls, particularly those whose sizes are incompatible with the cosmological principle, such as the Hercules–Corona Borealis Great Wall, Giant GRB Ring, and Huge-LQG, etc. Another category is extraordinarily supermassive black holes, particularly those whose masses exceed the theoretical limits, such as Phoenix A, TON 618, and MS 0735.6+7421, etc.

3.4.4. Conformal Cyclic Cosmology

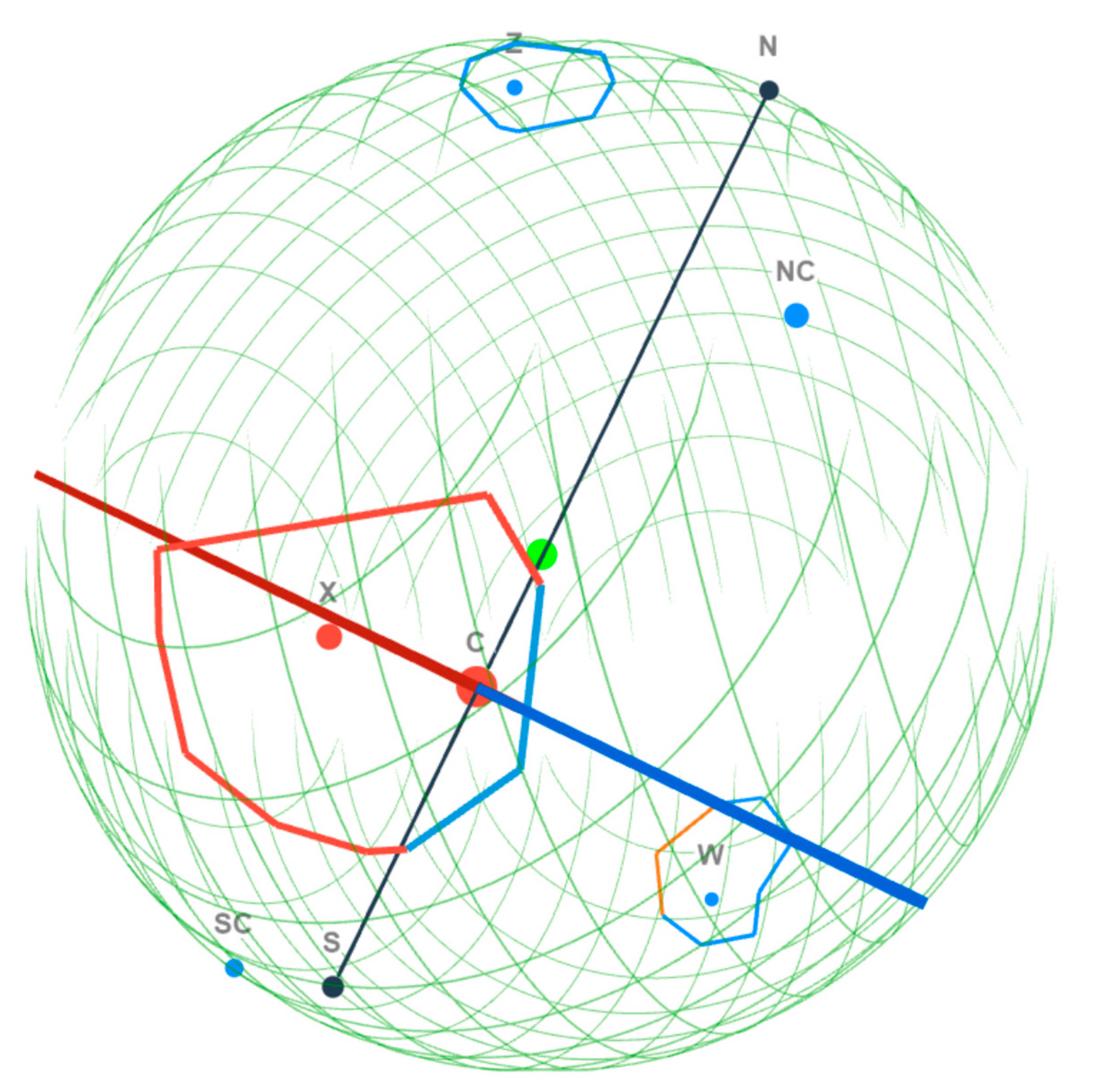
While we were looking for support to our finding that the universe originated from the collapse of a spinning precursor hypoatom or neutrino star, a piece of direct evidence was already present. Penrose⁵⁸ proposed conformal cyclic cosmology (CCC) that predicts there was an aeon preceding this universe. To support this theory, Gurzadyan and Penrose found multiple concentric low-variance circles (LVC) in the CMB maps. From the WMAP data, they⁵⁹ found region X, a large, higher-temperature LVC region concentrated around

(l, b) = (280 °, - 30 °)

, and a small, lower-temperature LVC region Y at around

(l, b) = (330 °, - 20 °)

. When they updated their search on the Planck data⁶⁰, region X was confirmed to have the strongest LVC signal at the same coordinates, while region Y was insignificant. Instead, they found two other large lower-temperature LVC regions. Since they did not name them, we assign names accordingly: region Z concentrated around

(l, b) = (290 °, 65 °)

, and region W concentrated around

(l, b) = (90 °, - 32 °)

. To explain the existence of this inhomogeneous pattern in the CMB, Gurzadyan and Penrose proposed that it is the non-uniform galactic matter distribution in the previous aeon that resulted in the LVCs. They believed that the LVCs with high temperatures come from distant previous-aeon galactic conglomerations, while the low-temperature LVCs correspond to closer ones. Very recently, Bodnia et al.⁶¹ performed a high-resolution search and obtained almost the same results. From the WMAP data, they obtained an anomalously bright spot at

(l, b) = (279.5 °, - 31.8 °)

, which is region X. From the Planck COMMANDER data, they obtained 11 anomalies, three of which with the highest temperature changes are:

(l, b) = (280.1 °, - 31.5 °)

which is region X,

(l, b) = (290.2 °, 64.9 °)

which is region Z, and

(l, b) = (86.1 °, - 38.2 °)

which is region W. From both CMB data, they also obtained a pronounced higher baseline variance (HBV) region at region X, with a sharp circular boundary.

These results prove our model in a direct manner. Region X, either from the WMAP or Planck data, either from Gurzadyan and Penrose^59,60 or Bodnia et al.⁶¹, as well as the HBV region⁶¹, all centered near

(l, b) = (280 °, - 30 °)

, is on the equatorial plane close to the center of the universe (Figure 10). Like the hot half ring observed in Figure 7, it was the collision between the V_BB and V_s flows and the Doppler effect that resulted in higher temperatures of region X. Region Z is located at the lower-temperature half of the equatorial plane (Figure 10). Region W is the result of less collisions between the outward V_b flow and the V_BB flow, because it has almost the same latitude as the NC (the angle between the line passing through

(l, b) = (86.1 °, - 38.2 °)

and the Center and the equatorial plane is ca. 59.8

°

In addition, we noticed an incredible detail about the regions on the equatorial plane: Region X has a cold corner near

(l, b) = (296 °, - 41 °)

, while Region W has a hot corner near

(l, b) = (98 °, - 28 °)

⁶⁰. Figure 10 clearly shows that the cold corner of Region X is in the cold half of the equatorial plane, while the hot corner of Region W is close to the hot half. This detail can hardly be explained without our finding.

Based on CCC, Gurzadyan and Penrose believed that the low variances result from the addition of light from the previous aeon. This mechanism is not supported in this work. By analyzing our model, we found that the low variances would be generated similar to the mechanism of baryon acoustic oscillations (BAO)⁶². All the collisions between flows, including that between the V_b and V_BB flows, would result in overdense regions in the primordial plasma. The overdense regions produced high outward pressure. Thus, the inward gravity and outward pressure created oscillations or spherical sound waves. By enhancing local heat transfer, the waves, like smoothers, reduced the temperature differences originated by quantum turbulence, leaving behind with the LVCs. Of course the smoothing requires time to process. Therefore, following the low temperature tail in the Northern hemisphere (NC-k-j-i-h, Figure 7c), there is a low-temperature LVC region, region Z. Similarly, no tail can be observed in the Southern hemisphere, neither are the LVC regions.

Other than the flows discussed above, individual objects could also be attracted and enter the precursor black hole. Therefore, our model is compatible with the Hawking points observed by Penrose and his colleagues⁶³.

In short, the LVC regions in the CMB prove that the Big Bang is the result of the collapse of a spinning precursor black hole. This black hole is indeed in the previous aeon defined by Penrose.

3.4.5. Fate of the universe

Based on our model, the universe is a flat, open system; the fate of the universe would end up with many new Big Bangs. This naturally explains the accelerating expansion of the current universe. Black holes, or their mergers, would be the seeds of the universes of the next generation, and hence require space or energy to grow. Our universe is still at her young age!

3.5. Parity non-conservation in weak interactions

Using our model, we have proven Einstein’s general theory of relativity. The frame dragging effect is also observed from the precursor black hole. Gravitoelectromagnetism (GEM) thus exists in a significant manner in the very early universe. Analogs to Maxwell’s equations, we have the GEM equations⁶⁴, one of which is:

\nabla \times B_{g} = - \frac{4 π G}{c^{2}} J_{g} + \frac{1}{c^{2}} \frac{\partial E_{g}}{\partial t}

(30)

where

E_{g}

is the gravitational field,

B_{g}

the gravitomagnetic field, and

J_{g}

the mass flux:

J_{g} = ρ_{g} V_{ρ}

, where

ρ_{g}

is mass density, and

V_{ρ}

is the velocity of the mass flow. After reactions (II) and (III), there was no process to significantly alter the gravitational field (by the creation or annihilation of aether particles). Therefore, the second term of equation (30) can be omitted:

\nabla \times B_{g} = - \frac{4 π G ρ_{g}}{c^{2}} V_{g}

(31)

Therefore, with the outward mass flow

V_{ρ}

of the V_BB flow, there existed a gravitomagnetic field

B_{g}

whose curl is negative. Because they spin against the vorticity of the

B_{g}

, antihypoatoms or antineutrinos would be more difficult to form by the recombination reaction (XIII). The created particles would mostly be those with left-handed spin, i.e. hypoatoms or neutrinos. This is the parity non-conservation in weak interactions that was discovered by Lee and Yang⁶⁵. Note that once created, the spin maintains its direction unless the motion of particles A within hypoatoms can be manipulated.

Acknowledgements

J.B.B. would like to thank Profs. Z. Shen, K. Yao, X. Jiang, F. Bo, Y. Cheng, S. Han, G. Chen, and Q. Yu at Zhejiang University for their inspiration. N.P.B. would like to dedicate this work to his grandparents in China.

References

Einstein, A. Ether and the theory of relativity (Address Univ. Leiden, 5 May 1920).
Guth, A. H. Inflationary universe: a possible solution to the horizon and flatness problems. Phys. Rev. D 23, 347-356 (1981). [CrossRef]
Linde, A. D. A new inflationary universe scenario: a possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. 108B, 389-393 (1982).
Kolb, E. W. & Turner, M. S. The early universe (Addison-Wesley, Redwood, 1990).
Starobinsky, A. A. Multicomponent de Sitter (inflationary) stages and the generation of perturbations. JETP Lett. 42, 152-155 (1985).
Silk, J. & Turner, M. S. Double inflation. Phys. Rev. D 35, 419-428 (1987).
Sinha, K. P., Sivaram, C. & Sudarshan, E. C. G. Aether as a superfluid state of particle-antiparticle pairs. Found. Phys. 6, 65-70 (1976). [CrossRef]
Pethick, C. J. & Smith, H. Bose-Einstein condensation in dilute gases (Cambridge Univ. Press, Cambridge, 2002).
Schive, H.-Y., Chiueh, T. & Broadhurst, T. Cosmic structure as the quantum interference of a coherent dark wave. Nat. Phys. 10, 496-499 (2014). [CrossRef]
Dirac, P. A. M. Is there an aether? Nature 168, 906-907 (1951).
Fagnocchi S. et al. Relativistic Bose-Einstein condensates: a new system for analogue models of gravity. New J. Phys. 12, 095012 (2010). [CrossRef]
Planck Collaboration: Aghanim N. et al. Planck 2018 results. VI. cosmological parameters. Astron. Astrophys. 641, A6 (2020).
Linde, A. D. The inflationary universe. Rep. Prog. Phys. 47, 925-986 (1984).
Guth, A. H. Lecture 23: inflation (MIT Open Course Ware, 2013).
Weiler, T. Resonant absorption of cosmic-ray neutrinos by the relic-neutrino background. Phys. Rev. Lett. 49, 234-237 (1982). [CrossRef]
Weiler, T. J. Cosmic-ray neutrino annihilation on relic neutrinos revisited: a mechanism for generating air showers above the Greisen–Zatsepin–Kuzmin cutoff. Astropart. Phys. 11, 303-316 (1999). [CrossRef]
Formaggio, J. A. & Zeller, G. P. From eV to EeV: neutrino cross sections across energy scales. Rev. Mod. Phys. 84, 1307-1341 (2012). [CrossRef]
18. IceCube Collab., Measurement of the multi-TeV neutrino interaction cross-section with IceCube using Earth absorption. Nature, 551, 596-600 (2017).
Barbieri R. et al., Baryogenesis through leptogenesis. Nucl. Phys. B 575, 61-77 (2000). [CrossRef]
Abada A. et al., Flavour matters in leptogenesis. J. High Eng. Phys. 09, 010 (2006). [CrossRef]
Grossman, Y. & Tanedo, P. Chapter 4: just a taste: lectures on flavor physics. Anticipating the Next Discoveries in Particle Physics. pp. 109-295 (World Scientific, Singapore, 2018).
Olive, K. A. et al. (Particle Data Group), Review of particle physics. Chin. Phys. C 38, 090001 (2014).
Agostini, M. et al. (Borexino Collaboration), Test of electric charge conservation with Borexino. Phys. Rev. Lett. 115, 231802 (2015). [CrossRef]
24. https://en.wikipedia.org/wiki/Proton_decay.
Taylor, E. F., Wheeler, J. A. & Bertschinger, E. Exploring black holes: introduction to general relativity. 2nd ed. (Addison-Wesley, Redwood, 2010).
Moore, B. et al. Resolving the structure of cold dark matter halos. Astrophys. J. 499, L5-L8 (1998). [CrossRef]
Feynman, R. P., Leighton, R. B. & Sands, M. The Feynman lectures on physics: quantum mechanics. The new millennium ed. vol. III (Basic books, New York, 2010).
Van der Klis, M. et al. Intensity-dependent quasi-periodic oscillations in the X-ray flux of GX 5-1. Nature 316, 225-230 (1985). [CrossRef]
29. https://images.nasa.gov/details-PIA21418.
Prakash, N. Dark matter, neutrinos, and our solar system (World Sci., Singapore, 2013).
Perkins, D. Particle Astrophysics. 2nd ed. (Oxford Univ. Press, New York, 2003).
http://pla.esac.esa.int/pla/#maps.
Cruz, M. et al. A cosmic microwave background feature consistent with a cosmic texture. Science 318, 1612-1614 (2007). [CrossRef]
Gott III, J. R. et al. A map of the universe. Astrophys. J. 624, 463-484 (2005).
Kovács A. et al. The DES view of the Eridanus supervoid and the CMB Cold Spot. MNRAS, 510, 216-229 (2021). [CrossRef]
Gödel, K. An example of a new type of cosmological solutions of Einstein’s field equations of gravitation. Rev. Mod. Phys. 21, 447-450 (1949). [CrossRef]
37. https://en.wikipedia.org/wiki/Gödel_metric.
Hawking, S. On the rotation of the universe. MNRAS 142, 129-141 (1969).
https://en.wikipedia.org/wiki/Big_Bang.
https://en.wikipedia.org/wiki/Lemaître-Tolman_metric.
Gamow, G. Rotating universe? Nature 158, 549 (1946).
Longo, M. J. Detection of a dipole in the handedness of spiral galaxies with redshifts z ∼ 0.04. Phys. Lett. B 699, 224-229 (2011). [CrossRef]
Shamir, L. Handedness asymmetry of spiral galaxies with z < 0.3 shows cosmic parity violation and a dipole axis. Phys. Lett. B 715, 25-29 (2012).
Hutsemékers D. et al. Mapping extreme-scale alignments of quasar polarization vectors. Astro. Astrophys. 441, 915-930 (2005). [CrossRef]
Hudson M. J. et al. A large-scale bulk flow of galaxy clusters. Astrophys. J. 512, L79-L82 (1999). [CrossRef]
Kashlinsky A. et al. A measurement of large-scale peculiar velocities of clusters of galaxies: results and cosmological implications. Astrophys. J. 686, L49-L52 (2008). [CrossRef]
Migkas K. et al. Cosmological implications of the anisotropy of ten galaxy cluster scaling relations. Astro. Astrophys. 649, A151 (2021). [CrossRef]
Nusser, A. & Davis, M. The cosmological bulk flow: consistency with ΛCDM and z ≈ 0 constraints on σ₈ and γ. Astrophys. J. 736, 93 (2011).
Salehi, A., Yarahmadi, M. & Fathi, S. The cosmological bulk flow in QCDM model: (in)consistency with ΛCDM. MNRAS 504, 1304-1319 (2021).
Planck Collaboration: Ade, P. A. R. et al. Planck intermediate results. XIII. constraints on peculiar velocities. Astron. Astrophys. 561, A97 (2014).
Migkas K. et al. Probing cosmic isotropy with a new X-ray galaxy cluster sample through the L_X-T scaling relation. Astro. Astrophys. 636, A15 (2020).
Riess, A. G. et al. A comprehensive measurement of the local value of the Hubble constant with 1 km/s/Mpc uncertainty from the Hubble Space Telescope and the SH0ES team. arXiv:2112.04510v2, 2022. [CrossRef]
Riess A. G. et al. Large Magellanic Cloud Cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond ΛCDM. Astrophys. J. 876, 85 (2019).
Colin J. et al. Evidence for anisotropy of cosmic acceleration. Astron. Astrophys. 631, L13 (2019). [CrossRef]
Battye, R. A., Charnock, T. & Moss, A. Tension between the power spectrum of density perturbations measured on large and small scales. Phys. Rev. D 91, 103508 (2015). [CrossRef]
Witze, A. Four revelations from the Webb telescope about distant galaxies. Nature 608, 18-19 (2022). [CrossRef]
Clery, D. Webb reveals early universe’s galactic bounty. Science 377, 700-701 (2022).
Penrose, R. Cycles of time: an extraordinary new view of the universe. (Bodley Head, London, 2010).
Gurzadyan, V.G. & Penrose, R. On CCC-predicted concentric low-variance circles in the CMB sky. Eur. Phys. J. Plus. 128, 22 (2013). [CrossRef]
Gurzadyan, V.G. & Penrose, R. CCC and the Fermi paradox. Eur. Phys. J. Plus. 131, 11 (2016). [CrossRef]
Bodnia, E. et al. Conformal cyclic cosmology signatures and anomalies of the CMB sky. arXiv: 2208.06021.
https://en.wikipedia.org/wiki/Baryon_acoustic_oscillations.
An, D. et al. Apparent evidence for Hawking points in the CMB Sky. MNRAS, 495, 3403-3408 (2020). [CrossRef]
https://en.wikipedia.org/wiki/Gravitoelectromagnetism.
Lee, T. D. & Yang, C. N. Question of parity conservation in weak interactions. Phys. Rev. 104, 254-258 (1956). [CrossRef]

Figure 1. Creation of the fundamental particles of nature. a) First episode of inflation: the pure energy (E) of the singularity turned into a globe of A and A (reaction I). The lowest temperature is taken from ref. 4. b) First reheating: numerous annihilations of A and A raised the temperature back to what the adiabatic standard cosmology describes. While one or a small number of aether pairs annihilated into energy (reaction II), n pairs of aether, by competition, produced photons (reaction III). Some aether particles were left along and therefore survived. c) Second episode of inflation: the photons collided to create particles B and antiparticles B (reaction IV). The temperature drop in this episode is much smaller than that in the first episode. d) Second reheating: the annihilations of particles B and B, without and with aether particles, raised the temperature again

Figure 2. A schematic diagram of a hypoatom, the fabric of space, and the generation of the sink flow of aether. Hypoatom BAn: a particle B (blue, open) is the nucleus; n particles A (slashed red area) surround the particle B. Fabric of space: composed of aether particles A (red, filled) and A (blue, open). Sink flow: an A (blue, open) in the fabric of space oscillates and contacts with an A (red, filled) at the hypoatom and gets annihilated (step 1). The vacancy is then filled by another A (red, filled) in the fabric of space (step 2). The hypoatom BAn constantly annihilates the aether particles, converting them into ultralong-wavelength photons, and thus produces a 3-dimensional sink flow of aether, warping spacetime and generating gravity. Spin of the hypoatom: the circlar motion (green) of particles A around the particle B, driven by steps 1 and 2.

Figure 3. A plot of the lifetimes of the pseudoscalar mesons

q \bar{q}

composed of symmetric quark q and antiquark

\bar{q}

versus their masses. By extrapolating the line: log(τ/sec) = -5.2123 - 5.0000 log(m/GeV) to 8 meV, the upper limit of the mass of a hypoatom, then the lifetime would be ca

2 \times 10^{35}

sec. Based on our postulate, annihilation only happens if all of the n+1 bodies that form an asymmetric hypoatom contact simultaneously. Therefore, the lifetime of a hypoatom would be much longer than

2 \times 10^{35}

sec, a value projected for a 2-body meson-like particle.

Figure 3. A plot of the lifetimes of the pseudoscalar mesons

q \bar{q}

composed of symmetric quark q and antiquark

\bar{q}

versus their masses. By extrapolating the line: log(τ/sec) = -5.2123 - 5.0000 log(m/GeV) to 8 meV, the upper limit of the mass of a hypoatom, then the lifetime would be ca

2 \times 10^{35}

2 \times 10^{35}

sec, a value projected for a 2-body meson-like particle.

Figure 4. A schematic diagram on the entanglement of particles. A standing wave (blue, solid curves) exists between two entangled particles (yellow). Once one of the particles is observed, the standing wave between them is overwritten. Therefore, the entangled system collapses into a pair of particles that are spinning in opposite directions (grey). The dashed line (red) between the entangled particles is a watershed.

Figure 5. A schematic diagram of a black hole. The circle (yellow) is the event horizon. The center (red) is a neutrino star. The vertical line (black) is the axis of spin. The horizontal zone (blue) represents the falling spiral flows, going in on the left and coming out on the right. The slashed lines (dark red) are the emission beams, emitting along the magnetic axis from the neutrino star (red). The dashed curves (dark red) represent the back falling flows (the thicker the curves, the larger the possibilities), either immediately surrounding the beams (dark red) or further into the spiral plane (blue). The filling (light yellow) within the event horizon (yellow) is a lit fire due to the annihilation of the fabric of space.

Figure 6. The size of a universe before and after a Big Bang. Before the Big Bang (blue): it is a growing black hole. At ca. 10^-34 ~ 10^-32 sec before the Big Bang when its mass exceeds ca.

3 \times 10^{22} M_{⊙}

, the core of the black hole collapses from ca. 2 m into a singularity. After the Big Bang (red): the universe expanded with zigzagging inflation and reheating processes, creating the fundamental particles of nature. After the first episode of inflation and reheating at ca. 10^-41 sec, the size of the universe is ca. 0.25 mm. After the second episode of inflation and reheating at ca. 10^-34 ~ 10^-32 sec, the universe returns to its size before the collapse.

Figure 6. The size of a universe before and after a Big Bang. Before the Big Bang (blue): it is a growing black hole. At ca. 10^-34 ~ 10^-32 sec before the Big Bang when its mass exceeds ca.

3 \times 10^{22} M_{⊙}

Figure 7. The center of the universe. The lines in this figure are for guidance only. a, Hot (red, number) and cold (black, letter) spots are labelled in the CMB. The zone between the white dashed curves is a hot ring. b, 3D globe of the SLS (green), on which half of the hot ring (dark red), 1-2-3&4-5-6-7-8-9, is visible. The plane of the hot ring and the line (blue) between the SC and NC (blue) intersect at the center of the universe (red). If we look from the Local Group (green), the universe is spinning clockwise. The plane of the hot ring is the equatorial plane, and the Local Group is inside the North half-ball. c, The axis of spin is the line (black) between the N and S (black), perpendicular to the equator (dark red). The observed angle between the equatorial plane and the beams (blue) is ca. 58°. With this angle, the rotating precursor black hole dragged the beams (blue) to sweep. On the Northern hemisphere, a low-temperature tail, NC-k-j-i-h, is following the cold spot NC. The regions immediately surrounding the Northern beam, 29-28-27-26-25-17-18-19-20, show higher temperatures. d, The North half-ball, looking from the N (black). Higher temperatures are close to the edge of the Northern hemisphere, 33-34-13-14(15)-16, together with those surrounding the beam. The space below them is uniform. e, The South half-ball, smaller than the North half-ball. The regions immediately surrounding the beam, 35(11)-12(23)-32-31-30, show higher temperatures. The regions immediately close to the hot equator, u-s-r-t-v and a-b-c, have lower temperatures. The thin blue line from the SC shows the position of a tail if it exists.

Figure 8. The anisotropic universe. a, Inside the SLS (green gridlines), the Local Group (green) rotates about the axis of spin (black, perpendicular to the paper) on the plane (yellow) above the center of the universe (red). The rotation

v_{rot}

points towards

(l, b) = (39 °, - 23 °)

(blue). The Big Bang radial direction

v_{rad}

points towards

(l, b) = (106 °, 43 °)

(red). The anisotropic motion

v_{LG}

of the Local Group (green) points towards the combined direction of

v_{rot}

and

v_{rad}

, such as

(l, b) = (74 °, 19 °)

(calculated from the parameters that we assumed for the simulation:

v_{rad} = 53,000 km s^{- 1}

and

v_{rot} = 38,000 km s^{- 1}

). The bulk flow (not to scale) points towards the opposite direction,

(l, b) = (254 °, - 19 °)

(black). b, The space anisotropy of the Hubble constant. Space is divided into four quadrants by the line between

(l, b) = (286 °, - 43 °)

and

(106 °, 43 °)

and the line between

(l, b) = (219 °, 23 °)

and

(39 °, - 23 °)

. The typical velocity components

{∆ u}_{rad}

(red) and

{∆ v}_{rot}

(blue) of the galaxy groups and clusters at different distances (near: yellow; far: pink) are shown relative to the motion of the Local Group (green). c, Simulated contour map of the Hubble constant.

v_{rot}

points towards

(l, b) = (39 °, - 23 °)

(blue). The Big Bang radial direction

v_{rad}

points towards

(l, b) = (106 °, 43 °)

(red). The anisotropic motion

v_{LG}

of the Local Group (green) points towards the combined direction of

v_{rot}

and

v_{rad}

, such as

(l, b) = (74 °, 19 °)

(calculated from the parameters that we assumed for the simulation:

v_{rad} = 53,000 km s^{- 1}

and

v_{rot} = 38,000 km s^{- 1}

). The bulk flow (not to scale) points towards the opposite direction,

(l, b) = (254 °, - 19 °)

(black). b, The space anisotropy of the Hubble constant. Space is divided into four quadrants by the line between

(l, b) = (286 °, - 43 °)

and

(106 °, 43 °)

and the line between

(l, b) = (219 °, 23 °)

and

(39 °, - 23 °)

. The typical velocity components

{∆ u}_{rad}

(red) and

{∆ v}_{rot}

(blue) of the galaxy groups and clusters at different distances (near: yellow; far: pink) are shown relative to the motion of the Local Group (green). c, Simulated contour map of the Hubble constant.

Figure 9. Anisotropic distribution of the first galaxies. The first galaxies would be found more frequently in the following high-density zones. Zone C (dark red arc) is near the center of the universe (red dot). The intersected zone between the equatorial plane (dark red line) and the spherical surface (dark red circle) of a radius of 11.5 Gpc (z~30) where the universe was 100 million years after the Big Bang. Zone N (dark red arc) is located in the North half-ball, with the latitude viewing from the center (red), i.e. the angle with the equator (dark red line), lower than 58°. Zone S is located in the South half-ball, with the latitude lower than 58°. The center dot (green) represents where we are or the LG, and the largest circle (green) is the SLS. The horizontal wide zone (grey) represents the Zone of Avoidance. This schematic diagram is not in accurate scale.

Figure 10. Regions of concentric low-variance circles (LVC) in the CMB: region X (closed by orange and blue lines, front), a higher-temperature LVC region concentrated around

(l, b) = (280 °, - 30 °)

with a cold corner (blue) around

(l, b) = (296 °, - 41 °)

; region Z (closed by blue lines, top), a lower-temperature LVC region; and region W (closed by blue and orange lines, far end), a lower-temperature LVC region with a hot corner (orange)

.

All the coordinates are taken from fig. 2 of Gurzadyan and Penrose⁶⁰. The points (orange or blue) within each of the regions are taken from Bodnia et al.⁶¹ The equator is drawn into two halves: the hot half (dark red) and the cold half (blue). The angle of the line between Z and the Center (red) with the equatorial plane is ca. 59.8°. The center point (green) represents where we are or the LG, and the largest 3D globe (green) is the SLS. NC and SC (blue) are the cold spots.

Figure 10. Regions of concentric low-variance circles (LVC) in the CMB: region X (closed by orange and blue lines, front), a higher-temperature LVC region concentrated around

(l, b) = (280 °, - 30 °)

with a cold corner (blue) around

(l, b) = (296 °, - 41 °)

; region Z (closed by blue lines, top), a lower-temperature LVC region; and region W (closed by blue and orange lines, far end), a lower-temperature LVC region with a hot corner (orange)

.

Table 1. List of particles created in the early universe.

Time	Energy	Events	Particles created
< 10^-43 s	> 10¹⁹ GeV	Symmetry breaking (gravity separated from other three forces)	A & $\bar{A}$
10^-34 ~ 10^-32 s	10¹⁵ ~ 10¹⁴ GeV	Electrostrong symmetry breaking	B & $\bar{B}$ , or UHE neutrinos
(10^-22 s)	(10⁸ GeV)	Gauge desert	Intermediates
10^-12 ~ 10^-6 s	100 ~ 0.1 GeV	Electroweak symmetry breaking	u, d & e
1 ~ 10 s	1 ~ 0.1 MeV		Nuclei
~ 10¹³ s	~ 0.4 eV		Atoms

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Fundamental Particles and Reactions of Nature

Abstract

I. INTRODUCTION

II. BASIC THEORY

2.1. Creation of fundamental particles

2.2. Fabric of space

2.3. Hypoatoms

2.4. Dark energy

2.5. An earlier inflation

2.6. Neutrinos

2.7. Stability of hypoatoms

2.8. Creation strategy

III. DISCUSSION

3.1. General theory of relativity

3.2. Dark matter

3.3. Quantum mechanics

3.4. Black hole

3.4.1. Birth of the universe

3.4.2. Where we are

3.4.3. Anisotropic universe

3.4.4. Conformal Cyclic Cosmology

3.4.5. Fate of the universe

3.5. Parity non-conservation in weak interactions

Acknowledgements

References

MDPI Initiatives

Important Links

Subscribe