Oscillating Universe with a Quantized Black Hole

Preprint

Article

Oscillating Universe with a Quantized Black Hole

Altmetrics

Downloads

614

Views

793

Comments

Sascha Kulas^*

This version is not peer-reviewed

Submitted:

10 November 2023

Posted:

15 November 2023

You are already at the latest version

Alerts

Abstract

In cosmology dark energy and dark matter are included in the ΛCDM model, but they are still completely unknown. Because in black holes Lorentz invariance seems not to be applicable for curved space-time, we introduce a model for a reduced speed of light in black holes due to quantum gravity effects and the Heisenberg uncertainty relation. Then black holes are a source for a scalar field with dark energy characteristics. This model has no information paradox for black holes because particles / radiation entering the black hole are redshifted in their wavelength that far that the wavelength has the size of the Schwarzschild radius and thus they are in some way "frozen" in the black hole. We show that the scalar field also has characteristics of dark matter shortly after Planck time, when we use a Big Bounce model. This model also presents an alternative to cosmological inflation with the possibility to solve the flatness and horizon problem and the problem of density fluctuations.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

Introduction

The

Λ

CDM model is very successful in describing the universe from the early beginning (assuming a big bang) and compatible to the cosmic microwave background (CMB) in a lot of details. In this model the scenario of an inflation phase is included, that solves different problems: amongst others the flatness problem, the horizon problem and the problem of density fluctuations [1]. Since it has difficulties, e.g. the big choice of physical parameters [2], it motivates for other views. One other view is the scenario of a big bounce without inflation. That means at some point the expansion of a universe stops and it contracts again [3]. After a rebound the next cycle begins. Among others the Loop Quantum Gravity (LQG) theory demands a minimal length where the contraction stops [4]. A contracting black hole, due to Hawking radiation, would stop the contraction at the Planck length or several orders of magnitude before.

Since we will use a reduced speed of light in black holes and want to show the effects by this reduced speed, we will use SI-units in the following. We use the Schwarzschild metric and no Kerr metric with rotating black holes as a first iteration. This model can in principle be adapted to rotating black holes.

1. The Reduced Speed of Light and the Scalar Field in Black Holes

For this new model we start with a minimum length in black holes. E.g. Loop Quantum Gravity (LQG) demands a minimal length, the Planck length

L_{P}

[3]. Then the Heisenberg uncertainty relation can not be fulfilled any more and has to be adjusted.

In an arbitrarily small area around a space-time-point in globally curved space-time, local flatness and Lorentz invariance apply. This cannot be sustained in black holes. By assuming a reduced speed of light the Heisenberg uncertainty can be maintained.

We start with the Heisenberg uncertainty relation for a particle with mass m:

Δ x Δ p = Δ x Δ m Δ v \geq ℏ / 2

(1)

Here x is the position,

p = m v

the momentum of the particle and v its speed, ℏ is the reduced Planck constant. To reach the extremal states the uncertainty for the mass m has to be extremal and we use the mass of a black hole with its Schwarzschild radius

R_{S} = \frac{2 G m}{c^{2}}

and the gravitational constant G:

Δ x Δ m Δ v = Δ x \frac{c^{2} R_{S}}{2 G} Δ v \geq ℏ / 2

(2)

To reach the extremal states the next step is that the uncertainty for

Δ x

has to be the smallest, the Planck length

L_{P}

, and the uncertainty for

Δ v

has to be the greatest, the speed of light c. Then we reach the state where the uncertainty relation would not hold true any more because we cannot reduce

Δ x = L_{P}

any more:

L_{P} \frac{C^{2} R_{S}}{2 G} c \geq ℏ / 2

(3)

On this scale and in the black hole we assume that the speed of light is variable. The equation does not forbid that the speed of light already changed before the Planck scale was reached. Here we use the capital letter for C for the variable speed of light, which is connected to black holes by the Schwarzschild radius. We do not use it as a speed of light c in general. After rearranging the equation we have

C^{2} \geq \frac{ℏ G}{L_{P} R_{S} c} = \frac{ℏ G L_{P}}{L_{P} R_{S} c L_{P}} = c^{2} \frac{L_{P}}{R_{S}}

(4)

Here we expand the equation by the Planck length

L_{P} = \sqrt{\frac{ℏ G}{c^{3}}}

When we look at black holes on the greatest and smallest scales we have a black hole with a Planck mass

m_{P}

on the one side. It has a Schwarzschild radius of the Planck length

L_{P}

L_{P} = \frac{G m_{P}}{c^{2}}

(5)

Here

c \approx 3 \times 10^{8}

m/s is the known speed of light. On the other side we have massive black holes with their masses M and their different Schwarzschild radii

R_{S}

R_{S} = \frac{2 G M}{c^{2}}

(6)

When the Schwarzschild radius of equation 6 gets smaller and smaller by Hawking radiation the speed of light C gets higher, see equation 4. For the Schwarzschild radius of a Planck length in equation 5 the reduced speed of light in equation 4 is not reduced any more and

C = c

. This makes sense because then particles / radiation in the black hole interact such short time with the black hole and with potential quantum gravity effects that the speed is not reduced. We add the factor 2 to the Planck length for this special case

C = c

at the Planck length. This leads to

C = c \sqrt{\frac{2 L_{P}}{R_{S}}}

(7)

That means a bigger Schwarzschild radius leads to a smaller speed of light of the photons inside the black hole and a black hole close to the Planck size has photons with nearly the speed of light c in it.

Here equation 7 is derived with the instruments of quantum mechanics: the Heisenberg uncertainty relation with the reduced Planck constant ℏ.

Equation 7 can also be derived with only the instruments of gravity theory and the conservation of energy. We use equation 6 and imagine the largest possible black hole. E.g. if their would be a Big Crunch scenario in the future there would be one black mega hole with all the mass of the universe

M_{U}

. When we assume that there is a reduced speed of light in this black hole and all the particles / radiation / information is "frozen" we can have the same mass only by the Planck energy, which is makable by the smallest black hole (see equation 5) and a reduced speed of light C:

M_{U} = \frac{E_{P}}{C^{2}}

(8)

By using equation 6 for

M_{U}

and

E_{P} = m_{P} c^{2}

the equation changes to:

\frac{c^{2} R_{S}}{2 G} = \frac{m_{P} c^{2}}{C^{2}}

(9)

Now we use

m_{P}

of equation 5 and end up with

C = c \sqrt{\frac{2 L_{P}}{R_{S}}}

(10)

This is the result we already know (see equation 7).

The reduced speed of light in black holes of equation 7 / 10 is plotted in Figure 1.

It can be seen that even very small black holes with a Schwarzschild radius of some meters trap extremely slow photons with a typical speed of

10^{- 9}

m/s.

Together with this reduced speed of light C we can derive an effective rest mass for these photons with energy E in the black hole

m_{e f f} = \frac{E}{C^{2}} = \frac{E R_{S}}{2 L_{P} c^{2}}

(11)

We call these photons with an effective rest mass massive photons (MP) in the following. For these massive photons in the black hole we have:

E = m_{e f f} C^{2} = m_{e f f} c^{2} \frac{2 L_{P}}{R_{S}} = 2 π ℏ c / λ

(12)

Then the wavelength is:

λ = \frac{2 π ℏ}{m_{e f f} c} \frac{R_{S}}{2 L_{P}} = λ_{0} \frac{R_{S}}{2 L_{P}}

(13)

Here we used

λ_{0} = \frac{2 π ℏ}{m_{e f f} c}

with the dynamical mass of normal photons (NP) in the last step. That means the photons in the black hole are strongly redshifted by

\frac{R_{S}}{2 L_{P}}

. That redshift factor is that immense due to the Planck length in the denominator that even photons with the smallest imaginable wavelength, the Planck length, would have wavelengths in the black hole about the Schwarzschild radius. That means all the photons in the black hole must have a wavelength about the Schwarzschild radius because nothing can leave the black hole and larger wavelengths are not possible then. Thus, the typical wavelength

λ_{0}

can be set to

4 L_{P} π

, which results in the longest possible wavelength in the black hole, by definition the circumference:

λ = 2 π R_{S}

. Then this results in a mass, which is half the Planck mass

m_{P}

m_{e f f} = \frac{1}{2} m_{P}

(14)

Also massive particles (baryonic matter) like electrons are redshifted inside the black hole, which can be seen by the De Broglie wavelength

λ_{D B}

λ_{D B} = \frac{2 π ℏ}{m_{0} v} \sqrt{1 - \frac{v^{2}}{C^{2}}} = \frac{2 π ℏ}{m_{0} v} \sqrt{1 - \frac{v^{2}}{c^{2}}} \sqrt{\frac{R_{S}}{2 L_{P}}}

(15)

That means the massive particles are redshifted by the factor

\sqrt{\frac{R_{S}}{2 L_{P}}}

. Here we have a similar scenario and we can assume

R_{S}

for the typical wavelength of particles in the black hole.

The mass m with its rest mass

m_{0}

is changed in the following way:

m = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{C^{2}}}} = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{C^{2}}}} \sqrt{\frac{2 L_{P}}{R_{S}}}

(16)

In massive black holes the particle mass gets extremely small, which is in harmony with the giant wavelength. When the black hole shrinks down to the Planck length the particles leave the black hole with their original mass.

Equations 13 and 15 show that everything that enters the black hole is strongly redshifted. The original information can still be deciphered by reducing the redshift.

When the photons enter the black hole and gain an effective mass similar to the Planck mass they nearly do not move any more, e.g.

\approx 10^{- 14}

m/s for SgrA*, see Appendix A. That means these photons span a scalar field very similar to the cosmological quintessence [5], but with

ω = p / ρ = - 1

and here similar to a cosmological constant, we see in the following. Here p is the pressure and

ρ

the density. These photons do not interact with other particles of effective mass in the field in the first order because of their photonic properties.

Since their speed is so low, their energy density is not changing over time in the first approximation. Due to the characteristics of a growing black hole and the statistics of black holes absorbing photons from its environment, space inside the black hole is filled with these particles in an orderly pattern.

When considering a perfect fluid, described by its density

ρ

and pressure p filling a Robertson Walker space time, the Friedmann equation for such a fluid is

\dot{ρ} + \frac{3 \dot{a}}{a} (ρ + \frac{p}{c^{2}}) = 0

(17)

Here a dot means derivative with respect to time t. That means every change of the energy density is proportional to the sum of positive energy density and pressure. For our scalar field the change is approximately zero and thus the pressure is negative and

ω = - 1

\dot{ρ} + \frac{3 \dot{a}}{a} (ρ + \frac{p}{c^{2}}) \approx 3 H (ρ + \frac{p}{c^{2}}) = 0

(18)

Then

ρ + \frac{p}{c^{2}} \approx 0

(19)

and

ω = \frac{p}{ρ} \approx - 1

(20)

In the last step

c = 1

is used for the typical convention in natural units. In the following SI-units are used again.

That means normal matter, which is surrounded by the massive photons, realizes a repulsive force and our scalar field acts as a fifth force and similar to dark energy. When the temporal derivative of the energy density is bigger than the energy density itself the approximation of a not changing energy density is not correct any more and we have the behaviour of dark matter, which is the case for early times, we will see in Section 4.

That means every black hole would consist of slow photons which posses something really similar to a dark energy and are very similar to Dark Energy Stars [6], but with a theoretical singularity, which does not have a practical significance (see Section 2). For massive black holes a cosmological coupling was measured ([7,8]), which indicates that massive black holes are growing with the same growing rate than the universe is growing due to dark energy. This would mean that massive black holes could save massive photons in their inner that act as dark energy and could be cosmological coupled. This is in agreement with [9], who show that nonsingular BHs are unlikely to be the source of dark energy.

For today we can calculate the energy density of the scalar field. As already mentioned, in a Big Crunch scenario there would be one massive black mega hole at the end with its mass

M_{U}

. If the Big Crunch is slow enough the black hole would shrink due to Hawking radiation [10]. By the shrinking radius

R_{S}

more and more MPs would stay behind and when

R_{S}

reaches the Planck length the original sphere is filled with MPs with their Planck masses

m_{P}

. When this scenario is thought through further and since the black hole cannot fall below the Planck length (see Appendix B), a rebound leads to a new Big Bang embedded in the scalar field of a predecessor universe. For calculating the energy density of this scalar field we use equation 8. And since the original mass

M_{U}

of the black hole is divided up to N effective masses (see equation 14), we can write

E_{P} = N m_{e f f} C^{2}

(21)

Here N is a natural number. With this number we can calculate the number density and then the mass density and end up with an equation for the scalar field mass density:

ρ_{M} = \frac{3 m_{P}}{8 π L_{P} R_{S}^{2}}

(22)

By taking the radius of the observable universe of

1.3 \times 10^{26}

m for

R_{S}

which the Hubble parameter

H = 67.7 \frac{K m / s}{M p c}

delivers [11], we end up with a mass density of

ρ_{M} = 9.5 \times 10^{- 27}

K g / m^{3}

and slightly above the critical density

ρ_{C} = 8.5 \times 10^{- 27}

K g / m^{3}

. This means in our model that the universe did not reach the Schwarzschild radius of the former mega black hole yet where the scalar field drops. By using the density of dark energy of the

Λ

CDM model of

ρ_{D E} = 5.95 \times 10^{- 27}

K g / m^{3}

, which includes a density parameter of

Ω_{Λ} = 0.7

, we end up with a Schwarzschild radius of

R_{S} * = 1.65 \times 10^{26}

m. Then this would mean for the future, when the radius of the observable universe reaches

R_{S} *

, the scalar field would end and according to equation 17 the temporal derivative of the energy density would have a dropping negative value because the scalar field is "washed out" more and more during the further expansion. That means the scalar field would switch to a field with gravitative attraction leading to an already mentioned Big Crunch, because then there is no dark energy equivalent any more, but a lot of additional normal matter in this scalar field.

The late universe has a value for the Hubble parameter of

H_{0} = 74.03 \pm 1.42 \frac{K m / s}{M p c}

[12]. This is the so called Hubble tension we explain by this model in Section 3.

In Appendix B the temperature in the black hole is derived by the model of the scalar field with effective photon mass. The temperature is the Hawking temperature. This shows that the temperature in the black hole (transmitted by the effective mass particle) is the same than around the black hole, transmitted by Hawking radiation, and there is a temperature coupling between inside and outside of the black hole.

2. Post-Schwarzschild-Metric

In the derivation of the new metric, we call Post-Schwarzschild-Metric (PSM), we start with the Schwarzschild metric (SM) and a change of the speed of light c by the reduced speed of light C in the expression for the Schwarzschild radius and the time coordinate. The original Schwarzschild metric is the following:

d s^{2} = \frac{d r^{2}}{1 - \frac{2 G M}{c^{2} r}} + r^{2} (d θ^{2} + s i n^{2} (θ) d ϕ^{2}) - (1 - \frac{2 G M}{c^{2} r}) c^{2} d t^{2}

(23)

We can do the following transformation when jumping form the surroundings of the black hole into the black hole:

\begin{matrix} c & \to C = c \sqrt{\frac{2 L_{P}}{R_{S}}} \\ R_{S} = \frac{2 G M}{c^{2}} & \to R_{S} * = \frac{2 G m_{P}}{C^{2}} = \frac{2 G m_{P}}{c^{2}} \frac{R_{S}}{2 L_{P}} = \frac{L_{P} R_{S}}{L_{P}} = R_{S} = \frac{2 G M}{c^{2}} \end{matrix}

Here the Schwarzschild radius for the Planck mass (Planck length) of equation 5 was used. During transformation mass M has to be changed by the Planck mass. Otherwise the Schwarzschild radius of the inner solution (PSM) does not fit with the Schwarzschild radius of the outer solution (SM). Since C is that small the Schwarzschild radius would be much higher. That means

d r^{2}

stays the same under transformation. Then the PSM-metric with

d S^{2}

instead of

d s^{2}

(SM) is:

d S^{2} = \frac{d r^{2}}{1 - \frac{R_{S}}{r}} + r^{2} (d θ^{2} + s i n^{2} (θ) d ϕ^{2}) - (1 - \frac{R_{S}}{r}) c^{2} \frac{2 L_{P}}{R_{S}} d t^{2}

(24)

For the interior of the black hole that means there is a core with the Planck mass

m_{P}

in the center and all particles / radiation entering the black hole (leaving the Schwarzschild radius behind) are slowed down massively. In some way radiation and particles are "frozen" inside the black hole. This is no violation of energy conservation since the mass of the black hole

M = E / c^{2}

is now saved in the mass of all the particles / radiation inside the black hole with a much lower speed of light and thus a much higher (effective) mass. The difference compared to the SM is a massive shift of the time coordinate in the black hole. Particles /radiation inside a black hole with a typical size will never enter the center of the black hole in the life time of the black hole. So the question if there is in anyway a singularity in the center makes no practical sense any more because no particle / radiation will enter this center in typical black holes in the universe. Apart from this we introduced a minimum length, the Planck length.

Now we look at the massive photons in the black hole in more details. We assume that the photon is taking a constant radius and

d r = 0

. Of course we have a massive photon and thus

d s \neq 0

. We rotate the coordinate system in a way that

θ

stays constant and

d θ = 0

. This leads to:

d S_{M P}^{2} = r^{2} s i n^{2} (θ) d ϕ^{2} - 2 (\frac{1}{R_{S}} - \frac{1}{r}) c^{2} d t^{2}

(25)

To see if this metric still holds true for normal photons (NP) at the surroundings of the black hole we set

d S_{M P} = 0 = d S_{N P}

and end up with

\frac{d ϕ^{2}}{d t^{2}} = (\frac{1}{R_{S}} - \frac{1}{r}) \frac{2 L_{P} c^{2}}{r^{2} s i n^{2} (θ)}

(26)

The geodesic equation provides an expression for

\frac{d ϕ^{2}}{d t^{2}}

\frac{d ϕ^{2}}{d t^{2}} = \frac{C^{2} R_{S}}{2 r^{3} s i n^{2} (θ)} = \frac{c^{2} R_{S} 2 L_{P}}{2 r^{3} s i n^{2} (θ) R_{S}} = \frac{c^{2} 2 L_{P}}{2 r^{3} s i n^{2} (θ)}

(27)

When we equate equations 26 and 27 we end up with

r = \frac{3}{2} R_{S}

, which is the well known photon sphere or photon orbit around Schwarschild black holes. That means the metric holds true for normal photons, which can not get closer to the center of the black hole than the photon sphere. When they get closer they transform to massive photons with a strongly reduced speed by a probably still unknown quantum gravity effect. That also means that they directly transform hitting the milestone

r = \frac{3}{2} R_{S}

. Maybe this can be detected in the future in characteristics of the photon ring(s) of M87* [13].

3. The Hubble Tension

For the Hubble parameter we can use the following simple correlation by using

H = \sqrt{Λ c^{2} / (3 Ω_{Λ})}

, equation 5 and equation 22 with

ρ_{M} = ρ_{Λ}

H = \frac{c}{R_{S}^{*} \sqrt{Ω_{Λ}}} = 2.18 \times 10^{- 18} 1 / s = 67.4 \frac{K m / s}{M p c}

(28)

The sphere with the radius

R_{S}^{*}

, filled with the scalar field, leads to the Hubble parameter measured in the CMB by the Planck satellite.

But new precise and different measurements of the Hubble constant lead to the so called Hubble tension. On the one hand there are above mentioned Planck data which lead to a Hubble constant of

67.4 \pm 0.5 \frac{K m / s}{M p c}

[11]. On the other hand measurements of the late universe by Riess et al. yield a Hubble constant

H_{0} = 74.03 \pm 1.42 \frac{K m / s}{M p c}

[12]. A reason for this in our model could be that when the previous universe was shrinking on the way to the Big Bounce there was not one mega black hole formed, but giant black holes first, which merged to the mega black hole. The giant black holes were smaller than the mega black hole and thus had a smaller Schwarzschild radius

R_{S G}

. Equation 28 shows that a smaller Schwarzschild radius leads to a higher Hubble parameter in our universe. Since we go the other way round and by expansion of our universe first the smaller Hubble parameter is noticed due to the evaporation of the mega black hole and later a higher Hubble parameter is noticed due to the evaporation of a giant black hole. The Hubble parameter of

H_{0} = 74.03 \frac{K m / s}{M p c}

would have its origin in a previous black hole with a Schwarzschild radius

R_{S G} = 0.75 \times 10^{26}

4. Dark Matter

When the mega black hole in the predecessor universe was evaporating and shrinking its Schwarzschild radius decreased. That means due to equation 7 the reduced speed of light grew. As already specified closer to the Planck length the reduced speed of light was to high to realize a stable energy density in the scalar field and the photons with effective mass had properties like the postulated dark photon. In [14] a standard deviation of

6.5 σ

is found for dark photons with typical energies of

E_{D P} = m_{P} C^{2} = 5

GeV. This leads to a reduced speed of light of

C_{D P} = 0.2

m/s and to a Schwarzschild radius of

R_{S D P} = 1.8 \times 10^{- 17}

m. That means that the black hole created dark photons with energies of around 5 GeV when the black hole in the predecessor universe had a size on the sub femtometer scale. After the repelling these photons act as dark matter. It is important to say that this model includes a whole range of different energies for the dark photons. The Big Bounce produces dark photons when the typical reduced velocity of

m_{e f f}

is too high. We can estimate

R_{S D P}

for this. Since the change in energy over time for black holes [15] is

\dot{E} = \frac{ℏ c^{6}}{15360 π G^{2} M^{2}}

(29)

and

M = \frac{c^{2} R_{S}}{2 G}

, this leads to

\dot{ρ} = \dot{E} / V = \frac{3 ℏ c^{2}}{15360 π^{2} R_{S}^{5}} \approx 1.86 \times 10^{- 22} \frac{J m^{2}}{s} \frac{1}{R_{S D P}^{5}}

(30)

For

R_{S D P} \approx 3.2

mm the change in energy density over time is equal to the energy density and with smaller radius the change grows further with

1 / R^{5}

. That means during the Big Bounce dark matter was produced when the radius during the shrinking process fell below the mm-range. Before that the change was small enough that dark energy was produced.

5. Alternative to Inflation Theory

Inflation theory solves these main problems: the flatness problem, the horizon problem and the problem of density fluctuations. In the following we show how our model can solve these problems.

Flatness Problem: We start with the following equation from [16]:

\dot{ϵ} = (1 + ϵ) ϵ \frac{\dot{a}}{a} (1 + 3 ω) + 2 \frac{\dot{c}}{c} ϵ

(31)

Here

ϵ = Ω - 1

with

Ω = ρ / ρ_{c}

and

ω

is the energy density. As we see in Appendix B: when the Planck length is reached, the speed of light grows above the value c. That means when there is a repelling effect (see Appendix B) a sharp phase transition would happen back to the value c and thus

(\frac{\dot{c}}{c}) < 0

. Then

ϵ

strives towards 0 and the flatness problem is solved because then

Ω

strives towards 1 and the density strives towards the critical density.

Horizon problem: Since the scalar field, which was generated during the collapse of the predecessor universe, acts as a background field in the new universe we live in, there was already a structure when the big bang began. These background photons with their effective mass have their temperature imprinted for such a long time (see Appendix B) that the field is completely homogeneous.

Problem of density fluctuations: Inflation theory solves this problem by quantum fluctuations which are inflated during the inflation phase. In our model this effect can be the same. The scalar field acts as a vacuum field and quantum fluctuations which "borrow" their energy from this scalar field can happen the same way.

6. Entangled Vacuum

Different experiments like [17,18], which simulate a black hole, show that the radiation from these simulated black holes is entangled. When we speculate that the massive photons with their origin in the black holes in our model are entangled too, this would mean that the whole scalar field that runs through our observable universe is entangled. That means we have the basic framework for "the spooky action at a distance" (Einstein).

7. Entropy

For the model of the oscillating universe the entropy has to be at a low value every time before the Big Bounce happens. That means first we have to know how the entropy changes when the black mega hole shrinks and the scalar field remains.

We start with equation 11 for the energy of a massive photon in the black hole:

E = \frac{m_{P} L_{P} c^{2}}{R_{S}} = \frac{c ℏ}{R_{S}}

(32)

Here

m_{P} L_{P} = ℏ / c

is used. After expanding the equation by

4 π R_{S}

, we have en expression that includes the surface of the event horizon

A = 4 π R_{S}^{2}

E = \frac{4 π R_{S} c ℏ}{A}

(33)

With

E = m_{P} c^{2}

, where

m_{P}

is the Planck mass, and equation 6,the following is obtained:

m_{e f f} = \frac{8 π ℏ G M}{A c^{3}}

(34)

When the black hole is completely radiated by Hawking radiation, all the massive photons which remain should sum up to the mass M of the black hole again and thus

M = N m_{P}

. Here N is a natural number. Then

N = \frac{A c^{3}}{8 π G ℏ} = \frac{A c^{3}}{G' ℏ}

(35)

Then the entropy S is the following:

S = N k_{B} l n (f) = \frac{A c^{3} k_{B}}{G' ℏ} l n (f)

(36)

This entropy is the Beckenstein-Hawking entropy

S_{B H} = \frac{A c^{3} k_{B}}{4 ℏ G'}

when

f \approx 1.28

. This can be explained by the mixture of degrees of freedom. Since the massive photons have

f = 1

(see Appendix B), but their is also massive baryonic matter in M, that has

f = 3

and both should be saved with their share in the black hole,

f \approx 1.28

is a result of the mixture, that indicates that more massive photons are saved than baryonic matter.

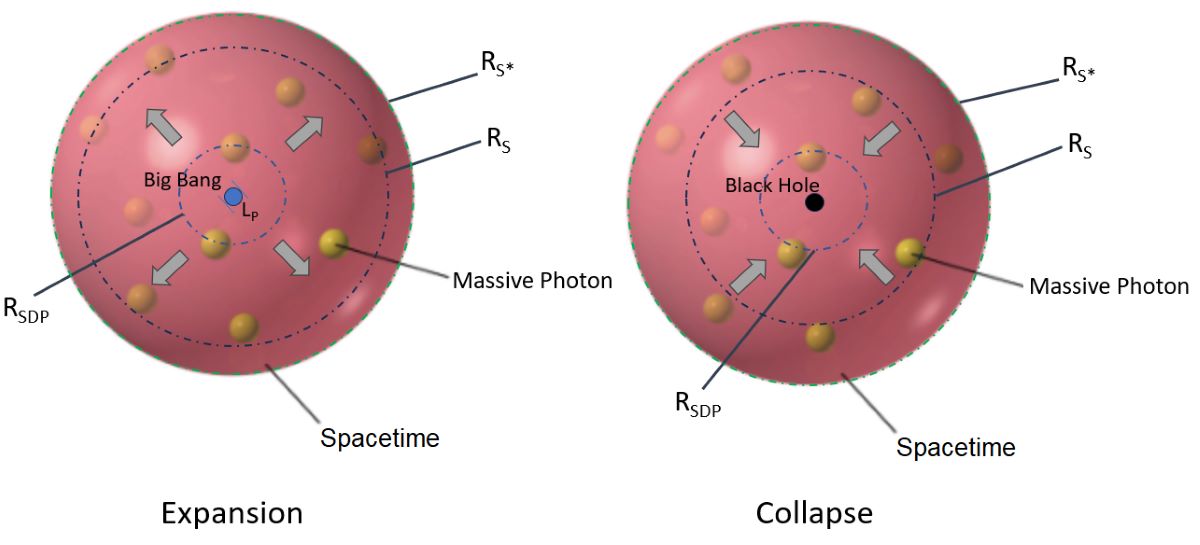
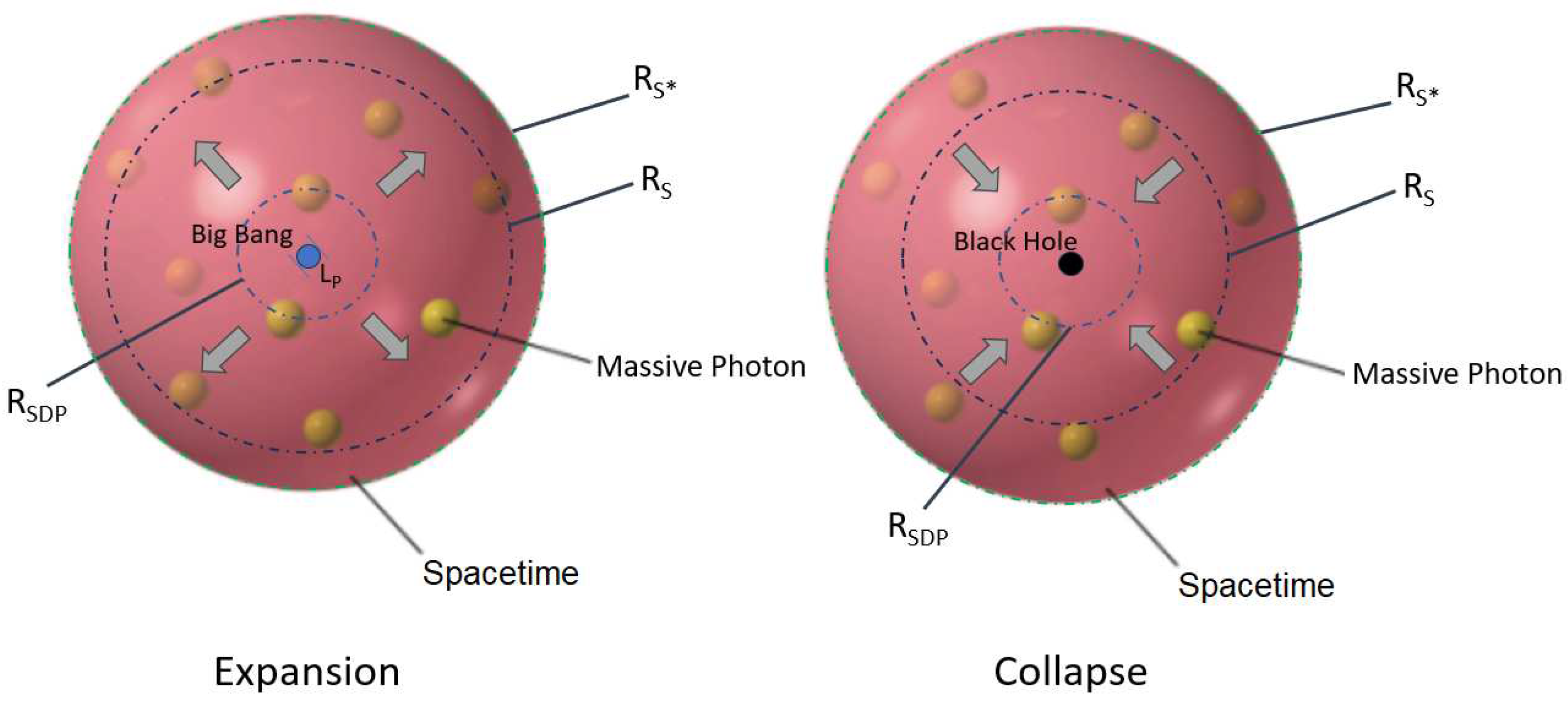
The whole model scenario can be seen in Figure 2. When the universe expands, it is embedded in a dark photon environment until it reaches

R_{S D P}

. Then the expanding universe is embedded in a scalar field of massive photons with an effect like the cosmological constant. During the expansion the entropy is growing. Today our universe has the size

R_{S}

. When it will reach

R_{S}^{*}

M_{U}

, it will shrink by Hawking radiation, generating a new scalar field and the entropy stays constant. When the shrinking black hole reaches the Planck length the pressure gets that high (see Appendix B), that this results in a Big Bounce and the next oscillation starts. In our model there is a reset of entropy during this process, which is shown in the following. We start with the Beckenstein Hawking entropy S

S = \frac{k_{B} A}{4 L_{P}^{2}}

(37)

The surface depends on the mass M of the black hole

A = 16 π {(\frac{G M}{c^{2}})}^{2} = 16 π {(\frac{G}{c^{2}} \frac{E_{P}}{C^{2}})}^{2}

(38)

Here equation 8 is used. Then the entropy is the following:

S = \frac{k_{B}}{L_{P}^{2}} 4 π {(\frac{G}{c^{2}} \frac{E_{P}}{C^{2}})}^{2}

(39)

When the black hole reaches the Planck length the reduced speed C reaches c and

\frac{E_{P}}{C^{2}} \to \frac{E_{P}}{c^{2}} = m_{P}

. Thus

S = \frac{k_{B}}{L_{P}^{2}} 4 π {(\frac{G}{c^{2}} m_{P})}^{2} = 1.73 \times 10^{- 22} J / K

(40)

This shows that the entropy is reset to a quite low value and the next cycle starts.

Conclusion

We show a mostly phenomenological approach for the solution of the information paradox in black holes. Since the Lorentz invariance does not hold true for strong gravitational curved backgrounds, we assume a variable speed of light in black holes. This variable speed explains the Heisenberg uncertainty relation close to the Planck length and below. Then the information of matter and radiation is saved in the black holes with typical (Compton) wavelengths in the range of the size of the black hole for matter or radiation. The characteristics of radiation in the black hole are quite similar to dark energy, which could explain the cosmological coupling and the mass growth of black holes similar to the cosmological growth due to the Hubble constant. When black holes decay by Hawking radiation the slow photons are left as remnants. They put up a scalar field for the next universal cycle. That means in every oscillating universe cycle this scalar field is the reason for a later expansion phase and has the same characteristics like the cosmological constant. When the radius of the former mega black hole is exceeded, the scalar field changes its properties to a gravitational field and the universe starts to collapse again. Shortly before the remnant black hole falls below the Planck length a repelling effect with a speed of light much higher than c leads to a new Big Bounce with a phase transition back to c. This change in the speed can explain the flatness problem and no additional field for inflation is necessary.

Appendix A

Average photon velocity in sphere with shrinking radius from

R_{S}

2 L_{P}

\bar{c (R_{S})} = \frac{1}{R_{S} - 2 L_{P}} \int_{2 L_{P}}^{R_{S}} c_{0} \sqrt{\frac{2 L_{P}}{R_{S}}} d R_{S} \approx \frac{2 c_{0} \sqrt{2 L_{P}}}{R_{S}} (\sqrt{R_{S}} - \sqrt{2 L_{P}})

(A1)

For a Schwarzschild blackhole (no electric charge, no angular momentum) with a Schwarzschild radius of

R_{M W} = 1.2 \times 10^{10}

m, which is the Schwarschild radius of SgrA* in our milky way, the average photon velocity is

\bar{c (R_{M W})} \approx 3 \times 10^{- 14}

m/s.

For the sphere with the radius

R_{S}^{*} = 1.65 \times 10^{26}

m in Section 1 the average photon velocity is

c (R_{S}) = 1.32 \times 10^{- 22}

m/s.

Appendix B

By assuming a scalar field with the Planck mass we can derive the temperature of massive photons in the black hole. We start with the kinetic energy of one photon with effective mass

m_{e f f}

. Since these photons are massive, they can have a temperature.

\frac{1}{2} m_{e f f} C^{2} = \frac{1}{2} m_{e f f} c^{2} \frac{2 L_{P}}{R_{S}} = \frac{f}{2} k_{B} T

(A2)

Here f is the number of degrees of freedom. That means the temperature is

T = \frac{2 m_{e f f} c^{2} L_{P}}{f R_{S} k_{B}}

(A3)

By using

R_{S} = \frac{2 G' M}{c^{2}}

we get

T = \frac{m_{e f f} c^{4} L_{P}}{f k_{B} G' M}

(A4)

By using the expression of

m_{e f f} = \frac{1}{2} m_{P}

(equation 14) we end up with

T = \frac{ℏ c^{3}}{2 k_{B} f G' M} = \frac{ℏ c^{3}}{2 k_{B} f 8 π G M}

(A5)

This temperature is the Hawking temperature when

f = 1 / 2

. For a photon gas

f = 2

applies and for massive spin-1-particles

f = 3

. We suppose that since the massive photons are restricted in their movements due to the black hole, the degrees of freedom are reduced.

When the black hole shrinks and the Schwarzschild radius is close to the Planck length, the reduced speed is similar to the speed c (see equation 7). Then we can assume the pressure of a black-body photon gas for the massive photons:

p = \frac{π^{2} k_{B}^{4}}{45 c^{3} ℏ^{3}} T^{4}

(A6)

The temperature is given in equation A3. Below the Planck length the decreasing Schwarzschild radius leads to a massive temperature increase

\propto \frac{1}{R_{S}}

and a pressure increase

\propto T^{4}

. That means the pressure acts as

p \propto \frac{1}{R_{S}^{4}}

(A7)

For

R_{S} = L_{P}

this is already the Planck pressure and with decreasing

R_{S}

the pressure gets that high that it could lead to the next Big Bang in the Big Bounce scenario. Then the Planck length is not the absolute minimum of length but due to the dependency in equation A7 the minimum length cannot be far below the Planck length. References

References

Guth, A. H. and Steinhardt, P. J. ( 250(5), 116–129.
Earman, J. and Mosterin, J. ( 66(1), 1–49.
Brizuela, D., Marugán, G. A. M. and Pawłowski, T. (2010). Big bounce and inhomogeneities. Classical and Quantum Gravity, 27(5), 052001.
Rovelli, C. (2011). Loop quantum gravity: the first 25 years. Classical and Quantum Gravity, 28(15), 153002.
Caldwell, R.R. et al, Phys. Rev. Lett, 80, 1582-1585, (1998).
Chapline, G., "Dark Energy Stars". Proceedings of the Texas Symposium on Relativistic Astrophysics: 101. arXiv:astro-ph/0503200.
Farrah, D. et al 2023 ApJ 943 133.
Farrah, D. et al 2023 ApJL 944 L31.
Cadoni, M. et al. Cosmological coupling of nonsingular black holes, [arXiv:2306.11588 [gr-qc]]. arXiv:2306.11588 [gr-qc]].
Hawking, S.W. Particle creation by black holes. Commun.Math. Phys. 43, 199–220 (1975).
Planck Collaboration, N. Aghanim,et al., (2018) [arXiv:1807.06209[hep-ph]]. arXiv:1807.06209[hep-ph]].
A. G. Riess,et al., (2019) [arXiv:1903.07603[hep-ph]]. arXiv:1903.07603[hep-ph]].
Gan, Q. et al. Photon Ring and Observational Appearance of a Hairy Black Hole, [arXiv:2105.11770 [gr-qc]]. arXiv:2105.11770 [gr-qc]].
Hunt-Smith, N.T. et al. Global QCD Analysis and Dark Photons, [arXiv:2302.11126]; et al. arXiv:2302.11126].
M. Lopresto, The Physics Teacher, 41, 299-301 (2003).
J. Magueijo, Reports on Progress in Physics. 66. 10.1088/0034-4885/66/11/R04 (2003).
J. Steinhauer, nature physics, 12, 959-965 (2016).
Shi, J.H., Yang, RQ., Xiang, Z. et al. Quantum simulation of Hawking radiation and curved space time with a superconducting on-chip black hole. Nat Commun 14 , 3263 (2023).

Figure 1. The reduced speed of light in black holes with different

R_{S}

Figure 1. The reduced speed of light in black holes with different

R_{S}

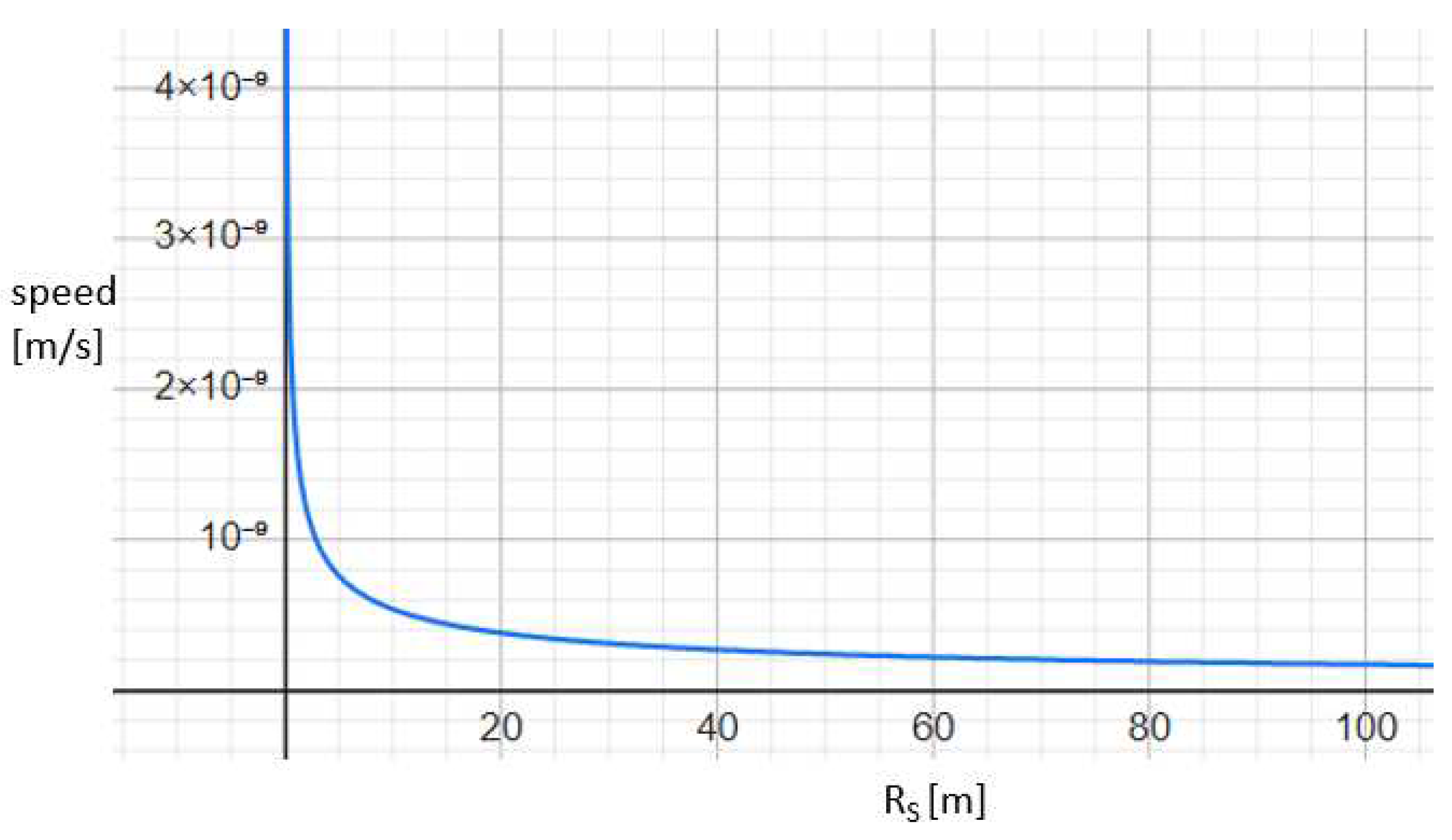
Figure 2. The Oscillating Universe with its expansion (left) and collapse (right) as an artistic representation. When the universe expands, it is embedded in a dark photon environment until it reaches

R_{S D P}

. Then the expanding universe is embedded in a scalar field of massive photons with an effect like the cosmological constant. Today our universe has the size

R_{S}

. When it will reach

R_{S}^{*}

, the background scalar field will be "washed out" more and more and due to the Friedmann equation (see equation 17) the scalar field will act as a gravitational field and the universe will collapse. The massive photons in the scalar field will be absorbed by a mega black hole, which will shrink by Hawking radiation, generating a new scalar field. When the shrinking black hole reaches the Planck length the pressure gets that high (see Appendix B), that this results in a Big Bounce and the next oscillation starts.

R_{S D P}

. Then the expanding universe is embedded in a scalar field of massive photons with an effect like the cosmological constant. Today our universe has the size

R_{S}

. When it will reach

R_{S}^{*}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Oscillating Universe with a Quantized Black Hole

Abstract

Introduction

1. The Reduced Speed of Light and the Scalar Field in Black Holes

2. Post-Schwarzschild-Metric

3. The Hubble Tension

4. Dark Matter

5. Alternative to Inflation Theory

6. Entangled Vacuum

7. Entropy

Conclusion

Appendix A

Appendix B

References

MDPI Initiatives

Important Links

Subscribe