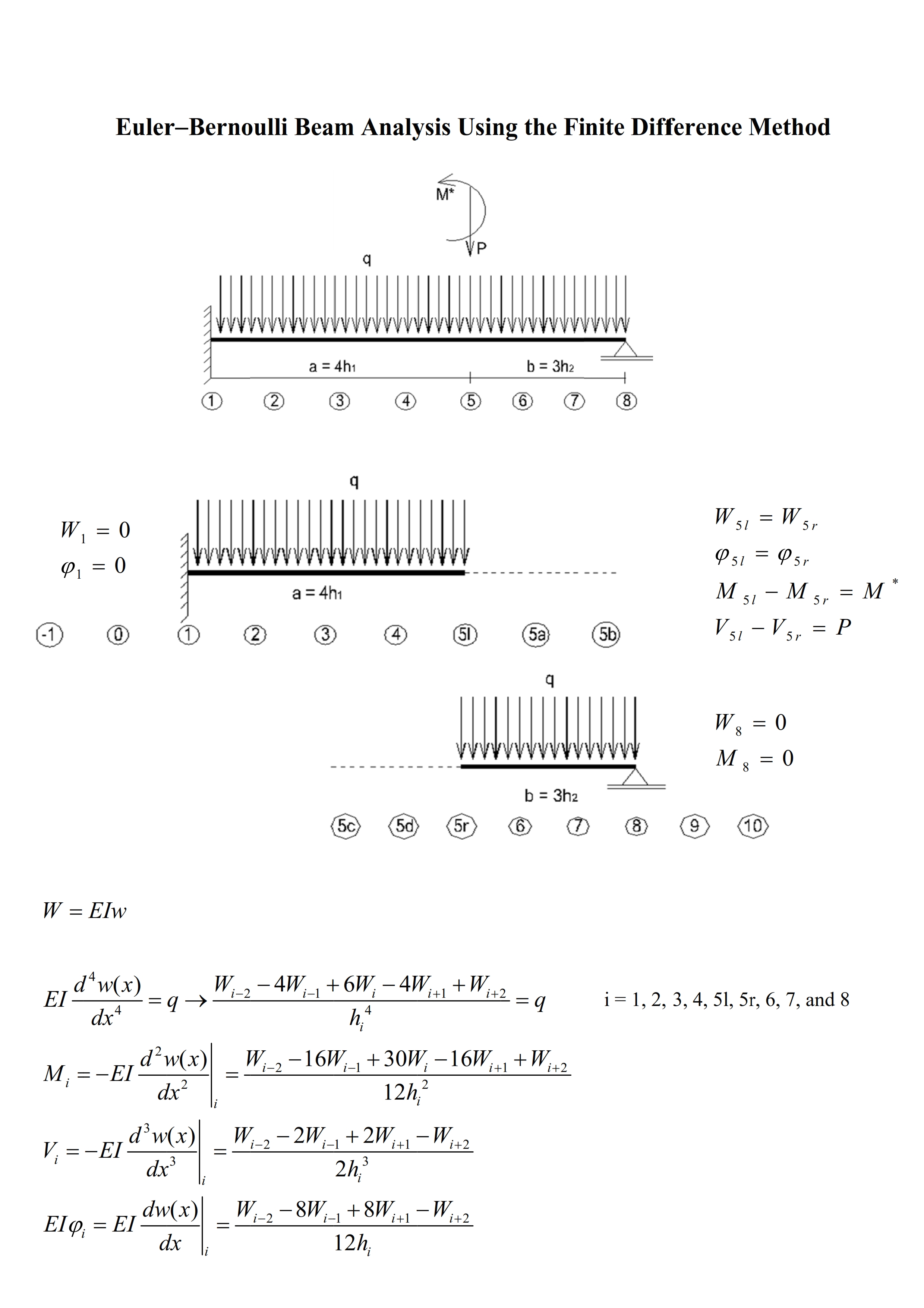
This paper presents an approach to the Euler-Bernoulli beam theory (EBBT) using the finite difference method (FDM). The EBBT covers the case of small deflections, and shear deformations are not considered. The FDM is an approximate method for solving problems described with differential equations. The FDM does not involve solving differential equations; equations are formulated with values at selected points of the structure. Generally, the finite difference approximations are derived based on fourth-order polynomial hypothesis (FOPH) and second-order polynomial hypothesis (SOPH) for the deflection curve; the FOPH is made for the fourth and third derivative of the deflection curve while the SOPH is made for its second and first derivative. In addition, the boundary conditions and not the governing equations are applied at the beam’s ends. In this paper, the FOPH was made for all of the derivatives of the deflection curve, and additional points were introduced at the beam’s ends and positions of discontinuity (concentrated loads or moments, supports, hinges, springs, etc.). The introduction of additional points allowed us to apply the governing equations at the beam’s ends and to satisfy the boundary and continuity conditions. Moreover, grid points with variable spacing were also considered, the grid being uniform within beam segments. First-order analysis, second-order analysis, and vibration analysis of structures were conducted with this model. Furthermore, tapered beams were analyzed (element stiffness matrix, second-order analysis). Finally, a direct time integration method (DTIM) was presented. The FDM-based DTIM enabled the analysis of forced vibration of structures, with damping taken into account. The results obtained in this paper showed good agreement with those of other studies, and the accuracy was increased through a grid refinement. Especially in the first-order analysis of uniform beams, the results were exact for uniformly distributed and concentrated loads regardless of the grid. Further research will be needed to investigate polynomial refinements (higher-order polynomials such as fifth-order, sixth-order…) of the deflection curve; the polynomial refinements aimed to increase the accuracy, whereby non-centered finite difference approximations at beam’s ends and positions of discontinuity would be used.