Introduction

Methods

Results and Discussion

1.1. Parallelism of Frames and the Interpretation of Einstein’s Principle

To begin with, we ought to reckon that physical laws tend to find analogies in areas other than their original area of enunciation, as reflected by the set of isomorphic laws discussed below. This is potentially the result of the physical universe functioning according to one and a single blueprint which takes on varying hues as we move from one area of scientific investigation to another. The applicability of physical laws in areas other than their original area of enunciation is encapsulated in Einstein's special principle of relativity, which states:

“Physical laws remain the same in all inertial reference frames,” [7]

which, diluted, means:

“If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K' moving in uniform translation relatively to K.” [8,9]

(Emphasis original)

The special principle of relativity has so far been understood as referring only to inertial reference frames while it, in fact, finds applications in more than just inertial reference frames. However, as we acknowledge that the ‘reference frames’ Einstein referred to are not just physical or inertial frames of reference but include multiple types of frames, so do we have to reckon that ‘translation,’ as he put it, does not mean just literal physical translation. Indeed, translation here refers to any existing parallelism between the multiple reference frames in presence.

As an example, Darcy's Law in fluid dynamics holds in heat conduction by having analogies with Fourier's Law of Heat Conduction. Then, Fourier's Law holds in electrical science by having analogies with Ohm's Law of Electrical Resistance. Then, Ohm's Law holds in diffusion theory by having analogies with Fick's Law of Diffusion; so forth. In other words, although Einstein's special principle of relativity has traditionally been understood to describe only space-time reference frames, it does describe more than just space-time reference frames. Beyond space-time frames, the types of frames the principle refers to also include what can be called ‘experimental reference frames.’ And the ‘uniform translation’ condition stated in the principle, in addition to referring to physical translation, also means the replication of all the defining experimental characteristics of one experimental reference frame in another experimental reference frame. This gives rise to a form of parallelism between the experimental reference frames in presence. Then, this parallelism subsequently allows the laws of one experimental reference frame to hold true and, therefore, stay applicable, sometimes upon slight adjustments of coefficients, in another experimental reference frame parallel to the former. This causes Einstein's special principle of relativity to remain valid beyond actual physical translation and beyond space-time reference frames and to cover other types of frames among which experimental reference frames.

As stated, uniform translation in experimental reference frames takes the form of replication of all of the defining characteristics of one experimental reference frame into another experimental reference frame. Translation means that there occurs a replication of the defining experimental features of one reference frame into the second reference frame, and then the translation is uniform because the replication involves all of the defining features of the first reference frame.

As an illustration, let us consider Darcy's Law which describes groundwater flow in a soil medium and Ohm's Law which describes the flow of electrons in an electrical wire. We know that the mathematical expressions of those two laws (as in the case of Fourier's, Hopkinson's, and Fick's Laws) show analogies or resemblance, as can be seen in their expressions below. However, beyond the analogies observable in their mathematical expressions, the construct or design of each experimental frame does show analogies with the construct or design of the other experimental frame, as explained below.

Darcy's Law

Darcy's Law [10] is a relationship between the discharge rate of water through a porous medium and the hydraulic conductivity of the said medium, the cross-sectional area of the flow, and the pressure drop between point a and point b over a given length of the medium [11]:

Q = – KA(P_b – P_a)/L

where:

Q = discharge rate

K = hydraulic conductivity

A = cross-sectional area

P_b – P_a = pressure drop between point a and point b (expressed in height or depth of water)

L = length traveled

The flux, q, which is discharge per unit area (m/s), is obtained by dividing Q by the cross-sectional area:

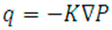
where ∇P is the pressure gradient vector.

Ohm's Law

Ohm's Law [12] relates the current between two points of an electrical conductor to the potential difference across those two points. It states that the current is directly proportional to the potential difference across the two points and inversely proportional to the resistance between them:

I = V/R

where:

I = current

V = voltage or potential difference across the conductor

R = resistance of the conductor

NB: The negative sign is absent but is incorporated into the direction of the potential difference i.e., the potential difference between two points a and b is such that (V_b – V_a) = – (V_a – V_b).

Hopkinson's Law

Hopkinson's Law [13] relates the magnetomotive force across a magnetic element to the magnetic flux through the element by means of the magnetic reluctance of that element:

where:

Ø = magnetic flux

F = magnetomotive force across the magnetic element

R_m = magnetic reluctance (or resistance) of the element

Fourier's Law

In Fourier's Law [14], the local heat flux density is equal to the product of thermal conductivity and the negative local temperature gradient, – ∇T:

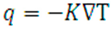
where:

q = local heat flux

K = conductivity of the material

∇T = temperature gradient

Fick's Law

In Fick's First Law [15], the diffusion flux is related to the concentration, with a magnitude proportional to the concentration gradient:

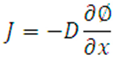
where:

J = diffusion flux

D = diffusion coefficient

Ø (for ideal mixtures) = concentration

In two or more dimensions, J becomes:

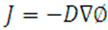
As can be seen, the five laws, through their respective equations, are isomorphic / analogous with each other.

Let us now zoom into just Darcy's and Ohm's Laws. Here, we are in the presence of two experimental frames of reference: water and soil in one, and then electrons and wire in the other. Because we are in the presence of two reference frames, Einstein's special principle of relativity will apply if the dual conditions of uniformity of translation are met. In fact, the first condition, that of the translation (or replication of the key features) of one reference frame into the other reference frame, is met: here, flowing water in the first reference frame is replicated in the second reference frame as flowing electrons, soil medium in the first is replicated in the second as wire medium, soil particles in the first are replicated in the second as atom particles, soil pores in the first are replicated in the second as space within atom lattices, and resistance offered by the soil medium to the flow of water in the first is replicated in the second as resistance offered by the wire medium to the flow of electrons. So, the first condition (translation) is met because we are in the presence of two experimental reference frames in which there occurs a replication of the defining features of one into the other.

However, the second condition, that of uniformity of the translation, is also met because the translation involves all of the defining features of any one reference frame into the other reference frame—meaning that if the replication or translation had been partial and had involved just a few of the defining features [for example, if there is replication of the soil particles of the first reference frame as atom particles in the second reference frame but nothing is flowing in the second reference frame], then there would be translation but then that translation would not have been uniform and, therefore, Einstein's principle would not and cannot apply. However, in this case, all of the defining characteristics of one reference frame are translated (replicated) into the second reference frame. Therefore, both conditions (uniformity of translation) are met. Both conditions being met, the special principle of relativity applies and the same law ‘holds good,’ as Einstein put it, in all of those reference frames—barring an adjustment of coefficients where necessary. In fact, the English phrase ‘holds good’ as used in the enunciation of Einstein’s principle [7,8,9] does mean that the law in question might not remain exactly the same in the second reference frame as it is in the first and that some adjustments, as in the case of coefficients, may be necessary.

The foregoing analysis between Darcy's Law and Ohm's Law applies equally to the other laws in the set listed above. As another illustration, let us compare Ohm's Law and Fourier's Law:

Observations of an analogy between Ohm's Law and Fourier's Law have also been reported by other observers, as follows:

“Ohm's principle predicts the flow of electrical charge (i.e. current) in electrical conductors when subjected to the influence of voltage differences. Jean-Baptiste-Joseph Fourier's principle predicts the flow of heat in heat conductors when subjected to the influence of temperature differences. The same equation describes both phenomena, the equation's variables taking on different meanings in the two cases. Specifically, solving a heat conduction (Fourier) problem with temperature (the driving “force”) and flux of heat (the rate of flow of the driven “quantity”, i.e. heat energy) variables also solves an analogous electrical conduction (Ohm) problem having electrical potential (the driving “force”) and electric current (the rate of flow of the driven “quantity”, i.e. charge) variables.” [16] —Emphasis added.

Furthermore, the following additional observation is also made:

“By comparing the steady state heat flow equation with Ohm's Law for current flow through a resistor, we see that they have similar forms:

“We can therefore draw the following analogies:

Heat Flow, Q	↔	[Electron flow =] Current, I
Temperature Difference, T1 - T2	↔	Voltage Difference, V1 - V2
Thermal Resistance, RT = ∆x/K*A	↔	Electrical Resistance, RE = ∆V/I

“The electric-to-heat conduction analogy allows one to apply laws from circuit theory to solve more complicated conduction problems, such as heat flow through conducting layers attached in parallel or series.” [17].

Similar analogies can be observed between Fick's Law and any of the remaining laws, and, generally, between any two of the five laws. Furthermore, similar analogies exist between other scientific laws whose experimental reference frames share design analogies. Essentially, it is one fundamental expression of a law which ‘mutates’ as it gets displaced or translated, taking on various forms from one experimental reference frame to another parallel experimental reference frame.

This principle is further illustrated in physics with the classical mechanics and quantum mechanics duo. Here, the Hamilton–Jacobi equation is known to allow the motion of a solid particle to be represented as the motion of a wave—although a wave is not a solid particle. As such, the Hamilton–Jacobi equation establishes an analogy between the propagation of light (which is a wave) and the motion of a particle (which is solid) [18]. Here as well, we are in the presence of two phases: a dense, solid phase and then a subtle, ethereal phase. Those are two experimental reference frames to which the principle can apply if they are parallel with each other. Then, it can be observed that the two conditions required for the principle to apply are met: a) the reference frames are in translation one in relation to the other and b) the said translation is uniform.

There is translation because there is a replication of the features of one reference frame into the other reference frame: 1) an object is involved in each reference frame: a solid particle in one and a photon in the other, 2) travel/motion occurs in both frames, and 3) the motion occurs in 3-D in both frames. So, the defining features of each frame are replicated in the other frame, and the first condition (translation) is therefore met. However, the said translation is uniform because the replication does involves all of the defining features (all three listed) of each reference frame. As a result, the second condition (uniformity) is also met, and we therefore have a uniform translation. Consequently, the special principle of relativity applies and the same equation holds true in both the Classical Mechanics and Quantum Mechanics reference frames [19,20].

A further illustration is found in attractive/repulsive forces. Here, two types of forces are in presence: the one in Newton's Law of Universal Gravitation and the one in Coulomb's Law of Electrostatic Interaction.

Newton's Law of Universal Gravitation states: “Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them.” [21]. That means that any two bodies 1 and 2, respectively of mass M₁ and M₂, attract each other with a force F given by:

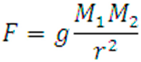
where:

g = gravitational constant

M₁ = mass of object 1

M₂ = mass of object 2

r = separation distance

On the other hand, Coulomb's Law states: “The magnitude of the electrostatics force of interaction between two point charges is directly proportional to the scalar multiplication of the magnitudes of charges and inversely proportional to the square of the distances between them.” [22]. That means that any two electrical point charges 1 and 2, respectively with charges Q₁ and Q₂, attract or repulse each other with an electrostatic force F' given by:

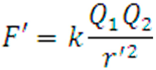
where:

k = proportionality constant

Q₁ = magnitude of point charge 1

Q₂ = magnitude of point charge 2

r' = separation distance

In those two experimental reference frames, there is evident analogy between the two equation laws. This analogy, also called parallelism between the electrostatic and gravitational fields, has also been reported by other observers [23].

Here, there is uniform translation of one experimental reference frame in relation to the other. The first condition, the translation condition, is met because there is replication of the defining characteristics of one experimental reference frame in the other experimental reference frame: 1) two objects are involved in both frames, 2) a distance separates both objects in either frame, 3) interaction is taking place between the two objects involved in either frame, and 4) force is present in both frames. As a result, the translation condition is met. But the translation is uniform because the replication involves all of the defining features (all four listed) of each reference frame. Consequently, the second condition, the uniformity condition, is also met, and there is therefore uniform translation. As a result, the special principle of relativity applies and, as can be observed, the law of each reference frame holds in the second reference frame.

In particular, the force F₁ exerted on an object of mass m in a gravitational field g is given by [24]:

while the force F₂ exerted on an electrical charge q in an electric field E is given by [25]:

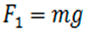
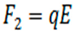
As before, there are two experimental reference frames: one characterized by a mass and the other characterized by an electrical charge. Because two frames are in presence, the principle will apply if the dual conditions of uniformity of translation are met. Indeed, there is uniform translation of one frame in relation to the other. There is translation because there is a replication of the defining characteristics of one experimental reference frame in the other experimental reference frame: 1) an object is involved in both frames, 2) the attribute of each object is involved: mass in the first and charge in the second, 3) a field is present in either frame, 4) force is exerted on each object in both frames. Therefore, the first condition (translation) is met. And the translation is uniform because the replication involves all of the defining characteristics (all four listed) of each frame. As a result, the second condition (uniformity) is also met, and we do have uniform translation. Consequently, the special principle applies and, as can be observed, the law of each reference frame holds in the other one.

Let us consider yet another illustration: Springs.

In the experimental reference frame made up of a linear spring and an applied force which compresses it, the potential energy stored in that spring is given by [26]:

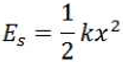
where:

E_s = energy

k = spring constant

x = linear displacement

In the experimental reference frame made up of a torsion spring and an applied force which deploys a torque twisting it, the potential energy stored in that spring is given by [27]:

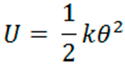
where:

U = energy

k = torsion constant

θ = angular displacement

Here again, there are two experimental reference frames: one characterized by a torsion spring and the other characterized by a linear one. Because two frames are in presence, the principle will apply if the dual conditions of uniformity of translation are met. Indeed, there is uniform translation of one frame in relation to the other. There is translation because of there is replication of the defining characteristics of one frame into the other frame: 1) a spring is involved in both reference frames, 2) energy is stored in both reference frames, and 3) displacement occurs in both reference frames: angular in one and linear in the other. Therefore, the first condition (translation) is met. However, the translation is also uniform because the replication involves all of the defining characteristics (all three listed) of each frame. As a result, the second condition (uniformity) is also met, and there occurs a uniform translation. Consequently, the special principle of relativity applies and, as is observable, the law of each reference frame holds in the other reference frame.

The isomorphism between the above laws is encapsulated in Einstein’s special principle of relativity. In fact, the special principle of relativity has already been found to be such that multiple meanings and interpretations can be derived from it for various conditions [9 and references therein]. Here, we introduce an additional interpretation of Einstein’s special principle of relativity as it specifically pertains to parallel experimental reference frames. In that regard, in the above discussed laws, one experimental reference frame is a uniform replicate of the other reference frame, however in another experimental ‘dimension.’ This phenomenon of uniform replication of features causes the laws of one experimental reference frame to stay valid in the other experimental reference frame—barring coefficients. Although the replication process takes the form of what Einstein called ‘uniform translation’ in the space-time reference frame that he investigated, ‘parallelism’ is perhaps a better terminology for experimental reference frames. The analogies observed in the series of laws discussed above (and in others not discussed here) show that the principle remains valid in experimental frames of reference, beyond the traditional space-time frames of reference. Consequently, we interpret Einstein's special principle of relativity specifically for experimental reference frames and submit the interpretation that follows:

• Ø Interpreted Einstein’s Special Principle of Relativity for Experimental Reference Frames

“Parallel experimental reference frames are governed by the same or similar laws.”

This pattern of applicability of the laws of a given experimental reference frame to other parallel reference frames is observable through the various manifestations of the physical universe. Illustrating this phenomenon, the ability of the principle to translate laws, with its associated capacity to accelerate the discovery of other laws, is manifest in the experimental reference frames made up by the solar system (Astronomy) and atoms (Atomic Physics).

Conclusion

References

1.  Hill JM and Cox BJ. Einstein's special relativity beyond the speed of light. Proc. R. Soc. A., Oct 3, 2012. [CrossRef]
2.  University of Adelaide. Extending Einstein's theory beyond light speed. Tuesday, 9 October 2012. University News and events. Online: http://www.adelaide.edu.au/news/news56901.html Accessed: November 2023.
3. Andréka H, Madarász JX, Németi I, Székely G. 2013 A note on ‘Einstein’s special relativity beyond the speed of light by James M. Hill and Barry J. Cox’. Proc R Soc A 469: 20120672. [CrossRef]
4.  Moskowitz C. Five reasons we may live in a multiverse. December 2012. Online: http://www.space.com/18811-multiple-universes-5-theories.html Accessed: November 2023.
5.  Feeney SM, et al. First observational tests of eternal inflation. Phys. Rev. Lett. 107, 071301 (2011). [CrossRef]
6. Fullybright R. The Unified Theory of Biological Resistance for Successful Antibiotic Resistance Control—with Applications in Medicine, Agriculture, and Beyond. Independently published, Feb 20, 2023; 2^nd Edition. 260 p. ISBN: 9798372146136 or 9798372146136; Online: https://www.amazon.com/dp/B0BW2CNKLZ Accessed: November 2023.
7.  Amit Goswami. The physicists' view of nature: From Newton to Einstein, Part 1. Springer New York. 2000. p 291.
8.  Einstein A, et al. (1952). The principle of relativity: a collection of original memoirs on the special and general theory of relativity. Courier Dover Publications; Mineola, NY. p. 111. ISBN 0-486-60081-5.
9.  Madaras JX, Szkely G, and Stannett M. 2017. Three Different Formalisations of Einstein’s Relativity Principle. Arxiv. https://arxiv.org/pdf/1702.08519.pdf.
10.  W. G. Gray and C. T. Miller. Examination of Darcy's Law for Flow in Porous Media with Variable Porosity. Environ. Sci. Technol., 2004, 38 (22), pp 5895–5901. [CrossRef]
11.  Hofmann JR and Hofmann PA. Darcy's Law and Structural Explanation in Hydrology, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association 1992, no. 1 (1992): 23-35. [CrossRef]
12.  Millikan AR and Bishop ES (1917). Elements of electricity: a practical discussion of the fundamental laws and phenomena of electricity and their practical applications in the business and industrial world. American Technical Society. p.54.
13.  Rowland HA. On magnetic permeability and the maximum of magnetism of iron, steel and nickel. Phil. Mag., 46 (1873) 140-159.
14.  Engineering Fundamentals (eFunda). Fourier law of Heat Conduction. eFunda, Inc. Sunnyvale, CA, USA. Online: http://www.efunda.com/formulae/heat_transfer/conduction/overview_cond.cfm Accessed: November 2023.
15.  John H Lienhard IV and John H Lienhard V. A heat transfer textbook. Third Edition. Phlogiston. Press. Cambridge. Massachusetts. Jan 2008.
16.  Wikipedia. Ohm's Law: Relation to heat conductions. Wikipedia, the free encyclopedia on-line. December 2017. Online: http://en.wikipedia.org/wiki/Ohm%27s_law Accessed: November 2023.
17.  Engineering Fundamentals (eFunda). Electrical analogy for 1-D heat conduction. eFunda, Inc. Sunnyvale, CA, USA. Online: http://www.efunda.com/formulae/heat_transfer/conduction/ee_analogy_cond.cfm Accessed: November 2023.
18.  Sivashinsky GI. Wave-Particle Duality and the Hamilton-Jacobi Equation. arXiv:0912.5156v1. Online: https://arxiv.org/pdf/0912.5156.pdf Accessed: November 2023.
19.  Goldstein H, Charles PP, John LS. (2001). Classical Mechanics. Addison Wesley, 3^rd edition. Upper Saddle River, NJ.
20.  Sakurai JJ (1985). Modern quantum mechanics. Benjamin/Cummings Publishing. San Francisco.
21.  Proposition 75, Theorem 35: p.956 – I. Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I. Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 // ISBN 0-520-08817-4.
22.  Nave R. Coulomb's Law: Like charges repel, unlike charges attract. Department of Physics and Astronomy. Georgia State University. 2010. Online: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elefor.html#c1 Accessed: November 2023.
23. Wikipedia. Electric Fields: Parallelism between electrostatic and gravitational fields. Wikipedia, the Free Encyclopedia. December 2017. Online: http://en.wikipedia.org/wiki/Electric_field Accessed: November 2023.
24. Barry N. Taylor and Ambler Thompson, ed. (2008). The international system of units (SI). NIST Special Publication 330 (2008 ed.). National Institute of Standards and Technology, US Dept of Commerce. NIST Special Publication 330, 2008 Edition. Online with the WayBack Machine Internet Archive: https://web.archive.org/web/20190802103224/https://www.nist.gov/sites/default/files/documents/2016/12/07/sp330.pdf Accessed: November 2023.
25.  Nave R. Electric field. Georgia State University. 2012. Online: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elefie.html Accessed: November 2023.
26.  Nave R. Spring potential energy. Georgia State University. 2012. Online: http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html Accessed: November 2023.
27.  Chakarov D, Tsveov M, Veneva I, Mitrouchev P. Adjustable Compliance Joint with Torsion Spring for Human Centred Robots. International Journal of Advanced Robotic Systems. Volume: 12 issue: 12. [CrossRef]
28.  Russell JL. Kepler's Laws of Planetary Motion: 1609-1666. The British Journal for the History of Science. Vol. 2, No. 1. (Jun., 1964), pp. 1-24.
29.  Papadatos K. The equations of planetary motion and their solution. Online: https://www.gsjournal.net/Science-Journals/Research%20Papers-Astrophysics/Download/3763 Accessed: November 2023.
30.  Barnes EJ. Shape of lunar orbit. Institute for Astronomy (IfA), University of Hawaii. April 2003. Online: http://www.ifa.hawaii.edu/~barnes/ASTR110L_S03/lunarorbit.html Accessed: November 2023.
31. The Editors of Encyclopædia Britannica. Rutherford atomic model. Encyclopædia Britannica, Sept, 15, 2023; Online: http://www.britannica.com/EBchecked/topic/514258/Rutherford-atomic-model Accessed: November 2023.
32. The Editors of Encyclopædia Britannica. Bohr atomic model. Encyclopædia Britannica? Oct 16, 2023: Online: http://www.britannica.com/EBchecked/topic/71700/Bohr-atomic-model Accessed: November 2023.
33. Heath JE. Jim Heath's Starry Site—Newton's Version of Kepler's Third Law. Austin Community College. Austin, Texas. 2018. Online: http://www.austincc.edu/jheath/Solar/Hand/NVK3L/nvk3l.htm Accessed: November 2023.
34. Bainbridge K. The masses of atoms and the structure of atomic nuclei. Journal of the Franklin Institute. Volume 215, Issue 5, May 1933, Pages 509-534. [CrossRef]
35. Peter J. Vickers. Bohr’s Theory of the Atom: Content, Closure and Consistency. Online: http://philsci-archive.pitt.edu/4005/1/Bohr_April_2008.pdf Accessed: November 2023.
36. Bartelborth, T. (1989a): ‘Is Bohr’s Model of the Atom Inconsistent?’, in P. Weingartner and G. Schurz (eds.), Philosophy of the Natural Sciences, Proceedings of the 13th International Wittgenstein Symposium, HPT, pp. 220-223.
37. Cho A. Focus: A tiny solar system after all. Phys. Rev. Focus. 13, 15 (April 7, 2004). Online: http://physics.aps.org/story/v13/st15 Accessed: November 2023. [CrossRef]
38. Maeda H and Gallagher TF. Nondispersing wave packets. Phys. Rev. Lett. 2004;92(13). [CrossRef]
39. Pillai SO. Solid state physics. Revised sixth edition. New Age Science. Tunbridge Wells, UK. 2009. 832 pp.
40.  Britton J. Occurrence of the conics. Camosun College, British Columbia, CA, March 2018. Online with the WayBack Machine Archive: https://web.archive.org/web/20180315015653/http://www.uhigh.ilstu.edu/math/thompson/Precalc/conics/Occurrence%20of%20the%20Conics.htm Accessed: November 2023.
41. Fullybright R. Characterization of Biological Resistance and Successful Drug Resistance Control in Medicine. Pathogens 2019, 8, 73. [CrossRef]
42.  Ohm GS (1827) Die galvanische Kette, mathematisch bearbeitet. (The galvanic cell: processed mathematically). Berlin: T. H. Riemann.
43.  Kamkarian P and Hexmoor H. Crowd evacuation for indoor public spaces using Coulomb’s Law. Advances in Artificial Intelligence (2012), Article ID 340615. [CrossRef]