Space Theory

Preprint

Article

Space Theory

Altmetrics

Downloads

818

Views

987

Comments

S. Chen^*

This version is not peer-reviewed

Submitted:

09 July 2023

Posted:

10 July 2023

Read the latest preprint version here

Alerts

Abstract

The author introduces a novel theoretical framework that suggests matter and energy are both converted from curved space. In Space Theory, gravitation is generated by the flow of space, instead of being transmitted by the graviton as in String Theory. This theory also suggests that Newton's gravitational constant, denoted as G, may not be truly constant but could vary over time. The equivalent equation of space is S=Ec²=mc⁴, and the gravitation of hollow sphere space is S_μν=4πGm=(4/3)π((r+a)³-r³). The Space Theory also predicts that the surface gravitational acceleration of the neutron star Crab Pulsar (PSR B0531+21) is approximately 8.21924883×10⁶ m/s².

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

When a star dies, it undergoes a contraction and blows off its outer envelope, forming a planetary nebula [6,7]. If the star collapses to within its Schwarzschild radius, it forms a black hole [8]. Newton's law of universal gravitation [1] provides the equation for this force, which states that:

Figure 1. A star forms a black hole.

Before the star collapses, the gravitational force between the planet and the star is represented by

F_{1}

. After the collapse, the gravitational force between the planet and the black hole is represented by

F_{2}

. In these equations,

m_{1}

represents the mass of the star,

m_{2}

represents the mass of the black hole,

m_{3}

represents the mass of the planet,

r

represents the distance between their centers of mass, and

G

is the gravitational constant. The gravitational force of a black hole is extremely strong and nothing, not even light, can escape it [9]. Therefore,

F_{2}

is greater than

F_{1}

. As the star collapses into a black hole, it blows off its outer envelope and loses mass [10]. Assuming the star loses

0.2 %

of its mass during this process, the mass of the black hole can be represented as

99.8 %

m_{1}

. This can be rewritten as:

F_{1} = G \frac{m_{1} m_{3}}{r^{2}} < F_{2} = G \frac{0.998 m_{1} m_{3}}{r^{2}} .

When the common parameters are removed, the equation can be simplified to:

1 < 0.998 .

How is it even possible that

1

is less than

0.998

? As the mass decreases from

m_{1}

m_{2}

and the distance

r

between the objects remains unchanged, it suggests that the gravitational constant

G

has increased. In Einstein's theory of relativity, matter curves spacetime, and the Einstein field equations [4] can be expressed in the following form:

G_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν} .

In this equation,

G_{μ ν}

is the Einstein tensor and

G

is the gravitational constant. However, if the gravitational constant

G

is constantly changing, it raises the question of whether Einstein's theory is still accurate.

2. Model

What if the situation were reversed, and both matter and energy were converted from curved space? Matter can release energy through annihilation, fission, and fusion [2,3], as matter and energy are different forms of the same thing. Therefore, matter curves spacetime because it is converted from curved space, and the flow of space released by matter creates gravitational force. The greater the amount of space released, the stronger the gravitational force generated. If one object releases much more space than another object, the flow of space will narrow the distance between the two objects. It is the space that moves, not the objects.

Figure 2. Gravitation.

When two galaxies are very far apart, the space they release accumulates in the middle, and this expands their distance. Therefore, the expansion of the universe and the phenomenon of redshift [11] are caused by the increase in space.

Figure 3. Expansion of the universe.

Thus, space curves in one dimension, converting matter and energy.

Figure 4. Curved space.

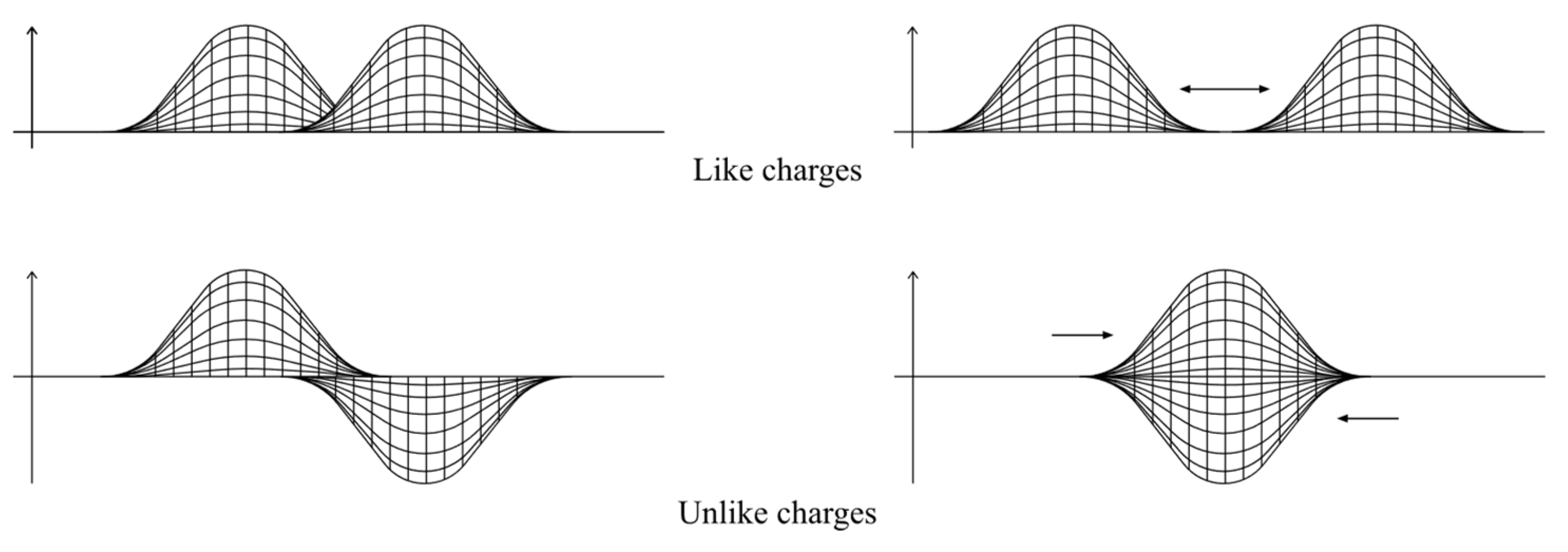
Since an electron is matter and there are only two directions in one dimension, matter curves in two different directions, creating two types of electric charges: positive and negative. Like charges repel each other because they occupy the same position in one dimension, while unlike charges attract each other because they occupy opposite positions in one dimension. Since they are all matter, they can only attract or repel each other, not annihilate.

Figure 5. Electric charges.

Quarks have three color charges: red, green, and blue [12], which are converted by matter curving in three different dimensions. The experimental discovery of neutrino oscillation [13,14,15] proves that those three values of quark color can be converted into each other: they are different forms of the same thing.

Figure 6. Quark color.

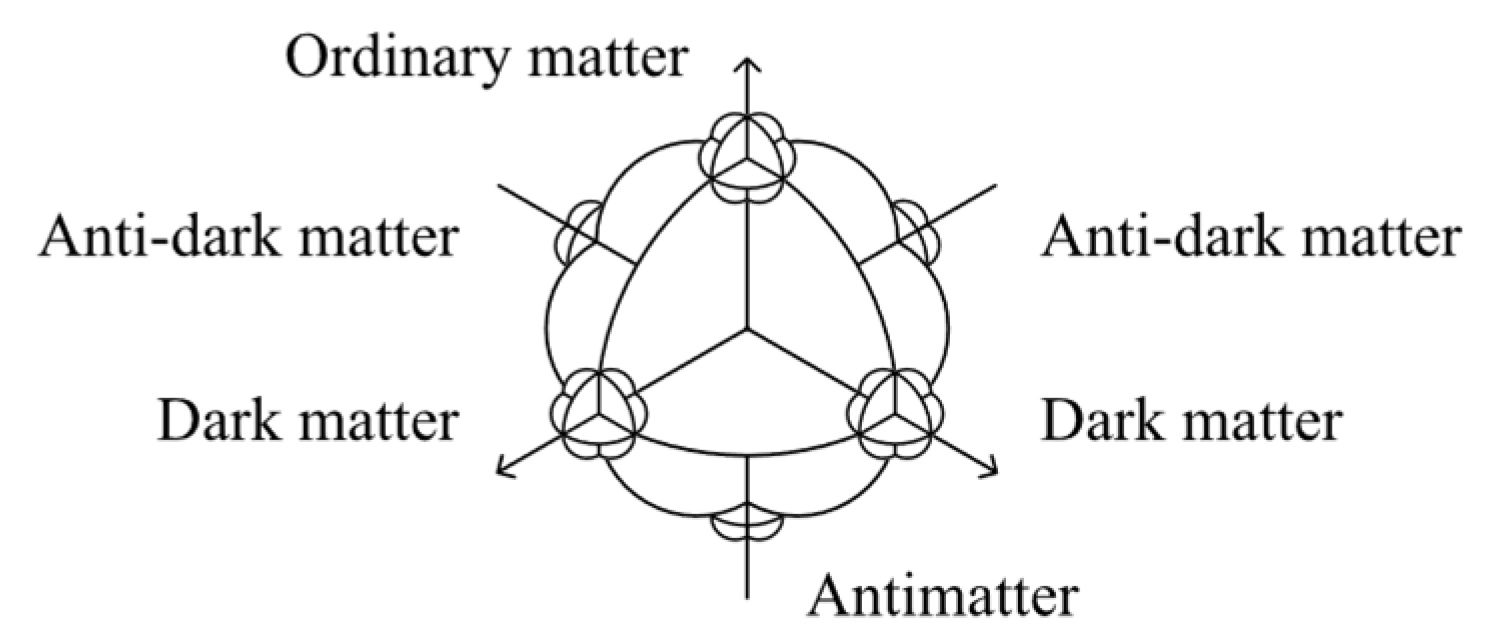
Since there are only three values of quark color, space has only three dimensions. Therefore, space curves in six different directions of these three dimensions, creating six types of matter: ordinary matter, antimatter, two types of dark matter, and two types of anti-dark matter.

Matter and antimatter in opposite directions attract and annihilate each other, while matter and dark matter perpendicular to each other in another dimension have no electromagnetic force. Both matter, antimatter, dark matter, and anti-dark matter are affected by gravitation.

During the Big Bang, matter and antimatter moved in opposite directions, so antimatter ended up on the other side of the universe. Currently, there is only dark matter and anti-dark matter in the observable universe. Particle collision experiments [16] prove that ordinary matter can be converted into antimatter: they are different forms of the same thing.

Figure 7. Six types of matter.

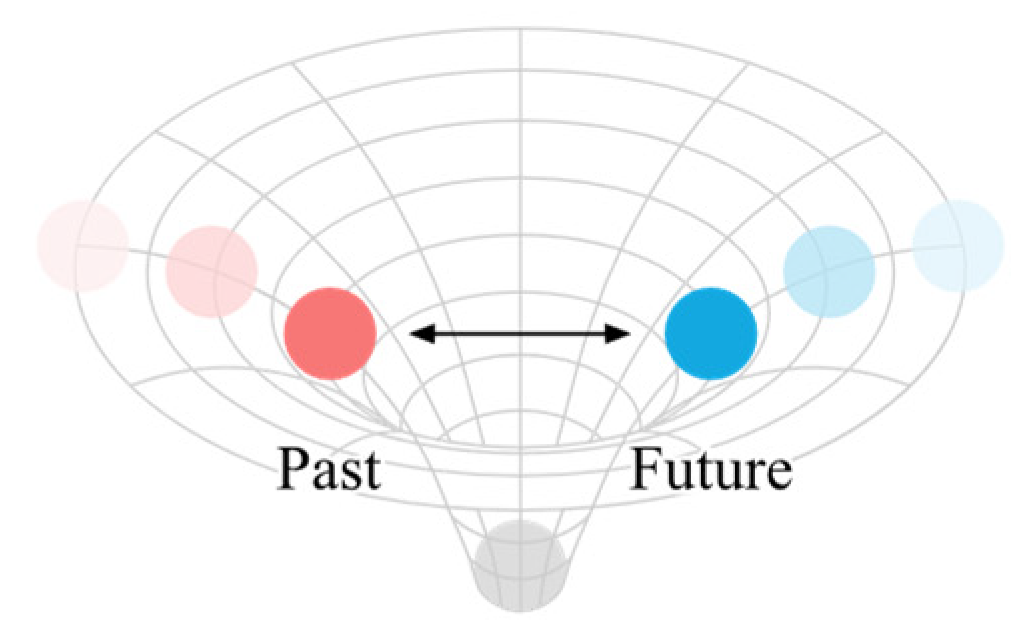
Matter is converted from curved space, and it also curves time. In the double-slit experiment, an interference pattern emerges as the particles build up one by one [17]. This occurs because matter curves time, causing the particle from the past to interfere with the particle from the future.

In which-way experiment, if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear [18]. The mass of the observer is much greater than the particle, and when the observation occurs, the time of the observer engulfs the time of the particle, similar to how a black hole swallows a star, resulting in wave function collapse.

The Wheeler's delayed choice experiment demonstrates that extracting "which path" information after a particle passes through the slits can appear to retroactively alter its previous behavior at the slits [19]. Because matter curves time, the particle from the future can interfere with the particle from the past, meaning that the present behavior can have an impact on the past.

The quantum eraser experiment further shows that wave behavior can be restored by erasing or making permanently unavailable the "which path" information [20]. Since the time of the particle has no connection with the time of the observer, no wave function collapse occurs.

Figure 8. Matter curves time.

Every elementary particle is matter, and they are all converted from curved space, which gives them rest mass. However, the current commonly accepted physical theories imply or assume that the photon is strictly massless [22]. The Lorentz factor

γ

is defined as [23]:

γ = \frac{1}{\sqrt{1 - {(v / c)}^{2}}} .

In Newton's law of universal gravitation, the gravitational acceleration is:

a = \frac{G m_{0} / r^{2}}{\sqrt{1 - {(v / c)}^{2}}} .

In Einstein's theory of relativity, the stress-energy tensor

T^{α β}

for a non-interacting particle with rest mass

m_{0}

and trajectory

x_{p} (t)

is given by [2,3]:

T^{α β} (x, t) = \frac{m_{0} v^{α} (t) v^{β} (t)}{\sqrt{1 - {(v / c)}^{2}}} δ (x - x_{p} (t)) .

If the photon has no rest mass, it would not be subject to gravitation and could escape from a black hole, contradicting observations [9].

Of course, there is no doubt that the Standard Model is

100 %

accurate, so the blame is on the photon. The mistake, therefore, lies with the photon, which should behave precisely as predicted by scientists. The photon is both a wave and a particle, both matter and antimatter, and both has and does not have rest mass.

By the way, the Standard Model also defines the rest mass of the neutrino as zero. Unfortunately, experimental observations by the Super-Kamiokande Observatory and the Sudbury Neutrino Observatories have shown that the neutrino actually has a non-zero rest mass [13,14,15], revealing the limitations of the Standard Model.

3. Gravitation of hollow sphere space

Since there are only three values for the color charge of quarks, so the space has only three dimensions. Therefore, the space released by matter takes the form of a three-dimensional sphere. As this space flows outward, it forms a hollow sphere, and its volume can be written in the following form:

V_{3} = \frac{4}{3} π r^{3}, S_{μ ν} = \frac{4}{3} π ({(r + α)}^{3} - r^{3}) .

where

S_{μ ν}

is the space released by the matter,

r

is the radius of the sphere, and

α

is the degree of space curvature. The greater the degree of space curvature, the greater the gravitational acceleration of the object, which can be expressed as:

α = a t^{2}, t = 1, S_{μ ν} = \frac{4}{3} π ({(r + a)}^{3} - r^{3}) .

When the outward flow of space occurs, its volume remains constant, allowing for the direct calculation of the gravitational acceleration

a_{2}

at a different distance using the gravitational acceleration

a_{1}

at a known distance. The equation can be rewritten to:

S_{μ ν} = \frac{4}{3} π ({(r_{1} + a_{1})}^{3} - {r_{1}}^{3}) = \frac{4}{3} π ({(r_{2} + a_{2})}^{3} - {r_{2}}^{3}),

a_{2} = \sqrt[3]{{(r_{1} + a_{1})}^{3} - {r_{1}}^{3} + {r_{2}}^{3}} - r_{2} .

The mass of the Earth is approximately

5.97237 \times 10^{24} k g

, and the average distance from its center to its surface is about

6.37123 \times 10^{6} m

[24,25]. According to Newton's law of universal gravitation, the value of the gravitational constant is approximately

6.67408 \times 10^{- 11} m^{3} / k g / s^{2}

[26]. The gravitational acceleration

a_{1}

at the Earth's surface can be calculated using this law and is given by:

a_{1} = \frac{G m}{{r_{1}}^{2}} \approx 9.81954911 m / s^{2} .

If the distance up to

10^{7} m

, the gravitational acceleration

a_{2}

is:

a_{2} = \frac{G m}{{r_{2}}^{2}} \approx 3.98600751 m / s^{2} .

When the gravitational acceleration

a_{1}

of the hollow sphere space is equal to the Newtonian gravitational acceleration

a_{1}

r_{1}

, the gravitational acceleration

a_{2}

of the hollow sphere space at

r_{2}

is:

a_{2} = \sqrt[3]{{(r_{1} + a_{1})}^{3} - {r_{1}}^{3} + {r_{2}}^{3}} - r_{2} \approx 3.98601207 m / s^{2} .

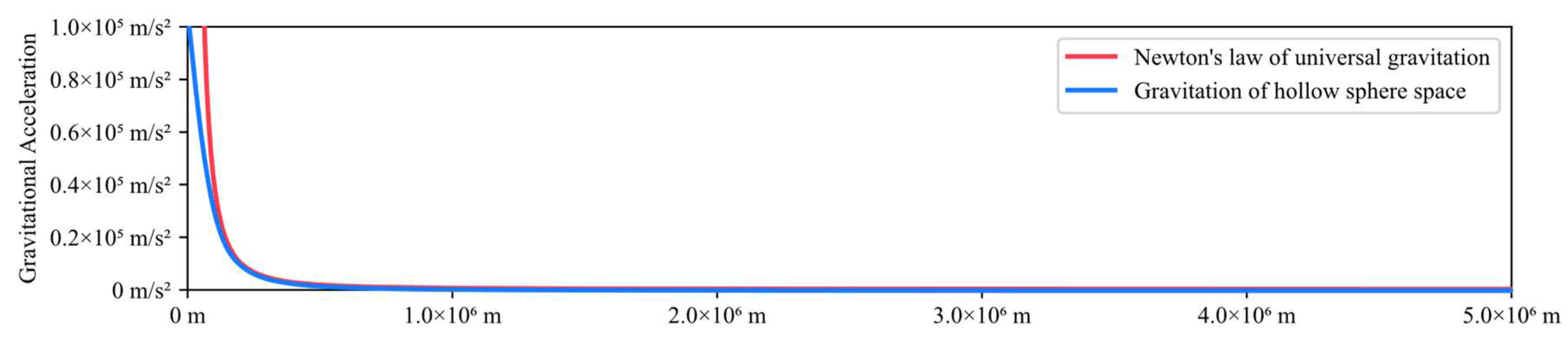
As you can see, the value of the gravitational acceleration

a_{2}

calculated using the gravitation of the hollow sphere space is extremely close to the value calculated using Newton's law of universal gravitation. This confirms that the gravitation of hollow sphere space can be used to accurately calculate the gravitational acceleration. However, when the distance is very large, it is advisable to use professional software to calculate the cube root, as calculators may return zero or negative values. The gravitational acceleration of the Earth at different distances in both models is shown in the following table:

Table 1. Gravitational acceleration of Earth.

Distance of Earth	$0 m$	$1.15 \times 10^{3} m$	$10^{4} m$	$10^{5} m$	$10^{6} m$	$10^{7} m$
Newton's law ofuniversal gravitation	$\infty$	$3 \times 10^{8} m / s^{2}$	$3986007 m / s^{2}$	$39860 m / s^{2}$	$398.600 m / s^{2}$	$3.986007 m / s^{2}$
Gravitation ofhollow sphere space	$106141 m / s^{2}$	$104991 m / s^{2}$	$96171 m / s^{2}$	$29976 m / s^{2}$	$398.442 m / s^{2}$	$3.986012 m / s^{2}$

When the distance is zero, Newton's gravitational acceleration becomes infinite, which is obviously incorrect. In contrast, the gravitation of hollow sphere space is more accurate and does not require the use of Newton's constant of gravitation. The Schwarzschild radius is a physical parameter that appears in the Schwarzschild solution to Einstein's field equations [5,8]. It corresponds to the radius defining the event horizon of a black hole and can be expressed as:

r_{s} = \frac{2 G m}{c^{2}} .

The Schwarzschild radius of Earth is approximately

0.00887 m

. However, when the distance is

1150 m

, the Newton's gravitational acceleration exceeds approximately

3 \times 10^{8} m / s^{2}

, it is greater than the speed of light in vacuum, approximately

2.9979 \times 10^{8} m / s

, and this leads to the formation of a black hole, which is obviously wrong.

The mass of the Moon is approximately

7.342 \times 10^{22} k g

, its mean radius is about

1.737 \times 10^{6} m

, and the time-averaged distance between the centers of the Earth and Moon is about

3.844 \times 10^{8} m

^{[27, 28, 29]}. When considering different distances, the gravitational acceleration of the Moon in two different models is shown in the following table:

Table 2. Gravitational acceleration of Moon.

Distance of Moon	$0 m$	${1.27 \times 10}^{2} m$	$10^{5} m$	$10^{6} m$	$10^{7} m$	${3.844 \times 10}^{8} m$
Newton's law ofuniversal gravitation	$\infty$	$3 \times 10^{8} m / s^{2}$	$490.01 m / s^{2}$	$4.900109 m / s^{2}$	$0.04900 m / s^{2}$	$0.00003316 m / s^{2}$
Gravitation ofhollow sphere space	$24496 m / s^{2}$	$24369 m / s^{2}$	$487.60 m / s^{2}$	$4.899863 m / s^{2}$	$0.04899 m / s^{2}$	$0.00003316 m / s^{2}$

The mass of the Sun is approximately

1.9885 \times 10^{30} k g

, with a mean radius of about

6.96342 \times 10^{8} m

, and the mean distance between the centers of the Earth and the Sun is about

1.496 \times 10^{11} m

^{[30, 31]}. The table below shows the gravitational acceleration of the Sun in two different models at varying distances:

Table 3. Gravitational acceleration of Sun.

Distance of Sun	$0 m$	${6.65 \times 10}^{5} m$	$10^{7} m$	$10^{9} m$	$10^{10} m$	${1.496 \times 10}^{11} m$
Newton's law ofuniversal gravitation	$\infty$	$3 \times 10^{8} m / s^{2}$	$1327140 m / s^{2}$	$132.71 m / s^{2}$	$1.3271 m / s^{2}$	$0.005929 m / s^{2}$
Gravitation ofhollow sphere space	$7356638 m / s^{2}$	$6693449 m / s^{2}$	$1181938 m / s^{2}$	$132.71 m / s^{2}$	$1.3271 m / s^{2}$	$0.005929 m / s^{2}$

Expanding the formula, the gravitational acceleration of the hollow sphere space can be derived as:

S_{μ ν} = \frac{4}{3} π (3 r^{2} a + 3 r a^{2} + a^{3}) = 4 π r^{2} a (1 + \frac{a}{r} + \frac{a^{2}}{3 r^{2}}) .

Then introduce a new variable

β

to represent

1 + a / r + a^{2} / 3 r^{2}

. The equation can be simplified to:

S_{μ ν} = 4 π r^{2} a β, β = 1 + \frac{a}{r} + \frac{a^{2}}{3 r^{2}}, \lim_{r \to \infty} β = 1 .

The expression implies that

β

can approach

1

as closely as desired by increasing the distance

r

to infinity. At the surface of the Earth, the ratio of the gravitational acceleration

a

to the distance

r

is approximately 0.00000153, which is negligible and can be omitted. The formula can be rewritten as:

S_{μ ν} = 4 π r^{2} a, β = 1 .

Since the accelerations of the two formulas are equal at long distances, the formula can be simplified to:

a = \frac{S_{μ ν}}{4 π r^{2}} = \frac{G m}{r^{2}} .

After removing the same parameters, the gravitation of hollow sphere space

S_{μ ν}

thus takes the form:

S_{μ ν} = 4 π G m .

The result demonstrates that the space released by matter per kilogram is precisely equal to

4 π G

, providing evidence that matter is converted from curved space, indicating that they are different forms of the same thing. In comparison to Newton's law of universal gravitation, the gravitation of hollow sphere space has only one more variable,

β

, which is extremely close to

1

at long distances.

S_{μ ν} = 4 π G m = 4 π r^{2} a β, a = \frac{4 π G m}{4 π r^{2} β} = \frac{G m}{r^{2}} \frac{1}{β} .

The further the distance between the objects, the closer the values of the formulas.

Figure 9. Gravitational acceleration of Earth.

In Einstein's theory of relativity, matter curves spacetime, and the Einstein field equations can be expressed in the following form:

G_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν}, κ = \frac{8 π G}{c^{4}} .

Where

G_{μ ν}

is the Einstein tensor,

T_{μ ν}

is the stress-energy tensor,

c

is the speed of light in vacuum, and

κ

is the Einstein constant of gravitation. In the geometrized unit system, the value of

4 π G

is set equal to unity. Therefore, it is possible to remove the Newton's constant of gravitation from the equations to avoid mistakes, especially since the Newton's law of universal gravitation does not apply to black holes. The equation can be rewritten as:

4 π G = 1, κ = \frac{2}{c^{4}} .

Since the theory is that matter and energy are both converted from curved space, the form should also be reversed. As space

S

is proportional to mass

m

and the fourth power of the speed of light in vacuum

c^{4}

, the equivalent equation for space

S

can be expressed as:

S = E c^{2} = m c^{4}, S_{μ ν} = \frac{4 π G}{c^{4}} S .

Of course, under ordinary circumstances, if the Newton's "constant" of gravitation doesn't change too much, it can still be used to calculate the gravitational acceleration, the form can be rewritten to:

S_{μ ν} = 4 π G m = \frac{4}{3} π ({(r + a)}^{3} - r^{3}), a = \sqrt[3]{3 G m + r^{3}} - r .

On the surface of Earth, the gravitational acceleration is:

a_{1} = \frac{G m}{r^{2}} \approx 9.81954911 m / s^{2},

a_{2} = \sqrt[3]{3 G m + r^{3}} - r \approx 9.81953396 m / s^{2} .

And the relative error is:

η = |1 - \frac{a_{2}}{a_{1}}| \approx 0.00000154284 .

As you can see, this value is still extremely close to the original. What's more, this formula does not introduce any new variables. Although this formula solves the problem at short distances, when the distance becomes too large, the software calculator may return zero or a negative value, which can be frustrating, so the author has made improvements to the original equation.

In 1665, Isaac Newton extended the binomial theorem to include real exponents, expanding the finite sum into an infinite series. To achieve this, he needed to give binomial coefficients a definition with an arbitrary upper index, which could not be accomplished through the traditional factorial formula. Nonetheless, for any given number

n

, it is possible to define the coefficients as:

(\binom{n}{k}) = \frac{n (n - 1) (n - 2) \dots (n - k + 1)}{k!} = \frac{{(n)}_{k}}{k!} .

The Pochhammer symbol

{(∙)}_{k}

is used to represent a falling factorial, which is defined as a polynomial:

{(n)}_{k} = n^{\underline{k}} = n (n - 1) (n - 2) \dots (n - k + 1) = \prod_{k = 1}^{n} (n - k + 1) .

This formula holds true for the usual definitions when

n

is a nonnegative integer. For any complex number

n

and real numbers

x

and

y

with

|x| > |y|

, the following equation holds:

{(x + y)}^{n} = \sum_{k = 0}^{\infty} (\binom{n}{k}) x^{n - k} y^{k} = x^{n} + n x^{n - 1} y + \frac{n (n - 1)}{2!} x^{n - 2} y^{2} + \frac{n (n - 1) (n - 2)}{3!} x^{n - 3} y^{3} + \dots .

The series for the cube root can be obtained by setting

n = 1 / 3

, which gives:

{(x + y)}^{\frac{1}{3}} = x^{\frac{1}{3}} + \frac{1}{3} x^{- \frac{2}{3}} y - \frac{1}{9} x^{- \frac{5}{3}} y^{2} + \frac{5}{81} x^{- \frac{8}{3}} y^{3} + \dots .

At long distances where

|r| > |\sqrt[3]{3 G m}|

, the equation becomes:

a = \sqrt[3]{r^{3} + 3 G m} - r = r + \frac{1}{3} r^{- 2} 3 G m - \frac{1}{9} r^{- 5} {(3 G m)}^{2} + \frac{5}{81} r^{- 8} {(3 G m)}^{3} + \dots - r,

a = \frac{G m}{r^{2}} - \frac{1}{r} {(\frac{G m}{r^{2}})}^{2} + \frac{5}{3 r^{2}} {(\frac{G m}{r^{2}})}^{3} + \dots,

Then introduce a new variable

β

, the equation can be simplified to:

a = \frac{G m}{r^{2}} + β, β = - \frac{1}{r} {(\frac{G m}{r^{2}})}^{2} + \frac{5}{3 r^{2}} {(\frac{G m}{r^{2}})}^{3} + \dots, \lim_{r \to \infty} β = 0 .

At the surface of the Earth, the variable

β

is approximately

- 0.00001513417

, which is negligible and can be omitted. This is the reason why it is extremely close to Newton's value at long distances. At short distances where

|\sqrt[3]{3 G m}| > |r|

, the form of the equation is different:

a = \sqrt[3]{3 G m + r^{3}} - r = {(3 G m)}^{\frac{1}{3}} + \frac{1}{3} {(3 G m)}^{- \frac{2}{3}} r^{3} - \frac{1}{9} {(3 G m)}^{- \frac{5}{3}} r^{6} + \frac{5}{81} {(3 G m)}^{- \frac{8}{3}} r^{9} + \dots - r,

a = \sqrt[3]{3 G m} - r (1 - \frac{1}{3} {(\frac{r}{\sqrt[3]{3 G m}})}^{2} + \frac{1}{9} {(\frac{r}{\sqrt[3]{3 G m}})}^{5} - \frac{5}{81} {(\frac{r}{\sqrt[3]{3 G m}})}^{8} + \dots) .

In Chapter 7 of the book "Why String Theory?", it is mentioned that there is no direct experimental evidence for the String Theory [32]. To avoid encountering the same issue of unverifiability as String Theory, the author makes a prediction about the surface gravity of neutron star.

The Crab Pulsar (PSR B0531+21) has a mass of

1.4

solar masses (M☉) and a radius of approximately

10500 m

[33]. The solar mass (M☉) is a standard unit of mass in astronomy, equal to approximately

1.98847 \times 10^{30} k g

. On the surface of Crab Pulsar, the gravitational acceleration is:

a_{1} = \frac{G m}{r^{2}} \approx 1.68523274 \times 10^{12} m / s^{2},

a_{2} = \sqrt[3]{3 G m + r^{3}} - r \approx 8.21924883 \times 10^{6} m / s^{2} .

Newton's prediction of

1.68523274 \times 10^{12} m / s^{2}

, which is significantly greater than the speed of light in vacuum,

2.9979 \times 10^{8} m / s

, clearly deviates from what is expected. In contrast, the predicted value from the Space Theory,

8.21924883 \times 10^{6} m / s^{2}

, aligns more closely with reality.

4. Discussion

As of this writing, graviton has not been found yet.

Funding

None.

Acknowledgments

None.

Conflicts of Interest

None.

References

Newton. (1687). "Philosophiae Naturalis Principia Mathematica". The Mathematical Principles of Natural Philosophy.
A. Einstein. (1905). "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig". Annalen der Physik, 4, 18, 639–641.
Einstein, M. Grossmann. (1913). "Entwurf einer verallgemeinerten Relativitätstheorie und eine Theorie der Gravitation". Zeitschrift für Mathematik und Physik, 62, 225–244, 245–261.
Einstein, A.D. Fokker. (1913). "Nordströmsche Gravitationstheorie vom Standpunkt des absoluten Differentialkalküls". Annalen der Physik, 4, 40, 551–560.
Einstein. (1916). "Die Grundlage der allgemeinen Relativitätstheorie". Annalen der Physik, Vierte Folge, Band 49, 769-822.
R. Penrose. (1965). "Gravitational Collapse and Space-Time Singularities". Physical Review Letters. American Physical Society, 14, 57-59. [CrossRef]
A. Frankowski, N. A. Frankowski, N. Soker. (2009). "Very late thermal pulses influenced by accretion in planetary nebulae". New Astronomy, 14, 8, 654-658. [CrossRef]
K. Schwarzschild. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, Seite 189-196.
D. Clery. (2020). "Black holes caught in the act of swallowing stars". Science, 367, 6477, 495. [CrossRef]
S.W. Hawking. (1974). "Black hole explosions". Nature 248, 30–31. [CrossRef]
E. Hubble. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". PNAS 15, 3, 168-173. [CrossRef]
Greenberg. (1964). "Spin and Unitary Spin Independence in a Paraquark Model of Baryons and Mesons". Physical Review Letters, 13, 598–602.
Pontecorvo. (1958). "Mesonium and Antimesonium". Soviet Journal of Experimental and Theoretical Physics, 6, 429–431.
E. Kearns, T. E. Kearns, T. Kajita, Y. Totsuka. (1999). "Detecting Massive Neutrinos". Scientific American, 281, 64–71. [CrossRef]
A. McDonald, J. A. McDonald, J. Klein, D. Wark. (2006). "Solving the Solar Neutrino Problem". Scientific American, 288, 40–49. [CrossRef]
V. Hatton. (1991). "Operational history of the SPS collider 1981-1990". Conference Record of the 1991 IEEE Particle Accelerator Conference, 2952-2954. [CrossRef]
R. Pfleegor, L. R. Pfleegor, L. Mandel. (1967). "Interference of Independent Photon Beams". Physical Review, 159, 5, 1084–1088. [CrossRef]
W. Wootters, W. W. Wootters, W. Zurek. (1979). "Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle". Physical Review D, 19, 2, 473–484. [CrossRef]
A. Peruzzo, P. A. Peruzzo, P. Shadbolt, et al. (2012). "A Quantum Delayed-Choice Experiment". Science, 338, 6107, 634–637. [CrossRef]
X. Ma, J. X. Ma, J. Kofler, et al. (2012). "Quantum erasure with causally disconnected choice". Proceedings of the National Academy of Sciences, 110, 4, 110–1226. [CrossRef]
M. Alonso, E. M. Alonso, E. Finn. (1968). "Fundamental University Physics Volume III: Quantum and Statistical Physics". Addison Wesley, ISBN 978-0-201-00262-1.
R. Oerter. (2006). "The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics". Penguin Group, ISBN 978-0-13-236678-6.
J. Forshaw, G. J. Forshaw, G. Smith. (2014). "Dynamics and Relativity". John Wiley & Sons, ISBN 978-1-118-93329-9.
Luzum, N. Capitaine, A. Fienga, et al. (2011). "The IAU 2009 system of astronomical constants: The report of the IAU working group on numerical standards for Fundamental Astronomy". Celestial Mechanics and Dynamical Astronomy, 110, 293–304. [CrossRef]
F. Chambat, B. F. Chambat, B. Valette. (2001). "Mean radius, mass, and inertia for reference Earth models". Physics of the Earth and Planetary Interiors, 124, 3–4, 234–253. [CrossRef]
P. Mohr, D. P. Mohr, D. Newell, B. Taylor. (2016). "CODATA Recommended Values of the Fundamental Physical Constants: 2014". Journal of Physical and Chemical Reference Data, 45, 4, 1527–1605. [CrossRef]
M. Wieczorek, B. M. Wieczorek, B. Jolliff, A. Khan, et al. (2006). "The Constitution and Structure of the Lunar Interior". Reviews in Mineralogy and Geochemistry, 60, 1, 221–364. [CrossRef]
Hirt, W.E. Featherstone. (2012). "A 1.5 km-resolution field model of the Moon". Earth and Planetary Science Letters, 329–330, 22–30. [CrossRef]
J. Battat, T. J. Battat, T. Murphy, E. Adelberger, et al. (2009). "The Apache Point Observatory Lunar Laser-ranging Operation (APOLLO): Two Years of Millimeter-Precision Measurements of the Earth-Moon Range". Astronomical Society of the Pacific, 121, 875, 29–40. [CrossRef]
G. Poole. (2019). "Cosmic Power Generation and Gravity". Journal of High Energy Physics, Gravitation and Cosmology, 5, 920-927. [CrossRef]
Pitjeva, E. Standish. (2009). "Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit". Celestial Mechanics and Dynamical Astronomy, 103, 365–372. [CrossRef]
J Conlon. (2016). "Why string theory?". CRC Press.
D. Jeffery. (n.d.). "Neutron Stars and the Crab Nebula". University of Nevada, Las Vegas. https://www.physics.unlv.edu/~jeffery/astro/neutron_star/crab_nebula.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Space Theory

Abstract

1. Introduction

2. Model

3. Gravitation of hollow sphere space

4. Discussion

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe