Prerpints.org logo
Preprint
Article

Space Theory

Altmetrics

Downloads

816

Views

980

Comments

0

supplementary.pdf (43.51KB )

S. Chen  *

This version is not peer-reviewed

Submitted:

06 March 2024

Posted:

07 March 2024

Read the latest preprint version here

Alerts
Abstract
The author introduces a novel theoretical framework that suggests matter and energy are both converted from curved space. In Space Theory, gravitation is generated by the flow of space, instead of being transmitted by the graviton as in String Theory. This theory also suggests that Newton's gravitational constant, denoted as G, may not be truly constant but could vary over time. The equivalent equation of space is S=Ec2=mc4, and the gravitation of hollow sphere space is Sμν=4πGm=(4/3)π((r+a)3-r3). The Space Theory also predicts that the surface gravitational acceleration of the neutron star Crab Pulsar (PSR B0531+21) is approximately 8.21924883×106 m/s2.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

Introduction

When a star dies, it undergoes a contraction and blows off its outer envelope, forming a planetary nebula. [6,7] If the star collapses to within its Schwarzschild radius, it forms a black hole. [8] Newton’s law of universal gravitation [1] provides the equation for this force, which states that:
Preprints 100733 g001
Figure 1. A star forms a black hole.
Figure 1. A star forms a black hole.
Preprints 100733 g001
Before the star collapses, the gravitational force between the planet and the star is represented by F 1 . After the collapse, the gravitational force between the planet and the black hole is represented by F 2 . In these equations, m 1 represents the mass of the star, m 2 represents the mass of the black hole, m 3 represents the mass of the planet, r represents the distance between their centers of mass, and G is the gravitational constant.
The gravitational force of a black hole is extremely strong and nothing, not even light, can escape it [9]. Therefore, F 2 is greater than F 1 . As the star collapses into a black hole, it blows off its outer envelope and loses mass [10]. Assuming the star loses 0.2 % of its mass during this process, the mass of the black hole can be represented as 99.8 % of m 1 . This can be rewritten as:
F 1 < F 2 , G m 1 m 3 r 2 < G 0.998   m 1 m 3 r 2 .
When the common parameters are removed, the equation can be simplified to:
1 < 0.998.
How is it even possible that 1 is less than 0.998 ? As the mass decreases from m 1 to m 2 and the distance r between the objects remains unchanged, it suggests that the gravitational constant G has increased. In Einstein’s theory of relativity, matter curves spacetime, and the Einstein field equations [4] can be expressed in the following form:
G μ ν = 8 π G c 4 T μ ν .
In this equation, G μ ν is the Einstein tensor and G is the gravitational constant. However, if the gravitational constant G is constantly changing, it raises the question of whether Einstein’s theory is still accurate.

Model

What if the situation were reversed, and both matter and energy were converted from curved space?
Matter can release energy through annihilation, fission, and fusion [2,3], as matter and energy are different forms of the same thing. Therefore, matter curves spacetime because it is converted from curved space, and the flow of space released by matter creates gravitational force. The greater the amount of space released, the stronger the gravitational force generated. If one object releases much more space than another object, the flow of space will narrow the distance between the two objects. It is the space that moves, not the objects.
Preprints 100733 g002
Figure 2. Gravitation.
Figure 2. Gravitation.
Preprints 100733 g002
When two galaxies are very far apart, the space they release accumulates in the middle, and this expands their distance. Therefore, the expansion of the universe and the phenomenon of redshift [11] are caused by the increase in space.
Preprints 100733 g003
Figure 3. Expansion of the universe.
Figure 3. Expansion of the universe.
Preprints 100733 g003
Thus, space curves in one dimension, converting matter and energy.
Preprints 100733 g004
Figure 4. Curved space.
Figure 4. Curved space.
Preprints 100733 g004
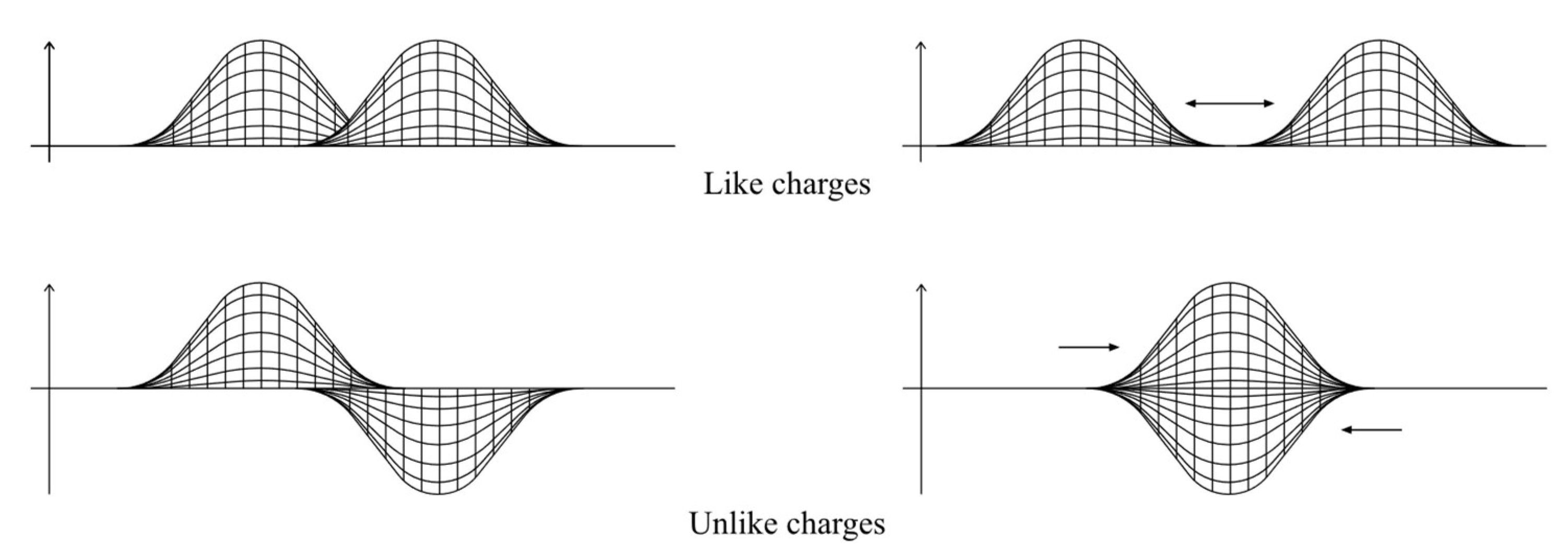
Since an electron is matter and there are only two directions in one dimension, matter curves in two different directions, creating two types of electric charges: positive and negative. Like charges repel each other because they occupy the same position in one dimension, while unlike charges attract each other because they occupy opposite positions in one dimension. Since they are all matter, they can only attract or repel each other, not annihilate.
Preprints 100733 g005
Figure 5. Electric charges.
Figure 5. Electric charges.
Preprints 100733 g005
Quarks have three color charges: red, green, and blue [12], which are converted by matter curving in three different dimensions. The experimental discovery of neutrino oscillation [13,14,15] proves that those three values of quark color can be converted into each other: they are different forms of the same thing.
Preprints 100733 g006
Figure 6. Quark color.
Figure 6. Quark color.
Preprints 100733 g006
Since there are only three values of quark color, space has only three dimensions. Therefore, space curves in six different directions of three dimensions, creating six types of matter: ordinary matter, antimatter, two types of dark matter, and two types of anti-dark matter.
Matter and antimatter in opposite directions attract and annihilate each other, while matter and dark matter perpendicular to each other in another dimension have no electromagnetic force. Both matter, antimatter, dark matter, and anti-dark matter are affected by gravitation.
During the Big Bang, matter and antimatter moved in opposite directions, so antimatter ended up on the other side of the universe. Currently, there is only dark matter and anti-dark matter in the observable universe. Particle collision experiments [16] prove that ordinary matter can be converted into antimatter: they are different forms of the same thing.
Preprints 100733 g007
Figure 7. Six types of matter.
Figure 7. Six types of matter.
Preprints 100733 g007
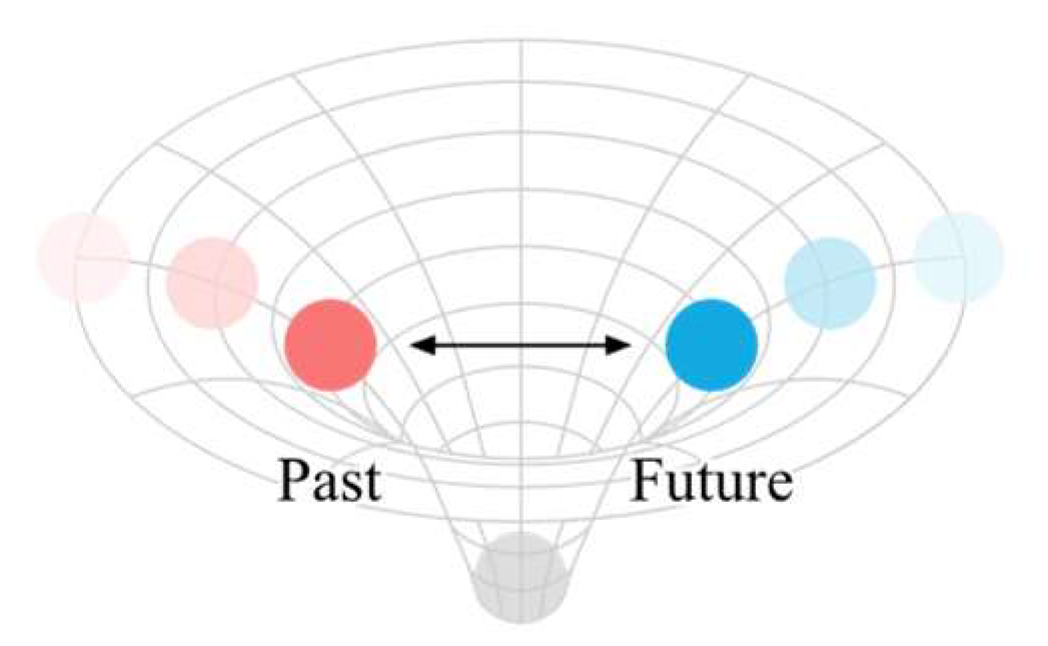
Matter is converted from curved space, and it also curves time. In the double-slit experiment, an interference pattern emerges as the particles build up one by one. [17] This occurs because matter curves time, causing the particle from the past to interfere with the particle from the future.
In which-way experiment, if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear. [18] The mass of the observer is much greater than the particle, and when the observation occurs, the time of the observer engulfs the time of the particle, similar to how a black hole swallows a star, resulting in wave function collapse.
The Wheeler’s delayed choice experiment demonstrates that extracting “which path” information after a particle passes through the slits can appear to retroactively alter its previous behavior at the slits. [19] Because matter curves time, the particle from the future can interfere with the particle from the past, meaning that the present behavior can have an impact on the past.
The quantum eraser experiment further shows that wave behavior can be restored by erasing or making permanently unavailable the “which path” information. [20] Since the time of the particle has no connection with the time of the observer, no wave function collapse occurs.
Preprints 100733 g008
Figure 8. Matter curves time.
Figure 8. Matter curves time.
Preprints 100733 g008
Every elementary particle is matter, and they are all converted from curved space, which gives them rest mass. However, the current commonly accepted physical theories imply or assume that the photon is strictly massless [22]. The Lorentz factor γ is defined as [23]:
γ = 1 1 − v / c 2 .
In Newton’s law of universal gravitation, the gravitational acceleration is:
a = G m 0 / r 2 1 − v / c 2 .
In Einstein’s theory of relativity, the stress-energy tensor T α β for a non-interacting particle with rest mass m 0 and trajectory x p t is given by [2,3]:
T α β x , t = m 0 v α t v β t 1 − v / c 2 δ x − x p t .
If the photon has no rest mass, it would not be subject to gravitation and could escape from a black hole, contradicting observations [9].
Of course, there is no doubt that the Standard Model is 100 % accurate, so the blame is on the photon. The mistake, therefore, lies with the photon, which should behave precisely as predicted by scientists. The photon is both a wave and a particle, both matter and antimatter, and both has and does not have rest mass.
By the way, the Standard Model also defines the rest mass of the neutrino as zero. Unfortunately, experimental observations by the Super-Kamiokande Observatory and the Sudbury Neutrino Observatories have shown that the neutrino actually has a non-zero rest mass [13,14,15], revealing the limitations of the Standard Model.
Furthermore, as is widely known, dark matter possesses mass. Is this mass conferred by the Higgs field? If the answer is yes, does the Higgs boson composed of both matter, antimatter, and dark matter? If the answer is no, where does the mass of dark matter originate from?

Gravitation

Since there are only three values for the color charge of quarks, so the space has only three dimensions. Therefore, the space released by matter takes the form of a three-dimensional sphere. As this space flows outward, it forms a hollow sphere, and its volume can be written in the following form:
V 3 = 4 3 π r 3 , S μ ν = 4 3 π r + α 3 − r 3 .
Where S μ ν is the space released by the matter, r is the radius of the sphere, and α is the degree of space curvature. The greater the degree of space curvature, the greater the gravitational acceleration of the object, which can be expressed as:
α = a t 2 , t = 1 , S μ ν = 4 3 π r + a 3 − r 3 .
When the outward flow of space occurs, its volume remains constant, allowing for the direct calculation of the gravitational acceleration a 2 at a different distance using the gravitational acceleration a 1 at a known distance. The equation can be rewritten to:
S μ ν = 4 3 π r 1 + a 1 3 − r 1 3 = 4 3 π r 2 + a 2 3 − r 2 3 , a 2 = r 1 + a 1 3 − r 1 3 + r 2 3 3 − r 2 .
The mass of the Earth is approximately 5.97237 × 10 24   kg , and the average distance from its center to its surface is about 6.37123 × 10 6   m . [24,25] According to Newton’s law of universal gravitation, the value of the gravitational constant is approximately 6.67408 × 10 − 11   m 3 / kg / s 2 . [26] The gravitational acceleration a 1 at the Earth’s surface can be calculated using this law and is given by:
a 1 = G m r 1 2 ≈ 9.81954911   m / s 2 .
If the distance up to 10 7   m , the gravitational acceleration a 2 is:
a 2 = G m r 2 2 ≈ 3.98600751   m / s 2 .
When the gravitational acceleration a 1 is equal to the Newtonian gravitational acceleration a 1 at r 1 , the gravitational acceleration a 2 at r 2 is:
a 2 = r 1 + a 1 3 − r 1 3 + r 2 3 3 − r 2 ≈ 3.98601207   m / s 2 .
As you can see, the value of the gravitational acceleration a 2 calculated using the Space Theory is extremely close to the value calculated using Newton’s law of universal gravitation. This confirms that the Space Theory can be used to accurately calculate the gravitational acceleration. However, when the distance is very large, it is advisable to use professional software to calculate the cube root, as calculators may return zero or negative values. The gravitational acceleration of the Earth at different distances in both models is shown in the following table:
Table 1. Gravitational acceleration of Earth.
Table 1. Gravitational acceleration of Earth.
Preprints 100733 i001
The mass of the Moon is approximately 7.342 × 10 22   kg , its mean radius is about 1.737 × 10 6   m , and the time-averaged distance between the centers of the Earth and Moon is about 3.844 × 10 8   m . [27,28,29] When considering different distances, the gravitational acceleration of the Moon in two different models is shown in the following table:
Table 2. Gravitational acceleration of Moon.
Table 2. Gravitational acceleration of Moon.
Preprints 100733 i002
The mass of the Sun is approximately 1.9885 × 10 30   kg , with a mean radius of about 6.96342 × 10 8   m , and the mean distance between the centers of the Earth and the Sun is about 1.496 × 10 11   m . [30,31] The table below shows the gravitational acceleration of the Sun in two different models at varying distances:
Table 3. Gravitational acceleration of Sun.
Table 3. Gravitational acceleration of Sun.
Preprints 100733 i003
When the distance is zero, Newton’s gravitational acceleration becomes infinite, which is obviously incorrect. In contrast, the gravitation of the Space Theory is more accurate and does not require the use of Newton’s constant of gravitation. The Schwarzschild radius [8] is a physical parameter that appears in the Schwarzschild solution to Einstein’s field equations. It corresponds to the radius defining the event horizon of a black hole and can be expressed as:
r s = 2 G m c 2 .
The Schwarzschild radius of Earth is approximately 0.00887   m . However, when the distance is 1150   m , the Newton’s gravitational acceleration exceeds approximately 3 × 10 8   m / s 2 , it is greater than the speed of light in vacuum, approximately 2.9979 × 10 8   m / s , and this leads to the formation of a black hole, which is obviously wrong.
Expanding the formula, the gravitational acceleration of the Space Theory can be derived as:
S μ ν = 4 3 π 3 r 2 a + 3 r a 2 + a 3 = 4 π r 2 a 1 + a r + a 2 3 r 2 .
Then introduce a new variable β to represent 1 + a / r + a 2 / 3 r 2 . The equation can be simplified to:
S μ ν = 4 π r 2 a β , β = 1 + a r + a 2 3 r 2 , lim r → ∞ β = 1.
The expression implies that β can approach 1 as closely as desired by increasing the distance r to infinity. At the surface of the Earth, the ratio of the gravitational acceleration a to the distance r is approximately 0.00000153, which is negligible and can be omitted. The formula can be rewritten as:
S μ ν = 4 π r 2 a , β = 1.
Since the accelerations of the two formulas are equal at long distances, the formula can be simplified to:
a = S μ ν 4 π r 2 = G m r 2 .
After removing the same parameters, the gravitation of the Space Theory S μ ν thus takes the form:
S μ ν = 4 π G m .
The result demonstrates that the space released by matter per kilogram is precisely equal to 4 π G , providing evidence that matter is converted from curved space, indicating that they are different forms of the same thing. In comparison to Newton’s law of universal gravitation, the gravitation of the Space Theory has only one more variable, β , which is extremely close to 1 at long distances.
S μ ν = 4 π G m = 4 π r 2 a β , a = 4 π G m 4 π r 2 β = G m r 2 1 β .
The further the distance between the objects, the closer the values of the formulas.
Preprints 100733 g009
Figure 9. Gravitational acceleration of Earth.
Figure 9. Gravitational acceleration of Earth.
Preprints 100733 g009
In Einstein’s theory of relativity, matter curves spacetime, and the Einstein field equations can be expressed in the following form:
G μ ν = 8 π G c 4 T μ ν , κ = 8 π G c 4 .
Where G μ ν is the Einstein tensor, T μ ν is the stress-energy tensor, c is the speed of light in vacuum, and κ is the Einstein constant of gravitation. In the geometrized unit system, the value of 4 π G is set equal to unity. Therefore, it is possible to remove the Newton’s constant of gravitation from the equations to avoid mistakes, especially since the Newton’s law of universal gravitation does not apply to black holes. The equation can be rewritten as:
4 π G = 1 , κ = 2 c 4 .
Since the theory is that matter and energy are both converted from curved space, the form should also be reversed. As space S is proportional to mass m and the fourth power of the speed of light in vacuum c 4 , the equivalent equation for space S can be expressed as:
S = E c 2 = m c 4 , S μ ν = 4 π G c 4 S .
Of course, under ordinary circumstances, if the Newton’s “constant” of gravitation doesn’t change too much, it can still be used to calculate the gravitational acceleration, the form can be rewritten to:
S μ ν = 4 π G m = 4 3 π r + a 3 − r 3 , a = 3 G m + r 3 3 − r .
On the surface of Earth, the gravitational acceleration is:
a 1 = G m r 2 ≈ 9.81954911   m / s 2 , a 2 = 3 G m + r 3 3 − r ≈ 9.81953396   m / s 2 .
And the relative error is:
η = 1 − a 2 a 1 ≈ 0.00000154284.
As you can see, this value is still extremely close to the original. What’s more, this formula does not introduce any new variables. Although this formula solves the problem at short distances, when the distance becomes too large, the software calculator may return zero or a negative value, so the author has made improvements to the original equation.
In 1665, Isaac Newton extended the binomial theorem to include real exponents, expanding the finite sum into an infinite series. [1] To achieve this, he needed to give binomial coefficients a definition with an arbitrary upper index, which could not be accomplished through the traditional factorial formula. Nonetheless, for any given number n , it is possible to define the coefficients as:
n k = n n − 1 n − 2 ⋯ n − k + 1 k ! = n k k ! .
The Pochhammer symbol · k is used to represent a falling factorial, which is defined as a polynomial:
n k = n k _ = n n − 1 n − 2 ⋯ n − k + 1 = ∏ k = 1 n n − k + 1 .
This formula holds true for the usual definitions when n is a nonnegative integer. For any complex number n and real numbers x and y with x > y , the following equation holds:
x + y n = ∑ k = 0 ∞ n k x n − k y k = x n + n x n − 1 y + n n − 1 2 ! x n − 2 y 2 + n n − 1 n − 2 3 ! x n − 3 y 3 + ⋯ .
The series for the cube root can be obtained by setting n = 1 / 3 , which gives:
x + y 1 3 = x 1 3 + 1 3 x − 2 3 y − 1 9 x − 5 3 y 2 + 5 81 x − 8 3 y 3 + ⋯ .
At long distances where r > 3 G m 3 , the equation becomes:
a = r 3 + 3 G m 3 − r = r + 1 3 r − 2 3 G m − 1 9 r − 5 3 G m 2 + 5 81 r − 8 3 G m 3 + ⋯ − r , a = G m r 2 − 1 r G m r 2 2 + 5 3 r 2 G m r 2 3 + ⋯ .
Then introduce a new variable β , the equation can be simplified to:
a = G m r 2 + β , β = − 1 r G m r 2 2 + 5 3 r 2 G m r 2 3 + ⋯ , lim r → ∞ β = 0.
At the surface of the Earth, the variable β is approximately − 0.00001513417 , which is negligible and can be omitted. This is the reason why it is extremely close to Newton’s value at long distances.
At short distances where 3 G m 3 > r , the form of the equation is different:
a = 3 G m + r 3 3 − r = 3 G m 1 3 + 1 3 3 G m − 2 3 r 3 − 1 9 3 G m − 5 3 r 6 + 5 81 3 G m − 8 3 r 9 + ⋯ − r , a = 3 G m 3 − r 1 − 1 3 r 3 G m 3 2 + 1 9 r 3 G m 3 5 − 5 81 r 3 G m 3 8 + ⋯ .
In Chapter 7 of the book “Why String Theory?”, it is mentioned that there is no direct experimental evidence for the String Theory. [32] To avoid encountering the same issue of unverifiability as String Theory, the author makes a prediction about the surface gravity of neutron star.
The Crab Pulsar (PSR B0531+21) has a mass of 1.4 solar masses (M☉) and a radius of approximately 10500   m . [33] The solar mass (M☉) is a standard unit of mass in astronomy, equal to approximately 1.98847 × 10 30   kg . On the surface of Crab Pulsar, the gravitational acceleration is:
a 1 = G m r 2 ≈ 1.68523274 × 10 12   m / s 2 , a 2 = 3 G m + r 3 3 − r ≈ 8.21924883 × 10 6   m / s 2 .
Newton’s prediction of 1.68523274 × 10 12   m / s 2 , which is significantly greater than the speed of light in vacuum, 2.9979 × 10 8   m / s , and this leads to the formation of a black hole, clearly deviates from what is expected. In contrast, the predicted value from the Space Theory, 8.21924883 × 10 6   m / s 2 , aligns more closely with reality.
In addition, the distance can also be determined by the gravitational acceleration, it can be rewritten as:
r 1 = G m a , r 2 = G m a − 1 12 a 2 − 1 2 a .
And the product of variables, G and m , becomes:
G m 1 = a r 2 , G m 2 = a r 2 + a 2 r + 1 3 a 3 .
As you can see, when the acceleration is very small, the results between the two formulas will be very close. Due to the modification of the Newton’s law, the orbital velocity also requires a corresponding adjustment, and it can be expressed in the following form:
V 2 = π r 2 , S α β = π r + α 2 − r 2 .
The temporary variables, S α β and α , will be removed in the final formula. Assuming the new formula is equal to the original one at long distances, it can be rewritten as:
S α β = 2 π r α 1 + α 2 r , α = S α β 2 π r = G m r , S α β = 2 π G m .
Therefore, the equation can be simplified to:
S α β = 2 π G m = π r + α 2 − r 2 , α = 2 G m + r 2 − r .
At long distances where r > 2 G m , the equation becomes:
α = 2 G m + r 2 − r = G m r − 1 2 r G m r 2 + 1 2 r 2 G m r 3 + ⋯ . Therefore, the new orbital velocity formula is:
α = v 2 , v = 2 G m + r 2 − r .
The mass of the Earth is approximately 5.97237 × 10 24   kg , and the mass of the Moon is approximately 7.342 × 10 22   kg . [25,27] The time-averaged distance between the centers of the Earth and Moon is about 3.844 × 10 8   m . [29] The orbital velocity is:
v 1 = G m 1 + m 2 r ≈ 1024.54383   m / s , v 2 = 2 G m 1 + m 2 + r 2 − r ≈ 1023.84606   m / s .
And the relative error is:
η = 1 − v 2 v 1 ≈ 0.0006815.
The modified formula resolves the issue of approaching infinity as the distance nears zero. Similarly, the distance of the orbit can also be determined by velocity, it can be rewritten as:
v 2 + r 2 = 2 G m + r 2 , r = G m v 2 − 1 2 v 2 .
When the orbital velocity is 1024   m / s , the distance is:
r 1 = G m 1 + m 2 v 2 ≈   3.84808   × 10 8   m , r 2 = G m 1 + m 2 v 2 − 1 2 v 2 ≈ 3.84284   × 10 8   m .
And the relative error is:
η = 1 − r 2 r 1 ≈ 0.0013643.

Electromagnetism

The same formula can also be used to calculate the electrostatic force. Interpret the formula as describing the propagation of photons in three-dimensional space, extending as a hollow sphere, with the number of particles remaining constant, and the density decreasing with distance, causing changes in the electric field. Therefore, the electric field can also be represented using the formula:
E μ ν = 4 π k e q = 4 3 π r + a 3 − r 3 , E = 3 k e q + r 3 3 − r .
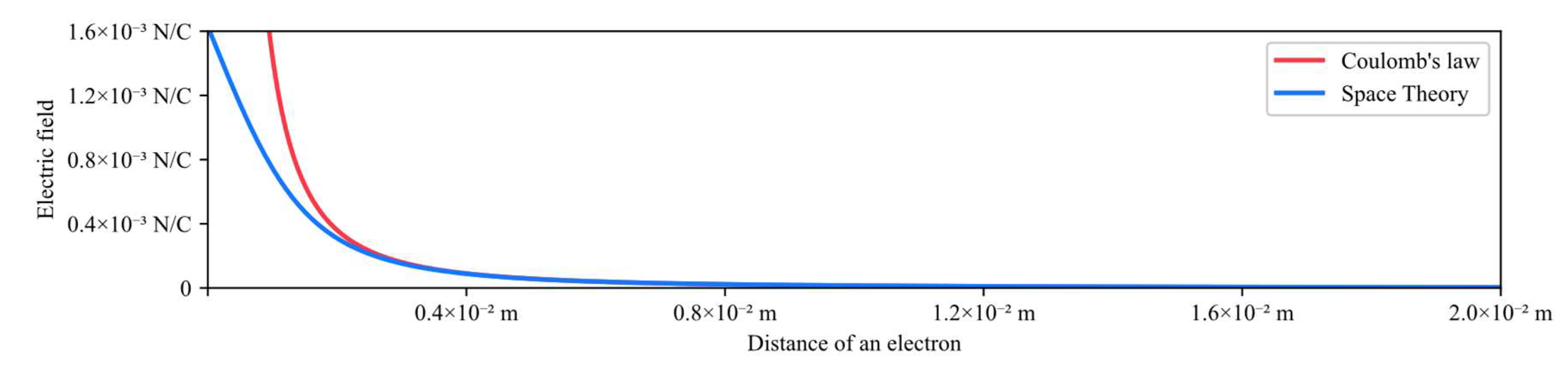
Where E μ ν is the electric field of photons, k e is the Coulomb constant, and q is the quantity of each charge. The Coulomb constant is about 8.98755179 × 10 9   N m 2 / C 2 , and the electric charge of a single electron is approximately 1.602176634 × 10 − 19   C [34]. If the distance of an electron is 1   m , the electric field is:
E 1 = k e q r 2 ≈ 1.43996426069 × 10 − 9   N / C , E 2 = 3 k e q + r 3 3 − r ≈ 1.43996425861 × 10 − 9   N / C .
And the relative error is:
η = 1 − E 2 E 1 ≈ 0.0000000014399642593.
The further the distance between the objects, the closer the values of the formulas.
Preprints 100733 g010
Figure 10. The electric field of an electron.
Figure 10. The electric field of an electron.
Preprints 100733 g010
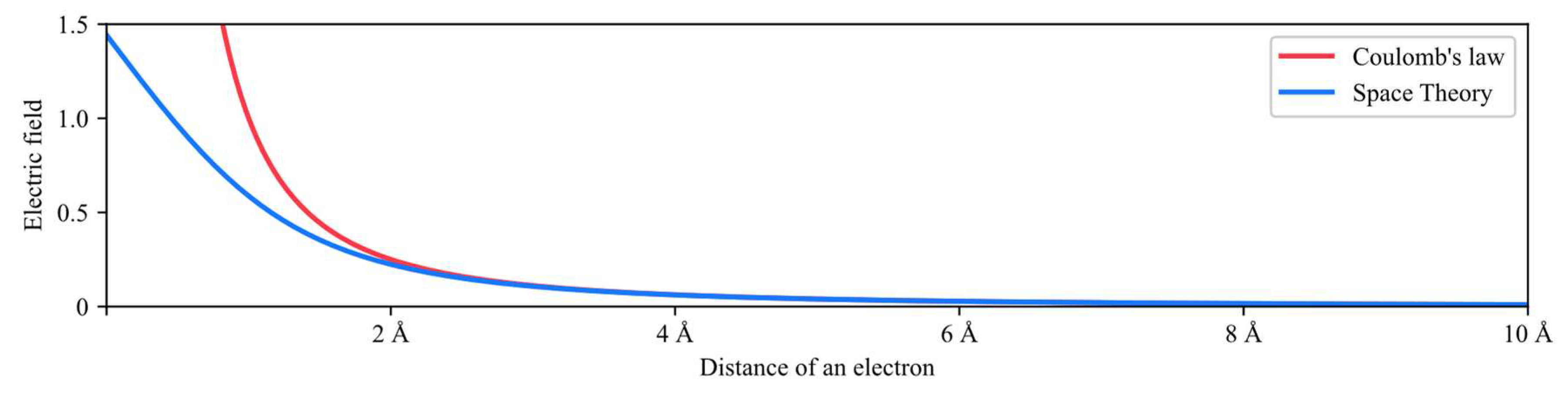
In the geometrized unit system, where ℏ = e = G = k e = 1 and ε 0 = 1 / 4 π . For the convenience of calculation, here Z represents the atomic number of the atom, and the quantity of charge is set to 1 . Therefore, at a distance of 2 Å, the electric field of the hydrogen atom Z = 1 is:
E 1 = Z r 2 ≈ 0.25 , E 2 = 3 Z + r 3 3 − r ≈ 0.22398009.
And at a distance of 1 Å, the electric field is:
E 1 = Z r 2 ≈ 1 , E 2 = 3 Z + r 3 3 − r ≈ 0.58740105.
However, when the distance is zero, the electric field obtained from the classical method is infinite:
E 1 = Z r 2 ≈ ∞ , E 2 = 3 Z + r 3 3 − r ≈ 1.44224957.
By modifying the formula, the calculated values are corrected, and at the same time, there is no longer a need to calculate the interaction between molecules through extremely complex methods like probability clouds. The variation in the geometrized unit system is illustrated in the diagram.
Preprints 100733 g011
Figure 11. The electric field of a hydrogen atom.
Figure 11. The electric field of a hydrogen atom.
Preprints 100733 g011
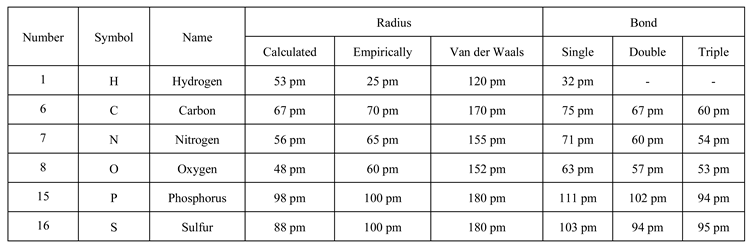
Carbon, hydrogen, nitrogen, oxygen, phosphorus, and sulfur are the six most important chemical elements whose covalent combinations make up most biological molecules on Earth. [35] The following table shows atomic radius, Van der Waals radius and covalent bond from theoretical models. [36,37,38,39,40]
Table 4. Atomic radius from theoretical models.
Table 4. Atomic radius from theoretical models.
Preprints 100733 i004
And the typical bond lengths and bond energies are: [41]
Table 5. Typical bond lengths and bond energies.
Table 5. Typical bond lengths and bond energies.
Preprints 100733 i005
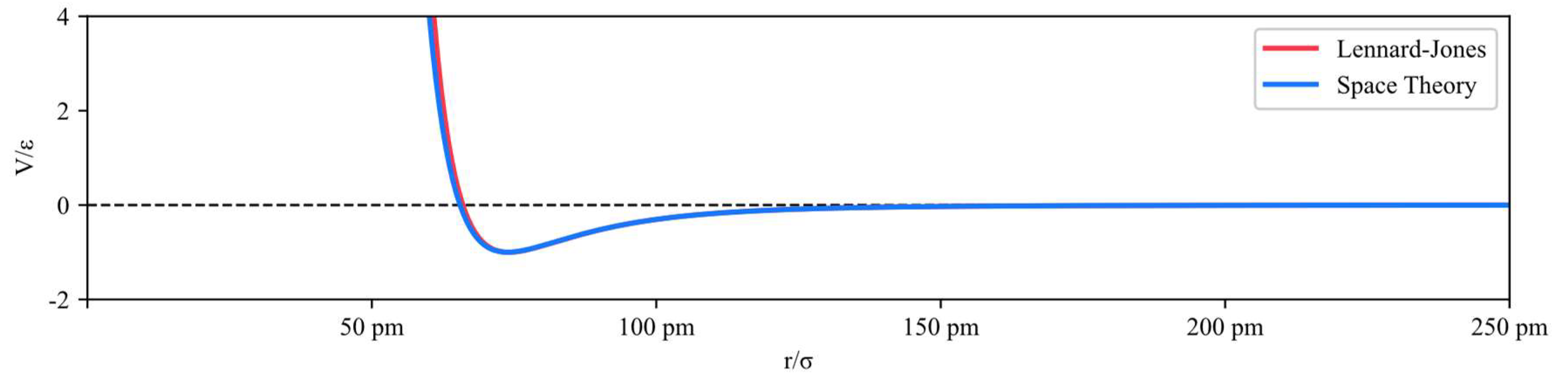
The Lennard-Jones potential characterizes intermolecular interactions within pairs. This potential model accounts for both soft repulsive and attractive (van der Waals) forces and is applicable to electronically neutral atoms or molecules. The commonly employed expression for the Lennard-Jones potential is: [42,43,44]
V r = 4 ε σ r 12 − σ r 6 .
Where r represents the distance between two interacting particles, ε represents the depth of the potential well, commonly known as the ‘dispersion energy’, and σ represents the distance at which the particle-particle potential energy V r equals zero, often termed the ‘size of the particle’. To simplify the formula the potential energy term can be rewritten as:
x 2 − x = x − 1 2 2 − 1 4 , x = σ r 6 , V r = 4 ε σ r 6 − 1 2 2 − 1 4 .
However, as the distance approaches zero, the result tends toward infinity. Therefore, the formula is rewritten using the hollow sphere model:
The temporary variables, S α β and α , will be removed in the final formula. Assuming the new formula is equal to the original one at long distances, it can be rewritten as:
α = 15 16 S α β π 3 r 6 = σ 6 r 6 , S α β = 16 15 π 3 σ 6 .
So the equation becomes:
S α β = 16 15 π 3 σ 6 = 16 105 π 3 r + α 7 − r 7 , α = 7 σ 6 + r 7 7 − r .
Therefore, the modified formula of Lennard-Jones potential is:
V r = 4 ε 7 σ 6 + r 7 7 − r − 1 2 2 − 1 4 .
The bond length of the H − H molecule is 74   p m , so the σ is:
σ = r 1 2 6 ≈ 65.9265   p m ,
σ = 1 7 1 2 + r 7 − r 7 6 ≈ 66.1498   p m .
When r is 74   p m and σ is 66   p m , the result is:
V r ε = 4 σ r 6 − 1 2 2 − 1 4 ≈ − 0.999955 , V r ε = 4 7 σ 6 + r 7 7 − r − 1 2 2 − 1 4 ≈ − 0.999824.
And the relative error is:
η ≈ 0.0001305948.
When r is 25   p m , the result is:
V r ε = 4 σ r 6 − 1 2 2 − 1 4 ≈ 457111.776567 , V r ε = 4 7 σ 6 + r 7 7 − r − 1 2 2 − 1 4 ≈ 2018.975417.
As you can see, when the distance decreases to 25   p m , the distance corresponds to the empirically measured atomic radius, the result become quite absurd. When the distance is zero, the result is infinite:
V r ε = 4 σ r 6 − 1 2 2 − 1 4 ≈ ∞ , V r ε = 4 7 σ 6 + r 7 7 − r − 1 2 2 − 1 4 ≈ 2246.52951.
The variation is illustrated in the diagram.
Preprints 100733 g012
Figure 12. Lennard-Jones potential of a hydrogen bond.
Figure 12. Lennard-Jones potential of a hydrogen bond.
Preprints 100733 g012
In summary, formulas inversely proportional to the distance r raised to the power of n can all be replaced with the hollow sphere model.
lim r → ∞ x r n = lim r → ∞ n + 1 x + r n + 1 n + 1 − r .
This paper is not yet complete.

Discussion

To ensure the accuracy of calculations, the author recommends using the Decimal Module in Python, and suggests setting precision to 100 digits. As of this writing, graviton has not been found yet.

Funding

None.

Acknowledgments

I would like to thank the scientists who study String Theory and make outstanding contributions to physics. The thickening speed of physics journals has surpassed the speed of light, but this doesn’t violate the theory of relativity, because those journals aren’t transmitting any information.
Competing interests: None.

References

  1. I. Newton. (1687). “Philosophiae Naturalis Principia Mathematica.” The Mathematical Principles of Natural Philosophy.
  2. A. Einstein. (1905). “Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig.” Annalen der Physik, 4, 18, 639–641.
  3. A. Einstein, M. Grossmann. (1913). “Entwurf einer verallgemeinerten Relativitätstheorie und eine Theorie der Gravitation.” Zeitschrift für Mathematik und Physik, 62, 225–244, 245–261.
  4. A. Einstein, A.D. Fokker. (1913). “Nordströmsche Gravitationstheorie vom Standpunkt des absoluten Differentialkalküls.” Annalen der Physik, 4, 40, 551–560.
  5. A. Einstein. (1916). “Die Grundlage der allgemeinen Relativitätstheorie.” Annalen der Physik, Vierte Folge, Band 49, 769-822.
  6. R. Penrose. (1965). “Gravitational Collapse and Space-Time Singularities.” Physical Review Letters. American Physical Society, 14, 57-59. [CrossRef]
  7. A. Frankowski, N. Soker. (2009). “Very late thermal pulses influenced by accretion in planetary nebulae.” New Astronomy, 14, 8, 654-658. [CrossRef]
  8. K. Schwarzschild. (1916). “Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie.” Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, Seite 189-196.
  9. D. Clery. (2020). “Black holes caught in the act of swallowing stars.” Science, 367, 6477, 495. [CrossRef]
  10. S.W. Hawking. (1974). “Black hole explosions.” Nature 248, 30–31. [CrossRef]
  11. E. Hubble. (1929). “A relation between distance and radial velocity among extra-galactic nebulae.” PNAS 15, 3, 168-173. [CrossRef]
  12. O.W. Greenberg. (1964). “Spin and Unitary Spin Independence in a Paraquark Model of Baryons and Mesons.” Physical Review Letters, 13, 598–602. [CrossRef]
  13. B. Pontecorvo. (1958). “Mesonium and Antimesonium.” Soviet Journal of Experimental and Theoretical Physics, 6, 429–431.
  14. E. Kearns, T. Kajita, Y. Totsuka. (1999). “Detecting Massive Neutrinos.” Scientific American, 281, 64–71. [CrossRef]
  15. A. McDonald, J. Klein, D. Wark. (2006). “Solving the Solar Neutrino Problem.” Scientific American, 288, 40–49. [CrossRef]
  16. V. Hatton. (1991). “Operational history of the SPS collider 1981-1990.” Conference Record of the 1991 IEEE Particle Accelerator Conference, 2952-2954. [CrossRef]
  17. R. Pfleegor, L. Mandel. (1967). “Interference of Independent Photon Beams.” Physical Review, 159, 5, 1084–1088. [CrossRef]
  18. W. Wootters, W. Zurek. (1979). “Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr’s principle.” Physical Review D, 19, 2, 473–484. [CrossRef]
  19. A. Peruzzo, P. Shadbolt, et al. (2012). “A Quantum Delayed-Choice Experiment.” Science, 338, 6107, 634–637. [CrossRef]
  20. X. Ma, J. Kofler, et al. (2012). “Quantum erasure with causally disconnected choice.” Proceedings of the National Academy of Sciences, 110, 4, 110–1226. [CrossRef]
  21. M. Alonso, E. Finn. (1968). “Fundamental University Physics Volume III: Quantum and Statistical Physics.” Addison Wesley, ISBN 978-0-201-00262-1.
  22. R. Oerter. (2006). “The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics.” Penguin Group, ISBN 978-0-13-236678-6.
  23. J. Forshaw, G. Smith. (2014). “Dynamics and Relativity.” John Wiley & Sons, ISBN 978-1-118-93329-9.
  24. B. Luzum, N. Capitaine, A. Fienga, et al. (2011). “The IAU 2009 system of astronomical constants: The report of the IAU working group on numerical standards for Fundamental Astronomy.” Celestial Mechanics and Dynamical Astronomy, 110, 293–304. [CrossRef]
  25. F. Chambat, B. Valette. (2001). “Mean radius, mass, and inertia for reference Earth models.” Physics of the Earth and Planetary Interiors, 124, 3–4, 234–253. [CrossRef]
  26. P. Mohr, D. Newell, B. Taylor. (2016). “CODATA Recommended Values of the Fundamental Physical Constants: 2014.” Journal of Physical and Chemical Reference Data, 45, 4, 1527–1605. [CrossRef]
  27. M. Wieczorek, B. Jolliff, A. Khan, et al. (2006). “The Constitution and Structure of the Lunar Interior.” Reviews in Mineralogy and Geochemistry, 60, 1, 221–364. [CrossRef]
  28. C. Hirt, W.E. Featherstone. (2012). “A 1.5 km-resolution field model of the Moon.” Earth and Planetary Science Letters, 329–330, 22–30. [CrossRef]
  29. J. Battat, T. Murphy, E. Adelberger, et al. (2009). “The Apache Point Observatory Lunar Laser-ranging Operation (APOLLO): Two Years of Millimeter-Precision Measurements of the Earth-Moon Range.” Astronomical Society of the Pacific, 121, 875, 29–40. [CrossRef]
  30. 30. G. Poole. (2019). “Cosmic Power Generation and Gravity.” Journal of High Energy Physics, Gravitation and Cosmology, 5, 920-927. [CrossRef]
  31. E. Pitjeva, E. Standish. (2009). “Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit.” Celestial Mechanics and Dynamical Astronomy, 103, 365–372. [CrossRef]
  32. J. Conlon. (2016). “Why string theory?” CRC Press.
  33. D. Jeffery. (n.d.). “Neutron Stars and the Crab Nebula.” University of Nevada, Las Vegas.https://www.physics.unlv.edu/~jeffery/astro/neutron_star/crab_nebula.html.
  34. NIST. (2019). “2018 CODATA Value: vacuum electric permittivity.” The NIST Reference on Constants, Units, and Uncertainty.
  35. E. Frieden. (1972). “The chemical elements of life.” Scientific American, 227(1), 52-64.
  36. E. Clementi, D. L. Raimondi, W. P. Reinhardt. (1967). “Atomic screening constants from SCF functions. II. Atoms with 37 to 86 electrons.” The Journal of chemical physics, 47(4), 1300-1307.
  37. A. V. Bondi. (1964). “van der Waals volumes and radii.” The Journal of physical chemistry, 68(3), 441-451.
  38. P. Pyykkö, M. Atsumi. (2009). “Molecular single-bond covalent radii for elements 1–118.” Chemistry–A European Journal, 15(1), 186-197.
  39. P. Pyykkö, M. Atsumi. (2009). “Molecular double-bond covalent radii for elements Li–E112.” Chemistry–A European Journal, 15(46), 12770-12779.
  40. P. Pyykkö, S. Riedel, M. Patzschke. (2005). “Triple-bond covalent radii.” Chemistry–A European Journal, 11(12), 3511-3520.
  41. Carruth, Gorton, Ehrlich, Eugene. “Bond Energies.” Volume Library. Ed. Carruth, Gorton. Vol 1. Tennessee: Southwestern, 2002.
  42. Jones, John Edward. “On the determination of molecular fields.—I. From the variation of the viscosity of a gas with temperature.” Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 106.738 (1924): 441-462.
  43. Jones, John Edward. “On the determination of molecular fields.—II. From the equation of state of a gas.” Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 106.738 (1924): 463-477.
  44. Lennard-Jones, John E. “Cohesion.” Proceedings of the Physical Society 43.5 (1931): 461.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated