Preprint
Article
Primordial Planets with an Admixture of Dark Matter Particles and Baryonic Matter
Altmetrics
Downloads
208
Views
276
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 June 2023
Posted:
28 June 2023
You are already at the latest version
Alerts
Abstract
It has been suggested that primordial planets could have formed in the early Universe and the missing baryons in the Universe could be explained by primordial free-floating planets of solid hydrogen. Many such planets were recently discovered around the old and metal poor stars and such planets could have formed at early epochs. Another possibility for missing baryons in the Universe could be that these baryons are admixed with DM particles inside the primordial planets. Here we discuss the possibility of admixture of baryons to the DM primordial planets discussed earlier. We consider gravitationally bound DM objects with the DM particles constituting them varying in mass from 20 to100GeV. Different fractions of DM particles mixed with baryonic matter in forming the primordial planets are discussed. For the different mass range of DM particles forming DM planets, we have estimated the radius and density of these planets with different fractions of DM and baryonic particles. It is found that for heavier mass DM particles with the admixture of certain fractions of baryonic particles, the mass of the planet increases and can reach or even substantially exceed Jupiter-mass. The energy released during the process of merger of such primordial planets is discussed. Also the energy required for the tidal breakup of such an object in the vicinity of a black hole is also discussed.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Dark Matter (DM), almost five times more abundant than ordinary matter, is theorized as one of the basic constituents of the Universe. Many experiments are running worldwide to detect these DM particles but till now the interaction of these particles with the ordinary matter has proven to be so feeble that they have escaped direct detection [1]. In the cosmic structure formation, the lightest objects would have formed first, i.e. the structure formation is a bottom-up scenario. It is of interest to note that the earliest objects to form could perhaps have been primordial planets dominantly composed of DM. The formation of such objects and their presence in large numbers in our galaxy could significantly reduce the number of free DM particles moving around in the Universe. The typical mass of such objects, made up mostly of DM particles of mass , is given by [2,3].
where is the Planck mass given by . If we consider the mass of DM particles to be 60𝐺𝑒𝑉, favored from the detection of excess of gamma rays from the galactic centre, attributed to the decay of 60𝐺𝑒𝑉 DM particles [4], the mass of the DM object works out to be which is the mass of Neptune. The radius of the DM object is given by [5]
where 𝐺 is the gravitational constant and is the DM particle mass [6].
As the density of these objects fall of as , the objects formed at later epochs would have a lower mass. If we consider the object density at a value 100 times the ambient density, say at , we get a lower mass limit of the object as ≈ (typical asteroid mass). So the mass range of these DM objects will be from (asteroid mass) extending to the mass of Neptune. These objects could have formed in the early epochs of the Universe (when local DM density was much higher) and be in existence even now.
Existence of (baryonic) primordial planets have been considered earlier by many authors [7,8]. In the recent paper [9] we had discussed possibility of DM at high redshifts forming primordial planets composed entirely of DM to be one of the reasons for not detecting DM as the flux of ambient DM particles would be consequently reduced. The evolution of these DM primordial planets is discussed in detail in [10]. In [11], we had proposed that the hypothesised Planet 9, in our solar system ([12,13]), could indeed be such a DM planet, with a mass about that of Neptune. This might explain why it has not been visibly detected so far.
Here we discuss the possibility of baryons getting mixed with the DM particles in forming these primordial objects. During the phase of formation of these primordial objects, as the primeval ambient cloud collapses we consider the presence of baryonic matter in addition to the DM particles.
2. Mass and Radius of DM Planet Admixed with Baryonic Matter
If is the total mass of DM particles and is the total mass of baryonic particles in forming the primordial planet, then the total mass () of the planet is given by
The gravitational binding energy density () of such a planet of radius 𝑅 admixed with both baryons and DM is given by
As the DM particles gets admixed with baryonic particles in forming these structures, the DM particles will exert pressure and the DM degeneracy pressure is given by [14]
where 𝑅 is the radius of planet and is the mass of DM particle forming the planet. On the other hand, baryonic particles when they get admixed, in addition to degeneracy pressure like DM particles, they will also exert thermal and radiation pressure. The degeneracy pressure exerted by the baryons is given by [15]
where is proton mass. It is assumed that the gravitational self energy goes into heating only the baryonic particles of mass as it is assumed that the DM does not interact with radiation. Thus . This leads to equation (7) and equation (8). The thermal pressure and the radiation pressure exerted by the baryonic particles is given by
where is the gas constant, and 𝑇 is the temperature of baryonic matter given by
where is Boltzmann constant. The radiation pressure is given by
where 𝑎 is Stefan’s constant.
For forming the planet admixed with DM and baryonic particles, the gravitational binding energy density of the planet must be in balance with the radiation pressure, thermal pressure and degeneracy pressure of baryonic and DM particles. Thus,
where is the total mass of the planet, is the total mass of baryonic particles, is the total mass of DM particles, 𝑅 is the radius of the planet, is the mass of DM particle, is mass of proton, is Stefan’s constant and is Boltzmann constant.
If we assume a fraction of baryonic particles getting mixed with fraction of DM particles, then and in equation (1) can be replaced by and respectively. Thus equation (10) becomes,
The mass of the planet formed with these particles [3] will be given by
where is the effective mass of the constituent particles forming the planet given by
When the effective mass is considered for the planetary formation, the mass of the object will increase (can be more than Jupiter mass) beyond the maximum limit () proposed for DM planets [11]. This happens because the effective mass is reduced, since .
Consider such a planet with 50% of DM (assuming of 60GeV) and 50% of baryonic matter, the mass of the planet is , where is the mass of Jupiter. For the planet of this mass, the baryonic radiation pressure will be very small compared to the degeneracy and thermal pressures. Hence the radiation pressure can be neglected from equation (11). Thus
Thus, the radius of the object from the above equation becomes
For the planet with mass , as discussed in the above case, the radius works out to be cm.
Table 1 shows the mass and radius of the primordial planets with an admixture of DM and baryonic particles of different fractions and for 60GeV DM particles. Figure 1 shows that the mass of DM planets with an admixture of baryonic particles increases their mass limit beyond the Neptune mass. For planets made entirely of DM, the maximum mass limit was Neptune mass and it can go down to asteroid mass. But with an admixture of DM and baryonic particles, the mass of the planet increases with the increase in the fraction of baryonic matter. When the baryonic fraction to that of DM particle increases, the planetary mass can increase and go beyond the Jupiter mass (up to about fifty Jupiter mass). It is also found that some objects can have sub stellar masses (above 50 Jupiter mass), like that of brown dwarfs. The radius of these planets (admixed with DM and baryonic matter) also increases with an increase in the fraction of baryonic matter. It is found from Figure 2 that if the DM particles involved in the formation of these planets are heavier, the size of the planets increases compared to the planets being formed by lighter DM particles.
3. Rotating DM Object Admixed with Baryonic Matter
In the previous section, we had discussed the possibility of formation of DM planets with an admixture of baryonic and DM particles. There could be one such object within half a light year for the density of DM around the solar neighbourhood [11]. These objects can rotate about their axis, thus emitting gravitational waves.
Consider such an object with DM and baryonic matter made up of DM particles of mass . The mass and radius of the object from Table 1 is and , where is Jupiter mass. The gravitational wave energy emitted per unit time by the rotating individual object is given by
where is the moment of inertia of object given by , is the frequency of rotating object and is the ellipticity of object. Then equation (16) becomes
The rotational frequency of DM object spinning close to breakup is given by
where is the gravitational constant. Thus, the maximum rotational frequency of the DM object is given by
Considering for the object of mass and , energy emitted per second works out to be with the frequency of which is well within the frequency of LIGO [16]. The typical period of rotation of object is . As the object rotates, it can break up emitting gravitational waves. The binding energy of the object will be emitted as gravitational waves. The binding energy of the object is given by
For the above object, the binding energy works out to be . The strain (in the gravitational wave detector) is calculated using the formula
where is the binding energy of the object, is speed of light and is the distance of object from Earth. If we consider this object at a distance of . from Earth, then the corresponding strain is .
4. Binary Systems of DM Objects Admixed with Baryonic Matter
These primordial planetary objects can form binary systems. Considering a binary system with each component of mass and size of 𝑐𝑚. and separation about ten times their size, the orbital period 𝑃 is given by
where is the orbital radius and is the total mass of the system. The orbital period works out to be 𝑃 = 0.27𝑠 and the corresponding frequency is 𝜔 = 23𝐻𝑧. The binary system will be emitting gravitational wave energy as it revolves and the energy emitted per unit time is given by
where 𝜖 is the eccentricity of orbit and 𝜇 is the reduced mass of system given by
and are the masses of individual objects in the binary system. During their orbit around one another they lose energy and the orbital radius keeps decreasing until it becomes . The final merger period and merger frequency of the binary system will be and . This frequency is also within the existing range of LIGO. The binding energy of the binary system will be emitted as gravitational waves and is given by
where
Figure 3 shows the orbital frequency of binary system of primordial objects admixed with baryonic matter versus fraction of baryonic matter. From the figure we can conclude that most of the frequency emitted by these binary systems falls under the LIGO range of frequency. Table 2 shows the gravitational wave energy emitted by the binary system for different fractions of baryons admixed with DM particles of mass ranging from 20 to 100 GeV in forming the planet. It is found that for greater mass DM particles, the energy emitted as gravitational waves decreases. As the fraction of baryons increases, the energy emitted by the binary system will increase. If we consider these binary systems to be situated at distance 𝑟 distance from Earth, then the strain, ℎ on earth due to the gravitational radiation emission from them is given by equation (21). If this binary system is assumed to be at distances and from Earth, then the strain due to the gravitational wave is and . The corresponding flux on Earth at these distances will be and 8 × .
5. Tidal Breakup of DM Object Admixed with Baryonic Matter Near a Black Hole
If a primordial degenerate object (as discussed in the above sections) of mass and radius approaches a BH of mass , the tidal force is given by
where d is the separation between the BH and the primordial object. The self-gravitational force of the object is given by
For the object to break up, the tidal force must be greater than the self-gravitational force of the object, i.e.,
Considering the distance between the BH and object to be around 10 times Schwarzchild radius (), the minimum mass of BH required for tidal break up of the object is given by
Figure 1 shows the mass of BH required for the tidal break-up of the primordial planet when it comes near the BH. The mass of the BH required for tidal break up increases with increase in mass of DM particles as well as with the fraction of baryons in the primordial planet. As these objects orbit the BH, they lose energy according to equation (23). Table 3 shows the gravitational wave energy emitted per second by the DM object consisting of different mass DM particles with different fractions of baryons in forming the primordial object. It is found that energy decreases with increase in the mass of DM particles.
When they lose energy, the orbital radius keeps decreasing until the radius becomes equal to Schwarzchild radius (𝑅𝑠𝑐ℎ). At the swarschild radius the frequency is given by [17]
where is the total mass of the system and the orbital radius . The orbital binding energy will be emitted as gravitational waves at this frequency. The time of merger of the primordial object with the BH is given by [18]
where 𝑐 is speed of light, 𝑟𝑖 is the initial orbital radius, 𝑀 is the total mass of system involving BH and object, 𝜇 is reduced mass of system and G is gravitational constant. For an object with 50% DM and 50% baryonic matter and made of 60GeV DM particle the merger time is .
Figure 5 shows the relation between the merger time and fraction of baryons in forming the primordial planet. It is found that the merger time increases with increase in DM particle mass. Also, the merger time increases with fraction of baryons, reaches a maximum for planets made of 60% baryonic matter.
6. Primordial Planetary Object at Galactic Centre
At the center of our galaxy is a BH of mass 4 million solar masses (. It appears reasonable to assume that stars near the Galactic center (several stellar clusters are known to exist near galactic center [19,20] have planets and other small orbiting bodies, such as asteroids and comets. When the parent star approaches the central black hole, tidal interaction may either strip these bodies off their parent stars or cause them to become more tightly bound. If we consider the primordial object orbiting around this BH, at . where R is the orbital radius, then according to Kepler’s law, the orbital frequency is given by
The system will lose energy as the object orbits around the central BH and the orbital radius keeps decreasing. The energy emitted per second is given by equation (23). For the primordial planet of mass and , energy emitted per unit time works out to be . At orbital radius equal to Schwazchild radius of central BH, the binding energy will be emitted as gravitational waves. The final orbital frequency and Energy emitted as gravitational waves for the above object works out to be and . The flux per unit time falling on Earth from the gravitational waves is given by
where is the energy emitted per unit time from the system and 𝑟 is the distance of Earth from center of galaxy equal to . The merger time of the object with the BH is given by equation (31) and for the above object .
Table 4 shows the variation of merger time with different fractions of baryons mixed with DM and with different mass of DM particles ranging from to .It is found that the merger time of the planet with the BH decreases as fraction of baryons increases in the primordial planet and also increases with increase in mass of DM particles in forming the planet. Considering the primordial planet at center of galaxy from Earth) the flux per unit time on Earth is very low, of the order of .
7. Possible Electromagnetic Radiation from Baryonic Fraction of the Merging Objects
If the objects were made of pure DM, the binding energy of the merging objects would be released as gravitational waves. In the case of primordial planet admixed with DM and baryons, the binding energy due to baryons will be emitted as electromagnetic waves (like merging neutron stars). Thus, during the merger, there will be emission of gravitational waves and electromagnetic waves by the baryonic particles inside the object. For objects with equal proportion of DM and baryonic matter, the energy released as EM waves will be of the order of and it will be emitted in the frequency range of gamma radiation. These gamma rays emitted would be in short duration bursts with the period same as final orbital period before merger (around 5 milli-second).
8. Conclusions
Here we discussed the possibility of admixture of baryons to the DM primordial planets with the DM particles varying in mass from 20GeV to 100 GeV. We have considered different fractions of admixture to form the planet. The mass of the primordial planet made completely of DM, ranges from asteroid mass to Neptune mass. Whereas, the mass of primordial planets (admixed with DM and baryonic matter) is found to increase with the fraction of baryonic matter in the planets and the mass of these objects can go well beyond the mass of Jupiter (around 40 times Jupiter mass) and can also approach sub stellar mass (Brown dwarf mass). So far, thousands of exoplanets have been discovered by the Kepler mission and more will be found by NASA’s Transiting Exoplanet Survey Satellite (TESS) mission, which is observing the entire sky to locate planets orbiting the nearest and brightest stars. Many exoplanets (Exo Jupiters) discovered so far fall in this mass range and we are not very sure whether these exoplanets are entirely made of baryons. Some of the exoplanets with mass several times Jupiter mass could be possible signatures of the presence of primordial planets with an admixture of baryonic and DM particles. It is also found that some of these planets could reach even sub stellar mass like that of brown dwarf [21]. Also, even if a small fraction of DM particles is trapped in these objects, the flux of ambient DM particles would be reduced significantly. This could be one of the many reasons for not detecting the DM particles in various experiments like XENON1T experiment etc. as suggested earlier. If two such primordial planets merge, they will release a lot of energy. The energy released and the time scale of merger of these objects is found to increase with the mass of primordial objects. The frequency of gravitational waves emitted during the merger is found to match with the frequency range of LIGO. The objects near the galactic center could consists of such primordial objects, planets, comets etc. Here we have also discussed the possibility of tidal break up of these primordial objects in the presence of a BH. The mass of BH required for tidal break up is calculated and it is found that the mass of BH required for tidal break up increases with the DM particle mass and also with the increase in fraction of baryons in these objects. The energy released in the form of gravitational waves as well as the frequency of emission is tabulated and again it is found that the frequency falls in the sensitivity range of LIGO.
Author Contributions
All authors contributed equally to the preparation of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arun K., Gudennavar S., Sivaram C., 2017, Advances in Space Research, 60, 166.
- Sivaram C., Arun K., 2011b, Astrophysics and Space Science, 334, 225.
- Sivaram C., 1994, Astrophysics and Space Science, 219, 135.
- Huang X.-J., Zhang W.-H., Zhou Y.-F., 2016, Physical Review D, 93, 115006.
- Sivaram C., Arun K., 2011a, arXiv preprint arXiv:1109.5266.
- Gelmini G. B., 2006, in Journal of Physics: Conference Series. p. 040.
- Shchekinov Y. A., Safonova M., Murthy J., 2013, Astrophysics and Space Science, 346, 31.
- Wickramasinghe N. C., Wallis J., Wallis D. H., Schild R. E., Gibson C. H., 2012, Astrophysics and Space Science, 341, 295.
- Sivaram ., Arun K., Kiren OV., 2019, Earth, Moon, and Planets, 122, 115.
- Kiren OV., Arun K., Sivaram C., 2021, Advances in Space Research, 68, 2050.
- Sivaram C., Kenath A., Kiren O., 2016b, Astrophysics and Space Science, 361, 1.
- Batygin K., Brown M. E., 2016, The Astronomical Journal, 151, 22.
- Trujillo C. A., Sheppard S. S., 2014, Nature, 507, 471.
- Sivaram, C. , Arun K., 2009, arXiv preprint arXiv:0910. 2306. [Google Scholar]
- Agrawal V., Barr S. M., Donoghue J. F., Seckel D., 1997, arXiv preprint hep-ph/9707380.
- Abbott B. P., et al., 2016, Physical review letters, 116, 061102.
- Sivaram C., Arun K., Kiren O., 2016a, 100 Years of Einstein’s Theory of Relativity: An Introduction to Gravity and Cosmology.
- Sivaram C., Arun K., 2010, arXiv preprint arXiv:1005.3431.
- Figer D. F., Kim S. S., Morris M., Serabyn E., Rich R. M., McLean I. S., 1999, The Astrophysical Journal, 525, 750.
- Cotera A. S., Erickson E. F., Colgan S. W., Simpson J. P., Allen D. A., Burton M. G., 1996, The Astrophysical Journal, 461, 750.
- Kirkpatrick J. D., et al., 2021, The Astrophysical Journal Letters, 915, L6.
Figure 1.
Mass of the primordial planet versus fraction of baryons in the.
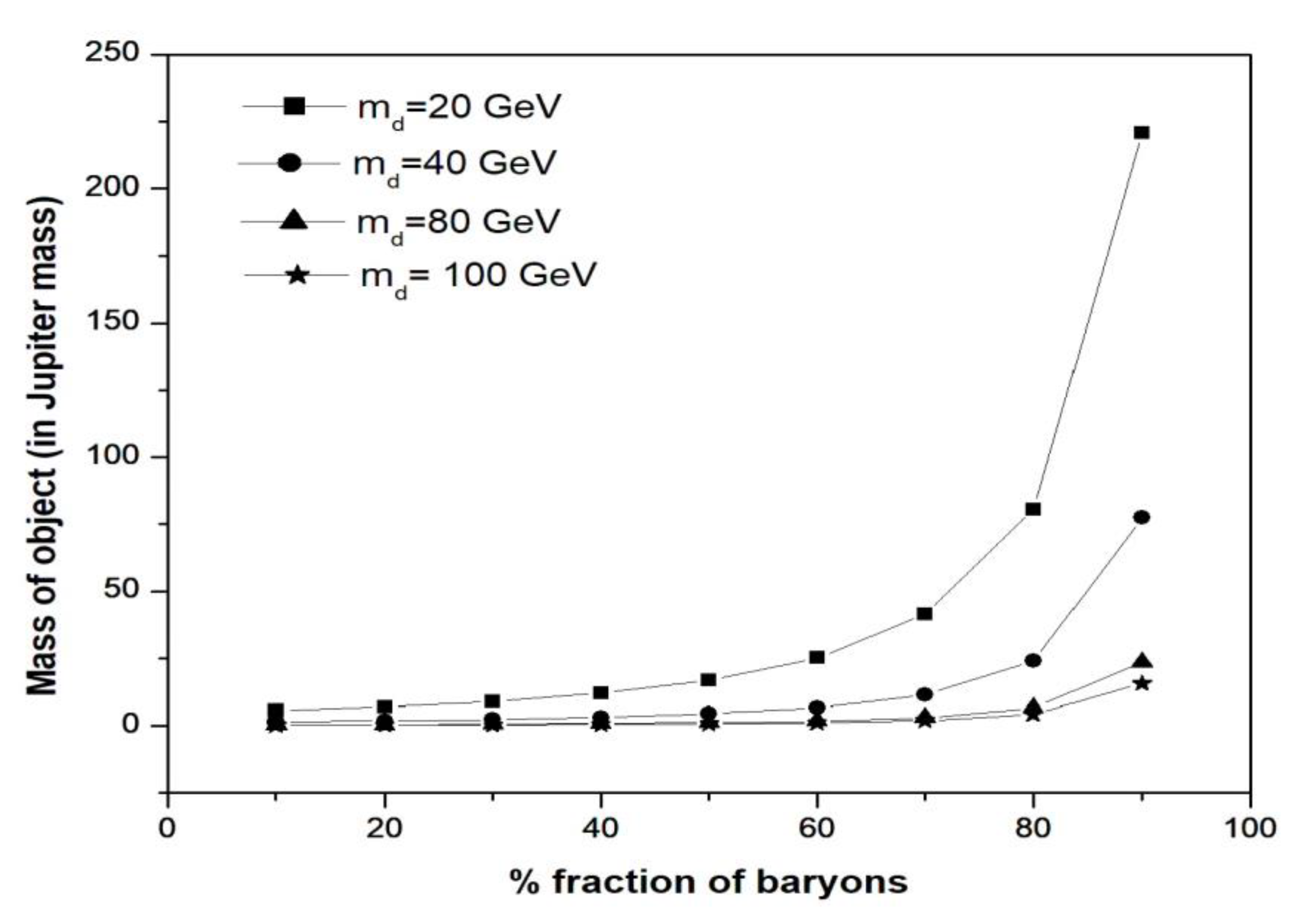
Figure 2.
Radius of the primordial planet versus fraction of baryons in the.
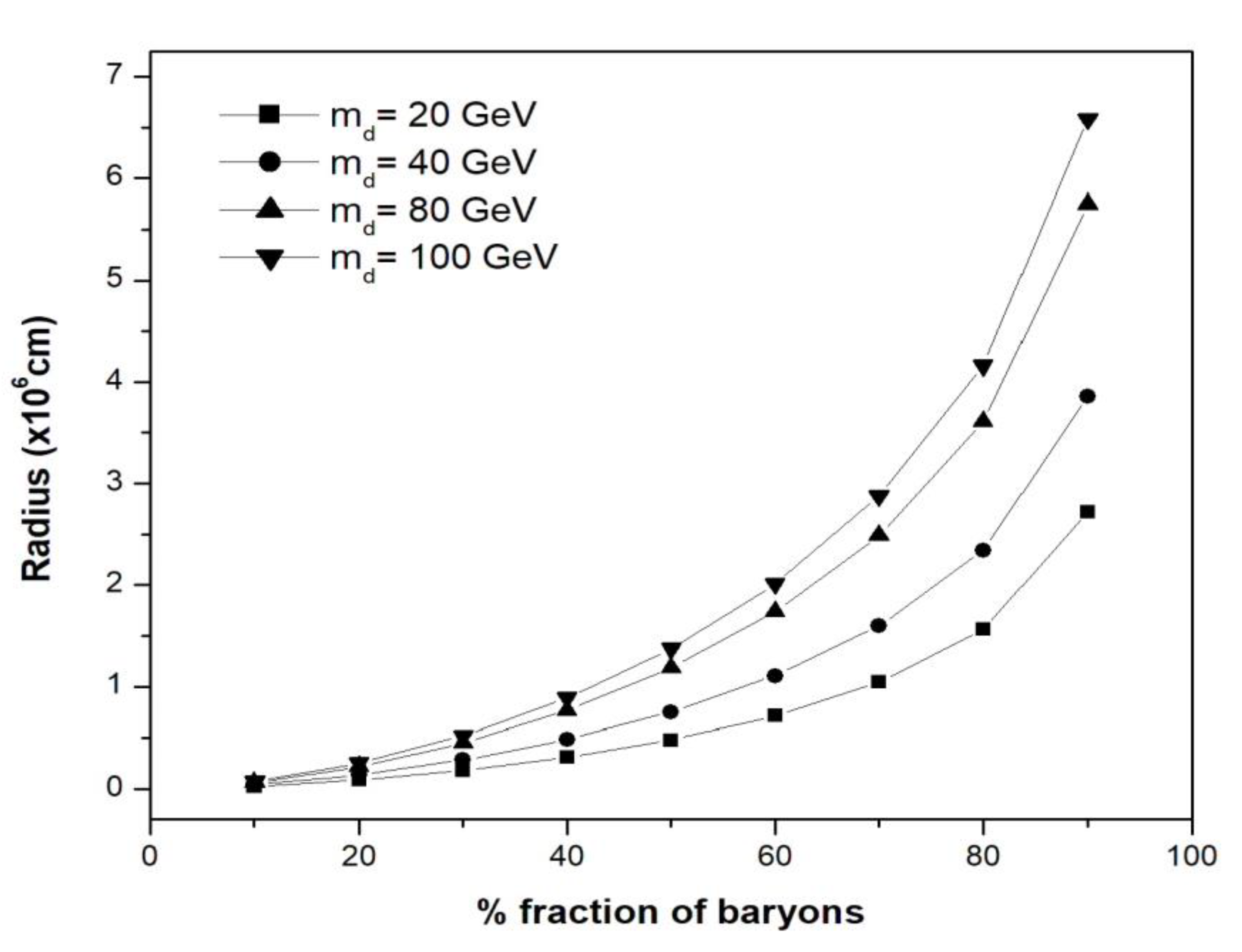
Figure 3.
Orbital Frequency of binary system of primordial planets admixed.
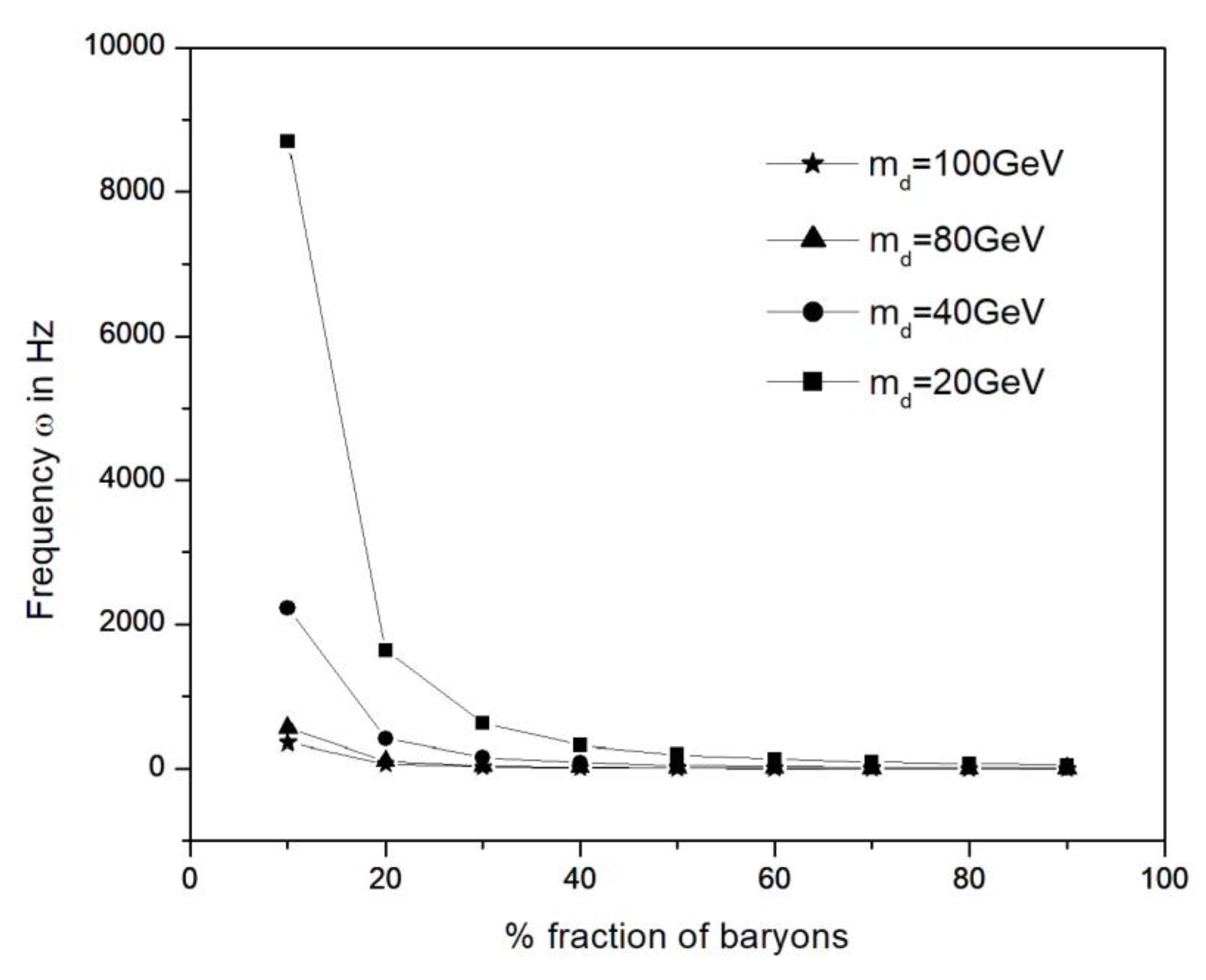
Figure 4.
Mass of BH for tidal break up versus fraction of baryonic particles admixed to form the primordial planet.
Figure 4.
Mass of BH for tidal break up versus fraction of baryonic particles admixed to form the primordial planet.
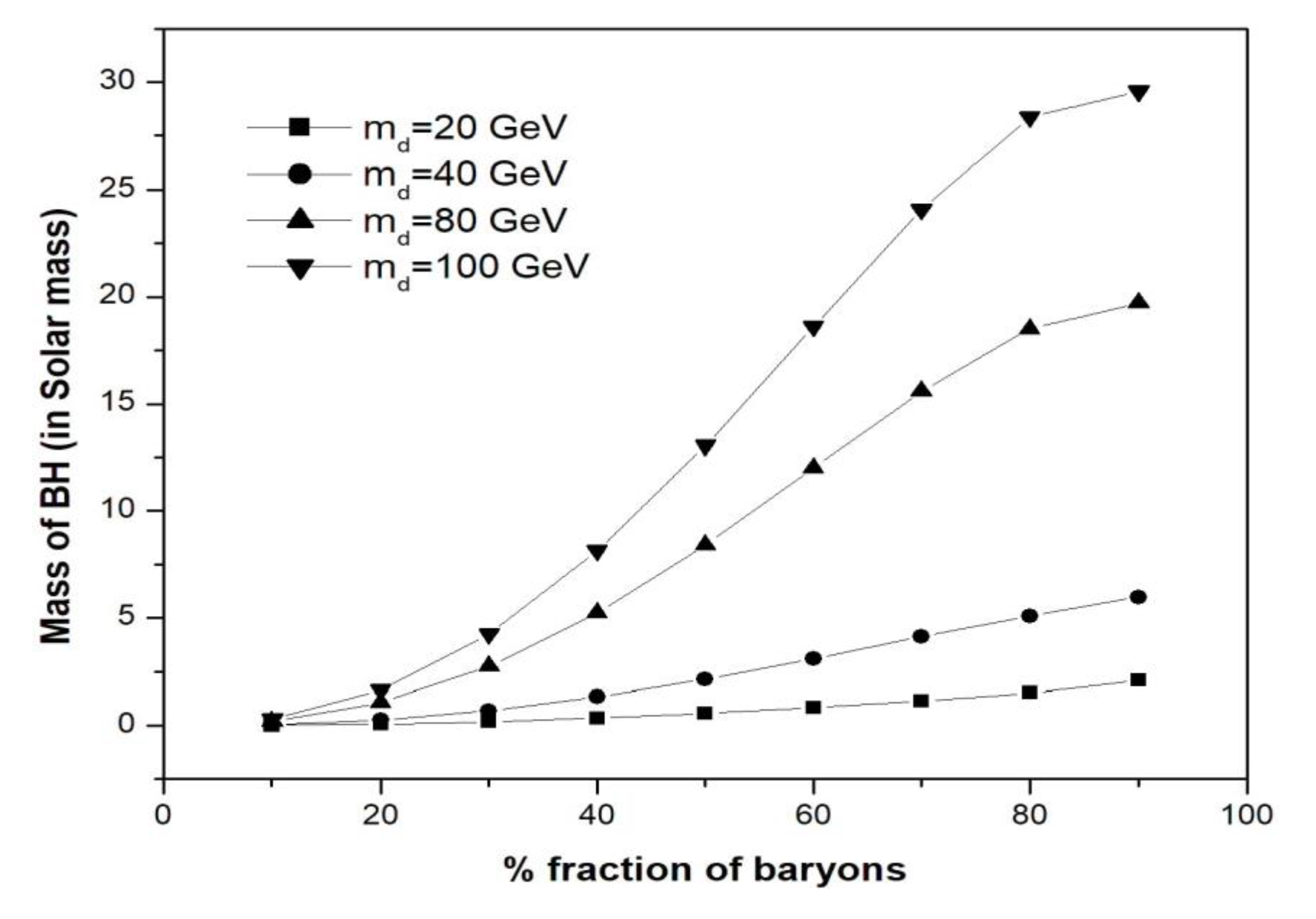
Figure 5.
Merger time versus fractions of baryons in forming the primordial planet for DM particles of mass 40GeV and 100 GeV.
Figure 5.
Merger time versus fractions of baryons in forming the primordial planet for DM particles of mass 40GeV and 100 GeV.
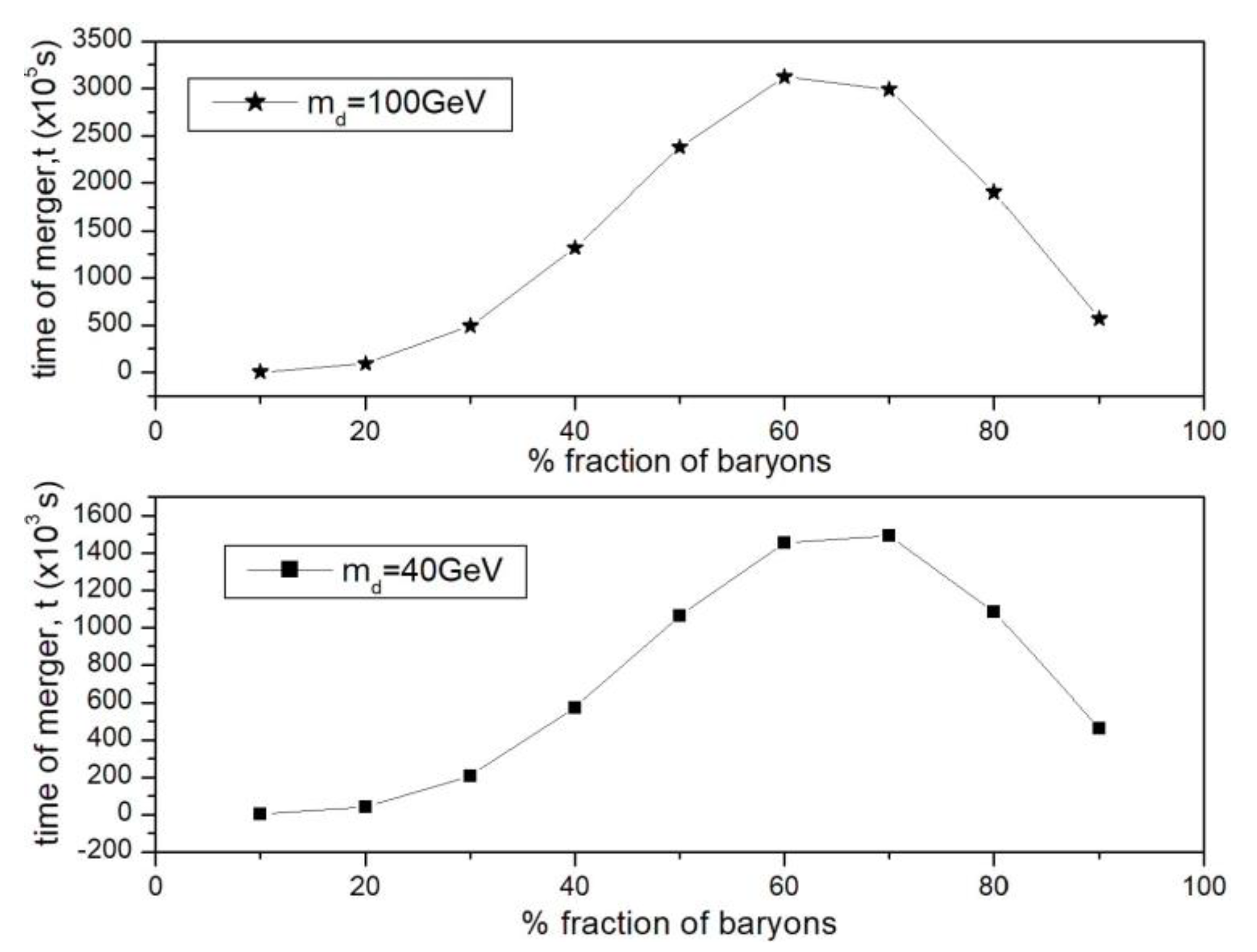
Table 1.
Mass and radius of primordial planet made of DM particle mass = 60GeV. Here is the Jupiter mass.
Table 1.
Mass and radius of primordial planet made of DM particle mass = 60GeV. Here is the Jupiter mass.
| f% | 1-f % | meff(GeV) | Mass of Object (g) | Radius of Object (cm) |
|---|---|---|---|---|
| 10 | 90 | 54.1 | 1.21X1030 | 5.47X104 |
| 20 | 80 | 48.2 | 1.52X1030 | 1.81X105 |
| 30 | 70 | 42.3 | 1.97X1030 | 3.72X105 |
| 40 | 60 | 36.4 | 2.66X1030 | 6.34X105 |
| 50 | 50 | 30.5 | 3.79X1030 | 9.81X105 |
| 60 | 40 | 24.6 | 5.83X1030 | 1.44X106 |
| 70 | 30 | 18.7 | 1.01X1031 | 2.07X106 |
| 80 | 20 | 12.8 | 2.15X1031 | 3.01X106 |
| 90 | 10 | 6.9 | 7.41X1031 | 4.85X106 |
Table 2.
Total energy emitted as gravitational waves by the binary system for different mass of DM particle and with different fractions of baryons for forming the planet.
Table 2.
Total energy emitted as gravitational waves by the binary system for different mass of DM particle and with different fractions of baryons for forming the planet.
| f(%) | E(ergs)for mD= 20𝐺𝑒V |
E(ergs)for mD= 40𝐺𝑒V |
E(ergs)for mD= 80𝐺𝑒V |
E(ergs)for mD= 100𝐺𝑒V |
|---|---|---|---|---|
| 10 | 1.16x1050 | 4.68x1048 | 1.86x1047 | 6.57x1046 |
| 20 | 5.51x1049 | 2.24x1048 | 8.94x1046 | 3.17x1046 |
| 30 | 4.40x1049 | 1.82x1048 | 7.35x1046 | 2.61x1046 |
| 40 | 4.54x1049 | 1.93x1048 | 7.90x1046 | 2.81x1046 |
| 50 | 5.67x1049 | 2.50x1048 | 1.04x1047 | 3.72x1046 |
| 60 | 8.50x1049 | 3.95x1048 | 1.69x1047 | 6.08x1046 |
| 70 | 1.58x1050 | 8.00x1048 | 3.59x1047 | 1.30x1047 |
| 80 | 4.00x1050 | 2.36x1049 | 1.16x1048 | 4.27x1047 |
| 90 | 1.73x1051 | 1.49x1050 | 9.21x1048 | 3.58x1048 |
Table 3.
Gravitational radiation energy emitted per second by the DM planet admixed with baryons for different mass DM particles.
Table 3.
Gravitational radiation energy emitted per second by the DM planet admixed with baryons for different mass DM particles.
| f(%) 𝐸˙(ergs/s)for 𝑚𝐷=20 GeV |
𝐸 ˙(ergs/s)for 𝑚𝐷=40 GeV |
𝐸 ˙(ergs/s)for 𝑚𝐷=60 GeV |
˙ 𝐸 ˙(ergs/s)for 𝑚𝐷=80 GeV |
˙ 𝐸 ˙(ergs/s)for 𝑚𝐷=100 GeV |
|---|---|---|---|---|
| 10 9.39X1051 | 2.79X1049 | 1.08X1048 | 1.08X1047 | 1.82X1046 |
| 20 3.97X1050 | 1.51X1048 | 5.95X1046 | 6X1045 | 1.01X1045 |
| 30 9.13X1049 | 3.72X1047 | 1.49X1046 | 1.51X1045 | 2.56X1044 |
| 40 4.21X1049 | 1.82X1047 | 7.41X1045 | 7.58X1044 | 1.29X1044 |
| 50 3.01X1049 | 1.39X1047 | 5.79X1045 | 5.98X1044 | 1.02X1044 |
| 60 3.06X1049 | 1.55X1047 | 6.65X1045 | 6.99X1044 | 1.21X1044 |
| 70 4.43X1049 | 2.58X1047 | 1.16X1046 | 1.26X1045 | 2.2X1044 |
| 80 9.85X1049 | 7.38X1047 | 3.67X1046 | 4.17X1045 | 7.55X1044 |
| 90 4.03X1050 | 5.59X1048 | 3.58X1047 | 4.66X1046 | 9.21X1045 |
Table 4.
Merger time of DM planet admixed with baryons for different mass DM particles.
| f | t(s) for mD=20GeV | t(s) for mD=40GeV | t(s) for mD=80GeV | t(s) for mD=100GeV |
|---|---|---|---|---|
| 10 | 2.91 X 1018 | 1.16 X 1019 | 4.62 X 1019 | 7.21 X 1019 |
| 20 | 2.33 X 1018 | 9.2 X 1018 | 3.66 X 1019 | 5.71 X 1019 |
| 30 | 1.82 X 1018 | 7.11 X 1018 | 2.81 X 1019 | 4.39 X 1019 |
| 40 | 1.37 X 1018 | 5.29 X 1018 | 2.08 X 1019 | 3.24 X 1019 |
| 50 | 9.79 X 1017 | 3.73 X 1018 | 1.46 X 1019 | 2.26 X 1019 |
| 60 | 6.57 X 1017 | 2.45 X 1018 | 9.43 X 1018 | 1.46 X 1019 |
| 70 | 3.99 X 1017 | 1.43 X 1018 | 5.42 X 1018 | 8.37 X 1018 |
| 80 | 2.05 X 1017 | 6.87 X 1017 | 2.51 X 1018 | 3.84 X 1018 |
| 90 | 7.47 X 1016 | 2.13 X 1017 | 7.03 X 1017 | 1.05 X 1018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






