Prerpints.org logo
Preprint
Article

P − V Criticality of the Non-linear Charged Black Hole Solutions in Massive Gravity

Altmetrics

Downloads

323

Views

274

Comments

1

Submitted:

15 January 2023

Posted:

16 January 2023

You are already at the latest version

Alerts
Abstract
In this paper, we explore the black hole solutions with the rainbow deformed metric in the presence of the exponential form of the nonlinear electrodynamics with asymptotic Reissner- Nordstr ̈om properties. We calculate the exact solution of metric function and explore the geometri- cal properties in the background of massive gravity. From the obtained solution, the existence of the singularity is confirmed in proper limits. Using the solutions we also investigate the thermodynamic properties of the solutions by checking the validity of the first law of thermodynamics. Continuing the thermodynamic study, we investigate the conditions under which the system is thermally stable from the heat capacity and the Gibbs free energy. We also discuss the possible phase transition and the criticality of the system. It was found that the quantum gravitational effects of gravity’s rain- bow render the thermodynamic system stable in the vicinity of the singularity. Hence, we obtained a first order phase transition which is interpreted as the large/small black hole phase transition. From the equation of state it was found that after diverging at the singularity, the system evolves asymptotically into pressure-less dust as one moves away from the central singularity. We also calculated the quantum work using the change of the Helmholtz free energy.
Keywords: 
Subject: Physical Sciences  -   Thermodynamics

1. Introduction

Black hole thermodynamics is one of the best way to gain insight into the black holes. Such studies are important steps towards increasing information about the dark side of universe which needs a quantum gravity description. It can not be achieved using the General Relativity (GR). The inconsistency of GR [1] at the cosmological scales has been the biggest problem of modern cosmology since the discovery of the recent cosmic acceleration [2,3]. For the last two decades extensive research in this direction paved the way for two alternative theories that can provide proper theoretical framework to explain the cosmic acceleration. These theories are known as dark energy [4] and modified gravity [5,6,7]. While the former deals with the nature of matter that fills up the universe, the latter modifies the spacetime geometry of the Einstein’s universe. In this work we will concentrate on the second alternative in order to explore the dynamics of the universe and its properties.
There are various ways in which Einstein gravity may be modified in order to incorporate the late cosmic acceleration. Almost all of them modifies the Einstein-Hilbert (EH) action of GR, by replacing the Ricci scalar R with suitable invariants or their functions [5,6,7]. Apart from explaining the cosmic acceleration cosmological models face other important challenges, such as the singularity problem. To solve such issues a complete theory of Quantum Gravity (QG) is needed that can reconcile GR with Quantum Mechanics (QM). Such a theory has been termed in literature as the Theory of Everything (TOE), because of its ability to span over all length scales and all energy levels. Over a century of extensive research resulted in the development of quantum gravity theories like the String theory [8,9], Loop Quantum Gravity (LQG) [10,11], Horava-lifshitz (HL) gravity [12,13], etc. In the Horava-Lifshitz mechanism a UV complete theory of GR is achieved, such that it reduces to GR in the IR limit. An alternative mechanism to attain the UV completeness of GR was proposed by Magueijo and Smolin in Ref. [14], which was termed as Gravity’s Rainbow. The striking feature of the theory is that the geometry of the spacetime depends on the energy of the test particle, and hence the geodesics (particle trajectories) are dependent on the energy of the particle. It is known that in order to establish the Special Theory of Relativity (STR) from the Galilean theory, a universal speed limit must be considered, which is the speed of light c. With this approach, particles can be limited to a threshold of receiving energy called the Planck Energy Scale. This high energy limit may lead to the correction of the dispersion relation, which is known as Doubly Special Relativity (DSR) [15]. Here the spacetimes used in STR is generalized for high energy scales comparable to Planck energy ( E P = 10 19 G e V ) . By generalizing the DSR to incorporate acceleration (non-zero curvature of spacetime), we finally arrive at doubly general relativity (DGR) or gravity’s rainbow [14]. However the cost of introducing these modifications to standard theories are not trivial at all. In any theory of quantum gravity including gravity’s rainbow, there is a natural breakdown of the Lorentz symmetry [16,17,18,19]. Due to the energy dependent nature of the spacetime there is also a clear violation of the equivalence principle which forms the physical basis for GR.
There are significant features in the dynamics of gravity’s rainbow that makes it worthy of exploring. One of these features is the correction of energy-momentum dispersion relation Which have been confirmed in research of quantum gravity [20], experimental observation [21] and string theory [22]. In this theory the modifications to the usual energy-momentum dispersion relations are introduced through the energy-dependent rainbow functions f ( ϵ ) and g ( ϵ ) as,
ϵ 2 f 2 ( ϵ ) − p 2 g 2 ( ϵ ) = m 2
In the above relation ϵ = E s / E P , where E s is the maximum energy that a spacetime can support, and E P is the Planck energy. The choice of the rainbow functions have been a real tough job for the researchers. A fundamental compliance behind such choices is that the rainbow functions must respect the correspondence principle, i.e. the usual energy-momentum dispersion relations of GR must be recovered in the IR limit. Mathematically such a requirement may be represented by,
lim E s / E P → 0 f ( ϵ ) = 1 , lim E s / E P → 0 g ( ϵ ) = 1 .
In literature, various types of rainbow functions have been addressed depending on their theoretical motivations. From the LQG and κ − Minkowski non-commutative spacetime the following rainbow functions have been proposed [23,24],
f ( ϵ ) = f ( E s / E P ) = 1 , g ( ϵ ) = g ( E s / E P ) = 1 − η E s E P n
Spectral observations from the gamma ray bursters have proposed the following rainbow functions [25],
f ( ϵ ) = f ( E s / E P ) = e a 2 E s / E P − 1 a 2 E s / E P , g ( ϵ ) = g ( E s / E P ) = 1
where a 2 is a constant. Now the metric in gravity’s rainbow is given by,
g μ ν ( ϵ ) = η a b e a μ ( ϵ ) e b ν ( ϵ ) .
where e 0 = f − 1 ( E s / E P ) e 0 ˜ and e i = g − 1 ( E s / E P ) e i ˜ . The tilde quantities actually correspond to frames that are not dependent on the energy, thus correlating with lower energy quanta. Equation (5) actually represents a family or bundle of metrics each of which depend on the energy of the probe. Thus different particles with different energy will experience a different geometry in the rainbow spacetime. Due to its quantum gravity background gravity’s rainbow has gained popularity and has been extensively studied in the past two decades [26,27,28,29,30,31,32,33].
It was found that, an IR modification of GR can be obtained by considering a massive graviton in the system. This is the basic principle of massive gravity. Initially it was done by simply introducing a Fierz-Pauli mass term in the action of GR [34,35], but there are discrepancies with the zero mass limit, due to the force derived from the scalar graviton. Moreover such a theory violates the solar system constraints [36,37]. The solution to the above problem was provided by the Vainshtein mechanism, which required the inclusion of non-linear terms in the field equations [38,39]. The higher derivative terms which are present in this mechanism produces negative norm Boulware-Deser ghosts [40]. A sub-class of massive potentials are introduced to get rid of the ghost terms in this theory [41,42,43,44], via the dRGT mechanism with a dynamical metric [45]. It is interesting to note that Lorentz symmetry breakdown at large scales can generate a mass term in the gravitational action, thus providing other mechanisms to develop a theory of massive gravity [46,47]. Substantive developments in massive gravity can be found in the refs. [48,49,50,51,52,53].
An interesting feature is the presence of black hole (BH) remnants in gravity’s rainbow [54] that can be used to solve the problem of information paradox [55]. In addition to the above, the principle of common uncertainty applies to this theory [56,57]. In recent times, we have witnessed increased interest in the study of BHs in energy-dependent space-time [55,58,59,60,61,62,63,64]. Different classes of black holes in gravity’s rainbow have been studied in the Refs. [65,66,67,68]. The equation of hydrostatic equilibrium of stars in the presence of the gravity’s rainbow has been derived in Ref.[69]. Moreover there are studies on the non-singular rainbow universes [70], effect of gravity’s rainbow on gravitational force [71], wormholes and compact stars [72]. Investigating the effects of gravity’s rainbow on the early universe is one of the most interesting studies in this field [73,74,75]. There are some key motivations for studying black holes in the presence of gravity’s rainbow. The most important idea is that, due to the high energy in black holes, quantum corrections must be considered from a classical point of view. One method that involves quantum corrections of gravitational fields is to consider the space-time dependence on energy, which is exactly what is done in gravity’s rainbow [76,77]. When we consider an energy-dependent space-time, it is also interesting to study the effects on the thermodynamics of black holes, which is another incentive to study gravity’s rainbow. Among the various achievements of studying black holes in the presence of gravity’s rainbow, the most important one is the possible solution to the singularity problem. Other achievements include the existence of remnants of black holes, the possibility of solving the information paradox, and the correction of the uncertainty principle.
Maxwell’s theory of electromagnetism, which is one of the most successful theories of nature, is however unable to explain many natural events. It has been observed that many electromagnetic phenomena behave non-linearly. For this reason, the study of nonlinear electromagnetic theories have increased and various theories have been proposed so far in this connection. Among the most important nonlinear electrodynamic theories are Born-Infield, exponential, logarithmic and power-law models [78,79,80,81] all of which reduce to Maxwell’s theory in certain limits. Motivated by the above discussion, here we are interested in exploring black hole solutions in gravity’s rainbow in the background of massive gravity equipped with non-linear electrodynamics (NLD). Our set-up will include a modified gravity theory with a quantum gravitational flavor. We also intend to include the NLD, which will bring in the Maxwell’s theory. Exploring black hole solutions in such an environment should be really interesting. One would always be interested to know that how far will the quantum gravity effects help in alleviating the singularity spike in the spacetime. Moreover the repulsive effects of the charged environment may also have a contribution in this scenario. We are also interested in studying the thermodynamic state of the derived system. The paper is organized as follows: We start with the field equations of massive gravity with non-linear electrodynamics and obtain the the exact solution of metric function in Section 2. In Section 3, we examine the first law of thermodynamics and calculate the basic thermodynamic quantities. Then, we study the thermal stability of the solutions in the canonical ensemble in Section 4. Section 5 is dedicated to the investigation of the possibility of P − V criticality and phase transition. In Section 6 we discuss about the quantum work. Finally the paper ends with a conclusion in Section 7.

2. Basic Field Equations

The four-dimensional action of massive gravity with a NLED field in the presence of cosmological constant is given by [82],
I = − 1 16 π G ∫ M d 4 x − g R − 2 Λ + m g 2 ∑ i = 1 2 c i U i ( g , f ) + L F ,
where R is the Ricci scalar and Λ denotes the cosmological constant related to the AdS radius (ℓ) by Λ = − 3 ℓ 2 . Besides, m g is the parameter of graviton’s mass, c i ’s are arbitrary constants and U i ’s are graviton’s self-interaction potentials constructed by the building blocks K ν μ = g μ α f α ν as
U 1 = K , U 2 = K 2 − K 2 .
In addition, L F is the Lagrangian of nonlinear electrodynamics that is a function of Maxwell invariant F = F μ ν F μ ν where F μ ν = ∂ μ A ν − ∂ ν A μ is electromagnetic tensor field and A μ is the gauge potential. Here we will consider an exponential form of non-linear electrodynamics given by [81],
L ( F ) = β 2 exp − F β 2 − 1 ,
where β is the nonlinearity parameter. Varying the bulk action (6) with respect to the physical metric ( g μ ν ) and the gauge vector ( A μ ), we can find the following field equations
G μ ν + Λ g μ ν − m g 2 c 1 2 U 1 g μ ν − K μ ν + c 2 2 U 2 g μ ν − 2 U 1 K μ ν + 2 K μ ν 2 = 1 2 g μ ν L ( F ) − 2 L F F μ λ F ν λ ,
and
∇ μ L F F μ ν = 0 ,
where L F = ∂ L ( F ) ∂ F .
Here, we take the following static ansatz for the physical metric g μ ν
g μ ν = d i a g − ψ ( r ) f ( ε ) 2 , 1 g ( ε ) 2 ψ ( r ) , r 2 g ( ε ) 2 g k ,
where g k is the metric of 2-dimensional (unit) surface with the constant curvature 6 k and area ω 2 with the following line element ( x i ’s are dimensionless coordinates)
d Ω k 2 = d x 1 2 + sin 2 x 1 d x 2 2 , k = 1 d x 1 2 + sinh 2 x 1 d x 2 2 , k = − 1 d x 1 2 + d x 2 2 , k = 0 .
Now, we can consider an appropriate static ansatz for the gauge potential A μ = h ( r ) δ μ 0 to obtain the electric field. Regarding Equation (9), we can obtain the following differential equation ( A ′ = d A d r )
4 r f ε 2 g ε 2 E r 2 + r β 2 ln E r ′ + 2 β 2 = 0 ,
with the following exact solution
E r = − F t r = − h ′ r = β 2 f ε g ε L W 1 / 2 ,
where L W = L a m b e r t W 4 q 2 f ε 2 g ε 2 β 2 r 4 with an integration constant q which is related to the total electric charge of spacetime. It is also notable that the scalar potential can directly obtain via the integration of E ( r ) as
h r = − 1 10 2 β q f ε g ε L W 1 / 4 2 L W + 1   F [ 1 ] , [ 9 4 ] , L W 4 + 5 exp L W 4 .
where F represents the hypergeometric function of the arguments. Here, we should calculate the exact solution of metric function ψ ( r ) . To do so, we follow the below ansatz for the reference metric
f μ ν = d i a g 0 , 0 , c 2 g ( ε ) 2 g k .
It is straightforward to calculate the self-interaction potentials with the following explicit form
U 1 = 2 c r , U 2 = 2 c 2 r 2 .
It is worth mentioning that only U 1 and U 2 are nonzero in four dimensions and higher orders ( U i , i ≥ 3 ) vanishes, and therefore, we have ignored higher orders in the action (6). Collecting the mentioned information, one finds that the nonzero components of the gravitational field Equation (8) can be written as
r ψ ′ ( r ) + ψ ( r ) − k g ( ε ) 2 + 2 Λ + β 2 r 2 2 − m g 2 c c 1 r + c 2 c 2 − β 2 r 2 2 1 − L W exp L W 2 = 0 ,
r ψ ′ ′ ( r ) + 2 ψ ′ ( r ) g ( ε ) 2 + 2 Λ + β 2 r − m g 2 c c 1 − r β 2 exp L W 2 = 0 ,
with the following analytic solution
ψ r = k − 2 m 0 r − 2 Λ + β 2 6 g ( ε ) 2 r 2 + c m g 2 g ( ε ) 2 c 1 r 2 + c c 2 + β q f ε 15 g ( ε ) L W 1 / 2 4 L W 2 F [ 1 ] , [ 9 4 ] , L W 4 + 5 1 + L W ,
in which m 0 is an integration constant related to the finite mass of black hole. Considering the massless graviton limit ( m g → 0 ), Equation (19) reduces to the case of nonlinearly charged black hole in massive gravity’s rainbow scenario.
The existence and detection of a singularity and the possible event horizon can help us to investigate the geometric properties of the spacetime. It is easy to calculate the Ricci and Kretschmann scalars (scalar curvatures) as below,
R = − g ε 2 ψ ″ r + 4 ψ ′ r r + 2 ψ r − k r 2 ,
R α β γ δ R α β γ δ = g ε 4 ψ ″ r 2 + 4 ψ ′ r 2 r 2 + 4 ψ r − k r 2 2 .
Inserting Equation (19) into the Equations (20) and (), we find
lim r ⟶ 0 R ⟶ ∞ , lim r ⟶ 0 R α β γ δ R α β γ δ ⟶ ∞ ,
lim r ⟶ ∞ R = 4 Λ + O ( 1 r ) , lim r ⟶ ∞ R α β γ δ R α β γ δ = 8 3 Λ 2 + O ( 1 r ) .
Strictly speaking, these scalars diverge at the origin and are finite for r ≠ 0 . Therefore, we conclude that there is only one curvature singularity located at r = 0 . In addition, Equation (23) hints us that the asymptotic behavior of the solutions may be of the AdS nature. However, in order to confirm that the solutions are asymptotically AdS, one have to examine the asymptotic symmetry group of the solutions which can be independently addressed elsewhere.

3. First Law of Thermodynamics

To examine the first law of thermodynamics, we have to calculate the conserved and thermodynamic quantities. At first, we use the definition of Hawking temperature arisen from the concept of surface gravity on the event horizon r + to find
T = g ( ε ) 4 π f ( ε ) ψ ′ ( r )   r = r + = k g ( ε ) 4 π f ( ε ) r + − r + Λ 4 π f ( ε ) g ( ε ) + m 2 c 2 c 2 + c c 1 r + 4 π f ( ε ) g ( ε ) r + + β q 1 − L W + 4 π r + L W + 1 / 2 − r + β 2 8 π f ( ε ) g ( ε ) ,
where L W + = L W | r = r + . It is worth mentioning that such temperature reduces to that of Reissner-Nordstrom (RN) black hole for β ⟶ ∞ with f ( ε ) = g ( ε ) = 1 .
Besides, due to the fact that we are working in the context of Einstein gravity, we can use the area law to calculate the entropy. It is easy to find that the entropy per unit volume ω 2 can be written as
S = r + 2 4 g ε 2 .
The electric charge, Q, can be found by calculating the flux of the electric field at infinity. Moreover, the electric potential, U, can be defined as the gauge potential at the event horizon with respect to the reference at spatial infinity. So, we can obtain the total charge per unit volume ω 2 and electric potential as
Q = f ( ε ) 4 π g ( ε ) q ,
U = A μ χ μ   r → ∞ − A μ χ μ   r → r + = 1 10 2 β q f ε g ε L W + 1 / 4 2 L W +   F [ 1 ] , [ 9 4 ] , L W + 4 + 5 exp L W + 4 .
It was shown that by using the Hamiltonian approach, one can find the finite mass M of the black hole for massive gravity’s rainbow as
M = ω 2 m 0 4 π f ( ε ) g ( ε ) ,
in which by evaluating metric function on the event horizon ( ψ r = r + = 0 ), one can obtain the finite mass per unit volume ω 2 is
M = r + 8 π f ( ε ) g ( ε ) k − 2 Λ − β 2 r + 2 6 g ( ε ) 2 + m 2 ( 2 c 2 c 2 + c c 1 r + ) 2 g ( ε ) 2 + β q f ε 15 g ( ε ) L W + 1 / 2 4 L W + 2 F [ 1 ] , [ 9 4 ] , L W + 4 + 5 1 + L W + ,
Here F represents hypergeometric function of the arguments. Now, we are in a position to examine the validity of the first law of thermodynamics for our solutions. By using thermodynamic quantities such as entropy (25), charge (26) and mass (28), in the first law of black hole thermodynamics we get,
d M = T d S + U d Q ,
we can define the intensive parameters conjugate to S and Q. These quantities are the temperature and the electric potential respectively as given below,
T = ∂ M ∂ r + Q ∂ r + ∂ S Q U = ∂ M ∂ q S ∂ q ∂ Q S ,
These are coincident with the ones calculated for the temperature and the electric potential in Equations (24) and (27) respectively. As a result, the first law of thermodynamics is valid while some of quantities are modified due to the nonlinear modification of electrodynamics and the presence of rainbow functions.

4. Thermal Stability in the Canonical Ensemble

To study thermal stability of the solutions in the canonical ensemble, we investigate the behavior of the heat capacity. The negative heat capacity represents an unstable state which hints us to look for a possible phase transition. The heat capacity is given by
C Q = T ∂ S ∂ T Q ,
which by using Equations (24), (25) and (28), we achieve
C Q = − 2 π r + 2 g ( ε ) 2 k − r + 2 Λ − r + 2 β 2 2 + m 2 ( c 2 c 2 + c c 1 r + ) L W + 1 / 2 + β q f ε ( 1 − L W + ) g ( ε ) 2 g ( ε ) 2 k + r + 2 Λ + r + 2 β 2 2 + m 2 c 2 c 2 L W + 1 / 2 − β q f ε ( 1 + L W + )
If C Q ≥ 0 , we have a stable thermodynamic system, otherwise the system is unstable in nature. Since the functional form of the heat capacity is complicated, we have to use the numerical analysis in the study. We plot C Q against r + in Figure 1 for open, closed and flat universe, to get an idea of the stability of the system. We can see a first order phase transition which may be interpreted as large/small black hole phase transition. It means that a large black hole is in the thermodynamically stable phase, while a small black hole is unstable due to the quantum gravitational effects of gravity’s rainbow. While the black hole size is reduced due to the Hawking radiation, a first order phase transition happen to yield the black hole in the unstable phase.

5. Extended Phase Space

From the first law in Equation (30), one may think about the relevant Smarr relation of the system. However, it is easy to find that if we consider the five conserved thermodynamic parameters M, T, U, Q and S, the Smarr relation is not valid anymore. In order to obtain the consistent Smarr relation, we may follow the approach of extended phase space thermodynamics.
After some calculations, we can find that the following Smarr relation is valid for the obtained solutions
M = 2 T S + Q U − 2 P V − C 1 c 1 − B β ,
where
P = − Λ 8 π , V = ∂ M ∂ P S , Q , β , c 1 = r + 3 3 f ( ε ) g 3 ( ε ) , C 1 = ∂ M ∂ c 1 S , Q , β , P = 1 4 r + 2 m 2 c ( ε ) g ( ε ) 3 , B = ∂ M ∂ β S , Q , P , c 1 = 2 r + 15 q 1 − 2 L W + F [ 1 ] , [ 9 4 ] , L W + 4 g 2 ( ε ) L W + − 5 2 ( 1 + L W + ) − 9 q F [ 2 ] , [ 13 4 ] , L W + 4 2 g 2 ( ε ) L W + − 5 2 ( 1 + L W + ) + 5 q 2 + L W + + L W + 2 4 g 2 ( ε ) L W + ( 1 + L W + ) − 4 β r + 2 4 f ( ε ) g ( ε ) 3 ,
where V, C 1 and B are, respectively, the conjugating quantities of the pressure P, massive parameter c 1 and nonlinearity parameter β . We should note that the related differential form of the first law in the extended phase space can be written as
d M = T d S + U d Q + V d P + C 1 d c 1 + B d β .
Here, we intend to employ the analogy between the cosmological constant and thermodynamical pressure to study the critical behavior of the system. By using Equation (24) and the relation between P and Λ , we can obtain the following equation of state
P = f ( ε ) g ( ε ) T 2 r + − k g 2 ( ε ) 8 π r + 2 − m 2 c 2 c 2 + c c 1 r + 8 π r + 2 − β q f ( ε ) g ( ε ) 1 − L W + 8 π r + 2 L W + 1 / 2 + β 2 16 π .
Due to modification in interpretation of the total mass of the black holes in extended phase space (M is interpreted as the enthalpy instead of internal energy), the Gibbs free energy is given by
G = H − T S = M − T S ,
where by using Equations (24), (25) and (28) with (37), one can obtain
G = ω 2 r + 8 π f ( ε ) g ( ε ) k 2 − 4 π P r + 2 3 g 2 ( ε ) + 5 β 2 r + 2 12 g 2 ( ε ) + m 2 ( c 2 c 2 ) 2 g 2 ( ε ) + β q f ε 6 g ( ε ) L W + 1 / 2 8 L W + 2 5 F [ 1 ] , [ 9 4 ] , L W + 4 + 5 − L W + .
The obtained relation for the volume could be used to define a specific volume which is related to horizon radius. This relation enables us to use horizon radius instead of volume for studying the critical behavior of the system. In order to obtain critical values, one can use the following properties of inflection point in the isothermal P − r + diagrams
∂ P ∂ r + T = ∂ 2 P ∂ r + 2 T = 0 ,
in which after some manipulations, we find
e q 1 = 2 k g ( ε ) f ε − 4 π T r + + m 2 ( 2 c 2 c 2 + c c 1 r + ) f ε g ε − 2 β q L W + 1 / 2 = 0 ,
is corresponding to ∂ P ∂ r + T = 0 while for ∂ 2 P ∂ r + 2 T = 0 , we can find the following equation
e q 2 = 3 g ε k f ε − 4 π T r + + m 2 ( 3 c 2 c 2 + c c 1 r + ) f ε g ε − 4 β q L W + 1 / 2 5 + 3 L W + 3 ( 1 + L W + ) = 0 .
In order to obtain the critical quantities, we should use e q 1 , e q 2 and the equation of state, simultaneously. In general, due to the contributions of massive term and nonlinear electrodynamics, it is not possible to obtain the critical parameters, analytically. Thus, we apply the numerical calculations to overcome this issue. To do so, we plot different figures and tables. Since there is no analytical solution for the system coexistence curve, we use the numerical method to calculate critical thermodynamic values for different case and study the behavior of the swallowtail in Gibbs free energy diagram.
For this purpose, we present various parameter values in tabular form to show the effects of space-time curvature, nonlinear electrodynamic parameter, mass gravity coefficients, and the effect of f ε and g ε functions on critical pressure and temperature. We have generated the plots for P − r + and G − r + at critical points and analyze the results in Figs. Figure 2 and Figure 3 respectively. One of the advantages of the P − r + diagram is that the pressure behavior can be viewed as a function of the horizon radius. In addition, in this diagram information about behavior of pressure near critical points can be obtained. By studying these diagrams, we can see the similarities between the van der Waals like behavior in structure of black holes. From the P − r + diagram we see that near the central singularity pressure diverges positively for open universe and negatively for closed and flat universe. As r + increases P settles near the zero value assuming a dust equation of state. Initially for all universes (open, closed and flat) there is a region of negative pressure, which indicates the presence of dark energy, that will actually ease out the singularity by reducing its strength. The presence of exotic component in the system is basically due to presence of modified gravity effects of massive gravity. The G − r + diagram in Figure 3 shows the different energy levels that changes near the phase transition. A striking feature of the plot is that the trajectories for closed, open and flat universes almost coincide with each other. The lowest levels of G correspond to the most stable configuration of the system. From the figure we see that this is attained around r + = 7 (in our scale). This can be validated with the result obtained from the plot of C Q , where we see that around r + = 7 , the trajectory remains at the positive level, confirming the stability of the system.
In this paper, we study the phase transition points in different topological black holes and then we present the effects of nonlinear electrodynamic parameters and mass gravity coefficients, and finally we present the effects of f ( ε ) and g ( ε ) coefficients. As it can be seen from Table 1 that under the identical conditions, the event horizon has the lowest value at critical points in positively curved space and the highest value at negatively curved space (see the last column in both the left and right pane). In all of these cases, we can see swallowtail behavior for P < P c , which represents first-order of phase transition. This configuration will disappear at P = P c which is the second-order phase transition. In Table 2 critical temperature and pressure have the maximum (minimum) value in the space with positive (negative) curvature. This means that in a space with a positive curvature, more energy is needed to reach the critical temperature and the phase transition occurs. This indicates that space with positive curvature is more stable compared to space with negative curvature.
By examining the criticality for different values of β in Table 3, we find that critical temperature and critical pressure are descending functions of beta. As the β increases, the nonlinear electrodynamics get closer to the linear state (Maxwell theory) and the critical temperature and pressure reduce. Therefore, the phase transition is a difficult proposition in the presence of the nonlinear electrodynamics compared to its linear counterpart. So, as the power of non-linearity grows, the critical temperature of the system for phase transition also grows. This is because, by increasing the nonlinear parameter (approaching the linear state), black holes require less mass absorption for the phase transition. In addition, the length of the critical isobars is an ascending function of the nonlinear parameter. These results are in complete agreement with the existing literature. Finally we see that, as β increases, the Gibbs free energy value at the critical point will also increase. This means that the system is more stable at the larger value of β (closer to Maxwell’s definition).
In Table 4 and Table 5, we examine the rainbow coefficients f ε and g ε that influence the metric to find the effects of the metric on the phase transition. As the tables show, the volume increases with increasing f ε or g ε and the critical temperature and pressure decrease correspondingly. This indicates that a greater deviation from classical spacetime, will trigger easier phase transition. If we increase f ε , the Gibbs free energy will increase for critical states, but if we increase g ε , then the Gibbs free energy will decrease. Therefore, with these findings, it can be concluded that Gibbs free energy does not necessarily increase with increasing temperature. By examining different values for the coefficients c 1 and c 2 , we investigate the effect of mass on the phase transition. The volume is independent of c 1 and so the temperature increases by increasing c 1 , but the critical pressure remains constant as seen in Table 6. In Table 7 as c 2 increases, the volume decreases and the critical temperature and pressure increase.
By comparing the results in general, we find that nonlinear electrodynamics and the rainbow coefficients f ε and g ε have opposite effects on critical pressure and temperature. Nonlinear electrodynamics and gravitational effects also have opposite effects on critical points. Therefore, phase transitions are fundamentally related to electrodynamics, gravity and the spacetime.

6. Quantum Work

In fact, one can imagine a dual picture of a black geometry in a superconformal field theory. The black geometry of a non-linear charged black hole solutions in massive gravity emit Hawking radiation. Its corresponding energy is described by heat, which is yields to information loss paradox in quantum thermodynamics. Such an information loss paradox may be solved using a dual picture in a superconformal field theory, when we study the quantum behavior. It is indeed characteristic of the superconformal side in the mentioned duality. Therefore, a non-linear charged black hole solutions in massive gravity is represented by the unitary superconformal field theory. Hence, we are able to use the quantum non-equilibrium thermodynamics to study this black geometry. In that case we are able to calculate quantum work of a non-linear charged black hole in massive gravity. This quantum work is denoted by an unitary information preserving process which is the dual picture of a non-linear charged black hole solutions in massive gravity.
Hence, in the other side of duality we have a non-equilibrium quantum thermodynamics. The non-equilibrium quantum thermodynamics enables a non-linear charged black hole in massive gravity to lose its mass through an unitary process. We have shown that a non-linear charged black hole in massive gravity is unstable through a first order phase transition and will evaporate at the final state. So information can leak out of a non-linear charged black hole solutions in massive gravity during the last stages of its evaporation from the mentioned unitary information preserving process. Therefore, we can resolve the information loss paradox in the given system using the non-equilibrium quantum thermodynamics. It is clear that at the quantum scale, we need to analyze a given system using the non-equilibrium quantum thermodynamics [83].
Black hole entropy, at quantum scales, is related to the microstates. Hence, a change in the black hole microstates yields to the change in the entropy. So, one can express the change in the quantum corrected entropy of a non-linear charged black hole in massive gravity as,
Δ S = S f − S i ,
where S f is the final entropy, while S i is the initial entropy in an evolution. Now, the quantum work is expressed as [84],
W Q ≡ < e W T > = e Δ F T ,
where Δ F is the change in the Helmholtz free energy ( F = G − P V ) which is given by,
Δ F = F f − F i .
We can fix F i for the large horizon radius and consider r + f ≡ r + as a variable. Hence F f ≡ F ( r + f ) is considered as a variable and help us to extract the quantum work in terms of the horizon radius. In Figure 4 we can see behavior of the quantum work for three different geometries. We can see increasing the quantum work by decreasing horizon radius during the evaporation (as expected). It is also possible to construct a microscopic model for the non-linear charged black hole in massive gravity, where the black hole event horizon consists of the discrete constituents. Therefore, it is possible to write the explicit form of the black hole partition function.
It is well-known that the black hole partition function may be constructed through string theory. Due to the black hole evaporation, the corresponding partition function will change. As the non-linear charged massive gravity black hole evaporates from an initial partition function Z i with the large event horizon radius at the large black hole phase to a final partition function Z f at the small black hole phase, the relative weight of these partition functions Z f / Z i can be related to the average quantum work of black hole as 〈 exp ( − β W ) 〉 = Z f / Z i . Therefore, using the relationship between the average quantum work and the equilibrium free energies, the mentioned relative weights of the partition function may be related to the difference between the equilibrium free energies of the non-linear charged massive gravity black hole as exp β Δ F = Z f / Z i . Hence, it is possible to obtain information about the non-linear charged massive gravity black hole behavior, using the average quantum work.

7. Conclusions

In this paper, we combined three classes of black hole solutions in gravitating systems. Indeed, we considered massive gravity’s rainbow with an exponential form of nonlinear electrodynamics. We first focused on the geometrical properties by studying the scalar curvatures and found a point singularity located at the origin. Then, we calculated thermodynamic and conserved quantities to examine the first law of thermodynamics. The stability of the thermodynamic system was investigated by plotting the specific heat C Q against r + . From the plot it was evident that after just a little phase of instability close to the singularity, the system evolved into a perfectly stable system. Besides, we checked the Smarr relation and found that the rainbow functions could not behave like a thermodynamic quantity. We also investigated thermal stability and possible phase transition. We plotted the P − r + and G − r + diagrams and found a van der Waals like behavior for the solutions. From the plots we found that at the singularity pressure diverge and as the distance from the singularity is increased it settles into a dust equation of state. For almost all of the open, closed and flat models there are regions where pressure is negative indicating the presence of dark energy originating from the modified gravity. The settling down of the system to such an equilibrium condition quite close to the central singularity may be attributed to the presence of the quantum gravitational effects of gravity’s rainbow. From the G − r + diagram we equilibrium configuration of the system is identified in the vicinity of the singularity. This again is the result of the quantum gravity effects, which keep the Gibbs free energy to a minimum level in the surrounding of the singularity. We also discussed the effects of different model parameters on the critical parameters of the thermodynamic system. Effects of curvature, non-linearity, rainbow functions and the massive gravity parameters are investigated on the critical points leading to phase transition of the thermodynamic system. This work shows the role of gravity’s rainbow in easing out a singularity as a pathology of the spacetime and helping it to gradually evolve into a stable configuration. In fact the the quantum gravity effects of gravity’s rainbow renders the singularity weak, thus shallowing the hole in the spacetime caused due to the singularity. Eventually for suitable initial conditions it may be possible to completely get rid of the singularity.
For the future works it is interesting to study the perturbative and non-perturbative correction on the entropy of the black hole when the black hole size becomes infinitesimal due to Hawking radiation [85,86,87]. In that case, massive gravity black hole corrected thermodynamics is already discussed [88,89].

Author Contributions

All the authors have equal contributions in the manuscript.

Acknowledgments

We are indebted to S. H. Hendi for useful discussions and for reading the manuscript. P.R. acknowledges the Inter University Centre for Astronomy and Astrophysics (IUCAA), Pune, India for granting visiting associateship.

References

  1. A. Einstein, Annalen der Physik 354, 769 (1916).
  2. S. Perlmutter et. al., Astrophys. J. 517 565 (1999).
  3. A. G. Riess et al., Astron. J. 116 1009 (1998).
  4. P. Brax, Rep. Prog. Phys. 81 016902 (2018).
  5. S. Nojiri, S. D. Odintsov, V. K. Oikonomou, Phys. Rep. 692 1 (2017).
  6. S. Nojiri and S. D. Odintsov, Int. J. Geom. Methods Mod. Phys. 04 115 (2007).
  7. S. Capozziello, R. D’Agostino, O. Luongo, Int. J. Mod. Phys. D 28 1930016 (2019).
  8. M. Kaku, K. Kikkawa, Phys.Rev. D 10 1110 (1974).
  9. M. Kaku, K. Kikkawa, Phys.Rev. D 10 1823 (1974).
  10. C. Rovelli, Class. Quantum Grav. 8 1613 (1991).
  11. C. Rovelli, Living Rev.Rel. 1 1 (1998).
  12. P. Horava, Phys. Rev. Lett. 102 161301 (2009).
  13. P. Horava, Phys. Rev. D 79 084008 (2009).
  14. J. Magueijo and L. Smolin, Classical and Quantum Gravity 21 1725-1736 (2004).
  15. J. Magueijo, L. Smolin, Phys. Rev. Lett. 88 19 (2002).
  16. R. Iengo, J.G. Russo, M. Serone, JHEP 0911 020 (2009).
  17. B. M. Gripaios, JHEP 0410 069 (2004).
  18. J. Alfaro, P. Gonzalez, R. Avila, Phys. Rev. D 91 105007 (2015).
  19. H. Belich, K. Bakke, Phys. Rev. D 90 025026 (2014).
  20. R. Gambini and J. Pullin, Phys. Rev. D. 59 124021, (1999).
  21. J. Abraham, P. Abreu, M. Aglietta et al., Phys. Lett. B 685 239 (2010).
  22. V. A. Kosteleck and S. Samuel, Phys. Rev. D 39 683 (1989).
  23. G. Amelino-Camelia, J.R. Ellis, N.E. Mavromatos, D.V. Nanopoulos, Int. J. Mod. Phys. A 12 607 (1997).
  24. G. Amelino-Camelia, Living Rev. Relativ. 16 5 (2013).
  25. G. Amelino-Camelia, J.R. Ellis, N.Mavromatos, D.V.Nanopoulos, S. Sarkar, Nature 393 763 (1998).
  26. P. Rudra, M. Faizal, A. F. Ali, Nucl. Phys. B 909 725 (2016).
  27. Y. Heydarzade, P. Rudra, F. Darabi, A. F. Ali, M. Faizal, Phys. Lett. B 774 46 (2017).
  28. P. Rudra, S. Maity, Eur. Phys. J. C 78 828 (2018).
  29. P. Rudra, Nucl.Phys.B 956 115014 (2020).
  30. M. Dehghani, Phys. Lett. B 777 351 (2018).
  31. S. H. Hendi, A.Dehghani, M. Faizal, Nucl. Phys. B 914 117 (2017).
  32. S. H. Hendi, S. Panahiyan, B.E. Panah, M. Faizal, M. Momennia, Phys. Rev. D 94 024028 (2016).
  33. A.F. Ali, M. Faizal, B. Majumder, Europhys. Lett. 109 20001 (2015).
  34. W. Pauli, M. Fierz Helv, Phys. Acta 12, 297 (1939).
  35. M. Fierz Helv, Phys. Acta 12, 3 (1939).
  36. H. van Dam, M. J. G. Veltman, Nucl. Phys. B 22, 397 (1970).
  37. Y. Iwasaki, Phys. Rev. D 2, 2255 (1970).
  38. A. I. Vainshtein, Phys. Lett. B 39, 393 (1972).
  39. E. Babichev, C. Deffayet, Class. Quant. Grav. 30, 184001 (2013).
  40. D. G. Boulware, S. Deser, Phys. Rev. D 6, 3368 (1972).
  41. C. de Rham, G. Gabadadze, A. J. Tolley, Phys. Rev. Lett. 106, 231101 (2011).
  42. S. F. Hassan, R. A. Rosen, A. Schmidt-May, JHEP 1202, 026 (2012).
  43. S. F. Hassan, R. A. Rosen, Phys. Rev. Lett. 108, 041101 (2012).
  44. S. F. Hassan, R. A. Rosen, JHEP 1204, 123 (2012).
  45. K. Hinterbichler, Rev. Mod. Phys. 84, 671 (2012).
  46. A. H. Chamseddine, V. Mukhanov,, JHEP 1208, 036 (2012).
  47. G. Goon, K. Hinterbichler, A. Joyce, M. Trodden, JHEP 1507, 101 (2015).
  48. S. H. Hendi, S. Panahiyan, B. E. Panah, JHEP 01, 129 (2016).
  49. Y. Heydarzade, P. Rudra, B. Pourhassan, M. Faizal, A. F. Ali, JCAP 06 038 (2018).
  50. M. Wyman, W. Hu, P. Gratia, Phys. Rev. D 87, 084046 (2013).
  51. M. S. Volkov, Phys.Rev. D 90, 024028 (2014).
  52. X. X. Zeng, H. Zhang, L. F. Li, Phys. Lett. B 756, 170 (2016).
  53. H. Aounallah, B. Pourhassan, S. H. Hendi, M. Faizal, Eur. Phys. J. C 82, 351 (2022).
  54. A. F. Ali, M. Faizal, and M. M. Khalil, Nuclear Physics B, 894, 341-360 (2015).
  55. A. F. Ali, M. Faizal, and B. Majumder, Europhysics Letters, 109, Article ID 20001 (2015).
  56. Y. Ling, X. Li, and H. Zhang, Modern Physics Letters A, 22, 2749-2756 (2007).
  57. H. Li, Y. Ling, and X. Han, Classical and Quantum Gravity, 26, Article ID 065004 (2009).
  58. R. Garattini and B. Majumder, Nuclear Physics B, 884, 125-141 (2014).
  59. Z. Chang and S. Wang, The European Physical Journal C, 75, article 259 (2015).
  60. Grasiele Santos et al, JCAP, 08,005 (2015).
  61. A. F. Ali and M. M. Khalil, Europhysics Letters, 110, Article ID 20009 (2015).
  62. G. Yadav, B. Komal, and B. R. Majhi, Int. J. Mod. Phys. A, 32,1750196 (2017).
  63. S. H. Hendi, S. Panahiyan, B. Eslam Panah, M. Faizal, and M. Momennia, Physical Review D, 94, 024028(2016).
  64. P. Galan and G. A. Mena Marugan, Physical Review D, 74, 044035 (2006).
  65. A. F. Ali, Physical Review D, 89, 104040 (2014).
  66. Y. Gim and W. Kim, JCAP, 5, 002 (2015).
  67. S. H. Hendi, S. Panahiyan, and B. Eslam Panah, JHEP, 01, 129 (2016).
  68. S. H. Hendi, G. H. Bordbar, B. Eslam Panah, and S. Panahiyan, JCAP, 09, 013 (2016).
  69. R. Garattini and G. Mandanici, arXiv:1601.00879 [physics.gen-ph].
  70. A. Awad, A. F. Ali, and B. Majumder, JCAP, 10, 052 (2013).
  71. A. S. Sefiedgar, IJMPD, 25, 1650101 (2016).
  72. R. Garattini and F. S. N. Lobo, arXiv:1512.04470 [physics.gen-ph].
  73. Y. Ling, JCAP, 8, 017 (2007).
  74. S. H. Hendi, M. Momennia, B. Eslam Panah, and M. Faizal, Astrophys. J., 827, 153 (2016).
  75. L. Smolin, Nuclear Physics B, 742, 142-157 (2006).
  76. R. Garattini and G. Mandanici, Physical Review D, 85, 023507 (2012).
  77. M. Dehghani, Phys. Rev. D, 99, 024001 (2019).
  78. A. Sheykhi, F. Naeimipour, S.M. Zebarjad, Phys. Rev. D, 91, 124057 (2015).
  79. M. Dehghani, S.F. Hamidi, Phys. Rev. D, 96, 104017 (2017).
  80. M. Dehghani, Phys. Rev. D, 98, 044008 (2018).
  81. S. H. Hendi, JHEP, 03, 065 (2012).
  82. S. Chougule, S. Dey, B. Pourhassan, M. Faizal, Eur. Phys. J. C 78, 685 (2018).
  83. B. Pourhassan, H. Aounallah, M. Faizal, S. Upadhyay, S. Soroushfar, Y. O. Aitenov, S. S. Wani, JHEP 2022, 30 (2022).
  84. B. Pourhassan, S. S. Wani, S. Soroushfar and M. Faizal, "Quantum work and information geometry of a quantum Myers-Perry black hole", JHEP10, 027 (2021).
  85. B. Pourhassan, M. Atashi, H. Aounallah, S. S. Wani, M. Faizal, B. Majumder, Nuclear Physics B 980, 115842 (2022).
  86. S. Upadhyay, N. Islam, P. Ganai, J. Hol. App. Phys. 2(1), 25-48 (2022). [CrossRef]
  87. B. Pourhassan, K. Kokabi, S. Rangyan, Gen Relativ Gravit 49, 144 (2017).
  88. B. Pourhassan, M. Faizal, Z. Zaz, A. Bhat, Phys. Lett. B 773, 325 (2017).
  89. S. Upadhyay, B. Pourhassan, H. Farahani, Phys. Rev. D 95, 106014 (2017).
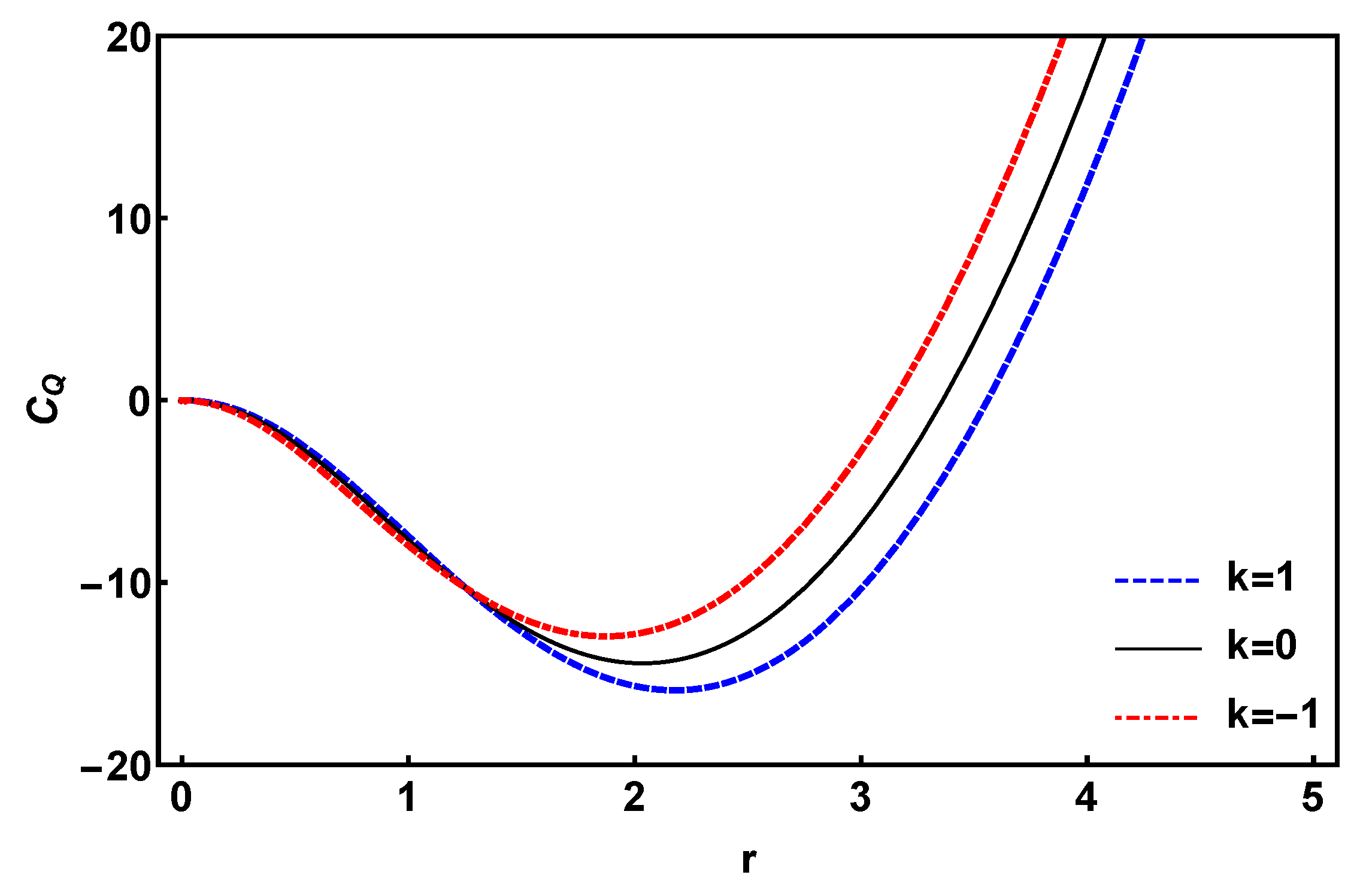
Preprints 67429 g001
Figure 1. Plot of heat capacity C Q against r + for closed, open and flat universe. The initial conditions are β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , Λ = 1 .
Figure 1. Plot of heat capacity C Q against r + for closed, open and flat universe. The initial conditions are β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , Λ = 1 .
Preprints 67429 g001

                       
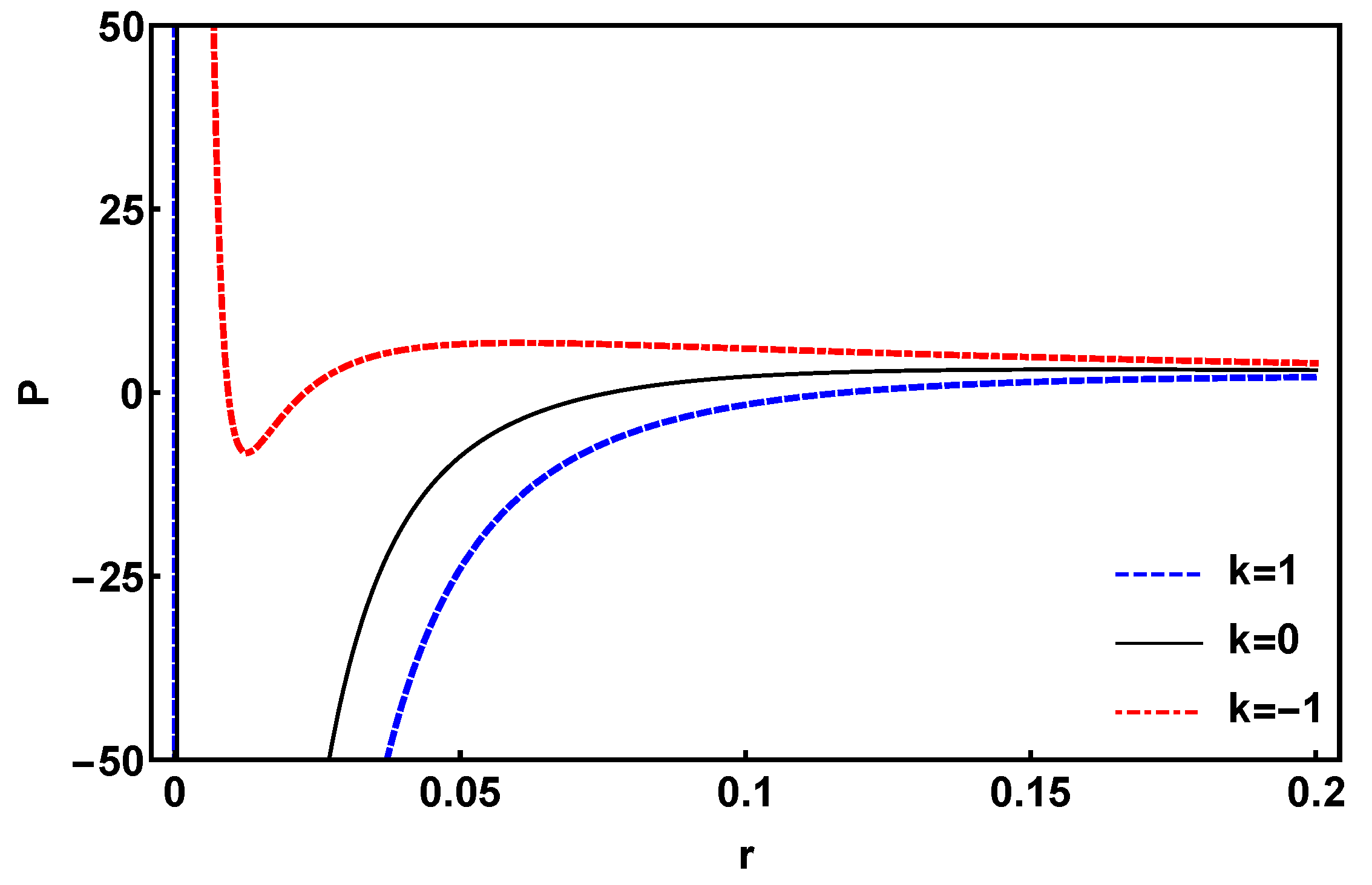
Preprints 67429 g002
Figure 2. Plot of pressure P vs r + for closed, open and flat universe. The initial conditions are β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , T = 2.55 .
Figure 2. Plot of pressure P vs r + for closed, open and flat universe. The initial conditions are β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , T = 2.55 .
Preprints 67429 g002
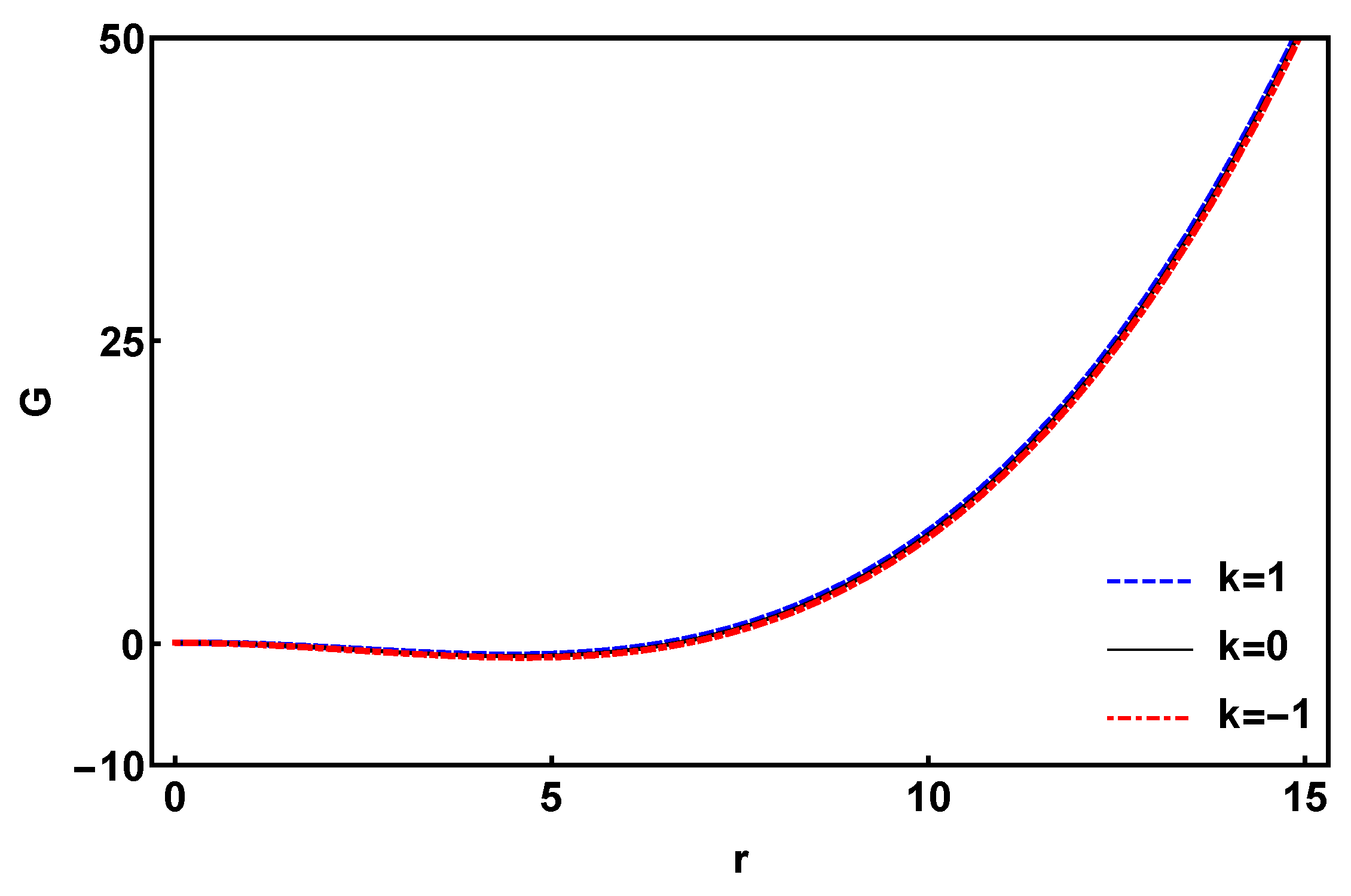
Preprints 67429 g003
Figure 3. Plot of Gibbs free energy G vs r + for closed, open and flat universe. The initial conditions are β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , T = 2.55 .
Figure 3. Plot of Gibbs free energy G vs r + for closed, open and flat universe. The initial conditions are β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , T = 2.55 .
Preprints 67429 g003
Preprints 67429 g004
Figure 4. Quantum work in terms of r + for β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , T = 2.55 .
Figure 4. Quantum work in terms of r + for β = 0.9 , m = 1.4 , c = 1 , c 1 = 1 , c 2 = 2.4 , q = 1 , f ( ε ) = 1 , g ( ε ) = 1 − η E s E p n , η = 1 , n = 2 , E s = 1 , E p = 5 , T = 2.55 .
Preprints 67429 g004
Table 1. For q = c = c 1 = c 2 = c 3 = c 4 = 1 , λ = 0.3 and d = 6 . Left: variation of m; ε = 0.5 . Right: variation of ε ; m = 1 .
Table 1. For q = c = c 1 = c 2 = c 3 = c 4 = 1 , λ = 0.3 and d = 6 . Left: variation of m; ε = 0.5 . Right: variation of ε ; m = 1 .
k m rc Tc Pc P c r c T c k ξ rc Tc Pc P c r c T c
−1 0.9 1.12051 1.81518 0.71931 0.44403 −1 0.1 1.18122 1.58593 0.73735 0.54919
0 0.9 1.10542 2.24425 0.86508 0.42610 0 0.1 1.16385 1.99321 0.90108 0.52615
1 0.9 1.09189 2.67889 1.01467 0.41357 1 0.1 1.14843 2.40625 1.06948 0.51043
−1 1 1.06499 2.61700 1.08930 0.44329 −1 0.6 1.03965 2.93556 1.19082 0.42173
0 1 1.05428 3.06763 1.25010 0.42963 0 0.6 1.03007 3.39697 1.35094 0.40965
1 1 1.04441 3.52267 1.41406 0.41924 1 0.6 1.02120 3.86252 1.51395 0.40027
−1 1.1 1.01777 3.60572 1.57104 0.44345 −1 1.0 0.94982 4.50073 1.65745 0.34978
0 1.1 1.00989 4.07669 1.74668 0.43269 0 1.0 0.94356 5.00510 1.81508 0.34218
1 1.1 1.00250 4.55123 1.92499 0.42402 1 1.0 0.93764 5.51273 1.97475 0.33587
Table 2. For β = 1 , q = 1 , Λ = − 1 , g ε = f ε = 1.1 , c = 1 , c 2 = 2.4 , m = 1 , 2 .
Table 2. For β = 1 , q = 1 , Λ = − 1 , g ε = f ε = 1.1 , c = 1 , c 2 = 2.4 , m = 1 , 2 .
k − 1 0 + 1
r c 1.38531 0.36867 0.05614
T c 0.20841 0.43250 1.66784
P c 0.01576 0.01262 3.86927
Table 3. For q = 1 , Λ = − 1 , K = − 1 , g ε = f ε = 1.01 , c = c 1 = 1 , c 2 = 2.4 , m = 1 , 4 .
Table 3. For q = 1 , Λ = − 1 , K = − 1 , g ε = f ε = 1.01 , c = c 1 = 1 , c 2 = 2.4 , m = 1 , 4 .
β 0.9 1 1.1 1.2 1.3
r c 0.03894 0.08498 0.15217 0.23800 0.33788
T c 2.10447 1.27249 0.92033 0.74464 0.69706
P c 5.87870 1.51472 0.57317 0.28426 0.17210
Table 4. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , g ε = 1 , c = c 1 = 1 , c 2 = 2.4 , m = 1 , 4 .
Table 4. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , g ε = 1 , c = c 1 = 1 , c 2 = 2.4 , m = 1 , 4 .
f 0.9 1 1.5 2
r c 0.02770 0.06985 0.75396 1.78753
T c 3.13625 1.47939 0.29574 0.16606
P c 11.12268 2.14542 0.04800 0.01566
Table 5. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , f ε = 1 , c = c 1 = 1 , c 2 = 2.4 , m = 1 , 4 .
Table 5. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , f ε = 1 , c = c 1 = 1 , c 2 = 2.4 , m = 1 , 4 .
g 0.9 1 1.5 2
r c 0.01720 0.06985 1.83632 5.79142
T c 4.68734 1.97939 0.18531 0.08440
P c 27.53819 2.1959 0.01113 0.00041
Table 6. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , g ε = f ε = 1.01 , c = 1 , c 2 = 2.4 , m = 1 , 4 .
Table 6. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , g ε = f ε = 1.01 , c = 1 , c 2 = 2.4 , m = 1 , 4 .
c = c 1 0.9 1 1.1 1.2
r c 0.08498 0.08498 0.08498 0.08498
T c 1.25720 1.27249 1.28778 1.30307
P c 1.51472 1.51472 1.51472 1.51472
Table 7. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , g ε = f ε = 1.01 , c = 1 , c 1 = 1 .
Table 7. For β = 1 , q = 1 , Λ = − 1 , K = − 1 , g ε = f ε = 1.01 , c = 1 , c 1 = 1 .
c = c 2 2.2 2.5 2.7 2.9
r c 0.17690 0.05753 0.02511 0.08498
T c 0.76506 1.71200 3.35833 1.27249
P c 0.39310 3.14607 15.0919 1.51472
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated