1. Introduction
1.1. Representing Even Numbers from Primes
Since the set of prime numbers is infinite, and since all prime numbers greater than 2 are odd numbers, then one knows immediately that there are infinitely many even numbers that can be represented as the sum of two primes, and, infinitely many even numbers that can be represented as the difference of two primes. Having said that, the following questions then naturally arise:
- (i)
Can every even number be represented as the sum of two primes?
- (ii)
Can every even number be represented as the difference of two primes?
- (iii)
Can any even number, or indeed all even numbers, be represented as the difference of two primes, in infinitely many ways?
- (iv)
If questions and are answered in the affirmative, can they also hold for consecutive primes, in representing even numbers greater than 4 as the difference of two primes?
The earliest known record to have posed question
, known as the Goldbach conjecture, dates back to 1742, in a correspondence between C. Goldbach and L. Euler, where it is propositioned that every even number greater than 2 can be represented as the sum of two primes [
1]. The Goldbach conjecture has more lately become known as the binary Goldbach conjecture, or the strong Goldbach conjecture, in order to distinguish it from the ternary Goldbach conjecture, or the weak Goldbach conjecture, which states that every odd number greater than 5 can be represented as the sum of three primes. The binary Goldbach conjecture has to date been shown empirically to hold for every even number up to
[
2], however, a rigorous proof, or disproof, remains elusive.
Nevertheless, some related theoretical results to the binary Goldbach conjecture have been achieved, the closest of which is due to J. R. Chen, who in 1973, proved that every sufficiently large even number can be represented as the sum of a prime and another prime or a semiprime, that is, the product of two primes [
3,
4,
5,
6]. On the other hand, significant results have been achieved for the ternary Goldbach conjecture, culminating with a proof given by H. Helfgott in 2014 [
7,
8,
9].
The earliest known record to have posed questions
are due to Alphonse de Polignac, who in 1849, conjectured that every even number can be represented as the difference of two consecutive primes, in infinitely many ways [
10]. The most significant special case of Polignac’s conjecture, is the so-called ‘twin prime conjecture’, which comprises of the number 2 being represented as the difference of two primes, in infinitely many ways. The twin prime conjecture is hugely supported by empirical data, where, over the past few decades, increasingly large twin prime pairs have been found to exist [
11], with the current world record for a twin prime pair, found in the year 2016, standing at
decimal digits long [
12].
As with the binary Goldbach Conjecture, the closest theoretical result to Polignac’s conjecture is given by J. R. Chen, who in the same article, proved that every even number can be represented as the difference of a prime and another prime or semiprime, that is, the product of at most two primes [
6]. More recently, D. A. Goldston, J. Pintz, and C. Y. Yildirim, introduced the now known ‘GPY method’, which uses approximations to the prime k-tuples conjecture, to study small numbers that can be represented as the difference of two primes [
13]. In 2013, Yitang Zhang built on the GPY method, thereby proving for the first time the existence of some even number less than
, which can be represented as the difference of two primes in infinitely many ways [
14]. Within a year after Zhang’s result, J. Maynard presented an independent proof that lowered the bound to 600, which, by assuming the Elliott-Halberstam conjecture, could be further lowered down to 12 [
15]. With some refinements to Zhang’s method and a combination of that with Maynard’s approach, the bound was lowered to 246 unconditionally, by an on-line collaborative project known as
Polymath 8, organised by T. Tao [
16].
1.2. Sieve Theory
Sieve theory is a technique for distinguishing specific subsets of integers, amongst the set of natural numbers. Sieve theory began with Eratosthenes of Cyrene (276-194 B.C.), who constructed a method with which one could isolate the subset of prime numbers, from the set of natural numbers [
17]. It starts by first crossing the multiples of 2 in the number line up to
x, then the multiples of 3, then the multiples of 5, and then the multiples of all the primes up to
. If an integer
is not divisible by any prime
, then
n is necessarily a prime. Upon completion of the sieve, one has
Having the means of constructing the complete subset of prime numbers, from the set of natural numbers up to x, one would be naturally interested in quantifying these primes. To this end, there are fundamentally two approaches that one could take, in order to quantify the set of prime numbers generated by the sieve of Eratosthenes. We describe each approach, as follows.
(I) In the first approach, one quantifies the proportion of integers that are sifted out at each round of the sieve, as
The appeal of this approach lies in the straightforward quantitative definition of both the subset of the multiples of p up to x and the complete set of integers up to x. However, the challenging aspect of this approach arises from the fact that integers which have multiple prime factors are necessarily counted at multiple rounds of the sieve, which must be accounted for. This is the approach taken by A. Legendre (1752-1833), who was the first to turn the sieve of Eratosthenes into a quantitative technique, and this has been the approach taken since.
In the sieve of Legendre, one counts the integers that are sifted out at each round, and then one subtracts those that are counted at multiple rounds, according to the multiplicity of times that this has happened, as follows
from which, one obtains Legendre’s formula
where
is the Möbius function, introduced by A. F. Möbius (1790–1868), and defined as
In efforts to evaluate the right-hand side of (3), one has
where the remainder
R is
which doubles at each round of the sieve, and thus quickly becomes larger than
x.
In modern sieve methods, one tries to replace by a function , referred to as the “sieve weights”, which mimics the and gives satisfactory estimates on upper bounds, lower bounds, and asymptotics for smoother number sets such as almost primes, which leads to upper bounds for primes. However, obtaining lower bounds for primes has proved much more difficult, thus leaving Goldbach’s and Polignac’s conjectures out of reach. This has been due to the so-called “parity barrier", where the sieve struggles to distinguish integers with an odd number of prime factors from integers with an even number of prime factors. Although the parity barrier has been broken for certain specific sequences, it still remains the fundamental obstacle in the treatment of primes via this approach of sieve theory.
(II) In the second approach, one quantifies the proportion of integers that are sifted out at each round of the sieve, as
This means that every integer is sifted out according to its least prime factor, out of a set of integers whose least prime factors are greater than, or equal to, the least prime factors of the integers being sifted out at the given round, with the exception of the number 1. This is best illustrated by the following example.
In the 1
st round of the sieve, one quantifies the subset of the multiples of 2 up to 26, as a ratio over the set of all integers up to 26. That is,
In the 2
nd round, one quantifies the subset of the multiples of 3 that survived the preceding round of the sieve, as a ratio over the set of all the integers that survived the preceding round of the sieve. That is,
In the 3
rd round, one quantifies the subset of the multiples of 5 that survived the preceding rounds of the sieve, as a ratio over the set of all the integers that survived the preceding rounds of the sieve. That is,
Since that completes the sieve, then the subset of integers that survives the sieve is
which consists of the number 1, and the complete set of primes in the interval
.
The appeal of this approach lies in the fact that every integer is sifted out only once; and therefore, one does not have the issue of certain integers appearing at multiple rounds of the sieve, which one has with the first approach, as described above. However, the challenging aspect of this approach is the difficulty that one has in defining quantitatively the two subsets of integers that survive the sieve up to the given round. Nevertheless, since at each round of the sieve, the subset of the multiples of p that survive the preceding rounds consists of the complete set of integers up to x for which p is the least prime factor; and, the subset of all the integers that survive the preceding rounds contains the complete set of primes in the interval ; then, one is able to define quantitatively the two sets of integers, at least to the extent where one can determine upper and/or lower bounds.
1.3. Our Results
In the present paper, we take the second approach as outlined above, in order to describe quantitatively the sieve of Eratosthenes. On the condition that x is sufficiently large; at each round of the sieving of integers, we define quantitatively both the subset of the multiples of p up to x that survive the preceding rounds of the sieve and the subset of all the integers up to x that survive the preceding rounds of the sieve; to the extent where we are then able to determine an upper bound to the proportion of integers that are sifted out at each round of the sieve. To the best of our knowledge, we are the first to take this approach for these purposes.
Definition 1. (Additive representation). Let , let , and let x be an even number, then we say that is an additive representation of x, if .
Definition 2. (Subtractive representation). Let , let , and let k be an even number, then we say that is a subtractive representation of k, if .
We then extend our approach taken in the sieving of integers, to the sieving of representations, whereby we quantify the subset of the additive representations of
x, and the subset of the subtractive representations of
k up to
x, that survive the sieve of Eratosthenes. As with the sieving of integers, we quantify the proportion of representations that are sifted out at each round of the sieve, as
This means that additive representations, and subtractive representations, are sifted out according to either a or b, depending on whose least prime factor is the smaller (or equal to) of the two. This allows for every representation that contains at least one multiple of p to be sifted out once only, while every representation that does not contain multiples of p, survives the sieve. Therefore, upon completion of the sieve, we have a subset of representations where or a prime in the interval , and b is a prime in the interval ; with the quantity of representations where being at most one.
By relating the sieving of representations to the sieving of integers for the same x, we determine an upper bound to the proportion of additive representations that are sifted out at each round of the sieve, and an upper bound to the proportion of subtractive representations that are sifted out at each round of the sieve, on the condition that x is sufficiently large. Following on from the upper bounds, we then determine a positive lower bound to the subset of additive representations that survive the sieve, where both a and b are primes in the interval , and a positive lower bound to the subset of subtractive representations that survive the sieve, where both a and b are primes in the interval . Therefore, we prove the following:
Theorem 1. Every sufficiently large even number is the sum of two primes.
Theorem 2. Every even number is the difference of two primes in infinitely many ways.
Theorem 1 partially addresses question as posed above; and, to date is the closest theoretical result to the binary Goldbach conjecture. Theorem 2 fully addresses questions as posed above; fully establishes the Twin Prime conjecture; and, to date is the closest theoretical result to the Polignac conjecture.
2. Notation
and : the set of natural numbers and the set of prime numbers respectively.
x and k : even numbers. p and q : prime numbers. : the prime number.
w : a sufficiently large positive integer, not necessarily the same at every occurrence.
: the integer in the sequence .
: positive real numbers.
: non-negative real numbers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
; that is, is a multiset, with e being the multiplicity of d.
.
Any other notation used, is defined at the point of use.
3. Sieve Outline
3.1. Sieving Integers
Let
then
Since
, then
Let
, then
and therefore
Empirical data for the sieving of
, as shown in
Figure 1, suggest that
oscillates about 1, before approaching 0 as
. We determine an upper bound to
, for
and
.
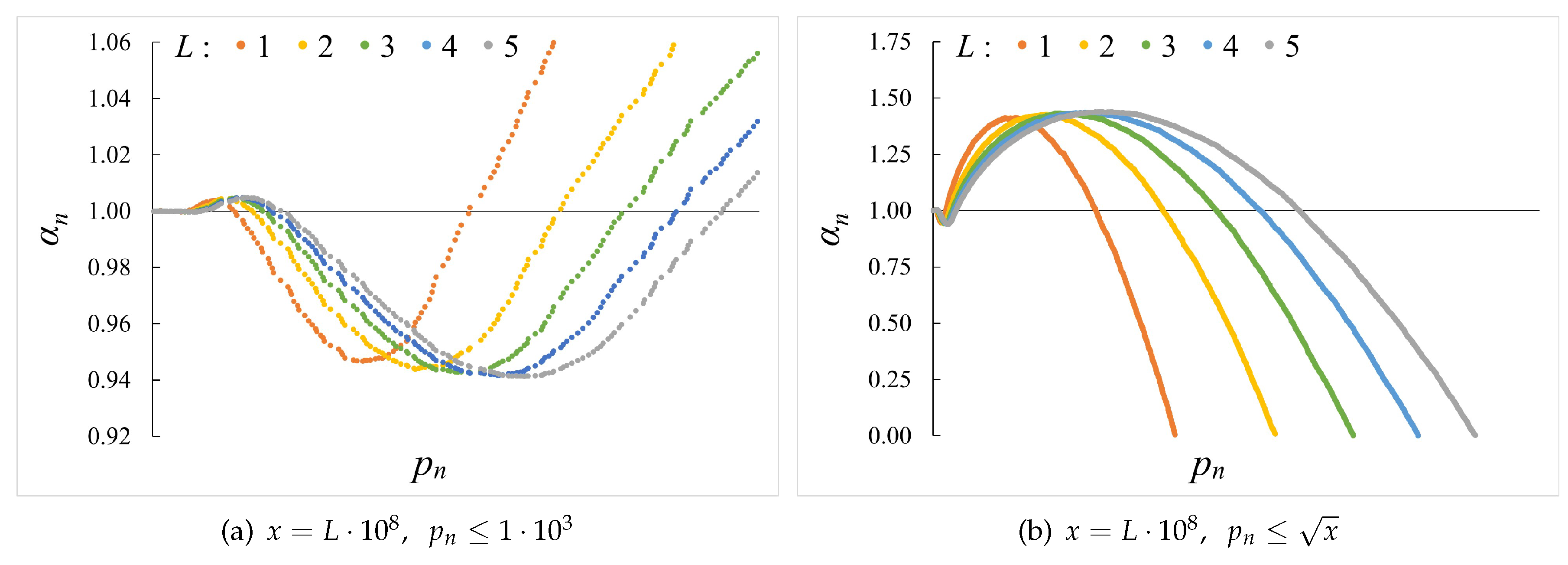
3.2. Sieving Additive Representations
Let
then
Since
, then
Let
, then
where
; and therefore,
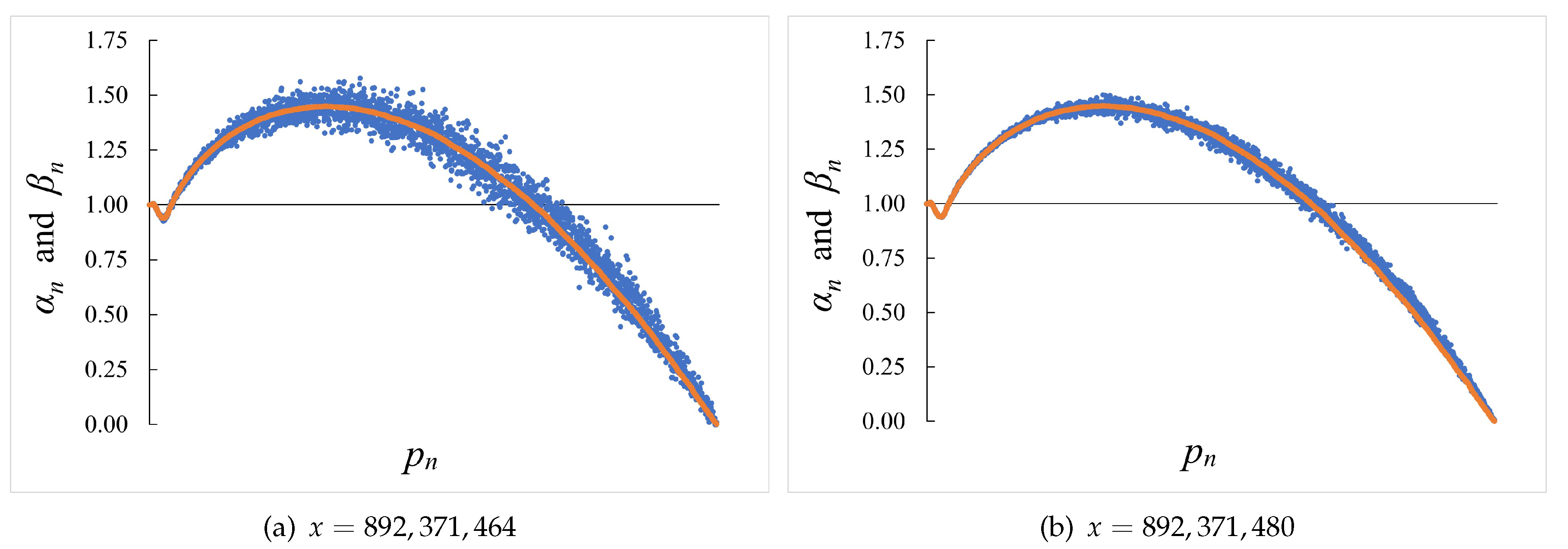
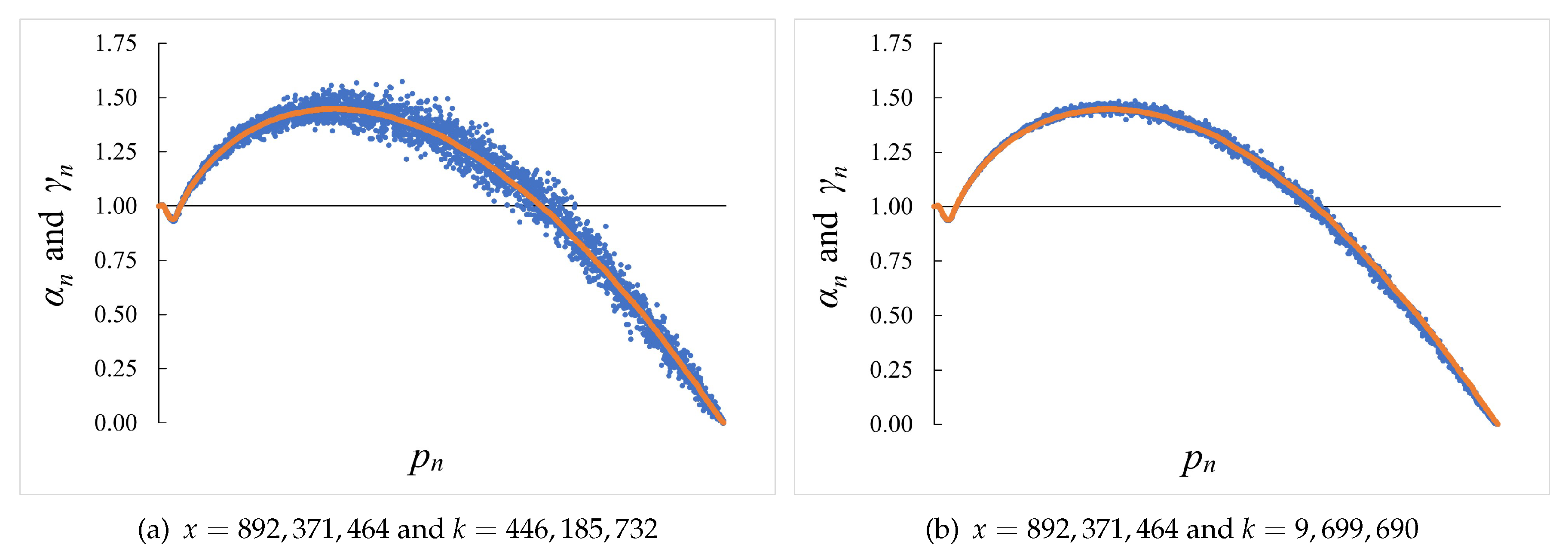
Empirical data for the sieving of
and for that of
, as shown in
Figure 2 for
, suggest that
which we generalise for
. Through (17), we determine upper bounds to
for
and
. Following on from the upper bounds for
, we determine a positive lower bound to (16) for
, and thus we prove Theorem 1.
3.3. Sieving Subtractive Representations
Let
then
Since
, then
Let
, then
where
; and therefore,
Empirical data for the sieving of
and for that of
, as shown in
Figure 3 for
, suggest that
which we generalise for
. Through (23), we determine upper bounds to
for
and
. Following on from the upper bounds for
, we determine a positive lower bound to (22) for
, and thus we prove Theorem 2.
4. Preliminaries
Proposition 1.
Let . Since consists of the complete set of integers () for which is the least prime factor, then due to the Fundamental Theorem of Arithmetic, we have
where , if .
Proposition 2.
In the following, we describe the sieving process of by , where . Thus, let
Then, in light of distribution effects at finite range, we have
Therefore, due to (25) we have
Therefore, due to (26) we have
where the width of approximation tends to decrease as , as can be deduced from Proposition 1.
Proposition 3.
then, in light of Proposition 2, we have
Proposition 4.
Let , then we have
where is the set of the remaining multiples of the primes in the interval ; and therefore, . Since x is an even number, then is non-prime; and therefore, if , then
If , then and is the 1st prime after the ; where, the is non-prime. Therefore; if , then . Therefore; if , then
Proposition 5.
Since and , then
where, due to the Prime Number Theorem, we have
Proposition 6.
Proposition 7.
Proposition 8.
In the following, we describe the sieving process of by ; in relation to the sieving process of , also by ; as outlined in Proposition 2. Thus; let x, , and , be the same as in Proposition 2; and, in light of Proposition 6, let
Then, in light of distribution effects at finite range, we have
Therefore, due to (43) we have
then, due to (47) and (48), in conjunction with (29) and (30), we have
where, the width of approximation tends to decrease, as and as .
Proposition 9.
In the following, we describe the sieving process of by ; in relation to the sieving process of , also by ; as outlined in Proposition 2. Thus; let x, , and , be the same as in Proposition 2; and, in light of Proposition 7, let
Then, in light of distribution effects at finite range, we have
Therefore, due to (51) we have
then, due to (55) and (56), in conjunction with (29) and (30), we have
where, the width of approximation tends to decrease, as and as .
5. an Upper Bound on the Sifted Out Integers
In this section, we determine an upper bound to , as follows.
Let
, then
where, due to the Prime Number Theorem, we have
where
for
. Since
as
, then
as
. Therefore, if
; then, from Proposition 1, we can see that
as
. Therefore, if
and
; then, due to Proposition 3, we have
It remains to determine an upper bound to for , which we do as follows.
Let
; then, due to Proposition 1, we have
where
Therefore, if
; then, due to Proposition 4, we have
which we quantify as follows.
Let
; then
Since
, then
Due to the Prime Number Theorem, we have
and therefore; if
, then
Therefore; if
and
, then
which, in conjunction with (62), holds for
and
.
6. Upper Bounds on the Sifted Out Additive Representations
In this section, we determine upper bounds to , as follows.
Let
and let
x be the same for both
and
; then, we have
and, due to Proposition 6, we have
and therefore, we have
Therefore, due to Proposition 8, we have
where
. We determine an upper bound to (74), as follows.
Let
and let
; then, due to (74) and (70), we have
where
as
. Let
, where
J is a constant arbitrarily large; then, due to (74) and (42), we have
where
. Therefore, if
; then,
such that
, or
Therefore; if
and
, then
and therefore
Furthermore, due to empirical observations, we have
and
and
Then, as with (78), we have
for
.
7. Upper Bounds on the Sifted Out Subtractive Representations
In this section, we determine upper bounds to , as follows.
Let
and let
x be the same for
,
, and
; then, we have
and, due to Proposition 7, we have
and therefore, we have
Since
then
Therefore, due to Proposition 9, we have
where
. We determine an upper bound to (89), as follows.
Let
and let
; then, due to (89) and (70), we have
where
as
. Let
, where
J is a constant arbitrarily large; then, due to (89) and (42), we have
where
. Therefore, if
; then,
such that
, or
Therefore; if
and
, then
and therefore
Furthermore, due to empirical observations, we have
and
and
Then, as with (93), we have
for
.
8. Lower Bounds on the Surviving Representations
In this section, we determine lower bounds to (16) and (22), as follows.
Let
; then, due to the upper bounds for
in (79), (80), (81), and (83), we have the following lower bound for (16):
which we quantify as follows. Since
and
then
Since
, then
and therefore
Since
where
and
, then
This completes the proof for Theorem 1.
Let
and let
; then, due to the upper bounds for
in (94), (95), (96), and (98), we have the following lower bound for (22):
Therefore, as with (106), we have
and therefore,
as
.
This completes the proof for Theorem 2.
Acknowledgments: In constructing the proofs presented in this paper, we were constantly guided by observations of empirical data, such as those presented in
Section 3. To this end, we give very special thanks to our dear friends, Abdul Karim and Zhuen Xie, with the assistance of whom we were able to obtain the data in a much shorter time frame than we would have otherwise. We’re also very grateful for the free access to the following websites, which we’ve made extensive use of:
oeis.org/ and
onlinenumbertools.com/calculate-prime-factors.
About authors
Ali Shehu has a background in Chemistry / Materials Science from London Metropolitan University, UK, and University College London, UK. He was awarded the PhD degree in Chemistry, from Queen Mary University of London, UK, in April 2018.
Jetmira Uka has a background in Chemistry / Chemical Engineering from the University of Tirana, Albania, and she is currently Head of Physics at Notre Dame School, UK. She is also a PhD student in Mechanical and Aerospace Engineering, at Brunel University, UK. Ali and Jetmira are husband and wife.
References
- L. E. Dickson. Goldbach’s Empirical Theorem: Every Integer is a Sum of Two Primes, in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. Dover Publications, New York, 1952, pp. 421-424.
- T. O. Silva, S. Herzog, and S. Pard. Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4·1018. Math. Comp. 83 (2014), 2033–2060. [CrossRef]
- V. Brun. The Sieve of Eratosthenes and the Theorem of Goldbach, in Goldbach Conjecture. World Scientific, Singapore, 2002, pp. 99–136.
- H. L. Montgomery and R. C. Vaughan. The exceptional set in Goldbach’s problem. in Acta. Arith. 27 (1975), 353–370.
- O. Ramare. On Šnirel’man’s constant. Ann. Scuola. Norm. Sup. Pis. 22 (1995), 645–706.
- J. R. Chen. On the representation of a larger even integer as the sum of a prime and the product of at most two primes. Sci. Sinica. 16 (1973), 157–176.
- I. M. Vinogradov. Representations of an odd integer as a sum of three primes. in Goldbach Conjecture. World Scientific, Singapore, 2002, pp. 61–64.
- T. Tao. Every odd number greater than 1 is the sum of at most five primes. Preprint, arxiv.org/abs/1201.6656, July 2012.
- H. Helfgott. The ternary Goldbach conjecture is true. Preprint, arxiv.org/abs/1312.7748, December 2013.
- L. E. Dickson. Theorems Analogous to Goldbach’s. in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. Dover Publications, New York, 1952, pp. 424-425.
- H. Rezgui. Conjecture of twin primes (Still unsolved problem in Number Theory). An expository essay. Sur. Math. App. 12 (2017), 229–252.
- L. Bethune. Found: New World Record Twin Primes!, 2016: available at: https://www.epcc.ed.ac.uk/blog/2016/09/27/found-new-world-record-twin-prime.
- D. A. Goldston, J. Pintz, and C. Y. Yıldırım. Primes in tuples. I. Ann. of Math. 170, No. 2, (2009), 819–862. [CrossRef]
- Y. Zhang. Bounded gaps between primes. Ann. Math. 179 (2014), 1121–1174. [CrossRef]
- J. Maynard. Small gaps between primes. Ann. Math. 181 (2015), 1–31. [CrossRef]
- D. H. J. Polymath. The "bounded gaps between primes" Polymath project - a retrospective. Preprint, arxiv.org/abs/1409.8361, September 2014.
- S. Horsley. The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers. Phil. Trans. 62 (1772), 327–347.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).