Multi-Host Pathogen Transmission and the Disease-Diversity Relationship

Preprint

Concept Paper

Multi-Host Pathogen Transmission and the Disease-Diversity Relationship

Altmetrics

Downloads

660

Views

674

Comments

Marjolein E.M. Toorians^*,Ailene MacPherson,T. Jonathan Davies

This version is not peer-reviewed

Submitted:

12 August 2024

Posted:

20 August 2024

You are already at the latest version

Alerts

Abstract

Disease transmission in wildlife is linked to ecosystem and human health, and host community structure can mediate pathogen spread. Here, we decompose the well-known susceptible-infected (SI) compartmental models of disease transmission for multi-host communities to explore the disease-biodiversity relationship. We examine the parameters involved in interspecific transmission and link them to the multi-host outbreak potential, R0. We partition R0 into its separate elements that can be associated with either the recipient or donating host, and show how this allows us to identify maintenance versus spillover hosts, allowing us to quantify separate stages of spillover into a novel, recipient host. We further suggest that the evolutionary relatedness between donating and recipient host may play a role in the probability a pathogen establishes in a novel species, as illustrated by the observed phylogenetic signal in the host-breadth of multi-host pathogens. We discuss how anthropogenic changes to the environment and wildlife communities, such as the reduction and fragmentation of wildlife habitat, might alter the mode and dynamics of disease transmission. This discussion contributes to the ongoing debate on the relationship between disease incidence and biodiversity. Through a synthesis of classic ecological theory, we illustrate how pathogens can affect host populations through phenomena such as in/direct symbioses, that can save a pathogen from extinction or suppress competing host species, but we highlight how host diversity can simultaneosuly influence the survival and success of the pathogen, suggesting a complex feedback between hosts and parasites in multi-host communities. Our review provides a guide to common derivations of interspecific transmission, and underscores the critical connections between community and disease-ecology.

Keywords:

Subject: Biology and Life Sciences - Ecology, Evolution, Behavior and Systematics

1. Introduction

Epidemics caused by zoonotic spillovers are increasing worldwide [1]. Most emerging pathogens in humans are directly transmitted viruses or bacteria that have crossed the species barrier, perhaps multiple times, likely facilitated by changes to the environment by humans [2,3]. Recent demographic changes have led to increasing contact between humans and livestock with wildlife, providing new opportunities for disease spillover [4,5], and we are seeing a concomitant rise in disease outbreaks originating from wildlife [1,3,6]. A key strategy to prevent emergence of novel infectious diseases, is to reduce transmission from the reservoir (a population of one - or multiple - species that maintain the disease) to a susceptible, novel target population [7]. Understanding the process of transmission within and between species, and especially from reservoir hosts to previously unexposed hosts, is thus critical for mitigating the risk of future disease emergence events.

Predicting the likelihood of interspecific transmission of a pathogen from an endemic donor host into a novel host population requires information on host behaviour and abundance, host and pathogen geographical overlap, host phylogeny and the pathogen’s mode of transmission [8,9,10,11,12]. Most commonly, transmission is modelled using compartmental disease models, which include host behaviour, and can provide predictions of pathogen outbreak potential (the basic reproductive ratio,

R_{0}

) — the number of secondary infections that can arise from a single infected individual [13]. In these models, transmission describes the process by which an infected individual transmits a pathogen to an uninfected individual, a critical step in disease spread [14]. When interspecific transmission is sufficiently high, a pathogen may invade a novel host [6,15,16]. This can occur when a new pathway between an infected host and a susceptible host is established, for example, due to travel, translocation of the pathogen or other mechanisms facilitating spillover. Here, we describe the steps of interspecific transmission and the role of anthropogenic changes in the environment on transmission dynamics, and how these different components determine disease spillover and endemic equilibria.

Mathematically defining interspecific transmission is not straightforward, and requires specific information on the contact structure between donating and recipient hosts. A subset of pathogens have been suggested to transmit through the environment in addition to spreading via vectors or direct contact between hosts [17]. Anthrax is one well-known example of a pathogen with environmental transmission [18]. Another example is bovine Tuberculosis (bTB, caused by Mycobacterium bovis), which has a wide host range, with environmental transmission playing a dominant role in interspecific transmission [19,20]. There is some evidence that survival rate of the bacterium also differed between sterile and unsterile soil samples, suggesting an even more complex role of environmental context in mediating disease transmission [21]. Survival rates in the environment vary by pathogen, and generally tend to be relatively low for viruses, which have short generation times and rely on their hosts for reproduction, whereas some bacteria and ectoparasites, can survive outside their hosts for extended periods of time. For example, Rabies (Rabies lyssavirus) has no known record of environmental transmission [22], whereas prions causative agents of Chronic Wasting Disease (CWD), can persist in the environment, providing a pathway for indirect disease transmission between racoons (Procyon lotor) and white-tailed deer [23]. These multiple possible pathways of transmission pose a significant challenge to developing predictive models of disease spread.

The relationship between biodiversity and disease is also complex; there exist contrasting hypotheses for this relationship both of which depend on assumptions about the dynamics of transmission. Biodiversity has been suggested to buffer disease outbreaks, a theory which is known as the dilution effect [24,25,26], and the increase in frequency of epidemics has been suggested to be linked to the loss of biodiversity worldwide [24,27,28]. However, biodiversity may also increase pathogen prevalence, an amplification effect, making it difficult to generalise about the role that biodiversity plays with diseases.

To examine how interspecific disease transmission is influenced by changes in biodiversity, here we explore the role of host community composition in disease outbreaks. We examine how the biology of transmission, and the mathematical assumptions in the general interspecific transmission model, shape the disease-diversity relationship and how anthropogenic disturbances may shift transmission modes. We also explore how pathogens effect host communities and contact structures, for example, by altering community composition through indirect competition. We start by defining interspecific transmission and outbreak potential in a multi-host system. We then explore how host community structure influences transmission dynamics, linking to the much debated disease-biodiversity relationship. Finally, we discuss the evolution of multi-host pathogens and disease emergence.

2. Decomposing Interspecific Transmission

To derive expressions for transmission between host species, we need to first describe the general transmission process. We can decompose interspecific transmission into five stages (Figure 1. These stages are analogous to those outlined by [29] for intraspecific transmission except with the additional consideration of the identity of the donating and receiving hosts. Figure 1 illustrates the five stages of transmission for bTB transmitting from its reservoir, African buffalo (Syncerus caffer), to a novel host, African elephants (Loxodonta africana), a species in which bTB has recently been discovered [30]. Bovine TB is a generalist pathogen able to infect almost all mammals [31,32], including threatened wildlife species and livestock. Because of its high prevalence in both wildlife and livestock, it serves as a useful model for interspecific transmission.

Mathematical models of transmission, as illustrated in the susceptible-infected (SI) model considered below, represent a series of simplifying assumptions and are the net result of the five transmission stages. The first stage (Figure 1) illustrates dynamics of the pathogen load within the donor host, a process mediated by the donor host’s immune response. Stage 2 is the production of infective propagules, which determines the interspecific transmission potential, and depends on both the donor species’ immune response and the phase of infection. In the case of bTB, a chronic infection, propagule production increases with time, whereas for many acute infections, such as influenza, there is a peak in propagule production early in infection [33]. Once shed into the environment the pathogen must first survive (Stage 3), and then may be picked up by a novel host species (in Figure 1, the African elephant). The probability of a pathogen spreading via the environment depends on the environmental conditions, such as light exposure and humidity, as in the case of M. bovis [21,34]. The recipient hosts is then exposed (Stage 4) in a process depending crucially on host behaviour, geography, disease prevalence and density of hosts, as we discuss in further detail below. Finally, the pathogen must replicate within the exposed host (Stage 5), a process that is again dependent on host immune defences, completing the transmission cycle.

Figure 1. Interspecific transmission of bovine Tuberculosis (bTB) from its reservoir, the African buffalo (Syncerus caffer), to the African elephant (Loxodonta africana). Graphs show an approximation of the stages of transmission as described by [35]: 1) Propagule load (y-axis) within donor host over time (x-axis), 2) Production of pathogen-infective stages in donor host (y-axis) depending on host traits (x-axis), 3) Survival and growth of pathogen propagules in the environment (y-axis) over time (y-axis), including the environment of an intermediate host, 4) Acquired dose by recipient host at exposure (y-axis) depends on the prevalence of the donor host (x-axis), 5) Recipient host pathogen load (y-axis) over time (x-axis). Both direct and indirect (environmental) transmission modes are shown. Intraspecific transmission is shown between buffaloes, which can occur through aerosols. The illustrations in orange (circles with rod-shaped bacteria) represent the progression of the mycobacterium, in the lungs of both hosts, as well as in their dispersal propagules. The figure is illustrative of the complexity of a pathogen’s transmission cycle. Figure credit: Sylvia Herediaz, UBC Zoology.

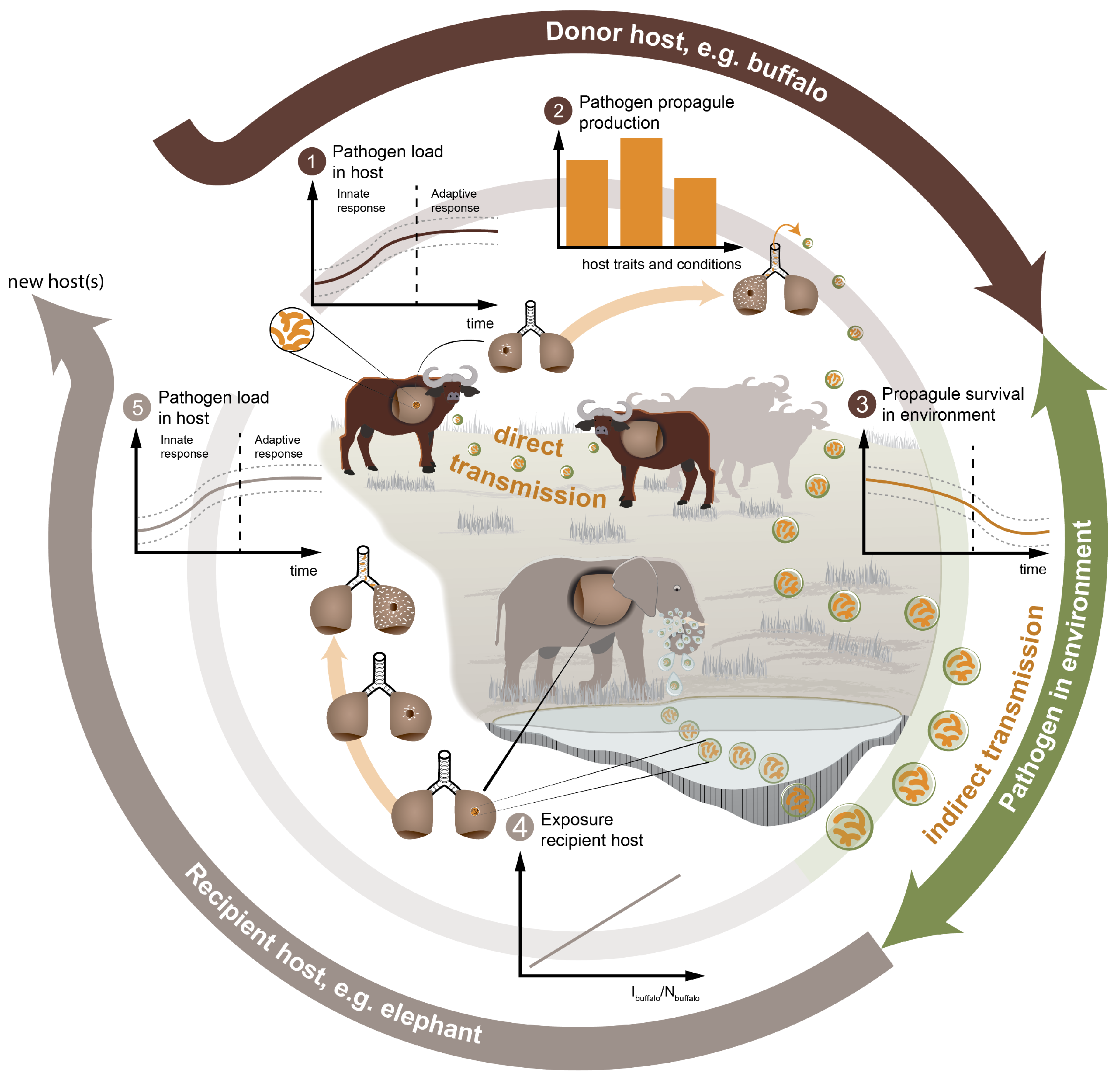
The first and second stages of transmission are solely dependent on the donating host, as represented by the buffalo in Figure 1. The propagule load in this host, and the production of dispersing propagules depends on the level of infection and host immune system, and is therefore species-specific as well as individual-specific. For example, the establishment and growth of bTB in individual buffalo is facilitated by co-infection with helminths, which can increase the population-level transmission rate [36,37]. In some cases, the mediating effect of co-infection was strong enough to inhibit bTB infection in the absence of helminth infection. Infected host individuals shed pathogen propagules into the environment (Figure 1, Stage 3), and this transmission pathway may be more important in interspecific dynamics, because transmission by direct or close contact may be less likely between individuals of different species (with some exceptions). Mycobacterium bovis has been found in the soils of bTB-positive farms, and can survive up to four weeks in the environment [21,38,39], allowing for possibility of extended environmental transmission (Figure 1, Stages 3 and 4). Environmental transmission of bTB has also been shown in a controlled experiment with white-tailed deer (Odocoileus virginianus) in Michigan, and wild boar in Doñana National Park, Spain [38,40]. Finally, the subsequent pathogen load in the recipient host (Stage 5) depends on the pathogen type and the host’s immune response. This may reflect the strength of co-evolution of the pathogen with the reservoir host, and the recipient’s host evolutionary relatedness to the donor host, with a higher likelihood of pathogen sharing when donor and recipient hosts are more closely related [41,42], we expand upon this in Section 4. These and more examples show that defining interspecific transmission is complex, and that the contribution of environmental transmission can be important.

Pathogen transmission is most commonly modelled using classic compartmental models [i.e., the Susceptible-Infected-Recovered model [13,43]. To illustrate some common approaches to modelling disease transmission, both within and between species, we begin with a simple SI model where we disregard resistance as many wildlife infections are either chronic or fatal, and recovered individuals will not directly impact transmission. While limited in epidemiological complexity, starting from the simplified susceptible-infected (SI) compartmental model allows us to easily expand to consider interspecific disease transmission and the much-debated disease-diversity relationship [27]. This model captures classic expressions for intraspecific transmission in the case where the donor (subscript d) and recipient species (subscript r) are the same, but easily allows for analogous expressions for models of interspecific transmission. The disease incidence in the recipient host is given by the following:

\frac{d I_{r}}{d t} = \underset{Transmission}{\underset{︸}{\sum_{d} (β_{d, r} S_{r} \frac{I_{d}}{N_{d}})}} - \underset{Removal}{\underset{︸}{Γ I_{r}}}

(1)

where t is time,

Γ

is the removal rate (recovery and mortality rates, combined), S and I are the number of susceptible and infected individuals, respectively, and the host population size is defined as

N = S + I

, these variables are measured in counts. When

r = d

, this function represents intraspecific transmission. Here,

β_{d, r}

is a general transmission rate and describes the rate of new infections per unit time per recipient host. Transmission is often asymmetric, for example, [44] suggest that for a fox with rabies to infect another species, such as a dog or cat, requires a million times more virus particles than would be necessary to infect another fox. Usefully, while the generalized transmission term of Equation (1) is usually referred to as Frequency-Dependent (FD) transmission [45], by changing the contact rate to include density (see Section 2.1) we can also derive Density-Dependent (DD) transmission. This single constant implicitly captures the biological complexity of the five transmission stages as well as chains of transmission between recipients and hence, unsurprisingly, can result in a wide range of possible epidemiological dynamics. As a result of the numerous underlying assumptions, its value cannot easily be interpreted, particularly in the context of interspecific transmission.

This simple SI transmission model assumes that all individuals within and between species mix homogeneously, such that the identity and/or characteristics of individual hosts need not be modelled explicitly. As illustrated in transmission stages 1 and 2 of Figure 1, we ignore the individual variation in propagule load. However, the model in Equation (1) can easily be extended to including additional discrete donor and recipient classes (e.g., varying in exposure or other attributes that might place them within high or low risk classes) or continuous variation among individuals (e.g., age-dependent, activity, or space-use related variation), capturing key features of individual heterogeneity. Including such information can also help capture interspecific differences in disease establishment in novel host populations. For example, in trophic transmission of bTB from infected buffalo to lions (Panthera leo), subadult buffalo are at highest risk of carrying bTB, while all age classes of lions are equally exposed [31]. We explore some examples of modelling heterogeneous populations in Appendix Section 5.

2.1. The Transmission-Rate, $β_{d, r}$

The modelled interspecific transmission rate,

β_{d, r}

, between the donor, d, and recipient, r, hosts is a simplification of the process in Figure 1. It can be approximated by the product of the interspecific contact rate,

κ_{d, r}

, capturing stages 1-4, and the probability that the recipient host becomes infectious given contact,

c_{r}

, capturing stage 5. We can represent this as

β \approx κ \cdot c

[see [46]. To explore multi-host pathogen dynamics, we can easily extend this formulation:

β_{d, r} \approx κ_{d, r} c_{r}

(2)

This approximation holds as long as the probability of infection per contact,

c_{r}

, is small (see Appendix Equation (A2) for derivation), but it implicitly ignores donor host heterogeneity, as described above, by averaging over the duration of infection (e.g. pathogen load and propagule production, Stages 1 and 2), the possibility of environmental transmission and the lifespan of the pathogen outside of the host (Stage 3), the novel host’s susceptibility and immune response to the novel pathogen (Stage 4) and the potential for onward transmission in order to become epidemic (Stage 5). Below, we decompose Equation (2) further and discuss how each component contributes to the interspecific transmission process.

2.1.1. The Contact-Rate, $κ_{d, r}$

The contact rate between hosts, measured as the number of recipient hosts contacted per donor host per unit of time, determines the shape of transmission dynamics [45]. There are multiple approaches for describing the spread of a pathogen through a host population, the most common distinction is between density-dependent (DD) and frequency-dependent (FD) dynamics, but there are numerous variations, reflecting differences in the biology of the pathogen and the behaviour of the hosts. A general form for this contact rate in a single-species system is:

κ (N) = ξ N^{q}

(3)

Here, the parameter q (0

\leq q \leq

1) determines the transmission mode [47], modifying the unit of measurement of the per-capita contact rate

ξ

. Wildlife diseases are almost always modeled assuming DD transmission (

q =

1), regardless of the pathogen, as host behaviour, including local heterogeneities, is more likely to approximate mass-action dynamics at larger scales [48]. In contrast, local dynamics in human interactions commonly depart from assumptions of DD (people frequently form small contact networks) and might thus be better modelled using FD transmission (

q =

0) or, more realistically, assuming asymptotic transmission (transmission that can shift from DD to FD with increasing host density).

Extending this to the interspecific contact rate

κ_{d, r}

, representing the contact rate between donor, d, and recipient, r, species. The per-recipient contact rate depends on the density of donor recipients,

N_{d}

κ_{d, r} (N_{d}) = ξ_{d, r} N_{d}^{q_{d, r}}

(4)

Here,

ξ_{d, r}

is the per-capita contact rate and represents the theoretical maximum number of contacts between d and r, and

q_{d, r}

is the DD-FD modifier of interactions between the r and d species pair, such that

q_{d, r}

= 1 represents DD and

q_{d, r}

= 0 is FD. In FD transmission, recipients hosts come into contact with a fixed number of donor hosts per unit of time regardless of the population density of the donor. In contrast, DD transmission occurs when the number of contacts per recipient host per unit time increases with donor host population density. For the case of a single donor and single recipient host species this simplifies to:

Transmission = β_{d, r} S_{r} \frac{I_{d}}{N_{d}}

(5)

Inserting Equations (2) and (4), we get:

Transmission = ξ_{d, r} c_{r} N_{d}^{q_{d, r}} S_{r} \frac{I_{d}}{N_{d}} = \{\begin{matrix} l r ξ_{d, r} c_{r} S_{r} I_{d}, & when q = 1 \\ ξ_{d, r} c_{r} S_{r} \frac{I_{d}}{N_{d}}, & when q = 0 \end{matrix}

(6)

The mode of transmission may differ between versus within populations (see following section and Figure 3A and B). For example, transmission can be DD within a household (or herd) but FD between households, where contacts may be constant per time-unit. Many empirical studies show evidence of both FD and DD dynamics in the same system, with DD dynamics more often observed at low population densities and FD dynamics more common at higher densities as contacts saturate [49,50]. Feline Leukaemia Virus (FeLV) provides one good example: At low host densities, infrequent encounters make contact rates insensitive to changes in densities (FD), at intermediate densities contact rate becomes proportional to density (DD), at higher densities contacts again approximate FD dynamics due to increased territoriality, and at very high densities, individual territories decrease in size, causing the contact rate to become DD again due to home range overlap [51]. Behaviour, such as territoriality, can thus have a large effect on contact rates within and between species. When modelling multi-species pathogens, we therefore need to carefully consider how transmission mode may differ both between versus within species and within versus between populations in each species. We elaborate on this complexity in Section 3 and Figure 3 using the spillover of a filovirus, such as Ebola, as example.

Contact structures within species are very unlikely to resemble contact structures between species. For directly transmitted diseases in populations with strong social and spatial structuring, we thus need to revisit assumptions of homogeneity and random host mixing assumed within density-dependent transmission [48,52,53]. Epidemic network models based on graph-theory, where the realized per-capita transmission rate

\hat{β}

is scaled to the mean neighbourhood size [48,52], provide one useful approach. In these models, the degree of connectivity within a population has a large effect on disease dynamics. For example, triangular contacts (three connected individuals) reduces both the initial spread and final disease outbreak size [54]. We discuss examples of single-species heterogeneity using graph-theory in Appendix Section 5. However, contacts in complex networks tend to homogenize over time [55]. Therefore over longer timescales, heterogeneity can average out, providing an opportunity to simplify otherwise complex models.

2.1.2. The Probability of Successful Transmission, $c_{r}$

Accurately quantifying the probability that a pathogen will establish in the recipient host after contact with an infected donor host or environmental propagules from that donor host is challenging. Within a species there is large variation in terms of susceptibility that depends on, for example, co-infection, sex, age, and genetic variation [56,57,58]. In a community of multiple species, it is becoming increasingly clear that the evolutionary relationship between species is also important for disease transmission, with strong evidence of phylogenetic signal in the likelihood of pathogen sharing among hosts [41,59,60,61]. It is likely, for example, that similarity in the immune defenses of closely related species due to evolutionary conservation of cellular, immunological, or metabolic traits, favours virus exchange between them [62,63]. Similar phylogenetic signature in pest and pathogen sharing is observed in plants [42,64,65,66,67], and phylogeny is also suggested to be a strong predictor of pathogen impact, with declining severity of the disease with increasing evolutionary distance from the reservoir host [68,69]. However, parasites infecting hosts outside of their typical host range can cause lethal damage, presumable due to a lack of resitance [70].

It would be relatively straightforward to include information on host phylogeny in our compartmental disease models, for example, scaling the probability of successful transmission, c, by the evolutionary relationship between hosts (see [42]). By incorporating the evolutionary distance separating hosts as an additional weight modifying transmission success, e.g.

c = 1 / ({Phylogenetic distance}_{species A \to species B}

), we can then describe the projected disease dynamics in host communities using commonly-used phylogentic metrics. It could additionally be possible to modify the probability of establishment to

c (r | d)

, so that the establishment depends on both the recipient and donor hosts identity, as in the example shown in Figure 1, Stage 4. We discuss further the implications of host phylogenetic diversity in multi-host diseases in Section 4.

2.2. Calculation of the Outbreak Potential in the Recipient Host, $R_{0, r}$

To calculate the probability of a disease outbreak in a host population with a single host species, we can use the previously described basic reproductive number:

R_{0} = \frac{Transmission}{Removal} = \frac{β}{Γ}

. An

R_{0}

= 1 describes dynamics in which each infected individual gives rise to one additional infection (before death or recovery). When

R_{0} > 1

there is more transmission within the population than removal through death or recovery, and the disease will spread exponentially, the larger

R_{0}

, the faster the rate of spread. If

R_{0} < 1

the disease will (eventually) die out.

In a system with multiple hosts contributing to the spread of a pathogen, we have multiple dimensions of

R_{0}

R_{0, r r}

, describing the contribution to disease spread within a single host species from intraspecific transmission,

ii)

R_{0, r}

, describing the contribution to disease spread within a single host species from both interspecific and intraspecific transmission from all donating hosts (D),

iii)

R_{0, D r}

, describing the contribution to disease spread within a single host from interspecific transmission,

iv)

R_{0, t o t a l}

, the outbreak potential across the whole community, considering the contributions of both interspecific and intraspecific transmission.

These various

R_{0}

expressions determine the pathogen’s endemicity in a host (at endemic equilibrium), and whether each hosts is an obligate mutualists (at spillover equilibrium), as we illustrate in Figure 2. We can calculate these

R_{0}

expressions from Equation (1). For a more detailed derivation, see Appendix section 3.

In a multi-host community, an ’outbreak’ can always occur in a recipient host given an influx of disease propagules through interspecific transmission. When intraspecific transmission does not occur then the disease will be at a non-zero "Spillover" equilibrium (Figure 2), hence

R_{0, r} > 1

. To find both this "spillover" equilibrium and the "endemic" equilibrium that exists in the presence of intraspecific transmission for the recipient host, we consider the case when Equation (1) > 0, such that there is a greater influx of disease into the population than outflux through mortality (and potentially recovery):

\frac{d I_{r}}{d t} = \sum_{d} β_{d, r} \frac{I_{d}}{N_{d}} S_{r} - Γ_{r} I_{r} > 0

(7)

This can be rewritten and partitioned into the respective intraspecific and interspecific transmission components (see Appendix Section 3 for the derivation):

\frac{d}{d t} Y_{r} = \underset{intraspecific}{\underset{︸}{β_{r r} Y_{r} (1 - Y_{r})}} + \underset{interspecific}{\underset{︸}{\sum_{d \neq r} β_{d, r} Y_{d} (1 - Y_{r})}} - Γ_{r} Y_{r}

(8)

Where

Y_{r} = \frac{I_{r}}{N_{r}}

and

Y_{d} = \frac{I_{d}}{N_{d}}

. We can similarly partition

R_{0}

which can be derived by assuming, as per definition, that the disease is initially rare,

Y_{r} \approx

R_{0, r} = \underset{R_{0, r r}}{\underset{︸}{\frac{β_{r r}}{Γ_{r}}}} + \underset{R_{0, D r}}{\underset{︸}{\sum_{d \neq r} \frac{β_{d r}}{Γ_{r}} \frac{Y_{d}}{Y_{r}}}} > 1

(9)

Hence,

R_{0, r}

is composed of

R_{0, r r}

and

R_{0, D r}

, where D stands for all donating hosts. Thus, when

R_{0, r r} \neq

0, the community can go from a disease-free equilibrium to a spillover equilibrium if

R_{0, D r} + R_{0, r r} > 1

. Only when the intraspecific transmission (

β_{r r}

) is significantly increased (or,

Γ_{r}

decreased), will the community converge on the endemic equilibrium,

R_{0, r r} > 1

(Figure 2).

Interspecific transmission and the community

R_{0}

has most often been described using Who-Acquired-Infection-From-Whom (WAIFW) matrices, representing the transmission rates,

β_{d r}

, between all species pairs [71,72]. The WAIFW-matrix can be expanded to include transition between stages, such as the recovery and mortality rates, to create the Next-Generation-Matrix (NGM), as shown by [72,73]. We can find all

R_{0, r r}

values on the diagonal of the NGM-matrix, and the off-diagonals represent the respective

R_{0, D r}

. This framework allows us to simply derive the outbreak potential over all the hosts in the community, calculated as the maximum eigenvalue of the NGM matrix. The sum of each the row in the matrix is equivalent to our Equation (9).

The separate definitions of

R_{0}

, derived above, allow us to easily describe multi-host dynamics. For example, in the case of bTB (Figure 1), buffalo are primary reservoirs and are able to maintain the disease in the population (i.e.

R_{0, b b} >

1, where b = buffalo). However, some spillover hosts, such as lions, have high disease-induced mortality rate (high

Γ_{l}

), and cannot maintain bTB without reinfection [74]. Thus for lions

R_{0, l l} < 1

(where l = lion), but with sufficient transmission from other hosts,

R_{0, D l}

can be

> 1

. Other likely examples include bTB in elephants (Loxodonta africana), and rabies in jackals (Canis adustus), which need to be frequently reinfected from domestic dogs to support an infection in the population [25,75]. Spillover hosts such as jackals may nonetheless contribute to disease maintenance, and increase the pathogen burden within host communities [76]. Even when a pathogen does establish in a novel host species, it may still not drive a disease outbreak (

R_{0} <

1), and there may be an evolutionary lag as it adapts to its novel host before emerging as an outbreak. The separate derivations of the basic reproductive number we introduce here provide us with a useful perspective for better understanding the contribution of each species in disease maintenance within multi-host communities.

3. The Role of Host Community Structure in Interspecific Transmission

Changing host community structure alters intraspecific and interspecific contact rates, and can thus reshape disease dynamics. As we described in Section 2.2, not all host species have similar susceptibility or transmission potential, so different species may uniquely alter disease prevalence and outbreak potential [26]. Additionally, abiotic conditions, including anthropogenic factors, can affect spatial structure of hosts, and host immunology and competence [77]. To understand how a diseases emerges in a novel host, for example, a zoonotic disease emerging from a wildlife reservoir into human populations, we need to consider the spatial scales and behaviour of both originating and novel host populations. The nature of the transmission (e.g. DD versus FD) contributes to the probability of a disease being able to establish in a novel population, and whether host diversity dilutes or amplifies disease prevalence. However, as discussed above, the mode of transmission within each species is often not so simply categorised, and as we add additional hosts we add further complexity to transmission dynamics.

Here, we use an example of Ebola (Zaire ebolavirus), where spillover occurs between human households, H, and wildlife, W, to illustrate the complexity of multi-host transmission (Figure 3A.). We might assume FD transmission between households within villages, because the rate a family or individual interacts with another family, does not change with the human density. In contrast, within households, transmission might approximate DD dynamics. Wildlife disease dynamics are commonly modelled assuming DD transmission [48]; however, contacts between wildlife and people, for example, through hunting, which may be a time-dependent, not density-dependent, are more likely to be FD. In addition, transmission dynamics can shift even within wildlife species between FD and DD, depending, for instance, host density, as was the case for feline leukemia virus (FeLV) in cats [51].

Behaviour is an important modifier of transmission dynamics; however, it is becoming increasingly evident that land use change in the form of habitat loss and fragmentation, agricultural intensification, and urbanisation has also had a dramatic effect on disease emergence and risk of epidemics [27,78,79,80]. These changes to the natural landscape in combination with a growing human population have likely increased the contact zone between human and wildlife hosts, providing new opportunity for interspecific transmission at the interface between natural and converted landscapes [79,81] (Figure 3C). For example, there is evidence for increased bacterial transmission between primates and humans on forest edges [82]. We might initially predict DD transmission to dominate if habitat degradation decreases the habitat area to support hosts, elevating host densities and thus intraspecific contact rates (Equation (3) and Figure 3C). However, over time, a reduction in natural habitat might force species to forage further, elevating interspecific contacts, and community disease dynamics might oscillate along the DD-FD spectrum. This switching between DD and FD dynamics is important when we consider how the mode of transmission determines the effects of host community structure on pathogen prevalence, which in turn feeds back to shape host communities.

4. Linking Host Community- and Disease-Ecology

Host community structure can both affect and be affected by pathogen dynamics. In multi-host systems, transmission is determined by multiple shedding hosts species, each of which can contribute differently to disease prevalence, depending on their interspecific and intraspecific ecological interactions [7,76,83]. This variation complicates models and how we estimate transmission, which may be asymmetric among hosts, with some hosts acting as pathogen reservoirs and others as sinks. In this section, we review both the sides of host communities on pathogen transmission and vice versa in multi-host disease systems, connecting classical community ecology theory and revisiting the much debated disease-diversity relationship.

4.1. Host Community Effects on Pathogen Prevalence

The dilution effect suggests a higher diversity of hosts reduces the probability of a pathogen infecting another host species, for example, by reducing encounters, and therefore transmission between hosts or indirectly by changing total host abundance [9,25]. One well-modelled example of encounter reduction (also known as frequency-dependent dilution) is provided by [84]; here, one host is rescued from pathogen mediated-extinction by a second host that is infected by the same disease (apparent mutualism). In this model the secondary host is assumed less competent, and therefore functions as a buffer, reducing further disease spread by replacing contacts (and therefore transmission events) with the original host, effectively reducing frequency of contacts between competent hosts. Lyme disease is a frequently cited empirical example of the FD dilution effect, where diversity of vertebrate hosts decreases the risk of spillover to humans. The bacterial pathogen (Borrelia burgdorferi) is vectored by the black legged tick (Ixodes scapularis), and uses the white-footed mouse (Peromyscus leucopus) as a primary host. Prevalence of B. burgdorferi decreases in white-footed mice when a secondary, less competent host, the eastern chipmunk (Tamias striatus), increases in density [25]. The dilution effect becomes more complex when species have high levels of sociality, as FD dilution assumes homogeneous contacts. A summary of diseases with dilution effect can be found in [9].

Host species richness and abundance have been the focus of most discussion on the disease-diversity relationship, but species identities are another important driving factor [42], and host competence may be more important than densities [85]. The replacement effect describes the replacement of a high competent host with a less competent host. One variation of the replacement effect is the phylogenetic dilution effect, in which host competence is assumed to covary with phylogenetic relatedness such that the addition of a phylogenetically distant species to a host community would be predicted to result in a decline in prevalence [42,86]. It is, therefore, possible to see a dilution effect through changes in the phylogenetic community composition even when host species richness remains constant, as has been suggested for bTB in sub-Saharan mammals [87,88]. It is challenging to decompose communities into separate components capturing richness, competences and abundances, but understanding how disease dynamics will shift with community change will require consideration of all three components.

In contrast to dilution, the amplification effect suggests that higher host diversity increases disease prevalence. This may be directly, via elevating contact rates by increasing total host density [84] or by the addition of a highly competent, super-spreader host (a phenomenon parallel to the selection effect in biodiversity science [89]), or indirectly by changing host densities through competition [90] (Figure 4B). For example, higher amphibian diversity is thought to have increased Chytrid disease (Batrachochytrium dendrobatidis) prevalence in some species of frogs, as highly competent (amplifying) hosts are more abundant in species-rich habitats [26]. Another example comes from a model for Lyme disease where the addition of a competent alternative rodent host increases the number of infected tick larvae and therefore increases disease prevalence [91]. These examples show that the amplification effect may also arise in vectored diseases (often modelled as FD) through indirect competition (host regulations) when increased host diversity supports more competent host species [24,84].

In all cases of amplification and dilution (Figure 4), it is assumed that the pathogen is a generalist but hosts may differ in competence. In FD transmission, amplification depends explicitly on host competence, and thus host identity (Figure 4A). Under strict assumptions of DD transmission, amplification will always occur, as contacts increase with host density, and contacts are always additive and never substitutive [72,84], as we illustrate in Figure 4A, column 2. Thus, increasing the number of hosts simply increases encounter rates between S and I individuals, and will therefore always amplify the disease, regardless of the competence of the hosts. In contrast, the direct effect of diversity in FD transmission, assuming a constant number of contacts per time unit and varying competence, are mixed. The addition of a less competent host will always have a diluting effect, whereas the addition of a highly competent host may have an amplifying effect (Figure 4A, column 1, row 3). Predicting the indirect effects of diversity is more challenging. For example, a model by [92] suggests that the substitutive behaviour (encounter reduction) of dilution in DD systems can only occur when we assume that species richness scales linearly with species density, which is not always the case. However, dilution can occur in DD systems indirectly, when the abundance of a competent host is reduced by an introduced, non-competent host that outcompetes the former (Figure 4A, column 3).

Most wildlife diseases are modelled assuming DD transmission, we might thus expect amplification effects to dominate in natural systems. However, host contacts likely saturate at higher densities [49], such that disease dynamics may switch from DD to FD transmission (c.f. asymptotic transmission), and therefore we might predict dilution effects to be relatively more common at higher densities.

4.2. Pathogen Effects on Host Community

While we expect a pathogen’s persistence to be influenced by the abundance of its hosts, host abundance might also be influenced by the pathogen. Most obviously, a pathogen can suppress host abundance directly through disease induced mortality. In multi-host systems, pathogen sharing among hosts can result in apparent competition [93]. For example, a reservoir host may indirectly suppress a spillover host by acting as a source of infection, and if the reservoir host has a better adapted immune system to the pathogen, it can reduce the relative density of the spillover host via pathogen induced mortality. One example of apparent competition is provided by the spillover of the vector-transmitted Barley Yellow Dwarf virus (genus Luteovirus) from wild oats (Avena fatua), which reduced the abundance of the spillover host species, Setaria, allowing the wild oat to maintain ecological dominance [94]. Although disease dynamics may appear similar, and feedback into dilution or amplification effects, apparent competition describes the effect of pathogen prevalence on hosts, whereas, dilution and amplification describe the effects of host diversity on pathogen prevalence. Apparent competition is typically only a property of DD systems, but may be possible in FD systems if the pathogen is not directly diluted by less susceptible, spillover hosts.

Apparent mutualism can occur in FD systems when hosts have equal competence. In this case, the introduction of a novel host can reduce the disease prevalence in the original host by replacing contacts. There is no ’competition’ as all hosts are equally affected by the pathogen [90], and all hosts benefit from additional hosts. Apparent mutualism differs from dilution, as dilution assumes difference in host competence, while apparent mutualism assumes hosts are identical in their competence.

Pathogens are also thought to play an important role in maintaining host diversity. The Janzen-Connell effect describes a process in which pathogens drive density-dependent mortality in hosts, allowing for heterospecifics to coexist [95,96]. Pathogens can thus counteract the process of competitive exclusion by preventing any one host becoming too dominant [97]. Originally describing seedling mortality in forests, the Janzen-Connell effect also includes a spatial component: seedlings have lower survival rates when grown in proximity to conspecifics as their genetic similarity in immune responses makes them equally susceptible to pathogen infection. Both distance-dependent and density-dependent effects can be viewed as examples of apparent intraspecific competition, mediated by pathogens. These dynamics give rise to a rare-species advantage, when we assume that closely related species have an increased probability of disease-sharing this may be reflected in their evolutionary distinctiveness from other host species [42].

In summary, under assumptions of DD transmission dynamics, increasing diversity results in amplification, irrespective of differences in host competence, assuming each host adds to overall disease transmission. Under assumptions of FD dynamics, increasing host diversity can result in apparent mutualism when hosts are equal in their competence, and dilution can occur when hosts have unequal competence. However, apparent competition is possible under both FD and DD dynamics if hosts vary in competence and one host experiences lower pathogen related mortality, for example, through having a superior immune system.

5. Pathogen Adaptation in Multi-Host Systems

Heterogeneity in host susceptibility, infectivity and mixing affects the likelihood of disease emergence. This is more commonly referenced as within-host heterogeneity, [57,98] but can be easily extended to encompass species-heterogeneity in the context of generalist pathogens. Models show that greater heterogeneity reduces the probability of emergence [99,100], but see [101], this is because the risk of encountering a poor-quality host increases the extinction probability of the pathogen. However, if

R_{0}

is initially

< 1

in the novel host following spillover, adaptation of the pathogen to the new host is required for emergence. Thus, rate of pathogen adaptation can be more important than host heterogeneity in determining the probability of disease emergence in novel hosts.

In general, pathogens always benefit from a longer duration of infection (low recovery rates) and higher transmission, and in a single-host system we would expect pathogen evolution to maximise transmission [102]. In a multi-host system, it has been suggested that generalism in a heterogeneous environment may be costly, resulting in selection for host specialization [103]. There is a large body of work on the evolution of generalism, and while we do not review this literature here (see [14,104] for recent reviews), we emphasise the importance of evolution in driving emergence in spillover hosts. We also note that pathogens appear to be limited in their generalism by the phylogenetic distance between hosts, suggesting evolutionary constraints to host range expansion, and therefore host-phylogeny may also play an important role in the probability of emergence [14,16,63,105].

6. Future Directions

Accelerating rates of biodiversity loss and habitat degradation worldwide, have been accompanied by increasing disease outbreaks in wildlife, domestic animals and human populations, generating an urgent need for studies on how biodiversity and changes in the environmental carrying capacity of wild species may modify pathogen transmission.

As most hosts and pathogens exist within multi-host systems, we need to better understand how transmission affects disease outbreaks in such systems. However, the complexity in quantifying transmission with asymmetries in interspecific rates and between reservoir and novel hosts following spillover events [16,106], can make the application of SIR models models fraught. Defining the shape of the transmission function between hosts is challenging, and seemingly small differences can have dramatic effects on predictions in multi-species models [72]. Additional challenges include accounting for spatial heterogeneity and contact structure, although over longer timescales transmission dynamics may appear more homogeneous [55].

It is also becoming increasingly clear that the evolutionary relationship between species plays a role in disease transmission, with strong evidence of phylogenetic signal in the likelihood of pathogen sharing among hosts [41,59,60,61]. It is likely, for example, that similarity in the immune defenses of closely related species due to evolutionary conservation of the cellular, immunological, or metabolic traits, favours pathogen exchange between them [62,63]. Similar phylogenetic signature in pest and pathogen sharing is observed in plants [42,64,65,66]. Phylogeny is also suggested to be a predictor of pathogen impact, with declining severity of the effect of the disease with increasing evolutionary distance between hosts [68,69], although evidence from livestock diseases suggest that the relationship may be more complex [70]. Information on the phylogenetic structure of host communities may help determine both the probability of interspecific transmission and predict novel host shifts [42,58]. Additionally, the greater the shared evolutionary history between reservoir and spillover species, the greater the probability of onward transmission in the novel host [10], providing us with information on the potential for disease emergence. Phylogenetic approaches, therefore, provide powerful tools for modelling future disease threats.

As habitat transformation and climate change continue to impact species distributions and population sizes, host communities are being disassembled and reassembled; understanding the role of community structure in transmission will be critical for forecasting disease dynamics in the Anthropocene.

7. Conclusion

By reviewing and decomposing the process of disease transmission in multi-host communities, we illustrate how the separate components contribute to determining disease outbreak potential.
We describe how the outbreak potential, $R_{0}$ , within a host is composed of intraspecific and interspecific components which determine whether a disease can be maintained within a host in isolation, or whether interspecific transmission is required to a spillover equilibrium.
We highlight that mode of transmission plays an important role in the disease-diversity relationship. Anthropogenic global changes are decreasing space for wildlife and increasing the contact rates between humans and wildlife. In some cases, this can switch interspecific transmission dynamics from density-dependent to frequency-dependent, which can lead to changes in the amplifying or diluting effects of biodiversity on disease prevalence.
We draw parallels between well-known disease-diversity relationships and theories of community ecology, and highlight that host competencies and identities play an important role in potential disease dilution and amplification. The well-known and disputed dilution effect can exist of a contact-dependent (FD dilution) as well as a community phylogeny component (phylogenetic dilution).
In multi-host communities, density-dependent transmission favours the amplifying effect of biodiversity as it assumes indefinitely increasing contacts. However, we expect that contacts will saturate at high host densities, causing a switch to FD transmission. At high host densities we might, therefore, additionally expect a shift in the amplifying/diluting effects of biodiversity.
Interspecific contacts also play an important role in determining the relationship between host diversity and disease prevalence and we argue there should be a greater focus on the full scale of ecological interactions between hosts when examining the effect of host diversity on disease prevalence.
Future work is needed to better understand how the composition of host communities determines the prevalence, maintenance and onward transmission of disease, and the likelihood of novel pathogen emergence via host shifts. Accurately defining the interspecific transmission process will be a critical first step.

Appendix A. Derivation of transmission rate β

The transmission rate for a single-species model was defined by [46] as:

β = - κ \cdot ln (1 - c)

(A1)

When the probability of infection given contact, c, is small this equation can be simplified into the more intuitive form of the product of the contact rate (

κ

) and the proportion of those contacts resulting in infection (c),

β = κ \cdot c

[35,107]. Assuming probability of successful transmission after contact (

c \to 0

), we can perform a second order Taylor expansion of

κ

around c = 0:

\begin{matrix} β \approx - κ \cdot ln (1 - c) |_{c = 0} + \frac{d}{d c} (- κ \cdot ln (1 - c)) |_{c = 0} \cdot c \\ = 0 + \frac{κ}{1 - c} |_{c = 0} \cdot c \\ β \approx κ \cdot c \end{matrix}

(A2)

Therefore,

β = κ \cdot c

is the approximation of Equation (A1) at low probability of successful transmission.

Appendix B. Generalizing the Derivation of Transmission Rate from the Single-Species Context

Generalizing the derivation of transmission rate from the single species context, as described by [46], we begin by considering the probability that a recipient host is infected by a donor host in a small time interval

Δ t

Δ p_{d, r}

. The probability that the recipient remains un-infected, is then given by;

1 - Δ p_{d, r} = {(1 - c_{r})}^{κ_{d, r} \frac{I_{d}}{N_{d}} Δ t}

(A3)

Here,

\frac{I_{d}}{N_{d}}

is the proportion of infected individuals in the donor host population, with homogeneously mixed individuals within a species population, allowing for random contacts.

The term

(1 - c_{r})

gives the probability that an exposed recipient (following step 4 in Figure 1) is not infected. Note that here we have defined

c_{r}

to be dependent on the recipient host alone, this implies that establishment depends solely on the pathogen, as in the case of environmental transmission, and the identity of the donating host is irrelevant. This may not always be the case, as we discuss in Section 2.1.2 of the Main text). Defining

β_{d, r} = - κ_{d, r} ln (1 - c_{r})

we get the probability a recipient host is infected by a donor host:

Δ p_{d, r} = e^{β_{d, r} \frac{I_{d}}{N_{d}} Δ t}

(A4)

Appendix C. Derivation of Endemic Equilibrium for Species r, R 0,r

We describe a system of equations where we have donating host d infecting recipient host, r:

\frac{d I_{r}}{d t} = \sum_{d} β_{d, r} \frac{I_{d}}{N_{d}} S_{r} - Γ_{r} I_{r} > 0

(A5)

Dividing over

N_{r}

\frac{d}{d t} \frac{I_{r}}{N_{r}} = \sum_{d} β_{d, r} \frac{I_{d}}{N_{d}} \frac{S_{r}}{N_{r}} - Γ_{r} \frac{I_{r}}{N_{r}}

(A6)

Rewriting this as

Y_{r} = \frac{I_{r}}{N_{r}}

and

Y_{d} = \frac{I_{d}}{N_{d}}

, where

\frac{S_{r}}{N_{r}} = X_{r} = 1 - Y_{r}

, we get:

\frac{d}{d t} Y_{r} = \sum_{d} β_{d, r} Y_{d} (1 - Y_{r}) - Γ_{r} Y_{r}

(A7)

We can then separate the inter and intraspecific transmission:

\frac{d}{d t} Y_{r} = \underset{intraspecific}{\underset{︸}{β_{r r} Y_{r} (1 - Y_{r})}} + \underset{interspecific}{\underset{︸}{\sum_{d \neq r} β_{d, r} Y_{d} (1 - Y_{r})}} - Γ_{r} Y_{r}

(A8)

The classic definition of

R_{0}

is the ability for a disease to spread in an almost fully susceptible population. Therefore we assume:

Y_{r} \approx 0

and thus

(1 - Y_{r}) \approx 1

, which simplifies Eqn (8) to:

\frac{d Y_{r}}{d t} = β_{r r} Y_{r} + \sum_{d \neq r} β_{d r} Y_{d} - Γ_{r} Y_{r} > 0

(A9)

Rearranging this by bringing the last term over to right hand side and dividing over

Y_{r}

β_{r r} + \sum_{d \neq r} \frac{β_{d r} Y_{d}}{Y_{r}} > Γ_{r}

(A10)

Then we divide over

Γ_{r}

to get the expression for

R_{0, r}

R_{0, r} = \underset{R_{0, r r}}{\underset{︸}{\frac{β_{r r}}{Γ_{r}}}} + \underset{R_{0, d r}}{\underset{︸}{\sum_{d \neq r} \frac{β_{d r}}{Γ_{r}} \frac{Y_{d}}{Y_{r}}}} > 1

(A11)

Appendix D. Interspecific Transmission through WAIFW

Interspecific transmission can be modeled in a WAIFW-matrix (Who Acquired Infection From Who), an n by n - matrix showing the transmission between species in an n-species system, where intraspecific transmission can be found on the diagonal, and interspecific transmission on the off-diagonals [2,108]. Transmission is defined as

β_{i, j}

, where i is the receiving host and j the donating host (j infects i). This matrix can be used to form the Next Generation Matrix which calculates the community

R_{0}

, and determines the overall disease prevalence in the system, as well as the contributions of each individual host [108].

One way to estimate the interspecific transmission rate is to take the average of the intraspecific transmission rates, using a scaling parameter to account for differences in transmission potential between species i and j [72]. This scaling parameter can determine the magnitude of diluting and amplifying behaviour of each host species in the system. Alternatively, one can parameterize the probability of successful transmission, c, per host species-pair, assuming that disease competence, and therefore transmission, is dependent on the donating and receiving host species’ identities [12], and can be asymmetrical. A similar approach can also be applied to contact rates,

κ

, if one wants to define c separately for individual host species (or species pairs), rather than the community average [109]. There can also be asymmetrical transmission between hosts, as in the example of foxes infected with rabies, which require a million times more virus particles to infect a dog or cat than would be necessary to infect another fox [110]. This also goes for different pathways of transmission. For example, a larger number of propagules is necessary for transmission of M. bovis through ingestion than inhalation [32]. Such asymmetries may be overlooked when simply averaging intraspecific transmission rates. The next-generation matrix [108], which allows us to calculate the community

R_{0}

and each host’s relative contribution, is a useful framework for modelling the dynamics of multi-host pathogens and disease maintenance in the reservoir. However, it has been most often applied using the scaling methods as described above.

Appendix E. Contact Network Model Distributions

Within a host population, not all individuals are the same, and they may vary in susceptibility and infectivity, as captured by the concept of superspreaders, which dramatically influences outbreak potential and disease dynamics [99]. Similar concepts can be extended to super-movers, super-recipients, super-shedders, and super-susceptibles [48,53,83]. Additionally, hosts likely do not have a homogeneous contact structure, as these may be modified through networks or variation in population density. Various case studies provide an illustration of how contact structure is important for modeling wildlife diseases [29,48,111,112].

Many animals aggregate in flocks, herds or other social networks. For directly transmitted diseases in populations with strong social and spatial structuring, we need to revisit the assumption of homogeneity and random host mixing assumed within density-dependent transmission [48,52,53]. Epidemic network models are based on graph-theory, where the realized per capita transmission rate

\hat{β}

is scaled to the mean neighbourhood size [48,52]. It has been shown that the degree of connectivity within a population has a large effect on disease dynamics. For example, triangular contacts (three connected individuals) reduces both the initial spread and final disease outbreak [54]. The transmission via a given connection is weighted by parameter

< k >

, the mean degree number of connections of a node, or dispersion parameter, which can be scaled in three ways [52,99]:

Independent of total population size, N. This is similar to the assumptions of the classic frequency-dependent transmission function
Increasing linearly with population size, N
Increasingly less than linear $C \cdot \sqrt{N}$ , C being a constant, an intermediate between 1 and 2. This is analogous to the density-dependent transmission function, assuming a constant area.

In epidemic network models, the calculation of

R_{0}

differs from the original compartmental models, as it is assumed that some individuals, such as superspreaders, contribute more to the spread of the disease than others [48,53,99]. This is similar to some of the previously introduced multi-host models, as in both cases the population consists of individuals contributing differently to disease spread. However, the former models do not take into account the heterogeneity of individuals, group formation and the extent of mixing within these groups. Fortunately, epidemic network models, that are often used to track contact in human epidemics [113], have the advantage of being able to take into account both the heterogeneous nature of contacts between hosts and the topology of the contact network, using the mean and variance of the number of contacts per individual (the number of connections). This can be done by choosing from a number of degree distributions. Some common examples are listed below [52].

Appendix E.1. Poisson Distribution

In the Poisson distribution, the variance to mean ratio is close to one. Due to this relatively low variance this distribution is closest to homogeneous mixing. A Poisson distribution is based on the assumption that events happen at a constant rate per time unit, irrespective of the time that has passed. For example, an individual contacts another individual with a constant contact rate, with a constant probability of being infected, independent of the number of previously infected individuals. Increasing the number of nodes either has a slight to strongly decreasing effect on

\hat{β}

, depending on whether

< k >

increases linearly with population size (case 3), increases with

\sqrt{N}

(case 2) or if it is constant with population size (case 1), respectively [52].

Appendix E.2. Power-Law Truncated Distribution

This distribution consists of two power law functions that intersect at a value that represent the size at which the behavior of the group changes. This threshold value can be an optimal group size, such as for animals living in herds [114]. Here, the variance to mean ratio

> >

1, such that some individuals have many contacts, and others almost none, capturing the phenomenon of super-spreaders [52]. The Power-law truncated distribution assumes extreme heterogeneity in local contacts;

\hat{β}

either slightly increases (case 3), slightly decreased (case 2) or decreases strongly (case 1) with the number of nodes in a network.

Appendix E.3. The Exponential Distribution

This is the intermediate case between the Poisson and the truncated power-law distributions. It is another example of a memory-less distribution, like the Poisson process, as it models the time between two events in a Poisson process. This distribution has, like the power-law distribution, a greater proportion of superspreaders.

Here, either

\hat{β}

remains unchanged (case 3), slightly decreases (case 2) or linearly decreases (case 1) with increasing number of nodes.

References

Jones, K.E.; Patel, N.G.; Levy, M.A.; Storeygard, A.; Balk, D.; Gittleman, J.L.; Daszak, P. Global trends in emerging infectious diseases. Nature 2008, 451, 990–993. [Google Scholar] [CrossRef] [PubMed]
Dobson, A.; Foufopoulos, J. Emerging infectious pathogens of wildlife. Philosophical Transactions of the Royal Society B: Biological Sciences 2001, 356, 1001–1012. [Google Scholar] [CrossRef] [PubMed]
Smith, K.F.; Goldberg, M.; Rosenthal, S.; Carlson, L.; Chen, J.; Chen, C.; Ramachandran, S. Global rise in human infectious disease outbreaks. Journal of the Royal Society Interface 2014, 11, 1–6. [Google Scholar] [CrossRef] [PubMed]
Graham, J.P.; Leibler, J.H.; Price, L.B.; Otte, J.M.; Pfeiffer, D.U.; Tiensin, T.; Silbergeld, E.K. The animal-human interface and infectious disease in industrial food animal production: Rethinking biosecurity and biocontainment. Public Health Reports 2008, 123, 282–299. [Google Scholar] [CrossRef]
Bar-On, Y.M.; Phillips, R.; Milo, R. The biomass distribution on Earth. Proceedings of the National Academy of Sciences of the United States of America 2018, 115, 6506–6511. [Google Scholar] [CrossRef]
Daszak, P.; Cunningham, A.A.; Hyatt, A.D. Emerging infectious diseases of wildlife - Threats to biodiversity and human health. Science 2000, 287, 443–449. [Google Scholar] [CrossRef] [PubMed]
Haydon, D.T.; Cleaveland, S.; Taylor, L.H.; Laurenson, M.K. Identifying reservoirs of infection: A conceptual and practical challenge. Emerging Infectious Diseases 2002, 8, 1468–1473. [Google Scholar] [CrossRef] [PubMed]
Pedersen, A.B.; Jones, K.E.; Nunn, C.L.; Altizer, S. Infectious diseases and extinction risk in wild mammals. Conservation Biology 2007, 21, 1269–1279. [Google Scholar] [CrossRef]
Keesing, F.; Belden, L.K.; Daszak, P.; Dobson, A.; Harvell, C.D.; Holt, R.D.; Hudson, P.; Jolles, A.; Jones, K.E.; Mitchell, C.E.; Myers, S.S.; Bogich, T.; Ostfeld, R.S. Impacts of biodiversity on the emergence and transmission of infectious diseases. Nature 2010, 468, 647–652. [Google Scholar] [CrossRef]
Mollentze, N.; Streicker, D.G.; Murcia, P.R.; Hampson, K.; Biek, R. Virulence mismatches in index hosts shape the outcomes of cross-species transmission. Proceedings of the National Academy of Sciences of the United States of America 2020, 117, 28859–28866. [Google Scholar] [CrossRef]
Gougherty, A.V.; Davies, T.J. Host phylogenetic diversity predicts the global extent and composition of tree pests. Ecology Letters 2022, 25, 101–112. [Google Scholar] [CrossRef]
Stewart Merrill, T.E.; Calhoun, D.M.; Johnson, P.T. Beyond single host, single parasite interactions: Quantifying competence for complete multi-host, multi-parasite communities. Functional Ecology 2022, 36, 1845–1857. [Google Scholar] [CrossRef]
Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character 1927, 115, 700–721. [Google Scholar]
Park, A.W.; Farrell, M.J.; Schmidt, J.P.; Huang, S.; Dallas, T.A.; Pappalardo, P.; Drake, J.M.; Stephens, P.R.; Poulin, R.; Nunn, C.L.; Davies, T.J. Characterizing the phylogenetic specialism-generalism spectrum of mammal parasites. Proceedings of the Royal Society B: Biological Sciences 2018, 285. [Google Scholar] [CrossRef] [PubMed]
Fenton, A.; Pedersen, A.B. Community epidemiology framework for classifying disease threats. Emerging Infectious Diseases 2005, 11, 1815–1821. [Google Scholar] [CrossRef]
Wolfe, N.D.; Dunavan, C.P.; Diamond, J. Origins of major human infectious diseases. Nature 2007, 447, 279–283. [Google Scholar] [CrossRef]
Manlove, K.; Wilber, M.; White, L.; Bastille-Rousseau, G.; Yang, A.; Gilbertson, M.L.; Craft, M.E.; Cross, P.C.; Wittemyer, G.; Pepin, K.M. Defining an epidemiological landscape that connects movement ecology to pathogen transmission and pace-of-life. Ecology letters 2022. [Google Scholar] [CrossRef]
Huang, Y.H.; Kausrud, K.; Hassim, A.; Ochai, S.O.; van Schalkwyk, O.L.; Dekker, E.H.; Buyantuev, A.; Cloete, C.C.; Kilian, J.W.; Mfune, J.K.; others. Environmental drivers of biseasonal anthrax outbreak dynamics in two multihost savanna systems. Ecological Monographs 2022, 92, e1526. [Google Scholar] [CrossRef]
Michel, A.L.; De Klerk, L.M.; Van Pittius, N.C.; Warren, R.M.; Van Helden, P.D. Bovine tuberculosis in African buffaloes: Observations regarding Mycobacterium bovis shedding into water and exposure to environmental mycobacteria. BMC Veterinary Research 2007, 3, 1–7. [Google Scholar] [CrossRef]
Miller, M.; Olea-Popelka, F. One Health in the shrinking world: Experiences with tuberculosis at the human-livestock-wildlife interface. Comparative Immunology, Microbiology and Infectious Diseases 2013, 36, 263–268. [Google Scholar] [CrossRef]
Young, J.S.; Gormley, E.; Wellington, E.M. Molecular detection of Mycobacterium bovis and Mycobacterium bovis BCG (Pasteur) in soil. Applied and environmental microbiology 2005, 71, 1946–1952. [Google Scholar] [CrossRef] [PubMed]
Brunker, K.; Mollentze, N. Rabies virus. Trends in microbiology 2018, 26, 886–887. [Google Scholar] [CrossRef] [PubMed]
Cassmann, E.D.; Frese, A.J.; Moore, S.J.; Greenlee, J.J. Transmission of raccoon-passaged chronic wasting disease agent to white-tailed deer. Viruses 2022, 14, 1578. [Google Scholar] [CrossRef] [PubMed]
Ostfeld, R.S.; Keesing, F. Biodiversity series: the function of biodiversity in the ecology of vector-borne zoonotic diseases. Canadian Journal of Zoology 2000, 78, 2061–2078. [Google Scholar] [CrossRef]
Keesing, F.; Holt, R.D.; Ostfeld, R.S. Effects of species diversity on disease risk. Ecology Letters 2006, 9, 485–498. [Google Scholar] [CrossRef]
Ostfeld, R.S.; Keesing, F. Effects of host diversity on infectious disease. Annual Review of Ecology, Evolution, and Systematics 2012, 43, 157–182. [Google Scholar] [CrossRef]
Halliday, F.W.; Rohr, J.R. Measuring the shape of the biodiversity-disease relationship across systems reveals new findings and key gaps. Nature Communications 2019, 10, 1–10. [Google Scholar] [CrossRef]
Keesing, F.; Ostfeld, R.S. Impacts of biodiversity and biodiversity loss on zoonotic diseases. Proceedings of the National Academy of Sciences 2021, 118, e2023540118. [Google Scholar] [CrossRef] [PubMed]
McCallum, H. Models for managing wildlife disease. Parasitology 2016, 143, 805–820. [Google Scholar] [CrossRef]
Miller, M.A.; Kerr, T.J.; de Waal, C.R.; Goosen, W.J.; Streicher, E.M.; Hausler, G.; Rossouw, L.; Manamela, T.; van Schalkwyk, L.; Kleynhans, L.; others. Mycobacterium bovis Infection in Free-Ranging African Elephants. Emerging Infectious Diseases 2021, 27, 990. [Google Scholar] [CrossRef]
Jolles, A.E.; Cooper, D.V.; Levin, S.A. Hidden effects of chronic tuberculosis in African buffalo. Ecology 2005, 86, 2358–2364. [Google Scholar] [CrossRef]
Spickler, A.R. Zoonotic Tuberculosis in Mammals, including Bovine and Caprine Tuberculosis 2019. pp. 1–20.
Handel, A.; Brown, J.; Stallknecht, D.; Rohani, P. A multi-scale analysis of influenza A virus fitness trade-offs due to temperature-dependent virus persistence. PLoS computational biology 2013, 9, e1002989. [Google Scholar] [CrossRef]
Fine, A.E.; Bolin, C.A.; Gardiner, J.C.; Kaneene, J.B. A study of the persistence of mycobacterium bovis in the environment under natural weather conditions in Michigan, USA. Veterinary Medicine International 2011, 2011. [Google Scholar] [CrossRef]
McCallum, H.; Fenton, A.; Hudson, P.J.; Lee, B.; Levick, B.; Norman, R.; Perkins, S.E.; Viney, M.; Wilson, A.J.; Lello, J. Breaking beta: Deconstructing the parasite transmission function. Philosophical Transactions of the Royal Society B: Biological Sciences 2017, 372. [Google Scholar] [CrossRef] [PubMed]
Ezenwa, V.O.; Etienne, R.S.; Luikart, G.; Beja-Pereira, A.; Jolles, A.E. Hidden consequences of living in a wormy world: Nematode-induced immune suppression facilitates tuberculosis invasion in African buffalo. American Naturalist 2010, 176, 613–624. [Google Scholar] [CrossRef]
Ezenwa, V.O.; Jolles, A.E. Opposite effects of anthelmintic treatment on microbial infection at individual versus population scales. Science 2015, 347, 175–177. [Google Scholar] [CrossRef]
Palmer, M.V.; Waters, W.R.; Whipple, D.L. Investigation of the transmission of Mycobacterium bovis from deer to cattle through indirect contact. American journal of veterinary research 2004, 65, 1483–1489. [Google Scholar] [CrossRef] [PubMed]
Palmer, M.V.; Whipple, D.L. Survival of Mycobacterium bovis on feedstuffs commonly used as supplemental feed for white-tailed deer (Odocoileus virginianus). Journal of Wildlife Diseases 2006, 42, 853–858. [Google Scholar] [CrossRef]
Barasona, J.A.; Vicente, J.; Díez-Delgado, I.; Aznar, J.; Gortázar, C.; Torres, M.J. Environmental presence of Mycobacterium tuberculosis complex in aggregation points at the wildlife/livestock interface. Transboundary and emerging diseases 2017, 64, 1148–1158. [Google Scholar] [CrossRef]
Davies, T.J.; Pedersen, A.B. Phylogeny and geography predict pathogen community similarity in wild primates and humans. Proceedings of the Royal Society B: Biological Sciences 2008, 275, 1695–1701. [Google Scholar] [CrossRef]
Parker, I.M.; Saunders, M.; Bontrager, M.; Weitz, A.P.; Hendricks, R.; Magarey, R.; Suiter, K.; Gilbert, G.S. Phylogenetic structure and host abundance drive disease pressure in communities. Nature 2015, 520, 542–544. [Google Scholar] [CrossRef] [PubMed]
Anderson, R.M.; May, R.M. Coevolution of Hosts and Parasites. Parasitology 1982, 85, 411–426. [Google Scholar] [CrossRef]
Blancou, J.; Aubert, M. Transmission of rabies virus: importance of the species barrier. Bulletin de L’academie Nationale de Medecine 1997, 181, 301–11. [Google Scholar] [PubMed]
Begon, M.; Bennett, M.; Bowers, R.G.; French, N.P.; Hazel, S.M.; Turner, J. A clarification of transmission terms in host-microparasite models: Numbers, densities and areas. Epidemiology and Infection 2002, 129, 147–153. [Google Scholar] [CrossRef]
Keeling, M.J.; Rohani, P. Modeling infectious diseases in humans and animals; Princeton university press, 2011.
Smith, M.J.; Telfer, S.; Kallio, E.R.; Burthe, S.; Cook, A.R.; Lambin, X.; Begon, M. Host-pathogen time series data in wildlife support a transmission function between density and frequency dependence. Proceedings of the National Academy of Sciences of the United States of America 2009, 106, 7905–7909. [Google Scholar] [CrossRef]
White, L.A.; Forester, J.D.; Craft, M.E. Using contact networks to explore mechanisms of parasite transmission in wildlife. Biological Reviews 2017, 92, 389–409. [Google Scholar] [CrossRef]
Antonovics, J. Transmission dynamics: Critical questions and challenges. Philosophical Transactions of the Royal Society B: Biological Sciences 2017, 372. [Google Scholar] [CrossRef]
Roberts, M.G.; Heesterbeek, J.A. Quantifying the dilution effect for models in ecological epidemiology. Journal of the Royal Society Interface 2018, 15. [Google Scholar] [CrossRef]
Fromont, E.; Pontier, D.; Langlais, M. Dynamics of a feline retrovirus (FeLV) in host populations with variable spatial structure. Proceedings of the Royal Society B: Biological Sciences 1998, 265, 1097–1104. [Google Scholar] [CrossRef] [PubMed]
Ferrari, M.J.; Perkins, S.E.; Pomeroy, L.W.; Bjrnstad, O.N. Pathogens, social networks, and the paradox of transmission scaling. Interdisciplinary Perspectives on Infectious Diseases 2011, 2011. [Google Scholar] [CrossRef]
Craft, M.E. Infectious disease transmission and contact networks in wildlife and livestock. Philosophical Transactions of the Royal Society B: Biological Sciences 2015, 370. [Google Scholar] [CrossRef]
Keeling, M.J. The effects of local spatial structure on epidemiological invasions. Philosophical Transactions of the Royal Society B: Biological Sciences 1999, 266, 859–867. [Google Scholar] [CrossRef] [PubMed]
Cross, P.C.; Lloyd-Smith, J.O.; Bowers, J.A.; Hay, C.T.; Hofmeyr, M.; Getz, W.M. Integrating association data and disease dynamics in a social ungulate: Bovine tuberculosis in African buffalo in the Kruger National Park. Annales Zoologici Fennici 2004, 41, 879–892. [Google Scholar]
Altizer, S.; Harvell, D.; Friedle, E. Rapid evolutionary dynamics and disease threats to biodiversity. Trends in Ecology and Evolution 2003, 18, 589–596. [Google Scholar] [CrossRef]
Lively, C.M. The effect of host genetic diversity on disease spread. American Naturalist 2010, 175, 17–20. [Google Scholar] [CrossRef] [PubMed]
Poullain, V.; Nuismer, S.L. Infection genetics and the likelihood of host shifts in coevolving host-parasite interactions. American Naturalist 2012, 180, 618–628. [Google Scholar] [CrossRef] [PubMed]
Farrell, M.J.; Govender, D.; Hajibabaei, M.; Van Der Bank, M.; Davies, T.J. Bacterial diversity in the waterholes of the Kruger National Park: An eDNA metabarcoding approach. Genome 2019, 62, 229–242. [Google Scholar] [CrossRef] [PubMed]
Streicker, D.G.; Fallas González, S.L.; Luconi, G.; Barrientos, R.G.; Leon, B. Phylodynamics reveals extinction–recolonization dynamics underpin apparently endemic vampire bat rabies in Costa Rica. Proceedings of the Royal Society B: Biological Sciences 2019, 286. [Google Scholar] [CrossRef]
Olival, K.J.; Hosseini, P.R.; Zambrana-Torrelio, C.; Ross, N.; Bogich, T.L.; Daszak, P. Host and viral traits predict zoonotic spillover from mammals. Nature 2017, 546, 646–650. [Google Scholar] [CrossRef]
Kuiken, T.; Holmes, E.C.; McCauley, J.; Rimmelzwaan, G.F.; Williams, C.S.; Grenfell, B.T. Host species barriers to influenza virus infections. Science 2006, 312, 394–397. [Google Scholar] [CrossRef]
Streicker, D.G.; Turmelle, A.S.; Vonhof, M.J.; Kuzmin, I.V.; McCracken, G.F.; Rupprecht, C.E. Host phylogeny constrains cross-species emergence and establishment of rabies virus in bats. Science 2010, 329, 676–679. [Google Scholar] [CrossRef] [PubMed]
Gilbert, G.S.; Webb, C.O. Phylogenetic signal in plant pathogen–host range. Proceedings of the National Academy of Sciences 2007, 104, 4979–4983. [Google Scholar] [CrossRef] [PubMed]
Gilbert, G.S.; Magarey, R.; Suiter, K.; Webb, C.O. Evolutionary tools for phytosanitary risk analysis: Phylogenetic signal as a predictor of host range of plant pests and pathogens. Evolutionary Applications 2012, 5, 869–878. [Google Scholar] [CrossRef] [PubMed]
Ssebuliba, E.; Davies, T.J. Assessing the phylogenetic host breadth of millet pathogens and its implication for disease spillover. Ecological Solutions and Evidence 2021, 2, 1–11. [Google Scholar] [CrossRef]
Gougherty, A.V.; Davies, T.J. A global analysis of tree pests and emerging pest threats. Proceedings of the National Academy of Sciences 2022, 119, e2113298119. [Google Scholar] [CrossRef]
Gilbert, G.S.; Briggs, H.M.; Magarey, R. The impact of plant enemies shows a phylogenetic signal. PLoS ONE 2015, 10, 1–11. [Google Scholar] [CrossRef]
Gougherty, A.V.; Davies, T.J. Towards a phylogenetic ecology of plant pests and pathogens. Philosophical Transactions of the Royal Society B 2021, 376, 20200359. [Google Scholar] [CrossRef] [PubMed]
Farrell, M.J.; Davies, T.J. Disease mortality in domesticated animals is predicted by host evolutionary relationships. Proceedings of the National Academy of Sciences of the United States of America 2019, 116, 7911–7915. [Google Scholar] [CrossRef]
De Leo, G.A.; Dobson, A.P. Allometry and simple epidemic models for microparasites. Nature 1996, 379, 720–722. [Google Scholar] [CrossRef]
Dobson, A. Population Dynamics of Pathogens with Multiple Host Species 2004. 164.
Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. Journal of mathematical biology 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
Renwick, A.; White, P.; Bengis, R.G. Bovine tuberculosis in southern African wildlife: a multi-species host–pathogen system. Epidemiology & Infection 2007, 135, 529–540. [Google Scholar]
Rhodes, C.J.; Atkinson, R.P.D.; Anderson, R.M.; Macdonald, D.W. Rabies in Zimbabwe : reservoir dogs and the implications for disease control 1998.
Fenton, A.; Streicker, D.G.; Petchey, O.L.; Pedersen, A.B. Are all hosts created equal? Partitioning host species contributions to parasite persistence in multihost communities. American Naturalist 2015, 186, 610–622. [Google Scholar] [CrossRef]
Becker, D.J.; Albery, G.F.; Kessler, M.K.; Lunn, T.J.; Falvo, C.A.; Czirják, G.Á.; Martin, L.B.; Plowright, R.K. Macroimmunology: The drivers and consequences of spatial patterns in wildlife immune defence. Journal of Animal Ecology 2020, 89, 972–995. [Google Scholar] [CrossRef]
Faust, C.L.; Dobson, A.P.; Gottdenker, N.; Bloomfield, L.S.; McCallum, H.I.; Gillespie, T.R.; Diuk-Wasser, M.; Plowright, R.K. Null expectations for disease dynamics in shrinking habitat: Dilution or amplification? Philosophical Transactions of the Royal Society B: Biological Sciences 2017, 372. [Google Scholar] [CrossRef] [PubMed]
Faust, C.L.; McCallum, H.I.; Bloomfield, L.S.; Gottdenker, N.L.; Gillespie, T.R.; Torney, C.J.; Dobson, A.P.; Plowright, R.K. Pathogen spillover during land conversion. Ecology Letters 2018, 21, 471–483. [Google Scholar] [CrossRef]
Murray, K.A.; Daszak, P. Human ecology in pathogenic landscapes: two hypotheses on how land use change drives viral emergence. Current opinion in virology 2013, 3, 79–83. [Google Scholar] [CrossRef]
Wolfe, N.D.; Daszak, P.; Kilpatrick, A.M.; Burke, D.S. Bushmeat hunting, deforestation, and prediction of zoonotic disease. Emerging infectious diseases 2005, 11, 1822. [Google Scholar] [CrossRef]
Goldberg, T.L.; Gillespie, T.R.; Rwego, I.B.; Estoff, E.L.; Chapman, C.A. Forest fragmentation as cause of bacterial transmission among nonhuman primates, humans, and livestock, Uganda. Emerging infectious diseases 2008, 14, 1375. [Google Scholar] [CrossRef]
Streicker, D.G.; Fenton, A.; Pedersen, A.B. Differential sources of host species heterogeneity influence the transmission and control of multihost parasites. Ecology Letters 2013, 16, 975–984. [Google Scholar] [CrossRef] [PubMed]
Rudolf, V.H.; Antonovics, J. Species coexistence and pathogens with frequency-dependent transmission. American Naturalist 2005, 166, 112–118. [Google Scholar] [CrossRef]
Johnson, P.T.; Preston, D.L.; Hoverman, J.T.; Richgels, K.L. Biodiversity decreases disease through predictable changes in host community competence. Nature 2013, 494, 230–233. [Google Scholar] [CrossRef] [PubMed]
Carlson, C.J.; Albery, G.F.; Merow, C.; Trisos, C.H.; Zipfel, C.M.; Eskew, E.A.; Olival, K.J.; Ross, N.; Bansal, S. Climate change increases cross-species viral transmission risk. Nature 2022, 607, 555–562. [Google Scholar] [CrossRef] [PubMed]
Huang, Z.Y.; de Boer, W.F.; Van Langevelde, F.; Xu, C.; Ben Jebara, K.; Berlingieri, F.; Prins, H.H. Dilution effect in bovine tuberculosis: Risk factors for regional disease occurrence in Africa. Proceedings of the Royal Society B: Biological Sciences 2013, 280, 1–7. [Google Scholar] [CrossRef]
Huang, Z.Y.; Xu, C.; Van Langevelde, F.; Prins, H.H.; Ben Jebara, K.; De Boer, W.F. Dilution effect and identity effect by wildlife in the persistence and recurrence of bovine tuberculosis. Parasitology 2014, 141, 981–987. [Google Scholar] [CrossRef]
Loreau, M.; Hector, A. Partitioning selection and complementarity in biodiversity experiments. Nature 2001, 412, 72–76. [Google Scholar] [CrossRef]
Holt, R.D.; Bonsall, M.B. Apparent Competition. Annual Review of Ecology, Evolution, and Systematics 2017, 48, 447–471. [Google Scholar] [CrossRef]
Ogden, N.H.; Tsao, J.I. Biodiversity and Lyme disease: Dilution or amplification? Epidemics 2009, 1, 196–206. [Google Scholar] [CrossRef]
Mihaljevic, J.R.; Joseph, M.B.; Orlofske, S.A.; Paull, S.H. The scaling of host density with richness affects the direction, shape, and detectability of diversity-disease relationships. PloS one 2014, 9, e97812. [Google Scholar] [CrossRef]
Holt, R.D.; Pickering, J. Infectious Disease and Species Coexistence : A Model of Lotka-Volterra Form Author ( s ): Robert D . Holt and John Pickering Source : The American Naturalist , Vol . 126 , No . 2 ( Aug ., 1985 ), pp . 196-211 Published by : The University of Chicago Press. The American naturalist 1985, 126, 196–211. [Google Scholar] [CrossRef]
Power, A.G.; Mitchell, C.E. Pathogen spillover in disease epidemics. the american naturalist 2004, 164, S79–S89. [Google Scholar] [CrossRef]
Janzen, D.H. Herbivores and the number of tree species in tropical forests. The American Naturalist 1970, 104, 501–528. [Google Scholar] [CrossRef]
Connell, J.; Den Boer, P.; Gradwell, G. Dynamics of populations. Centre for Agricultural Publishing and Documentation, Wageningen, The Netherlands. chapter On the role of natural enemies in preventing competitive exclusion in some marine animals and in rain forest trees, 1971; 298–313. [Google Scholar]
Gilbert, G.S.; Parker, I.M. The evolutionary ecology of plant disease: a phylogenetic perspective. Annual Review of Phytopathology 2016, 54, 549–578. [Google Scholar] [CrossRef] [PubMed]
Levine, J.M. Species diversity and biological invasions: Relating local process to community pattern. Science 2000, 288, 852–854. [Google Scholar] [CrossRef]
Lloyd-Smith, J.O.; Schreiber, S.J.; Kopp, P.E.; Getz, W.M. Superspreading and the effect of individual variation on disease emergence. Nature 2005, 438, 355–359. [Google Scholar] [CrossRef]
Gandon, S.; Hochberg, M.E.; Holt, R.D.; Day, T. What limits the evolutionary emergence of pathogens? Philosophical Transactions of the Royal Society B: Biological Sciences 2013, 368. [Google Scholar] [CrossRef]
Yates, A.; Antia, R.; Regoes, R.R. How do pathogen evolution and host heterogeneity interact in disease emergence? Proceedings of the Royal Society B: Biological Sciences 2006, 273, 3075–3083. [Google Scholar] [CrossRef] [PubMed]
Gandon, S. Evolution of multihost parasites. Evolution 2004, 58, 455–469. [Google Scholar] [CrossRef]
Remold, S. Understanding specialism when the jack of all trades can be the master of all. Proceedings of the Royal Society B: Biological Sciences 2012, 279, 4861–4869. [Google Scholar] [CrossRef] [PubMed]
Leggett, H.C.; Buckling, A.; Long, G.H.; Boots, M. Generalism and the evolution of parasite virulence. Trends in Ecology and Evolution 2013, 28, 592–596. [Google Scholar] [CrossRef]
Pedersen, A.B.; Davies, T.J. Cross-species pathogen transmission and disease emergence in primates. EcoHealth 2009, 6, 496–508. [Google Scholar] [CrossRef] [PubMed]
Auld, S.K.; Searle, C.L.; Duffy, M.A. Parasite transmission in a natural multihost-multiparasite community. Philosophical Transactions of the Royal Society B: Biological Sciences 2017, 372, 1–10. [Google Scholar] [CrossRef] [PubMed]

Figure 2. Alternative equilibria for a recipient host, r. The y-axis shows disease prevalence in the recipient population. The yellow dashed line represents the unstable disease-free spillover equilibria. The solid yellow line is the endemic equilibrium of the disease in the recipient host. The tan symbols represent recipient host individuals, the red, brown and green symbols represent donating hosts, each of a different species. These donating hosts can also transmit the disease among themselves

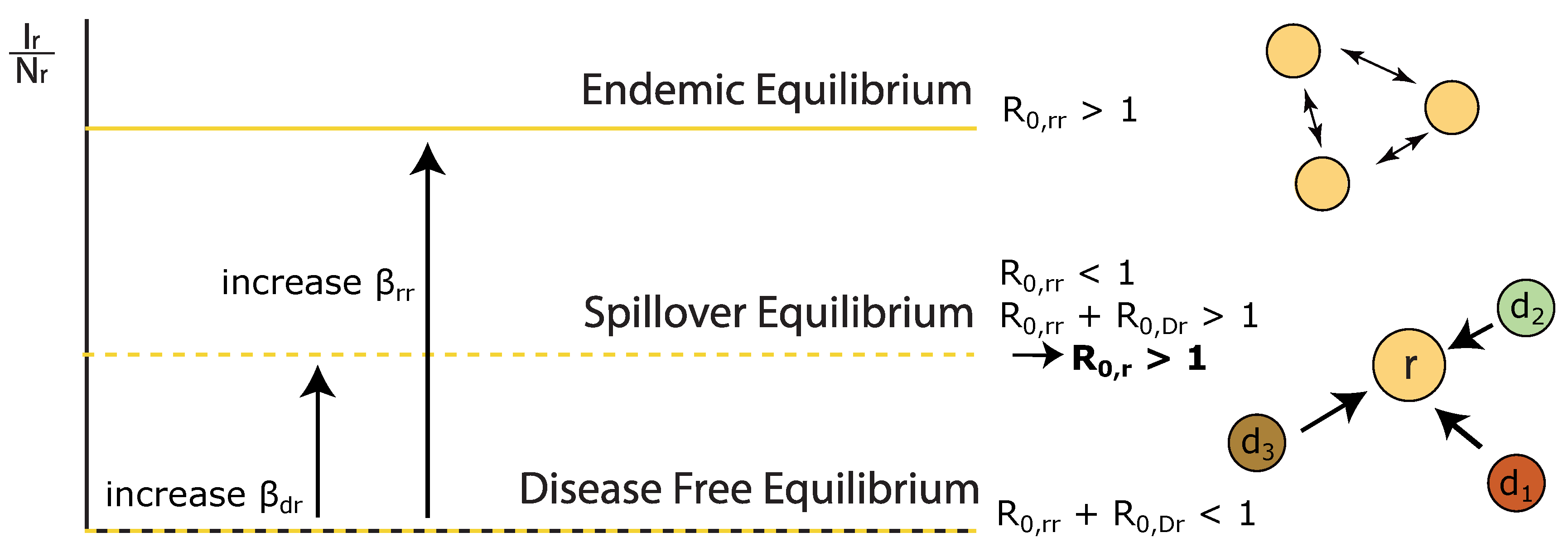
Figure 3. Determinants of inter- and intraspecific transmission mode. A: The mode of transmission (e.g., FD vs. DD) may differ among the hosts in a multi-species infection or even within levels of the hierarchical social structure. Transmission is often DD within households/herds but FD between them (see Panel B). Transmission mode in wildlife populations is also known to change with host density (right hand graph, [adapted, with permission, from [51]). Interspecific transmission between human and wildlife is appropriately modelled using FD transmission when the interaction occurs along a linear boundary (grey bar), see Panel C. B: Schematic showing the phenomenological distinction between DD (left) and FD (right) transmission in the relationship between contacts and host density as illustrated by the transmission within versus between households/herds. C: The relationship between density and interspecific contacts may be impacted by habitat fragmentation. The blue and green squares represent habitat patches for households and wildlife, respectively, the grey bar represents the contact zone between species. Whereas increasing densities along a single linear boundary (grey bar) has and FD effect, fragmentation of the habitat resulting in many species boundaries shifts transmission toward a DD mode. Fragmentation increases along the x-axis, density of individuals within each patch is on the y-axis.

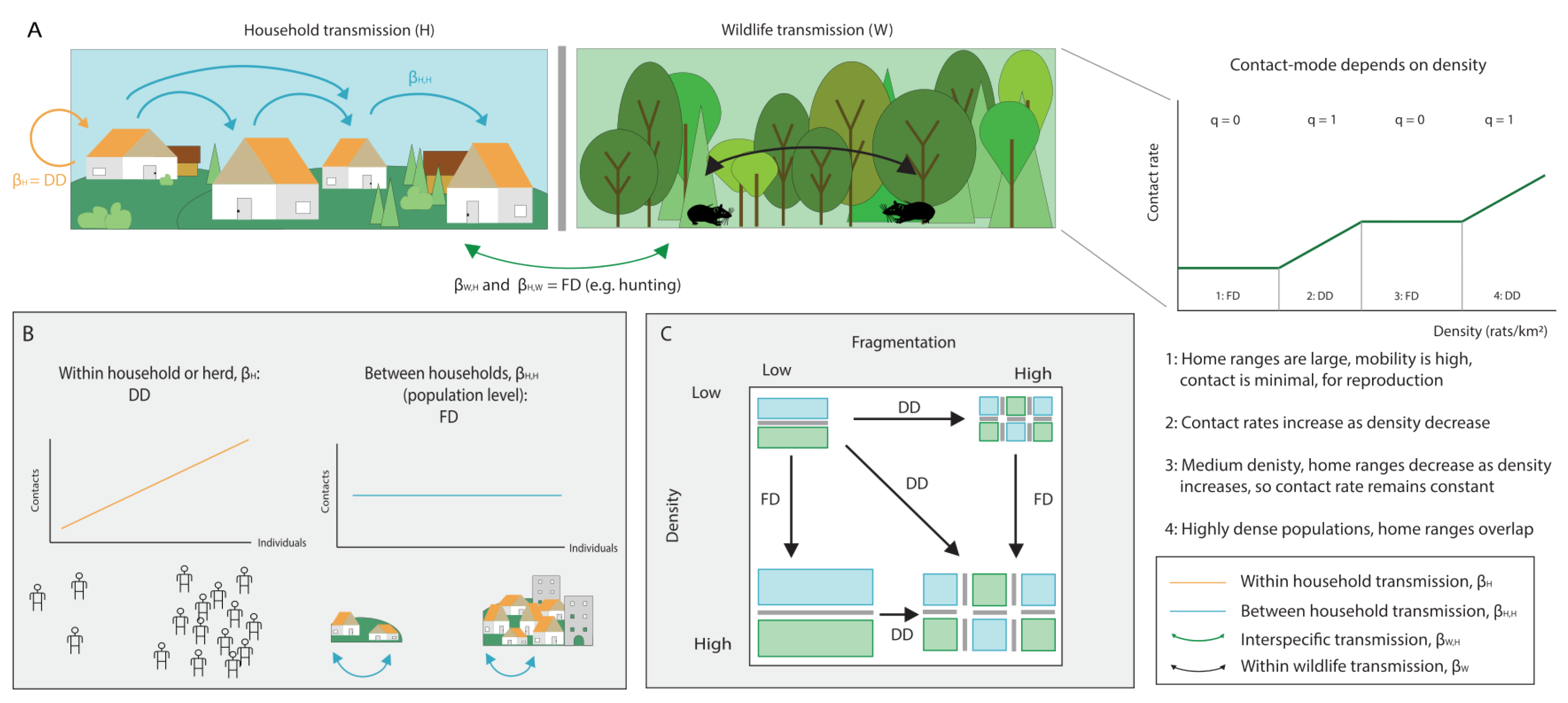
Figure 4. A: Illustration of how dilution and amplification effects can occur in FD and DD transmission systems. Nodes represent species and edge-width the transmission-strength. Highly competent species have higher probability of transmission, represented by thicker edges. Grey nodes represent extirpated hosts due to competition. The first column shows direct dilution and amplification through encounter reduction with the addition of a less or more competent host, respectively. The second and third column show DD dynamics, column two shows the classic amplification effect caused by increase in contacts, while the third column shows an indirect dilution effect due to competition with the purple host reducing the density (and therefore transmission) between the blue host. B: Table summarizing the mechanisms leading to dilution and amplification for FD and DD transmission modes, as illustrated in A.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multi-Host Pathogen Transmission and the Disease-Diversity Relationship

Abstract

1. Introduction

2. Decomposing Interspecific Transmission

2.1. The Transmission-Rate, β d , r

2.1.1. The Contact-Rate, κ d , r

2.1.2. The Probability of Successful Transmission, c r

2.2. Calculation of the Outbreak Potential in the Recipient Host, R 0 , r

3. The Role of Host Community Structure in Interspecific Transmission

4. Linking Host Community- and Disease-Ecology

4.1. Host Community Effects on Pathogen Prevalence

4.2. Pathogen Effects on Host Community

5. Pathogen Adaptation in Multi-Host Systems

6. Future Directions

7. Conclusion

Appendix A. Derivation of transmission rate β

Appendix B. Generalizing the Derivation of Transmission Rate from the Single-Species Context

Appendix C. Derivation of Endemic Equilibrium for Species r, R 0,r

Appendix D. Interspecific Transmission through WAIFW

Appendix E. Contact Network Model Distributions

Appendix E.1. Poisson Distribution

Appendix E.2. Power-Law Truncated Distribution

Appendix E.3. The Exponential Distribution

References

MDPI Initiatives

Important Links

Subscribe

2.1. The Transmission-Rate, $β_{d, r}$

2.1.1. The Contact-Rate, $κ_{d, r}$

2.1.2. The Probability of Successful Transmission, $c_{r}$

2.2. Calculation of the Outbreak Potential in the Recipient Host, $R_{0, r}$