Minimum Uncertainty as Bayesian Network Model Selection Principle

Preprint

Article

Minimum Uncertainty as Bayesian Network Model Selection Principle

Altmetrics

Downloads

386

Views

422

Comments

This version is not peer-reviewed

Submitted:

07 June 2023

Posted:

07 June 2023

Read the latest preprint version here

Alerts

Abstract

In this paper study, we develop a Bayesian Network model selection principle that address addresses the incommensurability of network features obtained from incongruous datasets and overcomes performance irregularities of the Minimum Description Length model selection principle. This is achieved (i) by approaching model evaluation as a classification problem, (ii) by estimating the effect that sampling error has on the satisfiability of conditional independence criterion, as reflected by Mutual Information, and (iii) by utilizing this error estimate to penalize uncertainty in the Minimum Uncertainty (MU) model selection principle. We validate our findings numerically and demonstrate the performance advantages of the MU criterion. Finally, we illustrate the advantages of the new model evaluation framework on a tRNA structural biology example.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Probabilistic Bayesian Network (BN) modeling is a prominent tool in modern medical and life sciences. Apart from the standard array of data-analytic uses that are common to all probabilistic models, it has the advantage of capturing the complex structure of the web of relationships underlying the biological reality. When used for extraction of meaning from data, BN modeling generates valid, data-driven, evidence-based, and directly interpretable hypotheses, adding mechanistic value (for both theoretical and applied research) to the more conventional numerical replication of phenomenology.

BN-based dependency modeling has firmly established itself in computational biology and gained significant traction in secondary data analysis. Recent BN work runs the gamut of high-dimensional data analysis applications from pathway analysis [1,2] to serology [3] to cell communications [4,5] to connectomics [6] to genomics [7,8,9,10,11] to epigenomics [12,13] to transcriptomics [14]. Our prior BN application work ranged from flow cytometry [15] to chromatin interactions [16] to molecular evolution [17] to genetic epidemiology [18]; it is precisely this wide variety of biomedical domains and datasets that stimulated the present study, aiming at standardizing the BN evaluation across the different domains, datasets and modalities.

The specific problem that we address in this communication arises in the context of analyzing BNs coming from different sources. Even if such BNs share an identical set of variables, comparing them is a non-trivial matter because certain structural features, although visually different, may belong to classes of equivalence, while structural similarities may obscure subtle but important differences. The task becomes more complicated when it comes to assessing variable dependence strengths and their interplay with the rest of the network. The fact that edge strengths are evaluated via scoring criteria used in the structure recovery process, which offer only relative ordering of edges on an arbitrary scale, renders the interpretation of these relative strengths difficult and non-portable in biological and biomedical settings. In our experience, this significantly impedes BN modeling adoption in the life sciences and in translational and clinical practice.

The outlined issue motivates designing a scoring criterion that could serve not only as an objective function for structure recovery, but as a measure of dependency strength on an absolute scale, enabling direct comparison of individual edges and structural features between networks, without parsing massive conditional probability tables and factorizations in search of explanations for local network behavior.

We will proceed by first considering possible modifications of a well-known and reliable Minimum Description Length (MDL) criterion that, under certain conditions (large i.i.d. sample), is also equivalent to another well-established criterion, Bayesian Information Criterion (BIC) [19,20]. Although the end results may vary from one criterion to the next, the reasoning that follows is applicable to most optimizing model selection principles (e.g., Akaike Information Criterion, Bayesian Dirichlet, etc.).

For a BN structure G, MDL can be expressed in the following form

M D L (G) = L L (G) - \frac{1}{2} C (G) log (N)

where the term

L L (G) = - N \sum_{i} H (X_{i} | π_{i})

is the log-likelihood of G, written in terms of conditional entropy H, of individual nodes

X_{i}

of G and their parent node sets

π_{i}

, and where the term

\frac{1}{2} C (G) log (N)

represents the description length of G with

C (G)

(or complexity) usually taken to be proportional to the number of free parameters necessary to represent the factorization of the joint probability of G. While MDL performs well as an objective function, its composition gets in the way of interpreting the scores that it generates. First of all, the log-likelihood term is proportional to the sample size N, which means that for every new dataset this portion of the score is bound to a different scale unless the sample size remains constant. Second, the description length term is itself on a different scale than the log-likelihood, meaning that the relative contribution to the total score varies at a different rate between the two terms across different datasets. To illustrate with a common data analysis scenario example: given a specific dataset, a network obtained via subsampling would be numerically not comparable with the network obtained using the entire data, crippling robustness and stability analysis.

The most obvious way to address this would be to do away with sample size dependence. Conveniently,

L L (G)

can be easily rescaled to the sum of local conditional entropies. However, simply rescaling MDL by

1 / N

leaves the description length term proportional to

log (N) / N

, failing to eliminate sample size dependence or provide adequate motivation for it. Clearly, this "naive" approach defers rather than resolves the problem and certainly does not explain why these seemingly incommensurate terms should appear together in the first place. After all, the measure of complexity, which is what the description length essentially is, is neither proportional to the measure of entropy, nor does it stand in a one-to-one correspondence to it [21].

The analysis of the relative role the constituent components of MDL play in model selection reveals that the monotonic behavior of the log-likelihood or, equivalently, the conditional entropy with the increasing number of variables is counterbalanced by an ad hoc construct that demands higher description efficiency for sparse data but becomes close to irrelevant for larger sample sizes. This trade-off irregularity is an indication of misalignment between the competing objectives.

To be more precise, maximizing log-likelihood (or minimizing conditional entropy), which is what MDL engages in, should not be the principal objective, even if it partially coincides with the goal of finding an optimal structure. This is apparent from the fact that the conditional entropy minimum is achieved in the situation where every sample gets its own class, or where the joint events of the ancestor variables are fine-grained enough to homogenize the conditioned variable, which clearly does not have to coincide with the true solution. Even more importantly, the true solution should correspond to the correct conditional probability distribution, as opposed to the distribution with minimum entropy (maximum likelihood), whatever its description efficiency may be.

On the other hand, perhaps the most important quality of MDL from the BN perspective is that the conditional entropy minimization serves the purpose of finding locally dependent variables via an iteration update of the form

Δ H = H (X | π) - H (X | π, Y)

which is essentially an independence test, in the sense that

Δ H = 0

when X is independent of Y given its ancestor set

π

. It is worth noting that

Δ H

is also known as the Conditional Mutual Information (CMI), another information-theoretic quantity that frequently arises in the context of machine learning.

The above suggests that one does not have to worry so much about the justification of conditional entropy application and its congruence with the true solution — one can succeed by consistently maximizing the local dependence, without running into an overfitting problem, by maintaining a stringent independence test policy. With all of this in mind, we are ready to rederive the score, starting from these basic principles, in a way that would make all the terms contextually congruent and free of any irregularities. For now, we will accept the general form of the objective function to be

S (G) = \sum_{i} H (X_{i} | π_{i})

but let the improvement update for the node

X_{i}

have the form

Δ S (X_{i}) = H (X_{i} | π_{i}) - H (X_{i} | π_{i}, Y) - μ (X_{i})

where the third term

μ

should perform the function of the uncertainty penalty, reflecting the acceptable local independence policy. In the following sections, we will construct a suitable penalty term, grounding our reasoning in numerical satisfiability considerations, and investigate its performance.

2. Methods: Numerical satisfiability and sampling resolution in independence criteria.

One of the difficulties in assessing independence lies in the fact that analytical criteria, such as, for example, separability of the joint probability, i.e.

P (X, Y) = P (X) P (Y)

, can only be satisfied approximately in practice. Here we will be interested primarily in the degree to which finite sample resolution affects the numerical satisfiability of the independence criterion expressed in terms of the information-theoretic entropy H, e.g.

H (X | Y) = H (X)

For a finite sample of size N the probability of the smallest non-zero event is

p_{min} = 1 / N

. This probability is also the smallest observable difference between the probabilities of any two events. Hence, for any two events the difference in their probabilities below the resolution limit

r = p_{min}

will be undetectable, rendering the probabilities of these observations equivalent. Conversely, the probability evaluations that produce magnitudes falling below r are meaningless and can be considered noise or numerical error, at least from the data-centric perspective of the information contained in the sample. For the time being, we will assume the sample size to be ample for other sources of error to be negligible.

Suppose

h

is a small perturbation of some simplex element

p

, such that

h \cdot 1 = 0

, so that

p + h

is again an element of the same simplex. Since entropy is a continuously differentiable function of its argument, the approximation of the entropy function by its Taylor expansion is

H (p + h) \approx H (p) + \nabla H (p) \cdot h + \frac{1}{2} h^{T} \cdot D^{2} H (p) \cdot h + R (p, h)

At the

r = p_{min}

resolution the smallest acceptable perturbation

h

must have

h_{n} = r

as its n-th component and

h_{m} = - r

as its m-th component, with all other components being identically zero, e.g.

h = (0, \dots, 0, r, 0, \dots, 0, - r, 0, \dots, 0)

. Evaluating the second term of the expansion for this

h

gives

\nabla H (p) \cdot h = - \sum_{k} h_{k} (log (p_{k}) + 1) = - r (log (p_{n}) - log (p_{m})) = - r log (p_{n} / p_{m})

because

\sum_{k} h_{k} = 0

. Since the nontrivial components of

p

lie between r and

1 - r

, and the extreme values of

log (p_{n} / p_{m})

at the prescribed resolution are achieved when either

p_{n} = r

and

p_{m} = 1 - r

, or the other way around, the following inequality holds

- r log ((1 - r) / r) \leq \nabla H (p) \cdot h \leq - r log (r / (1 - r))

In the same spirit, the third term of the expansion evaluates to

\frac{1}{2} h^{T} \cdot D^{2} H (p) \cdot h = - \frac{1}{2} \sum_{k} \frac{h_{k}^{2}}{p_{k}} = - \frac{r^{2}}{2} (1 / p_{n} + 1 / p_{m})

and for the same reason as above the following holds

- \frac{r^{2}}{2} (1 / r + 1 / r) \leq \frac{1}{2} h^{T} \cdot D^{2} H (p) \cdot h \leq - \frac{r^{2}}{2} (1 / (1 - r) + 1 / (1 - r))

Higher order terms

R_{k}

of the expansion, that comprise the residual

R (p, h) = \sum_{k} R_{k} (p, h)

, present the following pattern

R_{1} (p, h) = \frac{1}{3!} \sum \frac{\partial^{3} H (p)}{\partial p_{i} \partial p_{j} \partial p_{k}} h_{i} h_{j} h_{k} = - \frac{1}{3!} \sum \frac{- h_{i}^{3}}{p_{i}^{2}} = \frac{1}{3!} r^{3} (1 / p_{n}^{2} - 1 / p_{m}^{2})

R_{2} (p, h) = \frac{1}{4!} \sum \frac{\partial^{4} H (p)}{\partial p_{i} \partial p_{j} \partial p_{k} \partial p_{l}} h_{i} h_{j} h_{k} h_{l} = - \frac{1}{4!} \sum \frac{2 h_{i}^{4}}{p_{i}^{3}} = - \frac{2 r^{4}}{4!} (1 / p_{n}^{3} + 1 / p_{m}^{3})

R_{3} (p, h) = - \frac{1}{5!} \sum \frac{- 2 \cdot 3 \cdot h_{i}^{5}}{p_{i}^{4}} = \frac{3! r^{5}}{5!} (1 / p_{n}^{4} - 1 / p_{m}^{4})

R_{4} (p, h) = - \frac{1}{6!} \sum \frac{3! \cdot 4 \cdot h_{i}^{6}}{p_{i}^{5}} = - \frac{4! r^{6}}{6!} (1 / p_{n}^{5} + 1 / p_{m}^{5})

Since the even terms are strictly negative and the odd terms can be split into positive and negative parts, the residual R can be bounded above by

R^{+} = \sum_{k = 1}^{\infty} \frac{(2 k - 1)! \cdot r^{2 k + 1}}{(2 k + 1)! \cdot r^{2 k}} = r \sum_{k = 1}^{\infty} \frac{1}{(2 k) (2 k + 1)} \leq r \sum_{k} \frac{1}{{(2 k)}^{2}} = r \frac{π^{2}}{24}

and bounded below by

R^{-} = \sum_{k = 1}^{\infty} \frac{- 2 \cdot k! \cdot r^{k + 2}}{(k + 2)! \cdot r^{k + 1}} - R^{+} = - 2 r \sum_{k = 1}^{\infty} \frac{1}{(k + 1) (k + 2)} - R^{+} = - 2 r / 2 - R^{+} \geq - r - r \frac{π^{2}}{24}

One can now estimate the effect that limited resolution has on the independence criterion in the near-conditional-independence situation:

\begin{matrix} Δ H = H (X) - H (X | Y) = H (X) - \sum_{k} P (Y = y_{k}) H (X | Y = y_{k}) \\ \approx H (X) - \sum_{k} P (Y = y_{k}) (H (X) + \nabla H (X) \cdot h_{k} + \frac{1}{2} h_{k}^{T} \cdot D^{2} H (X) \cdot h_{k} + R (X, h_{k})) \\ = - \sum_{k} P (Y = y_{k}) (\nabla H (X) \cdot h_{k} + \frac{1}{2} h_{k}^{T} \cdot D^{2} H (X) \cdot h_{k} + R (X, h_{k})) \end{matrix}

Lower and upper bounds for the deviation

Δ H

under the circumstances of near-conditional-independence can then be estimated as

Δ H \leq - \sum_{k} (- r_{k} log ((1 - r_{k}) / r_{k}) - r_{k} - r_{k} (1 + π^{2} / 24)) P (Y = y_{k}) = \sum_{k} (log (N_{k} - 1) + 2 + π^{2} / 24) / N

and

\begin{matrix} Δ H \geq - \sum_{k} (- r_{k} log (r_{k} / (1 - r_{k})) - r_{k}^{2} / (1 - r_{k}) + r_{k} π^{2} / 24) P (Y = y_{k}) \\ = \sum_{k} (- log (N_{k} - 1) + 1 / (N_{k} - 1) - 1) / N \end{matrix}

where

r_{k} = 1 / N_{k}

is the sampling resolution in the set of observations conditioned on

(Y = y_{k})

, and

P (Y = y_{k}) = N_{k} / N

. We will not concern ourselves with obtaining tighter bounds for now, although it is clearly possible.

Noting that, in general,

Δ H \geq 0

, and that the obtained above lower bound is negative, i.e.

\sum_{k} (- log (N_{k} - 1) + 1 / (N_{k} - 1) - 1) / N \leq 0

we can safely exclude the lower bound from consideration for now.

For the upper bound, we note that it is satisfiable only when

N_{k} \geq 2

. This makes sense, because

N_{k} < 2

is the sampling resolution territory. However, for practical purposes we may actually prefer an upper bound that affords computation without additional constraints on

N_{k}

other than that of positivity, thereby arriving at the final result in the following form

Δ H \leq \sum_{k} (log (N_{k} - 1) + 2 + π^{2} / 24) / N \leq \sum_{k} (log (N_{k}) + 2 + π^{2} / 24) / N

Identical reasoning applies in a situation with several conditioning variables

\begin{matrix} H (X | Y) - H (X | Y, Z) = \sum_{j, i} [H (X | Y = y_{i}) - P (Y = y_{i}, Z = z_{j}) H (X | Y = y_{i}, Z = z_{j})] \\ \approx - \sum_{i, j} P (Y = y_{i}, Z = z_{j}) (\nabla H (X) \cdot h_{i j} + \frac{1}{2} h_{i j}^{T} \cdot D^{2} H (X) \cdot h_{i j} + R (X, h_{i j})) \\ \leq \sum_{i j} (log (N_{i j}) + 2 + π^{2} / 24) / N \end{matrix}

where the sampling resolution

1 / N_{i j}

corresponds to the joint event with the probability

P (Y = y_{i}, Z = z_{j}) = N_{i j} / N .

Having obtained these bounds we can now restate the local independence policy (selection criterion) as the requirement that at the n-th iteration,

X_{i}

and Y are dependent only if

Δ S_{n} (X_{i}) > 0

, where

Δ S_{n} (X_{i}) = H (X_{i} | π_{i}) - H (X_{i} | π_{i} \cap Y) - μ (π_{i} \cap Y)

with the uncertainty penalty

μ

given by

μ (π_{i} \cap Y) = \sum_{k} (log (N_{k}) + 2 + π^{2} / 24) / N

and

N_{k}

being the sample count associated with the k-th state of

π_{i} \cap Y

. Note that even though we have retained N in the penalty term this no longer presents an issue because now this term is commensurable with entropy and is nothing more than the amount of uncertainty or error acceptable in the evaluation of the independence criterion that arises due to sampling error; no additional interpretation should be ascribed to it.

Since, all else being equal, this selection policy prioritizes dependencies with the least uncertainty, the guiding model selection principle can be defined as the principle of Minimum Uncertainty (MU). Under MU, the appearance, fixation, and strength of dependencies in the network can now be interpreted in terms of representational accuracy and precision, instead of relying on idealized criteria like maximum likelihood, maximum posterior probability, or maximum parsimony.

3. Results

3.1. Numerical verification and the sensitivity profile.

In this section, we will use pairs of multivariate independent variables, obtained from a multinomial distribution with a uniform Dirichlet prior, to investigate and verify numerically the behavior of the uncertainty penalty term obtained in the previous section.

An example of the data obtained from a sequence of

10^{5}

8-variate categorical pairs of independent variables with sample size

N = 10^{3}

is shown in Table 1. For brevity, we only include the results for 5 pairs (this is sufficiently representative given that the statistical behavior across all pairwise comparisons is summarized in Table 2 below). The negative sign retained in the table arises due to the effect the penalty terms play in the evaluation of both

Δ M D L = Δ H - Δ c and Δ S = Δ H - μ

where

Δ c

and

μ

represent the MDL complexity penalty and the uncertainty penalty (obtained in this work), respectively. More importantly, the negative sign is an indicator that the update should be rejected due to near-independence in the case of

Δ S

, and due to high storage requirements in the case of

Δ M D L

. As we shall see further, the update rejection, equivalent to the detection of near-independence within the framework developed in this study, is not guaranteed for all independent variables, at least for the MDL score (see Table 4).

Table 2 summarizes the statistical behavior across the same sequence of

10^{5}

pairs. Note that the

Δ c

is constant, while

Δ S

reacts to the local properties of every pair of variables under consideration, and is a tighter bound for the deviation from independence, given by

Δ H

Table 3 summarizes the results of

10^{5}

pairwise comparisons of 4-variate independent variables and

N = 1000

. Note that the lower category count resulted in a decrease in the deviation from perfect independence, and that this effect is also accounted by the drop in both penalty terms, although at vastly different rates.

Table 4, on the other hand, indicates a failure of MDL to properly detect near-independent pair, as can be seen in the last row of the

Δ M D L

column. Here, the pairwise comparisons are carried out for 2-variate independent pairs with sample size

N = 1000

, and MDL misclassifies 920 independent pairs out of

10^{5}

, approximately

1 %

Table 4. Statistical summary for

10^{5}

independent variable pairs with 2 categories and

N = 1000

Table 4. Statistical summary for

10^{5}

independent variable pairs with 2 categories and

N = 1000

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.00050636	0.01663084	0.00345388	-0.01612448	-0.00294752
median	0.00023039	0.01696400	0.00345388	-0.01647059	-0.00322349
$σ$	0.00071399	0.00087238	0.00000000	0.00112515	0.00071399
max	0.00953119	0.01725168	0.00345388	-0.00693925	0.00607731

Note that the failure of

Δ M D L

to identify independent variables is not mitigated by an order of magnitude increase in the sample size, i.e.

N = 10000

, as can be observed in Table 5. But the total number of misclassifications of independent pairs falls to 227, which is approximately

0.23 %

. These observations are consistent with the well-known observation that the MDL complexity term tends to under-penalize low category count variable pairs, causing at times severe overfitting in the context of BN recovery from data. Observed sample size dependence in MDL’s ability to classify independent variables correctly, however, fails to explain why

Δ c

needs to be sensitive to sample size, given the relatively well-behaved, well-represented profile of conditional and joint events of the scenario presented here. Clearly, this undesirable under-penalizing property of MDL complexity term cannot be easily dismissed as the shortcoming of the data (see Figure 1), particularly given the fact that

Δ c

depends only on N and reflects nothing else about the variable pairs in question.

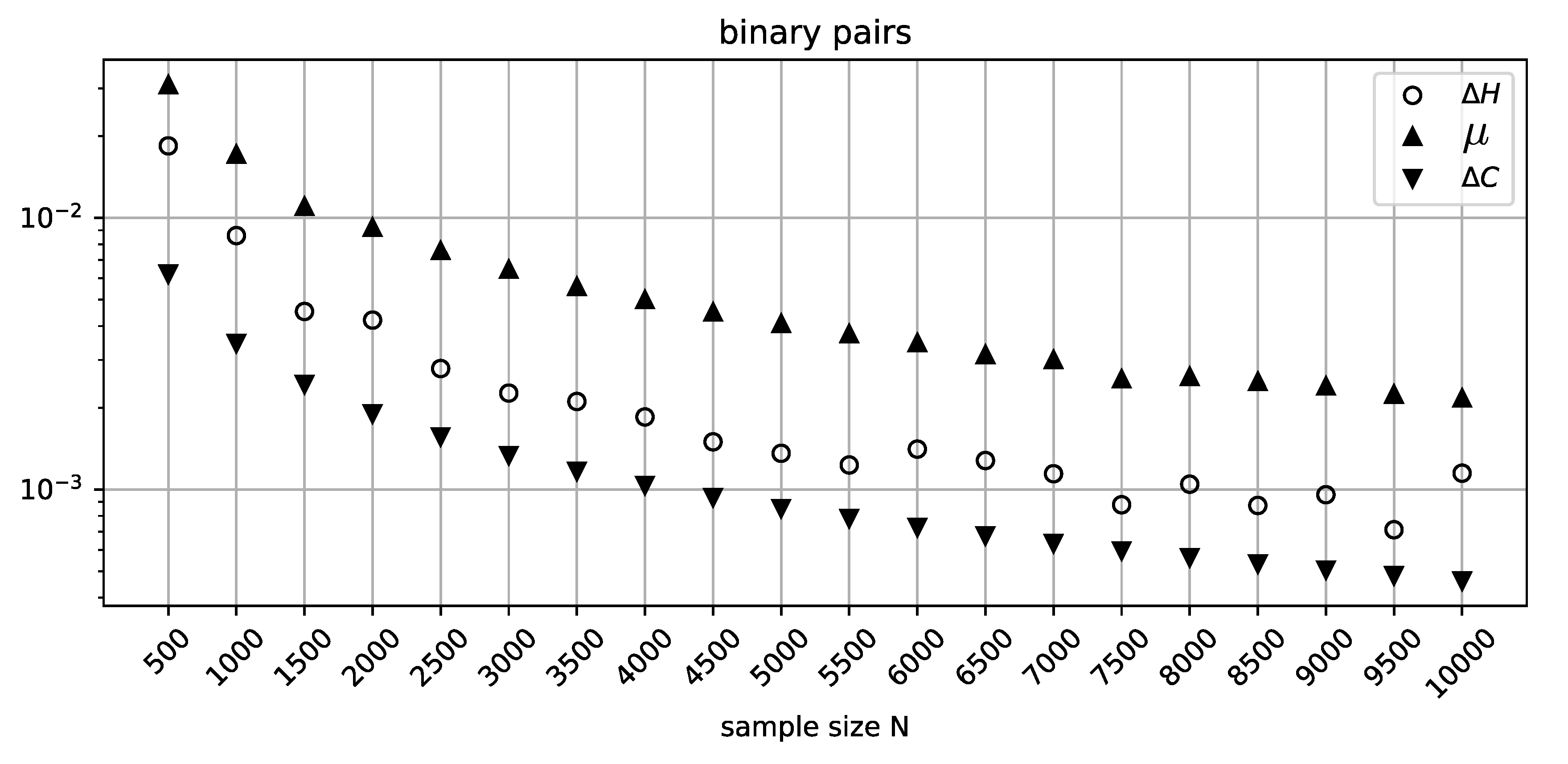
To investigate this misclassification further we consider batches of 10000 randomly generated pairs of binary variables for a range of sample sizes. For every batch, we extract the pair that gives the maximum value of

Δ H

and evaluate the corresponding values of

Δ c

and

μ

. These values are then plotted against the increasing sample size in Figure 1. The MDL penalty term

Δ c

clearly fails to bound the deviation from independence

Δ H

across the whole range of sample sizes.

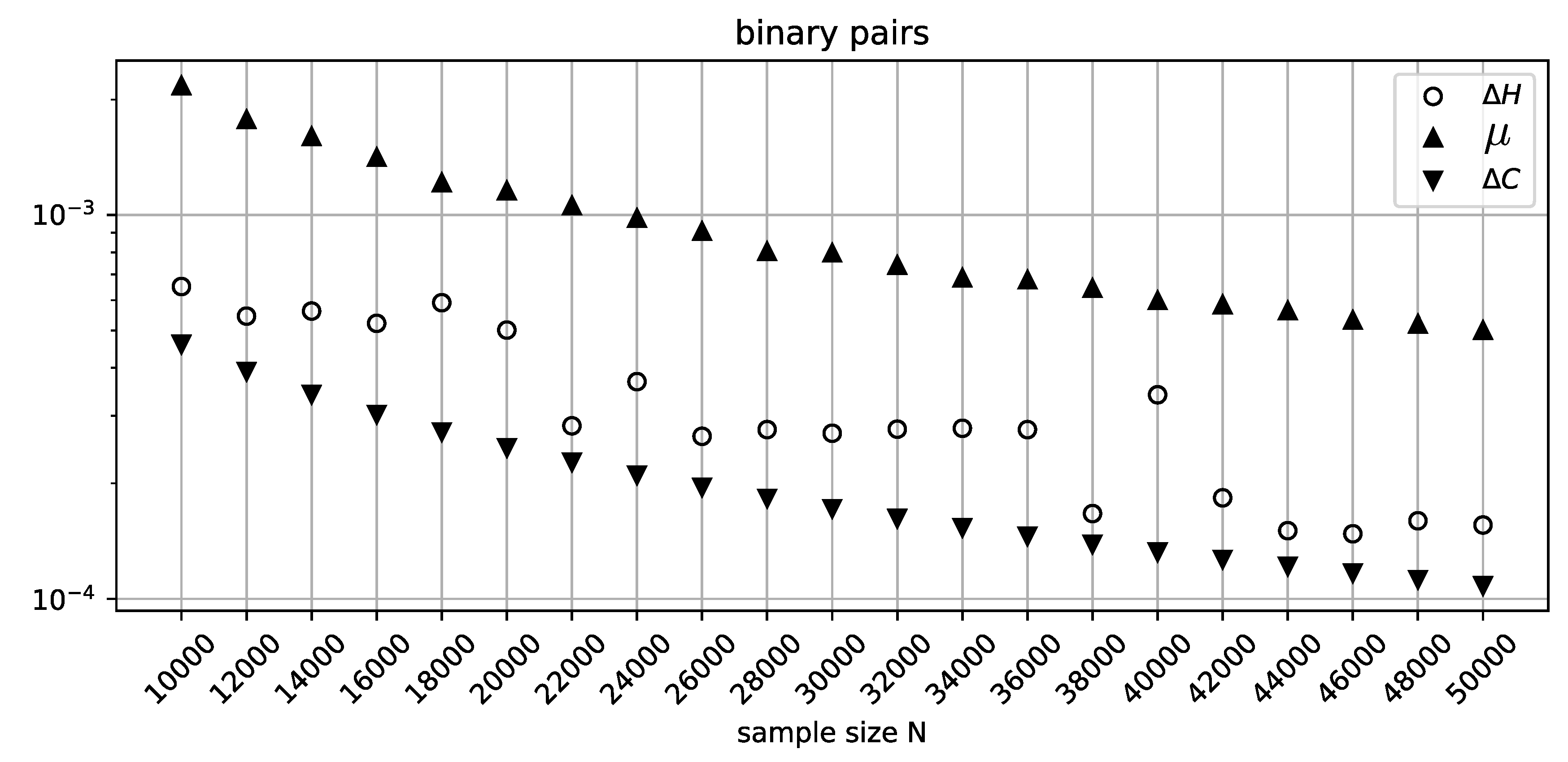
In Figure 2, the range of sample sizes is extended to 50000 with a coarser increment to show that the misclassification rate of

Δ c

sees general improvement as N increases, although at

N = 46000

the MDL penalty term once again fails to identify an independent pair. As expected,

μ

has no trouble in this range of parameters, and its stricter penalization profile is justified by the general volatility exhibited by

Δ H

To continue, we return to our previous setup generating

10^{5}

independent pairs and consider the scenario with 4-variate variables and

N = 10000

. Table 6 reveals the behavior consistent with the expectations, where both updates identify near-independent pairs equally well. In this range of data parameters the terms are very close in their magnitude, so it is not surprising that the behavior is almost identical.

In Table 7 (8-variate pairs,

N = 10000

), the MDL penalty term is on average several times greater than

μ

. Both scores, however, perform equally well in this range of parameters, identifying all independent pairs correctly.

Table 8 reveals a misclassification on the part of

Δ S

, as can be seen in the last row of the

Δ S

column. Further investigation reveals approximately

2.6 %

of misclassified pairs and sample size dependence of the misclassification rate which is completely resolved by increasing the sample size by one order of magnitude (Table 9). This observation is fully consistent with the general understanding of the effect that limited sample size may have on conditional or joint events.

In the scenario presented here, a 16-variate random variable can be expected to have unconditional events of the size

P (X = x_{i}) \approx 0.0625

. Therefore, any joint event will necessarily be smaller, in the order of the square of the unconditional events due to independence, i.e.

P (X = x_{i}, Y = y_{j}) = P (X = x_{i}) P (Y = y_{j}) \approx 0.00390625

This corresponds to only roughly 40 samples per joint event in the case of

N = 10^{4}

, on average. Clearly, for such small probabilities the sample size should be larger to be adequately representative, otherwise the unaccounted-for effects of sampling error may dominate the landscape.

It is not surprising that MDL falters in these circumstances, given how much it over-penalizes

Δ H

. This comes at the cost of specificity, i.e. MDL would clearly fail to classify dependent pairs as such for all values of

Δ H

that would fall between, say, the values

max Δ H

and

Δ c

presented in the table.

Table 9 reveals the ability of

Δ S

to recover its sensitivity under the condition of sufficient sample size. This is to be expected, since for

N = 10^{5}

a joint event will correspond to roughly 400 samples, on average. Note that while the MDL complexity term continues to over-penalize

Δ H

significantly even when provided data of ample size, the sensitivity of

μ

attains a new degree of refinement.

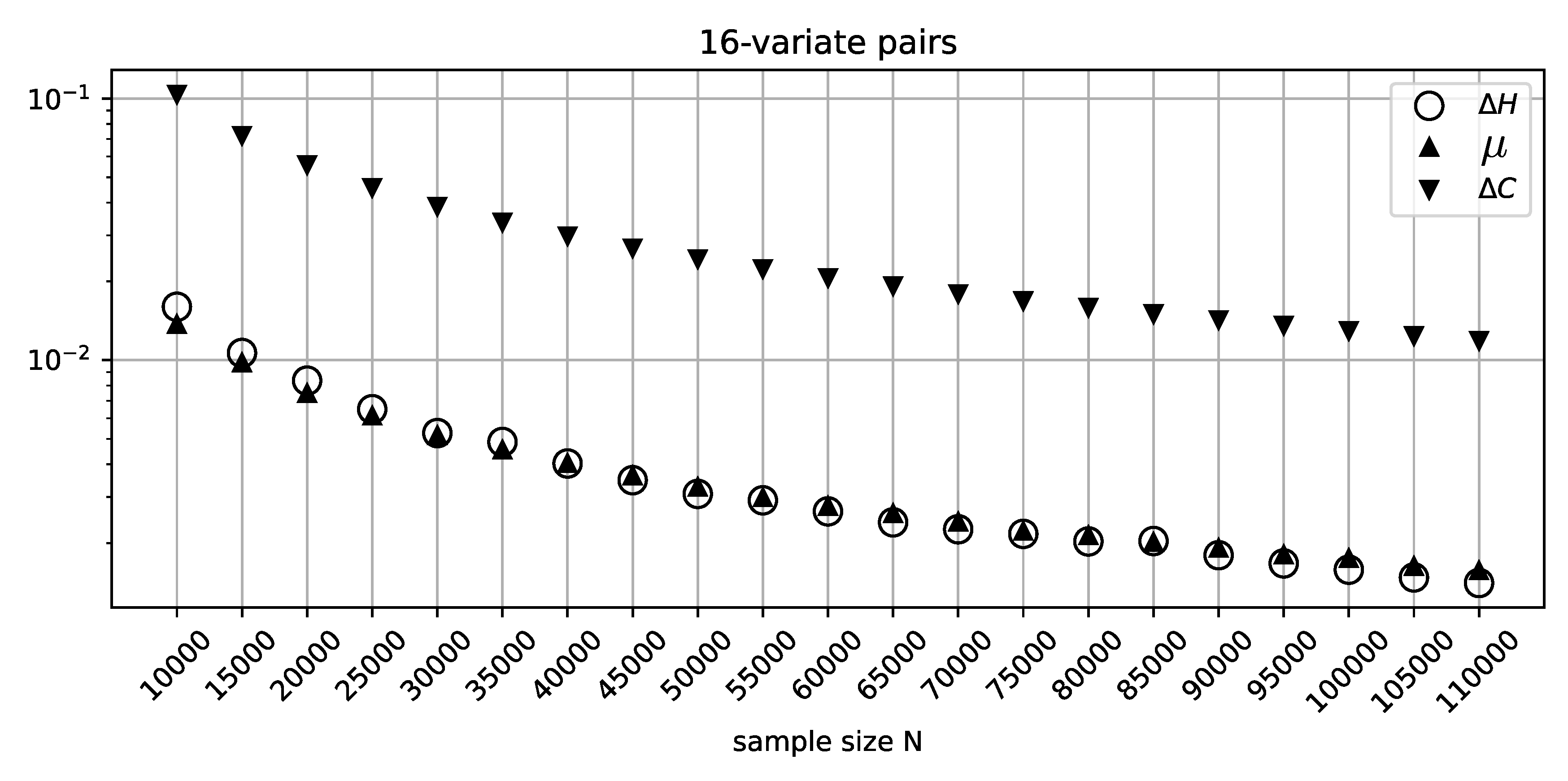
Figure 3 recapitulates the misclassification analysis (that was performed for the binary variables above) for the batches of 10000 random 16-variate independent variable pairs for every value of N. The figure shows consistently improving classification precision of

μ

, with a somewhat elevated sensitivity profile for smaller sample sizes, as expected due to the unaccounted-for effect of sampling error. On the other hand, the excessive over-penalization imposed by

Δ c

, clearly visible in this figure, is difficult to justify, given the abundant sample size and very consistent behavior on the part of

Δ H

These results demonstrate that not only does the uncertainty penalty term

μ

have an edge in interpretability, but that it is also far more balanced and consistent in its sensitivity profile, a matter of direct relevance to practical performance.

3.2. Application to the structural biology of tRNA molecules: Sample size invariance study.

In our prior work [17], we used BN modeling (with conventional scoring criteria) to study and dissect the structure of intra-tRNA-molecule residue/position relationships across the three domains of life, with an eye toward identifying informative positions and sections of the tRNA molecule in different tRNA subclasses. In this study, we have recapitulated this analysis with the current version of our BN modeling software BNOmics [18] using the "standard" MDL, and evaluated the resulting BN across different sample sizes using the standard MDL and the novel criterion, MU. The tRNA sequences and alignment were assembled as in [17] with slight modifications, amounting to 9378 tRNA sequences.

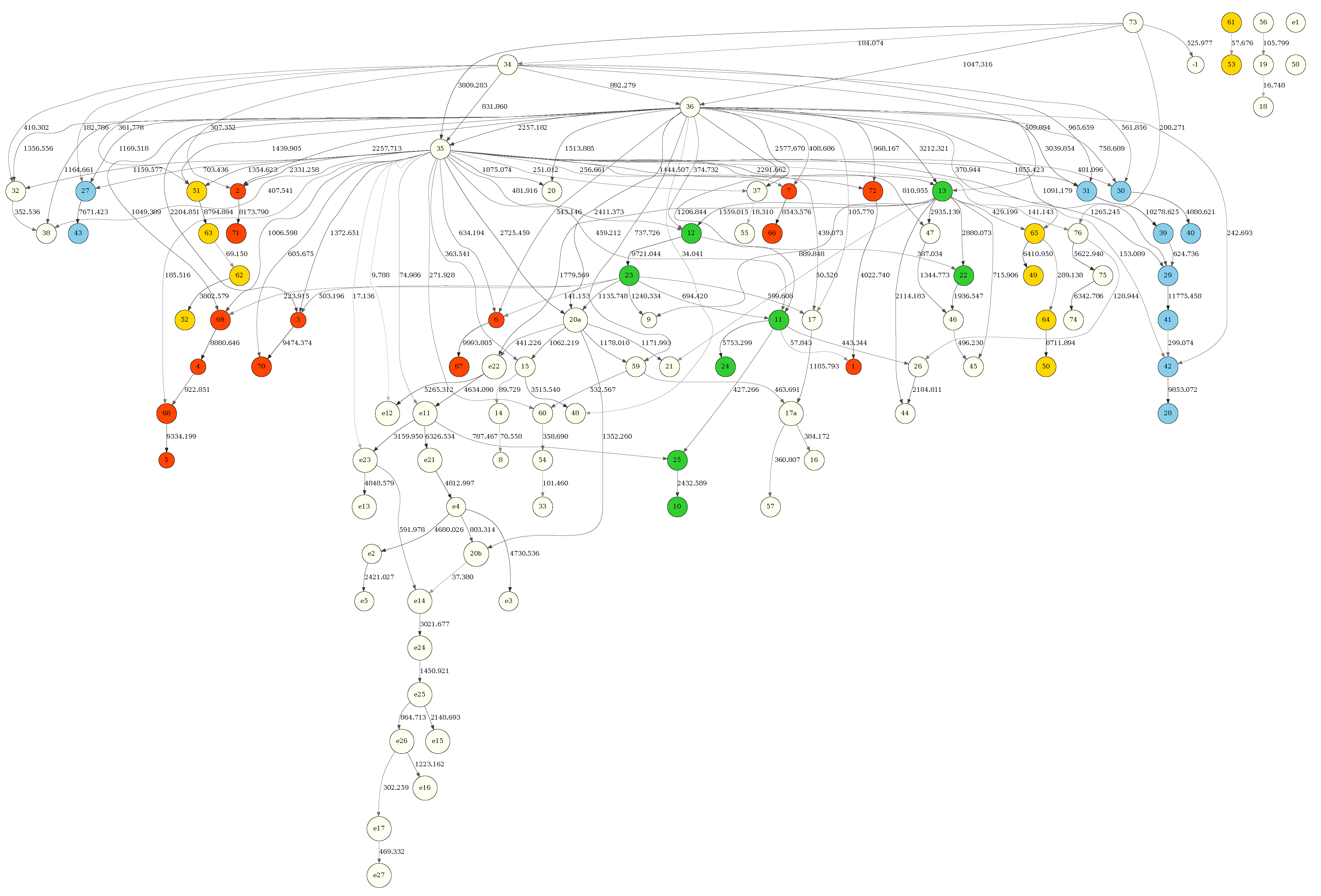
Figure 4 depicts the BN obtained from the full (9378 tRNAs) sample with the MDL criterion. The tRNA residues in the network were colored according to the tRNA molecule structural domains — red (acceptor stem), green (D-arm), blue (anticodon 131 arm) and yellow (T-arm). The tRNA residue positions, shown inside the network node labels, followed the universally accepted tRNA position numbering standard [22]. Figure S1 depicts the same structure but scored, also with MDL, against a random subsample of 4689 tRNAs (50 percent of the full sample). Figure S2 depicts the same structure scored with the MU criterion against the full (9378 tRNAs) sample. Finally, Figure S3 depicts the same structure scored with the MU criterion against a random subsample of 4689 tRNAs (50 percent of the full sample). It is clear that edge strengths obtained with the MDL scoring criterion strongly depend on sample size (Figure 4 vs Figure S1), just as expected. In contrast, the edge strengths obtained with the MU score are practically independent of sample size (Figure S2 vs Figure S3).

A "naive" alternative, described above in the introduction, would be to rescale MDL scores by

1 / N

, thereby eliminating sample size dependence in the likelihood term (converting it to conditional entropy). However, this transformation fails to eliminate sample size dependence from the complexity term, demanding a separate interpretation for its contribution. The results of the "naive" rescaling can be observed in Figure S4 and Figure S5 which exhibit significant instability in the strengths of many weaker edges across the two sample sizes. For reference, Figures S6 and S7 show the scores as calculated by

Δ H

alone, i.e. with the penalty term omitted, where we can see a much more predictable and relatively stable behavior across the two considered sample sizes. Notably, a more stable score behavior is demonstrated in Figures S2 and S3, suggesting that the MU penalty derived in this study is in congruence with

Δ H

Note that the effect of the penalty term on the score can be one of the primary deciding factors in network configuration preference, and play the role of a termination criterion for seeking dependencies. Since MDL penalizes the arity of ancestor variable bundles, i.e. complexity, one has to account for description efficiency when interrogating MDL score fluctuations. On the contrary, the MU score derived in this study seamlessly integrates its penalty term as an acceptable evaluation uncertainty. This allows the interpretation of score fluctuations directly in terms of satisfiability of the independence criterion.

In summary, the MU principle overcomes the limitations of the MDL principle in that it (i) naturally handles data of varying sample size, (ii) seamlessly integrates an adaptive penalty term commensurate with

Δ H

into edge scores, thereby simplifying interpretation, (iii) implicitly penalizes model complexity with higher regularity.

4. Discussion and Conclusions

Numerical verification of the effect that the resolution limit has on independence assessment has shown that the uncertainty-driven reasoning, as outlined in this study, is a valid and effective framework for managing near-independence scenarios, directly applicable in the context of data-driven recovery of BNs. The preliminary tests of the MU principle in BN recovery display all the desired characteristics, i.e. computational performance comparable to the MDL-driven method, but with consistently higher regularity across varying scales and scenarios, and, on average, better convergence rates. Importantly, the edge strengths, obtained via the application of MU criterion, are directly interpretable in a way independent from the data source, allowing for direct comparison of the recovered BNs not only in robustness/stability studies, but also under scenarios where different data spans diverse sets of variables. That being said, the consistently superior behavior of MU in situations where MDL typically tends to overfit or underfit suggests that with this relatively simple approach we can successfully address several problems, intrinsic to the model selection criteria in general, that go well beyond the interpretability of the score.

We intend to develop this work further along the axis of a comprehensive power-analytic methodology, with the aim to modify the scoring criterion to consistently work on an absolute scale, reflecting classification rates. This would improve the usefulness of the feature and model scoring in the judgment of proximity/similarity between networks, as well as in the assessment of dependencies in the general sense. The focus on the statistical behavior of the scoring criterion is, in part, motivated by the need to overcome the computational limitations associated with the relative nature of information-theoretic quantities in the assessment of variable dependencies in BNs. However, this statistical focus will also help with the broader integration and acceptance of BN modeling in the biomedical data analysis practice, where the interplay between sample size considerations and the effect size is often the dominant driving factor behind both the study design and the evaluation of its results.

A number of our ongoing multidisciplinary secondary biomedical data analysis studies, including (i) comparative BN analyses of multidimensional fluorescence-activated cell sorting (FACS) and other immuno-oncology datasets [15], (ii) -omics of Alzheimer’s disease, (iii) BN modeling of G-protein/GPCR molecular dynamics simulation data, and (iv) BN-centered construction of gene regulatory networks from the scRNA-seq data, stimulated a significant portion of the work detailed in this communication. Indeed, rigorous dissection of the underlying BN fundamentals and mechanics is essential for robust construction, interpretation, and comparison of BNs in any biomedical data analysis setting. In the future, we intend to use the novel MU criterion to increase the rigor of our ongoing and prospective applied BN work, across many biomedical domains.

In summary, our experience in working with multimodal high-dimensional biomedical data led us to the conclusion that every BN analysis should, ideally, allow direct comparative, possibly cross-study, interrogation of the recovered networks’ structural and quantitative features. The technical advancement detailed in this study has the potential to alleviate many difficulties typically encountered when trying to gain biological and mechanistic insights from a series of BN models generated at the secondary data analysis / network modeling stage of a typical data-driven research project.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org

Author Contributions

Grigoriy Gogoshin: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Software; Validation; Visualization; Writing - original draft. Andrei S. Rodin: Conceptualization; Funding acquisition; Investigation; Project administration; Supervision; Writing - original draft.

Data Availability Statement

Relevant code and software are available directly from the authors, or as part of the BNOmics package, at https://bitbucket.org/77D/bnomics.

Acknowledgments

The authors are grateful to Sergio Branciamore, Arthur D. Riggs, Russell C. Rockne, Peter P. Lee, Nagarajan Vaidehi and Amanda J. Myers for stimulating discussions and useful comments about the interpretability of Bayesian networks in various biomedical contexts. This work was supported by the NLM R01LM013138 grant (to A.S.R.), NCI Cancer Biology System Consortium U01CA232216 grant (to A.S.R.), Susumu Ohno Chair in Theoretical Biology (held by A.S.R.), and Susumu Ohno Distinguished Investigator Fellowship (to G.G.). Funding sources played no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Conflicts of Interest

The authors declare that no competing financial interests exist.

References

Wang, Y.; Li, J.; Huang, D.; Hao, Y.; Li, B.; Wang, K.; Chen, B.; Li, T.; Liu, X. Comparing Bayesian-Based Reconstruction Strategies in Topology-Based Pathway Enrichment Analysis. Biomolecules 2022, 12, 906. [Google Scholar] [CrossRef] [PubMed]
Sato, N.; Tamada, Y.; Yu, G.; Okuno, Y. CBNplot: Bayesian network plots for enrichment analysis. Bioinformatics 2022, 38, 2959–2960. [Google Scholar] [CrossRef] [PubMed]
Dickson, B.F.R.; Masson, J.J.R.; Mayfield, H.J.; Aye, K.S.; Htwe, K.M.; Roineau, M.; Andreosso, A.; Ryan, S.; Becker, L.; Douglass, J.; Graves, P.M. Bayesian Network Analysis of Lymphatic Filariasis Serology from Myanmar Shows Benefit of Adding Antibody Testing to Post-MDA Surveillance. Trop.Med. Infect. Dis. 2022, 7, 113. [Google Scholar] [CrossRef]
Gupta, S.; Vundavilli, H.; Osorio, R.S.A.; Itoh, M.N.; Mohsen, A.; Datta, A.; Mizuguchi, K.; Tripathi, L.P. Integrative Network Modeling Highlights the Crucial Roles of Rho-GDI Signaling Pathway in the Progression of non-Small Cell Lung Cancer, IEEE J. Biomed. Health Inform. 2022, 26, 4785–4793. [Google Scholar] [CrossRef]
Klinke, D.J., II.; Fernandez, A.; Deng, W.; Razazan, A.; Latifizadeh, H.; Pirkey, A.C. Data-driven learning how oncogenic gene expression locally alters heterocellular networks 2022, 13, 1986.
Zhao, Y.; Chen, T.; Cai, J.; Lichenstein, S.; Potenza, M.N.; Yip, S.W. Bayesian network mediation analysis with application to the brain functional connectome. Stat. Med. 2022, 41, 3991–4005. [Google Scholar] [CrossRef] [PubMed]
Tuo, S.; Li, C.; Liu, F.; Zhu, Y.; Chen, T.; Feng, Z.; Liu, H.; Li, A. A Novel Multitasking Ant Colony Optimization Method for Detecting Multiorder SNP Interactions, Interdiscip. Sci. 2022, 5. [Google Scholar]
Wang, Y.; Gao, X.; Ru, X.; Sun, P.; Wang, J. Identification of gene signatures for COAD using feature selection and Bayesian network approaches, Sci. Rep. 2022, 12, 8761. [Google Scholar]
Chen, Z.; Lu, Y.; Cao, B.; Zhang, W.; Edwards, A.; Zhang, K. Driver gene detection through Bayesian network integration of mutation and expression profiles. Bioinformatics 2022, 38, 2781–2790. [Google Scholar] [CrossRef]
Cherny, S.S.; Williams, F.M.K.; Livshits, G. Genetic and environmental correlational structure among metabolic syndrome endophenotypes, Ann. Hum. Genet. 2022, 86, 225–236. [Google Scholar] [CrossRef]
Wang, L.; Audenaert, P.; Michoel, T. High-dimensional bayesian network inference from systems genetics data using genetic node ordering, Front. Genet. 2019, 10, 1196. [Google Scholar]
Videla Rodriguez, E.A. , P´ertille F., Guerrero-Bosagna C., Mitchell J.B.O., Jensen P., Smith V.A., Practical application of a Bayesian network approach to poultry epigenetics and stress. BMC Bioin-formatics, 2022, 23, 261. [Google Scholar]
Liao, H.; Luo, X.; Huang, Y.; Yang, X.; Zheng, Y.; Qin, X.; Tan, J.; Shen, P.; Tian, R.; Cai, W.; Shi, X.; Deng, X. Mining the Prognostic Role of DNA Methylation Heterogeneity in Lung Adenocarcinoma, Dis. Markers May 2022, 28, 9389372. [Google Scholar]
Mortazavi, A.; Rashidi, A.; Ghaderi-Zefrehei, M.; Moradi, P.; Razmkabir, M.; Imumorin, I.G.; Peters, S.O.; Smith, J. Constraint-Based, Score-Based and Hybrid Algorithms to Construct Bayesian Gene Networks in the Bovine Transcriptome. Animals 2022, 12, 1305. [Google Scholar] [CrossRef]
Rodin, A.S.; Gogoshin, G.; Hilliard, S.; Wang, L.; Egelston, C.; Rockne, R.C.; et al. , Dissecting response to cancer immunotherapy by applying bayesian network analysis to flow cytometry data, Int. J. Mol. Sci. 2021, 22, 2316. [Google Scholar] [CrossRef]
Zhang, X.; Branciamore, S.; Gogoshin, G.; Rodin, A.S. Analysis of high-resolution 3d intrachro-mosomal interactions aided by bayesian network modeling, Proc. Natl. Acad. Sci. USA 2017, 114, E10359–E10368. [Google Scholar] [CrossRef]
Branciamore, S.; Gogoshin, G.; Di Giulio, M.; Rodin, A.S. Intrinsic properties of TRNA molecules as deciphered via bayesian network and distribution divergence analysis. Life 2018, 8, E5. [Google Scholar] [CrossRef]
Gogoshin, G.; Boerwinkle, E.; Rodin, A.S. New algorithm and software (bnomics) for inferring and visualizing bayesian networks from heterogeneous “big” biological and genetic data, J. Comp. Bio. 2017, 24, 340–356. [Google Scholar] [CrossRef]
de Campos, C.; Ji, Q. Efficient Structure Learning of Bayesian Networks using Con-straints, J. Mach. Learn. Res. 2011, 12, 663–689. [Google Scholar]
de Campos, Luis M. , A Scoring Function for Learning Bayesian Networks based on Mutual Information and Conditional Independence Tests, J. Mach. Learn. Res. 2006, 7, 2149–2187.
Li, W. On the Relationship between Complexity and Entropy for Markov Chains and Regular Languages. Complex Syst. 1991, 5. [Google Scholar]
Quigley, G. A. Rich. Structural domains of transfer RNA molecules. Science 1976, 194, 796–806. [Google Scholar] [CrossRef] [PubMed]

Figure 1. The behavior of the deviation from independence

Δ H

, the MDL penalty term

Δ c

, and the MU penalty

μ

for random binary independent variable pairs across varying sample size.

Figure 1. The behavior of the deviation from independence

Δ H

, the MDL penalty term

Δ c

, and the MU penalty

μ

for random binary independent variable pairs across varying sample size.

Figure 2. The behavior of

Δ H

Δ c

, and

μ

for random binary independent variable pairs across the extended sample size range.

Figure 2. The behavior of

Δ H

Δ c

, and

μ

for random binary independent variable pairs across the extended sample size range.

Figure 3. The behavior of

Δ H

Δ c

, and

μ

for random 16-variate independent variable pairs across varying sample sizes.

Figure 3. The behavior of

Δ H

Δ c

, and

μ

for random 16-variate independent variable pairs across varying sample sizes.

Figure 4. BN obtained from the full sample (9378 tRNAs) with the MDL criterion. Nodes in the network correspond to the tRNA positions, and edges — to the dependencies between the tRNA positions. The “boldness” of the edge is proportional to the dependency strength, also indicated by the number shown next to the edge. See text for further details.

Table 1. The data generated for

10^{5}

pairs of 8-variate independent variables with N=1000. Five representative pairs are shown. The 1st column is the conditional entropy deviation

Δ H = H (X) - H (X | Y)

; 2nd column is the corresponding uncertainty penalty, obtained in this work; 3rd column is the MDL complexity; 4th column is the update of the uncertainty penalized score; 5th column is the update of MDL.

Table 1. The data generated for

10^{5}

pairs of 8-variate independent variables with N=1000. Five representative pairs are shown. The 1st column is the conditional entropy deviation

Δ H = H (X) - H (X | Y)

$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
0.02403642	0.05743832	0.16924000	-0.03340190	-0.14520358
0.01683616	0.05483424	0.16924000	-0.03799808	-0.15240385
0.03657420	0.05738811	0.16924000	-0.02081391	-0.13266580
0.02864827	0.05710318	0.16924000	-0.02845492	-0.14059174
0.02562050	0.05696398	0.16924000	-0.03134347	-0.14361950

Table 2. Statistical summary for

10^{5}

independent variable pairs with 8 categories and N=1000.

Table 2. Statistical summary for

10^{5}

independent variable pairs with 8 categories and N=1000.

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.02480604	0.05363642	0.16924000	-0.02883038	-0.14443397
median	0.02450248	0.05409550	0.16924000	-0.02908602	-0.14473752
$σ$	0.00503776	0.00237667	0.00000000	0.00520181	0.00503776
max	0.04983589	0.05785563	0.16924000	-0.00333894	-0.11940411

Table 3. Statistical summary for

10^{5}

independent variable pairs with 4 categories and N=1000.

Table 3. Statistical summary for

10^{5}

independent variable pairs with 4 categories and N=1000.

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.00457969	0.02989537	0.03108490	-0.02531568	-0.02650521
median	0.00425591	0.03029054	0.03108490	-0.02564577	-0.02682899
$σ$	0.00214034	0.00153177	0.00000000	0.00258117	0.00214034
max	0.01933179	0.03173017	0.03108490	-0.01002770	-0.01175311

Table 5. Statistical summary for

10^{5}

independent variable pairs with 2 categories and

N = 10000

Table 5. Statistical summary for

10^{5}

independent variable pairs with 2 categories and

N = 10000

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.00004980	0.00212434	0.00046052	-0.00207455	-0.00041072
median	0.00002275	0.00215681	0.00046052	-0.00210780	-0.00043777
$σ$	0.00007025	0.00008392	0.00000000	0.00010969	0.00007025
max	0.00092597	0.00218569	0.00046052	-0.00113677	0.00046545

Table 6. Statistical summary for

10^{5}

independent 4-variate pairs with

N = 10000

Table 6. Statistical summary for

10^{5}

independent 4-variate pairs with

N = 10000

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.00045291	0.00391531	0.00414465	-0.00346240	-0.00369174
median	0.00042035	0.00395117	0.00414465	-0.00349716	-0.00372430
$σ$	0.00021309	0.00014345	0.00000000	0.00025671	0.00021309
max	0.00198022	0.00409401	0.00414465	-0.00179072	-0.00216443

Table 7. Statistical summary for

10^{5}

independent 8-variate pairs with

N = 10000

Table 7. Statistical summary for

10^{5}

independent 8-variate pairs with

N = 10000

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.00247550	0.00722180	0.02256533	-0.00474630	-0.02008983
median	0.00244186	0.00725890	0.02256533	-0.00478098	-0.02012347
$σ$	0.00049640	0.00021950	0.00000000	0.00054044	0.00049640
max	0.00532519	0.00762947	0.02256533	-0.00136958	-0.01724014

Table 8. Statistical summary for

10^{5}

pairs of 16-variate independent variables with

N = 10^{4}

Table 8. Statistical summary for

10^{5}

pairs of 16-variate independent variables with

N = 10^{4}

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.01140676	0.01327543	0.10361633	-0.00186866	-0.09220957
median	0.01137637	0.01331589	0.10361633	-0.00189549	-0.09223996
$σ$	0.00109037	0.00032421	0.00000000	0.00110517	0.00109037
max	0.01673620	0.01408294	0.10361633	0.00326571	-0.08688013

Table 9. Statistical summary for

10^{5}

pairs of 16-variate independent variables with

N = 10^{5}

Table 9. Statistical summary for

10^{5}

pairs of 16-variate independent variables with

N = 10^{5}

	$Δ H$	$- μ$	$- Δ c$	$Δ S$	$Δ M D L$
mean	0.00112990	0.00174350	0.01295204	-0.00061361	-0.01182214
median	0.00112681	0.00174529	0.01295204	-0.00061679	-0.01182523
$σ$	0.00010648	0.00001485	0.00000000	0.00010760	0.00010648
max	0.00166940	0.00177954	0.01295204	-0.00006718	-0.01128264

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Minimum Uncertainty as Bayesian Network Model Selection Principle

Abstract

1. Introduction

2. Methods: Numerical satisfiability and sampling resolution in independence criteria.

3. Results

3.1. Numerical verification and the sensitivity profile.

3.2. Application to the structural biology of tRNA molecules: Sample size invariance study.

4. Discussion and Conclusions

Supplementary Materials

Author Contributions

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe