Preprint
Article
On the Mass of the Nucleons from "First Principles"
Altmetrics
Downloads
221
Views
223
Comments
1
This version is not peer-reviewed
Submitted:
14 July 2023
Posted:
17 July 2023
You are already at the latest version
Alerts
Abstract
The mass of the nucleons is calculated from first principles by defining the quark as a non-gravitational particle, subject to Dirac’s equation with non-canonical gamma matrices. Unlike the canonical electron-type, this Dirac particle has two real dipole moments, which allows a structural modelling of hadrons. It is shown how such modelling reveals striking correspondences and differences between dually related particles and properties like electrons and quarks, photons and gluons, pions and nucleons, spin and isospin and protons and neutrons. It is a stepping stone to the actual calculation, which competes in precision with lattice QCD. The appendix contains a Lorentz covariance proof of hadrons composed by such particular Dirac-type quarks.
Keywords:
Subject: Physical Sciences - Nuclear and High Energy Physics
1. Introduction
One of the issues in particle physics is the challenge to calculate the masses of hadrons “from first principles” or “ab initio”. It is commonly taken for granted that lattice QCD is the best way, if not the only one, to do so. The calculation of the proton mass is usually considered as a decisive proof of its capabilities. However, although the quark is considered as the ultimate building block of observable nuclear particles, lattice QCD is unable to use the attributes of quarks as the true reference for “ab initio”, for the simple reason that a quark escapes from observability. For that reason, the real reference values for lattice QCD are the masses of the pion and the kaon. Although these mesons are not observable either, their masses can be measured as a result from their fermionic decay products. The lattice QCD quark model is subsequently used as a means to establish the relevant quark attributes for the calculation “from first principles”. Several groups have claimed results from calculations on protons and other hadrons that are close to experimental results [1,2]. However, results from theory can still not compete in precision with results from experiments. Up to now, lattice QCD is unable to calculate the mass difference between a proton and a neutron. Moreover, the retrieved masses for the and the quark can only be established as an average over the two and lattice QCD calculations for the mass difference between a charged pion and a neutral pion are still missing. The lattice QCD calculations require highly-intensive computations. The results have to be believed on the reputation of the reporting scientists without any means for verification by the reader. It is my aim in this article to show that a more simple approach is capable to address these problems more adequately than lattice QCD can do. This will require, though, giving a motivation for choosing a different route. Similarly as in lattice QCD, the basic elements in this route are the quark and the gluon. And more particularly, their interrelationship, which will culminate into the statement that the quark-gluon relationship is the nuclear equivalent of the electromagnetic electron-photon relationship. This will require more precise definitions of the quark and the gluon than available in present theory. Before addressing the actual calculations, a review on the differences and correspondences between a quark and an electron will be instructive, as well as the differences and correspondences between a gluon and a photon (paragraphs 2 and 3). Next to those from spin-spin interactions (paragraph 5), their impact will be shown on other dualities, like pion and nucleon (paragraph 4), quark and topquark (paragraph 6), spin and isospin (paragraph 7), proton and neutron (paragraph 8). Prior to the discussion and conclusions (paragraph 9), the results of the mass calculations on nucleons are compared with those reported from lattice QCD.
2. The electron and the quark
Like all elementary fermions, electrons and quarks follow Fermi-Dirac statistics, obey the Pauli exclusion principle, have half integer spin and have distinct antiparticles. They can be modelled with the Dirac equation. The canonic formulation of Dirac’s particle equation reads as [3,4],
in which is a 4 x 4 unity matrix and in which the 4 x 4 gamma matrices have different properties for electrons and quarks.
For electrons,
while for quarks [5,8],
(For convenience, in Appendix A this quark model is shown once more). In both cases Dirac’s Equation (1) is satisfied by the spinor,
in which is the three-vector momentum and in which W is an energy relationship between the particle’s rest mass and its motional energy. For electrons,
while for quarks,
It has to be emphasized here (and derived in Appendix A once more), that the quark is different from a tachyon, because it maintains a real energy under subluminal conditions as long as .
Note: It may seem that Dirac’s Equation (1) under the constraints (3) is not Lorentz invariant, because of the violation of the invariance of the space-time interval if W is equated with the Einsteinean energy E. This invariance is a basic theorem in Einstein’s Relativity theory. Let us take into consideration, though, that this theorem applies to gravitational objects, in which energy is conceived as the sum of massive energy embodied in the rest mass and the kinetic energy of an object. Prior to Dirac’s relativistic electron theory, the concept of negative energy has been considered as a violation of physical principles. After all, it was realized that the concept of negative energy did not violate the Einsteinean space-time invariance. Dirac himself proved the Lorentz covariance of his electron theory. But…if a particle with negative energy is physically viable, why would a particle that eats its kinetic energy from its rest mass not physically viable? It requires to identify such a particle as being different from a gravitational object and to redefine the space-time interval variance for such particles. As shown in Appendix B, such a non-gravitational object in confinement with another one is compliant with the Lorentz covariance.
The electron as well as the quark is a pointlike source of non-baryonic energy that erupts a scalar field of non-baryonic energy to which an identical other electron or quark couples with a dimensionless coupling factor g.The fields are characterized by a Lagrangian density with the generic format
in which is the potential energy of an energetic background field and in which is the source term. If the background energy and the source are known, a spatial expression for can be found as the solution of a field equation obtained from the Lagrangian density after application of the Euler-Lagange equation. If the source is a scalar pointlike source in empty space, in which is zero, the result is the Coulomb field,
If the source is a scalar pointlike source in a background field that consists of polarizable dipoles, such that
the field equation is akin to the inhomogeneous Helmholtz equation [6], which for a pointlike source shows the solution
This is the shielded field from a charged particle in ionic plasma, known as the Debije effect [7].
Dirac’s Hamiltonian analysis on his spinor equation has revealed that a pointlike source is more than a pointlike scalar. His analysis has shown that a pointlike particle is subject to elementary virtual motions that show up in an intrinsic angular momentum with magnitude ℏ and in an intrinsic vibration momentum with magnitude . This means that the pointlike source is equipped with two dipoles. In the case of electrons, subject to gamma constraints (2), the former one shows up as the well known anomalous magnetic dipole moment, while the latter one remains hidden as the imaginary anomalous electric dipole moment . This is different for a quark. Unlike an electron, the quark, subject to the gamma constraints (3), shows two real dipole moments [8,9]. This is proven once more in Appendix C. Hence, in qualitative terms, the potential field of a quark along the axis of the polarisable dipole, can be expressed as,
in which (with dimension is a measure for the range of the nuclear potential, in which (in units of energy, i.e. joule) is a measure for the quark’s “charge”, and in which w is a dimensionless weigh factor that relates the strength of the monopole field to the dipole field. Because of the limited range of nuclear force, there must be a Debije-type energetic background field, such that the field decays as . As shown in [5], the similar result can be derived from the Lagrangian (7) in which the background field has the format,
thereby establishing and relating the two parameters and of the background field with the parameters and in the spatial expression of the quark’s potential.
For real values of and ,(12) is a broken field that is zero for
known as the vacuum expectation value. The field (12) is known as the Higgs field, which in the standard model has been adopted by axiom with a rather artificial interpretation [10]. Like discussed in this text, it can be explained in terms of the quark’s intrinsic vibration momentum in conjunction with a Debije-type background field.
3. The photon and the gluon
Similarly as the (fermionic) electron, the quark is a source of bosons. From an inspection of (11) it is obvious the quark field consists of a far field next to a near field. Whereas the far field is due to the quark’s monopole properties, the near field is due to its dipole properties. The far field has the same properties as an electric charge in an energetic background field as described by (9). Applying the action principle on the Lagrangian (7) yields a Proca-type wave equation,
in which is a Dirac-type pointlike source that can be expressed as,
in which and , respectively, are Heaviside’s step function and Dirac’s delta function. Figure 1 shows the solution of this wave function in a graphical format. The upper part shows the field building up to the eventual steady state shape. The lower part shows the transient pulse. This transient pulse is the nuclear equivalent of a gamma photon. Unlike a gamma photon, this equivalent is subject to dispersion. The dispersion is due to the term in the Proca wave Equation (14). This term is a consequence of the energetic ambient field, known as the Higgs field. Whereas a photon can be seen as a component of a gamma photon, a gluon can be seen as a component of a “gamma gluon”.
4. The pion and the nucleon
Conceiving the pion as a structure in which a quark couples to the field of the antiquark by the generic quantum mechanical coupling factor g, the pion can be modeled as the one-body equivalent of a two-body oscillator, described by the equation for its wave function . In its center of mass, this wave equation is the non-relativistic approximation of the Dirac spinor Equation (1). For its time-independent part, we may write [5],
in which is the quark’s scalar field as derived before and eventually expressed by (11), 2 d the quark spacing, the reduced mass that embodies the two massive contributions from the constituting quarks, its potential energy, and E the generic energy constant, which is subject to quantization. It will be clear from (16) that the potential energy can be expanded as,
in which and are dimensionless coefficients that depend on the spacing 2d between the quarks. To facilitate the analysis, (16) is normalized as,
in which
and
Invoking previous work [11, eq. (24)] we get for
This relationship is not trivial. As discussed in Appendix D once more, it has been derived by a general relativistic analysis, thereby connecting particle physics with gravity and showing the conversion of nuclear energy into baryonic mass.
The two quarks in the meson settle in a state of minimum energy, at a spacing such that [11,12],
Figure 2 shows the structural pion configuration.The archetype meson, the pion, is the two-quark oscillator in its ground state. The first excitation state transforms a pion into a kaon. The mass ratio between the two is the same as the mass ratio of the normalized energy constants . This is not trivial and it reflects the basic theorem of the theory. This theorem states that the energy wells of the two quarks are not massive. Instead, the mass attribute of two-quark junctions (mesons) and three-quark junctions (baryons) is made up by the vibration energy as expressed by the energy state of the quantum mechanical oscillator that they build. The distribution of this mass over constituent quarks is a consequence of this mechanism. Unfortunately, an analytical calculation of the ratio of kaons over pions, is only possible for the quadratic approximation of the series expansion of the potential energy . A more accurate calculation requires a numerical approach. A procedure to do so has been documented in [11, Appendix C]. It shows that some simple lines of code in Wolfram’s Mathematica [13] may do the job. The numerically calculated ratio of the energy constants appears to be 3.57 instead of 3 as it would have been in the harmonic case. The result explains the excitation of the 137 MeV/ pion mass to the 490 MeV/ mass of the pseudoscalar kaon. This result gives a substantial support for the viability of the theory as developed in previous work.
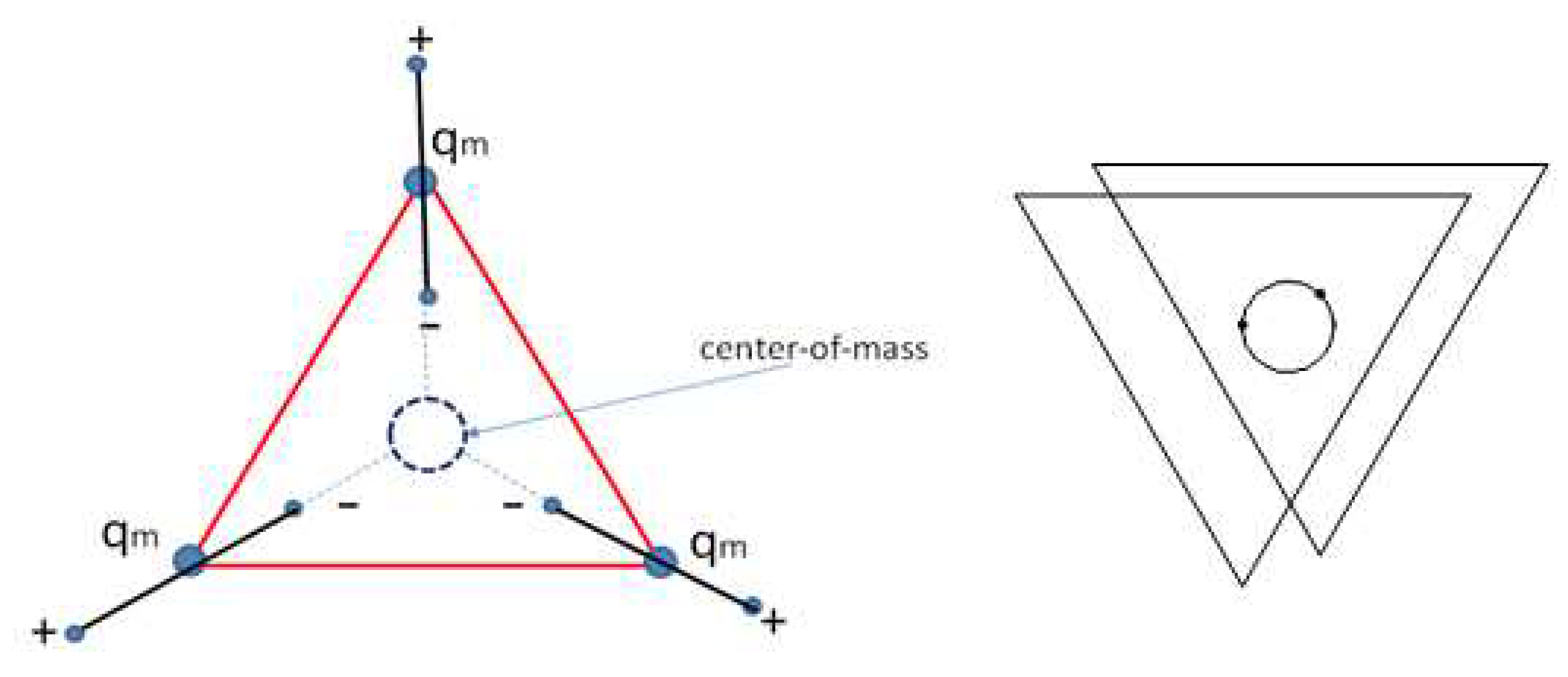
Figure 2.
A quark has two real dipole moments, hence two dipoles. One of these (horizontally visualized) is polarisable in a scalar potential field. The other one (vertically visualized) is not.. The polarity of the horizontal one is restrained by the bond: the horizontal dipoles are only oriented in the same direction: either inward to the centre or outward from the centre. The orientation of the dipole moments is unrelated from their isospin status.
Figure 2.
A quark has two real dipole moments, hence two dipoles. One of these (horizontally visualized) is polarisable in a scalar potential field. The other one (vertically visualized) is not.. The polarity of the horizontal one is restrained by the bond: the horizontal dipoles are only oriented in the same direction: either inward to the centre or outward from the centre. The orientation of the dipole moments is unrelated from their isospin status.
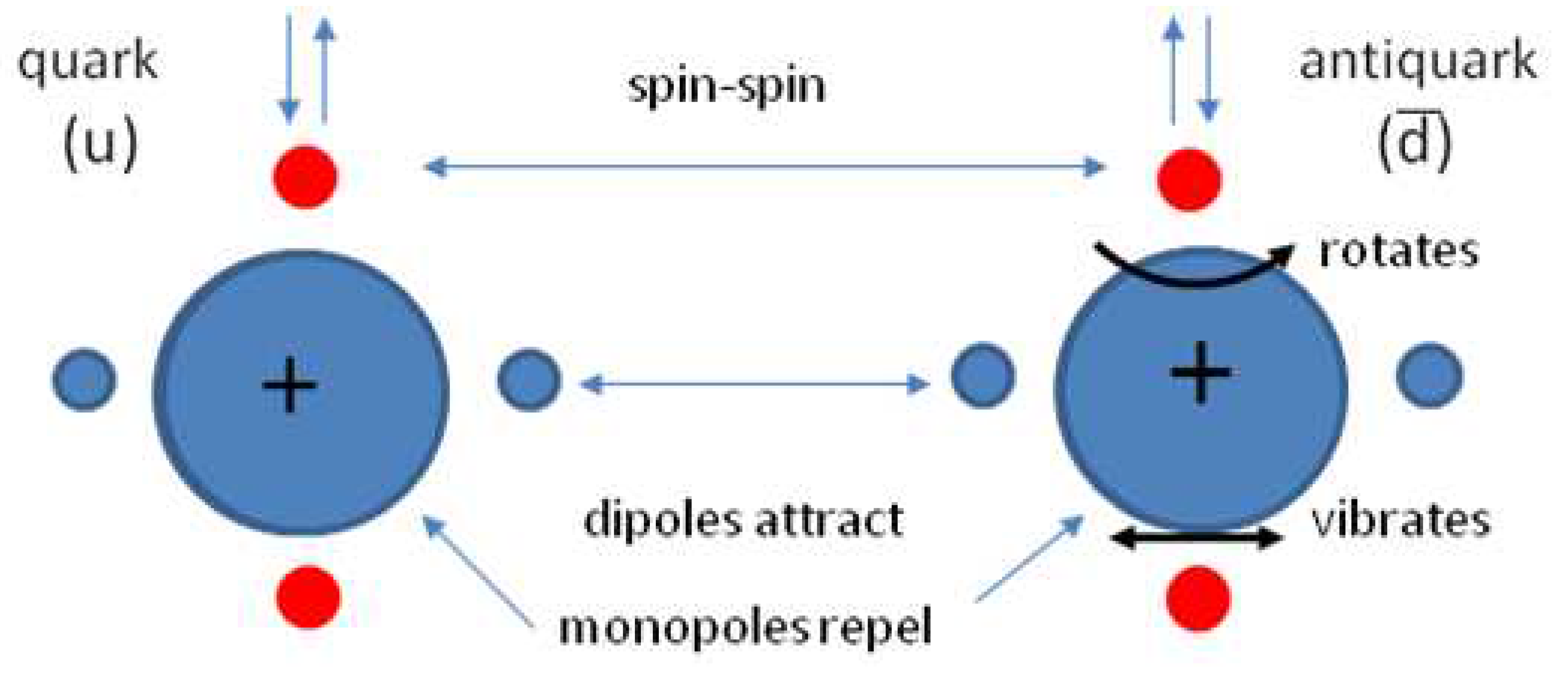
What about the nucleon? Figure 3 shows its basic configuration. It illustrates that the monopole fields of the quarks are balancing the fields of the polarisable dipole moments. Whereas a meson can be conceived as the one-body equivalent of a two-body harmonic oscillator, a baryon can be conceived as the one-body equivalent of a three-body harmonic oscillator. The one-body equivalent of the three-body quantum mechanical oscillator can be analyzed in terms of pseudo-spherical Smith Whitten coordinates [14]. The Smith-Whitten system of coordinates is six-dimensional. Next to a (hyper)radius , the square of which is the sum of the squared spacings between the three bodies, there are five angles in which and model the changes of shape of the triangular structure and in which and are the Euler angles. The latter ones define the orientation of the body plane in 3D-space. The planar forces between three identical interacting bodies not only are the cause of dynamic deformations of the equilateral structure, but also are the cause of a Coriolis effect that result in vibra-rotations around the principal axes of inertia of the three-body structure [15].
Figure 3.
Left: the basic baryon structure as a harmonic oscillator. The polarisable dipole moments balance the fields of the monopoles. The vibra-rotations of the monopoles have an equivalent in the behavior of the center-of-mass. Right: illustration of the frame spin of the baryon
Figure 3.
Left: the basic baryon structure as a harmonic oscillator. The polarisable dipole moments balance the fields of the monopoles. The vibra-rotations of the monopoles have an equivalent in the behavior of the center-of-mass. Right: illustration of the frame spin of the baryon
The application of this approach for baryons has been documented by the author in [16], showing that the wave equation of the quasi-equilateral baryon structure can be formulated as
in which,
and
This wave equation is the three-body equivalent of the pion’s two-body wave equation shown in (18). In the ground state we have . Hence,
The radial variable is the already mentioned hyper radius. The potential field is just the threefold of the potential field in the wave equation of the pion. There are three quantum numbers involved. Two of those are left in the ground state, effectively bundled to a single one. The quantum number k allows a visual interpretation, while v is difficult to visualize. The impact of k is shown in the right hand part of Figure 3. It illustrates the motion of the center of mass under influence of k . Note that this rotation is quite different from a rotation of the triangular frame around the center of mass. It is the center of mass itself that rotates, while the frame does not. Actually, the small motions of the individual quarks are responsible for this motion.
5. Spin-spin interactions
The simple anharmonic oscillator model described by (16-18) enables the mass spectrum calculation of the pseudoscalar mesons as excitations from the pion state. The excitation mechanism stops beyond the bottom quark due to the loss of binding energy. The mass spectrum calculation of the vector mesons requires the inclusion of the impact of the particle spin shown in the upper part of Figure 2. A spin flip marks the difference between the pseudoscalar pion and the vector type sisters rho. The massive energy difference between the two types is a consequence of a spin-spin interaction process. It is of a similar nature as the interaction process between the spin of electron and the spin of the proton nucleus in a hydrogen atom. Recognizing, though, that this is essentially a bosonic process, allows, in retrospect, a surprising simple approach. The step to be taken is conceiving the massive energy difference as a result of a bosonic interaction mediated by Z bosons in virtual state. Because of the asymmetry in the spin-spin interaction ( and ), we have,
in which and are the energies of, respectively, the rest masses of pion and the rho meson, the constituent massive energy of the quark and the energy of the Z boson in virtual state in the rest frame of mesons. The statement that the energy of the rest mass of the pion is equal to the non-relativistic equivalent of the energy of the W boson enables to calculate the energy of the boson in virtual state as,
Under use of (23) and (24), the constituent rest mass energy of the quark is calculated as
Under consideration of the rest mass of the pion 140 MeV/ and the energy values of the weak interaction bosons 80.4 GeV and 91.2 GeV, the energy of the constituent mass of the quark is calculated from (25) as 308 MeV. Under use of this value, the energy of the rho meson is calculated from (23) as 775 MeV. This is a perfect fit with experimental evidence!
We may go a step further by conceiving the spin-spin interaction energy as an add-on to the monopole interaction energy between the quarks. Doing so as described in Griffith’s textbook, but now supported by theory rather than by empirics, we may compose a mass table for the light sector as shown in Table 2. The constituent mass value for the s quark can now be calculated from the excitation result for the kaon as shown in Table 1 and the spin-spin interaction result as shown in Table 2 as,
Figure 4 is a graphical representation of Table 2. It has to be emphasized that the constituent masses of the quarks in the mesons don’t represent the (bare) inertial masses. The constituent masses represent the massive equivalent of the lab frame value of the meson energy distributed over the quarks. Doing the same for baryons, the constituent masses of the quarks in the baryon may show different values. Similarly as in the case of mesons, the baryon mass is the result of the monopole interaction energies between the constituent quarks corrected by spin-spin interaction energy carried by the Z boson in virtual state. This allows to compose the mass table for baryons in the light sector, like shown in Table 3, as derived in [16]. Similarly as with mesons, the application of the one-body anharmonic oscillator model for now the three-quark structure as shown in (21) enables the assessment of quantitative values for the baryonic constituent masses by theory instead of doing so by an empirical numerical fit on measured mass values. To do so, the energy ratio between the ground state value and the first (orbital) excitation () is calculated from (21) by the numerical model documented in [15]. This ratio happens to be
Figure 4.
Illustration of the excitation mechanism of mesons and the scaling mechanism of quarks in the light sector.
Figure 4.
Illustration of the excitation mechanism of mesons and the scaling mechanism of quarks in the light sector.
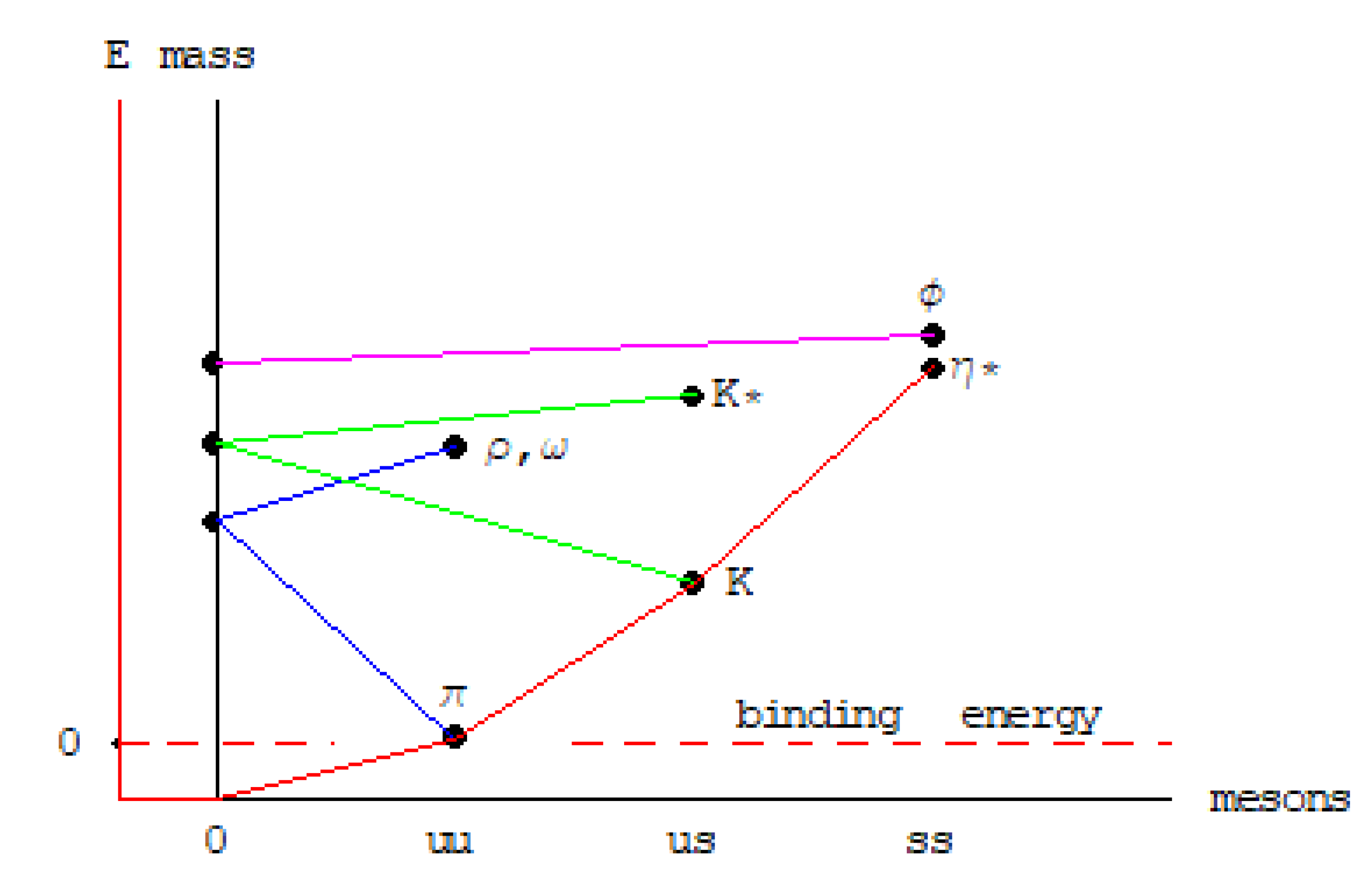
Figure 5.
Illustration of the excitation mechanism of baryons in the light sector. The dots on the vertical axis represent the baryonic constituent masses values 3u, 2u +s, 2s + u, 3s.
Figure 5.
Illustration of the excitation mechanism of baryons in the light sector. The dots on the vertical axis represent the baryonic constituent masses values 3u, 2u +s, 2s + u, 3s.
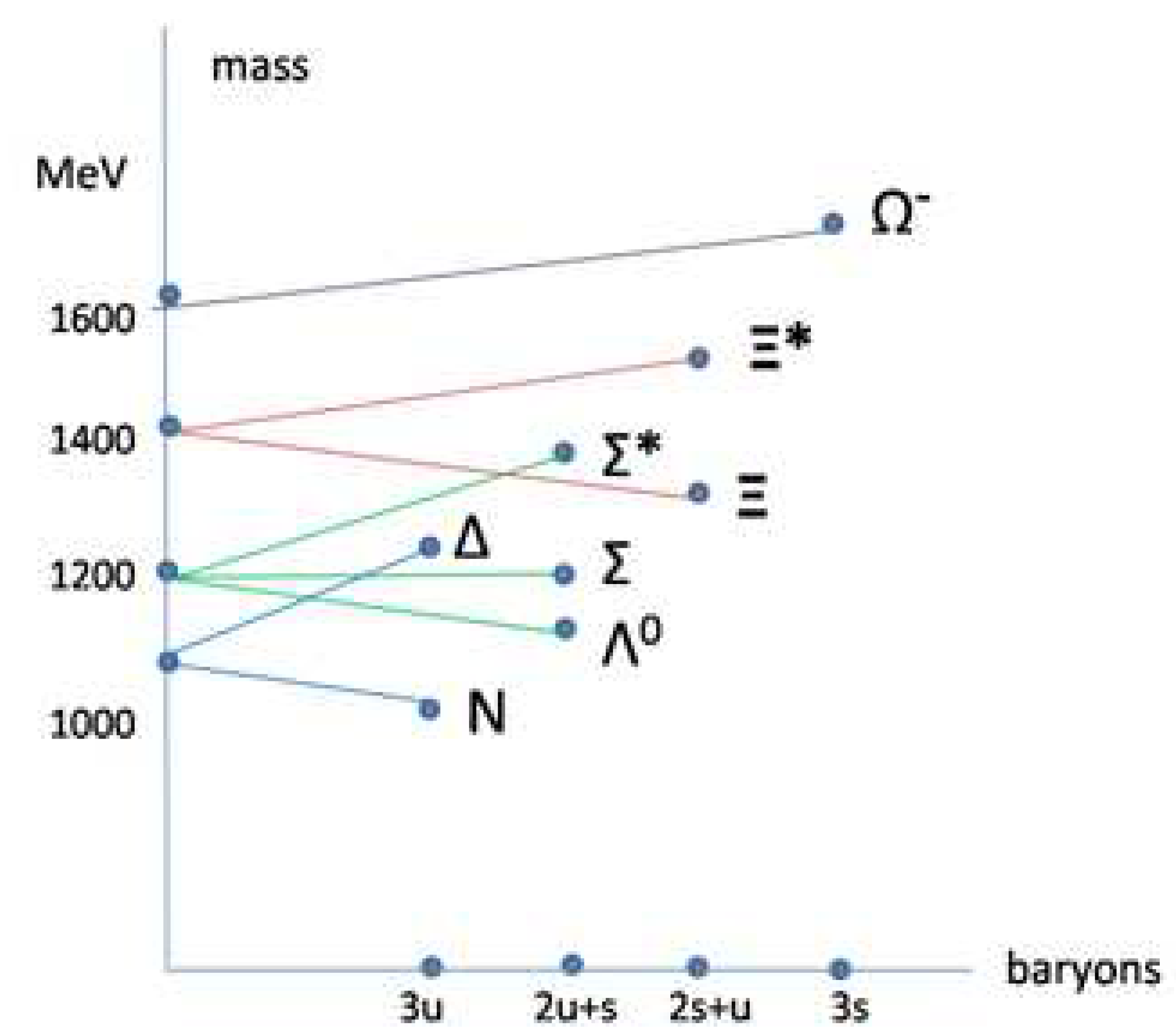
Table 1.
Meson excitation.
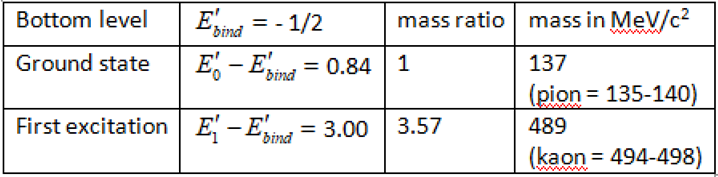
Table 2.
Mass formulae for mesons in the light sector.
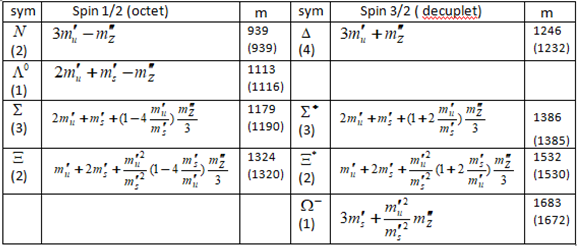
Table 3.
Mass formulae for baryons in the light sector.
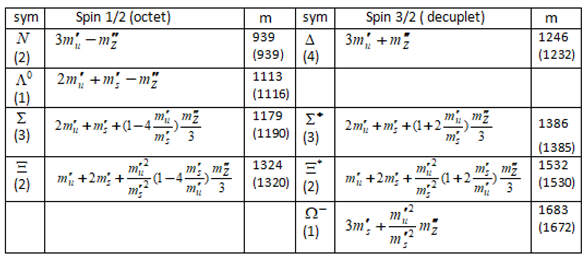
This ratio happens to be quite accurately the mass ratio of the nucleon in ground state (938.3 and 939.6 MeV/) over the baryon in excited orbital state (1882.7, 1383.7 and 1387.2 MeV/). It shows a similar accuracy as the mass ratio calculation from the pion state into kaon state. (Why the nucleon excites to instead of is not obvious, though). It gives an anchor point for the mass calculations shown in Table 3. The major one, however, is the calculation of the nucleon mass. Let us proceed by considering that in absence of spin-spin interaction, the excited three baryon would be equivalent with the ground state of a three baryon. Hence,
In the actual situation of spin-spin interaction, however, the baryon ground state, excites under the same ratio into the state. Hence,
From (28) and (29),
Moreover, from (24),
From (30) and (31) the nucleon mass as shown in Table 3 can be related with the mass of the pion as,
This expression relates the nucleon mass with the mass of the pion. It is not clear whether the neutral pion mass should be taken as reference or the mass of the charged pion. With the neutral pion mass ( 135 MeV) and the weak interaction bosons 80.4 GeV) and 91.2 GeV), the nucleon mass is calculated from (32) as 939 MeV/. It means that the mass value of the nucleon can be derived from the pion’s rest mass as reference.
6. The quark and the topquark
As stated in the previous paragraph and proven in [5], the excitation mechanism associated with simple anharmonic oscillator model described by (16-18) stops beyond the bottom quark due to the loss of binding energy. Nevertheless, there happens to be a topquark. Curiously however, the assigned rest mass of the topquark is out of scale. But if the topquark would be the constituent of the boson, its existence can be well understood. This is possible by invoking the relationship (23). expressing that the pion’s massive energy is built up by those from two archetype quarks, under a correction from Z bosons in virtual state. This result has been obtained by transforming the result found in the pion’s center-of-mass frame to the lab frame, under the recognition that the weak interaction massive energy is the relativistic equivalent of . Transforming back to the relativistic level, we have
in which is the relativistic value of the rest mass energy of the quark. Under consideration of 80.4 GeV for the W boson and 91.2 GeV for the Z boson, the result is 177 GeV. And this is just near to the energy of the topquark, found in 1995 [19], after an intensive search for the missing quark in the third generation predicted in 1973 [20]. The interpretation of (33), though, implies that the topquark is not the sixth member in the quark hierarchy, but, instead, the relativistic (at the pion’s speed) appearance of the quark. If so, it should have an isospin sister. Hence, the production of neutral and pairs from colliding beams of high-energy protons and antiprotons may result in the creation of charged pseudo-scalar topquark mesons. This view enables to conceive (charged) bosons as topquark mesons without violating the interpretation of the jets produced in topquark generating experiments. This means that the topquark should not be considered as the isospin sister of the bottom quark like taken for granted in the Standard Model.
The view just explained is not without problems, though. Whereas the non-relativistic equivalent (33) is rather precise in explaining the mass difference between the pion and its vector-type counterpart, the relativistic equivalent is somewhat less precise. Curiously, the difference of 4 GeV with the (172 +/- 0.3) GeV PDG value is just the same as the mass of a bottom quark. In the author’s view, the discrepancy is due to the interpretation of the topquark mass by retrieval from the associated decay paths, like illustrated in Figure 6.
The left-hand part of the figure shows the conventional model of the topquark generation and its decay path. It decays conventionally into a breal quark and via a weak interaction boson into high-energetic quarks as sources of hadronic jets. The weak interaction boson shown is not a meson, because it is not composed by a quark and an antiquark. At the right side the alternative representation, in which the weak interaction boson is conceived as a meson. Similarly as in the conventional representation, the output from the weak interaction boson are high-energetic quarks as sources of hadronic jets. The dual output may assume an energetic equivalent leptonic output. This means that the jets may either be full hadronic, mixed hadronic/leptonic or full leptonic with branch ratio probability of, respectively, 46%, 44% and 10%. [21]. It is probably not bold to suggest that the generation of topquarks and its decay into high energetic quarks can be viewed as the manifestation of a confinement break process. The figure shows a semantic difference between the topquark t as conceived in the Standard Model and the top quarks and as conceived in the context of this article. The experimental mass assessment from the final decay products, imposes the following relationship
in which are the masses of the theoretically assessed 177 GeV/, the constituent mass of the quark (4.18 +/-0.4 GeV/) and the empirically 172.8 +/-0.4GeV/ Standard Model topquark. This gives a perfect fit! This result is yet another proof for the viability of the views exposed in this article.
7. Spin aand isospin
While the particle spin-spin interaction has a significant impact on the mass attribute of mesons and baryons, it has no impact on the charge attribute. Charge is determined by the quark’s isospin. In the standard model of particle physics, this isospin is an axiomatic property of the quark without a known physical interpretation. Because it has similar properties as particle spin and because particle spin is related with the quark’s intrinsic (anomalous) angular dipole moment , one may expect that isospin is related with the quark’s (anomalous) intrinsic linear dipole moment . As discussed in paragraph 2, this property has remained unknown up to its description in 2021 [8,9]. However, whereas the particle spin state allows a direct interpretation as the spatial orientation of the intrinsic angular dipole moment, the spatial orientation of the intrinsic linear dipole moment is structurally bound. This seems to prevent the statistical freedom of isospin in the case of a one-to-one relationship between linear dipole moment and isospin. The relationship is however not as simple as that, because of another issue in this context, namely the not yet considered phenomenon that the particle spin-spin interaction as discussed in the previous paragraph is an equivalent of the Maxwellian spin-spin interaction between the spins of the electron and the proton in atomic Hydrogen. It is therefore a logic step to adhere Maxwellian properties to a quark. A straightforward way to do so is to conceive the quark as a Maxwellian magnetic monopole with a real electric dipole moment and a real magnetic dipole moment. This real magnetic dipole moment reveals the presence of an elementary pointlike amount of electric charge associated with the magnetic quark monopole. If so, the spin of this electric kernel may either belong to negative or to a positive electric kernel. This ambiguity is equivalent to assigning the (iso)spin status to the linear dipole moment. It is tempting to see this as a revival of Schwingers’s suggestion from 1969 that a quark is a dyon, i.e., both an electric monopole and a magnetic monopole [17]. However, whereas Schwinger proposed his dyon to explain the (quasi) stable hadron structures from a balance between an attracting magnetic force and a repelling electric force (or vice versa), the balance in the structure shown in Figure 2 is obtained by the balance between the monopole field and the field evoked by the polarizable dipole moment under a scalar potential. Electric charge pops up as a minor side effect, hence not as a gluing force. This marks a fundamental difference between Schwinger’s dyon (abandoned and replaced by QCD) and the structure shown in Figure 2.
8. The proton and the neutron
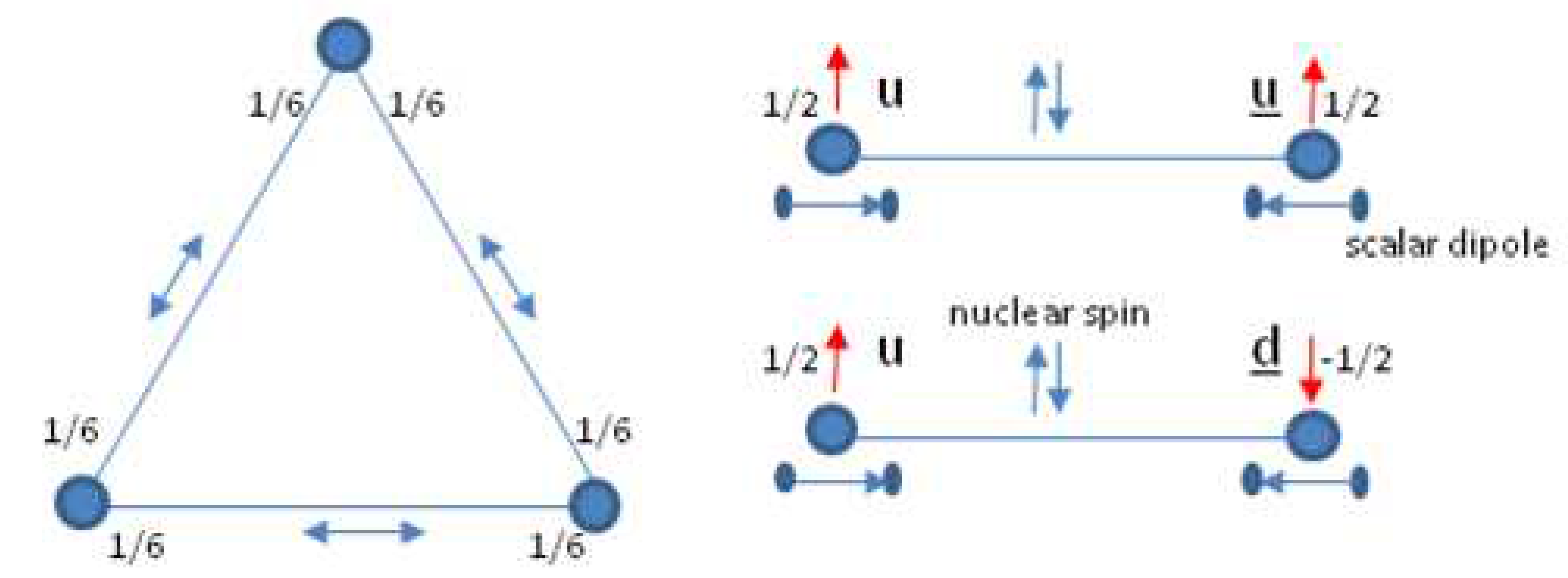
An intriguing problem in particle physics theory is the one how to explain the mass difference between a charged pion and a neutral pion on the one hand and the mass difference between the charged nucleon (proton) and the neutral nucleon on the other hand. It is too simple pointing to a difference in “running” mass between an u quark and a d quark, if such a difference would exist. Lattice QCD is unable to prove a mass difference between a u quark and a d quark, because it is only the average mass over the two that can be retrieved. Therefore, the differentiation between the mass values is hypothesized on the basis of their (supposed) charge difference. Accepting the difference would make the neutron (with two d and one u ) heavier than the proton (with two u and one d ). This, however, cannot explain why a charged pion (with two d and one u) is heavier than a neutral pion (with two u and one d). Before discussing this difference, let us first discuss the mass difference between the proton and the neutron. Under the acceptance of the existence of a second dipole moment next to the angular related one, the structural representation of baryons is shown by Figure 7. As discussed in the previous paragraph, the quarks in this picture have isospin statistics that are independent from the structural orientation their dipoles. By associating electric charge with isospin and considering the interaction between the electric charges along the peripheral axes a net amount of electric charge will cause a tiny increase of the baryon’s (hyper)radius . As a consequence, the energetic state of the baryon is reduced. It makes a charged baryon lighter than a neutral baryon. Although this phenomenon introduces some asymmetry in the symmetrical structure shown in Figure 3, the Smith Whitten model allows to model asymmetrical effects as an equivalent symmetrical one. This consideration allows to distribute the charge of the proton uniformly along the axes of the structure, like shown in the left-hand part of Figure 7.
The pion case is illustrated in the right-hand part. Here, the difference between the charged pion and the neutral pion is modeled by a distribution (+e/2, +e/2) for a charged pion. Unlike as in the representation for baryons, the picture shows a spin arrow associated with the charge. This is to symbolize the spin-spin interaction between isospins. Electric interaction at extreme short spacing is more than Coulombian. Electric charge kernels evoked by the quark’s second dipoles have their own (magnetic) spin, which can be seen as the manifestation of isospin. These spins interact. At extreme short spacing the interaction energy involved is larger than the Coulombian interaction energy. In charged pions, the isospins are parallel. This explains why charged pions are in a state of energy higher than neutral pions in spite of the opposite effect due to Coulombian interaction. A calculation of its quantitative effect can be found in [5]. It is beyond the scope of this article.
Although this isopin interaction effect is present in the baryon as well, the net effect of it is the same for protons and neutrons (their isospin sum is the same). Being interested in the mass difference between protons and neutrons only, there is no need for further elaboration on the isospin interaction. Let us model the impact of the electrical interaction instead. Concluding that the electromagnetic interaction increases the interaction strength of the far field of a quark, we may write for the latter,
in which is the far field part of the quark’s potential (11) and in which p is a measure for the effectiveness of the electric interaction force along the axes of the baryon. Under adoption of the symmetrical charge distribution as shown in Figure 6, we have 1/36. Let us rewrite (35) in terms of the electromagnetic fine structure relationship,
in which is the well-known fine structure constant . Hence, from (36) and (35), the far field potential can now be written after including the influence of the electric interaction as,
Now, the potential of the field built up by the quarks with inclusion of an electrical potential can be written as,
It is not difficult to modify the numerical procedure of the anharmonic oscillator accordingly, Doing so, we find
This corresponds with a mass difference of (1.00144 – 1) 936 = 1.35 MeV/. It is slightly above the known experimentally established value of 1.29 MeV/. It is closer than the 1.51 MeV/ value obtained by lattice QCD [2], which is built up as a QED correction of about 1 MeV/ on the retrieved masses of the quark (2.3 MeV/) and the quark (4.8 MeV/) [1,2]. Curiously, whereas in present canonical theory the masses are no longer be expressed in terms of constituent masses, it is still the case for the other quark flavors [1]. Within the view on quarks as presented in this article a retrieval of quark masses from the reference rest masses of the pion and the kaon is not required. Instead, it is based upon the theoretical view exposed in previous work [5], in which the charge asymmetry between the quark and the quark is challenged.
9. Discussion and conclusions
It has already been concluded at the end of paragraphs 5 and 8 that the capabilities to calculate the masses of the nucleons and the mass difference between a proton and a neutron on the basis of a rather simple structural model have a similar accuracy as those claimed from lattice QCD. This article is a summary, application and extension of previous work [5,8,9,11,12,16]. In [22], it has been summarized and put in a historic perspective. It is based upon a somewhat different view on quarks as compared to canonical theory. In this view the quark is a non-gravitational particle without baryonic mass that sources a nuclear field capable to bind other quarks in mesons and baryons, which behave as quantum mechanical oscillators in a state of baryonic energy. The quark is a Dirac particle, but in an unrecognized mode. This mode allows to interpret isospin as the physical manifestation of an anomalous real second dipole moment. This second dipole moment (which has an imaginary value in electron-type Dirac particles) enables to give hadrons a clear structural interpretation as a substitute for the axiomatically conceived electroweak GWS model (Glashow, Weinberg, Salam). The article is a rebuttal to opponents who have put the Lorentz invariance of the novel Dirac particle mode into doubt and who doubted about the capability to calculate the masses of nucleons from the same reference values as lattice QCD may do.
Data Availability Statement
The numerical data quoted in this article have been generated from rather simple computer programs written in Wolfram’s Mathemica [13]. The computer code can be made available on request.
Appendix A. Dirac particles with a polarisable dipole moment in a scalar potential field
The canonical set of gamma matrices in Dirac’s equation is given by,
The calculation of the excess energy of an electron in motion subject to a vector potential , gives [5,8],
in which is the Pauli vector, defined as
in which are the spatial unit vectors and in which and are generic field vectors (i.e. not necessarily of electromagnetic nature if e is a generic coupling factor) derived from the vector potential. The matrices are state variables with a real eigenvalue , such that the intrinsic angular momentum (associated with ) can be conceived as a spin vector with eigenvalue . Next to the intrinsic angular momentum , a second intrinsic pseudo vector (associated with ) can be identified with eigenvalue . In terms of these two dipole moments, eq. (2) can be written as,
The electron has a real first dipole moment (), known as the magnetic dipole moment, and an imaginary second dipole moment .The latter is one of the two anomalies of Dirac’s theory, pointed out by himself. He noticed a negative energy solution next to a positive energy solution. And he noticed a real magnetic moment next to an imaginary electrical dipole moment. About the first item he remarked that that the problem would disappear if the electron would change its polarity, but that “this is a phenomenon not yet observed”. About the second item he remarked that he doubted about the physical meaning of an imaginary electrical dipole moment. Curiously, like proven in [8] and its update [9] and shown once more in Appendix C, a different set of matrices may turn the imaginary electrical dipole moment into a real one. To show this modality, let us start from the canonic format of Dirac’s equation as captured by,
It can be rewritten after division by , in terms of wave function operators as,
in which with
and in which is the 4 x 4 identity matrix. Note that the variables are signed by ‘ to emphasize their normalization on . Note also that the temporal parameter is written as proper time to emphasize the (special) relativistic nature of Dirac’s equation in free space. Rewriting (1) in the Weyl format gives,
in which is the Pauli vector with the three Pauli matrices.
As known, Dirac’s equation is based upon a heuristic elaboration of the Einsteinean energy expression under use of particular properties of the matrices. These properties can be summarized as,
in which is the last matrix term in (8). The very same properties are met if (9) is modified into,
Note that the is modified from the 4 x 4 identity matrix into the imaginary value of the “fifth” gamma matrix . The two representations (8) and (10) are equivalent. Both represent the common electron-type Dirac particle with a real magnetic dipole moment and an imaginary electric dipole moment. If would have been modified into the real value of , we would have obtained the tachyon format, which reads as,
This tachyon format is studied in the context of the hypothetical existence of superluminal particles [18]. It violates constraint (9). Instead it meets,
Note the subtle difference between (9) and (12). The dipole moments of the tachyon are similar to those of the electron-type: the equivalent magnetic one is real and the equivalent electric one is imaginary.
Both dipole moments are real for a third modification of Dirac’s particle [8,9]. This modification reads as,
As compared with the electron-type (11), the matrix is imaginary and the matrix is real. It meets the constraints
To understand the violations of the constraints (9) and the modifications into (12) and (14), it is instructive to solve the various formats (10), (11) and (13) of Dirac’s equation. In full expansion mode, (13) reads as
and written differently,
Let
Applying (17) on (16) gives after some elaboration,
This homogeneous set of equations has the solution (17) indeed under the constraint of the determinant value
The canonical equations (8) or (10) show the same solution (17), but, different from (19), under the constraint,
The tachyon Equation (11) shows solution (17) for
For a meaningful wave function, and , hence W and , must be real. Hence, let us consider the condition (19) more closely. It can be rewritten as,
The condition for the momentum evolves as,
Hence,
The similar elaboration for the tachyon format results into,
The tachyon format shows real values for W and under superluminal conditions. It is a reason for speculations on the potential existence of superluminal particles. It is not meaningful under subluminal conditions, because the real values turn into imaginary ones. The properties of the “quark-type" format, though, as shown by (23,24) are real under subluminal conditions. The real value of its second dipole moment makes it of interest.
Appendix B. Lorentz invariance of a non-gravitational object
Whereas a gravitational object is subject to the Einsteinean energy expression,
the quark, as a non-gravitational object, is subject to
Defining
the Einsteinean energy expression (1) is conveniently expressed as,
which is equivalent with,
Note: is proper time.
Transforming this property to a different space-time frame, related by the Lorentz transform
we get, after substitution of (6) into (5),
Note that is different from proper time . This result (7) has the same format as (4). It proves the Lorentz covariance of the Einsteinean energy expression. In a similar view on the non-gravitational object (2),
which is equivalent with,
Transforming under the Lorentz transform gives
It is clear that the last term of the left hand part of (10) violates the Lorentz covariance. This seems being a show stopper for the existence of a non gravitational particle with the property shown in (2), as required for the existence of quarks with two real dipole moments. It is known however that quarks in isolation don’t exist, such as formalized in the confinement axiom. Taking this into consideration, it might be that the Lorentz violating term in (10) disappears for two and three quarks in conjunction. The structural meson (an)harmonic oscillator model, shown in Figure 2, demonstrates that the two quarks vibrate in opposite direction under a stationary position of their center-of-mass. Hence, showing opposite signs for . Consequently, the Lorentz violation of one of the quarks is cancelled by the opposite Lorentz violation of the other quark. This makes mesons composed by quarks with two real dipole moments Lorentz covariant in spite of the Lorentz covariance violation of quarks in isolation.
Appendix C. Dirac’s two anomalous dipole moments
The aim in this appendix is to show the correspondence as well as the difference between Dirac particles of the electron type and Dirac particles of the quark type. Basically, it is a refreshment of Dirac’s analysis that resulted into the conclusion that Dirac particles, possess two anomalous dipole moments, both purely quantum mechanical in nature. In this analysis, the original matrices will be invoked that Dirac defined in his classic paper. It all starts from two energy expression of a generic free moving particle with rest mass . For the electron type, it reads as,
while for the quark type,
in which is the three-vector momentum (, not to be confused with the fourvector momentum ).
Let us define, respectively
and normalize as,
As long as the temporal dimension is included, the bold italic notation for the vector will be maintained. Under particular number typing of a coefficient vector , eq. (3) can be rewritten as
This reflects the energy relationship (3) under the conditions for respectively, the electron type and the quark type,
This condition can be met if a coefficient vector is constructed from and for electrons and for quarks, with the canonical gamma matrices supplemented by the identity matrix
Hence,
in which,
and
Obviously, , because of (8,9). This remains so for a particle moving under influence of a conservative field of forces with a (generic) field potential . As before, is signed for indicating the normalization by . The field influence can be accounted for by,
The triviality disappears if the momenta are transformed into wave operators, like Dirac did by adopting the basic transform of quantum electrodynamics (QED),
Note for electrons and for quarks. As a consequence of the QED transform (15) and the minimum substitution rule (14), together known as the gauge covariant transform, the first term in (13) transforms as,
Note that quite some terms have disappeared because of , see (8,9) and, more importantly now, because of the sequence sensitivity of the operator action. Applying this on all terms of (13), the result is,
which can be rewritten as,
Regrouping under consideration of (8,9) gives,
Hence, from (19) and (15) for electrons,
while for quarks,
Elementary matrix multiplications reveal the following identities,
It can be written in terms of the grad operator, the curl operator and Dirac’s Pauli vector as
for electrons, while for quarks
Full expansion in terms of 4 x 4 matrices, gives
in which is the Pauli vector, defined as . Hence, for electrons and for quarks, respectively,
Note that still is a dimensionless quantity. It is the now non-zero excess energy term in expression (13) as a consequence of the particular characteristics of Dirac’s equation of motion. Hence for electrons and quarks, respectively,
in which v is the velocity of the particle in motion. As long as and the excess energy can be approximated in both cases as,
in which is given by (27,28). We are almost done, but not quite. So far, the Dirac particle has been considered in general terms, i.e., without identifying it as an electron or as a quark. To do so, a first step to do so is defining the four-vector potential for electrons and quarks, respectively, as
Note: The i factor in the scalar component for electrons is due to the metric (+,+,+,+) / (ict,x,y,z), used for electrons. It can be easily seen from the Lorenz gauge
Note also that in (32,33) the dimension of is energy. It is not the same as the electric potential .The relationship between the two can be found from the force equivalence,
From the Lorenz gauge and (35) obviously,
Hence, from (27), (36) and (31), for electrons and quarks, respectively,
Appendix D. The role of Einstein’s geodesic equation
Considering that two quarks may compose a stable structure under the balance of the scalar part of their monopole fields and the fields from their scalar dipole moments allows to describe the energy in their geometric center in terms of Einstein’s stress-energy tensor. This will allow to derive a geodesic equation for its center of equivalent baryonic mass. Because this equation is an equation of motion, it can be transformed into a wave equation. This can be done under application of the basic quantum mechanical theorem in which momenta are transformed into operators on a wave function. This approach has been described in earlier work [12] and has resulted into the derivation of a numerically verifiable expression for the gravitation constant in quantum mechanical parameters, thereby showing a bridge between gravity and quantum mechanics. Unfortunately, so far this work has not gained the momentum that it deserves. This appendix is meant to show its impact on the view as exposed in this article. In particular it is meant will serve to prove the validity of the relationship
as invoked in eq. (19) of the main text, which wouldn’t possible otherwise. To do so, three equations are needed. Two of those can be captured immediately from the harmonic oscillator description as described from eqs. (16,17) of the main text. The first of these says that the harmonic quantum mechanical oscillator characterized by quantum steps related with the effective mass , such that
Conventionally, represents is the central mass of the oscillator. In the non-relativistic center-of-mass model described in chapter 4, it does not represent the individual masses of the two bodies, but, like stated before, it is an equivalent mass that captures the energy of the field. As usual, is related with the vibration energy . Considering that the pion decays into a fermion via the weak interaction boson, it makes sense to equate the boson with the weak interaction boson. Hence,
The third equation is the more fundamental one. It reads as,
Its derivation is a rather tedious one, based upon the theorem stated above that a wave equation for fermions derived from Einstein’s geodesic equation must be equivalent with Dirac’s equation. The proof of (4) can be found in previous work [12]. Fortunately, this result can be physically readily understood. The harmonic oscillator model described by eqs. (16,17) of the main text shows a binding force to the amount of , with . The pion, as represented by this model decays via the weak interaction boson into the muon. Obviously, this binding energy represents the ground state energy of the harmonic oscillator, while represents the relativistic energy of the pion’s rest mass .
Some trivial algebraic on (2,3,4) reveals,
References
- S. Hashimoto, J. Laiho, S.R. Sharpe, Lattice Quantum Chromodynamics, pdg.libl.gov, rpp2020-rev-lattce-qcd (2020).
- Sz. Borsanyi et al., Ab initio calculation of the neutron-proton mass difference, Science 347, 6229 (2014).
- P.A.M. Dirac, The quantum theory of the electron, Proc.R. Soc. Lond. A 117 (778), 610 (1928).
- J.D. Bjorken, S.D, Drell, Relativistic Quantum Mechanics, McGraw-Hill Book , New York (1964).
- E. Roza, On the quark scaling theorem and the polarisable dipole moment of the quark in a scalar field. Available online: https://www.preprints.org/manuscript/202006.0304/v4.
- Encyclopedia of Mathematics, EMS Press, 2001 [1994].
- Debye, P., Hückel, E.: Zur Theorie der Elektrolyte, Physik. Zeitschrift, 24 (9), 185 (1923).
- E. Roza,. On the second dipole moment of Dirac’s particle, Found. Phys. 50, 829 (2020).
- E. Roza. Available online: https://www.preprints.org/manuscript/202002.0275/v3.
- D. Griffiths, Introduction to Elementary Particles, ISBN 3527406018, Wiley (2008).
- E. Roza, The H-type quark and the mass of mesons, Phys. Essays, 25, 2 (2012).
- E. Roza, The gravitational constant as a quantum mechanical expression, Results in Phys., 6, 149 (2016).
- Wolfram, S.: Mathematica (Addison-Wesley Publishing Inc. Redwood City, Ca (1991).
- Whitten, R.C., Smith, F.T.: Symmetric Representation for Three-Body Problems. II. Motion in Space, J. Math. Phys. 9, 1103 (1968).
- Bartlett, P., Howard, B.J.: The rotational-vibrational spectrum of symmetric non-rigid triatomics in hyperspherical coordinates: the H+ 3 molecule Molecular Physics, Vol. 70, No. 6, 1001 (1990).
- Roza, E., The H-type quark and the baryons, Phys. Essays, 27, 3, 390 (2014).
- J. Schwinger, A Magnetic Model of Matter, Science 165, 3895 (1969).
- U.D. Jentschura, Dirac Hamiltonian with imaginary mass and induced helicity-dependence by indefinite metric, Journ. Modern Phys, vol. 3, issue 9, 887 (2012).
- Abe, F.; et al. (CDF Collaboration) (1995). "Observation of top quark production in pp collisions with the Collider-Detector at Fermilab". Physical Review Letters. 74 (14), 2626 (1995).
- Abachi, S.; et al. (DØ Collaboration) (1995). Observation of the Top Quark. Physical Review Letters. 74 (14): 2632 (1995).
- Cortiana, G.: Top-quark measurements: Review and perspectives, Rev. In Phys., 1, 60 (2016).
- Roza,E.: From black body radiation to gravity, J. Phys. Astron. 11 (5), 342 (2023).
Figure 1.
The building of the quark’s potential far field as a result of a sudden energy eruption from its source. The field is the sum of the steady state solution shown at the right and the transient pulse shown in the lower part of the figure. This pulse is a “gamma gluon”. It propagates at light speed and it eventually disappears as a result of dispersion. If is zero, the transient is a never disappearing gamma photon and the stationary situation is shown by an unfinished rectangular shape of the upper most right graph. Note that the field is represented by
Figure 1.
The building of the quark’s potential far field as a result of a sudden energy eruption from its source. The field is the sum of the steady state solution shown at the right and the transient pulse shown in the lower part of the figure. This pulse is a “gamma gluon”. It propagates at light speed and it eventually disappears as a result of dispersion. If is zero, the transient is a never disappearing gamma photon and the stationary situation is shown by an unfinished rectangular shape of the upper most right graph. Note that the field is represented by
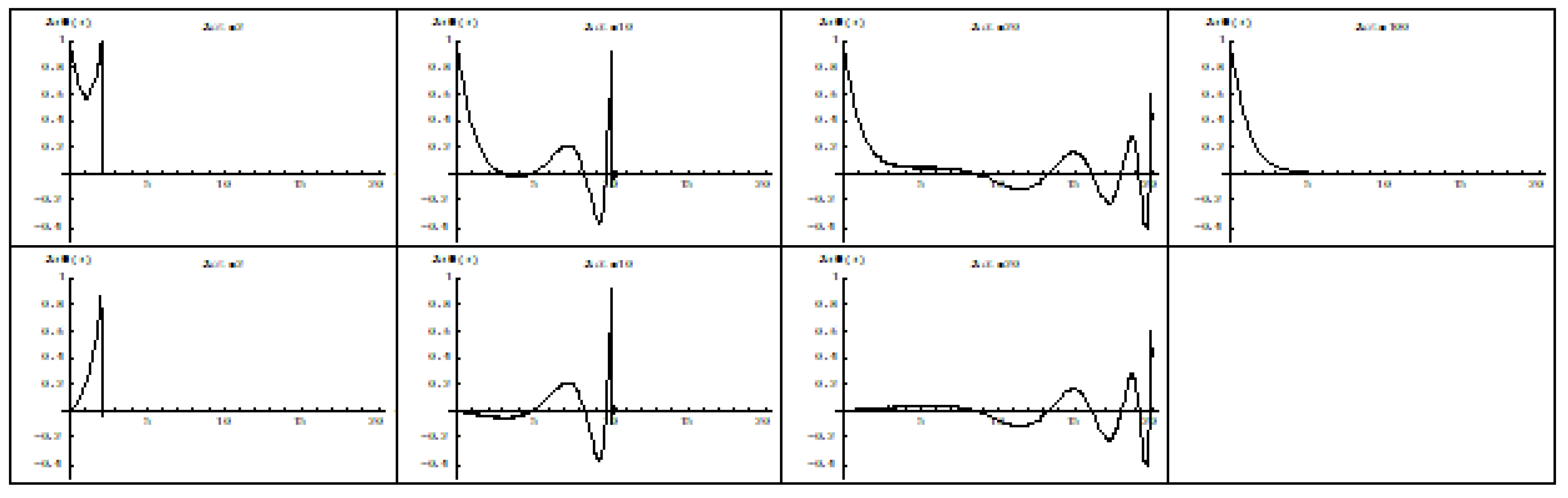
Figure 6.
Topquark generation from colliding proton anti-proton beams and subsequent decay. Left: conform the Standard Model. Right: conform the structural model.
Figure 6.
Topquark generation from colliding proton anti-proton beams and subsequent decay. Left: conform the Standard Model. Right: conform the structural model.
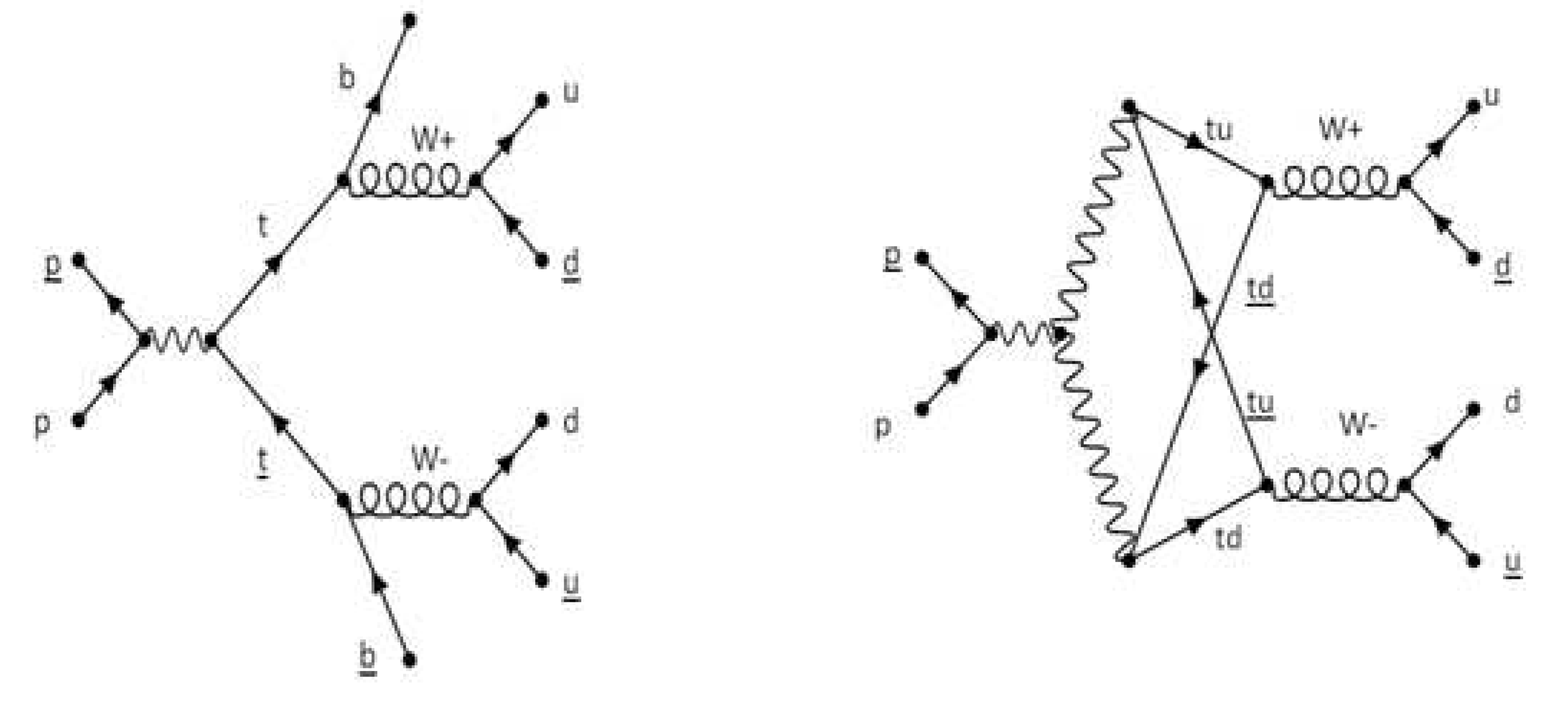
Figure 7.
The left-hand part shows the proton’s structural model with equal charge distribution along the axes. The upper part at the right shows the model for the charged pion, the lower part shows the model for the neutral pion. The nuclear dipoles are shown as up/down arrows in the middle, the second dipoles are shown as horizontal arrows. These latter dipoles evoke kernels of electric charge with their own (iso)spin. In parallel condition ( ) their spin-spin interaction increases the energetic state of the pion by an amount larger than the increase of electric interaction as present in the neutral pion.
Figure 7.
The left-hand part shows the proton’s structural model with equal charge distribution along the axes. The upper part at the right shows the model for the charged pion, the lower part shows the model for the neutral pion. The nuclear dipoles are shown as up/down arrows in the middle, the second dipoles are shown as horizontal arrows. These latter dipoles evoke kernels of electric charge with their own (iso)spin. In parallel condition ( ) their spin-spin interaction increases the energetic state of the pion by an amount larger than the increase of electric interaction as present in the neutral pion.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






