The weak principle of equivalence, which Einstein specifically laid down in his general theory of relativity, identifies the passive gravitational mass with the inertial mass, and these masses are identified with the active gravitational mass of matter [1]. The energy of the mass is determined according to the special theory of relativity and is equal to the energy of the inertial mass. This was the basis for introducing the hydrodynamic tensor $T_i^j=(c^2\rho +p)u^j{u}_i-{\delta }_i^{j}p$ with density $\rho$ and pressure p of an adiabatic fluid without friction as a source of matter gravity in the field equations. In [2,3], it is stated that the identification of the inertial and active gravitational masses is wrong, and the energy-momentum tensor $T_i^j$ must be determined by the density of the active gravitational mass and the potential of the scalar field. In the present work, the active gravitational mass of a rarefied cloud of relativistic material particles has been obtained based on properties of Lorentz transformations and Schwarzschild space-time geometry.

We study a weakly gravitating gas cloud consisting of identical particles with a rest mass m chaotically moving with the same absolute value of velocity v in a certain frame of reference $K^{\prime }=(t^{\prime },x^{\prime },y^{\prime },z^{\prime })$. It is assumed that at time $t^{\prime }=0$ the distances $\delta r$ between particles can be neglected to determine the gravity created by this cloud in the considered area. The rarefaction of the gas is determined by the condition where ${\alpha }_M=\frac{2\gamma M}{c^2}$ with cloud gravitational mass M and gravitational constant $\gamma$.

Statistically, the cloud can be represented as a set of systems consisting of two particles A and B, which move in opposite directions. The weak gravitational field of one particle is described approximately [4] in associated coordinates $K=(t,x,y,z)$ by linearised isotropic Schwarzschild metric with $r=\sqrt{x^2+y^2+z^2}$ and $\alpha =\frac{2\gamma m}{c^2}$.

Condition (1) means that the distortions of length and time caused by the presence of the Lorentz factor $\frac{1}{\sqrt{1-{\tilde{\beta }}^2}}$ with $\tilde{\beta }=\frac{\tilde{v}}{c}$ will be an order of magnitude greater than curvature of space-time by gravity. Therefore, the influence of gravity on the Lorentz transformations at or is insignificant and they can be applied to the metric (2). Transformation of coordinates with yields

In associated with bodies reference frames $K_A$, $K_B$ the gravity of each of them separately is described by the metric (2). Let us pass from these coordinate systems to $K^{\prime }$, using the Lorentz transformations for velocities (4), (5).

If we represent metric coefficients in the form where ${\eta }_{ij}$ correspond to the Minkovsky metric, then with weak gravity, [5] the ratio is performed for the total field created by n subsystems with metric coefficients Summing the fields obtained after substitutions of velocities (4) and (5) into the metric (7), we find approximate path interval in the vicinity of $t^{\prime }=0$ in a two-body system at ${\alpha }_1=2\alpha$ and $\beta =\frac{v}{c}$.

The equations of geodesics with Christoffel symbols ${\Gamma }_{ij}^l=\frac{1}{2}{g}^{lk}\left(\frac{\partial g_{jk}}{\partial x^i}+\frac{\partial g_{ik}}{\partial x^j}-\frac{\partial g_{ij}}{\partial x^k}\right)$ are used to search for the acceleration of a test material particle in described by metric (11) gravitational field. For spatial coordinates of particle at rest they turn out to be with indices $k=2,3,4$. These equations yield coordinate accelerations disregarding small quantities of a larger order.

The absolute value of acceleration imparted to the test particle by the two-body system will be provided that the size of the system is insignificant compared to the distance to the test particle. In spherical coordinate frame $(t^{\prime },r^{\prime },\phi ,\theta )$ defined by transformations we obtain Acceleration $a^{\prime }$ is caused by the gravitational mass

For each pair of particles, the direction of the axes of the coordinate system is chosen so that the axis $X^{\prime }$ is parallel to the line of their motion. 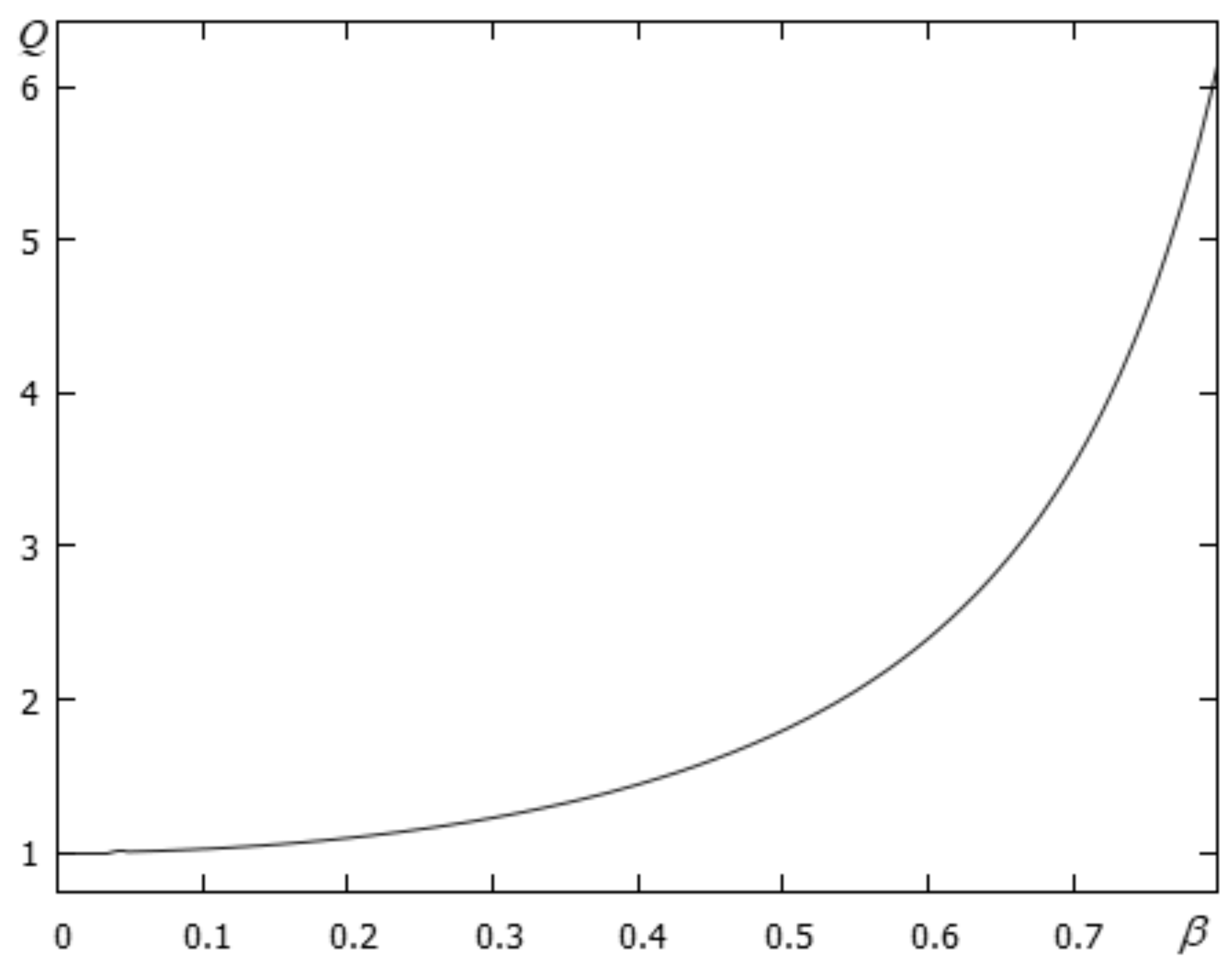Assuming a uniform distribution of the directions of their motion over the corners, the average gravitational mass of a pair of particles in the gas cloud will be It determines the gravitational mass of a cloud consisting of n particles where $E\left(\beta \right)$ is complete elliptic integral of the 2nd kind. Figure 1 shows how the ratio $Q=\frac{M}{nm}$ changes with increasing particles velocity.

The fallacy of assumption about the equality of the inertial and active gravitational masses follows from the analysis of a system of two bodies moving towards each other. The resulting gravitational mass of the gas cloud does not confirm concept of the mass density included in the hydrodynamic tensor, which is taken as the density of the source of gravity.