Prerpints.org logo
Preprint
Article

Light Dispersion in Gravitational Field

Altmetrics

Downloads

486

Views

1001

Comments

1

supplementary.pdf (129.76KB )

Yin Zhu  *

This version is not peer-reviewed

Submitted:

31 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
In any region of a space, the gravitational field cannot be eliminated. The speed of light in a vacuum has never been observed and cannot be observed with current technology. Till now, only the speed of light in a gravitational field has been observed. It results in that all the observed speed of light are always being varied by the gravity. Here, it is presented that light could be dispersion in a gravitational field analogous to the dispersion of light in the Newtonian prism experiment. The relativistic mass density on the surface of a neutron star is on the level of 1017kg/m3 while on the surface of the Earth is only 10-7kg/m3, the effect of the gravitational field acting on the speed of light by a neutron star is much larger than that by the Earth. Therefore, the dispersion of light in strong gravitational field could be generally observed from the image of a star and it should have been observed through the double-image gravitational lensing and the spectroscopic binary system. And, it should affect the observed numbers, spectrogram, size and distance of the celestial objects.
Keywords: 
Subject: Physical Sciences  -   Particle and Field Physics

 

In the Maxwell equations, the speed of light is expressed as
c = 1 ε 0 μ 0
ε0 and μ0 are the electric constant and magnetic constant in a vacuum. Partly for the Maxwell equations and partly for Einstein’s theory of relativity, in current physics, a very special role has been given to the speed of light from 1900s. It is believed, in the vacuum, the speed of light is a constant c = 3 × 108m/s which is the fastest speed in the universe. But, now, it was observed that the mass density of the gravitational field on the surface of the neutron star can be larger than the density of the neutron star which is almost 1017kgm−3 [1]. It is clearly unsuitable to treat a space filled with a field with a relativistic mass density of 1017kgm−3 as a vacuum. And, now, we cannot make the gravitational field eliminated from a space. So, we cannot have a vacuum which is radically “empty”. No vacuum does exist in our real world. Therefore, the speed of light need be understood with that it is always being acted by a gravitational field. The neutron stars can bend the light emitted on their far side around towards the front of the star [2]. The motion of a light in a super strong gravitational field is radically different from that in a weak field. Therefore, the action of the strong gravitational field on the speed of light need be studied to better understand the speed of light. The speed of light in gravitational field has been studied for a long time [3–6]. The conclusions are different from each other. Some of the conclusions is that the gravitational field could make the speed (or group/phase velocity) of light larger than the speed of light in a vacuum while other is less. Here, it is presented that light should be dispersion in gravitational field. And, the action of the centripetal force of the field on the speed of light is discussed.

1. Result

Dispersion of light in general medium was well studied. The speed of light in the medium can be written as
c n = 1 ε r μ r
Where, c is the speed of light measured on the Earth, n is the refractive index, ε r  and μ r  are the electric constant and magnetic constant in a medium. Here, c is also called the speed of light in a vacuum. The current concept of vacuum is presented by Torricelli in 1643 [7]. In this vacuum, the gravitational field is not eliminated. From the Newton’s prism  experiment, we know, for a material with a certain ε r  and μ r , the refractive indexes n  are different for the light ray with different wave length.
By analogy to other medium, it could be assumed that the electric constant and magnetic constant are different in the gravitational fields with different field strength. Therefore, Equation (1) could be rewritten as
c l = 1 ε l μ l
Where, l  indexes the location. It means that for the location around the Earth, the speed of light is c = 1 ε 0 μ 0 = 3 × 10 8 m / s  while around a neutron star, the ε l  and μ l  are different which results in that the speed of light is no longer c = 1 ε 0 μ 0 = 3 × 10 8 m / s .
Diffraction is produced from the property of wave, including sound wave, electromagnetic radiation, and small moving particles [8]. The Huygens’ principle [9] told us that as a plane wave is propagated from one medium into another one, this wave is refracted for that there is a time delay between different sides of the wavefront. Therefore, refraction of light is due to the wave propagation. As a light enters a strong gravitational field from a vacuum or a weak field, the Huygens’ principle shall certainly function. A refraction could be produced in this process. In addition, a gravitational field can make light redshift and bent. It clearly shows that the motion of a light is changed as it enters a new gravitational field.
Dispersion of light had been studied for a long history [10]. Cauchy, Briot, Hartmann, Corady and Sellmeier presented the formula for the dispersion. It showed that, for a given material, the refraction index is only determined with the wavelength of the light.
Therefore, dispersion of light in a gravitational field is such a result that only is produced by the property of wave propagation which can be well understood with classic physics.
The dispersion in gravitational field could be observed from the image of a star with a strong field. For convenience, here, only the simplest case that the light ray is vertical to the surface of the medium is studied. In the case, there is not refraction for the light. As the light emitted by a star is running through the gravitational field of the star, under the condition that the field is uniform, the light cannot be refracted by the field.
It is well known, for a star with a distance L relative to the observer, this star at the present position p and at the present time t cannot be observed for that a time t − t ′ = L / c  is needed for the light running from the star to the observer. It only can be observed at the retarded time t ′ = t − L / c  and at the retarded position which, at the retarded time, the star is at. Therefore, the observed image of the star is that the star is at the retarded position and at retarded time.
In a medium, the speed of light is determined with c λ = c n λ , where λ  is the wavelength of the light. Because of dispersion, for the speed of the light with different wavelength, the retarded time is determined with
t λ = n λ L / c
In Equation (4), n λ  is with different value. Therefore, under the condition of dispersion, there shall be two (or more) retarded positions for a star as shown in the Figure 1.
The distance S between two retarded positions p1 and p2 is determined with
S = v ( n λ 1 − n λ 2 ) L / c
From Figure 1 we know, observed on the Earth, the image of a star is directly determined with S. As S > 2 r , (where, r is the radius of the star,) a star shall appear two images in different colors as shown in Figure 2A. As S < 2 r , the image of a spherical star appears as a dumbbell in two colors as shown in Figure 2B.
If light is dispersive in gravitational field, it can have been generally observed. The first evidence for the dispersion of light in gravitational field is the double(multi-)-image gravitational lensing. Now, a large number of double-(multi-)image gravitational lensing was observed [11]. The two conditions are needed to form double-image in a gravitational lensing system. 1) There are two light curves. 2) There are different speeds and refractive angles for the two curves. The two conditions can just be produced from the dispersion of light in gravitational field. As a light ray is running through a strong field, it is being bent by the field. In the same time, it is being dispersed into two light curves with different speed and different refractive angle. It is emphasized, if a light ray could not be split into two rays, the double images could not be formed. In 1995, Pelt and coworkers [12] presented that the double-image in gravitational lensing system is originated from two different light curves. The time delay between the two light curves is determined with that one of the light curves is shifted by the dispersion spectra. They explained the time delay of QSO of 0957+561. With Pelt and coworkers’ conclusion, Burud and coworkers [13] explained the gravitationally lensed double QSO B1600+434. Therefore, although Pelt and coworkers [12,13] did not think that this dispersion spectra is related with the gravitational field, they used the key point in the concept of the dispersion of light in gravitational field: two light curves is shifted by dispersion spectra. Their description is almost as that described with our Figures 1 and 2 although the physical reason of the dispersion spectra in their work is different. It is shown that the dispersion of light in gravitational field is needed to wholly understand the double images in a gravitational lensing system.
In recent, it was observed that the observed size of the image of a galaxy is a function of the wavelength of the light 14,15]. It directly shows that the observed size and distance of a celestial object is affected by the wavelength of the light. A method is presented that the distance of extragalactic can be measured with “the time lag between variations in the short wavelength and long wavelength light from an active galactic nucleus” [16]. It should imply that, light dispersion in gravitational field is very important to have an accurate measured result. (Please reference the Supplementary material A.)
The second evidence for our conclusion should be the spectroscopic binary star. A spectroscopic binary is a star system that can only be seen as more than one star by looking at its spectrum; through a telescope, no matter what we do or how good our equipment is, it will always look like one star. It is highly accordant with the conclusion as described in the Figure 2A. Although it is thought that there are two stars in a spectroscopic binary system, it has not been excluded that it is a system that a star appears two images. We know, the binary stars have been well observed. But, it was presented that the Poincaré’s equation of Three-Body problem is invalid [17]. (The evidence is clear: the orbits of the Sun-Earth-Moon are absolutely stable. But, in the Poincaré’s equation, these orbits are chaotic.) It was also shown that the current theory of binary star is questioned. Therefore, further observation and study about the spectroscopic binary system is needed. Factually, the spectroscopic binary system is being studied [18,19]. Here, we found that, as shown in the Figure 3, a star in the retarded positions can completely appear a spectroscopic binary system. Here, it is emphasized that, any binary system is always orbiting around a large center but the large center is usually omitted [17]. And, it is noted that the retarded positions in the Figure 3 can be combined into many cases.
Third, the images of black hole [20,21] may be a possible evidence for the Figure 2B. Two features of the images of the black hole should be accordant with the Figure 2B. First, the images of the black hole are asymmetrical, or they are elongated. From Figure 1 and Equation (5) we know, as the band of the spectrum of a star is wider, the image of the star is longer. Second, the wavelengths of the light are different at different part of the image. 2B shows that the asymmetry is produced from the difference of the wavelength. Generally, Figure 2B is suitable to the celestial body with large radius and less distance L. It could be concluded that the observed image of a star is not always a sphere.
From Equation (5), assuming n λ 1 − n λ 2  is a constant, the image of a star is determined with L and v as shown in Figure 4.
In Equation (5), n λ 1 − n λ 2  can be treated as a constant and usually there is v < 10 3 k m / s . Therefore, in Figure 4, the distance L is the main factor to the observed result. The distance between two observed images can be very large as L is very large.
Figures 1–4 indicates that the spectroscopic binary system could be easily confirmed. (1) A large distance L is needed for the spectroscopic binary system. (2) As L is larger, the distance S between two spectroscopic binary stars is larger. (3) Each image of the spectroscopic binary in the Figure 2 is with a unique wavelength. (4) The spectroscopic binary has a same orbit around another center mass.
The possible forth evidence is very important but need further observation. Figures 2 and 4 indicate that, as L is larger, the spectra of the observed image of a star is less. In the very distant place, from Figure 2 we know, a star with several spectra should appear several images in which each image is with one unique spectrum. It means that the observed image of star in the very distant place is with only one spectrum and the numbers of the observed images of one star are usually large than one. Therefore, our conclusion could be further confirmed with the relationship between the spectrum of star and the distance L. But, form Equation (4) we know, the speed of the star and the difference of the refractive indexes n λ 1 − n λ 2  also have an effect on the spectrum. It is noted that, although n λ 1 − n λ 2  was treated as a constant in the above, n λ  is greatly different for different field. As the strength of a field is larger, n λ  is larger. It indicates that, for a super strong field, n λ 1 − n λ 2  should be important to the image of a star.
A gravitational field is a centripetal force. It is more complicated than a general medium, such as a water. Therefore, the real image of a star is more complicated than the Figure 2. First, usually, a gravitational field is not uniform. The light can be refracted by the field. Therefore, the image is related with the refracted angle of the light and the velocity v of the star. For the combinations of the directions of the star moving and that of the refracted angle, there should be different image. Second, light can be bent by gravity, it could result in that the motion of a light ray in a gravitational field is very complicated. As the dispersion is considered, the motion of a light ray in a strong field shall be complicated than that illustrated in the Ref. [2]. Under the conditions of both the bending of light by gravity and the dispersion, in a super strong gravitational field, for the moving of the star, the field strength is different relative to the light with different wavelength. For example, as shown in the Figure 1s in the Supplementary material B, as the light with λ 1  is being acting by the field with the strength g 1 , the light with λ 2  has not arrived at g 1 . The light with λ 2  only can be acted by g 2 . In a super strong field, ( g 1 − g 2 )  is very large in a short distance. It results in that the lines that the light with different wavelength running is radically different. And, it is emphasized that, the distance L between us and a star is very large. A little variation of the direction of a light shall result in that this light cannot be observed on the Earth. For example, as a little angle is between two light rays, one of the light rays can arrive at the Earth while the another shall arrive at a place very distant from the Earth. Therefore, as the angle of the light bent by gravity is very large, this effect could not be observed in a whole image. It indicates that only the effect that in the field with proper strength could be observed wholly. It indicates that many of the observable images of a stars could be only part of the images of the real stars. Therefore, in current theory, under the condition that the dispersion of light in gravitational field is not considered, many observed images of star are not a real star. Instead, it only is part of the images of a real star. For example, due to the gravitational lensing, a star can appear several images [22]. It is important to understand a galaxy. For example, in a galaxy, as the numbers of the images is much larger than that of the real stars, it should be an important factor to assess accurately the total mass of the galaxy.
Dispersion of light in free space was measured through that the speed of light can be slowed in a vacuum [23,24]. Two conclusions could be obtained from this measurement. First, the images analogous to that in the Figure 2 could be produced by the dispersion in free space. Second, dispersion in free space could be enlarged or varied in a strong gravitational field. (please reference the Supplementary material B.)

2. Discussion

The speed of light has been regarded as a cornerstone of current physics. It is believed that the speed of light in a vacuum is a constant which is the fastest velocity in our universe. However, as pointed out in the above, the speed of light in a vacuum has never been measured and cannot be measured with current technology. In fact, in Einstein’s theory of relativity, it was implied that the understandings about the speed of light can be developed. On one hand, it is claimed that the speed of light is constant in vacuum. On another hand, it is claimed that a light ray can be bent by gravity, and taking the bending of light by gravity as the main evidence for the general theory of relativity. Bending of light by gravity factually implies that the speed of light can be different in different gravitational field. It is easy to know that as the field is super strong, as illustrated in Ref [2]., the motion of light affected by gravity can be radically different from that on the Earth.
Till now, the only theory for the action of gravity on the speed of light is the bending of light by gravity. It is noted that it is Newton who first presented that light can be bent by gravity in 1660s [26]. And, von Soldner obtained the formula for it in 1804 [27]. This formula had not been improved in Einstein’s general relativity [28]. However, such old a theory need be developed. In quantum mechanics, the reflection of the wavelength of light to the gravity is an important subject.
Several other new observations about the speed of light were obtained. First, it is measured that the quantum teleportation is faster-than-light which can be used for communication [29–31]. In Refs [29–31]. it was clearly sentenced that the faster-than-light quantum teleportation can be used for communication. Second, it was measured that the speed of light in a vacuum is different due to the dispersion in free space [23–25]. It seems a strong supporter for our conclusion of the light dispersion in gravitational field. Third, it was measured that the photon can be accelerated along the direction vertical to its velocity [32–34]. It may lead to the new discovery of physics. Third, it was observed that the speed of gravity is much larger than the speed of light [35–37]. And, the negative speed of light and the fast light were measured.
And, we emphasize that the speed of light is with particular characteristic. First, in m = m 0 1 − v 2 / c 2   , no other particle is faster than light, and the velocity and mass of a particle are varied according to this formula. Second, astronomical observation shows that the speed of light is not affected by the speed of the source. If the speed of light was affected by the speed v of the source, the speed of light emitted from the sources should be c ′ = c ± v . Because of the orbital motion of the celestial body, relative to the observer on the Earth, it should lead to that, from the distant celestial bodies, the light emitted later could arrive at the Earth earlier. If it was so, for the binary star, it should appear that there are many stars, generally called as the “Phantom Phenomenon”. Third, the Fizeau experiment [38] also shows the special relationship between the speed of light and the source. In Fizeau experiment, the speed of light is not completely independent of the speed of the source, but the relationship is different from that of general objects such as that between the speed of a boat and that of the water in a river. Now, we have not known the reason for the particularities of the speed of light.
Additionally, it was well known that, there are many different cases for Equation (2). ε r  and μ r  are certain for a material. But, sometimes, μ r  is negative. For some materials, there are n → ε r . So, Equation (2) has not been completely understood.
These new observations and the particular characteristic showed that the speed of light is very complicated. It need be further studied and understood. As the strong gravitational field on the light is studied, some new features of the speed of light shall be discovered.

3. Conclusion

Light dispersion in gravitational field should have been observed through double-image gravitational lensing system and spectroscopic binary system. It was observed that the observed size of the image of a galaxy is a function of the wavelength of the light.[14,15] And, a method is presented that the distance of extragalactic system can be measured with “the time lag between variations in the short wavelength and long wavelength light from an active galactic nucleus”.[16] It should imply that, to have a right measurement of the numbers and spectrogram of the celestial objects and to have an accurate measurement of the size and distance of a celestial object, light dispersion in gravitational field need be considered.
The speed of light with the electric constant and magnetic constant is the fundamental physics constant in modern physics. Light dispersion in gravitational field means that a new understanding is needed for the fundamental constant. It is noted that, in the past time, the observation and experiment are mainly based on the physical event about the Earth and the solar system. These physical constants are universal to the solar system. The gravitational field in the solar system is very weak. The observational and experimental result acted by the field is correspondingly weak. Therefore, this field can be approximately treated as a vacuum. For example, although we have well known that a light ray is always being bent by the gravity of the Earth, we also treated this ray as a straight line. But, for a super strong gravitational field with a relativistic mass density of 10 17 k g m − 3 , the effect of the field on the observation is very large. It is clear, as the light ray emitted by a neutron star can be moved around the star by the gravitational field of the star [2], the speed of this light cannot be still understood as that this ray is moving in a vacuum. Therefore, although the concept of the speed of light in a vacuum is still useful in current theory of physics, it need be developed for studying the strong field. Factually, both observation and experiment showed that the speed of light can be varied by gravity and by the objects in laboratory [28–33]. The conditions for the new understanding about the fundamental physics constant were found. The deep space time is around the corner, the strong gravitational field is becoming one of the important subjects in physics. The new understanding should be helpful to better understand the physics fundamental constant in the future.

References

  1. Zhu, Y. , Gravitational Field and Mass. Preprints 2021, 2021090302. [Google Scholar] [CrossRef]
  2. Kraus U., Light Deflection Near Neutron Stars, Relativistic Astrophysics, 66-81 (1998). [CrossRef]
  3.    Whyte C., Neutron stars bend light so much we see their front and back at once, NewScientisits, (2018).
  4. Shapiro et al., Fourth Test of General Relativity: New Radar Result, Physical Review Letters, 26, 1132 (1971). [CrossRef]
  5. Drummond, I.T. and Hathrell S., QED vacuum polarization in a background gravitational field and its effect on the velocity of photons, Phys. Rev. D22 (1980) 343. [CrossRef]
  6. Shore G.M., Faster than light photons in gravitational fields II.: Dispersion and vacuum polarization, Nuclear Physics B, 633, 1-2, 271 (2002). [CrossRef]
  7. Franson J. D., Apparent correction to the speed of light in a gravitational potential, New J. Phys. 16, 065008 (2014). [CrossRef]
  8.    Yukio Tomozawa, Speed of Light in Gravitational Fields. https://www.arxiv-vanity.com/papers/astro-ph/0303047.
  9. Jervis-Smith and Frederick John, Evangelista Torricelli. Oxford University Press (1908).
  10. Zuccher S., Refraction of light, (2013).
  11. Enders P., Huygens’ Principle as Universal Model of Propagation, Lat. Am. J. Phys. Educ. 3, 1, (2009).
  12. Tan W.C., Koughia K., Singh J. and Kasap S.O., Fundamental Optical Properties of Materials I, Optical Properties of Condensed Matter and Applications, Edited by J. Singh (John Wiley & Sons, Ltd., 2006). [CrossRef]
  13. Burud I., et al., An Optical Time Delay Estimate for the Double Gravitational Lens System B1600+434*, ApJ, 544, 117 (2000). [CrossRef]
  14. Pelt J., Kayser R., Refsdal S., Schramm T., The Light Curve and Time Delay of QSO 0957+561, Astronomy and Astrophysics, 305, 97–106 (1996). [CrossRef]
  15. Pelt J., Hoff W., Kayser R., Refsdal S., Schramm T., Time delay controversy on QSO 0957+561 not yet decided, Astronomy and Astrophysics, 286, 775-785 (1994). [CrossRef]
  16. Fausnaugh M. M. et al., Space Telescope and Optical Reverberation Mapping Project. III. Optical Continuum Emission and Broadband Time Delays in NGC 5548, ApJ 821, 56 (2016). [CrossRef]
  17. J. H. H. Chan, K. Rojas, M. Millon, F. Courbin, V. Bonvin and G. Jauffret, Measuring accretion disk sizes of lensed quasars with microlensing time delay in multi-band light curves, A&A, 647, A115 (2021). [CrossRef]
  18. Yuzuru Yoshii, Yukiyasu Kobayashi, Takeo Minezaki, Shintaro Koshida, and Bruce A. Peterson, A New Method for Measuring Extragalactic Distances, 2014 ApJL 784 L11. [CrossRef]
  19. Zhu Y., Interaction of Gravitational Field and Orbit in Sun-planet-moon system[v1] | Preprints. [CrossRef]
  20. Matijevič G., et al., Double-lined spectroscopic binary stars in the RAVE survey, AJ., 140,184 (2010). [CrossRef]
  21. Pattnaik S., K. Kamila S., Roy G. S., Nayak M. K.,et al, Binary Star System- A Spectral Analysis, Lat. Am. J. Phys. Educ. 5, 2 (2011).
  22. Issaoun S., et al., The Size, Shape, and Scattering of Sagittarius A* at 86 GHz: First VLBI with ALMA, ApJ, 871, 30 (2019). [CrossRef]
  23. The Event Horizon Telescope Collaboration et al., First M87 Event Horizon Telescope Results. VII. Polarization of the Ring, ApJL, 910, L12 (2021). [CrossRef]
  24. Meneghetti M., Introduction to Gravitational Lensing, Introduction to Gravitational Lensing | SpringerLink. [CrossRef]
  25. Giovannini, D. et al. Spatially structured photons that travel in free space slower than the speed of light. Science 347, 857–860 (2015). [CrossRef]
  26. Bareza N., Hermosa N., Subluminal group velocity and dispersion of Laguerre Gauss beams in free space. Sci Rep 6, 26842 (2016). [CrossRef]
  27. Layton A. Hall and Ayman F. Abouraddy, Realizing normal group-velocity dispersion in free space via angular dispersion, Opt. Lett. 46, 5421-5424 (2021). [CrossRef]
  28. Sir Isaac Newton, Opticks (Dover, New York, 1952) p. 339.
  29. von Soldner J. G., Theorie der Landesvermessung; Ostwald’sKlassiker der Naturwissenschaften (Verlag von Wilhelm Engelmann, Leipzig, 1911).
  30. Sommerfeld H., Lorentz H., Einstein A., Minkowski & Weyl H., The principle of Relativity.
  31. Salart D., Baas A., Branciard C., Gisin N. & Zbinden H., Testing the speed of ‘spooky action at a distance’, Nature 454, 861-864 (2008). [CrossRef]
  32. Bancal J.-D., et al., Quantum non-locality based on finite-speed causal influences leads to superluminal signalling, Nature Physic, 8, 867-870 (2012). [CrossRef]
  33. Yin J., et al., Lower Bound on the Speed of Nonlocal Correlations without Locality and Measurement Choice Loopholes, Phys. Rev. Lett. 110, 260407 (2013). [CrossRef]
  34. Ballantine K. E., Donegan J. F., Eastham P. R., There are many ways to spin a photon: Half-quantization of a total optical angular momentum, Science Advances, 2(4), e1501748 (2016. [CrossRef]
  35. Bandres, M. A., et al., Accelerating optical beams. Optics and Photonics News 24, 30–37 (2013). [CrossRef]
  36. Webster J, Rosalesguzman C, Forbes A, et al., Radially dependent angular acceleration of twisted light, Optics Letters, 42(4): 675-678 (2017). [CrossRef]
  37. Van Flandern T., The speed of gravity — What the experiments say, Physics Letters A, 250, 1(1998). [CrossRef]
  38. Zhu Y., (17) (PDF) The speed of gravity: An observation on satellite motions (researchgate.net).
  39. Zhu Y., (17) (PDF) The speed of gravity: An observation on galaxy motions (researchgate.net).
  40. Fizeau H., On the hypotheses relating to the luminous æther, and an experiment which appears to demonstrate that the motion of bodies alters the velocity with which light propagates itself in their interior. [CrossRef]
Preprints 81110 g001
Figure 1. The double retarded positions of a star. A star is moving along the velocity v. p is the present position of the star. p1 is the first retarded position of the star which is determined with t λ 1 = n λ 1 L / c . And, p2 is the second retarded position which is determined with t λ 2 = n λ 2 L / c . S is the distance between the two retarded positions p1 and p2.
Figure 1. The double retarded positions of a star. A star is moving along the velocity v. p is the present position of the star. p1 is the first retarded position of the star which is determined with t λ 1 = n λ 1 L / c . And, p2 is the second retarded position which is determined with t λ 2 = n λ 2 L / c . S is the distance between the two retarded positions p1 and p2.
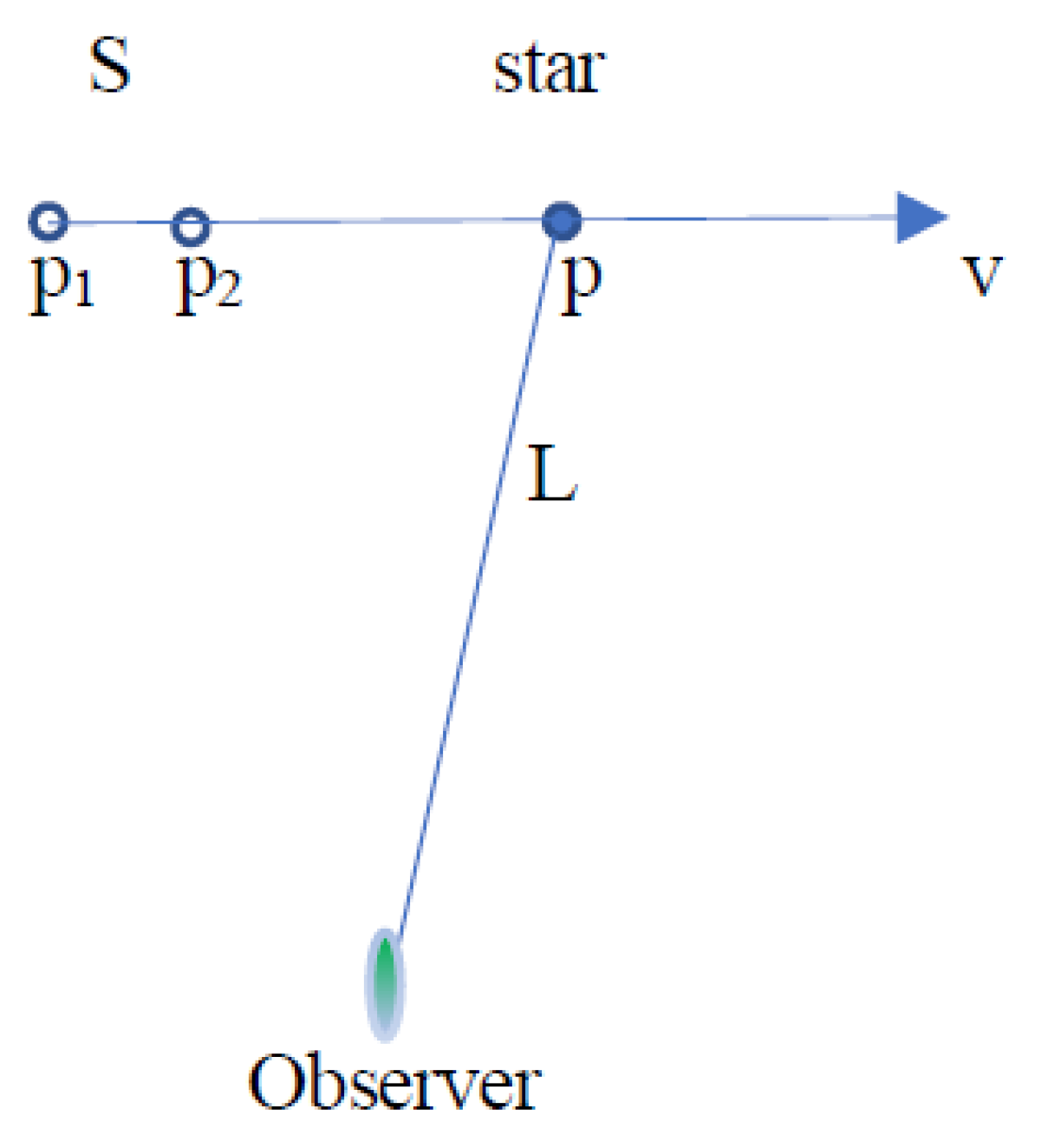
Preprints 81110 g001
Preprints 81110 g002
Figure 2. The picture of a star with a strong gravitational field. The original star is one sphere in violet. A. As S > 2 r , there should be two observed images in red and yellow for the original violet star. B. As S < 2 r , the observed image should be a dumbbell in red and yellow.
Figure 2. The picture of a star with a strong gravitational field. The original star is one sphere in violet. A. As S > 2 r , there should be two observed images in red and yellow for the original violet star. B. As S < 2 r , the observed image should be a dumbbell in red and yellow.
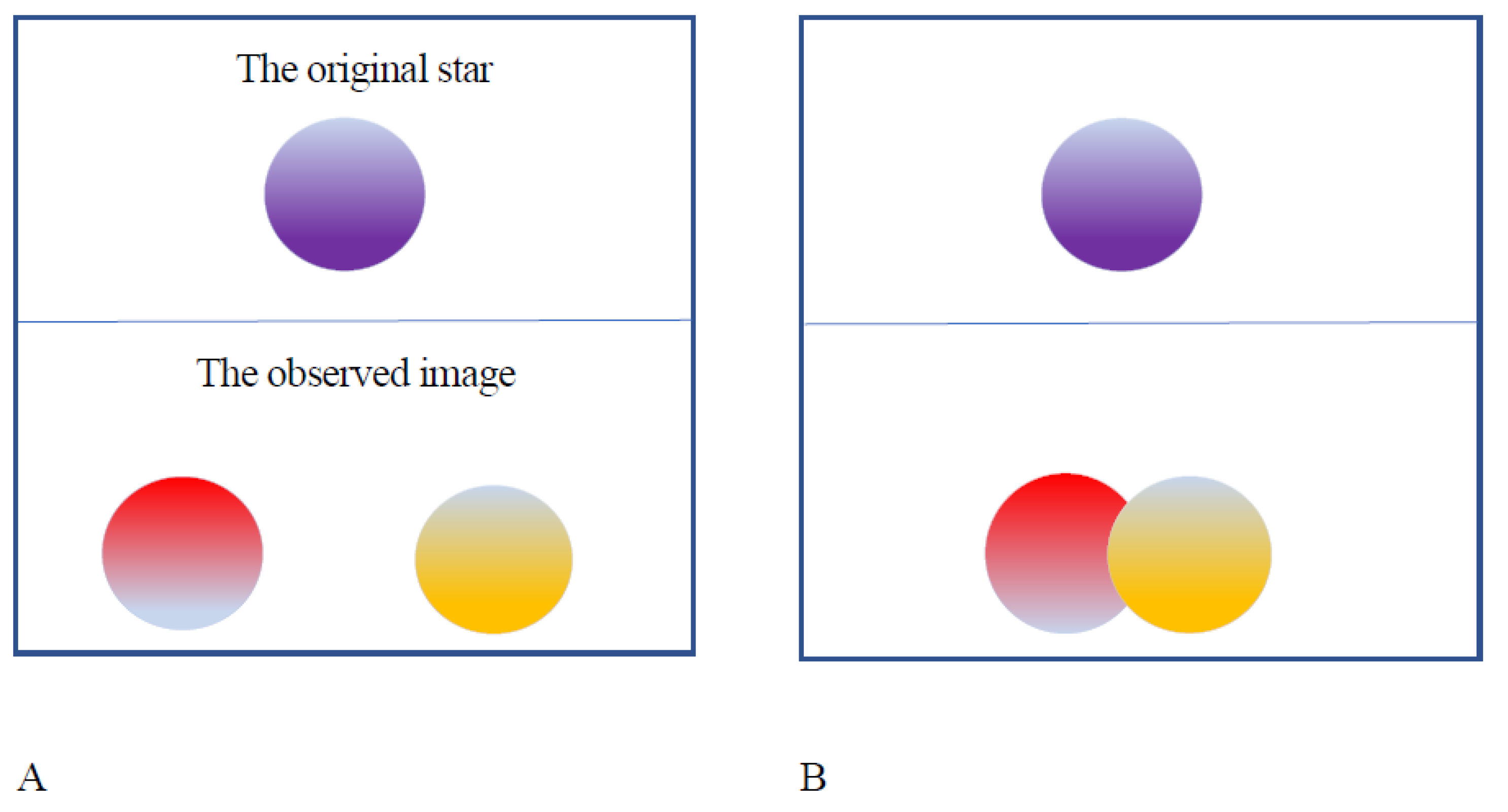
Preprints 81110 g002
Preprints 81110 g003
Figure 3. A star appears as spectroscopic binary system. A star is orbiting around a large center which cannot be observed by the observer. A the retarded position, because of the dispersion in gravitational field, there are two images for the star. The images of the star in the retarded position just appears a binary system.
Figure 3. A star appears as spectroscopic binary system. A star is orbiting around a large center which cannot be observed by the observer. A the retarded position, because of the dispersion in gravitational field, there are two images for the star. The images of the star in the retarded position just appears a binary system.
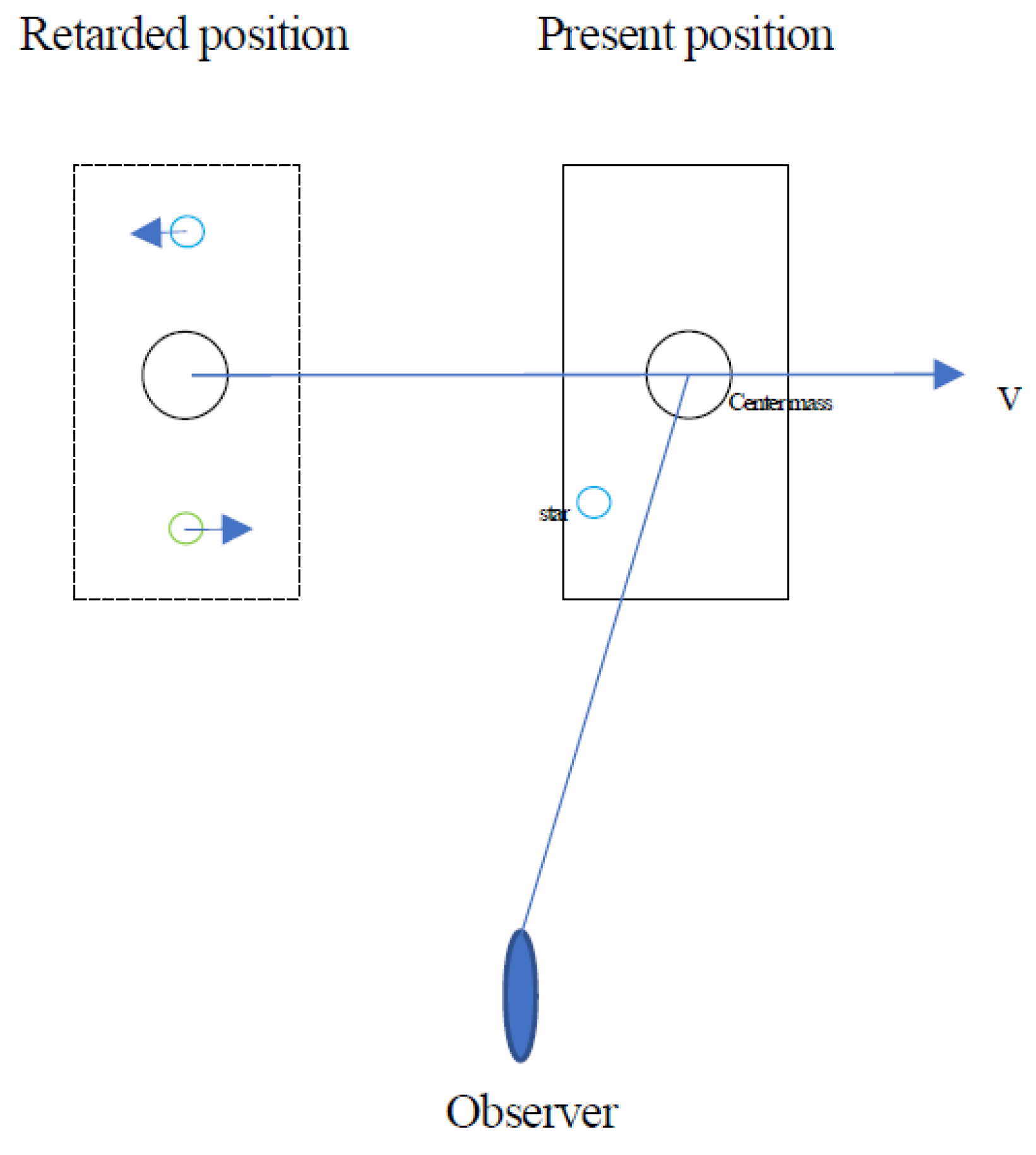
Preprints 81110 g003
Preprints 81110 g004
Figure 4. The distribution of the image of a star. The image of a star is determined with the distance between the star and observer and the velocity of the star. Out of the violet line, a star appears as two images in two colors. Between the two lines, the image of a spherical star appears as a dumbbell in two colors.
Figure 4. The distribution of the image of a star. The image of a star is determined with the distance between the star and observer and the velocity of the star. Out of the violet line, a star appears as two images in two colors. Between the two lines, the image of a spherical star appears as a dumbbell in two colors.
Preprints 81110 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated