Prerpints.org logo
Preprint
Article

Solving the Mystery of Time and Unifying Relativity with Quantum Mechanics

Altmetrics

Downloads

10730

Views

11128

Comments

1

This version is not peer-reviewed

Submitted:

03 January 2023

Posted:

03 January 2023

Read the latest preprint version here

Alerts
Abstract
Today's concept of time traces back to Albert Einstein's theories of special (SR) and general relativity (GR). In SR, uniformly moving clocks are slow with respect to my clocks. In GR, clocks in a more curved spacetime are slow with respect to my clocks. Many physicists anticipate that GR has an issue as it isn't compatible with quantum mechanics. Here we show: "Einstein time" (Einstein's concept of time) has an issue because it takes the proper time of an observer as the fourth coordinate of all objects in the universe. We replace Einstein time with "Euclidean time", which takes the proper time of an object as its fourth coordinate. SR and GR work very well as long as we describe the world on or close to Earth. Only then does time flow in one 4D direction for all objects. In all other cases, we must take a 4D vector "flow of time" into account. Unlike other models of Euclidean relativity (ER), we claim that reality is formed by projecting 4D Euclidean spacetime to an observer's 3D space. We prove: The Lorentz factor is recovered in ER; gravitational time dilation is also recovered in ER; ER is compatible with quantum mechanics. We solve 14 mysteries of physics, such as time's arrow, the c2 in mc2, dark energy, the wave–particle duality, and quantum entanglement. Our theory is supported by experimental data: ER empowers us to match the two competing values of the Hubble constant by adjusting redshift measurements of celestial objects.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

Albert Einstein coined today’s concepts of space and time. His theory of special relativity (SR) [1] is usually interpreted in Minkowski spacetime (MS) because Hermann Minkowski’s geometric interpretation [2] was very successful in explaining relativistic effects. MS comes with an indefinite Minkowski metric and is limited to inertial reference frames. General relativity (GR) [3] includes gravitation and turns flat MS into a curved spacetime with a pseudo-Riemannian metric. SR and GR are useful for describing the world that we perceive on or close to Earth. The lifetime of muons [4], the deflection of starlight during a solar eclipse [5], and the accuracy of GPS are a few examples. Quantum field theory [6] unifies classical field theory, SR, and quantum mechanics, but not GR.
Many physicists anticipate that GR has an issue as it isn’t compatible with quantum mechanics. In this paper, we give evidence for a basic issue in Einstein’s concept of time that can’t be fixed by adding “compensational concepts”, such as cosmic inflation or dark energy. We make three changes to the foundations of physics (new concepts of time, distance, and energy) that make relativity compatible with quantum mechanics. Be honest—isn’t that reason enough to give our theory a chance? We must ask this question because SR and GR have meanwhile turned into a dogma that must not be questioned. One editor informed us that some journals have an official policy not to consider any refutations of SR. Sorry, but why is that? According to Karl Popper, any theory is scientific if and only if it is falsifiable [7]. No scientific theory, not even SR or GR, is set in stone! What would science be like if editors weren’t to consider any refutations of the geocentric model?
For more than 100 years, physicists have been working with a flawed concept of time. It must be permitted to make this claim now that we explain why SR and GR work so well despite that flawed concept of time. And yet, five journals rejected our submission at the editor’s desk. One top journal argued that we wouldn’t provide extraordinary proof for our extraordinary claims. Isn’t solving 14 fundamental mysteries of physics extraordinary proof? Another journal argued that science would only deal with the observable world. Really? Do we observe time? It is irony that one of the journals, where Einstein published, refused to even look at our paper as we wouldn’t be experts. What constitutes an expert? Being a specialist in dark energy that we prove to be a redundant concept?
Our theory “Euclidean relativity” (ER) confirms relativity and quantum mechanics as the two solid pillars of physics. We formulate these three postulates: (1) In Euclidean spacetime (ES), the speed of light c is both absolute and universal—all energy is moving radially away from an origin at this speed. (2) The laws of physics have the same form in each “reality” (projection of ES to an observer’s 3D space). (3) All energy is “wavematter” (electromagnetic wave packet and matter in one). Our first postulate of ER is stronger than Einstein’s second postulate of SR. Everything is moving through ES at the same speed c . Our second postulate is the same as Einstein’s first postulate, except that ER isn’t limited to inertial frames and that we distinguish ES from an observer’s reality. Our third postulate paves the way for unifying relativity and quantum mechanics.
We aren’t the first physicists to investigate ER: In the early 1990s, Montanus made a first attempt to describe ES [8]. He also explored relativistic dynamics in ES [9]. Almeida tried to implement electrodynamics and gravitation in ES [10]. Gersten demonstrated that the Lorentz transformation in SR becomes an SO(4) rotation in ER [11]. van Linden studied energy and momentum in ES [12]. Pereira claimed a “hypergeometrical universe”, where matter is made from deformed space [13]. Yet by conceiving of ES as an observer’s reality, all these models run into geometric paradoxes (to be discussed in Sect. 4). Only Machotka [14] added a “boundedness postulate” to avoid such paradoxes, but that postulate sounds contrived. We overcome paradoxes for good by limiting reality with our second postulate: Reality is only formed by projecting ES to an observer’s 3D space.
It is helpful to compare our theory with Newton’s physics and Einstein’s physics. In Newton’s physics, all objects are moving through a non-deformable 3D space as a function of independent time. The speed of matter is v 3 D ≪ c . In Einstein’s physics, all objects are moving through a deformable spacetime given by 3D space and time, where time is linked to, but different from space (time is measured in seconds). The speed of matter is v 3 D < c . In our theory, all objects are moving through a non-deformable ES given by 4D distance (all distances are measured in light seconds), where time is a subordinate quantity derived from covered distance. The 4D speed of everything in ES is u 4 D = c . Immanuel Kant [15] provided the philosophical framework of Newton’s physics. Check out whether ER could be the philosophical framework of cosmology and quantum mechanics.
We kindly ask all readers including editors and reviewers: Be willing to question Einstein’s concept of time. Otherwise, you won’t understand! Here is a short roadmap of how we proceed: We start in Sect. 2 by revealing that there is an issue in Einstein’s concept of time. In Sect. 3, we offer an intuitive approach to Euclidean time. Instead of synchronizing clocks, we let a circle expand at the speed of light and then replace that circle with a sphere and a hypersphere. In Sect. 4, we derive the same Lorentz factor in ER as in SR. In Sect. 5, we solve 14 mysteries and declare five concepts of physics redundant. In our Conclusions, Occam’s razor knocks out Einstein’s concept of time.

2. An Issue in Einstein’s Concept of Time

The concept of time in today’s physics traces back to Albert Einstein. For this reason, we call it “Einstein time”. § 1 of SR [1] is an instruction of how to synchronize two clocks at the positions A and B. At “A time” t A , an observer sends a light pulse from A towards B. At “B time” t B , the light pulse is reflected at B towards A. And at “A time” t A * , the light pulse is back at A. Both clocks synchronize if
t B − t A   =   t A * − t B
In § 3 of SR [1], Einstein applies his synchronization procedure of clocks and derives the Lorentz transformation. The coordinates x 1 ,   x 2 ,   x 3 ,   t of a system K are transformed to the coordinates x 1 ′ ,   x 2 ′ ,   x 3 ′ ,   t ′ of a system K’ by
x 1 ′ =   γ   ( x 1 − v 3 D   t ) ,
x 2 ′   =   x 2 ,
x 3 ′   =   x 3 ,
t ′   =   γ   ( t − v 3 D   x 1 / c 2 ) ,
where the system K’ is moving relative to K in the axis x 1 and at the constant speed v 3 D . The factor γ = ( 1 − v 3 D 2 / c 2 ) − 0.5 is the Lorentz factor.
Millions of physicists read Einstein’s paper on SR [1], but didn’t object to it. Of course, we may subtract t A from t B in Eq. (1) if “A time” and “B time” are the same variables. Our theory reveals that this assumption is indeed a good approximation for all positions A and B on Earth or in our solar system. SR and GR work very well as long as we describe the world on or close to Earth. Yet Einstein’s Eq. (1) runs into a big problem once “A time” flows in a different 4D direction than “B time”. We claim that “A time” (or “B time”) is the absolute value of a 4D vector “flow of time” at A (or else B), which is an unknown quantity in SR and GR. In this general case, Einstein’s Eq. (1) is no longer applicable and must be replaced with a vector subtraction.
Albert Einstein was a theoretical physicist, and from his mathematical point of view there aren’t any objections against Eq. (1). Yet as we will prove in this paper, 14 mysteries of physics can all be solved if we only assume that there is a 4D vector “flow of time”. So, Einstein time does have an issue if it is evaluated from the perspective of physics. In Eq. (1), Einstein assumes that the time t B of any object in the universe flows in the very same direction as the time t A of an observer. So, Einstein time is egocentric! It takes the proper time of an observer as the fourth coordinate of all objects in the universe. No wonder that there are unsolved mysteries in cosmology and in quantum mechanics, where the “big picture” matters much more than the egocentric perspective of an observer.
In order to find an alternative concept of time, we now take a closer look at the effect of time dilation. In § 4 of SR [1], Einstein derives that there is a dilation in Einstein time: Clocks of an observer B in K’ are slow with respect to clocks of an observer R in K by the factor of γ . Time dilation by the factor of γ has been experimentally confirmed. So, any alternative concept of time must give rise to an Einstein time dilation by the same factor of γ . Now watch out as the next sentences are the most enlightening part of our paper: Most physicists aren’t aware that there are two variables in which this time dilation can be stored. Einstein and Minkowski assumed that clocks of B are slow with respect to R in the variable t ′ . Yet there is another variable in which clocks of B can be slow with respect to R: They can be slow in the variable t as we explain up next.
Figure 1 top illustrates a Minkowski diagram of two identical rockets—except for their color—with a proper length of 0.5 Ls (light seconds). They started at the origin and move relative to each other in the axis x 1 at a speed of 0.6   c . We choose these very high values to visualize relativistic effects. We display that moment when the red rocket has moved 1 s in time. Observer R is in the rear end of the red rocket r. His/her view is the red frame with the coordinates x 1 and t . Observer B is in the rear end of the blue rocket b. His/her view is the blue frame with the coordinates x 1 ′ and t ′ . Only for visualization do we draw our rockets in 2D although their width is in the dimensions x 2 ,   x 3 or x 2 ′ ,   x 3 ′ (not displayed in Figure 1). For R, the blue rocket contracts to 0.4 Ls because of length contraction. For B, the rear end of the blue rocket has moved 0.8 s in t ′  because of time dilation.
We now draw your attention to the values 0.8 and 0.5 printed at the blue rocket (Figure 1 top): In § 2 of SR [1], Einstein forces clocks inside b to synchronize with clocks inside r. So, all these clocks display the same time for R: t = 1.0   s . Yet the clocks inside b display a different time for B: t ′ = 0.8   s and t ′ = 0.5   s . This isn’t in line with experimental physics because a team of observers inside b would also synchronize all of its clocks! Reality is the other way around: Clocks inside b display the same time for B and a different time for R. We attribute the unfortunate assignment to a missing 4D vector “flow of time”.
Since we claimed both rockets to be identical, we must restore the symmetry. We can do so by rotating that blue rocket. Such a rotation is enabled by replacing the two asymmetric dimensions x 1 and t with two symmetric dimensions of ES: d 1 and d 4 (see our Sect. 3). We end up with an ES diagram (Figure 1 center), where the two values 0.8 and 0.5 are printed in the red frame. In SR (Figure 1 top), clocks inside b are slow with respect to R in t ′ . In ER (Figure 1 center), clocks inside b are slow with respect to R in t .

3. Introducing Euclidean Time and Euclidean Spacetime

Let us start with a very simple geometry. We imagine that all energy is in a 1D reality which is the line of a circle around some absolute point (origin O). The circle is expanding at the speed c . An observer sees only the projection of that circle to a straight 1D line. We add one dimension and imagine that all energy is in a 2D reality which is the surface of a sphere around that origin O. The surface is expanding at the speed c . An observer sees only the projection of that sphere to a flat 2D surface. We add one dimension and imagine that all energy is in a 3D reality which is the 3D hypersurface of a 4D hypersphere around that origin O. The 3D hypersurface is expanding at the speed c . An observer sees only the projection of that 4D hypersphere to a flat 3D space. We claim: This third scenario describes the world that we live in. For each observer, that 4D hypersphere is projected to a unique 3D space. The 3D hypersurface itself is absolute, but each observer’s 3D space is relative.
In all scenarios (circle, sphere, hypersphere), the radius r divided by time is always equal to c . The underlying concept of time isn’t egocentric, but universal, as it originates from an absolute point (origin O). We call it “Euclidean time” τ . Time can’t be observed. It is only felt as aging because the radial dimension disappears in a projection to 3D space. We define a new 4D vector “flow of time” r / c , where r is pointing from O to some object. The absolute value r / c is the same for all objects, but the orientation of r / c is unique for each object. Euclidean time itself is absolute, but each object’s flow of time is relative.
τ   =   r / c        ( Euclidean   time ) .
Eq. (3) tells us that Euclidean time isn’t a primary quantity, but a subordinate quantity derived from covered distance. Distance and speed are more significant than time! So, we suggest to reconsider the units of speed and time. The universal constant c shouldn’t be specified in “meters per second”, but in its own new unit to be given by the community. Euclidean time should be specified in “light seconds per that new unit”. These suggestions support claims by other authors that time isn’t fundamental to physics [16].
Mathematically, ES is an open 4D manifold with a Euclidean metric. We can describe ES either in four absolute hyperspherical coordinates ( ϕ 1 ,   ϕ 2 ,   ϕ 3 , r ), where each ϕ i is a hyperspherical angle and r is radial distance from an origin—or in four relative, symmetric Cartesian coordinates ( d 1 ,   d 2 ,   d 3 ,   d 4 ), where each d i is axial distance from an origin. In our new concept “distance”, we conceive of each distance (either the one radial distance r or the four axial distances d i ) as spatial and temporal distance in one. Distance isn’t covered as a function of independent time. Only by covering distance in ES is Euclidean time passing by for an object! In ES, all distances are measured in “light seconds” (Ls) by odometers. There is no need to calibrate these odometers as light seconds in ES are absolute.
Hyperspherical coordinates are good for grasping the “big picture” that physics tries to describe in cosmology. We claim that a huge amount of energy was injected into ES at some point that we take as our origin O. Right here our first postulate comes into play: In ES, all energy is moving radially away from this origin at the speed of light. That is, we live in the 3D hypersurface of an expanding 4D hypersphere. Hyperspherical coordinates have the great benefit of reducing all that is ever happening to one formula. So, this formula is the Theory of Everything (TOE) in hyperspherical coordinates: “All energy is covering radial distance r which, divided by Euclidean time τ , is equal to the speed of light c .”
r / τ   =   c       ( Theory   of   Everything ) .
Someone may argue that Eq. (4) couldn’t be a TOE as it doesn’t address the dynamics in 3D space. We disagree. In hyperspherical coordinates, there is indeed no motion within the hypersurface because everything is moving radially at the same speed. Yet as we will show in Sect. 5.4, motion in an observer’s view of the hypersurface (which is his 3D space, his reality, and his “universe”) is enabled by pure math—a rotation and a projection. So, Eq. (4) is the TOE in hyperspherical coordinates. Symmetry simplifies physics!
Cartesian coordinates are good for projecting 4D ES to an observer’s 3D space. They are calculated from hyperspherical coordinates by
d 1   =   r   cos ⁡ ϕ 1 ,
d 2   =   r   sin ⁡ ϕ 1   cos ⁡ ϕ 2 ,
d 3   =   r   sin ⁡ ϕ 1   sin ⁡ ϕ 2   cos ⁡ ϕ 3 ,
d 4   =   r   sin ⁡ ϕ 1   sin ⁡ ϕ 2   sin ⁡ ϕ 3 .
In Cartesian coordinates, too, all objects are moving at the speed of light c . Yet their 4D velocity u splits up into four components u i = d d i / d τ with
u 1 2 + u 2 2 + u 3 2 + u 4 2   =   c 2 .
In our ES diagrams, we often choose Cartesian coordinates in which an object starts moving from some origin P other than O. Because of the ES symmetry, we are free to label all four axes. We always assume that the axis d 4 coincides with the object’s flow of time r / c . That is to say: We take the proper time of an object as its fourth coordinate. Below our ES diagrams, we project ES to an observer’s 3D space. Here we are free to label the axis that we project onto. We always assume that two objects—moving relative to each other—will do so only in the axes d 1 and d 4 . This is why all of our ES diagrams display d 1 and d 4 . Our 3D projections display d 1 . Just keep in mind that d 1 stands for d 1 ,   d 2 ,   d 3 .

4. Geometric Effects in Euclidean Spacetime

Up next, we prove two effects in Cartesian ES coordinates: (1) If I observe a moving object, its 3D space is rotated with respect to my 3D space causing length contraction. (2) If I observe a moving object, its time flows in a 4D direction other than my time causing time dilation. So, these relativistic effects aren’t unique to MS. We consider the same two rockets as in Figure 1. They differ only in color (r = red rocket, b = blue rocket). Observer R in the rear end of the red rocket has the coordinates d 1 ,   d 2 ,   d 3 ,   d 4 (red frame). Observer B in the rear end of the blue rocket has the coordinates d 1 ′ ,   d 2 ′ ,   d 3 ′ ,   d 4 ′ (blue frame).
We assume that the rockets move relative to each other in 3D space (Figure 2 bottom). As explained in Sect. 3, this 3D motion is in d 1 and d 1 ′ . Our ES diagrams (Figure 2 top) must fulfill these three requirements: (1) According to our first postulate, both rockets must be moving at the speed c . (2) Our second postulate must be fulfilled. (3) Both rockets started at the same point P. There is only one way of how to draw our ES diagrams: We must rotate the two reference frames with respect to each other. Only a rotation guarantees full symmetry, so that the laws of physics have the same form in the 3D spaces of R and of B.
We define L i , R (or L i , B ) as length of the rocket with color i (r = red, b = blue) as seen from the perspective of observer R (or else B). From Figure 2, we derive
sin 2 ⁡ φ + cos 2 ⁡ φ   =   ( L b , R / L b , B ) 2 + ( v 3 D / c ) 2   =   1 ,
L b , R   =   γ − 1   L b , B      ( Length   contraction ) ,
where γ = ( 1 − v 3 D 2 / c 2 ) − 0.5 is the same Lorentz factor as in SR. The blue rocket appears contracted to observer R by the factor γ − 1 . Which distances will R observe in his axis d 4 ? For the answer, we mentally continue the rotation of the blue rocket (Figure 2 top left) until it is pointing vertically down ( φ = 0 ° ) and serves as R’s ruler in the axis d 4 . The projection to 3D space tells us that this ruler contracts to zero: The axis d 4 “is suppressed” (disappears) for R. He observes a 3D space, but only feels d 4 as aging. From Figure 2, we also derive
sin 2 ⁡ φ + cos 2 ⁡ φ   =   ( d 4 , B / d 4 , B ′ ) 2 + ( v 3 D / c ) 2   =   1 ,
d 4 , B   =   γ − 1   d 4 , B ′ ,
where d 4 , B and d 4 , B ′ are the distances that B has moved in d 4 and d 4 ′ . With d 4 , B ′ = d 4 , R (full symmetry in ES) and the substitutions d 4 , B = c t B and d 4 , R = c t R , we get
t R   =   γ   t B      ( Einstein   time   dilation ) ,
where t R (or t B ) is the distance that R (or else B) has moved in the Einstein time t of R. Be aware that t B in Eq. (11) is the Einstein time of R, whereas t B in Eq. (1) is the Einstein time at B. Clocks inside b are slow with respect to R in the variable t (0.8 and 0.5 printed in the red frame in Figure 1 center). In terms of Euclidean time, there is τ R = τ B .
The factor γ in Eqs. (8) and (11) is the same as in SR! Despite a Euclidean metric in ER, the Lorentz factor is recovered in the projection of ES to an observer’s 3D space and Einstein time. So, the Lorentz transformation and electrodynamics are recovered in ER if we take to heart that clocks inside b are slow with respect to R in the variable t . The recovery is no surprise. Hermann Weyl showed that the Lorentz group is generated by rotations [17].
Now we discuss three instructive, geometric paradoxes that demonstrate the benefit of our concept “distance”. Problem 1: A rocket moves along a guide wire at a high speed. The wire enters the rocket at its top and exits at its rear end. In ES, rocket and wire move at the speed c . We may assume that the wire moves in some axis d 4 . As the rocket moves along the wire, it can also move in the axis d 4 , but slower than the speed c . Wouldn’t the wire eventually be outside the rocket? Problem 2: In billiard, the cue ball is hit to collide with the red ball. In ES, cue ball and red ball move at the speed c . We may assume that the red ball moves in some axis d 4 . As the cue ball covers spatial distance to the red ball, it can also move in the axis d 4 , but slower than the speed c . How can the balls ever collide if their d 4 values never match? Problem 3: An observer in the tip of a rocket watches how a mirror is passing. He sends a light pulse to the mirror and tries to detect the reflection. In ES, all objects move at the speed c , but in different directions. We may assume that the rocket moves in some axis d 4 . How can the observer ever detect the reflection?
The questions in the last paragraph seem to imply that there are geometric paradoxes in ER, but there aren’t. The fallacy in all problems lies in the assumption that there would be four observable (spatial) dimensions. Yet only three distances of ES are observable! We solve all problems by projecting 4D ES to 3D space (Figure 3). Projections tell us what reality is like because “suppressing the axis d 4 ” is equivalent to “length contraction makes d 4 disappear”. The suppressed distance is felt as time. We easily verify in 3D space: The guide wire remains within the rocket; the cue ball collides with the red ball; the light pulse is reflected back to the observer. Other ER models [8,9,10,11,12,13,14] get caught up in paradoxes as they don’t project ES to an observer’s 3D space. They mistake ES for an observer’s reality.

5. Solving 14 Fundamental Mysteries of Physics

We just learned that the Lorentz transformation is recovered in ER. Hence, Euclidean time has no measurable consequences for SR and all theories that are based on SR, such as electrodynamics. Up next, we demonstrate that ER outperforms SR and GR in terms of understanding time, energy, cosmology, and quantum mechanics. We do so by solving 14 fundamental mysteries of physics.

5.1. Solving the Mystery of Time

Euclidean time is radial distance from an origin O in 4D ES divided by the speed c . This is why the concept of a linear time in a 3D space won’t let us grasp the “big picture”. I can’t observe time because I am moving in my flow of time at the speed c .

5.2. Solving the Mystery of Time’s Arrow

“Time’s arrow” is a synonym for time moving only forward. It traces back to the Big Bang (see our Sect. 5.4): We can’t reverse the 4D vector “flow of time” because radial momentum provided by the Big Bang drives all energy away from the origin O.

5.3. Solving the Mystery of the c 2   i n   m c 2

In SR, where forces are absent, the total energy E of an object is given by
E   =   γ   m   c 2   =   E k i n , 3 D + m   c 2 ,
where E k i n , 3 D is an object’s kinetic energy in 3D space and m c 2 is its “energy at rest”. SR doesn’t tell us why there is a c 2 in the energy of objects that in SR never move at the speed of light. ER gives us this missing clue and is thus superior to SR: m c 2 is the kinetic energy of moving through Euclidean time (of moving in the fourth dimension). The factor c 2 in Eq. (12) is strong evidence that everything is moving through ES at the speed c , while it is at rest in its 3D space. c 2 is passed through to 3D space. For the same reason, there is
E 2   =   p 2   c 2   =   p 3 D 2   c 2 + m 2   c 4 ,
where p and p 3 D are the momenta in ES and in 3D space. In ES, an object’s energy moves in its flow of time. Dividing Eq. (13) by c 2 gives us the vector addition of an object’s momentum in 3D space and its momentum m c of moving through Euclidean time.

5.4. Solving the Mystery of the Cosmic Microwave Background

Now we are ready for our new model of cosmology based on ER. There is no need to create ES. It exists just like numbers and can’t be deformed. Because of some reason that we don’t know, there was a Big Bang in ES. In today’s model of cosmology, it makes no sense to ask where the Big Bang occurred: Since space and time started as a singularity and space inflated thereafter, the Big Bang occurred “everywhere”. In ES, it is indeed possible to localize the Big Bang at what we take as our origin O. We claim that the Big Bang was a sudden incident that injected a huge amount of energy into ES all at once. Ever since has all this energy been moving radially away from O at the speed c . The adjective “sudden” allows for metaphysical speculations that aren’t a matter of physics.
During the initial stage after the Big Bang, there was a huge amount of concentrated energy inside ES. In the projection to any 3D space, this energy created a very dense and hot plasma. While the plasma was expanding, it cooled down. During the recombination of plasma particles, electromagnetic radiation was emitted that we still observe as cosmic microwave background (CMB) [18]. At a temperature of roughly 3,000 K, hydrogen atoms formed [19]. According to GR, this stage was reached 380,000 years “after” the Big Bang. In ER, these are 380,000 light years “away from” the Big Bang. The value of 380,000 needs to be recalculated if the universe has been expanding at the constant speed c .
Yet why is the CMB so isotropic? Here is our answer: The CMB is so isotropic because it is “swinging” equally from ES into all three dimensions of my 3D space (Figure 4). To grasp the process of swinging, we mentally continue the rotation of the blue rocket in Figure 2 top left until it is pointing vertically down. We then mentally replace that blue rocket with a photon and finally look at its projection to my 3D space. Here is what we learn from this thought experiment: In each photon, I actually observe energy from ES whose 4D motion swings “completely” (by an angle of 90 ° ) into my 3D space.
Our eyes aren’t made for perceiving all four dimensions of ES. Yet we can conceive of them with our brain by employing our trick: rotating that blue rocket in Figure 2 top left and looking at its projection to 3D space. This trick tells us that the process of swinging covers both operations: “Swinging” is one word for the combined action of rotating and projecting. In my 3D space, I observe the final result of this combined action.
We just learned that a photon is energy from ES whose 4D motion swings completely into my 3D space ( v 3 D = c ). Matter is energy from ES whose 4D motion swings “partly” (by an angle of < 90 ° ) into my 3D space, like that blue rocket in Figure 2 top left ( v 3 D < c ). The swing angle of Earth is 0 ° because Earth doesn’t move relative to myself ( v 3 D = 0 ). The process of swinging enables the motion of objects in my view of the hypersurface.
Photons are moving in my view of the hypersurface at the speed c , while the entire hypersurface is expanding at the speed c . Doesn’t a photon then exceed the speed c ? No, it doesn’t. Speeds in my view of the hypersurface must not be added to the speed of the hypersurface itself. A photon is energy from ES whose 4D motion swings completely into my 3D space. So, in the speed c of a photon I see the speed c of the hypersurface!

5.5. Solving the Mystery of Gravitational Time Dilation

Chronologically, this is the last of the 14 mysteries that we solved. Yet our solution is so simple that we consider it a very strong support for our theory. In ER, gravitation isn’t a property of spacetime. Gravitation is acting in 3D space like the other forces of physics. We now calculate time dilation in the gravitational field of Earth. Clock A is far away from Earth and continuously emitting time signals at infinitesimally short intervals. Receiver B is approaching Earth and detecting these time signals. The kinetic energy of B is
1 2   m u 1 , B 2   =   G   M   m / r ,
where m is the mass of B, u 1 , B is the speed of B in the axis d 1 of A, G is the gravitational constant, M is the mass of Earth, and r is the distance of B to Earth’s center. According to our first postulate, all energy is moving through ES at the speed c . So, we get
u 1 , B 2 + u 4 , B 2   =   2   G   M / r + u 4 , B 2   =   c 2 ,
u 4 , B 2 / c 2   =   1 − 2   G   M / ( r c 2 ) ,
where u 4 , B is the speed of B in the axis d 4 of A. With u 4 , B = d d 4 , B / d t A and d d 4 , B = c   d t B (there is no steady axis d 4 ′ because of the accelerated motion of B), we get
d t B   =   ( 1 − 2   G   M / ( r c 2 ) ) 0.5   d t A ,
d t A   =   γ g r a v   d t B ,
where d t A (or d t B ) is the distance that A (or else B) has moved in the Einstein time t of A in between consecutive time signals. The dilation factor γ g r a v = ( 1 − 2 G M / ( r c 2 ) ) − 0.5 is exactly the same as in GR [3]. It even has the same form as the Lorentz factor γ in Eqs. (8) and (11) if we only set 2 G M / r equal to v 3 D 2 .
In order to understand how acceleration manifests itself in ES, let us assume that the blue rocket b in Figure 2 bottom left accelerates in the axis d 1 . According to Eq. (6), the speed u 1 of b must then increase at the expense of its speed u 4 . That is, b is rotating in Cartesian ES coordinates! We didn’t specify what caused the acceleration. So, any acceleration of an object in 3D space—including an acceleration caused by gravitation—relates to a 4D rotation of this object in ES. I can’t observe a 4D rotation in my 3D space, but I do feel acceleration as a change in my 4D vector “flow of time”.

5.6. Solving the Mystery of Hubble’s Law

The 3D speed v 3 D at which a galaxy A is moving away from a galaxy B or from Earth relates to their distance D as c relates to the radius r of the hypersurface (Figure 4).
v 3 D   =   D   c / r   =   H 0   D       ( Hubble’s   law ) ,
where H 0 = c / r is the Hubble constant, c is in km/s, and r is in Mpc. There it is! Eq. (19) is Hubble’s law [20]: The farther a galaxy, the faster it is moving away from Earth. We derived it from the geometry of an expanding hypersurface. Because of Eq. (3), there is H 0 = 1 / τ . So, it does make sense to speak of a “Hubble function” H ( τ ) .

5.7. Solving the Mystery of the Flat Universe

Because the entire hypersurface is expanding at the speed of light (Figure 4), the radial dimension disappears for any observer inside the hypersurface. Together with this dimension, the 4D curvature of the 3D hypersurface disappears as well. He observes a flat 3D universe. His situation compares to that of an ant: Since it observes only two dimensions of space, the 3D curvature of Earth’s 2D surface disappears for the ant.

5.8. Solving the Mystery of Cosmic Inflation

Many physicists believe that an inflation of space in the early universe [21,22] would explain the isotropic CMB, the flatness of the universe, and large-scale structures (inflated from quantum fluctuations). We showed that an expanding 3D hypersurface can explain the first two of these observations. It also explains the third observation if we assume that there had been quantum fluctuations in energy in the early hypersurface. Their impacts have been expanding at the speed of light! Cosmic inflation is a redundant concept.

5.9. Solving the Mystery of the Two Competing Values of the Hubble Constant

There are several methods of calculating the Hubble constant H 0 , but unfortunately the results vary from one method to another. Here we consider measurements of the CMB made with the Planck space telescope [23]. We compare them with calculations of calibrated distance ladder techniques (measurement of distance and redshift of celestial objects) using the Hubble space telescope [24]. By taking the ES geometry into account, we now explain why the values of H 0 obtained by these two teams don’t even match within the specified error margins. According to team A [23], there is H 0 = 67.66 ± 0.42   k m / s / M p c . According to team B [24], there is H 0 = 73.52 ± 1.62   k m / s / M p c .
Team B made efforts to minimize the error margin by optimizing the distance measurement. Yet as we will prove now, it is a misinterpretation of the redshift measurements that causes a systematic error in team B’s value of H 0 . Let us assume that 67.66 km/s/Mpc would be today’s value of H 0 . Here we simulate a supernova at a distance of D = 400   M p c from Earth. It is moving at the 3D speed v 3 D away from Earth. Eq. (19) gives us
v 3 D   =   H 0   D   =   27,064   k m / s ,
z   =   Δ λ / λ 0   ≅   v 3 D / c   =   0.0903 ,
where the redshift parameter z tells us how any wavelength λ 0 of the supernova’s light is either passively stretched by an expanding space (team B)—or how it is redshifted by the Doppler effect of objects that are actively receding in ES (our model).
In the next paragraphs, we demonstrate that team B will measure a higher value of z , and thus calculate a higher value of v 3 D , and thus calculate a higher value of H 0 . Figure 5 left illustrates the geometry of the supernova and Earth in hyperspherical coordinates. We define one circle called “past”, where the supernova occurred, and a second circle called “present”, where its light is observed on Earth. Today, that supernova has turned into a neutron star. Figure 5 right shows the same geometry, but in Cartesian coordinates. Because everything is moving through ES at the speed c , Earth has moved the distance D in d 4 when the supernova’s light arrives. Hence, team B is receiving data from a time τ = 1 / H 0 ′ when there was a different radius r ′ and a different Hubble constant H 0 ′ .
1 / H 0 ′   =   r ′ / c   =   ( r − D ) / c   =   1 / H 0 − D / c .
H 0 ′   =   74.37   k m / s / M p c .
Because of this higher H 0 ′ value and Eq. (19), all data measured by team B are related to a higher 3D speed of the past v 3 D ′ = 29,748   k m / s for the same D . So, team B measures a redshift of z ′ = 0.0992 according to Eq. (21), which is indeed significantly higher than 0.0903. Team B isn’t aware of Eq. (22) and of the ES geometry shown in Figure 5. Yet because of that too high value of z ′ , team B will calculate v 3 D ′ = 29,748   k m / s from Eq. (21), and H 0 ′ = 74.37   k m / s / M p c from Eq. (19). So, team B will conclude that 74.37 km/s/Mpc would be today’s value of the Hubble constant. In truth, team B ends up with a Hubble constant of the past as it has been relying on redshift data from the past!
For a shorter distance of D = 400   k p c , Eq. (22) tells us that team B’s Hubble constant H 0 ′ deviates from team A’s Hubble constant H 0 by only 0.009 percent. Yet when plotting v 3 D ′ versus D for various distances (we chose 50 Mpc, 100 Mpc, 150 Mpc, … and 450 Mpc), the resulting slope (which is team B’s Hubble constant) is 8 to 9 percent higher than team A’s Hubble constant. So, we advise team B to improve its value of the Hubble constant by eliminating the systematic error in the redshift measurement. Team B should adjust the calculated speed of the past v 3 D ′ to today’s speed v 3 D by converting Eq. (22) to
H 0 ′   =   H 0   c   /   ( c − H 0   D )   =   H 0   /   ( 1 − v 3 D / c ) .
v 3 D   =   v 3 D ′   /   ( 1 + v 3 D ′ / c ) .
We conclude: The redshift is caused by the Doppler effect of objects that are actively receding in ES. Matching the two competing values of H 0 (team B’s published value is indeed 8 to 9 percent higher than team A’s value) is probably the strongest proof of our theory. Team A’s value is correct: H 0 ≈ 67 − 68   k m / s / M p c . If the 3D hypersurface has been expanding uniformly at the speed c , the age of today’s universe is equal to 1 / H 0 . In this case, its age wouldn’t be 13.8 billion years [25], but 14.5 billion years. The adjusted age would explain the observation that there are stars out there as old as 14.5 billion years [26].
As pointed out in Sect. 3, there is no motion within the hypersurface in hyperspherical coordinates. This is why we can’t draw the path of the supernova’s light in Figure 5 left. Only in Cartesian ES coordinates (Figure 5 top right) can we display the light’s path horizontally as we already did in Figure 3 top right. In order to see an observer’s reality, we have to project Cartesian ES coordinates to his 3D space (Figure 5 bottom right).
Of course, team B is well aware of the fact that the supernova’s light was emitted in the past. Yet in the Lambda-CDM model, all that counts is the timespan Δ t during which light is traveling from the supernova to Earth. Along the way, its wavelength is passively stretched by expanding space. So, the total redshift is only developing during the journey to Earth. We can put it this way: The redshift parameter z ′ starts from zero and increases continuously during the journey to Earth. The fact that the supernova occurred long ago in the past at a time t s is irrelevant for team B’s calculation.
In ER, the moment τ s (when a supernova occurs) is significant, but the timespan Δ τ (during which light is traveling to Earth) is irrelevant. The wavelength of the supernova’s light is initially redshifted by the Doppler effect. During its journey to Earth, the parameter z ′ remains constant. In GR, space itself is expanding. In ER, a hypersurface is expanding in ES. The hypersurface isn’t expanding space, but energy that is actively receding from the origin O. Here we can put it this way: The redshift parameter z ′ is tied up at the moment τ s “in a package” and sent to Earth, where it is measured.

5.10. Solving the Mystery of Dark Energy

The CDM model of cosmology assumes an expanding space to explain the distance-dependent recession of celestial objects. Meanwhile, it has been extended to the Lambda-CDM model, where Lambda is the cosmological constant. Cosmologists are now favoring an accelerated expansion [27,28] over a uniform expansion. This is because the measured recession speeds v 3 D deviate from values predicted by Eq. (19) if H 0 is considered an averaged constant. The deviations increase with distance D and are compensated by assuming an accelerated expansion of space. An acceleration would stretch the wavelength even more and thus increase v 3 D according to Eq. (21).
Our model gives a much simpler explanation for the deviations from Hubble’s law: Because of Eq. (3), there is H 0 = 1 / τ . So, H 0 isn’t a constant. H 0 ′ from every past is higher than today’s value H 0 . The older the considered redshift data are, the more will H 0 ′ deviate from today’s value H 0 , and the more will v 3 D ′ deviate from v 3 D . The small white circle in Figure 5 right helps us understand these deviations: If a new supernova S occurred today at the same distance D = 400   M p c as the mapped supernova S’ in the past, then S would recede slower (27,064 km/s) than S’ (29,748 km/s) just because of the different values of H 0 and H 0 ′ . As long as the ES geometry is unknown, the too-high redshifts are attributed to an accelerated expansion of space. Now that we know about the ES geometry, we can attribute different redshifts to data from different pasts.
We conclude that any expansion of space—uniform expansion as well as accelerated expansion—is only virtual. So, all that we ask for is to apply Occam’s razor even if a Nobel Prize was given “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae” [29]. We believe that cosmology has been misled by Einstein time and by GR. Expansion of space is a redundant concept.
The term “dark energy” [30] was coined to come up with a cause for an accelerated expansion of space. We gave strong evidence that there isn’t any expansion of space. So, dark energy is a redundant concept, too. It has never been observed anyway. The hypersurface isn’t driven by dark energy, but by intrinsic energy: Radial momentum provided by the Big Bang drives all energy away from the origin O.
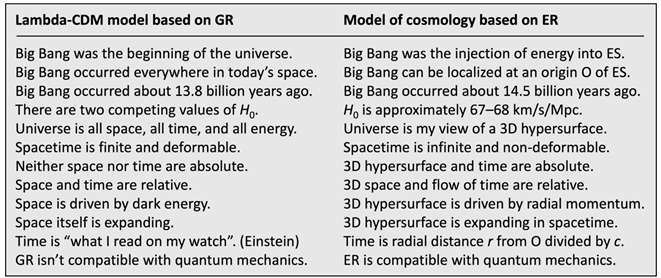
Table 1 summarizes huge differences in the meaning of the Big Bang, universe, space, and time. In the Lambda-CDM model, the Big Bang was the beginning of the universe. In our model, the Big Bang was the injection of energy into ES. In the Lambda-CDM model, the universe is all space, all time, and all energy. In our model, the universe is my view of a 3D hypersurface. In the Lambda-CDM model, spacetime is finite and deformable. In our model, spacetime is infinite and non-deformable. In the Lambda-CDM model, there is no definition of time other than “what I read on my watch” (attributed to Albert Einstein). In our model, time is radial distance r from an origin O in ES divided by the speed c . Most important of all, the Lambda-CDM model isn’t compatible with quantum mechanics. Our model is compatible with quantum mechanics.

5.11. Solving the Mystery of the Wave–Particle Duality

We can’t tell which solved mystery is the most important one. Yet the wave–particle duality has certainly kept physicists busy since it was first discussed by Niels Bohr and Werner Heisenberg [31]. The Maxwell equations tell us that electromagnetic waves are oscillations of an electromagnetic field that move through 3D space at the speed of light c . In some experiments, objects behave like “waves” (electromagnetic wave packets). But in other experiments, the same objects behave like particles. In MS, an object can’t be both at once because waves distribute energy in space over time, while the energy of particles is localized in space at a given time. This is why we added our third postulate: All energy is “wavematter” (electromagnetic wave packet and matter in one). By combining our new concepts of distance and wavematter, we now demonstrate: Waves and particles are actually the same thing (energy), but seen from two perspectives.
Figure 6 illustrates in Cartesian ES coordinates what our new concept of wavematter is all about. If I observe a wavematter (we call it the “external view”), that wavematter comes in four orthogonal dimensions: It propagates in my axis d 1 at some speed v 3 D ≤ c , and it oscillates in my axes d 2 (electric field) and d 3 (magnetic field); propagating and oscillating are functions of Euclidean time τ (related to my fourth axis d 4 ). So, I can observe how that wavematter is propagating and oscillating: I deem it wave.
From its own perspective (we call it the “internal view”), that wavematter propagates in its axis d 4 ′ at the speed c . Yet because of length contraction at the speed c , the axis d 4 ′ (its flow of time) disappears for that wavematter. So, its own propagating and oscillating disappears for itself: It deems itself matter at rest. It still observes other objects propagating and oscillating in its 3D space since it keeps on feeling Euclidean time, while it is invisibly propagating in its axis d 4 ′ . We thus conclude that there is an external view and an internal (in-flight) view of each wavematter. Be aware that “wavematter” isn’t just another word for the wave–particle duality, but a generalized concept of energy disclosing why there is wave–particle duality in an observer’s 3D space. In Einstein’s physics, there is no reference frame moving at the speed c and thus no internal view of a photon.
As an example, we now investigate the symmetry in three wavematters W M 1 , W M 2 , and W M 3 . We assume that they are all moving away from the same point P in ES, but in different directions (Figure 7 top left). d 1 ,   d 2 ,   d 3 ,   d 4 are Cartesian coordinates in which W M 1 moves only in d 4 . Hence, d 4 is that axis which W M 1 deems time multiplied by c , and d 1 ,   d 2 ,   d 3 span W M 1 ’s 3D space (Figure 7 bottom left). As the axis d 4 disappears because of length contraction, W M 1 deems itself matter at rest ( M 1 ). W M 3 moves orthogonally to W M 1 . d 1 ′ ,   d 2 ′ ,   d 3 ′ ,   d 4 ′ are Cartesian coordinates in which W M 3 moves only in d 4 ′ (Figure 7 top right). In this case, d 4 ′ is that axis which W M 3 deems time multiplied by c , and d 1 ′ ,   d 2 ′ ,   d 3 ′ span W M 3 ’s 3D space (Figure 7 bottom right). As the axis d 4 ′ disappears because of length contraction, W M 3 also deems itself matter at rest ( M 3 ).
Yet how do W M 1 and W M 3 move in each other’s view? We must fulfill our first two postulates and the requirement that they both started at the same point P. There is only one way of how to draw our ES diagrams: We must rotate the two reference frames with respect to each other. Only a rotation guarantees full symmetry, so that the laws of physics have the same form in the 3D spaces of W M 1 and of W M 3 . As the rotation angle is 90 ° , W M 3 ’s 4D motion swings completely into W M 1 ’s 3D space. W M 1 deems W M 3 wave ( W 3 ), while W M 3 deems W M 1 wave ( W 1 ). Regarding W M 2 , we split its 4D motion into a motion parallel to W M 1 ’s motion ( W M 1 views W M 2 internally) and a motion orthogonal to W M 1 ’s motion ( W M 1 views W M 2 externally). So, W M 1 deems W M 2 either matter ( M 2 ) or wave ( W 2 ). W M 3 likewise deems W M 2 either matter ( M 2 ) or wave ( W 2 ).
The secret to understanding our new concepts “distance” and “wavematter” is all in Figure 7. Here we see how they go hand in hand: We claim the symmetry of all four Cartesian coordinates in ES and—on top of that—the symmetry of all objects in ES. What I deem wave, deems itself matter. Just as distance is spatial and temporal distance in one, so is wavematter wave and matter in one. Here is a compelling reason for this unique claim of our theory: Einstein taught that energy is equivalent to mass. Full symmetry of matter and waves is a consequence of this equivalence! As the axis d 4 disappears because of length contraction, the energy in a propagating wave “condenses” to mass in matter at rest. Up next, we break the spell on the wave–particle duality (“wave–matter duality”) in its flagship experiments: the double-slit experiment and the outer photoelectric effect.
In the double-slit experiment, an observer detects coherent waves that pass through a double-slit and produce some pattern of interference on a screen. We already know that he observes wavematters from ES whose 4D motion swings by an angle of 90 ° into his 3D space. He deems all these wavematters waves because he isn’t tracking through which slit each wavematter is passing. If he did, the interference pattern would disappear immediately. So, he is a typical external observer. Experiments with low-noise video cameras have also been performed [32]. The results confirm our theory: There is interference of waves if photons aren’t tracked. Yet once we focus on the internal view of each wavematter (“Which CCD pixel will detect me?”), it behaves like a particle.
The outer photoelectric effect is quite different. Of course, we can externally witness how one photon is releasing one electron from a metal surface. But the physical effect itself (“Do I have enough energy to release one electron?”) is all up to the photon’s view. Only if its energy exceeds the binding energy of an electron is that electron released. Hence, we must interpret this experiment from the internal view of each wavematter. Here its view is crucial! It behaves like a particle, which is commonly called “photon”.
The wave–particle duality is also observed in matter, such as electrons [33]. How can electrons behave like waves in a double-slit experiment? According to our third postulate, electrons are wavematter, too. From the internal view (which is my view if the electrons are slow), electrons are particles: “Which slit will I go through?” From the external view (which is my view if the electrons are fast), electrons are waves. It all depends on the swing angle into my 3D space whether I deem a wavematter wave or matter. Figure 7 even tells us why I deem all macroscopic wavematters matter: Their speed in my 3D space is low compared with the speed c thus favoring the internal view. This argument justifies drawing solid rockets and celestial bodies in our ES diagrams rather than waves.
Be aware that in ER all wavematters are treated alike at once. Only in an observer’s 3D space is a wavematter deemed wave or matter. In SR and GR, there is no such superordinate frame of reference in which all objects could be treated alike at once. It is the same asymmetry that we encountered in Figure 1 top, where the two rockets aren’t treated alike at once. This shortcoming is due to the fact that Einstein time is egocentric.

5.12. Solving the Mystery of Quantum Entanglement

The term “entanglement” [34] was coined by Erwin Schrödinger when he published his comment on the Einstein–Podolsky–Rosen paradox [35]. The three authors argued that quantum mechanics wouldn’t provide a complete description of reality. John Bell proved that quantum mechanics is incompatible with local hidden-variable theories [36]. Schrödinger’s word creation didn’t solve the paradox, but demonstrates up to the present day the difficulties that we have in comprehending quantum mechanics. Several experiments have meanwhile confirmed that entangled particles violate the concept of locality [37,38,39]. Ever since has quantum entanglement been considered a non-local effect.
We will now “untangle” quantum entanglement without the issue of non-locality. All we need to do is discuss quantum entanglement in ES. Figure 8 illustrates two wavematters that were created at once at the same point P and move away from each other in opposite directions at the speed c . We claim that these wavematters are entangled. We assume that one wavematter is moving in the axis d 4 . The other wavematter is moving in the direction of − d 4 . If they are observed by a third wavematter that is moving in a direction other than d 4 , they are deemed two objects, especially if they are far away from each other. That third wavematter can’t understand how these entangled wavematters are able to communicate with each other in no time. This is again the external view.
And here comes the internal (in-flight) view in ES: For each entangled wavematter in Figure 8, the axis d 4 disappears because of length contraction at the speed c . That is to say: In the projection to its own 3D space spanned by d 1 ,   d 2 ,   d 3 , either wavematter deems itself at the very same position as its twin. From either perspective, they are one object that has never been separated. This is why they communicate with each other in no time! Entanglement is another strong evidence that everything is moving through ES at the speed c . Our solution to entanglement isn’t limited to photons. Electrons or atoms can be entangled as well. They are moving at a speed v 3 D < c in my 3D space, but in their axis d 4 they also move at the speed c . We conclude: Even non-locality is a redundant concept.

5.13. Solving the Mystery of Spontaneity

In spontaneous emission, a photon is emitted by an excited atom. Prior to the emission, the photon’s energy was moving with the atom. After the emission, that energy is moving by itself. Einstein’s physics can’t explain how that energy is boosted to the speed c in no time. In ES, both atom and photon are moving at the speed c . So, there is no need to boost any energy to the speed c . All it takes is energy whose 4D motion swings by an angle of 90 ° into an observer’s 3D space—and that energy is able to speed off at once. In absorption, a photon is spontaneously absorbed by an atom. Einstein’s physics can’t explain how the photon’s energy is slowed down to the atom’s speed in no time. In ES, both photon and atom are moving at the speed c . So, there is no need to slow down any energy. Similar arguments apply for pair production and annihilation. Spontaneity is another clue that everything is moving through ES at the speed c .

5.14. Solving the Mystery of the Baryon Asymmetry

According to the Lambda-CDM model, almost all matter in the universe was created shortly after the Big Bang. Only then was the temperature high enough to enable the pair production of baryons and antibaryons. Yet the density was also very high so that baryons and antibaryons should have annihilated each other again. Since we do observe a lot more baryons than antibaryons today (also known as the “baryon asymmetry”), it is assumed that more baryons than antibaryons must have been produced in the early universe [40]. However, an asymmetry in pair production has never been observed.
Our theory offers a unique solution to the baryon asymmetry: Since each wavematter deems itself matter, there was matter in 3D space right after the Big Bang. Pair production isn’t needed to create matter, and an asymmetry in pair production isn’t needed to explain that we observe a lot more matter than antimatter today. Even the baryon asymmetry is a redundant concept. One may ask why wavematter doesn’t deem itself antimatter, but this question misses the point. Energy has two faces: wave and matter. “Antimatter” is matter, too, but with the opposite electric charge. It is created only in pair production.

6. Conclusions

All attempts to unify GR and quantum mechanics have failed miserably. In Sects. 5.1 through 5.14, Euclidean time has solved mysteries that Einstein time either didn’t solve (time’s arrow, the c 2 in m c 2 , two competing values of the Hubble constant, the wave–particle duality, spontaneity)—or that it has solved, but with concepts (cosmic inflation, expansion of space, dark energy, non-locality, the baryon asymmetry) that we proved to be redundant. So now we finally let Occam’s razor, a powerful tool in science, do its job: As ER outperforms SR and GR, Occam’s razor knocks out Einstein time. Only ER lets us grasp the “big picture” and is compatible with quantum mechanics.
Many people believe that SR and GR are two of the greatest achievements of physics and have been confirmed many times over. Here we proved that they have a flawed concept of time. SR and GR work very well as long as we describe the world on or close to Earth. Albert Einstein, one of the most brilliant physicists ever, wasn’t aware of ER. It was a wise decision to award him with the Nobel Prize for his theory of the photoelectric effect [41], and not for SR or GR. We campaign for ER as it penetrates to a much deeper level. For the first time ever, mankind understands the nature of time: We live in the 3D hypersurface of an expanding 4D hypersphere—its radius, divided by the speed of light, is time! Just imagine: The human brain is able to grasp the idea that our energy is moving through ES at the speed of light. With that said, conflicts of mankind become all so small.
We solved 14 fundamental mysteries of physics: (1) time, (2) time’s arrow, (3) the c 2 in m c 2 , (4) the CMB, (5) gravitational time dilation, (6) Hubble’s law, (7) the flat universe, (8) cosmic inflation, (9) two competing values of the Hubble constant, (10) dark energy, (11) the wave–particle duality, (12) quantum entanglement, (13) spontaneity, and (14) the baryon asymmetry. These 14 solutions are 14 confirmations of ER. It was to our advantage that we, as non-cosmologists, aren’t dazzled by SR and GR. For quantum leaps in understanding, we must keep on questioning concepts. Einstein sacrificed the absoluteness of space and time. We sacrifice the absoluteness of wave and matter, but we restore absolute time and even pair it with an absolute 3D hypersurface. Quantum leaps can’t be planned. They just happen like the spontaneous emission of a photon. ☺
We introduced new concepts of time, distance, and energy: (1) There is absolute time. (2) Spatial and temporal distance are not two, but one. (3) Wave and matter are not two, but one. We explained these concepts and confirmed how powerful they are. We can even tell the source of their power: beauty and symmetry. Once you have cherished this beauty, you will never let it go again. Yet to cherish it, you first need to give yourself a little push—accepting that reality is only formed by projecting ES to an observer’s 3D space. Questions like “What is it good for that reality is only a projection?” must not be asked in physics. “Reality being a projection” is of a similar magic as “reality being a probability function”. It seems that philosopher Plato wasn’t all wrong with his allegory of the cave [42]. Should you have any doubts regarding our theory, take our advice: Think of a problem in physics and try to solve it in ER. Yet be fair and don’t expect us to solve all of physics, as one editor did. For example, we didn’t address gravitational lensing and gravitational waves. They support GR, but might be recovered in ER. We invite you to join us in this paradigm shift! Hopefully, we contribute to an improved understanding of physics.

Author Contributions

Markolf has a Ph.D. in physics and is a full professor at Heidelberg University, Germany. He studied in Frankfurt, Heidelberg, at UC San Diego, and Harvard. He found the issue in Einstein time, contributed the concepts “distance” and “wavematter”, and made ER compatible with quantum mechanics. He also drafted the report. Siegfried taught physics and math at the Waldorf School in Darmstadt, Germany. He contributed that Minkowski diagrams aren’t in line with experimental physics and solved the Hubble constant. Everything else was solved together.

Funding

No funds, grants, or other support was received.

Data Availability Statement

All data that support this study are included within the article.

Conflict of Interest

The authors have no competing interests to declare.

References

  1. Einstein A 1905 Zur Elektrodynamik bewegter Körper Ann. Phys. 17 891–921.
  2. Minkowski H 1910 Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern Math. Ann. 68 472–525. [CrossRef]
  3. Einstein A 1916 Die Grundlage der allgemeinen Relativitätstheorie Ann. Phys. 49 769–822. [CrossRef]
  4. Rossi B and Hall D B 1941 Variation of the rate of decay of mesotrons with momentum Phys. Rev. 59 223–229. [CrossRef]
  5. Dyson F W, Eddington A S and Davidson C 1920 A determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of May 29, 1919 Phil. Trans. R. Soc. London A 220 291–333.
  6. Peskin M E and Schroeder D V 1995 An Introduction to Quantum Field Theory (Boulder: Westview Press).
  7. Popper K 1989 Logik der Forschung (Tübingen: Mohr).
  8. Montanus J M C 1991 Special relativity in an absolute Euclidean space-time Phys. Essays 4, 350–356. [CrossRef]
  9. Montanus J M C 2001 Proper-time formulation of relativistic dynamics Found. Phys. 31 1357–1400. [CrossRef]
  10. Almeida J B 2001 An alternative to Minkowski space-time (arXiv: gr-qc/0104029).
  11. Gersten A 2003 Euclidean special relativity Found. Phys. 33 1237–1251. [CrossRef]
  12. van Linden R F J 2007 Dimensions in special relativity theory Galilean Electrodynamics 18, 12–18.
  13. Pereira M 2017 The hypergeometrical universe (available at: http://www.worldscientificnews.com/wp-content/uploads/2017/07/WSN-82-2017-1-96-1.pdf) (Accessed 30 December 2022).
  14. Machotka R 2018 Euclidean model of space and time J. Mod. Phys. 9 1215–1249.
  15. Kant I 1781 Kritik der reinen Vernunft (Riga: Hartknoch).
  16. Rovelli C 2018 The Order of Time (London: Allen Lane).
  17. Weyl H 1928 Gruppentheorie und Quantenmechanik (Leipzig: Hirzel) Chap. III, § 8c.
  18. Penzias A A and Wilson R W 1965 A measurement of excess antenna temperature at 4080 Mc/s Astrophys. J. 142 419–421. [CrossRef]
  19. Padmanabhan T 1993 Structure Formation in the Universe (Cambridge: Cambridge University Press).
  20. Hubble E 1929 A relation between distance and radial velocity among extra-galactic nebulae Proc. Nat. Acad. Sci. USA 15 168–173. [CrossRef]
  21. Linde A 1990 Inflation and Quantum Cosmology (Boston: Academic Press).
  22. Guth A H 1997 The Inflationary Universe (Reading: Perseus Books).
  23. Aghanim N, Akrami Y, Ashdown M et al. 2021 Planck 2018 results. VI. Cosmological parameters (arXiv: 1807.06209).
  24. Riess A G, Casertano S, Yuan W et al. 2018 Milky Way Cepheid standards for measuring cosmic distances and application to Gaia DR2: Implications for the Hubble constant (arXiv: 1804.10655).
  25. Choi S K, Hasselfield M, Ho S-P P et al. 2020 The Atacama Cosmology Telescope: A measurement of the cosmic microwave background power spectra at 98 and 150 GHz (arXiv: 2007.07289).
  26. Bond H E, Nelan E P, VandenBerg D A et al. 2013 HD 140283: A star in the solar neighborhood that formed shortly after the Big Bang (arXiv: 1302.3180).
  27. Perlmutter S, Aldering G, Goldhaber G et al. 1998 Measurements of Ω and Λ from 42 high-redshift supernovae (arXiv: astro-ph/9812133).
  28. Riess A G, Filippenko A V, Challis P et al. 1998 Observational evidence from supernovae for an accelerating universe and a cosmological constant (arXiv: astro-ph/9805201).
  29. The Nobel Prize 2011 (available at: https://www.nobelprize.org/prizes/physics/2011/summary/) (Accessed 30 December 2022).
  30. Turner M S 1998 Dark matter and dark energy in the universe (arXiv: astro-ph/9811454).
  31. Heisenberg W 1969 Der Teil und das Ganze (Munich: Piper).
  32. Aspden R S, Padgett M J and Spalding G C 2016 Video recording true single-photon double-slit interference Am. J. Phys. 84 671–677. [CrossRef]
  33. Jönsson C 1961 Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten Z. Phys. 161 454–474. [CrossRef]
  34. Schrödinger E 1935 Die gegenwärtige Situation in der Quantenmechanik Die Naturwissenschaften 23 807–849.
  35. Einstein A, Podolsky B and Rosen N 1935 Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47 777–780. [CrossRef]
  36. Bell J S 1964 On the Einstein Podolsky Rosen paradox Physics 1 195–200. [CrossRef]
  37. Freedman S J and Clauser J F 1972 Experimental test of local hidden-variable theories Phys. Rev. Lett. 28 938–941. [CrossRef]
  38. Aspect A, Dalibard J and Roger G 1982 Experimental test of Bell’s inequalities using time-varying analyzers Phys. Rev. Lett. 49 1804–1807. [CrossRef]
  39. Bouwmeester D, Pan J-W, Mattle K et al. 1997 Experimental quantum teleportation Nature 390 575–579. [CrossRef]
  40. Canetti L, Drewes M and Shaposhnikov M 2012 Matter and antimatter in the universe (arXiv: 1204.4186).
  41. Einstein A 1905 Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt Ann. Phys. 17 132–148. [CrossRef]
  42. Plato Politeia 514a–521b.
Preprints 66965 g001
Figure 1. Minkowski diagram, ES diagram, and 3D projection for two identical rockets. Top: The Minkowski diagram isn’t symmetric. For observer R, clocks inside the red rocket display the same time (1.0 printed in the red frame). For observer B, clocks inside the blue rocket display a different time (0.8 and 0.5 printed in the blue frame). Center: The ES diagram is rotationally symmetric. The values 0.8 and 0.5 are measured by R in the red frame. Bottom: Projection to the 3D space of R.
Figure 1. Minkowski diagram, ES diagram, and 3D projection for two identical rockets. Top: The Minkowski diagram isn’t symmetric. For observer R, clocks inside the red rocket display the same time (1.0 printed in the red frame). For observer B, clocks inside the blue rocket display a different time (0.8 and 0.5 printed in the blue frame). Center: The ES diagram is rotationally symmetric. The values 0.8 and 0.5 are measured by R in the red frame. Bottom: Projection to the 3D space of R.
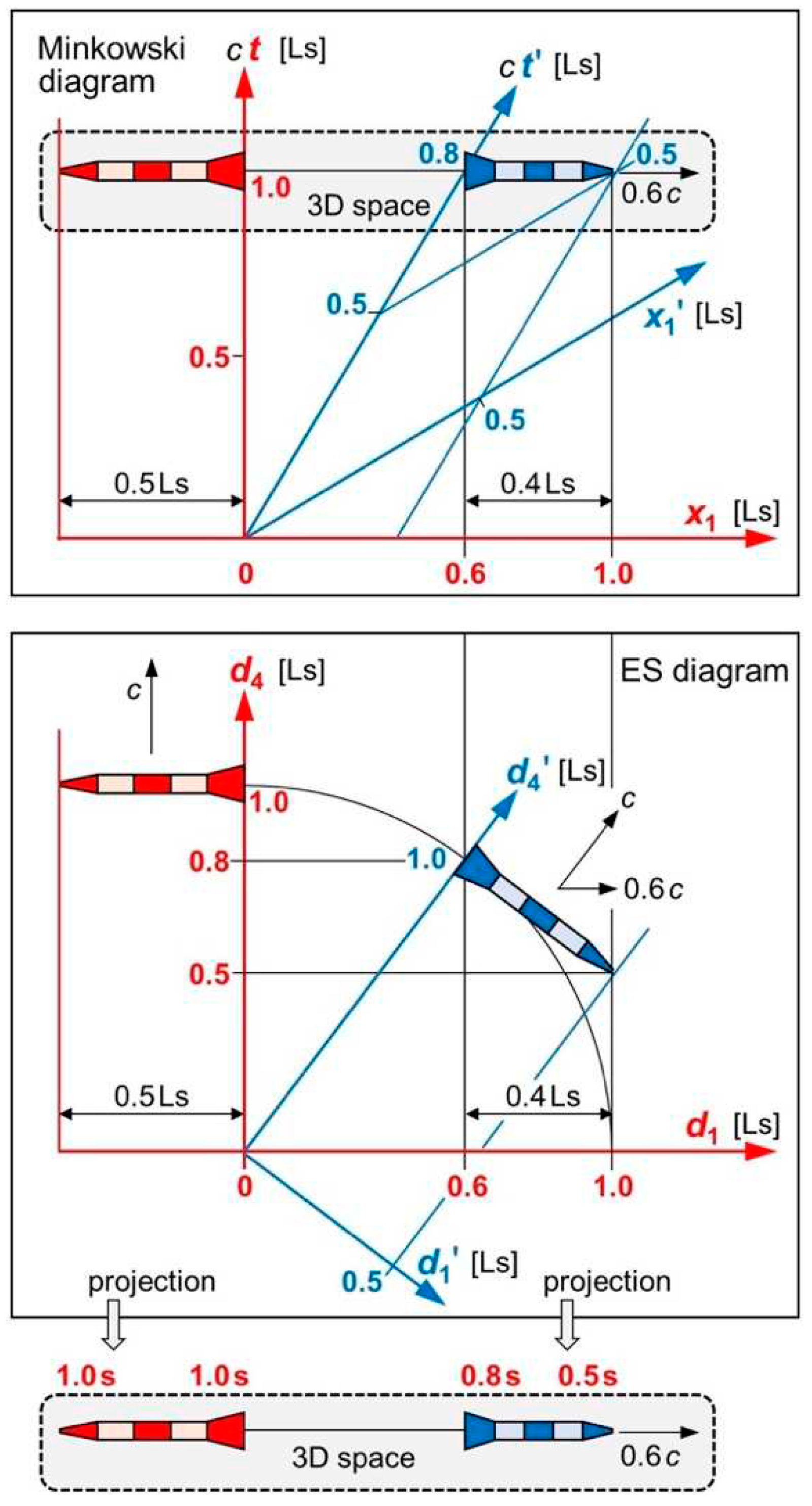
Preprints 66965 g001
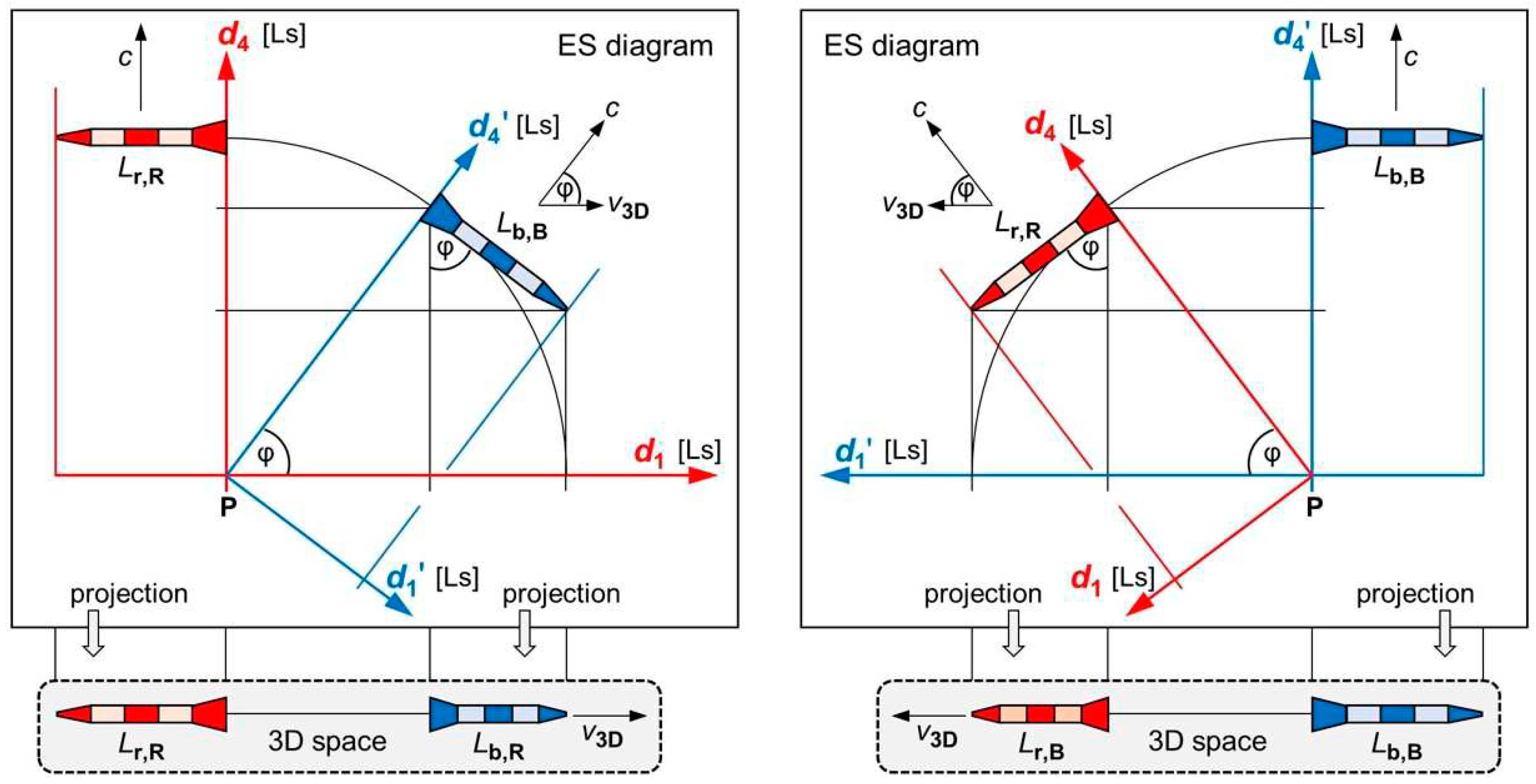
Preprints 66965 g002
Figure 2. ES diagrams and 3D projections for two identical rockets. All axes are in Ls (light seconds). Top left and top right: In the ES diagrams, both rockets are moving at the speed c , but in different directions. Bottom left: Projection to the 3D space of R. The relative speed is v 3 D . The blue rocket contracts to L b , R . Bottom right: Projection to the 3D space of B. The red rocket contracts to L r , B .
Figure 2. ES diagrams and 3D projections for two identical rockets. All axes are in Ls (light seconds). Top left and top right: In the ES diagrams, both rockets are moving at the speed c , but in different directions. Bottom left: Projection to the 3D space of R. The relative speed is v 3 D . The blue rocket contracts to L b , R . Bottom right: Projection to the 3D space of B. The red rocket contracts to L r , B .
Preprints 66965 g002
Preprints 66965 g003
Figure 3. Graphical solutions to three geometric paradoxes. Left: A rocket moves along a guide wire. In 3D space, the guide wire is always within the rocket. Center: A cue ball is hit to collide with the red ball. In 3D space, the cue ball collides with the red ball. Right: An observer inside a rocket tries to detect the reflection of a short light pulse. Between two snapshots (0–1 or 1–2), rocket, mirror, and light pulse move 0.5 Ls in ES. In 3D space, the light pulse is reflected back to the observer.
Figure 3. Graphical solutions to three geometric paradoxes. Left: A rocket moves along a guide wire. In 3D space, the guide wire is always within the rocket. Center: A cue ball is hit to collide with the red ball. In 3D space, the cue ball collides with the red ball. Right: An observer inside a rocket tries to detect the reflection of a short light pulse. Between two snapshots (0–1 or 1–2), rocket, mirror, and light pulse move 0.5 Ls in ES. In 3D space, the light pulse is reflected back to the observer.
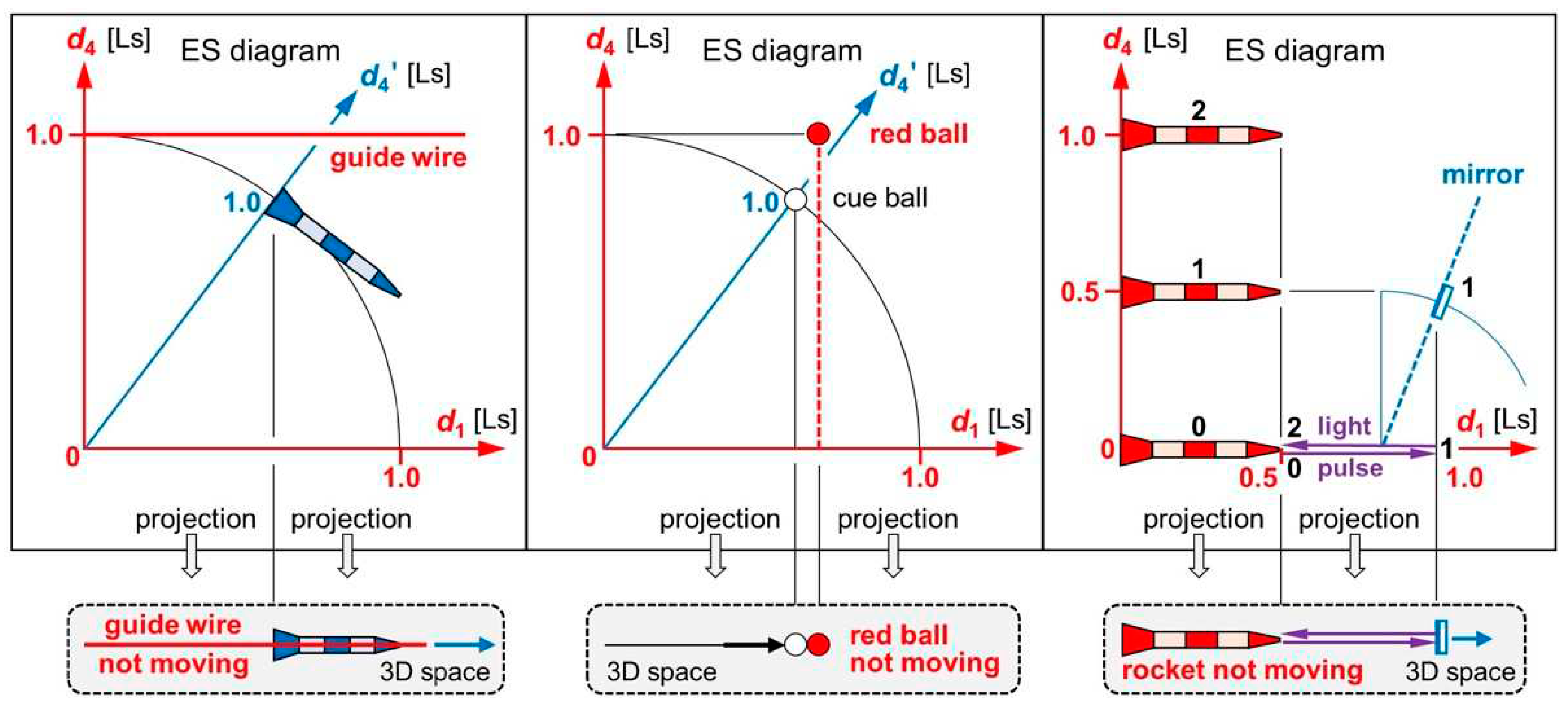
Preprints 66965 g003
Preprints 66965 g004
Figure 4. Model of cosmology based on ER (not to scale). Artwork illustrating how a 3D hypersurface is expanding in ES. Left: Non-observable ES in hyperspherical coordinates ( ϕ 1 ,   ϕ 2 ,   ϕ 3 , r ). The angle ϕ 3 can’t be displayed here. Hubble’s law is derived from the geometry of the hypersurface. Right: My 3D space in Cartesian coordinates ( d 1 ,   d 2 ,   d 3 ), which is my view of the hypersurface and my reality. The axis d 4 (related to time) disappears because of length contraction.
Figure 4. Model of cosmology based on ER (not to scale). Artwork illustrating how a 3D hypersurface is expanding in ES. Left: Non-observable ES in hyperspherical coordinates ( ϕ 1 ,   ϕ 2 ,   ϕ 3 , r ). The angle ϕ 3 can’t be displayed here. Hubble’s law is derived from the geometry of the hypersurface. Right: My 3D space in Cartesian coordinates ( d 1 ,   d 2 ,   d 3 ), which is my view of the hypersurface and my reality. The axis d 4 (related to time) disappears because of length contraction.
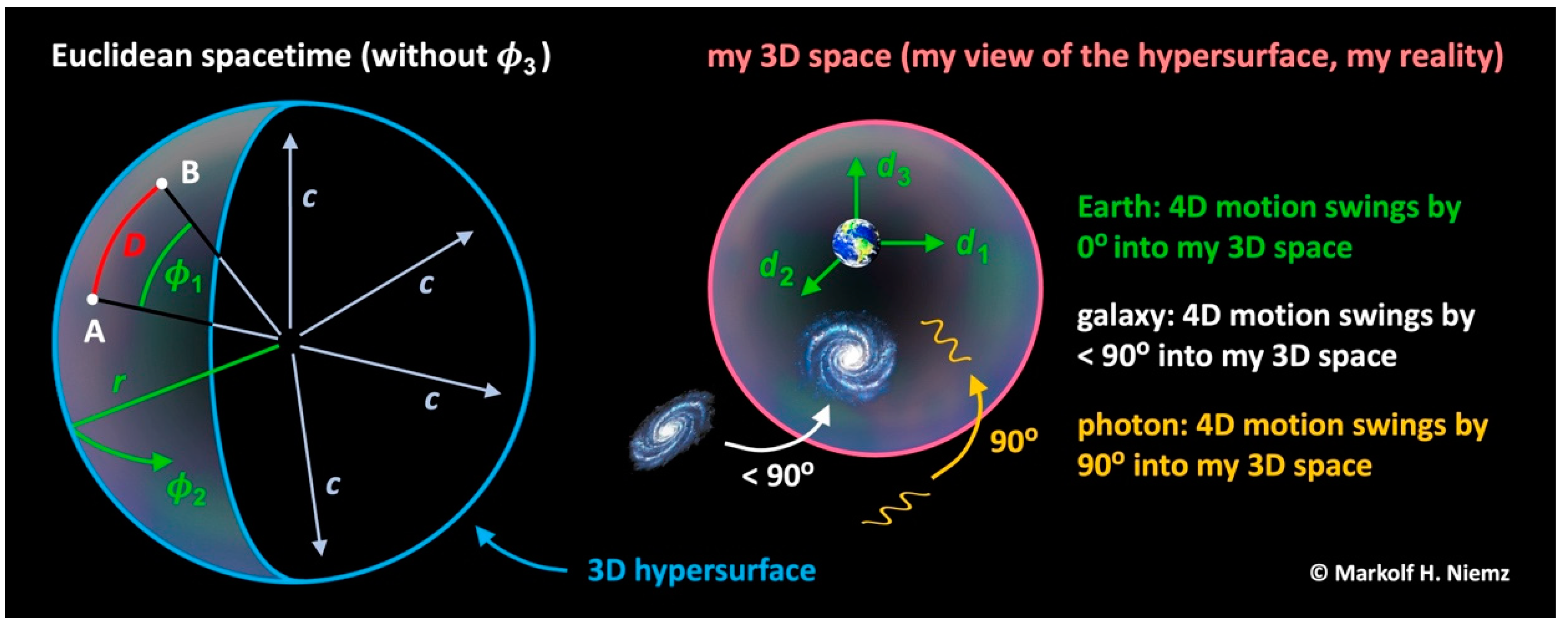
Preprints 66965 g004
Preprints 66965 g005
Figure 5. ES diagrams for team B’s calculation of the Hubble constant. The location of the Big Bang serves as the origin O. Left: We assume that 67.66 km/s/Mpc would be today’s value of the Hubble constant H 0 (present). A supernova S’ occurred in the past when the radius r ′ of the hypersurface was smaller than today’s radius r . Right: Team B observes S’ and measures a distance of 400 Mpc. Since the occurrence of S’, Earth has also moved 400 Mpc, but in the axis d 4 . Team B calculates a Hubble constant H 0 ′ of the past (74.37 km/s/Mpc). A supernova S occurring today (same distance, small white circle) recedes slower (27,064 km/s) than a supernova S’ in the past (29,748 km/s).
Figure 5. ES diagrams for team B’s calculation of the Hubble constant. The location of the Big Bang serves as the origin O. Left: We assume that 67.66 km/s/Mpc would be today’s value of the Hubble constant H 0 (present). A supernova S’ occurred in the past when the radius r ′ of the hypersurface was smaller than today’s radius r . Right: Team B observes S’ and measures a distance of 400 Mpc. Since the occurrence of S’, Earth has also moved 400 Mpc, but in the axis d 4 . Team B calculates a Hubble constant H 0 ′ of the past (74.37 km/s/Mpc). A supernova S occurring today (same distance, small white circle) recedes slower (27,064 km/s) than a supernova S’ in the past (29,748 km/s).
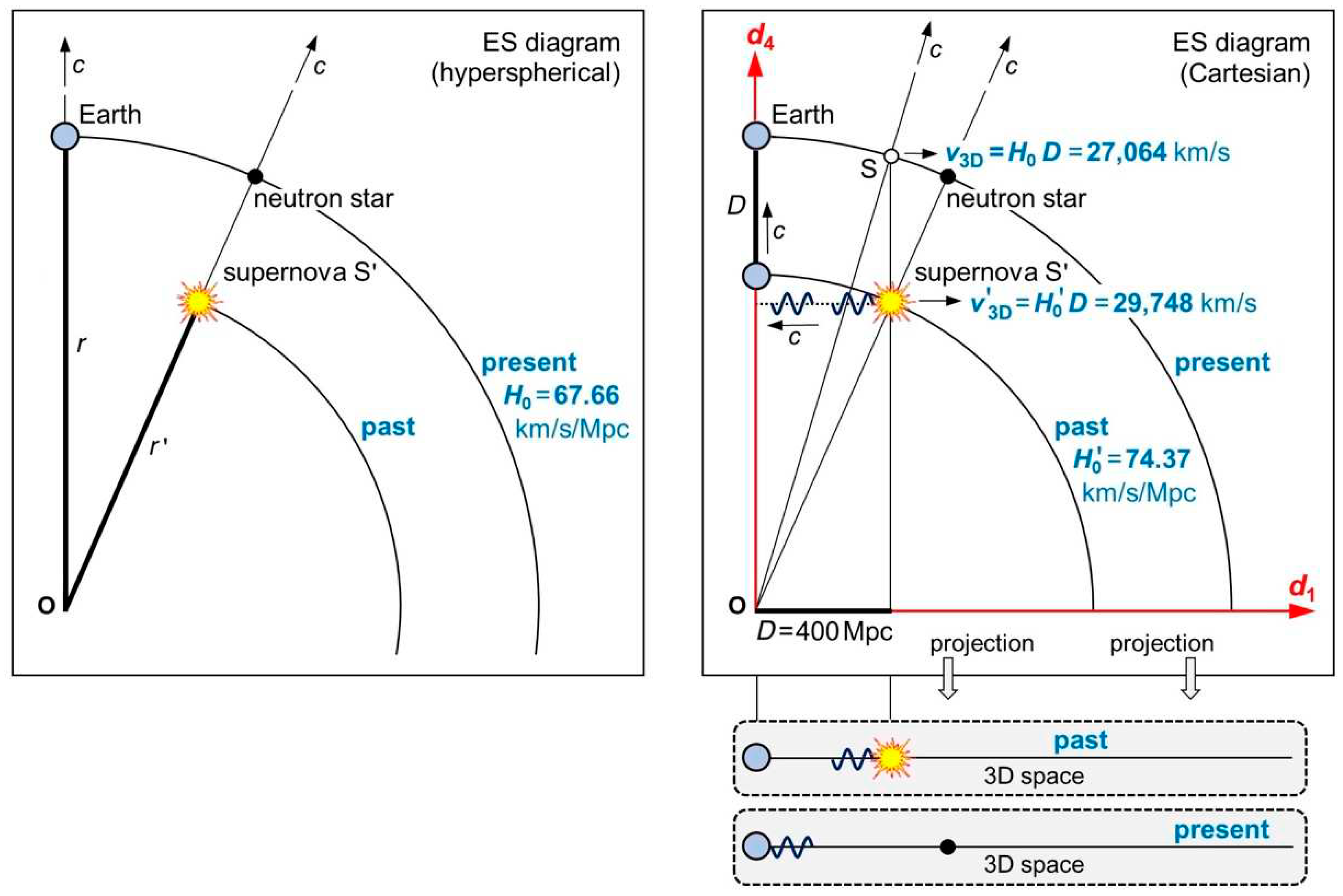
Preprints 66965 g005
Preprints 66965 g006
Figure 6. Concept of wavematter. Artwork illustrating how one object can be deemed wave or matter. Wavematter comes in four orthogonal dimensions: propagation, electric field, magnetic field, and Euclidean time. Each wavematter deems itself matter at rest (internal or in-flight view). If it is observed by some other wavematter (external view), it is deemed wave packet.
Figure 6. Concept of wavematter. Artwork illustrating how one object can be deemed wave or matter. Wavematter comes in four orthogonal dimensions: propagation, electric field, magnetic field, and Euclidean time. Each wavematter deems itself matter at rest (internal or in-flight view). If it is observed by some other wavematter (external view), it is deemed wave packet.
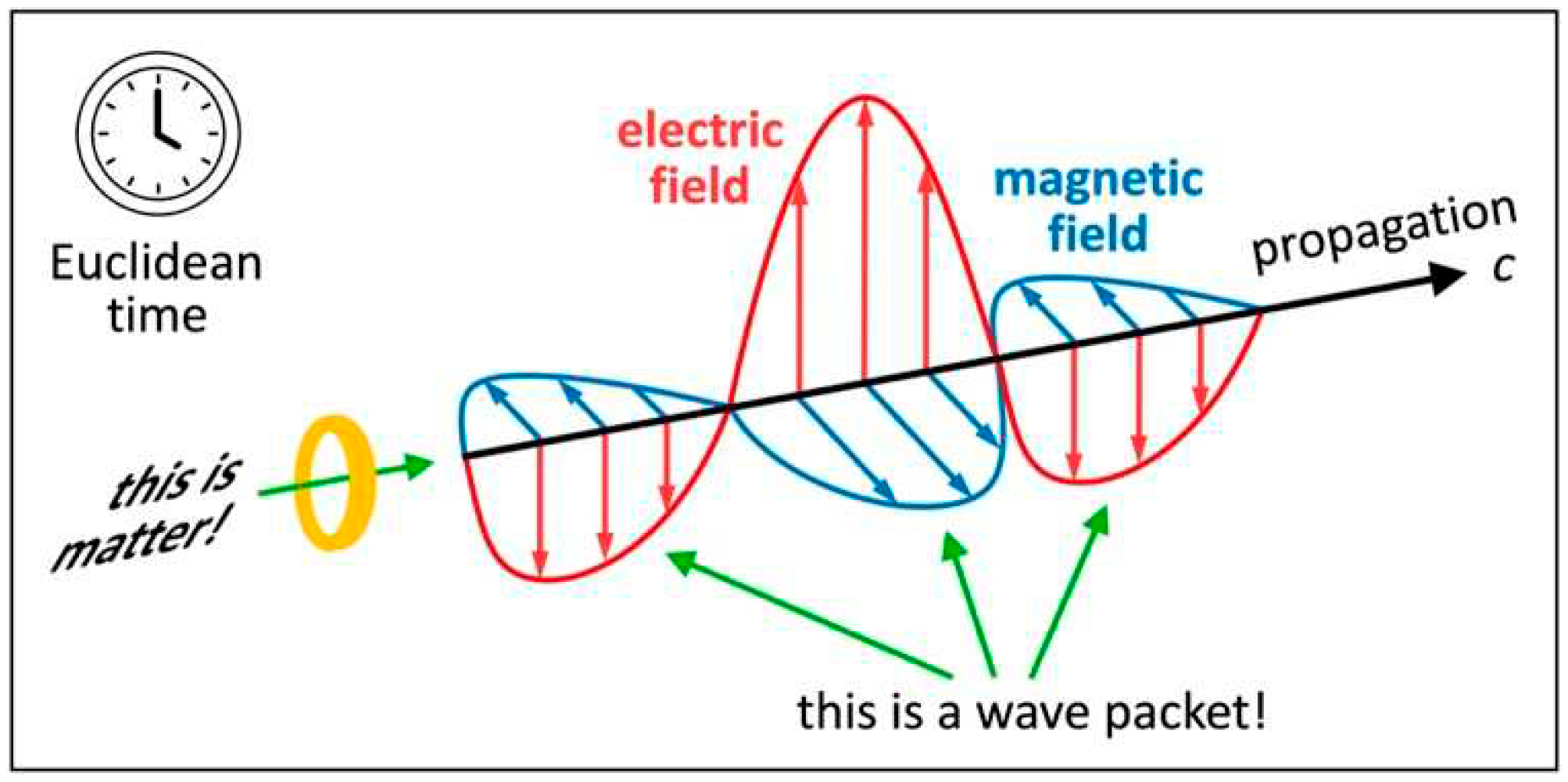
Preprints 66965 g006
Preprints 66965 g007
Figure 7. ES diagrams and 3D projections for three wavematters. Top left: ES in coordinates where W M 1 moves in d 4 . Top right: ES in coordinates where W M 3 moves in d 4 ′ . Bottom left: Projection to W M 1 ’s 3D space. Bottom right: Projection to W M 3 ’s 3D space.
Figure 7. ES diagrams and 3D projections for three wavematters. Top left: ES in coordinates where W M 1 moves in d 4 . Top right: ES in coordinates where W M 3 moves in d 4 ′ . Bottom left: Projection to W M 1 ’s 3D space. Bottom right: Projection to W M 3 ’s 3D space.
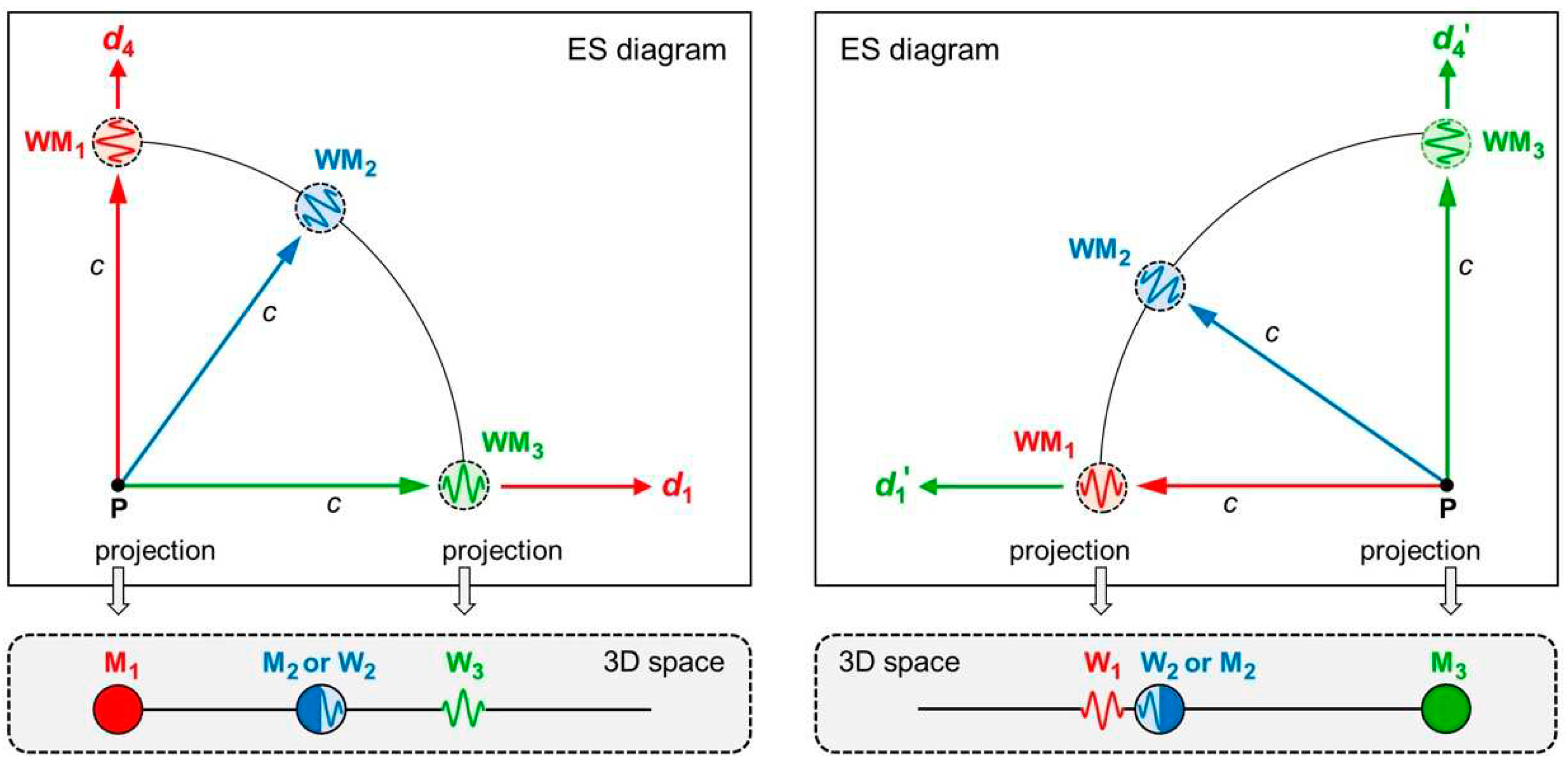
Preprints 66965 g007
Preprints 66965 g008
Figure 8. Quantum entanglement in ES. Artwork illustrating internal view and external view. For each displayed wavematter (internal view), the axis d 4 disappears because of length contraction. It deems its twin and itself one object. For a third wavematter that is moving in a direction other than d 4 (external view), the axis d 4 doesn’t disappear. It deems the displayed wavematters two objects.
Figure 8. Quantum entanglement in ES. Artwork illustrating internal view and external view. For each displayed wavematter (internal view), the axis d 4 disappears because of length contraction. It deems its twin and itself one object. For a third wavematter that is moving in a direction other than d 4 (external view), the axis d 4 doesn’t disappear. It deems the displayed wavematters two objects.
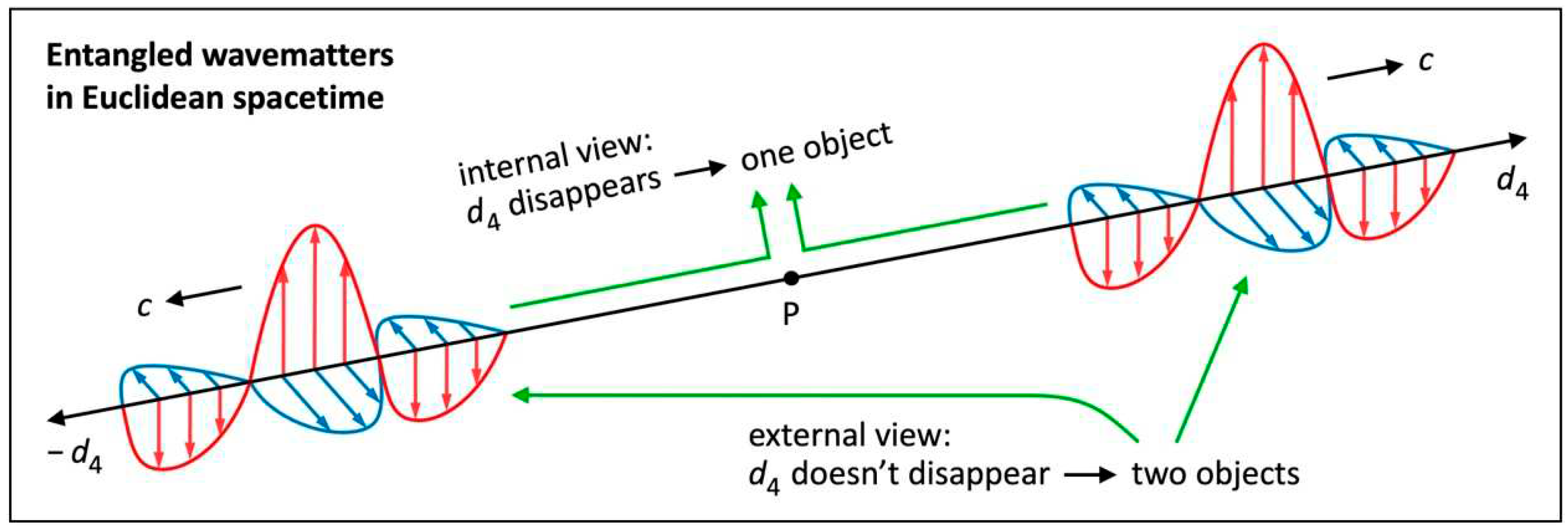
Preprints 66965 g008
Table 1. Comparing the Lambda-CDM model with our model of cosmology.
Table 1. Comparing the Lambda-CDM model with our model of cosmology.
Preprints 66965 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated