Prerpints.org logo
Preprint
Article

Physics at a Crossroads: Weird Concepts or Orthogonal Projections

Altmetrics

Downloads

10730

Views

11128

Comments

1

This version is not peer-reviewed

Submitted:

26 August 2024

Posted:

27 August 2024

Read the latest preprint version here

Alerts
Abstract
Einstein’s special relativity (SR) and general relativity (GR) describe nature in “subjective concepts” (concepts of observers), such as spatial and temporal distance, wave, particle, force, and field. The word “subjective” does not imply that SR/GR would be limited to one point of view. It implies that, despite the Lorentz covariance of SR and the general covariance of GR, any point of view in SR/GR is egocentric. Even coordinate-free formulations of SR/GR or all observers’ views taken together do not make a “holistic view” (comprehensive view from all possible perspectives at the same instant in time) because there is no absolute time in SR/GR. Here I show: Euclidean relativity (ER) describes nature in “objective concepts” (concepts that are immanent in all objects). “Pure distance” replaces spatial and temporal distance. “Pure energy” replaces wave and particle. Each object’s proper space d1, d2, d3 and its proper time τ span an absolute 4D Euclidean spacetime (ES), where d1, d2, d3 and d4 = cτ are pure distances. The invariant is absolute, cosmic time θ. All energy moves through ES at the speed c. An observer’s reality is created by orthogonally projecting the “master reality” ES to his proper space and to his proper time. In SR and GR, the two projections are reassembled to a non-Euclidean spacetime. Information is lost in projections. Thus, there will always be unsolved mysteries if we oppose ER. SR/GR are subordinate theories: Their subjective concepts describe an observer’s reality. ER describes ES and how his reality is created. On top, ER solves 15 mysteries purely geometrically, that is, without forces, fields, and weird concepts (cosmic inflation, expanding space, dark energy, non-locality). Why do physicists prefer weird concepts to two orthogonal projections?
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics
There are two legitimate approaches to describing nature: either in “subjective concepts” (concepts of observers) or else in “objective concepts” (concepts that are immanent in all objects). Only the second approach provides a “holistic view” (comprehensive view from all possible perspectives at the same instant in time), which solves mysteries in cosmology and quantum mechanics (QM). Special relativity (SR) and general relativity (GR) take the first approach [1,2]. Euclidean relativity (ER) takes the second approach. Top journals in physics rejected my theory. Often, I was told that manuscripts are not considered if they challenge SR or GR. This is not how science works! Many hints tell us that SR/GR cannot be the full story. Here is the basic message of my paper: Subjectively, we live in a curved, non-Euclidean spacetime. Objectively, we live in a flat, Euclidean spacetime.
Eight pieces of advice: (1) Do not reject ER unless you can provide a solid argument that would disprove ER. So far, no editor was able to provide a solid argument. (2) Do not pigeonhole ER as unscientific. My version of ER does not disprove but includes SR/GR. (3) Do not take SR/GR as the ultimate truth. Why not consider a theory that is more general than GR? (4) Be open-minded for new ideas. Rather than postulating dark energy and non-locality, ER postulates that my reality is a projection from a master reality. (5) Be fair. One paper cannot cover all of physics. SR/GR have been tested for 100+ years. ER deserves the same chance. (6) Do not be prejudiced against a theory that solves many mysteries. New concepts often do so. (7) Appreciate illustrations. As a geometric theory, ER complies with the stringency of math. (8) Consider that you may be biased. ER declares some concepts of today’s physics obsolete. If you are an expert in one of these concepts, you may easily feel offended.
To sum it all up: SR/GR remain valid in an observer’s reality, but they do not provide a holistic view. ER provides a holistic view, which is required for the solution to the Hubble constant tension and other mysteries. I do apologize for my several preprint versions, but I received almost no support. My final version is all that is needed. The earlier versions show how I got there. It was tricky to figure out why SR/GR work so well despite an issue. Sect. 2 is about this issue. Sect. 3 describes ER. In Sect. 4, I recover the Lorentz factor and gravitational time dilation. In Sect. 5, I outline the solutions to 15 mysteries.

1. Introduction

Today’s concepts of space and time were coined by Albert Einstein. In SR, space and time are merged into a flat spacetime described by the Minkowski metric. SR is often presented in Minkowski spacetime because this concept illustrates the invariance of the spacetime interval very well [3]. Predicting the lifetime of muons [4] is an example that supports SR. In GR, curved spacetime is described by the 4×4 Einstein tensor. The deflection of starlight [5] and the high accuracy of GPS [6] are examples that support GR. Quantum field theory [7] unifies classical field theory, SR, and QM, but it excludes GR.
The postulates of ER: (1) All energy moves through 4D Euclidean spacetime (ES) at the speed of light c . (2) The laws of physics have the same form in each observer’s reality. (3) An observer’s reality is created by orthogonally projecting ES to his proper space and to his proper time. In SR and GR, the two projections are reassembled to a non-Euclidean spacetime. It is not my task to show how this reassembly is done. Obviously, spacetime in SR/GR is non-Euclidean. My first postulate is stronger than the second SR postulate: c  is absolute and universal. My second postulate refers to realities and not to inertial frames. My third postulate is unique. I also introduce objective concepts: “Pure distance” replaces spatial and temporal distance. “Pure energy” replaces wave and particle. To improve readability, all my observers are male. To make up for it, Mother Nature is female.
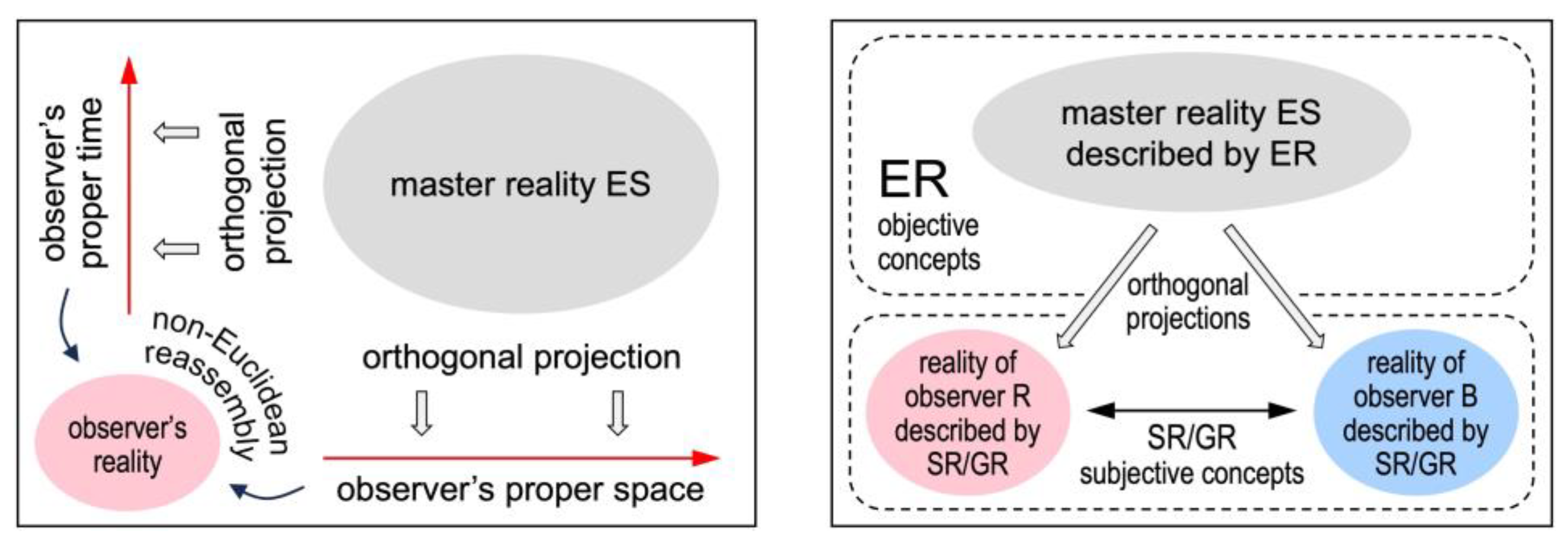
Since an observer’s reality is created by projecting ES, I call ES the “master reality”. Figure 1 left illustrates how ES relates to an observer’s reality. Information is lost in projections. Thus, there will always be unsolved mysteries if we oppose ER. Figure 1 right illustrates that SR/GR are subordinate theories: Their subjective concepts describe an observer’s reality and how the realities of two observers relate to each other. ER describes ES and how an observer’s reality is created. Note that ER describes nature but not an observer’s reality!
Preprints 116276 g001
Figure 1. Master reality ES and observer’s reality. Left: Illustration of how ES relates to an observer’s reality. Right: Illustration of where to apply ER and where to apply SR/GR.
Figure 1. Master reality ES and observer’s reality. Left: Illustration of how ES relates to an observer’s reality. Right: Illustration of where to apply ER and where to apply SR/GR.
Preprints 116276 g001
Newburgh and Phipps [8] pioneered ER. Montanus [9] described an absolute Euclidean spacetime with a “preferred frame of reference” (a pure time interval is a pure time interval for all observers). Montanus [10] claims: Without the preferred frame, we would face the twin paradox and a “character paradox” (confusion of photons, particles, antiparticles). I show that the preferred frame is obsolete. Whatever is proper time for me, it may be proper space for you. There is no twin paradox if we take cosmic time as the parameter. There is no character paradox if we apply “pure energy” (see Sect. 5.13). Montanus [11] tried to describe kinematics in ES using the Lagrange formalism. Montanus [10] even tried to formulate Maxwell’s equations in ES but wondered about a wrong sign. He overlooked that the SO(4) symmetry of ES is incompatible with waves. Montanus [10] calculated that ER predicts the same precession of Mercury’s perihelion as GR.
Almeida [12] studied geodesics in ES. Gersten [13] showed that the Lorentz transformation is an SO(4) rotation in a “mixed space” (see Sect. 3). van Linden [14] maintains a website about ER. Physicists are opposing ER because dark energy and non-locality make cosmology and QM work, waves are excluded, and paradoxes turn up if ER is expected to describe an observer’s reality. This paper marks a turning point: I disclose an issue in SR/GR. I justify the exclusion of waves. I avoid paradoxes by projecting ES.
It is instructive to contrast Newton’s physics, Einstein’s physics, and ER. In Newton’s physics, all energy moves through 3D Euclidean space as a function of independent time. There is no speed limit for matter. In Einstein’s physics, all energy moves through 4D non-Euclidean spacetime. The speed of matter is v 3 D < c . In ER, all energy moves through ES. The 4D speed of all energy is u 4 D = c . Newton’s physics [15] influenced Kant’s philosophy [16]. Will ER reform both physics and philosophy?

2. Disclosing an Issue in Special and General Relativity

The fourth coordinate in SR is an observer’s coordinate time t . In § 1 of SR, Albert Einstein provides an instruction on how to synchronize two clocks at the points P and Q. At t P , a light pulse is sent from P to Q. At t Q , the light pulse is reflected at Q. At t P * , the light pulse is back at P. The two clocks synchronize if
t Q − t P = t P * − t Q .
In § 3 of SR, Einstein derives the Lorentz transformation. The coordinates x 1 ,   x 2 ,   x 3 ,   t of an event in a system K are transformed to the coordinates x 1 ′ ,   x 2 ′ ,   x 3 ′ ,   t ′ in K’ by
x 1 ′ = γ ( x 1 − v 3 D t ) ,
x 2 ′ = x 2 ,   x 3 ′ = x 3 ,
t ′ = γ ( t − v 3 D x 1 / c 2 ) ,
where K’ moves relative to K in x 1 at the constant speed v 3 D and γ = ( 1 − v 3 D 2 / c 2 ) − 0.5 is the Lorentz factor. Mathematically, Eqs. (1) and (2a–c) are correct for observers in K. There are covariant equations for observers in K’. Physically, there is an issue in SR and also in GR: The subjective concepts applied in SR and GR fail to solve fundamental mysteries of physics. The word “subjective” does not imply that SR/GR would be limited to one point of view. It implies that, despite the Lorentz covariance of SR and the general covariance of GR, any point of view in SR/GR is egocentric. Even coordinate-free formulations of SR/GR or all observers’ views taken together do not make a holistic view because there is no absolute time in SR/GR and thus no same instant in time. Without absolute time, observers will not always agree on what is past and what is future. Physics has paid an enormous price for dismissing absolute time: ER restores absolute time (see Sect. 3) and solves 15 fundamental mysteries (see Sect. 5). Thus, the issue in SR/GR is real.
The issue in SR/GR is not about making wrong predictions. It has much in common with the issue in the geocentric model: In either case, there is no holistic view. Geocentrism is the egocentric view of mankind. In the old days, it was natural to believe that all celestial bodies would orbit Earth. Only the astronomers wondered about the retrograde loops of planets and claimed that Earth orbits the sun. In modern times, engineers have improved rulers and clocks. Today, it is natural to believe that it would be fine to describe nature as accurately as possible but from one or more egocentric perspectives. The human brain is very smart, but it often takes itself as the center/measure of everything.
The analogy of SR/GR to the geocentric model is stunningly close: (1) It holds despite all covariances. After a transformation in SR/GR (or after appointing another planet as the center of the Universe), the perspective is again egocentric (or else geocentric). (2) ER has much in common with a “heliocentric model 2.0”, where the sun is the center of our solar system but not of our galaxy. That model provides a holistic view from “beyond” (outside of) our galaxy. ER provides a holistic view from beyond each observer’s reality. (3) SR/GR and the geocentric model work by themselves, but only if we add weird concepts. Retrograde loops are obsolete but only in the heliocentric model. Dark energy and non-locality are obsolete but only in ER. (4) Our ancestors rejected heliocentrism. ER is rejected today. Have physicists not learned from history? Does history repeat itself?

3. The Physics of Euclidean Relativity

The Minkowski metric in SR is often written as
c 2 d τ 2 = c 2 d t 2 − d x 1 2 − d x 2 2 − d x 3 2 ,
where d τ is an infinitesimal distance in proper time τ , whereas d t and d x i ( i = 1 ,   2 ,   3 ) are infinitesimal distances in coordinate spacetime x 1 ,   x 2 ,   x 3 ,   t . This spacetime is construed because coordinate space x 1 ,   x 2 ,   x 3 and coordinate time t are subjective concepts: They are not immanent in rulers/clocks but are construed by observers. Rulers measure proper length. Clocks measure proper time. I introduce ER by defining its metric
c 2 d θ 2 = d d 1 2 + d d 2 2 + d d 3 2 + d d 4 2 ,
where d θ is an infinitesimal distance in cosmic time θ , whereas all d d i ( i = 1 ,   2 ,   3 ) and d d 4 = c   d τ are infinitesimal distances in 4D Euclidean spacetime d 1 ,   d 2 ,   d 3 ,   d 4 . The roles of θ and τ are switched: The invariant is absolute, cosmic time θ . The fourth coordinate is an object’s proper time τ . The metric tensor is the identity matrix. I choose the symbol θ because the initial of theta is “t” as in time. I prefer the indices 1–4 to 0–3 to stress the 4D symmetry. Each object’s proper space d 1 ,   d 2 ,   d 3 and its proper time τ span ES, where d 1 ,   d 2 ,   d 3 and d 4 = c τ are pure distances. This spacetime is natural because all d μ ( μ = 1 ,   2 ,   3 ,   4 ) are objective concepts: They are immanent in rulers/clocks because all rulers/clocks measure d μ . We must not confuse Eq. (4) with a Wick rotation [17], where coordinate time t is imaginary and proper time τ remains the invariant parameter.
Each object is free to label the axes of ES. We assume that it labels the axis of its current 4D motion as d 4 . Since it does not move in its proper space, it has to move in the d 4 axis at the speed c (my first postulate). Because of length contraction at the speed c , the d 4 axis disappears for itself and is experienced as proper time. Objects moving in the d 4 ′ axis at the speed c experience this axis as proper time. An object’s proper time flows in the direction of its 4D motion. Thus, there is a relative 4D vector “flow of proper time” τ .
τ = d 4 / c ,   τ ′ = d 4 ′ / c ,
τ = d 4 u / c 2 ,   τ ′ = d 4 ′ u ′ / c 2 ,
where u is an object’s 4D velocity in ES. For all objects, there is u μ = d d μ / d θ , where θ is absolute, cosmic time. Thus, Eq. (4) is equivalent to my first postulate.
u 1 2 + u 2 2 + u 3 2 + u 4 2 = c 2 .
My second postulate generalizes the principle of relativity to all observers’ realities. Since coordinate time t in Eq. (3) is not the same as cosmic time θ in Eq. (4), there is no continuous transition between Eqs. (3) and (4). In SR, objects are described by the coordinates x 1 ( τ ) ,   x 2 ( τ ) ,   x 3 ( τ ) , t ( τ ) , where proper time τ is the parameter and t is coordinate time. In ER, objects are described by the coordinates d 1 ( θ ) ,   d 2 ( θ ) ,   d 3 ( θ ) ,   d 4 ( θ ) , where cosmic time θ is the parameter and d 4 relates to τ according to Eq. (5). There also seems to be an issue in ER: Only in proper coordinates can we access ES, but the proper coordinates of other objects cannot be measured. In my Conclusions, I explain why this is not an issue. ER is a physical theory because it solves mysteries in an observer’s reality.
It is instructive to contrast the three concepts of time. Coordinate time t is a subjective measure of time: An observer uses his clock as the master clock. Proper time τ is an objective measure of time: Clocks measure τ independently of observers. Cosmic time θ is the total distance covered in ES (length of a worldline) divided by c . By taking θ as the parameter, all observers will agree on what is past and what is future. Since cosmic time is absolute, there is no twin paradox in ER. Twins are the same age in cosmic time.
Let us compare SR with ER. We consider two identical clocks “r” (red clock) and “b” (blue clock). In SR, “r” moves in the c t axis. Clock “b” starts at x 1 = 0 and moves in the x 1 axis at a constant speed of v 3 D = 0.6   c . Figure 2 left shows the instant when either clock moved 1.0 s in c t . Clock “b” moved 0.6 Ls (light seconds) in x 1 and 0.8 Ls in c t ′ . It displays “0.8”. In ER, Figure 2 right shows the instant when either clock moved 1.0 s in its proper time. Both clocks display “1.0”. Clock “b” moved 0.6 Ls in d 1 and 0.8 Ls in d 4 .
We now assume that an observer R (or B) is moving with the clock “r” (or else “b”). In SR and only from R’s perspective, clock “b” is at c t ′ = 0.8   L s when “r” is at c t = 1.0   L s (see Figure 2 left). Thus, “b” is slow with respect to “r” in t ′ (of B). In ER and independently of observers, clock “b” is at d 4 = 0.8   L s when “r” is at d 4 = 1.0   L s (see Figure 2 right). Thus, “b” is slow with respect to “r” in d 4 (of R). In SR and ER, “b” is slow with respect to “r”, but time dilation occurs in different axes. Experiments do not disclose the axis in which a clock is slow. Thus, SR and ER may claim that they describe time dilation correctly.
But why does ER provide a holistic view? Well, ES is independent of observers and thus absolute. This justifies the name “master reality”. Only the projections from ES are relative. Absolute ES shows up in the rotational symmetry of all ES diagrams: Figure 2 right works for R and for B at once. A second Minkowski diagram is required for B, where x 1 ′ and c t ′ are orthogonal. The absoluteness also shows up in Eq. (4): All d μ ( μ = 1 ,   2 ,   3 ,   4 ) are interchangeable. Only observers experience distance as spatial or temporal.
Gersten [13] showed that the Lorentz transformation is an SO(4) rotation in a “mixed space” x 1 ,   x 2 ,   x 3 ,   c t ′ , where only c t ′ is primed. The four mixed coordinates x 1 ,   x 2 ,   x 3 ,   c t ′ rotate to x 1 ′ ,   x 2 ′ ,   x 3 ′ ,   c t . I will not repeat the derivation. I consider it my task to turn ER into an accepted theory by revealing its power. However, a mixed space is physically pointless. In ER, unmixed d 1 ′ ,   d 2 ′ ,   d 3 ′ ,   d 4 ′ rotate with respect to d 1 ,   d 2 ,   d 3 ,   d 4 (see Sect. 4).
There is also a big difference in the synchronization of clocks: In SR, each observer is able to synchronize a uniformly moving clock to his clock (same value of c t in Figure 2 left). If he does, these clocks are not synchronized from the perspective of the moving clock. In ER, clocks with the same 4D vector τ are always synchronized, whereas clocks with different τ and τ ' are never synchronized (different values of d 4 in Figure 2 right).

4. Geometric Effects in 4D Euclidean Spacetime

We consider two identical rockets “r” (red rocket) and “b” (blue rocket). Let observer R (or B) be in the rear end of “r” (or else “b”). The 3D space of R (or B) is spanned by d 1 ,   d 2 ,   d 3 (or else d 1 ′ ,   d 2 ′ ,   d 3 ′ ). “3D space” is a synonym of “proper space”. The proper time of R (or B) relates to d 4 (or else d 4 ′ ) according to Eq. (5). Both rockets start at the point P and move relative to each other at the constant speed v 3 D . R and B are free to label the axis of relative motion. They label it as d 1 (or d 1 ′ ). The ES diagrams in Figure 3 must fulfill my postulates and the initial condition (point P). This is achieved by rotating the red and the blue frame with respect to each other. In all ES diagrams, objects maintain proper length and clocks display proper time. To improve readability, a rocket’s width is drawn in d 4 (or d 4 ′ ) rather than in d 2 ,   d 3 (or d 2 ′ ,   d 3 ′ ). Figure 3 bottom shows the projection to the 3D space of R (or B).
Up next, we verify: (1) Rotating the red and the blue frame with respect to each other causes length contraction. (2) The fact that proper time flows in different 4D directions for R and for B causes time dilation. The rotations are no surprise. Weyl [18] showed that the Lorentz group is generated by 4D rotations. Let L i , j be the length of rocket i for observer j . In a first step, we project the blue rocket in Figure 3 top left to the d 1 axis.
sin 2 ⁡ φ + cos 2 ⁡ φ = ( L b , R / L b , B ) 2 + ( v 3 D / c ) 2 = 1 ,
L b , R = γ − 1   L b , B ( length   contraction )
where γ = ( 1 − v 3 D 2 / c 2 ) − 0.5 is the same Lorentz factor as in SR. For observer R, rocket “b” contracts to L b , R . Which distances will R observe in his d 4 axis? We continue the rotation of “b” in Figure 3 top left until it serves as a ruler for R in his d 4 axis. In the 3D space of R, this ruler contracts to a point: The d 4 axis disappears for R because of length contraction at the speed c . In a second step, we project the blue rocket in Figure 3 top left to the d 4 axis.
sin 2 ⁡ φ + cos 2 ⁡ φ = ( d 4 , B / d 4 , B ′ ) 2 + ( v 3 D / c ) 2 = 1 ,
d 4 , B = γ − 1 d 4 , B ′ ,
where d 4 , B (or d 4 , B ′ ) is the distance that B moved in d 4 (or else d 4 ′ ). With d 4 , B ′ = d 4 , R (R and B cover the same distance in ES but in different directions), we calculate
d 4 , R   =   γ   d 4 , B ( time   dilation ) ,
where d 4 , R is the distance that R moved in d 4 . Eqs. (9) and (12) tell us: γ is recovered in ER if we project ES to the axes d 1 and d 4 of an observer. The rockets in Figure 3 serve as an example. Any other object is projected the same way to an observer’s reality. Orthogonal projections were discussed in detail by Nowinski [19].
Up next, we transform the proper coordinates of observer R to those of B. We recall that R (or B) is in the rear end of rocket “r” (or else “b”). We refer to Figure 3 again, but we now calculate the 4D motion of R and of B as a function of the parameter θ . R and B start at the point P. The starting time is θ 0 . R cannot measure the proper coordinates of B, and vice versa, but we can calculate them all by evaluating the ES diagrams in Figure 3.
d 1 , R θ = d 1 , R ( θ 0 ) ,
d 2 , R θ = d 2 , R ( θ 0 ) ,   d 3 , R θ = d 3 , R ( θ 0 ) ,
d 4 , R θ = d 4 , R θ 0 + c ( θ − θ 0 ) .
d 1 , B ′ θ = d 1 , B ′ ( θ 0 ) ,
d 2 , B ′ θ = d 2 , B ′ ( θ 0 ) ,   d 3 , B ′ θ = d 3 , B ′ ( θ 0 ) ,
d 4 , B ′ θ = d 4 , B ′ θ 0 + c ( θ − θ 0 ) .
To transform the proper coordinates of R (unprimed) to the proper coordinates of B (primed), we have to take the rotation angle 90 0 − φ into account (see Figure 3).
d 1 , R ′ θ = d 4 , R θ cos ⁡ φ = d 4 , R θ v 3 D / c ,
d 2 , R ′ θ = d 2 , R ( θ ) ,   d 3 , R ′ θ = d 3 , R ( θ ) ,
d 4 , R ′ θ = d 4 , R θ sin ⁡ φ = d 4 , R θ γ − 1 .
To understand how an acceleration manifests itself in ES, we return to our two clocks. Clock “r” and Earth move in the d 4 axis of “r” at the speed c (see Figure 4), but clock “b” accelerates in the d 1 axis of “r” toward Earth while maintaining the speed c . Because of Eq. (7), the speed u 1 , b of “b” in d 1 increases at the expense of its speed u 4 , b in d 4 .
Gravitational waves [20] support the idea of GR that gravity is a feature of spacetime. However, the SO(4) symmetry of ES is incompatible with waves. This is not an issue if we accept that waves occur in an observer’s reality only. There are no waves in ES. In ER, an objective concept of force has yet to be defined, which manifests as gravity or as another force in an observer’s reality. I suggest to take “process” as the objective concept of force. Typical processes are the transfer of energy or momentum [21]. As an example, we recover gravitational time dilation in ER. We consider the transfer of potential energy to kinetic energy. Initially, our clocks “r” and “b” are very far away from Earth. Eventually, “b” falls freely toward Earth as shown in Figure 4. The kinetic energy of “b” in d 1 is
1 2 m u 1 , b 2 = G M m / R ,
where m is the mass of “b”, G is the gravitational constant, M is the mass of Earth, and R is the distance of “b” to Earth’s center. By applying Eq. (7), we obtain
u 4 , b 2 = c 2 − u 1 , b 2 = c 2 − 2 G M / R .
With u 4 , b = d d 4 , b / d θ (“b” moves in the d 4 axis at the speed u 4 , b ) and c = d d 4 , r / d θ (“r” moves in the d 4 axis at the speed c ), we calculate
d d 4 , b 2 = ( c 2 − 2 G M / R ) ( d d 4 , r / c ) 2 ,
d d 4 , r = γ g r   d d 4 , b ( gravitational   time   dilation )
where γ g r = ( 1 − 2 G M / ( R c 2 ) ) − 0.5 is the same dilation factor as in GR. It does not depend on relative motion. Eq. (19) tells us: γ g r is recovered in ER if we project ES to the d 4 axis of an observer. More studies are required to confirm process as an objective concept. Force and field are subjective concepts. Thus, there are field equations in SR/GR only.
Summary of time dilation: In SR, a uniformly moving clock “b” is slow with respect to “r” in the time dimension of “b”. In GR, an accelerating clock “b” or a clock “b” in a stronger gravitational field is slow with respect to “r” in the time dimension of “b”. In ER, a clock “b” is slow with respect to “r” in the time dimension of “r” (!) if the 4D vectors τ of “r” and τ ′ of “b” are not the same. Since both dilation factors γ and γ g r are recovered in ER, the results of the Hafele–Keating experiment [22] do not only support SR/GR but also ER. Thus, GPS satellites work in ER as well as in SR/GR.
Three instructive problems teach us how to read ES diagrams correctly (see Figure 5). Problem 1: In billiards, the blue ball is approaching the red ball. In ES, both balls move at the speed c . Let the red ball move in its d 4 axis. As the blue ball covers distance in d 1 , its speed in d 4 must be less than c . How can the balls ever collide if their d 4 values do not match? Problem 2: A rocket moves along a guide wire. In ES, both objects move at the speed c . Let the wire move in its d 4 axis. As the rocket covers distance in d 1 , its speed in d 4 must be less than c . Doesn’t the wire escape from the rocket? Problem 3: Earth orbits the sun. In ES, both objects move at the speed c . Let the sun move in its d 4 axis. As Earth covers distance in d 1 ,   d 2 , its speed in d 4 must be less than c . Doesn’t the sun escape from Earth?
The questions in the last paragraph seem to disclose geometric paradoxes in ER. The fallacy lies in the assumption that all four dimensions of ES would be spatial. We solve all problems by projecting ES to the 3D space of the object that moves in d 4 at the speed c . In its 3D space, it is at rest. We see the solutions in the ES diagrams, too, if we read them correctly: For instance, the balls “r” and “b” in Figure 5 left collide if d i , r = d i , b ( i = 1 ,   2 ,   3 ) and if the same cosmic time has elapsed for both balls ( d 4 , r = d 4 , b ′ ). Thus, a collision in 3D space does not show up as a collision in ES. This is reasonable because only three out of the four d μ ( μ = 1 ,   2 ,   3 ,   4 ) are experienced as spatial by an observer.

5. Outlining the Solutions to 15 Fundamental Mysteries

We recall: (1) An observer’s reality is created by orthogonally projecting ES to his proper space and to his proper time. (2) There is a relative 4D vector τ . (3) Cosmic time θ is the correct parameter for a holistic view. In Sects. 5.1 through 5.15, I outline the solutions to 15 mysteries and declare four concepts of today’s physics obsolete. Note that all solutions are purely geometrical! They involve neither forces nor fields.

5.1. The Mystery of Time

Proper time τ is what clocks measure ( d 4 divided by c ). Cosmic time θ is the total distance covered in ES (length of a worldline) divided by c . An observer’s clock always displays both quantities: his proper time τ and cosmic time θ .

5.2. The Mystery of Time’s Arrow

Time’s arrow is a synonym for “time moving only forward”. The arrow emerges from the fact that covered distance ( d 4 or total distance) cannot decrease but only increase.

5.3. The Mystery of the Factor c 2 in the Energy Term m c 2

In SR, if forces are absent, the total energy E of an object is given by
E = γ m c 2 = E k i n , 3 D + m c 2 ,
where E k i n , 3 D is its kinetic energy in an observer’s 3D space and m c 2 is called its “energy at rest”. SR does not tell us why there is a factor c 2 in the energy of objects that in SR do not move at the speed c . ER gives us the missing clue: The object is never at rest but moves in its d 4 ′ axis. From the object’s perspective, E k i n , 3 D is zero and m c 2 is its kinetic energy in d 4 ′ . The factor c 2 is a hint that it moves through ES at the speed c . In SR, there is
E 2 = p 2 c 2 = p 3 D 2 c 2 + m 2 c 4 ,
where p is the total momentum of an object and p 3 D is its momentum in an observer’s 3D space. Again, ER is eye-opening: From the object’s perspective, p 3 D is zero and m c is its momentum in d 4 ′ . The factor c is a hint that it moves through ES at the speed c .

5.4. The Mystery of Length Contraction and Time Dilation

In SR, length contraction and time dilation can be derived from the Lorentz transformation, but their physical cause remains in the dark. ER discloses that length contraction and time dilation stem from projecting ES to the axes d 1 and d 4 of an observer.

5.5. The Mystery of Gravitational Time Dilation

In GR, gravitational time dilation is caused by a curved spacetime. ER discloses that gravitational time dilation stems from projecting curved worldlines in a flat ES to the d 4 axis of an observer. Eq. (7) tells us: If an object accelerates in his proper space, it automatically decelerates in his proper time. Thus, an accelerating object follows a curved worldline in a flat ES. More studies are required to understand other gravitational effects in ER.

5.6. The Mystery of the Cosmic Microwave Background (CMB)

In Sects. 5.6 through 5.12, I outline an “ER-based model of cosmology”. Distances are like numbers. In particular, they are not inflating/expanding. For some reason, there was a Big Bang. In the inflationary Lambda-CDM model, the Big Bang occurred “everywhere” because space inflated from a singularity. In the ER-based model, the Big Bang is locatable: It injected a huge amount of energy into ES at an origin O ( θ = 0 ). Cosmic time θ is also the total time that has elapsed since the Big Bang. The Big Bang was a singularity in providing energy and radial momentum. All energy started moving radially away from O. Shortly after θ = 0 , “pure energy” (objective concept, see Sect. 5.13) was highly concentrated in ES. In the projection to any 3D space, plasma particles (subjective concept) were created. Recombination radiation was emitted that we observe as CMB today [23].
The ER-based model must be able to answer these questions: (1) Why is the CMB so isotropic? (2) Why is the temperature of the CMB so low? (3) Why do we still observe the CMB today? Here are some possible answers: (1) The CMB is so isotropic because it has been scattered equally in the 3D space d 1 , d 2 , d 3 of Earth. (2) The temperature of the CMB is so low because the plasma particles had a very high recession speed v 3 D (see Sect. 5.7) shortly after the Big Bang. (3) The CMB has been scattered multiple times in d 1 ,   d 2 ,   d 3 and reaches Earth after having covered the same distance in d 1 ,   d 2 ,   d 3 as Earth in d 4 .

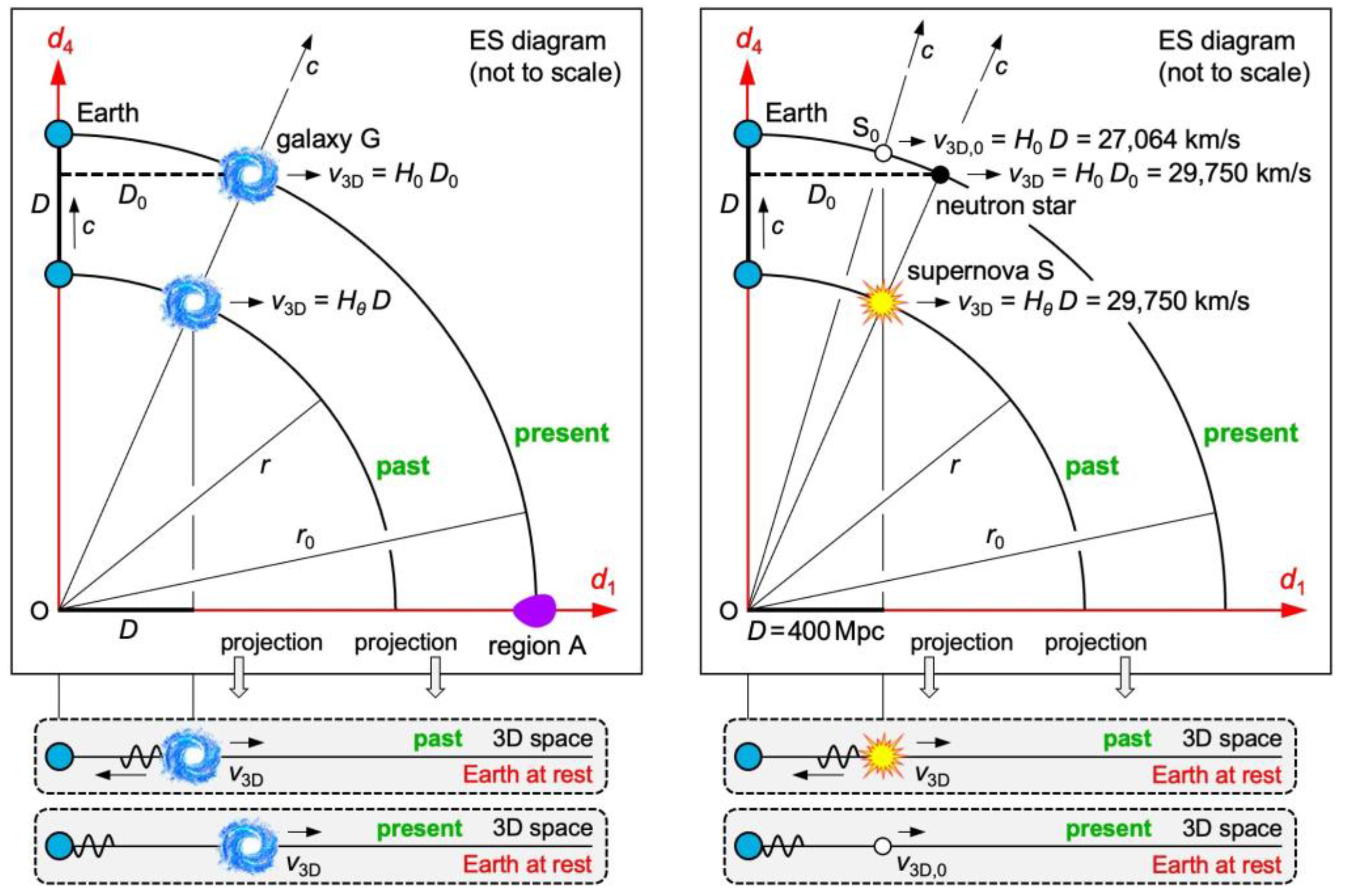
5.7. The Mystery of the Hubble–Lemaître Law

In Figure 6 left, Earth and a galaxy G recede from the origin O of ES. In Earth’s 3D space, G recedes from Earth at the 3D speed v 3 D . According to my first postulate, v 3 D relates to the 3D distance D of G to Earth as c relates to the radius r of a 4D hypersphere.
Preprints 116276 g006
Figure 6. ER-based model of cosmology. The circular arcs are part of an expanding 3D hypersurface. Left: Galaxy G recedes from the location of the Big Bang (origin O of ES) at the speed c , and from the d 4 axis in particular at the 3D speed v 3 D . Right: If star S 0 happens to be at the same distance D today at which the supernova of star S occurred, S 0 recedes more slowly from Earth than S .
Figure 6. ER-based model of cosmology. The circular arcs are part of an expanding 3D hypersurface. Left: Galaxy G recedes from the location of the Big Bang (origin O of ES) at the speed c , and from the d 4 axis in particular at the 3D speed v 3 D . Right: If star S 0 happens to be at the same distance D today at which the supernova of star S occurred, S 0 recedes more slowly from Earth than S .
Preprints 116276 g006
v 3 D = D c / r = H θ D ,
where H θ = c / r = 1 / θ is the Hubble parameter. If we observe G today at the cosmic time θ 0 , the recession speed v 3 D and c remain unchanged. Thus, Eq. (22) turns into
v 3 D = D 0 c / r 0 = H 0 D 0 ,
where H 0 = c / r 0 = 1 / θ 0 is the Hubble constant, D 0 = D   r 0 / r is today’s 3D distance of G to Earth, and r 0 is today’s radius of the 4D hypersphere. Eq. (23) is the Hubble–Lemaître law [24,25]. Cosmologists are aware of the Hubble parameter and of the quantity “cosmic time”. They are not yet aware that the 4D geometry is Euclidean, that Eq. (23) refers to D 0 rather than to D , and that there is no acceleration. Out of any two galaxies, the one farther away recedes faster, but each galaxy maintains its 3D speed v 3 D .

5.8. The Mystery of the Flat Universe

For each observer, ES is orthogonally projected to his proper space and to his proper time. Thus, he experiences two seemingly discrete structures: a flat 3D space and time.

5.9. The Mystery of Cosmic Inflation

Many cosmologists believe that an inflation of space shortly after the Big Bang [26,27] would explain the isotropic CMB, the flat universe, and large-scale structures (inflated from quantum fluctuations). I just showed that ER explains the first two effects. ER even explains large-scale structures if the impacts of quantum fluctuations have been expanding like the 4D hypersphere. In ER, cosmic inflation is an obsolete concept.

5.10. The Mystery of Cosmic Homogeneity (Horizon Problem)

How can the universe be so homogeneous if there are casually disconnected regions of space? In the Lambda-CDM model, a region A at x 1 = + r 0 and a region B at x 1 = − r 0 are casually disconnected unless we postulate a cosmic inflation. Without it, information could not have covered 2 r 0 since the Big Bang. ER solves the problem without a cosmic inflation: In Figure 6 left, A is at d 1 = + r 0 and B is at d 1 = − r 0 (not shown). From A’s or B’s perspective, their d 4 ′ axis (equal to Earth’s d 1 axis) disappears because of length contraction at the speed c . A and B are casually connected because they overlap spatially in either reality. Their opposite 4D vectors + τ ′ and − τ ′ do not affect casual connectivity.

5.11. The Mystery of the Hubble Constant Tension

Up next, I explain why the published values of the Hubble constant H 0 do not match each other (also known as the “Hubble constant tension”). I compare data of CMB measurements (Planck space telescope) with data of calibrated distance ladder measurements (Hubble space telescope). According to team A [28], there is H 0 = 67.66 ± 0.42   k m / s / M p c . According to team B [29], there is H 0 = 73.04 ± 1.04   k m / s / M p c . Team B made efforts to minimize the error margins in the distance measurements, but a systematic error in team B’s calculation of H 0 arises from assuming a wrong cause of the redshifts.
Let us assume that team A’s value of H 0 is correct. We simulate the supernova of a star S that occurred at a distance of D = 400   M p c from Earth (Figure 6 right). The recession speed v 3 D of S is calculated from measured redshifts. The redshift parameter z = Δ λ / λ tells us how each wavelength λ of the supernova’s light is either stretched by an expanding space (team B) or else Doppler-redshifted by receding objects (ER-based model). The supernova occurred at the cosmic time θ (arc called “past”), but we observe it at the cosmic time θ 0 (arc called “present”). While the supernova’s light moved the distance D in d 1 , Earth moved the same distance D but in d 4 (my first postulate). There is
1 / H θ = r / c = ( r 0 − D ) / c = 1 / H 0 − D / c .
For a very short distance of D = 400   k p c , Eq. (24) tells us that H θ deviates from H 0 by only 0.009 percent. However, when plotting v 3 D versus D for distances from 0 Mpc to 500 Mpc in steps of 25 Mpc (red points in Figure 7), the slope of a straight-line fit through the origin is roughly 10 percent greater than H 0 . Since team B calculates H 0 from similar but mirrored plots (magnitude versus z ), its value of H 0 is roughly 10 percent too high. This solves the Hubble constant tension. Team B’s value is not correct because, according to Eq. (23), we must plot v 3 D versus D 0 (blue points in Figure 7) to get a straight line.
Since we cannot measure D 0 (observable magnitudes relate to D rather than to D 0 ), the easiest way to fix the calculation of team B is to rewrite Eq. (23) as
v 3 D , 0 = D c / r 0 = H 0 D ,
where v 3 D , 0 is today’s 3D speed of another star S 0 (Figure 6 right) that happens to be at the same distance D today at which the supernova of star S occurred. I kindly ask team B to recalculate H 0 after converting all v 3 D to v 3 D , 0 . To perform this conversion, we only have to combine Eq. (24) with Eq. (25) and then with Eq. (22). This gives us
H θ = H 0 c / ( c − H 0 D ) = H 0 / ( 1 − v 3 D , 0 / c ) ,
v 3 D , 0 = v 3 D / ( 1 + v 3 D / c ) .
By applying Eq. (27) and plotting v 3 D , 0 versus D , all red points in Figure 7 drop down to the blue points. Figure 7 does not only solve the Hubble constant tension. It also explains why the H 0 tension increases if high-redshift data are included [29]: The higher the value of the redshift parameter z is, the more v 3 D deviates from a straight line. The moment of the supernova is irrelevant to team B’s calculation of H 0 . All that counts in the Lambda-CDM model is the duration of the light’s journey to Earth. The parameter z continuously increases during the journey. In the ER-based model, all that counts is the moment of the supernova. Each wavelength is initially redshifted by the Doppler effect. Here z remains constant during the journey. It was specified at the moment of the supernova and is eventually measured on Earth. Space is not expanding. Rather, energy is receding from O (the location of the Big Bang in ES). In ER, expanding space is an obsolete concept.

5.12. The Mystery of Dark Energy

Team B can fix the systematic error in its calculation of H 0 by converting all v 3 D to v 3 D , 0 according to Eq. (27). I now reveal another systematic error, but it is inherent in the Lambda-CDM model. It stems from assuming an accelerating expansion of space and can be fixed only by replacing this model with the ER-based model unless we postulate a dark energy. Many cosmologists advocate an accelerating expansion [30,31] because the calculated recession speeds v 3 D deviate from a straight line in the Hubble diagram and these deviations increase with D . An accelerating expansion would indeed stretch each wavelength even further and thus explain the increasing deviations.
In ER, the increasing deviations are much easier to understand: The older the redshift data are, the more H θ deviates from H 0 , and the more v 3 D deviates from v 3 D , 0 . If another star S 0 (Figure 6 right) happens to be at the same distance of D = 400   M p c today at which the supernova of star S occurred, Eq. (27) tells us: S 0 recedes more slowly (27,064 km/s) from Earth than S (29,750 km/s). As long as cosmologists are not aware of the 4D Euclidean geometry, they attribute the deviations to an accelerating expansion of space caused by “dark energy” [32]. Dark energy has not yet been confirmed. It is a stopgap for an effect that the Lambda-CDM model cannot explain. Older supernovae recede faster not because of an accelerating expansion but because of a larger H θ in Eq. (22).
The Hubble constant tension and dark energy are solved exactly the same way: In Eq. (23), we must not confuse D 0 with D . Because of Eq. (22) and H θ = c / ( r 0 − D ) , the recession speed v 3 D is not proportional to D but to D / ( r 0 − D ) . This is why the red points in Figure 7 run away from a straight line. Any expansion of space (uniform or else accelerating) is only virtual. There is no accelerating expansion of space even if the Nobel Prize in Physics 2011 was given “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae” [33]. There are two misconceptions in these words of praise: (1) In the Lambda-CDM model, Universe implies space, but space is not expanding. (2) There is no acceleration. All but the nearest galaxies recede from Earth, but they do so uniformly. In ER, dark energy is an obsolete concept.
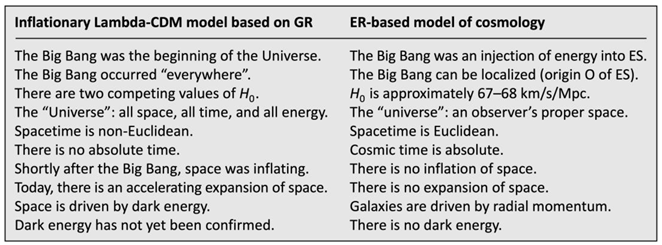
This result casts doubt on the Lambda-CDM model but not on GR. We have to accept that objective concepts are mandatory in cosmology. Radial momentum provided by the Big Bang drives all galaxies away from the origin O of ES. They are driven by themselves rather than by dark energy. Table 1 compares two models of cosmology. Note that “Universe” and “universe” are not the same thing! Observers may indeed experience different “universes”. In Sects. 5.6 through 5.12, objective concepts improve our understanding of cosmology. In the next two sections, they also prove very useful in QM.
Table 1. Comparing two different models of cosmology.
Table 1. Comparing two different models of cosmology.
Preprints 116276 i001

5.13. The Mystery of the Wave–Particle Duality

The wave–particle duality was first discussed by Niels Bohr and Werner Heisenberg [34] and has bothered physicists ever since. Electromagnetic waves are oscillations of an electromagnetic field, which propagate through an observer’s 3D space at the speed c . In some experiments, objects behave like waves. In other experiments, the very same objects behave like particles (also known as the “wave–particle duality”). In today’s physics, one object cannot be wave and particle at once because the energy of a wave is distributed in space, whereas the energy of a particle is always localized in space.
We solve the duality by introducing two objective concepts: “Pure distance” replaces spatial and temporal distance. “Pure energy” replaces wave and particle. My neologism “wavematter” visualizes pure energy (see Figure 8). In an observer’s reality (external view), a wavematter appears as a wave packet or as a particle. As a wave, it propagates in his x 1 axis at the speed c and it oscillates in his axes x 2 and x 3 (electromagnetic field). Since here we talk about an observer’s reality, the wave propagates and oscillates as a function of coordinate time. In its own reality (internal view), the axis of the wavematter’s 4D motion disappears because of length contraction at the speed c . It deems itself particle at rest. “Wavematter” is not just a substitute word for the duality. Rather, it visualizes an objective concept of energy that takes the internal view of photons into account.
Like spatial and temporal distance, wave and particle are subjective concepts: What I deem wave, deems itself particle at rest. For each wavematter, its own energy condenses (concentrates) to what we call “mass”. Albert Einstein taught us that energy is equivalent to mass [35]. Likewise, the polarization of a wave is equivalent to the spin of a particle. It is this very equivalence that inspired me to coin the word “wavematter”.
In a double-slit experiment, wavematters pass through a double-slit and produce an interference pattern on a screen. An observer deems them wave packets as long as he does not track through which slit each wavematter is passing. Here the external view applies. The photoelectric effect is different. Of course, I can externally witness how a photon releases an electron from a metal surface, but the physical effect is all up to the photon: The electron is released only if the photon energy exceeds the electron’s binding energy. Here the internal view of the photon is the crucial view. The photon behaves like a particle.
The wave–particle duality is also observed in matter, such as electrons [36]. Electrons, too, are wavematters. They behave like waves as long as they are not tracked. If they are tracked, they behave like particles. Since an observer automatically tracks objects that are slow in his 3D space, he deems all slow objects—and thus all macroscopic objects—matter rather than waves. To improve readability, I do not draw wavematters in my ES diagrams. I draw what they are deemed by observers: clocks, rockets, galaxies, etc.

5.14. The Mystery of Entanglement

The word “entanglement” was coined by Erwin Schrödinger [37] in his comment on the Einstein–Podolsky–Rosen paradox [38]. These three authors argued that QM would not provide a complete description of reality. Schrödinger’s neologism did not solve the paradox, but it demonstrates our difficulties in comprehending QM. John Bell [39] showed that local hidden-variable theories are not compatible with QM. Several experiments tell us that entanglement violates locality [40,41,42] but only “locality in an observer’s 3D space”. Entanglement has been considered a non-local 3D effect ever since.
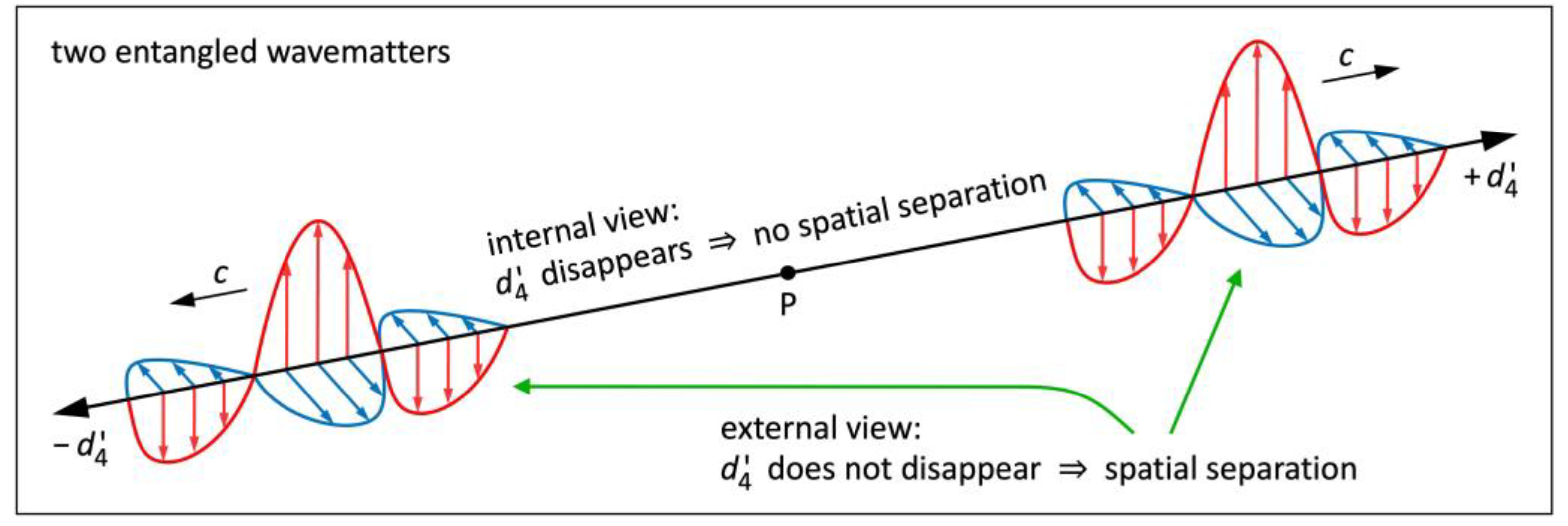
Up next, we untangle entanglement without the concept of non-locality. All we need is ER: The fact that all d μ ( μ = 1 ,   2 ,   3 ,   4 ) are interchangeable makes non-locality obsolete. Figure 9 illustrates two wavematters that were created at once at a point P. They move away from each other in opposite 4D directions ± d 4 ′ at the speed c . As it turns out, these two wavematters are automatically entangled. For an observer moving in any direction other than ± d 4 ′ (external view), the two wavematters are spatially separated. The observer has no idea how they are able to “communicate” with each other in no time.
For each wavematter (internal view), the d 4 ′ axis disappears because of length contraction at the speed c . In their common (!) proper space spanned by d 1 ′ ,   d 2 ′ ,   d 3 ′ , either of them is at the same position as its twin. From the internal view, the twins have never been separated spatially, but their proper time flows in opposite 4D directions. While the twins stay together spatially, they “communicate” with each other in no time. Their opposite 4D vectors + τ ′ and − τ ′ do not affect local “communication”. There is a “spooky action at a distance” (phrase attributed to Einstein) from the external view only.
This time, the horizon problem and entanglement are solved exactly the same way: An observer’s 4D vector τ and his proper space may differ from an observed region’s (object’s) 4D vector τ ′ and its proper space. This is possible only if all d μ ( μ = 1 , 2 , 3 , 4 ) are interchangeable. ER also explains the entanglement of matter, such as electrons [43]. In an observer’s proper space, electrons move at a speed v 3 D < c . In their ± d 4 ′ axis, electrons move at the speed c . Any measurement tilts the axis of 4D motion of one twin and thus destroys the entanglement. In ER, non-locality is an obsolete concept.

5.15. The Mystery of the Baryon Asymmetry

In the Lambda-CDM model, almost all matter was created shortly after the Big Bang. Only then was the temperature high enough to enable pair production. However, baryons and antibaryons should have annihilated each other because the energy density, too, was very high. Fact is that we observe more baryons than antibaryons today (also known as the “baryon asymmetry”). Pair production creates equal amounts of baryons and antibaryons. So, what caused the asymmetry? ER scores again: Each wavematter injected by the Big Bang deems itself particle at rest. The asymmetry was caused by the Big Bang.
But why do wavematters not deem themselves antiparticles at rest? Well, antiparticles are created in pair production only. They are not the opposite of particles but particles with the opposite electric charge. In particular, there is a reasonable “character paradox”: What I deem antiparticle, deems itself particle. It only seems that antiparticles flow backward in time because proper time flows in opposite 4D directions for any two wavematters created in pair production. In ER, these wavematters are automatically entangled. This gives us a chance to falsify ER. All scientific theories must be falsifiable [44].

6. Conclusions

ER solves mysteries that have not yet been solved, such as the Hubble constant tension, or that have been solved but with concepts that are obsolete in ER: cosmic inflation, expanding space, dark energy, non-locality. These weird concepts make cosmology and QM work, but Occam’s razor shaves them off: We should always surrender concepts if they are obsolete. Thus, I advise physics to teach ER, and three lessons in particular: (1) SR/GR describe an observer’s reality and how the realities of two observers relate to each other. (2) ER describes ES and how an observer’s reality is created, but ER does not describe his reality. (3) Objective concepts are mandatory in cosmology and QM.
SR/GR are considered two of the greatest achievements of physics because they have been confirmed over and over. I showed that SR/GR do not provide a holistic view. Physics got stuck in its own concepts. The stagnation in physics is of its own making. ER solves 15 mysteries purely geometrically, that is, without forces, fields, and weird concepts. It is very unlikely that 15 solutions in different (!) areas of physics are 15 coincidences. Only in natural concepts does Mother Nature disclose her secrets. If we think of an observer’s reality as an oversized stage, the key to understanding nature is beyond all stages.
It was a wise decision to award Albert Einstein the Nobel Prize for his theory of the photoelectric effect [45] and not for SR/GR. I showed that ER penetrates to a deeper level. Einstein—one of the most brilliant physicists ever—failed to realize that the fundamental metric chosen by Mother Nature is Euclidean. Einstein sacrificed absolute space and time. ER restores absolute, cosmic time, but it sacrifices the absolute nature of wave and particle. For the first time ever, mankind understands the nature of time: Cosmic time is the total distance covered in ES divided by c . The human brain is able to imagine that we move through ES at the speed c . With that said, conflicts of mankind become all so small.
Is ER a physical or a metaphysical theory? This is a very good question because only in proper coordinates can we access ES, but the proper coordinates of other objects cannot be measured. Make sure to get it right: Rulers/clocks do measure d μ ( μ = 1 ,   2 ,   3 ,   4 ), but I cannot measure d μ ′ of other objects. Yet I can calculate them as in Eqs. (13a–15c). Physics is the science of describing the universe and its interior. Our primary source of knowledge is observing, but even cosmology and QM would be metaphysical if we limit physics to observing: Dark matter and wave functions are non-observable. Observing is always wedded to egocentric perspectives. Information is lost in all projections from the master reality. ER is a physical theory because it solves mysteries in an observer’s reality.
Final remarks: (1) I only touched on gravity. We should not reject ER because gravity is still an issue. GR seems to solve gravity, but GR is not compatible with QM unless we add quantum gravity. (2) A promising objective concept of force is “process”. I gave just one example in Sect. 4, where potential energy is transferred to kinetic energy. It will help if we build physics on processes rather than on forces. (3) Mysteries, such as the retrograde loops of planets, disappear if we pick the appropriate symmetry. The SO(4) symmetry of ES is the appropriate symmetry in cosmology and QM. (4) Cosmic time puts an end to all speculations about time travel. Do other theories solve time’s arrow as beautifully as ER? (5) To cherish its beauty, we must work with ER. Physics does not ask: Why is my reality a projection? Nor does it ask: Why is it a wave function? Projections are less speculative than dark energy and non-locality. (6) It looks like Plato’s Allegory of the Cave [46] is correct: Mankind experiences projections that are blurred—because of QM.
It is not by chance that the author is an experimental physicist whose primary question is: How does all our insight fit together without adding highly speculative concepts? I laid the groundwork for ER and showed how powerful it is. Paradoxes are only virtual. The true pillars of physics are ER (including SR/GR as subordinate theories) and QM. Together, they describe everything from the very large to the very small. Introducing a holistic view to physics is what I consider my most significant contribution: All observers’ views taken together do not make a holistic view. The holistic view holds additional information that is hidden in absolute time and thus not available in SR/GR. Everyone is welcome to solve even more mysteries. May ER get the broad acceptance that it deserves!

Funding

No funds, grants, or other support was received.

Data Availability Statement

All data that support the findings of this study are included within the article.

Acknowledgements

I thank Siegfried W. Stein for his contributions to Sect. 5.11 and for the Figs. 3, 5 center, and 6 (partly). After several unsuccessful submissions, he eventually decided to withdraw his co-authorship. I also thank Matthias Bartelmann, Dirk Rischke, Jürgen Struckmeier, and Andreas Wipf for asking questions and commenting. In particular, I thank all reviewers and editors for the precious time that they spent on grappling with my manuscript.

Conflict of interest

The author has no competing interests to declare.

Comments

It takes open-minded, courageous editors and reviewers to evaluate a theory that heralds a paradigm shift. Whoever adheres to established concepts is paralyzing the scientific progress. I did not surrender when top journals rejected my theory. Interestingly, I was never given any solid arguments that would disprove my theory. Rather, I was asked to try a different journal. Were the editors dazzled by the success of SR/GR? Did they underestimate the benefits of ER? It seems to me that most editors hesitated to consider a theory that opposes the mainstream. Even friends refused to support me. Anyway, each setback inspired me to work out the benefits of ER even better. Finally, I succeeded in disclosing a physical issue in SR/GR and in formulating a holistic theory of relativity that is even more general than Albert Einstein’s “general” relativity. Some physicists have difficulties in accepting ER because the SO(4) symmetry of ES is incompatible with waves. ER is not disputing waves but limiting their occurrence to an observer’s reality. A well-known preprint archive suspended my submission privileges. I was penalized because I disclosed an issue in Einstein’s theories of relativity. One editor was unable to imagine that the Hubble constant tension is solved without GR. One editor-in-chief replied: “Publishing is for experts only.” I do not blame anyone. Paradigm shifts are always hard to accept. These comments shall encourage young scientists to stand up for promising ideas, but opposing the mainstream is exhausting. Here are some statements that I received: “Unscholarly research.” “Fake science.” “Too simple to be true.” Simplicity and truth are not mutually exclusive. Beauty is when they go hand in hand together.

References

  1. Einstein, A.: Zur Elektrodynamik bewegter Körper. Ann. Phys. 322, 891–921 (1905). [CrossRef]
  2. Einstein, A.: Die Grundlage der allgemeinen Relativitätstheorie. Ann. Phys. 354, 769–822 (1916). [CrossRef]
  3. Minkowski, H.: Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern. Math. Ann. 68, 472–525 (1910). [CrossRef]
  4. Rossi, B., Hall, D.B.: Variation of the rate of decay of mesotrons with momentum. Phys. Rev. 59, 223–228 (1941). [CrossRef]
  5. Dyson, F.W., Eddington, A.S., Davidson, C.: A determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of May 29, 1919. Phil. Trans. R. Soc. A 220, 291–333 (1920). [CrossRef]
  6. Ashby, N.: Relativity in the global positioning system. Living Rev. Relativ. 6, 1–42 (2003). [CrossRef]
  7. Ryder, L.H.: Quantum Field Theory. Cambridge University Press, Cambridge (1985).
  8. Newburgh, R.G., Phipps Jr., T.E.: A space–proper time formulation of relativistic geometry. Physical Sciences Research Papers (United States Air Force), no. 401 (1969).
  9. Montanus, H.: Special relativity in an absolute Euclidean space-time. Phys. Essays 4, 350–356 (1991).
  10. Montanus, H.: Proper Time as Fourth Coordinate. ISBN 978-90-829889-4-9. https://greenbluemath.nl/proper-time-as-fourth-coordinate/ (2023). Accessed 26 August 2024.
  11. Montanus, J.M.C.: Proper-time formulation of relativistic dynamics. Found. Phys. 31, 1357–1400 (2001). [CrossRef]
  12. Almeida, J.B.: An alternative to Minkowski space-time. (2001) arXiv:gr-qc/0104029.
  13. Gersten, A.: Euclidean special relativity. Found. Phys. 33, 1237–1251 (2003). [CrossRef]
  14. van Linden, R.: Euclidean relativity. https://euclideanrelativity.com (2024). Accessed 26 August 2024.
  15. Newton, I.: Philosophiae Naturalis Principia Mathematica. Joseph Streater, London (1687).
  16. Kant, I.: Kritik der reinen Vernunft. Hartknoch, Riga (1781).
  17. Wick, G.C.: Properties of Bethe-Salpeter wave functions. Phys. Rev. 96, 1124–1134 (1954). [CrossRef]
  18. Weyl, H.: Gruppentheorie und Quantenmechanik. Hirzel, Leipzig (1928).
  19. Nowinski, J.L.: Applications of Functional Analysis in Engineering. Plenum Press, New York (1981).
  20. Abbott, B.P., et al.: Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016). [CrossRef]
  21. Kalies, G., Do, D.D.: Momentum work and the energetic foundations of physics. I. Newton’s laws of motion tailored to processes. AIP Adv. 13, 065121 (2023). [CrossRef]
  22. Hafele, J.C., Keating, R.E.: Around-the-world atomic clocks: Predicted relativistic time gains. Science 177, 166–168 (1972). [CrossRef]
  23. Penzias, A.A., Wilson, R.W.: A measurement of excess antenna temperature at 4080 Mc/s. Astrophys. J. 142, 419–421 (1965). [CrossRef]
  24. Hubble, E.: A relation between distance and radial velocity among extra-galactic nebulae. Proc. Natl. Acad. Sci. U.S.A. 15, 168–173 (1929). [CrossRef]
  25. Lemaître, G.: Un univers homogène de masse constante et de rayon croissant, rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann. Soc. Sci. Bruxelles A 47, 49–59 (1927).
  26. Linde, A.: Inflation and Quantum Cosmology. Academic Press, Boston (1990).
  27. Guth, A.H.: The Inflationary Universe. Perseus Books, New York (1997).
  28. Aghanim, N., et al.: Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020). [CrossRef]
  29. Riess, A.G., et al.: A comprehensive measurement of the local value of the Hubble constant with 1 km s−1 Mpc−1 uncertainty from the Hubble Space Telescope and the SH0ES team. Astrophys. J. Lett. 934, L7 (2022). [CrossRef]
  30. Perlmutter, S., et al.: Measurements of Ω and Λ from 42 high-redshift supernovae. (1998) arXiv:astro-ph/9812133.
  31. Riess, A.G., et al.: Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 116, 1009–1038 (1998). [CrossRef]
  32. Turner, M.S.: Dark matter and dark energy in the universe. (1998) arXiv:astro-ph/9811454.
  33. The Nobel Foundation: The Nobel Prize in Physics 2011 (2011). https://www.nobelprize.org/prizes/physics/2011/summary/ Accessed 26 August 2024.
  34. Heisenberg, W.: Der Teil und das Ganze. Piper, Munich (1969).
  35. Einstein, A.: Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? Ann. Phys. 323, 639–641 (1905). [CrossRef]
  36. Jönsson, C.: Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Z. Phys. 161, 454–474 (1961). [CrossRef]
  37. Schrödinger, E.: Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 23, 807–812 (1935). [CrossRef]
  38. Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935). [CrossRef]
  39. Bell, J.S.: On the Einstein Podolsky Rosen paradox. Physics 1, 195–200 (1964). [CrossRef]
  40. Freedman, S.J., Clauser, J.F.: Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28, 938–941 (1972). [CrossRef]
  41. Aspect, A., Dalibard, J., Roger, G.: Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49, 1804–1807 (1982). [CrossRef]
  42. Bouwmeester, D., et al.: Experimental quantum teleportation. Nature 390, 575–579 (1997). [CrossRef]
  43. Hensen, B., et al.: Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015). [CrossRef]
  44. Popper, K.: Logik der Forschung. Julius Springer, Vienna (1935).
  45. Einstein, A.: Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Ann. Phys. 322, 132–148 (1905). [CrossRef]
  46. Plato: Politeia, 514a.
Preprints 116276 g002
Figure 2. Minkowski diagram and ES diagram of two identical clocks “r” (red) and “b” (blue). Left: In SR, “b” is slow with respect to “r” in t ′ . Coordinate time is relative (“b” is not at the same positions in c t and c t ′ ). Right: In ER, “b” is slow with respect to “r” in d 4 . Cosmic time is absolute (“r” is in d 4 at the same position as “b” in d 4 ′ ). Only the ES diagram is rotationally symmetric
Figure 2. Minkowski diagram and ES diagram of two identical clocks “r” (red) and “b” (blue). Left: In SR, “b” is slow with respect to “r” in t ′ . Coordinate time is relative (“b” is not at the same positions in c t and c t ′ ). Right: In ER, “b” is slow with respect to “r” in d 4 . Cosmic time is absolute (“r” is in d 4 at the same position as “b” in d 4 ′ ). Only the ES diagram is rotationally symmetric
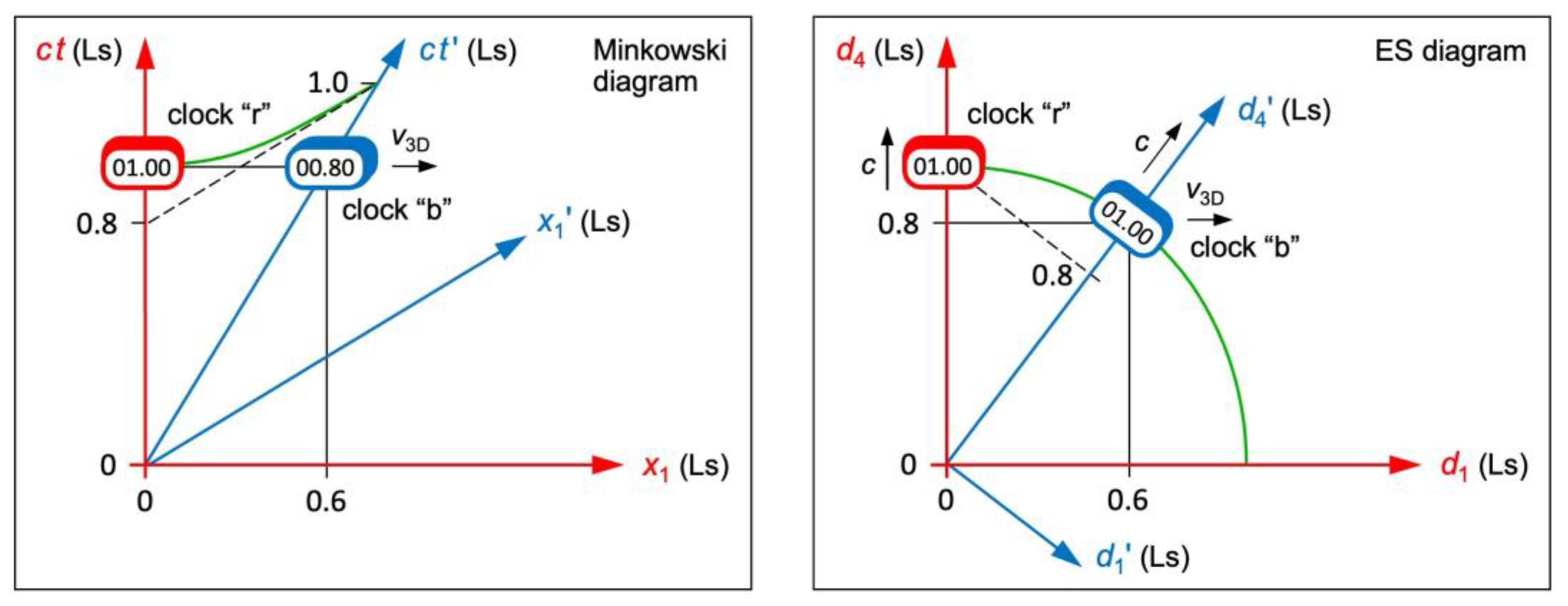
Preprints 116276 g002
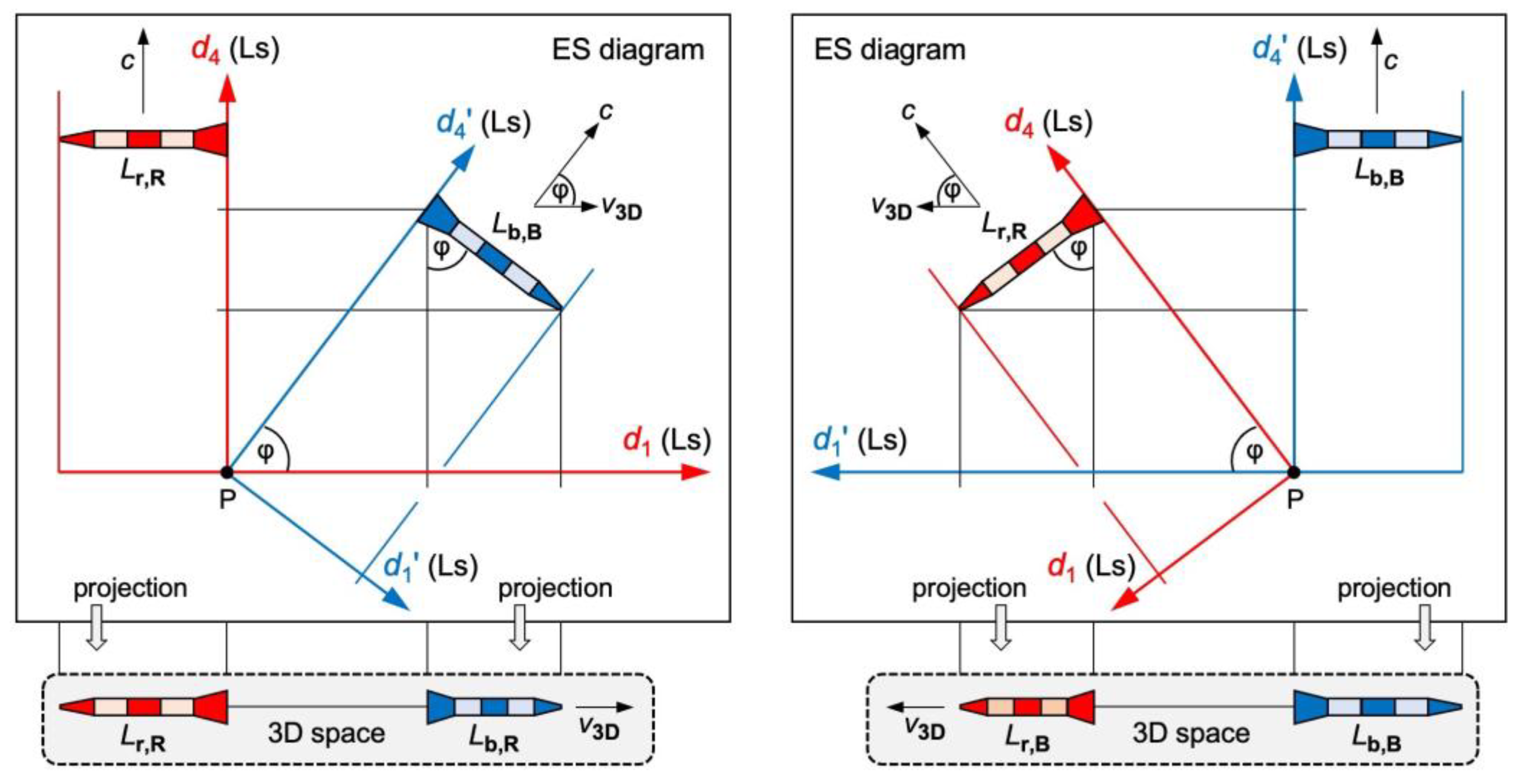
Preprints 116276 g003
Figure 3. ES diagrams and 3D projections of two rockets “r” (red) and “b” (blue). Top: Both rockets move in different 4D directions at the speed c . Bottom left: Projection to the 3D space of R. Rocket “b” contracts to L b , R . Bottom right: Projection to the 3D space of B. Rocket “r” contracts to L r , B .
Figure 3. ES diagrams and 3D projections of two rockets “r” (red) and “b” (blue). Top: Both rockets move in different 4D directions at the speed c . Bottom left: Projection to the 3D space of R. Rocket “b” contracts to L b , R . Bottom right: Projection to the 3D space of B. Rocket “r” contracts to L r , B .
Preprints 116276 g003
Preprints 116276 g004
Figure 4. ES diagram of two identical clocks “r” (red) and “b” (blue). Clock “r” and Earth move in the d 4 axis of “r” at the speed c . Clock “b” accelerates in the d 1 axis of “r” toward Earth.
Figure 4. ES diagram of two identical clocks “r” (red) and “b” (blue). Clock “r” and Earth move in the d 4 axis of “r” at the speed c . Clock “b” accelerates in the d 1 axis of “r” toward Earth.
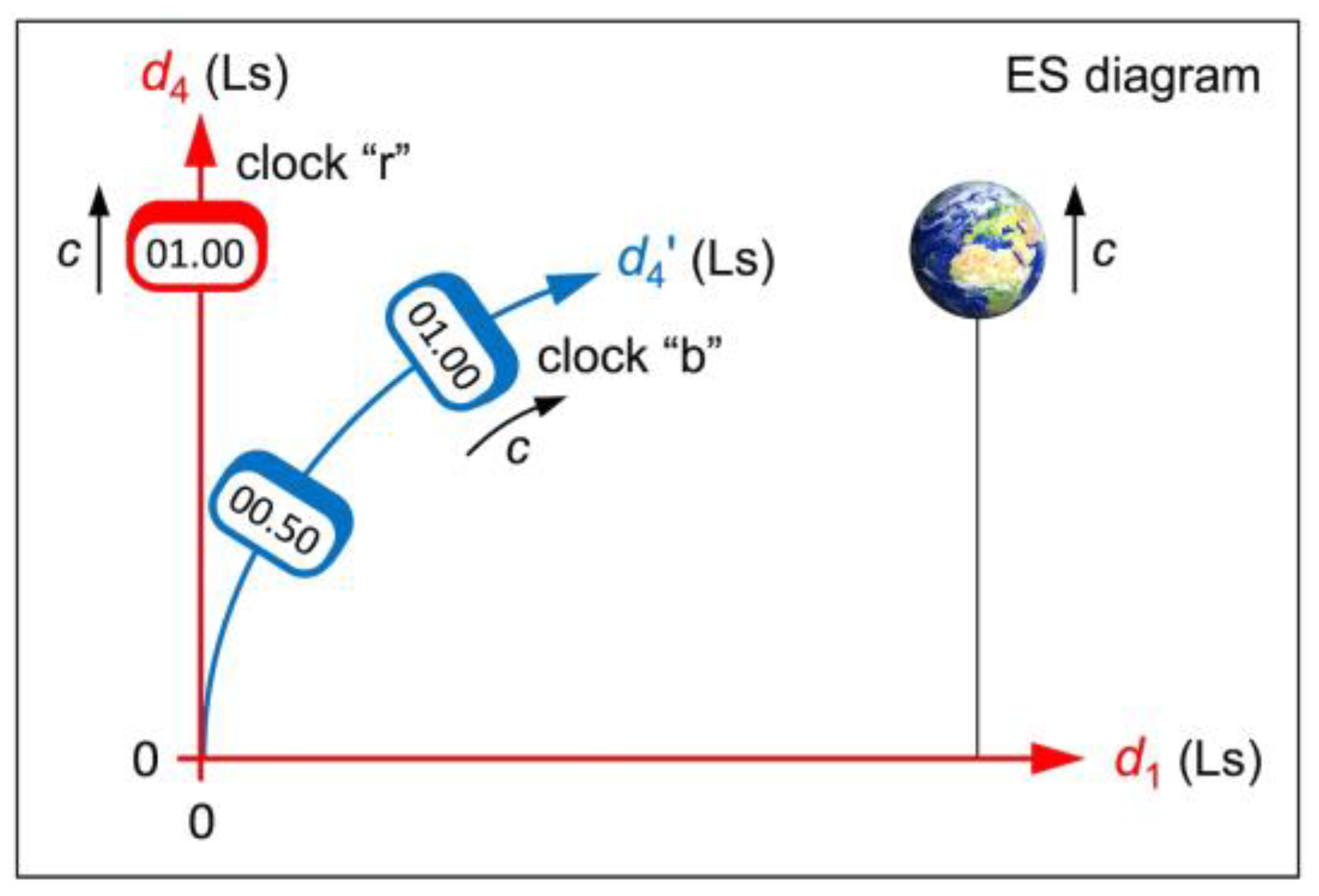
Preprints 116276 g004
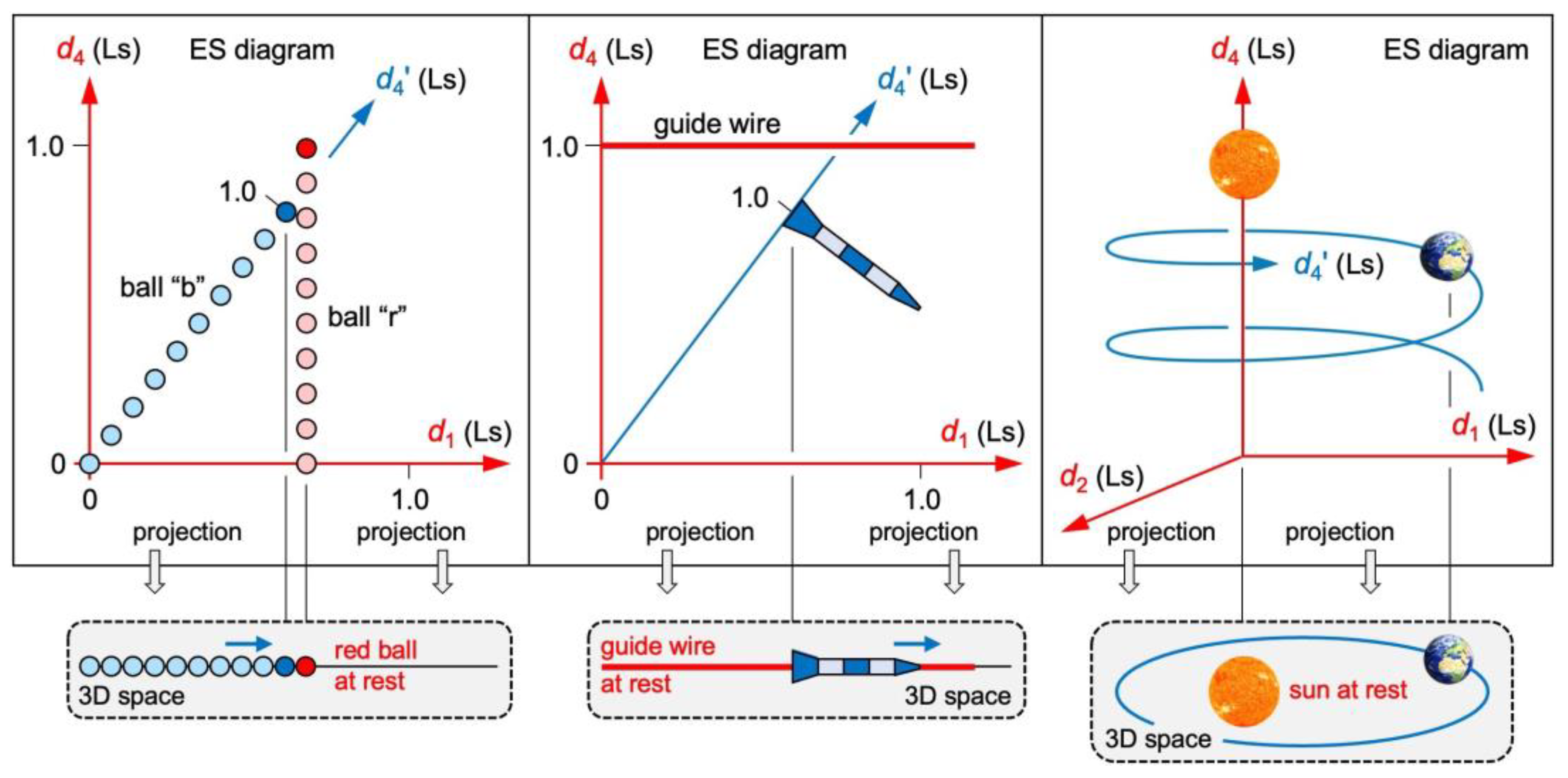
Preprints 116276 g005
Figure 5. Solving three instructive problems in ER. Each snapshot shows one instant in cosmic time. Left: The blue ball “b” is approaching the red ball “r”. In the 3D space of “r”, the balls collide. Center: A rocket moves along a wire. In the 3D space of the wire, the wire does not escape from the rocket. Right: Earth orbits the sun. In the 3D space of the sun, the sun does not escape from Earth.
Figure 5. Solving three instructive problems in ER. Each snapshot shows one instant in cosmic time. Left: The blue ball “b” is approaching the red ball “r”. In the 3D space of “r”, the balls collide. Center: A rocket moves along a wire. In the 3D space of the wire, the wire does not escape from the rocket. Right: Earth orbits the sun. In the 3D space of the sun, the sun does not escape from Earth.
Preprints 116276 g005
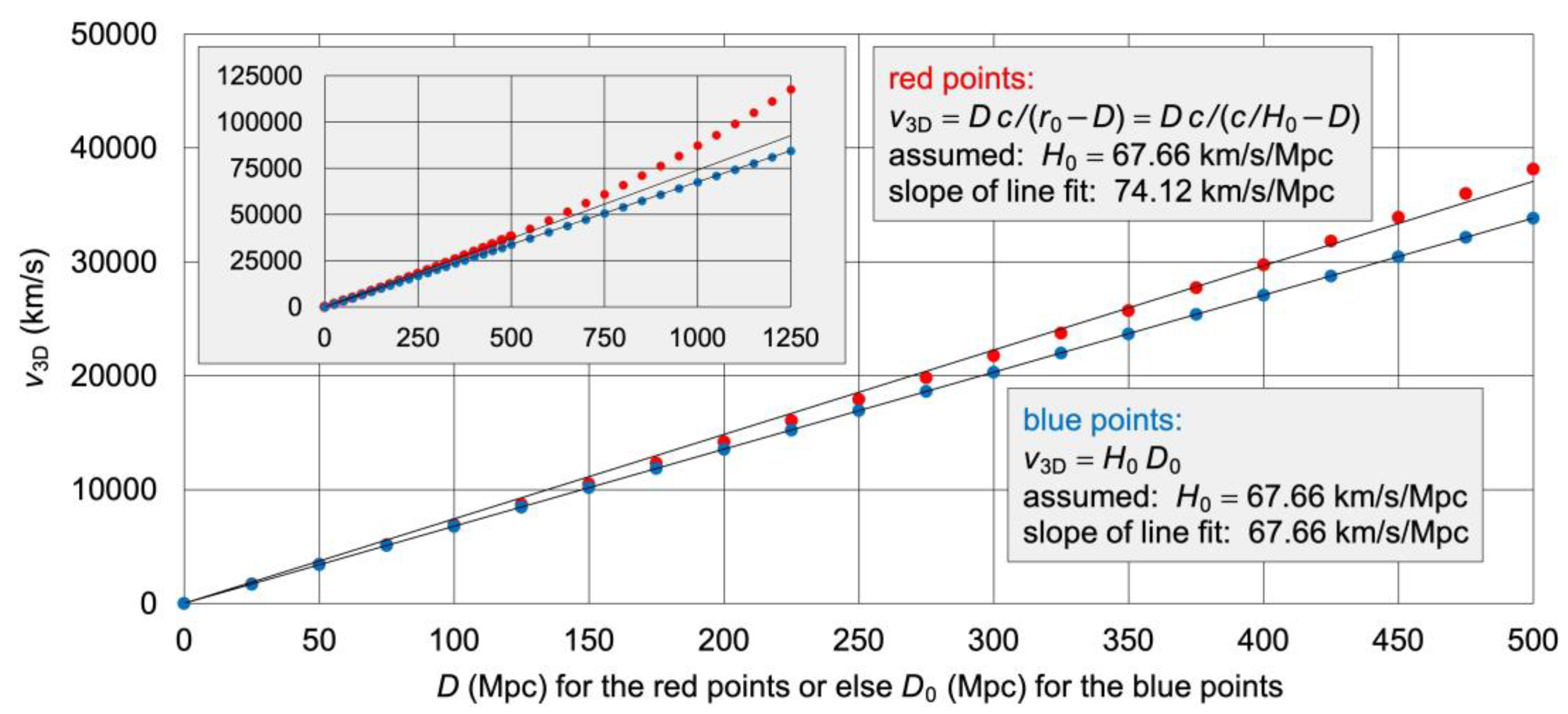
Preprints 116276 g007
Figure 7. Hubble diagram of simulated supernovae at distances up to 1250 Mpc. The horizontal axis is D for the red points or else D 0 for the blue points. The red points were calculated from Eq. (22). They do not yield a straight line because H θ is not a constant. The blue points were calculated from Eq. (23). They yield a straight line if we do not confuse D 0 with D .
Figure 7. Hubble diagram of simulated supernovae at distances up to 1250 Mpc. The horizontal axis is D for the red points or else D 0 for the blue points. The red points were calculated from Eq. (22). They do not yield a straight line because H θ is not a constant. The blue points were calculated from Eq. (23). They yield a straight line if we do not confuse D 0 with D .
Preprints 116276 g007
Preprints 116276 g008
Figure 8. Illustration of a wavematter. In an observer’s reality (external view), a wavematter appears as a wave packet or as a particle. As a wave (shown here), it propagates and oscillates as a function of coordinate time. In its own reality (internal view), the axis of the wavematter’s 4D motion disappears because of length contraction at the speed c . It deems itself particle at rest.
Figure 8. Illustration of a wavematter. In an observer’s reality (external view), a wavematter appears as a wave packet or as a particle. As a wave (shown here), it propagates and oscillates as a function of coordinate time. In its own reality (internal view), the axis of the wavematter’s 4D motion disappears because of length contraction at the speed c . It deems itself particle at rest.
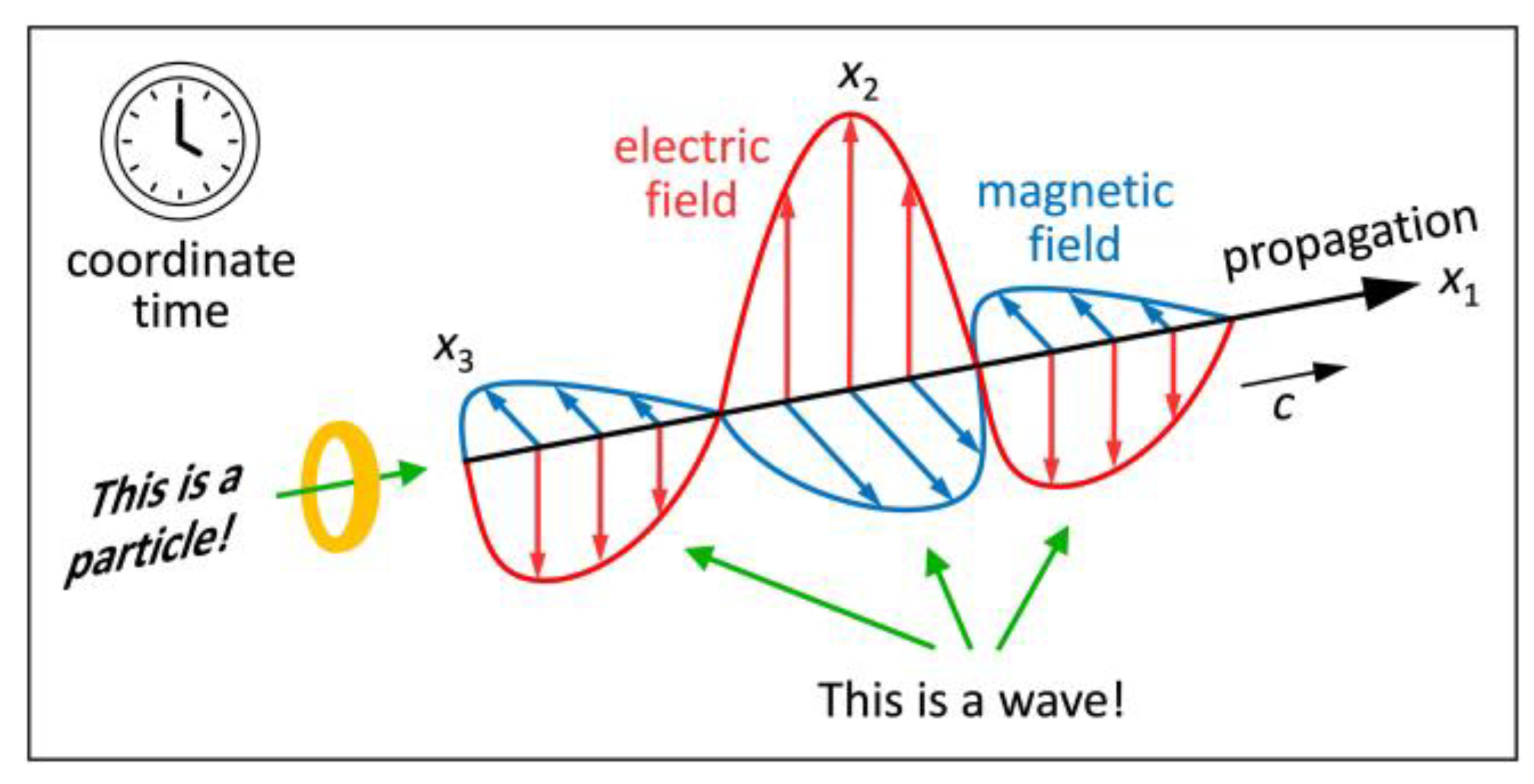
Preprints 116276 g008
Preprints 116276 g009
Figure 9. Two wavematters moving in ± d 4 ′ at the speed c are spatially separated for an observer moving in any direction other than ± d 4 ′ (external view). For each wavematter (internal view), the d 4 ′ axis disappears. From the internal view, the twins have never been separated spatially.
Figure 9. Two wavematters moving in ± d 4 ′ at the speed c are spatially separated for an observer moving in any direction other than ± d 4 ′ (external view). For each wavematter (internal view), the d 4 ′ axis disappears. From the internal view, the twins have never been separated spatially.
Preprints 116276 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated