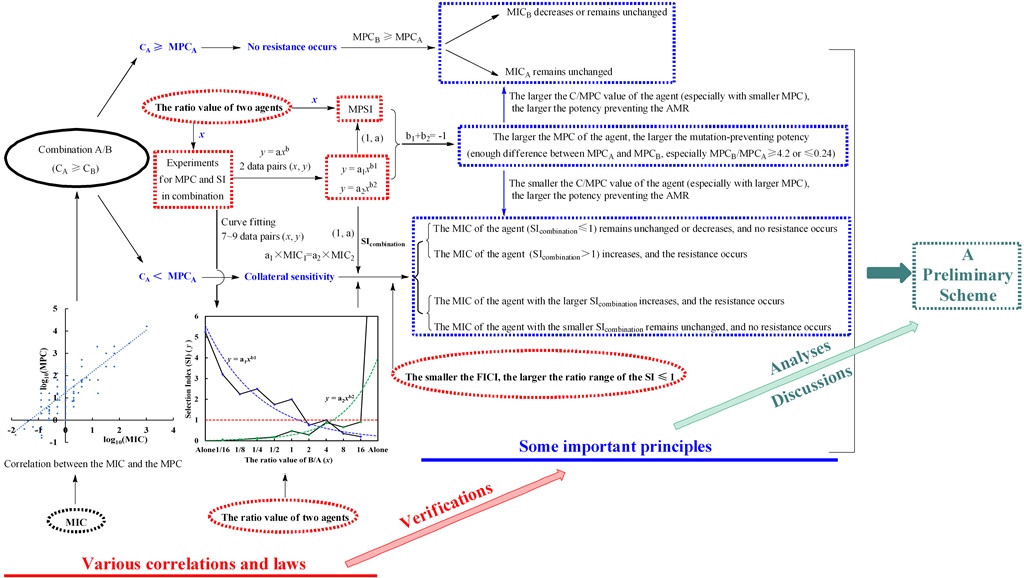
Antimicrobial resistance (AMR) has been a serious threat to human health, and combination therapy is proved to be an economic and effective strategy to fight the resistance. However, the abuse of drug combinations would conversely accelerate the spread of AMR. In our previous work, it had been concluded that the mutant selection indexes (SIs) of one agent against a specific bacterial strain are closely related to the proportions of two agents in a drug combination. To discover probable correlations, predictors and laws for further proposing feasible principles and schemes guiding the AMR-preventing practice, here three aspects were further explored. First, the power function (y=ax^b, a > 0) correlation between the SI (y) of one agent and the ratio value (x) of two agents in a drug combination was further established based on the mathematical and statistical analyses for those experimental data, and two rules a₁ × MIC₁ = a₂ × MIC₂ and b₁ + b₂ = -1 were discovered from both equations of y=a₁x^b1 and y=a₂x^b2 respectively for two agents in drug combinations. Simultaneously, it was found that one agent with larger MPC alone for drug combinations show greater potency for narrowing itself MSW and preventing the resistance. Second, a new concept as mutation-preventing selection index (MPSI) was proposed and used for evaluating the mutation-preventing potency difference of two agents in drug combinations, and the positive correlation between the MPSI and the mutant prevention concentration (MPC) or minimal inhibitory concentration (MIC) was subsequently established. Inspired by this, the significantly positive correlation, contrary to previous reports, between the MIC and the corresponding MPC of antimicrobial agents against pathogenic bacteria was established using one hundred and eighty-one of data pairs reported. These results together of above three aspects indicate that the MPCs in alone and combination are very important indexes for drug combinations to predict the mutation-preventing effects and the trajectories of collateral sensitivity, and while the MPC of an agent can be roughly calculated from its corresponding MIC. Subsequently, the former conclusion was further verified and improved by the antibiotic exposure to forty-three groups designed as different drug concentrations and various proportions. The results further proposed that the C/MPC for the agent with larger proportion in drug combinations can be considered as a predictor and is the key to judge whether the resistance and the collateral sensitivity occur to two agents. Based on these above correlations, laws, and their verification experiments, some principles were proposed, and a diagram of the mutation-preventing effects and the resistant trajectories for drug combinations with different concentrations and ratios of two agents was presented. Simultaneously, the reciprocal of MPC alone (1/MPC), proposed as the stress factors of two agents in drug combinations, together with their SI in combination, is the key to predict the mutation-preventing potency and control the trajectories of collateral sensitivity. Finally, a preliminary scheme for antimicrobial combinations preventing the AMR was further proposed for subsequent improvement research and clinic popularization, based on the above analyses and discussion. Moreover, some similar conclusions were speculated for triple or multiple drug combinations.