Prerpints.org logo
Preprint
Article

Effect of the Trip-Length Distribution on Network-Level Traffic Dynamics: Exact and Statistical Results

Altmetrics

Downloads

332

Views

253

Comments

1

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 January 2023

Posted:

31 January 2023

You are already at the latest version

Alerts
Abstract
This paper presents additional results of the generalized bathtub model for urban networks, including a simpler derivation and exact solutions for uniformly distributed trip lengths. It is shown that in steady state this trip-based model is equivalent to the more parsimonious accumulation-based model, and that the trip-length distribution has merely a transient effect on traffic dynamics, which converge to the same point in the macroscopic fundamental diagram (MFD). To understand the statistical properties of the system, a queueing approximation method is proposed to compute the network accumulation variance. It is found that (i) the accumulation variance is much larger than predicted by traditional queueing models, due to the nonlinear dynamics imposed by the MFD, (ii) the trip-length distribution has no effect on the accumulation variance, indicating that the proposed formula for the variance might be universal, (iii) the system exhibits critical behavior near the capacity state where the variance diverges to infinity. This indicates that the tools from critical phenomena and phase transitions might be useful to understand congestion in cities.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The aggregated modeling of urban networks has a long history dating back to [1], and numerous theories and models have been published since; see [2] for a recent review and reference therein. The starting point for all macroscopic urban models is the reservoir (or bathtub) model for cities, which simply states the conservation of Q ( t ) , the number of vehicles inside the network at time t:
Q ′ ( t ) = λ ( t ) − μ ( t )
where λ ( t ) , μ ( t ) give the inflow and outflow of the network, respectively, in units of flow. The main assumption in these models is that the speed of vehicles inside the network at time t, v ( t ) , is identical for all vehicles and given by the speed macroscopic fundamental diagram (speed-MFD):
v ( t ) = V ( Q ( t ) )
Unlike the inflow λ ( t ) , which can be easily determined, the network outflow μ ( t ) can be difficult to formalize due to its convoluted dependence on the probability distribution of trip lengths. Depending on the assumptions to formulate the outflow function μ ( t ) , the literature can be divided into accumulation-based [3,4,5] and trip-based models [6,7,8,9,10,11,12,13,14]. Accumulation-based models assume that the outflow is given by the network production divided by the average trip length, ℓ:
μ = Q V ( Q ) / ℓ . ( accumulation - based model )
This expression for the outflow was first derived in a seminal paper by [3] only assuming a constant trip length and that congestion is evenly spread across the network. He points out that extracting dynamic behavior from the model is possible for slow-varying demands, providing the foundations for the macroscopic modeling of cities. Despite some confusion in the literature [2,15,16,17,18], the role played by the exponential distribution in this model surfaced in the literature not until [6] who considers it an unrealistic assumption. As it turns out, this important observation that (3) follows from assuming exponentially distributed trip lengths, appears to have its origins in [19] although it was not published until [20] as described in [15].
[21] shows that the accumulation-based models suffer from significant numerical viscosity even when the time step is small. Outflows may then overreact to sudden demand surge leading to inconsistent information propagation between opposite perimeter boundaries. They also point out that the assumption of constant trip length for all vehicles inside a reservoir is not consistent with what is observed when the local dynamics are taken into account. This has prompted several extensions of the accumulation-based model, multi-reservoir systems with different categories of trip length over macroscopic routes, possibly changing with congestion levels, and delay-based models [13,22,23,24,25,26,27,28].
Trip-based reservoir models have been proposed that guarantee that all vehicles travel their own trip length, at the expense of mathematical tractability. Originally proposed by [6] on a footnote, these models recognize that each commuter i has different trip lengths, L i , which has to equal the distance traveled inside the network during their trip time T i ( t ) at the prevailing speeds:
L i = ∫ t t + T i ( t ) V ( Q ( s ) ) d s . ( trip length )
The resulting outflow function was proposed implicitly in [9] without proof, arguing that it is a direct consequence of (4) when the system is initially empty:
μ ( t ) = V ( Q ( t ) ) ∫ 0 t λ ( s ) f s ∫ s t V ( Q ( u ) ) d u d s , ( trip - based model )
where f s ( x ) is the probability density of trip lengths of vehicles entering the network at time s. [15] introduces one spatial dimension to the problem, x, the remaining distance to reach the destination. He shows that when the distribution of trip lengths f in (5) is exponential with mean ℓ, we obtain the accumulation-based model (3), a result that first appeared in [29]. All attempts in the literature to solve the trip-based model for other distributions have been numerical using discrete-event simulation [9,10,11] or more traditional time-stepping simulation [7]. Another advantage of trip-based models is the ease to incorporate slower vehicles such as buses [18], although moving bottlenecks have been incorporated into the accumulation-based models [30]. The interested reader is referred to [12] for additional properties of accumulation-based and trip-based models under fast-varying demands.
To the best of our knowledge, with the exception of [15], no other attempts have been made to develop analytical solutions to the trip-based model. To fill this gap, section 2 below uses the framework proposed in [15] to derive analytical solutions of the trip-based model and to characterize its steady state, which coincides with the accumulation-based model independently of the trip-length distribution. Perhaps a more important gap in the literature is that the stochastic nature of arrival flows has been completely neglected, at least when it comes to analytical formulations; see [2]. Section 3 fills this gap by drawing the analogy with the M/G/∞ queue and shows that accumulations exhibit a much larger variance than predicted by the M/G/∞ queue, due to the nonlinear dynamics imposed by the MFD. Finally, discussion and outlook are presented in section 4.

2. Jin’s Formulation: Alternative Derivation and Additional Results

The framework proposed in [15] introduces one spatial dimension to the problem, x, such that a vehicle trajectory x i ( t ) gives the remaining distance to reach commuter i’s destination, and x i ′ ( t ) = − v ( t ) . By considering the probability density function of remaining trip distances, [15] derives the conservation law that unifies existing reservoir models. Alternatively, one can simply note that these vehicle trajectories must obey the conservation law partial differential equation (PDE):
∂ ∂ t k ( t , x ) + ∂ ∂ x q ( t , x ) = Λ ( t , x )
where k ( t , x ) is the density of vehicles in the region at time t whose remaining distance is x, q ( t , x ) is the corresponding flow, and the source term Λ ( t , x ) is the net inflow to the system in units of flow per km. As opposed to regular traffic, in our problem (i) there is no fundamental diagram relating flow to density and therefore (6) it is not a hyperbolic conservation law such as the kinematic wave model. Instead, given assumption (2) above, the flow is given by the fundamental traffic flow relationship:
q ( t , x ) = v ( t ) · k ( t , x ) ,
which turns the conservation law (6) into the transport PDE:
∂ ∂ t k ( t , x ) − v ( t ) ∂ ∂ x k ( t , x ) = Λ ( t , x )
where the negative sign follows from x i ′ ( t ) = − v ( t ) . Other important differences compared to regular traffic are that (ii) the spacing between vehicle trajectories is immaterial because these vehicles could be in different links of the network; (iii)  Λ ( t , x ) , x > 0 only includes arrivals to the region because all departures take place at x = 0 . It follows from (iii) that the outflow from the region is simply the flow at x = 0 , i.e. μ ( t ) = q ( t , 0 ) , or equivalently using (7)1:
μ ( t ) = v ( t ) · k ( t , 0 ) ( generalized bathtub model )
It follows that all we need to solve the model is k ( t , 0 ) but unfortunately its analytical derivation quickly becomes intractable. For clarity, let
z ( t ) ≡ ∫ 0 t V ( Q ( u ) ) d u
and the distance traveled by a vehicle during time interval ( s , t ) :
z s t ≡ z ( t ) − z ( s ) = ∫ s t V ( Q ( u ) ) d u .
The initial value problem solution to the transport PDE (8) is well known in the literature. Given initial densities k ( 0 , x ) = g ( x ) , the solution can be expressed as the following system of integral-differential equations:
k ( t , x ) = g ( x + z ( t ) ) + ∫ 0 t λ ( s ) f s x + z s t d s ,
z ′ ( t ) = V ( Q ( t ) ) ,
Q ( t ) = ∫ 0 ∞ k ( t , x ) d x
which cannot be solved analytically in our case. However, it can be used to show the following:
Proposition 2.1. 
Lamotte and Geroliminis’s [9] conjecture in (5) can now be proven.
Proof. 
From (13a) we see that for x = 0 and empty initial conditions:
k ( t , 0 ) = ∫ 0 t λ ( s ) f s z s t d s ,
which in combination with (10) gives the desired result. □

2.1. Analytical Solutions for Q ( t )

Although (13) cannot be solved analytically for k ( t , x ) , we have been able to find explicit solutions for Q ( t ) = ∫ 0 ∞ k ( t , x ) d x only for exponential and uniform trip length distributions under a time-independent conditions λ ( t ) = λ , f s ( · ) = f ( · ) and a Greenshields speed-accumulation relationship, V ( Q ) = 1 − Q , where we assume that both the free-flow speed and jam accumulation are 1, without loss of generality. These assumptions imply that both the accumulation and time are dimensionless, measured in units of the jam accumulation and free-flow travel time, respectively. Let μ ^ the maximum outflow of the accumulation-based model:
μ ^ ≡ max Q { Q ( 1 − Q ) / ℓ } = 1 4 ℓ ,
and let the intensity be ρ ≡ λ / μ ^ , or:
ρ ≡ 4 λ ℓ .
In this case, one needs to solve the following system of equations:
Q ′ ( t ) = λ − v ( t ) · k ( t , 0 ) ,
k ( t , 0 ) = g ( z ( t ) ) + ∫ 0 t λ ( s ) f z s t d s ,
z ′ ( t ) = V ( Q ( t ) ) ,
subject to appropriate boundary conditions. When the distribution of trip lengths f is exponential with mean ℓ, one obtains the accumulation-based model (3) as pointed out in [15], and therefore one may replace (17a) and (17b) with (1) and (3), which removes the mathematical intractability of (17). With initial conditions Q ( 0 ) = Q 0 , z ( 0 ) = 0 one obtains:
Q ( t ) = 1 2 1 − c 1 tan sec − 1 − c 2 − c 3 t ,
z ( t ) = t 2 + ℓ log c 2 cos c 3 t + sec − 1 c 2 ,
where c 1 ≡ ρ − 1 , c 2 = ρ − 4 Q 0 V Q 0 / c 1 , and c 3 = c 1 / ( 2 ℓ ) are constants; see Figure 1. Notice that (21a) was presented in [31] for occupancies, but the formulation here also allows us to obtain z ( t ) . Other distributions of trip lengths did not result in analytical solutions of (17) (using Mathematica v13.1). The only exception is the uniform distribution, but in “relaxed” form:
f ( x ) = 1 / ( 2 ℓ ) , x > 0
instead of f ( x ) = 1 / ( 2 ℓ ) , 0 < x < 2 ℓ , which is the uniform distribution in ( 0 , 2 ℓ ) with mean ℓ. This relaxed form implies that the following analytical solutions are valid only up to a time t * such that : z ( t * ) = 2 ℓ . The general case ρ > 0 , Q 0 > 0 gives:
Q ( t ) = 1 − e t c 2 2 t + c 1 1 − 2 ℓ π c 2 e c 4 2 erf c 2 t + c 4 − e c 3 erf c 4 + c 1
where here c 1 = Q 0 / ( 2 ℓ ) , c 2 = ρ / ( 4 ℓ ) , c 3 = Q 0 2 / ρ , c 4 = c 1 / ( 2 c 2 ) . Notice that solution for z ( t ) looks complicated and not particularly insightful, and therefore will be omitted in what follows; they can be easily retrieved using equation (17c). Two important special cases of (20) are arbitrary initial conditions and no inflow and empty initial conditions and constant inflow:
Q ( t ) = 1 − 1 − Q 0 e c 1 t , ( ρ = 0 , Q 0 > 0 )
Q ( t ) = 1 − 1 − 2 ℓ π c 2 erf c 2 t e c 2 2 t 2 , ( ρ > 0 , Q 0 = 0 )
and are used to compare with the exponential disagree in Figure 1. It can be seen in the first row of the figure that under uniform trip lengths the accumulation tends to zero much more slowly than in the exponential case for earlier times, while the opposite is true for later times. The second row shows an initially empty network being loaded at a constant intensity, where one can see that both distributions tend to the same equilibrium point but at slightly different speeds. Notice that models (18) and (21) are valid only in 0 ≤ Q ( t ) ≤ 1 , and as soon as we hit one of these boundaries one should stop the evaluation; see points “a” in the figure. Similarly, because we used the relaxed version of the uniform distribution, as soon as z ( t ) = 2 ℓ then (21) no longer applies as noted earlier.
We can conclude that, given an average trip-length ℓ, the effect of the trip-length distribution affects the time (as found in [22]) to reach steady state, but not the equilibrium point itself. This is confirmed in the next section.

2.2. Steady-State

In this section all input variables are time-independent, i.e. λ ( t ) = λ , f s ( · ) = f ( · ) , and all other steady-state variables denoted with a star.
Proposition 2.2 
(Steady-state models). The accumulation-based model under steady-state conditions is valid regardless of the (time-independent) distribution of trip lengths.
Proof. 
In steady-state the network production Q * v * , defined as the integral of the circulating flow over the total network distance, has to match the incoming production λ ℓ , therefore
Q * v * = λ ℓ ,
where v * = V ( Q * ) . From (10) we can see that the steady-state condition Q ′ ( t ) = 0 implies
μ * = λ ,
as expected. Combining (23) and (22) gives:
μ * = Q * v * / ℓ ,
which establishes the result. □
Notice that this proposition was mentioned in [29] without proof. It implies that in steady state one may use the simple accumulation-based model to evaluate traffic conditions, regardless of the distribution of trip lengths. For instance, as shown previously in [31], solving for Q * in (22) gives two equilibrium solutions; the first solution is stable and in the free-flow regime, and in the Greenshields approximation it reads as:
Q * ( ρ ) = 1 2 1 − 1 − ρ ,
while the second solution, 1 2 1 + 1 − ρ , is in the congested regime and acts as a repellor; see [31] for details.
Proposition 2.3 
(Steady-state density). In steady-state, the density is given by:
k * ( x ) = [ 1 − F ( x ) ] λ / v * .
Proof. 
In steady state, characteristics are straight lines of slope − v * , which means that the density k ( t , x ) = λ ∫ 0 t f ( x + z s t ) d s can be computed explicitly with the change of viable z = ( t − s ) v * to obtain:
k ( t , x ) = [ F ( x + t v * ) − F ( x ) ] λ / v * .
Taking the limit t → ∞ we obtain the steady-state density k * ( x ) = k ( t → ∞ , x ) as claimed. □
It follows that the probability density function (PDF) of remaining trip distances, f X ( x ) = k * ( x ) / Q * , is given by:
f X ( x ) = [ 1 − F ( x ) ] / E L ,
where E L = ℓ is the expected trip length. Denoting its coefficient of variation by C L , it can be shown that their moments are given by [32] as:
E X = E L 2 1 + C L 2 ,
E X m = E L m + 1 ( m + 1 ) E L .
Notice that for the exponential distribution, (28) gives f X = f , as expected given the memoryless property of this distribution2. This means that the expected remaining trip length is E X = E L , as can be verified in (29) with C L 2 = 1 . For other distributions this is not the case, however, where E X < E L for distributions with light tails, as it appears to be the case in practice [17,33]. However, it would not be surprising to find cases where the trip length distribution is heavy tailed, such as the power-law distribution which is so prevalent in complex systems [34], where E X > E L .

3. Queueing Approximation for the Stochastic Problem

In this section, we present a queuing approximation for the stochastic version of our problem. For simplicity, we start with empty initial conditions and assume that the only sources of randomness are the arrival process and trip lengths, while the travel speed remains deterministic given the accumulation, as in the previous sections. The network accumulation (or queue) Q ( t ) ≡ A ( t ) − D ( t ) is the difference between cumulative vehicle arrivals to the network, A ( t ) , and departures from the network, D ( t ) ; see Figure 2. The mean and variance of the accumulation is then given by:
E Q ( t ) = E A ( t ) − E D ( t ) ,
Var Q ( t ) = Var A ( t ) + Var D ( t ) − 2 Cov { A ( t ) , D ( t ) } .
In traditional queuing systems the departure rate is independent of the accumulation, which acts as a buffer between arrivals and departures: as long as the queue is not zero, departures tend to be independent of arrivals. As argued in [35], the more the accumulation in the system, the more independent the departure and arrival process will be and is typically assumed that the covariance term Cov { A ( t ) , D ( t ) } = 0 . This is true even for limited storage, which can be treated as a boundary condition. But in our case, by definition of the MFD there is a dependency between accumulation and service rate and therefore the covariance term Cov { A ( t ) , D ( t ) } in (31b) cannot be neglected. In any case, as long as the accumulation is not close to zero, its distribution should be approximately normal with mean and variance given above; see [35]. The challenge here is to characterize the terms Var D ( t ) and Cov { A ( t ) , D ( t ) } due to the nontrivial dependencies in the reservoir model.
As customary in the queueing literature, we introduce the variance-to-mean ratio of arrivals, I A , departures, I D , and accumulations, I Q :
I A ( t ) ≡ Var A ( t ) E A ( t ) , I D ( t ) ≡ Var D ( t ) E D ( t ) , I Q ( t ) ≡ Var Q ( t ) E Q ( t )
Notice that I A = 1 for Poisson arrivals, and that if service times are independent, then I D gives the squared coefficient of variation of service times [35], and equals one for exponential service times. It will be convenient to define:
I A D ( t ) ≡ Cov { A ( t ) , D ( t ) } E D ( t )
which is one for the M/G/∞ queue [35], and is in the range 0 ≤ I A D ≤ I D . With these definitions the variance-to-mean ratio of the accumulation can be written as:
I Q = E A ( t ) I A − E D ( t ) ( 2 I A D − I D ) E A ( t ) − E D ( t ) ,
which is the main focus of this section. Although this ratio is time dependent we will be interested in its state-state behavior in what follows.
The traditional queuing model most similar to our problem is the M/G/∞ queue, with Poisson arrivals (so I A = 1 ), a general service time distribution, and an infinite number of servers. The latter means that each customer (commuter) is its own server and the service time plays the role of the travel time from origin to destination. The main difference with our problem is that travel times are governed by the reservoir model dynamics, and as it turns out, these dynamics will make a big difference: It is known that for the M/G/∞ queue the distribution of departures is Poisson, so I D = I A D = 1 and therefore accumulations are also Poisson, as can be seen in (34) that gives I Q = 1 . But our discrete-event simulation (described in appendix) results presented in Figure 3 and Figure 4 show that I Q > 1 depending on the intensity ρ . The simulation experiments consider, separately, three trip-length distributions: exponential, uniform and the “square” distribution arising when origins and destinations are uniformly distributed on a square; see [36]. The parameters of these distributions were set such that they all have the same mean, but different coefficient of variation: the C L 2 is 1, 1/27 and 1/4 for the exponential, uniform and square distribution, respectively.
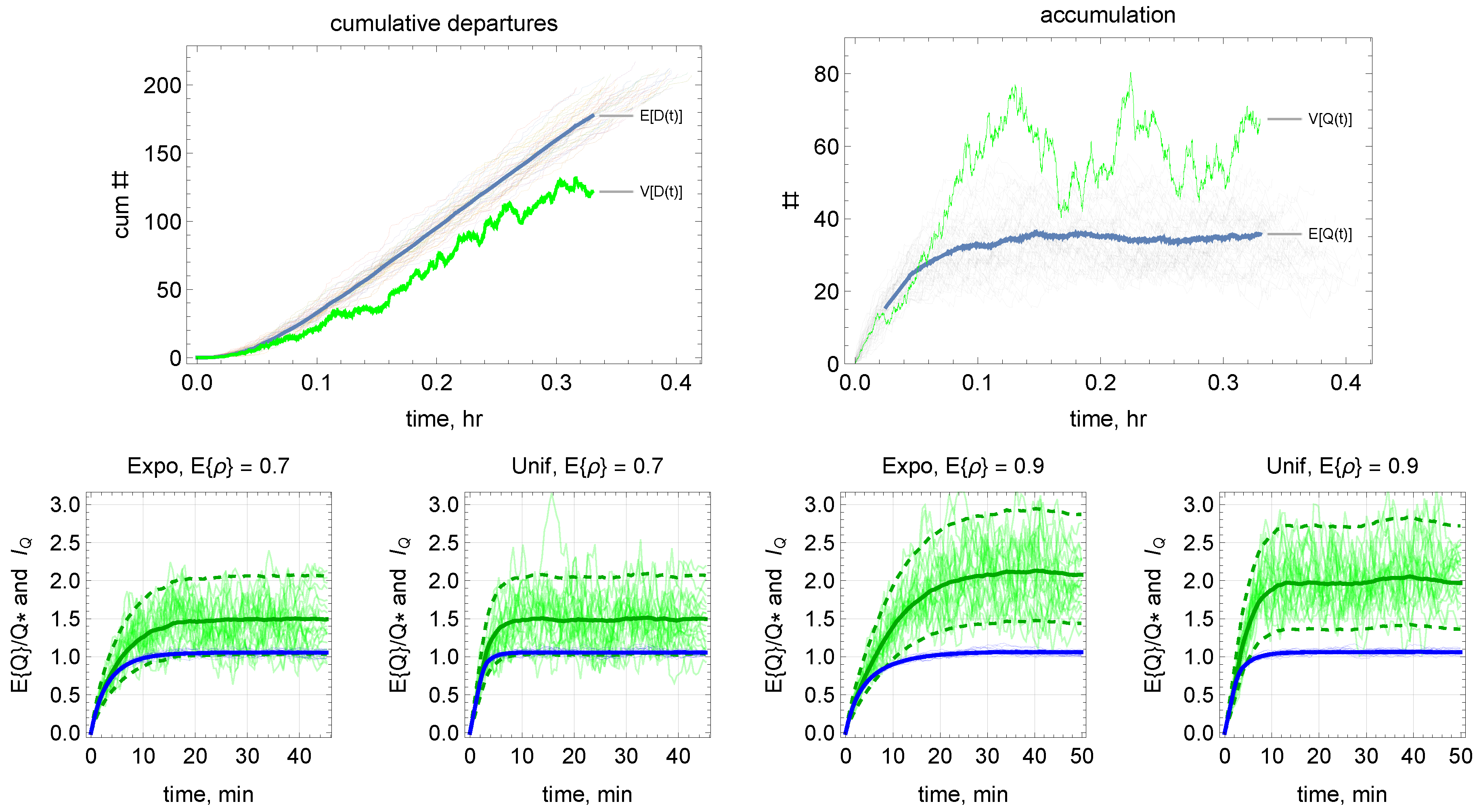
Figure 3(Top) shows a typical simulation output in terms of cumulative count curves for departures (left) and accumulations (right) for several realizations of the experiment. Arrivals are omitted as they look very similar to the departure plot. From these outputs one can calculate the sample means of E A ( t ) , Var A ( t ) , etc. to estimate the ratios I A , I D , I Q and I A D , all functions of time. The bottom part of the figure shows simulation time series showing the evolution of E Q ( t ) / Q * and I Q ≈ Var Q ( t ) / Q * with the exponential and uniform distributions for different values of E ρ . It becomes clear that the distribution with the highest coefficient of variation, the exponential distribution, implies longer relaxation times to reach the steady state, but this steady state is unaffected by the distribution of trip lengths.
Figure 4 shows the steady-state time-average values of parameters I A , I D , I A D and I Q as a function of the average intensity E ρ . It can be seen that all the columns in the figure look very similar, which indicates that the impact of the trip length distribution is almost negligible when it comes to the statistical properties of I A , I D , I A D and I Q . Notice that around intensity 0.9 there is a consistent drop in all the parameters, followed by a sudden increase at E ρ > 1 . The drop is a consequence of arrival flows being throttled in congestion (see appendix), which causes a reduction in the variance of the relevant variables since the system is forced to maintain the same accumulation. The sudden increase can be explained by the non-stationary of the system when ρ > 1 . Notice that for E ρ < 0.9 the first three columns of the figure are as expected, with 1 ≈ I A > I D ≈ I A D ≈ 0.9 as we have Poisson arrivals, whose variability is dampened slightly due to the interactions in the bathtub, leading to smaller I D and I A D .
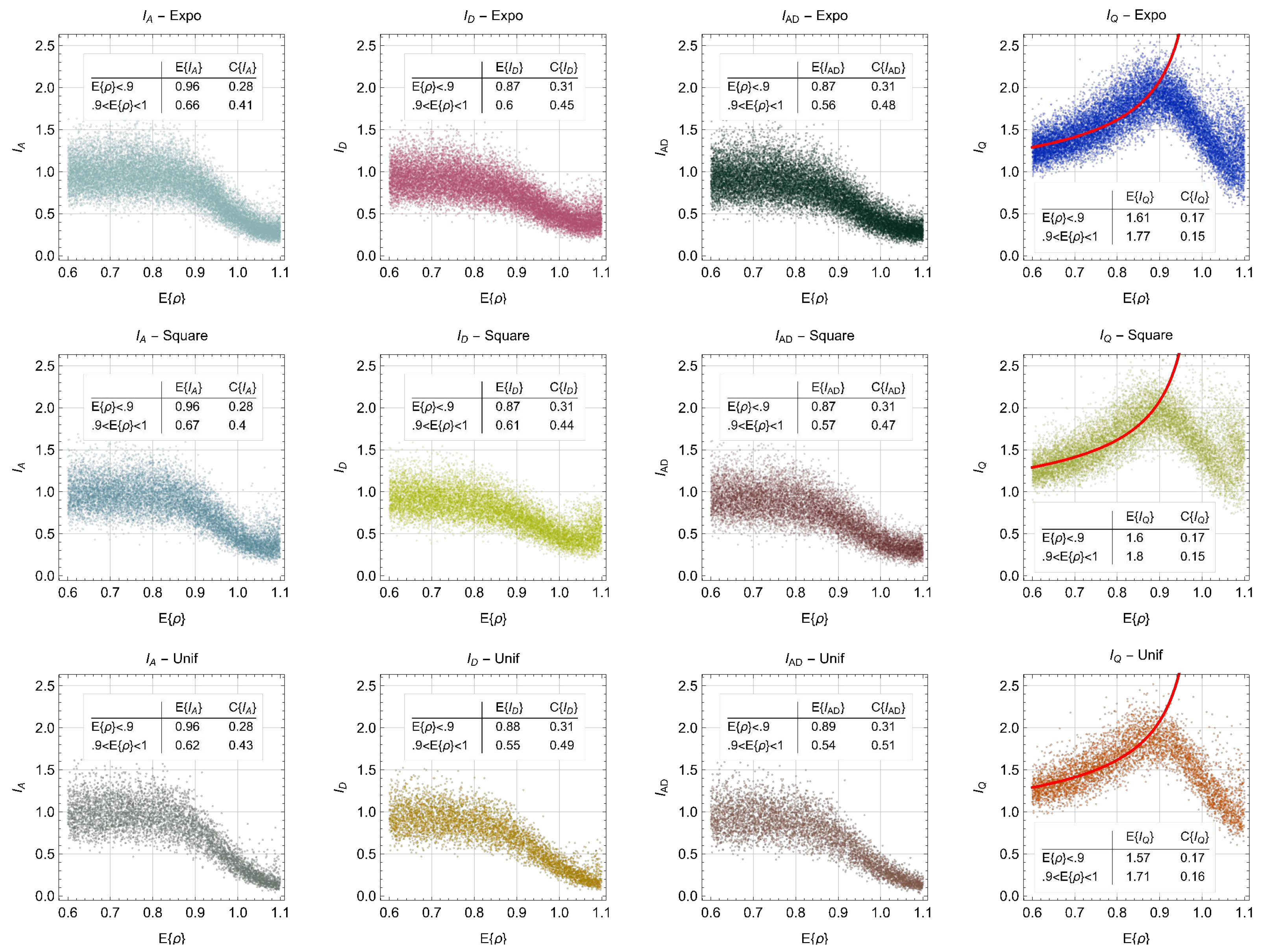
Preprints 68065 g004
Figure 4. Steady-state time-average values of parameters I A , I D , I Q and I A D as a function of the intensity ρ . Each row corresponds to a different distribution of trip length: exponential, uniform and square distribution. The red line corresponds to (36). The table on each panel gives the expected value and coefficient of variation of the relevant parameter for two ranges of E ρ .
Figure 4. Steady-state time-average values of parameters I A , I D , I Q and I A D as a function of the intensity ρ . Each row corresponds to a different distribution of trip length: exponential, uniform and square distribution. The red line corresponds to (36). The table on each panel gives the expected value and coefficient of variation of the relevant parameter for two ranges of E ρ .
Preprints 68065 g004
But not as expected is the behavior of I Q observed in the last column of Figure 4, which is not captured by (34). As shown next, this can be explained by the reservoir dynamics brought about by the MFD causing the variance to diverge to infinity near the critical point ρ = 1 . (Notice that this is not the case for the M/G/∞ queue because it has no exit capacity constraint such as μ ^ here; see (15).) To see this, we series expand (25) around the critical point ρ = 1 up to first order and compute its variance assuming Poisson arrivals, i.e. Var ρ = E ρ . This gives Var Q * ( ρ ) ≈ ( Q * ′ ( E ρ ) ) 2 E ρ = E ρ / ( 16 ( 1 − E ρ ) ) , which goes to infinity as E ρ → 1 . This behavior is typical of systems that undergo a phase transition [37], e.g. from liquid to solid or from free-flow to congestion in our case. The usual way to deal with this divergence in the phase transition literature is to assume a power-law divergence, in this case of the type:
Var Q * ( ρ ) = a E ρ ( 1 − E ρ ) − b ,
where a > 0 , b > 0 are constants and b is known as a critical exponent. Assuming E Q * ( ρ ) ≈ Q * ( E ρ ) we can compute:
I Q ≈ 1 2 1 + 1 − E ρ − 1 / 2
where we have used a = 1 / 4 , b = 1 / 2 that provide a good fit to the data. This is shown by the red line in Figure 4, which corresponds to (36). The good fit to the simulated data is apparent, and confirms that the steady-state behavior of the system is not affected by the different trip-length distributions. Therefore, we can conclude that the statistical properties of congestion are largely independent of the trip-length distribution, and mostly governed by the arrival process, whose stochastic fluctuations produced chaotic behavior thanks to the non-linear MFD dynamics.

4. Discussion

This paper has presented additional results of the generalized bathtub model for urban networks. Section 2 was devoted to deterministic arrivals, as is invariably the case in the literature until now, which included a simpler derivation of the model, exact solutions for uniformly-distributed trip lengths, and the characterization of the steady-state. While the variability of trip lengths has an impact on the time to reach steady-state as noted previously [14], it was found that under steady-state conditions the accumulation-based model remains valid regardless of the distribution of trip lengths. This is good news because in steady state or in the common case of slowly-varying demand, one may use the accumulation-based model, which is a much more parsimonious model that only requires a good estimation of the average trip length. Interestingly, similar findings have been reported for multi-reservoir models [13,38].
Section 3 examines the case of Poisson arrivals drawing the analogy with the well-know M/G/∞ queue, which predicts Poisson accumulations. In contrast, we found that accumulations exhibit a much larger variance than predicted by the M/G/∞ queue, which can be explained by the nonlinear dynamics imposed by the MFD, where the critical density acts as a critical point of a dynamical system subject to phase transitions. That traffic flow behaves as a fluid undergoing phase transitions has been known for a few decades now [39,40,41,42] but its consequences have not permeated the literature. Indeed, the values for I Q –a proxy for network reliability–found here are unusually high for traditional queuing systems, but perhaps as expected from the critical behavior that emerges in systems undergoing phase transitions. Future work should verify the conjecture found here that the discrete-event simulation of the trip-based model produces critical behavior. This result is important as it is currently believed that critical behavior can emerge only in fully microscopic models [42,43,44]. It would be interesting to see if other implementations [e.g. [45] also exhibit similar behavior under stochastic arrivals. As in [43], the results in section 3 strongly suggest that control can be used effectively to improve reliability simply by preventing the system to reach the critical region, e.g. by metering/perimeter control well below capacity. Another possibility might be nonlinear metering control [46]. In any case, more research is needed to explore the analogy with phase transitions to better understand the complex power-law dynamics taking place and the possible universal aspects of this problem.
As in the case with deterministic arrivals, we find that the trip length distribution has an impact only on the transient accumulation trajectory, but it does not affect its variance-to-mean ratio in steady-state. This indicates that the proposed approximation method for the variance-to-mean ratio I Q in (36) will be robust with respect to the trip length distribution, and perhaps universal as it is typically the case with power-law relationships arising in phase transitions. This universality would imply that the proposed approximation should be accurate independently of the shape of the MFD, so long as it is concave.
As pointed out in the introduction, assuming exponentially distributed trip lengths has been considered unrealistic, starting with [6] who argues that this is akin to assuming that commuters do not know their trip distance until initiating the trip. However, this is an unfair criticism. The fair statement here is that the commuter does not care how long the trip to the office is when applying for a job. Once he/she accepts the offer, that trip length becomes fixed for the commuter but it was drawn from a distribution, possibly exponential. So yes, we do know our trip distances even though they may be be exponential, or even heavy tailed as argued right before section 3.
Finally, the empirical trip length distributions from American and European cities [17,33] strongly suggest to the author that the exponential distribution exhibits the correct overall trend of the data, except for very short trips < 1.5 mi, which explains why the lognormal distribution was proposed as a good candidate by the authors in [17]. (Notice that this empirical data applies for a single-reservoir scenario, but not for a multi-reservoir context [13].) Adding the main result of this paper that the statistical properties of congestion are largely independent of the distribution choice, which only affects the transient behavior of the system, makes a compelling argument in favor of the exponential assumption. More research is needed, however, to settle the debate.

Acknowledgements

This research was partially funded by NSF Awards #1932451, #1826162 and by the TOMNET and STRIDE University Transportation Centers (USDOT) at Georgia Tech. I would like to thank the three anonymous reviewers, whose comments greatly improved the quality of this paper.

Appendix A. Simulation Experiments

This section explains the simulation experiments presented in section 3 of the paper, used to estimate the parameters I A , I D , I A D and I Q , and to verify the accuracy of the approximation presented here. Our simulation model implements the discrete-event simulation proposed in [10] with the exceptions that arrivals are driven by a Poisson processes instead of being deterministic. In the simulation, each vehicle has its own trip length and reservoir speeds are updated each time a vehicle either enters or leaves the system. As customary in the literature, in congestion the arrival flow is capped; i.e, restricted to remain at or below the prevailing flow on the network; see [3,11,12]. We also use the method in [10] to implement this. We use a Greenshields speed-accumulation relationship, V ( Q ) = 80 ( 1 − Q / 120 ) , where the free-flow speed is 80 km/hr and the jam accumulation is 120 vehs.
A single experiment consists of an initially empty system with Poisson arrivals with a constant rate λ . Each arrival has a trip length drawn from the distribution f, which can be the exponential, uniform distributions and the “square” distribution of trip length when origins and destinations are uniformly distributed on a square; see [36] for details. Notice that all these distributions have the same mean of ℓ = 3 , but different coefficient of variation: the C L 2 is 1, 1/27 and 1/4 for the exponential, uniform and square distribution, respectively. The simulation stops once a steady state has been reached for 30 minutes.

References

  1. Godfrey, J.W. The mechanism of a road network. Traffic Engineering and Control 11, 1969, pp. 323–327.
  2. Johari, M.; Keyvan-Ekbatani, M.; Leclercq, L.; Ngoduy, D.; Mahmassani, H.S. Macroscopic network-level traffic models: Bridging fifty years of development toward the next era. Transportation Research Part C: Emerging Technologies 2021, 131, 103334. [Google Scholar] [CrossRef]
  3. Daganzo, C.F. Urban gridlock: Macroscopic modeling and mitigation approaches. Transportation Research Part B: Methodological 2007, 41, 49–62. [Google Scholar] [CrossRef]
  4. Geroliminis, N. Dynamics of Peak Hour and Effect of Parking for Congested Cities. Transportation Research Board Annual Meeting 2009, 2009, number CONF. [Google Scholar]
  5. Yildirimoglu, M.; Ramezani, M.; Geroliminis, N. Equilibrium analysis and route guidance in large-scale networks with MFD dynamics. Transportation Research Procedia 2015, 9, 185–204. [Google Scholar] [CrossRef]
  6. Arnott, R. A bathtub model of downtown traffic congestion. Journal of Urban Economics 2013, 76, 110–121. [Google Scholar] [CrossRef]
  7. Daganzo, C.F.; Lehe, L.J. Distance-dependent congestion pricing for downtown zones. Transportation Research Part B: Methodological 2015, 75, 89–99. [Google Scholar] [CrossRef]
  8. Leclercq, L.; Sénécat, A.; Mariotte, G. Dynamic macroscopic simulation of on-street parking search: A trip-based approach. Transportation Research Part B: Methodological 2017, 101, 268–282. [Google Scholar] [CrossRef]
  9. Lamotte, R.; Geroliminis, N. The morning commute in urban areas with heterogeneous trip lengths. Transportation Research Part B: Methodological 2018, 117, 794–810. [Google Scholar] [CrossRef]
  10. Mariotte, G.; Leclercq, L.; Laval, J.A. Macroscopic urban dynamics: Analytical and numerical comparisons of existing models. Transportation Research Part B: Methodological 2017, 101, 245–267. [Google Scholar] [CrossRef]
  11. Mariotte, G.; Leclercq, L. Flow exchanges in multi-reservoir systems with spillbacks. Transportation Research Part B: Methodological 2019, 122, 327–349. [Google Scholar] [CrossRef]
  12. Leclercq, L.; Paipuri, M. Macroscopic Traffic Dynamics Under Fast-Varying Demand. Transportation Science 2019, 53, 1526–1545. [Google Scholar] [CrossRef]
  13. Batista, S.; Leclercq, L.; Geroliminis, N. Estimation of regional trip length distributions for the calibration of the aggregated network traffic models. Transportation Research Part B: Methodological 2019, 122, 192–217. [Google Scholar] [CrossRef]
  14. Paipuri, M.; Leclercq, L.; Krug, J. Validation of Macroscopic Fundamental Diagrams-Based Models with Microscopic Simulations on Real Networks: Importance of Production Hysteresis and Trip Lengths Estimation. Transportation Research Record 2019, 2673, 478–492. [Google Scholar] [CrossRef]
  15. Jin, W.L. Generalized bathtub model of network trip flows. Transportation Research Part B: Methodological 2020, 136, 138–157. [Google Scholar] [CrossRef]
  16. Batista, S.; Seppecher, M.; Leclercq, L. Identification and characterizing of the prevailing paths on a urban network for MFD-based applications. Transportation Research Part C: Emerging Technologies 2021, 127, 102953. [Google Scholar] [CrossRef]
  17. Martínez, I.; Jin, W.L. On time-dependent trip distance distribution with for-hire vehicle trips in Chicago. Transportation Research Record 2021, 2675, 915–934. [Google Scholar] [CrossRef]
  18. Johari, M.; Keyvan-Ekbatani, M.; Ngoduy, D. Traffic dynamics in bi-modal urban networks: a cross-comparison of outflow 2D-NMFD and 3D-NMFD. Transportmetrica B: transport dynamics 2022, 10, 555–585. [Google Scholar] [CrossRef]
  19. Vickrey, W. Congestion in midtown Manhattan in relation to marginal cost pricing. Technical report, Columbia University, 1991.
  20. Vickrey, W. Congestion in midtown Manhattan in relation to marginal cost pricing. Economics of Transportation 2020, 21, 100152. [Google Scholar] [CrossRef]
  21. Leclercq, L.; Parzani, C.; Knoop, V.L.; Amourette, J.; Hoogendoorn, S.P. Macroscopic traffic dynamics with heterogeneous route patterns. Transportation Research Part C: Emerging Technologies 2015, 59, 292–307. [Google Scholar] [CrossRef]
  22. Batista, S.; Leclercq, L.; Menendez, M. Dynamic Traffic Assignment for regional networks with traffic-dependent trip lengths and regional paths. Transportation Research Part C: Emerging Technologies 2021, 127, 103076. [Google Scholar] [CrossRef]
  23. Yildirimoglu, M.; Geroliminis, N. Approximating dynamic equilibrium conditions with macroscopic fundamental diagrams. Transportation Research Part B: Methodological 2014, 70, 186–200. [Google Scholar] [CrossRef]
  24. Batista, S.F.; Leclercq, L. Regional dynamic traffic assignment framework for macroscopic fundamental diagram multi-regions models. Transportation Science 2019, 53, 1563–1590. [Google Scholar] [CrossRef]
  25. Yildirimoglu, M.; Sirmatel, I.I.; Geroliminis, N. Hierarchical control of heterogeneous large-scale urban road networks via path assignment and regional route guidance. Transportation Research Part B: Methodological 2018, 118, 106–123. [Google Scholar] [CrossRef]
  26. Ramezani, M.; Haddad, J.; Geroliminis, N. Dynamics of heterogeneity in urban networks: aggregated traffic modeling and hierarchical control. Transportation Research Part B: Methodological 2015, 74, 1–19. [Google Scholar] [CrossRef]
  27. Huang, Y.; Xiong, J.; Sumalee, A.; Zheng, N.; Lam, W.; He, Z.; Zhong, R. A dynamic user equilibrium model for multi-region macroscopic fundamental diagram systems with time-varying delays. Transportation Research Part B: Methodological 2020, 131, 1–25. [Google Scholar] [CrossRef]
  28. Mariotte, G.; Leclercq, L.; Batista, S.; Krug, J.; Paipuri, M. Calibration and validation of multi-reservoir MFD models: A case study in Lyon. Transportation Research Part B: Methodological 2020, 136, 62–86. [Google Scholar] [CrossRef]
  29. Lamotte, R.; Murashkin, M.; Kouvelas, A.; Geroliminis, N. Dynamic modeling of trip completion rate in urban areas with MFD representations. 2018 TRB Annual Meeting Online. Transportation Research Board, 2018, pp. 18–06192.
  30. Castrillon, F.; Laval, J.A. Impact of buses on the macroscopic fundamental diagram of homogeneous arterial corridors. Transportmetrica B: Transport Dynamics 2017, 6, 1–16. [Google Scholar] [CrossRef]
  31. Laval, J.A.; Leclercq, L.; Chiabaut, N. Minimal parameter formulations of the dynamic user equilibrium using macroscopic urban models: Freeway vs city streets revisited. Transportation Research Part B: Methodological 2017, 23, 517–530. [Google Scholar] [CrossRef]
  32. Eick, S.G.; Massey, W.A.; Whitt, W. The Physics of the Mt/G/∞ Queue. Operations Research 1993, 41, 731–742. [Google Scholar] [CrossRef]
  33. Thomas, T.; Tutert, S. An empirical model for trip distribution of commuters in The Netherlands: transferability in time and space reconsidered. Journal of transport geography 2013, 26, 158–165. [Google Scholar] [CrossRef]
  34. Mori, T.; Smith, T.E.; Hsu, W.T. Common power laws for cities and spatial fractal structures. Proceedings of the National Academy of Sciences 2020, 117, 6469–6475. [Google Scholar] [CrossRef] [PubMed]
  35. Newell, G.F. Applications of queueing theory, second (monographs on statistics and applied probability) ed.; Chapman Hall: London, U.K., 1982. [Google Scholar]
  36. Aghamohammadi, R.; Laval, J.A. A continuum model for cities based on the macroscopic fundamental diagram: A semi-Lagrangian solution method. Transportation Research Part B: Methodological 2020, 132, 101–116. [Google Scholar] [CrossRef]
  37. Halperin, B.; Hohenberg, P. Scaling laws for dynamic critical phenomena. Physical Review 1969, 177, 952. [Google Scholar] [CrossRef]
  38. Batista, S.; Tilg, G.; Menéndez, M. Exploring the potential of aggregated traffic models for estimating network-wide emissions. Transportation Research Part D: Transport and Environment 2022, 109, 103354. [Google Scholar] [CrossRef]
  39. Nagatani, T. The physics of traffic jams. Reports on progress in physics 2002, 65, 1331. [Google Scholar] [CrossRef]
  40. Helbing, D. Traffic and related self-driven many-particle systems. Reviews of modern physics 2001, 73, 1067. [Google Scholar] [CrossRef]
  41. Chowdhury, D.; Santen, L.; Schadschneider, A. Statistical physics of vehicular traffic and some related systems. Physics Reports 2000, 329, 199–329. [Google Scholar] [CrossRef]
  42. Nagatani, T. Traffic flow on percolation-backbone fractal. Chaos, Solitons & Fractals 2020, 135, 109771. [Google Scholar]
  43. Laval, J. Self-organized criticality of traffic flow: There is nothing sweet about the sweet spot. (Under review)2021.
  44. Laval, J. Traffic Flow as a Simple Fluid: Towards a Scaling Theory of Urban Congestion. (Accepted in Transportation Research Record) 2022.
  45. Sirmatel, I.I.; Tsitsokas, D.; Kouvelas, A.; Geroliminis, N. Modeling, estimation, and control in large-scale urban road networks with remaining travel distance dynamics. Transportation Research Part C: Emerging Technologies 2021, 128, 103157. [Google Scholar] [CrossRef]
  46. Sirmatel, I.I.; Geroliminis, N. Stabilization of city-scale road traffic networks via macroscopic fundamental diagram-based model predictive perimeter control. Control Engineering Practice 2021, 109, 104750. [Google Scholar] [CrossRef]
1
This result can also be obtained by integrating the conservation law (8) for all trip distances, which gives the generalized bathtub model:
Q ′ ( t ) = λ ( t ) − v ( t ) · k ( t , 0 )
after noting that λ ( t ) = ∫ 0 ∞ Λ ( t , x ) d x , ∫ 0 ∞ ∂ k ( t , x ) / ( ∂ x ) d x = k ( t , ∞ ) − k ( t , 0 ) and that k ( t , ∞ ) = 0 .
2
For the exponential distribution with mean ℓ, F ( l ) = 1 − exp ( − l / ℓ ) , which gives f X ( x ) = f ( x ) = exp ( − x / ℓ ) / ℓ .
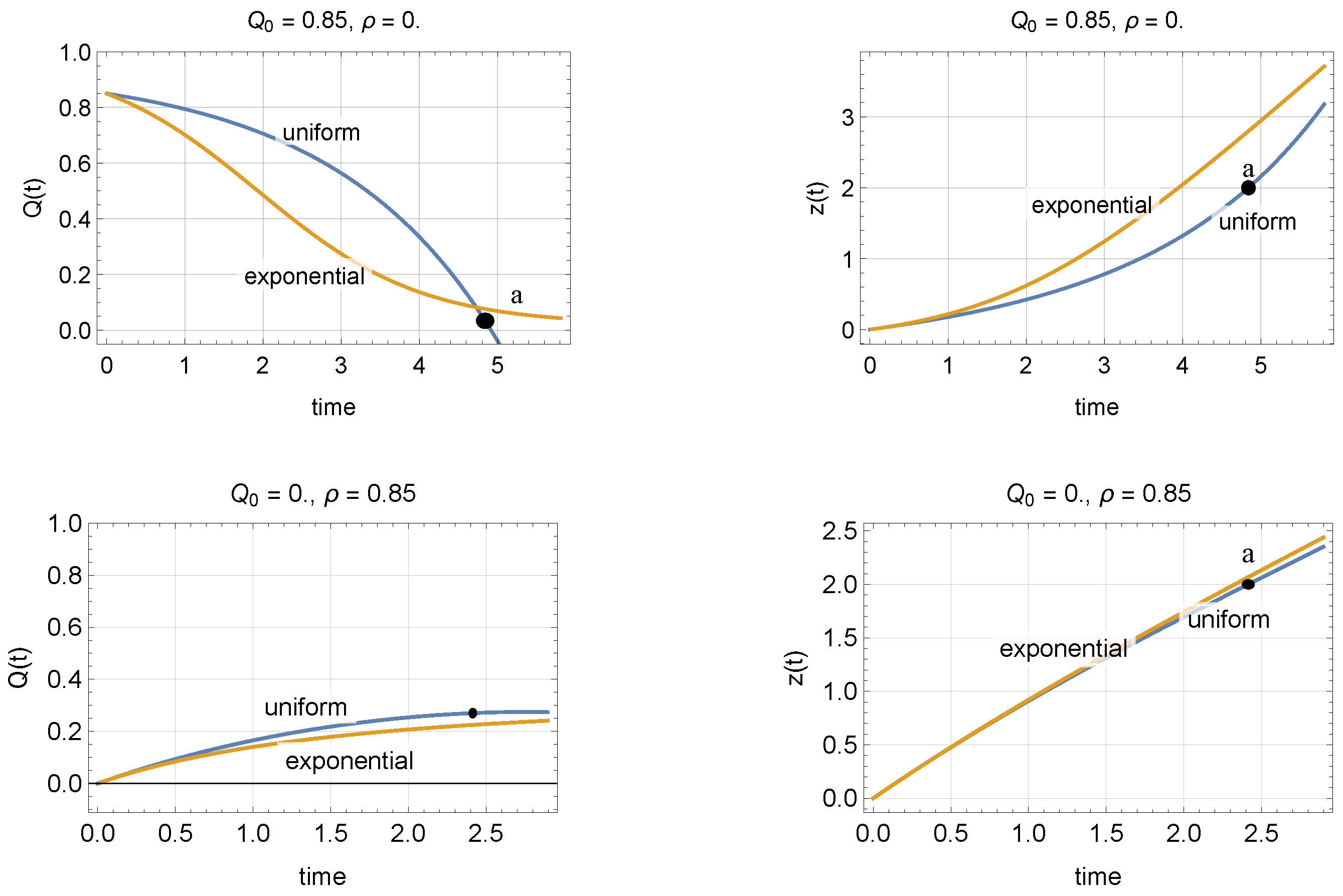
Preprints 68065 g001
Figure 1. Comparison of the exponential and uniform models with the same input parameters and ℓ = 1 .
Figure 1. Comparison of the exponential and uniform models with the same input parameters and ℓ = 1 .
Preprints 68065 g001
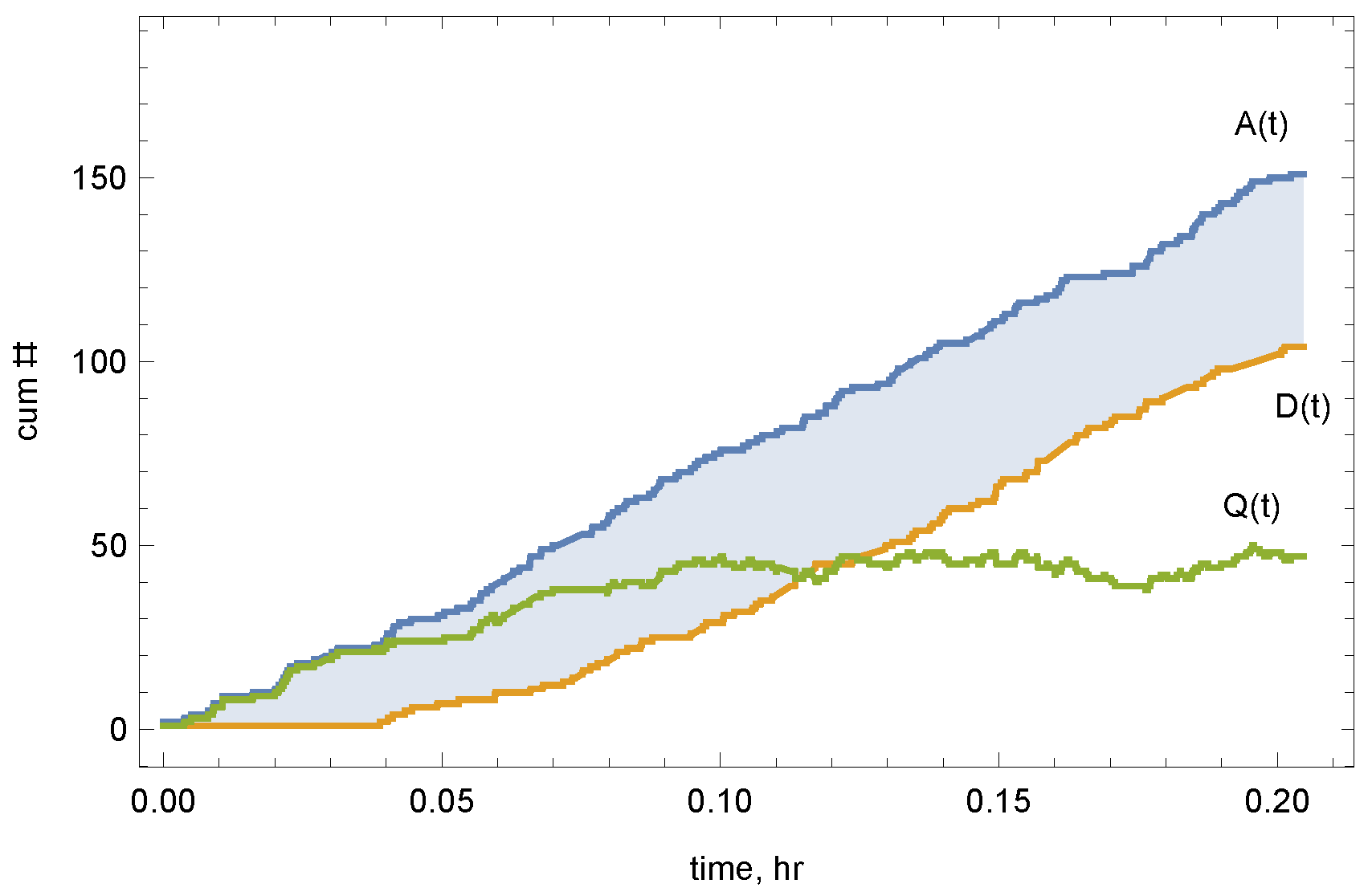
Preprints 68065 g002
Figure 2. The network accumulation Q ( t ) is the difference between cumulative vehicle arrivals to the network, A ( t ) , and departures from the network, D ( t ) .
Figure 2. The network accumulation Q ( t ) is the difference between cumulative vehicle arrivals to the network, A ( t ) , and departures from the network, D ( t ) .
Preprints 68065 g002
Preprints 68065 g003
Figure 3. Top: Typical simulation output in terms of cumulative count curves for departures (left) and accumulations (right), for 50 realizations of the experiment. Notice in the left panel that E D ( t ) > Var D ( t ) , which is typically the case, and from the right panel that E Q ( t ) < Var Q ( t ) . Bottom: Simulation time series with the exponential and uniform distributions for different values of E ρ , showing the evolution of E Q ( t ) / Q * in blue and I Q ≈ Var Q ( t ) / Q * in green. The solid thin lines represent these quantities for a single experiment as in the top part of the figure, while solid thick lines correspond to the average of 1000 such experiments. The dashed green lines give the 0.05 and 0.95 percentiles from the chi-square distribution with parameter 50-1=49.
Figure 3. Top: Typical simulation output in terms of cumulative count curves for departures (left) and accumulations (right), for 50 realizations of the experiment. Notice in the left panel that E D ( t ) > Var D ( t ) , which is typically the case, and from the right panel that E Q ( t ) < Var Q ( t ) . Bottom: Simulation time series with the exponential and uniform distributions for different values of E ρ , showing the evolution of E Q ( t ) / Q * in blue and I Q ≈ Var Q ( t ) / Q * in green. The solid thin lines represent these quantities for a single experiment as in the top part of the figure, while solid thick lines correspond to the average of 1000 such experiments. The dashed green lines give the 0.05 and 0.95 percentiles from the chi-square distribution with parameter 50-1=49.
Preprints 68065 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated