Preprint
Article
Omnidimensional Convex Polytopes
Altmetrics
Downloads
550
Views
344
Comments
1
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 February 2023
Posted:
24 February 2023
You are already at the latest version
Alerts
Abstract
The study shows that the volumes and surfaces of $n$-balls, $n$-simplices, and $n$-orthoplices are holomorphic functions of $n$, which makes those objects omnidimensional, that is well defined in any complex dimension. Applications of these formulas to the omnidimensional polytopes inscribed in and circumscribed about $n$-balls reveal previously unknown properties of these geometric objects. In particular, for $0 < n < 1$, the volumes of the omnidimensional polytopes are larger than those of circumscribing $n$-balls, and both their volumes and surfaces are smaller than those of inscribed $n$-balls. The surface of an $n$-simplex circumscribing unit diameter $n$-ball is spirally convergent to zero with real $n$ approaching negative infinity but first has a local maximum at $n=-3.5$. The surface of an $n$-orthoplex circumscribing unit diameter $n$-ball is spirally divergent with real $n$ approaching negative infinity but first has a local minimum at $n=-1.5$, where its real and imaginary parts are equal to each other; similarly, as its volume, where the similar local minimum occurs at $n=-3.5$. Reflection functions for volumes and surfaces of these polytopes inscribed in and circumscribed about $n$-balls are proposed. symmetries of products and quotients of volumes in complex dimensions $n$ and $-n$ and of surfaces in complex dimensions $n$ and $2-n$ are shown to be independent of the metric factor and the gamma function. Specific symmetries also hold between volumes and surfaces in dimensions $n = -1/2$ and $n = 1/2$.
Keywords:
Subject: Computer Science and Mathematics - Geometry and Topology
I. INTRODUCTION
The notion of dimension n is intuitively defined as a natural number of coordinates of a point within Euclidean space . However, this is not the only possible definition [1,2] of a dimension of a set. For example, analytic continuations from positive dimensions [2,3,4,5] can define negative dimensions [6]. Fractional (or fractal), including negative [7], dimensions are consistent with experimental results and enable the examination of transport parameters in multiphase fractal media [8,9]. This renders dimension n real, or at least a rational number. Complex [2], including complex fractional [10], dimensions can also be considered. Complex geodesic paths, for example, emerge in the presence of black hole singularities [11] and when studying entropic dynamics on curved statistical manifolds [12]. Complex wavelengths occur in Maxwell-Boltzmann, and Fermi-Dirac statistics on black hole event horizons [13]. Fractional derivatives of complex functions can describe different physical phenomena [14]. For example, it was recently shown [15] that magnetic monopole motion in 3-simplicial spin ice crystal lattice is limited to a fractal cluster.
In n-dimensional space, n-dimensional objects have -dimensional surfaces which have a dimension of volume in -dimensional space. However, this sequence has a singularity at . A 0-dimensional point in 0-dimensional space has a vanishing -surface being a vanishing volume of the -dimensional void. But the surface of the -dimensional void is not -dimensional. It is undefined. This discontinuity hints that thinking about dimension in terms of a point on a number axis, where negative dimensions are analytic continuations from positive ones, may be misleading. Thinking of the dimension as a point on a number semiaxis, similar to a point on a radius with -dimension corresponding to n-dimension, seems more appropriate. Considering the dimension of a set as the length exponent at which that set can be measured makes the negative dimensions refer to densities as positive ones refer to quantities [5]. Thus, the -dimensional pressure, for example, considered in terms of density (e.g., in units of N/m2) corresponds to a 2-dimensional area (in units of m2) that it acts upon. Following the same logic, gravitational force acting towards an inside of a 2-dimensional equipotential surface is -dimensional, whereas centripetal force acting towards an outside of a 1-dimensional curve is -dimensional.
The notion of distance intuitively defines how far apart two points are. Thus, intuition suggests that it is a non-negative quantity. However, intuition can be misleading1, and the Euclidean distance admits not only the principal, non-negative, square root but also a negative one. This fact, taken plainly, violates the nonnegativity axiom of the metric. However, diffuse metrics [16], including the Łukaszyk-Karmowski metric [17], are known to violate the identity of indiscernibles axiom of the metric. This hints that axiomatizing distance as a non-negative quantity may also be misleading. Complex effects (bivalence) extend real effects (classically one value), just as quantum theory extends classical physics.
The study shows that the recurrence relations of the prior research [18] allow removing indefiniteness present in known formulas for volumes and surfaces of the three polytopes present in all natural dimensions [19], thus making them holomorphic functions of a complex dimension n and omnidimensional (i.e., well defined ).
The paper is structured as follows. Section II summarizes known formulas and recurrence relations for volumes and surfaces of n-balls and regular, convex n-polytopes. Section III shows that these formulas and recurrence relations can be extended to all complex dimensions. Section IV examines the properties of the omnidimensional, regular, convex polytopes inscribed in and circumscribed about n-balls and their reflection functions. Section V presents metric-independent relations between volumes and surfaces of these polytopes and n-balls, whereas Section VI presents particular symmetries between volumes and surfaces for . Section sec:discussion concludes and discusses the findings of this study, hinting at their possible applications.
II. KNOWN FORMULAS
It is known that the volume of an n-ball (B) is
where is the Euler’s gamma function, , [18], and R denotes the n-ball radius. As the gamma function is meromorphic, volumes of n-balls are complex in complex dimensions. The volume of an n-ball can be expressed [20] in terms of the volume of an -ball of the same radius as a recurrence relation
where and . The relation (2) can be extended [18] into negative dimensions as
solving (2) for and assigning new n as the previous . A radius recurrence relation2 [18]
where , and , allow for expressing the volume n-ball as
where ”” is the floor function that yields the greatest integer less than or equal to its argument x. The relation (4) can be, analogously as formula (2), extended [18] into complex dimensions with a negative real part as
which allows to define to initiate the sequences (4) or (6). Known [20] surface of an n-ball3 is
Known volume of n-cube (C) is
where and A is the edge length. The known surface of n-cube is
where .
Known [21,22] volume of a regular n-simplex (S) is
where . The formula (10) can be written [18] as a recurrence relation
with , to remove the indefiniteness of the factorial for . Formula (11) can be solved for . Assigning new n as the previous , yields [18]
which also removes the singularity for present in the volume (10). n-simplex has -facets [20]. Therefore, its surface is
Formula (14) can be written [18] as a recurrence relation
where and , to remove the indefiniteness of the factorial for . Solving (15) for and assigning new n as the previous , yields [18]
which also removes singularity for present in formula (15). Any n-orthoplex has facets [20], which are regular -simplices. Therefore, its surface is
III. HOLOMORPHIZING KNOWN FORMULAS
Known formulas presented in the preceding section can be extended to all complex dimensions. We note that volumes and surfaces of n-cubes are already defined and thus holomorphic. We also note that a square root is bivalued in the complex domain4. Therefore, volumes and surfaces of n-balls and regular, convex n-polytopes are also bivalued in complex dimensions n. We call principal branch the branch with positive values in positive real dimensions.
Theorem 1
The volume of an n-ball is a holomorphic, bivalued function of a complex dimension n.
Proof.
First, we note that the initial bivalued values for the radius recurrence relations (4), (6) are , and . Then, we note that the recurrence relations (3) and (5) correspond to each other
which, after setting , yields
Comparing the non-recurrence general n-ball volume formula (1), which is bivalued for and valid within the domain of the gamma function, with the recurrence relation (3)
yields
Setting yields
which recovers (1), as , , . Thus we have proved that the recurrence relations (2), (3), and (5) correspond to the general n-ball volume formula (22) within this domain.
However, now we can use any of the backward recurrence relations (3) or (5) with (6) to determine the values of the n-ball volume outside this domain: we can find .
On the other hand
so the poles of the meromorphic gamma function present in (22), now defined in the sense of a limit of a function, vanish, which completes the proof. □
Corollary 1.1.
The surface of an n-ball is a holomorphic, bivalued function of a complex dimension n.
Proof.
If the volume of an n-ball is a holomorphic, bivalued function by Theorem 1, then, using formula (7), the surface of an n-ball is also a holomorphic function.
□
Theorem 2
The volume of a regular n-simplex is a holomorphic, bivalued function of a complex dimension n.
Proof.
Expressing the factorial in the volume of a regular n-simplex formula (10) by the gamma function extends the domain of applicability of (10) to complex dimensions
On the other hand, comparing the volume (25) with the recurrence relation (12)
yields
which, after setting , yields
and recovers (25) as and (cf. Appendix A). Thus, we have proved that the recurrence relation (12) corresponds to the generalized n-simplex volume formula (25) within this domain.
However, now we can use the recurrence relation (12) to determine the values of the n-simplex volume outside this domain: we can find . For example, even though is undefined for , we can determine that using the recurrence relation (12) with obtained from (25).
On the other hand
so the poles of the meromorphic gamma function present in (25), now defined in the sense of a limit of a function, vanish - which completes the proof. □
For }, n-simplex volume formula (25) is imaginary.
Corollary 2.1.
The surface of a regular n-simplex is a holomorphic, bivalued function of a complex dimension n.
Proof.
If the volume of a regular n-simplex is a holomorphic, bivalued function by Theorem 2, then its surface, using formula (13), is also a holomorphic, bivalued function.
□
Again, even though is undefined for , we can determine that directly from formula (13) knowing that .
For , n-simplex surface formula (30) is imaginary.
Theorem 3.
The volume of an n-orthoplex is a bivalued, holomorphic function of a complex dimension n.
Proof.
Expressing the factorial in the volume of an n-orthoplex formula (14) by the gamma function extends the domain of applicability of (14) to complex dimensions
On the other hand, comparing (31) with the recurrence relation (16)
yields
whereas setting in (33) yields
which recovers n-orthoplex volume (14), as . Thus, we have proved that the recurrence relation (16) corresponds to the general n-orthoplex volume formula (31) within this domain.
However, now we can use the recurrence relation (16) to determine the values of the n-orthoplex volume outside this domain: we can find . On the other hand
so the poles of the meromorphic gamma function present in (31), now defined in the sense of a limit of a function, vanish - which completes the proof. □
Corollary 3.1.
The surface of an n-orthoplex is a holomorphic, bivalued function of a complex dimension n.
Proof.
If the volume of a regular n-simplex is a holomorphic, bivalued function by Theorem 2, then, using formula (17), the surface of an n-orthoplex is a holomorphic, bivalued function.
□
For , n-orthoplex bivalued surface formula (36) is imaginary.
Thus, the volumes and surfaces of n-balls, n-simplices, and n-orthoplices, shown in Figs 1 and 2 for , are holomorphic functions of n, which makes those objects omnidimensional. They can be explicitly expressed in terms of the complex dimension (cf. Appendix B).
IV. OMNIDIMENSIONAL POLYTOPES INSCRIBED IN AND CIRCUMSCRIBED ABOUT n-BALLS
First, we will introduce the definition of a reflection function.
Definition 1.
For each function of a complex argument n given by the formula
where , , and is some nonzero function of n, we define its reflection function
where
Theorem 4.
Proof.
We note here that , such that
(with ) so that
and that
Therefore,
□
Each regular, omnidimensional polytope discussed in Section III can be inscribed in and circumscribed about an n-ball. This section presents their volumes, surfaces, and reflection functions (38). Particular values of their volumes and surfaces are listed in Tables I and II. Unless stated otherwise, and . Unit diameter n-balls are assumed.
A. Regular n-Simplices Inscribed in n-Balls
The diameter of an n-ball circumscribing a regular n-simplex () is known [22] to be
where A is the edge length. Hence, the edge length of a regular n-simplex inscribed () in an n-ball (B) with diameter D is
so that the regular n-simplex volume (25) becomes
For the inscribed n-simplex volume (49) is imaginary and divergent with n approaching negative infinity. It is complex for , with the real part equaling the imaginary part for . It is zero for , and for , it is larger than the volume of the circumscribing n-ball. The volume (49) does not have a reflection function (38), as d in (39) vanishes.
Similarly, the surface (30) of a regular inscribed n-simplex with edge length A given by (48) is
as shown in Fig. 4. For the inscribed n-simplex surface (50) is imaginary and divergent with n approaching negative infinity. It is complex for , with the real part equaling the imaginary part for . It is zero for , . The surface (50) does not have a reflection function (38), as d in (39) vanishes.
B. Regular n-Simplices Circumscribed About n-Balls
The diameter of an n-ball inscribed in a regular n-simplex () is known [22] to be
where A is the edge length. Hence, the edge length of a regular n-simplex circumscribed () about an n-ball (B) with diameter D is
so that its volume (25) becomes
For , the volume (53) is complex with a nonzero imaginary part, whereas both branches are left-handed spirals converging to zero with n approaching negative infinity. For , the volume (53) is smaller than the volume of the inscribed n-ball. It is zero for , and real for , where it amounts
Furthermore, for and , the real part of the volume (53) equals the imaginary part up to a modulus. For , . Otherwise, it amounts
The surface (57) is zero for , , and for , it is smaller than the surface of the inscribed n-ball. The surface (57) is complex for , with both branches being left-handed spirals converging towards zero with n approaching negative infinity. However, it is initially divergent to achieve a modulus maximum of about 2.9757 at (numerically calculated) and a real maximum of about at . For the imaginary part of the surface (57) vanishes and it amounts
The real part of the surface (57) is equal to the imaginary part up to a modulus for () and
C. n-Orthoplices Inscribed in n-Balls
The diameter of an n-ball circumscribing an n-orthoplex () is known [23] to be
where A is the edge length. Hence, the edge length of an n-orthoplex inscribed in an n-ball () with diameter D is
so that its volume (31) becomes
The inscribed n-orthoplex volume (63) is real, vanishes for , and for it is larger than the volume of the circumscribing n-ball. It does not have a reflection function.
D. n-Orthoplices Circumscribed About n-Balls
The diameter of an n-ball inscribed in an n-orthoplex () is known [23] to be
where A is the edge length. Hence, the edge length of an n-orthoplex circumscribed about an n-ball () with diameter D is
so that its volume (31) becomes
as shown in Fig. 9.
Circumscribed n-orthoplex volume (67) is complex for . It oscillates and is initially convergent to achieve a modulus minimum of about 0.1181 at (numerically computed) and then becomes divergent with n approaching negative infinity. For , it vanishes. For , it is smaller than the volume of the inscribed n-ball. For , the real part of the volume (67) equals the imaginary part up to a modulus, achieving a local minimum at and amounts
Similarly, the surface (36) of the circumscribed n-orthoplex with edge length A given by (66) becomes
as shown in Fig. 10.
Circumscribed n-orthoplex surface (70) is complex for . It oscillates and is initially convergent to achieve a modulus minimum of about 0.6244 at (numerical) and then becomes divergent with n approaching negative infinity. For , it vanishes. For , it is smaller than the surface of the inscribed n-ball. Furthermore, its real part equals the imaginary part up to a modulus for , . It achieves a local minimum at and amounts
E. n-Cubes Inscribed in and Circumscribed About n-Balls
The edge length of an n-cube circumscribed about an n-ball () corresponds to the diameter D of this n-ball. Thus, the volume of this cube is simply
and the surface is
However, the edge length of an n-cube inscribed in an n-ball () of diameter D is
which is singular for and complex for , rendering [18] the volume
and the surface
of an n-cube inscribed in an n-ball.
V. METRIC-INDEPENDENT RELATIONS
The following metric-independent relations hold, for , between volumes of n-balls (22)
n-simplices (25)
n-orthoplices (31) and n-orthoplices inscribed in n-balls (63)
n-simplices inscribed in n-balls (49)
n-simplices circumscribed about n-balls (53)
and n-orthoplices circumscribed about n-balls (67)
where we used Euler’s reflection formula, , with , and
as well as (for ), between surfaces of n-balls (24)
n-simplices (30),
n-orthoplices (36)
n-simplices inscribed in n-balls (50)
n-simplices circumscribed about n-balls (57)
n-orthoplices inscribed in n-balls (64)
n-orthoplices circumscribed about n-balls (70)
and n-cubes inscribed in n-balls (77) ()
where we again used and Euler’s reflection formula
These relations are independent of the distance value D and its particular form, whether negative () or complex (, ), including purely imaginary (). Furthermore, the relations (80)-(85) and (87)-(93) are independent of the gamma function. Relations (80)-(85) are shown in Fig. 13. The imaginary part of the surface relations (88)-(94) vanishes for .
Also, for , the following both metric and gamma function independent relations can be obtained between volumes (73), (76) and surfaces (74), (77) of circumscribed and inscribed n-cubes
between volumes (53), (49) and surfaces (57), (50) of circumscribed and inscribed n-simplices
and between volumes (67), (63) and surfaces (70), (64) of circumscribed and inscribed n-orthoplices
Notably, the ratio of the volume of n-cube circumscribed about n-ball to the volume of n-cube inscribed in n-ball (96) is the same as the ratio of the volume of n-orthoplex circumscribed about n-ball to the volume of n-orthoplex inscribed in n-ball (98), and the same holds for the ratio of their surfaces, . This is unsurprising: as n-cube is dual to n-orthoplex, these ratios remain invariant.
VI. VOLUME-SURFACE SYMMETRIES
Furthermore, the following particular symmetries between and hold for (22), (24); (25), (30); (31), (36); (49), (50); (53), (57); (63), (64); (67), (70); (76), (77); and (73), (74)
where ”*” denotes a complex conjugate.
Furthermore, if
VII. DISCUSSION
The volumes and surfaces of n-balls, n-simplices, and n-orthoplices have been defined in any complex dimension. As these geometric objects occur, along with n-cubes, in all natural dimensions [19], this result makes them omnidimensional, that is, present in any complex dimension.
Applications of these formulas to the omnidimensional polytopes inscribed in and circumscribed about n-balls revealed previously unknown properties of these geometric objects. In particular, for , the omnidimensional polytopes’ volumes are larger than those of circumscribing n-balls, while their volumes and surfaces are smaller than those of inscribed n-balls.
Reflection functions for volumes and surfaces of these polytopes inscribed in and circumscribed about n-balls are proposed.
Symmetries of products (80)-(85), (87)-(94) and quotients (96)-(98) of volumes of these circumscribed and inscribed omnidimensional polytopes and n-balls in complex dimensions n and and of surfaces in complex dimensions n and are shown to be independent of the metric factor and the gamma function.
Specific symmetries also hold between volumes and surfaces in dimensions and .
The results of this study could be applied in linguistic statistics, where the dimension in the distribution for frequency dictionaries is chosen to be negative [3], in fog computing, where n-simplex is related to a full mesh pattern, n-orthoplex is linked to a quasi-full mesh structure, and n-cube is referred to as a certain type of partial mesh layout [24]. Further possible applications include molecular physics and crystallography. Perhaps the results of this study are also related to the 2-dimensional quantum hall effect.
One can also investigate the properties of the examined geometric objects extending these concepts to quaternions. This can help us discover many interesting mathematical properties and physical phenomena. One of the challenges certainly involves characterizing all types of symmetries introduced by Definition 1.
Data Availability Statement
The public repository for the code written in Matlab computational environment is given under the link https://github.com/szluk/Omnidimensional-Polytopes.
Authors’ Contribution
AT: Proof that ; the proposition of the affine exponential function (37); remarks on the square root properties in the complex domain and the general bivalence that the latter brings (which renders volumes and surfaces bivalued) in the context of classical and quantum physics; numerous clarity and formal corrections and improvements; hinting at possible applications of the results of this study to quaternions. SŁ: Remaining part of the study.
ACKNOWLEDGMENTS
SŁ thanks his wife and Tomek for their motivation.
Appendix A: Bivalence of the complex square root
It is known that complex number has two square roots
for , that is
Thus,
The same holds for , setting .
Appendix B: Volumes and Surfaces in terms of the real and imaginary parts of the complex dimension
The volumes and surfaces of the omnidimensional objects can be explicitly expressed in terms of the real and imaginary part of the Complex Dimension .
In the case of n-balls, for example
and the volume (22) and surface (24) become
where we used and similarly .
In particular for , (spacetime dimensionality) the volume (B3) and the surface (B4) become
which forms reduce to familiar and for (i.e., at the present moment of perception). The trigonometric member also vanishes in (B5) and (B6) for . Notably, , where is the Planck length, is the radius of a 4-bit black hole [13], and one unit of a black hole entropy [25].
- D. Schleicher, “Hausdorff Dimension, Its Properties, and Its Surprises,” The American Mathematical Monthly, vol. 114, pp. 509–528, June 2007. [CrossRef]
- Y. I. Manin, “The notion of dimension in geometry and algebra,” Bulletin of the American Mathematical Society, vol. 43, pp. 139–162, Feb. 2006.
- V. P. Maslov, “Negative dimension in general and asymptotic topology,” Dec. 2006. arXiv:math/0612543.
- V. P. Maslov, “General notion of a topological space of negative dimension and quantization of its density,” Mathematical Notes, vol. 81, pp. 140–144, Feb. 2007. [CrossRef]
- Tglad, “Office chair philosophy: Generalised definition for negative dimensional geometry,” Aug. 2017.
- G. Parisi and N. Sourlas, “Random Magnetic Fields, Supersymmetry, and Negative Dimensions,” Physical Review Letters, vol. 43, pp. 744–745, Sept. 1979. [CrossRef]
- B. B. Mandelbrot, “Negative fractal dimensions and multifractals,” Physica A: Statistical Mechanics and its Applications, vol. 163, pp. 306–315, Feb. 1990. [CrossRef]
- B. Yu, “Fractal Dimensions for Multiphase Fractal Media,” Fractals, vol. 14, pp. 111–118, June 2006. [CrossRef]
- B. Yu, M. Zou, and Y. Feng, “Permeability of fractal porous media by Monte Carlo simulations,” International Journal of Heat and Mass Transfer, vol. 48, pp. 2787–2794, June 2005. [CrossRef]
- M. L. Lapidus, An overview of complex fractal dimensions:from fractal strings to fractal drums, and back, vol. 731 of Contemporary Mathematics. Providence, Rhode Island: American Mathematical Society, June 2019.
- L. Fidkowski, V. Hubeny, M. Kleban, and S. Shenker, “The Black Hole Singularity in AdS/CFT,” Journal of High Energy Physics, vol. 2004, pp. 014–014, Feb. 2004. [CrossRef]
- S. Gassner and C. Cafaro, “Information geometric complexity of entropic motion on curved statistical manifolds under different metrizations of probability spaces,” International Journal of Geometric Methods in Modern Physics, vol. 16, p. 1950082, June 2019. [CrossRef]
- Łukaszyk, Black Hole Horizons as Patternless Binary Messages and Markers of Dimensionality. Nova Science Publishers, 2023.
- E. Guariglia and S. Silvestrov, “Fractional-wavelet analysis of positive definite distributions and wavelets on D (C),” in Engineering Mathematics II (S. Silvestrov and M. Rančić, eds.), vol. 179, pp. 337–353, Cham: Springer International Publishing, 2016. [CrossRef]
- J. N. Hallén, S. A. Grigera, D. A. Tennant, C. Castelnovo, and R. Moessner, “Dynamical fractal and anomalous noise in a clean magnetic crystal,” Science, vol. 378, pp. 1218–1221, Dec. 2022. [CrossRef]
- P. S. Castro, T. Kastner, P. Panangaden, and M. Rowland, “MICo: Improved representations via sampling-based state similarity for Markov decision processes,” Jan. 2022. arXiv:2106.08229 [cs]. [CrossRef]
- S. Łukaszyk, “A new concept of probability metric and its applications in approximation of scattered data sets,” Computational Mechanics, vol. 33, pp. 299–304, Mar. 2004. [CrossRef]
- Łukaszyk, “Novel Recurrence Relations for Volumes and Surfaces of n-Balls, Regular n-Simplices, and n-Orthoplices in Real Dimensions,” Mathematics, vol. 10, p. 2212, June 2022. [CrossRef]
- “Platonic Solids in All Dimensions.”.
- H. S. M. Coxeter, Regular polytopes. New York: Dover Publications, 3d ed ed., 1973.
- B. C. Wong and D. M. Y. Sommerville, “An Introduction to the Geometry of n Dimensions,” The American Mathematical Monthly, vol. 38, p. 286, May 1931.
- R. H. Buchholz, “Perfect pyramids,” Bulletin of the Australian Mathematical Society, vol. 45, pp. 353–368, June 1992. [CrossRef]
- “Different Products, occurring with Polytopes.”.
- P. J. Roig, S. Alcaraz, K. Gilly, and C. Juiz, “Applying Multidimensional Geometry to Basic Data Centre Designs,” International Journal of Electrical and Computer Engineering Research, vol. 1, pp. 1–8, June 2021. [CrossRef]
- J. D. Bekenstein, “Black Holes and Entropy,” Phys. Rev. D, vol. 7, pp. 2333–2346, Apr 1973. [CrossRef]
| 1 | E.g., in aviation, where relying on a sense of orientation (aka intuition) can be fatal. |
| 2 | We choose the notation over , as . |
| 3 | Commonly, the surface is defined to correspond to -dimensional object. However, the authors find it confusing: -dimensional surface remains the property of the n-dimensional object. Thus, in this study denotes -dimensional surface of the n-dimensional object, not n-dimensional surface of the -dimensional object. |
| 4 | Furthermore . By choosing complex analysis, we enter into bivalence by its very nature. |
| 5 |
,
|
Figure 1.
Graphs of volumes (V) and surfaces (S) of unit edge length regular n-simplices (red), n-orthoplices (green), n-cubes (pink), and unit diameter n-balls (blue), along with the integer recurrence relations (dashed lines) for .
Figure 1.
Graphs of volumes (V) and surfaces (S) of unit edge length regular n-simplices (red), n-orthoplices (green), n-cubes (pink), and unit diameter n-balls (blue), along with the integer recurrence relations (dashed lines) for .
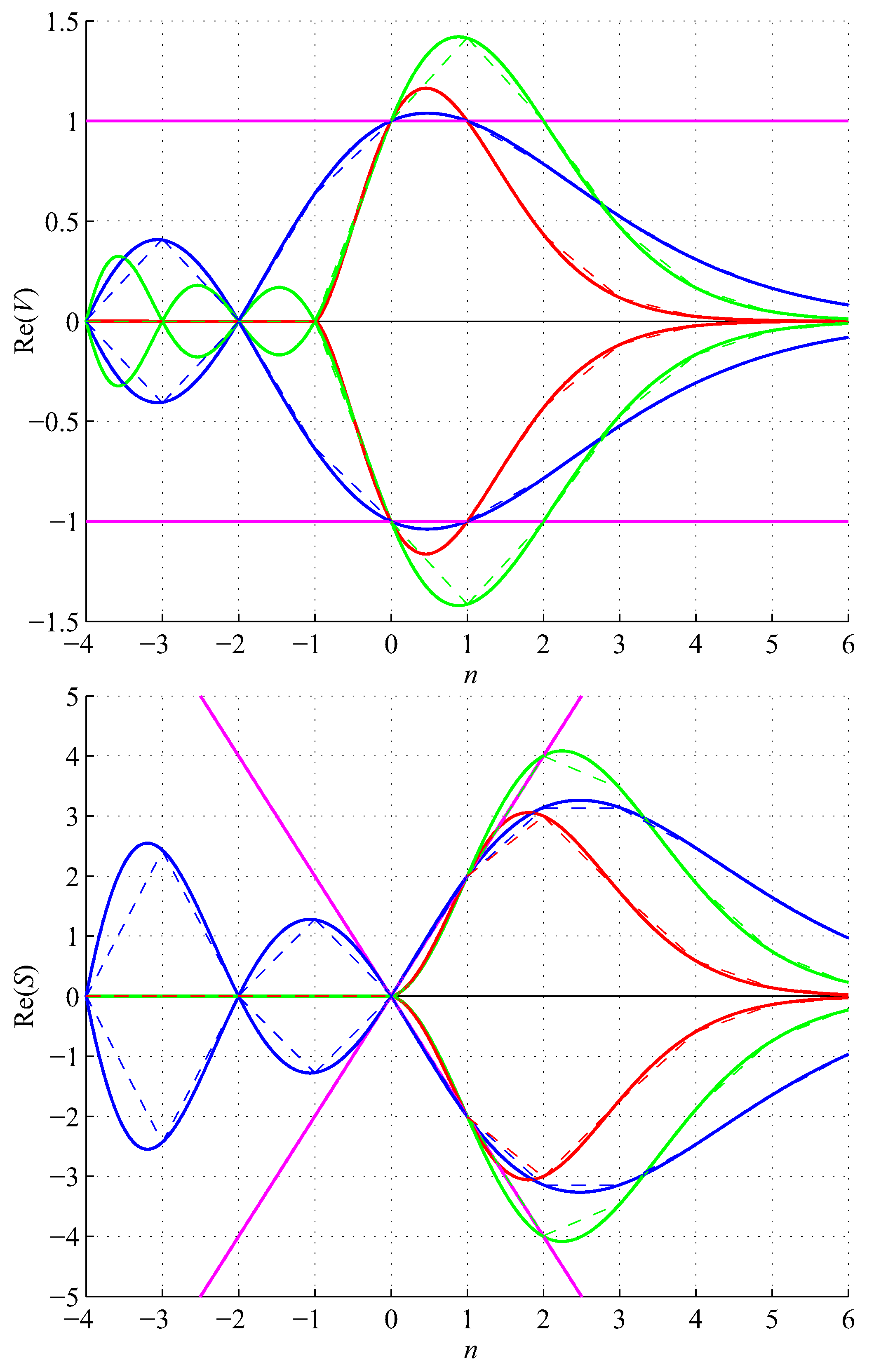
Figure 2.
Graphs of volumes (V) and surfaces (S) of unit edge length regular n-simplices (red), n-orthoplices (green), and unit diameter n-balls (blue) for .
Figure 2.
Graphs of volumes (V) and surfaces (S) of unit edge length regular n-simplices (red), n-orthoplices (green), and unit diameter n-balls (blue) for .
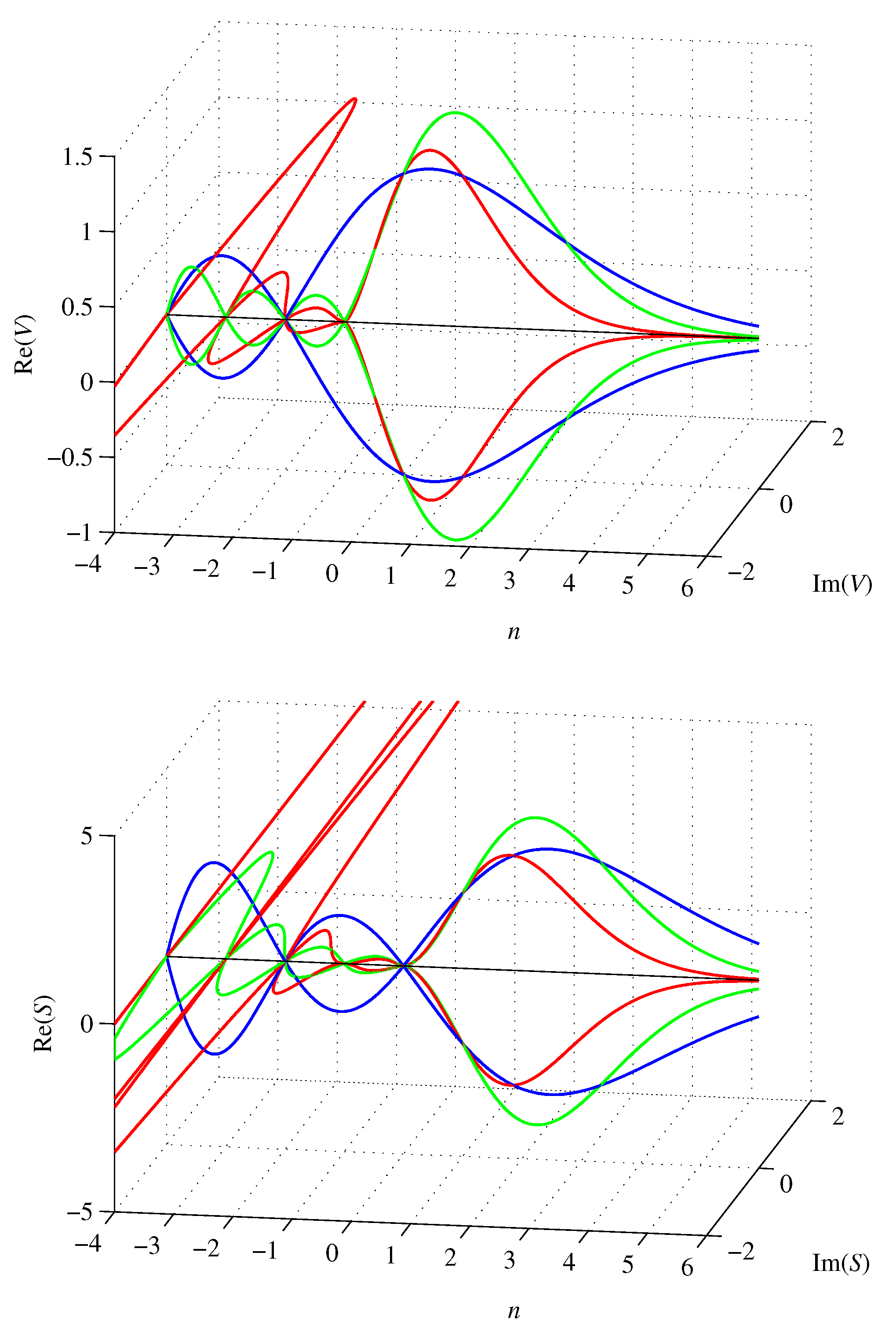
Figure 3.
Graphs of (red) and (blue) for .
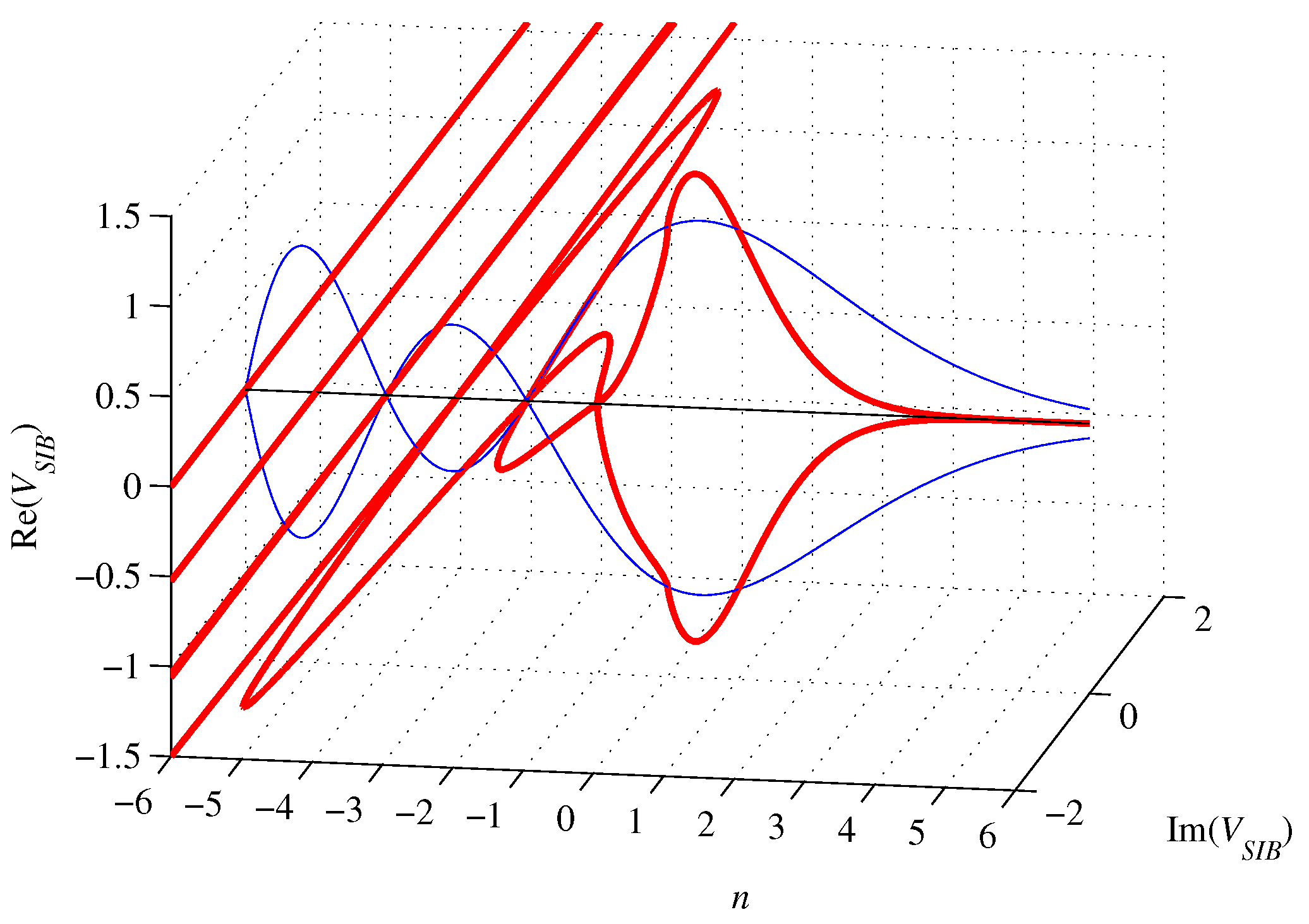
Figure 4.
Graphs of (red) and (blue) for .
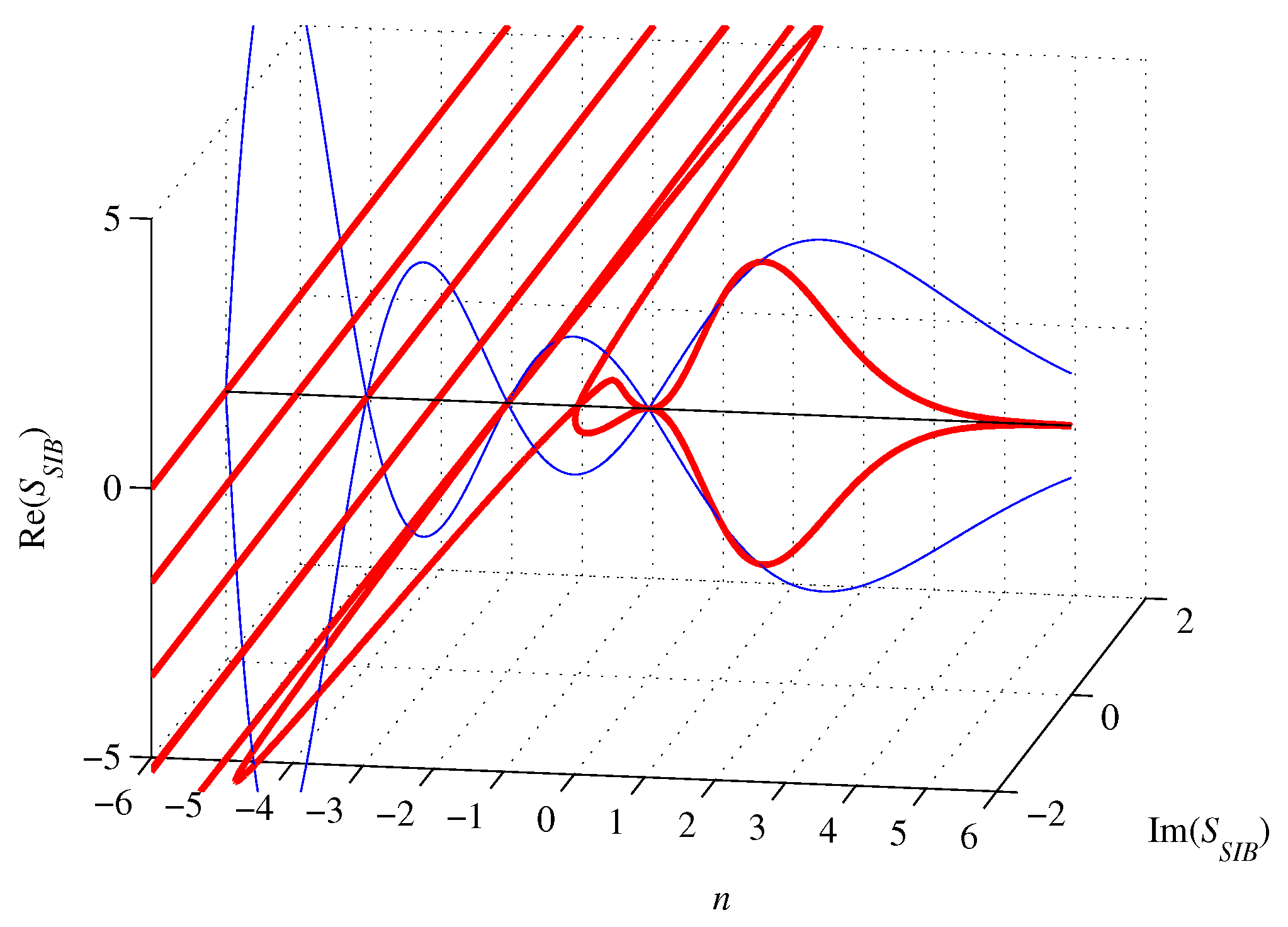
Figure 5.
Graphs of (red), (blue), and (dark red), for .
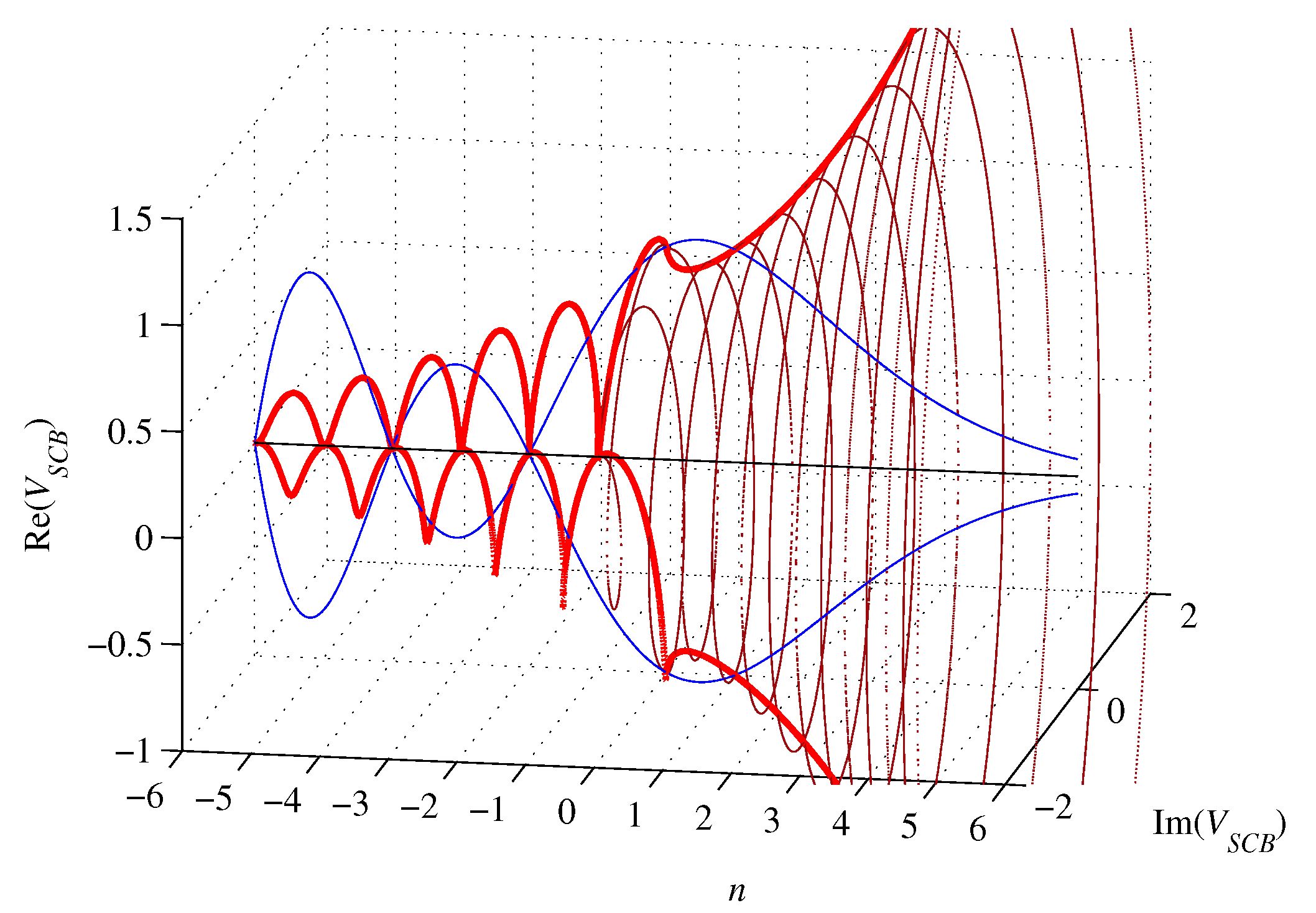
Figure 6.
Graphs of (red), (blue), and (dark red), for .
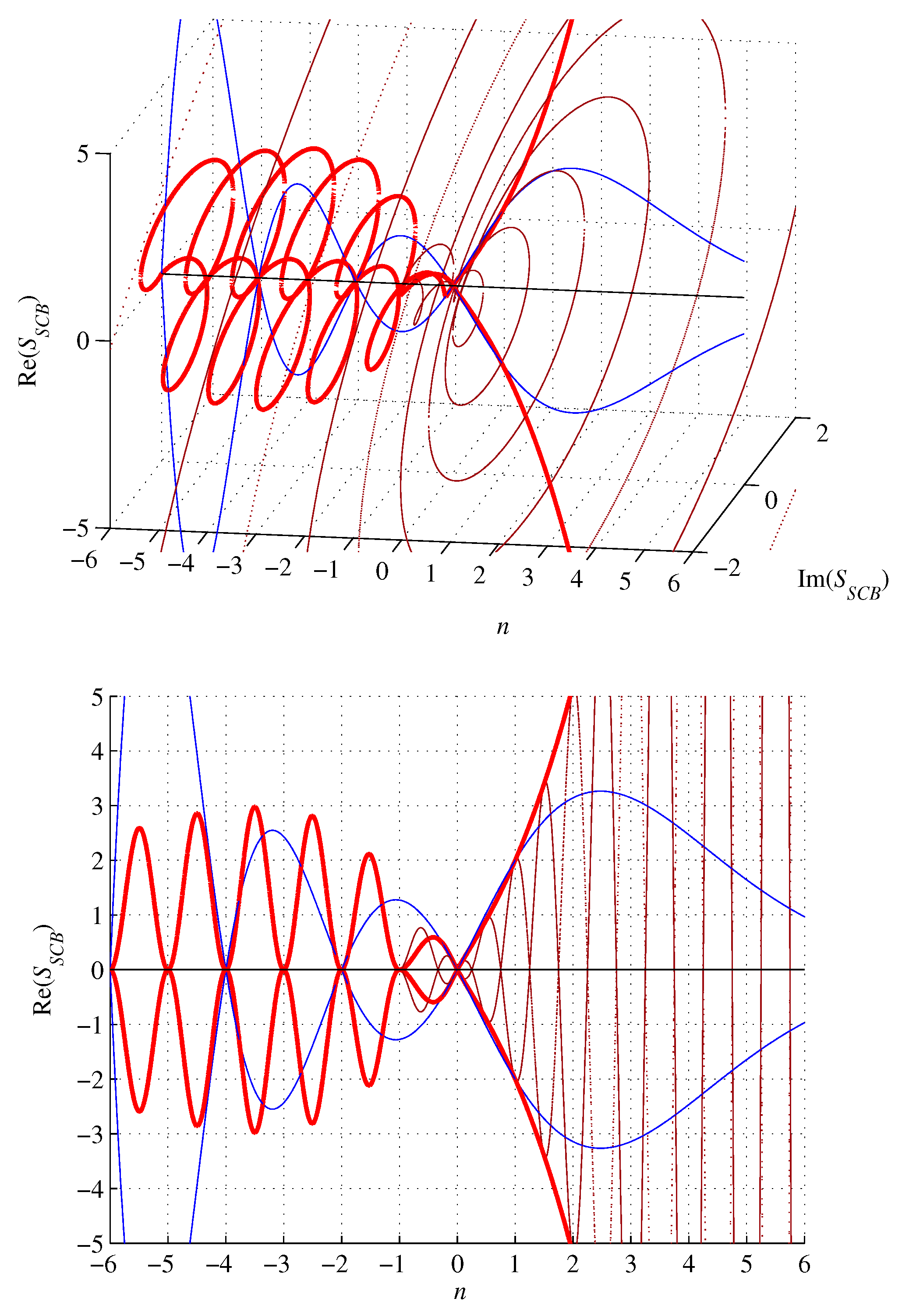
Figure 7.
Graphs of (green) and (blue), for .
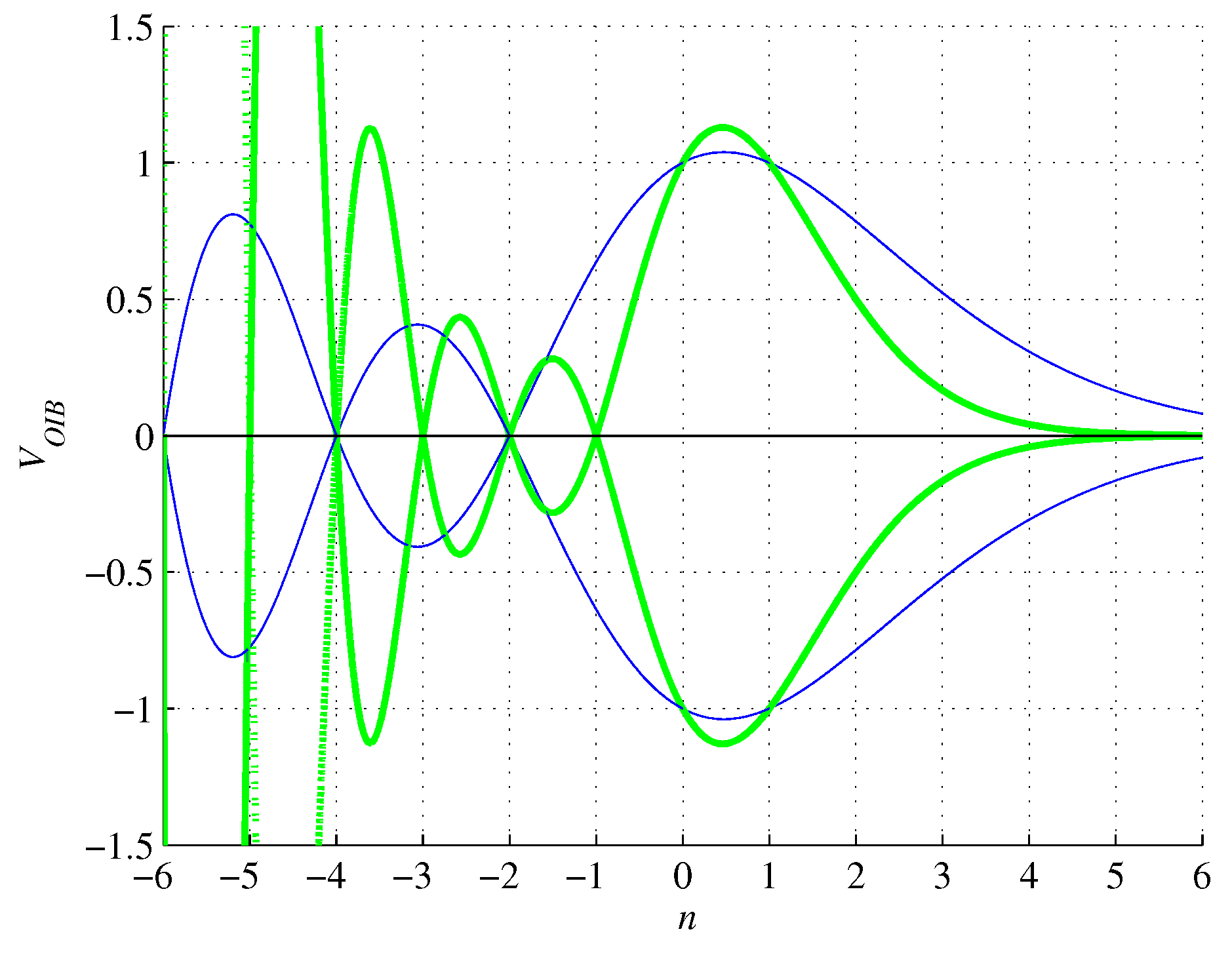
Figure 8.
Graphs of (green) and (blue), for .
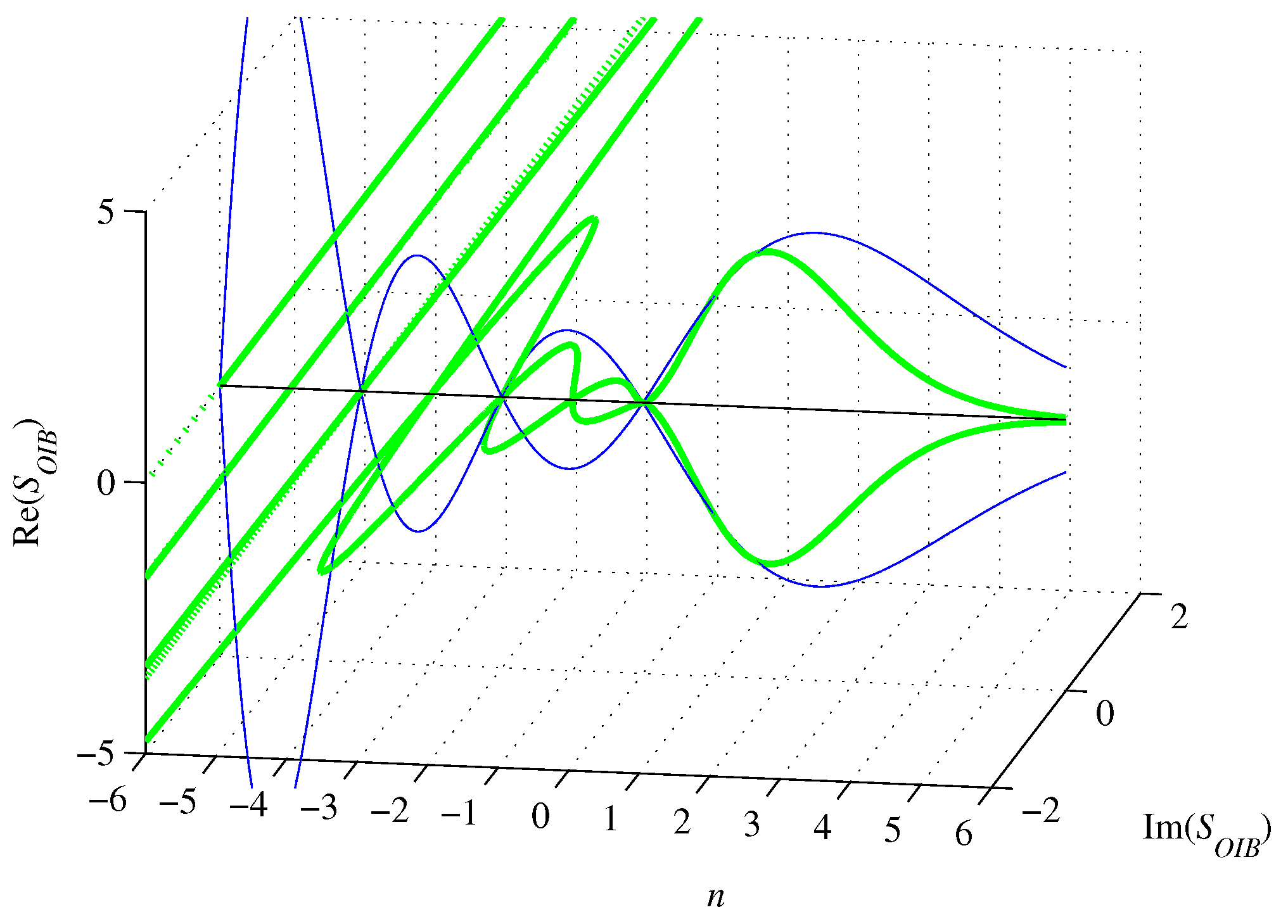
Figure 9.
Graphs of (green), (blue), and (dark green), for .
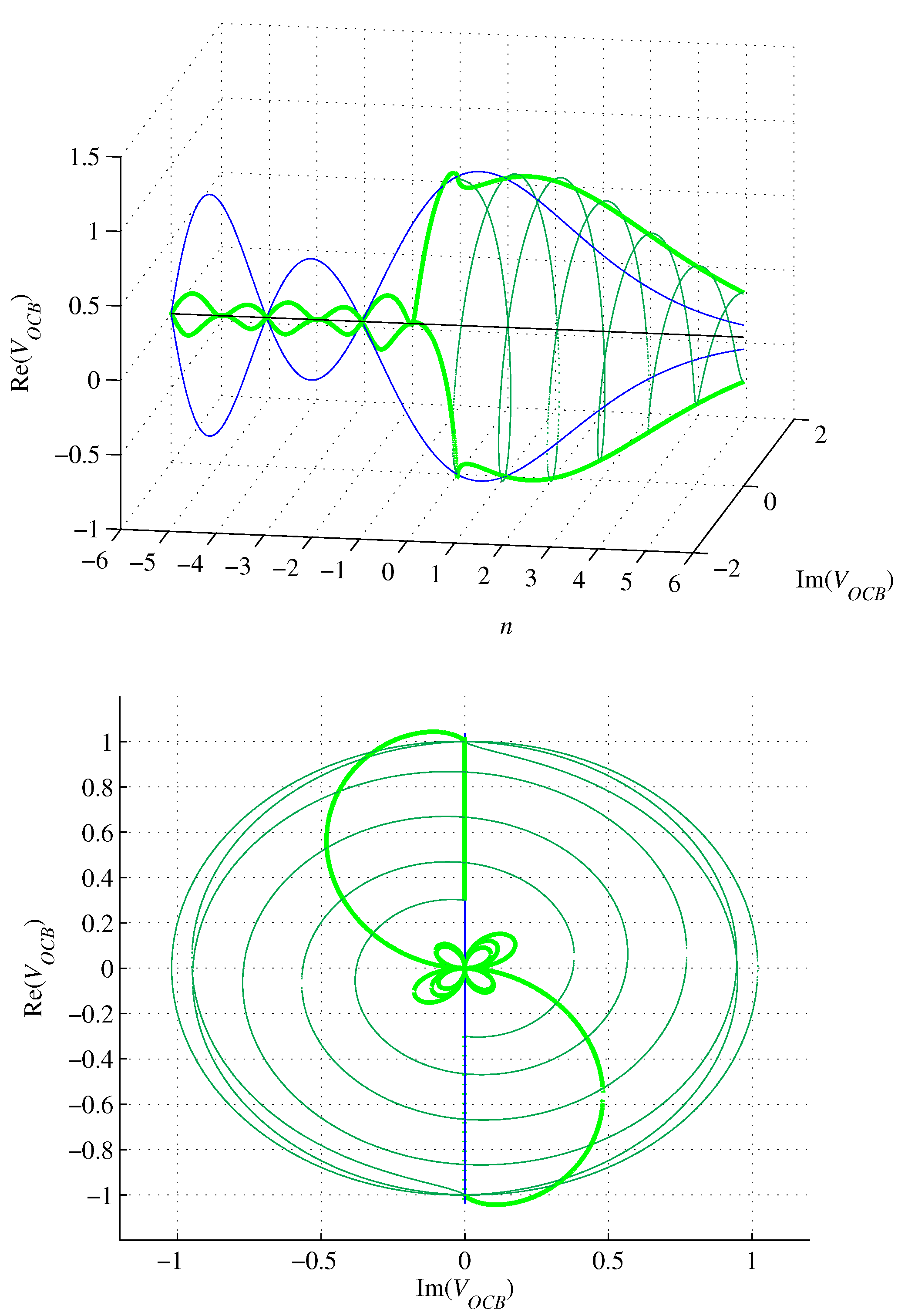
Figure 10.
Graphs of (green), (blue), and (dark green), for .
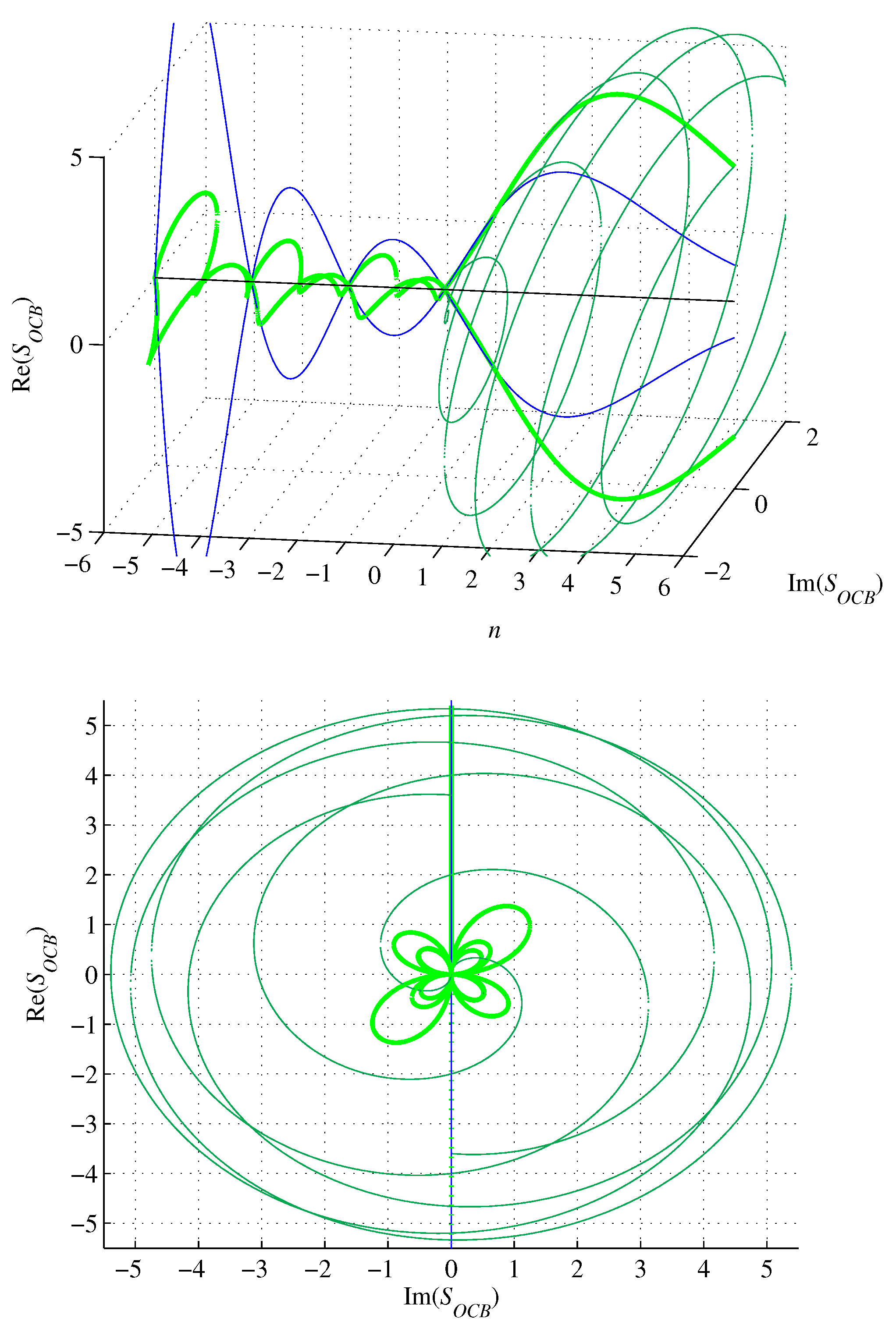
Figure 11.
Graphs of (pink), (blue), and (dark pink), for .
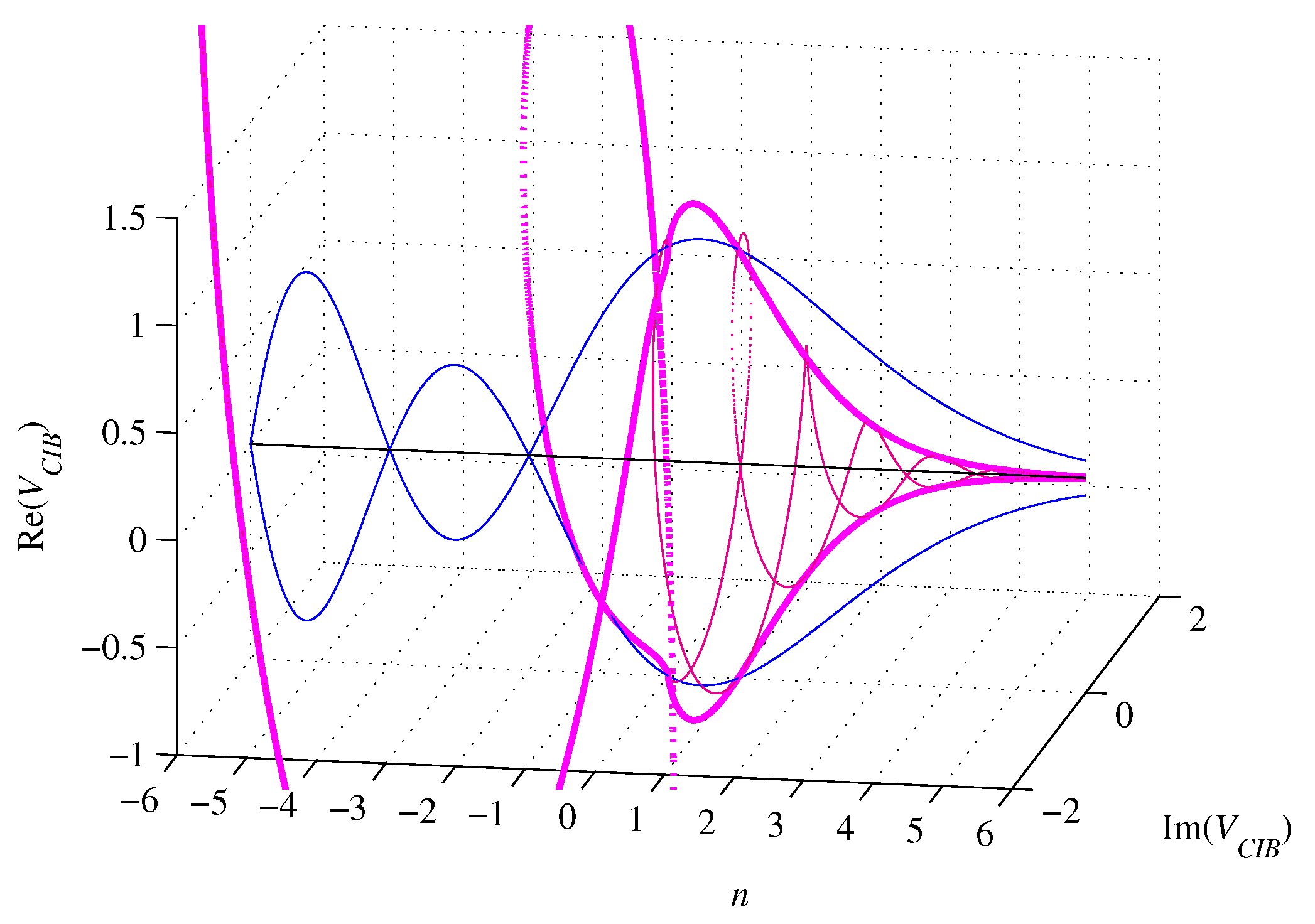
Figure 12.
Graphs of (pink), (blue), and (dark pink), for .
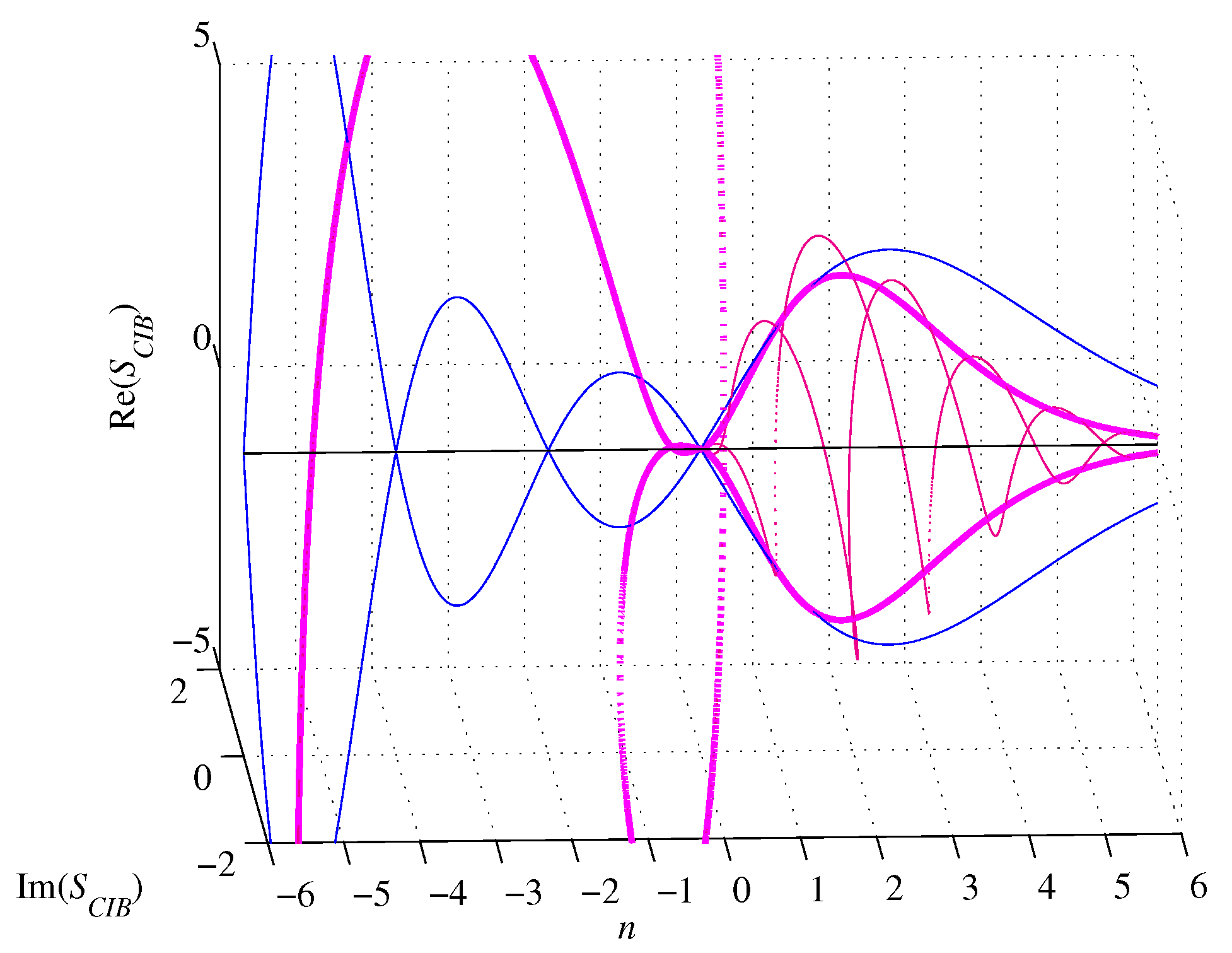
Figure 13.
Volume metric and gamma function independent relations. (blue), (red), (dark red), (orange red), (lime green), (yellow green), for .
Figure 13.
Volume metric and gamma function independent relations. (blue), (red), (dark red), (orange red), (lime green), (yellow green), for .
Table I.
Particular volumes of omnidimensional polytopes inscribed in and circumscribed about unit diameter n-balls (principal branch).
Table I.
Particular volumes of omnidimensional polytopes inscribed in and circumscribed about unit diameter n-balls (principal branch).
| n | −1 | 0 | 1 | ||||
| 0.331 | 1 | 1 | |||||
| 0 | 1 | 1 | |||||
| 0 | 1 | 1 | |||||
| 0 | 1 | 1 | |||||
| 0 | 1 | 1 | |||||
| i | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Table II.
Particular surfaces of omnidimensional polytopes inscribed in and circumscribed about unit diameter n-balls (principal branch).
Table II.
Particular surfaces of omnidimensional polytopes inscribed in and circumscribed about unit diameter n-balls (principal branch).
| n | −1 | 0 | 1 | ||||
| 0 | 2 | ||||||
| 0 | 0 | 2 | |||||
| 0 | 0 | 2 | |||||
| 0 | 0 | 2 | |||||
| 0 | 0 | 2 | |||||
| 2 | 0 | 2 | |||||
| 0 | 1 | 2 | 3 |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







