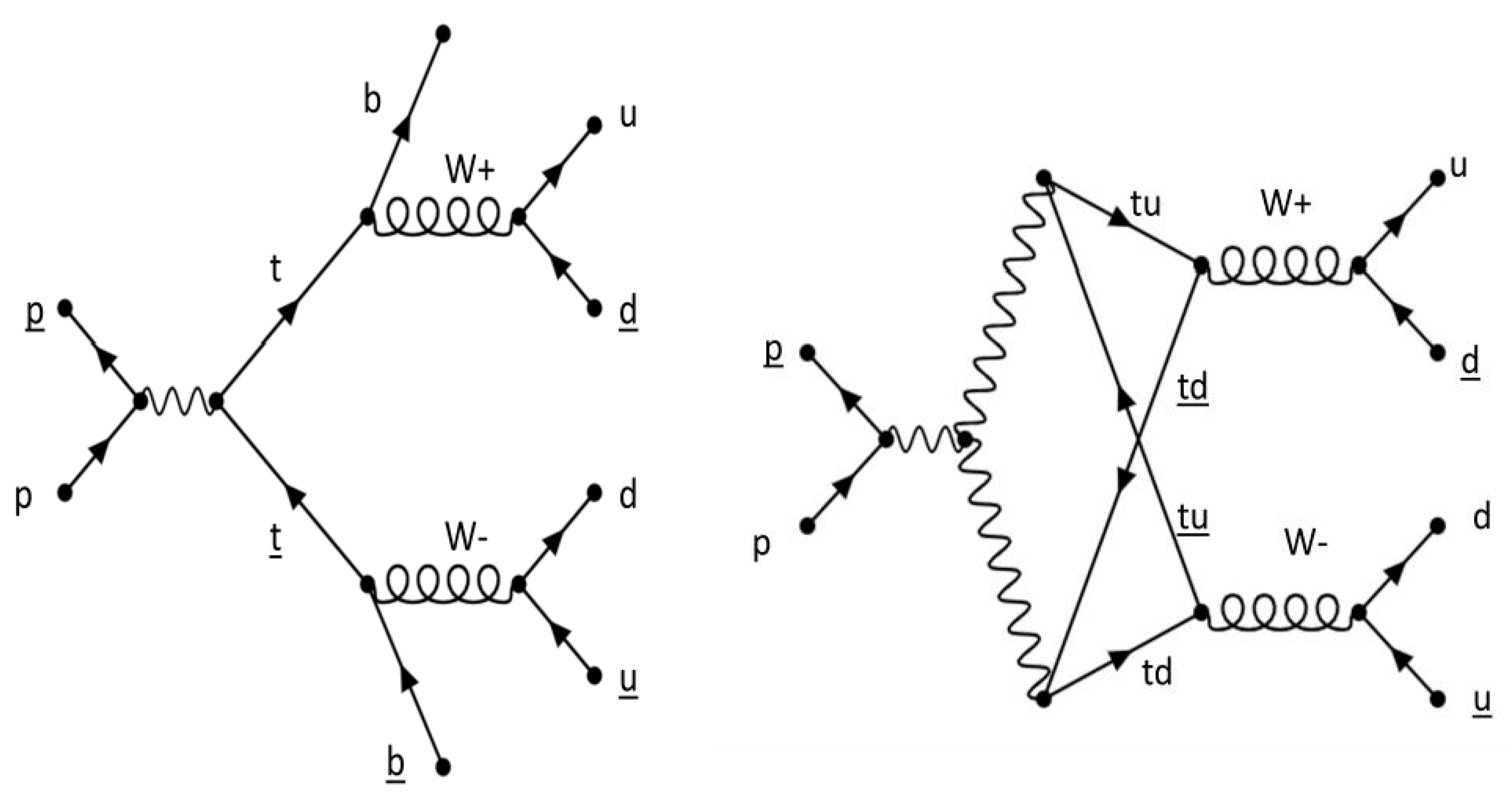
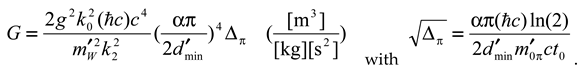1. Introduction
To explain physical phenomena and the outcome of physical experiments one needs a theory. It is not inconceivable that different theories can lead to the same results. In that case one will have to make a choice to which of those theories one should assign the highest value. That choice is usually determined by which of them is the simplest and which makes the most reliable predictions for expected new phenomena and outcomes of new experiments. A satisfactory outcome of such predictions is usually seen as proof for the correctness of a theory. In current physics, the Standard Model for the theory of particle physics is usually regarded as a particularly successful example of this view. Is that theory so simple and is there evidence for the correctness of predictions made in this theory? That is the question I want to address in this essay.
Actually, this would require a purely scientific treatise, provided with the necessary mathematical formulations. If one goes too far in this, one runs the risk that mathematics will mask the essence of the physical problem and one loses sight on the goal of the theory, which aims at simplicity and predictability. So, I want to try avoiding mathematics as much as possible, although at some places formulas will be necessary to succinctly summarize the train of thought.
2. Principle of covariance
The foundation on which the Standard Model is based is the application of Einstein's covariance principle. In the Standard Model this is commonly referred to as the “gauge principle”. What does this mean? That principle involves the conversion of physical laws that apply in empty space, in which no force fields are present, to laws that apply in a space in which force fields are present. If this is done according to certain prescriptions to be determined, then the laws in a space with force fields present have the same format as the laws in free space. The transformed laws are then called covariant. Formulating the prescriptions is called gauging. This principle has been successfully applied by Albert Einstein in the reformulation of the laws of gravity. It has also been successfully applied by Paul Dirac in the development of the theory for the electron. Although mathematical feats were necessary, the gauging was relatively easy to understand, because the force fields that fill the void for gravity and electromagnetism have been lawfully established by predecessors like Newton and Maxwell. In the Standard Model of particle theory, only Dirac's gauging is relevant, because as yet gravity is not part of the theory. What is part of it are the two other forces of nature, which are known as the “weak force”, later renamed weak interaction, and the “strong force”, later renamed strong interaction. That they exist is for sure, because otherwise there would be no explanation for gluing the protons and neutrons in atomic nuclei (due to the strong force) and for the phenomenon of radioactivity, in which the composition of nuclear particles changes (due to the weak force). In the Standard Model, efforts have been made to get a grip on these forces. The extent to which this has been achieved will become apparent in the remainder of this essay.
3. Planck's constant
To this end, it is useful to sketch a picture of the way in which the gauge-based Standard Model arose from classical physics. In the classical view there are particles and fields. The particles are observable and measurable as mass, and are force sensitive. They are characterized by momentum and energy. The forces are unobservable and manifest as fields that affect the momentum of the particles. The fields are characterized by their field strength. They have their source in force-producing particles and they are the medium for waves that propagate on a stationary field as fluctuations in place and time. Those waves appear to contain more energy the shorter their wavelength and the higher their frequency. This must be true, because otherwise there would be no explanation for the behavior of the so-called black-body radiator. This is a high-temperature black body that spreads heat radiation, which can be described as electromagnetic radiation. This radiation consists of wave components with a low frequency (infrared). In order to explain the spectrum of that heat radiation, in 1990 Max Planck formulated a relationship between the wavelength of electromagnetic radiation and energy. To this end, he hypothesized that, just as Boltzmann's constant establishes a relationship between temperature and the resulting kinetic energy of a molecule, so there should be a constant between the energy (of those molecules) and the wavelength of the heat radiation emitted from it. The consequence is E = ℏω. The unit ℏ was subsequently called Planck's constant (and later turned out to play a decisive role in other areas of physics as well). This hypothesis marks the beginning of the development of quantum mechanics, although particles and fields could still be seen as quantities with different physical contents.
4. De Broglie hypothesis
This changed when it was discovered that electromagnetic waves could behave like particles and that light particles, for which the electron serves as a role model, can interfere with each other as if they were waves. The elementary particle of an electromagnetic wave is the photon, to which a momentum
and an energy
can be assigned, while nevertheless the particle remains massless. This conclusion was in 1905 drawn by Albert Einstein as a consequence of Planck's hypothesis and given as an explanation for the photoelectric effect, in which electrons are released from a medium by irradiating the medium with monochromatic light. The massless character of the photons follows from Einstein's Theory of Relativity from 1916, in which the momentum
of a massless particle moving at the speed of light is given by the relativistic relation
, which remains finite for
and
. This observation led Louis-Victor de Broglie to think that the opposite could be true as well and that particles, such as electrons, could behave like waves. In 1923, he put this idea into a hypothesis, in which he related the momentum
of a particle to a wavelength with an amount
(i.e.
). In 1925, De Broglie's hypothesis led Erwin Schrödinger to hypothesize that the motion of particles should be built up in harmonic waves of the type
intended to be the solution of a wave equation. In order for the energy
and the momentum
to satisfy the energy relation
, which shows that energy is equal to the sum of kinetic energy and potential energy
, he formulated the wave equation as,
Indeed, it is easy to determine by substitution of the solution that,
But what was actually propagating physically was initially the subject of a discussion, which in 1927 was settled by Niels Bohr and Erwin Heisenberg. They came to the conclusion that the wave phenomenon of matter particles is not an energy phenomenon as is the case with electromagnetic waves, but that, instead, a matter wave is a statistical phenomenon. The real quantity
represents the probability that the particle can be found in a certain place at a certain time. This, by the way, also meant that the wave function of a particle of matter, unlike electromagnetic waves, must be a complex quantity.
5. Double slit experiment
The hypothesis of matter waves was first confirmed experimentally in 1927 in observations by Clinton Davisson and Lester Germer and, independently of them, by George Paget Thomson. In retrospect, these insights have been associated with the double slit experiment that Thomas Young performed in 1802 (!) in which he showed that, contrary to Newton's belief, light does not consist of particles, but of waves. By directing light onto a grating consisting of a double slit, a shadow pattern of dark and light trajectories at regular intervals is created behind the grating, which can only be explained if light is a wave phenomenon. This experiment was in 1960 (!) repeated by Claus Jönsson with particles, by shooting electrons at the double slit one by one, whereby he was able to record the expected interference pattern as blackening on a photographic plate behind the double slit. This result means that these particles must have passed one by one through both slits simultaneously.
Although particles appear to have wave properties and waves exhibit particle properties, the original difference between particles and fields, in which particles are force sensitive and fields force transmitting, has not disappeared. They can both be described, be it either as a particle or as a field, i.e., dual, but they remain different. The force-sensitive ones are called fermions, the force-transmitting ones are called bosons. These names have in 1945 been introduced by Paul Dirac.
To go a step further towards the goal of providing covariant descriptions of particles, also other than electrons, moving in force fields, including others than just electromagnetic ones, it is relevant to clarify the difference between wave and field. In short, a wave is a propagating disturbance in a stationary field. That field is essentially the stationary solution of a wave equation containing a source term. When the wave phenomenon has settled, the source has created a stationary field. In particle theory, the behavior of the field is central and relatively little attention is paid to the source of the field. Nevertheless, as will become apparent in the course of this essay, the behavior of the source is essential. The stationary field can be seen as a collection of an infinite amount of position-bound field particles. To each of those field particles an energy status can be assigned. Propagating waves can then be understood as bosons that influence the energy status of the field particles. This change of energy status is accompanied by a quantum leap. It introduces in particle theory a second quantum effect. The theory thus becomes a Quantum Field Theory (QFT).
For a proper understanding of boson and fermion, we return to their role models, namely the photon and the electron, respectively. They are best defined in terms of their wave equation as a free particle. The wave equation of the photon must, as stated earlier, contain a source. It is instructive to think of the photon as a boson produced by a force-producing particle. The force-producing element of such a particle is its charge. That charge is a measure for an elementary amount of energy, say . In the case of electromagnetism, the charge is electrical. But in general, the charge can be of a different nature as well. Therefore, the neutral measure of energy is more appropriate than a charge type, particularly if bosons other than photons and fermions other than electrons come into play.
The wave equation should describe what happens when a suddenly appearing pointlike particle produces an amount of energy . In that case, the source term can adequately be described by the formula . Therein is the step function of Heaviside. It has the value zero for 0 and is equal to 1 for 0. The pointlike character of the particle is expressed by a Dirac pulse that has the value 1 for 0 and the value zero for 0 . The wave equation is the relation from which the energy value can be determined at any time and in any place, assuming that the space is empty, i.e. contains no fields, and is spherically isotropic.
6. Principle of least action
In particle theory it is customary to start from a method which for brevity is called the action principle or “principle of least action”. This principle means that the equation of motion of a physical quantity is determined by an action in which the difference between the kinetic energy and the potential energy is kept as small as possible. The physical quantity can be the particle itself, but also, for example, the propagating field of the particle. A motion equation to be determined thus becomes a wave equation to be determined. The recipe for doing so consists of formulating the difference between the density of the kinetic energy and the density of the potential energy. For brevity, this difference is called the Lagrangian. The wave equation is the equivalent of an equation of motion and is obtained by applying the Euler-Lagrange equation to the Lagangian. The potential energy is the source energy plus the background energy of the field. The Lagrangian for a simple field can then be written as ,
The source term and the background energy together compose the density of the potential energy. The application of the Euler-Lagrange equation to this, yields a wave equation. In the case that and a suddenly occurring energetic pointlike source, that wave equation is no more than a time-dependent variant of Poisson's equation. Its solution is a stationary field the energy value of which decreases linearly with and a disturbance that manifests itself as a propagating Dirac pulse, the value of which decreases linearly with as well. This disturbance is thus a boson, which in the electromagnetic case manifests itself as a gamma photon. By associating to the source, in addition to the strength , a second index number , as a measure for the range of the source strength, the radius can be normalized as . This second characteristic therefore has the dimension [m-1].
The simple law of the potential function is of course disturbed if the space is not empty and contains energy fields from other sources. A simple disturbance shows up if a background energy hinders the outflow of energy from the source such that the stationary field generated by the source shows an exponential decay. The field of the source is, as it were, shielded. A well-known example of this is the shielded field of an electric charge in a plasma of ions, as in 1923 described by Peter Debije and Erich Hückel [
1]. An energy field with exponential decay, such as occurs in that process, arises as the consequence of a background potential
/2, giving the resulting wave equation the stationary solution,
disturbed by a Dirac transient pulse that decreases as
. Obviously, there is a physical cause for the exponential decay. That this is caused by a background field consisting of polarized dipoles in an ionic plasma cannot be seen from
. That relationship should be established from an analysis of the physical process [
2] .
In the Standard Model of particle theory, heuristics are played with the Lagrangian and with the background field. We will see later in this essay that, and why, instead of a field associated with a single particle, the fields of two particles are merged into a field doublet and why, as a hypothesis, the background field is modelled as a broken field with a potential function format [
3],
In which en are real constants to be determined. Unlike an empty background field or a field with polarisable dipoles , the zero point of the potential energy does not coincide with the zero state of the field energy. This will be explained in this essay later in more detail.
The field (or fields) thus determined is an energy field (or fields) spread out from sources. These fields influence the behavior of force-sensitive particles, which is described by the solution of Schrödinger's wave equation. However, this equation (1925) could not hold because it is not “relativistic”, or is, to put it another way, “not Lorentz invariant”. This is because the energy term
does not retain the same value in systems that move with respect to each other at different speeds. Attempts to modify the equation to solve this problem, initially failed due to the requirement that the wave function must remain complex in order to comply with the agreed wave function interpretation. This means that at any place and any time
must be equal to 1 (this is called “positive definite”). The impasse was in 1928 broken by Paul Dirac with the publication of his theory of the electron [
4] .
7. Dirac 's equation
Dirac concluded that the requirements set were compatible only through a multi-component wave function
. From a heuristic manipulation on Einstein's energy relationship, he constructed for free space (in which no potential energy is present) a wave equation with matrix coefficients,
in which
is a 4 x4 unity-matrix and in which the 4 x 4 gamma matrices have particular properties, viz.
This equation is relativistic and Lorentz-invariant, but not yet covariant. After all, our goal is to determine an equation that has the same format in empty space and in a space with a force field. To this end, Dirac's equation for the free space must be adjusted. How Dirac did so can be made clear by rewriting the equation in operator form as,
In which and ; .
Dirac made the equation covariant by exploiting the relationship between momentum
and operator
. Whereas under the influence of the vector potential
the momentum of a moving electron changes as
, Dirac transformed the operators as
. Thus, in the Dirac equation for free space, the ordinary derivatives
can be replaced by covariant derivatives
under the rule
In the later developed Standard Model of particle theory, a somewhat more formal way is defined to determine the covariant derivative. That recipe is derived from the way in which Einstein made the Lorentz transformation from a global property in free space to a local property in a space in which a force field is present. In a more general sense, this consists of identifying a suitable property which has the same value everywhere in empty space and which takes on locally a different value in a force field. In the wave mechanics of quantum theory, the property invoked for this purpose is the fact that a phase shift of the wave function makes no difference as long as the phase angle is an invariant global quantity. If this angle is not invariant under the influence of a force field present, the wave equation retains the same format if this equation is defined in terms of covariant derivatives undergoing a transformation in the same way as the wave function itself. The requirement to be imposed on the covariant derivative therefore is,
This is the same format as with Dirac if the vector potential
is interpreted as the derivative of a phase angle. The importance of the phase angle interpretation will be discussed later in this essay for couplings between two or three particles.
To appreciate the properties of Dirac's equation, it is instructive to split the four components of the wave function into two. To this end, the free space equation is rewritten as,
where
is Pauli’s state variable with the Pauli matrices. The solution of Dirac’s equation has the format,
For electrons the square of
equals the square of the Einsteinean energy expression, viz.
With a suitable alternative choice of the gamma matrices, the format of the solution can be preserved. That is, for example, the case for
The difference, though, is that now [
5,
6]
In this case, the Dirac particle inherits its kinetic energy from its rest mass. Although strange, it is theoretically viable. The problem, however, is that this wave equation is not Lorentz invariant. That is, the solution of this equation in systems moving at a different constant speed in free space is physically inconsistent.
An essential consequence of Dirac's equation is the implicit introduction of the "spin" concept. Spin is a statistical attribute associated with the unrest in the particle's motion. In the case of an electron, it is usually represented as an intrinsic (= imaginary) spin momentum. This is seen as the cause of the anomalous magnetic dipole moment of the electron. The projection of this spin momentum on the propagation direction of the electron has a quantized value. The electron is then said to have a spin of 1/2 (half an integer). Unrest in the motion, however, not only relates to its spatial dimension, but also to ihe temporal dimension (= time). Dirac's theory therefore shows a second dipole moment: an anomalous electric dipole moment. In the case of the electron, this electric dipole moment has an imaginary value. This means, for example, that an electron is not polarisable (i.e. cannot be directed) under the influence of a scalar potential field.
This is different for a Dirac particle that inherits its energy from the rest mass, because its second dipole moment turns out to be real as well. If two such Dirac particles with polarisable dipole moment are joined in a scalar field, a stable equilibrium of forces can arise between the particles, because the repulsive force of their monopole property is balanced by the attractive force of polarized dipoles. Although the two particles in isolation violate the Lorentz invariance, they don’t when bound together. In the scope of this essay, it will suffice to mention that this view has been substantiated and documented in recent work [
7] .
In fermions, such as the electron, the spin is semi-integer. In bosons, such as the photon, the spin is integer. The difference is caused by the format of the wave function. It is real with bosons, but complex with fermions.
8. The strong force
How do the nuclear forces, i.e. the strong force and the weak force fit into this picture? It was Hideki Yukawa who in 1935 initiated an adequate description of the strong force. He realized that the force that in atomic nuclei glues the protons and neutrons together cannot be of ordinary electromagnetic nature. Unlike the electric force, which has an unlimited, albeit decreasing, spatial effect, the nuclear force is limited to a very small range, to the size of approximately
10
-15 m (1 fermi). In principle, this could be explained by a generalization of the Maxwell equations, such as about the same time formulated by Alexandru Proca, who could turn a massless photon with a linearly decreasing effect into a mass-carrying photon with an exponentially decreasing effect. To this end, Proca generalized the electromagnetic Lagrangian as
where
are the four components of the electromagnetic vector potential and where
are the sources of the field. With a pointlike source as previously described, application of the Euler-Lagrange equation results into an source field
with the format,
which gives a shielded Coulomb field as a solution, i.e. just like with the Debije effect,
Although this Proca Lagrangian turned out to be subject to criticism, it was a source of inspiration for Yukawa, who hypothesized that nuclear particles such as protons and neutrons are associated with an internucleon potential that has a shape as outlined in
Figure 1
. The Proca potential, outlined as a red line, would result in the nuclear particles attracting each other unrestrained. In order for this not to happen and for a state of equilibrium to be established, an inhibitory corrective potential must exist, outlined as a black line.
The essential step taken by Yukawa is to posit that the equilibrium force that glues the nuclear particles together is carried by mass-carrying force particles. That couldn't be the massive photon of Proca's theory, because the force is of a balancing nature. To support his hypothesis, Yukawa made an estimation for the energy of this mesotron (corrected to meson in 1939), as he initially called his particle. In his estimate he invoked the uncertainty relationship as in 1927 postulated by Werner Heisenberg. That relation states that the uncertainty about the energy state of a particle and the uncertainty about the time of measurement is given by the relation
Figure 1.
The internucleon potential with the liquid drop profile.
Figure 1.
The internucleon potential with the liquid drop profile.
From this, Yukawa concluded that, within the lifetime of his particle, its energy can take any value. Knowing the distance between proton and neutron is about 1 fermi (= 10
-15 m) and assuming that in so-called virtual state, the particle would propagate at the speed of light, enabled him to guess a lifetime
to his particle. This gave him an estimated energy
The calculated distance of 1 fermi was only a rough estimate, which Yukawa derived from knowledge of the behavior of nuclear particles developed in many pioneering experiments and analyzes since the discovery of the alpha particle and its identification in 1907 by Ernest Rutherford and Thomas Royds as nuclei of the Helium atom. Yukawa himself was initially sceptical of his theory, but in 1937 two groups of researchers, Anderson and Neddermeyer on the one hand and Stevenson on the other, found in cosmic rays a particle that appeared to fit the Yukawa profile, because its energy was found to be 100 MeV. Later, when it was realized that this found particle was not a boson (with integer spin), but a (charged) fermion (with half integer spin), this opinion had to be revised. Finally, in 1947, the Yukawa particle was discovered by Cecil Powell. It was found to have a mass of 140 MeV/c2.
In retrospect, it is somewhat surprising that Yukawa neglected the wave aspect of particles when developing his theory. Afterall, one might expect a relationship between the de Broglie wavelength of the particle and the distance between the nucleons. Roughly estimated, the distance between the particles should correspond to half a wavelength. So at Yukawa's estimate of the distance between the nucleons of 1 fm, the energy of the particle would be equal
This does not match Yukawa's prediction. However, it corresponds to the later established actual distance between nucleons at which pion interacts, as outlined on the right in the figure. When it was later discovered that protons and neutrons could not be indivisible particles, but had to be regarded as composed by elementary building blocks, which were given the name quarks in 1963, the strong force was renamed as strong interaction. It is similar in nature, but primarily takes place between the quarks. The field of strong interaction also expands as an outer field beyond the quarks and manifests itself as the force that Yukawa envisioned. As early as 1930, George Gamow dubbed the internucleon potential as a “liquid droplet model”.
Later in this essay, this potential, which has the same format apart from the value of the parameters inside and outside the nucleon, will be modelled mathematically as
For
1/0.55 the Lagrangian of this potential function closely approaches the aforementioned potential of the Standard Model [
7] . It is made up of two fields, viz. the near field, determined by the first term
and the far field, determined by
.
9. The weak force
The history of the weak force dates back to 1933 when Enrico Fermi proposed a theory to explain beta decay. The beta decay is a mechanism that occurs with radioactivity. Radioactivity had been known since 1896 when Henri Bequerel discovered that uranium emits energetic radiation. Marie and Pierre Curie discovered the same phenomenon in thorium, polonium and radium. In 1899 this radiation was classified by Ernest Rutherford into alpha particles, which, as mentioned above, have been identified in 1907 as nuclei of the Helium atom, and beta particles, which have in 1900 been identified by Bequerel as electrons. In 1900, following the discovery of Paul Villard, gamma particles have been added, which in 1903 have been identified by Rutherford as a form of electromagnetic radiation. In Fermi's theory, beta decay had been explained as a mechanical process that causes a change in the statistical energy state of elementary fermions. It included the postulation of a new neutral virtually massless particle, dubbed as neutrino, which as yet could not be confirmed experimentally. In 1936 Hans Bethe and Robert Bacher argued that this would only be possible in an experiment in which a proton and a neutrino, a neutron and a positron would occur. Confirmation by such a process was in 1956 described in Science by a group of researchers at the Los Alamos laboratory in California.
Fermi's theory was a precursor to the description of the weak force, as it should occur within nucleons between subnucleon particles. In 1947, its existence was emphasized once again to explain the aforementioned difference between the 100 MeV particle discovered in 1937 and the 140 MeV particle discovered in 1947. In addition, since 1950, after the development of particle accelerators and the experiments conducted with them, new particles had been discovered all the time, some of which had properties similar to the pion and others with properties similar to nucleons. Both in antimatter form as well. The name meson was introduced for the former species, as had already in 1939 been used for the pion by Homi Bhabdha. The second species was by Abraham Pais in 1953 dubbed as baryon.
10. The Quark
In 1961, Murray Gell-Mann and, independently, Yuval Ne'eman proposed on heuristic grounds a classification scheme, in which the then known mesons and baryons have been systematically related to each other as combinations of three elementary building blocks, which in 1963 by Gell-Mann were given the name quarks. The eight spin 1/2 baryons, made up of three quarks, were grouped as an octet, the ten spin 3/2 baryons, made up of the same quarks, as a decuplet. Eight mesons, with integer spin and made up of two quarks, were grouped as an octet. This “eightfold way” scheme was so convincing that the three constituent quarks were subsequently assumed to be elementary. After the discovery of new baryons and mesons, this scheme was extended with new elementary quarks, so that ultimately six elementary quarks (and their antiparticles) were considered to exist, which were grouped into three groups of two quarks, viz., u(p ) and d(own), s(trange) and c(harme) and b(ottom) and t(op). The fact that the top quark has a mass that is incomprehensibly large in relation to the mass ratios between the other five quarks has been taken for granted, as is the fact that some particles are forced into the scheme or even fall beyond. It will be shown in this essay later that all quarks can be traced back to a single archetype, so they should not really be considered elementary. In addition, it will become clear why the top quark does not fit the scheme and what meaning should be assigned to it instead.
The quark as an elementary building block is a Dirac particle, with the associated properties, such as those of half-integer spin, subject to the Pauli’s exclusion principle, which prohibits two identical particles in the same energetic state from being in the same spin state, and having an antiparticle. That the quark, unlike the electron, is a Dirac particle with the special property of two real dipole moments, has remained unknown. However, it is found from experimental evidence that the base quark occurs in two modalities, which exhibit different electrical properties, just like the proton and the neutron. Because no theoretical substantiation has been found for this, these two modalities are per axiom considered as the same particle in a different state of isospin. It will be shown later in this essay that this isospin is a consequence from the second real dipole moment
It quickly became apparent that inside the baryons and mesons forces of the same nature are operational as outside. The strong force shows the exponential decay and the weak force is responsible for the change in composition of the hadrons (collective name for mesons and baryons). Within the hadrons, these forces are referred to as strong interaction and weak interaction, respectively. The quark is an elementary building block, which is sensitive to these two nuclear forces. In addition, the quark is apparently electrically charged because the hadrons made up of quarks having an electrical charge equal to or, in some cases, double that of the electron.
The detectors that are part of particle accelerators make the hadrons observable from analyzes of their decay products. This does not apply to the quark, which has remained an unobservable fundamental building brick. In that respect, the quark is different from the electron that can be considered as observable: its mass has even been experimentally determined since Robert Millikan did so in 1909 with his famous oil drop experiment. Because baryons are made up by three quarks and mesons by two quarks, and one wishes to regard charge as a quark attribute (instead of leaving open the possibility that the charge is a holistic property that allows charge distribution over the entire hadron), the quark charge is considered as being broken up into fractions 1/3-2/3 of the elementary electron charge. It is difficult to provide proof for this, nor to show a counter-evidence against it.
Another related problem that had to be solved by axiom, is the lack of understanding the origin of the difference in behavior of the two basic quarks ( and ) Similar in energy, but electrically different. Something similar was known from the behavior of the proton and the neutron: nearly equal in energy, similar behavior under the strong force, but electrically different. In order to emphasize the symmetry between proton and neutron on the one hand and to indicate their difference on the other, Heisenberg posited in 1932 a difference in state between the particles he referred to with a difference in isospin. When classifying the hadrons, the name isospin has been adopted as a quantum number to indicate the difference between the quark and the quark.
A second facet that makes the quark different from the electron is the vagueness of the nuclear forces. While electromagnetic forces associated with the electron can be accurately described with Maxwell's laws, something similar is a problem to be solved for nuclear forces. As a force-sensitive particle, the quark is a fermion on which nuclear forces act as bosons. So there should be a boson for the strong interaction and another boson for the weak interaction. Giving it a name, gluon for the strong interaction, and the W/Z boson for the weak interaction, obviously doesn't solve the problem. We will see that here mathematical formulations were posited per axiom as well. The dreamed wish is to provide a nuclear equivalent for the Dirac Lagrangian similarly like as being applied to the electron. Then, according to the principle of minimal action, a covariant wave equation for the quark could be derived, in which the three forces of nature would be incorporated by a covariance rule for the derivatives of the wave function.
11. A physical model for the two nuclear forces
Before giving a profile of the mathematical model that should lead to the intended covariant formulation of particle theory, we first take a step back by asking what could be the origin of the strong interaction and the weak interaction, instead of directly to choose the axiomatic approach and to construct an abstract formal mathematical model. The first question to be addressed is what could be the reason for the exponential decay of the strong force. As noted before, an example of such an exponential decay occurs with the shielding of the electric field from a pointlike charge in an ion plasma, known as the Debije effect. This suggests that the nuclear force exerted by a quark on other quarks, and on particles composed by quarks, is influenced by an energetic background field that is transparent to electromagnetism. To this end, we set up a nuclear equivalent of Poisson's equation as,
Herein
is the nuclear equivalent of a uniformly distributed space charge that models the assumed background field. Based on Debije's theory, we will assume that such background field consists of a uniform distribution of elementary dipoles. These must be dipoles that are polarisable in a scalar potential field that, without those dipoles, has a classical behavior with a linearly decreasing potential. It is a hypothesis intended to model the strong interaction. No more and no less hypothetical than the Higgs field modelling in the current Standard Model. However, more physically more comprehensible. A field of elementary dipoles can be modelled with a dipole density vector
. The concomitant space charge density can be written as its divergence [
2],
In the steady state, this field is fully polarized by the pointlike source. In that case
Since without a background field the potential
decays as
,
can also be written as a
With this side source, the solution of Poison's equation becomes,
This explains the exponential decay of a potential field as a consequence of a background field consisting of elementary dipoles that are polarisable in a scalar potential field. Now the far field of the interquark potential has been interpreted, the question remains how to do model the near field, assuming that the interquark potential has the same liquid drop shape as the internucleon potential.
Unlike the far field, which, apart from the exponential decay, has a monotonically decreasing gradient as
, the near field has a gradient as
. This suggests that it could have been caused by a dipole, which along its axis does exhibit such behaviour indeed. As described earlier in this essay, Dirac particles, in addition to their monopole property, have dipole properties as well. All Dirac particles have two anomalous dipole moments. An electron-type Dirac particle has a real anomalous magnetic dipole moment and an imaginary anomalous electric dipole moment. But Dirac particles of a special type, which for convenience we will refer to as a Dirac particle of the quark type, have two real dipole moments. The second dipole moment is polarisable under the scalar component of the vector potential. This makes the liquid drop model of the interquark potential easy to physically interpret: the far field is caused by the monopole property, the near field is caused by the scalar dipole. Both fields are shielded by a background field made up as a void of tiny elementary scalar dipoles.
With this interquark potential profile, the phenomenon of the weak force, which is defined as the force that can change the quark composition of the hadrons, is easily explained. To this end, it is sufficient to realize that two equal quarks can build a structure in which there is a balance between the repulsive effect of the far field and the attractive effect of the near field. It is easy to see that this structure can be described as a "one body" equivalent of a "two-body" harmonic oscillator. Its energetic field is quantized on the basis of its properties. We see here a “two-body” embodiment of QFT.
From an observer's point of view at the center of mass of the pion constructed by the described equilibrium of forces, the structure behaves like a harmonic oscillator, described by the wave equation determined by the Pauli-Schrödinger approximation of the Dirac equation.
Figure 2.
The structural meson model. A quark has two real dipole moments. One of them (shown horizontally) is polarisable in a scalar potential field. The other (shown vertically) is not. A stable configuration is created by a balance of forces between the repulsive effect of the monopoles and the attractive effect of the under-conditioned orientation of the dipoles.
Figure 2.
The structural meson model. A quark has two real dipole moments. One of them (shown horizontally) is polarisable in a scalar potential field. The other (shown vertically) is not. A stable configuration is created by a balance of forces between the repulsive effect of the monopoles and the attractive effect of the under-conditioned orientation of the dipoles.
The wave equation can be written as [
8,
9],
in which
is the previously derived interquark potential with the liquid drop profile,
a generic coupling factor,
the distance between the quark and the antiquark,
the effective mass of the two mass contributions of the quarks,
the potential energy of the field and in which
is the energy in the center of mass that is subject to quantization. The potential energy
can be expanded from the expression of the interquark potential as,
where
and
are dimensionless coefficients that depend on the interquark spacing. The wave equation can be normalized to the simple form,
in which
;
;
;
;
The structure is in a state of minimal energy where simple calculation shows that
If the expansion of the interquark potential is limited to two terms, the harmonic oscillator is harmonic. In that case, the energy quantization is determined by , so that the first excited level is a factor of 3 higher in energy than the ground state level. A simple numerical calculation with more terms in the expansion, or even better, with the analytic expression of the interquark potential, allows calculations of mass ratios with great precision. For example, the kaon, which arises from the pion ground state by excitation, turns out not to have a factor of three higher mass, but a factor of 3.57. This corresponds exactly to the experimentally determined ratio of the rest mass of the kaon (494-498 MeV/c2) overthe pion’s one (135-140 MeV/c2).
This simple model reveals much more than is shown within the scope of this essay. It reveals, among other things, that under excitation the binding energy between quark and antiquark, which is represented by
, shifts from the negative value -1/2 to, ultimately, a positive value. It also means that under excitation the quarks are scaled to heavier types, i.e., successively to
(trange),
(harm) and
(ottom). Due to the loss of binding energy, heavier types cannot occur. It is therefore incorrect to see the
(op) quark as the regular sixth quark. It is in itself strange that this has been posited in the Standard Model, because the mass of the top quark at 175 GeV/c2 is far beyond range. What the correct interpretation of the top quark should be will be discussed in this essay later.
12. Covariant description of the physical model
The question that now arises is how the description of the meson structure, as described so far in terms of the Schrödinger equation, can be converted into a covariant description that we have in mind. We already noted that there is a Lorentz invariance problem if the quark is described as an isolated quantity. But we have also stated, albeit with reference to documented scientific work [
7] , that the problem disappears with two quarks in a structural bond, such as with mesons. To covariantly describe the behavior of the meson structure, we need to derive the wave equation according to the principle of least action. To this end, the Lagrangian must be set up for the configuration. Because quarks are Dirac particles, their wave functions
are complex quantities. Their potential fields
, though, are real. In the Dirac model so far described, the particles interact by their fields. However, one could just as well argue that the fields interfere via the particles. This reversal of vision led to the introduction of quantum field theory (QFT). In that theory the fields are conceived as operators on fields.
In applying this view to the basic configuration of the structural model, consisting of the (basic) quark and the antiquark, we start from the Lagrangian description of their field energy densities. If the quark and the antiquark are mutually fully decoupled, the operational quantum fields of their potential fields will not affect each other. In that free state, their joint quantum field Lagrangian holds as,
in which
and
are the potential functions of the quark, respectively, the antiquark. The potential energy of both quarks is equal and match the profile described by,
It is a broken field that has a minimum value at
With
and
, this free Langrangian evolves as,
The influence of the two quarks on each other can now be taken into account under replacement of their free Lagrangian by a covariant Lagrangian. To this end, the ordinary derivatives in the free Lagrangian must be replaced by covariant derivatives. Because one quark acts as an operator on the other quark and vice versa, their wave functions will undergo a symmetrical change with respect to each other, such that, such that,
The Lagrangian thus becomes the sum of a common mode and a differential mode, so that
The field Lagrangian of the quark doublet is thus decoupled into two parts,
The common mode is not affected by the interaction, but the difference mode is. Since the
field is now decoupled from the
field, the Lagrangian allows for these fields separate boson equations. From the potential energy expression
it is deduced that the
field is the far field of the quark. In the Standard Model, the associated boson is known as the Higgs boson. The far field is omni-directional. Its stationary field can be calculated, after applying to the Lagrangian the principle of minimum action, as,
; ; so that .
Derivation of the full wave equation from the Lagrangian under normalization
;
;
;
, gives,
The stationary solution of this is the far field of the interquark potential. Hence,
The Higgs boson
is the wave disturbance on this. It is found from the time-dependent part of the solution. Its calculation is not trivial. It can be found as a Laplace transformation [
28] ,,
It is a boson that behaves like a gamma photon subject to dispersion.
Figure 3
illustrates the behavior of this boson.
Now that we've identified the far field boson as the carrier of the strong force as the Higgs boson, let's examine the near field. Unlike the far fields of both particles, the near fields of the particles influence each other. This influence can be accounted for by replacing the ordinary derivatives in the free field Lagrangian with covariant derivatives. so that,
which expresses that both quarks are coupled via a coupling factor
to a gauge field
to be determined that maintains the bond between the quark and the antiquark.
Figure 3.
The build-up of the far field of the interquark potential as a result of a sudden energy eruption from a pointlike source. The far field is the sum of the stationary solution, outlined as the rightmost image, and the transient phenomenon, shown in the lower part of the figure. In anticipation of later substantiation, we refer to this pulse as a “gamma gluon”. The pulse propagates at the speed of light and eventually disappears due to dispersion in the background energy. In the limit of the solution, λ is equal to zero and the gamma gluon turns into a never-disappearing gamma photon. In that case, the stationary solution is a progressing rectangle rΦ(r) that represents a field.
Figure 3.
The build-up of the far field of the interquark potential as a result of a sudden energy eruption from a pointlike source. The far field is the sum of the stationary solution, outlined as the rightmost image, and the transient phenomenon, shown in the lower part of the figure. In anticipation of later substantiation, we refer to this pulse as a “gamma gluon”. The pulse propagates at the speed of light and eventually disappears due to dispersion in the background energy. In the limit of the solution, λ is equal to zero and the gamma gluon turns into a never-disappearing gamma photon. In that case, the stationary solution is a progressing rectangle rΦ(r) that represents a field.
Since the coupling factor in this expression is not dimensionless, it is written as
and not as
. This coupling factor may be related to the coupling factor
entered in the structural model, but not necessarily equal to it. Later in this text, their relationship will be made clear.
Due to the coupling between the quarks, the near field is not omni-directional, but uni-directional. Hence, in this simple case of scalar interaction only, it has a single component
Taking into account a balanced interaction for establishing an equilibrium, the covariant form for the Lagrangians of the
field and the
field can be written as, respectively,
Combining the two together gives effectively,
The constant term in this Lagrangian is irrelevant, because, under application of the Lagrange-Euler equation, it does not give any contribution to the resulting wave equation. Hence, effectively, we have
Similarly as the far field, this near field now has the format of a mass-carrying boson. Hence, under proper dimensional correction of
, this boson can be written as,
The weak force boson
that maintains the bond between the two coupled particles can be seen as an interquark meson. In 1983, the free-state energy of this weak-force boson has been determined experimentally at CERN by the UA1 and UA2 collective. It turned out to have a value of
80.4 GeV. This fixes the product
. Within that product one of these quantities is freely selectable. In the Standard Model, the vacuum expectation value
has been adopted as the reference by defining
. See [
27] , (p.337).
It is a convention, allowed by the freedom to distribute the energy
over two quantities.
In the Standard Model, taking two wave functions together into the wave function of a single entity does not rely on structural considerations. The justification is derived from a common mathematical property of the associated particles. This property means that two particles in a mathematical sense belong to “the same special group”. That group has the property that every particle in the group can be converted into another particle of the group under the SU(2) transformation. That transformation is a change in isospin status. It will be clear that a
quark and a
quark therefore compose a SU(2) doublet in the sense of the Standard Model. In the Standard Model, particles other than quarks can constitute an
doublet as well. It will be explained in the next section.
13. The Z boson
The Standard Model of particle theory has three weak force bosons. In that respect there is a parallel with the pions. Afterall, if pions are the force-transmitting particles between the nucleons, one may expect, knowing that there are two charged pions and one neutral pion, that something similar must exist in the force-transferring particles between the quarks. Even before the experimental evidence of the third weak force boson, the GSW theory of Sheldon Glashow, Abdus Salam and Steven Weinberg, which took shape around 1967, predicted on theoretical grounds the third weak force boson. The starting point is the isospin doublet model. In its simplest form, the wave function
of the isospin doublet is represented as a 2 x 2 matrix of two complex fields,
Complex field in this context means that the already complex wave function can be in two different states of isospin.
Since the wave function of a doublet - which consists, for example, of two quarks bound together, as with a pion - must be seen as a single entity, with the semantics associated with it, the matrix is unitary, i.e. ⴕ = , in which is the unity matrix and in which ⴕ is obtained by transposing the matrix replacing the matrix elements with their complex conjugate values. Due to this property, only n – 1 of the n2 real parameters are independent quantities. If the wave function of the doublet is made subject to a conservative force field, the semantics is preserved under covariant conversion of the wave function of the doublet. In a conservative force field, this property is locally preserved under the transformation
with
en
provided the matrices
satisfy the matrix property of the isospin doublet. This is the case, for example, if matrices have the format of the three Pauli matrices,
Other valid formats can be traced back to this simplest form.
To give shape to covariance in the Lagrangian and the resulting wave equations, the transformation
must be accompanied by the similar transformation of the covariate derivative
. This is met if,
After rewriting
as
the covariant derivative takes the format
in which
can be seen as a coupling factor and
as a gauge field. This expression can be simplified to
in which the Pauli matrices are converted into real matrices,
and in which the gauge field is converted to,
Its further elaboration, which we will omit in this essay, can be done in the same way as before by substituting the covariant derivative in the Lagrangian described earlier. The three bosons
then acquire mass in the same way as in the simple model. Mass shows up from inhibition by the background field in analogy to the Debije mechanism. Two of the bosons have "charge" due to isospin. Whether this charge is electric is not a foregone conclusion. The third boson has no charge. There is as yet no reason why the coupling factors
and
are equal or not equal.
Thus, according to this view, there are three weak force bosons, two “charged” bosons and one “neutral” boson. In the mathematically conceived GSW SU(2) model it is unclear how these bosons are related to the weak force that physically manifests itself in the liquid drop profile. In spite of this, the model is based upon the view that each quark has an isospin equivalent. For the
junctions this can be readily understood. But the two quarks, of course, have “ordinary spin” as well. This must be the reason why in the mathematical model, next to two isospin related weak force bosons, a third one shows up. Experiments at CERN in 1983 by the UA1 and UA2 collective serve as evidence for the actual existence of three weak force bosons. They are considered as elementary particles, the mass of which must be determined empirically.
While three bosons are identified in the GSW doublet, only one has emerged in the structural model discussed thus far. This indicates that the structural model is not complete. Because the quark in the model is a Dirac particle, in addition to the scalar dipole moment included so far, it has the equivalent of an anomalous magnetic dipole moment as well. An extra term must therefore be added to the potential energy term of the quark. Adding a full equivalent of the electromagnetic field tensor is overdone, because the monopole property of the quark is already contained in the Lagrangian. However, because the energy field of the magnetic dipole equivalent behaves similarly to the energy field of the scalar dipole, the format of the Lagrangian is preserved and its effect manifests itself in a change in the magnitude of the coupling factor in the covariant derivative. The associated "spin" boson then has a different energy value from that of the "isospin" boson. Due to the ambiguity in the isospin status, the isospin boson has two modalities. Strictly speaking, this does not necessarily mean that the modality status is linked to electrical charge. The conclusion is that the structural model has three weak force bosons as well.
14. SU(2)
It has already been noted that in the Standard Model the merging of two complex wave functions into a wave function of a single entity is not based on structural considerations, but, instead, on a mathematical model. This model is based on the principle that if two wave functions are taken together into a composite wave function written as a matrix, the matrix must satisfy the special property of “unitarity”. If not, the assembly does not satisfy the semantics of a valid wave function. This SU(2) property is not a result of a physical proof, but rather the reverse. Assuming that two particles can be seen together as a unit, their individual wave functions must be written as a SU(2) doublet. It is for this reason, for example, that the decay product of a pion, which itself is built up as a doublet , must be a SU(2) doublet as well. So, a muon together with the muon antineutrino is an SU(2) doublet as well. The same applies to the electron-antineutrino doublet generated by the decay of a neutron into a proton. In 1970, a fourth quark was discovered from a newly discovered meson with mass 3.1 GeV/c2. The electric charge of this new quark, called charm ( ), was opposite to that of the quark. In 1976, a third lepton was discovered, named as tau, followed a year later by another new meson. This time with a mass of 10 GeV/c2, which could only be explained with a fifth quark, named as bottom ( ). Because three SU(2) lepton generations had been found, it was assumed that, like the doublet , the newly found quarks had to be regarded as three SU(2) doublets as well. So, and On the basis of this heuristic, the sixth quark was predicted in 1973 by Makoto Kobahashi and Toshihide Maskawa. In 1995 a particle was discovered with a mass of 173 GeV/c2, with properties like those of a quark. That discovery has been seen as a triumph for science and as further proof of the validity of the Standard Model. That the mass of this particle is completely out of range in the series of the constituent masses for and of 0.5 GeV/c2, 1.5 GeV/c2, 4.7 GeV/c2, respectively, was not (?) experienced as problematic.
While the axiomatically constructed SU(2) model relies on an empirical interpretation of particles and their attributes, the structural model provides answers with predictive scope (unfortunately only a posteriori). The mechanism by which new mesons and quarks arise is easy to understand. The simplest explanation is that in which one imagines that the energy of the first excitation of the pion modelled as an anharmonic oscillator is taken over by the ground state of two heavier quarks. However, the mechanism also allows only one of the two to be heavier and the other quark to remain as it was. Therefore, the kaon is not built up as
but as
or by the variants
en
.The generated new quark
has different numerical values for
and
, while preserving the invariance
. Why the ratio is invariant will become clear later. The scope of this essay does not allow detailed calculations. These can be found in documented work [
8,
9]. In that work it is shown that the meson mass spectrum can accurately be calculated from the base (
) quark. The same holds for the calculation of the constituent masses of the
and
quarks. These masses are the masses that can be attributed to the quarks as contributions to the energy of the hadrons (mesons and baryons). Since the masses can be calculated, the quarks, apart from the base quark, cannot be considered elementary. They are scaled versions of the base quark. As for the quark masses, it should be noted that since the emergence of the lattice QCD (Wilson, 1974), the convention as constituent masses has been abandoned for the light quarks quarks
and
, while those for
and
for the time being have been maintained [
10]. That doesn't seem very consistent. While the masses of the light quarks have been recalculated as so-called "running mass" from a theoretical concept that is still under development, this has not yet happened for
and
.
Besides the axiomatic SU(2) concept, unlike the structural model, imposes defining the quark flavors as elementary particles, there is another important difference. The structural model does not allow for quarks heavier than the bottom quark. The excitation mechanism in the anharmonic oscillator model is accompanied by a loss in binding energy as the quarks become more energetic. Therefore, as noted earlier, the bottom quark cannot have an isospin partner. This means that the top quark, the mass of which is completely out of range, must have a different interpretation. Which one will be made clear later in the essay. in the SU(2) concept the view that the bottom quark must have an isospin partner has no other justification than wishful thinking for classification, associated with the three lepton generations.
The baryons
With the establishment of the GSW theory, it was believed that the weak force was accurately portrayed as weak interaction. Strong force and strong interaction, though, remained a puzzle to be solved. That in the SU(2) model the strong interaction is implicit by accepting the Higgs potential has not been recognized because, in the absence of a physical interpretation of isospin, no structural interpretation for the SU(2) model was available. While with the SU(2) model the question of how quarks in isospin doublets, such as mesons, are glued together could in fact be avoided by a mathematical model, this question fiercely pops up in a baryon configuration.
Before discussing the theory in the Standard Model that aims answering the question, let's set up a simple structural model just like the meson.
Figure 4 shows a structure illustrating that the repulsive interaction between monopoles can be compensated by an attractive interaction between scalar dipoles in suitable orientation. This equilibrium state is the result of the liquid drop model of the interquark potential. It should be noted that, for the time being, the polarities of the dipoles don’t need an electrical interpretation.
Figure 4.
Structural baryon model: the repulsive forces between the monopoles are balanced by the attractive forces of well-oriented dipoles.
Figure 4.
Structural baryon model: the repulsive forces between the monopoles are balanced by the attractive forces of well-oriented dipoles.
This model can be described as a “one body” equivalent of a “three-body” harmonic oscillator. This structure is only fully symmetrical if the three quarks all are in the same spin state, because, as we have established, the nuclear spin interaction has a significant influence on the force balance between the quarks. This means that the sketched figure relates to, for example, a Δ+++ baryon (i.e. three quarks with spin 1/2, or a baryon (three quarks with spin -1/2). In the historic development of the Standard Model, such a configuration has been conceived as if three equal quarks were in the same state of energy. However, the Pauli exclusion principle prohibits an equal state of spin for two identical fermions in the same state of energy. A new axiom is the simplest way to break the deadlock. The new axiom is the assignment an extra attribute to the quarks, namely, in addition to electric charge, a second type of charge: a color charge red, green or blue. This can make each of the quarks different from the other quarks, under the requirement of the complementing white color for three color charges. There is a second problem with the baryons to solve as well. Because the electric charge of all mesons and baryons is equal to the charge of a single electron or, in the case of some baryons, to the double of it, and because a baryon consists of three quarks, the elementary electric charge has been broken up by axiom into two pieces 2/3-1/3, so that quarks either have a charge , or .
Without disputing in this essay the logic of these two axioms in this essay (they enable successful interpretations of many particle experiments to date), the axioms are mere hypotheses, because neither color charge, nor broken electric charge, can directly be experimentally proven. Experiments are usually interpreted with an axiomatic theory as a presupposition. As long as no conflict is found, the theory is considered as being correct. Nevertheless, both axioms are weak. Attributing color charge to quarks is justified on incorrect grounds. It happened on the assumption that the baryon
wave function is a ground state. A simple parallel with electrons in orbits around an atomic nucleus shows that caution is required here. After all, the orbits of two electrons with the same spin can be almost the same, but may slightly differ in state of energy. The energy difference is caused by the electrical interaction between the two electrons. Something similar happens in the
baryon, which can be seen as an excitation from a nucleon [
26] .
Figure 4 relates to the two nuclear forces that together determine the interquark potential of quarks. The interaction between electrical behavior is not included. If one does, then the three quarks will assume a different state of energy with respect to each other. Whether this should be modelled with color charges is highly questionable. Anyhow, as to be shown later, it can be done without as well. With regard to the broken electric charge axiom, it should be noted that it arises from the wish to regard electric charge of mesons and baryons as the sum of charges of individual quarks. An assumption that electric charge arises from interquark interactions and therefore might be a holistic attribute of meson or baryon as a whole is equally legitimate. This will be explained in more detail later as well.
However, the symmetry of the structural model now raises the question of why five baryons are asymmetric in their electrical behavior. After all, the positive charge of the baryon is twice as large as the negative charge of the baryon . The symmetry between these spin 3/2 baryons seems being disappeared. The spin 1/2 baryons from which they are excited, the proton and the neutron, are already asymmetrical as well. However, if the antiparticles are included in the scheme, the symmetry for these spin 1/2 baryons as well as for the related spin 3 /2 baryons is fully recovered. The loss in symmetry therefore arises from the difference in stability between the electron and the positron as its antiparticle. Other elementary particles show a similar difference as well. Such a difference in parity is basic in our universe. Without it, a stable universe is unthinkable.
In the Standard Model, a different route has been chosen. The formulation of the color charge axiom has led to the extension of the isospin SU(2) doublet of two nuclear particles to the color charge SU(3) triplet of three nuclear particles. By considering isospin as a carrier of electric charge (to what extent this is undisputed will be discussed later in this essay), the parallel SU(3) annex color charge and SU(2) annex electric charge seems plausible. Because, according to the color charge hypothesis, a quark is made up of three color charge components, the wave function of the quark is not twofold, as in the isospin doublet, but threefold. In its simplest form, the wave function of the SU(3) triplet is represented as a 3 x 3 matrix,
The components of the three constituent wave functions of the triplet are complex quantities. Because the wave function of a doublet consisting of, for example, two quarks bound together, as with a pion, must be seen as a single entity, with the associated semantics, the SU(3) matrix, just like the isospin doublet, is unitary , i.e. ⴕ = . However, the number of degrees of freedom n – 1 is now eight instead of three as in the doublet.
If the wave function of the triplet is made subject to a conservative force field, the semantics is preserved under covariant conversion of the wave function of the triplet ,
in which
are the eight 3 x 3 are Gell-Mann matrices, which, in the color charge triplet, are the equivalents for the three Pauli matrices in the isospin doublet. Based on this analogy, in the Standard Model eight new bosons, called gluons, have been conceived. These are seen as force-transmitting particles that in the triplet maintain the bond between the quarks.
Although the necessity of assigning the color charge attribute is disputable, modelling the wave function of a three-body entity as a SU(3) group is legitimate. However, the question now arises whether the gluons conceived in this way have more than an abstract meaning. And even, if it is legitimate to refer to them as media for strong interaction, are they the carrier of the strong nuclear force? Isn’t true that, as pointed out before, that the strong nuclear force is already included in the Lagrangian of the isospin doublet? Which physical phenomena can be explained with Quantum Chromo Dynamics (QCD) that are otherwise inexplicable? Have gluons been observed experimentally? Questions that arise because the assignment of the color charge attribute has been based on incorrect argumentation.
The concept of compiling covariant descriptions for the weak interaction and the strong interaction, based on the SU(N) group formalism of Sophius Lie from 1873, was originally described in 1954 by Chen Ning Yang and Robert Mills. However, in the Yang-Mills theory, just like in electromagnetism, the gauge fields have an unlimited range and the bosons are massless. In the 1967 GSW theory, the concept was made valid for SU(2) by inclusion of the Higgs field. About 1964, after identifying the quarks as building blocks of the nuclear particles, the SU(3) description was drawn up, more or less simultaneously by Murray Gell-Mann and by George Zweig, for the interaction mechanism between three quarks. So their gluons are massless. That was well before the introduction of the color charge hypothesis by Harald Fritsch, William Bardeen and Murray Gell-Mann in 1972.
Since the SU(3) description makes the gluon massless, their range seems unlimited, while the strong force should have the opposite effect of extremely small range. This paradox is explained in the Standard Model by pointing out that gluons mutually exchange their color charge, so that gluons are linked by strings. This limits their range. Again a new assumption that is not experimentally verifiable, but which cannot be refuted if experiments are interpreted on hypothetical grounds.
Instead of extending the abstract SU(2) model to the possibly even more abstract SU(3) model, one could have opted for a structural approach. In that case, one encounters a notoriously difficult three-body problem. The interaction between three particles, such as quarks in a nucleon, also occurs in the H3 molecule, as an interaction between three atomic nuclei. The analysis that in 1990 P. Bartlett and B.J. Howard [11] developed for this purpose can be applied to the interaction between three quarks as well. This problem appears to be solvable by using the interquark potential derived from the liquid drop internucleon model. The more so because, as we have seen, an analytical relationship for it is available. While a particle doublet, such as a meson, can be modelled as a "one-body" equivalent of an anharmonic "two-body" oscillator, a particle triplet, such as a baryon, can be modelled as a "one-body" equivalent of an anharmonic “three body” oscillator. This appears to be possible by the use of pseudo-spherical coordinates as in 1968 developed by R.C. Whitten and F.T. Smith [12]. The Smith-Whitten coordination system is six-dimensional. In addition to a hyperradius , the square of which is equal to the sum of the squares of the spacings between the three particles, there are five angles
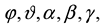
, in which
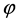
and
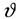
model the changes in the shape of the triangular structure and in which
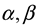
and
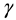
are the Euler angles. These are angles that determine the orientation of the triangle in 3D space. The interaction forces between the three particles not only cause dynamic shape changes in the equilaterality of the structure, but they also cause a Coriolis effect that results in vibra-rotations around the axis of the moment of inertia of the three-particle structure. Altogether, this results in a wave equation with the format of an anharmonic oscillator, which can be written as [13],
In which
;
;
, and
This format bears close resemblance to the wave equation for the meson discussed earlier. It is made up of the same parameters as those derived from the interquark potential. One of the main differences is the presence of the “grand angular quantum” number in the wave equation. For the ground state
, so that
As in the case of mesons, it appears that mass ratios for baryons can be accurately calculated with the anharmonic oscillator model as well. The calculated mass ratio of the excitation from ground state to first excitation is 1.475, which corresponds almost exactly to the experimentally determined masses for nucleon (938.3 and 936 MeV/c2) and the excited baryon (1382.7, 1383.7 and 1387.2 MeV/c2).
The structural model confirms that the strong force is an inherent component of the interquark potential. Just as the oscillator model of mesons can be deduced from a Lagrangian with interquark potential, it can be deduced for baryons as well.
15. Mass and charge
The structural models for meson and baryon show that baryonic mass arises from the nuclear energy of the quarks. In line with this, one might expect that the electrical energy contained in electrical charge of the quarks has its origin in their nuclear energy as well. Because the weak interaction and the electromagnetic interaction both have a Lagrangian, it is, in principle, possible to combine both interactions in a single description. Glashow, Salam and Weinberg have done so in their electroweak theory. In the structural model it can be done somewhat a easier. It suffices to extend the force derived from the far field component of the interquark potential with an electrical component, so that
where
1/4 for mesons and
1/36 for baryons. The numerical values are derived from a uniform charge distribution along the axes. Taking into account the electromagnetic fine structure expression
, this leads to a modification of the far field, so that
By including this adjustment in the numerical calculations of the mass ratios, the (modest) influence of the electrical interaction on the mass ratios of mesons and baryons can be calculated. This does require the invocation of the non-trivial relation
This analytical relationship, derived in documented work [
8] , can in retrospect be made plausible on the basis of the following consideration. A pion decays via a weak force boson
with an energetic value of 80.4 GeV. Its rest mass, calculated back from decay products, amounts to about 140 MeV/c
2. Since the pion moves at nearly the speed of light, the energy of the weak force boson can be seen as the relativistic equivalent of the rest mass of the pion. Afterall, a pion is in fact a boson. In the pion rest frame, the weak force boson maintains the bond between quark and antiquark. As noted earlier in this essay, the interquark distance should approximately equats half the wavelength of the weak force boson. Half the energy of the boson is contained in this half wavelength. The other half of the released energy therefore comes from the binding energy. According to the anharmonic oscillator model, this energy is equal to
. Because
1/2 , by virtue of these two considerations
, so that
in which
must be approximately of the order 1. Not quite, because in a harmonic oscillator there is no “brick wall” boundary. Therefore the gauging of
must be effected in a different way. Later it will be shown that
0.69 , based on a relation between the mass of the Higgs boson and the weak force boson, and, more importantly, on the basis of a deducible relation between quantum physics and gravity.
Note: It was stated earlier that the relationship between
and the weak interaction boson
has to be interpreted with care. In the structural model we have
, in which
has been defined as the square root of the electromagnetic fine structure constant
1/√137), thereby fixing a value for
. In the Standard Model, one has chosen for
, under adoption of relating
with Fermi’s constant
as
, thereby fixing a value for
. See [
27] , (p.337). This makes
in structural model numerically different from the
in the Standard Model.
The fact that nuclear interaction and electromagnetic interaction are computationally compatible does not mean that the origin of electromagnetism has been explained from the nuclear energy of quarks. This is not the case in the GSW theory either, although for this purpose more or less plausible theoretical considerations have been formulated. The structural model offers the possibility of a different explanation. The explanation given in this essay for the boson as a result of interaction between the nuclear spins of the quarks suggests that the properties of the quark can be described with Maxwell's equations. Like for electrons, one might also choose for assigning a charge, instead of describing the quark in terms of energy and a coupling factor . Symmetrically, if desired, one can may adopt energy as an attribute for the electron in association with a dimensionless coupling factor. Such descriptions are interchangeable.
It might therefore well be that that the quark is a monopole, which can be described in terms of the Maxwell equations. It could even be the long-sought magnetic monopole. In that case there is an immediate problem. The field of the magnetic monopole will have to behave differently from the field of an electric monopole such as that of an electron. Whereas the electromagnetic field of an electron is not shielded by an energetic background field, while, if the quark were a magnetic monopole, the magneto-electric field is shielded. Moreover, the magnetic monopole should have two real anomalous dipole moments, while the electric monopole has only one anomalous dipole moment. Yet, despite these two counter-arguments, the option remains, even though the properties of the electric monopole and the magnetic monopole will not be completely interchangeable. While an electron has an imaginary electric dipole moment, a quark, if it were a magnetic monopole, would have a real magnetic dipole moment. And such dipole moment could possibly be identified as the magnetic dipole moment of an elementary amount of electrical charge as well. Although the orientation of the dipole moment is fixed by the structural bond, the polarity of this charge can be positive or negative based on the spin statistics.
In this interpretation, electromagnetism has its origin in nuclear energy. In a documented elaboration of this hypothesis [
14] , the force of the nuclear interaction between two quarks has been compared to the interaction force between two electrons. It has been shown that the nuclear interaction force between two quarks corresponds to the interaction force between 18 electrons on each side. This makes the electrical influence on the mass of mesons and baryons very small (but calculable). If the quark were a magnetic monopole indeed, it would have a frame-invariant value of
8.64 x 10
-10 A m, calculated by analytical derivation from [
14] ,
This value is significantly smaller than the minimum value that Dirac has derived for his monopole. That one is determined by [
15]
where
is a natural number. Its minimum value is 3.29 x 10
-9 A m. This seems to exclude the possibility that the quark would be a magnetic monopole. It should be noted, however, that Dirac was driven by the wish to demonstrate that electric charge has a quantized character. As Eliayu Comay in 2011 showed in his Regular Charge Monopole Theory (RCMT), this wish has spoiled the symmetry of Dirac's monopole theory [
16] . Both Dirac's theory and Comay's theory are completely symmetrical under the substitutions
and
. H owever, whereas full symmetry requires a vector potential
such that
, Dirac maintained
under adoption of a string singularity. Comay's theory, on the other hand, is fully symmetrical. That theory, however, imposes the requirement that magnetic monopoles and electric monopoles cannot co-exist as sources. Comay's "magneto-electric" monopole can be described in terms of the Maxwell equations, but the fields do not interfere with the fields of an electro-magnetic monopole [
17] .
The generation of electric charge from the second anomalous dipole moment of the quark does not contradict Comay's theory. Because this charge arises from spin, the charge is quantized because the spin has only two states. An artificial construction with a Dirac string to explain quantization of electric charge is therefore not necessary. It should be noted that the hypothesis that the quark could be a magnetic monopole, or even simultaneously a magnetic monopole and electric monopole is not new. It was in 1969 proposed by Julian Schwinger [
18] . In his suggestion, the quark is a dyon, in which magnetic interaction is balanced by electrical interaction. However, as we have concluded, the electrical interaction is almost negligible compared to the nuclear interaction. The balancing by the interaction force from the near field due to the second dipole moment of the quark is of a completely different nature.
The main argument supporting the Maxwell character of the quark is the possibility, in 1980 demonstrated by Zakharov [
19] , to calculate fairly accurately the mass ratios in mesons and baryons from an assumed spin-spin mechanism between the quarks. Because this spin-spin mechanism is similar to the spin-spin interaction from which in electromagnetism the hyperfine energy spectrum of hydrogen is calculated, Zakharov's observation is an important pointer. Perhaps even more convincing, however, is the relationship between the energy of the boson and the mass difference between the pseudoscalar pion (with spins in antiparallel) and the rho meson excited by a spin flip (with spins in parallel). Due to the asymmetry in the spin-spin interaction of, respectively,
and
, this mass difference is,
wherein
the so-called constituent mass is of the
quark and
the mass is of the
boson in virtual, i.e. bound, state. It is therefore possible to calculate
from the structural model, because we know that the energy of the
boson is the relativistic equivalent of the rest mass of the pion. Hence, it may be stated that,
Because the rest masses of the pion (140 MeV/c2) and of the rho meson (775 MeV/c2) can be accurately determined experimentally, the energy value of the boson can be easily derived from the energy value of the W boson (80.4 GeV) on the basis of these two relations. This gives the
boson a value of 91.2 GeV. The very same value was collectively established at CERN in 1983 by the aforementioned UA1 and UA2 on purely experimental grounds. These simple relations, unknown in the Standard Model, gives a powerful support to the hypothesis that the quark is not only a Dirac particle with two real dipole moments, but that it is a magnetic (RCMT) monopole as well. Roughly speaking, one may say that the quark is a magnetic electron. It provides an insightful relationship between gravitation (mass), electromagnetics (electrical charge) and nuclear physics (nuclear interactions). Later in this text, the relationship with gravity will be developed toward a surprising result.
16. The Gluon
That the boson of electromagnetism is massless is understandable, because no inhibitory influence of a background field can be held responsible for giving inertia, i.e., mass. It is understandable as well that the boson of the weak force is mass-carrying, because the background field has an inhibitory effect, thereby giving inertia (mass). It thereby also limits the range of the weak force. From this perspective, it is therefore surprising that the strong force boson, if it were the gluon, would not have any inertia or mass. However, we have found that the Lagrangian of SU(3) is only covariant if the bosons are massless, as in electromagnetics, because interaction by color charge transfer is different from interaction with a background field. But to what extent can the gluon be associated with the strong force as originally identified by Yukawa? In the structural model there is in this respect no problem at all. It suffices to construct the interquark potential of a nucleon from the individual contributions of three quarks to see that the external potential of the nucleon has the same shape as the interquark potential. The external strong force bosons, mesons in that case, are therefore mass-carrying. The primary strong force boson is the boson that causes the exponential decay in the interquark potential. And that's the boson that belongs to the far field of the quark.
We identified that boson as a variant of a gamma photon. Although referred to as gluon in this essay, this strong force boson is different from the massless color charge transfer boson in the SU(3) model. Which brings us to the question of experimental evidence for the existence of gluons. For the energy of the far field boson, we found that,
where
is determined by the interquark distance spanned by half a wavelength of the weak force boson. That means that the energy value of the far-field boson is found from the previously found relationship between
and the weak-force boson, such that
With the previously mentioned value of 0.69 and the theoretical value for the normalized half interquark distance 0.853, this relationship shows that this boson has an energy value equal to 127/2 GeV. And that is equal to half the energy assigned to the Higgs boson in the Standard Model. What's wrong here? In the Standard Model, the energy value of the Higgs boson cannot be calculated. First predicted in 1964 by Francois Englert and Robert Brout, this particle was only discovered in 2012 by CERN using the Large Hadron Collder (LHC), as the signature of a collision experiment involving extremely high-energy accelerated nuclear particles. Since it is the far-field boson of a quark in the structure model and because quarks can only occur in even pairs due to their “confinement”, the signature must come from two bosons. That explains why the calculation results in half of the measured energy signature. The very fact that the calculation only yields half of the measured signature, which is in fact the sum of the rest masses of observable decay products, is proof for the correctness of the structural model. So, this strong force boson cannot be the massless SU(3) boson.
Nevertheless, it is believed that experimental evidence has been found for the physical existence of these SU(3) bosons. The so-called three-jet experiment is usually seen as proof of this [
20] . In 1979, collision experiments with high-energy beams of electrons and positrons were performed with the Petry accelerator in the DESY laboratory. As expected, it resulted into hadron bundles, which were scattered in two directions. Insofar as the energy and the momenta did not correspond to those of the electrons and the positrons, bremsstrahlung from electromagnetic radiation was held responsible. In sporadic cases, three bundles of hadrons occurred, scattered in different directions under 120
o. Because electromagnetic radiation cannot hadronize, the bremsstrahlung was attributed to gluons. There's nothing wrong with that. However, it is not proof that this bremsstrahlung is made up by gluons in the sense of the massless SU(3) bosons. The bremsstrahlung may just as well come from the dispersive radiation identified in the structural model as the boson seen as a Higgs particle in the Standard Model. This experiment is therefore not proof for the existence of color-carrying massless bosons. It might well be that they do not exist at all, especially since, as we have concluded, the necessity of the color charge attribute, which has been introduced into the theory on incorrect grounds, must be questioned.
17. The Top Quark
Apart from doubting the SU(3) boson, earlier in this essay the existence of the top quark as an isospin partner of the bottom quark (
) has been questioned. This doubt is based on two grounds. First, the structural model does not allow for heavier quarks than the bottom quark. Secondly, the mass of the top quark cannot be reconciled with the mass of the other quarks. The top quark was discovered in 1995 with the Tevatron accelerator at the Fermi laboratory in Chicago [
21,
22,
23] . In this case with a collision experiment between beams of protons and antiprotons. The collision also created jets of hadron beams under, in this experiment, an energy spectrum signature of 173 GeV. Assuming that the top quark is the missing isospin partner of the
quark, a Feynman diagram can be reconstructed as shown in the left half of figure 4. The top quark and the antitop quark arise from a gluon that is produced from a proton and an antiproton with the appropriate energy. Hadron jets can be formed from top quarks and
quarks via weak-force bosons. The necessary
quarks must then be derived from those same jets. We can conclude that with this experiment a particle with an energy of 173 GeV has been found that has the characteristics of a quark. No more and no less. But is this quark the isospin partner of the
quark?
In the Feynman reconstruction of this experiment, the weak force boson plays an essential role, because it is responsible for quark transformations. In the structural model, the weak force boson manifests itself in two ways. In bound state, also called virtual state, it binds two quarks with about half its wavelength, in free state it manifests itself as a particle with an energy of 80.4 GeV, moving at a speed close to that of light. Its rest mass, at least in this structural interpretation, is that of the pion. This boson is of a different nature from that of the gluon. We have come to know the gluon as an equivalent of the photon. This manifests itself as radiation, while the weak force boson at the interquark level shows similar properties to a meson at the internucleon level. This picture leads to the prediction that the weak force boson is not an elementary particle, but that it is a meson made up of a quark and an antiquark [
26] . But can such a prediction also be substantiated with an estimate of the energy of such a quark? A possible answer can be derived from the following consideration.
Figure 4.
Feynman reconstruction of the origin of the top quark from colliding bundles of protons and antiprotons. The emerging beams are hadron jets, formed from bremsstrahlung (gluons) generated weak-force bosons that decay into quark pairs. On the left the interpretation according to the Standard Model, on the right the interpretation according to the structural model.
Figure 4.
Feynman reconstruction of the origin of the top quark from colliding bundles of protons and antiprotons. The emerging beams are hadron jets, formed from bremsstrahlung (gluons) generated weak-force bosons that decay into quark pairs. On the left the interpretation according to the Standard Model, on the right the interpretation according to the structural model.
Assuming that
represents the relativistic state of the pion, one can calculate the relativistic value of the quark on the basis of the argument given earlier about the nature of the
Z boson. In that case, it must be ,
in which
represents the relativistic value of the (constituent) rest mass of the quark. With 80.4 GeV for the
boson and 91.2 GeV for the
boson, it gives 177 GeV for the relativistic value of the quark. The difference with the energy of 172.8
0.4 GeV assigned to the top quark is equal to the energy of 4.18
0.4 GeV assigned to the bottom quark. It may well be that the reconstruction model of the experiment was drawn up on the basis of the assumed correctness of the Standard Model. In that case, the difference is explainable. The right half of the figure shows another reconstruction, in which a top quark and an antitop quark are at the relativistic level bound by a
boson, in the same way as is the case at a non-relativistic level for the binding of a
quark to a
quark by a
boson in virtual state. If one accepts this analysis, the top quark is not the isospin partner of the bottom quark, but the base quark in relativistic state. In that case, the mass difference between bottom quark and top quark can be explained and the conclusion can be maintained that heavier quarks than the bottom quark can’t exist.
18. Gravity
It has been shown in this essay that the electron and the quark are fully on par. The same holds for the photon and the gluon. Of course there are differences. The gamma matrices of the quark are different from those of the electron. Moreover, the second dipole moment of the electron is imaginary and that of the quark is real. The radiation field of the photon is not shielded by an energetic background field, but that of the gluon is. And the source of a photon is an electromagnetic monopole while the source of a gluon quite probably is a magneto-electric monopole. As a result, the Lagrangian for a quark will differ from that for the electron. Generalizing the Lagrangian to that for a quark turns out to be a difficult task. In particular, correctly taking the influence of the two dipole moments into account is problematic. The Lagrangian also should embody the intrinsic bond between the quarks, called confinement, which imposes a requirement on the interquark distance. This makes constructing a Lagrangian for a single quark difficult and perhaps of little use. The situation is different for doublets and triplets. In the Standard Model, the joint of experimental results and theoretical abstractions has resulted in a Standard Model Lagrangian with many dozens of terms. One may have different thoughts whether such a complicated expression is meaningful.
In this essay, we will suffice with the conclusion that the description of the weak force and the strong force in a structural model reveals relationships that in the Standard Model are unexposed or unrecognized. The quarks, for instance, can all be calculated from the basic archetype. Therefore, only a single one is elementary. The Higgs boson, the top quark, the
boson and the
boson can be calculated from each other, so here only one is elementary as well. The
boson and the pion are relativistically related mesons, the top quark and the base quark are relativistically related as well. These are just a few examples from a longer list.
The model makes clear that the electric charge and baryonic mass are the product of the energy flow from a quark. It even turns out that the gravitational constant can be expressed in quantum mechanical quantities. That unites gravity with quantum mechanics. Although this was more than a decade ago deduced and documented [
24,
25] (albeit with the knowledge of the time and perhaps not transparent enough), no attention has been paid to it. I would like to conclude this essay with a brief description of the way in which this coupling between gravity and quantum mechanics takes shape.
The gravitational constant is a quantity with which in Einstein's Field Equation the energy of a conservative force field is expressed in a curvature (i.e. transformation) of the space-time coordinate system. Einstein's recipe for this is basically simple: instead of calculating the influence of the force field on the motion, one may pretend just as well that there is no influence on the motion, but instead, one may express the influence of the force field into a change of the coordinate system.
Since quantum mechanical wave equations are the equivalent of equations of motion, it is, in principle, possible to apply the same recipe in quantum mechanics. To this end, the wave equation for the anharmonic oscillator must be set up along two different paths and both results must be declared equivalent.
The energetic way is open. It suffices to construct the equation in the rest frame of the pion on the basis of the non-relativistic Pauli-Schrödinger approximation of Dirac's equation. It is also possible to derive the wave equation from Einstein's geodetic equation and to apply the non-relativistic approach to it as well. Afterall, just as Dirac derived his wave equation by transforming momenta from an equation of motion into differential operators on a wave function, one can do the same in the geodesic equation. The energetic path provides data for the stress-energy tensor
and the geodesic path provides data for Einstein tensor
. They constitute, respectively, the right-hand and the left-hand side of Einstein's Field Equation,
where
and
, respectively are the Ricci tensor and the Ricci scalar that can be calculated from the components to be determined of the metric tensor
. I once posed the question to a Nobel laureate whether this path would not be more principled and therefore more fundamental than Dirac's derivation. He confirmed, but pointed to the preventing complexity of Einstein's set of sixteen simultaneous equations. However, doing so for the pion, the problem becomes manageable, not only because of the simplicity on of the 1 + 1 dimensionality, but also because of plausible simplified conditions, such as stationarity (the metric components are independent of time), isotropy
0 ) and weak curvature (
with Δ(
x),Δ
2(
x)<<1). In that case the Einstein tensor and Ricci tensor reduce to,
The stress-energy tensor of the field within the pion has a single component
where for the pion system, as described earlier in the essay,
This relationship for the energy density is easily understood from the corresponding expression for an electric field. Because
and
, also is
What still is needed to find an expression for the gravitational constant, is the determination of the weak curvature by comparing the Pauli-Schrödinger wave equation with the result of the conversion of the geodetic equation to a wave function equivalent. Within the scope of this essay, it is sufficient to invoke by reference to published scientific work [
6] , that
Previously in this essay, it has been established that
With these ingredients both the relevant terms for the Einstein tensor and the momentum-energy tensor are available. The gravitational constant
can thus be found from simple algebra as,
Since we know all numerical values of the quantities involved,
can be calculated. However, nothing now appears being right. The
calculated with this formula is many orders of magnitude too large. So something is wrong. It has to be taken into account, though, that the result is made up in the rest frame of the pion. Hence, a relativistic correction is required for producing a proper result. That raises a new problem. How to determine the speed of the pion, which is close to the light velocity? Although the weak force boson eventually decays to the pion’s rest mass, this does not mean that the propagation speed of the pion can be determined from the associated mass ratio.
It is possible, though, to determine the pion speed from its life time. This requires the proper interpretation that the strong force, as originally conceived by Yukawa, is transmitted by pions as the consequence of the internucleon potential. That potential is the external result from the internal potential of the nucleon, set up by the individual contributions of three quarks. This means that the pion bond between nucleons can be described as an anharmonic oscillator, with new and parameters under invariance of and such that
From the rest mass energy of the pion (135.0/139.6 MeV) the internucleon distance can be calculated as
1.16 fm). This knowledge of the
parameter makes it possible to calculate the pion speed from its lifetime. The decay in proper time of a quantity
pions, shows the exponential behavior
The life
of the pion is defined as a half life value
, such that ,
The decay as a function of time is, of course, related to the decay as a function over distance, such that, taking into account relativistic correction, the lifetime of the pion can be written as,
Because
, the relativistic correction
can be found from the life time of the pion according to,
In summary, the derived expression
can now be corrected under relativistic correction for
as
In addition to the previously mentioned relationships that have been proven in the structural model, while being unrecognized in the Standard Model, this theoretically derived and numerically verifiable result for the relationship between gravity and quantum mechanics is a strong proof of its viability. It presents a challenge to the Standard Model to provide a similar proof.
| physical quantities |
determined by theory |
calculated |
|
193 MeV fm |
|
0.69 |
|
139.6 MeV |
2.36 |
1.59x10-16
|
|
2.603x10-8 s |
-1/2 |
6.67x10-11 m3kg-1s-2
|
|
80.4 GeV |
0.8526 |
|
|
1/137 |
|
|
19. Finally
I wrote this essay in response to the rejection of a scientific paper in which I calculated the mass of the nucleons on the basis of “first principles” [
7] . That article was and is the result of a challenge presented to me by a scientist friend who is convinced that the Standard Model is a perfect theory. I had sent him a list of nine points of what I believe to be shortcomings in the Standard Model and I asked him to name me a single problem that cannot be solved with the structural model, but can be solved with the Standard Model. As an example he then gave me the mass calculation of nucleons from first principles. This problem has been addressed by various groups of scientists using enormous computing power under application of the lattice QCD approach. It has been claimed that the mass of nucleons can be calculated using the “running mass” of the
quark (2.3 MeV/c
2) and of the
quark (4.6 MeV/c
2) as basic data. Quarks, however, are not observable. Those basic data have been recalculated, assuming that lattice QCD is correct, from observable particles. In this case, from the rest masses of the pion and the kaon (which, by the way, are only indirectly observable). Because lattice QCD cannot distinguish between the
quark and the
quark, their mass ratio is based on the 1/3-2/3 electrical charge distribution assumed in the Standard Model. In my rejected article I showed that with the structural model the mass of the nucleons can be calculated from the mass of the pion. Because the kaon in that model can be calculated from the pion, the pion mass as a first principle is sufficient and there is no need for invoking the mass of the kaon. Also accepting the 1/3-2/3 charge distribution is unnecessary. Moreover, the result of the mass calculation of the nucleons, especially if the mass difference between proton and neutron, appears to be more accurate than the published result from lattice QCD. And all with the structural model that requires only a few lines of computer code for accurate mass calculations. However, the article was not accepted for publication. This was not because the content was refuted on scientific grounds, but on the grounds that such an article, in which the Standard Model is not chosen as a starting point, must contain greater predictive power.
In the introduction of this essay, it was mentioned that different theories can lead to the same results. The structural model differs from the Standard Model. It is, like the Standard Model, based on a number of basic principles. Color charge as an attribute to explain the strong force is superfluous. By the way, as argued in this essay, color charge has been introduced on arguable grounds. This does not alter the fact that axiomatic principles can lead to a fruitful theory. The gauge principle, in which covariance to account for the influence of natural forces, is an example of this. That can be effective, even if the nature of the forces of nature is not understood, and the covariance is merely formatted in an abstract mathematical way. A physical model for those natural forces, such as those for the weak force and the strong force, can lead to a different description of the covariance. Ultimately, Occam's razor determines which of those theories is the simplest and makes the most reliable predictions for expected new phenomena and outcomes of new experiments.
In many respects, the described structural model can be fitted into the Standard Model. What makes it essentially different, however, are two aspects. The first of these is the description of the quark as a Dirac particle that has two real dipole moments. Its existence is defensible in Dirac's theory for the electron, although Lorentz invariance imposes the requirement that such a particle can only exist in confinement with a sister particle. The second aspect is the necessary recognition that empty space does not exist, but that space is filled with a polarisable energetic fluid. Actually, in the Standard Model this is the case as well, albeit being masked by the mathematically defined Higgs mechanism, in which a boson is generated that, in fact, is the carrier of the energy in the background field.
In this essay, I have mentioned, among a number of other examples, the relationship with gravity as a result that can be achieved with a structural model for particle physics. In addition, the strong force has been identified as an inhibitory effect from a polarisable energetic background field. In cosmology there is a background field as well, necessary to explain that the universe is expanding faster than before 1998 was thought. Although this phenomenon could not be explained, it was possible to bring it in line with Einstein's Field Equation by assigning to the cosmological constant a value different from zero. In other work I have documented [
14,
27] that the accelerated expansion relies on the reverse phenomenon of polarization inhibition. A sign difference in Einstein's Lambda explains why in cosmology the energetic background field has a stimulating effect, while in particle physics the field has an inhibitory effect.
References
- Debye, P.; Huckel, E. Physik. Zeitschrift 1923, 24, 185. [Google Scholar]
- Gonano, C.A.; Zich, R.E.; Mussetta, M. Definition for polarization P and magnetization M fully consistent with Maxwell's equations. Prog. Electromagn. Res. B 2015, 64, 83–101. [Google Scholar] [CrossRef]
- Griffiths, D.: Introduction to Elementary Particles, ISBN 3527406018, Wiley (2008).
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. A 1928, 117, 610–624. [Google Scholar]
- Roza, E. On the second dipole moment of Dirac’s particle. Found. Phys. 2020, 50, 828. [Google Scholar] [CrossRef]
- Roza, E. On the second dipole moment of Dirac’s particle. updated, www.preprints. [CrossRef]
- E. Roza, On the mass of nucleons from first principles, https://www.preprints.org/manuscript/202203.0282/v1 (2022).
- E. Roza, On the quark scaling theorem and the polarisable dipole moment of the quark in a scalar field, https://www.preprints.org/manuscript/202006.0304/v4.
- Roza, E. The H-type quark and the mass of mesons. Phys. Essays 2012, 25, 191–202. [Google Scholar] [CrossRef]
- M. Tanabashi et al. (Particle Data Group), “Review of Particle Physics”, Phys. Rev.
- Bartlett, P., Howard, B.J.: The rotational-vibrational spectrum of symmetric non-rigid triatomics in hyperspherical coordinates: the H+ 3 molecule Molecular Physics, Vol. 70, No. 6, 1001 (1990). 1001; 6.
- Whitten, R.C., Smith, F.T.: Symmetric Representation for Three-Body Problems. II. Motion in Space, J. Math. Phys. 9, 1103 (1968).
- E. Roza, The H-type quark and the baryons, Phys. Essays, 27, 3, 390 (2014).
- E. Roza, The Impact of the quark’s monopole properties on the unification of the fundamental physical forces, https://www.preprints.org/manuscript/202105.0147/v4.
- Dirac, P.A.M. Quantised singularities in the electromagnetic field, Proc. R. Soc. London. Ser. A, Contain. Pap. a Math. Phys. Character 1931, 133, 60–72. [Google Scholar] [CrossRef]
- E. Comay, “Spin, isospin and strong interaction dynamics”, Progr. In Phys., 4, 55 (2011).
- Comay, E. Inherent Differences between Bound and Radiation Fields. OALib 2018, 05, 1–18. [Google Scholar] [CrossRef]
- Schwinger, J. A Magnetic Model of Matter. Science 1969, 165, 757–761. [Google Scholar] [CrossRef] [PubMed]
- A.D. Sakharov, Sov. Phys. JETP 51 (6), (1980).
- S.L. Wu, Discovery of the gluon, Int. Journ. of Modrrn Phys. A, 29, 32, 1430076 (2014).
- Abe, F.; et al. (CDF Collaboration) (1995). "Observation of top quark production in pp collisions with the Collider-Detector at Fermilab". Physical Review Letters. 74 (14), 2626 (1995).
- Abachi, S.; Abbott, B.; Abolins, M.; Acharya, B.S.; Adam, I.; Adams, D.L.; Adams, M.; Ahn, S.; Aihara, H.; Alitti, J.; et al. Observation of the Top Quark. Phys. Rev. Lett. 1995, 74, 2632–2637. [Google Scholar] [CrossRef] [PubMed]
- Cortiana, G. Top-quark mass measurements: Review and perspectives. Rev. Phys. 2016, 1, 60–76. [Google Scholar] [CrossRef]
- Roza, E. A hypothetical H-particle. Phys. Essays 2011, 24, 72–84. [Google Scholar] [CrossRef]
- Roza, E. The gravitational constant as a quantum mechanical expression. Results Phys. 2016, 6, 149–155. [Google Scholar] [CrossRef]
- E. Comay, Broken Physics, ISBN 978-1-64153-417.8 (2021).
- E. Roza, On the vacuum energy of the universe at the galaxy level, the cosmological level and the quantum level, https://www.preprints.org/manuscript/202108.0159/v1.
- Roza, E. On the compatibility of the H-particle with the Standard Model. Phys. Essays 2011, 24, 395–412. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
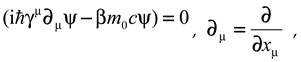
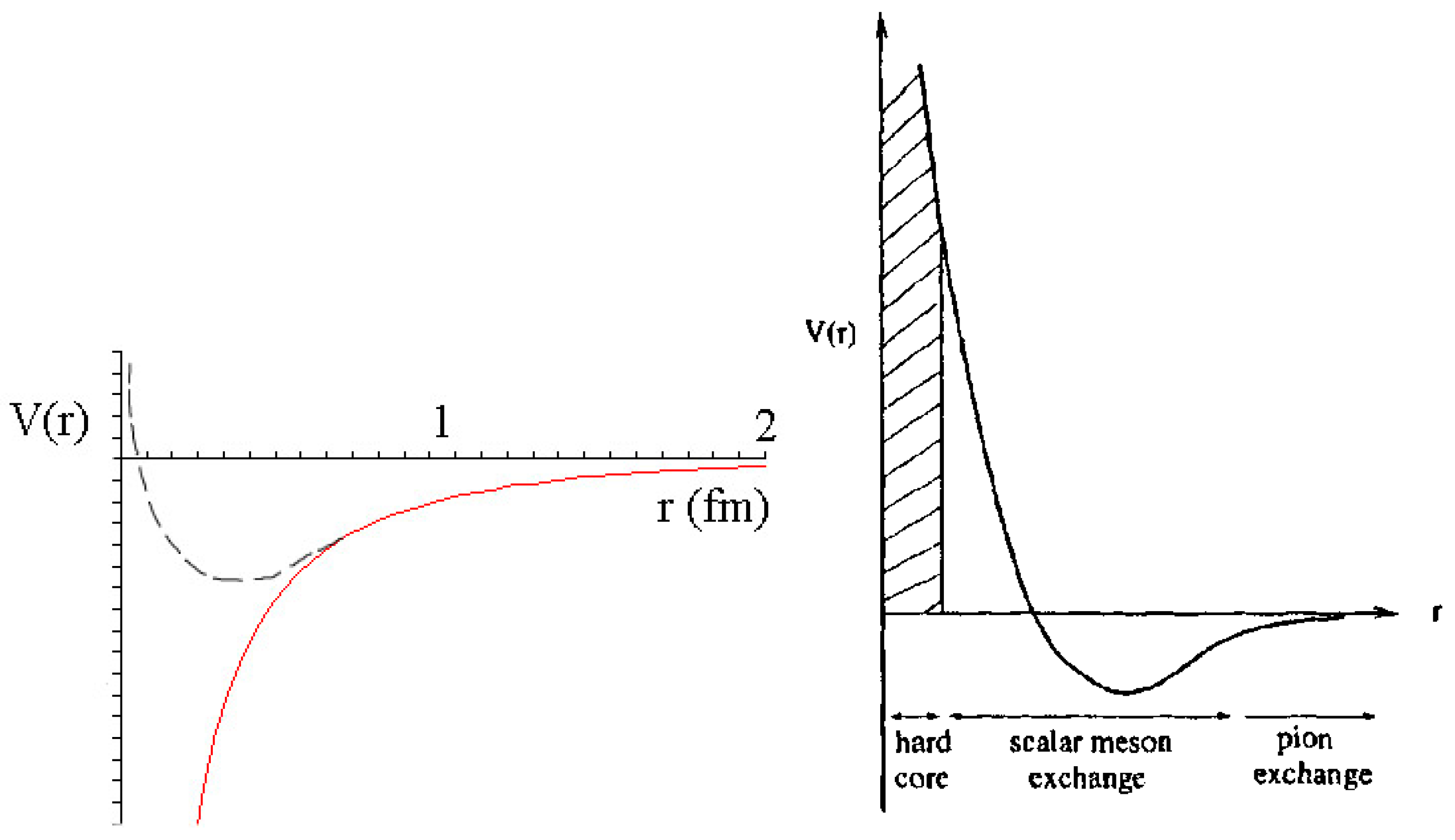
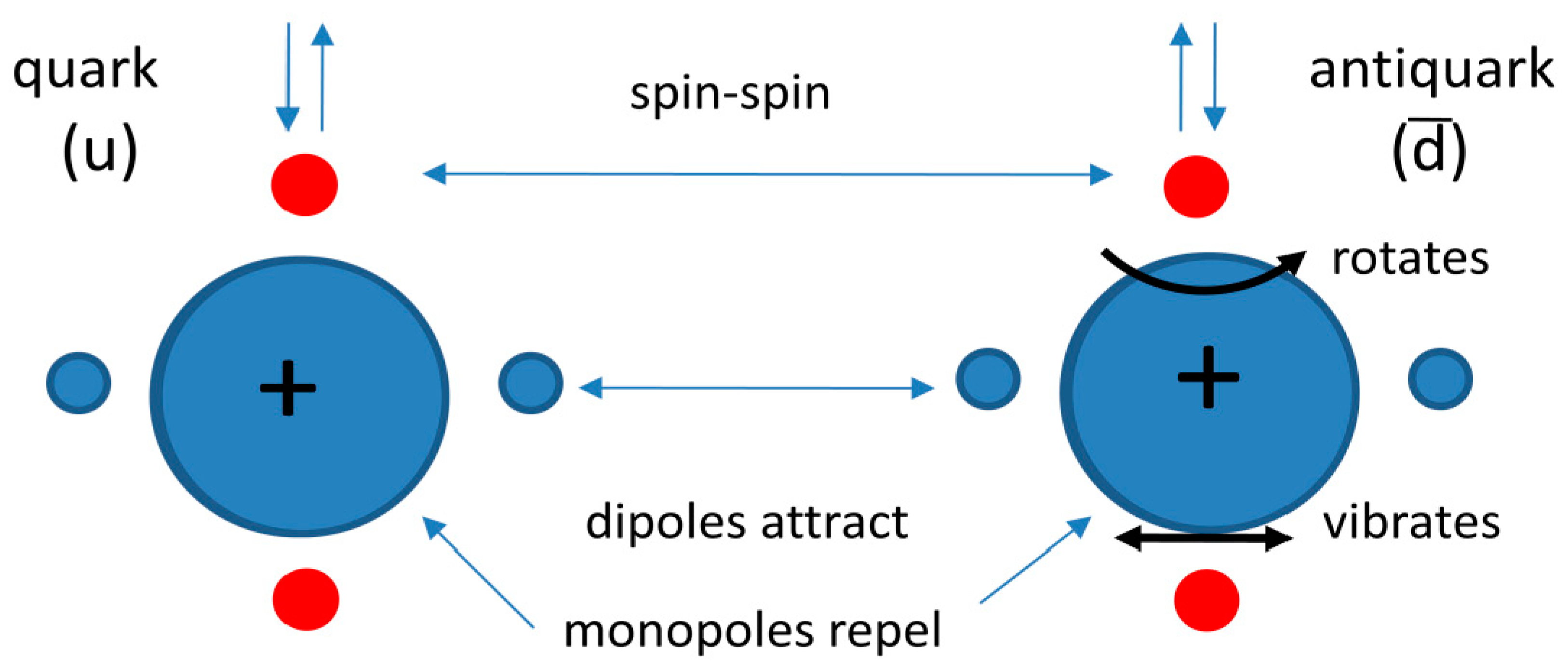
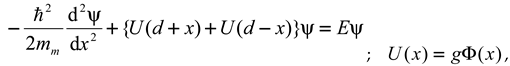
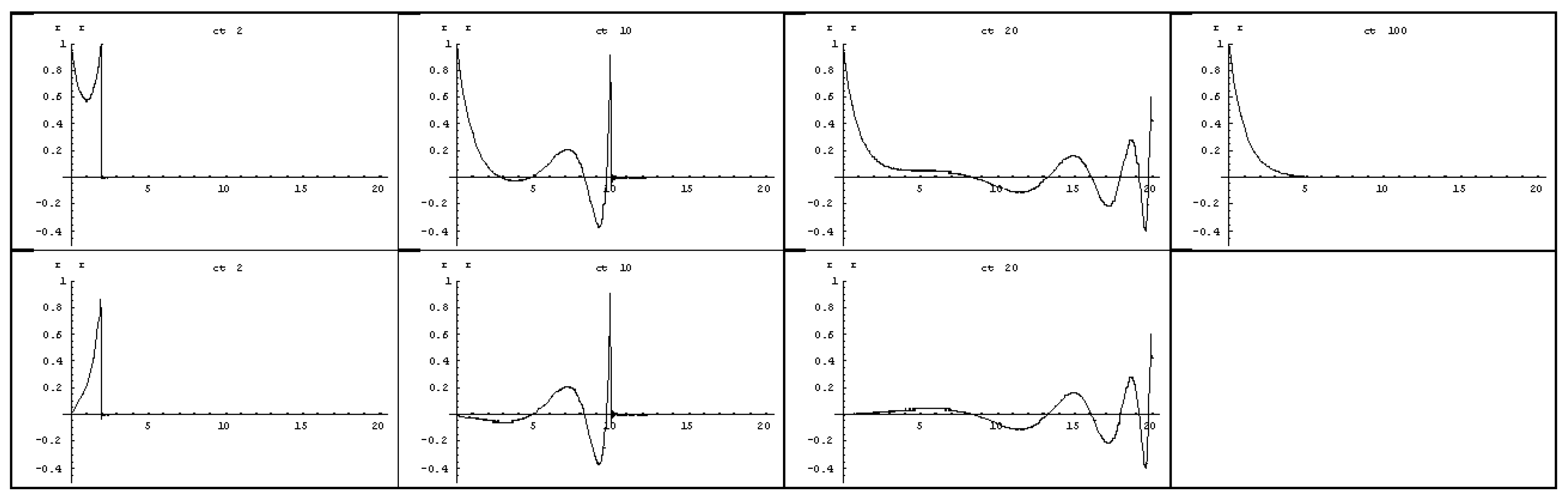
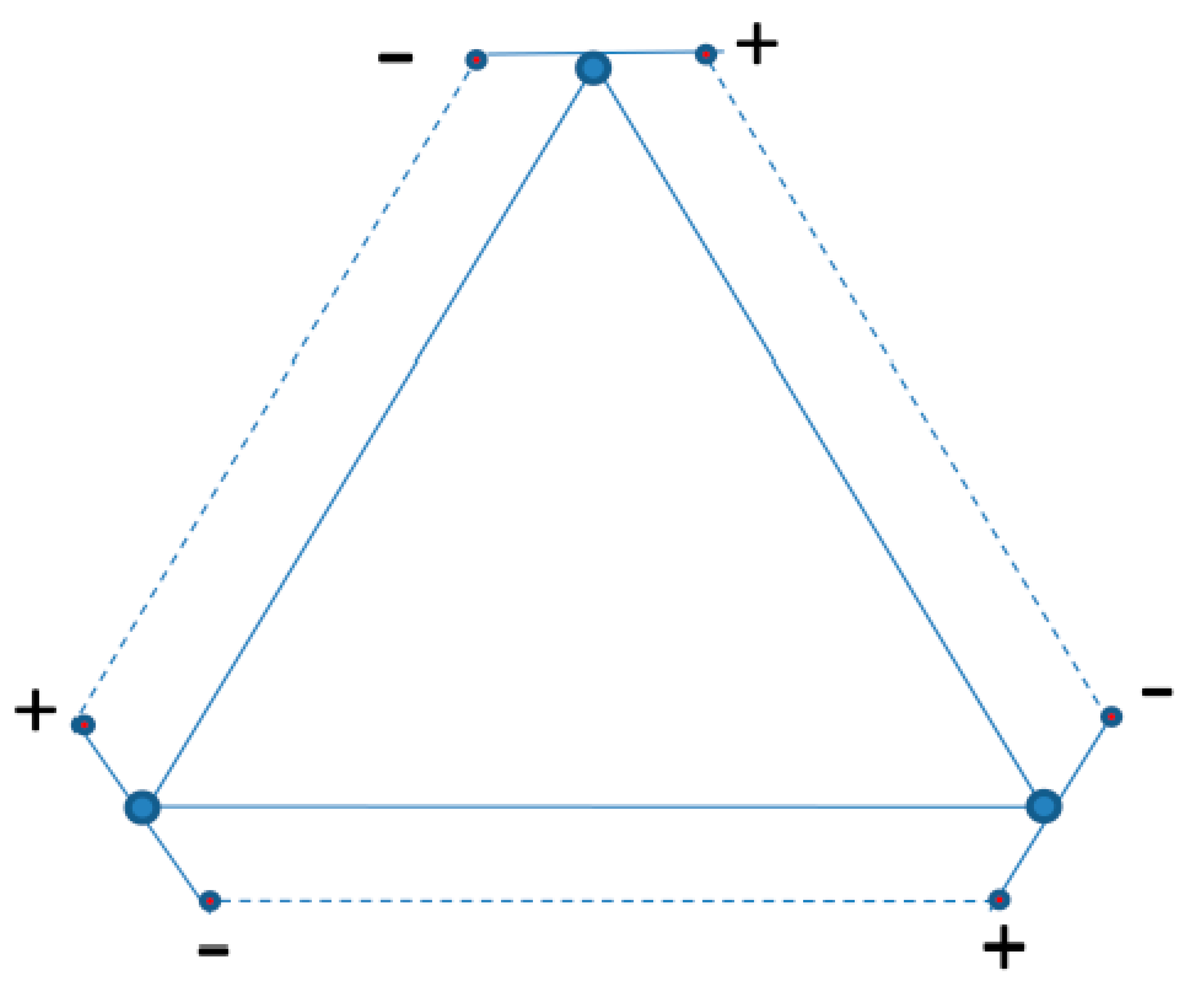
 , in which
, in which  and
and  model the changes in the shape of the triangular structure and in which
model the changes in the shape of the triangular structure and in which and
and are the Euler angles. These are angles that determine the orientation of the triangle in 3D space. The interaction forces between the three particles not only cause dynamic shape changes in the equilaterality of the structure, but they also cause a Coriolis effect that results in vibra-rotations around the axis of the moment of inertia of the three-particle structure. Altogether, this results in a wave equation with the format of an anharmonic oscillator, which can be written as [13],
are the Euler angles. These are angles that determine the orientation of the triangle in 3D space. The interaction forces between the three particles not only cause dynamic shape changes in the equilaterality of the structure, but they also cause a Coriolis effect that results in vibra-rotations around the axis of the moment of inertia of the three-particle structure. Altogether, this results in a wave equation with the format of an anharmonic oscillator, which can be written as [13],