Dirac Fermion of a Monopole Pair (MP) Model of 4D Space-Time and Its Wider Implications

Samuel Yuguru

doi:10.20944/preprints202210.0172.v15

Submitted:

23 December 2024

Posted:

25 December 2024

Read the latest preprint version here

Abstract

In quantum mechanics (QM), the electron of spin-charge, ±1/2 in probabilistic distribution about a nucleus of an atom is described by non-relativistic Schrödinger wave equation. Its transformation to Dirac fermion of a complex four-component spinor is incorporated into relativistic quantum field theory (QFT) based on Dirac theory. The link between QM and QFT on the basis of space-time structure remains lacking without the development of a proper, complete theory of quantum gravity. In this study, how a proposed MP model of 4D space-time mimicking hydrogen atom type is able to combine both QM and QFT into a proper perspective is explored. The electron of a point-particle and its transformation to Dirac fermion appears consistent with Dirac belt trick while sustaining unitarity of spin-charge and wave-particle duality with center of mass reference frame relevant to Newtonian gravity assigned to the point-boundary of the spherical model. Such a tool appears dynamic and is compatible with basic aspects of both QM and QFT such as non-relativistic wave function and its collapse, quantized Hamiltonian, Dirac spinors, Weyl spinors, Marjorana fermions and Lorentz transformation. How all these relate to space-time curvature for an elliptical orbit without invoking a framework of space-time fabric is plotted for general relativity and a multiverse of the MP models at a hierarchy of scales is proposed for further investigations.

Keywords:

Dirac fermion

;

Quantum mechanics

;

Quantum field theory

;

Dirac belt-trick

;

4D space-time

Subject:

Physical Sciences - Theoretical Physics

I. Introduction

In this section, the rationale for why it is necessary to consider an electron within a boundary of 4D space-time is explored by first outlining the transition from QM to QFT and then describing the transformation of the electron to composite Dirac fermion of four-component spinor. The MP model of 4D space-time resembling a hydrogen atom type is explored in Section II. Physical intuition on a geometry basis is applied to explain the transformation of the valence electron to a Dirac fermion by the process of Dirac belt trick (DBT) and how this is able to integrate charge conjugation (C), parity inversion (P) and time reversal (T) symmetry. Center of mass (COM) reference frame is assigned to a point-boundary of the spherical model and this offers a dynamic tool which appears compatible with QM and QFT as respectively explored in Sections III and IV by considering some of their features relevant to the discussions. In Section V, space-time geometry of the model is examined with respect to its framework of fabric and internal structure relevant to Lie group representation. How space-time curvature can be incorporated in a multiverse of the MP models at a hierarchy of scales is presented and some concluding remarks for future prospects are offered in Section VI.

A. Quantum space-time dilemma in field theory

The electron of a point-particle of mass is attributed to

i ℏ

with

i

a complex number assigned to a point of a rotating sphere and

ℏ

to Planck constant of infinitesimal radiation in quantized form [1,2]. The first order space-time derivative of the particle in motion is attributed to non-relativistic Schrödinger equation,

i ℏ \partial / \partial t

and it is a fundamental concept of particles in QM that cannot be derived by QFT [3]. For light-matter coupling, the energy and momentum operators of Schrödinger equation,

\hat{E} = i ℏ \frac{\partial}{\partial t}, \hat{p} = - i ℏ \nabla,

(1)

are adapted into QFT beginning with Klein-Gordon equation [4] by second derivation of space-time given in the expression,

({i^{2} ℏ}^{2} \frac{\partial^{2}}{\partial t^{2}} - c^{2} ℏ^{2} \nabla^{2} + m^{2} c^{4}) ψ (t, \bar{x}) = 0 .

(2)

Equation (2) is a relativistic form of Equation (1) and it incorporates special relativity,

E^{2} = p^{2} c^{2} + m^{2} c^{4}

with the first term representing momentum and second term to mass-energy equivalence,

E = {m c}^{2}

. The del operator,

\nabla

presents 3D space for a particle in motion in space-time. Only one component is considered in Equation (2) and is relevant to describe bosons of whole integer spin and their charges. However, it does not take into account fermions of spin 1/2 and negative energy contribution from antimatter. These are accommodated into the famous Dirac equation [3] of the generic form,

i ℏ γ^{u} \partial_{u} ψ (x) - m c ψ (x) = 0 . (3)

The symbol,

γ^{u}

is a set of 4 x 4 gamma matrices, i.e.,

γ^{u}

=

γ^{0}

,

γ^{1}

,

γ^{2}

,

γ^{3}

and this combines with partial derivative of space-time,

\partial_{u} =

x_{0}

,

x_{1}

,

x_{2}

,

x_{3}

to give a scalar quantity which is invariant under Lorentz transformation. The imaginary unit,

i

unifies space and time according to special relativity and distinguishes 1D time from 3D space by orthonormal relationship. The complex four-component spinor,

ψ

from Equation (3) is represented in the form,

ψ = (\begin{matrix} \begin{matrix} ψ_{0} \\ ψ_{1} \\ ψ_{2} \end{matrix} \\ ψ_{3} \end{matrix}), (4)

where

ψ_{0}

and

ψ_{1}

are spin-up and spin-down components of positive energy with

ψ_{2}

and

ψ_{3}

as corresponding antimatter for spin-up and spin-down of negative energy. Negative energy is associated with the creation and annihilation of virtual particles in a vacuum towards the emergence of real particles,

ψ_{0}

and

ψ_{1}

of superposition states like the electron of spin-charge, ±1/2 in probabilistic distributions [3]. In order to include space-time-energy matrices of the particles, standard Pauli matrix convention is applied such as [5,6],

{σ_{0} = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}), σ}_{1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}), σ_{2} = (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}), σ_{3} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) . (5)

These are a set of 2 x 2 complex Hermitian and unitarity matrices, each related to angular momentum operator for observable spin 1/2 particle respectively in three spatial directions. The combination of

({σ_{13})}^{2}

gives the negative identity matrix,

- I = (\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix})

with its square equal to

σ_{0}

for positive

I

. The orthonormal basis of

σ_{13}

and

σ_{0}

is the matrix

σ_{2}

by isomorphism is [6],

(\begin{matrix} a & - i b \\ i b & a \end{matrix}) = {a σ}_{0} + {b σ}_{13} ⟷ a + i b . (6)

Equation (6) considers real numbers

a

→

ψ_{0}

and

b

→

ψ_{1}

respectively as real and imaginary parts of

σ_{2}

. The orthonormal basis for vector space is relevant to Clifford group and Clifford algebra,

C ≅ C (0,1)

. The four matrices in

C (4)

generate the vector space

C (3,1)

or

C (1,3)

and by isomorphism is denoted

γ^{i}

with respect to Dirac matrices inclusive of a fifth related matrix [6],

γ^{0} = (\begin{matrix} I & 0 \\ 0 & - I \end{matrix}), γ^{i} = (\begin{matrix} 0 & σ_{i} \\ {- σ}_{i} & 0 \end{matrix}) ⟹ γ_{5} = (\begin{matrix} 0 & I \\ I & 0 \end{matrix}) . (7)

The matrix,

γ_{5} = {i γ}^{u}

couples the spinor field of i defined by modes of oscillation, stress-energy tensor and momentum to space-time structure. There is no space-time boundary to the quantum state defined by QFT with observation limited to partial derivative of space-time. Similarly, for QM, by 2^nd derivative of space-time, Schrödinger relationship of oscillation mode is conceived in the generic form,

i ℏ \frac{d ψ (x, t)}{d t} = \frac{{- ℏ}^{2}}{2 m} \frac{d^{2} ψ (x, t)}{{d x}^{2}} + V (x) ψ (x, t) . (8)

Equation (8) considers wave behavior of electrons permeating space and consisting of both kinetic and potential energies. Based on such notion, it becomes quite challenging to constrain space-time singularity towards Planck’s length on the basis of gravitational force without any new insights offered by experiments inclusive of observations made on black holes and gravitational waves. Thus, quantum space-time still remains a speculative notion when viewed from theoretical perspective of either a multidimensional structure pursued by string theory or finite loops of space woven into a network of fine fabric as in loop quantum gravity.

B. Rationale for 4D quantum space-time in field theory

In relativistic QFT,

γ^{u}

is broken up into four-position coordinates, four-momentum and four-vector for the force respectively given as [7],

\vec{R} = (\begin{matrix} \begin{matrix} c t \\ x \\ y \end{matrix} \\ z \end{matrix}), \vec{P} = (\begin{matrix} \begin{matrix} E \\ p_{x} c \\ p_{y} c \end{matrix} \\ p_{z} c \end{matrix}), χ^{μ} = (\begin{matrix} \begin{matrix} x^{0} \\ x^{1} \\ x^{2} \end{matrix} \\ x^{3} \end{matrix}) . (9)

The components of Equation (9) transformed contravariantly by continuity of rotation, translation and inversion. For covariant measures,

\partial_{u}

is adapted but the increase in entropy in accordance with the 2^nd law of thermodynamics presents the dilemma of electroweak baryogenesis [8] when matter is dominant over antimatter. Antimatter existence is readily observed from Stern-Gerlach experiment [9] and cosmic rays [10] and it requires time reversal to demonstrate violation of charge, parity or their combination as applied in Feynman diagrams for renormalization process [11]. However, conservation of CPT symmetry and exponential rise of Hilbert space linearly somehow necessitates negative energy of antimatter for both spin up and spin down as demonstrated in Equation (4). In massless quantum electrodynamics, the creation and annihilation of virtual particles is required [5,12]. Because of the dominance of classical thermodynamic arrow of time with microscopic arrow of time assigned to decay of neutral kaons [9], a proper 4D quantum space-time is required to describe the transformation of the electron of probability distribution,

{|ψ|}^{2}

, under Lorentz boost to composite Dirac fermion within an atom. In QM, the electron of a point-particle into 3D space about the nucleus of an atom and its shift in position of 1D time implies to quantum space-time. Its motion by derivation of space and time or space-time from a ground state as demonstrated in Equation (1) cannot be accounted by classical time especially within an atom of diameter about 0.1 to 0.5 nanometers. Comparable, Dirac’s string trick or belt trick [13] that describes the electron conversion to a positron at 360° rotation and its restoration at 720° rotation requires quantum space-time. The same extends to other related descriptions like Balinese cup trick [14] or Dirac scissors problem [15] for the Dirac fermion.

Leading theoretical approach to quantum space-time is to quantize both matter field and space-time such as the twister approach [16] analogous to theory of loop quantum gravity. It is based on non-commutative spin network of dynamical triangulations in 4D to mimic angular momenta. Its simulation using four

{}^{13}C

nuclei replicating quantum tetrahedra by nuclear magnetic resonance simulator is attempted to produce spinfoam vertex amplitude predicted by loop quantum gravity for quantum space-time [17]. The outcome looks promising for quantum computation of exponential rise in non-perturbative regimes of vectors in Hilbert space which cannot be easily done by classical computers. Nevertheless, the key ingredient for such novel undertaking and its similar kinds [18,19] is how to integrate both quantum gravity and quantum fluctuations of matter field into a Block sphere replicating an atom, where the theory of general relativity breaks down and the principles of QM come into the foreplay. At this stage, no such model exists because it is extremely difficult to isolate atoms and study their dynamics.

C. Motivation of this study

Both Schrödinger electron cloud model and Bohr model present spherical models for the hydrogen atom in 3D. Capitalizing on Rutherford’s atomic model, how an electron of a physical entity in an elliptical orbit is likely to generate 4D space-time spherical model mimicking the hydrogen atom type is examined in this study. The process includes demonstrating DBT and CPT symmetry to account for the electron spin of superposition states. The outcomes are able to integrate some basic aspects of both QM and QFT into a proper perspective on a geometry basis. Such a tool can become important to the pursuit of a multiverse of the MP models at a hierarchy of scales for a body-mass in an elliptical orbit and this warrants further investigations.

II. Dirac fermion of a MP model of hydrogen atom type

Additional details on the conceptualization path of the model from electron wave-diffraction is offered elsewhere [20]. In this section, the transformation of an electron of hydrogen atom type to a fermion by Dirac process within a spherical MP model of 4D space-time is unveiled (Figure 1a–d). First, a brief overview of the atomic models is provided on how it is not able to accommodate the electron spin, ± 1/2 superposition states. Then how this can be incorporated into the MP model by DBT consistent with combined CPT symmetry is demonstrated. This is ensued by outlining some of the model’s dynamics before exploring its compatibility to both QM and QFT on the basis of space-time geometry.

A. A brief overview of existing atomic models

The widely accepted model of the atom is the electron cloud model described by Schrödinger’s

ψ

. The probability of finding the electron at a time is relegated to orbitals of quantum waves. These are standing waves permeating the finite region of the atom and possess both kinetic and potential energies as demonstrated in Equation (8). However, it cannot explain how these collapse to a definite state at observation. Similarly, Bohr model depicts electron to occupy certain orbits of quantized energy around the nucleus. Any promotion to higher energy levels requires external energy inputs such as for light-atom coupling observed in the hydrogen spectrum. The model was developed to explain how electron(s) in orbit around the nucleus (consisting of proton(s) and neutron(s)) of Rutherford’s atomic model do not lose energy by radiation and collapse into the center. The major limitations to all these models is that they cannot account for the electron’s magnetic spin, ±1/2 in superposition states and its transition in orbit of indeterminacy. How the electron spin is applicable to the process of DBT by incorporating both Euclidean and Minkowski space-times for the MP model is elucidated next.

B. Unveiling of Dirac belt trick and CPT symmetry

The electron orbit of time reversal in discrete form of sinusoidal wave is defined by Planck radiation, h. In forward time, the orbit is transformed into an elliptical shape of a MP field mimicking Dirac’s string (Figure 1a). The electron at the vertex mimics a monopole as quantized state of the MP field of a dipole moment. Clockwise precession generates Euclidean space-time for the atomic state. Perturbations such as nonlinearity of differential gravitation acceleration between two body-masses, eccentricity of the reference orbit and its oblateness, and relative motion of one-body mass in motion against the other body-mass are evident in classical planetary orbit [21] and are considered negligible for the atomic state. Only the centrifugal force,

F_{c} = m v^{2} / r

is balanced out by nuclear attractive force,

F_{e} = Z e^{2} / 4 π ε_{0} r^{2}

to generate a stable orbit of the MP model (Figure 1a) comparable to Bohr model.

Clockwise precession of the MP field institutes the process of DBT, where the torque or right-handedness exerted on the vertex shifts the electron of spin up from positions 0 to 4 for 360° rotation. At position 4, maximum twist is attained due to time reversal orbit against clockwise precession. The electron then flips to spin down mimicking a positron to begin the unfolding process and emits radiation by,

E = n h v

. The positron is short-lived from possible repulsion of the proton and by another 360° rotation from positions 5 to 8, the electron is restored to its original state. The electron-positron transition is restricted to a hemisphere of the MP field that is interchangeable with the other hemisphere. In this way, CPT symmetry is sustained except the electron is chiral. Discrete symmetries of C, P or combined CP can be broken unlike T from light-matter coupling. These intuitions are analogous to DBT by the electron shift at positions 0 to 3 in continuous form to generate Dirac four-component spinor at spherical lightspeed. As a consequence, the four-components,

ψ_{0}, ψ_{1}, ψ_{2}, ψ_{3}

of Equation (4) are assigned respectively to positions 0, 1, 2, 3. The argument is made that negative energy from antimatter of spin-up and spin-down for both the electron and positron pair during their transition can emerge from the corresponding, interchangeable hemispheres. The moduli spaces at the vertices of the MP field by clockwise precession can resemble both Hermitian (hemisphere consisting of the electron) and non-Hermitian (hemisphere devoid of the electron) Hamiltonian spaces, i.e., P(0→8) =

\int_{τ} ψ^{*} \hat{H} ψ d τ

with time equal to

τ

. The vertex at position 0 accommodates the electron-positron transition of ZPE and serves as COM reference frame. In this case, the vertices can resemble virtual particles with the emergence of real particles accorded to electron shift at positions 0, 1, 2 and 3. Balancing out the charges at positions, 1, 3 and its conjugate positions 5,7 somehow transforms the hyperbolic surfaces of the pair of light-cones to form compact topological torus of Bohr orbit (BO) (Figure 1c) that somehow mimics angular momentum of quantized state,

m v r = n h / 2 π

. These levitates into n-dimensions or n-energy levels between the two hemispheres of the MP field into Minkowski space-time (Figure 1b) in accordance with Rydberg formula,

1 / λ = R (1 / n_{1} - 1 / n_{2})

. Oscillations between the hemispheres can produce Zeeman effects and cater for both exponentials in

R_{\infty} = m_{e} e^{4} / 8 ε_{0}^{2} h^{3} c

and fine-structure constant,

α = e^{2} / 4 π

. The former considers each hemisphere to be in superposition states for the electron-positron transition at spherical lightspeed with z-axis equivalent to nuclear isospin. The latter is applicable to fine-tuning of hydrogen spectral lines at the ground state of BO at n = 1 to the first excited state, n = 2 by setting,

ε_{0} = ℏ = c = 1

. The non-conducting electron as a physical entity rotates about z-axis of the MP field and generates both magnetic dipole moment,

u

due to its charge and angular momentum,

J_{z}

equivalent to BO by rotation of its mass. The relationship to gyromagnetic ratio or

g

-factor,

γ = u / |J_{z}|

is subjected to the anomalous magnetic moment,

a_{e} = g - 2 / 2

due to twisting and unfolding process by DBT at the vertex from the electron-positron transition. The one loop correction,

a_{e} = a / 2 π

is attributed to 720° rotation by DBT, while perpetual motion by clockwise precession to quantum perturbations pursued in quantum electrodynamics. The moduli of Hermitian spaces for the MP field vertices would mimic polarization states of electron-positron transition at position 0 to generate infinite Hamiltonian systems as mentioned above. The precession is balanced out by the electron’s time reversal orbit in accordance with Newton’s first law to generate an inertia reference frame, λ (Figure 1a) under the conditions,

λ_{\pm}^{2} = λ_{\pm},

T r λ_{\pm} =

2,

λ_{+} + λ_{-} =

1, (10)

where the trace function, Tr is the sum of all elements within the model from light-matter coupling. How this is applicable to incorporate the dynamics of the atom is examined next.

C. Dynamics of space-time geometry in an atom

In this subsection, the dynamics of the MP model of 4D space-time somewhat mimicking a hydrogen atom and its relevance to both QM and QFT on a geometry basis (Figure 1a–d) are briefly described. Some of these concepts are derived from ref. [22,23].

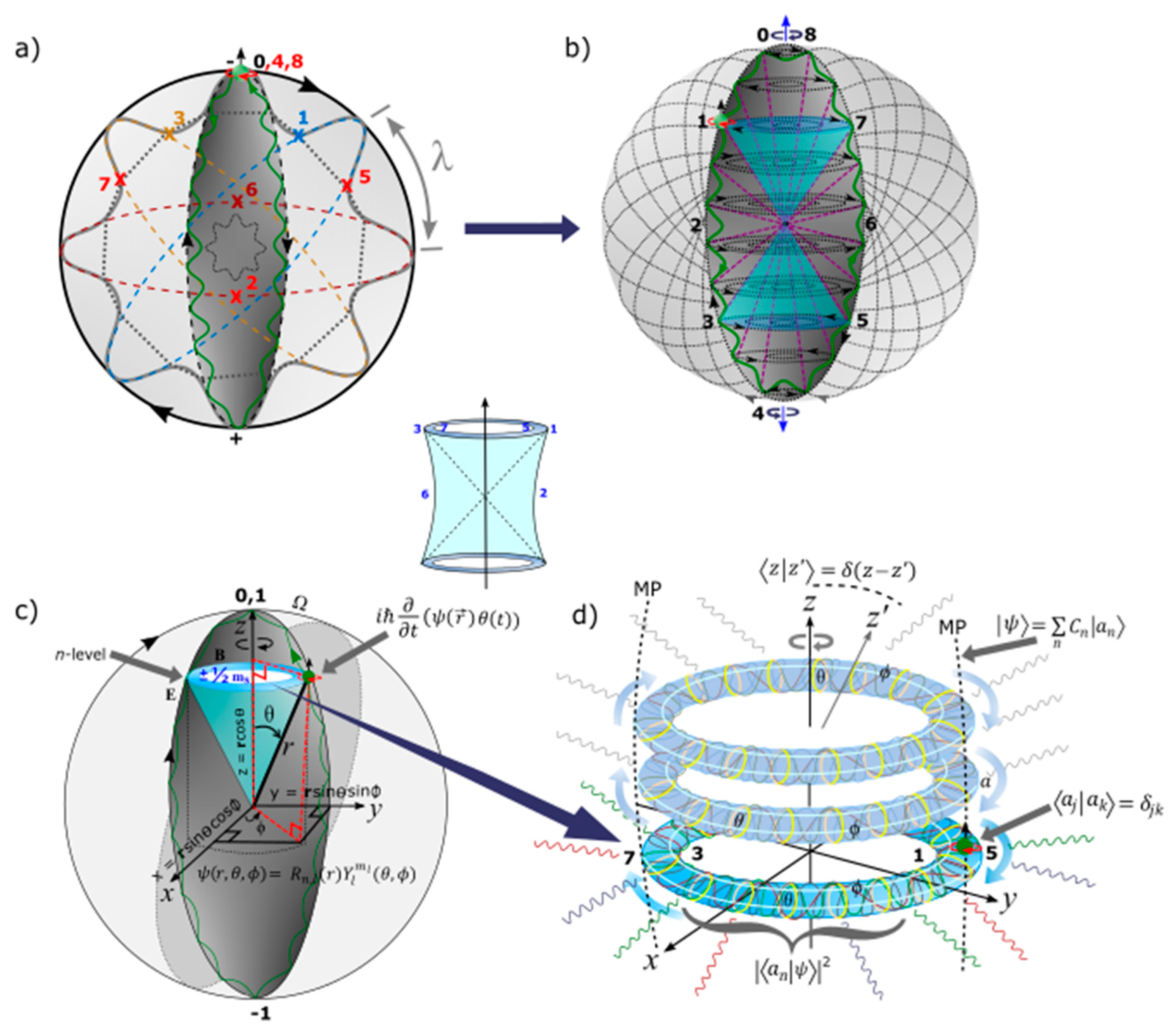
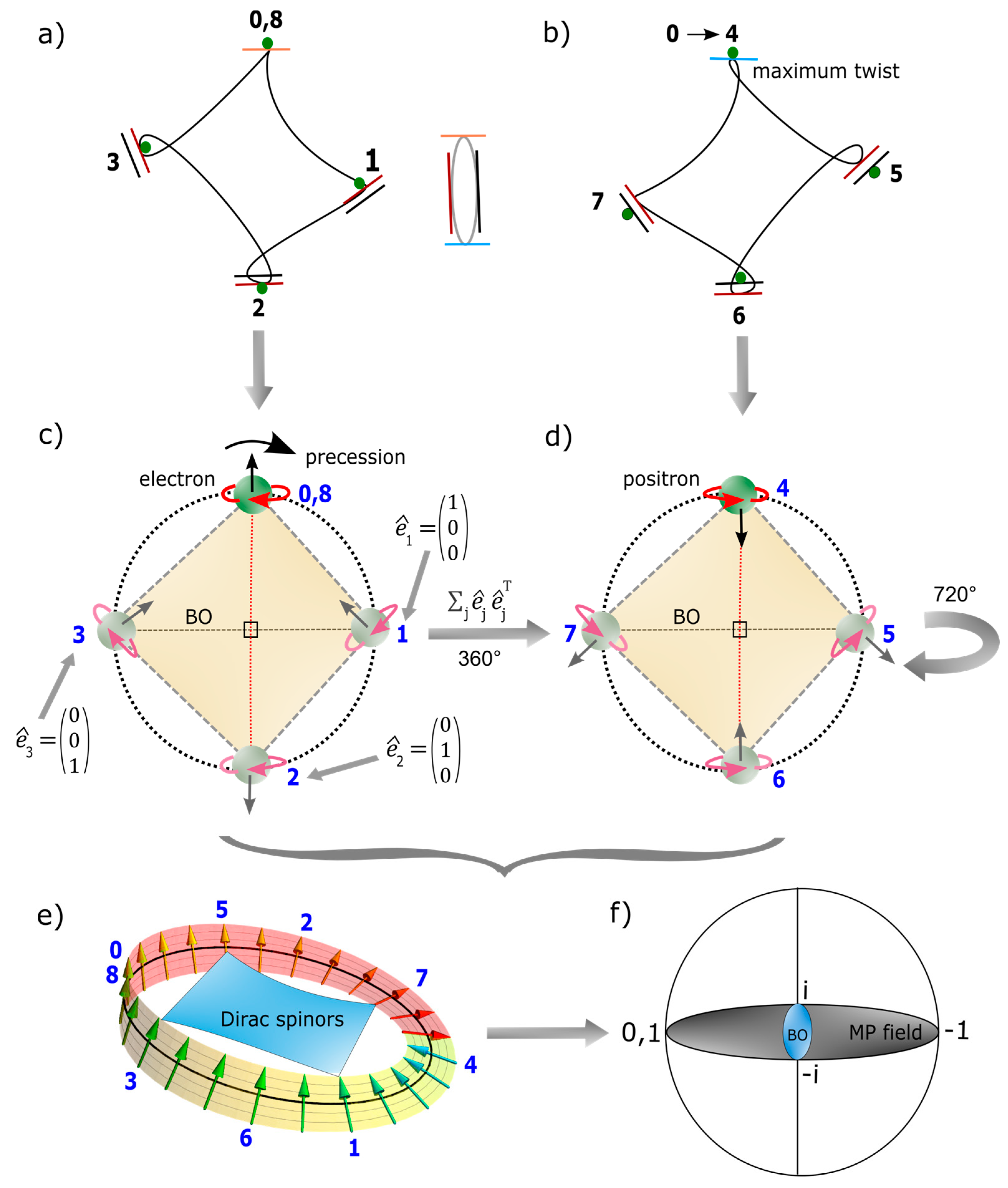
The electron defined by $ψ$ and its shift in positions, 0, 1, 2, 3 of continuity is envisioned for four-component complex spinor. The stretching of its elliptical orbit or MP field resembles Dirac’s string. Suppose the vertices of both the south and north poles are stretched out, the electron is expected to transit back and forth by DBT irrespective of the distance of separation. In the case, a dipole moment of weak electromagnetic field is generated beyond lightspeed by the particle’s motion and this somewhat parallels quantum entanglement or spooky action at a distance. Interception of the electron by traversing light waves or magnetic field should depict the characteristics of either the south or north poles or its hybrid state leaning towards either of the positions.
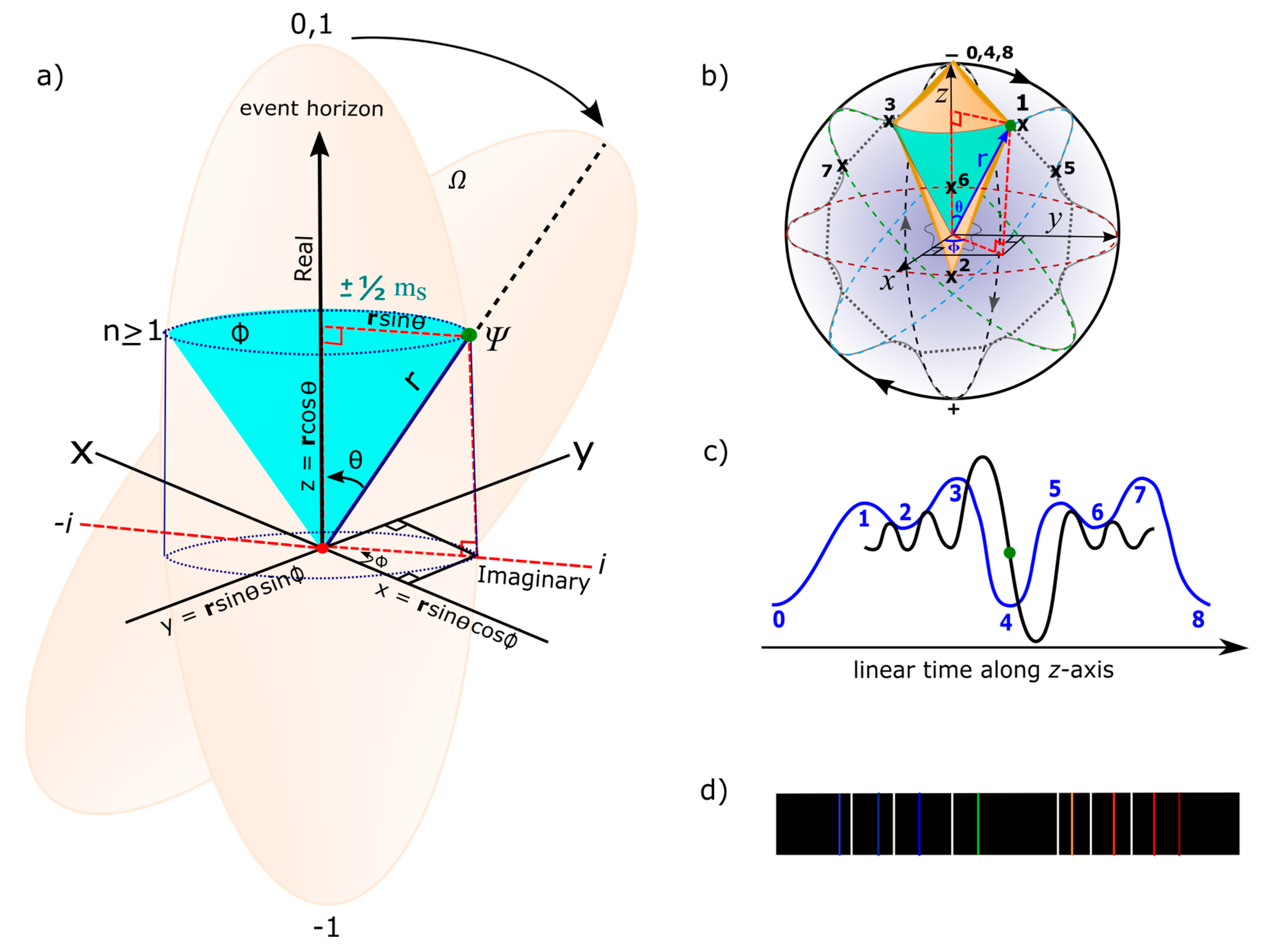
The two interchangeable hemispheres of the MP field of ±1/2 spin-charge by clockwise precession adheres to Pauli exclusion principle and these accommodate the electron shift in positions 0 → 8 by the process of DBT of continuity at spherical lightspeed. Time reversal for the emergence of antimatter is assumed by clockwise precession in accordance with 2^nd law of thermodynamics. Entanglement by von Neumann entropy for the polarization states of qubits, 0, 1 and hypercharge –1 (for z-axis mimicking nuclear isospin) at the vertex of the MP field for COM reference frame somehow upholds the holographic principle. Its translation to Shannon entropy is by light-MP model coupling with unitarity by Euler’s formula, $e^{i π}$ + 1 = 0 in real space sustained.
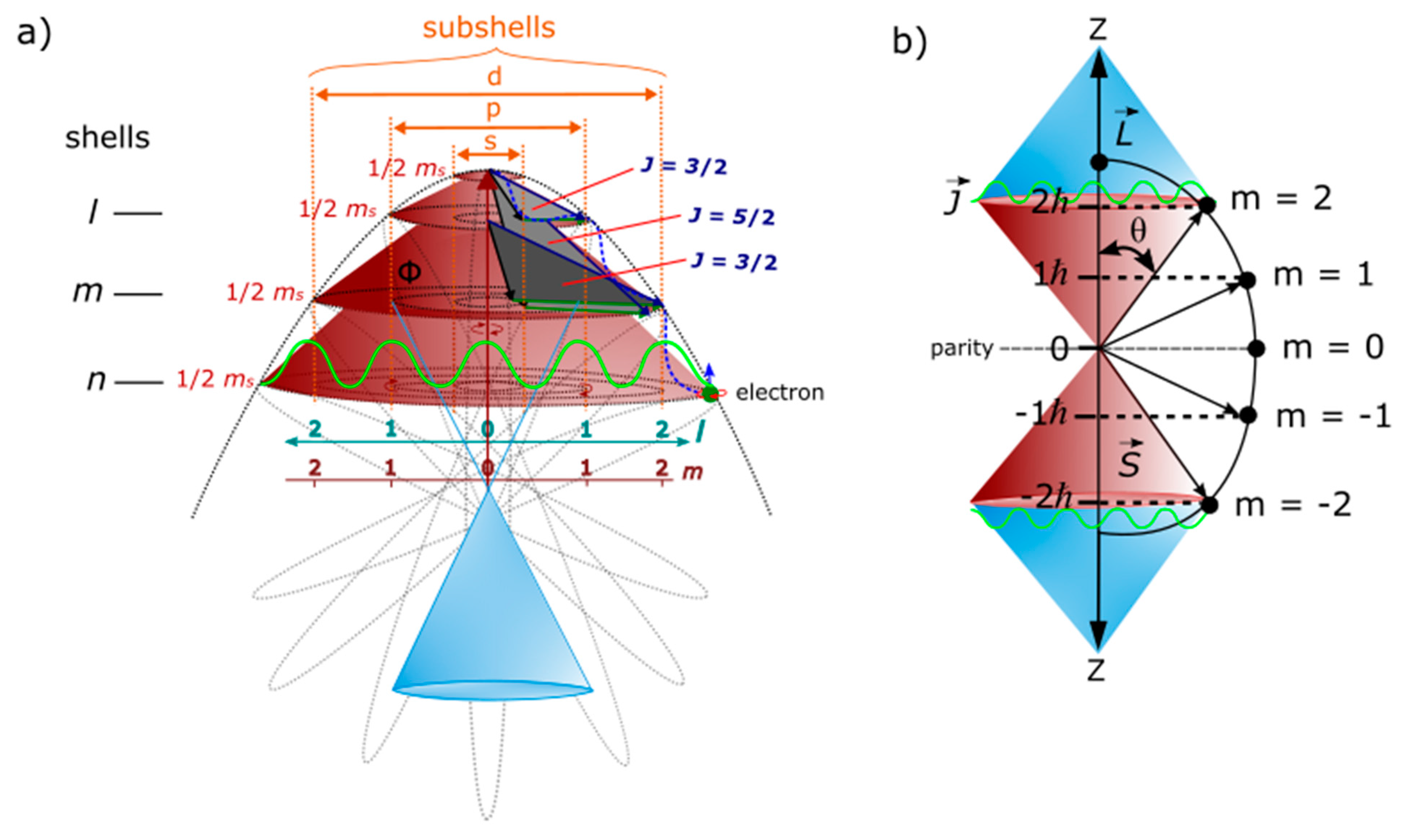
The electron at the vertex of the MP field at position 0 mimics monopole instanton (MI). It offers the base point for transmission of vortex electron through a helical solenoid which intersects topological torus of BO at n-dimensions by levitation between two hemispheres of the MP field. The base point presents COM reference frame from the electron-positron transition with time reversal orbit of the electron balanced out by clockwise precession in accordance with Newton’s second law of motion. The COM is about Planck length ~ 1.62 x 10^-35 meters) is aligned to the principal axis or z-axis of the MP field as nuclear isospin (about 1.1 angstroms for the hydrogen atom) and it depicts arrow of time in asymmetry. Infinitesimal radiation of Planck constant, $ℏ$ is assumed from twisting and unfolding process of the electron-positron transition by DBT at COM. It can cater for ZPE of the hydrogen atom at ultraviolet range in a potential well of a harmonic oscillator, $E_{v} = \frac{1}{2} ℏ ω$ for the value of -13.60 electronvolts.
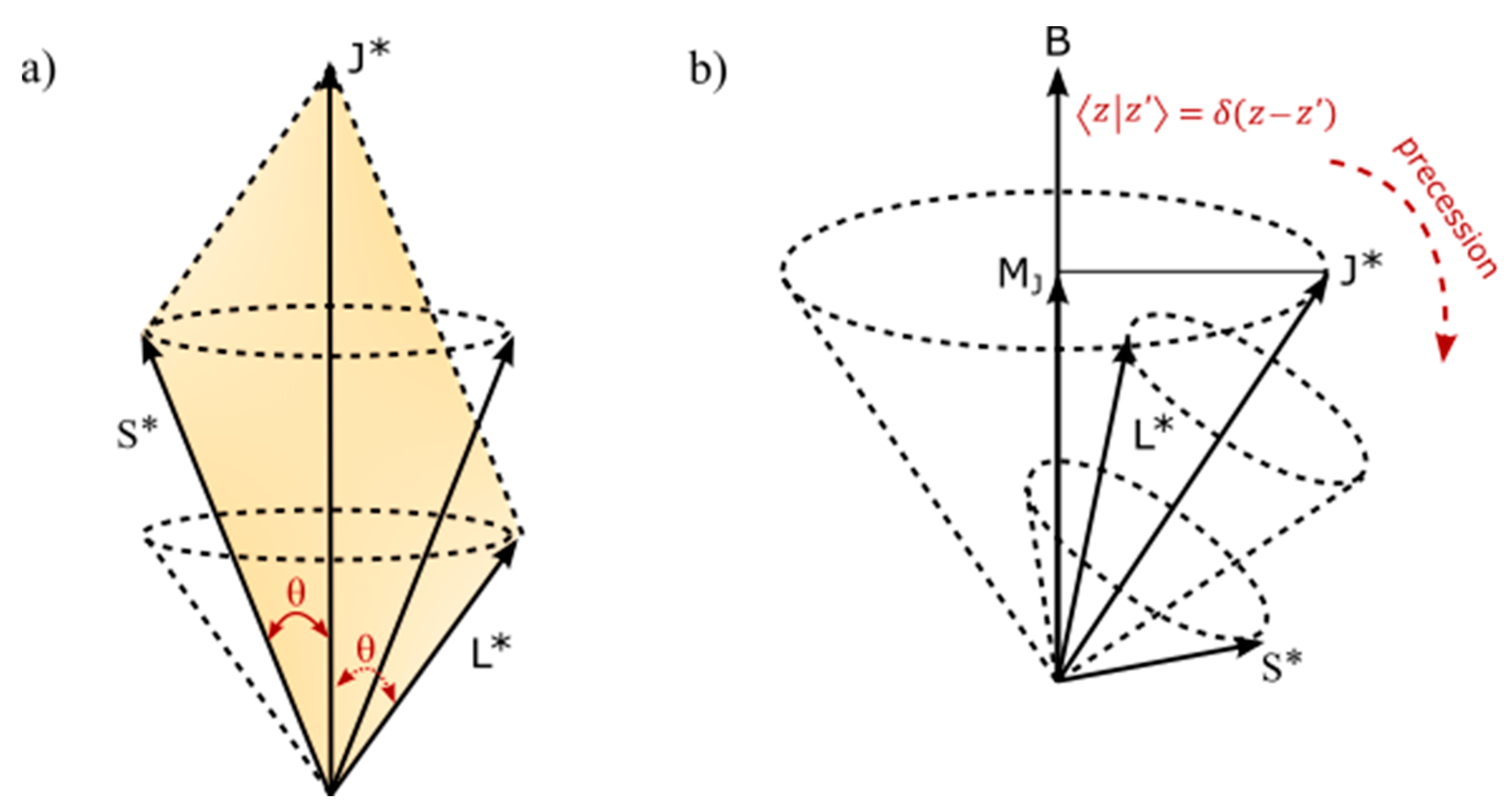
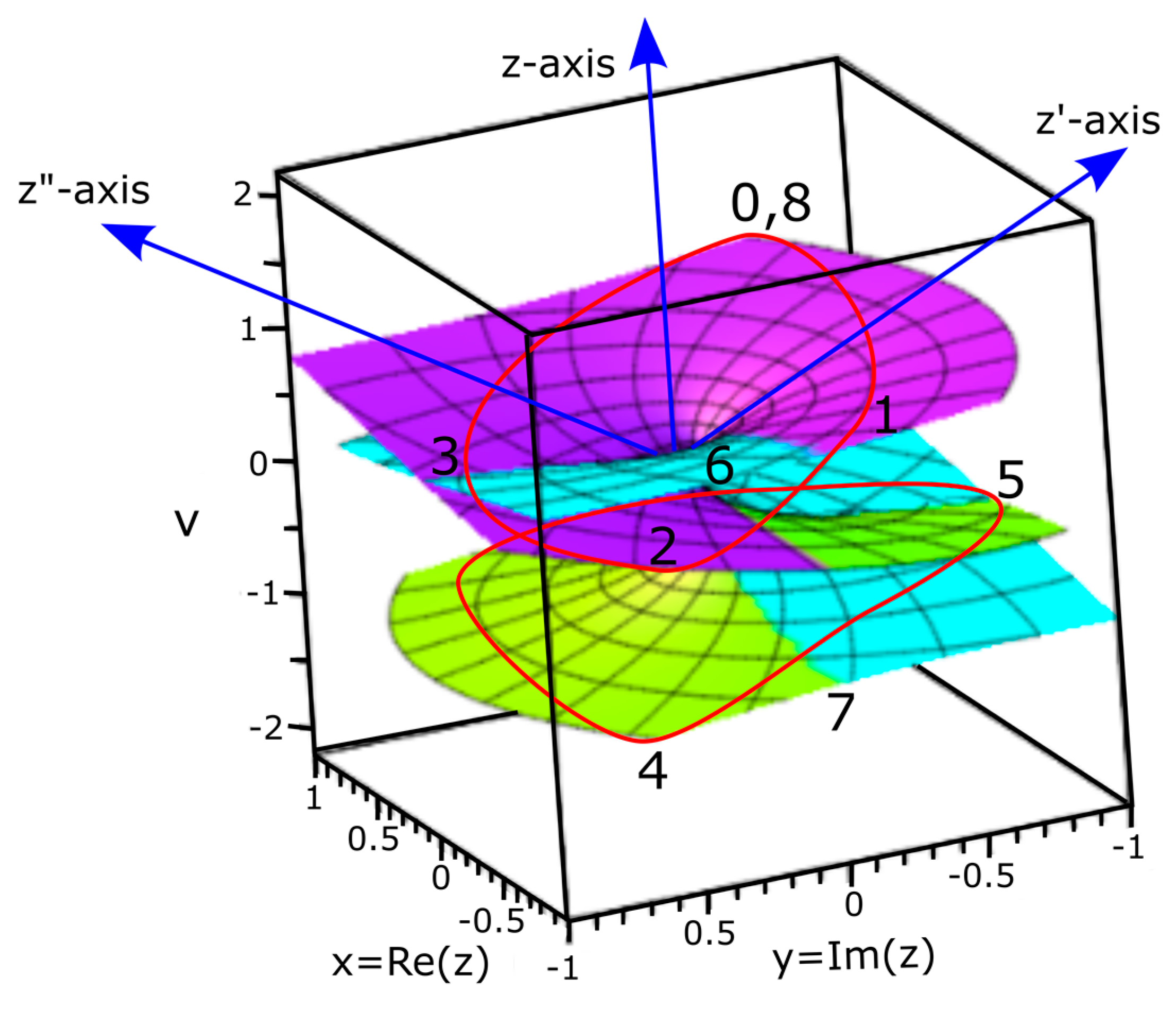
In flat Euclidean space-time of inertia frame (Figure 1a), any deviation from z-axis of the MP field by precession is trivial, $δ (z - z^{'}) = ⟨z| z'⟩$ (Figure 1d) and time remains absolute from a background of clock face with distances between any two points being positive and COM is assigned to point-boundary at position 0 as mentioned above. The electron position in space within the model is defined by the Cartesian coordinates, x, y, z. At positions 1 and 3 or 5 and 7, electron-positron transition of superposition states obey Born’s rule, ${|ψ|}^{2}$ and acquires spin angular momentum to mimic Weyl spinor of Minkowski space-time (Figure 1b). Hyperbolic surface of the light-cone of holonomic is contained within hypersurface of the MP field of Euclidean space towards position 0 of ZPE at N-1. Balancing out of charges at homomorphic positions 1, 3 and 5, 7 is isomorphic to compact topological torus of BO. By clockwise precession, time is relative, i.e., $z - z^{'} \equiv c t - c t^{'} = {t a n}^{- 1} v / c = α$ with $α = θ$ (Figure 1c). By Lorentz transformation in 1D for accelerated reference frame, the volume or dipole moment of the MP field remains constant so, $t^{'} = γ (t - v x / c^{2})$ and $x^{'} = γ (x - v t / c^{2})$ with Lorentz factor, $γ = 1 / (\sqrt{1 - v^{2} / c^{2}})$ and $y^{'} = y$ and $z^{'} = z$ . Its invariance, $t = γ (t' - v x' / c^{2})$ and $x = γ (x' - v t' / c^{2})$ sustains the unitarity of the model. Observation by light-MP model coupling is confined to the electron and its motion and this can relate to Lorentz transformation with any outgoing radiation being of linear time. In this way, 4D Minkowski space-time (Figure 1b) is applicable to multidimension of Euclidean space-time (Figure 1a) with COM by Newtonian gravity assigned to position 0 as mentioned above.
Singularity towards the nucleus is constrained by the dipole moment of the MP field to generate an irreducible spinor. Stochastic behavior from the emergence of envelop solitons at positons 2 and 6 insinuates a chaotic system. Combined with the quantum critical region of the light-cones at positions 1 and 3, the quest towards quantum critical point at the baseline of the hemisphere remains elusive by quantum chaos of butterfly effect for the hydrogen atom (e.g., Figure 1a). Such intuition is important in the pursuit of quantum critical point in condensed matter physics for an array of atoms in one-dimensional line.
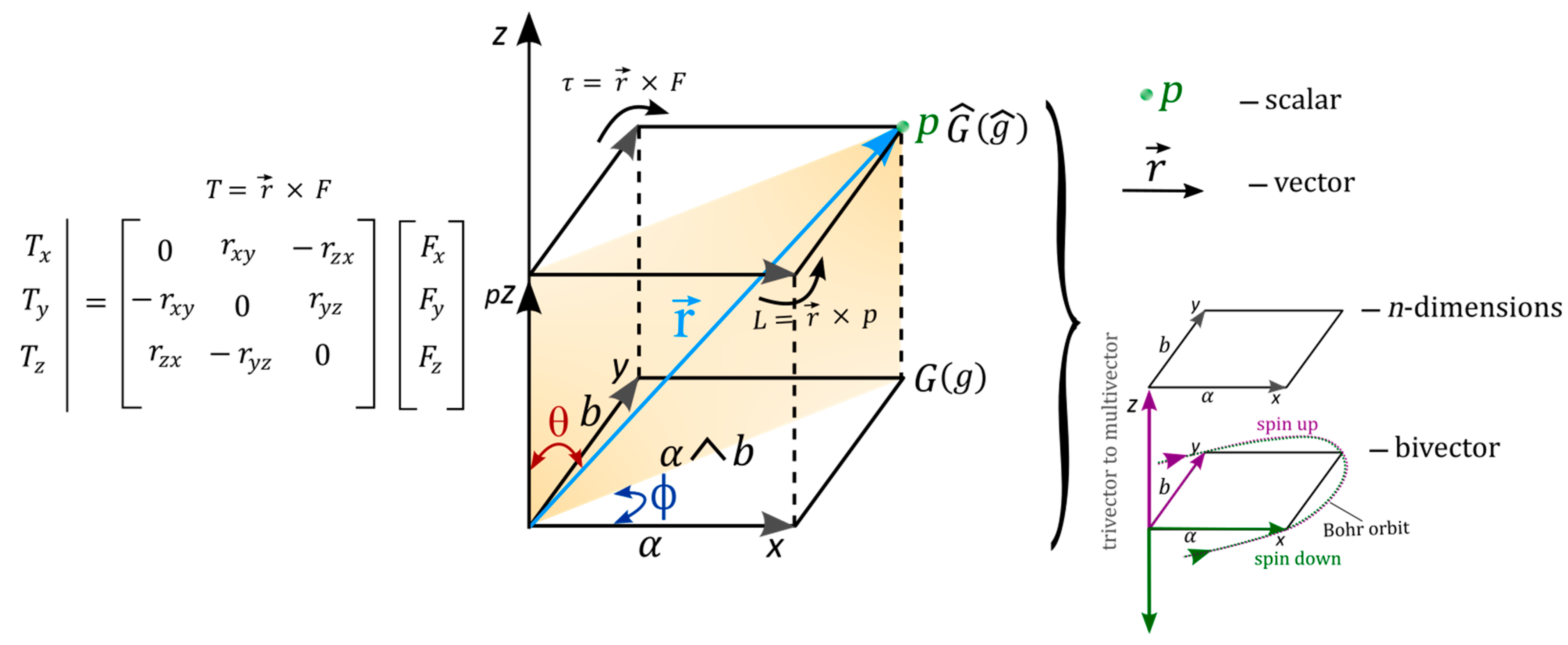
The electron is a point-particle at constant motion, mv acquires $J_{z}$ and further offers wave-particle duality for the overall spherical reference frame, $λ = h / m v$ in accordance with de Broglie relationship. In this case, ±h is assigned to the electron-positron transition of a sinusoidal orbital. The electron is defined by the wave function, $ψ$ and its orbit of time reversal by time derivative is accorded to Schrödinger equation, $i ℏ \frac{\partial}{\partial t} (ψ (\vec{r}) θ (t))$ . It is a fundamental equation with the basis vector, $\vec{r}$ and $θ$ assumed into Minkowski space-time (Figure 1c) against z-axis as time axis and x-axis equal to distance.
The electron’s spin-charge of superposition states is linked to BO of topological torus defined by $ϕ$ and this is projected in the x-y plane (Figure 1c). Its inner product, ${⟨ψ| ϕ⟩}^{*} = ⟨ψ| ϕ⟩$ sustains unitarity for the electron of weak isospin into n-dimensions of topological torus by disturbance (Figure 1d). The electron’s position can be split into both radial and angular wave functions, $ψ (r, θ, ϕ) = R_{n, l} (r) Y_{l}^{m_{l}} (θ, ϕ)$ . The radial part, $R_{n, l}$ is attributed to the principal quantum number, n and angular momentum, l of a light-cone with respect to r (Figure 1c). The angular part, $Y_{l}^{m_{l}}$ of degenerate states, ${\pm m}_{l}$ is assigned to the BO defined by both $θ$ and $ϕ$ (Figure 1d).
The BO of a constant structure, ɑ is orthogonal to z-axis by linearization (Figure 1d). Its tangential link to electron-positron pair of anticommutation is, $⟨a_{j}| a_{k}⟩ = \int d x ψ_{a_{j}}^{*} (x) ψ_{a_{k}} (x) = δ_{j k}$ for continuous derivation of MP field due to clockwise precession. Linear translation of n-dimensions or n-levels by Fourier transform is by the generalized state, $E = n h v$ and this is standardized to the z-axis. By continuity, the sum of expansion coefficients, $C_{n}$ , from the electron’s position offers the expectant value, $|ψ⟩ = \sum_{n} C_{n} / a_{n}⟩$ with its probability given as, ${⟨a_{n}| ψ⟩}^{2}$ .

The list is not exhausted and these can be explored in many facets of physics in both low and high energy regimes. The limitations are that the electron is considered to be a physical entity of a spherical MP model in orbit of perpetual motion balanced out by clockwise precession. In the subsequent sections, the compatibility of the model to QM, QFT and general relativity on a geometry basis are explored to pave the path for further researches by conventional methods.

III. Relevance of quantum mechanics on the MP model

The attributes of QM related to the MP model is dissected into three parts. First, its non-relativistic aspect is presented ensued by its translation at observations with respect to wave function collapse and quantized Hamiltonian. These are relevant towards demonstrating the transition of non-relativistic MP model described by the electron towards relativistic QFT related to the fermion. There a numerous literatures available for QM and for this undertaking only a few ref. [3,24,25,26,27,28,29] are selected.

A. Non-relativistic wave function

The difference of classical oscillator to the quantum scale is the application of Schrödinger wave equation (e.g., Figure 1c) and it forms the basis for QM. This satisfactory accounts for the probability distribution of the electrons within the atom. However, QM cannot account for the combination of orbital angular momenta, spin angular momenta and magnetic moments of valence electrons observed in atomic spectra [24]. Thus, light-MP model coupling is needed to explain the emergence of energy shells of BOs at the n-levels by levitation between the hemispheres and this can possibly accommodate complex fermions of ±1/2, ±3/2, ±5/2 and so forth (Figure 2a). By Russell-Saunders orbital-spin (L-S) coupling with Clebsch-Gordon series, the eigenvalue of total angular momentum,

\vec{J} = \vec{l} + \vec{s}

for orbitals in 3D combines eigenvalues of both orbital angular momentum, l and spin angular momentum, s (Figure 2b). Complete rotation

towards the point-boundary by the process of DBT at 720° rotation equates to 2π with the positron-electron transition related to h. The magnitude of l by precession then takes the form,

|l| = \sqrt{l_{i} (l_{i} + 1)} ℏ, (11 a)

where i is equal to subshells (Figure 2a). For n = 2 is split into s and p orbitals with each one accommodating ±1/2 spin from the electron-positron transition at spherical lightspeed (Figure 1a) in accordance with Pauli exclusion principle. The total angular momentum,

\vec{J} = l \pm \frac{1}{2}

, equates to

\frac{3}{2}

and

\frac{1}{2}

at n = 2, l = 1. Comparably, the summation of spin, 1/2 + 1/2 + 1/2 from combined s and p subshells of

n_{2}

+

n_{1}

=

\frac{3}{2}

, when both orbital and spin angular momenta are aligned in the same direction (Figure 2b), and this also provides the resultant spin angular momentum, S. When orbital and spin are not aligned at low energy, then

n_{2} -

n_{1}

=

\frac{1}{2}

in the form, 1/2 +1/2 −1/2. This is assigned to p orbital by cancelling out 1s orbital while the orientation such as dumbbell shape can be attributed to levitation into n-dimensions between two hemispheres and by subjecting this to DBT. The resultant orbital angular momentum L from the combination of

\sum l_{i}

in a complete loop of BO at n-dimension by amalgamation of degenerate states is,

|L| = \sqrt{L_{n} (L_{n} + 1)} ℏ, (11 b)

where the values of 0,

\sqrt{2} ℏ

and

\sqrt{6} ℏ

are respectively generated at n = 0, n =1 and n = 2. Their projection along z-axis for the irreducible MP field is of the form,

|L_{Z}| = M_{L} ℏ . (11 c)

Equation (11c) is applicable to levitation of the light-cone of Minkowski space-time (Figure 3a), where its precession in the presence of applied external magnetic field corresponds to hyperbolic surface (Figure 3b). Comparable to Equation (11c), the magnitude of

\vec{J}

along the z-axis of the MP

field is of the form,

J_{Z} = m_{l} ℏ, (12 a)

where

m_{l}

can take (2l + 1) values as eigenfunciton of

M_{L}

. Both S and L combine to generate J (Figure 3b) in the form,

J = L + S . (12 b)

The distinction of these parameters is offered in Figure 3b with orientations by precession referenced to

M_{j}

and these are necessary for quantization of space. These explanations can relate to Zeeman effect for fermions of odd spin types,

\frac{1}{2}, \frac{3}{2}, \frac{5}{2}

and possibly apply to lamb shift for COM of ZPE assigned to position 0 (Figure 1a). Similarly,

\pm \vec{J}

splitting for Landé interval rule for on-shell momentum of weak isospin is assigned to BO at the n-levels of the two hemispheres of MP model (e.g., Figure 2b).

B. Wave function collapse

Dirac fermion of a complex four-component spinor is denoted ψ(x) in 3D Euclidean space (Figure 1a) with time aligned to z-axis of the MP field so any variation in it becomes trivial,

(z - z^{'}) = ⟨z| z'⟩

in flat space. The distance between two events such as at position 1 and 3 in space is positive of the form [25],

{d s}^{2} = {d x}^{2} + {d y}^{2} + {d z}^{2} = {(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2} . (13)

In Equation (13), changes in time appears trivial and is hidden among any of the axes applied as the vertical axis. Once the electron gains spin angular momentum by the process of DBT, the Euclidean space-time is transformed into 4D Minkowski space-time, ψ(x,t) (Figure 1b). The hyperbolic space of the light-cone for both the inertia reference frame (position 0) and accelerated reference frame (at the vertices of the MP field at clockwise precession other than position 0), is subjected to Lorentz transformation of time invariance such as [25],

{d s}^{2} = {d x}^{2} + {d y}^{2} + {d z}^{2} - {c t}^{2} . (14)

Both Equations (13) and (14) appear independent of both an internal observer stationed at the nucleus and external observations for the measurement of electron probability distribution. The emergence of the pair of light-cones coincides with Minkowski space-time (Figure 1b) and these are dissected by z-axis as arrow of time into asymmetry. Both positive and negative curvatures of non-Euclidean space are normalized to straight paths of Euclidean space (Figure 4a). It is important to note that while the electron position is non-abelian, its transition to induce a dipole moment allows for the transformation of hyperbolic space to compact topological torus into extra dimensions by levitation between the two hemispheres of the MP field as demonstrated in Figure 4a. In this case, the Dirac four-component spinor,

ψ = (\binom{ψ_{0}}{\begin{matrix} ψ_{1} \\ \binom{ψ_{2}}{ψ_{3}} \end{matrix}})

is attributed to positions 0 to 3 of 3D space in repetition rather than to negative energy of antimatter of spin-up and spin-down as implied in Equation (4). Convergence of positions 1 and 3 at either position 0 at the point-boundary or towards the nucleus of time infinite is relevant to the equivalence principle for Euclidean space superimposed on the surface of the spherical MP model mimicking Poincaré sphere (Figure 4b). In this case, the quantum aspect of de Sitter space by geodetic clockwise

precession is balanced out by anti-de Sitter form of the electron transition in its orbit of time reversal for COM assigned to the point-boundary at position 0. Light-MP model coupling is expected for linear light paths tangential to BOs at n-energy levels due to balancing out of charges, where the hyperbolic surfaces are transformed into compact topological torus (Figure 1d). These are expected to translate to Fourier transform along z-axis of the MP field as time axis by wave function collapse (Figure 4c). Constraining the electron’s position insinuates the uncertainty principle with on-shell momentum of BO susceptible to levitation between the two hemispheres of the MP model. The generated wave amplitudes from the electron shift in position and its location in real-time can somehow mimic a typical hydrogen emission spectrum (Figure 4d).

C. Quantized Hamiltonian

Two ansatzes adapted from Equation (3) are given by,

ψ = u (p) e^{- i p . x}, (15 a)

and

ψ = v (p) e^{i p . x}, (15 b)

where outward projection of electron spin is

v

and inward projection is

u

. Equations 15(a) and 15(b) relates to oscillations between the two hemispheres of the MP field from the electron-positron transition. Linear transformation along z-axis of the MP field as time axis in asymmetry can accommodate the Hermitian plane wave solutions and this forms the basis for Fourier components in 3D space (Figure 4c). Decomposition for quantized Hamiltonian becomes [26],

ψ (x) = \frac{1}{{(2 π)}^{3 / 2}} \int \frac{d^{3}}{2 E_{p}} \sum_{s} (a_{P}^{s} u^{s} (p) e^{- i p . x} + b_{P}^{s †} v^{s} (p) e^{i p . x}), (16 a)

where the constant,

\frac{1}{{(2 π)}^{3 / 2}}

is attributed to dissection of BOs between two hemispheres along z-axis. Its conjugate is,

\bar{ψ} (x) = \frac{1}{{(2 π)}^{3 / 2}} \int \frac{d^{3}}{2 E_{p}} \sum_{s} (a_{P}^{s †} {\bar{u}}^{s} (p) e^{i p . x} + {b_{P}^{s} \bar{v}}^{s} (p) e^{- i p . x}) . (16 b)

The coefficients

a_{P}^{s}

and

a_{P}^{s †}

are ladder operators for u-type spinor and

b_{P}^{s}

and

b_{P}^{s †}

for v-type spinor. These are attributed to n-dimensions of BOs mimicking topological torus by levitation between the two hemispheres of the MP model (e.g., Figure 1d). The Dirac spinors of two spin states, ±1/2 with

{\bar{v}}^{s}

and

{\bar{u}}^{s}

as their antiparticles is reflected by clockwise precession of IM at the vertices of the MP field. Dirac Hamiltonian of one-particle for the MP model of hydrogen atom type is [27],

H = \int d^{3} x ψ^{†} (x) [- i \nabla . α + m β] ψ (x), (17)

where the electron, i acquires vectors of momentum,

\nabla

with shift in its position and gamma matrices represented by the standard Pauli matrices,

α

,

β

. Parity transformation by levitation between the hemispheres provide both observable and holographic oscillators of canonical conjugates. The associated momentum is,

π = \frac{\partial L}{\partial ψ} - \bar{ψ} i γ^{0} = i ψ^{†} . (18)

For the time axis along z-axis of the MP field, V-A currents are projected in either x or y directions in 3D space analogous to Fourier transform (e.g., Figure 4c). The projections are of the relationship [28],

[ψ_{α} (x, t), ψ_{β} (y, t)] = [ψ_{α}^{†} (x, t), ψ_{β}^{†} (y, t)] = 0 . (19 a)

Equation (19a) by unitarity is attained at position 0 at the point-boundary. Because the electron of a physical entity is non-abelian (Figure 1a), the matrix form for anticommutation is,

[ψ_{α} (x, t), ψ_{β}^{†} (y, t)] = δ_{α β} δ^{3} (x - y), (19 b)

where α and β denote the spinor components of

ψ

. In 3D space independent of time, electron’s position, p and momentum, q, of conjugate operators commute by,

\{a_{P}^{r}, a_{q}^{s †}\} = \{b_{p}^{r}, b_{q}^{s †}\} = {(2 π)}^{3} δ^{r s} δ^{3} (p - q) . (20)

Equation (20) relates the uncertainty principle to the MP model, where the electron pops in and out of existence at spherical lightspeed with observations of real particles applicable at positions 1 and 3. The hemisphere devoid of the electron is interchangeable with its counterpart so that only positive-frequency is generated such as [29],

⟨0| ψ (x) \bar{ψ} (y)| 0⟩ = ⟨0 │ \int \frac{d^{3} p}{{(2 π)}^{3}} \frac{1}{\sqrt{{2 E}_{p}}} \sum_{r} a_{p}^{r} u^{r} (p) e^{- i p x}

\times \int \frac{d^{3} q}{{(2 π)}^{3}} \frac{1}{\sqrt{{2 E}_{q}}} \sum_{s} a_{q}^{s †} {\bar{u}}^{s} (q) e^{i q y} │ 0⟩ . (21)

Equation (21) implies to the dominance of matter over antimatter with the spinor,

ψ_{0 ⟶ 3}

attributed to the electron shift in positions. In this way, both antimatter and matter are combined by clockwise precession into forward time for the interchangeable hemispheres of the MP field.

IV. Relevance of quantum field theory on the MP model

Extending from the preceding section on QM, this section explores the relevance of QFT on space-time geometry of the MP model by examining some of its components like Dirac spinors, Weyl spinors and Marjorana fermions plus Lorentz transformation based on ref. [3,6,28,29]. These are succinctly plotted to pave the path for future researches which can also extend to other related components.

A. Dirac spinors

The helical property of the electron within the MP model towards the generation of Dirac fermion by the process of DBT is expounded in here. The elliptical MP field of Dirac’s string is warped and unwarped by twisting and unfolding process (Figure 5a and 5b). As a result, the electron-positron transition is restricted to a pair of interchangeable hemispheres (Figure 5c and 5d). At spherical lightspeed, these combine to generate an irreducible spinor (Figure 5e) and this is applicable to a spherical geometry (Figure 5f) incorporating Euler’s formula for hyperbolic and parabolic complex number with respect to the electron’s position about BO in orbit. Components of Pauli matrices,

i, 0, - 1, 1

are distinct from those of Dirac matrices,

ψ_{0 \to 3}

. The latter is depended on the shift in the electron’s position, 0 → 3 for the transition to positron by DBT. In the former, the matrices are [6] traceless, Hermitian and of unitarity with determinant –1 and satisfy the relations

\sum_{j} {\hat{e}}_{j} {\hat{e}}_{j}^{T} = [e_{i} e_{j}] = c_{i j}^{k} e_{k}

with

c_{i j}^{k}

is expansion coefficients at angular frequency,

ω^{2} = k / m

for the electron of a body-mass in continuous oscillation mode. The unit matrices,

{\hat{e}}_{k}

is applied to the electron-positron pair,

i

and

j

is the angular momentum along BO

(Figure 5f) at positions 1 and 3. Anti-commutation and its square for the electron-positron transition offers the identity matrix,

σ_{0} \equiv I

and is relevant to Clifford multiplication. These provide orthonormal basis like,

{\hat{e}}_{i}, {\hat{e}}_{j}

for the vector space of Clifford algebra as described in Equations (5 to 7). In this case, breaking of CPT symmetry in discrete form for charge-parity emanates from the chirality of the electron in a hemisphere versus the devoid hemisphere. Time reversal symmetry is sustained for electron-positron transition at spherical lightspeed. These properties are revealed by light-matter coupling and are incorporated into Dirac equation of the extended form, coupling, this can be described by the famous Dirac equation,

(i γ^{0} \frac{\partial}{\partial t} + c A \frac{\partial}{\partial x} + c B \frac{\partial}{\partial y} + c C \frac{\partial}{\partial z} - \frac{{m c}^{2}}{ℏ}) ψ (t, \vec{x}), (22)

where c acts on the coefficients A, B and C and transforms them to

γ^{1} {, γ}^{2}

and

γ^{3}

. The exponentials of

γ

are denoted i for off-diagonal Pauli matrix for the light-cone of irreducible spinor and

γ^{0}

to 0, 1 polarization states at position 0 of COM reference frame. These are demonstrated in Equation (7). Hypercharge, –1 is expected at position 4 along z-axis as nuclear isospin and

σ^{i}

can relate to oscillations from on-shell momentum of BOs of topological torus into n-dimensions (Figure 2a) with anticommutation relationship,

e^{+} (ψ) \neq e^{-} (\bar{ψ})

of chiral symmetry. The associated vector gauge invariance for the electron-positron transition in continuum form exhibits the following relationships,

ψ_{L} \to e^{i θ L} ψ_{L}

(23a)

and

ψ_{R} \to e^{i θ L} ψ_{R}

. (23b)

The exponential factor, iθ refers to the position, i of the electron of a complex number and θ, is its angular momentum (Figure 4a). The unitary rotations of right-handedness (R) or positive helicity and left-handedness (L) or negative helicity are applicable to the electron transformation to Dirac fermion (Figure 5c and 5d). The process is confined to a hemisphere and it is interchangeable with its counterpart to generate spin ±1/2. The helical symmetry from projections operators resembles nuclear isospin of z-axis acting on the spinors and is established by the following relationships,

P_{L} = \frac{1}{2} (1 - γ_{5}) (24 a)

and

P_{R} = \frac{1}{2} (1 - γ_{5}), (24 b)

where

γ_{5}

relates to I matrices (Equation (7)) based on the electron shift in positions 0

\to

3 in repetition. The chirality of the electron and its shift in position of helical solenoid further attest to the dynamics of the MP model. In addition, the usual properties of projection operators like: L + R = 1; RL = LR = 0; L² = L and R² = R are relatable to the interchangeable hemispheres accommodating the electron shift in its position and these can be explored within the geometry of the model.

B. Weyl spinors and Majorana fermions

In condensed matter physics, Dirac fermion can be converted to Weyl spinor and possibly to Marjorana fermion of a natural neutrino type. Usually, these are pursued for an array of atoms in lattice structure and it is difficult to examine them for individual atoms. Theoretically, how this is applicable to the Dirac fermion incorporated within the MP model of the hydrogen atom type is examined in here. Acquisition of angular momentum by the electron shift in position is related to the pair of light-cones (Figure 1b). The process is linked to DBT associated with the electron-positron transition within a hemisphere of the MP field of parity violation to the other hemisphere (Figure 5c and 5d). The four-component spinor demonstrated in Equation (4) is reduced to the two-component bispinor of the form,

ψ = (\begin{matrix} \begin{matrix} ψ_{0} \\ ψ_{1} \\ ψ_{2} \end{matrix} \\ ψ_{3} \end{matrix}) = (\begin{matrix} u_{+} \\ u_{-} \end{matrix}), (25)

where

u_{\pm}

are Weyl spinors of chirality assigned to the pair of light-cones (e.g., Figure 1b). Because only spin up and spin down fermions are observed in experiments, i.e.,

ψ_{0}

,

ψ_{1}

then the antifermions of spin up and spin down,

ψ_{2}

and

ψ_{3}

are ruled out. Instead, creation and annihilation of virtual particles are attributed to the vertices of the MP field by clockwise precession to generate instanton magnetic monopoles. In this case,

ψ_{0 ⟶ 3}

is attributed to the electron shift in position from 0

⟶ 3

as mentioned earlier to generate the four-component spin (e.g., Figure 1a). By the process of DBT, the exchanges of left- and right-handed Weyl spinor between the pair of hemispheres of the MP field assumed the process,

(\begin{matrix} ψ_{L}^{'} \\ ψ_{R}^{'} \end{matrix}) = (\begin{matrix} ψ_{R} (x) \\ ψ_{L} (x) \end{matrix}) \Rightarrow \begin{matrix} ψ^{'} (x^{'}) = γ^{0} ψ (x) \\ {\bar{ψ}}^{'} (x^{'}) = \bar{ψ} (x) γ^{0} . \end{matrix} (26)

Equation (26) conserves local symmetry and the correspondence global symmetry by continuity of clockwise precession. Because the electron forms its own antimatter, it is difficult to extract each individual component, other than to observe them collectively in experiments. In its orbit confined to a hemisphere, the electron levitates between the hemispheres by clockwise precession of the MP field. It is also important to noted that the electron-positron transition,

ψ_{0 ⟶ 3}

in repetition generates own antimatter at these positions. So Dirac fermion becomes Majorana fermions with toroidal moments of topological torus by clockwise precession of the MP field. The moduli of vertices are accorded to creation and annihilation operators

γ (E), γ^{†} (E)

. The Fermi level

γ (0) \equiv γ = γ^{†}

is assigned to position 0 of ZPE at the point-boundary of the spherical MP model so particle and antiparticle change charges by undergoing twisting and unfolding process of DBT. The generated anticommutation relation for the Majorana is of the form [31],

γ_{n} γ_{m} + γ_{m} γ_{n} = {2 δ}_{n m} . (27)

The product of Equation (27),

γ_{n}^{2} = 1

is assumed at the potential well and the value can equate to a bosonic field of qubit 1. Qubit 0 is also expected at position 0 at the initiation of the process of DBT with increase in n-levels of BO in degeneracy forming canonical ensemble towards infinity along the horizontal axis dissecting the nucleus. Majorana fermion analog of Dirac fermion or the electron is non-abelian based on Equation (27) and it assumes the valence state at position 0. Its displacement akin to quantum tunneling offers particle-hole symmetry for conservation of the model. The ejected fermion is promoted to the conductance band. If Majorana fermion naturally resemble neutrino, the potential well of ZPE assigned to COM exerts gravitational force and there is no barrier to the passage of neutrinos. Whether this can also apply to the electrons poses an interesting prospect for condensed matter physics dealing with semi-conductors to superconductors for an array of atoms in dimensional lines.

C. Lorentz transformation

The Hermitian pair,

ψ^{†} ψ

for the electron-positron transition at the vertex of the MP field in modulus space undergo Lorentz boost in the form,

u^{†} u = (ξ^{†} \sqrt{p . σ,} ξ \sqrt{p . \bar{σ}} . (\begin{matrix} \sqrt{p . σ} ξ \\ \sqrt{p . \bar{σ}} ξ \end{matrix}), = 2 E_{P} ξ^{†} ξ . (28)

Conversion of Weyl spinors to Dirac bispinor,

ξ^{1}

ξ^{2}

are of transposition state (e.g., Figure 5c and 5d). The two-component spinor,

ξ^{1}

ξ^{2}

= 1 are normalized to the point-boundary at position 0 of the spherical model similar to Equation (27). The corresponding Lorentz scalar applicable to scattering from on-shell momentum tangential to the BOs (Figure 1d) is,

\bar{u} (p) = u^{†} (p) γ^{0} . (29)

Equation (29) is referenced to z-axis of the MP field as time axis and is relevant to Fourier transform into linear time (see also subsection IIIc). By identical calculation to Equation (29), the Weyl spinors are of chirality due to the electron presence (Figure 1b) are given by,

\bar{u} u = 2 m ξ^{†} ξ . (30)

Equation (30) is applicable to time and distance aligned respectively to the z-axis of the MP field and perpendicular distance along x-axis. By acceleration, light-matter coupling at distance, r with an angle,

θ

(Figure 1c) of infinite n-dimensions is curved towards one dimension setting of

n_{\infty} =

ε_{0} = c = ℏ = 1

about the horizontal plane at positions 2 and 6. This generates particle property, where Weyl spinor of a light-cone (Figure 2a) and Majorana fermion becomes indistinguishable to Dirac spinor.

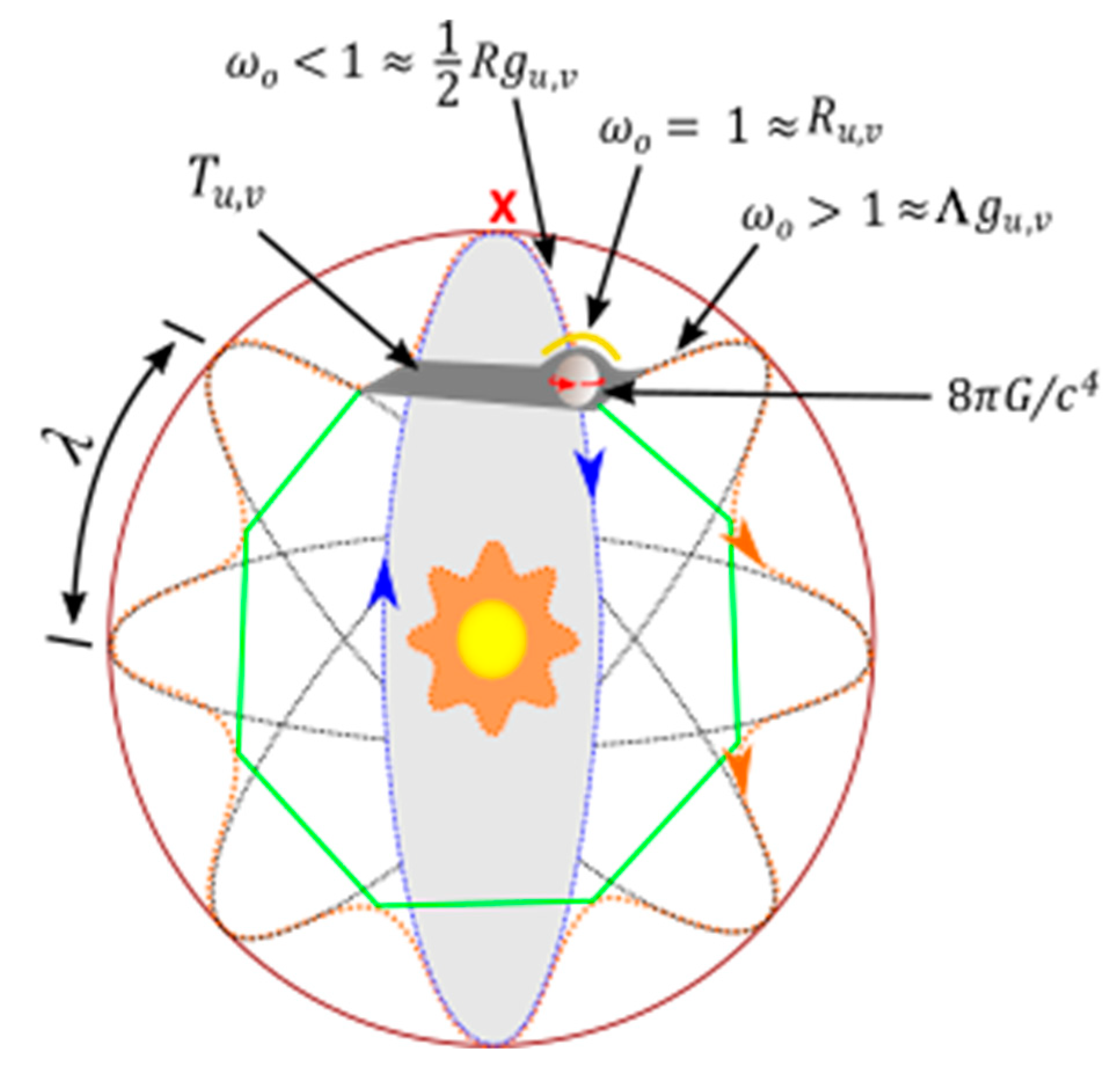
V. Space-time geometry of the MP model

General relativity portrays the framework of space-time fabric in 3D flat Euclidean space. It is bend by the gravitational force of an object in orbit. However, such geometry of space-time is not realistic to merge with singularity, where field equations describing space-time and matter becomes infinite. How a proper space-time fabric should apply to an elliptical orbit is considered first before examining its relevance to Lie group, 2D manifolds into 4D space-time and space-time curvature. These are demonstrations are important to show the possible link of general relativity to high energy physics and condensed matter physics and how all these can be incorporated by both QM and QFT on a geometry basis.

A. Space-time fabric of an elliptical orbit

The framework of space-time fabric in an elliptical orbit is warped and unwarped for a pair of interchangeable light-cones akin to traversable wormholes and is intersected on a path of vortex electron of helical solenoid resembling Riemann surface (Figure 6). The description mimics how DBT is interwoven into the spherical MP model (see section II). Translation of t, x, y, z Cartesian

coordinates to spherical polar coordinates is,

δ (z - z^{'}) = c t

,

r, θ,

ϕ and this resembles Euclidean space-time transition to Minkowksi space-time (Figure 1a and 1b). In the former, clock face background is envisioned in flat space of n-dimensions

\geq 1

akin to Bohr model of the atom with distance between any two points being positive. In the latter, space-time is dynamic and a body-mass at a distance, r of n-dimension attains angular momentum,

θ

with respect to z-axis of the MP field as time axis. Its associated spin, ϕ is referenced to BO. Projection of the basis vector, r and

θ

for time-distance relationship along x-y plane is referenced to z- and x-axes (Figure 7). The plane wave solution,

e^{r θ} = c o s θ + r s i n θ

incorporates positions 1 and 3 for the emergence of real particles with spin angular momentum is translated along z-axis of continuum form with the electron popping in and out of existence by the process of DBT (Figure 1a). Access to singularity at the nucleus is constrained by the irreducible spinor of a dipole moment and the same is assumed either for the sun in the solar system or a black hole. The transition from flat Euclidean space-time to Minkowski space-time resembles Riemann surface and this incorporates both Ricci scalar and Ricci tensor. The magnetic field of helical solenoid is,

B = μ N (γ^{u} \partial_{u}) I {(ε}_{0}) L, (31)

where

μ

is permeability of space, N is number of turns akin to BOs of n-dimensions by levitation between the two hemispheres and is subjected to Dirac matrices, I is the current from the electron path generated from the electric dipole moment,

ε_{0}

and L is length of extension between the poles. Along BO at n-dimension,

R_{μ ν} = 0

. The electron path by DBT of positive curvature is,

R_{μ ν} > 0

and negative curvature as,

R_{μ ν} < 0

. Contraction by Pauli matrix from the vortex electron of a helical solenoid is [33],

R_{α β} \equiv {R^{γ}}_{α γ β,} R_{μ, ω} \equiv {R_{α β} μ}^{α} ω^{β}, (32)

where the electron emergence at positions 1, 3 intersecting the BO is defined by

μ^{α} ω^{β}

and coupling to light is traceless,

R_{α β} = 1

and this preserves the model. The reduction towards the vertex at position 0 (Figure 1a) of the point-boundary is,

R \equiv g^{α β} R_{α β}, (33)

where

g

is subset of space applicable to the metric tensor field and R is Ricci scalar. The metric of the two space-time spheres of Euclidean and Minkowski (Figure 1a and 1b), S² is

{d s}^{2} = {d θ}^{2} + {s i n}^{2} θ d ϕ^{2} . (34)

The coordinates

\{θ, ϕ\}

are ordered into the forms,

g_{i j} = (\begin{matrix} 1 & 0 \\ 0 & {s i n}^{2} θ \end{matrix}), g^{i j} = (\begin{matrix} 1 & 0 \\ 0 & \frac{1}{{s i n}^{2} θ} \end{matrix}) . (35 a)

Equation (35a) has discreet non-zero Christoffel symbols such as

Γ_{ϕ θ}^{ϕ} = \frac{c o s θ}{s i n θ}, Γ_{ϕ ϕ}^{θ} = - c o s θ s i n θ . (35 b)

Equation (35b) is for the basis vector,

\vec{e} θ

and

\vec{e} r

of continuity in space-time. These brief illustrations demonstrate basic aspects of general relativity applicable to the model.

B. Internal structure by Lie group representation

The rotation matrices of the type,

{R r}_{y z} (θ)

and

R_{z x} (θ)

for the MP model (e.g., Figure 1c) are attributed to precession of the MP field. The precession stage is referenced to the original z-axis at position 0 such as,

⟨z| z'⟩ = δ (z - z^{'})

and this translates to linear time as plane wave solutions (e.g., Figure 4c and subsection IIIc). The rotation matrix,

R_{x y} (θ)

intersects BO of topological torus at n-dimension. These matrices are relevant to describe both integer and half-integer spins like, 0, 1/2 and 1 towards complete rotation at position 0 of the spherical point-boundary (see also Figure 2a). At position 0, COM and ZPE of oscillation mode is relevant to the pursuit of both Bose-Einstein statistics and Fermi-Dirac statistics similar to the potential well of a harmonic oscillator. In here, some illustrations of the Lie group by Lorentz transformation are explored based on refs. [34,35].

The chirality of the electron of non-abelian in a symmetric MP field is described by,

g \in G

, (36)

where g is electron’s position at subset of space tangential to the manifolds of BOs and G represents the Lie group (Figure 7). For the conjugate positions pairs, 1, 3 and 5, 7 of BO (Figure 1d), Equation (36) validates the operations,

g_{1,5} + g_{3,7} \in G

(37a)

and

g + (- g) = i

, (37b)

where

i

is spin matrix for both spin ±1/2. The form,

g_{1} + g_{3} \neq g_{5} + g_{7}

due to electron-positron (±

g

) transition and radiation loss,

E = n h v

tangential to the manifolds of the spherical model. For linear transformation along z-axis in 1D space, the hyperbolic surface of the light-cones are compacted to isomorphic BOs with respect to the particle position,

|ψ⟩ = \sum_{n} C_{n} / a_{n}⟩

(e.g., Figure 1d and 7). By intermittent precession, the inner product of r is a scalar and relates to the

boundary of the MP field in the form,

{\vec{r}}_{1} {. \vec{r}}_{2} = |{\vec{r}}_{1}| |{\vec{r}}_{2}| c o s θ

(38)

where rotation of both vectors preserve the lengths and relative angles (e.g., Figure 1c). By assigning rotation matrix, R to Equation (38), its transposition becomes,

{(R r_{1})}^{T} (R r_{2}) = r_{1}^{T} r_{2} I,

(39)

where the identity matrix,

I = R^{T} \times R

by reduction and compaction of vector bundles in homogenous spaces spaces (Figure 7). The rotation by

\vec{r}

is a four 3-fold axis in 3D and its matrices are defined by Cartesian coordinates, x, y and z. These are related to shift in both

θ

and

Φ

as double cover of SU(2) for vector to multivectors assumed within the BOs (refer also to Figure 1d). They are applicable to the Lie group ladder operators,

G (g)

and

\hat{G} (\hat{g})

of 3D space and 4D space-time (Figure 7). By linearization akin to Fourier transform (e.g., Figure 4c), the cubes by isomorphism are translated along the z-axis as time axis in asymmetry by commutation between the poles of the MP field. The BO of bivector field is related to

z / p z

of integers modulo p of prime with respect to the vertices of the MP field. Both forward (F) and backward (B) transforms can be performed on the rotational matrix of the tensors for Levi-Civita connection,

{\hat{e}}_{θ} = {\hat{e}}_{r}

as basis factors with any changes of square infinitesimals,

d θ = d r

.

The orthogonal relationship of BO to clockwise precession along z-axis at 90° for all rotations suggests,

R \in S O (3)

. The SO(3) group rotation for integer spin 0 or 1 in 3D space for the irreducible spinor can be expanded into a series such as,

Π_{μ} (g_{ϕ}) = Π_{μ} [(\begin{matrix} c o s ϕ & - s i n ϕ & 0 \\ s i n ϕ & c o s ϕ & 0 \\ 0 & 0 & 1 \end{matrix})] = \pm (\begin{matrix} e^{i \frac{ϕ}{2}} & 0 \\ 0 & e^{- i \frac{ϕ}{2}} \end{matrix}) = R_{x y} (ϕ) (40 a)

and

Π_{μ} (g_{θ}) = Π_{μ} [(\begin{matrix} 1 & 0 & 0 \\ 0 & c o s θ & - s i n θ \\ 0 & s i n θ & c o s θ \end{matrix})] = \pm (\begin{matrix} c o s \frac{θ}{2} & i s i n \frac{θ}{2} \\ i s i n \frac{θ}{2} & c o s \frac{θ}{2} \end{matrix}) = R_{y z} (θ) . (40 b)

By inserting exponential indices, the gauge symmetry is preserved akin to Christoffel symbols (Equation (35b)). Equation (40a) relates to counterclockwise rotation about positive x-y plane by the angle,

ϕ

along BO for the lattice point, P (Figure 7). It is related to the electron spin –1/2 and its clockwise rotation to positron of spin +1/2 by twisting and unfolding process of DBT (Figure 1a). Similarly, Equation (40b) incorporates both the electron orbit of time reversal (–) and clockwise rotation (+) at the boundary of the spherical model (see also Figure 1b). The resultant shift in the position of the electron or planet (e.g., Figs 5c and 5d) is accorded to the form,

Π_{ν} (g_{ψ}) = Π_{ν} [\begin{matrix} c o s ψ & 0 & s i n ψ \\ 0 & 1 & 0 \\ - s i n ψ & 0 & c o s ψ \end{matrix}] = R_{z x} (ψ) . (40 c)

The algebraic relationship for irreducible representation,

Π

is given by [36],

ρ (g) = [Π (\hat{g})], (41)

where

ρ

is composed of algebraic structure (

p z

,

+ p

and

x p

) for vectorization, V into p-dimensional space defined by

α \land b

(Figure 7). The two operators,

T_{a}

and

S_{a}

acting on V are

(T_{a} f) (b) = f (b - a) (42 a)

and

(S_{a} f) (b) = e^{2 π i a b} f (b), (42 b)

where T is identified by the rotational matrices,

T = \vec{r} \times F

(Figure 7) and

S_{a}

is the shift in frequency in space by outsourcing of radiation along z-axis (see also Figure 4c).

SO(3) group is distinct from compact topological torus,

S U (2) \times S U (2) = S 0 (4)

for the pair of light-cones between the hemispheres (e.g., Figure 1c). When rotating as 2 x 2 Pauli vector for SU(2) symmetry at n-dimensions (Figure 1d), Equation (40b) translates to the form,

\pm (\begin{matrix} c o s \frac{θ}{2} & i s i n \frac{θ}{2} \\ i s i n \frac{θ}{2} & c o s \frac{θ}{2} \end{matrix}) = (\begin{matrix} z & x - y_{i} \\ x + y_{i} & - z \end{matrix}) = |\begin{matrix} ξ_{1} \\ ξ_{2} \end{matrix}| |\begin{matrix} - ξ_{2} & ξ_{1} \end{matrix}|,

(43)

where

ξ_{1}

and

ξ_{2}

are Pauli spinors of rank 1 to rank 1/2 tensor relevant for Dirac matrices (see also Equation (28)). By orthogonal geometry, the column is attributed θ at n-levels along z-axis and the row to BO defined by ϕ in degeneracy. In this case, the following relationship is established for metric tensor of general relativity and identity matrix I of quantum mechanics such as,

g_{r θ} = [\begin{matrix} 1 & 0 \\ 0 & r^{2} \end{matrix}] \equiv I = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] . (44)

The metric tensor,

g_{r θ} = g_{\vec{v} . \vec{ω}}

for speed, v and angular frequency,

ω = 2 π / τ

considers the reference point of rotation at the nucleus with COM reference frame assigned to the point-boundary at position 0. In this case, discrete Christoffel symbols such as,

Γ_{r θ}^{r}

or

Γ_{θ r}^{θ}

and their variations for

g_{r θ}

are applicable to the body-mass position in an elliptical orbit of 2D and this can easily translates to 3D when spin, ϕ of BO is considered (e.g., Figure 7). With precession, both the metric and stress-energy tensors are symmetric given that

g_{μ v} = g_{v μ}

and

T_{μ v} = T_{v μ}

so each one requires 10 independent components from the 4 x 4 matrices owed to reference time axis equivalent to the principal axis of the MP field at position 0. The relationship between the two in a rest frame is given as [37],

g_{v μ} = k T_{v μ} = η_{α β} (45)

where

k = 8 π G / C^{4}

is Einstein constant and

η_{α β}

is Minkowski space-time (Figure 1b). The space-time metric,

g_{v μ}

is incorporated into the two space-time spheres similar to Equation (34) in the form,

{d s}^{2} = {g_{μ v} d x}^{μ} {d x}^{ν}, (46)

where

μ ν = 0,1, 2,3

. The relevance of the indices for the electron path suggests that

T_{v μ}

is the result of the presence of a body-mass comparable to either the electron or a planet in the solar system (Figure 1c and 8). Its matrices of the generalized form,

T_{μ ν} = (\begin{matrix} \begin{matrix} T_{t t} & T_{t x} \\ T_{x t} & T_{x x} \end{matrix} \begin{matrix} T_{t y} & T_{t z} \\ T_{x y} & T_{x z} \end{matrix} \\ \begin{matrix} T_{y t} & T_{y x} \\ T_{z t} & T_{z x} \end{matrix} \begin{matrix} T_{y y} & T_{y z} \\ T_{z y} & T_{z z} \end{matrix} \end{matrix}), (47)

can be dissected as follows [38]. Energy density,

T_{t t}

is attributed to twisting and unfolding process of the electron-positron transition within the space of the MP model. The momentum density,

T_{x t} T_{y t} T_{z t}

or

T_{t x} T_{t y} T_{t z}

for the plane wave solutions is referenced to the z-axis of the MP model as arrow of time in asymmetry (see also subsection IIIc for quantized Hamiltonian). Shear stress like the rate of change in x-momentum in the y-direction is given by

T_{x y}

and for y-momentum in the z-direction by,

T_{y z}

and so forth can relate to invariant rotation of the x-y plane diagonal (Figure 7). The plane is part of the four 3-fold rotational axes for a body-mass at a lattice point of a cube defined by x, y, z coordinates. In a cube, there are also three 4-fold rotational axes on the faces and six 2-fold rotational axes at the edges. The negative pressure force,

T_{x x}

T_{y y}

T_{z z}

directions are balanced out between the two hemispheres of the MP model. Based on the relationship offered in Equation (45), the matrix of the form,

η_{α β} = [\begin{matrix} \begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix} \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix} \end{matrix}], (48)

is consistent with the interpretation made in Equation (44) and also for the relationship,

η^{α β} = T^{μ ν}

for the rest mass with the polarization of 0, –1, 1 assumed at position 0 of COM at the spherical point-boundary. Anti-de Sitter and de Sitter spaces are balanced out by the two hemispheres of the MP field of Dirac string so the electron transits back and forth between the poles by DBT irrespective of distance of separation akin to entanglement process (see also Figure 5a–5f). Accelerated expansion and space-time inflation can be viewed for disturbance of body-mass at BO into n-dimensions of a massive MP model at a hierarchy of scales. Such a scenario can be applied to the galaxy, Milky Way as a point-particle subjected to the process of DBT in a clockwise precession of an elliptical MP field of cosmic microwave background radiation as proposed in ref. [20]. In a multielectron or multigalaxy, multiple MP fields are expected to undergo clockwise rotation. So any two points will generate positive space of flat Euclidean space-time. The time frame for a gigantic clock face can be enormous to an observer stationed on Earth so both blue shift and red shift are expected for an object coupled to linear lightpath at constant speed. In a universe of MP model, visualization of 2D manifolds into 4D space-time (e.g., Figure 1c) sustains gauge symmetry as briefly explored next.

C. Visualization of 2D manifolds into 4D space-time

For ladder operators of BO into n-dimension along z-axis such as the topological torus (Figure 1d), SU(2) is irreducible with the shift in θ and ϕ of the type,

(\begin{matrix} S U (2) \\ n \times n \end{matrix}) \neq (\begin{matrix} S U (2) \\ l \times l \end{matrix}) ⨁ (\begin{matrix} S U (2) \\ m \times m \end{matrix})

between the two hemispheres of the MP field. Translation of SU(2) by

(\begin{matrix} S U (2) \\ 2 \times 2 \end{matrix}) ⨁ (\begin{matrix} S U (2) \\ 2 \times 2 \end{matrix})

to SO(4) somewhat resembles Dirac spinor described within the MP model. The particle’s position, when y = 0, z = x is a real number with the imaginary number at x = 0,

z = y

(see also Figure 6). The BO for SO(2) group in 2D is,

(\begin{matrix} c o s θ & s i n θ \\ - s i n θ & c o s θ \end{matrix}) ≅ (\begin{matrix} 1 & θ \\ - θ & 1 \end{matrix}) = I + θ (\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}), (49)

where,

θ \in [0,2 π]

is related to the electron-positron transition at 720° rotation by DBT. Similar relationships can be forged for

R_{x y} (ϕ)

with respect to the BO along x-y plane comparable to Equation (40a) in the form,

R_{x y} (ϕ) = (\begin{matrix} c o s ϕ & - s i n ϕ & 0 \\ s i n ϕ & c o s ϕ & 0 \\ 0 & 0 & 1 \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) = \pm (\begin{matrix} e^{i \frac{ϕ}{2}} & 0 \\ 0 & e^{- i \frac{ϕ}{2}} \end{matrix}) .

(50)

Substitution of Equation (50) with

R_{x y} (ϕ) = e^{θ}

can relate to polarization states, -1, 1 and 0 at the vertices of the MP field (Figure 1c) from the electron-positron transition such as,

e^{θ} [\begin{matrix} 0 & - 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}] = [\begin{matrix} c o s θ & - s i n θ & 0 \\ s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}] .

(51)

The matrices are relevant to describe manifolds of BOs of topological torus (Figure 1d) between the two hemispheres and its propagation along z-axis into extra dimensions. These demonstrations of Lie group and topology are only teasers of otherwise very complex themes and these can be explored further in high energy physics. Similarly, the crystallography of the cube demonstrated in Figure 7 can be applied to fermions at the lattice points such as in condensed matter physics and this unveils a possible link to high energy physics to be explored further.

D. Space-time curvature

Based on the descriptions of the geometry of MP model of 4D space-time offered so far in the preceding sections, an alternative interpretation of Einstein field equation described in ref. [20] is reproduced in Figure 8 for the planetary model at a higher hierarchy of scale. How this can accommodate perturbations from nonlinearity of differential gravitation acceleration, eccentricity of the reference orbit and its oblatenes including the relative motion of the planet against the sun appears to be more complex phenomena [21] and these are not covered in here the conventional way. It is possible that some of them could become more pronounced by DBT at a higher hierarchy of scales in a multiverse of the MP models. For an elliptical orbit undergoing clockwise precession, its curvature of space-time does not require framework of space-time fabric into smaller infinitesimal forms. Time reversal orbit of Earth is balanced out by clockwise precession of its elliptical orbit and this generates an inertia frame at the spherical boundary. At

position 0 or vertex of the MP field, COM of ZPE is assumed and it forms an aphelion for Earth,

ψ

with respect to the sun. At positions 2 and 6, the planet is perihelion to the sun and the orbit obeys Newton’s first law of motion. Newton’s gravity,

F = G \frac{m_{1} m_{2}}{r^{2}}

is localized to the planet of COM at position 0 of scalar quantity. Its shift from position 0 to 1 by Dirac process intersects the lattice point of the cube (e.g., Figure 7) and the body-mass is subjected to tensors, vectors and Fourier transform along z-axis of inertia frame. The tensors are accorded to warping and unwarping of space-time curvature of the spherical model (Figure 8) akin to helical solenoid of Riemann surface (Figure 6). Thus, coulomb’s law of electrostatic force,

F = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{r^{2}}

for the electron-positron pair can be extended to neutral matter such as the planet of irreducible spinor in a MP model on the geometry basis. Because of the scale, both are of different time frames but are of superposition states and obey Pauli exclusion principle by the process of DBT. Then multielectron atom is equivalent to the solar system of multiple planets. So the approximate resemblance of the MP model at a hierarchy of scales for the atom and the solar system by correspondence is given as [20],

{8 π G T}_{μ, ν} \equiv {i ℏ}_{μ, ν} . (52)

Equation (52) can relate to Equation (1) for the plausible reconciliation path, where both

T_{μ, ν}

and

ℏ_{μ, ν}

are initiated at position 0 and the gravitation constant, G is a weak force for classical COM. Twisting and unfolding by DBT on a body-mass in orbit of space can institute the change,

8 π G \int_{- \infty}^{\infty} {(d R d T d g)}_{u, v} \equiv i \int_{- \infty}^{\infty} {(d Ω d ϕ d θ)}_{u, v} . (53)

Equation (53) considers an alternative interpretation of Einstein’s field equation such that

{R g}_{μ ν}^{λ} - {Λ g}_{μ ν}^{λ} = R_{μ v}

at position 0 (Figure 8) for a body-mass in constant motion of an elliptical orbit without inferring framework of space-time fabric. Preexistence of the MP field is implied with observation limited to light-matter coupling. Strong nuclear force is not considered here similar to the core of the sun. However, for COM assigned to position 0 at the spherical boundary, it forms a composite Dirac fermion of a four-component spinor. If this is also assigned to the nucleus, then a miniature of the MP model is expected and both COMs are linked by nuclear isospin or z-axis as arrow of time in asymmetry (Figure 1a). By asymptotic freedom, the composite nucleons are confined to the atomic MP model. Similarly, the sun’s electromagnetic radiation by nuclear fusion is confined to the planetary MP model in order to sustain life on Earth. Any possible outsourcing of radiation beyond the boundary is by tunneling effect when both Earth and Sun are at aphelion to each other. In this case, how the elliptical cosmic microwave background of MP field can accommodate black hole, cosmic inflation, cosmological principle, dipole anisotropy, dark matter, dark energy and so forth has been previously inferred [20] and these provide fertile grounds for further researches. Similarly, entanglement and measurement appear to be an intrinsic property of the model for linear light paths tangential to a body-mass undergoing the process of DBT in an atom. All these prospects look promising to explore QM at both the microscale and cosmic level in a multiverse of the MP models at a hierarchy of scales.

VI. Conclusion

The dynamics of the MP model of 4D space-time of hydrogen atom type is able to incorporate non-relativistic form of the electron described by QM to its transformation to Dirac fermion of four-component spinor pursued by QFT. COM reference frame is assigned to the spherical point-boundary of ZPE at the vertex of the elliptical MP field undergoing clockwise precession. The vertex is the point of transition to antimatter by the process of DBT for a body-mass undergoing time reversal in its orbit. In this way, the COM at Planck length forms a composite particle for the Dirac fermion. If the process is replicated at the nucleus for a miniature MP model, this is subjected to confinement within the MP model by asymptotic freedom. Similarly, the sun’s electromagnetic radiation by nuclear fusion is confined to the planetary MP model at a hierarchy of scale in a multiverse of the models. Such a prospect can cater for both QM associated with space-time geometry to space-time curvature at the classical scale described by the theory of general relativity. In this case, the model offers fertile grounds for further researches into both the quantum state of matter as well as astrophysics and cosmology and this warrants further investigations.

Data availability statement

The modeling data attempted for the current study are available from the corresponding author upon reasonable request.

Competing financial interests

The author declares no competing financial interests.

References

Lanciani, P. A model of the electron in a 6-dimensional spacetime. Found. Phys. 1999, 29, 251–265. [Google Scholar] [CrossRef]
Nahin, P. Dr. Euler’s fabulous formula: cures many mathematical ills (Vol. 52). Princeton University Press (2011).
Thaller, B. The Dirac Equation. Springer Science & Business Media (2013).
Sun, H. Solutions of nonrelativistic Schrödinger equation from relativistic Klein–Gordon equation. Phys. Lett. A, 2009. [Google Scholar]
Grandpeix, J. Y. and Lurçat, F. Particle Description of Zero-Energy Vacuum I: Virtual Particles. Found. Phys. 2002. [Google Scholar]
Nicol, M. Mathematics for physics: an illustrated handbook (2018).
Chanyal, B. C. A relativistic quantum theory of dyons wave propagation. Can. J. Phys. 2017, 95, 1200–1207. [Google Scholar] [CrossRef]
Trodden, M. Electroweak baryogenesis. Rev. Mod. Phys. 1999, 71, 1463. [Google Scholar] [CrossRef]
Meshkov, I. N. Experimental studies of antihydrogen and positronium physics: problems and possibilities. Phys. Part. Nucl. 1997. [Google Scholar]
Blasi, P. Origin of the positron excess in cosmic rays. Phys. Rev. Lett. 2009, 103, 051104. [Google Scholar] [CrossRef] [PubMed]
S. Santos, T. R. and Sobreiro, R. F. Remarks on the renormalization properties of Lorentz-and CPT-violating quantum electrodynamics. Braz. J. Phys. 2016.
Fox, T. Haunted by the spectre of virtual particles: a philosophical reconsideration. J. Gen. Philos. Sci. 2008. [Google Scholar]
Weiss, L. S.; et al. Controlled creation of a singular spinor vortex by circumventing the Dirac belt trick. Nat. Commun. 2019. [Google Scholar]
Silagadze, Z. K. Mirror objects in the solar system?. arXiv preprint astro-ph/0110161 (2001).
Rieflin, E. Some mechanisms related to Dirac’s strings. Am. J. Phys. 1979. [Google Scholar]
Penrose, R. and MacCallum, M. A. Twistor theory: an approach to the quantisation of fields and space-time. Phys. Rep. 1973. [Google Scholar]
Li, K.; et al. Quantum spacetime on a quantum simulator. Commun. Phys. 2019. [Google Scholar]
Cohen, L.; et al. Efficient simulation of loop quantum gravity: A scalable linear-optical approach. Phys. Rev. Lett. 2021, 126, 020501. [Google Scholar] [CrossRef] [PubMed]
van der Meer, R.; et al. Experimental simulation of loop quantum gravity on a photonic chip. Npj Quantum Inf. 2023. [Google Scholar]
Yuguru, S. P. Unconventional reconciliation path for quantum mechanics and general relativity. IET Quant. Comm. 2022. [Google Scholar]
Jiang, F.; et al. Study on relative orbit geometry of spacecraft formations in elliptical reference orbits. J. Guid. Control Dyn. 2008. [Google Scholar]
Jaffe. R. L. Supplementary notes on Dirac notation, quantum states, etc. https://web.mit.edu/8.05/handouts/jaffe1.pdf (September, 2007).
Recami, E., Zamboni-Rached, M. and Licata, I. On a Time–Space Operator (and other Non-Self-Adjoint Operators) for Observables in QM and QFT. In Beyond peaceful coexistence: The Emergence of Space, Time and Quantum (pp. 371-417) (2016).
Singh, R. B. Introduction to modern physics. New Age International (2008).
Machotka, R. Euclidean model of space and time. J. Mod. Phys. 2018, 9, 1215. [Google Scholar] [CrossRef]
Burdman, G. Quantum field theory I_Lectures. http://fma.if.usp.br/~burdman (October, 2023).
Oshima, S. , Kanemaki, S. and Fujita, T. Problems of Real Scalar Klein-Gordon Field. arXiv preprint hep-th/0512156, 2005. [Google Scholar]
Peskin, M. E. and Schroeder, D. V. An introduction to quantum field theory. Addison-Wesley, Massachusetts, USA (1995).
Alvarez-Gaumé, L. and Vazquez-Mozo, M. A. Introductory lectures on quantum field theory. arXiv preprint hep-th/0510040 (2005).
https://en.wikipedia.org/wiki/Spinor (updated February 2024).
Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 2013. [Google Scholar]
Jeffrey, D. J. Branch cuts and Riemann surfaces. arXiv preprint arXiv:2302.13188 (2023).
Callahan, J. J. The geometry of spacetime: an introduction to special and general relativity. Springer Science and Business Media (2013).
Zhelobenko, D. P. Compact Lie groups and their representations. J. Amer. Math. Soc. 1973. [Google Scholar]
Freed, D. S., Hopkins, M. J., Lurie, J. and Teleman, C. Topological quantum field theories from compact Lie groups. arXiv preprint arXiv:0905.0731 (2009).
Monteiro, R., Nicholson, I. and O’Connell, D. (2019). Spinor-helicity and the algebraic classification of higher-dimensional spacetimes. Class. Quantum Gravity 36(6), 065006 (2019).
Naber, G. L. The geometry of Minkowski spacetime. Springer (2012).
Markley, L. C. and Lindner, J. F. Artificial gravity field. Results Phys. 2013, 3, 24–29. [Google Scholar] [CrossRef]

Figure 1. The MP model [20]. (a) In flat Euclidean space-time, arrow of time is aligned with the principal axis or z-axis of the MP as time axis in asymmetry of a clock face. A spinning electron (green dot) in orbit of sinusoidal form (green curve) assumes time reversal and it is normalized to an elliptical MP field (black area) mimicking Dirac’s string of a small magnet. Clockwise precession of the MP field (black arrows) against time reversal generates an inertia frame, λ. The electron at position 0 is assigned center of mass and is subjected to Newton’s first law of motion,

F = m a

. The shift in the electron’s position from positions 0 to 4 at 360° rotation offers maximum twist and the electron is converted to a positron. The unfolding process from positions 5 to 8 for another 360° rotation restores the electron to its original state at position 0 analogous to DBT and this is associated with zero-point energy (ZPE). A dipole moment (±) of an electric field, E is induced at the total of 720° rotation between two interchangeable hemispheres of the MP so both CPT symmetry and Pauli exclusion principle are sustained. (b) Twisting and unfolding by electron-positron transition generates hyperbolic solenoid of spin angular momentum, ±1/2 (navy colored pair of light-cones) into Minkowski space-time. This levitates into n-dimensions (purple dotted diagonal lines) between the hemispheres and are linked to smooth manifolds of Bohr orbit (BO) perpendicular to the light-cones. The undisturbed helical solenoid of a magnetic field, B by unitarity is referenced to the hypersurface of the MP field. (c) In a Bloch sphere, the precession stages,

Ω

, is polarized by electron-positron transition with qubits, 0 and ±1 assumed at positions, 0, 4 and 8 at the vertices of the MP field. The polar coordinates (r, θ, Φ) with respect to the electron’s position in space are applicable to Schrödinger wave function. (d) Hyperbolic surface of the light-cone of holonomic is contained within hypersurface of the MP field towards position 0 of ZPE at n-1. Balancing out of charges at homomorphic positions 1, 3 and 5, 7 is isomorphic to compact topological torus of BO. The BO is defined by

ϕ

(white loops) and dissected orthonormal by

θ

(yellow circles) from hypersurface of the MP field by clockwise precession. The reach of singularity towards the nucleus is constrained by the irreducible spinor field (insert centered image). The embedded terms and equations are described in the text.

Figure 1. The MP model [20]. (a) In flat Euclidean space-time, arrow of time is aligned with the principal axis or z-axis of the MP as time axis in asymmetry of a clock face. A spinning electron (green dot) in orbit of sinusoidal form (green curve) assumes time reversal and it is normalized to an elliptical MP field (black area) mimicking Dirac’s string of a small magnet. Clockwise precession of the MP field (black arrows) against time reversal generates an inertia frame, λ. The electron at position 0 is assigned center of mass and is subjected to Newton’s first law of motion,

F = m a

. The shift in the electron’s position from positions 0 to 4 at 360° rotation offers maximum twist and the electron is converted to a positron. The unfolding process from positions 5 to 8 for another 360° rotation restores the electron to its original state at position 0 analogous to DBT and this is associated with zero-point energy (ZPE). A dipole moment (±) of an electric field, E is induced at the total of 720° rotation between two interchangeable hemispheres of the MP so both CPT symmetry and Pauli exclusion principle are sustained. (b) Twisting and unfolding by electron-positron transition generates hyperbolic solenoid of spin angular momentum, ±1/2 (navy colored pair of light-cones) into Minkowski space-time. This levitates into n-dimensions (purple dotted diagonal lines) between the hemispheres and are linked to smooth manifolds of Bohr orbit (BO) perpendicular to the light-cones. The undisturbed helical solenoid of a magnetic field, B by unitarity is referenced to the hypersurface of the MP field. (c) In a Bloch sphere, the precession stages,

Ω

, is polarized by electron-positron transition with qubits, 0 and ±1 assumed at positions, 0, 4 and 8 at the vertices of the MP field. The polar coordinates (r, θ, Φ) with respect to the electron’s position in space are applicable to Schrödinger wave function. (d) Hyperbolic surface of the light-cone of holonomic is contained within hypersurface of the MP field towards position 0 of ZPE at n-1. Balancing out of charges at homomorphic positions 1, 3 and 5, 7 is isomorphic to compact topological torus of BO. The BO is defined by

ϕ

(white loops) and dissected orthonormal by

θ

(yellow circles) from hypersurface of the MP field by clockwise precession. The reach of singularity towards the nucleus is constrained by the irreducible spinor field (insert centered image). The embedded terms and equations are described in the text.

Figure 2. Light-MP model coupling. (a) To an external observer, the topological point-boundary provides the origin for the emergence of the oscillator (maroon light-cones). Total angular momentum,

J_{z} = S + L

is minimal with S and L in opposite directions. Levitation of BOs into n-dimensions from n to k for the pair of interchangeable hemispheres coalesces at the point-boundary of COM assigned to electron-positron transition at position 0. The BOs in degeneracy, Φ_i (see also Figure 1d) can accommodate Fermi-Dirac statistics (green wavy curve) and possibly Fock space for non-relativistic many-particle systems if multielectron are assigned to multiple MP fields. The observable oscillator is partitioned at an infinite boundary towards the center of the MP field and is equivalent to atomic wave of linear time. The blue light-cone is from the perspective of the observer at the center and is relevant to Schrödinger wave function (e.g., Figure 1c) with subshells assigned to spectroscopic notations at n-dimensions. (b) Dirac bispinor, where the emergence of quantized magnetic moment,

{\pm J}_{z} = m_{j} ℏ

from the point-boundary (maroon light-cones) levitates about the internal frame of the model (blue light-cones). Parity transformation for the conjugate pairs is confined to a hemisphere and it is dissected along z-axis as nuclear isospin. Scatterings (green wavy curves) at n-dimensions of BOs for light-MP model coupling are related to the eigenfunction,

\vec{J} = \vec{L} + \vec{S}

.

Figure 2. Light-MP model coupling. (a) To an external observer, the topological point-boundary provides the origin for the emergence of the oscillator (maroon light-cones). Total angular momentum,

J_{z} = S + L

is minimal with S and L in opposite directions. Levitation of BOs into n-dimensions from n to k for the pair of interchangeable hemispheres coalesces at the point-boundary of COM assigned to electron-positron transition at position 0. The BOs in degeneracy, Φ_i (see also Figure 1d) can accommodate Fermi-Dirac statistics (green wavy curve) and possibly Fock space for non-relativistic many-particle systems if multielectron are assigned to multiple MP fields. The observable oscillator is partitioned at an infinite boundary towards the center of the MP field and is equivalent to atomic wave of linear time. The blue light-cone is from the perspective of the observer at the center and is relevant to Schrödinger wave function (e.g., Figure 1c) with subshells assigned to spectroscopic notations at n-dimensions. (b) Dirac bispinor, where the emergence of quantized magnetic moment,

{\pm J}_{z} = m_{j} ℏ

from the point-boundary (maroon light-cones) levitates about the internal frame of the model (blue light-cones). Parity transformation for the conjugate pairs is confined to a hemisphere and it is dissected along z-axis as nuclear isospin. Scatterings (green wavy curves) at n-dimensions of BOs for light-MP model coupling are related to the eigenfunction,

\vec{J} = \vec{L} + \vec{S}

.

Figure 3. Vectors of orbital angular momentum. (a) J results from precession of vectors L and S. The shaded area of bivector is extended to the point-boundary of the MP model (see also Figure 2a). (b) Precession of J of hyperbolic surface in Minkowski space-time corresponds to applied external magnetic field B. Both images are adapted from ref. [24].

Figure 4. Wave function collapse (a) Irreducible MP field of Dirac’s string. Electron shift in position 0 by clockwise precession places the particle along a diagonal line, r by the process of DBT. The polar coordinates (r, θ, Φ) are linked to a light-cone (navy colored) and it incorporates Euler’s formula,

e^{i π} = c o s π + i s i n π

with θ = π. The real part, cosπ is aligned with z-axis and the imaginary part, isinπ about x-y plane. Unitarity,

{|ψ|}^{2} = x^{2} + y^{2} = 1

is sustained, where qubits, 0,-1,1 are respectively assumed at positions, 0, 4, 8 in a (b) vector space of Dirac spinor (shaded yellow) superimposed on hyperbolic surface of Poincaré sphere. The vector space is made up of both Euclidean (straight paths) and non-Euclidean (negative and positive curves) spaces from electron-positron transition. (c) On-shell momentum of BO tangential to the MP field for the electron path is applicable to Fourier transform (blue wavy curve) into linear time. Constraining the particle’s position presents the Heisenberg uncertainty principle (black wavy curve). (d) Light-MP model coupling can incorporate both the shift in the electron’s position and its position in real time akin to a typical hydrogen emission spectrum. Thus, from the wave function collapse shown in (c), the amplitudes of both Fourier transform and particle property by uncertainty principle are respectively shown by white and colored spectral lines. This presents a combination for the discrete series of infinite n-dimensions to n = 1, such as Humphery series > Pfund series > Brackett series > Pachen series > Balmer series > Lyman series. .

Figure 4. Wave function collapse (a) Irreducible MP field of Dirac’s string. Electron shift in position 0 by clockwise precession places the particle along a diagonal line, r by the process of DBT. The polar coordinates (r, θ, Φ) are linked to a light-cone (navy colored) and it incorporates Euler’s formula,

e^{i π} = c o s π + i s i n π

with θ = π. The real part, cosπ is aligned with z-axis and the imaginary part, isinπ about x-y plane. Unitarity,

{|ψ|}^{2} = x^{2} + y^{2} = 1

is sustained, where qubits, 0,-1,1 are respectively assumed at positions, 0, 4, 8 in a (b) vector space of Dirac spinor (shaded yellow) superimposed on hyperbolic surface of Poincaré sphere. The vector space is made up of both Euclidean (straight paths) and non-Euclidean (negative and positive curves) spaces from electron-positron transition. (c) On-shell momentum of BO tangential to the MP field for the electron path is applicable to Fourier transform (blue wavy curve) into linear time. Constraining the particle’s position presents the Heisenberg uncertainty principle (black wavy curve). (d) Light-MP model coupling can incorporate both the shift in the electron’s position and its position in real time akin to a typical hydrogen emission spectrum. Thus, from the wave function collapse shown in (c), the amplitudes of both Fourier transform and particle property by uncertainty principle are respectively shown by white and colored spectral lines. This presents a combination for the discrete series of infinite n-dimensions to n = 1, such as Humphery series > Pfund series > Brackett series > Pachen series > Balmer series > Lyman series. .

Figure 5. Dirac spinors. (a) Light-matter coupling is reduced to the electron’s position of an irreducible spinor field of close loop generated within a hemisphere at spherical lightspeed. The electron’s (green dot) shift in position of time reversal is balanced out by clockwise precession of the MP model (see also Figure 1a). The position of the particle on a straight path (colored lines) is referenced to the MP field of elliptical shape (centered image). (b) Maximum twist is attained at position 4 as detectable energy and the unfolding process by another 360° rotation for a total of 720° rotation restores the electron at position 8 or 0 akin to DBT. (c) Precession normalizes the loop to generate an electron of positive helicity or right-handedness. Spin up vector at the point-boundary correlates with the direction of precession. (d) At position 4, the electron flips to a positron of negative helicity or left-handedness. The spin down vector is in opposite direction to the direction of precession to begin the unfolding process. Transposition is attained at 720° rotation,

\sum_{j} {\hat{e}}_{j} {\hat{e}}_{j}^{T} = [e_{i} e_{j}] = c_{i j}^{k} e_{k}

as described in the text. (e) Irreducible spinor field at spherical lightspeed. Cancelation of charges at conjugate positions, 1, 3 and 5, 7 from on-shell momentum offers close loops of BOs into 3D of discrete form to stabilize the electron to only generate either spin up or spin down states respectively at position 0 and 4. The point of singularity at the center is evaded by shift in the electron orbit. The slight tilt at position 4 compared to position 0 is attributed to energy loss from the electron-positron transition in the form,

E = h v = g β B

. (f) Polarization of the model either horizontally or vertically with respect to the electron-positron pair, ±i at position 0 by 720° rotation generates qubits 0, 1 and hypercharge of –1 respectively at positions 0, 8 and 4 (see also Figure 4a). These are relevant to classical computing and accessibility to quantum computing for the nucleons are restricted by the chaotic system of envelop solitons at positions 2 and 6. Image (e) adapted from ref. [30].

Figure 5. Dirac spinors. (a) Light-matter coupling is reduced to the electron’s position of an irreducible spinor field of close loop generated within a hemisphere at spherical lightspeed. The electron’s (green dot) shift in position of time reversal is balanced out by clockwise precession of the MP model (see also Figure 1a). The position of the particle on a straight path (colored lines) is referenced to the MP field of elliptical shape (centered image). (b) Maximum twist is attained at position 4 as detectable energy and the unfolding process by another 360° rotation for a total of 720° rotation restores the electron at position 8 or 0 akin to DBT. (c) Precession normalizes the loop to generate an electron of positive helicity or right-handedness. Spin up vector at the point-boundary correlates with the direction of precession. (d) At position 4, the electron flips to a positron of negative helicity or left-handedness. The spin down vector is in opposite direction to the direction of precession to begin the unfolding process. Transposition is attained at 720° rotation,

\sum_{j} {\hat{e}}_{j} {\hat{e}}_{j}^{T} = [e_{i} e_{j}] = c_{i j}^{k} e_{k}

as described in the text. (e) Irreducible spinor field at spherical lightspeed. Cancelation of charges at conjugate positions, 1, 3 and 5, 7 from on-shell momentum offers close loops of BOs into 3D of discrete form to stabilize the electron to only generate either spin up or spin down states respectively at position 0 and 4. The point of singularity at the center is evaded by shift in the electron orbit. The slight tilt at position 4 compared to position 0 is attributed to energy loss from the electron-positron transition in the form,

E = h v = g β B

. (f) Polarization of the model either horizontally or vertically with respect to the electron-positron pair, ±i at position 0 by 720° rotation generates qubits 0, 1 and hypercharge of –1 respectively at positions 0, 8 and 4 (see also Figure 4a). These are relevant to classical computing and accessibility to quantum computing for the nucleons are restricted by the chaotic system of envelop solitons at positions 2 and 6. Image (e) adapted from ref. [30].

Figure 6. A periodic Riemann surface for the cube-root function. The period resembles integration of the two hemispheres and BOs along the pair of light-cones of the MP model. The 3D warping and unwarping by DBT for the electron-positron transition is numbered (red loops). The top hemisphere (purple colored) combines with the pair of light-cones (turquoise colored) and bottom hemisphere (greenish yellow colored) to provide a complex spinor field. The hidden hypersurface is provided by clockwise precession of the MP field along its z-axis from z’, z” to z. Both real and imaginary potentials are referenced to the z-axis (e.g., Figure 4a). Image modified after ref. [32].

Figure 7. The basis of vectors to multivectors, matrices, tensors and Fourier transform for the electron position (P) in space (see also Figure 1c). Time axis is assumed along z-axis as the principal axis of the MP field and distances projected in the x-y directions. Fourier transform of tensor matrices along z-axis is by commutation,

p Z

to

Z

. The electron of a resultant vector,

\vec{r}

of four 3-fold rotational axes (shaded orange plane) in 3D of a cube can relate to the vector space,

\vec{J} = \vec{L} + \vec{S}

offered in Figure 3a and 3b. These are ascribed to 4-gradient Dirac operator,

\nabla

for vectors to multivector of n-dimensions by the cube translation along z-axis. Stress-energy tensor of BO mimicking rotation into forward time,

τ = \vec{r} \times F

by the emergence of spin up is balanced out by spin down of time reversal,

L = \vec{r} \times p

. The spin rotation matrices applicable to Clifford algebra are shown to the left. The half-integer spins of SU(2) group provide double cover (bivector) with shift in both

θ

and

ϕ

for BOs of topological torus (Figure 1d) between two interchangeable hemispheres of the MP field. These are relevant to the Lie group ladder operators,

G (g)

and

\hat{G} (\hat{g})

into n-dimension. Some key features of the dimensional cube are expounded to the right.

Figure 7. The basis of vectors to multivectors, matrices, tensors and Fourier transform for the electron position (P) in space (see also Figure 1c). Time axis is assumed along z-axis as the principal axis of the MP field and distances projected in the x-y directions. Fourier transform of tensor matrices along z-axis is by commutation,

p Z

to

Z

. The electron of a resultant vector,

\vec{r}

of four 3-fold rotational axes (shaded orange plane) in 3D of a cube can relate to the vector space,

\vec{J} = \vec{L} + \vec{S}

offered in Figure 3a and 3b. These are ascribed to 4-gradient Dirac operator,

\nabla

for vectors to multivector of n-dimensions by the cube translation along z-axis. Stress-energy tensor of BO mimicking rotation into forward time,

τ = \vec{r} \times F

by the emergence of spin up is balanced out by spin down of time reversal,

L = \vec{r} \times p

. The spin rotation matrices applicable to Clifford algebra are shown to the left. The half-integer spins of SU(2) group provide double cover (bivector) with shift in both

θ

and

ϕ

for BOs of topological torus (Figure 1d) between two interchangeable hemispheres of the MP field. These are relevant to the Lie group ladder operators,

G (g)

and

\hat{G} (\hat{g})

into n-dimension. Some key features of the dimensional cube are expounded to the right.

Figure 8. The components of Einstein field equation are applied to the MP model of 4D space-time [20]. At the solar scale, the planet,

ψ

shifts in its position at point X of position 0 as COM of ZPE towards position 1. As a consequence, it warps space-time akin to the DBT (see also Figure 1a) and the emergence of angular momentum,

\vec{J}

at position 1 and 3 of superposition states mimics stress-energy tensor,

T_{μ, ν}

. Note, because of the irreducible spinor presented by the MP field mimicking Dirac’s string, space-time does not curve towards singularity. Instead, the Hamiltonian of quantized states (green outline) of moduli space undergo the process of DBT to generate Riemann surface,

R_{μ, ν}

.

Figure 8. The components of Einstein field equation are applied to the MP model of 4D space-time [20]. At the solar scale, the planet,

ψ

shifts in its position at point X of position 0 as COM of ZPE towards position 1. As a consequence, it warps space-time akin to the DBT (see also Figure 1a) and the emergence of angular momentum,

\vec{J}

at position 1 and 3 of superposition states mimics stress-energy tensor,

T_{μ, ν}

. Note, because of the irreducible spinor presented by the MP field mimicking Dirac’s string, space-time does not curve towards singularity. Instead, the Hamiltonian of quantized states (green outline) of moduli space undergo the process of DBT to generate Riemann surface,

R_{μ, ν}

.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Dirac Fermion of a Monopole Pair (MP) Model of 4D Space-Time and Its Wider Implications

Abstract

Keywords:

Subject:

I. Introduction

A. Quantum space-time dilemma in field theory

B. Rationale for 4D quantum space-time in field theory

C. Motivation of this study

II. Dirac fermion of a MP model of hydrogen atom type

A. A brief overview of existing atomic models

B. Unveiling of Dirac belt trick and CPT symmetry

C. Dynamics of space-time geometry in an atom

III. Relevance of quantum mechanics on the MP model

A. Non-relativistic wave function

B. Wave function collapse

C. Quantized Hamiltonian

IV. Relevance of quantum field theory on the MP model

A. Dirac spinors

B. Weyl spinors and Majorana fermions

C. Lorentz transformation

V. Space-time geometry of the MP model

A. Space-time fabric of an elliptical orbit

B. Internal structure by Lie group representation

C. Visualization of 2D manifolds into 4D space-time

D. Space-time curvature

VI. Conclusion

Data availability statement

Competing financial interests

References

MDPI Initiatives

Important Links

Subscribe