Dirac Fermion of a Monopole Pair (MP) Model

1. Introduction

At the fundamental level of matter, particles are described by wave-particle duality, charges and their spin property. These properties are revealed from light interactions and are pursued by the application of relativistic quantum field theory (QFT) [1,2]. The theory of special relativity defines lightspeed, c to be constant in a vacuum and the rest mass of particles to be, $m=E/c^2$ with E as energy. The particle-like property of light waves consists of photons possessing spin 1 of neutral charge. Any differences to its spin, charge and mass-energy equivalence provide the inherent properties of particles for matter at the fundamental level and this is termed causality [3,4]. Based on QFT, particles appear as excitation of fields permeating space at less than lightspeed. A level of indetermination is associated towards unveiling of charge-spin property, whereas the wave-particle duality is depended on the instrumental set-up [5,6]. The probability of locating the electron within the atom is defined by non-relativistic Schrödinger’s electron field,$\psi$, and it is not compatible to the excitation of the electromagnetic field for particle manifestation [7]. In other words, it is difficult to imagine wavy form of particles freely permeating space without interactions and this somehow collapses to a point at observation [8].

At the atomic state, the energy is radiated in discrete energy forms in infinitesimal steps of Planck radiation, ±h. The interpretation is consistent with observations except for the resistive nature of proton decay [9]. The preferred quest for particle observation at the atomic level is to make non-relativistic equations become relativistic due to the shared properties of both matter and light at the fundamental level as mentioned above.

Beginning with Klein-Gordon equation [10], the energy and momentum operators of Schrödinger equation,

$$\widehat{E}=i\hslash \frac{\partial }{\partial t}, \widehat{p}=-i\hslash \nabla ,\mathrm{}$$

(1)

are adapted in the expression,

$$\left({\hslash }^2\frac{{\partial }^2}{\partial t^2}-c^2{\hslash }^2{\nabla }^2+m^2{c}^4\right)\psi \left(t,\overline{x}\right)=0.$$

(2)

Equation (2) incorporates special relativity, $E^2=p^2{c}^2+m^2{c}^4$ for mass-energy equivalence, $\nabla$ is the del operator in 3D space, ℏ is reduced Planck constant and $i$ is an imaginary number, $i=\sqrt{-1}$. Only one component is considered in Equation (2) and it does not take into account the negative energy contribution from antimatter. In contrast, the Hamiltonian operator,$\widehat{H}$ of Dirac equation [11] for a free particle is, 

$$\widehat{H}\psi =\left(-i\nabla .\mathit{a}\mathit{}+m\beta \right)\psi .$$

(3)

The $\psi$ has four-components of fields, $i$ with vectors of momentum,$\nabla$ and gamma matrices, α, β represent Pauli matrices and unitarity. The concept is akin to, e⁺ e^– ⟶ 2𝛾, where the electron annihilates with its antimatter to produce two gamma rays. Antimatter existence is observed in Stern-Gerlach experiment and positron from cosmic rays. While the relativistic rest mass is easy to grasp, how fermions acquire mass other than Higgs field remains yet to be solved at a satisfactory level [12]. But perhaps, the most intriguing dilemma is offered by the magnetic spin ±1/2 of the electron and how this translates to a Dirac fermion of four-component spinor field. Such a case remains a very complex topic, whose intuitiveness in terms of a proper physical entity remains lacking and it is often described either by Dirac belt trick [13] or Balinese cup trick [14]. Others relatable descriptions include Klein bottle [15] and Dirac scissors problem [16]. These descriptions dwell on the possible formation of Dirac strings from atom decay. However, suppose the atom is preserved, how the electron can be physically transformed into Dirac fermion is examined within a proposed MP model. Such a process appears compatible with Dirac belt trick, quantum mechanics and Lie group, while gravity is considered to be a classical force for an irreducible spinor field. These outcomes are compatible with Dirac field theory and its associated features such as wave function collapse, quantized Hamiltonian, non-relativistic wave function, Weyl spinor, Lorentz transformation and Feynman diagrams. Though the model remains somewhat speculative, it can become important towards defining the fundamental state of matter and its field theory subject to further investigations.

2. An Electron Conversion to a Fermion by Dirac Process

In this section, the transformation of a lone electron in a hydrogen atom type to a fermion by Dirac process is speculated within a spherical MP model. The process includes examination of Dirac belt trick by assuming energy conservation and this is ensued by the model’s relevance to the basic interpretations of quantum mechanics and Lie group.

a) Unveiling Dirac belt trick within the spherical MP model

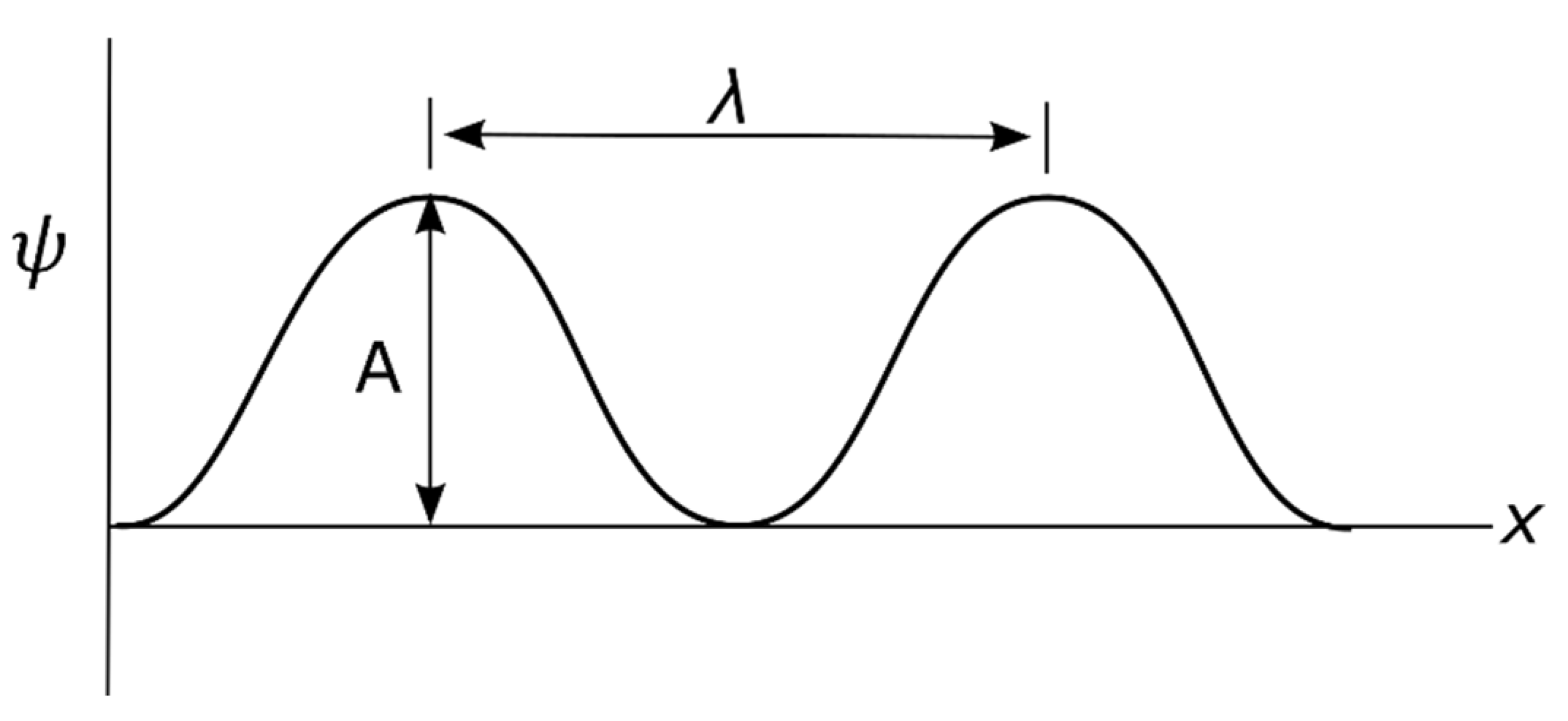
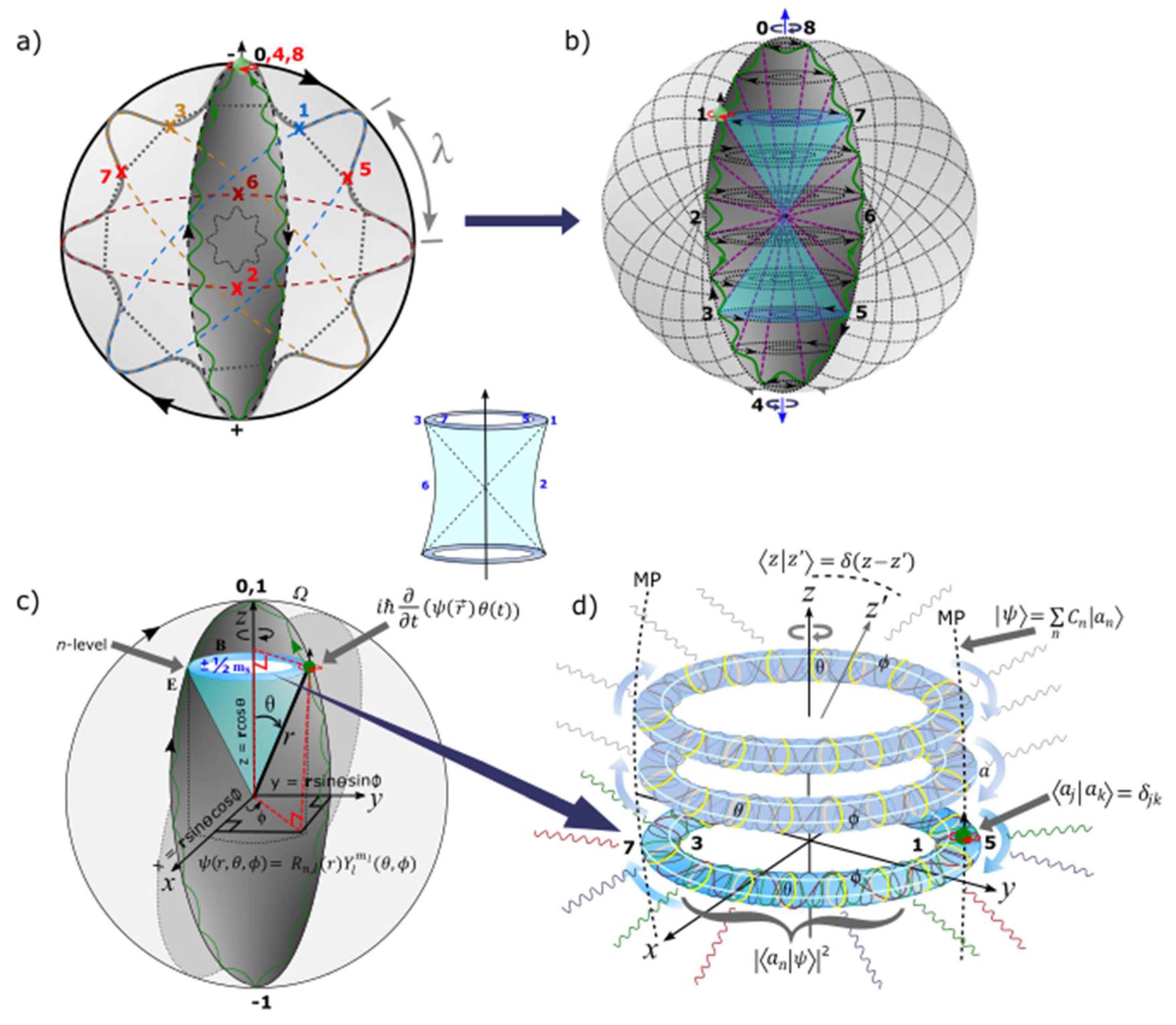
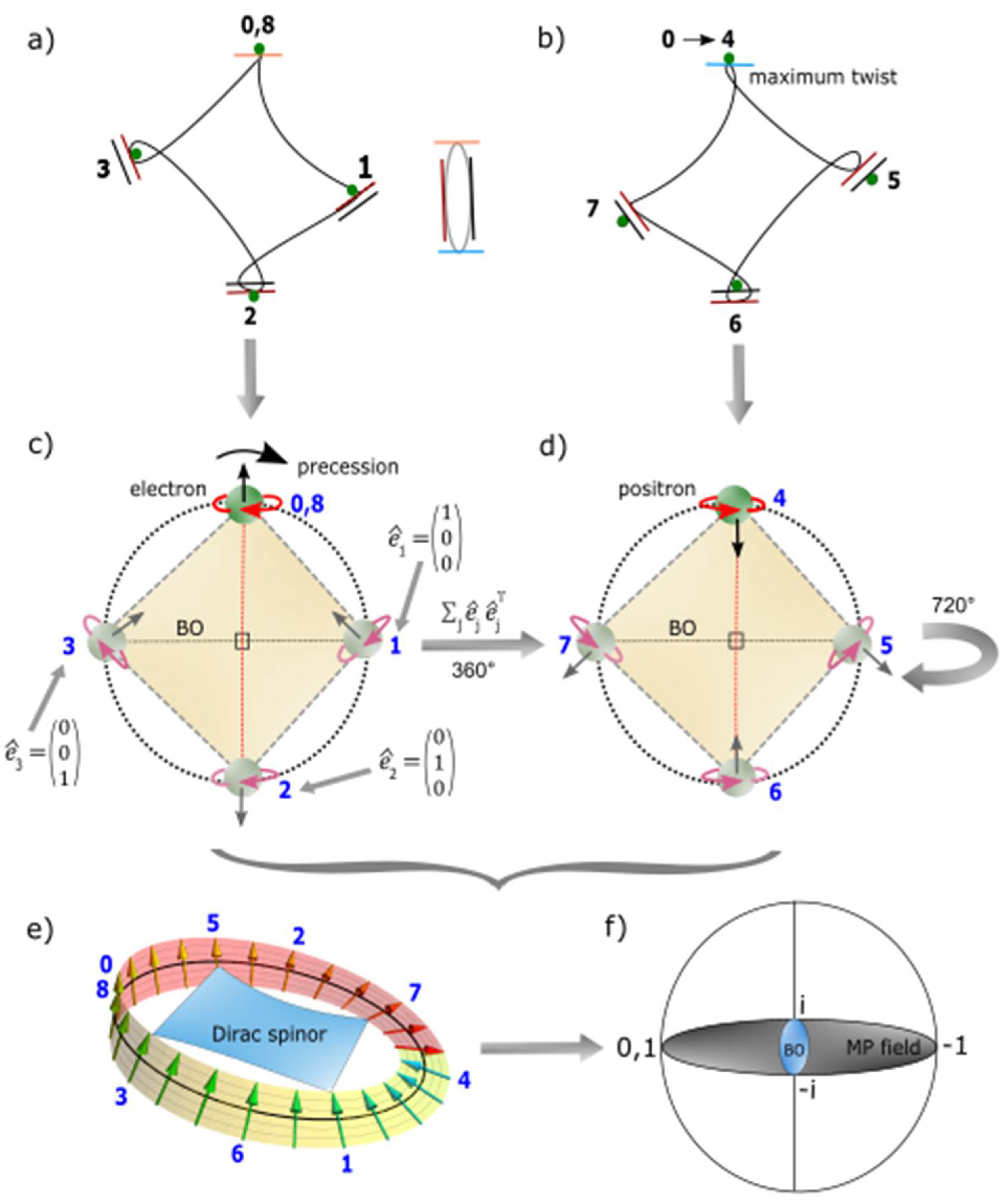
The electron’s orbit of time reversal in discrete continuum form of sinusoidal wave is defined by Planck radiation, h. In forward time, the orbit is transformed into an elliptical shape of a monopole pair (MP) field mimicking Dirac string (Figure 1a). It is dissected perpendicular by Bohr orbits (BOs) into n-dimensions of energy levels. By clockwise precession, the torque or right-handedness exerted on the MP field shifts the electron of spin up from positions 0 to 4 to assume 360° rotation. Time reversal orbit against clockwise precession allows for maximum twist at the point-boundary or vertex of the MP field at position 4. The electron then flips to spin down mimicking a positron to begin the unfolding process and emits radiation by, $E=nhv$. Another 360° rotation from positions 5 to 8 restores the electron to its original state. These intuitions are relatable to Dirac belt trick at 720° rotation for the Dirac four-component spinor, $\psi =\left(\genfrac{}{}{0pt}{}{{\psi }_0}{\begin{array}{c}{\psi }_1\\ \genfrac{}{}{0pt}{}{{\psi }_2}{{\psi }_3}\end{array}}\right)$ assigned to positions 0 to 3 and its transposition at positions 4 to 8 assumed at spherical lightspeed. In Minkowski space-time, the conjugate pairs of positions, 1, 3 and 5,7 offer light-cone depicting Weyl spinor of 4D space-time (Figure 1b). The point of singularity for the light-cone is out of reach due to the electron’s shift at positions, 2 and 6 for the irreducible spinor field (centered image of Figure 1a–d). Additional details on the conceptualization path of the model from electron wave-diffraction is offered elsewhere [17]. Clockwise precession at spherical lightspeed offers an inertia reference frame, λ at the microscale (Figure 1a) under the conditions,

$${\lambda }_{\pm }^2={\lambda }_{\pm }\hspace{1em}Tr{\lambda }_{\pm }=2 {\lambda }_{+}+{\lambda }_{-}=1,$$

(4)

where the trace function, Tr is the sum of all elements within the model. These elements are applicable to both quantum mechanics and Lie group as examined next.

b) Quantum mechanics and Dirac notations

The transformation of the electron to a Dirac fermion within the MP model can further accommodate some basic concepts in quantum mechanics (Figure 1c and Figure 1d). Some of them are outlined below in bullet points based on ref. [18].

• The electron of wave-particle duality obeys de Broglie relationship, $\lambda =h/mv$ with h assigned to its sinusoidal orbit and mv to BO. It is defined by the wave function, $\psi$ and its orbit of time reversal adheres to the Schrödinger equation, $i\hslash \frac{\partial }{\partial t}\left(\psi \left(\overrightarrow{r}\right)\theta \left(t\right)\right)$ in space-time (Figure 1c) (see also Appendix A for further explanations). Its superposition state (electron-positron pair) in space is linked to BO defined by $\varphi$ and thus, its inner product is, ${⟨\psi |\varphi ⟩}^{*}=⟨\psi |\varphi ⟩$ with respect to z-axis. Conjugate charges at positions, 1, 3 and 5 and 7 cancels each other out at spherical lightspeed to form close loops, where the electron is stabilized to generate only either spin up or spin down in its orbit at an energy n-level in accordance with Pauli exclusion principle. At 360° rotation, an electron of spin up is produced and at 720° rotation, a positron of spin down is formed. The loops of BOs are topology construct of differential manifolds into n-levels or n-dimensions (Figure 1d). In this way, the electron forms a weak isospin, whereas the z-axis mimicking spin up and spin down resembles nuclear isospin.
• Both radial and angular wave functions are applicable to the electron, $\psi \left(r,\theta ,\varphi \right)=R_{n,l}\left(r\right)Y_l^{m_l}(\theta ,\varphi )$. The radial part,$R_{n,l}$ is attributed to the principal quantum number, n and angular momentum, l of a light-cone with respect to r (Figure 1c). The angular part, $Y_l^{m_l}$ in degenerate states, ${\pm m}_l$ with respect to the z-axis is assigned to the BO defined by both $\theta$ and $\varphi$ (Figure 1d).
• The BO is defined by a constant structure, ɑ and its orthogonal (perpendicular) to z-axis by linearization (Figure 1d). Its link to electron-positron pair is, $⟨a_j|a_k⟩=\int dx{\psi }_{a_j}^{*}\left(x\right){\psi }_{a_k}\left(x\right)={\delta }_{jk}$ for continuous derivation by rotation and is relevant to Fourier transform (see also Appendix B). Linear translation for the n-levels along z-axis can relate to the sum of expansion coefficients, $C_n$, where the electron’s position offers an expectant value, $\left|\psi \right.⟩=\sum _n{C}_n/a_n⟩$. Its probability is of the type, ${⟨a_n|\psi ⟩}^2$.
• The shift in the electron’s position of hermitian conjugates by Dirac process, P(0→8) = ${\int }_{\tau }{\psi }^{*}\widehat{H}\psi d\tau$ assumes Hamiltonian space with $\tau$ by precession (Appendix B). The complete spherical rotation towards the point-boundary for the polarization states, 0, 1 assumes U(1) symmetry and incorporates Euler’s formula, $e^{i\pi }$ + 1 = 0 in real space.
• Singularity at Planck’s length is assigned to the point-boundary at position 0 and this promotes radiation of the type, $E=nhv$ by the electron-positron transition. Somehow it sustains the principle axis of the MP field or z-axis as nuclear isospin in asymmetry so ±h values are applicable. The inertia frame can substitute for centripetal force if gravity is assumed to be a classical force rather than an atomic force. Coulomb’s law, $F_{orce}=\frac{m_e{v}^2}{r}$, for the electron-positron pair at constant velocity, v can apply to the MP model accommodating irreducible spinor field.

c) Lie Group

The Lie group of differential smooth manifolds are attributed to both the BO of a circle and the spherical model (Figure 1c). The BO in degeneracy offers a topology of Lie groups and its translation along z-axis of orthogonality by linearization (Figure 1d). The electron-positron transition from positions 0 → 8 is tangential to the boundaries of the manifolds. Rotation matrices of the type, ${Rr}_{yz}\left(\theta \right)$ and $R_{zx}\left(\theta \right)$ is attributed to the MP field by precession with any shift in z-axis of nuclear isospin is trivial, $⟨z|z\prime ⟩=\delta (z-z^{\prime })$ (Figure 1d). The rotation matrix, $R_{xy}\left(\theta \right)$ is accorded to the BO. These are relevant to describe both integer and half-integer spins such as, 0, 1/2 and 1 towards complete rotation at position 0 at the point-boundary. These attributes are relatable to Figure 2A in Appendix B and some these examples are explored in here based on refs. [19,20].

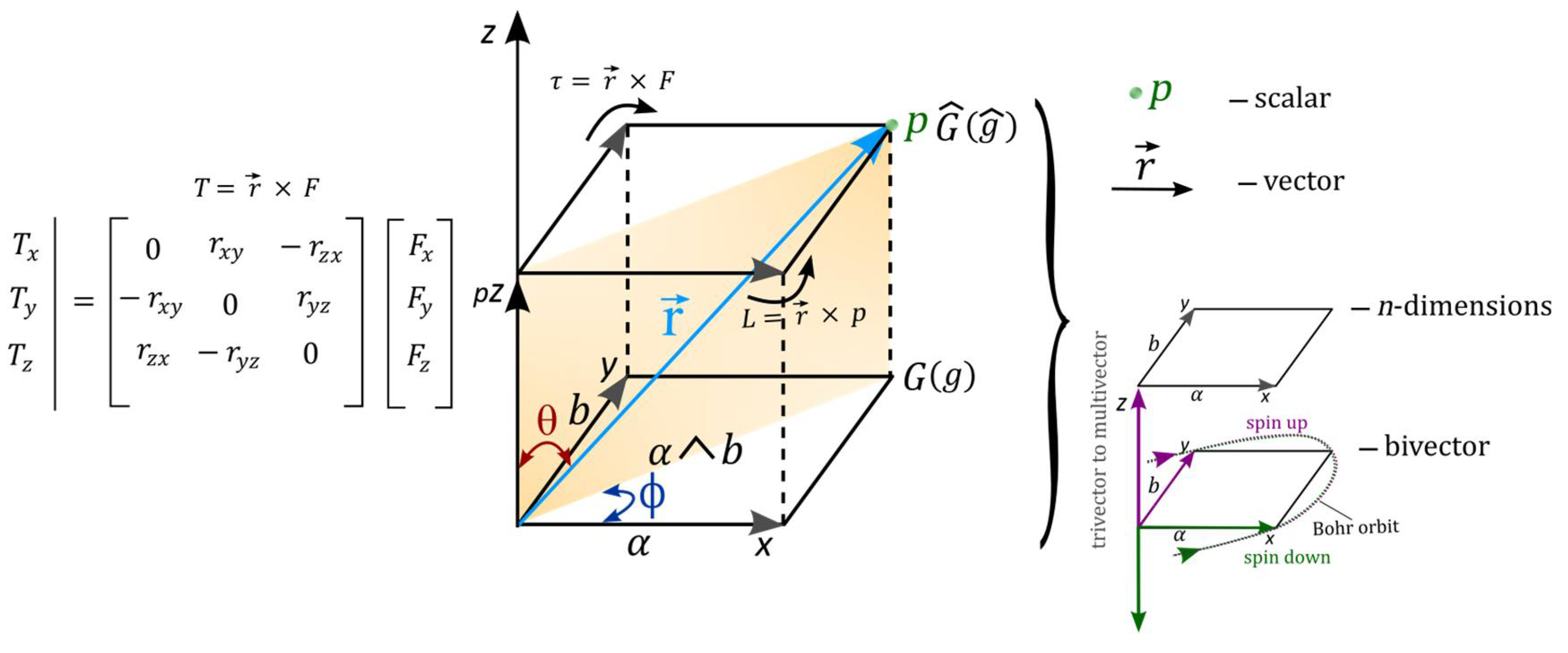
The electron of chiral form can be described by,

$$g\in G,$$

(5)

where g is the electron’s position as subset of the space tangential to the manifolds and G is Lie group (see also Figure 2A). For the conjugate numbered pairs, 1, 3 and 5, 7 of BO (Figure 1d), Equation (5) validates the operations,

$$g_{\mathrm{1,5}}+g_{\mathrm{3,7}}\in G$$

(6a)

and

$$g+\left(-g\right)=i,$$

(6b)

where $i$ is spin matrix for both spin ±1/2 (Figure 2A). The form, $g_1+g_3\ne g_5+g_7$ due to electron-positron (±$g$) transition and radiation loss, $E=nhv$ tangential to the manifolds. For linear transformation along z-axis in 1D space, the BOs are isomorphic with respect to the particle position, $\left|\psi \right.⟩=\sum _n{C}_n/a_n⟩$ (Figure 1d and Figure 2A). By intermittent precession, the inner product of r is a scalar and relates to the boundary of the MP field in the form,

$${\overrightarrow{r}}_1 {. \overrightarrow{r}}_2=\left|{\overrightarrow{r}}_1 \right|\left|{ \overrightarrow{r}}_2\right|cos\theta$$

(7)

where rotation of both vectors preserve the lengths and relative angles (e.g., Figure 1c). By assigning rotation matrix, R to Equation (7), its transposition is,

$${\left(R{r}_1\right)}^T\left(R{r}_2\right)=r_1^T{r}_{2}I,$$

(8)

where the identity matrix, $I=R^T\times R$ by reduction (Figure 2A). The orthogonal relationship of BO to clockwise precession along z-axis at 90° for all rotations suggests, $R\in \mathrm{S}\mathrm{O}\left(3\right)$. The SO(3) group rotation for integer spin 1 in 3D space is,

$$R_{yz}\left(\theta \right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right).$$

(9)

Equation (9) can also be pursued for integer spin 0 and higher spin particles. When rotating as 2 x 2 Pauli vector for SU(2) symmetry with respect to a light-cone of half-integer spin (Figure 1d), Equation (9) translates to the form,

$$\pm \left(\begin{array}{cc}cos\frac{\theta }{2}& isin\frac{\theta }{2}\\ isin\frac{\theta }{2}& cos\frac{\theta }{2}\end{array}\right)=\left(\begin{array}{cc}z& x-y_i\\ x+y_i& -z\end{array}\right)=\left|\begin{array}{c}{\mathsf{\xi }}_1\\ {\mathsf{\xi }}_2\end{array}\right|\left|\begin{array}{cc}-{\mathsf{\xi }}_2& {\mathsf{\xi }}_1\end{array}\right|,$$

(10)

where ${\mathsf{\xi }}_1$ and ${\mathsf{\xi }}_2$ are Pauli spinors of rank 1 to rank 1/2 tensor relevant for Dirac matrices (Figure 2A). By orthogonal geometry, the column is attributed θ at n-levels along z-axis and the row to BO defined by 𝜙 in degeneracy. For ladder operators at n-dimension along z-axis, SU(2) is irreducible for the shift in θ and 𝜙 such as, $\left(\begin{array}{c}SU\left(2\right)\\ n\times n\end{array}\right)\ne \left(\begin{array}{c}SU\left(2\right)\\ l\times l\end{array}\right)⨁\left(\begin{array}{c}SU\left(2\right)\\ m\times m\end{array}\right)$. Translation of SU(2) by accentuating precession at high energy like, $\left(\begin{array}{c}SU\left(2\right)\\ 2\times 2\end{array}\right)⨁\left(\begin{array}{c}SU\left(2\right)\\ 2\times 2\end{array}\right)$ matrices is reduced to the upright MP field position (e.g., Figure 1b). For the particle’s position, when y = 0, z = x is a real number. At x = 0, $z=y$ becomes an imaginary number. The BO linked to the electron’s position can be assigned to SO(2) group in 2D such as,

$$\left(\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right)\cong \left(\begin{array}{cc}1& \theta \\ -\theta & 1\end{array}\right)=I+\theta \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),$$

(11)

where, $\theta \in \left[\mathrm{0,2}\pi \right]$ incorporates Dirac process at 720° rotation (e.g., Figure 1a). Similar relationships can be forged for $R_{xy}\left(\varphi \right)$ with respect to the BO along x-y plane with respect to Equation (9) in the form,

$$R_{xy}\left(\varphi \right)=\left(\begin{array}{ccc}cos\varphi & -sin\varphi & 0\\ sin\varphi & cos\varphi & 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\pm \left(\begin{array}{cc}{e}^{i\frac{\varphi }{2}}& 0\\ 0& e^{-i\frac{\varphi }{2}}\end{array}\right).$$

(12)

Substitution of Equation (12) with $R_{xy}\left(\varphi \right)=e^{\theta }$can relate to polarization states, -1, 1 and 0 at the vertices of the MP field (Figure 1c) from the electron-positron transition such as,

$$e^{\theta }\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right].$$

(13)

The physical perspective of Equation (13) is provided in Figure 2A for the rotation of BOs into n-dimensions. These explanations offer the basics to the complexities of compact Lie group similar to those demonstrated for quantum mechanics and Dirac notations in the preceding subsection.

d) Summary

Dirac fermion of a complex four-component spinor field appears compatible with the MP model with respect to Dirac belt trick. The first 360° rotation involves matter (electron) and the next 360° rotation is associated with the emergence of positron (antimatter) before the electron is restored at the point-boundary or vertex of the MP model. Clockwise precession is reduced to the irreducible MP field of Dirac string of magnetic dipole moment whose principal axis (i.e., z-axis) mimics nuclear isospin (Figure 1b). The physicality of the electron of weak isospin tangential to the manifolds for both the spherical model and BOs (Figure 1d) somewhat mimics monopole or quantized electric charge for Dirac string. In turn, the electron in orbit at spherical lightspeed offers an electric dipole moment or dielectric constant to the space defined by the MP field and this is relevant to the pursuit of Coulomb’s interaction without requiring the necessity of gravitational force.

3. Dirac Field Theory and Its Related Components

An alternative demonstration of the application of Dirac belt-trick based on the MP model is offered in Figure 2a–f. The electron’s time reversal orbit of a MP field mimics Dirac string and it is subjected to twisting and unfolding process by clockwise precession. Cancellation of charges at conjugate positions 1, 3 and 5, 7 allows for the emergence of BOs in manifolds and these generate only spin up and spin down states. How these relate to Dirac theory and its associated components [1,2,10,11] are succinctly described in bullet points for future undertakings.

⇒Dirac theory and helical property. The fermion field is defined by the famous Dirac equation of the generic form,

$$i\hslash {\gamma }^u{\partial }_u\psi \left(x\right)-mc\psi \left(x\right)=0,$$

(14)

where ${\gamma }^u$ are gamma matrices. The exponentials of the matrices, $\left\{{\gamma }^o{\gamma }^1{\gamma }^2{\gamma }^3\right\}$ are attributed to the electron’s position by clockwise precession acting on its time reversal orbit. For example, ${\gamma }^o$is assigned to the vertex of the MP field and by electron-positron transition at position 0, it sustains z-axis as arrow of time in asymmetry. The ${\gamma }^1{\gamma }^2{\gamma }^3$ variables of Dirac matrices are related to the electron shift in its positions. Orthogonal projections of the space-time variables, $\frac{1}{2}\left(1\pm i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3\right)$ are confined to a hemisphere and assigned to a light cone (e.g., Figure 1c). These are incorporated into the famous Dirac equation,

$$\left(i{\gamma }^0\frac{\partial }{\partial t}+cA\frac{\partial }{\partial x}+cB\frac{\partial }{\partial y}+cC\frac{\partial }{\partial z}-\frac{{mc}^2}{\hslash }\right)\psi \left(t,\overrightarrow{x}\right),$$

(15)

where c acts on the coefficients A, B and C and transforms them to ${\gamma }^1{, \gamma }^2$and ${\gamma }^3$. The exponentials of $\gamma$ are denoted i for off-diagonal Pauli matrices for the light-cone (Figure 1d) and is defined by,

$${ \gamma }^i=\left(\begin{array}{cc}0& {\sigma }^i\\ {-\sigma }^i& 0\end{array}\right),$$

(16a)

and zero exponential, ${\gamma }^o$ is,

$${ \gamma }^0=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right).$$

(16b)

${\sigma }^i$ is relevant to oscillations assumed at the BOs (Figure 1d) with anticommutation relationship, $e^{+}\left(\psi \right)\ne e^{-}\left(\overline{\psi }\right)$ of chiral symmetry (Figure 2c and Figure 2d). The associated vector gauge invariance for the electron-positron transition exhibits the following relationships,

$${\psi }_L\to e^{i\theta L}{\psi }_L$$

(17a)

And

$${\psi }_R\to e^{i\theta L}{\psi }_R.$$

(17b)

The exponential factor, iθ refers to the position, i of the electron of a complex number and θ, is its angular momentum (e.g., Figure 1c). The unitary rotations of right-handedness (R) or positive helicity and left-handedness (L) or negative helicity are applicable to the electron transformation to Dirac fermion (e.g., Figure 2A in Appendix B). The process is confined to a hemisphere and this equates to spin 1/2 property of a complex spinor. Two successive rotations of the electron in orbit by clockwise precession of the MP field is identified by $i\text{ћ}$. The chirality or vector axial current at the point-boundary is assigned to polarized states, ±1 of the model (Figure 1c). The helical symmetry from projections operators or nuclear isospin of z-axis acting on the spinors (Figure 2e) is,

$${ P}_L=\frac{1}{2} \left(1-{\gamma }_5\right)$$

(18a)

and

$${ P}_R=\frac{1}{2} \left(1-{\gamma }_5\right),$$

(18b)

where ${\gamma }_5$ is likened to thermal radiation of a black body. The usual properties of projection operators are: L + R = 1; RL = LR = 0; L² = L and R² = R (e.g., Figure 2a–d).

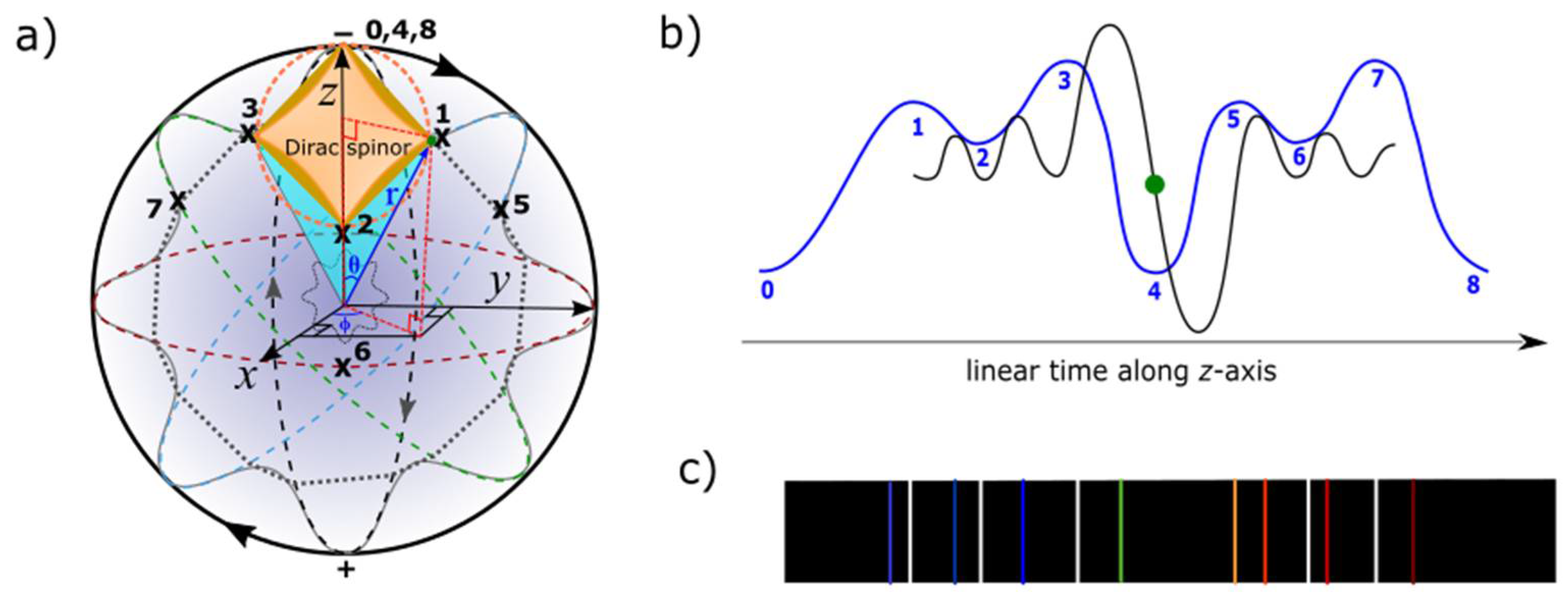
Wave function collapse. Dirac fermion or spinor is denoted ψ(x) in 3D Euclidean space and it is superimposed onto the MP model of 4D space-time, ψ(x,t) by clockwise precession (Figure 3a). The former includes both positive and negative curvatures of non-

Euclidean space (e.g., Figure 2a and Figure 2b) normalized to straight paths of Euclidean space (Figure 2c and Figure 2d) and these are imposed on the surface of Poincaré sphere. The latter resembles Minkowski space-time and consists of a light-cone dissected by z-axis as arrow of time. The Dirac four-component spinor, $\psi =\left(\genfrac{}{}{0pt}{}{{\psi }_0}{\begin{array}{c}{\psi }_1\\ \genfrac{}{}{0pt}{}{{\psi }_2}{{\psi }_3}\end{array}}\right)$ is attributed to positions 0 to 3 of conjugate pairs in 3D space. Convergence of positions 1 and 3 at either position 0 or 2 is relevant to the equivalence principle based on general relativity. Any light paths tangential to the point-boundary of the n-energy manifolds of BOs is expected to transform the spinor into linear time mimicking Fourier transform for wave function collapse scenario (Figure 3b). Constraining the electron’s position along the z-axis offers the uncertainty principle due to the particle’s link to the BO. The wave amplitudes can relate to a typical hydrogen emission spectrum for external light-matter interactions with respect to the electron’s position in orbit (Figure 3c). In this way, wave function collapse of probabilistic distribution by Born’s rule,${\left|\psi \right|}^2$, where the spherical model is reduced to linearization along z-axis.

Quantized Hamiltonian. Two ansatzes adapted from Equation (14) are given by,

$$\psi =u\left(\mathbf{p}\right)e^{-ip.x},$$

(19a)

and

$$\psi =v\left(\mathbf{p}\right)e^{ip.x},$$

(19b)

where outward project of spin at positions 5, 7 is represented by $v$ and inward projection at positions 1, 3 by $u$ (e.g., Figure 2c and Figure 2d). By linear transformation, the hermitian plane wave solutions form the basis for Fourier components in 3D space (Figure 1d and Figure 3b). Decomposition of quantized Hamiltonian [22] ensues as,

$$\psi \left(x\right)=\frac{1}{{\left(2\pi \right)}^{3/2}}\int \frac{d^3}{2E_{\mathbf{p}}}\sum _s\left(a_{\mathbf{P}}^s{u}^s\left(p\right)e^{-ip.x}+b_{\mathbf{P}}^{s†}{v}^s\left(p\right)e^{ip.x}\right),$$

(20a)

where the constant, $\frac{1}{{\left(2\pi \right)}^{3/2}}$ is attributed to the dissection of BOs along z-axis. Its conjugate form is by,

$$\overline{\psi }\left(x\right)=\frac{1}{{\left(2\pi \right)}^{3/2}}\int \frac{d^3}{2E_{\mathbf{p}}}\sum _s\left(a_{\mathbf{P}}^{s†}{\overline{u}}^s\left(p\right)e^{ip.x}+{b_{\mathbf{P}}^s\overline{v}}^s\left(p\right)e^{-ip.x}\right).$$

(20b)

The coefficients $a_{\mathbf{P}}^s$ and $a_{\mathbf{P}}^{s†}$ are ladder operators for u-type spinor and $b_{\mathbf{P}}^s$ and $b_{\mathbf{P}}^{s†}$ for v-type spinor at n-dimensions along BOs (e.g., Figure 1d). These related to Dirac spinors of two spin states, ±1/2 and ${\overline{v}}^s$ and ${\overline{u}}^s$ as their antiparticles. Dirac Hamiltonian of one-particle quantum mechanics relevant to the MP model of hydrogen atom type is,

$$H=\int d^{3}x{\psi }^{†}\left(x\right)\left[-i{\gamma }^0\gamma . \nabla +m{\gamma }^0\right]\psi \left(x\right).$$

(21)

The quantity in the bracket is provided in Equation (3). By parity transformation, the observable and holographic oscillators are canonically conjugates (e.g., Figure 2c and Figure 2d). The associated momentum is,

$$\pi =\frac{\partial \mathcal{L}}{\partial \psi }-\overline{\psi }i{\gamma }^0=i{\psi }^{†}.$$

(22)

With z-axis of the MP field aligned to the vertex in asymmetry (Figure 1c), the V-A currents comparable to Fourier transform are projected in either x or y directions in 3D space (Figure 1d and Figure 3b). These assume the relationships,

$$\left[{\psi }_{\alpha }\left(\mathbf{x}, t\right),{\psi }_{\beta }\left(\mathbf{y}, t\right) \right]=\left[{\psi }_{\alpha }^{†}\left(\mathbf{x}, t\right),{\psi }_{\beta }^{†}\left(\mathbf{y}, t\right) \right]=0,$$

(23a)

and its matrix form,

$$\left[{\psi }_{\alpha }\left(\mathbf{x}, t\right),{\psi }_{\beta }^{†}\left(\mathbf{y}, t\right) \right]={\delta }_{\alpha \beta }{\delta }^3\left(\mathbf{x}-\mathbf{y}\right),$$

(23b)

where α and β denote the spinor components of $\psi$. Equations (23a) refers to unitarity of the model and Equation (23b) is assumed by the electron-positron transition about the manifolds of BOs in 3D space (Figure 1d). The $\psi$ independent of time in 3D space obeys the uncertainty principle with respect to the electron’s position, p and momentum, q, as conjugate operators (Figure 1c). The commutation relationship of p and q is,

$$\left\{a_{\mathbf{P}}^r,a_{\mathbf{q}}^{s†} \right\}=\left\{b_{\mathbf{p}}^r,b_{\mathbf{q}}^{s†} \right\}={\left(2\pi \right)}^3{\delta }^{rs}{\delta }^3\left(\mathbf{p}-\mathbf{q}\right).$$

(24)

Equation (24) incorporates both matter and antimatter and their translation to linear time (Figure 3b). The electron as a physical entity generates a positive-frequency such as,

$$\begin{gathered} ⟨0|\psi \left(x\right)\overline{\psi }\left(y\right)|0⟩=⟨0│\int \frac{d^{3}p}{{\left(2\pi \right)}^3}\frac{1}{\sqrt{{2E}_{\mathrm{p}}}} \sum _r{a}_{\mathrm{p}}^r{u}^r\left(p\right)e^{-ipx} \\ \times \int \frac{d^{3}q}{{\left(2\pi \right)}^3}\frac{1}{\sqrt{{2E}_{\mathrm{q}}}} \sum _s{a}_{\mathrm{q}}^{s†}{\overline{u}}^s\left(q\right)e^{iqy}│0⟩. \end{gathered}$$

(25)

Equation (25) could explain the dominance of matter (electron) over antimatter if the latter is accorded to the conceptualization process of Dirac fermion provided by the model (e.g., Figure 2a and Figure 2b).

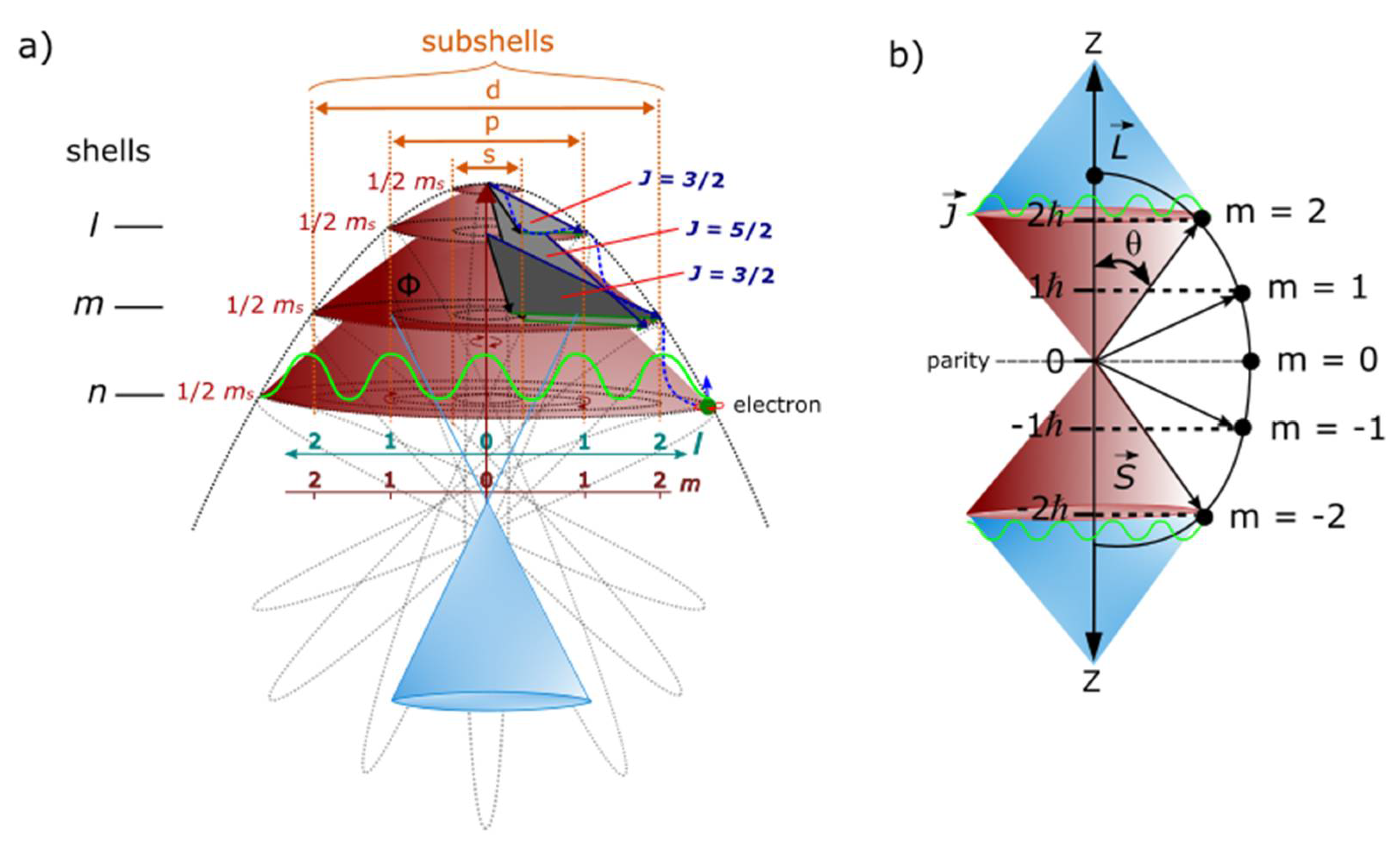
Non-relativistic wave function. Observation by light-matter interaction allows for the emergence of the model from the point-boundary at Planck length. Subsequent energy shells of BOs at the n-levels by excitation accommodates complex fermions, ±1/2, ±3/2, ±5/2 and so forth (Figure 4a). The orbitals of 3D are defined by total angular momentum, $\overrightarrow{J}=\overrightarrow{l}+\overrightarrow{s}$ and this incorporates both orbital angular momentum, l and spin angular momentum, s (Figure 4b). These are aligned with Schrödinger wave function (e.g., Figure 1c). The reader is also referred to Appendix A, Appendix B and Appendix C. Within a hemisphere, the model is transformed to a classical oscillator. By clockwise precession, a holographic oscillator from the other hemisphere of the MP field remains hidden. One oscillator levitates about the other (Figure 4b) and both are not simultaneously accessible to observation by Fourier transform (e.g., Figure 3b). The n-levels for the fermions can be pursued for Fermi-Dirac statistics with the point-boundary assigned to zero-point energy (ZPE). The $\pm \overrightarrow{J}$ splitting (Figure 4a) can apply to Landé interval rule due to the electron isospin and this can somehow accommodate lamb shift and thus, hyperfine structure constant. Such a scenario is similar to how vibrational spectra of a harmonic oscillator for diatoms like hydrogen molecule incorporates rotational energy levels. The difference of the classical oscillator to the quantum scale is the application of Schrödinger wave equation (e.g., Figure 1c).

is minimal with S and L in opposite directions. Increase into n-dimensions, k to l offers asymptotic boundary to the energy shells and subshells inclusive of the hidden oscillator. The BOs in degeneracy, Φ_i (see also Figure 1d) at the n-levels can accommodate Fermi-Dirac statistics (green wavy curve) and possibly Fock space for non-relativistic many-particle systems if multielectron are assigned to multiple MP fields. The observable oscillator is partitioned at the infinite boundary at the center of the MP field and is equivalent to classical limit. The blue light cone is from the perspective of the observer at the center and is relevant to Schrödinger wave function (e.g., Figure 1c). (b) The emergence of quantized magnetic moment, ${\pm J}_z=m_j\hslash$ from the point-boundary (maroon light cones) levitates about the internal frame of the model (blue light cones). Parity transformation for the conjugate pairs is confined to a hemisphere (e.g., Figure 2a and Figure 2b) and it is related to z-axis of nuclear isospin. Minimal scatterings (green wavy curves) are applicable to light-MP model interactions along the BOs for the eigenfunction, $\overrightarrow{J}=\overrightarrow{L}+\overrightarrow{S}$.

Weyl spinor. The light cone from the point-boundary within a hemisphere accommodates both matter and antimatter by parity transformation to generate Dirac spinor (Figure 1c, Figure 2a–d and Figure 4b). It is described in the form,

$$\psi =\left(\begin{array}{c}\begin{array}{c}{\psi }_0\\ {\psi }_1\\ {\psi }_2\end{array}\\ {\psi }_3\end{array}\right).$$

(26)

Equation (26) corresponds to spin up fermion, a spin down fermion, a spin up antifermion and a spin down antifermion (e.g., Figure 2c and Figure 2d). By forming its own antimatter, Dirac fermion somewhat resembles Majorana fermions. It is difficult to observe them simultaneously due to the wave function collapse long z-axis of linear time (e.g., Figure 3b). Non-relativistic Weyl spinor of a pair of light cones in 4D space-time are relevant to Schrödinger wave equation in 3D space (Figure 1c, Figure 3a and Figure 4a). These are defined by reduction of Equation (26) to a bispinor in the form,

$$\psi =\left(\begin{array}{c}{u}_{+}\\ u_{-}\end{array}\right),$$

(27)

where $u_{\pm }$ are Weyl spinors of chirality with respect to the electron position. By parity operation, x → x’ = (t, ‒ x), qubits 1 and −1 are generated at the vertices of the MP field (e.g., Figure 1c). Depending on the reference point-boundary of the BO (Figure 1d), the exchanges of left- and right-handed Weyl spinor assumed the process,

$$\left(\begin{array}{c}{\psi }_L^{\prime }\\ {\psi }_R^{\prime }\end{array}\right)=\left(\begin{array}{c}{\psi }_R\left(x\right)\\ {\psi }_L\left(x\right)\end{array}\right)\Rightarrow \begin{array}{c}{\psi }^{\prime }\left(x^{\prime }\right)={\gamma }^0\psi \left(x\right)\\ {\overline{\psi }}^{\prime }\left(x^{\prime }\right)=\overline{\psi }\left(x\right){\gamma }^0.\end{array}$$

(28)

Conversion of Weyl spinors to Dirac bispinor, ${\xi }^1$ ${\xi }^2$ are of transposition state (e.g., Figure 2c and Figure 2d)). The two-component spinor, ${\xi }^1$ ${\xi }^2$ = 1 are normalized at the point-boundary at position 0 of the spherical model (Figure 1a).

Lorentz transformation. The Hermitian pair, ${\psi }^{†}\psi$ of Dirac fermion based on Equation (27) undergo Lorentz transformation in the form,

$$u^{†}u=({\xi }^{†}\sqrt{p.\sigma ,} \xi \sqrt{p.\overline{\sigma }} . \left(\begin{array}{c}\sqrt{p. \sigma }\xi \\ \sqrt{p.\overline{\sigma }}\xi \end{array}\right), =2{\mathrm{E}}_{\mathrm{P}}{\mathsf{\xi }}^{\text{†}}\mathsf{\xi } .$$

(29)

Equation (29) basically relates to the transformation of the model of 4D space-time to linear time at observation comparable to Fourier transform (e.g., Figure 3b). The corresponding Lorentz scalar applicable to scattering at the BOs (Figure 1d) is,

$$\overline{u}\left(p\right)=u^{†}\left(p\right){\gamma }^0.$$

(30)

Equation (30) is referenced to z-axis as the principle axis of the MP field of a dipole moment in asymmetry (Figure 1c). By identical calculation to Equation (29), the Weyl spinor becomes,

$$\overline{u}u=2m{\xi }^{†}\xi ,$$

(31)

with respect to the light-cone (Figure 4a). It is difficult to distinguish Weyl spinor and Majorana fermion from Dirac spinor by observations due to superposition of electron-positron pairings and the point of singularity is evaded by shift in the electron’s position (e.g., Figure 2e).

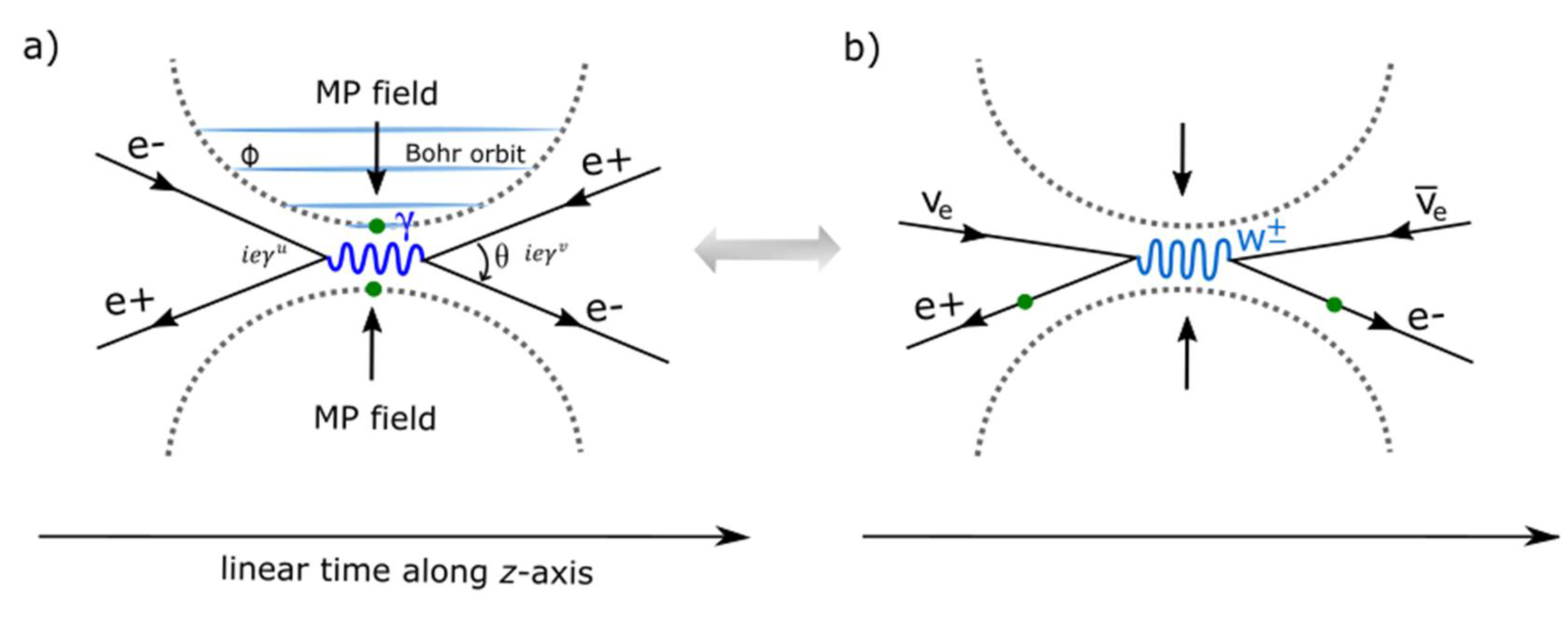
Feynman diagrams. The two types of particles pursued by Dirac field theory consist of bosons and fermions. The former of whole integer spin 0 and 1 vectors are force-carrying particles and the latter of spin 1/2 are fundamental building blocks of matter. Their relevance to bivector to multivector, matrices and tensors are described in section 2 and Appendix B. Within the prospects of the MP model, both spin 1 and 0 are attributed to the point-boundary of ZPE of a classical oscillator (Figure 4a). By conservation of the model, ejection of the electron (object) of weak isospin permits electroweak symmetry breaking. The emergence of a particle-hole at the vertex somewhat mimics Higgs boson. At position 0, it assumes center of mass (COM) when aligned with the z-axis of nuclear isospin and this becomes massive somewhat mimicking Nambu-Goldstone boson. These are not transferrable by linearization (e.g., Figure 3b). The outgoing electron (or positron) by beta decay, ${\beta }^{\pm }$ can insinuate neutrino types of helical property from the separation of particle hole and z-axis (nuclear isospin) as COM during rotation by Dirac process. Such a shift will correspond to change of color charges by exchange of gluons from up and down quarks (Figure 5b). Any scatterings along the BOs of unidirectional (e.g., Figure 1d and Figure 4a) would mimic electron-positron pair as the base point of the manifolds (e.g., Figure 1d) and accommodate the fine-structure constant, $a=\frac{e^2}{\hslash c}=\frac{e^2}{4\pi }\approx \frac{1}{137}$ . These explanations are relevant to electroweak interactions but these could apply to hadron collisions at high energy for ionized hydrogen atoms if the z-axis assumes nuclear isospin and for quark confinement, the nuclear shell model was to mimic the electron shell (e.g., Figure 4a). Photon-MP model coupling is assumed by Einstein mass-energy equivalence of the form,

$$E^2-{\left|\overrightarrow{p}\right|}^2{c}^2=m^2{c}^2.$$

(32)

The emitted particles are energized by, $\gamma$ or $\frac{{-ig}_{uv}}{p^2}$ from on-shell momentum ($p^2=m^2$) along the BO at fixed orbit by precession (Figure 4a). Translation to linear time along the z-axis from the vertices as COM are of the type, ${ie\gamma }^u$, ${ie\gamma }^v$ by wave function collapse (e.g., Figure 3b). These interpretations can somehow relate to deviations in the anomalous magnetic moment of the electron with respect to the value, $a$ such as for the lamb shift and possibly account for baryon asymmetry.

Summary and further undertakings. The above themes offered for Dirac field theory with respect to the MP model are compatible with quantum mechanics, compact Lie group and total angular momentum (Appendix A, Appendix B and Appendix C). These provide the foundations for further explorations into more depth in both quantum electrodynamics and Standard Model of particle physics. Such undertaking can warrant the removal of infinite terms for fermion and boson types to comply with baryon asymmetry.

4. Conclusion

The dynamics of the MP model of 4D space-time offered in this study allows for the transformation of the electron of hydrogen atom type to Dirac fermion of a complex four-component spinor. These are compatible with Dirac belt trick, quantum mechanics and Lie group, while gravity is considered to be a classical force rather than an atomic force for the irreducible spinor field represented by the model. Such outcomes relate well to Dirac field theory and some of its associated components such as wave function collapse, quantized Hamiltonian, non-relativistic wave function, Weyl spinor, Lorentz transformation and Feynman diagrams. Though the model still remains a speculative tool, it can become important towards defining the fundamental state of matter and its field theory subject to further investigations.