1. Introduction
The Collatz conjecture is one of the unsolved problems in mathematics. Introduced by German mathematician Lothar Collatz in 1937 [
1], it is also known as the 3n + 1 problem, 3x + 1 mapping, Ulam conjecture (Stanislaw Ulam), Kakutani’s problem (Shizuo Kakutani), Thwaites conjecture (Sir Bryan Thwaites), Hasse’s algorithm (Helmut Hasse), or Syracuse problem [
2,
3,
4].
The Collatz conjecture or 3n+1 problem can be summarized as follows:
Take any positive integer n. If n is even, divide n by 2 (n/2). Otherwise, if n is odd, multiply n by 3 and add 1 (3.n+1). By repeatedly applying this rule of the conjecture to the chosen number n, we obtain a sequence. The next term in the sequence is found by applying arithmetic operations (n/2 or 3n+1) to the previous term according to the assumption rule. The conjecture states that no matter what number you start with, you will always reach 1 eventually.
For example, if we start with 17, multiply by 3 and add 1, we get 52. If we divide 52 by 2, 26, and so on, the rest of the sequence is: 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Or if we start 76, the sequence is: 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
This sequence of numbers involved is sometimes referred to as the hailstone sequence, hailstone numbers or hailstone numerals (because the values are usually subject to multiple descents and ascents like hailstones in a cloud) [2,6], or as wondrous numbers [2,5].
In this paper, {, the symbol represents the natural numbers. {, the symbol represents the positive integers. {, the symbol represents the positive odd integers.
2. The Conjecture and Related Conversions
Definition 2.1. Let
and a function
, Collatz defined the following map:
The Collatz conjecture states that the orbit formed by iterating the value of each positive integer in the function will eventually reach 1. The orbit of n under f is ().
In the following sections, we will call these two arithmetic operations ( and ), which we apply to any positive integer n according to the rule of assumption, Collatz operations (CO).
Remark 2.2. According to the definition of the Collatz conjecture, if the number we choose at the beginning is an even number, then by continuing to divide all even numbers by 2, one of the odd numbers is achieved. So it is sufficient to check whether all odd numbers reach 1 by the Collatz operations.
Therefore, if we prove that it reaches 1 when we apply the Collatz operations to all the elements of the set {, we have proved it for all positive integers.
Remark 2.3. If the Collatz operations are applied to the numbers (), then eventually 1 is reached. If we can convert to numbers by applying the Collatz operations to all the elements of the set, we get the result. Therefore, our goal is to convert all positive odd integers to numbers by applying Collatz operations.
2.1. Collatz Inverse Operation (CIO)
Let
and
; for
a to be converted to
by the Collatz operation (CO), it must satisfy the following equation,
then,
Lemma 2.4. In (1) , a cannot be an integer if n is a positive odd integer.
Proof. If
n is a positive odd integer, we can take
(
), then substituting
for
n in (1) we get,
if we factor
,
we get , which is a multiple of 3 ().
Since ,
() is not a multiple of 3 (), so in (2) a is not an integer for any number n.
If we substitute
for
n in (1), we get equation
Lemma 2.5. In (3) , for each number n there is a different positive odd integer a, ().
Proof. When we factorize for all n numbers, (), if
n=2, (24 -1) = (2-1)(2+1)(22+1)=3.5
n=3, (26 -1) = (23-1)(23+1)=3.3.7
n=4, (28-1) = (2-1)(2+1)(22+1)(24+1)=3.(...)
n=5, (210-1) = (25- 1)(25+1)= (2-1)(24+...+1)(2+1)(24- ...+1)=3.(...)
n=6, (212-1)= (23- 1)(23 + 1)(26+1)=3.3.(...)
n=7, (214 -1)= (27- 1)(2+1)(26- 25+...+1)=3.(...)
...
...
if we substitute 2n to ,(m ∈);
...
or
in these equations, is a positive odd integer and , , ... are positive even integers. Since is a positive odd number,
so,
Since each of these numbers has a multiplier of 3, we can find positive odd integers a for all n, and when we apply Collatz operations to these a numbers, we always get 1.
is not a multiple of 3, since is a multiple of 3, for all n ().
If ,
,
,
,
,
... ...
Corollary 2.6. We get a set A with infinite elements, these numbers reach 1 when we apply the Collatz operations. This is because when we apply the Collatz operations to these numbers, they become numbers (Remark 2.3). (In the following sections, we will refer to the elements of the set A and other numbers that satisfy the Collatz conjecture as Collatz numbers).
Example 2.7. 5 → odd number, 16 →8→4→2→1.
21→ odd number, 64→32→16→8→4→2→1.
If we can generalize the elements of the set to all positive odd numbers, we have proved the Collatz conjecture.
2.2. Transformations in the Set A with Infinite Elements
Let the elements of the set be respectively.
Lemma 2.8. In the set A\
, if
, from each we get sets with infinite elements (Collatz numbers), these numbers satisfy the conjecture. And then, from each we get sets with infinite elements, from each we get sets with infinite elements, ... and so on forever.
Proof. If (mod 3), we can take as ,
substituting in (4),
is divisible by 3 (Lemma 2.5.). So we get an infinite number of different
elements, which can be converted to
, i.e. 1, by the Collatz operation. The
elements are Collatz numbers.
Example 2.9. Let , then ≡1 (mod 3),
in (4),
Lemma 2.10. In the set A\
}, if
≡2 (mod 3),
, from each
we get
sets with infinite
elements (Collatz numbers), these numbers satisfy the conjecture. And then, from each
we get
sets with infinite elements, from each
we get
sets with infinite elements, ... and so on forever.
Proof. If ≡2 (mod 3), we can take as
substituting in (5),
is divisible by 3 (Lemma 2.5). So we get an infinite number of different elements, which can be converted to , i.e. 1, by the Collatz operation. The elements are Collatz numbers.
Example 2.11. Let , then ;
, ,
, ,
Lemma 2.12. In the set A\
}, if
≡0 (mod 3),
, there is no such integer .
Proof . If 0 (mod 3), we can take as
substituting in (6),
is not integer.
In the following sections, we will call the operations of deriving new Collatz numbers from Collatz numbers by equations (3), (4) or (5) as Collatz inverse operations (CIO).
2.3. Conversion of Collatz Numbers to all Positive Odd Integers
In the previous sections, when we applied the Collatz operations, we called the numbers that reached 1 as Collatz numbers. Now let’s see how these Collatz numbers can be converted to all positive integers.
If we apply the Collatz inverse operations [equations (4) or (5)] continuously to each Collatz number, we get infinitely many new Collatz numbers.
→ Set of A →→ 1 (conversion direction of numbers with CO).
← Set of A ← (conversion direction of numbers with CIO).
Example 2.13. A small fraction of the Collatz numbers, that can be converted to , i.e. 1, by applying CO. These numbers are obtained by applying the CIO to each of the numbers. New numbers are obtained by repeatedly applying CIO to any number that is not a multiple of 3.
Example 2.14. Collatz numbers that can be converted to , i.e. 1, by applying CO.
21 ← There are no other Collatz numbers. Because the resulting number is a multiple of 3. (Lemma 2.12).
Lemma 2.15. There is only one different Collatz number, which is converted to each of the numbers ; (, , , ...) .
Proof. If we factor - 1,
, there is always a multiplier of () in this equation. Because when we factor () and ();
if n is even, () = ... (), is odd integer.
if n is odd in (), is odd integer.
And if or are odd,
Therefore . (odd integer)
And, when we divide () by 3, we get only one Collatz number. We can’t obtain another Collatz number because it is a multiple of 3 (Lemma 2.12).
Example 2.16. There is only one different Collatz number for each of , because the resulting Collatz numbers are the multiples of 3 (Lemma 2.12).
... ...
But, for , and , when all numbers (except ) are divided by 3, we get positive odd integers that are not multiples of 3. This is because when we factor , there is only one multiplier of 3.
or
In these equations, is a positive odd integer and not a multiple of 3, and , , , ... are positive even integers. and do not have a multiplier of 3 (Lemma 2.4. and Lemma 2.5). And since is not a multiple of 3, has only one multiplier of 3, so an infinite number of Collatz numbers are converted to each of the numbers with CO.
Example 2.17. A small fraction of the Collatz numbers that can be converted to , i.e. 1, by applying CO. These numbers are obtained by applying the CIO to each of the numbers. New numbers are obtained by repeatedly applying CIO to any number that is not a multiple of 3.
Similarly, all positive odd integers are converted to ( ), i.e. to 1 by applying CO. These numbers are obtained by repeatedly applying the Collatz inverse operations to each element of the set A and the Collatz numbers generated from these numbers.
Lemma 2.18. We obtain new Collatz numbers by applying the Collatz inverse operation () (), to the Collatz numbers, all of these Collatz numbers are different from each other.
Proof. Let and be arbitrary Collatz numbers, when we apply the Collatz inverse operation to each of them, the resulting numbers are and . If then,
and for odd positive integers, must be and .
Lemma 2.19. If 0 (mod 3) and numbers are odd Collatz numbers, we can derive from other Collatz numbers.
Proof. If 0 (mod 3) and numbers are odd Collatz numbers, then by applying CO to , we find odd positive integers . Since numbers are the Collatz numbers, numbers are also the Collatz numbers and .
→ (apply CO to )
← (apply CIO to )
since Collatz numbers cover numbers, by applying the Collatz inverse operation to we get ,
Corollary 2.21. By applying the Collatz inverse operations [Equation (
3)] to the numbers
, we get a set A with infinite elements of positive odd numbers. The elements of the set A are the Collatz numbers. We get new Collatz numbers by applying Collatz inverse operations [Equation (
4) or (5)] to each element of this set A. From these new infinite Collatz numbers, infinitely many new Collatz numbers are formed by applying the Collatz inverse operations (CIO) again and again, and this goes on endlessly. So we get the whole set of positive odd numbers as Collatz numbers and we prove the Collatz conjecture for all
(Remark 2.2).
3. The Absence of any Positive Integer other than Collatz Numbers
In this section, we prove that there are no positive integers that do not satisfy the conjecture.
Lemma 3.1. There cannot be any positive integer other than Collatz numbers.
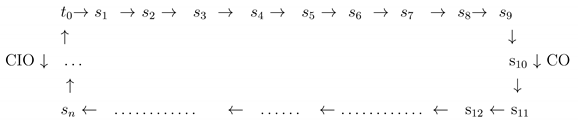
Proof. Let be a number that is not a Collatz number and (), then when we apply Collatz inverse operations to ,
CIO we get , and the elements of the set T are not Collatz numbers.
Also, when we apply the Collatz operation to , until we find odd numbers;
, → → → → → → → s → → ...
we get and the elements of the set S are not Collatz numbers .
If is a multiple of 3, the CIO cannot be applied to , so we take instead of the set T.
If we apply the Collatz inverse operations to every number in the sets T and S, we get infinitely many new numbers that are not Collatz numbers.
(Numbers obtained by applying CIO to . New numbers are obtained by repeatedly applying CIO to any number that is not a multiple of 3.)
(Numbers obtained by applying CIO to . New numbers are obtained by repeatedly applying CIO to any number that is not a multiple of 3.)
In the same way, an infinite number of new numbers are formed by applying CIO to each of ( and ). We get infinite new numbers that are not Collatz numbers, repeated application of CIO to these numbers produces infinite new numbers, this result contradicts (Corollary 2.21).
Lemma 3.2. The elements of the set S do not loop with any element of the sets S or T.
Proof. We assume that such a loop exists.
For such a loop to be exist, if we choose , or any other number as the starting and ending terms of the loop, which cannot be a number other than 1. If we choose as the first and last terms of the loop, when CO is applied to all elements of the loop, they all turn into , but when CO is applied to , it cannot produce a number other than the loop numbers. In other words, while infinitely different numbers turn into with CO, cannot turn into a number different from those numbers. Such a restriction is only possible if is 1. Then the other elements of the loop are also 1. For such a loop to be exist in positive odd integers, all the elements of the loop must be 1.
By another method, all the elements of the loop must be equal, because the infinite set of numbers obtained by applying the CIO to each element of the loop is the same, that is, . In the positive odd integers, only the number 1 can form a loop with itself, so all elements of the loop are 1.
Example 3.3.Lets take in the loop, and ( ), then if ,
,
cannot be any positive odd integer other than 1 in this equation.
Since we assume that there is a number which is not a Collatz number, we obtain two sets (T and S) with infinite elements from this number. The elements of the sets T and S are not Collatz numbers. By repeatedly applying the Collatz inverse operations (CIO) to these numbers and the new numbers formed from them, an infinite number of new numbers are created, and this continues indefinitely. And they don’t form a loop. If there were such a number , there would be no Collatz number. This is because from each of the infinite numbers in the sets T and S, new numbers are continuously generated without any limitation by repeated application of Collatz inverse operations, thus covering all positive odd numbers. This result contradicts the result we found above (Corollary 2.21). So there cannot be any positive integer that is not a Collatz number.