Preprint
Article
The Imaginary Universe (on the Three Complementary Sets of Measurement Units Defining Three Dark Electrons)
Altmetrics
Downloads
1854
Views
1399
Comments
0
This version is not peer-reviewed
Social Change and Transition
Submitted:
27 August 2024
Posted:
28 August 2024
You are already at the latest version
Alerts
Abstract
Three Fresnel coefficients for the normal incidence of electromagnetic radiation on monolayer graphene establish three complementary fine-structure constants, two of which are negative. Each introduces its own specific set of Planck units. Hence, two sets of basic Planck units are real and two are imaginary. The elementary charge is the same in all those sets of Planck units, establishing equality between the products of each fine-structure constant and the speed of light it is associated with, and defining the dark electron in each of these three complementary systems. All fine-structure constants are related to each other through the constant of pi, which indicates that they do not vary over time. The negative complementary fine-structure constant established by the graphene reflectance is dual to the fine-structure constant. The assumption of universality of the black hole entropy formula to the remaining two stellar objects emitting perfect black-body radiation less dense than a black hole (neutron stars and white dwarfs) renders their energies exceeding their mass-energy equivalence. To accommodate this unphysical result, we introduced an imaginary mass and defined three complex energies in terms of real and imaginary Planck units, storing the surplus energy in their imaginary parts. It follows that black holes are fundamentally uncharged and have a vanishing imaginary mass. We have derived the lower bound on the mass of a charged black-body \textit{object}, the upper bound on a white dwarf radius, and the equilibrium density of all three complex energies. The complex force between real masses and imaginary charges leads to the complex black-body \textit{object's} surface gravity and generalized Hawking radiation complex temperature. Furthermore, based on the Bohr model for the hydrogen atom, we show that complex conjugates of this force represent atoms and antiatoms. The proposed model considers the value(s) of the fine-structure constant(s), which is(are) otherwise neglected in general relativity, and explains the registered (GWOSC) high masses of neutron star mergers and the associated fast radio bursts (CHIME) without resorting to any hypothetical types of exotic stellar objects.
Keywords:
Subject: Physical Sciences - Mathematical Physics
1. Introduction
The universe began with the Big Bang, a prevailing scientific opinion. However, this Big Bang was not an explosion of 4-dimensional spacetime, which is also a current prevailing scientific opinion, but an explosion of dimensions that started in -dimensional void. The only exception to the general formula for the integral of a volume unit , where a is the length of an edge in any dimension n is , where a jump discontinuity occurs and . A first 0-dimensional point appeared in the -dimensional void, inducing the appearance of other points that were indistinguishable from the first. The breach made by the first operation of the dimensional successor function of the Peano axioms inevitably continued leading to the formation of 1-dimensional, real and imaginary lines, allowing for an ordering of points using multipliers of real units (ones) or imaginary units (, and , where ). Then, out of the two lines of each kind, crossing each other only at one initial point , the dimensional successor function formed 2-dimensional , , and Euclidean planes, with being a mirror reflection of . Thus, forming n-dimensional Euclidean spaces with real and imaginary lines, , and the scalar product defined by
where . With the appearance of the first 0-dimensional point, information has begun to evolve [1,2,3,4,5,6,7,8,9], initially using undirected exploration in a selectionless [8] and a timeless [9] assembly process.
Mathematics is theoretically infinite, so determining why some math corresponds to our observable universe and the rest does not is a highly nontrivial problem [10]. Fortunately, the mathematical properties of particular dimensions are not the same. For regular convex n-polytopes, for example, there are countably infinitely many regular convex polygons, five regular convex polyhedra (Platonic solids), six regular convex 4-polytopes and only three regular convex n-polytopes if and [11]. In particular, a 4-dimensional Euclidean space is endowed with a peculiar property known as exotic [12], absent in other dimensionalities. Owing to this property, Euclidean space provides a continuum of homeomorphic but non-diffeomorphic differentiable structures and this is necessary for biological evolution, as it allows the variation of phenotypic traits within populations of individuals [13]: each piece of individually memorized information is homeomorphic to the corresponding piece of individually perceived information but remains non-diffeomorphic (non-smooth). Hence, selection [8] and time [9] emerged and the evolution of information had to inevitably exploit directed exploration provided by biological evolution. Exotic solves the problem of extra dimensions of nature, and perception requires a natural number of (thus independent) dimensions to form perceived space [14]. Each biological cell and each biological agent perceives an emergent space of three real dimensions and one imaginary (time) observer-dependently [15] and at present, when is real, through a spherical Planck triangle corresponding to one bit of information in units of , where c is the speed of light in vacuum. This is the principle of emergent dimensionality (ED) [5,6,9,13,16,17].
Human perception involves measuring and measuring requires measurement units. In 1899 Max Planck derived the natural units of measure as "independent of special bodies or substances, thereby necessarily retaining their meaning for all times and for all civilizations, including extraterrestrial and nonhuman ones" [18]. Planck units utilize the Planck constant h introduced in his black-body radiation formula. Earlier, in 1881, George Stoney derived a system of natural units [19] based on the elementary charge e (Planck’s constant was unknown at this time). The ratio of Stoney units to Planck units is , where is the fine-structure constant. This study derives three complementary sets of Planck units based on the three complementary fine-structure constants established by the Fresnel coefficients for the normal incidence of electromagnetic radiation on monolayer graphene (MLG) and hints at certain areas of their applicability. We chose Planck units over other natural unit systems not only because they incorporate the fine-structure constant and the Planck constant h. Other systems of natural units (except for Stoney units) also incorporate them. This is because only the Planck area defines one bit of information on a patternless black hole surface given by the Bekenstein bound (52) and the binary entropy variation [5,6].
The paper is organized as follows. Section 2 shows that the Fresnel coefficients for the normal incidence of electromagnetic radiation on MLG include three complementary fine-structure constants, including two negative ones and hinting that the negative complementary fine-structure constant established by the graphene reflectance is dual to the fine-structure constant . Section 3 presents complementary sets of -Planck units established by these three fine-structure constants. Section 4 introduces the concept of a black-body object in thermodynamic equilibrium that emits perfect black-body radiation and reviews its necessary properties. Section 5 introduces complex energies expressed in terms of real and imaginary -Planck units and applies them to black-body objects to show that in this model and are indeed dual to each other. Section 6 defines complex forces based on the products of the complex energies. The complex force between real masses and imaginary charges is applied in Section 7 to the Bohr model of the hydrogen atom and in Section 8 to derive a black-body object surface gravity and the generalized Hawking radiation temperature. Section 9 considers the observed mergers of black-body objects to show that the observed data can be explained without the need to introduce hypothetical exotic stellar objects. Section 10 discusses fluctuations of black-body objects. Section 11 summarizes the findings of this study.
2. Three Complementary Fine-Structure Constants
Numerous publications provide Fresnel coefficients for the normal incidence of electromagnetic radiation (EMR) on monolayer graphene (MLG), which are remarkably defined only by and the fine-structure constant having the inverse
where is the Planck charge, ℏ is the reduced Planck constant, is the vacuum permittivity (electric constant), and e is the elementary charge. We choose this set of units over [F] for , since the mass, length, time, and charge units can express all the electrical units and together with temperature, amount of substance, and luminous intensity, these are the base units of the International System of Quantities (ISQ). Furthermore, in this notation we see that is dependent on the unit of time. Transmittance (T) of MLG
for normal EMR incidence was derived from the Fresnel equation in the thin-film limit [20] (Eq. 3), whereas a spectrally flat absorptance (A) has been reported [21,22] for photon energies between approximately and [J]. T is related to reflectance (R) [23] (Eq. 53) as , i.e,
The above equations for T and R, as well as the equation for the absorptance
were also derived [24] (Eqs. 29-31) based on the thin-film model (setting for the substrate). The sum of the transmittance (3) and reflectance (4) at normal EMR incidence on the MLG was derived [25] (Eq. 4a) as
where [] is the vacuum impedance, [] is the MLG conductivity [26], k is the wave vector of light in vacuum, and is the electric susceptibility of vacuum. Therefore, these coefficients are well established both theoretically and experimentally [20,21,22,25,27,28].
As a consequence of the conservation of energy
In other words, the transmittance in the Fresnel equation describing the reflection and transmission of EMR at normal incidence on a boundary between different optical media is, in the case of the 2-dimensional (boundary) MLG, modified to include its absorption (cf. Appendix C). Furthermore, and . Notably for Fresnel coefficients (A12) (cf. Appendix C), solves to which implies no refraction. We note that each conservation law is associated with a certain symmetry, as asserted by Noether’s theorem. In this case, the symmetry involves the fine-structure constant and .
2.1. Reflectance
The reflectance (4) of the MLG can be expressed as a quadratic equation of
which can be expressed in terms of the reciprocal of , defining as
The quadratic equation (9) has two roots
Therefore, equation (8) includes the second negative fine-structure constant . It turns out that the sum of the reciprocals of these fine-structure constants (10) and (11)
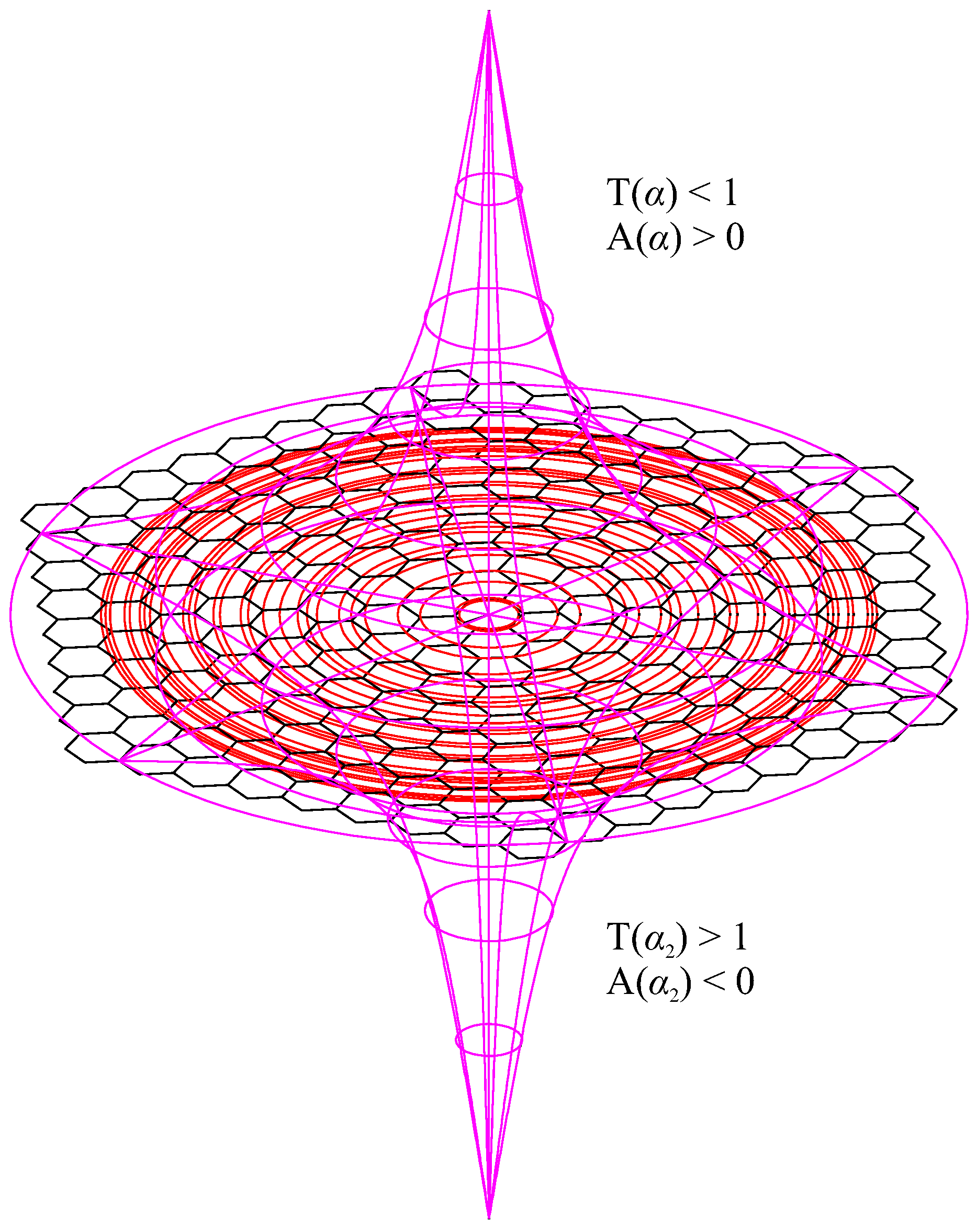
is a transcendental number independent of the value of the reflectance R. Furthermore, the minimum of parabola (9) amounts and occurs at , as shown in Figure 1. Also, these values are independent of the reflectance.
These results are also intriguing in the context of a peculiar expression of the fine-structure constant [29] as a transcendental number
that contains a free term and is very close to the physical definition (2) of , which according to the CODATA 2022 value is . We note that CODATA values are computed by averaging the measurements.
2.2. Transmittance and Absorptance
The transmittance (3) of MLG can also be expressed as a quadratic equation of
having two roots
where is the third negative fine-structure constant. Their sum hints taxicab geometry (where )
and is also independent of the value of the transmittance T. The third complementary fine-structure constant expressed by using relations (13) and (17) is
Finally, the absorptance (5) of MLG can be expressed as a quadratic equation of
having two roots
where is the fourth positive fine-structure constant. Their product
is also a transcendental number independent of the value of the reflectance A. The minimum of parabola (19) amounts and occurs at . The fourth complementary fine-structure constant expressed by using relations (13) and (21) is
2.3. Summary
The form of the relations (13), (14) is the same (contains the same like-terms with respect to ) as the relation (126) describing the information capacity of a black body object after absorption or emission of a particle. Furthermore, the relation (12) corresponds to the following identity
between the roots (10) and (11), which is also derivable from the Fresnel equations and the corresponding Euclid formula (cf. Appendix C). Because the fine-structure constants are expressible by only, we conjecture that they do not vary over time. They could not vary in the first undirected [8] and timeless [9] part of the evolution of information in the universe. Also, combining relations (23) with (17) and (21) yield
Furthermore, we can interpret as a phase of a complex number, as shown in Figure 2. Using relations (13) and (14) along with angle sum and difference trigonometric identities we obtain
Finally, . Therefore, we conclude that only and are dual to each other and we introduce for or .
Using relations (13), (14), (18), and (22) the MLG coefficients (3)-(5) can be expressed simply by (cf. Appendix A) and introduce three pairs of -like constants for two surfaces with positive and negative Gaussian curvatures (cf. Appendix B). Interestingly, and .
In the following section, we derive the complementary sets of Planck units corresponding to the complementary fine-structure constants . We shall use the subscript "*" as a placeholder for all four fine-structure constants, and the subscripts "+", "−" to describe respectively positive or and negative or and quantities associated with them. Occasionally we use the subscript 1 for quantities associated with .
3. Complementary Sets of Planck Units
Natural units can be derived from numerous starting points [6,30] (cf. Appendices Appendix E). The central assumption in all systems of natural units is that the quotient of the unit of length and time is a unit of speed; we call it . It is the speed of light in vacuum c in all systems of natural units, except for Hartree and Schrödinger units, where it is , and Rydberg units, where it is . Hence, is coupled with c in Hartree, Schrödinger, and Rydberg measurement units.
The fine-structure constant can be defined as the quotient (2) of the squared (and thus positive) elementary charge e and the squared Planck charge . To accommodate the negativity of the fine-structure constants discovered in the preceding section, we must introduce the imaginary Planck charge such that its square would yield a negative value.
For example, in the case of
Therefore
We note that an imaginary , which must have a physical definition analogous to , requires either a real, negative speed of light or some complementary real, negative electric constant (h is positive). Let us call them and
From this equation, we find that , because the values of the other constants are known.
We assume the universality of the Planck constant h and the gravitational constant G. However, this assumption may be too far-reaching, given that we do not need to know the gravitational constant G or Planck constant h to find the product of the Planck length and c, [31], i.e., we know how to express three physical constants by two only. This resembles a qubit, which in general requires three real numbers to be described, whereas if it encodes only one of its states, then just two real numbers suffice.
The fine-structure constant can also be defined as the ratio of Coulomb’s law for two elementary charges to Newton’s law of gravity for two Planck masses separated by the same distance. Constructing the same ratio for the remaining leads to
where the area of a 3-ball () in the denominator of the Coulomb force requires further investigation. Hence, the quotient of the squared Planck charge and mass must be the same for all sets of Planck units. Therefore
is independent of the unit of time (even though and G are) and introduces the imaginary Planck masses . The masses can be calculated from equation (30) by determining the value of the Planck charge from equation (27). From (30) we also conclude that and then by (31) that and . Next, we assume that the solution of Maxwell’s equations in vacuum is valid for other values of the constants involved. Let us call the unknown magnetic constant, corresponding to , . Therefore,
from which the bivalued can be obtained. Unlike the electric constant , magnetic constants are independent of the unit of time. Furthermore, Maxwell’s equations in vacuum are not directly dependent on the fine-structure constant(s), which is included in the magnetic constant . Finally, combining relations (27) and (28) yields
which establishes the universality of the elementary charge e that defines both matter and antimatter and leads to the following important relation between the speeds of light in vacuum , and the fine-structure constants
is also the velocity of the electron in the first circular orbit in the Bohr hydrogen atom model to which we shall return in Section 7. Because each derivable from the final Maxwell equation (31) is bivalued, all sets of -Planck units have four forms equal in modulus: real positive, real negative, imaginary positive and imaginary negative. However, due to the relation (33), we consider mostly real, positive -Planck units and imaginary, positive -Planck units. We note that switching the signs of in the relation (33) would require the imaginary elementary charge . Therefore, we consider real Planck units associated with the positive speed of light associated with in the Appendix D only.
Complementary speeds of light (33) introduce complementary sets of Planck units, wherein basic -Planck units are imaginary since they are defined as square roots containing raised to odd powers (1, 3, 5). Furthermore, the speed of electromagnetic radiation is the product of its wavelength and frequency, and these quantities would be imaginary in terms of imaginary Planck units; a negative speed of light is necessary to accommodate this.
-Planck units that can be expressed, using the relation (33), in terms of base Planck units , , , , and are
Most Planck units derived from the -Planck base units (34)-(38) are also imaginary. These include the Planck volume
the Planck momentum
the Planck energy
and the Planck acceleration
However, the -Planck density
and the -Planck area
are real and negative. Interestingly, both Planck forces and
are strictly positive. The remaining sets of Planck units are listed in Table 1.
Contrary to the elementary charge e (27), there is no physically meaningful elementary mass satisfying the relation (36)
There is no physically meaningful elementary length satisfying the relation (35)
or an elementary temperature satisfying the relation (38)
and close to the Hagedorn temperature of grand unified string models, or an elementary period satisfying the relation (37)
However, the relations between periods (49) and temperatures (48) are inverted. Hence, the energy-time version of Heisenberg’s uncertainty principle (HUP) is saturated using energy from the equipartition theorem for one bit of information [5,6,32] both by Planck temperatures and times and elementary temperatures and periods (49), (48)
The Planck charge relation (27) and charge conservation principle imply that the elementary charge e, unlike mass is the same in all systems of Planck units, even though the same forms of the relations (27) and (46) reflect the same forms of Coulomb’s law and Newton’s law of gravity, which are inverse-square laws.
Condensed-matter systems having two pairs of sublattices located at half-translation positions and related by multiple glide-reflection symmetries, such as palladium diselenide, make their relative quantum phases polarized into only four kinds, three of which become dark due to double destructive interference [33]. This is akin to two qubits with one fixed quantum phase. The dark quantum state does not absorb or emit photons and, therefore, is undetectable by spectroscopic means. Considering this result and the equality of the elementary charge e in all systems of Planck units that we derived based on a condensed-matter system having only one pair of sublattices, and thus analogous to only one qubit, we note the elementary charge e in these three complementary systems defines the dark electron of these systems. Thus (blue) dark state disclosed in [33] corresponds to -electron, (red) state corresponds to -electron, and (green) and (yellow) states correspond to - and -electrons.
In the following, where deemed appropriate, we express the physical quantities in Planck units:
where uppercase letters M, E, Q, , R, and D denote masses, energies, charges, Compton wavelengths, radii, and diameters (or lengths), lowercase letters m, l, etc. denote multipliers of the real and imaginary Planck units, respectively, and q is an integer multiplier of the elementary charge e. The latter assumption is most likely too far-reaching, considering the fractional charges of quasiparticles, particularly in the open research problem of the fractional quantum Hall effect (cf. Appendix G) and energy-dependent fractional charges in electron pairing [34].
4. Black Body Objects
There are only three observable objects in nature that emit perfect black-body radiation: unsupported black holes (BHs, the densest), neutron stars (NSs), supported, as believed, by neutron degeneracy pressure, and white dwarfs (WDs), supported, as believed, by electron degeneracy pressure (the least dense). We collectively refer to these black-body objects (BBs). The spectral density in sonoluminescence, that is light emission by sound-induced collapsing gas bubbles in fluids, was also shown to have the same frequency dependence as black-body radiation [35,36]. Thus, sonoluminescence, particularly shrimpoluminescence [37], is probably emitted by collapsing micro-BBs. Micro-BH induced in glycerin by modulating acoustic waves has also been reported [38].
The term black-body object is not used in general relativity (GR) and standard cosmology, but standard cosmology scrunches under embarrassingly significant failings, not just tensions as is sometimes described, as if to somehow imply that a resolution will eventually be found [39]. In addition, James Webb Space Telescope data show multiple galaxies that grew too massive too soon after the Big Bang, which is a strong discrepancy with the cold dark matter model (CDM) expectations of how galaxies formed at early times at both redshifts, even when considering observational uncertainties [40]. For example, the supermassive BH of J1120+0641 quasar with mass assembled in less than 0.77 billion years after the Big Bang [41,42]. This is an important unresolved issue, indicating that fundamental changes to the reigning CDM model of cosmology are required [40]. In particular, it is well known that entropic gravity [32] explains the galaxy rotation curves without resorting to dark matter (dark matter is not required to explain the rotation curves of certain galaxies, such as the massive relic galaxy NGC 1277 [43]), has been experimentally confirmed [44], and is decoherence-free [45].
The term object as a collection of matter is a misnomer because it neglects the (quantum) nonlocality [9,46] that is independent of the entanglement among particles [47], as well as the Kochen-Specker contextuality [48], and increases as the number of particles increases [49,50]. Macro-realistic theories are false [51]. Thus, we use emphasis for (perceivably indistinguishable) particle and (perceivably distinguishable) object, as well as matter and distance. The ugly duckling theorem [52,53] asserts that every two objects we perceive are equally similar (or equally dissimilar). These terms do not have an absolute meaning in the ED. In particular, given the observation of quasiparticles in classical systems [54]. Within the ED framework, no object is enclosed in space. The interiors of the BBs are inaccessible to an exterior observer [55], which makes them similar to interior-less mathematical points representing real numbers on a number line. Thus, the term object is a particularly staring misnomer if applied to BBs.
It has been experimentally confirmed that (so-called) accretion instability is a fundamental physical process [56]. We conjecture that this process, which has already been recreated under laboratory conditions [57], is common for all BBs. As black-body radiation is a radiation of global thermodynamic equilibrium, it is patternless [58] (thermal noise) radiation that depends only on one parameter. In the case of BHs, this is known as Hawking [59] radiation, and this parameter is the BH temperature corresponding to the BH diameter [6] . Furthermore, BHs absorb patternless information [6,60]. Therefore, because Hawking radiation depends only on the diameter of a BH, it is the same for a given BH, even though it fluctuates (cf. Section 10).
As black-body radiation is patternless, triangulated [6] BBs contain a balanced number of Planck area triangles, each having binary potential , as has been shown for BHs [6], based on the Bekenstein-Hawking (BH) entropy [55] , where is the information capacity of the BH surface, i.e., the Planck triangles corresponding to bits of information [5,6,32,55,61], and the fractional part triangle(s) having the area too small to carry a single bit of information [5,6], where "" is the floor function that yields the greatest integer less than or equal to its argument x.
BH entropy can be derived from the Bekenstein bound
which defines an upper limit on the thermodynamic entropy S that can be contained within a sphere of radius R and energy E. Substituting BH (Schwarzschild) radius and mass-energy equivalence , where is the BH mass, into the bound (52), it reduces to the BH entropy. In other words, the BH entropy saturates the Bekenstein bound (52). Furthermore, the Bekenstein bound can be derived from the BH entropy
where we used and .
The patternless nature of perfect black-body radiation was derived [6] by comparing the BH entropy with the binary entropy variation ([6] Eq. (55)), which is valid for any HS, where denotes the number of active Planck triangles with a binary potential . Thus, the entropy of all BBs is
Furthermore, confirms the patternless thermodynamic equilibrium of BBs by maximizing Shannon entropy [6]. In complex Euclidean space, a n-ball () is spherical only for , i.e., when perceived. Not only BBs are perfectly spherical when perceived; their mergers (cf. Section 9) are also perfectly spherical. Furthermore, the trigonometric member of its volume and surface formulas vanishes for the radius [5,17]. This is an important result since is a dimensionless mathematical value like or , while , providing the information capacity and hence one unit of BB entropy (54) is a physical one. Anyway, this corroborates the universality and applicability of BH entropy (54) to all BBs. Furthermore, some binary strings of of length can be assembled in less than steps. There is no disorder or uncertainty in a binary string of length [9].
We shall define the generalized radius of a BB (this definition applies to all HSs) having mass as a function of multiplier
and the generalized BB energy (this definition also applies to all HSs) as a function of multiplier
Substituting from the generalized radius definition (55) into the generalized BB energy definition (56) and the latter into the Bekenstein bound (52), we obtain
which equals BB entropy (54) if . Thus, the energy (56) of all BBs with a generalized radius (55) turns into
with in the case of the BHs, setting the lower bound for the other BBs. We further call coefficient k the size-to-mass ratio (STM). This is similar to the specific volume (reciprocal of density) of BB. We derive the upper STM bound in Section 5. The energy (58) of BBs other than BHs (i.e., for ) exceeds the mass-energy equivalence , which is the limit of the maximum real energy. Therefore, we consider this surplus energy that exceeds as related to charge and we shall model it as imaginary and thus unmeasurable.
According to the no-hair theorem, all BHs general relativity (GR) solutions are characterized by only three parameters: mass, electric charge, and angular momentum. However, BHs are fundamentally uncharged, because the parameters of any conceivable BH, in particular, charged (Reissner–Nordström) and charged-rotating (Kerr–Newman) BH, can be arbitrarily altered, provided that the BH area does not decrease [62] using Penrose processes [63,64] to extract the electrostatic and/or rotational energy of BH [65]. Thus, any BH is defined by only one real parameter: its diameter, mass, temperature, energy, etc., each differing from the other by a multiplicative constant. A BH can embrace the real number that defines it as a curvature of a spherical triangle corresponding to one bit of classical information. The area of a spherical triangle is larger than that of a flat triangle defined by the same vertices and depends on its curvature.
However, it is accepted that in the case of NSs, electrons combine with protons to form neutrons, such that NSs are composed almost entirely of neutrons. However, it is never the case that all electrons and protons of an NS become neutrons. WDs are charged by definition because they are believed to be mostly composed of electron-degenerate matter. But how can a charged BB store both its curvature corresponding to its mass and an additional parameter corresponding to its charge? Fortunately, the relation (27) ensures that the elementary charge is the same in all systems of Planck units. Therefore, the charge of a spherical Planck triangle of a BB surface can link the perceivable Euclidean space parameterized by Planck units with the parameterization provided by one of the remaining negative fine-structure constants . This can be considered in a polyspherical coordinate system, in which gravitation/acceleration acts in a radial direction (with the entropic gravitation acting inwardly and acceleration acting in both radial directions) [6], while electrostatic acts in tangential directions. Contrary to the no-hair theorem, we characterize BBs only by mass and charge, neglecting the angular momentum because the latter introduces the notion of time, which we find redundant in the BB description of a patternless thermodynamical equilibrium. Time is required for directed exploration only [8,9].
5. Complex Energies
A complex energy formula
where and represent the real and imaginary energies of an object having mass and charge was proposed in ref. [66]. Equation (59) considers the real masses and charges which in ref. [66] are defined in CGS units. We adopted SI units and modified this formula to a form involving real physical expressed in terms of real -Planck units and imaginary quantities expressed in terms of the imaginary -Planck units using relations (33), (36), (41), (51), and (32) as
To this end, we defined the following three complex energies linking mass, imaginary mass, and charge: the complex energy of real mass and imaginary charge
of real charge and imaginary mass
and of real mass and imaginary mass
We neglected the energy of real and imaginary charges , because by equation (27), the elementary charge is the same in all systems of measurement units, and hence we use the same elementary charge multiplier q in (51). Furthermore, the mass-energy equivalence relates the mass or to the speed of light or , which subsequently parameterizes both parts of the energies and (cf. Appendix F). We express all energies (61)-(63) in terms of the same Planck energy in order to be able to compare them, as we assume that they are fundamental to any object and particle. We also note that the complex conjugates and of the energy (61) represent respectively particle and antiparticle. We note that antimatter obeys gravity [67], which is consistent with the definition (61) and the findings of this study.
In the remainder of this section we shall analyze the energies (61)-(63) for different pairs of in order , , , and . Our aim is to determine which pair is the most plausible physically.
Energies (61) and (62) yield two different charge energies corresponding to the elementary charge, imaginary quantum
and the - larger in modulus - real quantum
Furthermore, , . The universal character of the charges is additionally emphasized by the real multiplied by i in the imaginary charge energy (61) and imaginary in the real charge energy (62).
Proof.
The complex energies and are balanced if their real and imaginary parts are equal in modulus. This holds for
However, if balanced with each other, they cannot be balanced with the energy , which is balanced for
defining the energy balance of uncharged masses. Similarly, the complex energies and can be balanced with each other but not with since
and likewise for and . □
The squared moduli of the complex energies (61)-(63), expressed in terms of the Planck energy, are
ad shown in Figure 3.
Equalities of the squared moduli of the complex energies lead to the following results
Because the mass multiplier , the square root argument must be nonnegative in equation (72), which leads to (the sign of this inequality changes, as )
which is imaginary for ruling out the third pair of alphas . Otherwise, we would have to exclude objects having the same energies and from our model. Furthermore, for equation (72) yields
which corresponds to equation (67).
Furthermore, the relation (75) means that the masses of the uncharged micro-BHs () can be arbitrary (). However, micro NSs and micro WDs, which are also in thermodynamic equilibrium, are charged. Thus, even a single elementary charge () of a white dwarf renders its minimum allowable mass (75) comparable to the mass of a sand grain.
Proof.
If the squared moduli (69)-(71) are equal to some constant energy then drops out by subtracting , yielding
Subtracting this from yields
which substituted into the relation (79) yields
□
We can interpret the squared generalized energy of the BBs (58) as the squared modulus of each of the complex energies (69)-(71). That is, for (61) and for (63), we assume that the real mass energy of the BB is the observable real part of this complex energy. For (69) we have
where represents the charge surplus energy exceeding . We note that implies , confirming the vanishing charge of BHs. For (71) we have
where the square root argument must be nonnegative, which implies (along with (83)), as expected, , where implies . Finally, for (70) we have
where we substituted as a function of from equation (83). Comparison of given by (85) with given by (72) also leads to , and for or corresponds to the balance of uncharged masses (67), (76) which are unrelated to any assumptions regarding BB energy and independent of STM. Comparing equations (72), as a function of charge q, and (85), as a function of the STM k, leads, as expected, to the relation (83).
Furthermore, the square root argument in equation (85) must be nonnegative, because . This leads to the maximum STM-bound
where again third pair of examined alphas must be ruled out, while pairs and do not allow to extend our model above the STM of BH. The relations (83) and (85) are shown in Figure 4 for and .
The maximum STM-bound (86) sets the bounds on BB energy (58), mass, and radius (55)
In particular, using the relations (51), or .
From the relation (78) we see that uncharged BHs () cannot remain in a nonvanishing equilibrium of complex energies (77), even though they are in thermodynamic equilibrium. It was shown [5] based on the Mandelstam-Tamm [68], Margolus–Levitin [69], and Levitin-Toffoli [70] theorems on the quantum orthogonalization interval that a BH is represented by a qubit in an equal superposition of the eigenstates corresponding to the BH energy and vanishing ground state energy. However, such a nonvanishing equilibrium of complex energies (77) is possible for charged BBs. We obtain it by substituting squared generalized energy of the BBs (58) into equation (77) as and solving for . This yields
where all three energies are equal. The equilibrium (88) and maximum (86) STMa satisfy (which resolves to ).
The relations (75), (86), and (88) show that the negative fine-structure constant corresponding to is not . As we have seen in Section 2.3, and are dual to each other. The BB having the STM (88) and the elementary charge () would have mass , imaginary mass , corresponding to the Compton wavelength , and the imaginary Compton wavelength . On the other hand, equation (83) provides the BB charge in equilibrium (77) as and the limit of the BB charge .
We note that BBs with STMs are referred to as ultracompact [71], where is a photon sphere radius, at which, according to an accepted photon sphere definition, the strength of gravity forces photons to travel in orbits. The author wonders why the photons would not travel in orbits at a radius corresponding to the orbital velocity of mass M. Obviously, according to the ED principle, photons do not travel. Any object that undergoes complete gravitational collapse passes through an ultracompact stage [72], where . Collapse can be approached by gradual accretion, increasing the mass to the maximum stable value, or by the loss of angular momentum [72]. During the loss of angular momentum, the star passes through a sequence of increasingly compact configurations until it finally collapses and becomes a BH. It was also pointed out [73] that for a neutron star of constant density, the pressure at the center would become infinite if , which is the radius of the maximal sustainable density for gravitating spherical matter given by Buchdahl’s theorem. It was shown [74] that this limit applies to any well-behaved spherical star, where the density increases monotonically with the radius. Furthermore, some observers would measure a locally negative energy density if thus breaking the dominant energy condition, although this may be allowed [75]. As the surface gravity increases, photons from further behind the NS become visible. At the entire NS surface becomes visible [76]. The relative increase in brightness between the maximum and minimum of a light curve is greater for than for [76]. Furthermore, defining a photon capture radius [77], the effective radius for capturing photons that approach the black hole from infinity is about of (86). Therefore, the equilibrium and maximum STM ratios (88), (86) satisfying are well within the range of radii of ultracompact objects researched in the state-of-the-art within the GR framework.
However, aside from the Schwarzschild radius, derivable from the escape velocity of mass M by setting , and discovered in 1783 by John Michell [78], all the remaining significant radii of GR are only approximations. GR neglects the value of the Planck constant and the fine-structure constants and , which, similar to or the base of the natural logarithm, are fundamental constants of nature. Constructive criticism of GR can be found, for example, in [79,80,81,82,83,84,85].
Therefore, we conjecture that is the correct value of the photon sphere radius and is the correct value of a photon capture radius. These radii are indirectly measured by the Event Horizon Telescope (EHT), a telescope array consisting of a global network of radio telescopes, each associated with an atomic clock. The signals collected by each telescope are stored along with time stamps and subsequently shipped to one location to be synchronized and processed. The EHT observational targets are the Milky Way’s BH, Sagittarius A* (Sgr A*) and the M87* BH at the center of the Messier 87 galaxy. The EHT data processing model assumes a Kerr BH (uncharged, spinning) [77,86] and is suitable for prograde accretion disks [86] (spinning in the same direction as a BH). The first assumption is congruent with our results; in this and in the preceding sections we have shown that BHs are fundamentally uncharged.
The processed Sgr A* and M87* signals revealed ring-like structures surrounding these BHs, which were compared with a large suite of general-relativistic magnetohydrodynamics (GRMHD) simulations [77,86]. However, the GRMHD simulations turned out to be more variable than the observed signals and only a few configurations could satisfy the full set of observational constraints apart from variability, hinting that more work is needed to fully explore the physical parameter space and to understand this variability, as these variations challenge standard approaches to interferometric analysis. Subsequently, measurements of the first in an infinite series of photon rings around M87* were reported [87] based on simultaneous modeling and imaging of the EHT signals. However, the photon ring calculated by this method turned out to be much brighter than expected, while it should be emitting only around 20 percent of the light in the image, as general relativity predicts [88]. Therefore, it may be just picking out an unrelated structure in the image [89] and M87* and Sgr A* EHT observations have yet to experimentally resolve any photon ring [90,91,92,93]. This ambiguity requires further research of these ring-like structures revealed by the EHT within the ED framework, considering the equilibrium and maximum STM ratios (88) and (86) that may accurately describe them.
6. Complex Forces
The complex energies (61)-(63) define the complex forces (similarly to the complex energy of real masses and charges (59); cf. ref. [66] Eq. (7)). Using the relations (51), we obtain the following three complex products of energies
where is the energy of object 1 and is the energy of object 2. Their squared moduli are
Products of energies (89)-(91) define three complex forces acting over a real distance
and three complex forces acting over an imaginary distance
where and . We express the forces (93) and (94) in terms of the Planck force in order to compare them, which yields
7. Extended Bohr Model
The Bohr model of the hydrogen atom is based on three assumptions that can be conveniently expressed in terms of Planck units using relations (51). The first assumption of a natural number of electron wavelengths that fits along the circumference of the electron’s orbit of radius R becomes:
The second assumption, de Broglie’s relation between electron mass , velocity and wavelength becomes
Finally, the third assumption postulated equality between the centripetal force exerted on the electron orbiting around the proton (assuming an infinite mass of the latter) and the Coulomb force between the electron and proton becomes:
It is remarkable that such a simple postulate alone, expressed in terms of Planck units, introduces the fine-structure constant . Joining relations (96) and (97) yields
which combined with (98) and using the relation (33) yields
Thus, in the first circular orbit () of this model, the electron velocity factor . In the Bohr model of atoms other than hydrogen this equality of forces is extended to a point-like set of Z electrons orbiting around a nucleus, where Z is the atomic number.
Furthermore, since the proton and the electron have different signs of the elementary charge e, the Coulomb force should be considered negative in this model.
To quantify charges, we assume that the centripetal force acting on the electron is equal to the complex force (93) with the product of real mass and imaginary charge energies (89) and, motivated by the short multiplication formula and the two-body problem we describe, use the reduced mass of the proton-electron system. This yields
where we set and as the electron and proton charges, respectively, from the electron mass [kg] and the proton mass [kg]. The equation (101) yields complex velocity
assuming that R is equal to the Bohr radius or the complex radius
assuming that the Bohr model gives the velocity of the electron, that is, . However, neglecting their insignificant imaginary parts, they correspond to their Bohr model counterparts. This is because the gravitational attraction between the proton and the electron in hydrogen atom ( N) is negligible compared to the Coulomb force between them ( N).
We further note that switching the signs of charges (, ) provides complex conjugates of the relation (101), which in this case describes the antihydrogen. Thus, we conjecture that the energy generated by a hydrogen-antihydrogen collision, predicted by this extended Bohr model, is
Expressed in terms of Planck units and the reduced mass of the proton-electron system, the Rydberg constant for hydrogen is
The inverse of the corresponding Rydberg formula for hydrogen can be expressed using the relation (13) for as
using the wavelength relation (51) and expression (13). The coefficients form part of the OEIS sequence A158565 for .
8. BB Complex Gravity and Temperature
We can use the complex force (93) with the product (89) (i.e., complex Newton’s law of universal gravitation) to calculate the BB surface gravity , assuming an uncharged () test mass and comparing this force with Newton’s 2nd law of motion
where , . Substituting from the BB energy relation (83) and the mass taken from the generalized BB radius (55) into the relation (107) yields
which reduces to BH surface gravity for and in modulus
for all k and is remarkably independent of . In particular,
The BB surface gravity (108) leads to the generalized complex Hawking blackbody radiation equation:
describing the BB temperature by including its charge in the imaginary part, which also for and in modulus reduces to the BH temperature for all k. In a commonly used, equivalent form it is
In particular,
reduce to the BH temperature for . Therefore, a universe without the negative fine structure constants (i.e., with ) would be a black hole disallowing the directed exploration [8,9] of the evolution of information [1,2,3,4,6,7]. This kind of exploration requires imaginary time [6]. And we cannot zero as we would have to neglect the existence of graphene, estimated to form about of total interstellar carbon [94] and recently discovered on the Moon [95].
9. BB Mergers
As the entropy (Boltzmann, Gibbs, Shannon, von Neumann) of independent systems is additive, a merger of BB1 and BB2 having entropies (54) and , produces a BBC with entropy (we drop the HS subscripts in this section for clarity)
which shows that the resultant information capacity is the sum of the information capacities of the merging components. Thus, a merger of two primordial BHs, each with the Planck length diameter, the reduced Planck temperature (the largest physically significant temperature [5]) produces a BH having which represents the minimum BH diameter allowing for the notion of time [5]. In comparison, a collision of the latter two BHs produces a BH with and the triangulation defining only one precise diameter between its poles (cf. [6] Figure 3(b)), which is also recovered from HUP (cf. Appendix E).
Substituting the generalized diameter (55) into the entropy relation (116) establishes a Pythagorean relation between the generalized energies (58) of the merging components and the merger
It is accepted that gravitational events observations alone allow measuring the masses of the merging components, setting a lower limit on their compactness, but it does not exclude mergers that are more compact than neutron stars, such as quark stars, BHs, or more exotic objects [96]. We note in passing that describing the registered gravitational events as waves is misleading: normal modulation of the gravitational potential, registered by LIGO and Virgo interferometers, and caused by rotating (in the merger case, inspiral) objects is wrongly interpreted as a gravitational wave understood as a carrier of gravity [97]. It has also been shown that from a mathematical point of view, the quadrupolar waves in a quantum spin nematic are in one-to-one correspondence with quantized gravitational waves in a flat, 4-dimensional spacetime [98].
The accepted value of the Chandrasekhar WD mass limit, which prevents its collapse into a denser form, is [99] and the accepted value of the analogous Tolman-Oppenheimer-Volkoff NS mass limit is [100,101]. There is no accepted value for the BH mass limit. The conjectured value is . We note in passing that a BH with a surface gravity equal to the Earth’s surface gravity (9.81 m/s2) would require a diameter of (slightly less than one light year) [6] and mass exceeding the conjectured limit. The masses of most registered merging components go well beyond . From those that do not, most of the total or final masses exceed this limit. Therefore, these mergers (, , , , , ) are classified as BH mergers. Only a few were classified otherwise, including GW170817, GW190425, GW200105, and GW200115, as listed in Table 2.
Equation (117) explains the measurements of large masses of BB mergers with at least one charged merging component without resorting to any hypothetical types of exotic stellar objects such as quark stars. Interferometric data, available online at the Gravitational Wave Open Science Center (GWOSC) portal1, indicates that the total mass of a merger is the sum of the masses of the merging components. Thus
We can use the squared moduli , , and (83)-(84) and the relation (117) to derive some information about the merger from equation (117). We shall initially assume , since negative masses, similar to negative lengths, and their products with positive ones, are (in general [102]) inaccessible for direct observation, unlike charges. (83) with the first inequality (118) yields:
On the other hand, (85) with inequality (119) leads to (, and thus the direction of the inequality is reversed):
But (84) with the first inequality (118) leads to:
contradicting inequality (120) (), while with inequality (120) leads to:
contradicting the first inequality (118) and is consistent with the second inequality (118) introducing the product of positive and negative masses. with inequality (121) yields:
contradicting the inequality (120) and so on.
The additivity of the entropy (116) of statistically independent merging BBs, both in global thermodynamic equilibrium, defined by their generalized radii (55), introduces the energy relation (117). This relation, universality of the charges (27), and the BB complex energies (69)-(71) establish imaginary, negative, and mixed masses during the merger. The BB merger spreads as a gravitational event associated with a fast radio burst (FRB) event, as reported [103] based on the gravitational event GW1904251 and FRB 20190425A event2. Furthermore, IXPE3 observations show that the polarized X-rays detected from 4U 0142+61 pulsar exhibit a linear polarization swing from low to high photon energies [104]. In addition, direct evidence for a magnetic field strength reversal based on the observed sign change and extreme variation of FRB 20190520B’s rotation measure, which changed from to between June 2021 and January 2022, has been reported [105], and such extreme rotation measure reversal has never been observed before in any FRB or any astronomical object. It has been suggested that outside the GR, merging BHs may differ from their GR counterparts [106]. Furthermore, it was experimentally confirmed [107], based on the registered gravitational event GW170817, that BB mergers are perfectly spherical. It is concluded [107] that an additional process seems necessary to make the merger distribution uniform. However, one can hardly expect the collision of two perfectly spherical, patternless thermal noises to produce an aspherical pattern instead of another perfectly spherical patternless noise. Where would information about this pattern come from at the moment of collision? From the point of impact? No point of impact can be considered unique on the patternless surface.
During the merger, the STM ratio decreases, making the BBC denser until it becomes a BH for and no further charge reduction is possible (see Figure 4). From equation (117) and the first inequality (118), we see that this holds for
For two merging BHs and the relation (124) yields . On the other hand, if then . The tendency to decrease the STM, given by relation (124), is reflected in the merger statistics registered by LIGO and Virgo interferometers: the registered fraction of BH mergers is much higher than might be expected by chance.
10. BB Fluctuations
A relation [108] (p.160) describing a BH information capacity, having an initial information capacity4 , after absorption of a particle having the Compton wavelength equal to the BH radius
was subsequently generalized [6] (Eq. (18)) to all Compton wavelengths (or frequencies ) and thus to all radiated Compton energies , absorbed (+) or emitted (−) by a BH as
Equation (126) can be further generalized, using the generalized diameter (55), to all BBs as follows
where represents the BB mass, and its roots are
where it vanishes. Thus, in general, BB changes its information capacity by:
absorbing or emitting energy m with at , as shown in Figure 5. Equation (129) shows that, depending on its mass , a BB can expand or contract by emitting or absorbing energy m [6]. However, expansion by emission (), for example, requires energy exceeding the mass-energy equivalence of BB for , which is consistent with the results presented in Section 5. We note that the same form of the relation (127), expressed as
contains the same like terms with respect to as the transcendental expressions for the fine-structure constants (13) and (14), which requires further investigation. The forms of the fine-structure constants (18) and (22) are different.
11. Discussion
Complex, imaginary, and negative physical quantities are the subject of research. In particular, the subject of scientific research is the thermodynamics in the complex plane. For example, Lee–Yang zeros [109,110] and photon-photon thermodynamic processes under negative optical temperature conditions [111] have been experimentally observed. Furthermore, the rendering of synthetic dimensions through space modulations has recently been suggested because it does not require any active materials or other external mechanisms to break time-reversal symmetry [112]. Complexified geodesics are investigated [113] and it was shown that from a geometric point of view the unitary symmetries U(1) and SU(2) stem fundamentally from Schwarzschild and Reissner-Nordström metrics through spacetime complexification if a new Euclidean metric on a complex Hermitian manifold is provided [114]. In Lorentz signature, a Hermitian structure must necessarily be complex-valued, so its integrability properties are more subtle than in the Euclidean case [115].
Physical quantities accessible for direct everyday observation are mostly real and positive with the negativity of distances, velocities, accelerations, etc., induced by the assumed orientation of space. Quantum measurement results, for example, are the necessarily real eigenvalues of Hermitian operators. Unlike charges, negative, real masses are also generally inaccessible for direct observations. However, dissipative coupling between excitons and photons in an optical microcavity leads to the formation of exciton polaritons with negative masses [102]. In Section 9, we show that negative masses also result from the merging of BBs.
The notion of atemporality, related to the prebiotic, timeless [9] part of the evolution of information in the universe, was also investigated [116] on a black hole (BH) surface as the dynamical mechanism responsible for the transition from a regime with a real-valued interval to an imaginary interval via the Wick rotation. The Wick rotation between real and imaginary intervals was also analyzed in the context of kinematics on holographic spheres [6] and quantum orthogonalization intervals of BHs [5].
By Noether’s theorem, the conservation of energy (7) between three Fresnel coefficients for the normal incidence of electromagnetic radiation on monolayer graphene is associated with a symmetry between the fine-structure constant and . This symmetry establishes three complementary fine-structure constants, of which two are negative, wherein all fine-structure constants are related to each other through the constant of , which indicates that they do not vary over time. The complementary fine-structure constants are associated with their own sets of Planck units that allow for different parameterization of the perceivable space Euclidean space parameterized by the fine-structure constant . Since the elementary charge and the products are the same in all these four parameterizations, the complementary electrons correspond to dark states recently discovered in condensed-matter systems having two pairs of sublattices.
As the two sets of basic Planck units are real and two are imaginary, we have applied four complex pairs of masses and charges defined by to the complex energy formula [66] defining three complex energies (61) and (62). The generalized energy (58) of all perfect black-body objects (black holes, neutron stars, and white dwarfs) with a generalized radius , where is the Schwarzschild radius, exceeds the mass-energy equivalence if . However, the complex energies (61)-(63) allow storage of this excess energy in their imaginary parts. Further analysis of this model showed that the negative complementary fine-structure constant established by the graphene reflectance is dual to the fine-structure constant and Appendix D presents some arguments to support the claim that parameterization sets favorable conditions for biological evolution to emerge. The lower bound on the mass of a charged black-body object is and the upper bound on a white dwarf radius is , where is the Schwarzschild radius of the white dwarf mass. A charged black-body object is in the equilibrium of complex energies if its radius , which is close to the photon sphere radius , and is marginally greater than the locally negative energy density bound of . The maximum radius of the black-body object is , which is close to the photon capture radius . The complex force between real masses and imaginary charges leads to the complex black-body object’s surface gravity and generalized Hawking radiation complex temperature. Furthermore, on the basis of the Bohr model for the hydrogen atom, we show that complex conjugates of this force represent atoms and antiatoms. The proposed model considers the value(s) of the fine-structure constant(s), which is(are) otherwise neglected in general relativity, and explains the registered (GWOSC) high masses of neutron star mergers and the associated fast radio bursts (CHIME) without resorting to any hypothetical types of exotic stellar objects.
MLG is a truly 2-dimensional material with no thickness. Although its thickness is reported [117] as 0.37 [nm] with other reported values up to 1.7 [nm], these results are not credible, considering that 0.335 [nm] is the established interlayer distance and consequently the thickness of bilayer graphene: the thickness of bilayer graphene is not [nm]. In the context of the results of this study, graphene is a keyhole to ED. The history of graphene is also instructive. Discovered in 1947 [118], graphene was long considered an academic material until it was eventually pulled from graphite in 2004 [119] using ordinary Scotch tape (introduced into the market in 1932). These fifty-seven years, along with twenty-nine years (1935-1964) between the condemnation of quantum theory as incomplete [120] and Bell’s mathematical theorem [121] asserting that it is not true, and the fifty-eight years (1964-2022) between the formulation of this theorem and the 2022 Nobel Prize in Physics for its experimental loophole-free confirmation, should remind us that Max Planck, the genius who discovered Planck units, has also discovered Planck’s principle.
Acknowledgments
The author truly thanks his wife, Magdalena Bartocha, for her support since this research [122,123] began; Wawrzyniec Bieniawski for inspiring discussions, constructive ideas concerning the layout of this paper, and his feedback concerning the sections on BB mergers and BB fluctuations; Piotr Masierak for constructive and insightful remarks; Mariola Bala for handling these esoteric vapors under control; and Andrzej Tomski for defining the scalar product for the real/imaginary Euclidean spaces (1).
Abbreviations
The following abbreviations are used in this paper:
| ED | emergent dimensionality |
| EMR | electromagnetic radiation |
| MLG | monolayer graphene |
| T | transmittance |
| R | reflectance |
| A | absorptance |
| any of the fine-structure constants | |
| or | |
| or | |
| or | |
| BH | black hole |
| NS | neutron star |
| WD | white dwarf |
| BB | black-body object |
| HS | holographic sphere |
| STM | size-to-mass ratio |
| GR | general relativity |
| HUP | Heisenberg’s uncertainty principle |
Appendix A. Mlg Transmittance, Absorptance, and Reflectance as Functions of π Only
With definitions of (13), (14), (18), and (22) MLG Fresnel coefficients (3), (4), and (5) can be expressed simply by . For (13) and for (22) they are
For (14) they are
with and for (18) they are
with . and imply a sink and source, respectively, whereas the opposite holds for T, as illustrated schematically in Figure A1. We conjecture that the negative A and T values exceeding 100% for (11) and (14) could be explained in terms of graphene spontaneous EMR emission.
Figure A1.
Illustration of the concepts of negative absorptance and excessive transmittance of EMR under normal incidence on MLG for .
Figure A1.
Illustration of the concepts of negative absorptance and excessive transmittance of EMR under normal incidence on MLG for .
Appendix B. π-like Constants
The quadratic equation (8) can also be solved for , which yields two roots.
dependent on R and , where indicates or . This can be further evaluated using the MLG reflectance R (4) or (A3), yielding four, yet only three, distinct possibilities,
The modulus of (A9) corresponds to a convex surface with a positive Gaussian curvature, whereas the modulus of (A11) corresponds to a negative Gaussian curvature. The product is independent of , the quotient is not directly dependent on , and . It remains to be determined whether each of these -like constants describes the ratio of the circumference of a circle drawn on the respective surface to its diameter () or the ratio of the area of this circle to the square of its radius (). These definitions produce different results for curved surfaces, whereas on convex surfaces and on saddle surfaces [124]. The remaining -like constants corresponding to and are listed in Table 1.
Appendix C. Mlg Fresnel Equation and Euclid’s Formula
The Fresnel equation for the normal incidence of EMR at the boundary of two media with refractive indices and is
Substituting MLG reflectance (4) and the sum of transmittance (3) and absorptance (5) into the Fresnel equation (A12) yields
which resolves to independent on and two roots for
satisfying
which corresponds to the identity (23). The refractive index is close to that of liquid helium at 3 K. The refractive index is close to the refractive index of water for X-ray radiation at a photon wavelength of nm. We note that these results are different from the complex refractive index of MLG ( at 532 nm to at 633 nm at room temperature). However, because , the equation (A14) relates to the absolute () refractive indices; it models MLG as a boundary between vacuum and some other bulk medium. Refractive indices (A14) correspond to the phase velocities
using the relation (33). We note that the phase velocity of light does not carry information and thus can be faster than the speed of light in vacuum c.
On the other hand, the Fresnel equation (A12) has the same form as the Euclid’s formula for generating Pythagorean triples , ,
with and . Substituting MLG reflectance (4) and the sum of transmittance (3) and absorptance (5) into the Euclid formula (A17) yields
generating four right triangles with edges
and
In each case, different edge lengths satisfy , which also corresponds to the identity (23). Furthermore
We further note that , (A2), (A5) and , (A1), (A4).
Appendix D. Why α Is Better for Biological Evolution than α 2 ?
The probability that two nuclear particles a and b will undergo nuclear fusion by overcoming their electrostatic barriers is given by Gamow–Sommerfeld factor
where
is the Gamow energy, , are the masses of those particles in terms of or Planck units (51) and , are their respective atomic numbers.
As is larger than , the probability (A22) is higher for the same dimensionless parameters , . Therefore, perceivable -space provides more favorable conditions for the evolution of information (by nuclear fusion) than nonperceivable -space parameterized with negative , positive and with imaginary charge due to the relation (33).
Furthermore, the -Planck energy and temperature are higher than the Planck energy and temperature . Therefore, the perceivable -space provides more favorable conditions for the evolution of information than would be provided by nonperceivable -space, also owing to the minimum energy principle.
Appendix E. Planck Units and HUP
Perhaps the simplest derivation of the squared Planck length is based on HUP
where , , , and denote momentum, position, energy, and time uncertainties, respectively. Replacing energy uncertainty with mass uncertainty using mass-energy equivalence, and time uncertainty with position uncertainty using [30] yields
Interpreting as the BH mass in (A25) we derive the Planck length as and recover [6] the BH diameter .
However, using the same procedure but inserting the BH radius instead of the BH mass into the uncertainty principle (A25) leads to . In general, using the generalized radius (55) in both procedures, we obtain
Thus, if k increases, the mass decreases, and increases and the factor is the same for i.e., for the orbital speed radius or orbital speed mass.
Appendix F. Other Definitions of Complex Energies
Appendix G. Hall Effect
The fractional quantum Hall (FQHE) effect shows a stepwise dependence of the conductance on the magnetic field (as compared to the linear dependence of the Hall effect) with steps quantized as
where is an integer or fraction (for example, for , ). The relations (A29) and (33) suggest that the 2D FQHE links real and imaginary Planck units, similar to 2D graphene, establishing the complementary fine-structure constants.
References
- de Chardin, P.T. The Phenomenon of Man; Harper, New York, 1959.
- Prigogine, I.; Stengers, I. Order out of Chaos: Man’s New Dialogue with Nature; Bantam Books, 1984.
- Melamede, R. Dissipative Structures and the Origins of Life. Unifying Themes in Complex Systems IV; Minai, A.A.; Bar-Yam, Y., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; pp. 80–87.
- Vedral, V. Decoding Reality: The Universe as Quantum Information; Oxford University Press, 2010. [CrossRef]
- Łukaszyk, S. Life as the Explanation of the Measurement Problem. Journal of Physics: Conference Series 2024, 2701, 012124. [CrossRef]
- Łukaszyk, S., Black Hole Horizons as Patternless Binary Messages and Markers of Dimensionality. In Future Relativity, Gravitation, Cosmology; Nova Science Publishers, 2023; chapter 15, pp. 317–374. [CrossRef]
- Vopson, M.M.; Lepadatu, S. Second law of information dynamics. AIP Advances 2022, 12, 075310. [CrossRef]
- Sharma, A.; Czégel, D.; Lachmann, M.; Kempes, C.P.; Walker, S.I.; Cronin, L. Assembly theory explains and quantifies selection and evolution. Nature 2023, 622, 321–328. [CrossRef]
- Łukaszyk, S.; Bieniawski, W. Assembly Theory of Binary Messages. Mathematics 2024, 12, 1600. [CrossRef]
- Walker, S.I. Life as no one knows it: The physics of life’s emergence; Riverhead Books: New York, 2024.
- Platonic Solids in All Dimensions, 2020.
- Taubes, C.H. Gauge theory on asymptotically periodic {4}-manifolds. Journal of Differential Geometry 1987, 25. [CrossRef]
- Łukaszyk, S. Four Cubes, 2021. arXiv:2007.03782 [math].
- Lukaszyk, S. Solving the black hole information paradox. Research Outreach 2023. [CrossRef]
- Brukner, Č. A No-Go Theorem for Observer-Independent Facts. Entropy 2018, 20. [CrossRef]
- Łukaszyk, S. Novel Recurrence Relations for Volumes and Surfaces of n-Balls, Regular n-Simplices, and n-Orthoplices in Real Dimensions. Mathematics 2022, 10, 2212. [CrossRef]
- Łukaszyk, S.; Tomski, A. Omnidimensional Convex Polytopes. Symmetry 2023, 15. [CrossRef]
- Planck, M. Über irreversible Strahlungsvorgänge, 1899.
- Stoney, G.J. LII. On the physical units of nature. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1881, 11, 381–390. [CrossRef]
- Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal dynamical conductance in graphite. Physical Review Letters 2008, 100, 117401. arXiv:0712.0835 [cond-mat], . [CrossRef]
- Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Physical Review Letters 2008, 101, 196405. [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Universal Dynamic Conductivity and Quantized Visible Opacity of Suspended Graphene. Science 2008, 320, 1308–1308. arXiv:0803.3718 [cond-mat], . [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Physical Review B 2008, 78, 085432. [CrossRef]
- Wang, X.; Chen, B. Origin of Fresnel problem of two dimensional materials. Scientific Reports 2019, 9, 17825. [CrossRef]
- Merano, M. Fresnel coefficients of a two-dimensional atomic crystal. Physical Review A 2016, 93, 013832. [CrossRef]
- Ando, T.; Zheng, Y.; Suzuura, H. Dynamical Conductivity and Zero-Mode Anomaly in Honeycomb Lattices. Journal of the Physical Society of Japan 2002, 71, 1318–1324. [CrossRef]
- Zhu, S.E.; Yuan, S.; Janssen, G.C.A.M. Optical transmittance of multilayer graphene. EPL (Europhysics Letters) 2014, 108, 17007. [CrossRef]
- Ivanov, I.G.; Hassan, J.U.; Iakimov, T.; Zakharov, A.A.; Yakimova, R.; Janzén, E. Layer-number determination in graphene on SiC by reflectance mapping. Carbon 2014, 77, 492–500. [CrossRef]
- Varlaki, P.; Nadai, L.; Bokor, J. Number Archetypes in System Realization Theory Concerning the Fine Structure Constant. 2008 International Conference on Intelligent Engineering Systems; IEEE: Miami, FL, 2008; pp. 83–92. [CrossRef]
- Scardigli, F. Some heuristic semi-classical derivations of the Planck length, the Hawking effect and the Unruh effect. Il Nuovo Cimento B (1971-1996) 1995, 110, 1029–1034. [CrossRef]
- Haug, E.G. Finding the Planck length multiplied by the speed of light without any knowledge of G, c, or h, using a Newton force spring. Journal of Physics Communications 2020, 4, 075001. [CrossRef]
- Verlinde, E. On the origin of gravity and the laws of Newton. Journal of High Energy Physics 2011, 2011, 29. [CrossRef]
- Chung, Y.; Kim, M.; Kim, Y.; Cha, S.; Park, J.W.; Park, J.; Yi, Y.; Song, D.; Ryu, J.H.; Lee, K.; Kim, T.K.; Cacho, C.; Denlinger, J.; Jozwiak, C.; Rotenberg, E.; Bostwick, A.; Kim, K.S. Dark states of electrons in a quantum system with two pairs of sublattices. Nature Physics 2024. [CrossRef]
- Schneider, L.; Ton, K.T.; Ioannidis, I.; Neuhaus-Steinmetz, J.; Posske, T.; Wiesendanger, R.; Wiebe, J. Proximity superconductivity in atom-by-atom crafted quantum dots. Nature 2023. [CrossRef]
- Hiller, R.; Putterman, S.J.; Barber, B.P. Spectrum of synchronous picosecond sonoluminescence. Physical Review Letters 1992, 69, 1182–1184. [CrossRef]
- Eberlein, C. Theory of quantum radiation observed as sonoluminescence. Physical Review A 1996, 53, 2772–2787. [CrossRef]
- Lohse, D.; Schmitz, B.; Versluis, M. Snapping shrimp make flashing bubbles. Nature 2001, 413, 477–478. [CrossRef]
- Rietman, E.A.; Melcher, B.; Bobrick, A.; Martire, G. A Cylindrical Optical-Space Black Hole Induced from High-Pressure Acoustics in a Dense Fluid. Universe 2023, 9, 162. [CrossRef]
- Melia, F. A Candid Assessment of Standard Cosmology. Publications of the Astronomical Society of the Pacific 2022, 134, 121001. [CrossRef]
- Boylan-Kolchin, M. Stress testing ΛCDM with high-redshift galaxy candidates. Nature Astronomy 2023. [CrossRef]
- Mortlock, D.J.; Warren, S.J.; Venemans, B.P.; Patel, M.; Hewett, P.C.; McMahon, R.G.; Simpson, C.; Theuns, T.; Gonzáles-Solares, E.A.; Adamson, A.; Dye, S.; Hambly, N.C.; Hirst, P.; Irwin, M.J.; Kuiper, E.; Lawrence, A.; Röttgering, H.J.A. A luminous quasar at a redshift of z = 7.085. Nature 2011, 474, 616–619. [CrossRef]
- Bosman, S.E.I.; Álvarez Márquez, J.; Colina, L.; Walter, F.; Alonso-Herrero, A.; Ward, M.J.; Östlin, G.; Greve, T.R.; Wright, G.; Bik, A.; Boogaard, L.; Caputi, K.; Costantin, L.; Eckart, A.; García-Marín, M.; Gillman, S.; Hjorth, J.; Iani, E.; Ilbert, O.; Jermann, I.; Labiano, A.; Langeroodi, D.; Peißker, F.; Rinaldi, P.; Topinka, M.; Van Der Werf, P.; Güdel, M.; Henning, T.; Lagage, P.O.; Ray, T.P.; Van Dishoeck, E.F.; Vandenbussche, B. A mature quasar at cosmic dawn revealed by JWST rest-frame infrared spectroscopy. Nature Astronomy 2024. [CrossRef]
- Comerón, S.; Trujillo, I.; Cappellari, M.; Buitrago, F.; Garduño, L.E.; Zaragoza-Cardiel, J.; Zinchenko, I.A.; Lara-López, M.A.; Ferré-Mateu, A.; Dib, S. The massive relic galaxy NGC 1277 is dark matter deficient: From dynamical models of integral-field stellar kinematics out to five effective radii. Astronomy & Astrophysics 2023, 675, A143. [CrossRef]
- Brouwer, M.M.; others. First test of Verlinde’s theory of emergent gravity using weak gravitational lensing measurements. Monthly Notices of the Royal Astronomical Society 2017, 466, 2547–2559. [CrossRef]
- Schimmoller, A.J.; McCaul, G.; Abele, H.; Bondar, D.I. Decoherence-free entropic gravity: Model and experimental tests. Physical Review Research 2021, 3, 033065. [CrossRef]
- Lukaszyk, S. A No-go Theorem for Superposed Actions (Making Schrödinger’s Cat Quantum Nonlocal). In New Frontiers in Physical Science Research Vol. 3; Purenovic, D.J., Ed.; Book Publisher International (a part of SCIENCEDOMAIN International), 2022; pp. 137–151. arXiv:1801.08537 [quant-ph], . [CrossRef]
- Qian, K.; Wang, K.; Chen, L.; Hou, Z.; Krenn, M.; Zhu, S.; Ma, X.s. Multiphoton non-local quantum interference controlled by an undetected photon. Nature Communications 2023, 14, 1480. [CrossRef]
- Xue, P.; Xiao, L.; Ruffolo, G.; Mazzari, A.; Temistocles, T.; Cunha, M.T.; Rabelo, R. Synchronous Observation of Bell Nonlocality and State-Dependent Contextuality. Physical Review Letters 2023, 130, 040201. [CrossRef]
- Tran, D.M.; Nguyen, V.D.; Ho, L.B.; Nguyen, H.Q. Increased success probability in Hardy’s nonlocality: Theory and demonstration. Phys. Rev. A 2023, 107, 042210. [CrossRef]
- Colciaghi, P.; Li, Y.; Treutlein, P.; Zibold, T. Einstein-Podolsky-Rosen Experiment with Two Bose-Einstein Condensates. Phys. Rev. X 2023, 13, 021031. [CrossRef]
- Kreuzgruber, E.; Wagner, R.; Geerits, N.; Lemmel, H.; Sponar, S. Violation of a Leggett-Garg Inequality Using Ideal Negative Measurements in Neutron Interferometry. Physical Review Letters 2024, 132, 260201. [CrossRef]
- Watanabe, S. Knowing and Guessing: A Quantitative Study of Inference and Information; Wiley, 1969.
- Watanabe, S. Epistemological Relativity. Annals of the Japan Association for Philosophy of Science 1986, 7, 1–14. [CrossRef]
- Saeed, I.; Pak, H.K.; Tlusty, T. Quasiparticles, flat bands and the melting of hydrodynamic matter. Nature Physics 2023. [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [CrossRef]
- Vincentelli, F.M.; et al.. A shared accretion instability for black holes and neutron stars. Nature 2023, 615, 45–49. [CrossRef]
- Valenzuela-Villaseca, V.; Suttle, L.; Suzuki-Vidal, F.; Halliday, J.; Merlini, S.; Russell, D.; Tubman, E.; Hare, J.; Chittenden, J.; Koepke, M.; Blackman, E.; Lebedev, S. Characterization of Quasi-Keplerian, Differentially Rotating, Free-Boundary Laboratory Plasmas. Physical Review Letters 2023, 130, 195101. [CrossRef]
- Chaitin, G.J. On the Length of Programs for Computing Finite Binary Sequences. J. ACM 1966, 13, 547–569. [CrossRef]
- Hawking, S. Black hole explosions? Nature 1974, 248, 30–31. [CrossRef]
- Alsing, P.M.; Milburn, G.J. Teleportation with a Uniformly Accelerated Partner. Phys. Rev. Lett. 2003, 91, 180404. [CrossRef]
- Hooft, G.t. Dimensional Reduction in Quantum Gravity, 1993. [CrossRef]
- Gould, A. Classical derivation of black-hole entropy. Physical Review D 1987, 35, 449–454. [CrossRef]
- Penrose, R.; Floyd, R.M. Extraction of Rotational Energy from a Black Hole. Nature Physical Science 1971, 229, 177–179. [CrossRef]
- Christodoulou, D.; Ruffini, R. Reversible Transformations of a Charged Black Hole. Physical Review D 1971, 4, 3552–3555. [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. [CrossRef]
- Zhang, T. Electric Charge as a Form of Imaginary Energy, 2008.
- Anderson, E.K.; Baker, C.J.; Bertsche, W.; Bhatt, N.M.; Bonomi, G.; Capra, A.; Carli, I.; Cesar, C.L.; Charlton, M.; Christensen, A.; Collister, R.; Cridland Mathad, A.; Duque Quiceno, D.; Eriksson, S.; Evans, A.; Evetts, N.; Fabbri, S.; Fajans, J.; Ferwerda, A.; Friesen, T.; Fujiwara, M.C.; Gill, D.R.; Golino, L.M.; Gomes Gonçalves, M.B.; Grandemange, P.; Granum, P.; Hangst, J.S.; Hayden, M.E.; Hodgkinson, D.; Hunter, E.D.; Isaac, C.A.; Jimenez, A.J.U.; Johnson, M.A.; Jones, J.M.; Jones, S.A.; Jonsell, S.; Khramov, A.; Madsen, N.; Martin, L.; Massacret, N.; Maxwell, D.; McKenna, J.T.K.; Menary, S.; Momose, T.; Mostamand, M.; Mullan, P.S.; Nauta, J.; Olchanski, K.; Oliveira, A.N.; Peszka, J.; Powell, A.; Rasmussen, C.; Robicheaux, F.; Sacramento, R.L.; Sameed, M.; Sarid, E.; Schoonwater, J.; Silveira, D.M.; Singh, J.; Smith, G.; So, C.; Stracka, S.; Stutter, G.; Tharp, T.D.; Thompson, K.A.; Thompson, R.I.; Thorpe-Woods, E.; Torkzaban, C.; Urioni, M.; Woosaree, P.; Wurtele, J.S. Observation of the effect of gravity on the motion of antimatter. Nature 2023, 621, 716–722. [CrossRef]
- Mandelstam, L.; Tamm, I. The Uncertainty Relation Between Energy and Time in Non-relativistic Quantum Mechanics. J. Phys. (USSR) 1945, 9, 249––254.
- Margolus, N.; Levitin, L.B. The maximum speed of dynamical evolution. Physica D: Nonlinear Phenomena 1998, 120, 188–195. [CrossRef]
- Levitin, L.B.; Toffoli, T. Fundamental Limit on the Rate of Quantum Dynamics: The Unified Bound Is Tight. Physical Review Letters 2009, 103, 160502. [CrossRef]
- Iyer, B.R.; Vishveshwara, C.V.; Dhurandhar, S.V. Ultracompact (R<3 M) objects in general relativity. Classical and Quantum Gravity 1985, 2, 219–228. [CrossRef]
- Nemiroff, R.J.; Becker, P.A.; Wood, K.S. Properties of ultracompact neutron stars. The Astrophysical Journal 1993, 406, 590. [CrossRef]
- Lightman, A.P.; Press, W.H.; Price, R.H.; Teukolsky, S.A. Problem Book in Relativity and Gravitation; Princeton University Press, 2017. [CrossRef]
- Weinberg, S. Gravitation and cosmology: Principles and applications of the general theory of relativity; Wiley: New York, 1972.
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. American Journal of Physics 1988, 56, 395–412. [CrossRef]
- Pechenick, K.R.; Ftaclas, C.; Cohen, J.M. Hot spots on neutron stars - The near-field gravitational lens. The Astrophysical Journal 1983, 274, 846. [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. The Astrophysical Journal Letters 2019, 875, L1. [CrossRef]
- Montgomery, C.; Orchiston, W.; Whittingham, I. Michell, Laplace and the Origin of the Black Hole Concept. Journal of Astronomical History and Heritage 2009, 12, 90–96. [CrossRef]
- Szostek, K.; Szostek, R. The derivation of the general form of kinematics with the universal reference system. Results in Physics 2018, 8, 429–437. [CrossRef]
- Szostek, R. The Original Method of Deriving Transformations for Kinematics with a Universal Reference System. Jurnal Fizik Malaysia 2022, 43, 10244–10263.
- Szostek, R.; Szostek, K. The Existence of a Universal Frame of Reference, in Which it Propagates Light, is Still an Unresolved Problem of Physics. Jordan Journal of Physics 2022, 15, 457–467. [CrossRef]
- Szostek, R. Explanation of What Time in Kinematics Is and Dispelling Myths Allegedly Stemming from the Special Theory of Relativity. Applied Sciences 2022, 12, 6272. [CrossRef]
- Unnikrishnan, C.S. Cosmic Gravity and the Quantum Spin. In New Relativity in the Gravitational Universe; Springer International Publishing: Cham, 2022; Vol. 209, pp. 373–405. [CrossRef]
- Unnikrishnan, C.S. Cosmic Relativity—The Theory and Its Primary Fundamental Results. In New Relativity in the Gravitational Universe; Springer International Publishing: Cham, 2022; Vol. 209, pp. 255–306. [CrossRef]
- Szostek, Karol and Szostek, Roman. The concept of a mechanical system for measuring the one-way speed of light. Technical Transactions 2023, 2023, 1–9. [CrossRef]
- Event Horizon Telescope Collaboration.; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bauböck, M.; Benson, B.A.; Bintley, D.; Blackburn, L.; Blundell, R.; Bouman, K.L.; Bower, G.C.; Boyce, H.; Bremer, M.; Brinkerink, C.D.; Brissenden, R.; Britzen, S.; Broderick, A.E.; Broguiere, D.; Bronzwaer, T.; Bustamante, S.; Byun, D.Y.; Carlstrom, J.E.; Ceccobello, C.; Chael, A.; Chan, C.k.; Chatterjee, K.; Chatterjee, S.; Chen, M.T.; Chen, Y.; Cheng, X.; Cho, I.; Christian, P.; Conroy, N.S.; Conway, J.E.; Cordes, J.M.; Crawford, T.M.; Crew, G.B.; Cruz-Osorio, A.; Cui, Y.; Davelaar, J.; Laurentis, M.D.; Deane, R.; Dempsey, J.; Desvignes, G.; Dexter, J.; Dhruv, V.; Doeleman, S.S.; Dougal, S.; Dzib, S.A.; Eatough, R.P.; Emami, R.; Falcke, H.; Farah, J.; Fish, V.L.; Fomalont, E.; Ford, H.A.; Fraga-Encinas, R.; Freeman, W.T.; Friberg, P.; Fromm, C.M.; Fuentes, A.; Galison, P.; Gammie, C.F.; García, R.; Gentaz, O.; Georgiev, B.; Goddi, C.; Gold, R.; Gómez-Ruiz, A.I.; Gómez, J.L.; Gu, M.; Gurwell, M.; Hada, K.; Haggard, D.; Haworth, K.; Hecht, M.H.; Hesper, R.; Heumann, D.; Ho, L.C.; Ho, P.; Honma, M.; Huang, C.W.L.; Huang, L.; Hughes, D.H.; Ikeda, S.; Impellizzeri, C.M.V.; Inoue, M.; Issaoun, S.; James, D.J.; Jannuzi, B.T.; Janssen, M.; Jeter, B.; Jiang, W.; Jiménez-Rosales, A.; Johnson, M.D.; Jorstad, S.; Joshi, A.V.; Jung, T.; Karami, M.; Karuppusamy, R.; Kawashima, T.; Keating, G.K.; Kettenis, M.; Kim, D.J.; Kim, J.Y.; Kim, J.; Kim, J.; Kino, M.; Koay, J.Y.; Kocherlakota, P.; Kofuji, Y.; Koch, P.M.; Koyama, S.; Kramer, C.; Kramer, M.; Krichbaum, T.P.; Kuo, C.Y.; Bella, N.L.; Lauer, T.R.; Lee, D.; Lee, S.S.; Leung, P.K.; Levis, A.; Li, Z.; Lico, R.; Lindahl, G.; Lindqvist, M.; Lisakov, M.; Liu, J.; Liu, K.; Liuzzo, E.; Lo, W.P.; Lobanov, A.P.; Loinard, L.; Lonsdale, C.J.; Lu, R.S.; Mao, J.; Marchili, N.; Markoff, S.; Marrone, D.P.; Marscher, A.P.; Martí-Vidal, I.; Matsushita, S.; Matthews, L.D.; Medeiros, L.; Menten, K.M.; Michalik, D.; Mizuno, I.; Mizuno, Y.; Moran, J.M.; Moriyama, K.; Moscibrodzka, M.; Müller, C.; Mus, A.; Musoke, G.; Myserlis, I.; Nadolski, A.; Nagai, H.; Nagar, N.M.; Nakamura, M.; Narayan, R.; Narayanan, G.; Natarajan, I.; Nathanail, A.; Fuentes, S.N.; Neilsen, J.; Neri, R.; Ni, C.; Noutsos, A.; Nowak, M.A.; Oh, J.; Okino, H.; Olivares, H.; Ortiz-León, G.N.; Oyama, T.; Özel, F.; Palumbo, D.C.M.; Paraschos, G.F.; Park, J.; Parsons, H.; Patel, N.; Pen, U.L.; Pesce, D.W.; Piétu, V.; Plambeck, R.; PopStefanija, A.; Porth, O.; Pötzl, F.M.; Prather, B.; Preciado-López, J.A.; Psaltis, D.; Pu, H.Y.; Ramakrishnan, V.; Rao, R.; Rawlings, M.G.; Raymond, A.W.; Rezzolla, L.; Ricarte, A.; Ripperda, B.; Roelofs, F.; Rogers, A.; Ros, E.; Romero-Cañizales, C.; Roshanineshat, A.; Rottmann, H.; Roy, A.L.; Ruiz, I.; Ruszczyk, C.; Rygl, K.L.J.; Sánchez, S.; Sánchez-Argüelles, D.; Sánchez-Portal, M.; Sasada, M.; Satapathy, K.; Savolainen, T.; Schloerb, F.P.; Schonfeld, J.; Schuster, K.F.; Shao, L.; Shen, Z.; Small, D.; Sohn, B.W.; SooHoo, J.; Souccar, K.; Sun, H.; Tazaki, F.; Tetarenko, A.J.; Tiede, P.; Tilanus, R.P.J.; Titus, M.; Torne, P.; Traianou, E.; Trent, T.; Trippe, S.; Turk, M.; Van Bemmel, I.; Van Langevelde, H.J.; Van Rossum, D.R.; Vos, J.; Wagner, J.; Ward-Thompson, D.; Wardle, J.; Weintroub, J.; Wex, N.; Wharton, R.; Wielgus, M.; Wiik, K.; Witzel, G.; Wondrak, M.F.; Wong, G.N.; Wu, Q.; Yamaguchi, P.; Yoon, D.; Young, A.; Young, K.; Younsi, Z.; Yuan, F.; Yuan, Y.F.; Zensus, J.A.; Zhang, S.; Zhao, G.Y.; Zhao, S.S.; Agurto, C.; Allardi, A.; Amestica, R.; Araneda, J.P.; Arriagada, O.; Berghuis, J.L.; Bertarini, A.; Berthold, R.; Blanchard, J.; Brown, K.; Cárdenas, M.; Cantzler, M.; Caro, P.; Castillo-Domínguez, E.; Chan, T.L.; Chang, C.C.; Chang, D.O.; Chang, S.H.; Chang, S.C.; Chen, C.C.; Chilson, R.; Chuter, T.C.; Ciechanowicz, M.; Colin-Beltran, E.; Coulson, I.M.; Crowley, J.; Degenaar, N.; Dornbusch, S.; Durán, C.A.; Everett, W.B.; Faber, A.; Forster, K.; Fuchs, M.M.; Gale, D.M.; Geertsema, G.; González, E.; Graham, D.; Gueth, F.; Halverson, N.W.; Han, C.C.; Han, K.C.; Hasegawa, Y.; Hernández-Rebollar, J.L.; Herrera, C.; Herrero-Illana, R.; Heyminck, S.; Hirota, A.; Hoge, J.; Hostler Schimpf, S.R.; Howie, R.E.; Huang, Y.D.; Jiang, H.; Jinchi, H.; John, D.; Kimura, K.; Klein, T.; Kubo, D.; Kuroda, J.; Kwon, C.; Lacasse, R.; Laing, R.; Leitch, E.M.; Li, C.T.; Liu, C.T.; Liu, K.Y.; Lin, L.C.C.; Lu, L.M.; Mac-Auliffe, F.; Martin-Cocher, P.; Matulonis, C.; Maute, J.K.; Messias, H.; Meyer-Zhao, Z.; Montaña, A.; Montenegro-Montes, F.; Montgomerie, W.; Moreno Nolasco, M.E.; Muders, D.; Nishioka, H.; Norton, T.J.; Nystrom, G.; Ogawa, H.; Olivares, R.; Oshiro, P.; Pérez-Beaupuits, J.P.; Parra, R.; Phillips, N.M.; Poirier, M.; Pradel, N.; Qiu, R.; Raffin, P.A.; Rahlin, A.S.; Ramírez, J.; Ressler, S.; Reynolds, M.; Rodríguez-Montoya, I.; Saez-Madain, A.F.; Santana, J.; Shaw, P.; Shirkey, L.E.; Silva, K.M.; Snow, W.; Sousa, D.; Sridharan, T.K.; Stahm, W.; Stark, A.A.; Test, J.; Torstensson, K.; Venegas, P.; Walther, C.; Wei, T.S.; White, C.; Wieching, G.; Wijnands, R.; Wouterloot, J.G.A.; Yu, C.Y.; Yu, W.; Zeballos, M. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. The Astrophysical Journal Letters 2022, 930, L12. [CrossRef]
- Broderick, A.E.; Pesce, D.W.; Gold, R.; Tiede, P.; Pu, H.Y.; Anantua, R.; Britzen, S.; Ceccobello, C.; Chatterjee, K.; Chen, Y.; Conroy, N.S.; Crew, G.B.; Cruz-Osorio, A.; Cui, Y.; Doeleman, S.S.; Emami, R.; Farah, J.; Fromm, C.M.; Galison, P.; Georgiev, B.; Ho, L.C.; James, D.J.; Jeter, B.; Jimenez-Rosales, A.; Koay, J.Y.; Kramer, C.; Krichbaum, T.P.; Lee, S.S.; Lindqvist, M.; Martí-Vidal, I.; Menten, K.M.; Mizuno, Y.; Moran, J.M.; Moscibrodzka, M.; Nathanail, A.; Neilsen, J.; Ni, C.; Park, J.; Piétu, V.; Rezzolla, L.; Ricarte, A.; Ripperda, B.; Shao, L.; Tazaki, F.; Toma, K.; Torne, P.; Weintroub, J.; Wielgus, M.; Yuan, F.; Zhao, S.S.; Zhang, S. The Photon Ring in M87*. The Astrophysical Journal 2022, 935, 61. [CrossRef]
- Johnson, M.D.; Lupsasca, A.; Strominger, A.; Wong, G.N.; Hadar, S.; Kapec, D.; Narayan, R.; Chael, A.; Gammie, C.F.; Galison, P.; Palumbo, D.C.M.; Doeleman, S.S.; Blackburn, L.; Wielgus, M.; Pesce, D.W.; Farah, J.R.; Moran, J.M. Universal interferometric signatures of a black hole’s photon ring. Science Advances 2020, 6, eaaz1310. [CrossRef]
- Conover, E. Physicists dispute a claim of detecting a black hole’s ‘photon ring’, 2022.
- Gralla, S.E.; Lupsasca, A.; Marrone, D.P. The shape of the black hole photon ring: A precise test of strong-field general relativity. Physical Review D 2020, 102, 124004. [CrossRef]
- Lockhart, W.; Gralla, S.E. How narrow is the M87* ring – II. A new geometric model. Monthly Notices of the Royal Astronomical Society 2022, 517, 2462–2470. [CrossRef]
- Tiede, P.; Johnson, M.D.; Pesce, D.W.; Palumbo, D.C.M.; Chang, D.O.; Galison, P. Measuring Photon Rings with the ngEHT. Galaxies 2022, 10, 111. [CrossRef]
- Cárdenas-Avendaño, A.; Lupsasca, A. Prediction for the interferometric shape of the first black hole photon ring. Physical Review D 2023, 108, 064043. [CrossRef]
- Chen, X.H.; Li, A.; Zhang, K. On Graphene in the Interstellar Medium. The Astrophysical Journal 2017, 850, 104. [CrossRef]
- Zhang, W.; Liang, Q.; Li, X.; Ma, L.P.; Li, X.; Zhao, Z.; Zhang, R.; Cao, H.; Wang, Z.; Li, W.; Wang, Y.; Liu, M.; Yue, N.; Liu, H.; Hu, Z.; Liu, L.; Zhou, Q.; Li, F.; Zheng, W.; Ren, W.; Zou, M. Discovery of natural few-layer graphene on the Moon. National Science Review 2024, p. nwae211. [CrossRef]
- Abbott, B.P.; et al.. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Physical Review Letters 2017, 119, 161101. [CrossRef]
- Szostek, R.; Góralski, P.; Szostek, K. Gravitational waves in Newton’s gravitation and criticism of gravitational waves resulting from the General Theory of Relativity (LIGO). Bulletin of the Karaganda University. "Physics" Series 2019, 96, 39–56. [CrossRef]
- Chojnacki, L.; Pohle, R.; Yan, H.; Akagi, Y.; Shannon, N. Gravitational wave analogs in spin nematics and cold atoms. Physical Review B 2024, 109, L220407. [CrossRef]
- Hawking, S.W., Ed. Three hundred years of gravitation, transferred to digital print ed.; Cambridge University Press: Cambridge, 2003.
- Kalogera, V.; Baym, G. The Maximum Mass of a Neutron Star. The Astrophysical Journal 1996, 470, L61–L64. [CrossRef]
- Ai, S.; Gao, H.; Zhang, B. What Constraints on the Neutron Star Maximum Mass Can One Pose from GW170817 Observations? The Astrophysical Journal 2020, 893, 146. [CrossRef]
- Wurdack, M.; Yun, T.; Katzer, M.; Truscott, A.G.; Knorr, A.; Selig, M.; Ostrovskaya, E.A.; Estrecho, E. Negative-mass exciton polaritons induced by dissipative light-matter coupling in an atomically thin semiconductor. Nature Communications 2023, 14, 1026. [CrossRef]
- Moroianu, A.; Wen, L.; James, C.W.; Ai, S.; Kovalam, M.; Panther, F.H.; Zhang, B. An assessment of the association between a fast radio burst and binary neutron star merger. Nature Astronomy 2023. [CrossRef]
- Lai, D. IXPE detection of polarized X-rays from magnetars and photon mode conversion at QED vacuum resonance. Proceedings of the National Academy of Sciences 2023, 120, e2216534120. [CrossRef]
- Anna-Thomas, R.; Connor, L.; Dai, S.; Feng, Y.; Burke-Spolaor, S.; Beniamini, P.; Yang, Y.P.; Zhang, Y.K.; Aggarwal, K.; Law, C.J.; Li, D.; Niu, C.; Chatterjee, S.; Cruces, M.; Duan, R.; Filipovic, M.D.; Hobbs, G.; Lynch, R.S.; Miao, C.; Niu, J.; Ocker, S.K.; Tsai, C.W.; Wang, P.; Xue, M.; Yao, J.M.; Yu, W.; Zhang, B.; Zhang, L.; Zhu, S.; Zhu, W. Magnetic field reversal in the turbulent environment around a repeating fast radio burst. Science 2023, 380, 599–603. [CrossRef]
- Li, D.; Wagle, P.; Chen, Y.; Yunes, N. Perturbations of Spinning Black Holes beyond General Relativity: Modified Teukolsky Equation. Physical Review X 2023, 13, 021029. [CrossRef]
- Sneppen, A.; Watson, D.; Bauswein, A.; Just, O.; Kotak, R.; Nakar, E.; Poznanski, D.; Sim, S. Spherical symmetry in the kilonova AT2017gfo/GW170817. Nature 2023, 614, 436–439. [CrossRef]
- Susskind, L. Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics; Little, Brown and Company, 2008.
- Peng, X.; Zhou, H.; Wei, B.B.; Cui, J.; Du, J.; Liu, R.B. Experimental Observation of Lee-Yang Zeros. Physical Review Letters 2015, 114, 010601. [CrossRef]
- Gnatenko, K.; Kargol, A.; Tkachuk, V. Lee–Yang zeros and two-time spin correlation function. Physica A: Statistical Mechanics and its Applications 2018, 509, 1095–1101. [CrossRef]
- Marques Muniz, A.L.; Wu, F.O.; Jung, P.S.; Khajavikhan, M.; Christodoulides, D.N.; Peschel, U. Observation of photon-photon thermodynamic processes under negative optical temperature conditions. Science 2023, 379, 1019–1023. [CrossRef]
- Wang, S.; Hu, Z.; Wu, Q.; Chen, H.; Prodan, E.; Zhu, R.; Huang, G. Smart patterning for topological pumping of elastic surface waves. Science Advances 2023, 9, eadh4310. [CrossRef]
- Fidkowski, L.; Hubeny, V.; Kleban, M.; Shenker, S. The Black Hole Singularity in AdS/CFT. Journal of High Energy Physics 2004, 2004, 014–014. [CrossRef]
- Ali, A.F.; Moulay, E.; Jusufi, K.; Alshal, H. Unitary symmetries in wormhole geometry and its thermodynamics. The European Physical Journal C 2022, 82, 1170. [CrossRef]
- Aksteiner, S.; Araneda, B. Kähler Geometry of Black Holes and Gravitational Instantons. Physical Review Letters 2023, 130, 161502. [CrossRef]
- Capozziello, S.; De Bianchi, S.; Battista, E. Avoiding singularities in Lorentzian-Euclidean black holes: The role of atemporality. Physical Review D 2024, 109, 104060. [CrossRef]
- Jussila, H.; Yang, H.; Granqvist, N.; Sun, Z. Surface plasmon resonance for characterization of large-area atomic-layer graphene film. Optica 2016, 3, 151. [CrossRef]
- Wallace, P.R. Erratum: The Band Theory of Graphite [Phys. Rev. 71, 622 (1947)]. Physical Review 1947, 72, 258–258. [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 1935, 47, 777–780. [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics Physique Fizika 1964, 1, 195–200. [CrossRef]
- Łukaszyk, S. A short note about graphene and the fine structure constant, 2020. [CrossRef]
- Łukaszyk, S. A short note about the geometry of graphene, 2020. [CrossRef]
- Mahajan, S. Calculation of the pi-like circular constants in curved geometry. ResearchGate, 2013.
- The 2023 Pole Marker, 2023.
- Schrinski, B.; Yang, Y.; Von Lüpke, U.; Bild, M.; Chu, Y.; Hornberger, K.; Nimmrichter, S.; Fadel, M. Macroscopic Quantum Test with Bulk Acoustic Wave Resonators. Physical Review Letters 2023, 130, 133604. [CrossRef]
- Tobar, M.E. Global representation of the fine structure constant and its variation. Metrologia 2005, 42, 129–133. [CrossRef]
- Lin, X.; Du, R.; Xie, X. Recent experimental progress of fractional quantum Hall effect: 5/2 filling state and graphene. National Science Review 2014, 1, 564–579. [CrossRef]
| 1 | |
| 2 | Data available online at the Canadian Hydrogen Intensity Mapping Experiment (CHIME) portal (https://www.chime-frb.ca/catalog). |
| 3 | X-ray Polarimetry Explorer (https://ixpe.msfc.nasa.gov). |
| 4 | We drop the HS subscripts in this section for clarity. |
Figure 1.
MLG reflectance as a function of .
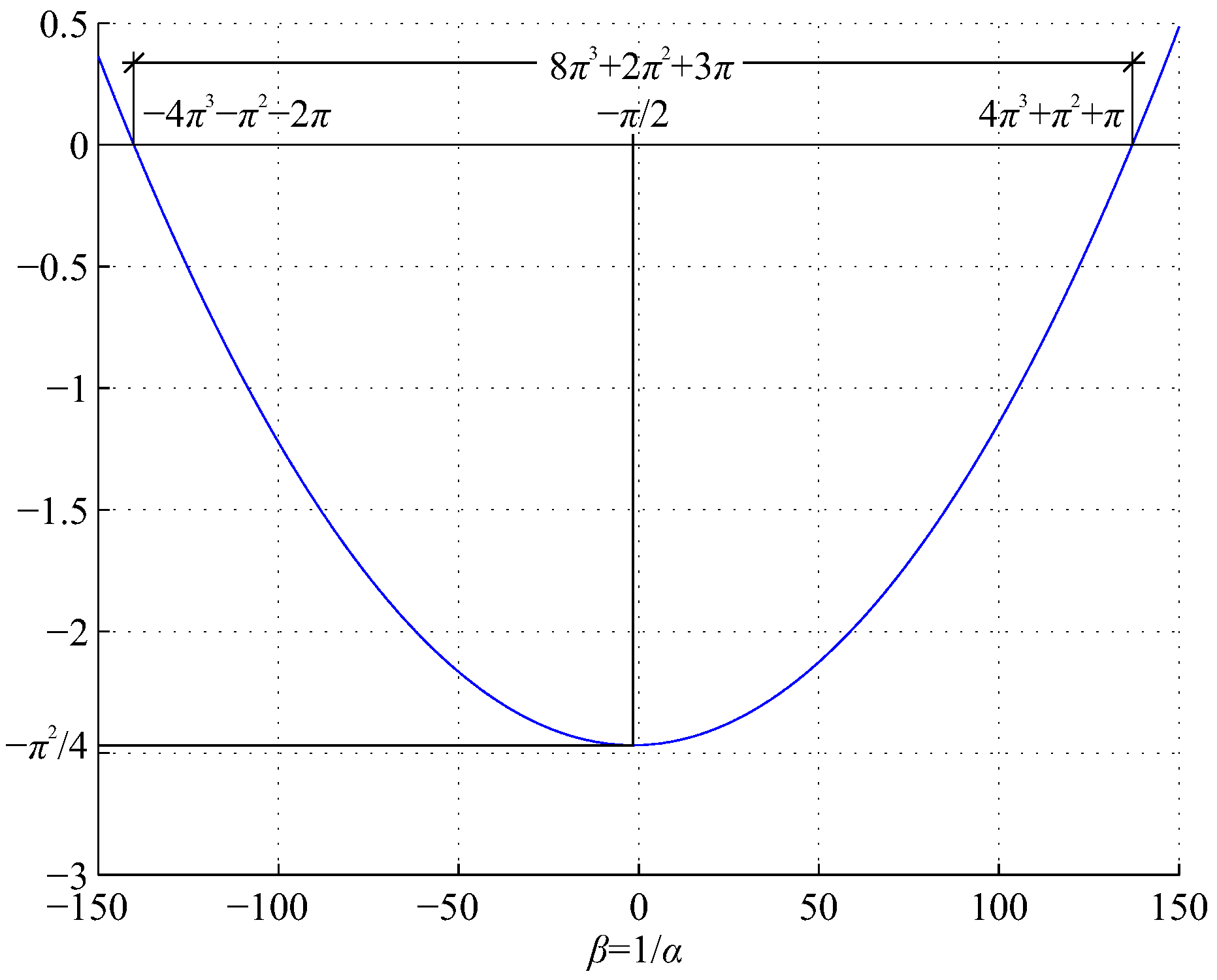
Figure 2.
Four fine-structure constants as phases of a complex number in order , , , from left to right.
Figure 2.
Four fine-structure constants as phases of a complex number in order , , , from left to right.
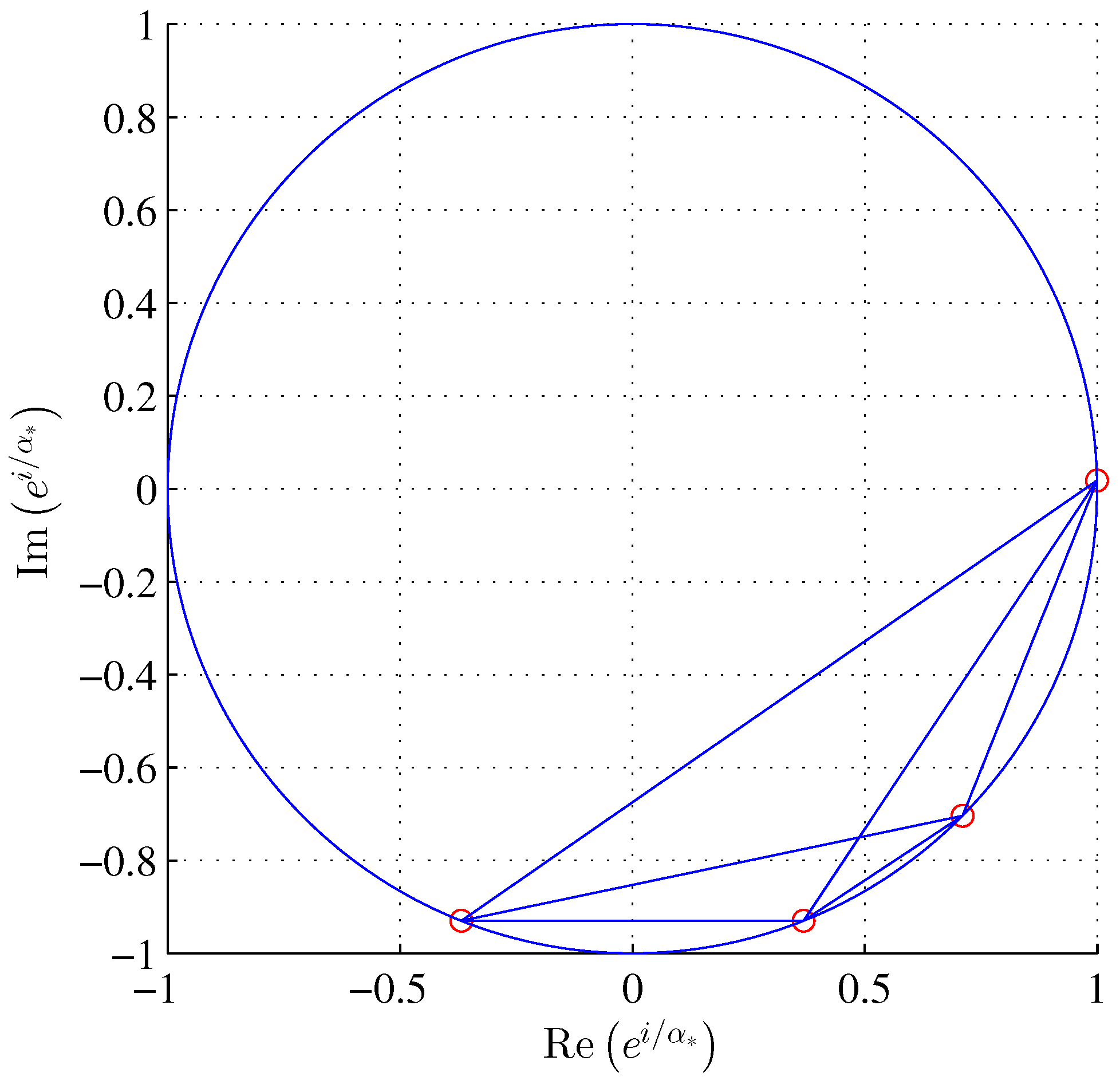
Figure 3.
Squared moduli of three complex energies linking mass , imaginary mass , and charge q through pairs of positive and negative fine-structure constants.
Figure 3.
Squared moduli of three complex energies linking mass , imaginary mass , and charge q through pairs of positive and negative fine-structure constants.
Figure 4.
Ratios of imaginary mass to real mass (green) and real charge to (red) of a BB as a function of the size-to-mass ratio for . The mass is imaginary for . The charge is real for .
Figure 4.
Ratios of imaginary mass to real mass (green) and real charge to (red) of a BB as a function of the size-to-mass ratio for . The mass is imaginary for . The charge is real for .
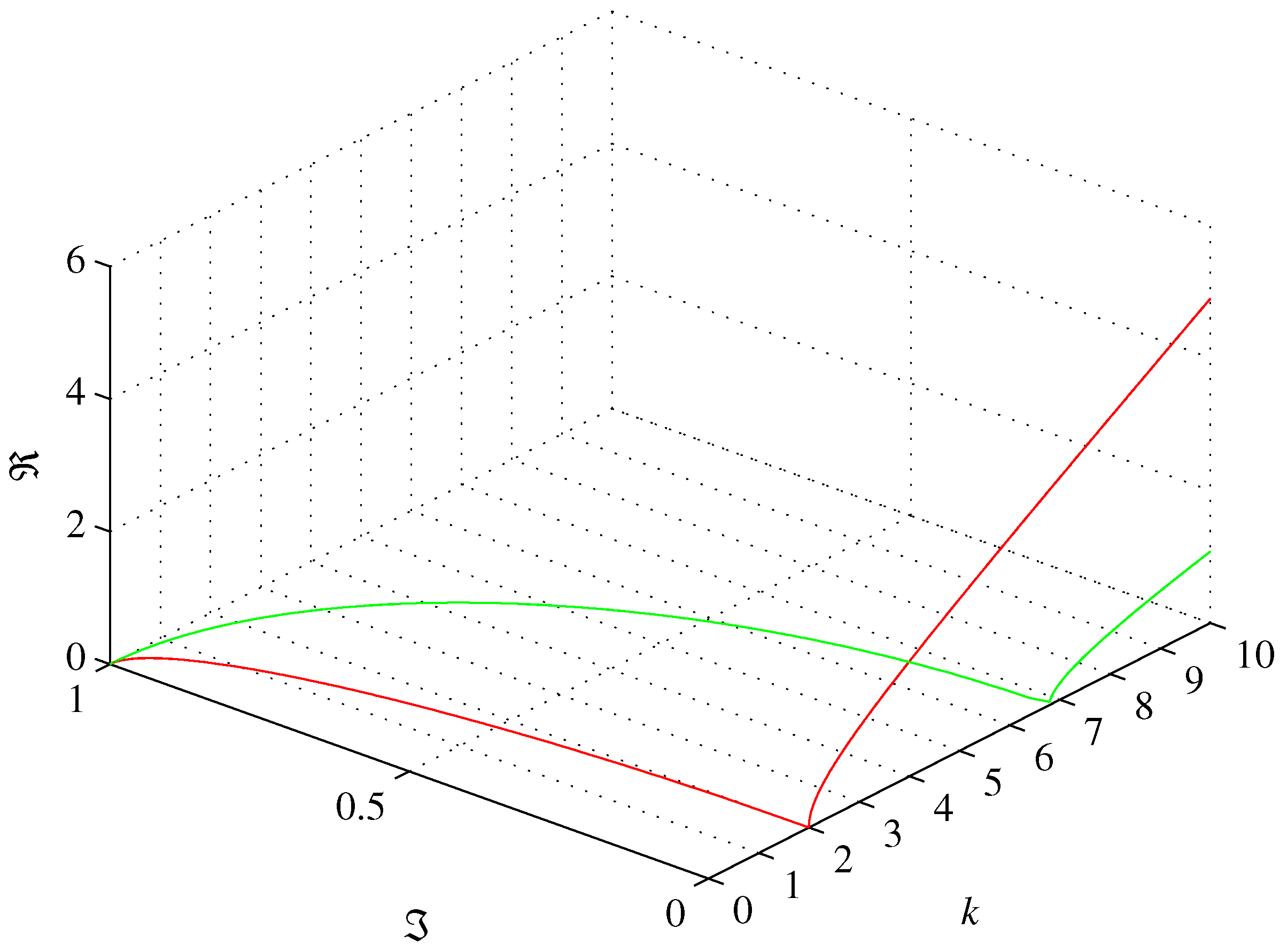
Figure 5.
BB information capacity variations after absorption (red) or emission (green) of energy m (, ).
Figure 5.
BB information capacity variations after absorption (red) or emission (green) of energy m (, ).
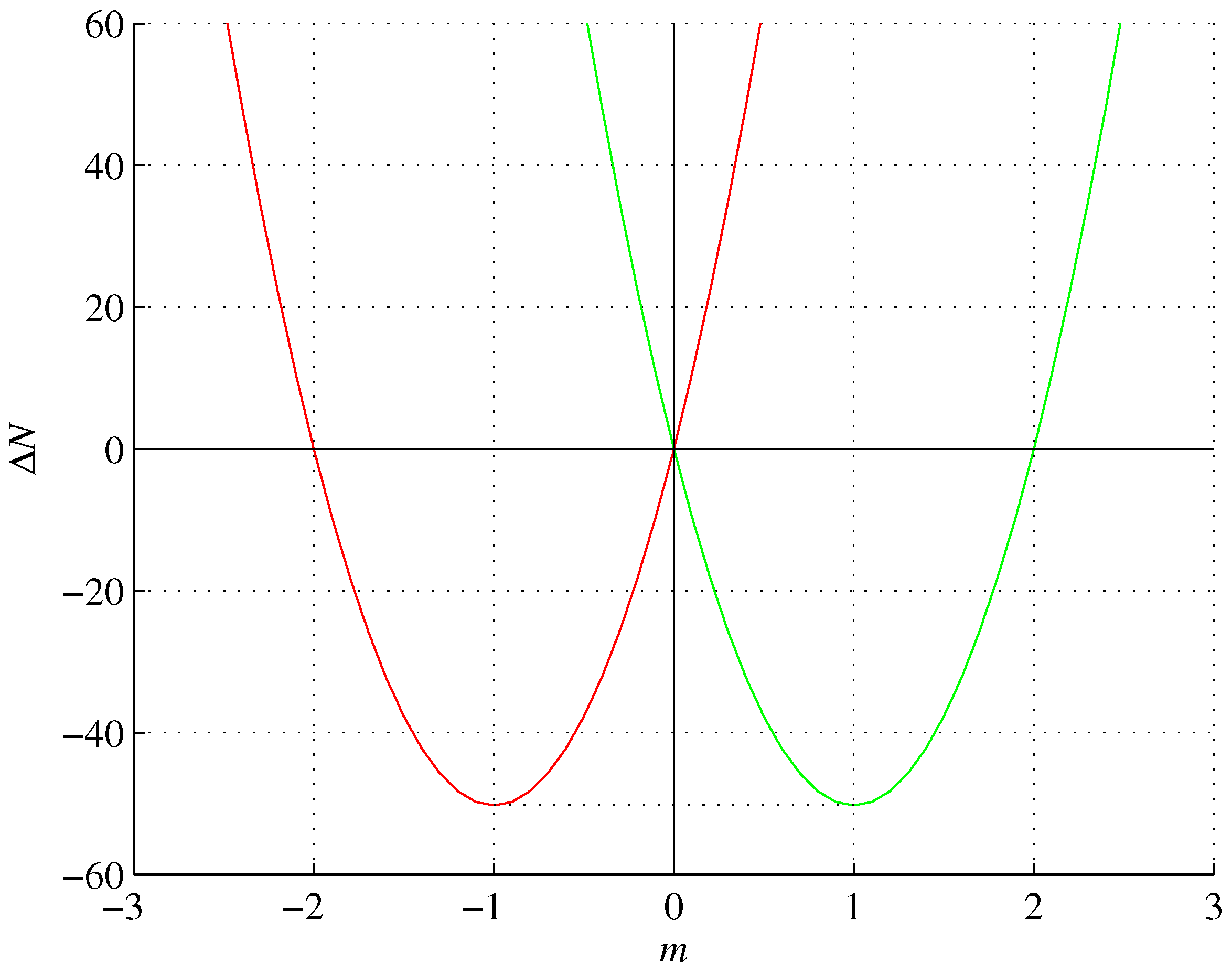
Table 1.
Complementary fine-structure constants - and the associated physical quantities and sets of Planck units.
Table 1.
Complementary fine-structure constants - and the associated physical quantities and sets of Planck units.
| -form | ||||
| [m/s] | 299792458 | |||
| [C] | ||||
| [m] | ||||
| [kg] | ||||
| [s] | ||||
| [K] | ||||
| [m3] | ||||
| [kg m/s] | ||||
| [J] | ||||
| [m/s2] | ||||
| [kg/m3] | ||||
| [m2] | ||||
| [N] | ||||
| [kg m C−2] | 1.2569e-6 | 1.2012e-6 | 0.0387 | 72.8061 |
| T | ||||
| A | ||||
| R | ||||
| -3.0712 | -551.2868 | |||
| -3.2136 | -0.0179 |
Table 2.
Selected BB mergers discovered with LIGO and Virgo. Masses in .
| Event | ||||||
| GW170817 | 4.39 | 4.39 | 3.03 | |||
| GW190425 | 4.39 | 4.39 | 3.15 | |||
| GW200105 | 2.76 | 4.39 | 2.38 | |||
| GW200115 | 3 | 4.39 | 2.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






