Graphene Introduces the Second Negative Fine Structure Constant and the Imaginary Set of Base Planck Units

Szymon Łukaszyk

doi:10.20944/preprints202212.0045.v6

Submitted:

20 January 2023

Posted:

23 January 2023

Read the latest preprint version here

Abstract

The reflectance $R$ of monolayer graphene for the normal incidence of electromagnetic radiation is known to be remarkably defined only by $\pi$ and the fine-structure constant $\alpha$. It is shown in this paper that the reflectance (or the sum of transmittance and absorptance) of monolayer graphene, expressed as a quadratic equation with respect to the fine-structure constant $\alpha$ must unsurprisingly introduce the 2$^\text{nd}$ fine-structure constant $\alpha_2$, as the 2$^\text{nd}$ root of this equation, as well as two $\pi$-like constants for a convex and a saddle surface. It turns out that this 2$^\text{nd}$ fine-structure constant is negative, and the sum of its reciprocal with the reciprocal of the fine-structure constant $\alpha$ is independent of the reflectance value $R$ and remarkably equals $-\pi$. Particular algebraic definition of the fine-structure constant $\alpha^{-1} = 4\pi^3 + \pi^2 + \pi \approx 137.036$, containing the free $\pi$ term and agreeing with the physical definition of this dimensionless constant to the 5$^\text{th}$ significant digit, when introduced to this sum, yields $\alpha_2^{-1} = -4\pi^3 - \pi^2 - 2\pi \approx -140.178$. Assuming universal validity of the physical definition of $\alpha$, $\alpha_2$ defines the negative speed of light in vacuum $c_n$. The average of this speed $c_n$ and the speed of light in vacuum $c$ is in the range of the Fermi velocity ($10^6$ m/s). Furthermore, the 2$^\text{nd}$ negative fine-structure constant $\alpha_2$ alone introduces the imaginary set of base Planck units.

Keywords:

Planck units

;

the fine-structure constant

;

speed of light in vacuum

;

emergent dimensionality

Subject:

Physical Sciences - Mathematical Physics

I. Introduction

Numerous publications provide Fresnel coefficients for the normal incidence of electromagnetic radiation (EMR) on monolayer graphene (MLG), which are remarkably defined only by

π

and the fine-structure constant

α

having the reciprocal

α^{- 1} = {(\frac{q_{P}}{e})}^{2} = \frac{4 π ϵ_{0} ℏ c}{e^{2}} \approx 137.036,

(1)

where e is the elementary charge,

q_{P}

is the Planck charge,

ϵ_{0}

is vacuum permittivity, ℏ is the reduced Planck constant, and c is the speed of light in vacuum.

Transmittance (T) of MLG

T = \frac{1}{{(1 + \frac{π α}{2})}^{2}} \approx 97.746 %

(2)

for normal EMR incidence was derived from the Fresnel equation in the thin-film limit [1] (Equation 3), whereas spectrally flat absorptance (A)

A \approx π α \approx 2.3 %

was reported [2,3] for photon energies between about 0.5 and 2.5 eV. T was related to reflectance (R) [4] (Equation 53) as

R = π^{2} α^{2} T / 4

, i.e,

R = \frac{\frac{1}{4} π^{2} α^{2}}{{(1 + \frac{π α}{2})}^{2}} \approx 0.013 %,

(3)

The above formulas for T and R, as well as the formula for the absorptance

A = \frac{π α}{{(1 + \frac{π α}{2})}^{2}} \approx 2.241 %,

(4)

were also derived [5] (Eqs. 29-31) based on the thin film model (setting

n_{s} = 1

for substrate).

The sum of transmittance (2) and the reflectance (3) at normal EMR incidence on MLG was also derived [6] (Equation 4a) as

\begin{matrix} T + R & = 1 - \frac{4 σ η}{4 + 4 σ η + σ^{2} η^{2} + k^{2} χ^{2}} \\ = \frac{1 + \frac{1}{4} π^{2} α^{2}}{{(1 + \frac{π α}{2})}^{2}} \approx 97.759 %, \end{matrix}

(5)

where

η = \frac{4 π α ℏ}{e^{2}} = \frac{1}{ϵ_{0} c}

(6)

is the impedance of vacuum,

σ = e^{2} / (4 ℏ) = π α / η

is the MLG conductivity [7], and

χ = 0

is the electric susceptibility of vacuum.

These coefficients are thus well-established theoretically and experimentally confirmed [1,2,3,6,8,9].

As a consequence of the conservation of energy

(T + A) + R = 100 % .

(7)

In other words, the transmittance in the Fresnel equation describing the reflection and transmission of EMR at normal incidence on a boundary between different optical media is, in the case of the 2-dimensional (boundary) of MLG, modified to include its absorption.

The paper is structured as follows. Section II shows that Fresnel coefficients for the normal incidence of EMR on MLG introduce the second, negative fine-structure constant

α_{2}

. Section III shows that this second fine-structure constant introduces the negative speed of light in vacuum

c_{n}

, which in turn introduces the imaginary set of base Planck units. Section IV shows that the negativity of the

α_{2}

alone is sufficient to introduce the

α_{2}

-set of Planck units. Section V presents Fresnel coefficients for the normal incidence of EMR on MLG expressed just by

π

. Section VI shows that Fresnel coefficients for the normal incidence of EMR on MLG introduce two

π

-like constants for a convex and a saddle surface having respectively positive and negative Gaussian curvatures. Section VII outlines certain prospects of further research, whereas Section VIII concludes the findings of this study.

II. The second Fine-Structure Constant

The reflectance

R = 0.013 %

(3) of MLG can be expressed as a quadratic equation with respect to

α

\frac{1}{4} (R - 1) π^{2} α^{2} + R π α + R = 0,

(8)

having two roots with reciprocals

α^{- 1} = \frac{π - π \sqrt{R}}{2 \sqrt{R}} \approx 137.036, and

(9)

α_{2}^{- 1} = \frac{- π - π \sqrt{R}}{2 \sqrt{R}} \approx - 140.178 .

(10)

Therefore, the quadratic equation (8) introduces the second, negative fine-structure constant

α_{2}

.

The sum of the reciprocals of these fine-structure constants (9) and (10)

α^{- 1} + α_{2}^{- 1} = \frac{π - π \sqrt{R} - π - π \sqrt{R}}{2 \sqrt{R}} = - π,

(11)

is remarkably independent of the reflectance R. The same result can be obtained for the sum of T and A, as shown in Appendix A.

Furthermore, this result is intriguing in the context of a peculiar algebraic definition of the fine-structure constant [10]

α^{- 1} = 4 π^{3} + π^{2} + π \approx 137.036

(12)

that contains a free

π

term and agrees with the physical definition (1) of

α

to the 5^th significant digit. Therefore, using Equations (11) and (12), we can express the negative reciprocal of the 2^nd fine-structure constant

α_{2}^{- 1}

that emerged in the quadratic equation (8) also as a function of

π

only

α_{2}^{- 1} = - π - α_{1}^{- 1} = - 4 π^{3} - π^{2} - 2 π \approx - 140.178 .

(13)

This result supports the validity of the algebraic definition (12).

But how can this negative value be interpreted physically?

III. Negative Speed of Light and the $α_{2}$ -set of Planck Units based on it

Almost all physical constants of

α = e^{2} / (4 π ϵ_{0} ℏ c)

in the physical definition of the fine-structure constant (1) are positive1, whereas the charge e is squared. Only the velocity can be negative, as it is a directional quantity. Therefore, if

α^{- 1} = \frac{π - π \sqrt{R}}{2 \sqrt{R}} = \frac{4 π ϵ_{0} ℏ c}{e^{2}} \approx 137.036,

(14)

then

α_{2}^{- 1} = \frac{- π - π \sqrt{R}}{2 \sqrt{R}} = \frac{4 π ϵ_{0} ℏ c_{n}}{e^{2}} \approx - 140.178,

(15)

where

c_{n}

is the negative speed of light in vacuum that, using Equations (11) with (1) and (15), amounts

\begin{matrix} \frac{4 π ϵ_{0} ℏ c}{e^{2}} + \frac{4 π ϵ_{0} ℏ c_{n}}{e^{2}} = - π \\ c_{n} = - \frac{e^{2}}{4 ϵ_{0} ℏ} - c \approx - 3.066653 \times 10^{8} [m / s], \end{matrix}

(16)

which is greater that the speed of light in vacuum c in modulus, whereas their average

\frac{c + c_{n}}{2} \approx - 3.436417 \times 10^{6} [m / s]

(17)

is in the range of the Fermi velocity.

Furthermore, we can express the

e^{2} / (4 ϵ_{0} ℏ)

term in (16) using the impedance of vacuum (6) as

c_{n} = - c (α π + 1)

which, using the algebraic definitions of

α

(12) and

α_{2}

(13), yields the following relation between the speed of light in vacuum c, negative speed of light

c_{n}

, the fine-structure constant

α

and the negative fine-structure constant

α_{2}

c α = c_{n} α_{2} (= v_{e}),

(18)

where

v_{e}

is the electron’s velocity at the first circular orbit in the Bohr model of the atom.

The concept of the negative speed of light in vacuum

c_{n}

might seem to be a nonsence or unsettling for the reader. If this is the case, the reader is advised to skip to the subsequent Section 1.

The negative speed of light in vacuum

c_{n}

(16) introduces the imaginary set of base Planck units {

q_{P i}

,

ℓ_{P i}

,

m_{P i}

,

t_{P i}

,

T_{P i}

} that redefined by square roots containing

c_{n} < 0

raised to an odd (1, 3, 5) power become imaginary and bivalued2:

\begin{matrix} q_{P i} & = \pm \sqrt{4 π ϵ_{0} ℏ c_{n}} = \pm q_{P} \sqrt{\frac{α}{α_{2}}} \\ \approx \pm i 1.8969 \times 10^{- 18} [C] (> q_{P}), \end{matrix}

(19)

\begin{matrix} ℓ_{P i} & = \pm \sqrt{\frac{ℏ G}{c_{n}^{3}}} = \pm ℓ_{P} \sqrt{\frac{α_{2}^{3}}{α^{3}}} \\ \approx \pm i 1.5622 \times 10^{- 35} [m] (< ℓ_{P}), \end{matrix}

(20)

\begin{matrix} m_{P i} & = \pm \sqrt{\frac{ℏ c_{n}}{G}} = \pm m_{P} \sqrt{\frac{α}{α_{2}}} \\ \approx \pm i 2.2012 \times 10^{- 8} [kg] (> m_{P}), \end{matrix}

(21)

\begin{matrix} t_{P i} & = \pm \sqrt{\frac{ℏ G}{c_{n}^{5}}} = \pm t_{P} \sqrt{\frac{α_{2}^{5}}{α^{5}}} \\ \approx \pm i 5.0942 \times 10^{- 44} [s] (< t_{P}), \end{matrix}

(22)

\begin{matrix} T_{P i} & = \pm \sqrt{\frac{ℏ c_{n}^{5}}{G k_{B}^{2}}} = \pm T_{P} \sqrt{\frac{α^{5}}{α_{2}^{5}}} \\ \approx \pm i 1.4994 \times 10^{32} [K] (> T_{P}), \end{matrix}

(23)

and can be expressed3, using (18), in terms of base Planck units

ℓ_{P}

,

m_{P}

,

t_{P}

, and

T_{P}

.

We note in passing, that imaginary and negative physical quantities are the subject of research. In particular, thermodynamics in the complex plane is the subject of research. In particular, Lee–Yang zeros have been experimentally observed [11,12].

Both charge

α_{2} q_{P i}^{2} = α q_{P}^{2}

(19) and mass

α_{2}

Planck units

α_{2} m_{P i}^{2} = α m_{P}^{2}

(21) are related with base Planck units in the same way. It is not surprising: both Coulomb’s law and Newton’s law of gravity are inverse-square laws. We also note that the relations between time (22) and temperature

α_{2}

Planck units (23) are inverted:

α^{5} t_{P i}^{2} = α_{2}^{5} t_{P}^{2}

, whereas

α_{2}^{5} T_{P i}^{2} = α^{5} T_{P}^{2}

. Furthermore, eliminating

α

and

α_{2}

from (19)-(23) yields the following relations

\frac{q_{P}^{2}}{m_{P}^{2}} = \frac{q_{P i}^{2}}{m_{P i}^{2}} = 4 π ϵ_{0} G,

(24)

T_{P}^{2} t_{P}^{2} = T_{P i}^{2} t_{P i}^{2} = \frac{ℏ^{2}}{k_{B}^{2}},

(25)

and

\frac{ℓ_{P}}{ℓ_{P i}} = \frac{q_{P i}^{3}}{q_{P}^{3}} = \frac{m_{P i}^{3}}{m_{P}^{3}},

(26)

independent of the velocity of light.

The first relation (24) is interesting. A complex energy formula

E = E_{M} + i E_{Q} = (1 + i β) M c^{2},

(27)

where

E_{M} = M c^{2}

represents the real energy, M is the mass of a particle,

E_{Q}

represents the imaginary energy, and

β ≐ \frac{E_{Q}}{E_{M}} = \frac{Q}{2 M \sqrt{π ϵ_{0} G}},

(28)

is the imaginary-real energy ratio4, where Q is the charge5 of the particle, was proposed in [13] (Eqs. (1), (3), and (4)). Squared imaginary-real energy ratio (28) can be expressed as

β^{2} = \frac{Q^{2}}{4 π ϵ_{0} G M^{2}}, \frac{Q^{2}}{β^{2} M^{2}} = 4 π ϵ_{0} G,

(29)

which certainly supports the complex energy formula (27). We see that for

β^{2} = 1

,

Q^{2} / M^{2} = q_{P}^{2} / m_{P}^{2} = q_{P i}^{2} / m_{P i}^{2}

(24). In such a case, the complex energy (27) is real-to-imaginary balanced, i.e.,

E = (1 \pm i) M c^{2} .

Such a balanced situation is also specific to black holes, the horizons of which comprise a balanced number of Planck areas with binary potentials equal to

- c^{2}

and zero [14]. Furthermore, the complex energy (27) of an antiparticle is defined as a conjugate of the complex energy of its associated particle. The complex energy (27) also unifies Coulomb’s law and Newton’s law of gravity (cf. [13] Eqs. (7), (8)) between two particles with masses

M_{1}

,

M_{2}

, charges

Q_{1}

,

Q_{2}

, a distance of R apart, in a complex force formula

\begin{matrix} F & = \frac{G}{c^{4}} \frac{E_{1} E_{2}}{R^{2}} = \\ = G \frac{M_{1} M_{2}}{R^{2}} - \frac{1}{4 π ϵ_{0}} \frac{Q_{1} Q_{2}}{R^{2}} + i \frac{\sqrt{G}}{2 \sqrt{π ϵ_{0}}} (\frac{Q_{1} M_{2} + Q_{2} M_{1}}{R^{2}}) = \\ = G \frac{M_{1} M_{2}}{R^{2}} [1 + i (β_{1} + β_{2})] - \frac{1}{4 π ϵ_{0}} \frac{Q_{1} Q_{2}}{R^{2}} . \end{matrix}

(30)

We note that the imaginary term vanishes if

M_{1} = M_{2}

and

Q_{1} = - Q_{2}

(particle vs. antiparticle). Also, the quantum of the imaginary energy (corresponding to the elementary charge e)

E_{Q} (e) = e c^{2} / (2 \sqrt{π ϵ_{0} G})

([13] Equation (10)) can be expressed, using the impedance of vacuum (6), in terms of the fine-structure constant as

E_{Q} (e) = \sqrt{α} k_{B} T_{P} .

(31)

Planck units derived from imaginary base units (20)-(23) are not imaginary in general.

The

α_{2}

Planck volume

\begin{matrix} ℓ_{P i}^{3} & = \pm {(\frac{ℏ G}{c_{n}^{3}})}^{3 / 2} = \pm ℓ_{P}^{3} \sqrt{\frac{α_{2}^{9}}{α^{9}}} \\ \approx \pm i 3.8127 \times 10^{- 105} [m^{3}] (< ℓ_{P}^{3}), \end{matrix}

(32)

the

α_{2}

Planck momentum

\begin{matrix} p_{P i} & = \pm m_{P i} c_{n} = \pm \sqrt{\frac{ℏ c_{n}^{3}}{G}} = \pm m_{P} c \sqrt{\frac{α^{3}}{α_{2}^{3}}} \\ \approx \pm i 6.7504 [kg m / s] (> m_{P} c), \end{matrix}

(33)

the

α_{2}

Planck energy

\begin{matrix} E_{P i} & = \pm m_{P i} c_{n}^{2} = \pm \sqrt{\frac{ℏ c_{n}^{5}}{G}} = \pm E_{P} \sqrt{\frac{α^{5}}{α_{2}^{5}}} \\ \approx \pm i 2.0701 \times 10^{9} [J] (> E_{P}), \end{matrix}

(34)

and the

α_{2}

Planck acceleration

\begin{matrix} a_{P i} & = \pm \frac{c_{n}}{t_{P i}} = \pm \sqrt{\frac{c_{n}^{7}}{ℏ G}} = \pm a_{P} \sqrt{\frac{α^{7}}{α_{2}^{7}}} \\ \approx \pm i 6.0198 \times 10^{51} [m / s^{2}] (> a_{P}), \end{matrix}

(35)

are imaginary and bivalued.

However, the

α_{2}

Planck force

\begin{matrix} F_{P 2} & = \pm \frac{E_{P i}}{ℓ_{P i}} = \pm \frac{c_{n}^{4}}{G} = \pm F_{P} \frac{α^{4}}{α_{2}^{4}} \\ \approx \pm 1.3251 \times 10^{44} [N] (> F_{P}), \end{matrix}

(36)

and the

α_{2}

Planck density

\begin{matrix} ρ_{P 2} & = \pm \frac{m_{P i}}{ℓ_{P i}^{3}} = \pm \frac{c_{n}^{5}}{ℏ G^{2}} = \pm ρ_{P} \frac{α^{5}}{α_{2}^{5}} \\ \approx \pm 5.7735 \times 10^{96} [kg / m^{3}] (> ρ_{P}), \end{matrix}

(37)

are real and bivalued.

On the other hand, the

α_{2}

Planck area

ℓ_{P i}^{2} = \frac{ℏ G}{c_{n}^{3}} = ℓ_{P}^{2} \frac{α_{2}^{3}}{α^{3}} \approx - 2.4406 \times 10^{- 70} [m^{2}] (< ℓ_{P}^{2}),

(38)

is strictly negative. According to the holographic principle, each bit of information is physically represented on the holographic boundary by the Planck area [15,16,17] (having a positive value), whereas these areas are triangular [14]6. Notably, out of all four omnidimensional (i.e., present in all complex dimensions n) convex n-polytopes and n-balls, only n-simplices (i.e., triangles for

n = 2

) are bivalued, admitting both positive and negative volumes and surfaces [18].

IV. Alternative Derivation of the $α_{2}$ -set of Planck Units without the Negative Speed of Light

The

α_{2}

-set of Planck units, discussed in the preceding section, can also be derived without the negative speed of light

c_{n}

(16).

Using the definition of the fine-structure constant

α = e^{2} / q_{P}^{2}

(1) for the negative

α_{2}

(10) or (13), we see that it requires an introduction of some imaginary Planck charge

q_{P i}

, so that its square would yield a negative

α_{2}

\frac{q_{P i}^{2}}{e^{2}} = α_{2}^{- 1} \approx - 140.178 < 0 .

(39)

Thus, using the value of the elementary charge e in (39) and the value of the

α_{2}

(10) or (13), the imaginary Planck charge (39) can be derived without the negative speed of light

c_{n}

as

q_{P i} = \pm \sqrt{\frac{e^{2}}{α_{2}}} .

(40)

Furthermore, the concept of the negative speed of light

c_{n}

is not required to derive the imaginary Planck mass, which, using (40), (24) and the values of the Planck mass and charge is

m_{P i} = \pm \frac{q_{P i} m_{P}}{q_{P}} .

(41)

In the derivation of (41), we have used the relation (24) that was derived on the basis of the negative speed of light, but this relation, as such, is independent of any particular value of the speed of light, be it positive or negative.

Knowing that the Planck charge is

q_{P} = \sqrt{4 π ϵ_{0} ℏ c}

we can solve it for the speed of light to find

c = q_{P}^{2} / (4 π ϵ_{0} ℏ)

and introduce it to the Planck force

F_{P} = \pm c^{4} / G

making it is independent on the speed of light.

This relation must be valid also for the

α_{2}

Planck force that therefore can be derived without the negative speed of light

c_{n}

and using the imaginary Planck charge (40), or the relation (24) (with the second term) as

F_{P 2} = \pm \frac{1}{G} {(\frac{q_{P i}^{2}}{4 π ϵ_{0} ℏ})}^{4} = \pm \frac{G^{3}}{ℏ^{4}} m_{P i}^{8} .

(42)

Knowing the value of the

α_{2}

Planck force (42) and mass (41) we can derive the

α_{2}

Planck acceleration

a_{P i} = \pm \frac{F_{P 2}}{m_{P i}},

(43)

and the remaining

α_{2}

Planck units, using the imaginary Planck charge (40) instead of the negative speed of light

c_{n}

.

V. Algebraic Fresnel coefficients for the normal incidence of EMR on MLG

With algebraic definitions of

α

(12) and

α_{2}

(13) transmittance T (2), reflectance R (3) and absorptance A (4) of MLG for normal EMR incidence can be expressed just by

π

.

For

α^{- 1} = 4 π^{3} + π^{2} + π

(12) they become

T (α) = \frac{4 {(4 π^{2} + π + 1)}^{2}}{{(8 π^{2} + 2 π + 3)}^{2}} \approx 97.746 %,

(44)

A (α) = \frac{4 (4 π^{2} + π + 1)}{{(8 π^{2} + 2 π + 3)}^{2}} \approx 2.241 %,

(45)

while for

α_{2}^{- 1} = - 4 π^{3} - π^{2} - 2 π

(13) they become

T (α_{2}) = \frac{4 {(4 π^{2} + π + 2)}^{2}}{{(8 π^{2} + 2 π + 3)}^{2}} \approx 102.279 %,

(46)

A (α_{2}) = - \frac{4 (4 π^{2} + π + 2)}{{(8 π^{2} + 2 π + 3)}^{2}} \approx - 2.292 %,

(47)

with

R (α) = R (α_{2}) = \frac{1}{{(8 π^{2} + 2 π + 3)}^{2}} \approx 0.013 % .

(48)

Obviously (

T (α) + A (α)) + R (α) = (T (α_{2}) + A (α_{2})) + R (α_{2}) = 1

as required by the law of conservation of energy (7), whereas each conservation law is associated with a certain symmetry, as asserted by Noether’s theorem. Nonetheless, physical interpretation of

T (α_{2}) > 1

and

A (α_{2}) < 0

invites further research.

A (α) > 0

implies a sink, whereas

A (α_{2}) < 0

implies a source, whereas the opposite holds true for the transmittance T, as illustrated schematically in Figure 1. Perhaps, the negative absorptance and transmittance exceeding 100% for

α_{2}

(10) or (13) could be explained in terms of graphene spontaneous emission.

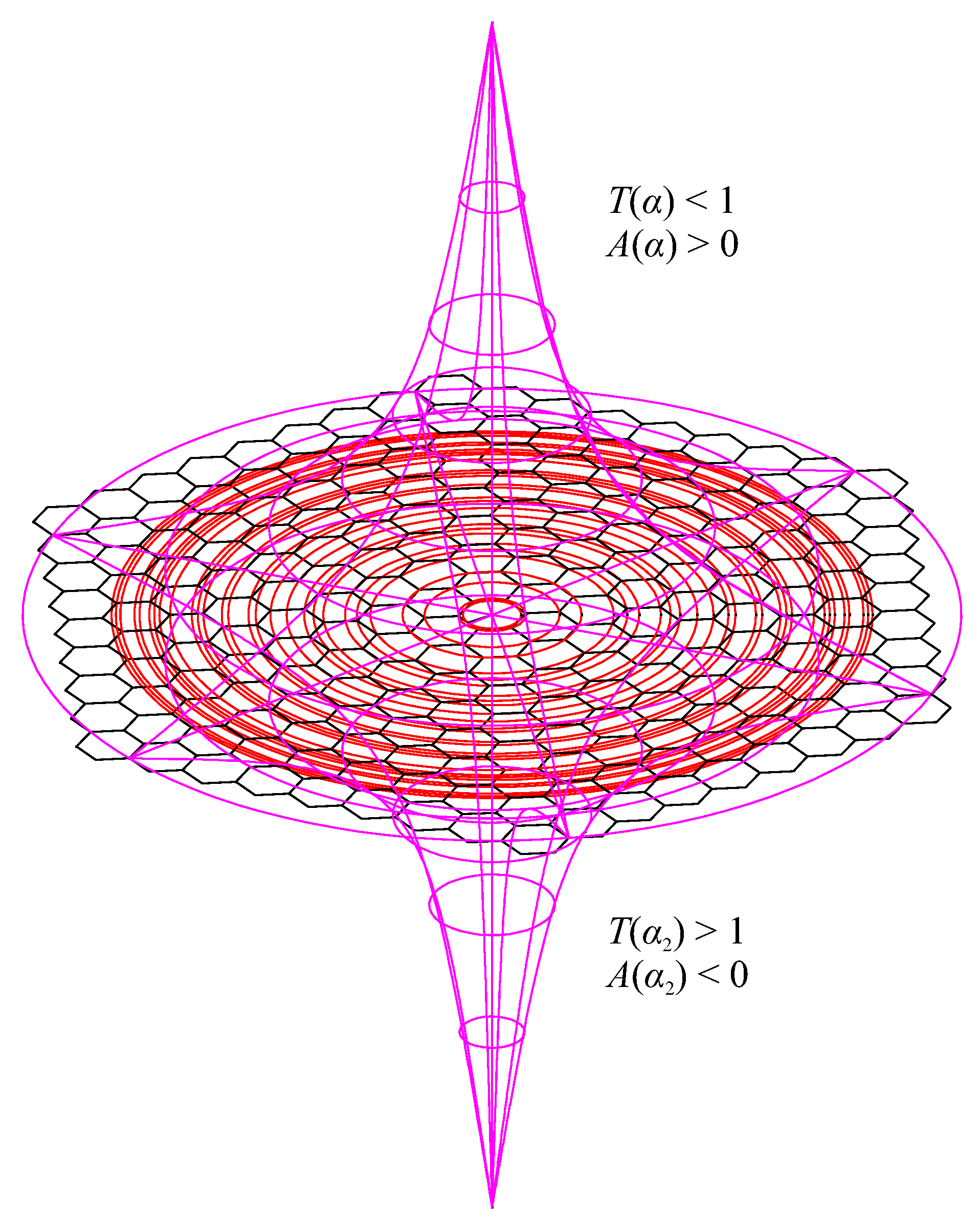
VI. FRESNEL COEFFICIENTS FOR THE NORMAL INCIDENCE OF EMR ON MLG introduce two $π$ -like constants for two surfaces with positive and negative Gaussian curvatures

The quadratic equation (8) describing the reflectance R of MLG under normal incidence of EMR (or alternatively (A1)) can also be solved for

π

yielding two roots

π {(R, α_{*})}_{1} = \frac{2 \sqrt{R}}{α_{*} (1 - \sqrt{R})}, and

(49)

π {(R, α_{*})}_{2} = \frac{- 2 \sqrt{R}}{α_{*} (1 + \sqrt{R})},

(50)

dependent on R and

α_{*}

, where

α_{*}

indicates

α

or

α_{2}

. This can be further evaluated, using the algebraic definition of R (48) (which is the same for both

α

and

α_{2}

), yielding four, yet only three distinct, possibilities

π_{1} = π {(α)}_{1} = - π \frac{4 π^{2} + π + 1}{4 π^{2} + π + 2} = π \frac{α_{2}}{α} \approx - 3.0712,

(51)

π {(α)}_{2} = π {(α_{2})}_{1} = π \approx 3.1416, and

(52)

π_{2} = π {(α_{2})}_{2} = - π \frac{4 π^{2} + π + 2}{4 π^{2} + π + 1} = π \frac{α}{α_{2}} \approx - 3.2136 .

(53)

The absolute value of

π_{1}

(51) corresponds to a convex surface having a positive Gaussian curvature, whereas the absolute value of

π_{2}

(53) - to a negative Gaussian curvature. Their product

π_{1} π_{2} = π^{2}

is independent of

α_{*}

, and their quotient

π_{1} / π_{2} = α_{2}^{2} / α^{2}

is independent of

π

. It remains to be found, whether each of them describes the ratio of circumference of a circle drawn on the respective surface to its diameter (

π_{c}

) or the ratio of the area of this circle to the square of its radius (

π_{a}

). These definitions produce different results on curved surfaces, whereas

π_{a} > π_{c}

on convex surfaces, while

π_{a} < π_{c}

on saddle surfaces [19].

VII. Discussion

A general relation describing the information capacity

N_{B H} = π d^{2}

(i.e., the number of the triangular Planck areas at the black hole horizon, corresponding to bits of information and the fractional part triangle

{π d^{2}}

to small to carry a bit) of a Schwarzschild black hole (BH) having the diameter D multiplier

d = D / ℓ_{P}

after absorption (

+ 16 π^{2} d / l

) or emission (

- 16 π^{2} d / l

) of a particle having the wavelength

λ

multiplier

l = λ / ℓ_{P}

has been disclosed in [14] (Equation (18)) as

N_{B H}^{A / E} (d, l) = 64 π^{3} \frac{1}{l^{2}} \pm 16 π^{2} \frac{d}{l} + π d^{2} .

(54)

This general geometric relation, originally derived only for particles having the Compton wavelength equal to the BH radius [20] (p. 153), is remarkably similar to the algebraic definitions of the inverses of

α

(12) and

α_{2}

(13) also containing

π^{3}

,

π^{2}

, and

π

terms. This raises the question of whether the inverses of the fine-structure constants themselves correspond to the number of bits. Remarkably, the floor function of the inverse of the fine-structure constant

α

represents the threshold on the atomic number (137) of a hypothetical element feynmanium that, in the Bohr model of the atom, still allows the 1s orbital electrons to travel slower than the speed of light. On the other hand, the negative

α_{2}

introduces the negative BH information capacity, which - taking into account the negative, triangular

α_{2}

Planck area

ℓ_{P i}^{2}

(38) - could be in the form

N_{B H} (α, α_{2}) = \frac{π d^{2} ℓ_{P}^{2}}{ℓ_{P i}^{2}} = π d^{2} \frac{α^{3}}{α_{2}^{3}} \approx - 1.0704 π d^{2},

(55)

or

N_{B H} (α_{2}, α) = \frac{π d^{2} ℓ_{P i}^{2}}{ℓ_{P}^{2}} = π d^{2} \frac{α_{2}^{3}}{α^{3}} \approx - 0.8728 π d^{2} .

(56)

To examine the conditions under which the BH information capacity would equal

α

(12) and

α_{2}

(13) after absorption or emission we compare (54) with (12), which yields

d_{A / E, α} = \mp \frac{8 π}{l} \pm \sqrt{4 π^{2} + π + 1},

(57)

whereas comparing (54) with (13) yields

d_{A / E, α_{2}} = \mp \frac{8 π}{l} \pm i \sqrt{4 π^{2} + π + 2},

(58)

in both cases with

- 8 π

for absorption and

+ 8 π

for emission. The emission first term in (57) and (58) corresponds to the BH Compton diameter multiplier [14] (Equation (9)). This issue certainly requires further research. We note in passing that the fine-structure constant has recently been reported as the quantum of rotation [21].

VIII. CONCLUSIONS

We have shown that the reflectance of graphene under the normal incidence of electromagnetic radiation (EMR), expressed as the quadratic equation with respect to the fine-structure constant

α

must introduce the 2^nd negative fine-structure constant

α_{2}

.

The sum of the reciprocal of this 2^nd fine-structure constant

α_{2}

with the reciprocal of the fine-structure constant

α

(1) is independent of the reflectance value R and remarkably equals simply

- π

.

Particular algebraic definition of the fine-structure constant

α^{- 1} = 4 π^{3} + π^{2} + π

(12), containing the free

π

term, when introduced to this sum, yields

α_{2}^{- 1} = - 4 π^{3} - π^{2} - 2 π < 0

.

Assuming universal validity of the physical definition of the fine-structure constant

α

(1), the 2^nd fine-structure constant

α_{2}

(13) defines the negative speed of light

c_{n}

(16), the average of which and the speed of light in vacuum is in the range of the Fermi velocity (

10^{6}

m/s).

Furthermore, the negative fine-structure constant

α_{2}

alone introduces the imaginary set of five base Planck units (19)-(23), whereas mass and charge units (24), as well as temperature and time units (25) are directly related to base Planck units.

The Planck volume (32), momentum (33), energy (34), and acceleration (35) derived from imaginary base units (20)-(23) are imaginary and bivalued, whereas the Planck force (36) and density (37) are real and bivalued.

The square of the imaginary Planck length (20) introduces the negative Planck area (38). If Planck areas correspond to bits of information [15,16,17] and if they are triangular [14], then the fact that among four basic geometrical structures present in all complex dimensions: n-balls, n-cubes, n-orthoplices, and n-simplices only the latter have bivalued (positive and negative) volumes and surfaces equal to the modulus [18] for any real dimension n, suggests a physical interpretation for this negative Planck area (38).

The findings of this study, in particular, the meaning of the relation (25) (which clearly hints at Heisenberg’s uncertainty principle) and the negative ratios

π_{1}

(51) and

π_{2}

(53), inquire further research in the context of information-theoretic approach [22,23,24] and emergent dimensionality [14,18,25,26].

In the context of the results of this study, monolayer graphene, a truly 2-dimensional material with no thickness7, is a keyhole to other, unperceivable [14], dimensionalities. Graphene history is also instructive. Discovered in 1947 [28], graphene was long considered academic material until it was eventually pulled from graphite in 2004 [29] by means of ordinary Scotch tape8. These fifty-seven years, along with twenty-nine years (1935-1964) between the condemnation of quantum theory as incomplete [30] and Bell’s mathematical theorem [31] asserting that it is not true, and the fifty-eight years (1964-2022) between the formulation of this theorem and 2022 Nobel prize in physics for its experimental loophole-free confirmation, should remind us that Max Planck, the genius who discovered Planck units, has also discovered Planck’s principle.

Acknowledgments

I truly thank my wife for her support when this research [32,33] was conducted.

Appendix A. Other Quadratic Equations

The quadratic equation for the sum of transmittance (2) and absorptance (4), putting

C_{T A} ≐ T + A

, is

\frac{1}{4} C_{T A} π^{2} α^{2} + (C_{T A} - 1) π α + (C_{T A} - 1) = 0,

(A1)

and has two roots with reciprocals

α^{- 1} = \frac{C_{T A} π}{2 (1 - C_{T A} + \sqrt{1 - C_{T A}})} \approx 137.036,

(A2)

and

α_{2}^{- 1} = \frac{C_{T A} π}{2 (1 - C_{T A} - \sqrt{1 - C_{T A}})} \approx - 140.178,

(A3)

whereas their sum

α^{- 1} + α_{2}^{- 1} = - π

is also independent of T and A.

Other quadratic equations do not feature this property. For example, the sum of

T + R

(5) expressed as the quadratic equation and putting

C_{T R} ≐ T + R

, is

\frac{1}{4} (C_{T R} - 1) π^{2} α^{2} + C_{T R} π α + (C_{T R} - 1) = 0,

(A4)

and has two roots with reciprocals

α^{- 1} = \frac{π (C_{T R} - 1)}{- 2 C_{T R} + 2 \sqrt{2 C_{T R} - 1}} \approx 137.036,

(A5)

and

α_{T R}^{- 1} = \frac{π (C_{T R} - 1)}{- 2 C_{T R} - 2 \sqrt{2 C_{T R} - 1}} \approx 0.0180,

(A6)

whereas their sum

α_{T R_{1}}^{- 1} + α_{T R_{2}}^{- 1} = \frac{- π C_{T R}}{C_{T R} - 1} \approx 137.054

(A7)

is dependent on T and R.

References

Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal dynamical conductance in graphite. Physical Review Letters 2008, 100, 117401, arXiv:0712.0835 [cond-mat]. [Google Scholar] [CrossRef] [PubMed]
Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Physical Review Letters 2008, 101, 196405. [Google Scholar] [CrossRef] [PubMed]
Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Universal Dynamic Conductivity and Quantized Visible Opacity of Suspended Graphene. Science 2008, 320, 1308–1308, arXiv:0803.3718 [cond-mat]. [Google Scholar] [CrossRef] [PubMed]
Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Physical Review B 2008, 78, 085432. [Google Scholar] [CrossRef]
Wang, X.; Chen, B. Origin of Fresnel problem of two dimensional materials. Scientific Reports 2019, 9, 17825. [Google Scholar] [CrossRef] [PubMed]
Merano, M. Fresnel coefficients of a two-dimensional atomic crystal. Physical Review A 2016, 93, 013832. [Google Scholar] [CrossRef]
Ando, T.; Zheng, Y.; Suzuura, H. Dynamical Conductivity and Zero-Mode Anomaly in Honeycomb Lattices. Journal of the Physical Society of Japan 2002, 71, 1318–1324. [Google Scholar] [CrossRef]
Zhu, S.E.; Yuan, S.; Janssen, G.C.A.M. Optical transmittance of multilayer graphene. EPL (Europhysics Letters) 2014, 108, 17007. [Google Scholar] [CrossRef]
Ivanov, I.G.; Hassan, J.U.; Iakimov, T.; Zakharov, A.A.; Yakimova, R.; Janzén, E. Layer-number determination in graphene on SiC by reflectance mapping. Carbon 2014, 77, 492–500. [Google Scholar] [CrossRef]
Varlaki, P.; Nadai, L.; Bokor, J. Number Archetypes in System Realization Theory Concerning the Fine Structure Constant. 2008 International Conference on Intelligent Engineering Systems; IEEE: Miami, FL, 2008; pp. 83–92. [Google Scholar] [CrossRef]
Peng, X.; Zhou, H.; Wei, B.B.; Cui, J.; Du, J.; Liu, R.B. Experimental Observation of Lee-Yang Zeros. Physical Review Letters 2015, 114, 010601. [Google Scholar] [CrossRef] [PubMed]
Gnatenko, K.; Kargol, A.; Tkachuk, V. Lee–Yang zeros and two-time spin correlation function. Physica A: Statistical Mechanics and its Applications 2018, 509, 1095–1101. [Google Scholar] [CrossRef]
Zhang, T. Electric Charge as a Form of Imaginary Energy, 2008.
Łukaszyk, S., Black Hole Horizons as Patternless Binary Messages and Markers of Dimensionality. In Future Relativity, Gravitation, Cosmology; Dvoeglazov, V.V.; Caldera Cabral, M.d.G.; Cázares Montes, J.A.; Quintanar González, J.L., Eds.; Nova Science Publishers, 2023. [CrossRef]
Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
Hooft, G.t. Dimensional Reduction in Quantum Gravity, 1993. [CrossRef]
Verlinde, E. On the origin of gravity and the laws of Newton. Journal of High Energy Physics 2011, 2011, 29. [Google Scholar] [CrossRef]
Łukaszyk, S. On the Omnidimensional Convex Polytopes and n-Balls in Negative, Fractional and Complex Dimensions. preprint, MATHEMATICS & COMPUTER SCIENCE, 2022. [CrossRef]
Mahajan, S. Calculation of the pi-like circular constants in curved geometry. ResearchGate, 2013.
Susskind, L. Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics, 2008.
Shuvaev, A.; Pan, L.; Tai, L.; Zhang, P.; Wang, K.L.; Pimenov, A. Universal rotation gauge via quantum anomalous Hall effect. Applied Physics Letters 2022, 121, 193101. [Google Scholar] [CrossRef]
de Chardin, P.T. The Phenomenon of Man, Harper: New York, 1959.
Prigogine, I.; Stengers, I. Order out of Chaos: Man’s New Dialogue with Nature, 1984.
Vedral, V. Decoding Reality: The Universe as Quantum Information, Oxford University Press, 2010. [CrossRef]
Łukaszyk, S. Four Cubes, 2021. arXiv:2007.03782 [math].
Łukaszyk, S. Novel Recurrence Relations for Volumes and Surfaces of n-Balls, Regular n-Simplices, and n-Orthoplices in Real Dimensions. Mathematics 2022, 10, 2212. [Google Scholar] [CrossRef]
Jussila, H.; Yang, H.; Granqvist, N.; Sun, Z. Surface plasmon resonance for characterization of large-area atomic-layer graphene film. Optica 2016, 3, 151. [Google Scholar] [CrossRef]
Wallace, P.R. Erratum: The Band Theory of Graphite [Phys. Rev. 71, 622 (1947)]. Physical Review 1947, 72, 258–258. [Google Scholar] [CrossRef]
Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 1935, 47, 777–780. [Google Scholar] [CrossRef]
Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics Physique Fizika 1964, 1, 195–200. [Google Scholar] [CrossRef]
Łukaszyk, S. A short note about graphene and the fine structure constant 2020. [CrossRef]
Łukaszyk, S. A short note about the geometry of graphene 2020. [CrossRef]
C. J. Shearer, A. D. Slattery, A. J. Stapleton, J. G. Shapter, and C. T. Gibson, “Accurate thickness measurement of graphene,” Nanotechnology, vol. 27, p. 125704, Mar. 2016.

1	Vacuum permittivity $ϵ_{0}$ is the value of the absolute dielectric permittivity of classical vacuum. Thus, $ϵ_{0}$ cannot be negative. The Planck constant h is the uncertainty principle parameter. Thus, it cannot be negative; negative probabilities do not seem to withstand Occam’s razor.
2	Base Planck units themselves admit negative values as negative square roots.
3	The notation $ℓ_{P i} (< ℓ_{P})$ , for example, means that the absolute value of the imaginary Planck length (20) is lower than the absolute value of the Planck length $ℓ_{P} = \sqrt{ℏ G / c^{3}}$ .
4	In the cited study it is called $α$ , so we shall call it $β$ to avoid confusion with the fine-structure constant $α$ .
5	Charges in the cited study are defined in CGS units; here we adopt SI.
6	This is also compatible with the Causal Dynamical Triangulation (CDT) approach, which does not assume a pre-existence of a dimensional space, but focuses on the evolution of the spacetime as such.
7	Thickness of MLG is reported [27] as 0.37 nm with other reported values up to 1.7 nm. However, taking into account that 0.335 nm is the established inter-layer distance, and thus the thickness of bilayer graphene, these results do not seem credible.
8	Introduced into the market in 1932.

Figure 1. Illustration of the concepts of negative absorptance and excessive transmittance of EMR under normal incidence on MLG.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Graphene Introduces the Second Negative Fine Structure Constant and the Imaginary Set of Base Planck Units

Abstract

Keywords:

Subject:

I. Introduction

II. The second Fine-Structure Constant

III. Negative Speed of Light and the α 2 -set of Planck Units based on it

IV. Alternative Derivation of the α 2 -set of Planck Units without the Negative Speed of Light

V. Algebraic Fresnel coefficients for the normal incidence of EMR on MLG

VI. FRESNEL COEFFICIENTS FOR THE NORMAL INCIDENCE OF EMR ON MLG introduce two π -like constants for two surfaces with positive and negative Gaussian curvatures

VII. Discussion

VIII. CONCLUSIONS

Acknowledgments

Appendix A. Other Quadratic Equations

References

III. Negative Speed of Light and the $α_{2}$ -set of Planck Units based on it

IV. Alternative Derivation of the $α_{2}$ -set of Planck Units without the Negative Speed of Light

VI. FRESNEL COEFFICIENTS FOR THE NORMAL INCIDENCE OF EMR ON MLG introduce two $π$ -like constants for two surfaces with positive and negative Gaussian curvatures