Prerpints.org logo
Preprint
Article

The Imaginary Universe

Altmetrics

Downloads

1854

Views

1399

Comments

1

This version is not peer-reviewed

Submitted:

17 March 2023

Posted:

20 March 2023

Read the latest preprint version here

Alerts
Abstract
Imaginary dimensions in physics require an imaginary set of base Planck units and some negative parameter cn corresponding to the speed of light in vacuum c. Fresnel coefficients for the normal incidence of electromagnetic radiation on monolayer graphene introduce the second, negative fine-structure constant α2−1≈−140.178 as a fundamental constant of nature and this constant introduces these imaginary base Planck units along with this negative parameter cn≈−3.06×108 [m/s]. Neutron stars and white dwarfs, considered as objects emitting perfect black-body radiation, are conjectured to possess energy exceeding their mass-energy equivalence ratios, wherein the imaginary parts of two complex energies inaccessible for direct observation make storing excess of these energies possible. With this assumption, black holes are fundamentally uncharged; charged micro neutron stars and white dwarfs with masses lower than 5.7275×10−10 [kg] cannot be observed; and the radii of white dwarfs' cores are limited to RWD<6.7933 GMWD/c2. A black-body object is in the equilibrium of complex energies of mass, charge, and electromagnetic radiation if its radius Req≈2.7665 GMBBO/c2.
Keywords: 
Subject: Biology and Life Sciences  -   Endocrinology and Metabolism

I. INTRODUCTION

The universe began with the Big Bang, which is a current prevailing scientific opinion. But this Big Bang was not an explosion of 4-dimensional spacetime, which also is a current prevailing scientific opinion, but an explosion of dimensions. More precisely, in the − 1 -dimensional void, a 0-dimensional point appeared implying the appearance of countably infinitely other points indistinguishable from the first one. The breach made by the first operation of the dimensional successor function of the Peano axioms inevitably continued leading to the formation of 1-dimensional, real and imaginary lines allowing for an ordering of points using multiples of real units (ones) or imaginary units ( a ∈ R ⇔ a = 1 b 1, a ∈ I ⇔ a = i b , b ∈ R ). Then out of two lines of each kind, crossing each other only at one initial point ( 0 , 0 ) , the dimensional successor function formed 2-dimensional R 2 , I 2 , and R × I Euclidean planes, with I 2 being a mirror reflection of R 2 . And so on, forming n-dimensional Euclidean spaces R a × I b with a ∈ N real and b ∈ N imaginary lines, n : = a + b , and the scalar product defined by
x · y = x 1 , … , x a , i x 1 ′ , … , i x b ′ y 1 , … , y a , i y 1 ′ , … , i y b ′ : = : = ∑ k = 1 a x k y k + ∑ l = 1 b x l ′ y l ′ ¯ ,
where x , y ∈ R a × I b .
With the onset of the first 0-dimensional point, information began to evolve [1,2,3,4,5,6].
However, dimensional properties are not uniform. Concerning regular convex n-polytopes in natural dimensions, for example, there are countably infinitely many regular convex polygons, five regular convex polyhedra (Platonic solids), six regular convex 4-polytopes, and only three regular convex n-polytopes if n > 3 [7]. In particular, 4-dimensional euclidean space is endowed with a peculiar property known as exotic R 4 [8]. This property allowed for variation of phenotypic traits within populations of individuals [9] perceiving emergent Euclidean R 3 × I space of three real and one imaginary (time) dimension observer-dependently [10] and at present [11] when i 0 = 0 is real. The evolution of information extended into biological evolution.
Each dimension requires certain units of measure. In real dimensions, the natural units of measure were introduced by Max Planck in 1899 as "independent of special bodies or substances, thereby necessarily retaining their meaning for all times and for all civilizations, including extraterrestrial and non-human ones" [12].
This study introduces the complementary set of Planck units applicable for imaginary dimensions, including the imaginary base units, and outlines certain prospects for their research. As the speed of electromagnetic radiation is the product of its wavelength and frequency (which are real and positive), and both these quantities are imaginary in imaginary dimensions, some real but negative parameter c n = ν i λ i corresponding to the speed of light in vacuum c (i.e., the Planck speed) is also necessary as i 2 = − 1 . It turns out that the imaginary Planck energy E P i and temperature T P i are larger in moduli than the Planck energy E P and temperature T P Thus, the minimum energy principle sets more favorable conditions for biological evolution to emerge in R 3 × I Euclidean space than in I 3 × R Euclidean one.
The study shows that the energies of neutron stars and white dwarfs exceed their mass–energy equivalences. Therefore, the excess of these energies must be stored in imaginary dimensions and is inaccessible to direct observations. This results in the upper bound on the slope of the radius of their cores as a function of their masses.
The paper is structured as follows. Section II shows that Fresnel coefficients for the normal incidence of electromagnetic radiation on monolayer graphene introduce the second, negative fine-structure constant α 2 as a fundamental constant of nature. Section III shows that nature endows us with the imaginary base Planck units by this second fine-structure constant. Section IV introduces the concept of a black-body object in thermodynamic equilibrium emitting black-body radiation and discusses its necessary properties. Section V introduces two complex energies of masses and charges and applies them to black-body objects. Section VI introduces four additional complex energies of masses, charges, and wavelengths to derive the black-body object equilibrium, correcting the photon sphere radius of general relativity. Section VII summarizes the findings of this study.

II. THE SECOND FINE-STRUCTURE CONSTANT

Numerous publications provide Fresnel coefficients for the normal incidence of electromagnetic radiation (EMR) on monolayer graphene (MLG), which are remarkably defined only by π and the fine-structure constant α
α − 1 = q P e 2 = 4 π ϵ 0 ℏ c e 2 ≈ 137.036 .
Transmittance (T) of MLG
T = 1 1 + π α 2 2 ≈ 0.9775 ,
for normal EMR incidence was derived from the Fresnel equation in the thin-film limit [13] (Eq. 3), whereas spectrally flat absorptance (A) A ≈ π α ≈ 2 . 3 % was reported [14,15] for photon energies between about 0 . 5 and 2 . 5 [eV]. T was related to reflectance (R) [16] (Eq. 53) as R = π 2 α 2 T / 4 , i.e,
R = 1 4 π 2 α 2 1 + π α 2 2 ≈ 1.2843 × 10 − 4 ,
The above equations for T and R, as well as the equation for the absorptance
A = π α 1 + π α 2 2 ≈ 0.0224 ,
were also derived [17] (Eqs. 29-31) based on the thin film model (setting n s = 1 for substrate).
The sum of transmittance (3) and the reflectance (4) at normal EMR incidence on MLG was also derived [18] (Eq. 4a) as
T + R = 1 − 4 σ η 4 + 4 σ η + σ 2 η 2 + k 2 χ 2 = 1 + 1 4 π 2 α 2 1 + π α 2 2 ≈ 0.9776 ,
where η is the vacuum impedance
η = 4 π α ℏ e 2 = 1 ϵ 0 c ≈ 376.73 [ Ω ] ,
ϵ0 is vacuum permittivity, σ = e 2 / ( 4 ℏ ) = π α / η is the MLG conductivity [19], and χ = 0 is the electric susceptibility of vacuum.
These coefficients are thus well-established theoretically and experimentally confirmed [13,14,15,18,20,21].
As a consequence of the conservation of energy
( T + A ) + R = 1 .
In other words, the transmittance in the Fresnel equation describing the reflection and transmission of EMR at normal incidence on a boundary between different optical media is, in the case of the 2-dimensional (boundary) of MLG, modified to include its absorption.
The reflectance R = 0 . 013 % (4) of MLG can be expressed as a quadratic equation with respect to α
1 4 R − 1 π 2 α 2 + R π α + R = 0 ,
having two roots with reciprocals
α − 1 = π − π R 2 R ≈ 137.036 , and
α 2 − 1 = − π − π R 2 R ≈ − 140.178 .
Therefore, the quadratic equation (9) includes the second, negative fine-structure constant α 2 .
The sum of the reciprocals of these fine-structure constants (10) and (11)
α − 1 + α 2 − 1 = π − π R − π − π R 2 R = − π ,
is remarkably independent of the reflectance R. (The same result can be obtained for the sum of T and A, as shown in Appendix A).
Furthermore, this result is intriguing in the context of a peculiar algebraic expression for the fine-structure constant [22]
α − 1 = 4 π 3 + π 2 + π ≈ 137.036303776
that contains a free  π term and is very close to the physical definition (2) of α − 1 , which according to the CODATA 2018 value is 137 . 035999084 . Notably, the value of the fine-structure constant is not constant but increases with time [23,24,25,26,27]. Thus, the algebraic value given by (13) can be interpreted as the asymptote of the α increase.
Using relations (12) and (13), we can express the negative reciprocal of the 2nd fine-structure constant α 2 − 1 that emerged in the quadratic equation (9) also as a function of π only
α 2 − 1 = − π − α 1 − 1 = − 4 π 3 − π 2 − 2 π ≈ − 140.177896429 ,
and this value can also be interpreted as the asymptote of the α 2 decrease with the current value ammounting to α 2 − 1 ≈ − 140 . 177591737 , assuming the rate of change is the same for α and α 2 .
Using relations (13) and (14), transmittance T (3), reflectance R (4), and absorptance A (5) of MLG for normal EMR incidence can be expressed just by π . Furthermore, equation (9) includes two π -like constants for two surfaces with positive and negative Gaussian curvatures (cf. Appendix B).

III. α 2 -SET OF PLANCK UNITS

Planck units can be derived from numerous starting points [5,28] (cf. Appendix C). The definition of the Planck charge q P = 4 π ϵ 0 ℏ c can be solved for the speed of light yielding c = q P 2 / ( 4 π ϵ 0 ℏ ) . Furthermore, the ratio of charges definition of the fine-structure constant α = e 2 / q P 2 (2) applied for the negative α 2 , requires an introduction of some imaginary Planck charge q P i so that its square would yield a negative value of α 2
q P i 2 e 2 = α 2 − 1 ≈ − 140.178 < 0 .
Since the elementary charge e is real
q P i = ± e 2 α 2 = ± 4 π ϵ 0 ℏ c n .
and almost all physical constants of the 4 π ϵ 0 ℏ c n term, almost all are positive2. Only the c n = ν i λ i parameter, corresponding to the speed of light, must be negative as both frequency ν i and wavelength λ i are imaginary in imaginary dimensions. Therefore, equation (16) can be solved for c n yielding
c n = q P i 2 / ( 4 π ϵ 0 ℏ ) ≈ − 3.066653 × 10 8 [ m / s ] ,
which is greater than the speed of light in vacuum c in modulus3.
The negative parameter c n (17) introduces the imaginary set of base Planck units q P i , ℓ P i , m P i , t P i , and T P i that redefined by square roots containing c n raised to an odd (1, 3, 5) power become imaginary and bivalued
q P i = ± 4 π ϵ 0 ℏ c n = ± q P α α 2 ≈ ≈ ± i 1.8969 × 10 − 18 [ C ] | q P i | > | q P | ,
ℓ P i = ± ℏ G c n 3 = ± ℓ P α 2 3 α 3 ≈ ≈ ± i 1.5622 × 10 − 35 [ m ] | ℓ P i | < | ℓ P | ,
m P i = ± ℏ c n G = ± m P α α 2 ≈ ≈ ± i 2.2012 × 10 − 8 [ kg ] | m P i | > | m P | ,
t P i = ± ℏ G c n 5 = ± t P α 2 5 α 5 ≈ ≈ ± i 5.0942 × 10 − 44 [ s ] | t P i | < | t P | ,
T P i = ± ℏ c n 5 G k B 2 = ± T P α 5 α 2 5 ≈ ≈ ± i 1.4994 × 10 32 [ K ] | T P i | > | T P | ,
and can be expressed, using the relation (31), in terms of base Planck units q P , ℓ P , m P , t P , and T P .
Planck units derived from the imaginary base units (19)-(21) are generally not imaginary. The α 2 Planck volume
ℓ P i 3 = ± ℏ G c n 3 3 / 2 = ± ℓ P 3 α 2 9 α 9 ≈ ≈ ± i 3.8127 × 10 − 105 [ m 3 ] < | ℓ P 3 | ,
the α 2 Planck momentum
p P i = ± m P i c n = ± ℏ c n 3 G = ± m P c α 3 α 2 3 ≈ ≈ ± i 6.7504 [ kg m / s ] | m P i c n | > | m P c | ,
the α 2 Planck energy
E P i = ± m P i c n 2 = ± ℏ c n 5 G = ± E P α 5 α 2 5 ≈ ≈ ± i 2.0701 × 10 9 [ J ] | E P i | > | E P | ,
and the α 2 Planck acceleration
a P i = ± c n t P i = ± c n 7 ℏ G = ± a P α 7 α 2 7 ≈ ≈ ± i 6.0198 × 10 51 [ m / s 2 ] | a P i | > | a P | ,
are imaginary and bivalued. However, the α 2 Planck force
F P 2 = ± E P i ℓ P i = ± c n 4 G = ± F P α 4 α 2 4 ≈ ≈ ± 1.3251 × 10 44 [ N ] | F P 2 | > | F P | ,
and the α 2 Planck density
ρ P 2 = ± m P i ℓ P i 3 = ± c n 5 ℏ G 2 = ± ρ P α 5 α 2 5 ≈ ≈ ± 5.7735 × 10 96 [ kg / m 3 ] | ρ P 2 | > | ρ P | ,
are real and bivalued. On the other hand, the α 2 Planck area
ℓ P i 2 = ℏ G c n 3 = ℓ P 2 α 2 3 α 3 ≈ ≈ − 2.4406 × 10 − 70 [ m 2 ] | ℓ P i 2 | < | ℓ P 2 | ,
is strictly negative, while the Planck area ℓ P 2 is strictly positive.
Both α 2 and c n introduce the second, negative vacuum impedance
η 2 = 4 π α 2 ℏ e 2 = 1 ϵ 0 c n ≈ − 368.29 [ Ω ] | η 2 | < | η | .
Solving both impedances (7) and (30) for 4 π ℏ ϵ 0 / e 2 and comparing with each other yields the following important relation between the speed of light in vacuum c, negative parameter c n , and the fine-structure constants α , α 2
c α = c n α 2 = v e ,
where, notably, v e is the electron’s velocity at the first circular orbit in the Bohr model of the hydrogen atom. This is not the only α to α 2 relation. Along with the two π -like constants (relations (B8) and (B10), cf. Appendix B)
α 2 α = c c n = π 1 π = π π 2 ≈ − 0.9776 .
The relations between time (21) and temperature (22) α 2 Planck units are inverted, α 5 t P i 2 = α 2 5 t P 2 , α 2 5 T P i 2 = α 5 T P 2 , and saturate Heisenberg’s (energy-time version) uncertainty principle taking energy from the equipartition theorem for one degree of freedom (or one bit of information [5,29])
1 2 k B T P t P = 1 2 k B T P i t P i = ℏ 2 .
Furthermore, eliminating α and α 2 from (18)-(20), yield
q P 2 m P 2 = q P i 2 m P i 2 = 4 π ϵ 0 G ,
and
ℓ P m P 3 = ℓ P i m P i 3 and ℓ P q P 3 = ℓ P i q P i 3 .
Base Planck units themselves admit negative values as negative square roots. By choosing complex analysis, within the framework of emergent dimensionality [5,9,11,30,31], we enter into bivalence by the very nature of this analysis. All geometric objects have both positive and negative volumes and surfaces [31] equal in moduli. On the other hand, imaginary and negative physical quantities are the subject of research. In particular, the subject of scientific research is thermodynamics in the complex plane. Lee–Yang zeros, for example, have been experimentally observed [32,33].
We note here that the imaginary Planck Units are not imaginary due to being multiplied by the imaginary unit i. They are imaginary numbers I due to the negativity of odd powers of c n being the square root argument; thus, they define imaginary physical quantities inaccessible to direct measurements4. The complementary Planck units do not apply only to the time dimension but to any imaginary dimension. However, in our four-dimensional Euclidean R 3 × I space-time, Planck units apply in general to the spatial dimensions, while the imaginary ones in general to the imaginary temporal dimension, wherein the seemingly interchangeable meaning of the Planck imaginary length ℓ P i and time t P i requires further research. All the complementary Planck units have physical meanings. However, some of them are elusive, like the negative area or imaginary volume, which require two or three orthogonal imaginary dimensions.

IV. Black Body Objects

There seem to be only three observable objects in nature that emit perfect black-body radiation: unsupported black holes (BH, the densest), neutron stars (NS), supported, as it is accepted, by neutron degeneracy pressure, and white dwarfs (WD), supported by electron degeneracy pressure (the least dense). We shall collectively call them black-body objects (BBO). It has recently been experimentally confirmed that the so-called accretion instability is a fundamental physical process [34] common for all BBOs.
As black-body radiation is radiation emitted by a body in global thermodynamic equilibrium, it is patternless (thermal noise) radiation and depends only on the temperature of this body. In the case of BHs, this is known as Hawking radiation, wherein the BH temperature T BH = T P / ( 2 π d BH ) , where T P is the Planck temperature, is a function of the BH diameter [5] D BH = d BH ℓ P , where d BH ∈ R . (in the following d is also called a diameter) and ℓP is the Planck length.
As Hawking radiation depends only on the diameter of a BH, it must be the same for a given BH, even though it is momentary as it fluctuates (cf. Appendix D). As the interiors of the BBOs are inaccessible to an exterior observer [35], BBOs do not enclose interiors and can only be defined by their diameters (cf. [5] Fig. 2(b)). The term object as a collection of matter is a misnomer in general, as it neglects quantum nonlocality. But it is a particularly staring misnomer if applied to BBOs. Thus we use emphasis for (indistinguishable) particle and (distinguishable) object, as well as for matter and distance, as these terms have no absolute meaning in emergent dimensionality. In particular, given the recent observation of quasiparticles in classical systems [36].
But not only BBOs are perfectly spherical. Also, the early epochs of their collisions must be perfectly spherical, as it has been recently, experimentally confirmed [37] for NSs based on the AT2017gfo kilonova data. One can hardly expect a collision of two perfectly spherical, patternless thermal noises to produce some aspherical pattern instead of another perfectly spherical patternless noise. Where would the information about this pattern come from at the moment of the collision? From the point of impact? No point of impact is distinct on a patternless surface.
As black-body radiation is patternless, the triangulated [5] BBOs, as well as their early epoch collisions, must contain a balanced number of Planck area triangles, each carrying binary potential δ φ k = − c 2 · { 0 , 1 } , as it has been shown for BHs [5], based on Bekenstein-Hawking entropy
S BH = 1 4 k B N BH ,
where N BH 4 π R BH 2 / ℓ P 2 = π d BH 2 is the BH information capacity (i.e., the number of the triangular Planck areas at the BH horizon, corresponding to bits of information [29,35,38] and the fractional part triangle { π d BH 2 } to small to carry a single bit of information), [sic!]) and R BH = 2 G M BH / c 2 is the BH (Schwarzschild) radius. The BH entropy (36) can be derived from the Bekenstein bound
S ≤ 2 π k B R E ℏ c ,
an upper limit on the thermodynamic entropy S that can be contained within a sphere of radius R having energy E, where kB is the Boltzmann constant and ℏ is the reduced Planck constant, after plugging the BH radius R BH and energy EBH = MBHc2 taken from mass-energy equivalence into the bound (37).
Since the patternless nature of the perfect black-body radiation was derived [5] by comparing BH entropy (36) with the binary entropy variation δ S = k B N 1 / 2 ([5] Eq. (55)), which is valid for any holographic sphere, where N 1 ∈ N denotes the number of active Planck areas with binary potential δ φ k = − c 2 , the BH entropy (36) must be valid also for NSs and WDs. Thus, defining the generalized radius of a holographic sphere of mass M as a function of G M / c 2 multiplier k [5]
R : = k G M c 2 ,
and the generalized energy E of this sphere as a function of M c 2 multiplier a
E : = a M c 2 ,
where k, a, a ∈ R : k ≤ 2 the generalized Bekenstein bound (37) becomes
S ≤ 1 2 k B a k N ,
where N 4 π R 2 / ℓ P 2 is the information capacity of this sphere, the surface of which contains N Planck triangles, where " x " is the floor function that yields the greatest integer less than or equal to its argument x.
The generalized Bekenstein bound (40) equals the BH entropy (36) if a 2 k = 1 4 ⇒ a = k 2 . Thus, the energy of all BBOs having a radius (38) is
E BBO = k 2 M BBO c 2 ,
with k = 2 in the case of BHs and k > 2 for NSs and WDs.
Schwarzschild BHs are fundamentally uncharged, contrary to NSs and WDs, since the entropy (36) of any BH is equal to that of the uncharged Schwarzschild BH with the same area by the Penrose process. It is accepted that in the case of NSs, electrons combine with protons to form neutrons, but it is never the case that all electrons and all protons become neutrons. WDs are charged by definition as they are composed mostly of electron-degenerate matter.
As the entropy of independent systems is additive, a collision of two BBOs, BBO1 and BBO2, having entropies S BBO 1 = 1 4 k B N BBO 1 = 1 4 k B π d BBO 1 2 and S BBO 2 = 1 4 k B π d BBO 2 2 , produces another B B O C having entropy
S BBO C = S BBO 1 + S BBO 2 ⇒ d BBO C 2 = d BBO 1 2 + d BBO 1 2 .
This shows that a collision of two primordial BHs, each having the Planck length diameter, the reduced Planck temperature T P 2 π (which is the largest physically significant temperature [11]), and no tangential acceleration a L L [5,11], produces a BH having d BH = ± 2 which represents the minimum BH diameter allowing for the notion of time [11], while a collision of the latter two BHs produces a BH having d BH = ± 2 having the triangulation defining only one precise diameter between its poles (cf. [5] Fig. 3(b)). Diameter d BH = ± 2 is also recovered [5] from Heisenberg’s Uncertainty Principle (cf. Appendix C).
The hitherto considerations may be unsettling for the reader, as the energy (45) of BBOs other than BHs exceeds mass-energy equivalence E = k M c 2 / 2 for k > 2 , which is the limit of the maximum real energy. Thus, a part of the energy of NSs and WDs must be imaginary and thus unmeasurable. We shall consider this question in the subsequent section.

V. COMPLEX ENERGIES

A complex energy formula
E R : = E M R + i E Q R = 1 + i β R M R c 2 ,
where E M R = M R c 2 and i E Q R represent respectively real and imaginary energy of an object having mass M R and charge Q R 5, and
β R : = E Q R E M R = Q R 2 M R π ϵ 0 G ,
is the imaginary-real energy ratio6, was proposed in [39] (Eqs. (1), (3), and (4)). Equations (43) and (44) consider real (physically measurable) masses M R and charges Q R .
Planck charge relations (2) and (16) imply that the elementary charge e is the same both in real and imaginary dimensions since
e 2 = α q P 2 = α 2 q P i 2 .
On the other hand, there is no physically meaningful elementary mass  m e = ± 3 . 4566 × 10 − 18 [ kg ] that would satisfy the relation (20)
m e 2 = α m P 2 = α 2 m P i 2 .
Thus, as to the modulus, charges are the same in real and imaginary dimensions, while masses are different. We note that the same form of the relations (45) and (46) reflect the same form of Coulomb’s law and Newton’s law of gravity, which are inverse-square laws.
In the following, where deemed appropriate, dimensional quantities were discretized using Planck units as
Q : = q e , Q i : = i Q = i q e , q ∈ Z M : = m m P , M i : = m i m P i , m , m i ∈ R , λ : = l ℓ P , λ i : = l i ℓ P i , l , l i ∈ R , R : = r ℓ P , R i r i : = ℓ P i , r , r i ∈ R ,
although the discretization of charges by integer multipliers q of the elementary charge e is far-fetched, considering the fractional charge of quasiparticles.
We shall now modify the equation (43) to a form involving imaginary masses M i and charges Q i by defining the following two complex energies, the complex energy of real mass M and imaginary charge Qi
E M Q i : = E M + E Q i = = 1 + β Q i M c 2 = M + i q α m P c 2 ,
and the complex energy of real charge Q and imaginary mass Mi
E Q M i : = E Q + E M i = = β Q i + 1 M i c n 2 = q α 2 m P i + M i c 2 ,
where
β Q i : = Q i 2 M π ϵ 0 G = i q α m P M ∈ I ,
β Q : = Q 2 M i π ϵ 0 G = q α 2 m P i M i ∈ I .
We note in passing that using the different speed of light parameters in energies E M Q i (49) and E Q M i (48) yields a contradiction (cf. Appendix F).
Equations (48)-(51) yield two different quanta of the charge-dependent energies corresponding to the elementary charge, the imaginary quantum
E Q i ( q = ± 1 ) = ± i α E P ≈ ± i 1.6710 × 10 8 [ J ] ,
and the - larger in modulus - real quantum
E Q ( q = ± 1 ) = ± α 2 E P i ≈ ± 1.7684 × 10 8 [ J ] .
Furthermore, ∀ q , α 2 E Q i = i α 2 2 E Q .
The squared moduli of the energies (48) and (49) can be expressed as
| E M Q i | 2 = M 2 c 4 1 − β Q i 2 = M 2 + q 2 α m P 2 c 4 ,
and (using relations (31) and (20))
| E Q M i | 2 = M i 2 c n 4 β M i 2 − 1 = q 2 α 2 m P i 2 − M i 2 c n 4 = = α 4 α 2 4 q 2 α m P 2 − M i 2 c 4 .
If we assume these moduli are equal, we shall obtain the value of the imaginary mass Mi corresponding to an object having mass M and charge Q
α 2 4 M 2 + q 2 α m P 2 = α 4 q 2 α m P 2 − M i 2 , M i = ± q 2 α m P 2 1 − α 2 4 α 4 − α 2 4 α 4 M 2 ,
as an equation with three unknowns M, Mi, and q.
In particular for an uncharged mass M ( q = 0 ) this yields
M i α 2 = ± i M α 2 2 or M i = ± i α 2 2 α 2 M ≈ ± 0.9557 i M .
Since mass M i is imaginary by definition, the argument of the square root in the relation (56) must be negative
M > | q | m P α α 4 α 2 4 − 1 ≈ | q | 5.7275 × 10 − 10 [ kg ] .
which means that masses of uncharged micro BHs ( q = 0 ) can be arbitrary but micro NSs and micro WDs cannot be observed, as achieving a net charge Q = 0 is impossible in this case. Even a single elementary charge renders the mass M = 5 . 7275 × 10 − 10 [ kg ] comparable to the mass of a grain of sand.
We conjecture that the threshold (58) pertains solely to charged distinguishable objects having masses larger than the threshold of distinguishability [5] of M < 2 π m P ≈ 1 . 3675 × 10 − 7 [ kg ] (i.e., masses having Compton wavelengths smaller than the Planck length). A hypothetical (indistinguishable) element at this threshold would have an atomic number Z = 2 π α α 4 α 2 4 − 1 = 238 , corresponding to q, which-as we conjecture - sets the limit on an extended periodic table, and is lower that the accepted limit of 300 [40].
We can interpret the modulus of the generalized energy of BBOs (41) as the modulus of the complex energy of real mass (54), taking the observable real energy E BBO = M BBO c 2 of the BBO as the real part of this energy. Thus
k 2 M BBO c 2 2 = M BBO 2 + q BBO 2 α m P 2 c 4 , q BBO = ± M BBO m P 1 α k 2 4 − 1 ,
which is real for k ≥ 2 and for k = 2 confirms vanishing net charge of BHs. Similarly, we can interpret the modulus of the generalized energy of BBOs (41) as the modulus of the complex energy of real charge (55). Thus
k 2 4 M BBO 2 = α 4 α 2 4 q BBO 2 α m P 2 − M i B B O 2 , M i B B O 2 = q BBO 2 α m P 2 − α 2 4 α 4 k 2 4 M BBO 2 .
Substituting q BBO 2 from the relation (59) into the relation (60) yields
M i BBO 2 = k 2 4 1 − α 2 4 α 4 − 1 M BBO 2 , M i BBO = ± M BBO k 2 4 1 − α 2 4 α 4 − 1 ,
which for BHs ( k = 2 ) also corresponds to the relation (57) between uncharged masses M and M i , where no assumptions concerning the BBO energy were made.
Furthermore, the argument of the square root in the relation (61) must be negative, as mass M i is imaginary by definition. This leads to the maximum G M / c 2 multiplier k max
| k | < k max = 2 1 − α 2 4 α 4 ≈ 6.7933 ,
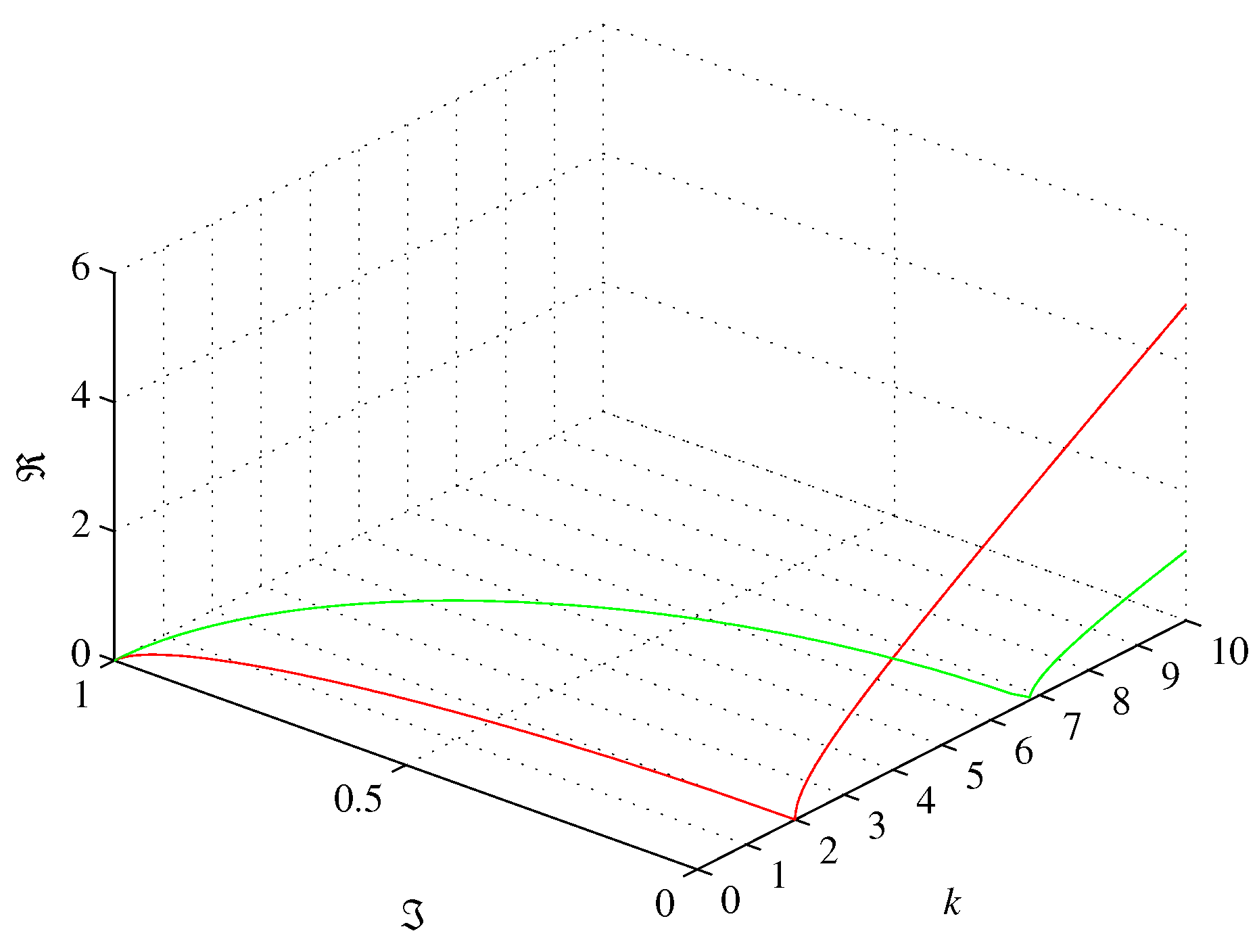
Relations (59) and (61) are shown in Figure 1.
The relation (62) sets the upper bound on the BBO radius (38) and energy (39)
R BBO < R B H 1 − α 2 4 α 4   and   E BBO < M BBO c 2 1 − α 2 4 α 4 ,
where RBH is the radius of the BH having a mass of the BBO. As WDs are the least dense BBOs, this bound defines the maximum radius of a WD core.
Furthermore, combining the minimum mass threshold (58) with the maximum mass multiplier threshold (62) of the charged BBO radius yields the minimum charge required for a given BBO diameter
q BBO > 1 4 α 2 4 α 5 d BBO .
Thus for example 1-bit BBO ( d BBO = 1 / π ) corresponds to q BBO > 1 . 5780 , π -bit BBO ( d BBO = 1 ) requires q BBO > 2 . 7969 .
These results show that the radius (42) of charged BBOs (i.e., BBOs other than BHs) is a continuous function of k ∈ R : 2 < k < k max ; the largest k satisfying the BBO entropy relation (36), a necessary condition of patternless perfect black body radiation [5]. We shall consider this question in the subsequent section.

VI. MASS, CHARGE, EMR - PHOTON SPHERE RADIUS

Besides complex energies of masses and charges (48), (49)
E M Q i : = M c 2 + Q i c 2 2 π ϵ 0 G = m + i q α E P ,
E M Q i : = Q i c 2 2 π ϵ 0 G + M c 2 = a a 2 a 2 2 q + m 1 a 2 E P ,
we can also define the complex energies of real wavelength and imaginary mass/charge ERMi, ERQi
E R M i : = h c λ + M i c n 2 = 2 π E P l + m i E P i = = 2 π l + α 5 α 2 5 m i E P ,
E R Q i : = h c λ + Q i c 2 2 π ϵ 0 G = 2 π l + i q α E P ,
and of imaginary wavelength and real mass/charge EMRi, EQRi,
E M R i : = M c 2 + h c n λ i = m E P + 2 π E P i l i = = m + α 5 α 2 5 2 π l i E P ,
E Q R i : = Q c n 2 2 π ϵ 0 G + h c n λ i = α 2 α 2 2 q α E P + 2 π l i E P i = = α 2 α 2 2 q α + α α 2 2 π l i E P ,
where we applied discretizations (47). The energies (67)-(70) link the electromagnetic radiation with gravity/inertia and electrodynamics within the framework of emergent dimensionality.
Complex energies (65)-(70) are real-to-imaginary balanced if moduli of their real and imaginary parts are equal. This holds for
M = i M i = m P q α , M i = i α 2 2 α 2 h c λ , | M | = i α α 2 h c λ i , λ = 2 π l P q α , λ i = i 2 π l P α 2 q α 3 .
Furthermore, complex energies (65)-(70) define complex forces between two objects acting over real and imaginary distances R , R i (cf. Appendix E).
This time, comparing the squared moduli of the energies(65)-(70) with the squared BBO energy (41) yield a solvable system of six equations with six unknowns k, q, m, mi, l, li
| E M Q i | 2 ⇒ q 2 α = m 2 k 2 4 − 1 , | E Q M i | 2 ⇒ α 4 α 2 4 q 2 α − α 5 α 2 5 m i 2 = k 2 4 m 2 , | E R M i | 2 ⇒ 4 π 2 l 2 − α 5 α 2 5 m i 2 = k 2 4 m 2 , | E R Q i | 2 ⇒ 4 π 2 l 2 + q 2 α = k 2 4 m 2 , | E M R i | 2 ⇒ m 2 1 − k 2 4 = α 5 α 2 5 4 π 2 l i 2 , | E Q R i | 2 ⇒ α 4 α 2 4 q 2 α − 4 π 2 l i 2 α 5 α 2 5 = k 2 4 m 2 .
Substituting q 2 α = m 2 k 2 4 − 1 from | E M Q i | 2 to | E R Q i | 2 recovers the Compton wavelength of the BBO, λ BBO = h M BBO c , in its discrete form l 2 = 4 π 2 m 2 .
Furthermore, by substituting q 2 α and the Compton mass m 2 = 4 π 2 l 2 into | E Q M i | 2 , and comparing the LHSs of | E Q M i | 2 and | E R M i | 2 we obtain the BBO equilibrium multiplier
k eq 2 4 = α 2 4 α 4 + 1 ⇒ | k eq | = 2 1 + α 2 4 α 4 ≈ 2.7665 ,
at which all the moduli (72) are equal. The equilibrium multiplier k eq (73) is related to the bound k max (62) by k eq 2 + 16 / k max 2 = 8 . Also, the following relations can be derived from the relations (72) for the BBO in the equilibrium k eq (73)
m i 2 = − α 2 9 α 9 m 2 ⇔ M i BBO eq = ± i α 2 4 α 4 M BBO eq ,
l i 2 = − α 9 α 2 9 l 2 ⇔ λ i BBO eq = ± i α 3 α 2 3 λ BBO eq ,
l 2 = 4 π 2 m 2 ⇔ λ BBO eq = h M BBO eq c
q 2 α = α 2 4 α 4 m 2 ⇔ α 2 4 α 4 = − β Q i BBO eq 2 = ± i M i BBO eq M BBO eq ,
where in the last relation, we used the definition (50) and applied the relation (74).
Notably, 2 . 25 < k eq < 3 , where 9 / 4 is the multiplier of a radius of the maximal sustainable density for gravitating spherical matter given by Buchdahl’s theorem, and 3 is the multiplier of a BH photon sphere radius.
This shows that k eq ≈ 2 . 766 is a true photon sphere radius, where BBO gravity, charge, and photon energies remain at equilibrium. Aside from the Schwarzschild radius (derivable from escape velocity v e s c 2 = 2 G M / R of mass M by setting v e s c 2 = c 2 ), all the remaining thresholds of general relativity, such as Buchdahl’s threshold ( k = 9 / 4 ) or a photon sphere radius ( k = 3 ), are only crude approximations. It must be so, since general relativity neglects the value of the fine-structure constants α and α 2 , which, similarly as π or the base of the natural logarithm, are the fundamental constants of nature.

VII. DISCUSSION

The reflectance of graphene under the normal incidence of electromagnetic radiation expressed as the quadratic equation for the fine-structure constant α includes the 2nd negative fine-structure constant α 2 . The sum of the reciprocal of this 2nd fine-structure constant α 2 with the reciprocal of the fine-structure constant α (2) is independent of the reflectance value R and remarkably equals simply − π . Particular algebraic definition of the fine-structure constant α − 1 = 4 π 3 + π 2 + π , containing the free π term, can be interpreted as the asymptote of the CODATA value α − 1 , the value of which increases with time. The negative fine-structure constant α 2 introduces the complementary set of Planck units applicable to imaginary dimensions, including imaginary Planck units (18)-(26). Real and imaginary mass and charge units (34), length and mass units (35) units, and temperature and time units (33) are directly related to each other. Also, the elementary charge e is common for real and imaginary dimensions (45).
Applying the complementary Planck units to a complex energy formula [39] yields complex energies (48), (49) setting the atomic number Z = 238 as the limit on an extended periodic table.
The generalized energy (41) of all perfect black-body objects (black holes, neutron stars, and white dwarfs) having the generalized radius R BBO = k G M / c 2 exceed mass-energy equivalence if k > 2 . Complex energies (50), (51) allow for storing the excess of this energy in their imaginary parts, inaccessible for direct observation. The results show that the perfect black-body objects other than black holes cannot have masses lower than 5 . 7275 × 10 − 10 [ kg ] and that the maximum slope of the radius of their cores as a function of mass is defined, as k max ≈ 6 . 7933 , by the relation (62). It is further shown that a black-body object is in the equilibrium of complex energies if its radius R eq ≈ 2 . 7665 G M BBO / c 2 (73). It is conjectured that this is the correct value of the photon sphere radius.
The findings of this study inquire further research in the context of information-theoretic approach [1,2,3,4,5,6] and emergent dimensionality [9,30,31].
In the context of the results of this study, monolayer graphene, a truly 2-dimensional material with no thickness7, is a keyhole to other, unperceivable [5], dimensionalities. Graphene history is also instructive. Discovered in 1947 [42], graphene was long considered an academic material until it was eventually pulled from graphite in 2004 [43] by means of ordinary Scotch tape8. These fifty-seven years, along with twenty-nine years (1935-1964) between the condemnation of quantum theory as incomplete [44] and Bell’s mathematical theorem [45] asserting that it is not true, and the fifty-eight years (1964-2022) between the formulation of this theorem and 2022 Nobel prize in physics for its experimental loophole-free confirmation, should remind us that Max Planck, the genius who discovered Planck units, has also discovered Planck’s principle.

ACKNOWLEDGMENTS

I truly thank my wife for her support when this research [46,47] was conducted. I thank Wawrzyniec Bieniawski for inspiring discussions and constructive ideas concerning the layout of this paper. I thank Andrzej Tomski for the definition of the scalar product for Euclidean spaces R a × I b (1).

Appendix A: Other quadratic equations

The quadratic equation for the sum of transmittance (3) and absorptance (5), putting C T A T + A , is
1 4 C T A π 2 α 2 + C T A − 1 π α + C T A − 1 = 0 ,
and has two roots with reciprocals
α − 1 = C T A π 2 1 − C T A + 1 − C T A ≈ 137.036 ,
and
α 2 − 1 = C T A π 2 1 − C T A − 1 − C T A ≈ − 140.178 ,
whereas their sum α − 1 + α 2 − 1 = − π is, similarly as the relation (12), also independent of T and A.
Other quadratic equations do not feature this property. For example, the sum of T + R (6) expressed as the quadratic equation and putting C T R : = T + R , is
1 4 C T R − 1 π 2 α 2 + C T R π α + C T R − 1 = 0 ,
and has two roots with reciprocals
α − 1 = π ( C T R − 1 ) − 2 C T R + 2 2 C T R − 1 ≈ 137.036 ,
and
α T R − 1 = π ( C T R − 1 ) − 2 C T R − 2 2 C T R − 1 ≈ 0.0180 ,
whereas their sum
α T R 1 − 1 + α T R 2 − 1 = − π C T R C T R − 1 ≈ 137.054
is dependent on T and R.

Appendix B: Two π-like constants

With algebraic definitions of α (13) and α 2 (14), transmittance T (3), reflectance R (4) and absorptance A (5) of MLG for normal EMR incidence can be expressed just by π . For α − 1 = 4 π 3 + π 2 + π (13) they become
T α = 4 4 π 2 + π + 1 2 8 π 2 + 2 π + 3 2 ≈ 0.9775 ,
A α = 4 4 π 2 + π + 1 8 π 2 + 2 π + 3 2 ≈ 0.0224 ,
while for α 2 − 1 = − 4 π 3 − π 2 − 2 π (14) they become
T α 2 = 4 4 π 2 + π + 2 2 8 π 2 + 2 π + 3 2 ≈ 1.0228 ,
A α 2 = − 4 4 π 2 + π + 2 8 π 2 + 2 π + 3 2 ≈ − 0.0229 ,
with
R α = R α 2 = 1 8 π 2 + 2 π + 3 2 ≈ 1.2843 × 10 − 4 .
( T ( α ) + A ( α ) ) + R ( α ) = ( T ( α 2 ) + A ( α 2 ) ) + R ( α 2 ) = 1 as required by the law of conservation of energy (8), whereas each conservation law is associated with a certain symmetry, as asserted by Noether’s theorem. Nonetheless, physical interpretation of T ( α 2 ) > 1 and A ( α 2 ) < 0 invites further research. A ( α ) > 0 implies a sink, whereas A ( α 2 ) < 0 implies a source, whereas the opposite holds true for the transmittance T, as illustrated schematically in Fig. 2. Perhaps, the negative absorptance and transmittance exceeding 100% for α 2 (11) or (14) could be explained in terms of graphene spontaneous emission.
The quadratic equation (9) describing the reflectance R of MLG under normal incidence of EMR (or alternatively (A1)) can also be solved for π yielding two roots
π ( R , α * ) 1 = 2 R α * ( 1 − R ) , and
π ( R , α * ) 2 = − 2 R α * ( 1 + R ) ,
dependent on R and α * , where α * indicates α or α 2 . This can be further evaluated using the MLG reflectance R (4) or (A12) (which is the same for both α and α 2 ), yielding four, yet only three distinct, possibilities
π 1 = π ( α ) 1 = − π 4 π 2 + π + 1 4 π 2 + π + 2 = π α 2 α ≈ − 3.0712 ,
π ( α ) 2 = π ( α 2 ) 1 = π ≈ 3.1416 , and
π 2 = π ( α 2 ) 2 = − π 4 π 2 + π + 2 4 π 2 + π + 1 = π α α 2 ≈ − 3.2136 .
Preprints 69918 g002
Figure 2. Illustration of the concepts of negative absorptance and excessive transmittance of EMR under normal incidence on MLG.
Figure 2. Illustration of the concepts of negative absorptance and excessive transmittance of EMR under normal incidence on MLG.
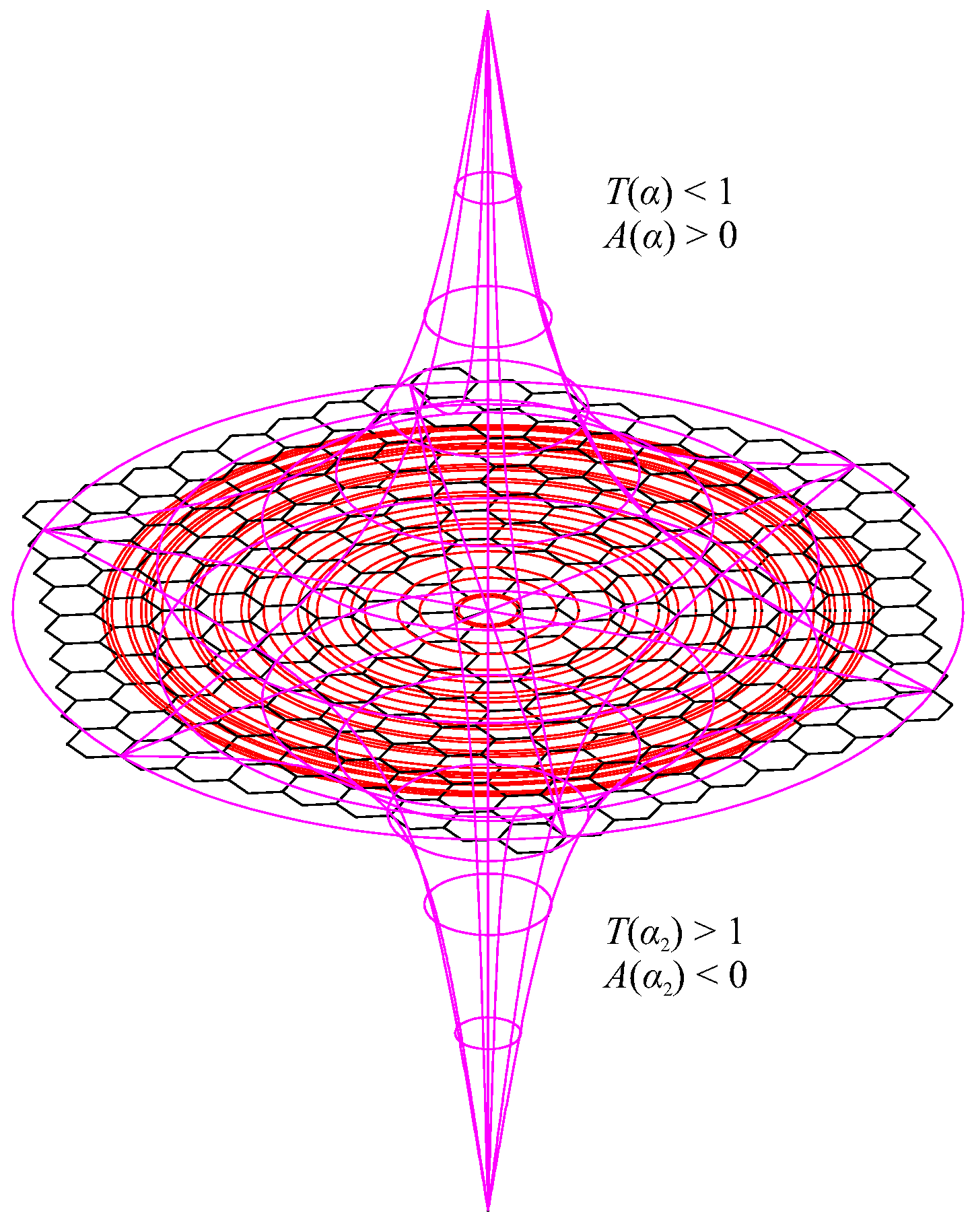
Preprints 69918 g002
The modulus of π 1 (B8) corresponds to a convex surface having a positive Gaussian curvature, whereas the modulus of π 2 (B10) - to a negative Gaussian curvature. Their product π 1 π 2 = π 2 is independent of α * , and their quotient π 1 / π 2 = α 2 2 / α 2 is independent of π . It remains to be found, whether each of them describes the ratio of circumference of a circle drawn on the respective surface to its diameter ( π c ) or the ratio of the area of this circle to the square of its radius ( π a ). These definitions produce different results on curved surfaces, whereas π a > π c on convex surfaces, while π a < π c on saddle surfaces [48].

Appendix C: Planck units and HUP

Perhaps the simplest derivation of the squared Planck length is based on Heisenberg’s uncertainty principle
δ P HUP δ R HUP ≥ ℏ 2 or δ E HUP δ t HUP ≥ ℏ 2 ,
where δ P HUP , δ R HUP , δ E HUP , and δ t HUP denote momentum, position, energy, and time uncertainties, by replacing energy uncertainty δ E HUP = δ M HUP c 2 with mass uncertainty and time uncertainty with position uncertainty, using mass-energy equivalence and δ t HUP = δ R / c HUP [28], which yields
δ M HUP δ R HUP ≥ ℏ 2 c .
Plugging δ M HUP = δ R HUP c 2 / ( 2 G ) for BH mass into (C2) we arrive at δ R HUP 2 = ℓ P 2 ⇒ δ D HUP = ± 2 ℓ P and recover BH diameter d BH = ± 2 .
However, using the same procedure but inserting the BH radius, instead of the BH mass, into the uncertainty principle (C2) leads to δ M HUP 2 = 1 4 ℏ c / G = 1 4 m P 2 . In general, using the generalized radius (38) in both procedures, one obtains
δ M HUP 2 = 1 2 k m P 2 and δ R HUP 2 = k 2 ℓ P 2 .
Thus, if k increases mass δ M HUP decreases, and δ R HUP increases and the factor is the same for k = 1 i.e., for orbital speed radius δ R = G δ M / c 2 or the orbital speed mass δ M = δ R c 2 / G .

Appendix D: Fluctuations of the holographic spheres

A simple relation describing the BH information capacity after absorption (+16π2dBH/l) or emission (−16π2dBH/l) of a particle having the wavelength λ multiplier l = λ/ℓP has been derived in [5] (Eq. (18)) as
N BH A / E ( d BH , l ) = 64 π 3 1 l 2 ± 16 π 2 d BH l + π d BH 2 .
Using the generalized radius (38), this equation can be generalized to all holographic spheres, including BBOs
N A / E ( d , l ) = 16 k 2 π 3 1 l 2 ± 8 k π 2 d l + π d 2 .

Appendix E: Complex forces

Complex energies (65)-(70) define complex forces between two objects, real R or imaginary R i  distance apart. We exclude mixed forces (of real and imaginary masses/charges) as real and imaginary dimensions are orthogonal. Thus, using discretizations (47), we obtain the following products
E 2 m q i E 2 m q i : = E 1 M Q i E 2 M Q i / E P 2 = = m 1 m 2 − q 1 q 2 α + i α ( m 1 q 2 + m 2 q 1 ) , E 1 q m i E 2 q m i : = E 1 Q M i E 2 Q M i / E P 2 = = α 5 α 2 4 q 1 q 2 + 1 α 2 m 1 i m 2 i + 1 α 2 q 1 m 2 i + q 2 m 1 i ,
E 1 r m i E 2 r m i : = E 1 R M i E 2 R M i / E P 2 = = 4 π 2 l 1 l 2 + α 5 α 2 5 m 1 i m 2 i + 2 π α 5 α 2 5 m 2 i l 1 + m 1 i l 2 , E 1 m r i E 2 m r i : = E 1 M R i E 2 M R i / E P 2 = = m 1 m 2 + α 5 α 2 5 4 π 2 l 1 i l 2 i + 2 π α 5 α 2 5 m 1 l 2 i + m 2 l 1 i ,
E 1 q r i E 2 q r i : = E 1 Q R i E 2 Q R i / E P 2 = = α 4 α 2 4 q 1 q 2 α + 4 π 2 l 1 l 2 α 5 α 2 5 + 2 π α 5 α 2 9 q 1 l 2 + q 2 l 1 , E 1 r q i E 2 q r i : = E 1 R Q i E 2 R Q i / E P 2 = = 4 π 2 l 1 l 2 + i 2 π α q 2 l 1 + q 1 l 2 − q 1 q 2 α ,
defining six complex forces; between two particles or objects acting over a real distance R
F A B i = G c 4 R 2 E 1 A B i E 2 A B i = F P r 2 E 1 a b i E 2 a b i ,
and six complex forces; between two particles or objects acting over an imaginary distance  R i
F ˜ A B i = G c n 4 R i 2 E 1 A B i E 2 A B i = α 2 α F P r i 2 E 1 a b i E 2 a b i ,
where A , B ∈ { M , Q , R } and a , b ∈ { m , q , r } , and
α 2 r 2 F A B i = α r i 2 F ˜ A B i .
In the case of masses and charges (65) and (66), the complex forces (E1) unify Coulomb’s law and Newton’s law of gravity (similarly to the complex energy of real masses and charges (43), [39] Eq. (7)).
Furthermore, under a simplifying assumption of r = r i , the forces acting over a real distance R are stronger and opposite to the corresponding forces acting over an imaginary distance R i (if these distances are equal in modulus) even though the Planck force is lower in modulus than the complementary (and, in this case, real) Planck force (27). This issue requires further research.

Appendix F: A mixed speeds hypothesis

Let us define the mass/charge energies with different speeds of light, i.e., the charge part of the energy E M Q i with c n and the charge part of the energy E Q M i with c
E ^ M Q i : = M c 2 + Q i c n 2 2 π ϵ 0 G = M c 2 ± i q α m P α 2 α 2 2 c 2 , E ^ Q M i : = Q c 2 2 π ϵ 0 G + M i c n 2 = ± q α m P c 2 + M i α 2 α 2 2 c 2 ,
If their moduli are equal, then
M 2 + q 2 α m P 2 α 4 α 2 4 = q 2 α m P 2 − M i 2 α 4 α 2 4 , M i = ± q 2 α m P 2 α 2 4 α 4 − 1 − α 2 4 α 4 M 2 .
For an uncharged mass M, this relation corresponds to (57). However, since mass M i is imaginary, the argument of the square root in the relation (F2) must be negative, i.e.,
| M | ≯ | q | m P α 1 − α 4 α 2 4 .
But α 4 > α 2 4 , yielding imaginary M, while M is real by definition. Therefore, complex energies E M Q i (48) and E Q M i (49) must be parametrized respectively by c and c n .

Notes

1
This is, of course, a circular definition, but it is given for clarity.
2
Vacuum permittivity ϵ 0 is the value of the absolute dielectric permittivity of classical vacuum. Thus, ϵ 0 cannot be negative. The Planck constant h is the uncertainty principle parameter. Thus, it cannot be negative; negative probabilities do not seem to withstand Occam’s razor.
3
Their average ( c + c n ) / 2 ≈ − 3 . 436417 × 10 6 [ m / s ] is in the range of the Fermi velocity.
4
Quantum measurement outcomes are real eigenvalues of hermitian operators.
5
Charges in the cited study are defined in CGS units; here we adopt SI.
6
In the cited study it is called α , so we shall call it β to avoid confusion with the fine-structure constant.
7
In which, according to an accepted photon sphere definition, the strength of gravity forces photons to travel in orbits. The author wonders why photons would not travel in orbits at radius R = G M / c 2 corresponding to the orbital velocity?
8
Thickness of MLG is reported [41] as 0.37 [nm] with other reported values up to 1.7 [nm]. However, considering that 0.335 [nm] is the established inter-layer distance and consequently the thickness of bilayer graphene, these results do not seem credible: the thickness of bilayer graphene is not 2 × 0 . 37 + 0 . 335 = 1 . 075 [nm].
9
Introduced into the market in 1932.

References

  1. de Chardin, P.T. The Phenomenon of Man; Harper, New York, 1959.
  2. Prigogine, I.; Stengers, I. Order out of Chaos: Man’s New Dialogue with Nature; 1984.
  3. Melamede, R. Dissipative Structures and the Origins of Life. Unifying Themes in Complex Systems IV; Minai, A.A.; Bar-Yam, Y., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; pp. 80–87.
  4. Vedral, V. Decoding Reality: The Universe as Quantum Information; Oxford University Press, 2010. [CrossRef]
  5. Łukaszyk, S., Black Hole Horizons as Patternless Binary Messages and Markers of Dimensionality. Nova Science Publishers, 2023. [CrossRef]
  6. Vopson, M.M.; Lepadatu, S. Second law of information dynamics. AIP Advances 2022, 12, 075310. [CrossRef]
  7. “Platonic Solids in All Dimensions.”.
  8. Taubes, C.H. Gauge theory on asymptotically periodic {4}-manifolds. Journal of Differential Geometry 1987, 25. [CrossRef]
  9. Łukaszyk, S. Four Cubes, 2021. arXiv:2007.03782 [math].
  10. Brukner, Č. A No-Go Theorem for Observer-Independent Facts. Entropy 2018, 20. [CrossRef]
  11. Łukaszyk, S. Life as the Explanation of the Measurement Problem 2018. doi:. [CrossRef]
  12. Planck, M. Über irreversible Strahlungsvorgänge, 1899.
  13. Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal dynamical conductance in graphite. Physical Review Letters 2008, 100, 117401. arXiv:0712.0835 [cond-mat]. [CrossRef]
  14. Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Physical Review Letters 2008, 101, 196405. [CrossRef]
  15. Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Universal Dynamic Conductivity and Quantized Visible Opacity of Suspended Graphene. Science 2008, 320, 1308–1308. arXiv:0803.3718 [cond-mat]. [CrossRef]
  16. Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Physical Review B 2008, 78, 085432. [CrossRef]
  17. Wang, X.; Chen, B. Origin of Fresnel problem of two dimensional materials. Scientific Reports 2019, 9, 17825. [CrossRef]
  18. Merano, M. Fresnel coefficients of a two-dimensional atomic crystal. Physical Review A 2016, 93, 013832. [CrossRef]
  19. Ando, T.; Zheng, Y.; Suzuura, H. Dynamical Conductivity and Zero-Mode Anomaly in Honeycomb Lattices. Journal of the Physical Society of Japan 2002, 71, 1318–1324. [CrossRef]
  20. Zhu, S.E.; Yuan, S.; Janssen, G.C.A.M. Optical transmittance of multilayer graphene. EPL (Europhysics Letters) 2014, 108, 17007. [CrossRef]
  21. Ivanov, I.G.; Hassan, J.U.; Iakimov, T.; Zakharov, A.A.; Yakimova, R.; Janzén, E. Layer-number determination in graphene on SiC by reflectance mapping. Carbon 2014, 77, 492–500. [CrossRef]
  22. Varlaki, P.; Nadai, L.; Bokor, J. Number Archetypes in System Realization Theory Concerning the Fine Structure Constant. 2008 International Conference on Intelligent Engineering Systems; IEEE: Miami, FL, 2008; pp. 83–92. [CrossRef]
  23. Webb, J.K.; Flambaum, V.V.; Churchill, C.W.; Drinkwater, M.J.; Barrow, J.D. Search for Time Variation of the Fine Structure Constant. Physical Review Letters 1999, 82, 884–887. [CrossRef]
  24. Murphy, M.T.; Webb, J.K.; Flambaum, V.V.; Dzuba, V.A.; Churchill, C.W.; Prochaska, J.X.; Barrow, J.D.; Wolfe, A.M. Possible evidence for a variable fine-structure constant from QSO absorption lines: motivations, analysis and results. Monthly Notices of the Royal Astronomical Society 2001, 327, 1208–1222. [CrossRef]
  25. Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Dzuba, V.A.; Barrow, J.D.; Churchill, C.W.; Prochaska, J.X.; Wolfe, A.M. Further Evidence for Cosmological Evolution of the Fine Structure Constant. Physical Review Letters 2001, 87, 091301. [CrossRef]
  26. Murphy, M.T.; Webb, J.K.; Flambaum, V.V. Further evidence for a variable fine-structure constant from Keck/HIRES QSO absorption spectra. Monthly Notices of the Royal Astronomical Society 2003, 345, 609–638. [CrossRef]
  27. Rosenband, T.; Hume, D.B.; Schmidt, P.O.; Chou, C.W.; Brusch, A.; Lorini, L.; Oskay, W.H.; Drullinger, R.E.; Fortier, T.M.; Stalnaker, J.E.; Diddams, S.A.; Swann, W.C.; Newbury, N.R.; Itano, W.M.; Wineland, D.J.; Bergquist, J.C. Frequency Ratio of Al + and Hg + Single-Ion Optical Clocks; Metrology at the 17th Decimal Place. Science 2008, 319, 1808–1812. [CrossRef]
  28. Scardigli, F. Some heuristic semi-classical derivations of the Planck length, the Hawking effect and the Unruh effect. Il Nuovo Cimento B (1971-1996) 1995, 110, 1029–1034. [CrossRef]
  29. Verlinde, E. On the origin of gravity and the laws of Newton. Journal of High Energy Physics 2011, 2011, 29. [CrossRef]
  30. Łukaszyk, S. Novel Recurrence Relations for Volumes and Surfaces of n-Balls, Regular n-Simplices, and n-Orthoplices in Real Dimensions. Mathematics 2022, 10, 2212. [CrossRef]
  31. Łukaszyk, S.; Tomski, A. Omnidimensional Convex Polytopes. Symmetry 2023, 15. [CrossRef]
  32. Peng, X.; Zhou, H.; Wei, B.B.; Cui, J.; Du, J.; Liu, R.B. Experimental Observation of Lee-Yang Zeros. Physical Review Letters 2015, 114, 010601. [CrossRef]
  33. Gnatenko, K.; Kargol, A.; Tkachuk, V. Lee–Yang zeros and two-time spin correlation function. Physica A: Statistical Mechanics and its Applications 2018, 509, 1095–1101. [CrossRef]
  34. Vincentelli, F.M.; Neilsen, J.; Tetarenko, A.J.; Cavecchi, Y.; Castro Segura, N.; Del Palacio, S.; Van Den Eijnden, J.; Vasilopoulos, G.; Altamirano, D.; Armas Padilla, M.; Bailyn, C.D.; Belloni, T.; Buisson, D.J.K.; Cúneo, V.A.; Degenaar, N.; Knigge, C.; Long, K.S.; Jiménez-Ibarra, F.; Milburn, J.; Muñoz Darias, T.; Özbey Arabacı, M.; Remillard, R.; Russell, T. A shared accretion instability for black holes and neutron stars. Nature 2023, 615, 45–49. [CrossRef]
  35. Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [CrossRef]
  36. Saeed, I.; Pak, H.K.; Tlusty, T. Quasiparticles, flat bands and the melting of hydrodynamic matter. Nature Physics 2023. [CrossRef]
  37. Sneppen, A.; Watson, D.; Bauswein, A.; Just, O.; Kotak, R.; Nakar, E.; Poznanski, D.; Sim, S. Spherical symmetry in the kilonova AT2017gfo/GW170817. Nature 2023, 614, 436–439. [CrossRef]
  38. Hooft, G.t. Dimensional Reduction in Quantum Gravity, 1993. [CrossRef]
  39. Zhang, T. Electric Charge as a Form of Imaginary Energy, 2008.
  40. B. Holdom, J. Ren, and C. Zhang, “Quark matter may not be strange,” Phys. Rev. Lett., vol. 120, p. 222001, May 2018.
  41. Jussila, H.; Yang, H.; Granqvist, N.; Sun, Z. Surface plasmon resonance for characterization of large-area atomic-layer graphene film. Optica 2016, 3, 151. [CrossRef]
  42. Wallace, P.R. Erratum: The Band Theory of Graphite [Phys. Rev. 71, 622 (1947)]. Physical Review 1947, 72, 258–258. [CrossRef]
  43. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [CrossRef]
  44. Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 1935, 47, 777–780. [CrossRef]
  45. Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics Physique Fizika 1964, 1, 195–200. [CrossRef]
  46. Łukaszyk, S. A short note about graphene and the fine structure constant 2020. [CrossRef]
  47. Łukaszyk, S. A short note about the geometry of graphene 2020. [CrossRef]
  48. Mahajan, S. Calculation of the pi-like circular constants in curved geometry. ResearchGate, 2013.
Preprints 69918 g001
Figure 1. Ratios of imaginary mass M i BBO to real mass M BBO (green) and real charge q BBO m P α to M BBO (red) of a BBO as a function of G M / c 2 multiplier k : 0 ≤ k ≤ 10 . Mass M i BBO is imaginary for k ⪅ 6 . 79 . Charge q BBO is real for k ≥ 2 .
Figure 1. Ratios of imaginary mass M i BBO to real mass M BBO (green) and real charge q BBO m P α to M BBO (red) of a BBO as a function of G M / c 2 multiplier k : 0 ≤ k ≤ 10 . Mass M i BBO is imaginary for k ⪅ 6 . 79 . Charge q BBO is real for k ≥ 2 .
Preprints 69918 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated