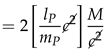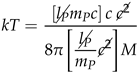The Natural Unit Expression of Classical Gravity

Preprint

Article

The Natural Unit Expression of Classical Gravity

Altmetrics

Downloads

168

Views

Comments

Supplementary Material

supplementary.xlsx (55.64KB )

David Humpherys^*

This version is not peer-reviewed

Submitted:

08 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts

Abstract

The gravitational constant is equivalent to natural units in its six unit dimensions. Evaluating the classical formulas in each unit dimension shows how inputs of mass and radius are transformed into the correct unit dimensions and magnitude of gravitational potential. Mass and radial distance are equivalent proportions of the Planck scale as the potentials they produce. Gravitational potentials of velocity, acceleration, energy, and force are proportional to a radial density limit of one Planck mass per Planck length of radial distance.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

The gravitational constant plays an important role in both Newton’s and Einstein’s formulation of the gravitational interaction. With a single value and six unit dimensions, the constant behaves as a function, transforming inputs of mass and radius into potentials of velocity, acceleration, energy, force, etc.

While the computational utility of the gravitational constant is incontrovertible, it is not immediately clear why the function works or what physical structure the constant represents. The magic of G is that combining it with the right inputs produces formulas which consistently fulfill two requirements:

The formulas produce the correct unit dimensions of the physical phenomenon you are solving for (acceleration, force, etc.)
The formulas produce the correct magnitude of the physical phenomenon from the given inputs.

That a single constant can produce the correct magnitude and unit dimensions of radial distance, velocity, acceleration, energy, and force—simply by adjusting the formula inputs—cries out for explanation. Evaluating the classical formulas in each unit dimension reveals how these transformations are accomplished.

The formula for gravitational acceleration combines the gravitational constant with inputs of mass and distance squared (inputs emphasized in red)

g = G \frac{M}{r^{2}} m / s^{2} .

(1)

The first requirement of the transformation is to reduce nine unit dimensions to three

\frac{L^{3}}{M T^{2}} \times \frac{M}{L^{2}} = \frac{L}{T^{2}} .

(2)

The six unit dimensions provided by G and three unit dimensions provided by formula inputs must form ratios which reduce the dimensionality. For example,

(\frac{L}{L}) \times (\frac{M}{M}) \times (\frac{L}{L}) \times \frac{L}{T^{2}} = \frac{L}{T^{2}}

(3)

The second requirement of the function is that it produce the correct magnitude of acceleration from the given set of inputs. This second requirement raises an important question about the role of dimensionless and dimensional components of 3 and whether the gravitational constant has meaningful quantities in each of its unit dimensions.

When Max Planck derived natural units of length, mass, and time, he combined the values and unit dimensions of c, G, and ℏ into ratios which isolate a single value in each unit dimension. His approach presumes that the universal constants contain natural units in their unit dimensions [1,2]. It is therefore equivalent to express the gravitational constant in natural units as [3,4,5,6]

G = \frac{l_{P}^{3}}{m_{P} t_{P}^{2}} = \frac{l_{P}}{m_{P}} c^{2} = 6.674 30 \times 10^{- 11} m^{3} / k g s^{2}

(4)

which agrees with the CODATA value [7].

Restating Equation 1 in natural units accounts for the mathematical transformation in each unit dimension, and reveals how formula inputs produce a corresponding magnitude of gravitational acceleration

g = G \frac{M}{r^{2}} = [\frac{l_{P}^{3}}{m_{P} t_{P}^{2}}] \frac{M}{r^{2}} = (\frac{l_{P}}{r}) (\frac{M}{m_{P}}) (\frac{l_{P}}{r}) \frac{l_{P}}{t_{P}^{2}}

(5)

The role of natural units in quantifying gravitational acceleration can be summarized in two parts.

Planck acceleration (the ratio of Planck length to Planck time squared) serves as a maximum limit or computational basis from which observable quantities of acceleration are determined.
A given magnitude of gravitational acceleration is determined by dimensionless ratios between the physical attributes of a system (mass and radial distance) and the Planck scale.

Figure 1. Classical formulas quantify gravitational acceleration in proportion to the Planck acceleration. Inputs of mass and radial distance are the same proportion of the Planck scale as the acceleration output. The gravitational constant injects natural units of length, mass, and time into the formula.

Natural units afford an opportunity for evaluating the physical meaning of the classical gravity formulas. A better understanding of the Planck scale structure in Equation 5 and the physical characteristics which quantify natural phenomena may be instrumental in the search for a theory of quantum gravity.

Table 1 shows the natural unit formulas for gravitational acceleration, energy, force, and escape velocity. The physical meaning of these formulas is explored in the following sections.

2. The Natural Unit Scale

The natural unit formulas in Table 1 give a consistent account by which the gravitational constant produces the correct magnitude and unit dimensions of each gravitational potential. While these formulas are computationally equivalent to equations written with G, they offer more information about the physical structures represented in the formulas. The occasional practice of setting universal constants equal to 1 gives an opaque view of this structure compared to the detail contained in each unit dimension of the formulas.

2.1. Natural units of length and time

The characteristic feature of natural units is an alignment of length, mass, and time units at the Planck scale. The alignment of length and time unit scales is evident in a one-to-one ratio of length to time at the velocity limit

c = \frac{l_{P}}{t_{P}} .

(6)

The familiar MKS ratio

299, 792, 458 m / s

quantifies the incongruence between length and time scales in the arbitrarily defined International System of Units. Natural units align the two unit scales in a 1:1 ratio at the speed of light

\frac{l_{P}}{t_{P}} = \frac{1.616 255 \times 10^{- 35} m}{5.391 247 \times 10^{- 44} s} = 2.997 924 \times 10^{8} m / s .

(7)

Because the Planck units are calculated from ratios of the three universal constants, the precision of the natural units is limited by the precision of G which has a relative standard uncertainty of

2.2 \times 10^{- 5}

[7]. But it is the physical structures these units represent that is important and not their utility in everyday experiments. Meters and seconds are convenient units on human scales, but the natural units reveal insightful correlations found in nature.

The natural unit structure shown in Section 1 is found repeatedly in formulas that feature universal constants. It appears, for example, when calculating the wavelength of a photon from its frequency or period

λ = \frac{c}{f} = c T = (\frac{T}{t_{P}}) l_{P}

(8)

In this case, the dimensionless number of natural time units (

T / t_{P}

) is equal to the number of natural length units. Multiplying the number of time units by one length unit gives the correct wavelength. In MKS units, the photon’s period and wavelength are proportional; but in natural units, the number of length units is equal to the number of time units.

The natural unit structure of the formulas can accommodate any arbitrary unit scale provided two conditions are met:

Formulas quantify the Planck scale basis of a phenomenon in arbitrary units of length, mass, and time.
Formulas quantify the magnitude of the phenomenon using dimensionless ratios of natural units to arbitrary units.

The formulas arrange universal constants in such a way as to meet both of these criteria. Some of the natural units embodied in the universal constants create the Planck scale phenomenon while others provide a Planck scale basis for quantifying the phenomenon in proportion to the Planck scale.

If the meter had been defined as twice its accepted value today, we would use the same formulas but the universal constants would be

c^{'} = 149, 896, 229 m / s

G^{'} = 8.343 \times 10^{- 12} m^{3} / k g s^{2}

, and

ℏ^{'} = 2.636 \times 10^{- 35} k g m^{2} / s

. Whether calculating in MKS units, natural units, or any arbitrary units, it is the same intensive ratio between the photon’s wavelength and period that gives the correct result.

Natural unit formulas reveal how physical structures like particles and fields change as their scale increases or decreases. Particularly interesting are symmetries which conserve certain physical quantities as constituent quantities change. For a photon in the vacuum, the ratio of wavelength to period is conserved for all combinations of wavelength and period

\frac{λ}{T} = \frac{l_{P}}{t_{P}}

(9)

Conserved relationships like the one in Equation 9 allow us to find the correct magnitude of a physical property in one unit dimension using a correlated quantity in another unit dimension. Writing the formula in terms of the oscillation period gives another example of this simple pattern

T = (\frac{λ}{l_{P}}) t_{P} .

(10)

2.2. Natural mass units

Perhaps less well-known is the natural unit scale for mass. Whereas Planck length and time are minimum units, the Planck mass is a maximum unit. Natural units of length and mass are equal to one at the Planck scale and changes in mass are inversely proportional to changes in length. Consider the relationship between a particle’s rest mass and Compton wavelength [8,9,10]

\frac{l_{P}}{λ_{C}} = \frac{m_{0}}{m_{P}} .

(11)

According to 11, a matter particle’s rest mass is equal to one divided by its Compton wavelength in natural units, perhaps implying that a standard mass unit becomes diluted over the particle’s Compton wavelength. Taken to the Planck scale, a matter particle with a Planck length Compton wavelength would have a rest mass of one Planck mass. This inversely proportional relationship is demonstrated by the charged leptons in Table 2.

The correlation between rest mass and Compton wavelength conserves the product of these two particle attributes

λ_{C} m_{0} = l_{P} m_{P} = 3.517 67 \times 10^{- 43} k g m .

(12)

The conservation of mass-wavelength conserves Planck’s constant and is the basis for quantizing spin in relation to a particle’s wavelength and oscillation period [8]. The correlation is so strong that the electron mass and Compton wavelength produce Planck’s constant with a precision comparable to measurements performed with the Kibble balance [11]

ℏ = λ_{C} m_{0} c = 1.054 571 8176 . . . \times 10^{- 34} k g m^{2} / s

(13)

Equations 11 and 12 provide another example of how structures with correlated physical properties enable the calculation of one property using the dimensionless ratio of a correlated property. For Compton wavelength and rest mass, the formulas can be stated as

m_{0} = (\frac{l_{P}}{λ_{C}}) m_{P}

(14)

and

λ_{C} = (\frac{m_{P}}{m_{0}}) l_{P} .

(15)

These formulas exhibit the same natural unit structure found in the gravitational potential formulas shown in Table 1. Correlations in the physical attributes of massive bodies play a similar role in the gravity formulas as correlations of mechanical properties in the quantum mechanical formulas.

2.3. Planck scale phenomena

The Planck scale gives a computational basis for calculating physical phenomena using a chosen unit scale, but it also provides a physical description of phenomena in unit dimensions of length, mass, and time. Planck scale attributes of length, mass, and time produce Planck scale phenomena of velocity, energy, force, etc. For example, a photon’s energy is the same proportion of the Planck energy as its wavelength to the Planck length

E = \frac{h c}{λ} = \frac{l_{P} m_{P} c^{2}}{λ} = (\frac{l_{P}}{λ}) E_{P} .

(16)

Furthermore, the formula characterizes Planck energy as a Planck length photon moving at the speed of light. If the Planck length gives a structural limit on a photon’s wavelength, then the Planck energy is a maximum quantum of energy.

3. The Structure of Classical Gravity

Evaluating the classical two-body formulas in Table 1 and Table 4 shows that G can be characterized in two parts:

The ratio $l_{P}$ / $m_{P}$ identifies the Planck scale as a computational basis or limit for quantifying the gravitational field generated by mass M and radius r.
The quantity $c^{2}$ in the gravitational constant gives a computational basis for quantifying the momentum and velocity of a test particle or second body.

A look at the formulas in each unit dimension suggests that gravitational potentials are not simply proportional to the gravitational constant, but to a Planck scale density limit expressed in units of length and mass. Only two of the constant’s six unit dimensions quantify the gravitational field in proportion to the Planck length and Planck mass; the remaining unit dimensions characterize gravitational field strength in terms of the mechanics of a second body.

Figure 2. The gravitational constant can be characterized in two parts. The ratio of Planck length to mass gives a computational basis for calculating the magnitude of gravitational field strength produced by mass M at distance r. Two units of c provide a basis for quantifying gravitational potential as the intensive ratios of momentum and velocity of a second body.

3.1. Radial Density

Beneath the compound unit dimensions of G, the classical formulas compare a body’s mass and radius to a Planck scale basis of Planck mass and Planck length. Two signature inputs into the formulas—mass in the numerator and radius in the denominator—produce a dimensionless ratio

\frac{l_{P}}{r} \frac{M}{m_{P}}

(17)

which quantifies the gravitational field on a scale of 0 to 1, where 1 represents a limit of radial density. Inputs of Planck length and mass yield a value of 1 and this ratio decreases as length increases with respect to mass. This single dimensionless value is the correct scaling factor for quantifying gravitational field potentials induced by mass M at distance r. The formulas in Table 4 highlight the essential role of this ratio in quantifying each of the gravitational potentials.

The physical meaning of the radial density ratio can be examined in the context of the Schwarzschild radius. The classical Schwarzschild radius formula can be stated in natural units as

\begin{matrix} R_{s} & = 2 G \frac{M}{c^{2}} \end{matrix}

(18)

(19)

\begin{matrix} = 2 (\frac{M}{m_{P}}) l_{P} . \end{matrix}

(20)

Re-arranging 18 gives a definition of the Schwarzschild radius in terms of the radial density

\frac{l_{P}}{R_{s}} \frac{M}{m_{P}} = \frac{1}{2} .

(21)

Equation 21 reflects an important consequence of the radial density limit. Since the relationship between Schwarzschild radius and mass is constant, the volumetric density of a black hole decreases as its radius increases. While the formula does not indicate how the mass of a black hole is distributed, it does support the view that black holes are not singularities.

Table 3 shows the radial density ratios of several massive bodies. Ratios for black holes are calculated using the Schwarzschild radius formula while the ratios of other bodies are calculated using current values of mass and radius.

A simple way of understanding the radial density ratio in the last column of Table 3 is to consider that each body’s mass is constant. The radial density ratio in the last column is then equal to the ratio between the body’s radius and one-half of its Schwarzschild radius. For example, multiplying the Earth’s radius by its radial density ratio in Table 3 yields one-half of its Schwarzschild radius

(6, 371, 000 m) \times (6.96 \times 10^{- 10}) = . 004 435 m .

(22)

The radial density ratio takes into account both the size and density of the massive body. Note that while the Earth and Sun have similar volumetric densities, the Sun’s radial density ratio is about four orders of magnitude larger. The sun’s larger radius gives it a larger surface area and volume accommodating more mass per unit of radial distance than Earth.

Given a fixed ratio between the radial density limit and a body’s Schwarzschild radius, the formulas in Table 1 and Table 4 can be stated in terms of the ratio between the Schwarzschild radius and distance r, irrespective of whether the massive body is a black hole. Separating the ratio

l_{P} / r

into two parts where

r > = R_{S}

\frac{l_{P}}{r} = \frac{l_{P}}{R_{s}} \frac{R_{s}}{r}

(23)

provides the statement that

\frac{l_{P}}{r} \frac{M}{m_{P}} = \frac{l_{P}}{R_{s}} \frac{R_{s}}{r} \frac{M}{m_{P}} .

(24)

From the Schwarzschild radius definition in Equation 21, the formula can be reduced to

\frac{l_{P}}{r} \frac{M}{m_{P}} = \frac{R_{s}}{2 r} .

(25)

With a relative uncertainty of

2 \times 10^{- 9}

[12], the standard gravitational parameter gives a fairly accurate value of the Earth’s radial density limit and Schwarzschild radius.

The principal role of the radial density limit in quantifying gravitational field potentials makes the ratio of Planck length to Planck mass an important physical constant

\frac{G}{c^{2}} = \frac{l_{P}}{m_{P}} = 7.426 16 \times 10^{- 28} m / k g .

(26)

Table 4. A summary of certain formulas for calculating classical gravitational potentials. Formulas are written in 1) the standard form using the gravitational constant, 2) natural units of length, mass, and time, 3) a radial index form using the ratio of a body’s Schwarzschild radius to distance r, and 4) a simple form that abbreviates natural units with the speed of light. The formulas in each row are equivalent.

Physical property	Sym	Standard	Natural Units	Radial Index	Simple
Schwarzschild radius	$R_{s}$	$\frac{2 G M}{c^{2}}$	$[\frac{l_{P}}{R_{S}} \frac{M}{m_{P}}] = \frac{1}{2}$		$2 \frac{M}{m_{P}} l_{P}$
Escape velocity	$v_{e}$	$- \sqrt{\frac{2 G M}{r}}$	$- \sqrt{2 [\frac{l_{P}}{r} \frac{M}{m_{P}}]} \frac{l_{P}}{t_{P}}$	$- \sqrt{\frac{R_{s}}{r}} \frac{l_{P}}{t_{P}}$	$- \sqrt{\frac{R_{s}}{r}} c$
Gravitational acceleration	g	$- \frac{G M}{r^{2}}$	$- [\frac{l_{P}}{r} \frac{M}{m_{P}}] \frac{l_{P}}{r} a_{P}$	$- \frac{R_{s}}{2 r} \frac{l_{P}}{r} a_{P}$	$- \frac{R_{s}}{2 r} \frac{c^{2}}{r}$
Gravitational potential energy	$U_{g}$	$- \frac{G M m}{r}$	$- [\frac{l_{P}}{r} \frac{M}{m_{P}}] \frac{m}{m_{P}} E_{P}$	$- \frac{R_{s}}{2 r} \frac{m}{m_{P}} E_{P}$	$- \frac{R_{s}}{2 r} m c^{2}$
Gravitational force	F	$\frac{G M m}{r^{2}}$	$[\frac{l_{P}}{r} \frac{M}{m_{P}}] [\frac{l_{P}}{r} \frac{m}{m_{P}}] F_{P}$	$\frac{R_{s, 1}}{2 r} \frac{R_{s, 2}}{2 r} F_{P}$	$\frac{R_{s}}{2 r} \frac{m c^{2}}{r}$
Gravitational binding energy	U	$- \frac{3 G M^{2}}{5 R}$	$- \frac{3}{5} [\frac{l_{P}}{R} \frac{M}{m_{P}}] \frac{M}{m_{P}} E_{P}$	$- \frac{3}{10} \frac{R_{s}}{R} \frac{M}{m_{P}} E_{P}$	$- \frac{3}{10} \frac{R_{s}}{R} M c^{2}$
Hawking radiation (energy)	$k T$	$\frac{ℏ c^{3}}{8 π G M}$	$\frac{1}{8 π} (\frac{m_{P}}{M}) E_{P}$	$\frac{1}{4 π} (\frac{l_{P}}{R_{S}}) E_{P}$	$\frac{1}{4 π} \frac{ℏ c}{R_{S}}$

The formulas in Table 4 offer a convenient method for evaluating how the radial density of a massive body determines its gravitational field at various distances from the center of mass.

3.2. Planck scale

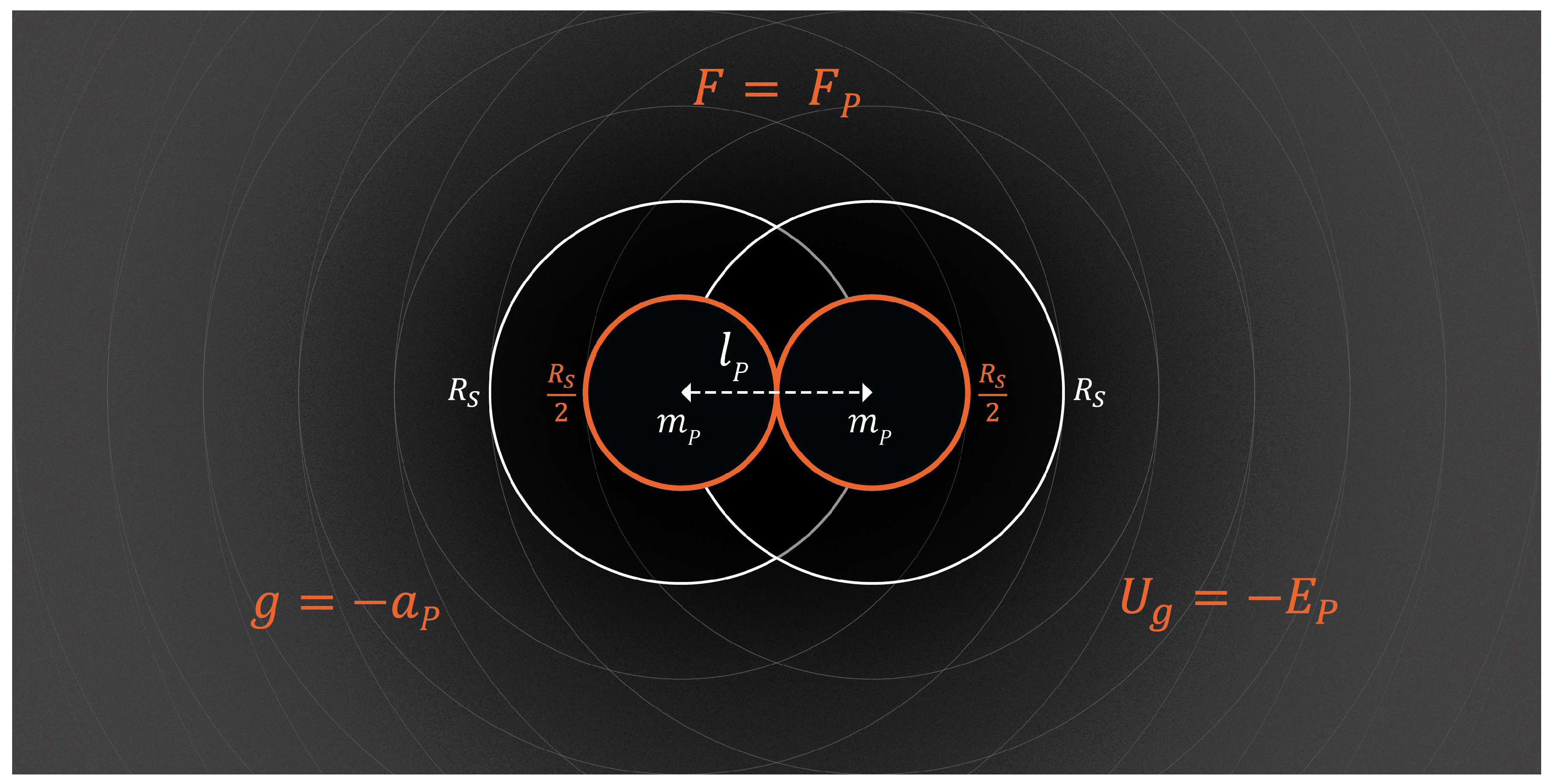
The natural unit formulas in Table 4 showcase the extreme conditions required to produce Planck scale gravitational potentials. Inputs of Planck length and Planck mass produce dimensionless coefficients of 1 in the formulas resulting in Planck scale quantities of acceleration, force, and energy. Figure 3 gives an illustrative representation of the conditions which produce Planck scale potentials. In the figure, two Planck mass bodies are positioned one Planck length apart from their centers of mass.

While these inputs of mass and distance would produce Planck scale gravitational potentials according to the formulas in Table 4, there is no observational evidence that such conditions are physically possible. But whether they are possible or not, the Planck scale serves as a computational basis in the formulas.

The natural unit formulas suggest that gravity is not necessarily a weak force; however, its magnitude is determined by the size, density, and distance between massive bodies. The relatively weak gravitational force we experience on Earth is simply due to the lack of nearby high-density objects.

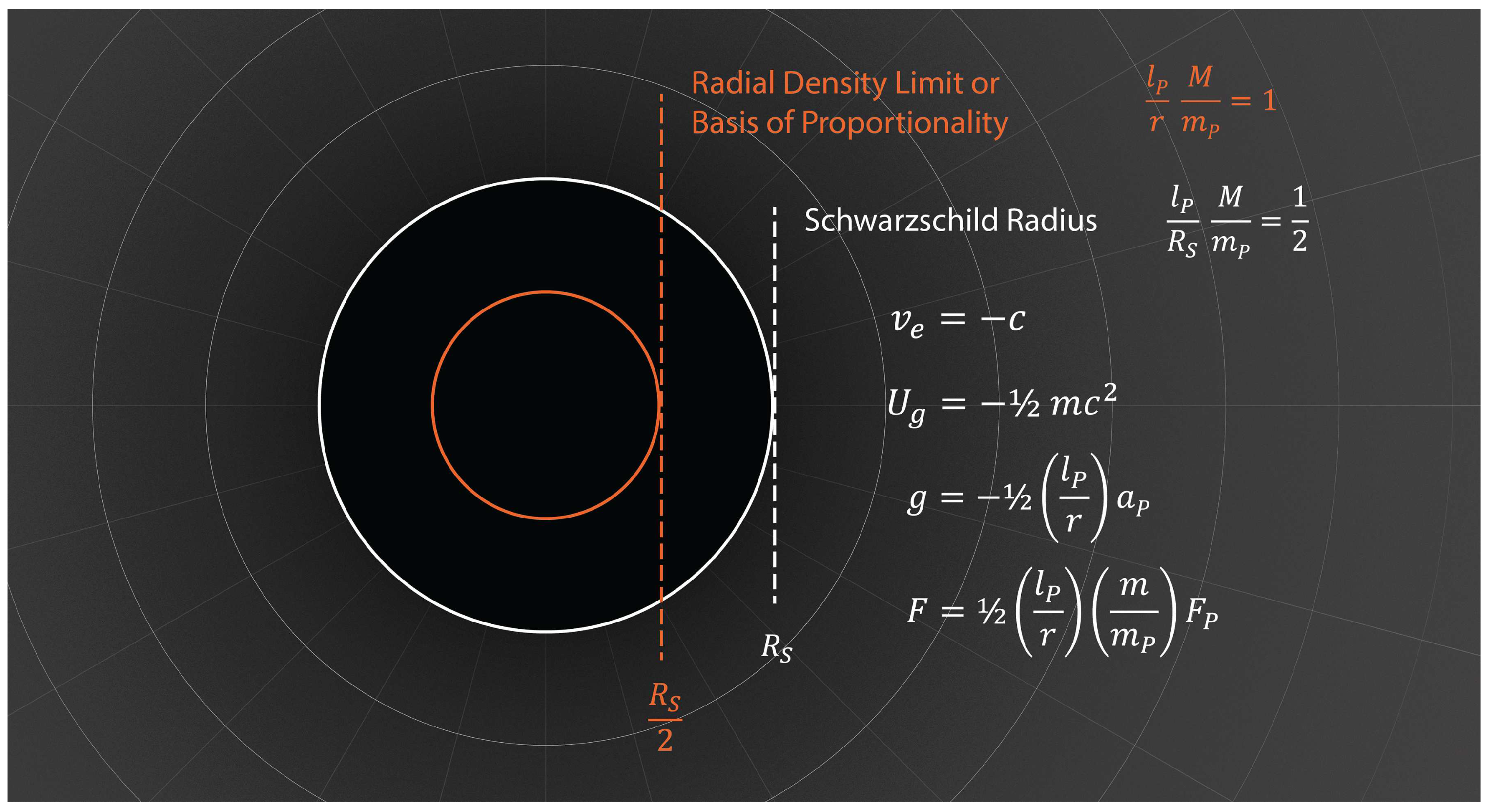
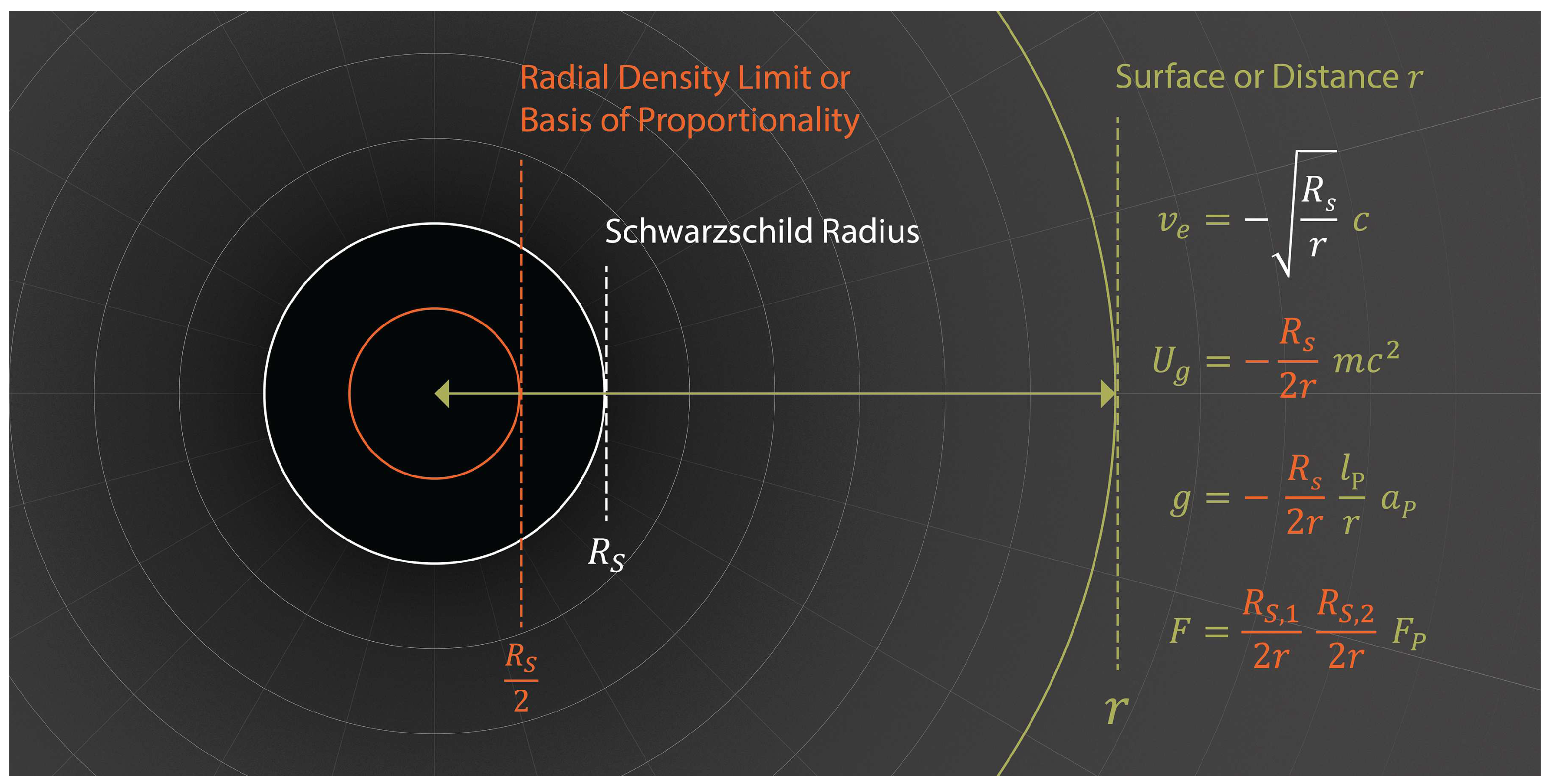
3.3. The Schwarzschild Radius

The gravitational potential formulas in Table 4 are simplified at the Schwarzschild radius by the constant one-half ratio of radial density. Substituting one-half for ratios of radius and mass at the horizon highlights the simple attributes which quantify gravitational potentials at this particular location. Figure 4 illustrates these formulas which are also given in Table 4.

Two of the potentials shown in the figure—escape velocity and gravitational potential energy—are constant regardless of the radial distance at the horizon. Escape velocity is equal to

- c

while gravitational potential energy depends only on the mass of the test particle. This energy is proportional to the Planck energy by the ratio of the particle’s mass to the Planck mass.

Acceleration and force potentials, on the other hand, decrease as the Schwarzschild radius increases. These two physical phenomena grow weaker by a factor of distance squared from the center of mass. However, the constant one-half ratio between mass and radial distance at the horizon represents offsetting influences on the acceleration and force potentials. Apart from this one-half coefficient, acceleration is only reduced from its Planck scale maximum by the inverse distance in natural units,

l_{P} / r

. Gravitational force is similarly proportional to the Planck force but includes an additional ratio between the mass of the test particle and the Planck mass.

3.3.1. Hawking Radiation

The Schwarzschild radius is the principal quantifier of Hawking radiation as the natural unit formula demonstrates. Restating temperature in terms of kinetic energy

k T = \frac{ℏ c^{3}}{8 π G M}

(27)

and replacing universal constants with natural units gives

(28)

which can be simplified to

k T = \frac{1}{8 π} (\frac{m_{P}}{M}) E_{P} .

(29)

Equation 29 quantifies energy as the ratio of mass to Planck mass, but we can restate the mass ratio in terms of the radius. Equation 21 gives the constant ratio between mass and Schwarzschild radius

\frac{m_{P}}{M} = 2 \frac{l_{P}}{R_{s}} .

(30)

Replacing the mass ratio with the ratio of Planck length to Schwarzschild radius gives

k T = \frac{1}{4 π} (\frac{l_{P}}{R_{s}}) E_{P} .

(31)

Comparing 31 to the natural unit form of the photon energy formula in 16 shows a close parallel between photon wavelength and Schwarzschild radius. In fact, Equations 27 through 31 can be stated in universal constants as

k T = \frac{1}{4 π} \frac{ℏ c}{R_{S}} .

(32)

The natural unit formulas show that kinetic energy approaches the Planck energy as the Schwarzschild radius approaches the Planck length. The equations highlight correlations between the length, mass, and energy of a black hole.

3.4. Outside the Schwarzschild radius

Gravitational potentials outside the Schwarzschild radius are proportional to the radial density limit, including potentials generated by bodies that are less dense than black holes. Figure 5 illustrates the ratio between distance r and the Schwarzschild radius or radial density limit.

The formula for gravitational potential energy says something interesting about the ratio between the Schwarzschild radius and distance r. Setting the gravitational potential energy equal to the kinetic energy of a second body

\frac{1}{2} (\frac{R_{S}}{r}) m c^{2} = \frac{1}{2} m (v^{2})

(33)

shows how the radial density of the first body influences the momentum and velocity of a second body and can be simplified to

\frac{R_{S}}{r} = \frac{v^{2}}{c^{2}}

(34)

where v is equal to the escape velocity. From Equation 25, the relationship can also be stated in terms of the radial density limit

2 \frac{l_{P}}{r} \frac{M}{m_{P}} = \frac{v^{2}}{c^{2}} .

(35)

Equation 34 gives a translation between the radial density of a massive body and the gravitational potential it produces.

4. Conclusion

The gravitational constant is a versatile quantity for computing gravitational potentials, but it provides little information about how or why the classical formulas work. Restating the constant in natural units reveals the mathematical means by which the formulas transform inputs of mass and radius into the correct magnitudes and unit dimensions of each potential. The physical attributes of the system and the field potentials they produce are equal proportions of a Planck scale limit or computational basis.

A better understanding of the classical gravity formulas may prove instrumental in the search for a theory of quantum gravity. An important next step is considering the physical structure of quantum particles in real dimensions of space and time, and how this structure influences the gravitational field. Natural units offer a common language for comparing the quantum mechanical structure of matter particles with a corresponding gravitational field expressed by the mechanics of a second body. The inversely proportional relationship between mass and wavelength is an important structural clue.

Another research opportunity is the restatement or reinterpretation of general relativity in natural units. The role of universal constants in the mathematical formulation of general relativity may yield valuable new insights. For example, natural units suggest that the Einstein gravitational constant—the Planck force—constitutes the same computational basis in General Relativity as it does in the classical formulas.

Planck’s derivation of the natural units requires that each of the universal constants embody natural units in their unit dimensions. The consistent and insightful role that these units play in describing gravitational and quantum mechanical phenomena suggests that greater emphasis should be placed on discovering their meaning. A theory of quantum gravity may follow.

References

Max Planck. Über irreversible strahlungsvorgänge. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin, 5(1):440–480, 1899.
David Humpherys. The Implicit Structure of Planck’s Constant. European Journal of Applied Physics, 4(6):22–25, 2022. [CrossRef]
Espen Gaarder Haug. Progress in the Composite View of the Newton Gravitational Constant and Its Link to the Planck Scale. Universe, 8(9):454, 2022. [CrossRef]
Barton Zwiebach. A First Course in String Theory. Cambridge university press, 2004.
V.A. Nastasenko. Otkrutie predelno vozmojnuh volnovuh parametrov: Theoria and tehnica peredachi, priema i pererabotki informacii. Proceedings of the 10-ja Jubilejnaja Megdunarodnaja Conferencia, Kharkov, Ukraine, 1, 2004.
Claude Mercier. Several Ways to Calculate the Universal Gravitational Constant G Theoretically and Cubic Splines to Verify Its Measured Value. Journal of Modern Physics, 11(9):1428–1465, 2020. [CrossRef]
Fundamental Physical Constants. https://physics.nist.gov/cuu/Constants/index.html, 2018.
David Humpherys. Natural Planck Units and the Structure of Matter and Radiation. International Journal of Quantum Foundations: Quantum Speculations, 3, 2021.
Espen Gaarder Haug. Extraction of the Planck Length from Cosmological Redshift without Knowledge of G or h. International Journal of Quantum Foundations: Quantum Speculations, 4, 2022.
Gordon R Kepner. Relating the de Broglie and Compton Wavelengths to the Velocity of Light? Applied Physics Research, 10(4), 2018. [CrossRef]
David Humpherys. Measuring Planck’s Constant With Compton Scattering. Applied Physics Research, 15(1):24–29, 2023.
C. Rothleitner and S. Schlamminger. Invited Review Article: Measurements of the Newtonian constant of gravitation, G. Review of Scientific Instruments, 88(11), 11 2017. 111101. [CrossRef]

Figure 3. Natural unit formulas describe the extreme conditions required to produce Planck scale gravitational potentials. Two Planck mass bodies separated by one Planck length produce gravitational potentials of Planck energy, acceleration, and force.

Figure 4. At the Schwarzschild radius, the countervailing influences of mass and distance produce a radial density coefficient of one-half, simplifying the gravitational potential formulas.

Figure 5. Gravitational potentials at distance r are proportional to the ratio between r and the Schwarzschild radius or radial density limit.

Table 1. Stating the gravitational constant in natural units shows how the physical attributes of a system quantify gravitational phenomena in proportion to a Planck scale basis. Formula inputs are highlighted in red.

Physical property	Symbol	Std Formula	Natural Unit Formula	Simple Formula
Escape velocity	$v_{e}$	$- \sqrt{\frac{2 G M}{r}}$	$- \sqrt{2 (\frac{l_{P}}{r}) (\frac{M}{m_{P}})} \frac{l_{P}}{t_{P}}$	$- \sqrt{2 \frac{l_{P}}{r} \frac{M}{m_{P}}} c$
Gravitational acceleration	g	$- \frac{G M}{r^{2}}$	$- (\frac{l_{P}}{r}) (\frac{M}{m_{P}}) (\frac{l_{P}}{r}) a_{P}$	$- \frac{l_{P}}{r} \frac{M}{m_{P}} \frac{c^{2}}{r}$
Gravitational potential energy	$U_{g}$	$- \frac{G M m}{r}$	$- (\frac{l_{P}}{r}) (\frac{M}{m_{P}}) (\frac{m}{m_{P}}) E_{P}$	$- \frac{l_{P}}{r} \frac{M}{m_{P}} m c^{2}$
Gravitational force	F	$\frac{G M m}{r^{2}}$	$(\frac{l_{P}}{r}) (\frac{M}{m_{P}}) (\frac{l_{P}}{r}) (\frac{m}{m_{P}}) F_{P}$	$\frac{l_{P}}{r} \frac{M}{m_{P}} \frac{m c^{2}}{r}$

Table 2. The inversely proportional relationship between Compton wavelength and rest mass gives a conserved constant of Planck length times mass. Compton wavelength and rest mass are equivalent proportions of the Planck scale allowing formulas to determine wavelength from mass and mass from wavelength.

Lepton	$λ_{C}$	$m_{0}$	$λ_{C} m_{0}$	$l_{P} m_{P}$	$l_{P} / λ_{C}$	$m_{0} / m_{P}$
	m	$k g$	$k g m$	$k g m$	—	—
e	$3.862 \times 10^{- 13}$	$9.109 \times 10^{- 31}$	$3.518 \times 10^{- 43}$	$3.518 \times 10^{- 43}$	$4.185 \times 10^{- 23}$	$4.185 \times 10^{- 23}$
$μ$	$1.868 \times 10^{- 15}$	$1.884 \times 10^{- 28}$	$3.518 \times 10^{- 43}$	$3.518 \times 10^{- 43}$	$8.654 \times 10^{- 21}$	$8.654 \times 10^{- 21}$
$τ$	$1.111 \times 10^{- 16}$	$3.168 \times 10^{- 27}$	$3.518 \times 10^{- 43}$	$3.518 \times 10^{- 43}$	$1.455 \times 10^{- 19}$	$1.455 \times 10^{- 19}$

Table 3. The ratio between a massive body’s radial density and the radial density limit in the last column quantifies its gravitational field. The table compares the relative radial densities of different types of massive bodies. The Schwarzschild radius is defined by a density of 0.50

Massive body	Type	$\frac{l_{P}}{R}$	$\frac{M}{m_{P}}$	$\frac{l_{P}}{R} \frac{M}{m_{P}}$
Sagittarius A*	Supermassive BH	$1.32 \times 10^{- 45}$	$3.80 \times 10^{44}$	$0.50$
GRO J1655-40	Steller mass BH	$1.03 \times 10^{- 39}$	$4.85 \times 10^{38}$	$0.50$
4U 1820-30	Neutron star	$1.78 \times 10^{- 39}$	$1.44 \times 10^{38}$	$0.26$
Sirius B	White dwarf star	$2.76 \times 10^{- 42}$	$9.45 \times 10^{37}$	$2.61 \times 10^{- 4}$
Sun	Yellow dwarf star	$2.32 \times 10^{- 44}$	$9.14 \times 10^{37}$	$2.12 \times 10^{- 6}$
Earth	Planet	$2.54 \times 10^{- 42}$	$2.74 \times 10^{32}$	$6.96 \times 10^{- 10}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Natural Unit Expression of Classical Gravity

Abstract

1. Introduction

2. The Natural Unit Scale

2.1. Natural units of length and time

2.2. Natural mass units

2.3. Planck scale phenomena

3. The Structure of Classical Gravity

3.1. Radial Density

3.2. Planck scale

3.3. The Schwarzschild Radius

3.3.1. Hawking Radiation

3.4. Outside the Schwarzschild radius

4. Conclusion

References

MDPI Initiatives

Important Links

Subscribe