Preprint
Article
A New Algorithm for Estimating Fast Variations in the Heart Rate
Altmetrics
Downloads
351
Views
123
Comments
1
Submitted:
03 February 2023
Posted:
06 February 2023
You are already at the latest version
Alerts
Abstract
Heart rate variability (HRV) is commonly intended as the variation in the heart rate (HR) and it is evaluated in the time and frequency domains with various well known methods. In the present paper, we first consider an abstract model in which the HR is the instantaneous frequency of an otherwise periodic signal such as the electrocardiogram (ECG). Thus the ECG is assumed as a frequency modulated signal, or carrier signal, where HRV or HRVt is a supposed time-domain signal which is frequency modulating the carrier ECG signal around its average frequency. Hence we describe an algorithm able to frequency demodulate the ECG signal to extract a continuous signal HRVt with possibly enough time resolution to analyse fast time-domain variations in the instantaneous HR. After exhaustive testing of the method on simulated frequency modulated sinusoidal signals, we have applied the procedure on actual ECG tracings. The purpose of the work is to eventually use the heart as a kind of biological sensor of the fast activity of the autonomic nervous system (ANS) to study the ANS ultra-short-term event-evoked responses. A few preliminary, not clinical, real examples are also given.
Keywords:
Subject: Medicine and Pharmacology - Cardiac and Cardiovascular Systems
1. Introduction
We tackle the problem of detecting the variation of the heart rate (HR) in the framework of the general theory of frequency modulated signals. Considering any physiologic signal periodic at the, variable, heart rate, we describe a method and algorithm for recovering a time continuous frequency modulating signal from the frequency modulated signal at hand. The problem above is solved for applications like frequency modulated (FM) radio broadcasting but it appears very tricky, and put to its physical limits, when considered for the heart rate and, in this case, when a large bandwidth of the recovered modulated signal is needed to preserve.
It is out of the scope of this paper that of discussing about the origin of heart rate modulations and heart rate variability. The method we present is completely disregarding the physiology of the heart and the mechanisms that influence and define in real time the heart rate. It is not our intention that of investigating the physiology of the heart nor to propose any new insight into it, on the contrary we are just proposing a method for extracting a clean heart rate variability signal from a heart-activity-related signal like the electrocardiogram (ECG). Our interest in the physiology of the phenomena implied in heart rate controlling is only limited to the understanding that the ECG is a frequency modulated signal (the times of occurrence of R-waves are not evenly spaced in time), thus we are looking for a continuous time signal reflecting the inverse of the instantaneous time spacing of the R events and we call this signal as the instantaneous heart rate indicated as . We recognize that this signal is not to be solely found in any particular organ or physiologic mechanism in the body: we consider it just from a black box point of view as depicted in Figure 1.
To the contrary to commonly known HRV analysis methods, we are looking for an algorithm able to detect very fast variations in the heart rate or fast not-rhythmic variations intervening in a few heart cycles. In a nutshell our method is going to frequency demodulate the signal to recover the assumed frequency modulating signal . The latter signal, no matter if it is periodical or not, will then be used for any particular heart rate variability analysis which might be required to study.
2. Intrinsic Signal Analysis Problems in Frequency Demodulating the ECG Signal
Comparing the frequency band occupation of a radio FM signal with the frequency occupation of the signal (simplifying the ECG as having a sinusoidal shape to avoid also considering the spectral content of the waveform of it) may be very much instructive to highlight the originality and importance of this study.
The FM radio broadcasting is very popular (although now made obsolete with the introduction of the digital audio broadcasting or DAB). In the famous 88-108 MHz radio band, many FM stations are allocated with a spacing of 200 KHz while a maximum modulation deviation of ± 75 KHz is permitted for sending stereo audio signals in a band from tens of Hz to 50 KHz (considering also stereo multiplexing). It is very well known that the intrinsic non-linearity of the frequency modulation process makes the calculation of the occupied band of the modulated signal very difficult to assess. The popular Carson bandwidth rule [1] gives an rough estimation of the bandwidth (Carson Bandwidth or CB) of a signal frequency modulated by another signal having a maximum frequency with a maximum permitted frequency deviation of the carrier from the non modulated carrier frequency:
For a FM radio emission with = 53 KHz and = 75 KHz, we get = 256 KHz which is even a bit larger than the allocated band for each FM radio channel. By the way the occupied band is just 0.26 percent of the carrier (at center band of 98 MHz).
The same calculation for the frequency modulated ECG signal is quite astonishing: first we may assume that the possible absolute maximum deviation of the heart rate from a given average (normal) heart rate would be in the order of 40 beats per minute (bpm) or 0.7 Hz, meaning that we might expect, for example, for the heart rate running at 70 bpm (1.17 Hz), to slow down to 30 bpm (0.5 Hz) or rise up to 110 bpm (1.8 Hz) although this is just an assumption with approximate figures; second, the maximum frequency of the variation might be assumed to be a bit larger than the breath frequency which is a well-known modulator of the heart rate, say a maximum of 15 events per minute (0.25 Hz). This is just for the sake of having some acceptable figures to let us compute the CB. Thus, for the heart rate, running on average at 70 bpm (1.17 Hz), we have = 0.25 Hz and = 0.7 Hz which gives = 1.9 Hz so explaining the intrinsic difficulty or even impossibility of a correct estimation of the HRV, as the signal modulating the heart rate has a larger bandwidth than the carrier (average heart rate) itself. Indeed, in the calculation above we considered just maximum values, as it is uncommon that the breath-frequency-induced HRV have a shift of 40 bpm, by the way the problem remains as the CB of the heart rate signal is still comparable to the average heart rate itself.
In conclusion, one must admit that the heart is running too slow for correctly carrying the expected heart rate variability modulation, hence we may say that in general the detection of the heart rate variability signal from any heart-activity-related physiologic signal, like the ECG, is conceptually impossible. We may surmise that this problem is at the basis of motivation for the large number of methods defined so far for heart rate variability assessment.
The concepts previously highlighted make the use of standard frequency de-modulators commonly used in radio technology impossible. Indeed, HRV has been always evaluated by the computing of the actual time delays of arrival of each individual heartbeat or instantaneous heart period, starting from the inter beat interval values.
There are two problems to underline. First is that no matter the demodulation process used to estimate , we will never obtain a continuous heart rate modulation signal as the instantaneous heart rate is not available at each instant of time but only at each heartbeat (by computing the inverse of the instantaneous heart period). Thus, the heart rate variability signal, which we assume in the black box model as a signal time continuous in nature, is not available in a continuous form (like the blood pressure signal for example) for us to acquire. Second, it is true that we are anyway digitally acquiring biological signals in a sampled form, but the sampling frequency is chosen by the experimenter while with the signal we should follow its own sampling frequency (which is the heart period), and the heart period, or heart rate, is exactly what we are looking for. So, the visible HRV signal is in general a non-continuous signal available at its own sampling frequency which is by the way the signal itself.
The authors think that there is no need here to review once again all the HRV acquisition and analyzing techniques developed so far. All these algorithms can be roughly divided into long term and short term HRV analyzing methods depending on the time length of the epoch of the ECG to study. The results can also be divided into time or frequency analysis. The readers well acquainted in this field know the story very well. For the other interested readers, the reference [2] is suggested.
Nevertheless, we think it is important to discuss and to review the current state of the research field with a special attention devoted to the papers dealing with the problem of HRV signal detection, recording and resampling. Of special interest for our work is the paper [3] where the effects of resampling frequency of RR interval and length of the epoch of analysis are considered toward the evaluation of the autonomic nervous system. Fast variations of acceleration and deceleration of heart rate were also analyzed in [4] where interest was given to the preprocessing of unevenly sampled RR interval signals using interpolation and resampling.
A special mention for comparing HRV analysis methods is the Lomb-Scargle periodogram [5,6] which can be used for a reliable estimation of the frequency spectrum of unevenly sampled signals like RR series. Lomb-Scargle periodogram is more common in the astronomy community but it is, quite unfortunately, less popular in the HRV research community mostly because the mathematical difficulties in understanding it. In any case, Lomb-Scargle is looking for rhythmical variations in the RR series, while we would like to remain general not assuming any particular behavior of the HR modulating signal.
The problem of resampling and actual final sampling rate of HRV signal has been studied also in [7] where another time domain measure of HRV has been introduced. Errors and effects introduced in the resampling process of HRV were also studied in [8-9].
The present paper introduces yet another method for obtaining a resampled and clean HRV signal out of a sequence of RR intervals with the aim of preserving the bandwidth of the frequency modulating signal even on short or ultra-short time epochs.
3. Algorithm for the Estimation of the Instantaneous Heart Rate Signal from the ECG
As already stated, the presented algorithm aims to obtain a signal representative of the “instantaneous” heart rate. This signal should be provided with a sampling rate even higher than the heart rate itself.
There are two standard and straightforward ways of extracting the heart rate signal from the ECG signal [2]: both methods start with the measuring each heart period and convert it to frequency by calculating the inverse. The resulting collection of measures will normally be unevenly spread in time as the time delay between a measure and the following is just equal to each heart period which is varying. Thus, we may say that the signal is available only in an unevenly sampled fashion where the actual sampling is the signal itself. Eventually, to create an evenly sampled, resampled, heart rate signal extracted from the set of measures, the first way is to distribute each sample measure on a reconstructed sampling frequency equal to the average heart rate in the epoch to be analyzed. The second way is that of leaving the measures at the instants of time where they were taken and interpolating them on an evenly distributed instants of time. Same interpolation is to be done also when using the first method, if a more significant number of points is required. This problem is commonly known as resampling. Both methods will provide the signal suitable for subsequent analysis in the frequency domain but relatively poor for direct study in the time domain. Indeed, time-domain studies of are almost never done on the waveform of but, more often, on indexes extracted from it [2].
We aim to obtain a kind of signal that might be directly analysed for the study of fast transitory events appearing in the signal itself. Indeed, the final goal, and the advantage of the algorithm, which is about to be described, is that of catching fast variations in the heart rate, although not rhythmical, which might be related to sudden correlated variations of the activity of the autonomic nervous system.
Thus, the problem we want to tackle is that of estimating the signal , or , from . At first, we must recognize that nor , neither , can be directly measured with appreciable time resolution. Indeed, even supposing that we have a reliable R-wave detector on the signal , we could just measure only at each nth heartbeat occurring at each instant of time . We might note that the signal is the only biological signal which is only naturally available in sampled form; moreover, as already noted above, its sampling instants of time are the signal itself.
In this new proposed method, we build a new signal as the cumulative sum of the heart beats (or complete cycles). We define a suitable evenly spaced sampling time for the signal. This means that the will be created as a signal sampled at a frequency . We may choose a convenient sampling frequency for , often even higher than the actual heart rate and for sure much higher than the frequency content of , and maybe we may even use the same sampling frequency at which the signal itself was acquired. Then, at each time instant of sampling , we apply the following first rule:
if a heartbeat (R-wave) has occurred (has been detected) at an instant of time where then otherwise .
This means that will be built as the running count function of the detected heartbeats. Obviously, it will be a not-descending function of time, it will be sampled at the frequency with an obvious [instantaneous] slope equal to beats per minute. Indeed, we used the word “instantaneous” in brackets because the signal is a sampled staircase signal which remains constant during many time samples between each heartbeat and the following. Please note that the signal rises as faster as higher will be the signal : indeed, supposing be constant at 70 bpm, then will obviously grow at a rate of 70 units per minute.
Thus, we might evaluate as just the first derivative of in the second rule:
As we may subtract the signal’s average (mean heart rate) to obtain in bpm.
Apart from a series of difficulties which we shall discuss in the following, it is worth noting that the signal so estimated is in principle known with a remarkable time resolution (it is sampled at a very high sampling frequency) hence it is helpful for ultra-short term heart rate variability (USTHRV) studies even to detect fast and short lived heart rate variations (time domain HRV studies), provided the required minimum signal epoch is available.
We are convinced that this proposed method is better than the standard method based on interpolation of the inverse of individual heart periods.
The attentive reader will note that computing the signal and then make the derivative of it, is somewhat like performing the inverse of the interbeat interval values followed by interpolation or smoothing. By the way, in the present proposed method the interpolation is still used on the signal before computing the derivative and it is also done through low pass filtering as described in the following. Nevertheless, the obtained signal still maintains a wide frequency content that shows fast heart rate variations, along with an even resampling at a high sampling frequency.
Details of the method will be presented here while applying the algorithm on a special artificial simulated signal which we used to better appreciate the performances of the processing.
The central assumption put forward in this paper is that any heart-activity-related biomedical signal (electrocardiogram ECG, phonocardiogram PCG, photoplethysmogram PPG, etc.) is a frequency modulated signal while its instantaneous frequency is known as the instantaneous heart rate. Considering the ECG, as the instantaneous frequency of it is time varying, then the instantaneous frequency is a time signal. Here it is useful to recall the definition of a “signal” as “any observable change of a quantity over time” [10]. That’s why we consider the heart rate signal as a signal . The purpose of this paper is to describe a method for the frequency demodulation of the ECG to obtain an estimation of the instantaneous heart rate signal. The carrier signal has a sinusoidal shape in conventional frequency modulated signals like those used in radio communications. In the case at hand here, the heart-activity-related biomedical signal is not sinusoidally shaped. Indeed, the ECG is not sinusoidal, although we may consider it as a periodical signal as well, made of repetitions of the well-known P-Q-R-S-T waves (instead of sinusoidally shaped periods). Now, no matter the actual frequency content of the biomedical signal, which depends on its wave shape, we consider the signal with its periodism as the carrier of a frequency modulating signal in the time domain, which we may name the heart rate signal. The heart rate signal is not directly available for acquisition from the real world. Still, we know that the heart rate signal is visible as the instantaneous frequency of other signals generated synchronously with the heart activity, being the electrocardiogram one of those. As the ECG has a large bandwidth between other heart-activity-related signals and it is simple to process for extracting the heart rate by detection of R-waves, then the heart rate is commonly inferred from the frequency of the ECG events as its jitter incertitude is at the minimum. Jitter may be defined as the deviation from the true periodicity of a presumably periodic signal [11]. As the ECG is, by its nature, not periodic, then it is evident that the jitter, in assessing the true instant of time at which the R-wave in the ECG is detected, will be made of two components: one component is the natural (physiological) wandering of the heart rate (the scope of our research) and the second component is the instrumental error in detecting the time of the R-wave (instant of the heart beat event). The first component is due to the heart rate variability signal (also made of two components: the real wandering of the cardiac physiological pace-maker, which generates P-waves, summed to the wandering of the transmission delay of the impulse from the physiological pace-maker through the specific heart conduction tissues to the ventricles, which generate the R-waves) and the second component is an unavoidable, although it can be minimized, instrumental error. Indeed, ECG is used thanks to its large bandwidth, so that on this signal the instrumental error can be kept at a minimum compared to other heart-activity-related biological signals. At the end of the preliminary description, we will use the ECG signal to infer the shape of the heart rate signal and we will always assume the instrumental jitter as zero.
First, we consider, obviously, the ECG as the time domain signal produced by the ventricles’ electrical activation: . To better describe our model, and without loss of generality, we may initially consider a sinusoidal signal as a classical kind of a periodical signal that is clearly simpler to manage than the ECG shape itself. Trivially, a sinusoidal period has the shape of a sinusoid while an ECG period has the well-known shape of the P-Q-R-S-T waves complex: in a sinusoidal signal we have repetitions of sinusoids and in a ECG signal we have repetitions of P-Q-R-S-T complexes. So, let’s first consider a sinusoidal signal instead of an ECG signal. As we are interested in the wandering of the frequency of repetitions, the shape of what repeats itself is meaningless. To help correctly understand the matter, we start from Figure 2 where the artificial generated “heart rate signal” is shown.
It might be surprising the use of a square wave for simulating the heart rate signal in Figure 2 as the heart rate variation has never this shape in nature. Indeed. The choice of a square wave, having a sudden and perpendicular rise in the waveform, has been made to show and test the performance of the algorithm in detecting fast transients in the heart rate variability signal even if a so fast variation is absolutely unlikely in nature.
, composed of a constant signal with an amplitude of 70.2 bpm summed to a square-wave signal having a peak-to-peak amplitude of 14.4 bpm and a frequency of 0.02 Hz; the resulting signal is a square-wave signal having an average value of 70.2 bpm alternating between 77.4 bpm and 63 bpm every 25 seconds. Lower tracing: the signal imposes the frequency of a sinusoidal signal creating a “sinusoidal ECG” signal whose frequency is, at each instant of time, precisely that shown in the upper tracing. Please note that the amplitude of the signal is purposely given in beats per minute (bpm) while the units of the simulated “sinusoidal ECG” signal are arbitrary.
4. Practical Implementation of the Algorithm
A deeper insight is now given into the details of practical implementation of the algorithm described above. We initially use the method on an artificial simulated signal showing a sudden variation in its frequency. The signal to use is of sinusoidal shape because it is much simpler to simulate than an actual ECG shaped signal. Therefore, the R detector will be temporarily changed in favour of a zero-crossing detector.
Thus, the first step in FM demodulation of the ECG signal is detecting the signal cycles. In case the simulated ECG signal is used (sinusoidal shape), positive zero-crossings are detected, while in the case of a real ECG signal, the peaks of R-wave will be detected. As in this paragraph we will be concerned about simulated signals, positive zero-crossings will be used. A positive zero-crossing event in the signal is detected at the instant of time when the signal is crossing the zero-line travelling from a negative value to a positive value (positive first derivative). As the signal is artificially generated without any noise component, the following very simple MATLAB function has been written for zero-crossing detection:

 In the following we will use the first simulated signal as described in subsection 4.1 above. Using the previous zerofind(y) function, the zeroes in the signal are found and, after this zero-crossing detection, the signal is created by the cumulative sum of the zero-crossing events in time as in Figure 3.
In the following we will use the first simulated signal as described in subsection 4.1 above. Using the previous zerofind(y) function, the zeroes in the signal are found and, after this zero-crossing detection, the signal is created by the cumulative sum of the zero-crossing events in time as in Figure 3.The method for obtaining the cumulative sum signal implies counting the number of cycles detected along time using the following MATLAB script:


In the above MATLAB script, the ecg vector is the simulated frequency modulated signal (or the sampled ECG epoch), the same vector passed to the zerofind function above.
The sumecg vector so obtained merits some discussion to be clearly understood. As already described, it is the summing count of the cycles (zero crossings in the simulated signal or R-waves detected in the ECG epoch). In Figure 3, apparently, it is shown as a rising straight line. But it must be noted that the higher the number of cycles (or R-waves) detected per unit time, the steeper will be the slope of the sumecg vector (which is, by the way, the signal), so it is not really a straight line! This means that the first derivative of the sumecg vector or the signal, should give the instantaneous signal frequency (or heart rate).
The obtained signal is not directly helpful in estimating its first derivative because it is composed of a series of steps (staircase shape) of one count for each cycle (or heartbeat) found. Numerical first derivative is quite a tricky procedure to obtain a sufficiently smooth and low noise output signal, so we used the following steps:
- a)
- b)
- then a downsampling of the signal is made to a sampling frequency of 8 Hz as the maximum bandwidth of the HRV signal is expected to be around 0.5 Hz at most (30 cycles/minute)
- c)
- eventually filtering is applied on the downsampled signal with a differentiating noise-robust filter to obtain the first derivative or the instantaneous heart rate signal; signal differentiation by FIR filtering is a classical procedure but we followed the original and robust method proposed by Holoborodko [12] using an 11-order one-sided noise-robust differentiator whose Bode plot is shown in Figure 5; a filter delay of 625 ms is to be expected. This filter has a linear characteristic at low frequencies (implying a multiplication by the s-variable in the Laplace domain), while at higher frequencies, it becomes a low pass.
- d)
- a final low pass filter is then applied to the signal with a moving average Kaiser-Bessel 16 points weighted filter whose Bode plot is shown in Figure 6 (corresponding, at the sampling frequency of 8 Hz, to approximately 2 seconds and giving a filter delay of 937,5 ms); following the differentiating filter, which provides the required first derivative, this further moving average filter is used to clean the output from residuals of original R-wave detection points (the original carrier frequency).
- e)
- eventually, the average value of it is subtracted from so to obtain the final signal or heart rate variation signal.
At last, the heart rate signal can be plotted as in Figure 7. This figure shows how the recovered heart rate signal (bottom trace) is closely resembling the simulated signal (top trace in red) which was used to frequency modulate the “sinusoidal ECG”. In particular the frequency variation step from 77.4 bpm to 63 bpm has been detected with a 2.5 second delay (known from the fixed delays applied by the filters) and the sudden step in the heart rate is detected with a 2 second gentle slope of the recovered signal, which has about two heart cycles time length. The beginning of the reconstructed signal is affected by initialization transition period of reconstructing filters or edge effect.
5. Testing the Algorithm on More Complex Artificial Heart Rate Variability Signals
Software implementation of the simulation in Figure 2 is relatively straightforward as the frequency varying sinusoidal signal is composed of epochs in which its frequency is constant (in the example, there are epochs in which frequency is 77.4 bpm alternating with epochs at 63 bpm). But this situation is not that we might expect in general in the frequency wandering of the natural ECG: indeed, in nature, we will expect a continuous variation of the instantaneous frequency of the ECG. Let’s put it in formulas. The sinusoidal signal that we will use must show a continuous frequency wandering behaviour, as we might see in the ECG. We continue using a sinusoidal signal instead of an ECG signal. From secondary school, the sinus function is presented as: , which is strictly an accurate periodical signal of period . For the scope of introducing frequency wandering in the formula, we must re-learn what a sinus function is all about: given a time domain function representing the instantaneous value of the frequency of the sinus signal, or heart rate, then this can be represented in formula as:
Should be reduced to a constant not depending on time, then the formula above will become the well-known formula for the actual periodic (not frequency wandering) sinus function:
Of course, as the frequency of our “heart sinusoidal signal” is not constant, we should keep the first representation as in formula (3) above.
Following the example in Figure 2, we say that the function is a time-domain signal whose amplitude is the instantaneous heart rate or the instantaneous frequency of the ECG signal. As a matter of fact, we consider the signal as composed of two parts, one constant and another variable in time such as:
where is the constant average value of and the function is the variable component or, more appropriately, the heart rate variability signal we are looking for. In the example simulated in Figure 2 we used the following values:
bpm, and bpm
where is the sign function and is the frequency of variation of the instantaneous signal frequency (0.02 Hz, meaning the heart rate is changing every 25 seconds).
In a more general case, we will define as the average (constant) heart rate during a given (short) epoch of signal acquisition and we will define as the wandering frequency signal, or the heart rate variability signal, whose amplitude is the instantaneous shift of the heart rate from the average heart rate (frequency modulation).
We can state the problem of recording the signal as the method by which this signal can be inferred from the quasi-periodic signal . The need to obtain a “continuous”, or “instantaneous”, signal comes from the interest in analysing very short or even ultra-short-term heart rate variations in the time domain instead of considering cyclical variations on very long epochs of time.
To describe the performances of the method described in the previous paragraph, we will initially use simulated signals for which we exactly know the signal used for simulating those. It must be noted that the use of simulated signals on which testing the algorithm is necessary because in this way we can compare the results of the method with the signal actually used in the simulations. We couldn’t apply the method on real ECG signals because in this case we cannot know the real frequency variability coded into the heart rate. Once the method is validated on simulated signals then it will be used reliably on real natural signals. Eventually, we will apply the method on real ECG biological signals as in next paragraph 6.
The simulator will produce a sinus shaped signal instead of an ECG shaped signal as there is no loss of generality. Just the periods in the sinusoidal signal will be detected by positive zero-crossings of the signal (inflections crossing the baseline from a negative value to a positive value) while, in the actual real application, the periods on a real ECG signal will be detected by the peaks of R-waves. Despite using a sinus waveform, we will call the simulated signal as as well. For the signal we have used a square waveform as already shown in Figure 2, and now are about to describe the performance of the algorithm on a mix of superposed sinusoidal signals of different frequencies.
Initially we restate:
then from (1):
In a this simulation we will consider:
(Hz) or (bpm) as the average heart rate and
as a heart rate variability signal produced by the sum of two sinusoidal waves with two different amplitudes and two different frequencies. We take the following values for the various parameters:
Hz or bpm, and as modulation width of the two modulating signals, Hz and Hz as the modulation frequencies of the two modulating signals.
With the indicated parameters the simulated ECG signal will have the following expression:
and, solving the integral:
finally:
Thus, the signal is a sinusoidal signal with a sinusoidal periodic variation of its frequency given by the sum of the two sinusoidal frequency modulating signals as in Figure 8.
Before analyzing our method’s performances on actual ECG signals, we present the algorithm’s performances on this complex modulating structure: the sum of two sinusoidal signals used to frequency modulate the sinusoidal carrier.
The sinusoidal carrier with an average frequency of 70.2 bpm is frequency modulated by two sinusoidal signals respectively at 0.19 Hz (11.4 cycles per minute) and 0.32 Hz (19.2 cycles per minute) with modulation depths respectively of 3.6 and 7.2 cycles per minute.
Application of the algorithm on this complex simulated signal, much more resembling the situation to be found in nature, gives the results depicted in Figure 9.
In an attempt to verify to quality of modulation recovery (i.e. the heart rate variability signal) from the simulated heart rate signal, we computed the Fast Fourier Transform (FFT) of the original modulating signal and of the recovered modulation signal. The FFT was computed on the simulation as shown in Figure 9 above thus on the middle and bottom tracings of Figure 9 above. Results are plotted in Figure 10.
6. Analysis of Real ECG Signals Epochs for Appreciation of Ultra-Short-Term HRV
As it was not the purpose of the present work that of analysing ECG signals for HRV estimation, but only to explain a method for doing so, nevertheless we initially tested the algorithm on a few epochs of our own ECG (that of one of the authors). No human subject was used for acquiring ECG tracings but the authors themselves just to show the application of the method on real tracings.
In Figure 11 the ECG of one of the authors (H.K.) was taken while he was busy in an emotional computer game. The idea was to acquire the fast variations of heart rate (if any) during the cognitive and emotional effort of computer gaming. Again, we were only interested in the ECG tracing per se, and no interest was given, at this stage of the research, to the meaning of HRV signals and correlation with the activity of the subject. Further papers will take care of this by using the present algorithm.
There are many different, robust and efficient algorithms for the real-time detection of the R-wave [13]. In this work, we programmed our own software detection based on an adaptive amplitude and time thresholds. The resulting peak finder R-wave detector function was written in MATLAB as follows:


As the underlying scope of our research is that of implementing a method for assessing vagus nerve activity using the heart (heart rate) as a sort of “vagus sensor” with the final ambitious goal of recording “vagus nerve event related activity”, we just tried to preliminary use the method on one of the well-known vagal maneuvers like the Valsalva maneuver. We would like to stress once more the fact that we didn’t perform clinical research on humans, we just used the newly developed algorithm on our own ECG tracings (the ones of the authors) to look at a real HRV signal out of the simulations which permitted us to test the method “in vitro” as explained before.
Methods to stimulate the vagus nerve are well known and clinically assessed. They all go under the name of vagal maneuvers. Most clinically useful are the Valsalva maneuver, the carotid sinus massage, the cold-water immersion, and the eyeball pressure. Effects of these maneuvers are different, but any of them provokes an increase or decrease in heart rate, which is often mediated by a concurrent vagal stimulation.
Valsalva maneuver was chosen as the simplest to qualitatively test our method. It is performed doing a forced expiratory effort against a closed airway and is considered a very low-risk procedure [14].
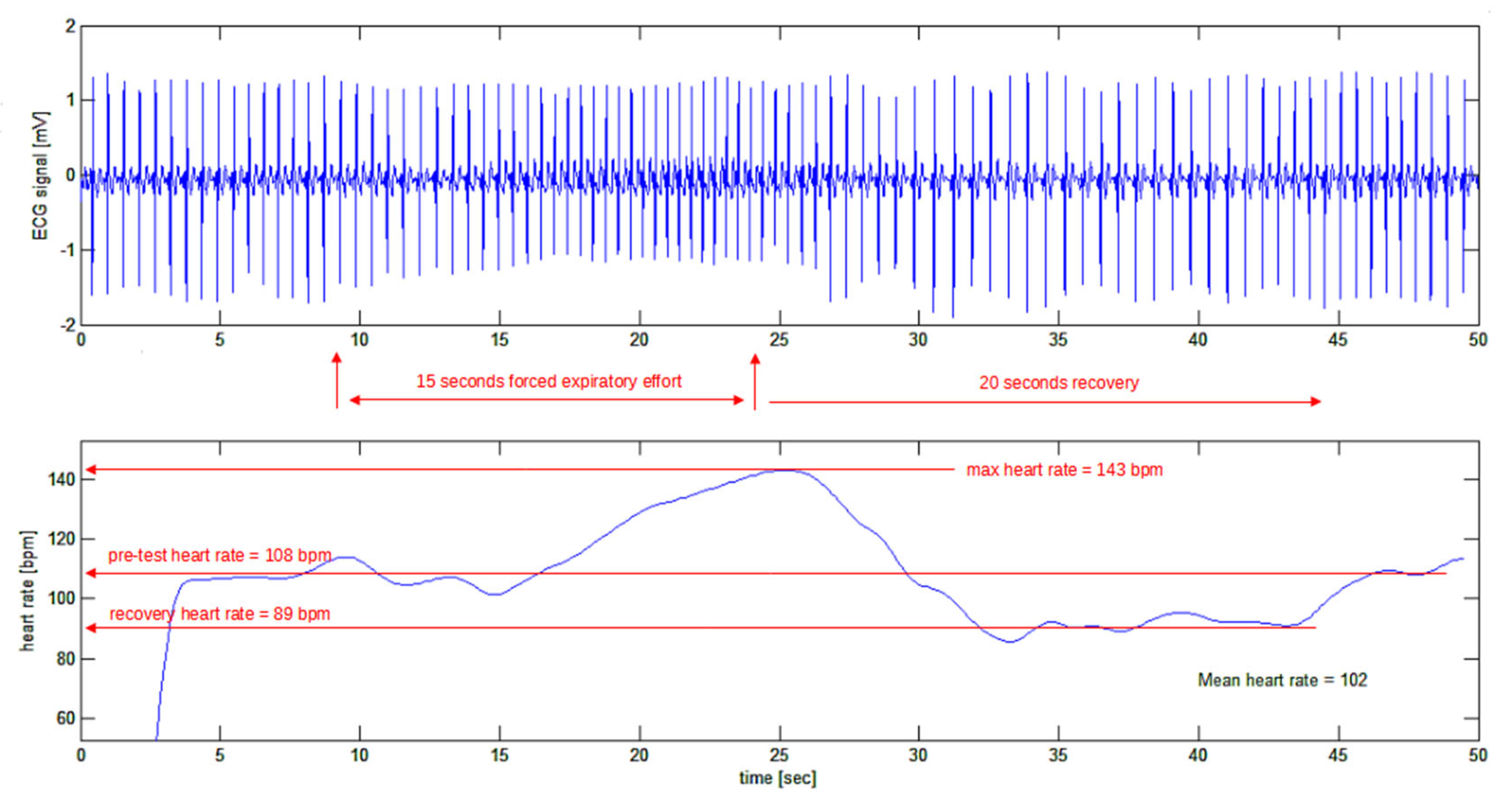
Using a custom made two channels ECG [15], we recorded the ECG tracings. The second channel was used for recording marks for the different phases of the Valsalva maneuver, namely exact beginning and ending times of forceful attempt of exhalation. Then we computed the ECG tracing so obtained using our algorithm and the results are given in Figure 12.
In Figure 12 a typical tracing is shown where the resting heart rate of the subject (one of the authors: H.K.) is 108 bpm. At the end of the force expiratory effort, the heart rate went up to 143 bpm (or 35 bpm above resting value). During the recovery phase the heart rate went down to 89 bpm in just 7 seconds (or 54 bpm down with a negative slew rate of 8 bpm per second) before restoring the resting heart rate to 108 bpm.
7. Conclusions
We have already highlighted the proposed method for HRV signal detection and tested the method extensively on simulated signal and real ECG tracings. Discussion text has been already put in the various paragraphs dealing with the description of the algorithm and its applications. In this place a particular attention should be put on the comparison of our method with others, more conventional, methods of HRV detection. We affirm the superiority of our method as it avoids completely any suspicious activity of resampling or interpolation on the RR periodogram. By the way a form of filtered interpolation is still to be detected in the use of low pass filtering before and after differentiation of the cumulative sum signal.
Nevertheless, the method appears to provide a very clean HRV signal which keep its frequency content even at high frequencies.
The method might also be used on other frequency modulated biomedical signals to extract a reliable modulation signal embedded into them.
Author Contributions
Literature search: All authors; Study design and conceptualization: Enrico M. Staderini and Harish Kambampati; Methodology and software: Enrico M. Staderini and Amith K. Ramakrishnaiah; Validation: Stefano Mugnaini, Sandro Gentili and Andrea Magrini; Writing and original draft preparation: Enrico M. Staderini; Review and editing: Harish Kambampati and Amith K. Ramakrishnaiah; Tables and figures: Enrico M. Staderini; Supervision and project administration: Enrico M. Staderini and Sandro Gentili (Coordinator of Prevention and Rehabilitation Occupational Medicine Laboratory); Funding acquisition and supervision: Andrea Magrini. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Tor Vergata” University of Rome Department of Biomedicine and Prevention – Occupational Medicine Section.
Informed Consent Statement
Actually, this article is not describing a study involving humans as the only real ECG tracings were obtained from the authors themselves for the purpose of rapidly having a signal at hand for testing the algorithm. Not having been real patients in the study, that’s why the consent was waived also considering it as not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
| 1 | Just to recall a basic signal theory concept: the time delay for a FIR filter having N taps (points or coefficients) at a sampling frequency is equal to . |
References
- Carson J.R. Notes on the theory of modulation. Proc. IRE 1922, 10, 57-64. [CrossRef]
- Kuusela, T. Methodological Aspects of Heart Rate Variability Analysis. In Heart Rate Variability (HRV) Signal Analysis. Clinical Applications; Kamath, M.V., Watanabe, M.A., Upton, A.R.M., Eds.; CRCPress: Boca Raton (FL), USA, 2013; pp. 9–42.
- Yamada, M.; Ayabe, M. Treatment of Resampling Frequency and Epoch Length for RR interval in Autonomic Nervous System Analysis. In Proceedings of the 2022 IEEE 4th Global Conference on Life Science and technologies (LifeTech), Osaka, Japan, 7-9 March 2022.
- Cao, P.; Ye, B.; Yang, L.; Lu, F.; Fang, L.; Cai, G.; Su, Q.; Ning, G.; Pan, Q. Preprocessing Unevenly Sampled RR Interval Signals to Enhance Estimation of Heart Rate Deceleration and Acceleration Capacities in Discriminating Chronic Heart Failure Patients from Healthy Controls. Computational and Mathematical Methods in Medicine 2020, 2020, Article ID 9763826. [CrossRef]
- VanderPlas J.T Understanding the Lomb-Scale Periodogram. The Astrophysical Journal Supplement Series 2018, 236:16. [CrossRef]
- Moody, G.B. Spectral Analysis of Heart Rate Without Resampling. In Proceedings of Computers in Cardiology Conference, London, UK, 5-8 September 1993.
- Vollmer, M.; A Robust, Simple and Reliable Mesure of Heart Rate Variability using Relative RR Intervals. Computing in Cardiology 2015, 42, 609-612. [CrossRef]
- Clifford, G.D. Quantifying Errors in Spectral Estimates of HRV Due to Beat Replacement and Resampling. IEEE Transactions on Biomedical Engineering 2005, 52, 630-638. [CrossRef]
- Singh, D.; Vinod, K.; Saxena, S.C. Sampling frequency of the RR interval time series for spectral analysis of heart rate variability. Journal of Medical Engineering & Technology 2004, 28, 263-272. [CrossRef]
- Chakravorty, P. What Is a Signal [Lecture Notes]". IEEE Signal Processing Magazine 2018, 35 (5), 175–177.
- Wolaver, D.H. Phase-Locked Loop Circuit Design; Prentice Hall; 1991; p. 211.
- Holoborodko, P. Smooth Noise Robust Differentiators. Available online: http://www.holoborodko.com/pavel/numerical-methods/numerical-derivative/smooth-low-noise-differentiators/ (accessed on 14 December 2022).
- Yadav, A.; Grover, N. A Review of R Peak Detection Techniques of Electrocardiogram (ECG). Journal of Engineering and Technology, 2017, 8.
- Pstras, L.; Thomaseth, K.; Waniewski, J.; Balzani, I.; Bellavere, F. The Valsalva manoeuvre: physiology and clinical examples. Acta Physiol, 2015. [CrossRef]
- Staderini, E.M.; Mugnaini, S.; Kambampati, H.; Magrini, A.; Gentili, S. Improved Multichannel Electromyograph Using Off-the-Shelf Components for Education and Research. Sensors, 2022, 10, 3616. [CrossRef]
Figure 1.
Abstract and almost black box model of the heart rate variability signal as a heart rate frequency modulator. A: a black box model of any physiologic factor (R pulses rate modulator shown upper left) is blindly considered to impose a certain discharge frequency on the cells in the sinus node which provide an electrical sinus node signal which propagate in the heart and eventually it will be responsible to produce an electrical signal recorded on the skin of the subject. An external R-wave detector produces a signal which is zero at any instant of time but when an R-wave is detected at which instant its value is set to one (detected R pulse). B: the R pulses rate modulator is now black box modelled as a R pulses rate variability signal generator producing a signal which is equal to the variation of the heart rate (over the average) at each instant of time , this signal is then summed to a constant value representing the average heart rate in the considered epoch, to produce a signal which is equal to the heart rate at each instant of time . All the time domain signals indicated in the figure are assumed to be continuous in time.
Figure 1.
Abstract and almost black box model of the heart rate variability signal as a heart rate frequency modulator. A: a black box model of any physiologic factor (R pulses rate modulator shown upper left) is blindly considered to impose a certain discharge frequency on the cells in the sinus node which provide an electrical sinus node signal which propagate in the heart and eventually it will be responsible to produce an electrical signal recorded on the skin of the subject. An external R-wave detector produces a signal which is zero at any instant of time but when an R-wave is detected at which instant its value is set to one (detected R pulse). B: the R pulses rate modulator is now black box modelled as a R pulses rate variability signal generator producing a signal which is equal to the variation of the heart rate (over the average) at each instant of time , this signal is then summed to a constant value representing the average heart rate in the considered epoch, to produce a signal which is equal to the heart rate at each instant of time . All the time domain signals indicated in the figure are assumed to be continuous in time.

Figure 2.
Upper tracing: the simulation of an artificial instantaneous “heart rate signal”, or
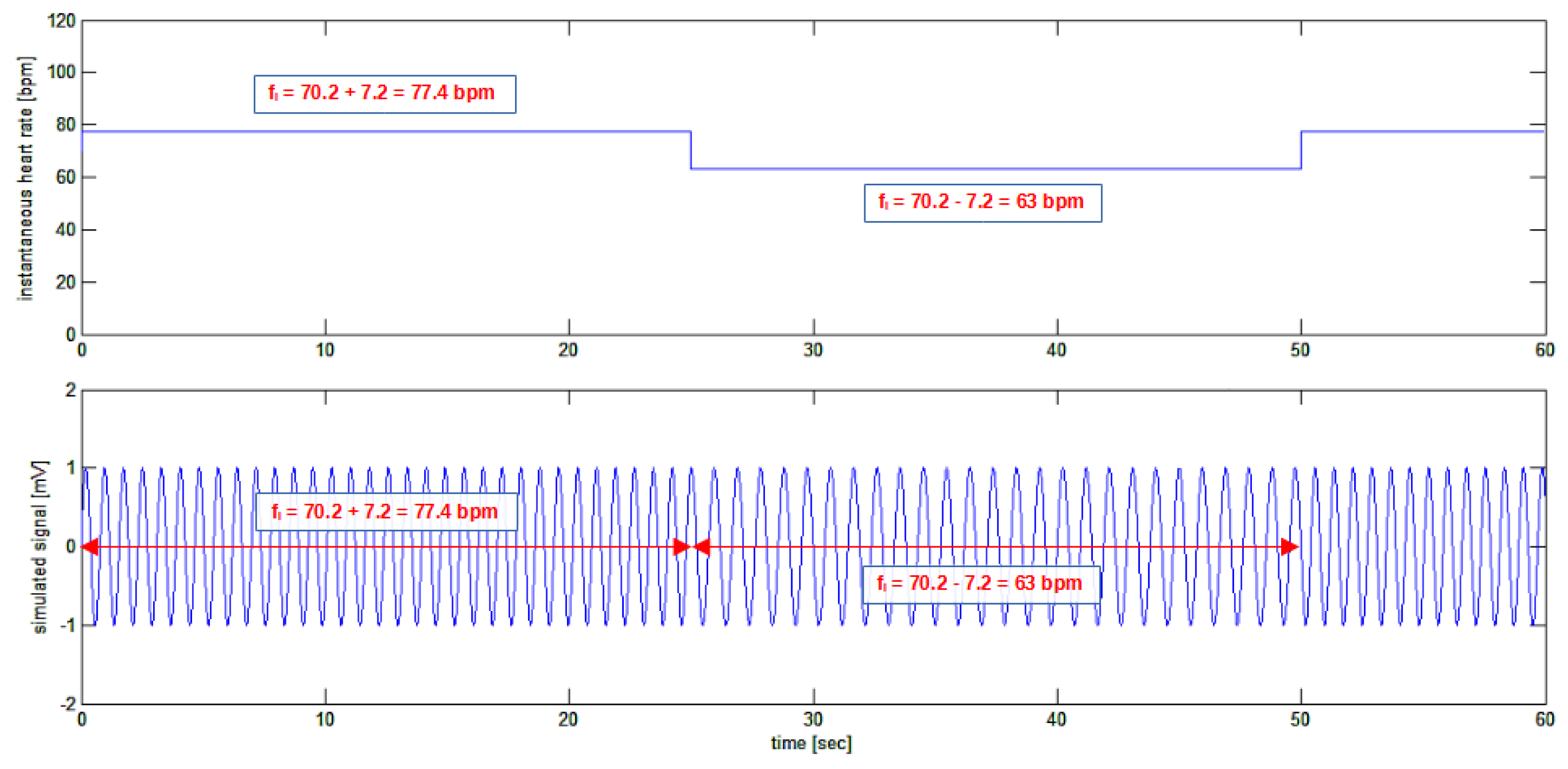
Figure 3.
Upper tracing shows frequency modulated signal with the square-wave modulating signal superposed in red. Zero-crossing detection points (red) on the signal ECG1(t) are shown in the middle tracing. Bottom tracing shows the created SR(t) signal with a slope depending on the local instantaneous frequency of the simulated ECG1(t) signal.
Figure 3.
Upper tracing shows frequency modulated signal with the square-wave modulating signal superposed in red. Zero-crossing detection points (red) on the signal ECG1(t) are shown in the middle tracing. Bottom tracing shows the created SR(t) signal with a slope depending on the local instantaneous frequency of the simulated ECG1(t) signal.
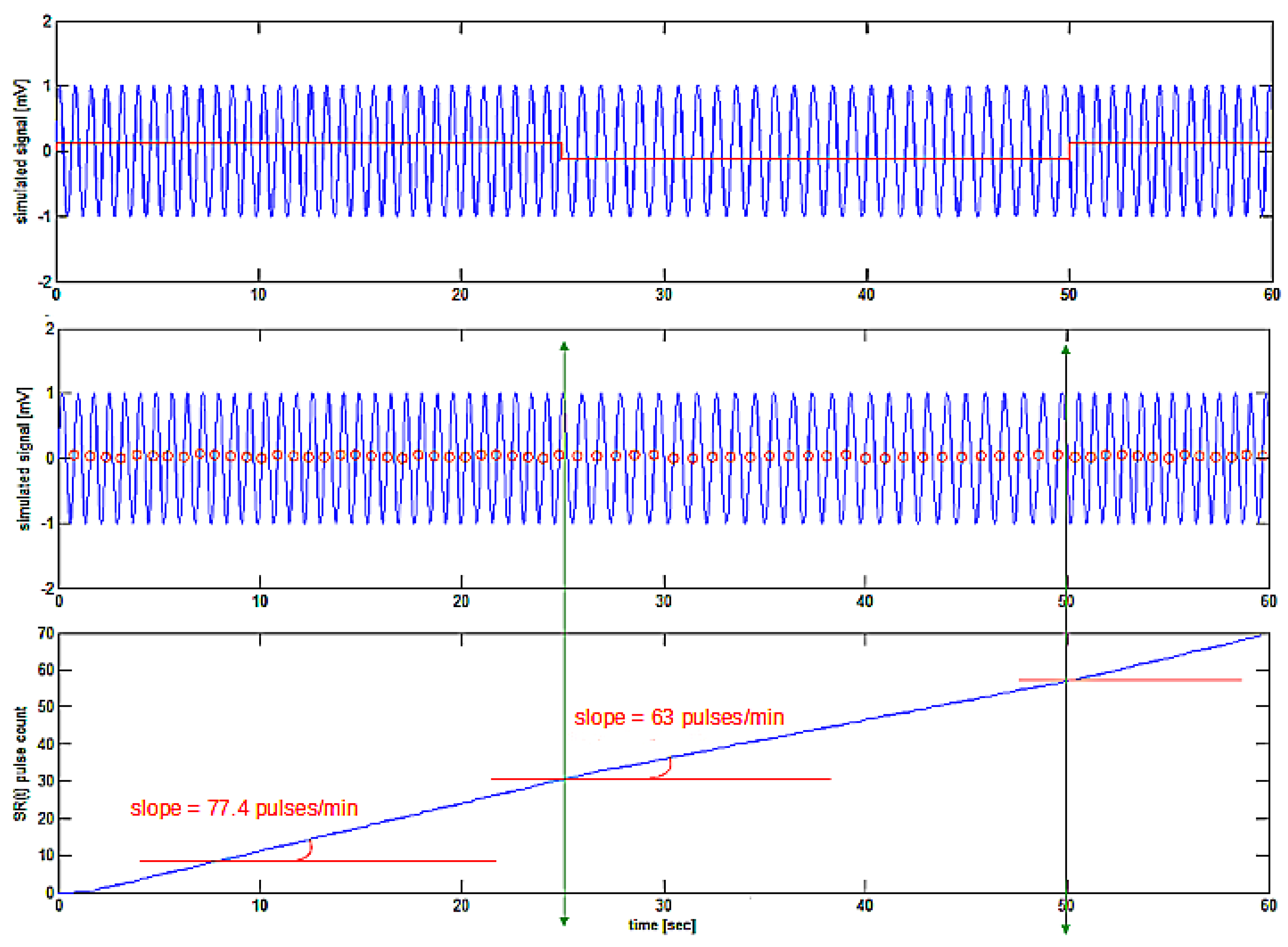
Figure 4.
Magnitude Bode plot of the moving average filter applied to the cumulative sum signal.
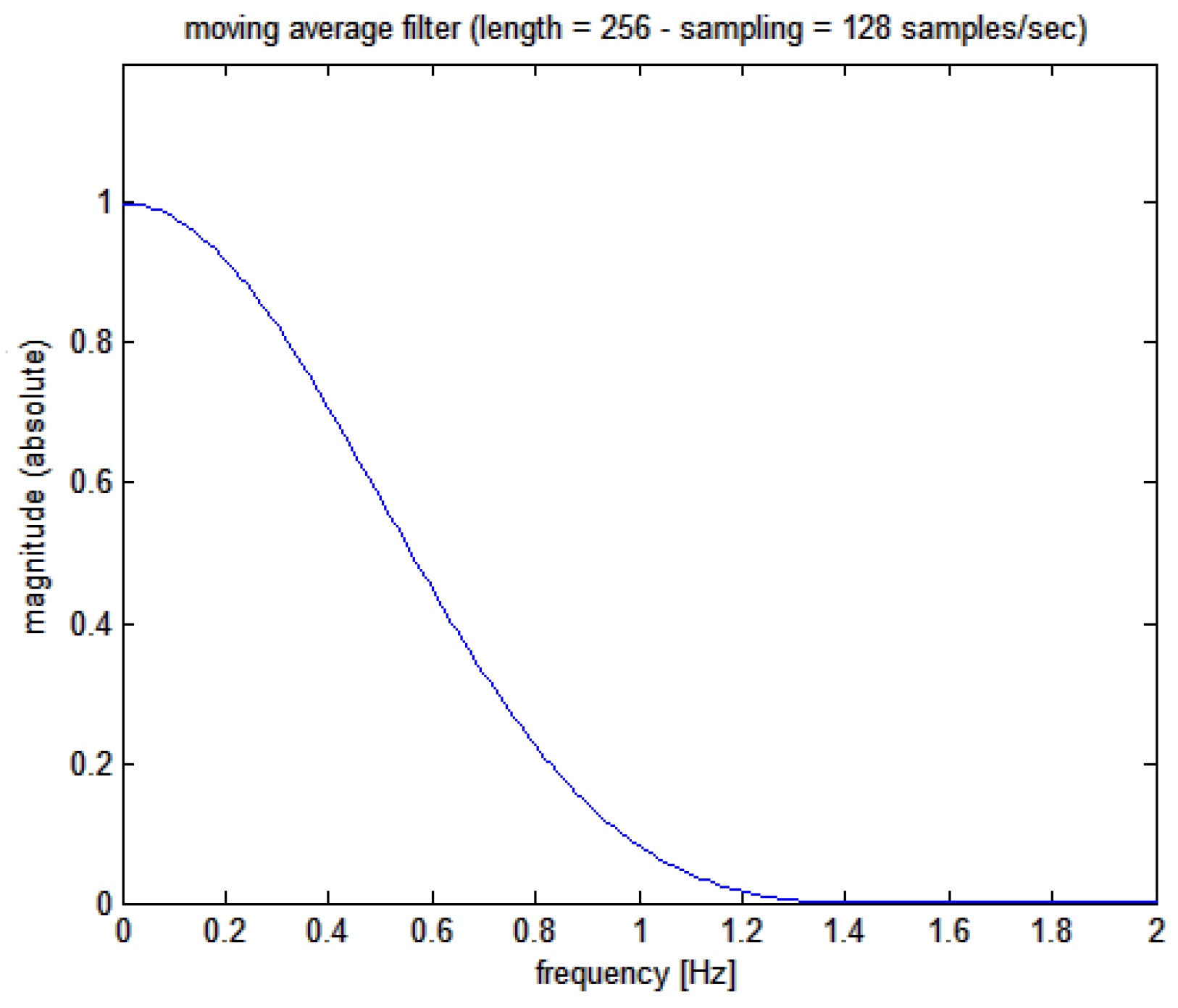
Figure 5.
Magnitude Bode plot of the Holoborodko’s differentiating filter applied to the cumulative sum signal. Please note the differentiating behavior at low frequencies thanks to the almost straight line of the graph (output linearly proportional of the frequency of the input signal).
Figure 5.
Magnitude Bode plot of the Holoborodko’s differentiating filter applied to the cumulative sum signal. Please note the differentiating behavior at low frequencies thanks to the almost straight line of the graph (output linearly proportional of the frequency of the input signal).
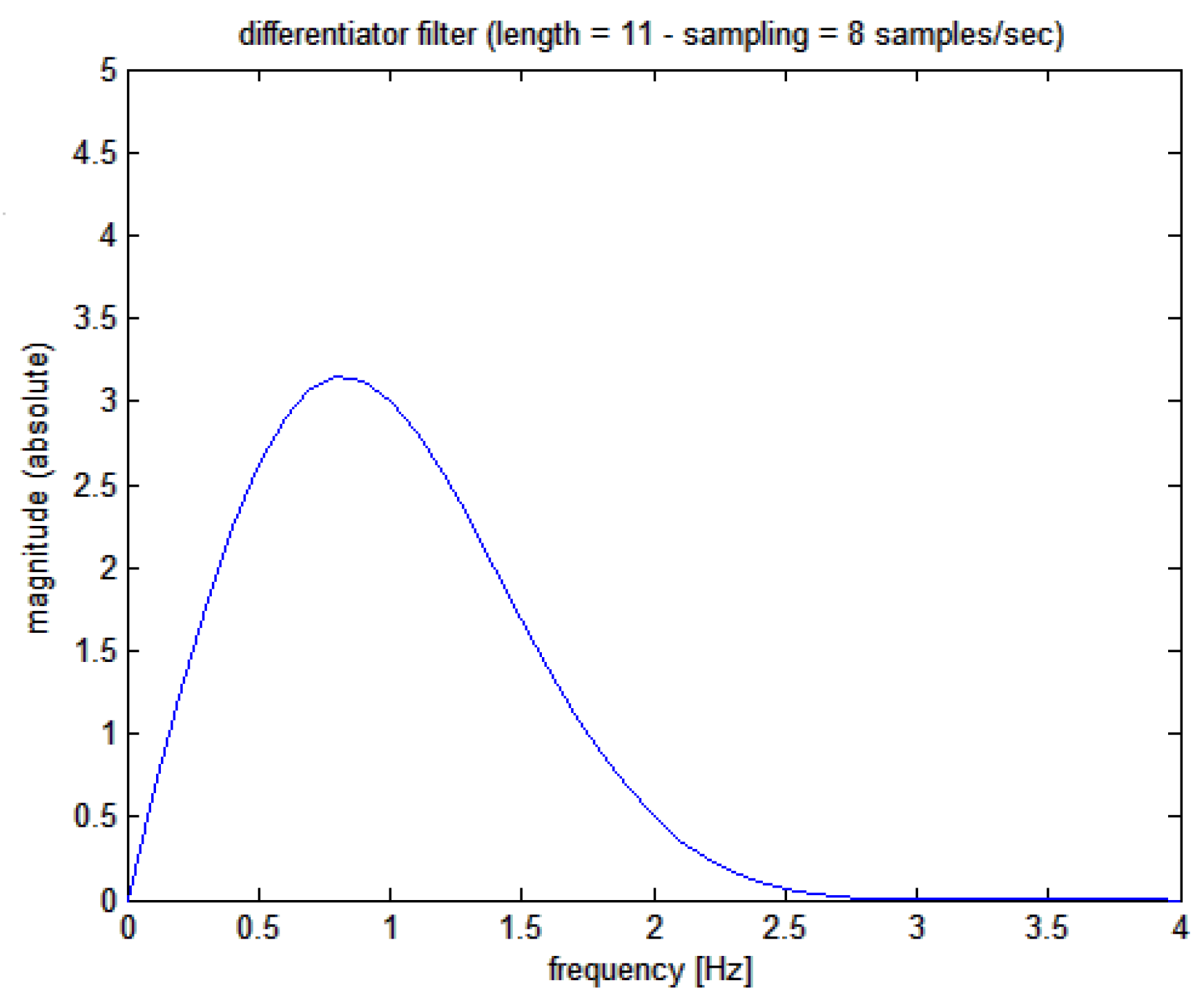
Figure 6.
Magnitude Bode plot of the moving average filter applied to the recovered first derivative signal or the heart rate signal.
Figure 6.
Magnitude Bode plot of the moving average filter applied to the recovered first derivative signal or the heart rate signal.
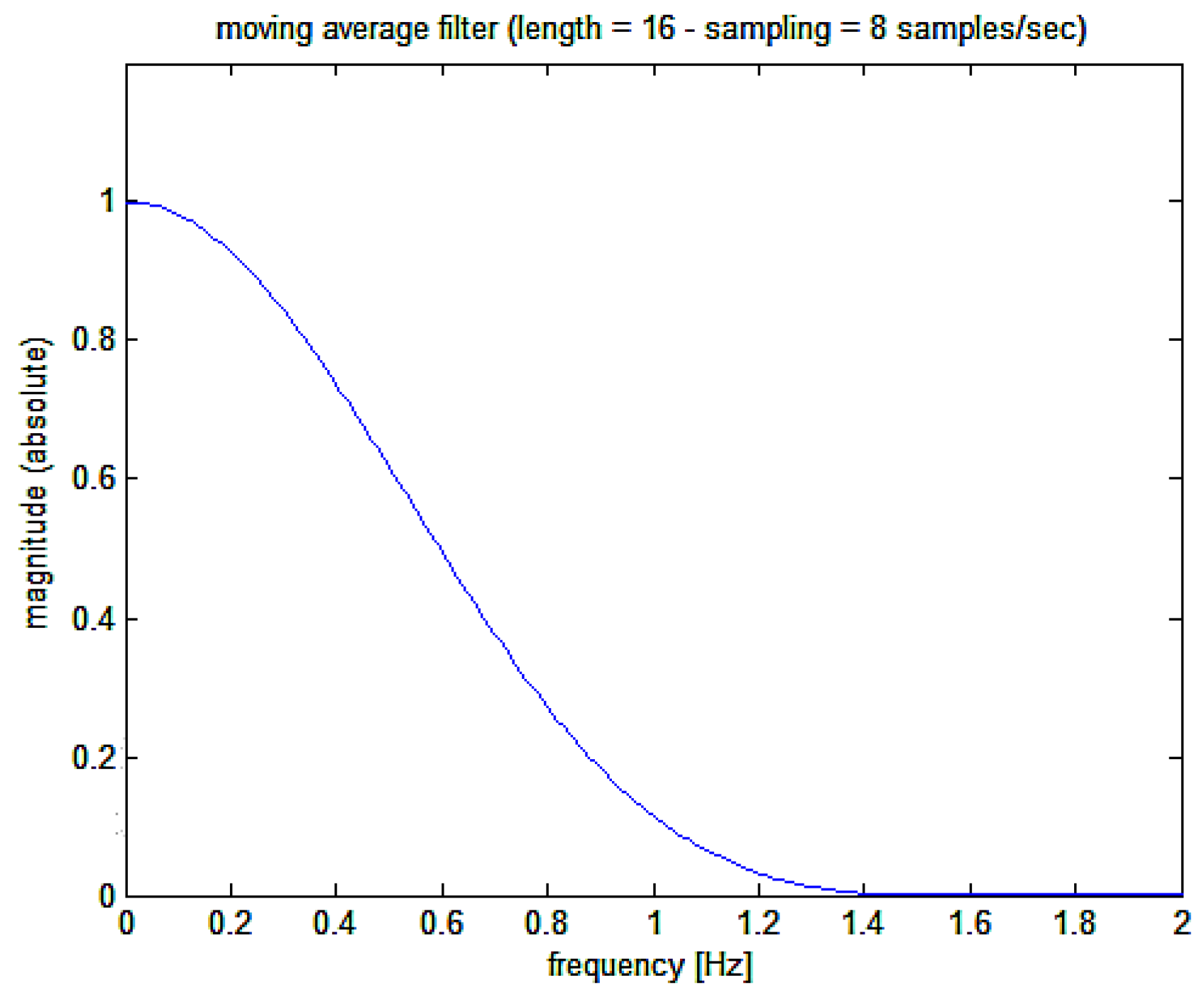
Figure 7.
Bottom tracing: the recovered heart rate signal. The 2.5 seconds delay of the recovered signal corresponds to the delays expected from the sequence of FIR filters.
Figure 7.
Bottom tracing: the recovered heart rate signal. The 2.5 seconds delay of the recovered signal corresponds to the delays expected from the sequence of FIR filters.
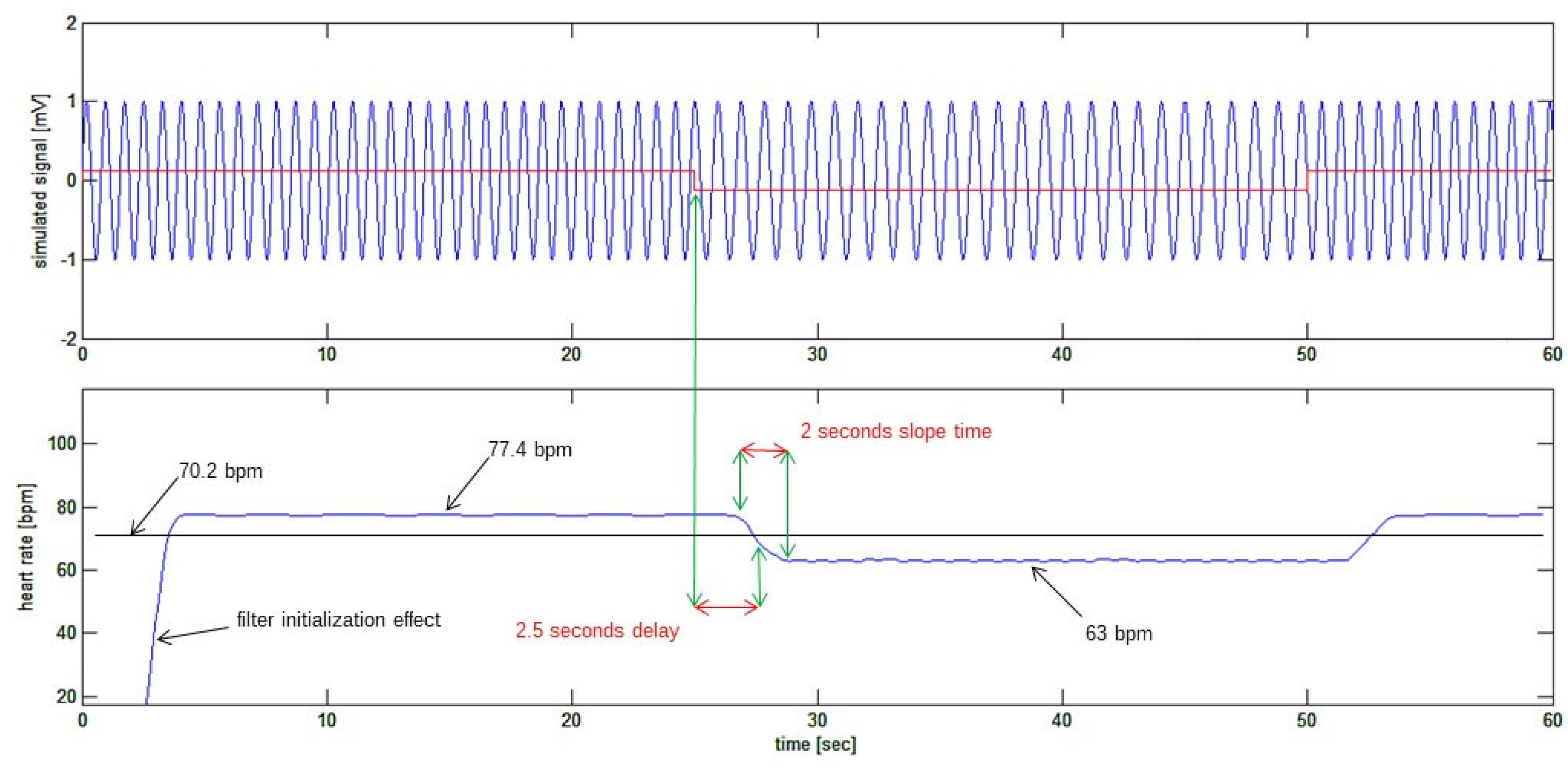
Figure 8.
Simulation of test signal : a sinusoidal signal (bottom tracing) which is frequency modulated with the sum of two sinusoidal waves (shown separately on upper tracing) producing a final modulating signal around the average frequency of 70.2 bpm (middle tracing).
Figure 8.
Simulation of test signal : a sinusoidal signal (bottom tracing) which is frequency modulated with the sum of two sinusoidal waves (shown separately on upper tracing) producing a final modulating signal around the average frequency of 70.2 bpm (middle tracing).
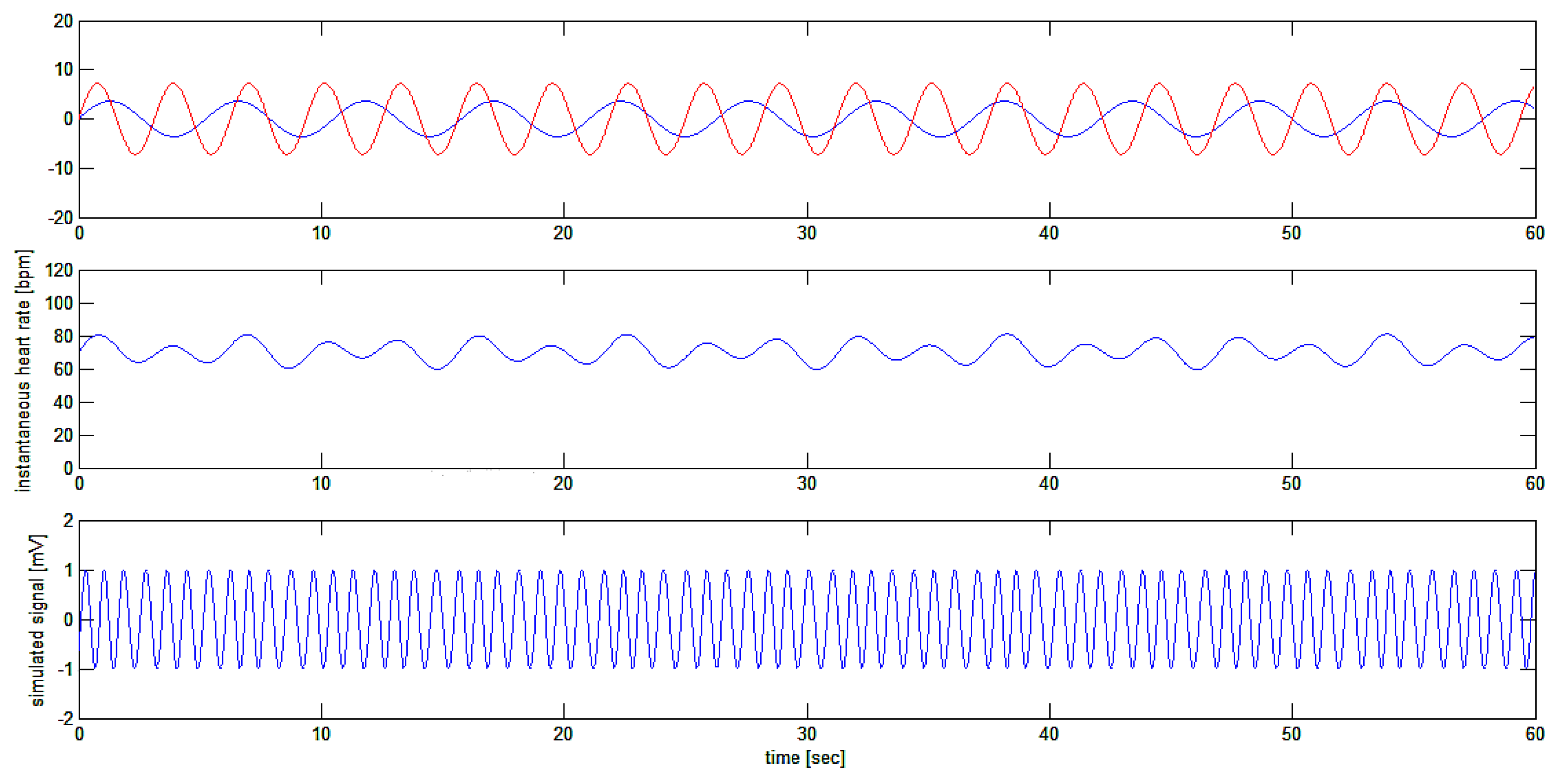
Figure 9.
Upper tracing: frequency modulated signal and modulating signal. Bottom tracing: the recovered heart rate signal. Middle tracing represents the modulating waveform (cfr. Figure 8).
Figure 9.
Upper tracing: frequency modulated signal and modulating signal. Bottom tracing: the recovered heart rate signal. Middle tracing represents the modulating waveform (cfr. Figure 8).
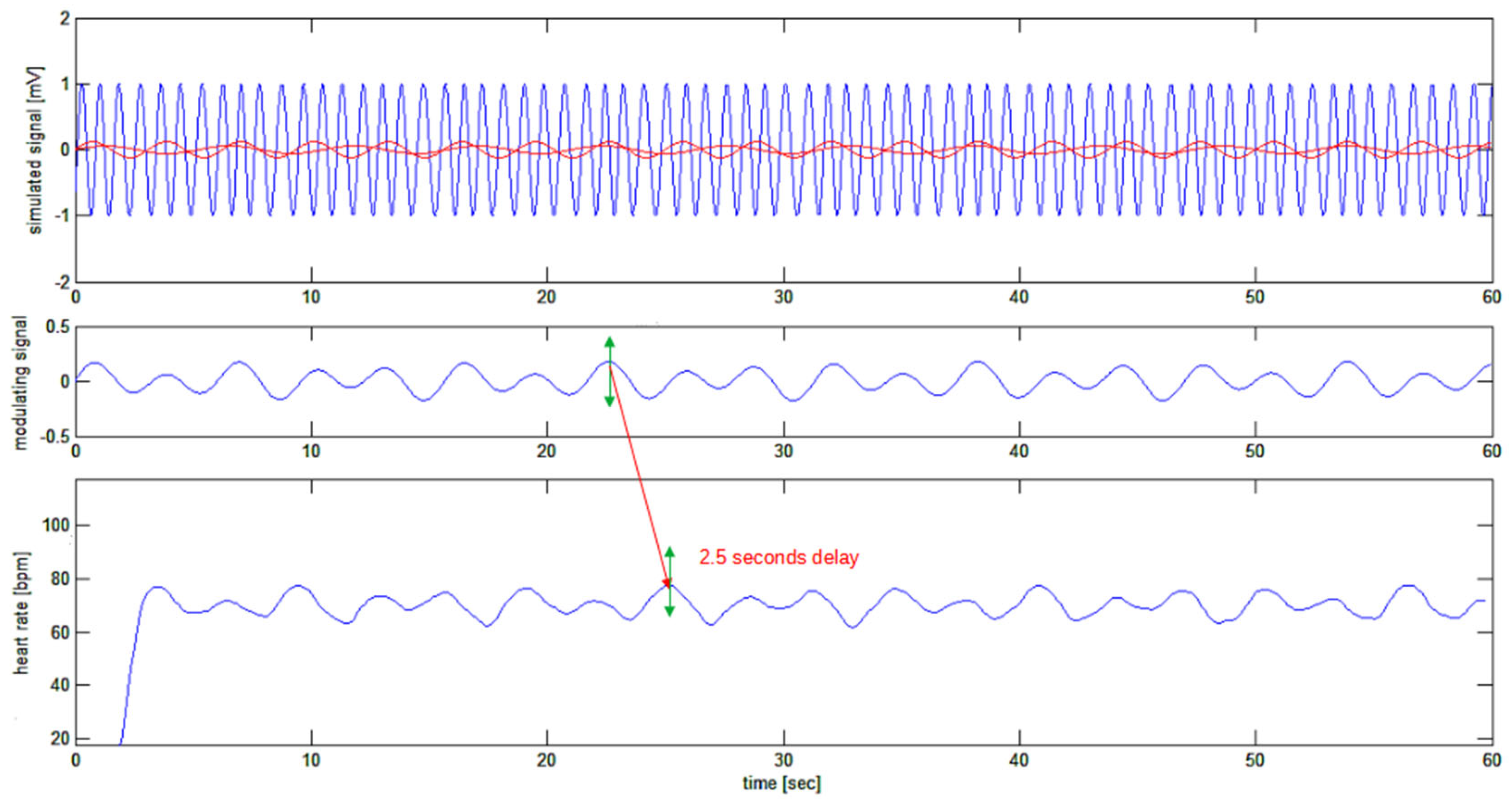
Figure 10.
Comparison of modulating and recovered simulation signals in the time and frequency domains. HRV frequencies are perfectly recovered. Different amplitudes of signals in the time domain come from changing the scale from beats per second to beats per minute. Different amplitudes in the frequency domain are also due to the windowing effect (a Blackman-Harris window was used before FFT calculation).
Figure 10.
Comparison of modulating and recovered simulation signals in the time and frequency domains. HRV frequencies are perfectly recovered. Different amplitudes of signals in the time domain come from changing the scale from beats per second to beats per minute. Different amplitudes in the frequency domain are also due to the windowing effect (a Blackman-Harris window was used before FFT calculation).
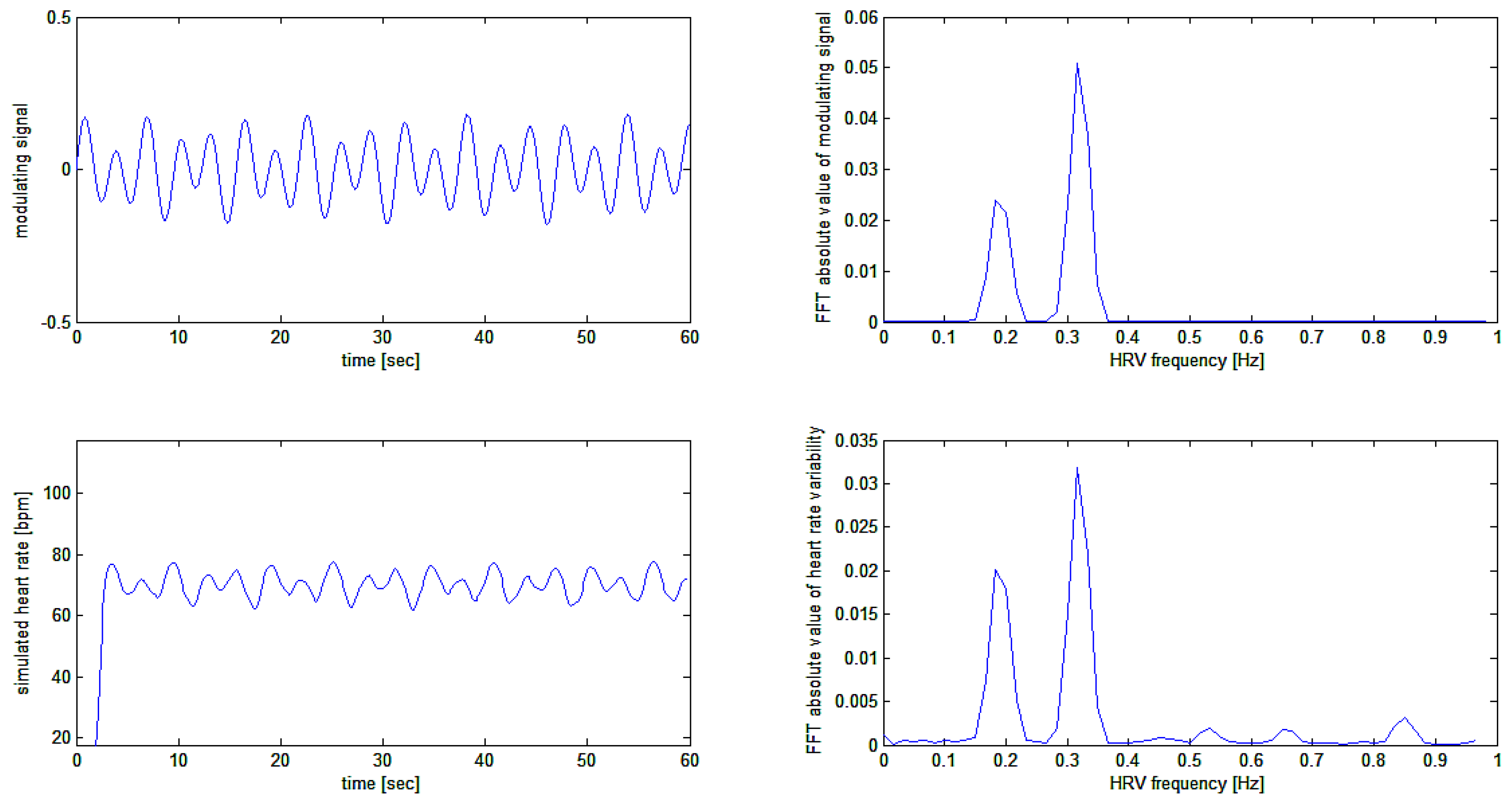
Figure 11.
First test of the algorithm on a real ECG tracing (top tracing). In the second tracing from the top, ECG R-waves are indicated as detected. In the third tracing the cumulative summing signal is shown and in the bottom trace, the filtered first derivative of the latter is plotted showing fast variations of the heart rate during the subject’s activity.
Figure 11.
First test of the algorithm on a real ECG tracing (top tracing). In the second tracing from the top, ECG R-waves are indicated as detected. In the third tracing the cumulative summing signal is shown and in the bottom trace, the filtered first derivative of the latter is plotted showing fast variations of the heart rate during the subject’s activity.
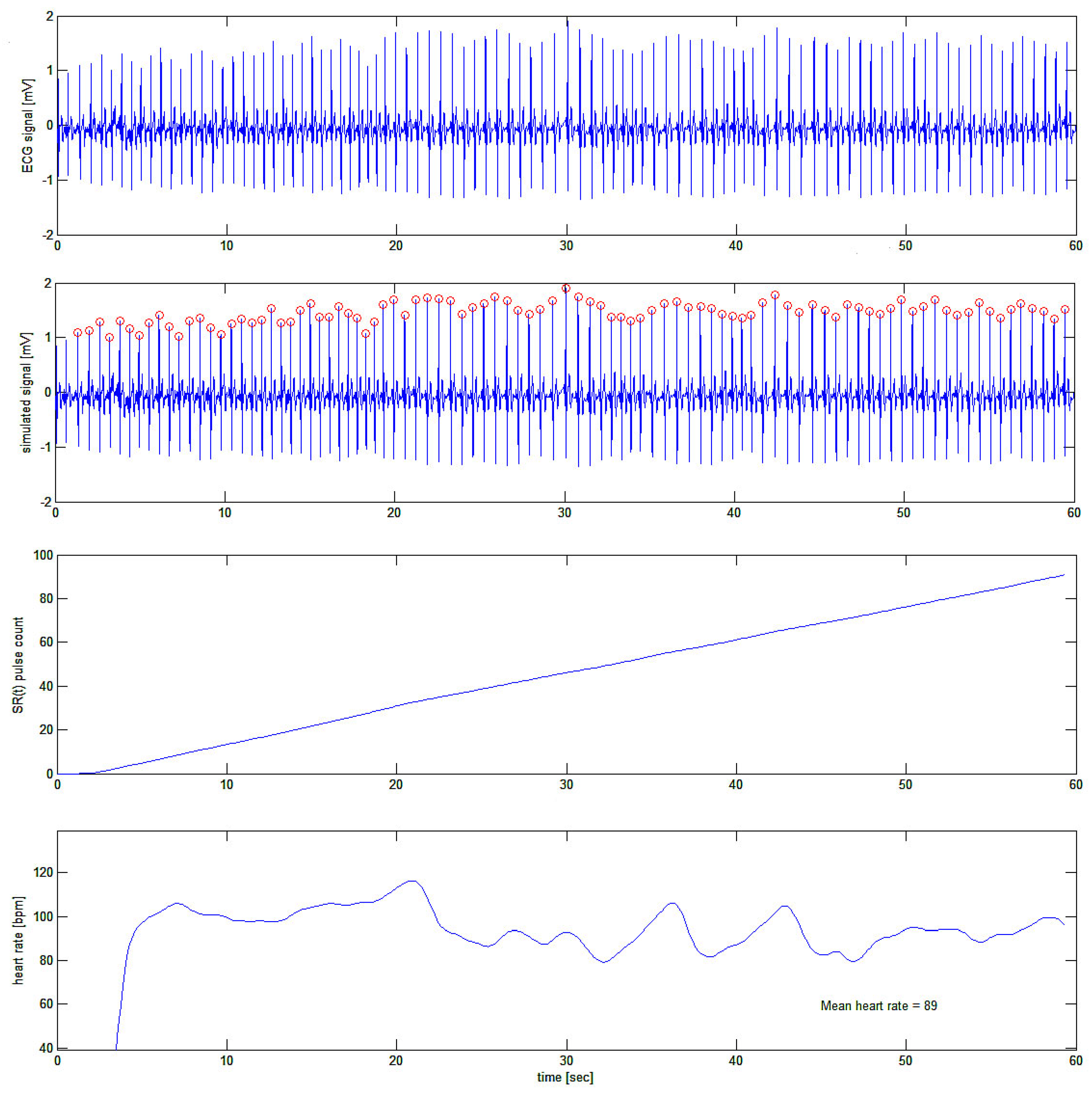
Figure 12.
Test of the algorithm on a real ECG tracing (top tracing) during the Valsalva manoeuvre.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






