Atmospheric CO2 Two Box Model Accurately Tracks 14C and 13C without Requiring the "Revelle Isotopic Anomaly"

Preprint

Article

Atmospheric CO2 Two Box Model Accurately Tracks 14C and 13C without Requiring the "Revelle Isotopic Anomaly"

Altmetrics

Downloads

280

Views

125

Comments

Stephen Taylor^*

This version is not peer-reviewed

This preprints belongs to the Topic

Climate Change and Environmental Sustainability, 2nd Edition

Submitted:

17 January 2023

Posted:

17 January 2023

You are already at the latest version

Alerts

Abstract

Although total nett CO₂atmospheric flow can be estimated with reasonable accuracy, the contributing gross fluxes between the atmosphere and the earth's surface are poorly understood. This paper presents a method, driven by the objective of simplicity, by which the global outflow and inflow of CO₂between atmosphere and a globally equivalent "mixing reservoir" can be estimated, using the isotopes ¹⁴C and ¹³C as tracers. It has been asserted that the isotopic carbon in CO₂ cannot be directly used as a tracer in flow studies because it is not subject to the Revelle factor. Evidence is provided showing that this view is mistaken. The model contains 7 key parameters which are used to create synthetic records of Δ¹⁴C and d¹³C spanning 200 years or more, including during the period of atmospheric weapons testing and its decay known as the "bomb pulse". By optimising the fit between these computed values and the historical records of d¹³C and Δ¹⁴C, all seven key parameters are determined. The effective "mixing reservoir" is thereby determined to have a size around six times that of the atmosphere, with global outflux rising from 39.7 GTC yr-1 in 1750 to 58.9 GTC/yr in 2020, this figure probably not including annually cycled carbon.

Keywords:

Subject: Environmental and Earth Sciences - Atmospheric Science and Meteorology

Environmental Significance

An accurate estimate of the flux between the atmospheric and sequestered CO₂ is important as it is key to our understanding of the carbon-cycle. However, estimates of these fluxes have large uncertainties. This paper describes a method of calculating the atmospheric CO₂ flux by using the historical variations of ¹⁴CO₂ and ¹³CO₂ for calibration, challenging the view that such studies cannot be carried out because of a supposed anomalous isotopic effect. It also provides a new estimate of the fossil fuel airborne fraction and the accumulation of carbon inventory.

Introduction

The components of global CO₂ flux between the atmosphere and the earth's surface are imprecisely known, with considerable uncertainties in their estimation. According to the Global Carbon Budget (GCB), CO₂ atmospheric growth is known to within 0.4%, the uncertainty in fossil fuel emissions are an order of magnitude greater at 5% while uncertainty in sink rates range from 14% to 20% for ocean and 21% for land, with the figure for equivalent emissions from land-use change being higher still at 29% to 50% (Friedlingstein et al. 2021). Yet this uncertainty is dwarfed by the uncertainty in gross flows, reported by IPCC as being more than 50% for both ocean and land (Ciais 2013). Although this level of uncertainty is surprising, it should be remembered that many useful experimental techniques are not available to climate scientists, including the use of a control experiment, or the ability to apply external stimuli in the form of periodic functions, step functions or spikes (the Heavyside and Dirac functions) to examine the system response. Therefore a reliance on models has evolved with over 35 recently being listed by IPCC, being categorised as Earth System Models (ESM) and coupled General Circulation Models (GCMs). Canadell reports that there is a "wide range of model responses", and "disagreement between models....in the relative contribution of land and ocean fluxes", with significant variation between model predictions being reported (Canadell et al. 2021). Furthermore, with many models there is a need for tuning (Flato et al 2013), there is the possibility of overfitting (Bindoff et al. 2013) and the fundamental question has also been raised of whether complexity rather than simplicity can ever contribute to our understanding (Paola et al. 2011). This paper bucks the trend towards micro-modelling and complexity. Its fundamental guiding principle is to find the simplest solution which best fits historical measurements. We describe, after consideration of a number of different models, a model which combines simplicity with an excellent quality of fit; a 7 parameter model of global CO₂ outflow and inflow using Dalton's mixing laws (i.e. paint) to calculate values of ¹⁴CO₂ and ¹³CO₂. The model indicates a rising influx of CO₂ from an internal reservoir. Such variations are known to have occurred during the deglaciation between 16ka and 12ka, when changes in global temperature accompanied century-scale variations in CO₂ and δ¹³C (Bauska et al. 2014, Bengtson et al 2020, Marcott et al. 2014). Therefore changes in nett CO₂ flux should not be disregarded, especially when accompanied by a significant global temperature change, such as is recently becoming apparent. Throughout this document the phrases "atmospheric mixing ratio" and "atmospheric CO₂ level" are used interchangeably, while the term CO2ff refers to the anthropogenic fossil fuel CO₂ emissions. The calculations are provided in the form of a working Excel Spreadsheet. Our analysis critically relies upon the variation of atmospheric ¹⁴CO₂ and ¹³CO₂ over the past 200 years, hence a brief historical perspective of atmospheric radiocarbon is now provided.

Radiocarbon Summary

The most abundant isotope of atmospheric carbon is the stable form ¹²C, while around 1 percent is the non-radioactive isotope ¹³C and around 1 part in 10¹² is the radioactive isotope ¹⁴C. Samples of wood, charcoal etc, provide an historical record of the atmospheric concentration of ¹⁴C and ¹³C, as carbon becomes embedded in the sample (Stenström 2011). However ¹⁴C and ¹³C exhibit very different properties; ¹⁴C undergoes radioactive decay with a half-life of 5700 ± 30 years (Kutschera 2013), while ¹³C is radioactively stable. Fossil fuels, being hundreds of millions of years old, contain virtually no ¹⁴C as it has already radioactively decayed. The combustion of fossil fuels therefore releases virtually no ¹⁴CO₂ into the atmosphere, thus diluting the ¹⁴C atmospheric concentration; a process known as the "Suess Effect" (Suess 1955). Stuiver & Quay (1981) confirmed the "Suess Effect", using ¹⁴C in archived tree-ring samples, but found it was only 32% of the expected value, a margin they called the "¹⁴CO₂/CO₂ attenuation factor" because "part of the radiocarbon deficit is stored in the oceans and biosphere". By contrast with ¹⁴C, the content of ¹³C in fossil fuels is just a few percent below background levels of ¹³C. This reduction is not due to radioactive decay but is caused by fractionation, arising because ¹³C atoms are slightly larger and heavier than ¹²C, and their corresponding reaction rates are slightly slower. During the conversion of atmospheric CO₂ to carbon within the sample, fractionation reduces the relative presence of ¹⁴C and ¹³C. Therefore, when fossil-fuel combustion adds CO₂ to the atmosphere, the ¹³C concentration falls because fossil fuels contain a lower concentration of ¹³C, in a similar but much less pronounced way than that for ¹⁴C. The ¹³C/C ratio is written as δ¹³C which incorporates an offset scale so that zero corresponds approximately the background level. Before 1900 δ¹³C remained remarkably constant over the previous 10,000 years, maintaining its value to within ± 0.1‰ (Bengston 2020). However, since 1900 δ¹³C has fallen sharply; by approximately 2‰. Similarly the ¹⁴C/C ratio is written as Δ¹⁴C which in addition to using an offset scale also incorporates the corrections for decay and fractionation so that comparison can be made across different ages. Δ¹⁴C has been less stable, falling on average by around 2‰ per century over the past 10,000 years, occasionally falling by 8‰ in one century (IntCal20). However, its fall between 1900 and 1950 is much steeper, being 25‰ in only 50 years. Thus δ¹³C and Δ¹⁴C both show exceptional falls since 1900. For ¹⁴CO₂ since 1950 the picture is even more complex, because of the creation of ¹⁴CO₂ in atomic weapons atmospheric tests. The decay of this "bomb pulse" (Figure 3) was initially exponential. By 2020, although the atmospheric ¹⁴C level was dipping below its pre-bomb value approximating zero, it continued to fall rather than levelling off. However calculation of Suess dilution suggested its rate of fall should be even quicker, with a theoretical reduction rate due to CO2ff dilution alone as 12-14‰ per year this being "partially compensated by ¹⁴CO₂ release from the biosphere, industrial ¹⁴CO₂ emissions and natural ¹⁴C production." (Levin 2009). Similarly, calculations of the Suess dilution for ¹³CO₂ show that it too should be falling more steeply than its measured value (see Appendix D). Thus both the fall of Δ¹⁴C and δ¹³C exhibit a dilution discrepancy, which this paper explains is due to the inflow of heavier isotopic gas back from the reservoir (ocean and land) mixing with the lighter isotopic gas inflow from fossil fuels CO2ff. The reader may be interested to note that while Δ¹⁴C continues to fall, the absolute atmospheric content of ¹⁴C has recently begun to increase (Svetlik 2010), reflecting the general atmospheric increase in CO₂.

Revelle Isotopic Anomaly

When atmospheric CO₂ dissolves in sea-water, the relative increase in dissolved inorganic carbon (DIC) is approximately only one tenth of the relative increase in dissolved CO₂, this factor being known as the Revelle factor, and being due to buffering by CO₃^2- ions. (Zeeb and Wolf 2001) When the CO₂ is partially isotopic carbon, an equilibrium is reached where the ratio of the two isotopic partial pressures match the inverse ratio of the fractionation factors (Appendix Equation (A7)). Although the fractionation factor for photosynthesis is approximately 0.98, the seawater fractionation factors are even closer to unity, so close as to be irrelevant (Bolin and Eriksson 1959). Irrespective of this, it has been asserted that analysis of the decay of the "¹⁴C bomb pulse" cannot be used to calculate atmospheric CO₂ flux because "bomb radiocarbon and anthropogenic CO₂ do not behave identically.....the equilibration time is about ten times longer for ¹⁴C than it is for anthropogenic CO₂" (Joos 1994) and more recently "The Revelle factor does not apply to isotopic equilibration because a ¹²CO₂ molecule is replaced by a ¹³CO₂ or vice versa. As a result, an isotopic anomaly disappears from the atmosphere more quickly than a total CO₂ anomaly." Tans 2022. The assertion of the existence of such a large difference in the behaviour of an isotope compared to its non-radioactive form is unusual, apparently originating from a mathematical derivation published by Tans (Tans 1993 Equation (16)). The assertion has been widely repeated (Ciais et al 1995, Harvey 2000, Tans 2022). The author contends that the notion arose because of an approximation in Tans’ calculation which in some cases is unjustified, and which gave rise to a misinterpretation (Appendix A). In 1959 Bolin and Eriksson published CO₂ flux calculations where both the Revelle factor and Suess effect were derived by consideration of isotopic flow at the seawater-atmosphere boundary. They did not make the same claim regarding unfettered anomalous isotopic diffusion. Furthermore, regarding fractionation they stated "The deviation of μ from unity will be completely irrelevant in the following discussion. We shall ... thus neglect fractionation." This approach was adopted in the model described here. Fractionation rates have been set to unity, and the mistaken Isotopic Revelle Anomaly is not included.

CO₂ Finite Reserve Model

The CO₂ Finite Reserve Model (CFR) is a two box model describing CO₂ fluxes between the atmosphere and a finite mixing reservoir, based upon 7 solution parameters, these being determined by curve fit to measured δ¹³C and Δ¹⁴C values, with the following assumptions.

There is a continuous CO₂ outflow A_OUT, from the atmosphere to a global carbon mixing reservoir, the flow being proportional to the CO₂ atmospheric level, A_CO2, as listed (Data Ref 1,2). The constant of proportionality is the inverse turnover time, T (IPCC 2013 Glossary); it determines the initial rate of fall of the 14C bomb pulse, (Figures 2 and 3), and is a solution parameter.
Carbon is returned to the atmosphere from the reservoir via an inflow of CO₂. The amount returned, A_IN, is calculated by "balancing the budget" of outflow with the known atmospheric growth of CO₂, Δ(A_CO2) and fossil fuel emissions input A_FF, as shown in Figure 1. CO₂ inflow from a reservoir in which atmospheric CO₂ has previously accumulated hinders the fall in value of ¹⁴C. Hence it predominantly determines the shape of the tail of the ¹⁴C bomb pulse, the rate of fall of δ¹³C, and recent δ¹³C levels, see Figure 3, Figure 4 and Figure 5. Note that some inflows are roughly independent of atmospheric CO₂ level (e.g., fire / respiration) while others may be dependant upon pressure difference (e.g., oceanic flux). Both types of inflow are computed within this balanced budget method. The relative reservoir size, R_CO2, is a solution parameter.
Total fossil fuel emissions inflows (CO2_FF) are derived from known listings (Data Ref 3). A portion of the inflow, as described by an Airborne Factor, A_F, is directly mixed into the atmosphere, while the remaining portion (1-A_F) is absorbed directly by the reservoir. This does not imply the absorption is instantaneous, because each cycle is annual. A_F is a solution parameter. It predominantly determines the shape of the tail of the ¹⁴C bomb pulse, the rate of fall of δ¹³C, and recent δ¹³C levels Figure 3, Figure 4 and Figure 5.
Inflow of ¹⁴CO₂ from known listed atmospheric atomic weapon detonations B₁₄, (Data Ref 5) are assumed to be linearly related to the bomb yield. The conversion factor Y_b (¹⁴C [in 1820 background units] per megaton) is a solution parameter. It has the main effect of scaling the bomb pulse portion of the graph after 1960, Figure 3.
Isotopic ¹³C and ¹⁴C concentrations are calculated using Dalton’s mixing laws, see Appendix B. Fractionation is considered negligible at the reservoir-atmosphere boundary so fractionation factors are implicitly unity. The isotopic equilibrium is identical for ¹³C ,¹⁴C and ¹²C hence there is no Revelle exception. In accounting for isotopic concentration, it is not necessary to explicitly embed Stuiver's attenuation factor, Suess dilution or a general Revelle factor (see Radiocarbon above), because they are implicitly represented. The initial values i.e. δ¹³C_init, Δ¹⁴C_init , determine the initial level of the curves in Figure 3 and Figure 4 and for δ¹³C_FF determine the curve slopes in Figure 4 and Figure 5. δ¹³C_init, Δ¹⁴C_init and fossil fuel δ¹³C_ff content are solution parameters.

Figure 1. CO₂ Finite Reservoir Two Box Model.

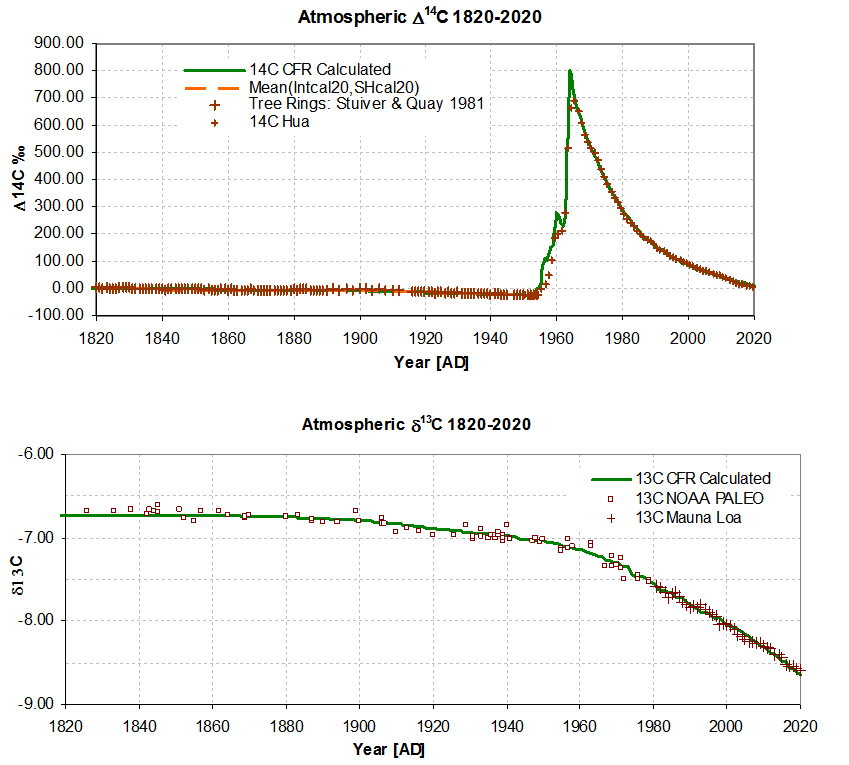
Figure 2. Atmospheric Δ¹⁴C 1820-2020. CFR calculated: (solid line). Mean (Intcal20,SHCal20) (dashed line). σ = 3.0‰, excl. values during the rising pulse from 1950 to 1968.

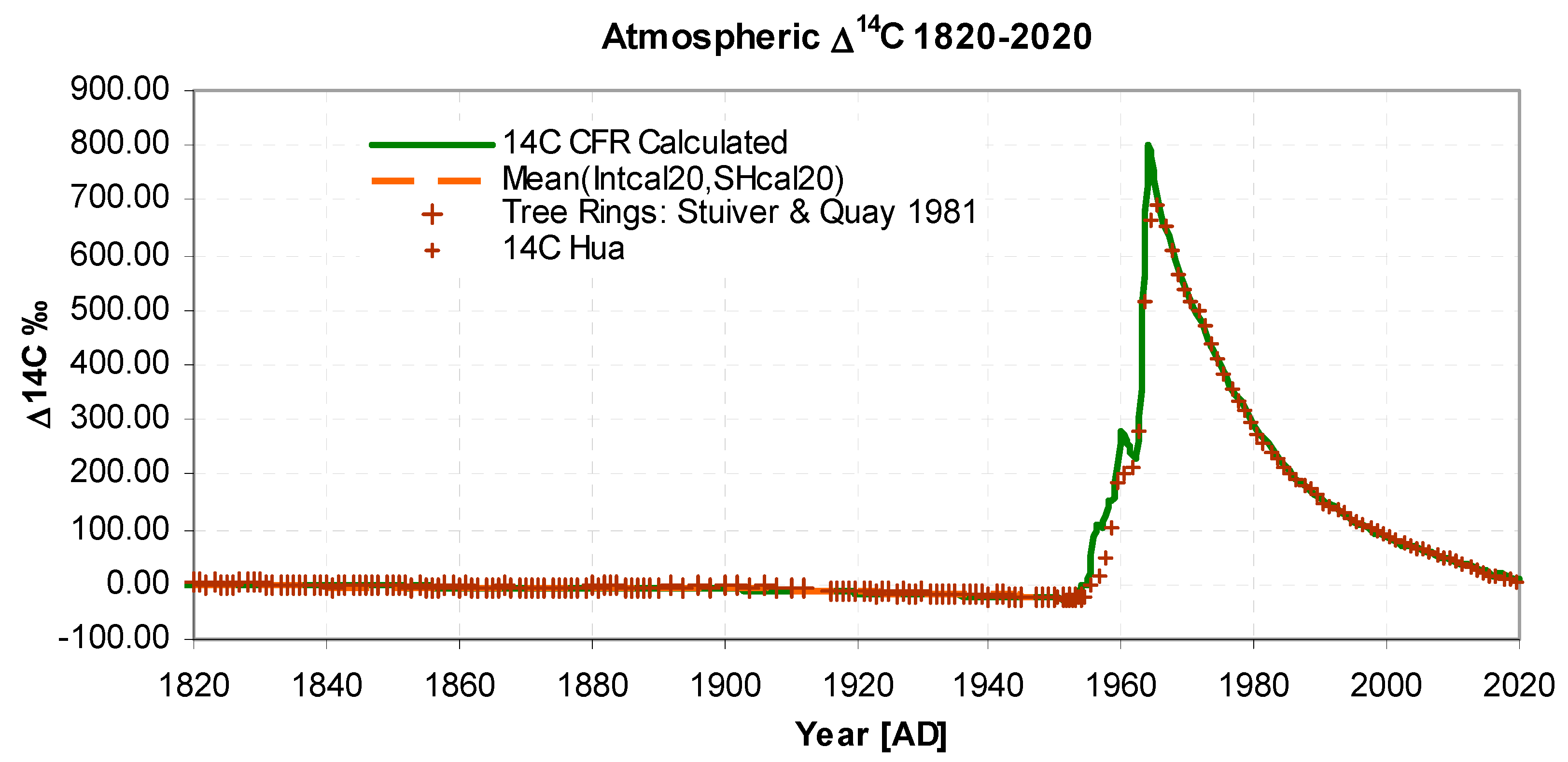
Figure 3. Atmospheric Δ¹⁴C. CFR calculated values: (solid line). Collated: Hua 2021 (crosses), Mean SHCAL20 and INTCAL20 (Square). For σ see Fig. 2.

Figure 4. Atmospheric δ¹³C 1820-2020. CFR calculated values (solid-line), Observed values: NOAA Paleo (squares), Mauna Loa (crosses) σ_1820-2020,= 0.05‰.

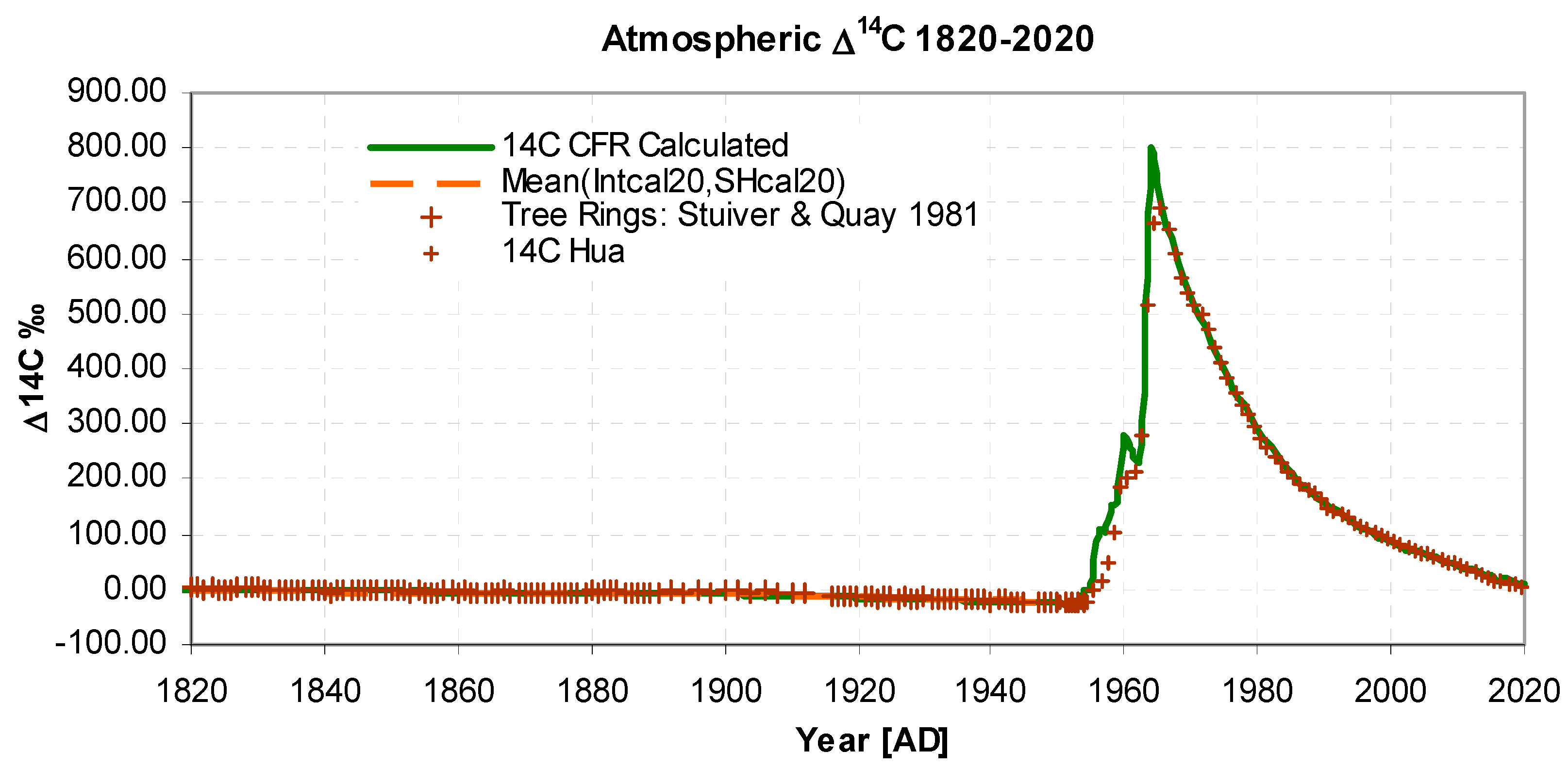
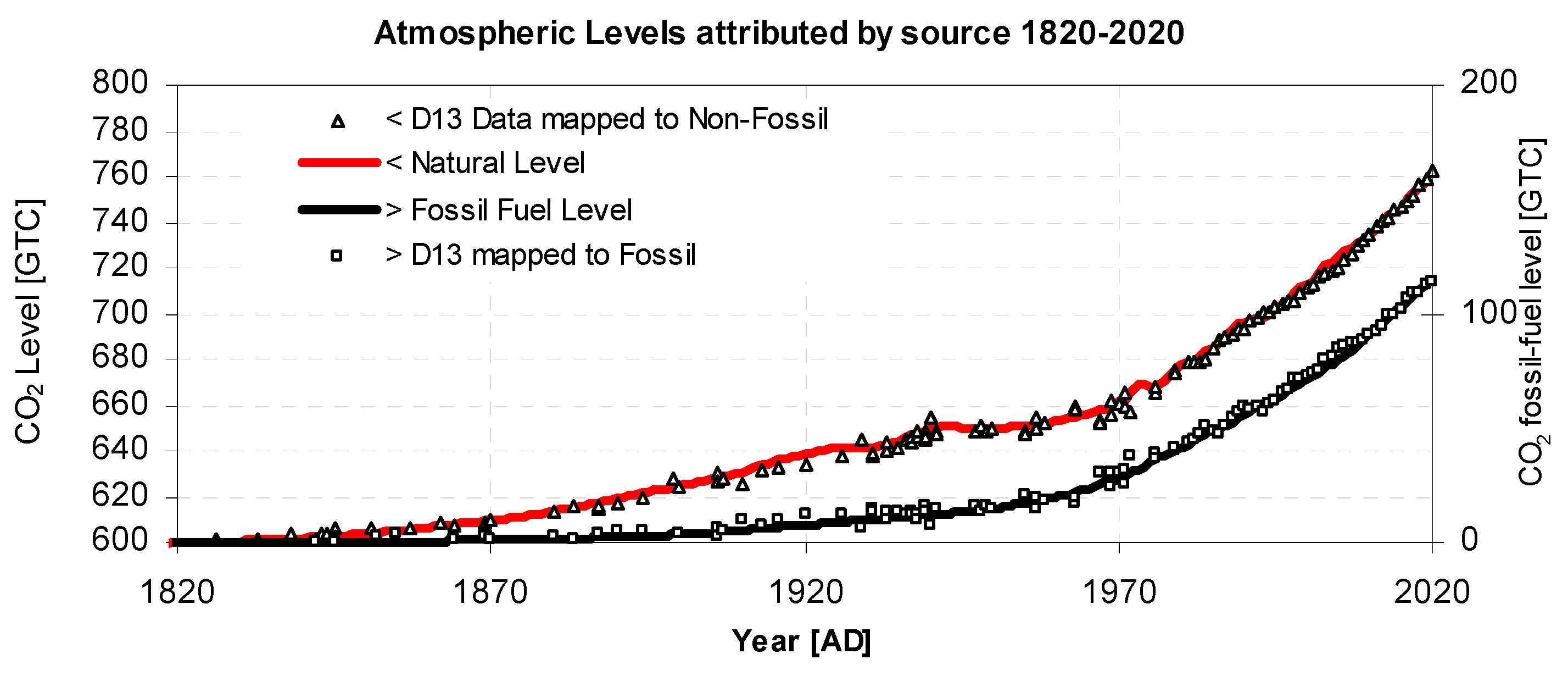
Figure 5. Atmospheric Levels as derived from δ¹³. CFR computed (fossil black-line, non-fossil red-line). Measured values mapped via Eq. A6 using δ¹³C_F, δ¹³C_B to fossil (square) and non-fossil (triangle). The slope represents Net flow indicating a similar nett flows of fossil and natural sources.

To be clear, the CFR does not use ad-hoc corrections to an exponential decay shape. Rather, it calculates year by year the amount of CO₂ in the biospheric reservoir, the change of ¹⁴C and ¹³C in atmosphere and reservoir and its release back to the atmosphere. The return flux is determined by "balancing the books" since atmospheric CO₂ mixing ratio is a data input. See Appendix C for annual iteration relations. The final solution is found by minimising the standard deviation between the observed and predicted values of δ¹³C, Δ¹⁴C as each parameter is adjusted. The entire model is re-calculated for each of these iterations. In practice the standard deviation between observed and predicted was calculated for each graph σ₁, σ₂ and a product was taken. The square root of this product gives the total standard deviation,σ. Hence

σ_j = √ 1/n Σ (obs_i - calc_i)²

σ = (σ₁ x σ₂)^1/2

The minimisation of standard deviation was carried out using the solver function in Microsoft Excel. Only one true constant was used, atmospheric capacity, which was taken to have a value of 2.124 ppm GTC^-1 (Ballantyne 2012).

Results

The input data was prepared and selected from Data References 1–5. The model was run from 1750 to 2020, with results from 1820 to 2020 being shown for ∆¹⁴C in Figure 2 and Figure 3 and δ13C in Figure 4. In total 340 observed data points were used giving a total overall standard deviation of 0.39‰. The individual quality of fit is indicated in the graph captions. The graphs show excellent agreement between the CFR model and the observed global measurements. Figure 2 shows Δ¹⁴C from 1820 to 2020 before, during and after the atomic bomb pulse, with 130 observed data points before 1950 and 70 observed data points from 1968 onwards taken from Hua 2021.

Note the quality of fit during the latter parts of the pulse. If the model is deliberately run with a different relative reservoir size the latter tail portion of the pulse tail ceases to fit, indicating the back flow is having the anticipated effect. Figure 3 shows just the period since the bomb pulse. Figure 4 shows the value of δ¹³C from 1820 to 2020 with the predicted values (green line) being from the model (after the global curve fitting process) and the experimental values (brown squares and brown cross) being from NOAA PALEO and MAUNA LOA respectively showing good agreement. Figure 5 shows two key quantities from the CFR model, the anthropogenic fossil-fuel level (black line) and the level attributable to the rest (red line) termed here “natural”. The values, see left and right axis labels, represent the level while the slope of the curves indicate flux rate. The similarity of the slopes of the natural level and fossil level curves shown in Figure 5, indicates similar fluxes from natural and fossil fuel inflow rates. The superimposed data points were derived uses Equation B6 as suggested to me by Tom Quirk (Quirk 2021). Essentially the method finds what quantities of the two gases (i.e., pre-industrial δ¹³C_B and fossil fuel δ¹³C_F), would mix to form the observed δ¹³C value?” Since Figure 4 shows a high level of agreement this is also the case in Figure 5. The solution of all 7 parameters values, is listed in Table 1, along with error SD.

In Table 1, the SD value was derived by variation of each parameter, whilst holding the other values constant, until the standard deviation approximately doubled. Table 2 and Figure 6 indicate cumulative CO₂ flows and storage as calculated by the CFR over various periods. The cumulative fossil-fuel within the atmospheric CO₂ relative to total fossil fuel emissions during the same period, has remained fairly constant, with 26% remaining in the atmosphere. However, the cumulative atmospheric increase due to fossil fuels relative to the atmospheric increase itself over the past 270 years is 43%, rising to 49% over the past 60 years. For further details see next section.

6. Discussion

In the CFR method described above, the reservoir size and outflow was determined by curve fitting of Δ¹⁴C and δ¹³C values (Figure 2 and Figure 4) whose rate of fall is a balance between Suess dilution and CO₂ inflow from the mixing reservoir. Table 6 shows that that atmospheric growth relative to fossil fuel input i.e., 282/454 is as high as 62%, with similar figures being listed in GCB (Friedlingstein 2021 Table 8). However at the same time only 13.7% of the atmosphere consists of fossil fuel CO₂. How is this possible? The answer is because the reservoir is considerably larger than the atmosphere. When the reservoir absorbs fossil fuel CO₂ its concentration of fossil fuel CO₂ increases only slowly. Therefore, although outflow from the atmosphere to the reservoir almost matches the opposing inflow there is a considerable nett transport of fossil fuel CO₂ (120GTC) from the atmosphere into the reservoir Figure 6. Hence only 13.7% of the atmosphere remains due to CO2ff. Whether this latter atmospheric inflow would have occurred without anthropogenic fossil fuel emission is an important question, but one this paper does not attempt to address. We now discuss each of the seven solution parameters in more detail.

a) Reservoir Size. The CFR method indicated that the atmosphere could be considered as if connected to a carbon reservoir with approximately six times the atmospheric carbon content (in 1820) and with a current size of 3770 ± 900 GTC, the errors being determined from the uncertainty in reservoir size, Table 1. This figure compares favourably with figures from IPCC WG1AR6 for the total reserve totalling 4250 GTC (Canadell et al. 2021)comprising 1700 GTC in soil, 450 GTC in vegetation, 1200 GTC in permafrost and 900 GTC in surface ocean.

b) Airborne Factor. It is clear that each year, the annual growth in the atmospheric level of CO₂ is smaller than the CO2ff. This ratio is known as the Airborne Factor. The model returns a figure of 54% ± 11% of CO2ff entering the atmosphere while 46% is removed each year, in good agreement with the value of airborne fraction averaged over 60 years recently published by IPCC of 44% ± 10% (Canadell et al. 2021).

c) Nuclear Bomb Yield. The model produces a figure of 1.6 ± 0.1 mills of 14C per MT. The number of atoms per unit of Δ¹⁴C can be found by calculating the number of carbon atoms for the CO₂ level in 1950 (A_CO2 = 6.7x10¹⁷), using Avogadro's number (N_A) and by dividing by the carbon atomic weight M_C = 12, then multiplying by the 14C/12C ratio which can itself be calculated from the specific activity, α = 0.226 decays per gram, ¹⁴C half life T_1/2 = 5730yr = 1.807 10¹¹ s, and ln(2) as follows giving

Nc = (A_CO2 N_A /M_C12 ) x ( α T_1/2 M_C14 / (N_A ln(2)) = 4.6 x 10^{28 14}C atoms per unit Δ¹⁴C

d) Turnover Time. The figure of turnover time T, was found to be 14.9 ± 1.7 years. The flux figure may be calculated as atmospheric size divided by turnover time (IPCC Glossary 2013, Harde 2017), and ranges from 39.7 GTC yr^-1 in 1720 to 59.0 GTC yr^- in 2020. These figures are around 1/3rd of the IPCC listed values who have in WG1 AR5 for 1750 an oceanic flux of 60 GTC yr^-1 and land flux of 108 GTC yr^-1, and for 2013 79 GTC yr^-1 and 120 GTC yr^-1 respectively, with uncertainties quoted as a minimum of 50% (Ciais 2013). WG1 AR6 has "rescaled values" giving oceanic flux as 54 GTC yr^-1 and land 111 GTC yr^-1 (Canadell et al. 2021). One consideration is that some of the carbon may not isotopically mix in the reservoir at each iteration, thereby leaving carbon trapped in an annual cycle or perhaps in soil or dense wood. Hence the figures may correspond to the amount of carbon which mixes each year in the ocean, but not the amount that is cycled. Indeed, the figure is not far from the oceanic flux quoted above. Furthermore the turnover time figure compare very reasonably with older estimates by Revelle & Suess 1957 ~ 10yrs, and Arnold & Anderson 1957 of 10 - 20yrs, these being referred to (respectively) as “the average lifetime of a CO₂, molecule in the atmosphere before it is dissolved into the sea” and “the mixing half-time between the atmosphere and ocean”.

e) Pre-industrial Δ¹⁴C_init, Pre-industrial δ¹³C_init. The solution values (-3‰, -6.7‰) from the model for these values represent the model aligning to the initial values and are in good agreement with values of Δ¹⁴C_init = -3.4‰ (Intcal20) and δ¹³C_init = 6.7‰. (Rubino et al 2013).

f) Fossil Fuel δ¹³C_ff. This figure from the model is δ¹³C_{f =} -20.8 ‰, in reasonable agreement but slightly low for fossil fuels. See Stuiver & Polach 1977 who have coal δ¹³C = -23.

It is extremely unlikely the above results would occur by chance given the excellent mean quality of fit for Δ¹⁴C and δ¹³C, and the reasonable values for six of the seven solution parameters, together with the reasonable explanation for the discrepancy in the other parameter, atmospheric outflow.

7. Conclusions

This paper presented a novel method for calculating global CO₂ flux, demonstrating that despite its apparent complexity, global flows can be approximated using a top-down approach. The CFR model provides a plausible explanation for the "¹⁴CO₂/CO₂ attenuation factor" suggested by Stuiver and it accounts for a similar discrepancy in ¹³C dilution, providing a means for estimating the influx. It has been asserted that the ¹⁴C bomb pulse cannot be used for CO₂ flux studies due to anomalous behaviour of ¹³C and ¹⁴C regarding the Revelle factor (Joos 1994, Tans 2022). Yet this study produces reasonable results, without incorporating an exception for the Revelle anomaly for ¹³C and ¹⁴C, thus showing that the Tans assertion is unfounded. The specific theoretical mistakes which may have led to this assertion are listed in Appendix. This conclusion restores the common-sense view that such anomalous behaviour of carbon isotopes is unlikely. The effects of this mis-step upon climate science may be considerable and wide reaching, since the isotopic ratiometric exception has almost certainly entered the internal coding for various climate models. Such models have been widely used for flux calibration using the partition method (Zeng et al, 2020) and for scenario testing of fossil fuel emissions (IPCC 2021). Although the CFR model is not itself a climate model it can usefully provide indications of effective bulk global parameters and provides a focus on the physics of internal processes. The CFR method thus offers a means by which estimates of effective bulk global quantities can be compared. The model can be downloaded as a Microsoft Excel Spreadsheet from https://www.geomatix.net/atmos2boxmodel.htm.

Acknowledgments

I would like to thank my colleagues Dr. Andrew Layfield (Engineering and Environmental Studies), City University, Hong Kong, and Dr. Michael Oates (Geologist) of Barrow-upon-Humber, UK for their detailed comments and proof reading. The author would like to thank and acknowledge all the data providers indicated in "Data References", without whom this work could never have been carried out. This research was self-funded and received no external funding. The author declares no conflict of interest. The author would like to thank the publisher for waiving the APC which was funded by the publisher.

Appendix A. Notes on Tans 1993 and Tans 2022

In 1993 Tans derived an expression for C_A dR_A/dt where C_A is the atmospheric CO₂ content, R is the isotopic composition with subscript A for atmospheric gaseous CO₂ Equation (13) and O for ocean, and F is flow and subscript FOS refers to fossil fuel CO₂ emissions. Tans 2022 Equation (1) is a simplified version of his Equation (13) obtained by setting all terms with subscripts lb or ph to zero. In either case Tans derives.

C_adR_a/dt = F_fos (R_fos - R_a) - (F_ao - F_oa) R_a ( α_ao - 1) + F_oa α_ao (R_a^eq - R_a) )

(T1)

It is claimed the last term, because it is a difference of ratiometrics, multiplied by a one way flux provides evidence of "pure isotopic equilibration that always takes place regardless of what the net total flux is". In 2022 he states "The Revelle factor does not apply to isotopic equilibration because a 12CO2 molecule is replaced by a 13CO2 or vice versa. As a result, an isotopic anomaly disappears from the atmosphere more quickly than a total CO2 anomaly." In the derivation Tans has.

d¹³C_a/dt = d (R_aC_a) /dt = C_adR_a/dt + R_adC_a/dt

(A2)

d¹³C_a/dt = R_fosF_fos + α_oaR_oF_oa - α_aoR_aF_ao

(A3)

dC_a/dt = F_fos + F_oa - F_ao

(A4)

where α_oa and α_ao are the fractionation rates to and from the atmosphere. At equilibrium between the two reservoirs R_fos=0, d¹³C_a/dt =0 and dC_a/dt =0 so we have.

α_oaR_o^eqF_oa^eq = α_aoR_a^eqF_ao^eq

(A5)

F_oa^eq = F_ao^eq

(A6)

Giving

α_oaR_o^eq = α_aoR_a^eq

(A7)

However Tans, after rearranging, has written eq. A7 as

The effect of the incorrect substitution is to enable the grouping in the last term in Equation (T1). Its effect upon the rate of isotopic transfer d¹³C_a/dt can be evaluated by adding Tans' expression for C_adR_a/dt (eq. T1) to the value of R_adC_a/dt (Equation (A4) multiplied by R_a) to provide a new “test” value for d¹³C_a/dt.

“d¹³C_a/dt” = F_fos (R_fos - R_a) - (F_ao - F_oa) R_a ( α_ao - 1) + F_oa α_ao (R_a^eq - R_a) + R_a (F_fos + F_oa - F_ao)

After some re-arranging and using the correct substitution of (A7) gives.

“d¹³C_a/dt” = F_fos R_fos + α_oa R_o^eq F_oa - α_ao R_a F_ao

It can be seen that the term R_o in eq. A3 is replaced by its equilibrium value R_o^eq . This is not justifiable as it prevents the ocean from exhibiting any isotopic variation when coming to an equilibrium, effectively clamping its isotopic ratio to the value R_o^eq, implying its volume is infinite. Furthermore Tans' expression for C_adR_a/dt (Equation (A1)) does not fully represent d¹³C_a/dt (which is the quantity required) because R_adC_a/dt is missing from the calculation. The same arguments apply to ¹⁴C as ¹³C. Equations (A3) and (A4) are the correct versions and are used throughout this paper neglecting fractionation (with α_oa = α_ao= 1) and in the production of the presented results.

Appendix B. Notes on Isotopic Mixtures and Radiocarbon Levels

Dalton's "Law of Partial Pressures" indicates that, when two gases having partial pressure P_A and P_B and concentration R_A and R_B, are mixed, then the total pressure, P_T of the mixture will be given by.

P_T = P_A + P_B

and its concentration R_M of the mixture or model is

R_M = (R_A P_A +R_B P_B) / P_T

Note: If the isotopic amount is described by an offset scale e.g., R = (m.δa + c) the above becomes

(m δm + c) P_T = ( m δa + c) P_A + ( m δa + c) P_B

which after rearranging gives equations of similar form, i.e.

δ_m Pt = δa P_A + δb P_B

(B1)

δ_m = (δa P_A + δb P_B) / P_T

(B2)

Conversely, for a mixture of total pressure P_T, whose concentration is δm, given the concentration of its two constituents δa and δb, the pressure of the constituent P_A, is given by (Quirk T. 2021).

P_A = P_T ( δm - δa ) / ( δa - δb )

(B3)

Conventionally δ¹⁴C is defined as an offset scale whose value is zero when A_s, the specific activity of the atmosphere or reservoir is equal to A_abs, the absolute specific standard, with both being in units of Bq per unit mass of carbon. Hence we may write

A = δ¹⁴C +1 = (A_s/A_abs)

where A refers to the relative specific ¹⁴C activity. Thus A contains no allowance for radioactive decay or fractionation. For the mixture M obtained by mixing natural N and fossil fuel derived F components we may write using Equation (A2) for A_M and δ¹³C_M

A_M = (A_N P_N / P_T) -1

(B4)

δ¹³C_M = (δ¹³C_F P_F + δ¹³C_N P_N) / P_T

(B5)

bearing in mind that A_F = 0. The inverse for δ¹³C_M,, used in Figure 6 to map from observed atmospheric values of δ¹³ to CO₂ levels by source from Equation (A3) is

P_N = P_T ( δ¹³C_M - δ¹³C_F ) / ( δ¹³C_N - δ¹³C_F )

(B6)

Fractionation

It is desired to compare values of A_M with collated measured values of Δ¹⁴C. However Δ¹⁴C incorporates a fractionation correction to "translate the measured activity to the activity the sample would have had if it had been wood" (Lund 2011) and is a function of δ¹³C. Therefore a fractionation correction must be applied to A_M, where δ¹³ for wood is taken as -25‰, given by

Δ¹⁴C_M = A_M . { (1+ δ¹³C_W)/(1+ δ¹³C_M) }² - 1

This formula decreases the values by around 35‰ compared to the values for A_M.

Age Correction

Sample age correction, common in radiocarbon calculations, is not included in the CFR or the definition of Δ¹⁴C. The ¹⁴C half-life of 5700± 30 years (Kutschera, W., 2013) translates to a decay of around 2% over the period 1820 to 2020. However, the steady level of stratospheric ¹⁴C production roughly balances the amount of ¹⁴C decay since the two are in approximate equilibrium, providing a buffering effect. Disregarding ¹⁴C decay introduces an error at most in the low percentage region and probably considerably smaller and is regarded as negligible. Therefore neither ¹⁴C decay nor natural stratospheric ¹⁴C production were included in the CFR model. Values of A were not artificially corrected for ¹⁴C decay before comparison with Δ¹⁴C.

Appendix C. Implementation

The implementation process involves a number of calculations at each iteration which are based upon "Daltons Law of Partial Pressures". The amount of CO₂ in the atmosphere is A_CO2, its turnover time is T, outflow is A_OUT and the amount of CO₂ initially in the reservoir is R_CO2 , with respective increases being written as Δ(A_CO2) and Δ(R_CO2) at each iteration, i, then the iteration relationships are:-.

Δ(R_CO2) = R_CO2[i] - R_CO2[i-1] Δ(A_CO2)= A_CO2 [i] - A_CO2[i-1]

A_OUT[i] = A_OUT /T A_IN[i] = A_OUT [i] + A_CO2 [i] - A_CO2 [i-1] - A_F CO2_FF [i]

R_CO2[i] = R_CO2[i-1 ]+ A_OUT[i] - A_IN[i] + (1-A_F)CO2_FF [i]

For the ratio of ¹⁴C to ¹²C in Atmosphere A₁₄[i] and Reservoir R₁₄[i] we have:-

A₁₄[i] = (A₁₄ [i-1].A_CO2 [i-1] + A_IN [i-1].R₁₄[i-1] - A_OUT[i-1]. A₁₄[i-1] + B₁₄[i-1]) / A_CO2 [i]

(¹⁴C previously + ¹⁴C coming in - ¹⁴C going out + Bomb ¹⁴C ) / Atmos C

R₁₄[i] = (R₁₄ [i-1].R_CO2 [i-1] - A_IN [i-1].R₁₄[i-1] + A_OUT[i-1]. A₁₄[i-1] ) / R_CO2 [i]

( ¹⁴C previously + ¹⁴C coming in - ¹⁴C going out ) /Reservoir C

Similarly the relative atmospheric and reservoir fossil fuel content A_FF[i], R_FF[i], on a scale of 0 to 1, are given by:-

A_FF[i] = (A_FF [i-1].A_CO2 [i-1] + A_IN [i-1].R_FF [i-1] - A_OUT[i-1].A_FF[i-1] + A_F CO2_FF [i]) / A_CO2 [i]

R_FF[i] = (R_FF [i-1].R_CO2 [i-1] - A_IN [i-1].R_FF [i-1] + A_OUT[i-1].A_FF[i-1] + (1-A_F) CO2_FF [i]) / R_CO2 [i]

FL[i] = A_CO2[i] A_FF[i] NL[i] = A_CO2[i] (1- A_FF[i])

where the absolute fossil fuel level, FL[i], and natural non-fossil level, NL[i], are shown in the final equation. The isotopic ratiometric measures for ¹³C, δ¹³C and ¹⁴C Δ¹⁴C are given by:-

δ¹³C = δ¹³C_FF . A_FF + δ¹³C_N ( 1- A_FF ) Δ¹⁴C = (A₁₄ -1)

Initial Conditions: A_IN [0] = A_OUT [0] , A₁₄ [0] = 1 , R₁₄ [0] = 1, A_FF[0] = 0 , R_FF[0] = 0

where A_OUT is the atmospheric outflow, A_CO2 is the atmospheric CO₂ mixing ratio, A_IN is the atmospheric inflow, R_CO2 is the reservoir CO₂ mixing ratio, R_FF is the relative fossil fuel level in the reservoir, R₁₄ is the f¹⁴C level in the reservoir, F_RSVR is the Fossil fuel CO₂ mixing ratio in the reservoir, A₁₄ is the f¹⁴C level in the atmosphere, B₁₄ is the annual ¹⁴C production due to atomic weapons testing Δ¹⁴C is the ¹⁴C/¹²C ratio and δ¹³C = is the ¹³C/¹²C ratio and the square brackets "[ ]" refer to the value at each iteration. The constant α is an output which in the case of an infinite reservoir represents the time constant in equations C1, C2.

Appendix D. Attenuation Factor of 14C and 13C

Stuiver & Quay proposed an "attenuation factor" for Δ¹⁴C because the Suess dilution of atmospheric CO₂ was not as great as expected. (Stuiver & Quay 198). Between 1820 and 1950 the actual reduction in Δ¹⁴C was around 20‰ using IPCCC-WG1AR5 WG1AR5 Figs. 4&6b, pp 493-4 (Ciais 2013) or Intcal20 data. During this time the atmospheric level increased from 600 to 667 GTC while listed CO2ff emissions totalled 61GTC. Setting in Equation B5 δ¹⁴C_F = -1000, P_F = 6, δ¹⁴C_N= 0 , P_N= 600, P_T=667 gives a reduction in Δ¹⁴C of 89‰, much larger than the measured decrease of 20‰. A similar argument can be made for δ¹³C. The actual annual reduction can be measured from Figure 4 or from IPCCC-WG1AR5 Figure 6b and is around 0.025‰ per year. Both the IPCC curve and Figure 4 from this paper indicate that the annual CO₂ emissions from fossil fuels in 2000AD was approximately 6 GTC yr^-1 around one 125th of the atmospheric size of around 750 GTC which was increasing at around 3GTC per year. For fossils d13 = -26V (or higher) while for the atmosphere in 2000AD δ¹³ = -8 (see) Setting in Equation (B5) δ¹³C_F = -26, P_F = 6, δ¹³C_N=-8, P_N= 750, P_T=756 gives δ¹³C_M = -8.14‰, indicating a decrease of 0.14‰ per year which is considerably greater than 0.025‰ per year. Some have suggested fossil fuels have even lower δ¹³ figures of approaching -44‰ (Bush et al 2007) which would make this discrepancy greater. Even allowing for the airborne fraction (i.e., the fact that the atmospheric increase was attributed to only half of the CO2ff) there still is a considerable discrepancy in both cases. The analysis given above of δ¹³C and Δ¹⁴C is entirely independent of the CFR model itself and is simply based on published data. It is postulated here that the above discrepancy can be accounted for by a CO₂ inflow from a reservoir in which previous atmospheric CO₂ has accumulated, which having higher Δ¹⁴C and δ¹³C values than those for fossil fuel would hinder the fall. The CFR model not only shows that this inflow is a plausible explanation, it accurately calculates the inflow, the δ¹³C and the value of Δ¹⁴C.

References

Archer, D et al. 2009. Atmospheric lifetime of fossil fuel carbon dioxide. Annu. Rev. Earth Planet. Sci., 2009. 37:117–134.
Arnold J.R. & Anderson E.C. 1957. The Distribution of Carbon-14 in Nature. Tellus IX 1957.
Ballantyne, A. P et al. 2012. Increase in observed net carbon dioxide uptake by land and oceans during the last 50 years. Nature, 488, 70–72.
Bauska et al. 2014 Carbon isotopes characterize rapid changes in atmospheric carbon dioxide during the last deglaciation. PNAS | March 29, 2016 | vol. 113 | no. 13 | 3465–3470.
Bengston et al. 2020 Lower oceanic δ13C during the last interglacial period compared to the Holocene. Clim. Past, 17, 507–528. [CrossRef]
Bindoff, N.L. et al. 2013, Detection and Attribution of Climate Change: from Global to Regional. Climate Change 2013: The Physical Science Basis. WG1 AR5, IPCC, Cambridge University Press.
Bolin B, Eriksson E. 1959. Changes in the carbon dioxide content of the atmosphere and sea due to fossil fuel combustion. In Rossby Memorial Volume, ed. B Bolin:130-42. New York: Rockefeller Institute Press, Oxford University Press. Number of 130-42 pp.
Broecker W. & Peng T, 1994. Stratospheric contribution to the global bomb radiocarbon inventory: Model versus observation.
Bush S.E. et al 2007. Sources of variation in d13C of fossil fuel emissions in Salt Lake City, USA , Applied Geochemistry 22 (2007) 715–723.
Canadell, J.G et al. 2021: Global Carbon and other Biogeochemical Cycles and Feedbacks. In Climate Change 2021: The Physical Science Basis. WG1 AR6 IPCC, [Masson-Delmotte V et al.]. Cambridge University Press, pp. 673–816. [CrossRef]
Ciais, P. et al, 2013. Carbon and Other Biogeochemical Cycles. Chapter 6. Climate Change 2013: The Physical Science Basis. [Stocker et. al] WG1 AR5 IPCC 2013.
Ciais, P. et al, 1995. Partitioning of ocean and land uptakeof CO2 as inferred by d13C measurements from the NOAA Climate Monitoring and Diagnsotics Laboratory Global Air Sampling Network, Journal of Geophysical Research Vol. 100 D3, 5051-5070, March 20, 1995.
Flato, G.et al., 2013: Evaluation of Climate Models. Climate Change 2013: The Physical Science Basis. WG1 AR5, IPCC. Cambridge University Press, UK and USA.
Friedlingstein P. et al, 2021. Global Carbon Budget 2021, Earth Syst. Sci. Data, 14,1917-2005, 2022. [CrossRef]
Gruber, N. et al. 2019. The oceanic sink for anthropogenic CO2 from 1994 to 2007. Science 363, 1193–1199 (2019).
Harde H. 2017. Scrutinizing the carbon cycle and CO2 residence-time in the atmosphere , Global and Planetary Change 152 (2017) 19–26.
Harvey Danny LD 2000, Global Warming: The Hard Science, Pearson Education Limited, UK. ISBN 0582-38167-3.
Hesshaimer, V et al. 1994, Radiocarbon evidence for a smaller oceanic carbon dioxide sink than previously believed. Nature Vol 370 21 July 1994.
Hua Q. et al. Atmospheric Radiocarbon For The Period 1950–2019, Radiocarbon Vol 0 Nr00 2021. Submitted. Private Communication.
IPCC 2013: Glossary. Climate Change 2013: The Physical Science Basis. [Stocker et. al] WG1 AR5 IPCC 2013.
IPCC, 2021: Annex II: Models [Gutiérrez, J M., A.-M. Tréguier (eds.)]. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte V. et al]. Cambridge University Press, 2087–2138. [CrossRef]
Joos F. 1994. , Imbalance in the Budget, Nature Vol 370 21July 1994.
Kutschera, W., (2013) Applications of accelerator mass spectrometry. International Journal of Mass Spectrometry 349, 203-218.
Levin I. et al. 2010 Observations and modelling of the global distriution and long-term trend of atmospheric 14CO2. Tellus B, 62: 26-46 2010.
Marcott A S et al., 2014. Centennial-scale changes in the global carbon cycle during the last deglaciation. Nature,Vol 514,30October 2014.
Paola, C. & Leeder M, Simplicity versus complexity. Nature 469, 38–39(2011).
Quirk T. 2021 Suggested method using inversion formulae for d13C. Private Communication 2021.
Revelle, R & Suess H, 1957. Carbon Dioxide Exchange Between Atmosphere and Ocean and the Question of an Increase of Atmospheric CO2 during the Past Decades. Tellus IX(1957).1.
Rubino, M et al 2013. A revised 1000 year atmospheric δ13C-CO2 record from Law Dome and South Pole, Antarctica. Journal of Geophysical Research: Atmospheres, 118(15), pp.8482-8499. 2013.
Physics, Division of Nuclear Physics. Sweden. 2011.
Stenström K. E. 2011. A guide to radiocarbon units and calculations, Lund University, Department of Stuiver, M. & Quay, P.D. 1981. Atmospheric ¹⁴C changes resulting from fossil fuel CO2 release and cosmic ray flux variability. Earth and Planetary Science Letters, 53 (1981) 349-362.
Stuiver M & Polach H A. 1977 Discussion: Reporting of 14C Data, Radiocarbon, Vol19 No 3 1977 P355-363.
Stuiver, M et al. 1998 "Intcal98 Radiocarbon Age Calibration, 24,000-0 Cal Bp", Radiocarbon, Vol. 40, No. 3, 1998, P.1041-1083.
Suess, H.E. 1955 Radiocarbon concentration in modern wood. Science 122, 415.
Svetlik I. 2010 Estimation of Long-Term Trends in the Tropospheric 14CO2 Activity Concentration. Proceedings of the 20th International Radiocarbon Conference, edited by A J T Jull, RADIOCARBON, Vol 52, Nr 2–3, 2010, p 815–822.
Tans, P., Berry J., Keeling R. 1993. Oceanic 13C/12C Observation: A new window on ocean CO2 uptake. Global Biogeochemical Cycles Vol 7 No2 P353-368) June 1993.
Tans P. 2022. Reminiscing On The Use And Abuse Of 14c And 13c In Atmospheric Co2. Radiocarbon, Vol 64, Nr 4, 2022, p 747–760. [CrossRef]
Zeebe, R.E. and Wolf-Gladrow, D.A. 2001. CO2 in Seawater: Equilibrium, Kinetics, Isotopes. Gulf Professional Publishing. http://store.elsevier.com/product.jsp?isbn=9780444509468.
Zeng J. et al. 2020. Global terrestrial carbon fluxes of 1999–2019 estimated by upscaling eddy covariance data with a random forest . Scientific Data (2020) 7:313. [CrossRef]

Figure 6. Atmospheric CO₂ cumulative flux 1750 to 2020. (GTC) The figures in red represent the increase over the time period, underscore indicates 2020 values. The atmospheric flux out contains more CO2ff than the flux in because the atmospheric concentration of CO2ff is higher than the reservoir concentration, removing CO2ff from the atmosphere. Atmospheric CO2ff = 246 - 292 + 166 = 120 corresponding to 120/871 = 13.7% of the atmosphere (See Table 2).

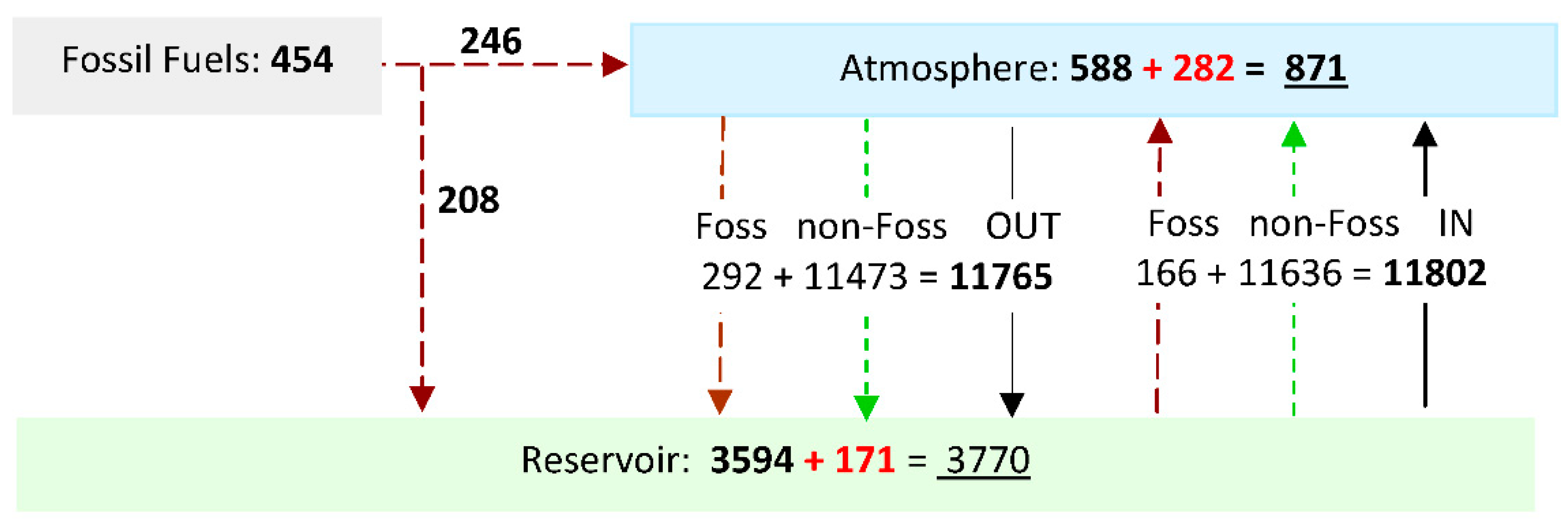
Table 1. Solved 7 Parameter Values.

Parameter	Symbol	Value	SD ±
Turnover Time = A_CO2 /A_OUT	T	14.9 yr	1.7
Fossil-fuel Inflow Fraction	A_F	0.54	0.11
Nuclear Bomb Yield*	Y_b	1.60	0.1
Rel. Reserve Size	R_CO2	6.1	1.4
¹⁴C Pre-industrial	Δ¹⁴C_init	-3.0‰	10‰
¹³C Pre-industrial	δ¹³C_init	-6.7‰	0.2‰
¹³C fossil fuel	δ¹³C_ff	-20.8‰	4‰

Table 2. Cumulative CO₂ Flow and Storage.

Duration	1750 -	2020	1850 -	2020	1960 -	2020
	GTC	%	GTC	%	GTC	%
CO2FF Supplied
CO2FF delivered to Atmos. (AF)	246	54	245	54	202	45
CO2FF delivered to Rsvr. (1-AF)	208	46	207	46	170	38
CO2FF Total	454	100	452	100	372	82
CO2FF Destination
CO2FF present in Atmos.	120	26	120	26	99	26
CO2FF present in Rsvr.	333	74	333	74	273	72
CO2FF Total	454	100	452	100	382	100
Atmospheric Growth
Atmos. CO2 Growth due to CO2FF	120	43	120	44	99	49
Atmos. CO₂ Growth due to non-Foss*	162	57	152	56	104	51
Atmospheric Growth Total	282	100	272	100	204	100
Reservoir Growth
Reservoir Growth due to CO2FF	333		333		273
Reservoir Growth due to non-Foss*	-158		-143		-97
Reservoir Growth Total	171		185		171
Atmospheric Outflow
Atmos Outflow CO2FF	292		291		245
Atmos Outflow non-Foss	11473		7459		2806
Atmospheric Outflow Total	11765		7750		3051
Reservoir Outflow
Reservoir Outflow CO2FF	166		166		143
Reservoir Outflow non-Foss	11636		7606		2907
Reservoir Outflow Total	11802		7772		3050
CO2FF rel. to CO2 atmos. 2020† (%)	120/876	13.7	120/876	13.7	99/876	11.3
Average Annual Flux from Reservoir	43.77		45.79		50.96
Average Annual Flux to Reservoir	43.63		45.67		50.99

* Non-Foss means “not due to anthropogenic fossil fuel CO2 emissions”. † The CO2 atmospheric mixing ratio in 2020, was 412.44 ppm, 876 GTC. These values take into account the backflow of fossil fuel CO₂ from reservoir to atmosphere. Year Intervals chosen to align with GCB Frieldingstein 2021 Table 8.

Data References

Institute for Atmospheric and Climate Science (IAC), CO2 Mean Global AD0 to AD2014 ftp://data.iac.ethz.ch/CMIP6/input4MIPs/UoM/GHGConc/CMIP/yr/atmos/UoM-CMIP-1-1- 0/GHGConc/gr3-GMNHSH/v20160701/ mole_fraction_of_ carbon_dioxide_in_air_input 4MIPs_GHGConcentrations_CMIP_UoM-CMIP-1-1-0_gr3-GMNHSH_0000-2014.csv
NOOAA GML. Accessed 04-March-2022. https://gml.noaa.gov/ccgg/trends/gl_data.html File: https://gml.noaa.gov/webdata/ccgg/trends/co2/co2_annmean_gl.txt
Global Carbon Budget: National_Carbon_Emissions_2021v0.4.xlsx Historical Budget, Global Fossil Emissions Visited 04 March 2022.Friedlingstein et al (2021),
World Data Service for Paleoclimatology, Boulder and NOAA Paleoclimatology Program, National Centers for Environmental Information (NCEI) https://www1.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/law/law2018d13c-co2.txt, https://doi.org/10.25919/5bfe29ff807fb
UNSCEAR: United Nations Scientific Committee on the Effects of Atomic Radiation 2000 Report To The General Assembly. Volume I: Sources. Annex C: Exposures To The Public From Man-Made Sources Of Radiation 207 Sources And Effects Of Ionizing Radiation. . Table 4. Annual Fission And Fusion Yields.
Calib: INTCAL20/SGCAL20. Stuiver, M. et al, 2022 CALIB 8.2 [WWW program] at http://calib.org, accessed 2022-3-4 Rev 8.1.0 intcal20.14c, shcal20.14c

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Atmospheric CO2 Two Box Model Accurately Tracks 14C and 13C without Requiring the "Revelle Isotopic Anomaly"

Abstract

Environmental Significance

Introduction

Radiocarbon Summary

Revelle Isotopic Anomaly

CO2 Finite Reserve Model

Results

6. Discussion

7. Conclusions

Acknowledgments

Appendix A. Notes on Tans 1993 and Tans 2022

Appendix B. Notes on Isotopic Mixtures and Radiocarbon Levels

Appendix C. Implementation

Appendix D. Attenuation Factor of 14C and 13C

References

Data References

MDPI Initiatives

Important Links

Subscribe

CO₂ Finite Reserve Model