Preprint

Article

Optimizing the Energy Consumption of the Porcelain Tile Manufacturing Process using Flowsheet Simulations

Altmetrics

Downloads

458

Views

172

Comments

A peer-reviewed article of this preprint also exists.

Carine Lourenco Alves^*

Vasyl Skorych

Agenor De Noni Jr,

Dachamir Hotza,Sérgio Yesid Gómez González,

Stefan Heinrich

Carine Lourenco Alves^*

Vasyl Skorych

Agenor De Noni Jr,

Dachamir Hotza,Sérgio Yesid Gómez González,

Stefan Heinrich

This version is not peer-reviewed

Submitted:

26 December 2022

Posted:

03 January 2023

You are already at the latest version

Alerts

Abstract

Porcelain tile manufacturing is an energy-intensive industry that is in dire need of increasing productivity, minimizing costs, and reducing CO2 emissions, while keeping the product quality intact to remain competitive in today’s environment. In this contribution, alternative processing parameters for the porcelain tile production sequence were proposed based on simulation-based process optimization. Flowsheet simulations in the Dyssol framework were used to study the impact of milling and firing process parameters on the electrical and thermal energy consumption, final product quality, and productivity of the entire processing sequence. For this, a new model of gas flow consumption in the sintering stage was proposed and implemented. During optimization, the primary condition was to maintain the product quality by keeping the final open porosity of the tile within the specified industrial range. The proposed simulation methodology proved to be effective in predicting the influence of processing parameters on the intermediate and final products of the manufacturing sequence, as well as in estimating production costs for the Brazilian and Spanish economic conditions. This approach has shown great potential to promote digitalization and establish digital twins in ceramic tile manufacturing for further in-line process control.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

The global porcelain tiles market is rising rapidly. It is projected to grow from $54.41 billion in 2021 to $77.82 billion in 2028 at a compound annual growth rate of 5.2% [1]. In 2017, global ceramic tile production was about 13500 million m² [2]. Brazil is currently the third largest producer and consumer and is alone responsible for an increase in production of 4.2k% from 4 million m² in 2001 to 168 million m² in 2020 [3]. In Europe, Spain is currently (2002) the leading manufacturer, increasing tile production by 20.3% (to 567 million m²) when compared to 2021.

The main manufacturing process used for porcelain tile production is the wet route shown in Figure 1. It consists of six principal unit operations: wet milling, spray drying, storage, uniaxial pressing, drying, and sintering.

The entire process consumes a large amount of thermal energy from natural gas combustion. Natural gas accounts for 92% of the sector’s total energy demand, and the remaining 8% corresponds to electric energy consumption [4]. The slurry’s spray drying, represent 36% of the thermal consumption. The drying of the recently formed tile bodies (known as green tiles) accounts for 9%, and the tile firing is responsible for 55% of energy demand, the largest within the manufacturing process. Moreover, all stages of the manufacturing process use electrical energy [4]. Milling is the step of the processing sequence that presents the highest electrical energy consumption, being responsible for nearly 22%. [5].

During milling, the raw materials are mixed with water for grinding and homogenization. The process usually occurs in a ball mill, either continuous or intermittent. Inadequate milling can increase water absorption of fired tiles and lead to staining problems in products that undergo polishing. In contrast, excessive grinding can compromise the shaping stage, resulting in parts with decreased apparent density and dry mechanical strength, as well as increased linear shrinkage of the tiles after firing [6,7].

Firing occurs mainly in roller kilns, particularly in the high-temperature or firing zone, where the green products are subjected to heat from fuel combustion. The process is continuous, so the porcelain tiles enter the kiln and are slowly transported through it. The temperature in the furnace steadily increases towards the center, where it reaches its maximum (firing). The tile’s period at the maximum set temperature is called firing time [2,8,9]. Then, the temperature is gradually reduced, so the products leave the kiln close to room temperature [10]. The preheating and cooling times are defined to safely change the tiles’ temperature to avoid defects caused by thermal shock. The firing time depends on the raw materials’ composition, particle size, and the density of the green tile after pressing. The total time of the firing cycle (cold-to-cold) comprises the preheating, firing, and cooling times.

The productivity of a ceramic tile plant is inversely proportional to the total firing cycle time [6]. The firing stage is responsible for the most significant thermal energy consumption and is often assumed as the main production bottleneck [4][11–13]. Heat recovery installations are applied to industrial plants to minimize the firing influence. Usually, the hot air exhausted from the cooling zone of the kiln is used to warm up the air for the drying stage. Due to corrosion issues, standard heat exchangers are used for transferring the heat from the flue gas of the cooling zone to the clean hot air, which will then be sent to the dryer and spray dryer, reducing natural gas consumption [11–13].

Additionally, special attention is paid to the environmental aspects of ceramic tile manufacturing in Europe due to the new 2030 climate and energy target by the European Commission and the goal of an 80-95% reduction in CO₂ emissions by 2050 [14,15]. Reducing pollutant gas emissions implies diminishing fuel consumption. This is a highly complex optimization challenge since the factors that improve one step can often harm another stage. Therefore, it is not trivial to achieve environmentally friendly tile manufacturing while minimizing costs, increasing productivity, and maintaining industry competitiveness.

Increasing the level of automation can assist in controlling the manufacturing processes, permitting the increase in production volume, guaranteeing high-quality indicators, finding or eliminating bottlenecks, and minimizing production costs [16]. In recent decades, numerical simulations have become a valuable tool for optimizing and designing industrial equipment and evaluating operation parameters. Flowsheet calculations can be effectively applied for numerical investigations of complex plants, where different production steps are connected by material and energy streams [17–19].

Alves et al. [20] developed an integrated flowsheet process model for producing porcelain tiles and applied it to simulate the entire plant. The obtained flowsheet simulation framework, created using the Dyssol software [21,22], proved effective for investigating the complete processing sequence and considering the interdependencies between individual unit operations in the entire process chain for analyzing the influence of the main process parameters.

Later, the developed model was extended to consider both thermal and electrical energy consumption and coupled with MATLAB to offer the possibility of creating a digital twin of the processing sequence and optimizing it [23]. However, additional costs that influence the industry’s productivity, such as fixed costs, raw materials, maintenance, and amortization, were not considered. In this work, the proposed methodology was further extended to increase the productivity of the porcelain tiles manufacturing process while maintaining product quality and minimizing production costs. Industrial data were used to improve the accuracy of the applied model of the roller kiln, recalling that it is the main bottleneck of the manufacturing chain, compromising its productivity. Herein, we created a database based on flowsheet simulations to determine how productivity, manufacturing costs, and manufacturing sustainability can be improved by analyzing the firing process and the milling stage.

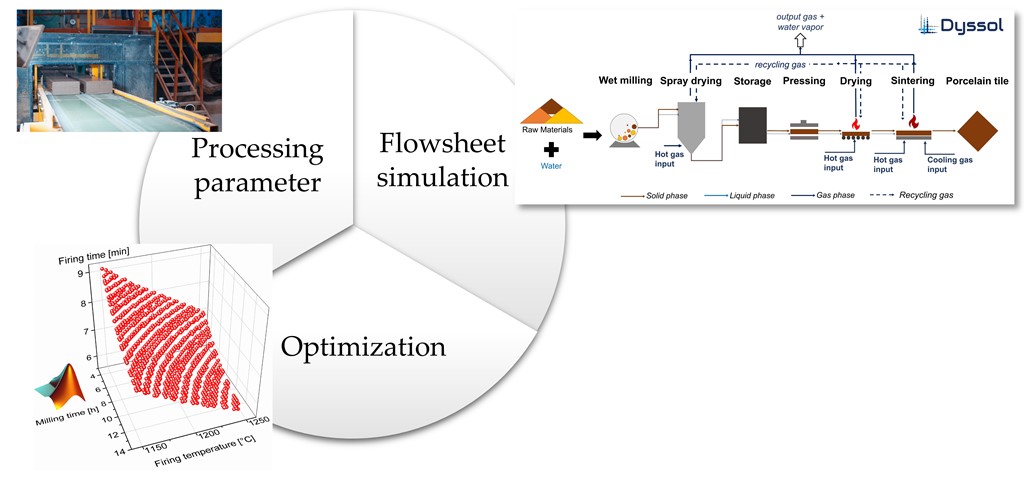
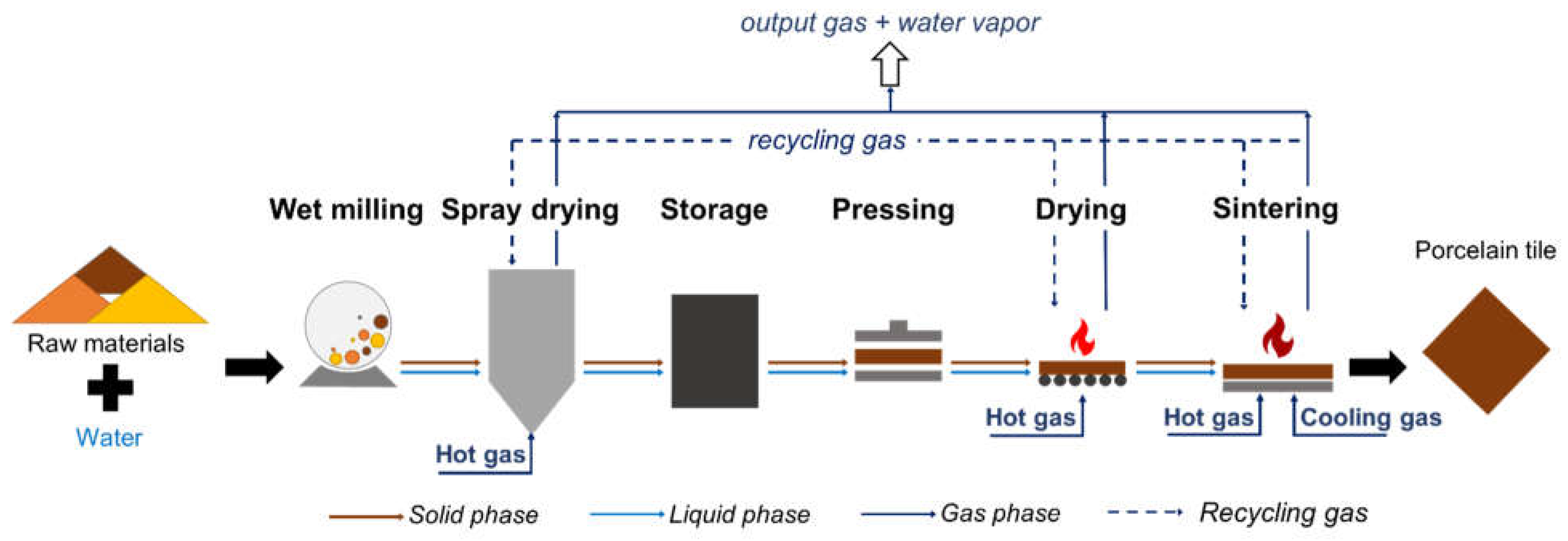
2. Materials and Methods

A flowsheet model for each unit was developed based on Alves et al. [20][23]. Nasetti et al. experimentally determined correlations between electrical energy consumption and processing parameters for each unit of the tile manufacturing sequence, and these relationships were used to implement the models of electrical energy consumption [24]. The thermal energy consumption for spray drying, drying, and firing units was modeled based on enthalpy and mass balances. The thresholds of thermal energy consumption from Nasetti et al. [24] were used to verify the obtained simulated values.

Wet milling involves mixing raw materials with water and grinding them in a ball mill for a set time to achieve the desired particle size and homogenization of the slurry components. The flowsheet model to describe the process was based on correlations proposed by Tsakalakis et al. [25] and Morell et al. [26].

During spray drying, the slurry from the wet milling is atomized, forming droplets consisting of liquid and primary particles, after which their moisture content is significantly reduced, reaching approximately 7 wt.%. For simplification, the spray drying unit was divided into an atomizer, where the droplets are formed, and a drying chamber. The atomizer was based on the model proposed by Walzel et al. [27]. The model proposed by Ali et al. [28] was adopted for drying the granules in a counter-current flow, which is the most widespread setup in spray drying for the ceramic tile industry.

After drying, the obtained granules are stored for moisture homogenization in a silo for approximately 24 h. It was assumed that moisture correlates with the size of the granules: bigger granules retain more water than smaller ones. Therefore, a liquid mass transfer model was developed based on the industrial data relating the moisture content in each granule and the average moisture content after spray drying [20].

The homogenized granules, after storage, are shaped into green tiles. A semi-empirical relationship proposed by Bal’shin et al. [32] was used to describe the uniaxial pressing, in which the porosity and, consequently, the density of the green tile depends on the density of the spray-dried powder, the applied pressure, and several semi-empirical parameters. Based on previous studies [5,33], the model was extended with the dependence of porosity on the average diameter d₅₀ of primary round particles [24]. Generally, the green tile porosity is 30% with a dry bulk density (ρpressing) of 1.9 g/cm³ [5,34].

During the subsequent drying, the moisture content of green tiles is further reduced from 6-8 wt% to less than 1 wt% by circulating hot gases in convective dryers. It was assumed that the change in the moisture distribution within a plate over time is controlled by diffusion, as stated by Fick’s law. The derived analytical solution by Henderson et al. [29,30] was used for the flowsheet model of this unit.

The final densification of tiles occurs in the roller kiln. The sintering stage of the firing process was assumed to be isothermal, and the porosity was modeled according to the approach developed by Gómez et al. [31]. The final total porosity of the tiles was fixed at nearly 5%, and the bulk density

(ρ_{f i r i n g})

was 2.35 g/cm³ [6,32,33]. At this level, the water absorption is assumed to be less than 0.5%, and the product rises to the standard level to be considered a porcelain tile.

All models were validated by experimental and industrial data. Alves et al. [20] laid the foundation for the models, materials database, and process parameters used to implement the energy consumption of each unit. Thermal and electrical energy consumption were considered separately for each unit, and the thermal consumption was based on energy and mass balances for every stream of the units. A more detailed description can be found in [23].

Despite previous models shown good accuracy, the volume gas flow required to keep a minimum firing temperature and the influence of the tiles load were not considered. These parameters are directly linked to productivity. Therefore, the gas consumption model for the kiln furnace was modified to include the productivity of the processing sequence and the effect of the load on the firing fuel consumption. The model was modified based on industrial data collected by SACMI, a supplier of ceramic tile equipment [37]. The new model additionally considers the fuel required to maintain the high temperature of the empty furnace, the heat generated from the fumes, and the endothermic reactions that take place during the firing of porcelain tiles. The main reactions are clay dehydroxylation and α → β quartz transformation, which require additional energy [34]. In the new model, the hot gas consumption by the kiln is given as follows:

{\dot{v}}_{f, f i r} = {\dot{v}}_{u l}^{F R} + X_{f / p} {C p}_{f} (T - T^{R F}) \frac{{\dot{m}}_{p}}{L H V} + (∆ H + C p (T - T^{a m b})) \frac{{\dot{m}}_{p}}{L H V},

(1)

Here,

{\dot{v}}_{f, f i r}

is the volume flow of the hot gas required for firing in Nm³/h;

{\dot{v}}_{u l}^{R}

is the flow of gas needed to keep the empty furnace at a high temperature in Nm³/h;

T

is the firing temperature in ˚C;

T^{R F}

is the reference temperature – the minimum at which firing takes place in ˚C;

X_{f / p}

is a mass ratio of combustion fumes and dilution air to the amount of the tiles in kcal/kg·°C;

{C p}_{f}

is the average specific heat capacity at a constant pressure of combustion fumes in kcal/kg·°C;

∆ H

is the energy consumption due to endothermic reactions in kcal/kg ,

C p

is the average specific heat capacity at a constant pressure of the tiles in kcal/kg·°C;

T^{a m b}

is the ambient temperature assumed to be 25 ºC;

{\dot{m}}_{p}

is the mass flow of tiles in kg/s; and

L H V

is lower heating value of natural gas in kcal/Nm³. The specific weight of the tile

γ

is used to convert the mass flow rate to the number of square meters of tiles produced. These variables’ values were based on the established values of SACMI that are applied to the industry [35,36], presented in Table 1.

The total productivity of the processing sequence

P r

is defined as [37]

P r = \frac{L w η_{g} {η_{l r}}^{2}}{t_{f}}

(2)

where

L

and

w

are the kiln length and width in m, respectively, with the values given in Table 1.

η_{g}

is the geometry efficiency,

η_{l r}

is the shrinkage efficiency and

t_{f}

is the firing time in s. The geometry efficiency

η_{g}

is the ratio of the area occupied by the tiles to the total area of the furnace. It is assumed to be 0.98, considering 1 cm of spacing between longitudinal rows and 2 mm spacing between transverse rows [38].

η_{l r}

is based on the linear shrinkage (

l r

) during firing, as seen in Equation (3). It is calculated based on the density of the tile after firing (

ρ_{f i r i n g}

) and the density of the green tile (

ρ_{p r e s s i n g}

), as shown in [39,40].

η_{l r} = {(1 - l r)}^{2}

(3)

l r = 1 - {(\frac{(1 - F L) ρ_{p r e s s i n g}}{ρ_{f i r i n g}})}^{\frac{1}{3}}

(4)

Here FL is the fire loss, which depends on the raw material composition and usually ranges from 2.5 wt% to 4.5 wt%. In all simulations, FL was assumed to be 3.5 wt%, considering it depends mainly on the composition of raw materials that were kept constant. The total firing cycle time cold-to-cold

t_{f}

(the sum of pre-heating, firing, and cooling time) depends on the firing or holding time

t_{s}

at the sintering temperature

T

. Typically,

t_{f}

can be assumed as

t_{f} = 6 t_{s}

(5)

The milling, total firing cycle time, and, consequently, the firing time, and the firing temperature, were identified as the most critical parameters that directly affect the productivity and cost of the process, in addition to product quality. The flowsheet simulation was used to establish their quantitative values. Therefore, the three indicated parameters were schematically studied, varying their values within the limits given in Table 2. These intervals have been chosen according to actual industrial data. A total of 64,000 simulations were carried out. The milling time, firing time, and temperature were generated using equidistant sampling, and the values were linearly generated for 40 points. Each simulation lasted about 10 s, so the total CPU time of the calculations was about 178 hours.

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

After sintering, the final open porosity of the tiles was used as the product quality. As standard, the final total porosity of porcelain tiles should remain between 4.8 to 5.1% [32,39,41]. The results of 89901 simulations showed porosity outside this range, so only the remaining 1099 were used for further analysis.

The costs assessment includes thermal and electrical energy, fixed costs, and taxes on CO₂ emissions. The utilized fuel was natural gas with a lower heating value (LHV) of 8500 kcal/Nm³ or 9.88 kWh/Nm³ and estimated CO₂ emissions estimated of 56100 kg CO₂ per TJ or approximately 0.2 kg CO₂ per kWh leading to the emission of 1.976 kg CO₂ per Nm³ of natural gas [36,42]. The current price and tax data for Brazil and Spain (Table 3), which are among the top five global producers were used [2,43] to calculate the cost indicators.

The total electrical energy consumption (

{\dot{E}}_{e l, t o t a l}

) in kWh/ton is given by the sum of the electrical energy consumption of each unit in the processing sequence (Equation (6)). Equations (6) to (11) describe the interplay between the mass load and the electrical energy consumption milling, pressing, spray drying, drying, and firing, respectively. The correlations were proposed by the collected data from Nassetti et al. [24] Specifically for milling, there is the additional consideration of the milling time (

t_{m i l l}

The sum of fuel consumption is determined by the sum of fuel required for spray drying, drying, and sintering (Equation (6)). For the Brazilian scenario, the adopted fuel for spray drying is biomass or coal instead of natural gas. In Europe, natural gas was maintained to fit accurate industry practices. The use of a cogeneration plant coupled with the spray-dried process was neglected. Accordingly, the value for the spray drying seen in Table 3 was kept constant, and it was not considered for determining the fuel amount sum presented in Equation (12).

{\dot{E}}_{e l, t o t a l} = {\dot{E}}_{e l, m i l l} + {\dot{E}}_{e l, s p d r y} + {\dot{E}}_{e l, p r e s s} + {\dot{E}}_{e l, d r y} + {\dot{E}}_{e l, f i r}

(6)

{\dot{E}}_{e l, m i l l} = 7.6 {\dot{m}}_{p} t_{m i l l}

(7)

{\dot{E}}_{e l, p r e s s} = 20 {\dot{m}}_{p}

(8)

{\dot{E}}_{e l, s p d r y} = 8 {\dot{m}}_{p}

(9)

{\dot{E}}_{e l, d r y} = 12 {\dot{m}}_{p}

(10)

{\dot{E}}_{e l, f i r} = 22 {\dot{m}}_{p}

(11)

{\dot{v}}_{f, t o t a l} = {\dot{v}}_{f, d r y} + {\dot{v}}_{f, f i r}

(12)

There is currently no CO₂ tax for the Brazilian industry, so this value was not considered in the cost calculation, differing from the industry conditions in Europe, where CO₂ emissions taxes currently exist [44–46]. The costs of raw material and glazing in Spain were assumed to be the same as in Brazil, given that these values do not vary because of the different processing parameters and consequently do not influence the variation in the total production cost. It is assumed that the glazing mass is 10% of the total mass of the tiles [35,36]. The entire energy spent was converted based on the fuel price and calorific value. The Brazilian cost of production (

C_{p r, B r a z i l})

and Spanish cost (

C_{p r, S p a i n})

can be seen in Eqs.(13) and (14), respectively. For both Brazil and Spain, extra charge for staffing, miscellaneous inputs, maintenance, and insurance are estimated to be 1/3 of the total production cost [37,38] (

C_{e x t r a} = 1 / 3 C_{p r}

). Additionally, packing is assumed to be 1/4 of the whole production cost (

C_{p a c k i n g} = 1 / 4 C_{p r}

). Hence, the total costs for Brazil and Spain are given by

C_{p r, B r a z i l} = (1 + \frac{1}{3} + \frac{1}{4}) [γ P r (C_{r a w} + C_{g l a z} 0.1 + C_{e l} E_{e l, t o t a l} + \frac{E_{t h, s d r y} C_{s d r y}}{L H V} + \frac{E_{t h, d r y} C_{f u e l}}{L H V}) + {\dot{v}}_{f, f i r} C_{f u e l}]

(13)

C_{p r, S p a i n} = (1 + \frac{1}{3} + \frac{1}{4}) [γ P r (C_{r a w} + C_{g l a z} 0.1 + C_{e l} E_{e l, t o t a l} + \frac{{(E}_{t h, s d r y} + E_{t h, d r y}) C_{f u e l}}{L H V}) + {\dot{v}}_{f, f i r} C_{f u e l}] + {1.976 C}_{C O 2} {\dot{v}}_{f, t o t a l}

(14)

The costs were evaluated based on the total cost per meter squared of produced porcelain tile (USD/m²), and the sustainability of the process sequence is evaluated based on the total CO₂ emission. The following exchange rates were used to calculate prices in US dollars: 0.19 USD/R$ and 0.98 USD/€.

3. Results and Discusion

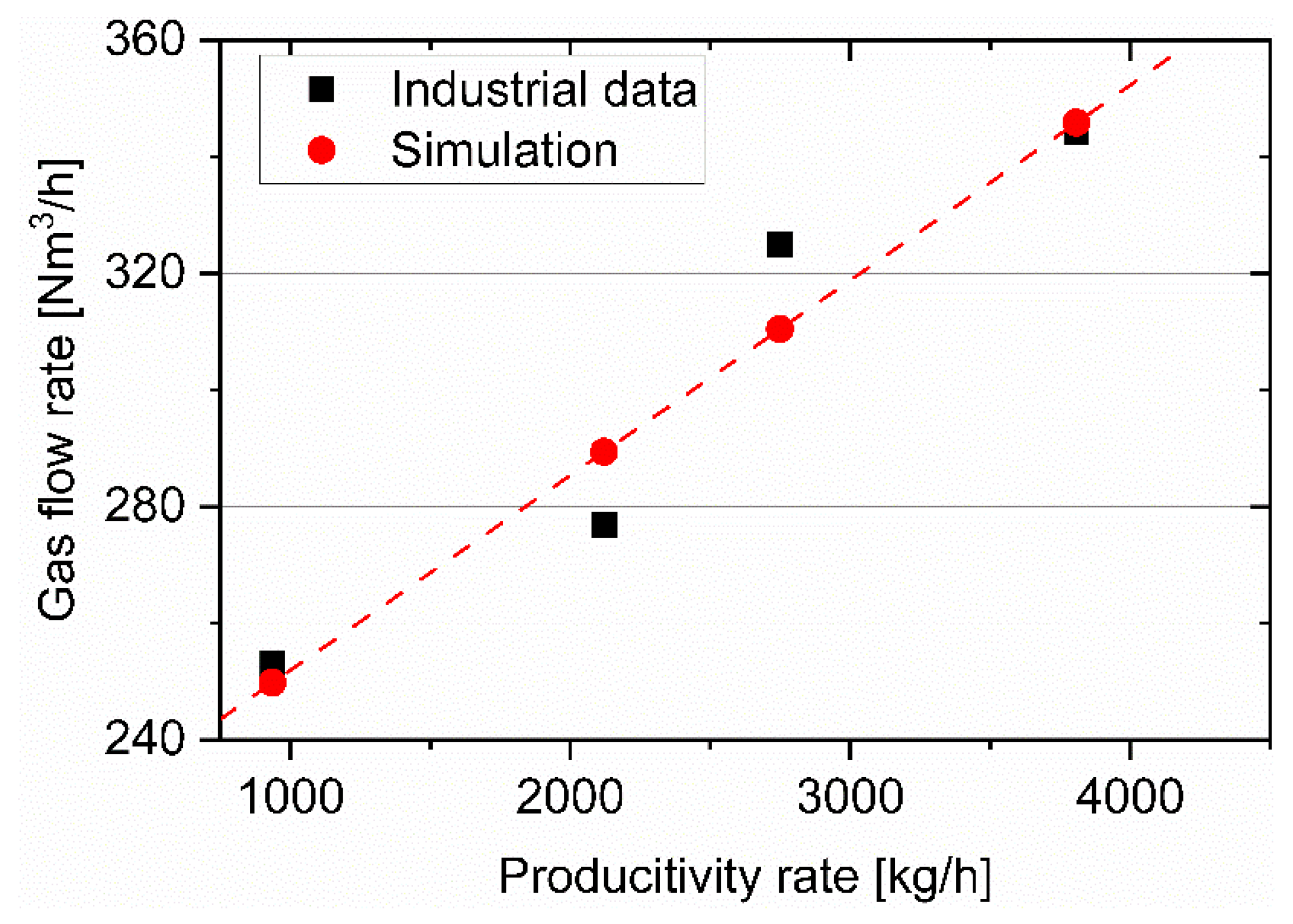
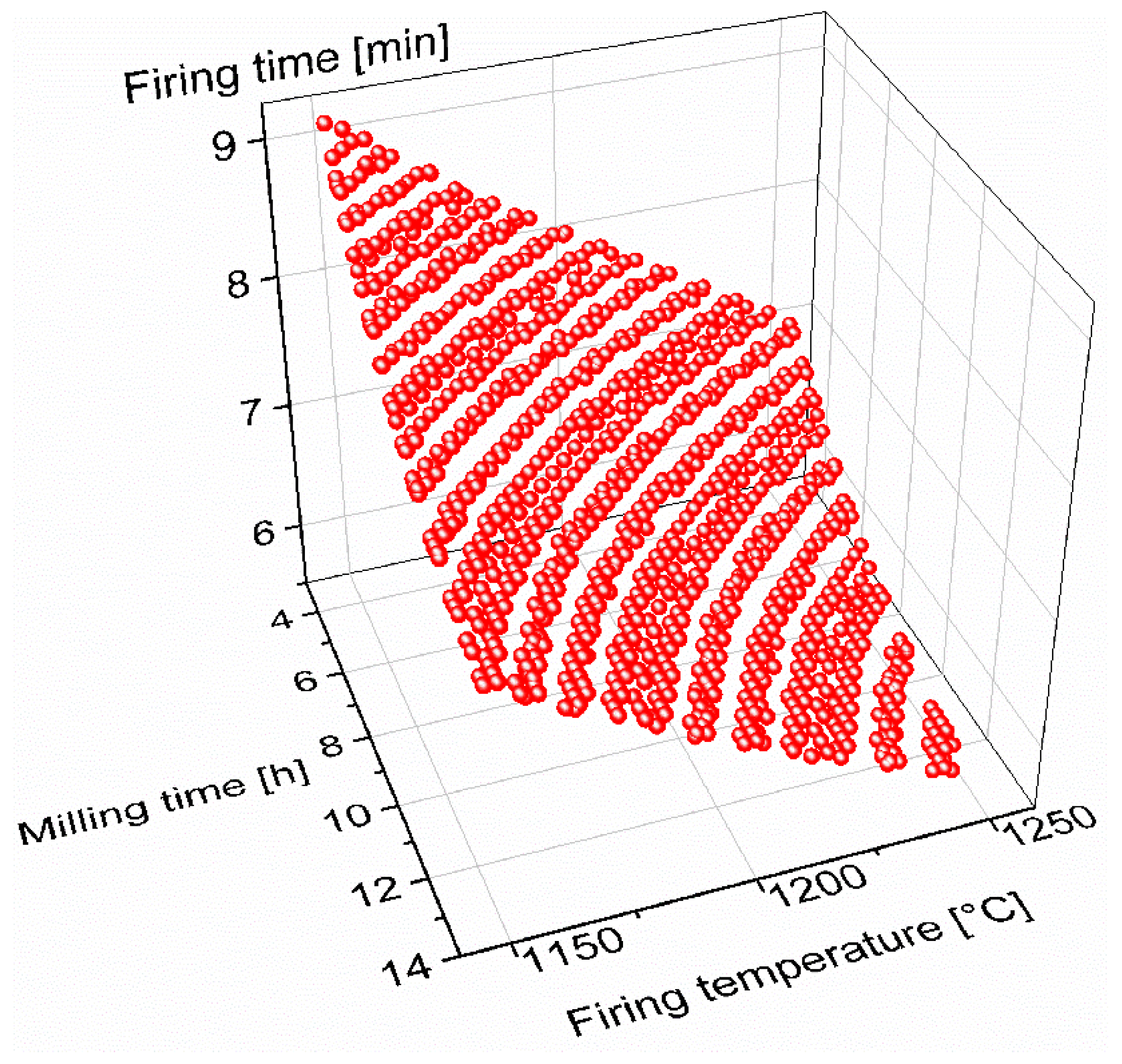
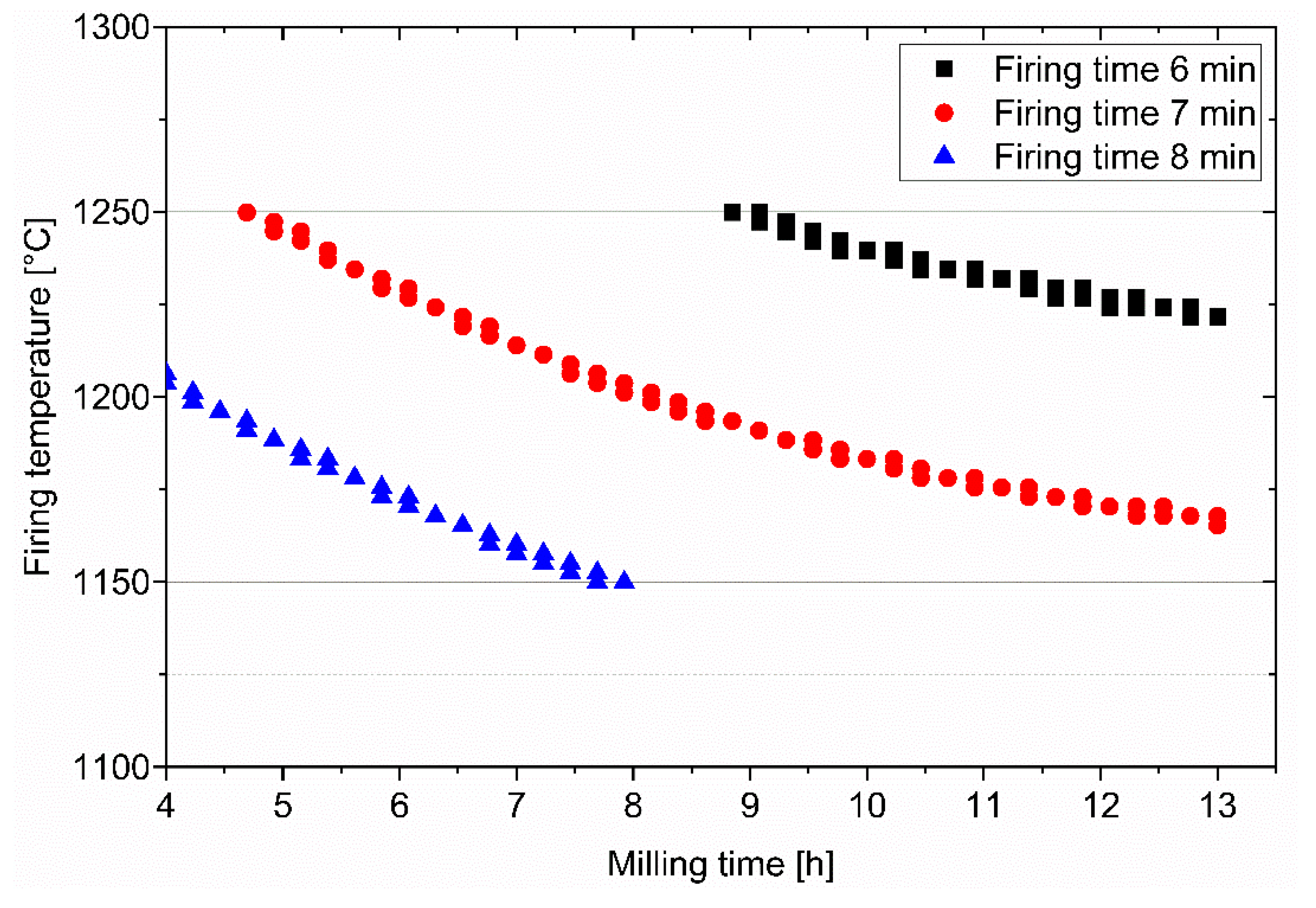
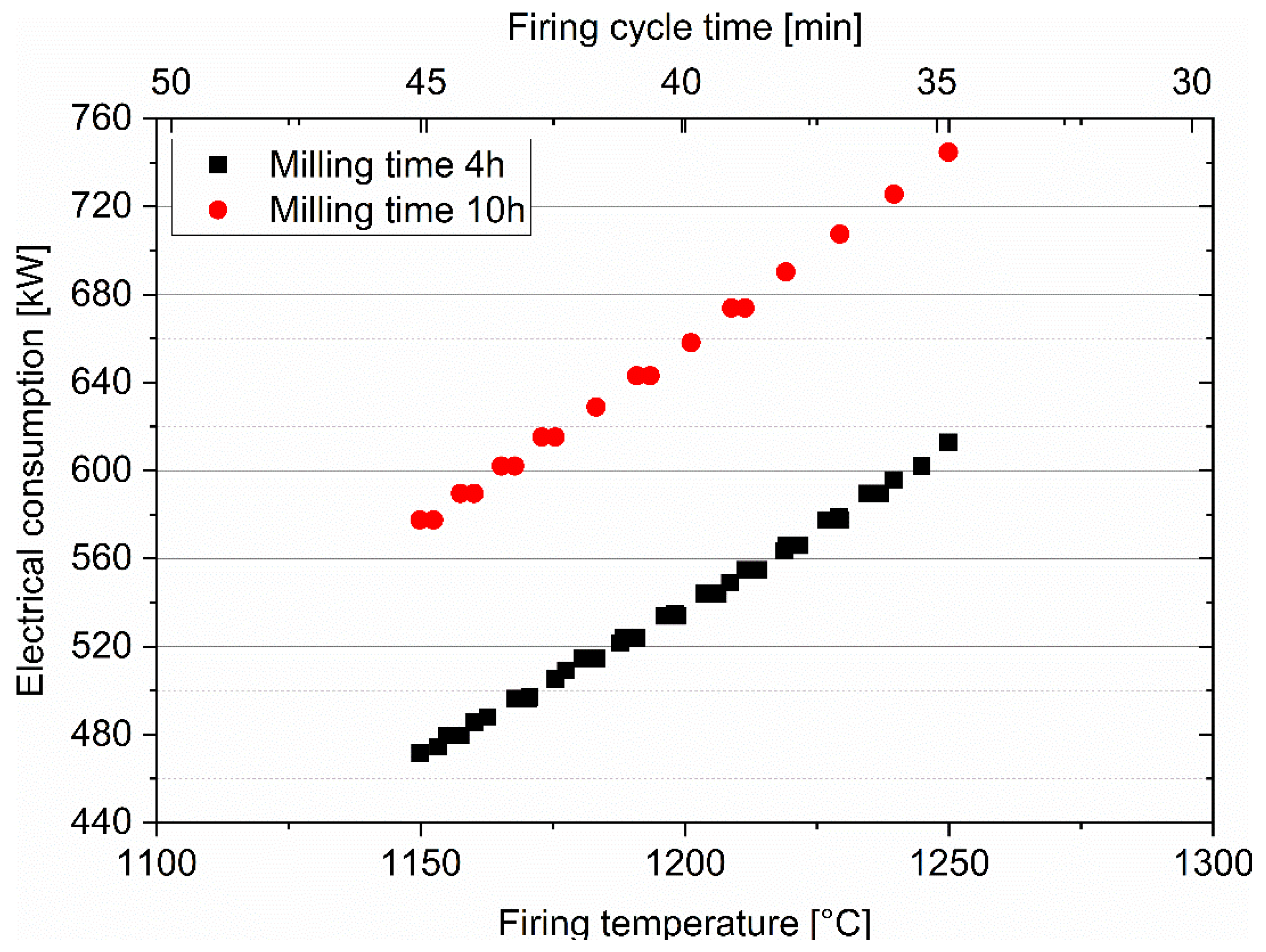
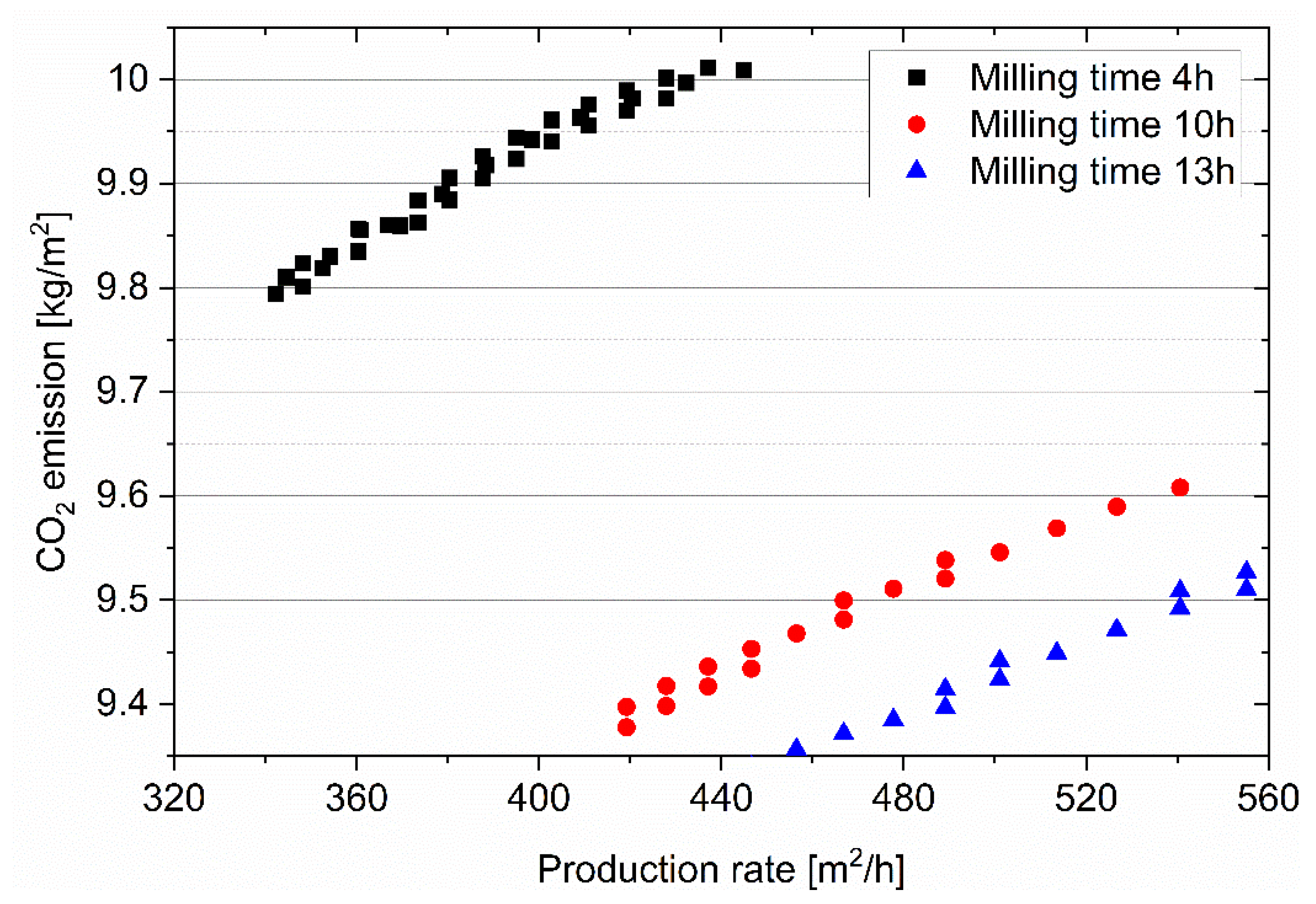
3.1. Simulation results

The dependence of the roller kiln productivity on the gas flow consumption obtained by the developed model was compared with industrial data and showed very good agreement (Figure 2). Variations can be justified by assumed constant simulation values such as endothermic reaction energy, the ratio of exhausting gases to the mass of the tiles, and averaged values of specific heat capacity for both fumes and tiles.

All found combinations of milling time, firing temperature, and the total firing cycle time required to reach the final total porosity in the range of 4.8 to 5.1% can be seen Figure 3.

From the data, a surface equation with the firing time, firing temperature and milling time can be derived (s. Eq.(15)) with and R² agreement of 99.75%.

t_{f i r i n g} = 36.59 - 1.09 t_{m i l l i n g} - 2.23 \cdot 10^{- 2} T_{f i r i n g} + 1.79 \cdot 10^{- 2} {t_{m i l l i n g}}^{2} + 5 \cdot 10^{- 4} t_{m i l l i n g} T_{f i r i n g}

(15)

To reach the same range of product quality, lower firing temperatures and firing times can be applied if longer milling times are adopted. Consequently, longer milling times can be beneficial for the reduction of fuel consumption. The same conclusion has been drawn by Darolt et al. [6] and Beltrán et al. [41]. The size of reactant particles governs the kinetics of sintering [47]. Small particles primarily induce the reaction because of the decrease distances among them and high available surface area.

The development of the solid-state reaction product in powder systems happens mostly at particle contact sites. As a result, the particle size directly affects porosity after sintering [20,48]. Figure 4 compares the requirement of firing temperature and milling times for different firing times. Two possibilities can be distinguished for the same firing time. Longer milling times can allow lower firing temperatures, which will greatly reduce thermal energy consumption. Therefore, the same productivity would be obtained while diminishing costs. Additionally, the same firing temperatures can be kept for shorter firing times, again, allowing higher productivity for the same energy thermal consumption.

To further explore dependencies, the production rate was compared for different firing cycle times and firing temperatures for milling times of 4, 10 and 13h as seen in Figure 5.

Longer milling time results in higher production rates at the same firing temperature to keep the same range of the tiles' final total porosity. Similarly, longer firing times are required to reduce milling time, leading to lower production rates to retain the same quality of the final product [49]. Thus, applying longer milling time and keeping the same firing temperatures, maintaining the same invested costs on firing, the productivity rate increases.

The dependency of the electrical consumption of the entire production plant on the firing cycle times and firing temperatures required to reach the determined product quality for different milling times is shown on Figure 6. As expected, the increased milling times lead to higher electrical consumption, considering milling relies exclusively on electrical energy. Nevertheless, this increase in electrical energy consumption did not increase the total production costs, as it will be shown in Section 3.2.

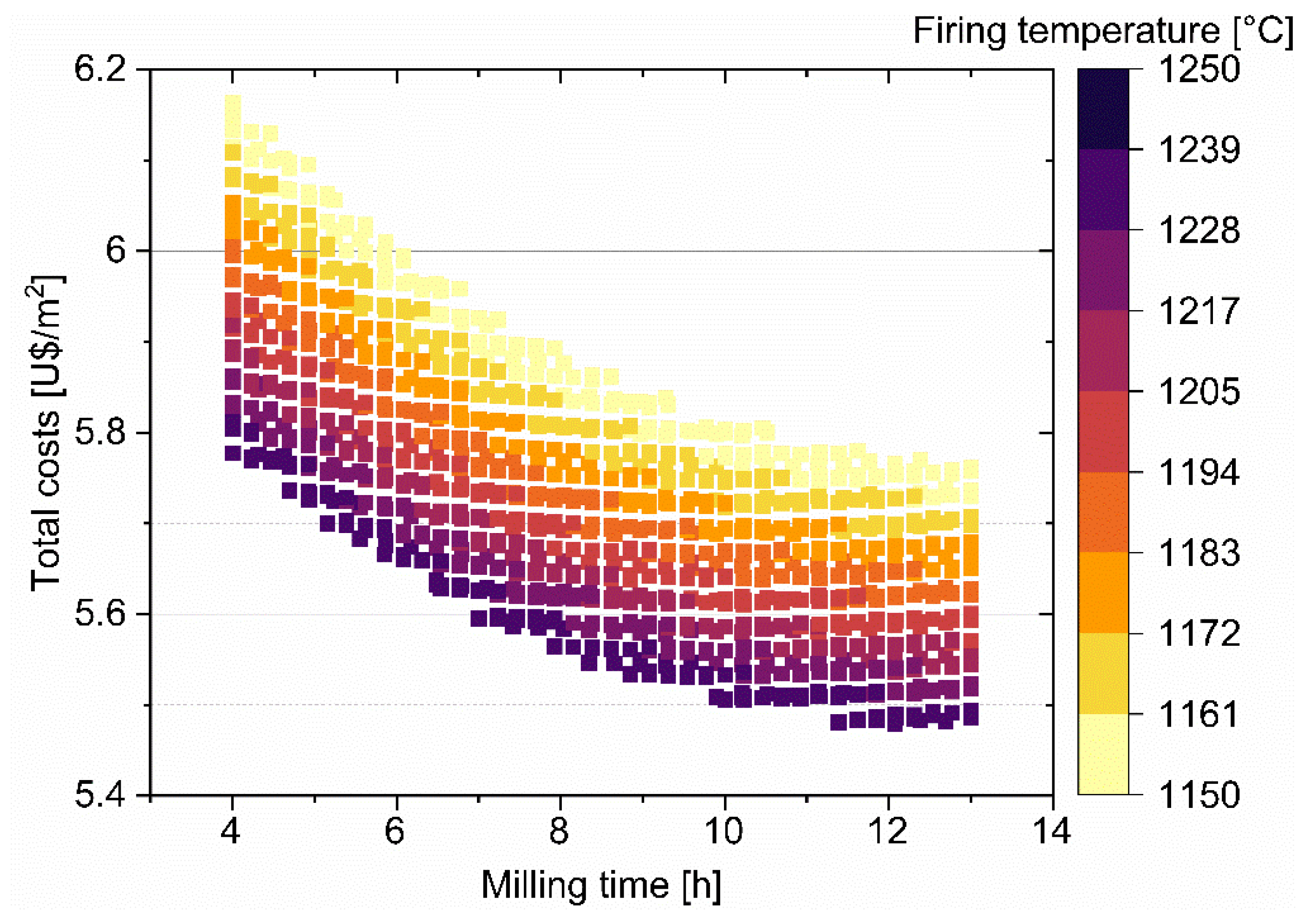
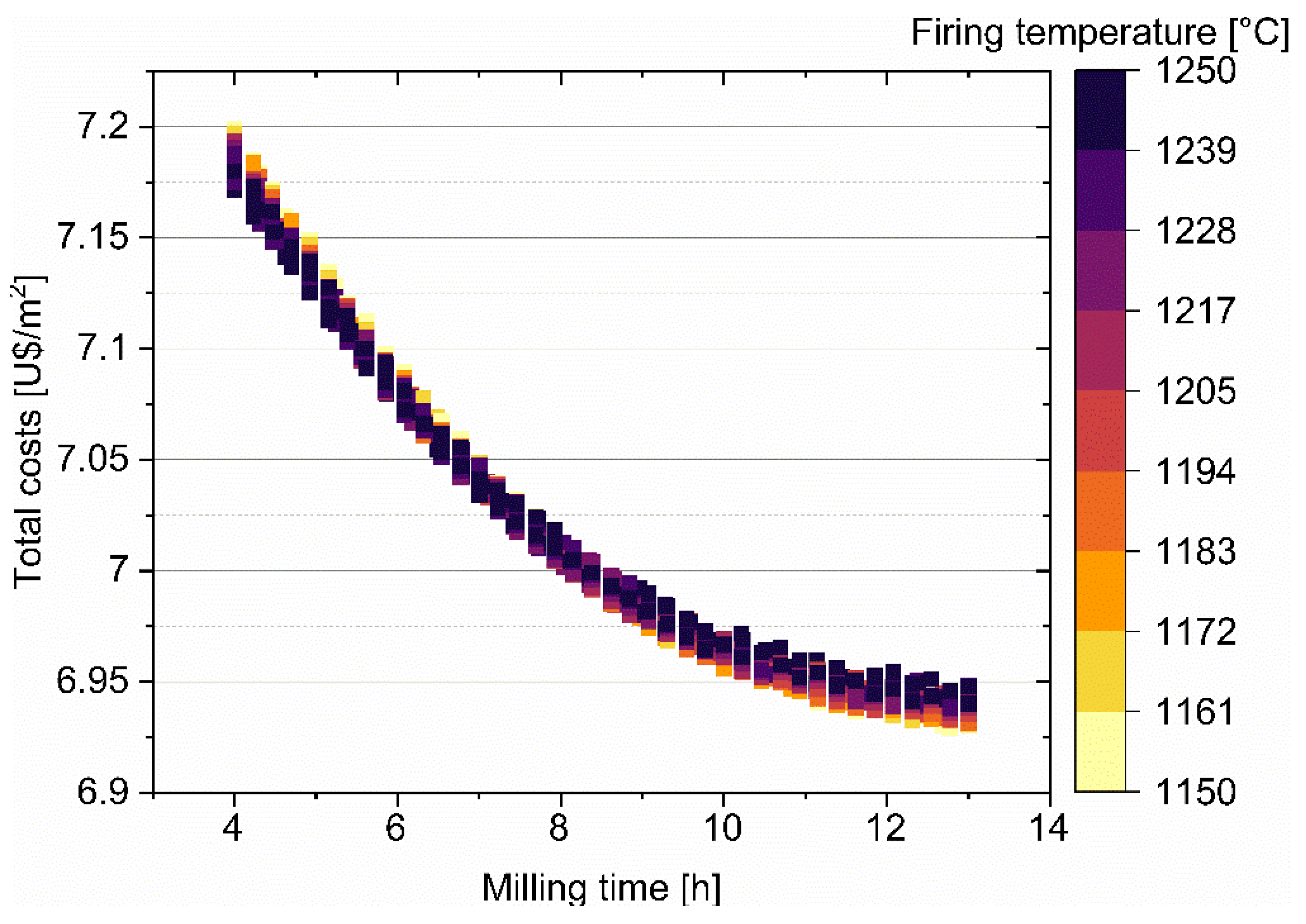
3.2. Economic impact

To evaluate the economic impact of different process parameters in Brazilian and Spanish economic environments, the total production costs, considering the expenses given in Table 3 were investigated as a dependency of different milling times, as seen in Figure 7and Figure 8.

Comparing both economic scenarios, it becomes clear that the reduction of costs occurs with increasing milling times in both cases. However, there is a smaller scattering of costs for the same milling time in the case of Spain. The scattering is attributed to the CO₂ emission tax, which is currently not applied to costs in Brazil, and the higher fuel cost in Spain. Even though extended milling increases the electrical costs proportionally, the direct impact of reducing the thermal energy costs results in smaller total expenses.

The sustainability of the process can be interpreted in terms of the CO₂ emission rate. It can be observed an increase of CO₂ emission per m² of tile with increasing production rate, as seen in Figure 9. Therefore, longer milling times can reduce the CO₂ emission without interfering with the production rate, keeping the product quality. These trends are an exciting result given the new climate and energy target the European Commission has established for the industries to meet in 2030 [15].

However, longer milling times lead to higher erosion of the gridding balls used during the process, which will result in higher expenses not accounted for here. Additionally, longer milling times result in smaller pores size after conformation, lower bulk density and dry strength [6,20]. Smaller particles originating from excessive milling have a higher tendency to adhesion and agglomeration that compromise the fluidity into the conformation die. Even though it is desired to increase the packing efficiency and uniformity in the die during pressing, and smaller granules can achieve this, the attractive forces retard the flow of small granules and reduce the fill density and flow rate. In general, narrow granule size distributions and small dimensions of die cavities determine a lower packing density. Increasing aspect ratio (i.e., height/diameter) in small dies makes the variability in packing density increase [50–52]. So, to increase press productivity, higher dry strength and higher density are beneficial to minimize the shock or vibration losses index.

Moreover, decreasing milling times and larger primary particles can reduce the product's thickness. Consequently, longer milling times might lead to the need of changing pressing dies to overcome dimensions mismatch and avoid hindering productivity by the pressing process. Also, the requirement of longer milling times might require additional ball mills to maintain the continuity of the production line. Therefore, these changes are not straightforward and require an initial investment, also highlighting the importance of the simulation approach presented here for the development of tools to aid decision-making.

Nassetti et al. [24] have reported a reduction in energy consumption using an additional attritor mill within the ceramic tile process after conventional milling. Darolt et al. [6] and Kucuker et al. [53] have also stated the benefits of high-energy milling employment in ceramic tiles manufacturing by reducing the particle size distribution of the composition compared to conventional milling, given this additional milling showed an increase in dry mechanical strength and increasing bulk density of the tile after. Consequently, additional equipment of an attritor mill can be proposed as an alternative to additional ball mills in the production line.

4. Conclusions

The market growth of porcelain tiles manufacturing emphasizes the requirement for higher productivity to keep the industry competitive. Concurrently, there is an increased demand for CO₂ emission reduction due to environmental aspects.

An optimization methodology utilizing flowsheet simulation was used to investigate alternative processing parameters to modify the firing stage specification to increase industrial productivity and reduce CO₂ emission. The simulations were used to create a database where the operating costs of each processing unit were coupled, including electrical and thermal costs and process productivity. The final total porosity of the tile was restricted to be in the range of 4.8 to 5.1%, representing about 1% of open porosity and 0.5% of water absorption to maintain the final product quality. The economic impact was investigated based on the current costs in Brazil and Spain, which are among the world’s greatest producers.

For the same firing time, longer milling times can result in lower firing temperatures to keep the same final porosity range, which can considerably save thermal energy, resulting in the same production but at a lower cost. In contrast, the same firing temperatures can be maintained for shorter firing times if longer milling times are used, resulting in increased productivity for the same thermal energy consumption. Increased milling times did not compromise the overall costs in both Brazil and Spain, even though there is an increase in electrical energy consumption. Similarly, longer milling times can reduce the CO₂ emission rate due to reduced firing temperature.

The increased milling periods can compromise the pressing stage due to a reduction in dry density. Consequently, changes in dies for the press can be required to maintain the press productivity. Also, the additional milling times can increase the erosion and wear of the ball mills and lead to extra costs not considered in the simulation framework. It can also transfer the production bottleneck from the kiln to the grinding operation. Alternatively, using high-energy milling may show great potential to overcome the requirement of additional ball mill units.

Numerical investigations and simulations using the Dyssol framework were proven to effectively predict the outcome of modified process parameters in the porcelain tile production line. The simulations can be used to propose modifications to increase productivity and process sustainability, towards developing tools for aid decision-making. The proposed methodology has shown great potential in digitizing the complete process sequence and establishing a digital twin of the ceramics production chain.

Author Contributions

Conceptualization, C. L. Alves, A. de Noni Jr. and S.Y.G. González; methodology, C. L. Alves.; software, C. L. Alves, V. Skorych; validation, A. de Noni Jr.; resources, S. Heinrich, A. de Noni Jr, D. Hotza.; writing—original draft preparation, C. L. Alves.; writing—review and editing, C. L. Alves, V. Skorych, A. de Noni Jr., S.Y.G. González, D. Hotza, S. Heinrich ; supervision, D. Hotza, S. Heinrich, A. de Noni Jr; funding acquisition, S. Heinrich, A. de Noni Jr, D. Hotza.;

Funding

This research was funded by German Research Foundation (DFG). Project ID: 418788750 (DFG DO 2026/ 6-1) and DFG Graduate School GRK 2462 ‘Processes in natural and technical particle fluid systems (PintPFS) (Project No. 390794421) as well the DAAD (Pro Bral 57447192) and CAPES-DFG program (PIPC 88881.207634/2018-01).

Acknowledgments

We thank Dr.-Ing Maksym Dosta for the assistance and help with the simulation methodology.

Conflicts of Interest

The authors declare no conflict of interest.

References

Market research report, Ceramic tiles market size: Share & COVID -19 Impact Analysis, by implaction area (Floor, Walls,Others), By End-Use (Residential, Non Residential), and Regional Forecast, 2021-2028, 2022. https://www.fortunebusinessinsights.com/ceramic-tiles-market-102377.
S. Ferrer, A. Mezquita, V.M. Aguilella, E. Monfort, Beyond the energy balance: Exergy analysis of an industrial roller kiln firing porcelain tiles, Applied Thermal Engineering 150 (2019) 1002–1015. [CrossRef]
J.L. Bombazaro, A.M. Bernardin, Improving plasticity of kaolins by high-energy milling for use in porcelain tile compositions, Open Ceramics 10 (2022) 100256. [CrossRef]
E. Monfort, A. Mezquita, R. Granel, E. Vaquer, A. Escrig, A. Miralles, V. Zaera, Analysis of energy consumption and carbon dioxide emissions in ceramic tile manufacture, Boletin De La Sociedad Espanola De Ceramica Y Vidrio 49 (2010) 303–310.
E.F.S. Ciacco, J.R. Rocha, A.R. Coutinho, The energy consumption in the ceramic tile industry in Brazil, Applied Thermal Engineering 113 (2017) 1283–1289. [CrossRef]
R.D. Darolt, M. Cargnin, M. Peterson, A. de Noni, Additional high-energy milling to enhance the performance of porcelain stoneware manufacturing, Int J Appl Ceram Technol 17 (2020) 1742–1751. [CrossRef]
M.U. Taskiran, N. Demirkol, A. Capoglu, Influence of mixing/milling on sintering and technological properties of anorthite based porcelainised stoneware, Ceramics International 32 (2006) 325–330. [CrossRef]
H.A. Refaey, A.A. Abdel-Aziz, M.R. Salem, H.E. Abdelrahman, M.W. Al-Dosoky, Thermal performance augmentation in the cooling zone of brick tunnel kiln with two types of guide vanes, International Journal of Thermal Sciences 130 (2018) 264–277. [CrossRef]
H.A. Refaey, A.A. Abdel-Aziz, R.K. Ali, H.E. Abdelrahman, M.R. Salem, Augmentation of convective heat transfer in the cooling zone of brick tunnel kiln using guide vanes: An experimental study, International Journal of Thermal Sciences 122 (2017) 172–185. [CrossRef]
H.A. Refaey, B.A. Almohammadi, A.A. Abdel-Aziz, H.E. Abdelrahman, H.A. Abd El-Ghany, M.A. Karali, M.W. Al-Dosoky, Transient thermal behavior in brick tunnel kiln with guide vanes: Experimental study, Case studies in thermal engineering (2022) 101959. [CrossRef]
B. Delpech, M. Milani, L. Montorsi, D. Boscardin, A. Chauhan, S. Almahmoud, B. Axcell, H. Jouhara, Energy efficiency enhancement and waste heat recovery in industrial processes by means of the heat pipe technology: Case of the ceramic industry, Energy 158 (2018) 656–665. [CrossRef]
Cogeneration systems in the ceramics tile sector, 1994.
C. Agrafiotis, T. Tsoutsos, Energy saving technologies in the European ceramic sector: a systematic review, Applied Thermal Engineering 21 (2001) 1231–1249. [CrossRef]
M. Castro Oliveira, M. Iten, P.L. Cruz, H. Monteiro, Review on Energy Efficiency Progresses, Technologies and Strategies in the Ceramic Sector Focusing on Waste Heat Recovery, Energies 13 (2020) 6096. [CrossRef]
European Commission, European Commission. https://ec.europa.eu/info/.
D.S. Barbosa, J.E. Silva, R.A.F. Machado, D. Hotza, Controle e automação na indústria cerâmica: estudo de caso na fabricação de porcelanato no Brasil, Revista Cerâmica Industrial 13 (2008) 23–30.
M. Dosta, J.D. Litster, S. Heinrich, Flowsheet simulation of solids processes: Current status and future trends, Advanced Powder Technology 31 (2020) 947–953. [CrossRef]
V. Skorych, M. Buchholz, M. Dosta, H.K. Baust, M. Gleiß, J. Haus, D. Weis, S. Hammerich, G. Kiedorf, N. Asprion, H. Nirschl, F. Kleine Jäger, S. Heinrich, Use of Multiscale Data-Driven Surrogate Models for Flowsheet Simulation of an Industrial Zeolite Production Process, Processes 10 (2022) 2140. [CrossRef]
J. Haus, E.-U. Hartge, S. Heinrich, J. Werther, Dynamic flowsheet simulation for chemical looping combustion of methane, International Journal of Greenhouse Gas Control 72 (2018) 26–37. [CrossRef]
C.L. Alves, A. de Noni Jr, R. Janssen, D. Hotza, J.B. Rodrigues Neto, S.Y. Gómez González, M. Dosta, Integrated process simulation of porcelain stoneware manufacturing using flowsheet simulation, CIRP Journal of Manufacturing Science and Technology 33 (2021) 473–487. [CrossRef]
V. Skorych, M. Dosta, S. Heinrich, Dyssol—An open-source flowsheet simulation framework for particulate materials, SoftwareX 12 (2020) 100572. [CrossRef]
V. Skorych, M. Dosta, E.-U. Hartge, S. Heinrich, Novel system for dynamic flowsheet simulation of solids processes, Powder Technology 314 (2017) 665–679. [CrossRef]
C.L. Alves, V. Skorych, A. de Noni Jr, D. Hotza, S.Y. Gómez González, S. Heinrich, M. Dosta, Improving the sustainability of porcelain tile manufacture by flowsheet simulation, Ceramics International.
G. Nassetti, F. Ferrari, A. Fregni, G. Maestri, Piastrelle Ceramiche & Energia: Banca dati dei consumi energetici nell' industria delle piastrelle di ceramica, Assopiastrelle, Bologna, 1998.
K.G. Tsakalakis, G.A. Stamboltzis, Modelling the specific griding energy and abll- mill scaleup, IFAC Proceedings Volumes 37 53–58.
Morrell, Power draw of wet tumbling mills and its relationship to charge dynamics- Part 1: a continuum apprach to a mathematical modelling of mill power draw, Mineral processing and Extractive metallurgy 105 (1996) C43-C53.
P. Walzel, Spraying and Atomizing of Liquids, Ullmann’s Encyclopedia of Industrial Chemestry; Wiley-VCH Verlag GmbH: Weinheim, Germany (2012) 79–98.
M. Ali, T. Mahmud, P.J. Heggs, M. Ghadiri, D. Djurdjevic, H. Ahmadian, L.M. Juan, C. Amador, A. Bayly, A one dimensional plug flow model of a counter current spray drying tower, chemical engineering research and design 92 (2014). [CrossRef]
W. Kriaa, S. Bejaoui, H. Mhiri, G. Le Palec, P. Bournot, Study of dynamic structure and heat and mass transfer of a vertical ceramic tiles dryer using CFD simulations, Heat and Mass Transfer 50 (2014) 235–251. [CrossRef]
K. Khalili, M. Bagherian, S. Khisheh, Numerical simulation of drying ceramic using finite element and machine vision, Procedia Technology 12 (2014) 388–393. [CrossRef]
S.Y. Gómez, D. Hotza, Predicting powder densification during sintering, Journal of the European Ceramic Society 38 (2018) 1736–1741. [CrossRef]
A. de Noni, D. Hotza, V.C. Soler, E.S. Vilches, Influence of composition on mechanical behaviour of porcelain tile. Part I: Microstructural characterization and developed phases after firing, Materials Science and Engineering: A 527 (2010) 1730–1735. [CrossRef]
A. de Noni Jr, Modelagem matemática aplicada ao controle dimensional de placas cerâmicas de monoqueima processadas por via úmida: Dissertação (Mestrado em Ciência e Engenharia de Materiais), Universidade Federal de Santa Catarina, Florianópolis (2005).
J. Martín-Márquez, J.M. Rincón, M. Romero, Effect of firing temperature on sintering of porcelain stoneware tiles, Ceramics International 34 (2008) 1867–1873. [CrossRef]
S.A. Sacmi Iberica, Tecnología cerámica aplicada, Vol I, Faenza Editrice Ibérica SL Faenza RA, Italia: Litográfica Faenza SRL (2001).
A. van Gelder, Tecnología cerámica aplicada, Volumen II. SACMI (2004).
F.G. Melchiades, A. Canavesi, A.O. Boschi, Dimensionamento de Revestimentos Cerâmicos Visando a Maximização da Produtividade (Por que os Revestimentos tem os Tamanhos que tem?), Cerâmica Industrial 3 (2006) 13–15.
SACMI, Asociación Española de Técnicos Cerámicos, Tecnología cerámica aplicada, Castellón de la Plana: Faenza Editrice Iberica (2004).
G.B. Remmey, Firing ceramics, World Scientific, 1994.
H.A. Refaey, E. Specht, M.R. Salem, Influence of fuel distribution and heat transfer on energy consumption in tunnel kilns, International Journal of Advances in Engineering & Technology 8 (2015) 281.
Beltrán, V., Ferrer, C., Bagán, V., Sánchez, E., Garcia, J., & Mestre, S. (Ed.), Influence of pressing powder characteristics and firing temperature on the porous microstructure and stain resistance of porcelain tile, 1996.
J. Peng, Y. Zhao, L. Jiao, W. Zheng, L. Zeng, CO2 Emission Calculation and Reduction Options in Ceramic Tile Manufacture-The Foshan Case, Energy Procedia 16 (2012) 467–476. [CrossRef]
T. Ros-Dosdá, P. Fullana-i-Palmer, A. Mezquita, P. Masoni, E. Monfort, How can the European ceramic tile industry meet the EU's low-carbon targets? A life cycle perspective, Journal of Cleaner Production 199 (2018) 554–564. [CrossRef]
P. Runst, D. Höhle, The German eco tax and its impact on CO2 emissions, Energy Policy 160 (2022) 112655. [CrossRef]
P. Härtel, M. Korpås, Demystifying market clearing and price setting effects in low-carbon energy systems, Energy Economics 93 (2021) 105051. [CrossRef]
A. Bengochea-Morancho, F. Higón-Tamarit, I. Martínez-Zarzoso, Economic Growth and CO2 Emissions in the European Union, Environmental and Resource Economics 19 (2001) 165–172. [CrossRef]
R.E. Carter, Kinetic Model for Solid-State Reactions, The Journal of Chemical Physics 34 (1961) 2010–2015. [CrossRef]
J.L. Amorós, M.J. Orts, J. García-Ten, A. Gozalbo, E. Sánchez, Effect of the green porous texture on porcelain tile properties, Journal of the European Ceramic Society 27 (2007) 2295–2301. [CrossRef]
E. Sánchez-Vilches, V. Sanz-Solana, M.C. Bordes, J. Sales, K. Kayaci, M. Taşkiran, Ü. Anil, S. Türk, M. Tarhan, Firing deformation in large size porcelain tiles. Effect of compositional and process variables (2018).
W.J. Walker, J.S. Reed, S.K. Verma, Influence of Slurry Parameters on the Characteristics of Spray-Dried Granules, Journal of the American Ceramic Society 82 (1999) 1711–1719. [CrossRef]
J.S. Reed, Principles of ceramics processing (1995) 378–393.
M. Dondi, Powder Granulation and Compaction 136–145. [CrossRef]
A.S. Küçüker, A. Kara, K. Kayacı, S. Gerl, Cost Effective Slurry Preparation in Porcelain Tile Production, 0173-9913 (2009).

Figure 1. Flowsheet of manufacturing wet route of porcelain tile manufacturing.

Figure 2. Simulated values of gas consumption in roller kiln for firing compared to industrial data for different productivity.

Figure 3. Correlation between firing temperature, time, and milling time to reach the final total porosity between 4.8 and 5.1%.

Figure 4. Influence of milling time on firing temperature for firing cycle times of 36, 42, and 48 min.

Figure 5. (a) Dependency of production rate over firing cycle time for different milling times.; (b) Dependency of production rate from the firing temperature for different milling times.

Figure 6. Electrical consumption compared to required firing cycles and temperatures to reach the determined final open porosity range from 4.8 to 5.1%.

Figure 7. Milling time influence in Brazilian cost production in USD/m².

Figure 8. Milling time influence in Spanish cost production in USD/m².

Figure 9. Influence of milling time on CO₂ emission and production.

Table 1. Reference values for variables of the kiln furnace gas flow model [35,36].

Variable		Value	Units
Reference temperature	$T^{R F}$	1190	ºC
Specific weight of the tile	$γ$	20	kg/m²
Mass ratio of combustion fumes and dilution air to the amount of tiles	$X_{f / p}$	2.15	-
Specific heat capacity of combustion fumes	${C p}_{f}$	0.25	kcal/kg·°C
Specific heat capacity of the tiles	$C p$	0.22	kcal/kg·°C
Lower heating value of natural gas	$L H V$	8500	kcal/Nm³
Endothermic reactions energy	$∆ H$	50	kcal/kg
Required gas flow for empty kiln	${\dot{v}}_{u l}^{F R}$	218.52	Nm³/h
Kiln length	$L$	150	m
Kiln width	$w$	2.5	m

Table 2. Minimum and maximum values for milling time, firing time, and temperature for the investigations.

	Minimum value	Maximum value	Unit
Milling time	4	13	h
Firing temperature	1150	1250	ºC
Total firing cycle time	24	60	min

Table 3. Unit costs for raw materials, electrical energy, fuel, and CO₂ emissions taxes for Brazil and Spain.

	Brazil	Spain	Units
$Raw material (C_{r a w})$	28.5	28.5	USD/ton
$Glazing (C_{g l a z})$	475	475	USD/ton
$Electrical energy (C_{e l})$	0.0665	0.0497	USD/kWh
$Spray drying \cos t (C_{s d r y})$	0.076	0.0606	USD/kg of dried material
$Fuel (C_{f u e l})$	0.7733	1.5609	USD/Nm³
$Taxes on {CO}_{2} emissions (C_{C O 2})$	-	16.58	USD/ton CO₂

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.