Prerpints.org logo
Preprint
Article

Educational Multi-agent PLM System for Threaded Connections

Altmetrics

Downloads

339

Views

66

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 December 2022

Posted:

04 January 2023

You are already at the latest version

Alerts
Abstract
The PLM concept implies the use of heterogeneous information resources at different stages of the product life cycle, the joint work of which allows you to effectively solve the problems of product quality and various costs. According to the principle of isomorphism of regularities of complex systems, an effective PLM system must have these regularities. Unfortunately, this principle is not often fundamental when designing PLM systems. The purpose of the work is to show, using a simple example, the principles of development, operation and use of an educational multi-agent PLM system, the main purpose of which is to study and research these regularities in the life cycle of a special threaded connection. The multi-agent approach to the development of a PLM system provides the necessary prerequisites for the emergence of system-wide regularities in it. The parallel work of agents is implemented using the actor model and the Ray Python-package. Agents for the logical inference of knowledge base facts, CAD/FEA/CAM/SCADA agents, agents for optimization by various methods, and other agents have been developed. Open source software was used to develop the system. Each agent has relatively simple behavior, implemented by its rule function, and can interact with other agents. The system can work in interactive mode with the user or in automatic mode according to a simple algorithm: the rule functions of all agents are executed until at least one of them returns a value other than None. Examples of the operation of the system are given and such system-wide regularities as emergence, historicity and self-organization are demonstrated in it.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The product life cycle consists of the stages of design preparation, technological preparation of production, production and operation. At each stage of life cycle, appropriate approaches, methods, tools, knowledge and other information resources are used that help improve the quality of the product. The PLM (Product Lifecycle Management) [1,2,3] concept provides for combining these resources into a system to achieve a super-additive (synergy, emergence) effect [4]. A PLM system is an information system of heterogeneous information resources, the purpose of which is to provide information support for the stages of the life cycle of a product in order to improve quality and reduce costs.

2. Materials and Methods

How to effectively combine these resources into a system? The answer must be sought by analyzing other complex systems. The most important principle of systems theory is the principle of isomorphism of regularities of systems [5]. According to this principle, a PLM system, as a complex system, must have such regularities of complex systems as emergence, “requisite variety”, hierarchy, historicity, non-linearity, self-organization, two-phase evolution, adaptation, feedbacks (negative and positive or “damping” and “amplification”), self-similarity, openness, memory, and also have a structure similar to them [4]. Unfortunately, when developing PLM systems, this important principle is not often paid attention to [3,4]. Partially, these regularities are used in systems engineering [6] and systems analysis [7] techniques. In particular, the regularities of emergence, historicity, “requisite variety” and spontaneous order are noticeable in the systems analysis method “gradual formalization of the decision-making model” [7]. The authors of the method note that most of projects of complex systems need to be described by a class of self-organizing systems, models of which must be constantly adjusted and developed. The product life cycle should be isomorphic to the life cycle of other complex systems. The work [4] shows its correspondence to the activity cycle. Methodologists point out the importance of studying the phenomenon of activity: “activity is the only thing that exists from the very beginning, and nature is a certain construction of activity itself” [8]. The Figure 1 shows the main stages of activities related to PLM [4].
At the Requirement-Idea stage, the requirements for the product and the idea of quality improvement are formulated, the resources of conceptual design, conceptual modeling (CAID - Computer Aided Industrial Design), heuristic methods, methods of activating the intuition of specialists (MAIS) [4,7] are used. The Motive-Analysis stage analyzes these requirements and ideas, typically using methods of formalized representation of systems (MFRS) [4,7], and indicates how these requirements and ideas can be implemented. At the Control-Decision stage, final decisions are made and the product is produced. At the Implementation-Evaluation stage, the product is operated with an assessment of its quality relative to its preliminary version. As a result of these assessments, new requirements and ideas for improving the product may arise. That is, several consecutive cycles actually form a helix, where all the turns are similar in structure, but correspond to different levels of product quality - with each turn of the helix, the quality improves and new requirements and ideas are implemented [4]. According to the regularities of hierarchy and fractality [5], each stage can be similar in structure to one turn and consist of sub-stages similar to the listed stages, which are also isomorphic to the life cycle, etc. For example, a technological preparation stage could have Requirement-Idea, Motive-Analysis, Control-Decision, Implementation-Evaluation sub-steps, but related to the technological process [9].
Complex systems such as biological, social or economic systems have life cycles that are driven by evolution and consist of a large number of heterogeneous, decentralized, autonomous and relatively simple elements. A multi-agent approach [10,11,12,13,14] can provide such a structure of an information system and create the prerequisites for the emergence of system-wide patterns in it.
Recent PLM solutions such as Siemens PLM Software (UGS), Dassault system software, Oracle/AgileSoft, PTC/ Windchill, SAP/mySAP PLM integrate functions such as Project/Portfolio, CAD/CAM, Product Data Management, Manufacturing Process Management, various types if collaboration, etc. [3]. Many implementations of multi-agent PLM, among which the ontology-based approach is often used, testify to their effectiveness. In particular, a new approach, based on the ontology, the Semantic Web and the concept of agent, was proposed in [15]. In [16] the multi-agent system integrates the problem-solving method 8D, Process Failure Mode and Effect Analysis, Case-Based Reasoning, and PLM. The architecture of the system is based on SEASALT [17] (Shared Experience using an Agent-based System Architecture LayouT), which is a multi-case base domain-independent reasoning architecture for extracting, analyzing, sharing, and providing experiences. In [18,19] the agent technology is used in the solution to support decision-making in the design of recycling-oriented products. In [20] a knowledge engineering multi-agent module integrated in a PLM-system which is based on a multi-domain scheme (project, product, process and use) taking into consideration several viewpoints (structural, functional, dynamic, etc.). In [21] a generic multi-agent framework using IoT-based protocol, as the communication medium, for PLM of the products having high collateral damage values and where monitoring and control of systems in real-time are vital, was developed. In [22] a multi-agent software architecture that allows the capitalization of distributed and heterogeneous knowledge was designed. The research [23] targets the development of a knowledge engineering multi-agent system integrated into a PLM–environment linked with virtual reality tools. In [24] a PLM-framework supported by a proactive approach based on intelligent agents was proposed. The work [25] describes the process and various details of developing the Semantic Object Model into an ontology using OWL-DL. The purpose of the study [26] is to create, analyze and reuse an ontology-based approach during implementation of a multi-agent system capable of integrating different elements of a distributed control system. In [27] a multi-agent software system for PLM and logistic support analysis related tasks solving and automation was presented.
Despite the fact that threaded connections seem to be simple products, there is a lot of scientific work related to the problems that appear at different stages of their life cycle, in particular during the design, manufacture and operation [28,29,30,31,32]. Specifically for threaded connections of oil and gas equipment, such areas of research as analytical modeling [33,34,35], investigation of manufacturing errors [36,37,38] and corrosion fatigue [39,40,41] are important. Due to the prevalence of such products, we chose an educational PLM-system for threaded connection for research. In [42], using a systematic approach and the Python language, a PLM-system for threaded connections was developed. However, only design components have been developed and methods for their asynchronous operation have not been proposed.
The purpose of this work is to show, using a simple example, the principles of development, operation and use of a PLM-system with asynchronous agents to maintain the life cycle of a special threaded connection.
A simple example of a multi-agent PLM system is shown in Figure 2.
Agents can implement knowledge base facts (facts, product requirements, hypotheses for its improvement), inference rules, inference engine, CAD, FEA, CAM, SCADA components, etc. Hypotheses and rules can be passed to the inference engine for analysis or to obtain new hypotheses, then passed to the “CAD + FEA1” agent for verification by finite element analysis (FEA) of the performability of the product model. If the analysis results confirm the hypothesis, the data is transferred to the “CAM1” agent to prepare the technological process for manufacturing the product. Otherwise, the hypothesis is not confirmed and the relevant facts are updated. Agent “ICS1” (Industrial Control System) manages the manufacturing process. The finished product is subjected to testing or operation, during which the “SCADA1” (Supervisory Control and Data Acquisition) agent monitors the technical condition of the product. Based on the results of monitoring, new requirements and hypotheses may appear, initiating a new turn of the spiral. At any stage of the life cycle, it should be possible to interrupt the cycle and return to the previous stages.
To develop a PLM system, the authors recommend first of all using free software, which is associated with the following advantages: open source, potentially unlimited developer community, intensive development, collaborative development opportunities, user independence from manufacturers, high degree of interoperability and scalability [43]. In particular, you can use the CalculiX [44] finite element analysis system, the Gmsh [45] finite element mesh generator, the OpenModelica [46] dynamic systems simulation environment, the Python [47] general-purpose programming language, and the GRBL [48] CNC machine control software. However, to expand the capabilities of the system, it should also be possible to use commercial programs available via the API. It can be: SOLIDWORKS – 3D CAD/CAE/CAM-system, Abaqus/CAE - finite element analysis system with Python API, fe-safe - fatigue life analysis system, and other software. Ideally, the system architecture should allow agents to be programmed in any language and not depend on the platform, for example, as service-oriented software architecture allows. You should also pay attention to such indicators of software quality as usability, maintainability and performance. Due to the fact that the components should be heterogeneous, decentralized, autonomous and relatively simple, their development should adhere to the well-known concept in a Unix philosophy “Do One Thing And Do It Well”. This concept is related with the regularity of specialization of elements and their “requisite variety”. To develop the components of the PLM educational system and their system integration, the authors used the popular Python language, for which many different packages have been developed. For the PLM system, Python packages can be used: pythonocc [49] - Python wrapper for the Open CASCADE Technology [50] geometry kernel, FreeCAD [51] - 3D CAD, NumPy [52] - package for N-dimensional arrays, SciPy [53] - basic library for scientific computing, Matploltlib [54] - creating 2D diagrams, Sympy [55] - symbolic mathematics, scikit-learn [56] - machine learning, Pycalculix [57] - FEA based on CalculiX and Gmsh, Jupyter [58] - interactive computing.
The following software versions were used in the work: Python 3.8.9x64, NumPy 1.22.4+mkl, SciPy 1.7.3, Matplotlib 3.5.0, Ray 1.8.0, Pycalculix 1.1.4, Pyserial 3.5, Jupyter Notebook 6.4.6, SymPy 1.10.1, Gmsh-4.8.4-Windows64, CalculiX 2.16.
An important performance problem of the PLM system is to ensure the parallel operation of agents. Ordinary synchronous functions are executed sequentially - before calling the function again, you should wait for the result of the previous call (Table 1). An asynchronous function can be called without such a wait.
To implement parallelism and asynchronous calls, the actor model and the Ray Python package were used. Ray is an open source package that makes it easy to scale any computationally intensive Python program [59]. The Ray Core package provides simple primitives for creating parallel and distributed Python programs with minimal code changes - you can easily convert synchronous code to asynchronous by adding the @ray.remote decorator [59]. With Ray, the code will run on a single machine and can be easily scaled up to a large cluster [59]. For the FEA example, the simulation can be lengthy and block the operation of a synchronous system [42]. But Ray allows you to create an FEA actor class, an instance of an actor, and run it asynchronously with other actors: Preprints 66849 i001
This class for finite element simulation uses the mypycalculix module described below.

3. Results

Let's consider an example of an educational PLM-system for threaded connection of plastic parts with special threads (Figure 3). This product is used for educational purposes only and was chosen due to the ability of the design to optimize parameters and the ability to cut threads with a conventional disc milling cutter on a CNC 3018 Pro 3-axis training milling machine.
The source code of the developed PLM system is available on GitHub [60]. Each agent of the system is a Ray-actor and has a rule() function that describes its behavior. This function can take arguments and return results.
The inference engine allows you to derive new facts from existing ones using inference rules, as is done in the CLIPS production rule system [61]. Facts are represented as triplets (subject, predicate, object) and stored in agents of the Fact class, whose rule() function returns a triple. For example, fact “An equivalent stress of 14 MPa occurs in a structure with a dimension h=0.1 mm” can be represented as a triple ("Seqv=14", "match", "h=0.1"). The inference rules “if A, then B” can be written as follows: A → B, where A , B are facts. For example, the inference rule (X, Y, Z) → (Z, Y, X) should be read as “If there is a fact (X, Y, Z), then infer a new fact (Z, Y, X)”, and the rule (X, Y, Z) & (Z, Y, W) → (X, Y, W) - “If there is a fact (X, Y, Z) and a fact (Z, Y, W), then infer a new fact (X, Y, W)”. Inference rule agents are created using actor classes (Rule1, Rule2), whose rule() functions search for facts corresponding to facts A of the rule and return the set of inferred facts B. The Reasoner actor class describes the concept of an inference engine. Its rule function runs in parallel (and once) the rules of the inference rule agents, which are passed triplets with facts, and returns a set of triplets with new facts.
The FEA actor class agent simulates the stress-strain state of the connection using an axisymmetric finite element model. The rule() function takes the value of the connection parameter and returns the maximum stress. It uses the mypycalculix.py [60] automated FEA module of a threaded connection, which is developed by the authors and in turn uses Pycalculix [57]. A feature of the Pycalculix package is the ability to easily create parametric models with the ability to automate all stages of model building and create FEA programs for fully automatic parametric studies and design optimization. Before using Pycalculix, you must specify the path to the CalculiX solver (ccx.exe) and Gmsh generator (gmsh.exe) executable files in the file system. The package has the ability to visualize geometry, mesh and results using Matplotlib. The disadvantage of the package is the ability to create only two-dimensional models (planar or axisymmetric).
The mypycalculix.py module builds a geometric model of a threaded connection with given parameters, meshes with Gmsh, generates an input solver file, runs a simulation with the CalculiX solver, and gets the results. The description of a parametric model contains all model parameters with their values. The parametric model is created using Python code in an object-oriented way. In particular, the objects of the geometric model of the part (lines and arcs) are created using Pycalculix functions, which are passed the values of the model parameters:Preprints 66849 i002 where r0, l, t1 are model parameters.
It is also possible to import a complex geometric model in DXF format. To facilitate the creation of parametric models, the findLine() function developed by the authors can be used, which searches for the edges of a geometric model by their various attributes: midpoint coordinates, extreme point coordinates, length, etc. In general, the description of the model is similar to the description of models in other FEA packages: geometry creation, description of the mechanical characteristics of materials, description of surface contact, description of the finite element mesh (Figure 4(a)), boundary conditions and loads. Instructions for building models, calculating and getting results are located in the run function, and model parameters are global variables. In the case of a parametric study (investigation of the influence of a parameter on stress or strain), the run() function should be called for various values of the model parameter, saving the results in a list. For example:Preprints 66849 i003
Using the FEA actor, you can perform these tasks in parallel, which, in the case of a multiprocessor system, will reduce the computation time:Preprints 66849 i004
After receiving the results (stresses or strains), the program can read their values at any node of the mesh or get the maximum values. The results (Figure 4(b)) correspond to the expected ones - in joints of this type, the greatest stresses occur in the zone of the first turns. Thus, according to the results of the analysis, some elements should be provided in the design that would reduce these stresses.
To demonstrate the operation of the module, the dependences of the maximum equivalent stresses in a threaded connection on such parameters as thread length, pitch, and clearance were obtained (Figure 5). However, the maximum stress in a joint is not always a criterion for its durability, so it is necessary to find the stress value in the most dangerous zones where fatigue cracks may appear, for example, in the zone of the first thread root. In many cases, such dependencies can be easily formalized, including automatically [42], and get knowledge base facts. For example, from the dependence σmax(l_) (Figure 5) one can get the fact: “an increase in the length of the thread leads to a decrease in the maximum stresses”.
The CAM [60] actor class agent uses the CNC_thread_mill.py [60] module developed by the authors to generate the G-code for thread milling on a three-axis CNC milling machine (Figure 6(a)). The rule() function takes the value of the connection parameter and returns the corresponding list of G-code points (Figure 6(b)). Milling of taper external and internal threads with multiple passes and an arbitrary thread profile specified by point coordinates in the X-Z plane is supported.
The helixPoints() function returns a list of helix points [60]. Its parameters are: r - minimum radius, h - height, p - pitch, fi - taper angle, n - number of points on one turn, z0 - axial displacement. The coordinates of the points are determined by the parametric helix equation.
The helixPoints2() function has also been developed, which also returns helix points, but allows you to build more complex and varied helixes. The function uses the SymPy symbolic mathematics package to construct a parametric helix equation by sequential transformations of a point object in the space [62].
For example, a point object is described by a position vector
P = 1 1 0 1
and there is a rotation path transformation around the z-axis
T 1 = c o s ⁡ ( f 1 ( t ) ) 0 0 0 0 s i n ( f 1 ( t ) ) 0 0 0 0 1 0 0 0 0 1
where f 1 t – arbitrary function. Then the position vector L = P · T 1 describes a circle in the xy plane. The x and y scaling transformation looks like this
T 2 = f 2 ( t ) 0 0 0 0 f 2 ( t ) 0 0 0 0 1 0 0 0 0 1
and the z translation transformation like this
T 3 = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 f 3 ( t ) 1
Here f 2 ( t ) and f 3 ( t ) – arbitrary functions. If the P vector describes not a point, but a curve, then by such transformations one can also obtain the equation of helical surfaces [62].
The developed helixPoints2() function uses the following transformations
L = P · T 1 · T 2 · T 3 = f 2 ( t ) · c o s ⁡ ( f 1 ( t ) ) f 2 ( t ) · s i n ( f 1 ( t ) ) f 3 ( t ) 1
However, the user can easily modify its code to apply additional transformations. If the user defines different functions f 1 ( t ) , f 2 ( t ) and f 3 ( t ) , this allows different helixes to be obtained. Some of these helixes are shown in the Figure 7. Along with helixes, their planar envelope curves obtained using SymPy are shown. Figure 7(a) shows a cylindrical helix with a radius of 100 and a pitch of 5, in the Figure 7(b) the helix has a parabolic envelope, an initial radius of 100 and a pitch of 5, in the Figure 7(c) the helix is different in that it has a variable pitch.
The parameters of the helixPoints2() function are the strings f1, f2, f3, which define the functions f 1 ( t ) , f 2 t , , the helix height h and the number of points on the helix num. By solving the equation z(t)=h, the algorithm determines the maximum value of the t parameter and generates a list of points. An example of using this function:Preprints 66849 i005
Functions f i t can even be piecewise-defined, which greatly increases the set of different types of curves that can be built. For example the function
f 3 t = t ,       t < 10 2 t − 10 ,       t ≥ 10
allows you to create a helix with different pitches - the second part of the curve will have twice the pitch of the first. Then the f3 parameter in the Python code should be like this "Piecewise((t, t <= 10), (2*t-10, t > 10))".
The function can be used at the design stage of a threaded connection to create different types of thread helixes. The user can build a morphological matrix in which there are various combinations of f 1 t , f 2 t , f 3 t , and then select the most promising options or transfer all elements of the matrix to CAD / FEA agents to identify the best options according to stress and strain criteria. Thus, the developed function complies with the principle of «requisite variety» in the threaded connection design subsystem.
The TreadMulti() function uses helixPoints() and returns a list of points for thread milling in multiple passes. Its parameters are: h – thread length (should be a multiple of pitch p), p – pitch, fi – taper angle, n – number of points on one turn, R, Z – lists with radii (x-coordinate) and z-coordinate of the first points helical lines. In other words, R and Z contain the x- and z-coordinates of the profile points. For one pass R=[r], Z=[0], where r is the minimum thread radius.
The Gcode() function returns a G-code from a list of points. The plotCNC() function plots points using Matplotlib. An example of code generation for thread milling in two passes (Figure 6):Preprints 66849 i006
The module supports threading on CNC systems that do not have tool radius compensation and circular interpolation. Using Python Streaming Scripts [63], the G-code is transmitted via a serial port to the GRBL program that controls the machine. There is the possibility of organizing a flexible manufacturing system that combines a CNC-machine with an industrial robot designed to install and remove a workpiece [64]. A CNC 3018 Pro educational machine equipped with a control board supporting GRBL software was used. An Arduino Uno can be used as such a board. The workpiece 1 (Figure 8) is installed on the table 3 on the cylindrical pin 4 and fixed with a bolt 2, a washer 5 and a nut 6. The thread is cut with a disc milling cutter 7 in several passes. You can use the free application Candle [65] to set up the machine.
A SCADA actor class agent is also proposed for monitoring the technical condition of a threaded connection at the testing or operation stage. Its rule function receives the value of the connection parameter and returns the dependence of the deformations on the running time. The agent uses a schema based on example from Proteus CAD «Arduino HX711 SparkFun Breakout Board with 200kg Load Cell» [66]. Strain monitoring is done using an Arduino UNO board, an HX711 chip (24-bit ADC with strain gauge amplifier) and a strain gauge glued to the threaded connection. The Arduino sketch sends the results via a serial port using pyserial package (Table 2) to the HX711proteus_client.py module, which developed by the authors and associated with the agent. The results can be analyzed, compared with the previous ones and new facts can be obtained.
To demonstrate an example of using the PLM system, the authors developed an interactive document Jupyter Notebook [60]. The document contains cells with Python code, cells with formatted text generated by the Markdown markup language, and execution results in the form of text and charts. Ray is initialized first. In this example, the resources of one computer are used for calculations, but a cluster can also be used. Next, the actor classes described above (Fact, Rule1, Rule2, Reasoner, FEA, CAM, SCADA) and their actor objects (agents) that can work asynchronously are created.Preprints 66849 i007
In this case, the facts f1, f2, f3 are represented, containing the correspondence between the values of the input and output parameters of the threaded connection model: the geometric parameter h (mm), the maximum equivalent stress in the thread Seqv (MPa) and the maximum total displacement utot (mm). These facts can be obtained as a result of modeling, experiments, industrial data at the preliminary stages of the life cycle. The inference rules r1 and r2 are for the “match” property, which is symmetric, i.e. (1, match, 3) -> (3, match, 1), and transitive, i.e. (1, match, 3) & (3, match, 4) -> (1, match, 4).
Each agent works autonomously, receives input and returns results. The agent may return None, which means no new results. The automatic operation of the system can be organized using a simple algorithm: while there are changes in the system, call the rule() function of each agent. If all agents return None, then automatic operation of the PLM system is terminated. For example, logical inference is implemented using a naive forward chaining algorithm: call the Reasoner agent's rule() function while new facts are inferred. Preprints 66849 i008
As a result, the set of knowledge base facts is supplemented by the following:Preprints 66849 i009
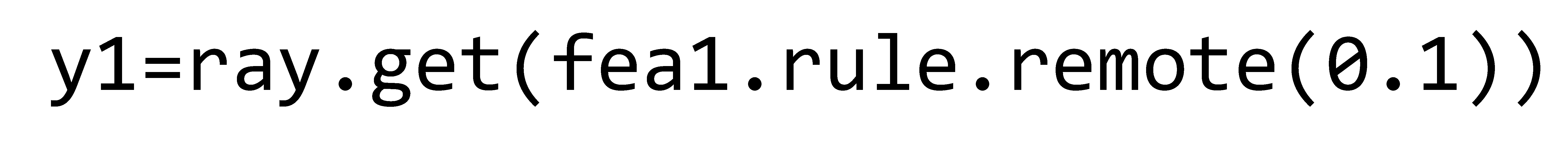
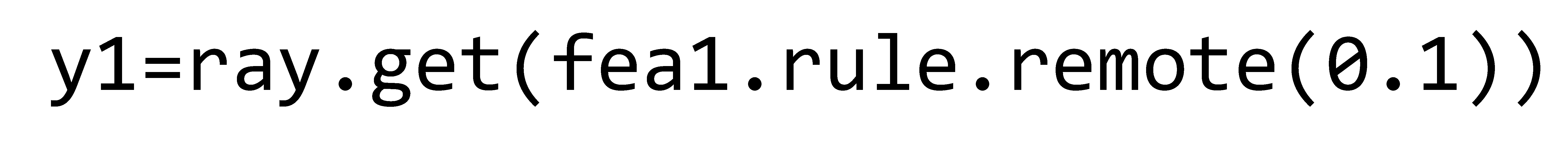
Further in the document, a threaded connection variant is simulated using the FEA agent. Using the fea1 agent, a threaded connection with the h=0.1 mm parameter (gap in the thread) is simulated. We wait results. Preprints 66849 i010
But all agents have the ability to run the simulation asynchronously, i.e. ro=fea1.rule.remote(0.1), and get the result in the cells below, i.e. y1=ray.get(ro).
The calculated maximum values of equivalent stresses and the distribution of strains and stresses in the thread are displayed (Figure 4). G-code generation for milling an external thread variant (h=0.1) is done using the CAM agent.Preprints 66849 i011
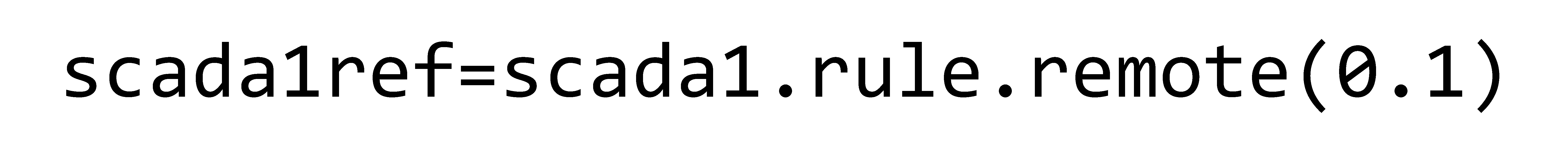
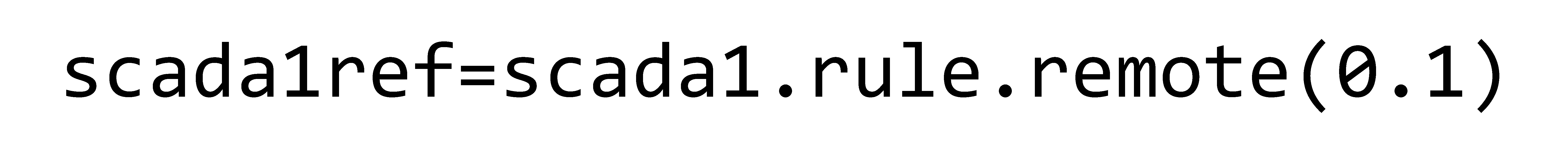
The coordinates of the first points of the generated trajectory and the plot of the trajectory are displayed using Matplotlib (Figure 6(b)). With the help of a SCADA agent, the technical condition of a threaded connection variant (h=0.1) is monitored during operation. Preprints 66849 i012
The following commands should be run when scada1.rule() has completed. A graph of the dependence of deformations on the operating time is displayed.Preprints 66849 i013
At any stage of the life cycle, you can access the desired cells, edit the code and get the results. The user can enter new data, change the model or parameter value, create new agents, and restart the system. Thus, at each iteration step, new knowledge appears and the system evolves, like the product itself. Thus, the multi-agent system works interactively with user interaction.
However, agents for optimization calculations have also been developed that can work autonomously. The Opti base class of agents for optimization has an f attribute which is the object of optimization and must be a function or ray.actor.ActorHandle. The attribute-function calc() calculates the value of f(x) using the FEA agent. The class also contains the attribute-function find(), which receives an XY dictionary of arguments and values of the function, and by analyzing these values using a special algorithm, returns the hypothesis of the argument x of the minimum. The attribute-function rule() describes the rule of the agent's behavior in the environment of X and Y values. For all optimization agents, this function has the same implementation with the following general algorithm:Preprints 66849 i014
The loop continuation condition is a condition for the continuation of optimization calculations. It may be different. For example like this:
SD y i − 2 ,   y i − 1 ,   y i ,   y i + 1 ,   y i + 1 ,   > 0.01 ,
where SD is the standard deviation, i is the index of the minimum value in the Y array. In Python, this condition can be written as Y[i-2:i+3].std()>0.01. But the restriction on the length of XY (len(XY)<20) is better to apply in case of a certain time limit for optimization calculations.
The OptiX class inherits from Opti and is designed to find the minimum using the grid-stochastic method. It differs from Opti only in the find() function. In this case, its algorithm is as follows:Preprints 66849 i015
This method is a combined global optimization method requiring an initial grid of x values with a desirably uniform step. At each step, finds x that is the same distance from the optimal value (found at the previous iteration) and neighbors to the right or left (random choice). In order not to get stuck in a local minimum, the algorithm provides for a random choice of x according to a given distribution law, the parameters of which can be changed.
The OptiR class inherits from Opti and is designed to find the minimum by building a regression model of the XY data. The F attribute is a function of the model, such as a second or third degree polynomial. The fit() function uses the method of least squares to find the best XY data model and returns the value of its coefficients and the coefficient of determination R2. The find() function finds the minimum of this model using a grid method with a sufficiently fine grid. This algorithm is deterministic, without stochastic elements, so it is the opposite of the find() algorithm of the OptiX class. The simultaneous use of these methods can provide a synergy effect and reduce the duration of calculations. In addition, not only agents of opposite optimization classes should be used, but also a set of agents of the same class with different parameters. As required by the “requisite variety” regularity. Advanced optimization algorithms, like basin-hopping [67] or differential evolution [68], often combine opposing methods.
The Environment class describes the environment of optimization agents and contains an XY dictionary in which the keys are the function arguments and the values are the function values. The getXY() and setXY() functions are for reading and writing the XY attribute. The setxy() function writes an (x, y) pair to an XY dictionary. If the place is already reserved, then the function only returns False.
The dict2arr() function is designed to convert an XY dictionary into NumPy arrays X and Y with values sorted by X. To test classes, you can use the f(x) test function to simulate long calculations using time.sleep. To do this, we need to modify the rule() function in the FEA class so that the s variable is assigned the value of f(x).
Let's consider an example of using these agents to optimize the parameter hh according to the criterion of minimum equivalent stresses in the joint.Preprints 66849 i016
Ray is initialized first. Next, the agent environment e is created. Then a uniform grid (array X) with 6 values of x in the interval [0.08, 0.2] is created. After that, agent-actors of the OptiX class are created for optimization. Each receives an FEA class agent and one value from the X array. By executing the agents' calc() function in parallel, the y value is calculated. After that, the XY data is written to the e environment. Two additional actors of the OptiR class are created that implement another optimization method. Since they use a deterministic algorithm, they must differ in F functions. The first uses a second degree polynomial, the second uses a third degree polynomial. Next, the rule() function of each agent is executed until they all return None. After the completion of the calculations, we read the XY attribute of the environment and find the minimum (hh=0.2). You can also visualize the XY points and the regression curve (Figure 9). Calculating the minimum of the function σ(hh) in this way on a computer with an Intel Xeon CPU E5-2630L v3 (eight cores) took 17 minutes, which is 5.6 times faster than sequential execution of tasks for 23 values of x. The maximum CPU load is 64%, RAM is 20 GB. In most cases, this optimization method allows you to immediately obtain the regression equation f(hh)
f h h = a · h h 3 + b · h h 2 + c · h h + d ,
a b c d = − 5.89538 e + 09 2.81486 e + 09 − 4.47734 e + 08 5.91554 e + 07 ,
R 2 = 0.9677
which, in the case of a high value of R2, can be formalized and placed in the knowledge base. Instead of R2, you can use other indicators of the model quality, for example, obtained using cross-validation.

4. Discussion

As a rule, all system-wide regularities explored by systems theory allow the system to be more efficient. This follows from the fact of the long-term evolution of various systems in which researchers observe these regularities.
The regularities of integrity are perhaps the most important. Many successes and failures in the life cycles of complex systems can be explained by the effects of synergy and dissynergy of their elements. This also applies to the PLM system. For example, the combination of conceptual design tools of a construction only with process design tools seems to be disenergy and threatens with additional costs, since the latter require the most accurate descriptions of the construction, and not the abstract ones that are generated in large numbers by the former. However, supplementing the first tools with CAD/FEA tools can significantly reduce costs by reducing the number of unsubstantiated hypotheses. In the developed system, emergence manifests itself in the interaction of agents of such classes as FEA and Opti, FEA and CAM, OptiX and OptiR, or various agents of the OptiR class. The “requisite variety” is manifested in the variety of types of agents used, the variety of solutions (helixPoints2() function, Opti classes). With an increase in variety, the efficiency of the system will increase, so you should try to expand the system with agents of a different type. This is quite easy to implement, since the behavior of the developed agents is described by relatively simple rules. Hierarchy and self-similarity is manifested in the possibility of creating hierarchical compositions of agents that are similar at different levels of the hierarchy (for example, the Opti agent-composition using FEA agents). Historicity is in the presence of cyclic optimization processes with access to a higher level of quality. Optimization agents can be used at various stages of the life cycle. The value of the function being optimized can be returned not only by FEA agents, but also, for example, by SCADA agents that determine the performance of the product at the stage of full-scale testing, or operation. Nonlinearity is in the stochastic behavior of OptiX agents. Part of the self-organization can be observed in the examples of using agents for the logical inference of facts and agents for optimization. Other regularities are planned to be investigated in the future.
The use of PLM system resources in the wrong place and at the wrong time, or in other words, the use for other purposes, threatens to significantly reduce the efficiency of the system. In many cases, the PLM system designer does not exactly know the purpose of a particular resource. Therefore, the system should provide mechanisms for self-identification and self-organization of resources, for example, those described in the work [69]. The easiest way is to endow agents with a memory mechanism in which the experience of positive or negative interaction of agents is stored. Then the choice by the agent of a partner of a certain class will take into account this experience. The level of synergy of interacting elements should be controlled on a certain scale, taking into account their hierarchy [9]. Thus, the effectiveness of the interaction can be unexpectedly high, medium, negligible, drop to zero, or even have devastating consequences. All developed agents can be classified according to the features of the stage of activity at which they are used, or according to other features, and pairs of classes with a high or low level of synergy can be identified [9]. The relationship class can be found using classification methods known in the field of machine learning [70]. This is planned to be implemented in the future.
The proposed system architecture based on the concept of actors and the use of the Ray package is not the only possible one. In the future, it is planned to supplement or replace it with a microservice architecture. To speed up the work of agents, the memoization technique can be used - in order to avoid re-computation with the same input data, the results are remembered. In the case of a large set of facts and rules, more productive algorithms or tools should be used, such as RETE [71] or pydatalog [42,72].
An important feature is the use of free software, which allows students and researchers to easily integrate other tools into the system and expand its capabilities. Using Python and its packages greatly facilitates this process due to their flexibility and easy understanding of Python code by other programmers.
More details about the project can be found on the project site on GitHub [60]. You can join the project and leave your wishes and comments.

5. Conclusions

1. Using the achievements of systems theory and the principle of isomorphism of system-wide regularities is a necessary condition for designing effective PLM systems. The presence in the developed system of such system-wide regularities as emergence, historicity, “requisite variety” and self-organization testifies to its effectiveness.
2. The example shows that today the development of PLM systems is available not only to large corporations. The available open-source software makes it relatively easy to develop a multi-agent PLM-system framework and components to support any stage of the product life cycle.
3. Thanks to the use of a systematic approach, an agent-oriented approach and high-level free tools (Python, Ray, Pycalculix, Jupyter, etc.), the proposed system has the ability to be easily studied, researched and improved. Additional research needs to be carried out to ensure self-organization at all stages of the life cycle, taking into account the level of synergy, improving the efficiency of existing and creating new components.
4. Using the developed PLM-system will help to reduce the costs of the optimization processes of the life cycle, in particular, those containing the stages: conceptual design, structural design, design of technological process, production, testing and operation.

Author Contributions

Conceptualization, V.K.; methodology, V.K. and O.O.; software, V.K. and O.O.; validation, O.O., V.P. and P.D.; formal analysis, O.O. and C.B.; investigation, C.B., V.P. and P.D.; resources, C.B.; data curation, C.B.; writing—original draft preparation, V.K.; writing—review and editing, P.D., C.B.; visualization, O.O.; supervision, V.P. and C.B.; project administration, O.O.; funding acquisition, C.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to the Ministry of Education and Science of Ukraine for the grant to implement the project D-2-22-P (RK 0122U002082). The team of authors expresses their gratitude to the reviewers for valuable recommendations that have been taken into account to significantly improve the quality of this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Saaksvuori, A; Immonen, A. Product lifecycle management, 3rd ed.; Springer-Verlag: Berlin, Heidelberg, Germany, 2008.
  2. Grieves, M. Product Lifecycle Management – Driving the Next Generation of Lean Thinking, McGraw-Hill: New York, USA, 2006.
  3. Liu, W.; Zeng, Y.; Maletz, M.; Brisson, D. Product lifecycle management: a survey. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (2009, January); vol. 48999, pp. 1213-1225.
  4. Kopey, V. B. Abstract model of product lifecycle management system. Precarpathian bulletin of the Shevchenko scientific society 2017, 2(38), pp. 71-96 (in Ukrainian).
  5. Bertalanffy von, L. General system theory: foundations, development, applications; George Braziller, Inc.: New York, USA, 1968.
  6. Kossiakoff, A.; Sweet, W. N.; Seymour, S. J.; Biemer, S. M. Systems engineering principles and practice, 2nd ed.; A John Wiley & Sons: Hoboken, New Jersey, USA, 2011.
  7. Volkova, V. N. Gradual formalization of decision-making models; Saint Petersburg State Technical University: Saint Petersburg, Russia, 2006 (in Russian).
  8. Shchedrovitsky, G. P. Selected writings. Moscow, Russia, 1995 (in Russian).
  9. Kopei, V. B. Scientific and methodological bases of computer-aided design of equipment for a sucker rod pumping unit. The dissertation for a doctor technical sciences degree in speciality 05.05.12 – Machines of Oil and Gas Industry. Ivano-Frankivsk National Technical University of Oil and Gas, Ivano-Frankivsk, 2020 (in Ukrainian).
  10. Wooldridge, M.; Jennings, N. R. Intelligent agents: Theory and practice. The Knowledge Engineering Review, 1995, 10(2), pp. 115‒152. [CrossRef]
  11. Wooldridge, M. An introduction to multi-agent systems, John Wiley & Sons, 2009.
  12. Shoham, Y.; Leyton-Brown, K. Multiagent systems: algorithmic, game-theoretic, and logical foundations, Cambridge University Press, 2008.
  13. Kravari, K.; Bassiliades, N. A survey of agent platforms. Journal of Artificial Societies and Social Simulation 2015, 18(1), 11.
  14. Shoham, Y. Agent-oriented programming. Artificial Intelligence, 1993, 60, pp. 51-92. [CrossRef]
  15. Abadi, A.; Sekkat, S.; Zemmouri, E. M.; Benazza, H. Using ontologies for the integration of information systems dedicated to product (CFAO, PLM...) and those of systems monitoring (ERP, MES..). In 2017 International Colloquium on Logistics and Supply Chain Management, LOGISTIQUA 2017, 2017, pp. 59-64.
  16. Camarillo, A.; Ríos, J.; Althoff, K. Knowledge-based multi-agent system for manufacturing problem solving process in production plants. Journal of Manufacturing Systems, 2018, 47, pp. 115-127. [CrossRef]
  17. Reichle, M.; Bach, K.; Althoff, K.D. The seasalt architecture and its realization within the docquery project. In: Proceedings of the 32nd annual German conference on Advances in artificial intelligence, KI’09, Springer-Verlag: Berlin, Heidelberg, 2009, pp. 556–563.
  18. Diakun, J.; Dostatni, E. End-of-life design aid in PLM environment using agent technology. Bulletin of the Polish Academy of Sciences: Technical Sciences, 2020, 68(2), pp. 207-214. [CrossRef]
  19. Dostatni, E.; Diakun, J.; Hamrol, A.; Mazur, W. Application of agent technology for recycling-oriented product assessment. Industrial Management and Data Systems, 2013, 113(6), pp. 817-839. [CrossRef]
  20. Gomes, S.; Monticolo, D.; Hilaire, V.; Mahdjoub, M. A multi-agent system embedded to a product lifecycle management to synthesise and reuse industrial knowledge. International Journal of Product Lifecycle Management, 2007, 2(4), pp. 317-336. [CrossRef]
  21. Kumar, V. V.; Sahoo, A.; Liou, F. W. Cyber-enabled product lifecycle management: A multi-agent framework. Procedia Manufacturing, 2019, 39, pp. 123-131. [CrossRef]
  22. Lahoud, I.; Gomes, S.; Hilaire, V.; Monticolo, D. A multi-agent platform to manage distributed and heterogeneous knowledge by using semantic web. In IAENG transactions on electrical engineering volume 1: Special issue of the international multiconference of engineers and computer scientists 2012, 2012, pp. 215-228.
  23. Mahdjoub, M.; Monticolo, D.; Gomes, S.; Sagot, J. A collaborative design for usability approach supported by virtual reality and a multi-agent system embedded in a PLM environment. CAD Computer Aided Design, 2010, 42(5), pp. 402-413. [CrossRef]
  24. Marchetta, M. G.; Mayer, F.; Forradellas, R. Q. A reference framework following a proactive approach for product lifecycle management. Computers in Industry, 2011, 62(7), pp. 672-683. [CrossRef]
  25. Matsokis, A.; Kiritsis, D. An ontology-based approach for product lifecycle management. Computers in Industry, 2010, 61(8), pp. 787-797. [CrossRef]
  26. Choiński, D.; Senik, M. Distributed control systems integration and management with an ontology-based multi-agent system, Bull. Pol. Ac.: Tech. 2018, (66)5, pp. 613‒620. [CrossRef]
  27. Karasev, V. O.; Sukhanov, V. A. Product lifecycle management using multi-agent systems models. Procedia Computer Science 2017, 103, pp. 142-147. [CrossRef]
  28. Birger, I. A.; Iosilevich, G. B. Threaded and flange connections. Mashinostroenie: Moscow, Russia, 1990 (in Russian).
  29. Yakushev, A. I.; Mustaev, R. Kh.; Mavlyutov, R. R. Increasing the strength and reliability of threaded connections. Mashinostroenie: Moscow, Russia, 1979 (in Russian).
  30. Blake, A. What every engineer should know about threaded fasteners: materials and design. M. Dekker: New York, USA, 1986.
  31. Bickford, J. H. An Introduction to the Design and Behavior of Bolted Joints, 3rd ed., revised and expanded, CRC Press; Taylor and Francis, 2017.
  32. Fukuoka, T. The Mechanics of Threaded Fasteners and Bolted Joints for Engineering and Design. Elsevier: Amsterdam, Netherlands, 2022.
  33. Shatskyi, I.; Ropyak, L.; Velychkovych, A. Model of contact interaction in threaded joint equipped with spring-loaded collet. Engineering Solid Mechanics, 2020, 8 (4), pp. 301-312. [CrossRef]
  34. Tutko, T.; Dubei, O.; Ropyak, L.; Vytvytskyi, V. Determination of Radial Displacement Coefficient for Designing of Thread Joint of Thin-Walled Shells. In Advances in Design, Simulation and Manufacturing IV. DSMIE 2021 Ivanov, V., Trojanowska, J., Pavlenko, I., Zajac, J., Peraković, D. (eds) Lecture Notes in Mechanical Engineering, 2021, pp. 153-162.
  35. Dubei, O.Ya.; Tutko, T.F.; Ropyak, L.Ya.; Shovkoplias, M.V. Development of Analytical Model of Threaded Connection of Tubular Parts of Chrome-Plated Metal Structures. Metallofizika i Noveishie Tekhnologii, 2022, 44 (2), pp. 251-272. [CrossRef]
  36. Pryhorovska, T.; Ropyak, L. Machining Error Influnce on Stress State of Conical Thread Joint Details. In Proceedings of the International Conference on Advanced Optoelectronics and Lasers, CAOL, 2019-September, 2019, 9019544, pp. 493-497.
  37. Bazaluk, O.; Velychkovych, A.; Ropyak, L.; Pashechko, M.; Pryhorovska, T.; Lozynskyi, V. Influence of heavy weight drill pipe material and drill bit manufacturing errors on stress state of steel blades. Energies, 2021, 14 (14), 4198. [CrossRef]
  38. Ropyak, L.Y.; Vytvytskyi, V.S.; Velychkovych, A.S.; Pryhorovska, T.O.; Shovkoplias, M.V. Study on grinding mode effect on external conical thread quality. IOP Conference Series: Materials Science and Engineering, 2021, 1018 (1), 012014. [CrossRef]
  39. Shats’kyi, I.P.; Lyskanych, O.M.; Kornuta, V.A. Combined Deformation Conditions for Fatigue Damage Indicator and Well-Drilling Tool Joint. Strength of Materials, 2016, 48 (3), pp. 469-472. [CrossRef]
  40. Severinchik, N.A.; Kopei, B.V. Inhibitive protection of steel drill pipes from corrosion fatigue. Soviet Materials Science, 1978, 13 (3), pp. 318-319. [CrossRef]
  41. Kopei, B.V.; Gnyp, I.P. A method for the prediction of the service life of high-strength drill pipes based on the criteria of corrosion fatigue. Materials Science, 1997, 33 (1), pp. 99-103. [CrossRef]
  42. Kopei, V. B., Onysko, O. R., Panchuk, V. G. Principles of development of product lifecycle management system for threaded connections based on the Python programming language. J. Phys.: Conf. Ser. 2020, 1426, 012033. [CrossRef]
  43. Artamonov, I. V. Free software: advantages and disadvantages Izvestiya of Irkutsk State Economics Academy, 2012, 5. pp. 122–125 (in Russian).
  44. Dhondt, G. The finite element method for three-dimensional thermomechanical applications, Wiley, 2004.
  45. Geuzaine, C.; Remacle, J. F. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering, 2009, 79(11), pp.1309-1331.
  46. Fritzson, P.; Aronsson, P.; Lundvall H.; Nyström, K.; Pop, A.; Saldamli, L.; Broman, D. The OpenModelica Modeling, Simulation, and Software Development Environment. Simulation News Europe, December 2005, 15(44/45), 8-16.
  47. Van Rossum, G.; Drake, F. L. Python 3 Reference Manual. Scotts Valley, CA: CreateSpace. 2009.
  48. Grbl : An open source, embedded, high performance g-code-parser and CNC milling controller written in optimized C that will run on a straight Arduino. URL: https://github.com/gnea/grbl (accessed 29-12-2022).
  49. Paviot, T. pythonocc-core : Python package for 3D CAD/BIM/PLM/CAM. URL: https://github.com/tpaviot/pythonocc-core (accessed 29-12-2022).
  50. OPEN CASCADE. URL: http://www.opencascade.com (accessed 29-12-2022).
  51. FreeCAD: Your own 3D parametric modeler. URL: https://www.freecadweb.org (accessed 29-12-2022).
  52. Harris, C. R.; Millman, K.J.; van der Walt, S.J. et al. Array programming with NumPy. Nature, 2020, 585, pp. 357–362. [CrossRef]
  53. Virtanen, P.; Gommers, R.; Oliphant, T. E.; Haberland, M.; Reddy, T., Cournapeau, D. et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 2020, 17, pp. 261–272.
  54. Hunter, J. D. Matplotlib: A 2D graphics environment, Computing in Science & Engineering, 2007, 9(3), pp. 90-95.
  55. Meurer, A.; Smith, C.P.; Paprocki, M. Čertík, O.; Kirpichev, S.B.; Rocklin, M. et al. SymPy: symbolic computing in Python. PeerJ Computer Science, 2017, 3:e103. [CrossRef]
  56. Pedregosa, F. et al. Scikit-learn: machine learning in Python, JMLR, 2011, 12, pp. 2825-2830.
  57. Black, J. Pycalculix. URL: https://github.com/spacether/pycalculix (accessed 29-12-2022).
  58. Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B. et al. Jupyter Notebooks – a publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas. Loizides, Fernando and Scmidt, Birgit (eds.), IOS Press, 2016, pp. 87-90. [CrossRef]
  59. Ray: Scaling Python made simple, for any workload. URL: https://www.ray.io (accessed 29-12-2022).
  60. Kopei V., Onysko O. Educational multi-agent PLM system for threaded connections. URL: https://github.com/vkopey/ThreadsPLM-MAS- (accessed 31-12-2022).
  61. CLIPS: A Tool for Building Expert Systems. URL: https://clipsrules.net (accessed 29-12-2022).
  62. Rogers, D. F.; Adams, J. A. Mathematical Elements for Computer Graphics. 2nd ed. McGraw-Hill, 1989.
  63. Python Streaming Scripts. URL: https://github.com/gnea/grbl/wiki/Using-Grbl#python-streaming-scripts-officially-supported-by-grbl-cross-platform (accessed 29-12-2022).
  64. Proniuk, I. V.; Kopei, V. B. Educational flexible manufacturing module software control system based on Arduino, GRBL and Python. In Young science - robotics and nano-technologies of modern mechanical engineering: a collection of scientific papers of the International Youth Scientific and Technical Conference, June 20, 2022. S.V. Kovalevsky, Dr. Tech. Science, Prof., and Hon.D.Sc., Prof. Predrag Dašić (eds.). DSEA: Kramatorsk, Ukraine, 2022. pp. 150-156 (in Ukrainian).
  65. GRBL controller application with G-Code visualizer written in Qt. URL: https://github.com/Denvi/Candle (accessed 29-12-2022).
  66. PCB Design and Circuit Simulator Software - Proteus. URL: https://www.labcenter.com (accessed 29-12-2022).
  67. Wales, D. J.; Doye, J. P. K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. Journal of Physical Chemistry A, 1997, 101, 5111. [CrossRef]
  68. Storn, R.; Price, K. Differential Evolution - a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces, Journal of Global Optimization, 1997, 11, pp. 341 - 359. [CrossRef]
  69. Kopei, V. B. Algorithm of an intelligent system based on interdisciplinary studies of system-wide regularities. In Materials IV-th International scientific-technical conference “Computer modeling and optimization of complex systems” (Dnipro, November 1-2, 2018). Ministry of Education and Science of Ukraine, Ukrainian State University of Chemical Technology. Balance-club: Dnipro, Ukraine, 2018. pp. 246-248 (in Ukrainian).
  70. Kopei, V. B. Synthesis of PLM systems of threaded connections using machine learning methods. In Comprehensive quality assurance of technological processes and systems (КЗЯТПС–2022) : materials of abstracts of reports of the XII International Scientific and Practical Conference (Chernihiv, May 26–27, 2022): in 2 vols. Chernihiv Polytechnic National University: Chernihiv, Ukraine, 2022, vol. 1, P.146 (in Ukrainian).
  71. Forgy, C. Rete: A Fast Algorithm for the Many Pattern/Many Object Pattern Match Problem. Artificial Intelligence, 1982, 19, pp. 17–37. [CrossRef]
  72. Datalog logic programming in Python. URL: https://sites.google.com/site/pydatalog (accessed 29-12-2022).
Preprints 66849 g001
Figure 1. Stages of PLM activity.
Figure 1. Stages of PLM activity.
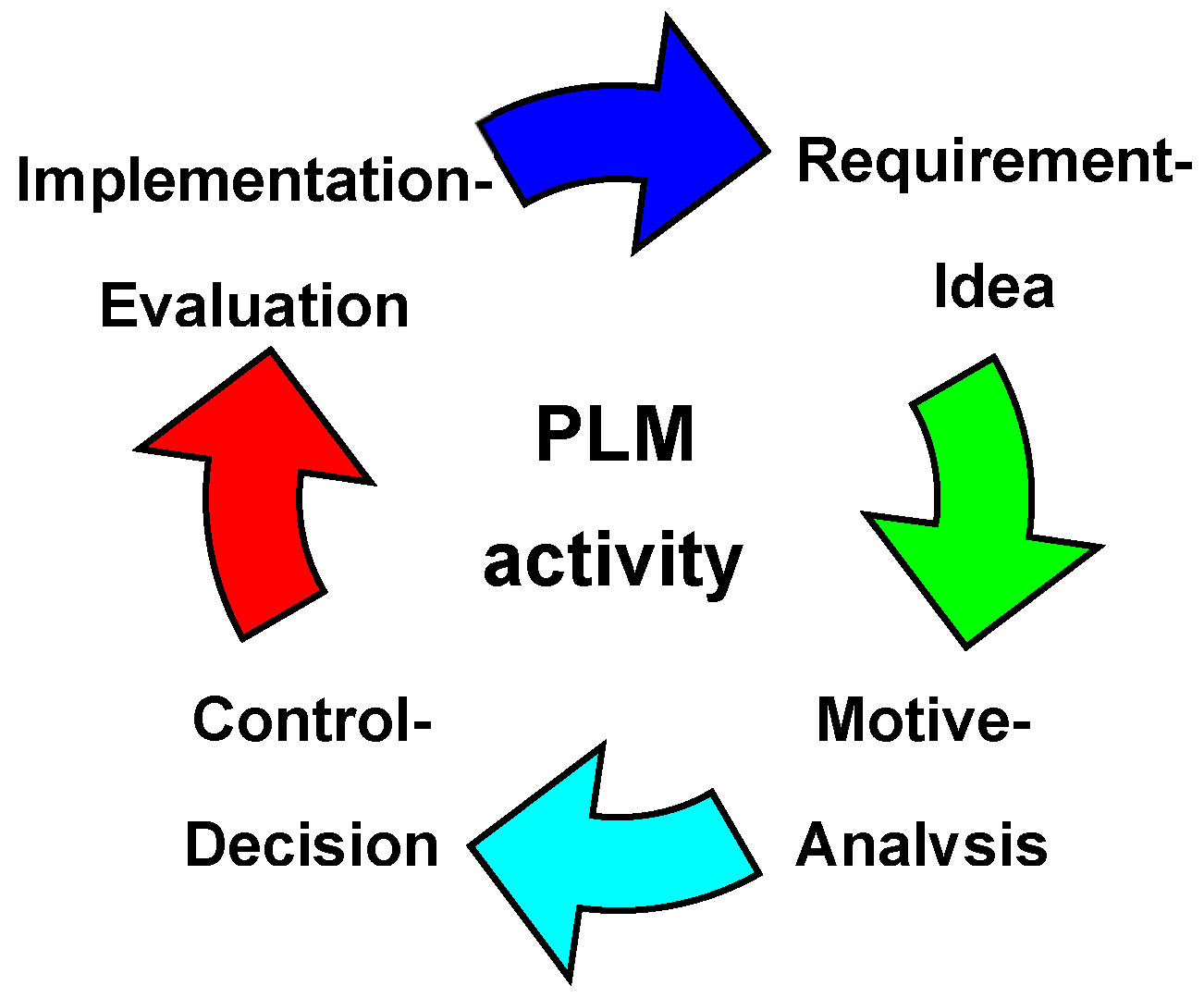
Preprints 66849 g001
Preprints 66849 g002
Figure 2. An example of a multi-agent PLM system.
Figure 2. An example of a multi-agent PLM system.
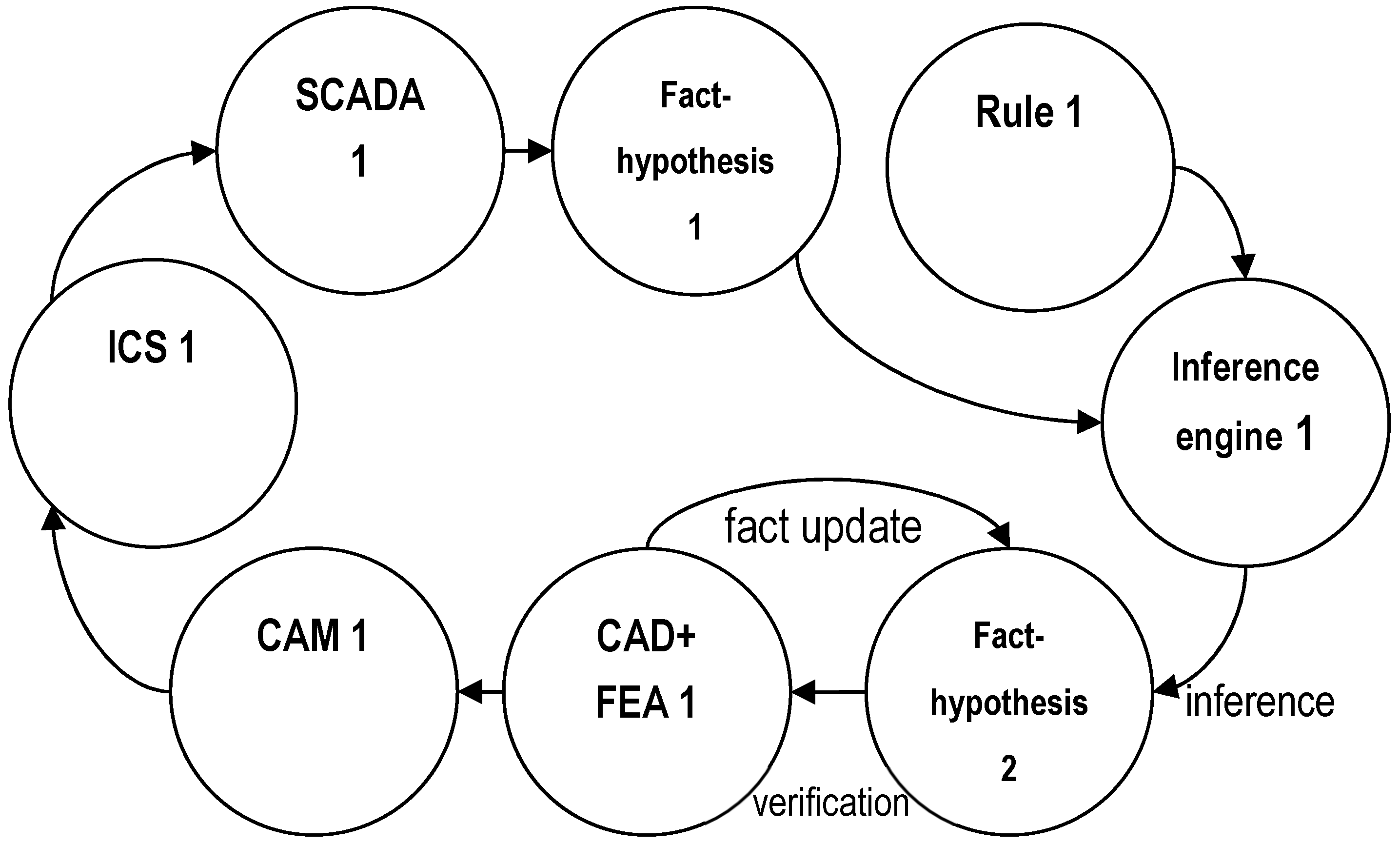
Preprints 66849 g002
Preprints 66849 g003
Figure 3. Threaded connection with special thread.
Figure 3. Threaded connection with special thread.
Preprints 66849 g003
Preprints 66849 g004
Figure 4. Finite element mesh (a) and distribution of equivalent stresses (b) in the area of the first turns (MPa).
Figure 4. Finite element mesh (a) and distribution of equivalent stresses (b) in the area of the first turns (MPa).
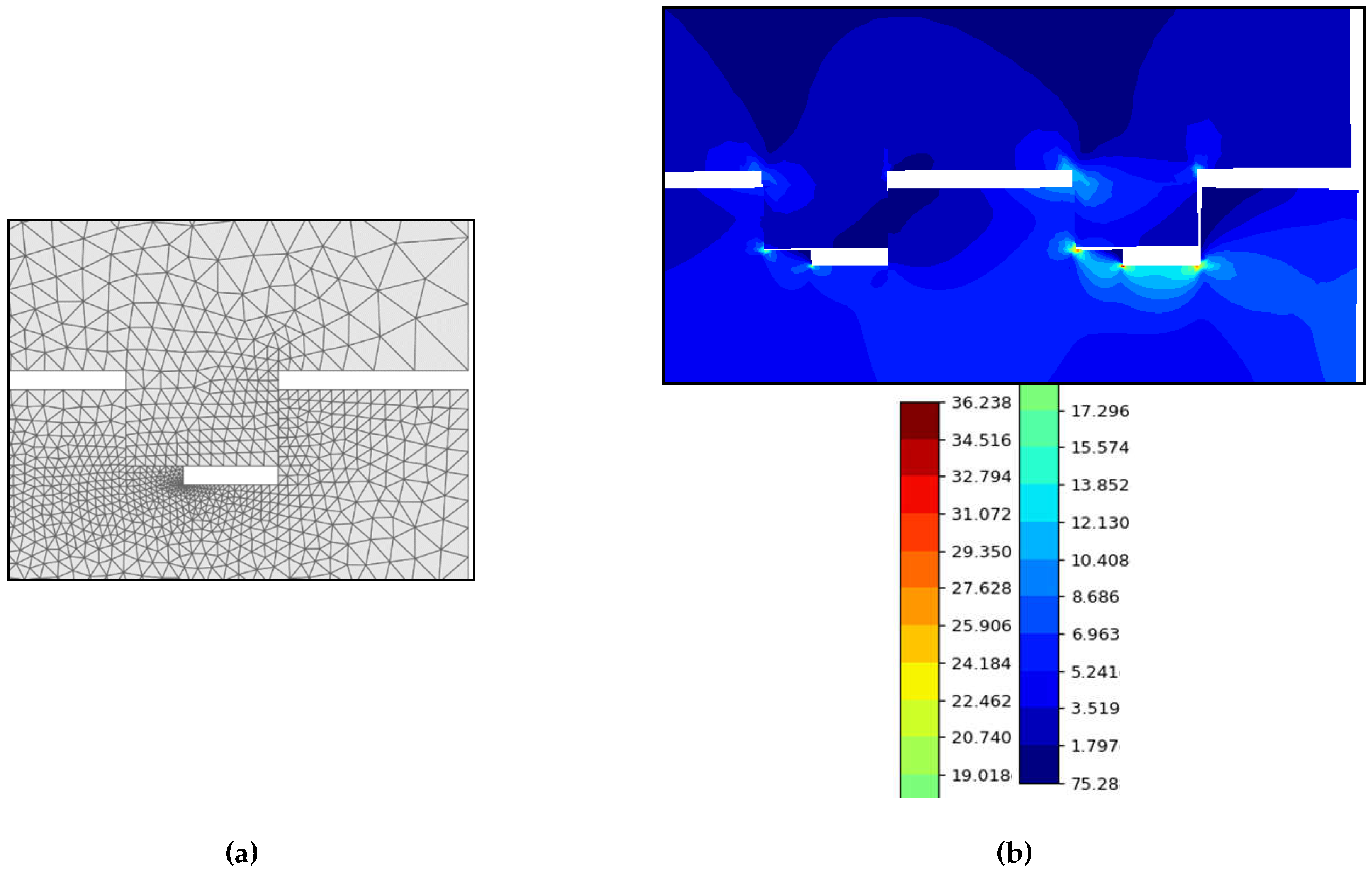
Preprints 66849 g004
Preprints 66849 g005
Figure 5. Dependences of the maximum equivalent stresses σmax in the connection on: radial clearance in the thread (hh), thread length (l_) and pitch (k)
Figure 5. Dependences of the maximum equivalent stresses σmax in the connection on: radial clearance in the thread (hh), thread length (l_) and pitch (k)
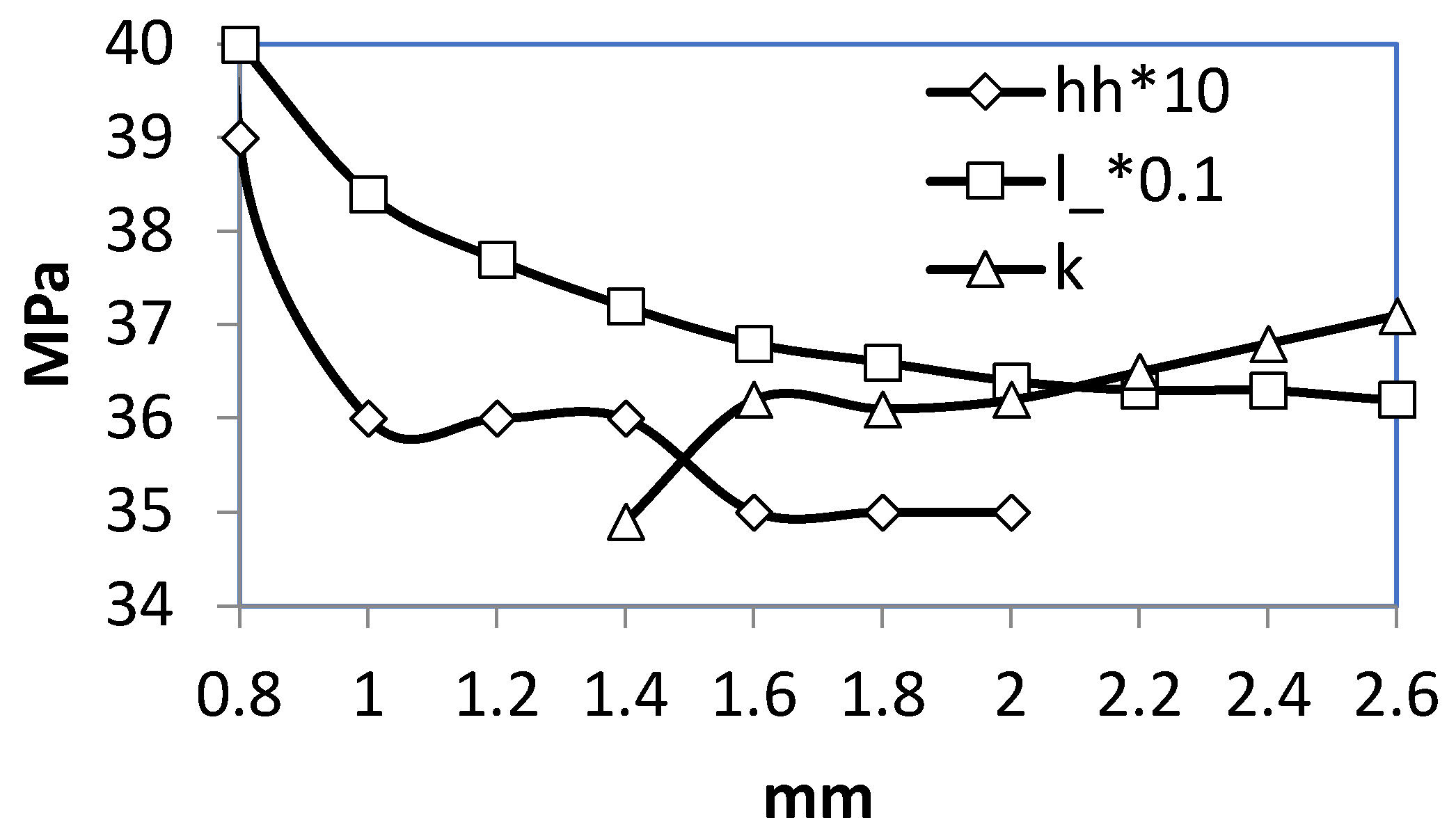
Preprints 66849 g005
Preprints 66849 g006
Figure 6. G-code snippet (a) and toolpath visualization with Matplotlib (b)
Figure 6. G-code snippet (a) and toolpath visualization with Matplotlib (b)
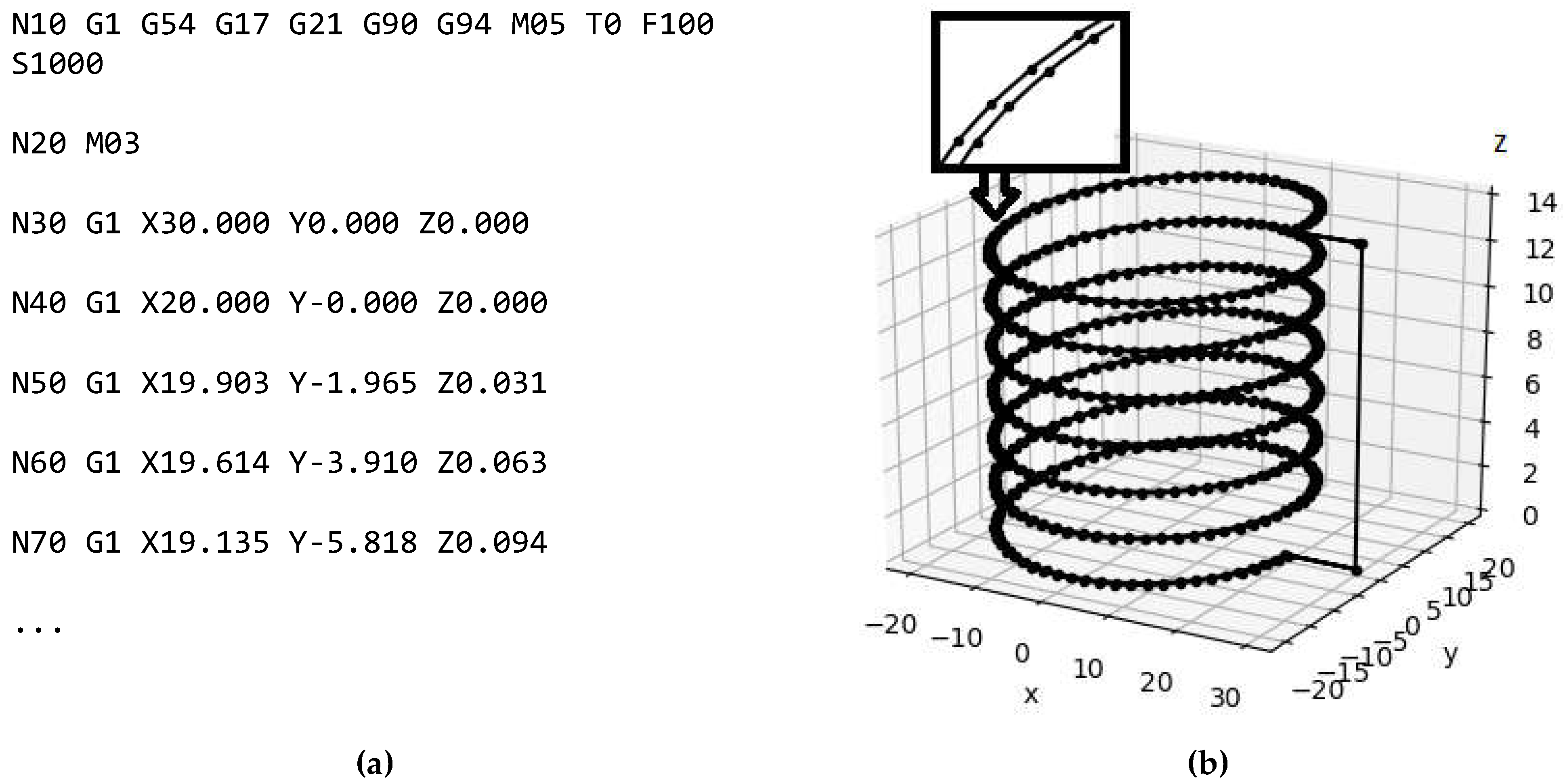
Preprints 66849 g006
Preprints 66849 g007
Figure 7. Helixes and their planar envelope curves
Figure 7. Helixes and their planar envelope curves
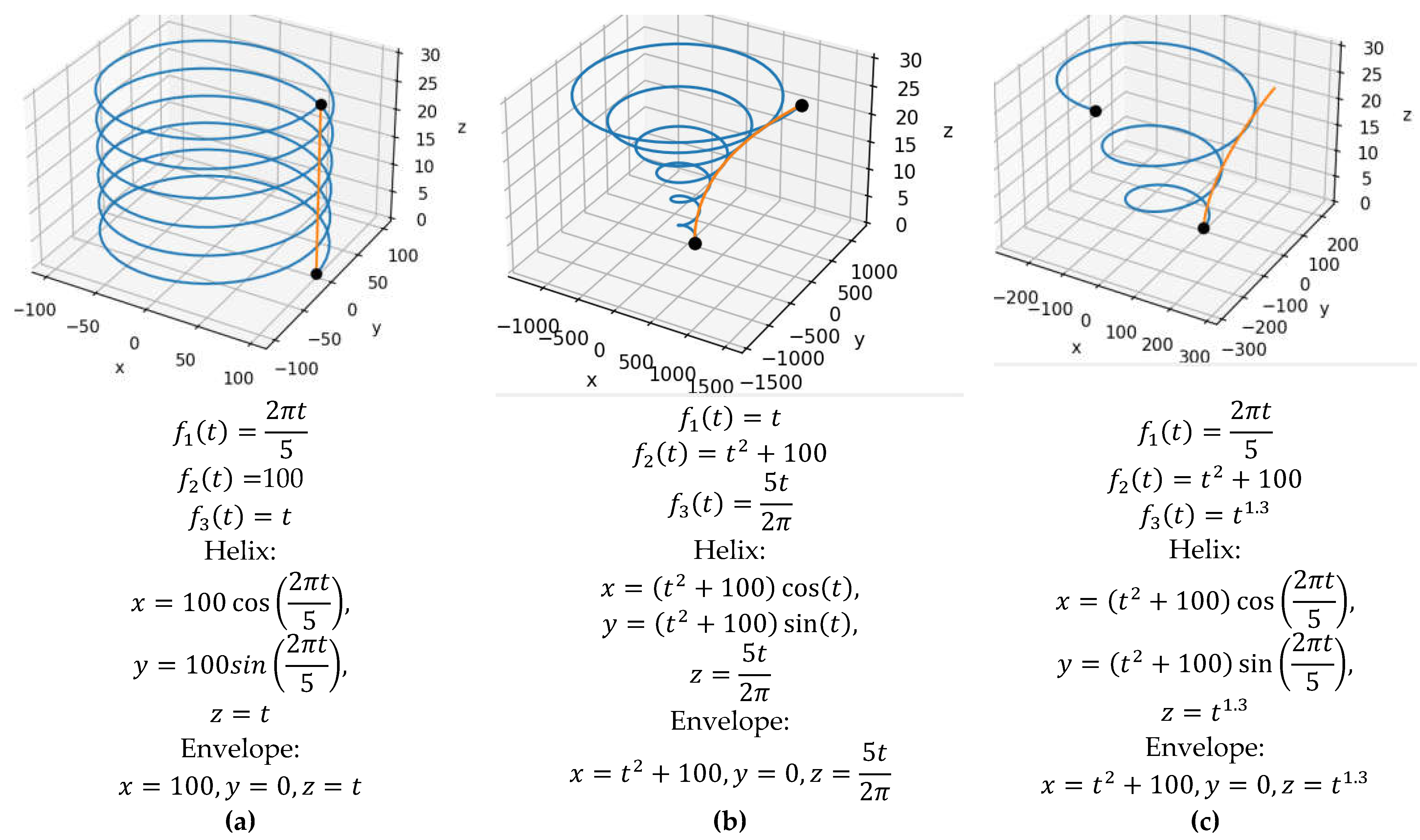
Preprints 66849 g007
Preprints 66849 g008
Figure 8. Technological sketch (a) and photograph (b) of milling a special thread on a CNC 3018 Pro machine.
Figure 8. Technological sketch (a) and photograph (b) of milling a special thread on a CNC 3018 Pro machine.
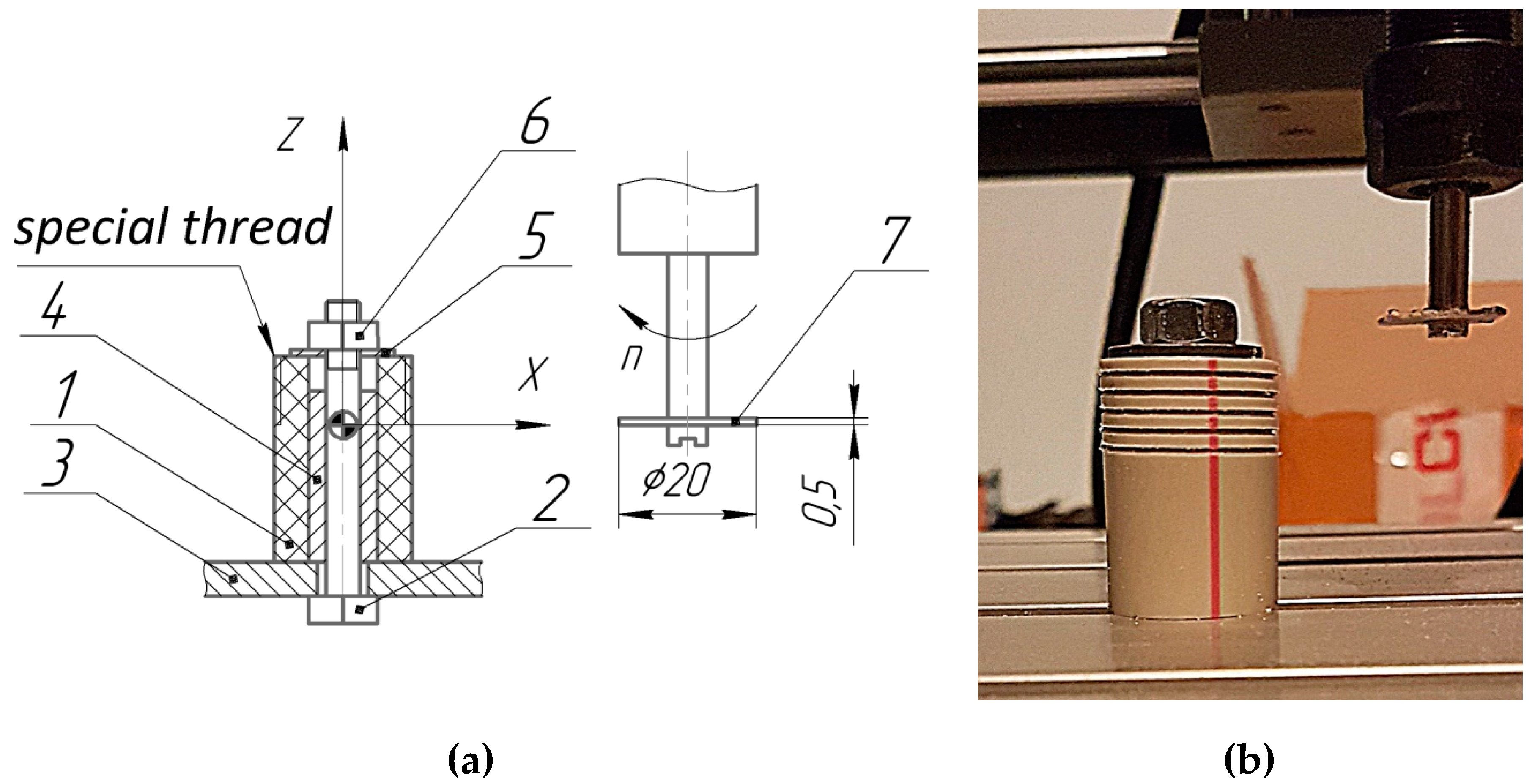
Preprints 66849 g008
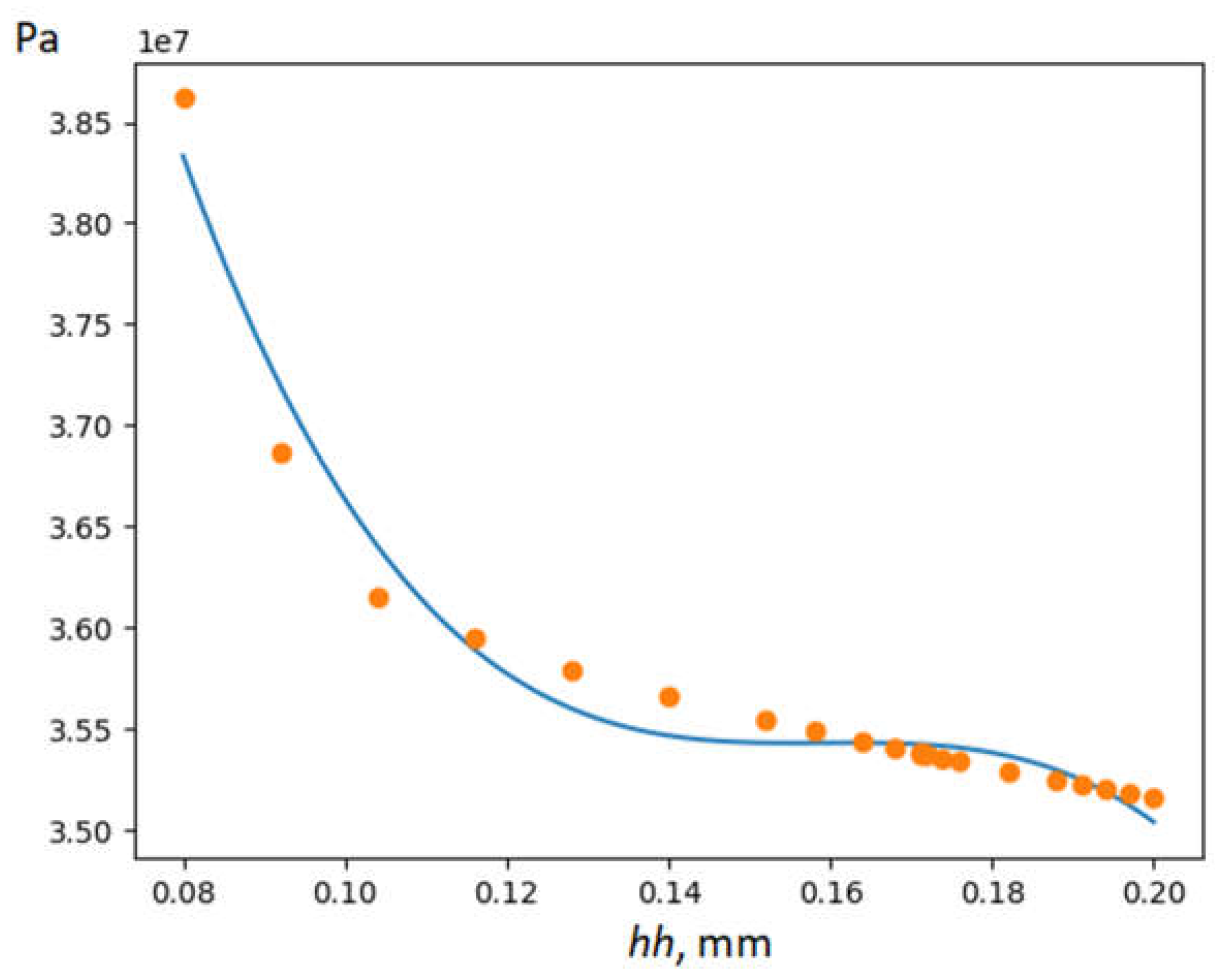
Preprints 66849 g009
Figure 9. Dependence points σ(hh) obtained during optimization and regression model f(hh)
Figure 9. Dependence points σ(hh) obtained during optimization and regression model f(hh)
Preprints 66849 g009
Table 1. Creation and use of synchronous and asynchronous Python-functions.
Table 1. Creation and use of synchronous and asynchronous Python-functions.
Synchronous function Asynchronous function Ray [59]
def f():
  return 1

f() # synchronous call
f() # one more
f() # and more 		@ray.remote
def f():
   return 1

obj_ref1 = f.remote() # asynchronous call
obj_ref2 = f.remote() # one more
obj_ref3 = f.remote() # and more
ray.get(obj_ref1) # result
ray.get(obj_ref2)
ray.get(obj_ref3)
Table 2. Programs for data transfer via serial port
Table 2. Programs for data transfer via serial port
Arduino-sketch Python-module HX711proteus_client.py
#include "HX711.h"
#define calibration_factor (18029.57)
#define DOUT 3
#define CLK 2
HX711 scale(DOUT, CLK);
void setup() {
 Serial.begin(9600);
 scale.set_scale(calibration_factor);
 scale.tare();
}
void loop() {
 Serial.println(scale.get_units(), 2);
 delay(1000);
  } 		# -*- coding: utf-8 -*-
import serial,time
def run():
  ser = serial.Serial(port='COM7',
        baudrate=9600)
  X, Y = [], []
  for x in range(10):
   y = ser.readline()
   y = float(y)
   X.append(x)
   Y.append(y)
   time.sleep(1)
ser.close()
return X, Y
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated