Preprint
Article
Matter as Pure 'Atoms' of Electricity
Altmetrics
Downloads
208
Views
158
Comments
1
This version is not peer-reviewed
Submitted:
09 January 2023
Posted:
10 January 2023
You are already at the latest version
Alerts
Abstract
Dirac’s equation depicts electron mass as either positive or negative. Taken as correct description of nature, the equation identifies electron mass as ‘electrically active’ and therefore fundamentally different from the ordinary, ‘electrically passive’ mass. Following this cue, I demonstrate that electron mass (me) is the natural elementary mass: positive (me+) and negative (me–) elementary masses neutralise to an elementary unit of the electrically passive mass (2me0). Further, I show that electron mass (me± ) and the electrostatic field (ef±) surrounding it compose an elementary charge (e±), thereby relating charge to mass. Two plain principles underlie these findings. 1) Electric charge and gravitational mass have a common root: positive (e+) and negative (e–) charges coexist as neutral charge (2e0), which is the quantum of gravitational mass. 2) Charge is a static (nonrelativistic) ‘atom of electricity’ and obeys the laws of electrostatics; electron is the same ‘atom of electricity’ at ultrahigh (relativistic) speed and obeys the laws of electrodynamics. That is, charges are electricity at rest; electrons are electricity in motion – ‘same physical entities two behavioural identities.’ A decisive proof that this paradigm shift correctly portrays is that it verifiably unifies Newton’s law of gravity and Coulomb’s law of electrostatics to: 8G/mpme = K/e2; where G and K are the respective constants, mp the proton mass, me the electron mass, and e the elementary charge. Ultimately, the insights simplify matter to pure ‘atoms’ of positive and negative electricity.
Keywords:
Subject: Physical Sciences - Particle and Field Physics
1. Introduction
The ancient Greek philosopher, Democritus, theorized that by repeatedly cutting a piece of matter one would end up with atomos or “the uncuttable”.[1] In 1808 Dalton proved that each chemical element comprises uniform building blocks[2] – the modern atoms. Dalton thought he had found the uncuttable particles in Democritus’s theory. However, in 1897 Thomson discovered the electron, which is 1,837 times lighter than the smallest atom, proving that nature has material particles smaller than the atom. Later, two more subatomic particles were found – the proton and the neutron. By 1932 physicists had proved beyond doubt that Dalton’s atom has a simple structure that comprises only three types of building blocks: electron, proton, and neutron. Griffiths observes: “Never before (and I’m sorry to say never since) has physics offered so simple and satisfying an answer to the question, ‘What is matter made of?’”[3] Logically, the next challenge would have been to further unify electron, proton, and neutron.
However, in the same year physicists started to observe additional subatomic particles from cosmic radiation, nuclear reactors and particle accelerators[4,5] and this diverted attention from further simplification of the three classical subatomic particles. The first was the positron; then a bewildering array of particles presently dubbed the “particle zoo.”[6] The new particles are short-lived and lack obvious places in the atomic structure. Nevertheless, all of them – paradoxically, even those considered ‘antimatter’ like the positron – originate from atoms of ordinary matter.[7] To establish order in the new and previously known particles, physicists embarked on a grand search for the ultimate building blocks of both ‘matter particles’ and the ‘forces’ that bind them.[8] Mendeleev’s Periodic Table of chemical elements influenced the search,[9] inspiring hope that nature arranges subatomic particles and Dalton’s atoms in analogous patterns. The effort culminated in the Standard Model (SM) of particle physics.[10] Formally, the SM explains matter and binding forces in 17 building blocks – 12 fermions and 5 bosons.[11] It recognizes negative electron as fundamental and irreducible, but suggests that proton and neutron consist of simpler particles – the quarks. Each quark, according to the SM, has one-third or two-thirds of the elementary charge.[12,13] However, credible experiments have repeatedly[14] failed to detect the proposed fractional charges.[15] Hence, as yet, the fractional charge hypothesis lacks a direct experimental proof.[16]
In contrast, Faraday,[17] Stoney,[18] and Millikan,[19] among others, provide conclusive evidence that electric charge exists naturally in integral multiples of the elementary charge (e). In electrical, chemical, and nuclear process, charge invariably occurs in integral units. Regardless, no one has ever utilised the proven ‘whole charges’, as opposed to the hypothetical ‘fractional charges’, to explain the subatomic particles – electron, proton, neutron and the ‘particle zoo’. The difficulty comes from the enigmatic nature of charge. Of course, a lot is known and applied about charge; but physicists have always skipped the question of its fundamental nature.[20,21,22] This is, perhaps, the most serious oversight in the history of physics. It means that the essence of the atom – hence matter – remains mysterious; and that any theory that deals with the physical nature of charge – such as its divisibility or indivisibility – is founded on the unknown.
A fresh synthesis of scattered pieces of scientific evidence, collected over the centuries, leads to a definite but surprising discovery: a charge (e) is the static (nonrelativistic) electron; and an electron (E) is the moving (relativistic) charge – one physical entity two behavioural identities. Put differently, charges are static ‘atoms’ of electricity and obey the laws of electrostatics; electrons are moving ‘atoms’ of electricity and obey the laws of electrodynamics. Thus, Thomson and Anderson observed negative and positive charges at relativistic speeds and, thinking they had discovered completely new particles, named them negative and positive electrons respectively. The current discovery opens a way to demonstrate that ‘atoms of electricity’[23] – collectively charges and electrons – are all there is in the known material universe. An ‘atom of electricity’, however, is fundamentally different from Dalton’s atom.
2. Positive-negative mass and field symmetry
Maxwell envisaged the unification of “field and substance”;[24] the intangible reality his equations describe and the tangible matter. The two realities are discernible in the electron. Thomson’s me/e ratio defines electron in just two parameters:[25] electron mass (me) and electric charge (e). The directly detectable entities, however, are the electron mass and the electrostatic field.[26] Like electron mass, electrostatic field – or Faraday’s lines of force[27] – is “very real.”[28] It underlies Maxwell’s equations, “contains energy, and its presence precludes a classical ‘true vacuum.’”[29] Thus, electron mass and electrostatic field, respectively, match Maxwell’s ‘tangible’ and ‘intangible’ realities. Besides electron mass and electrostatic field, the electron has nothing else (Figure 1). Conspicuously, it lacks any discrete ‘charge’. Mathematically, electron (E) is the sum of electron mass (me) and electrostatic field (ef):
Firm theoretical and experimental evidence, presented shortly, shows that electron mass and electrostatic field naturally exist in opposite types. That is, positive electron (E+) is the sum of positive electron mass (me+) and positive electrostatic field (ef+) as expressed in Equation (2); and negative electron (E–) is the sum of negative electron mass (me–) and negative electrostatic field (ef–) as expressed in Equation (3). Hence, opposite masses and fields differentiate positive and negative electrons (Figure 2). (For the sake of clarity, the terms positron and negatron are hereafter used, per the original proposal,[30] to denote positive and negative electrons respectively; and ‘electron’ to denote both).
In agreement with Equation (2) and Equation (3), Dirac, in Equation (4), shows that electron mass is either positive (me+) or negative (me–). Schrodinger was the first physicist to highlight this fact.[31]
Equation (4) is currently interpreted to mean that positive electron mass exists in nature but its negative counterpart does not. The negative mass is said to make mathematical[32] but no physical sense.[33,34] The reasoning is based on the tacit definition of all known mass, including electron mass, as always positive.[35,36,37] However, Dirac’s equation has such predictive power that its positive-negative mass symmetry cannot just be dismissed. The equation, for example, correctly predicted the existence of the positron before Anderson observed the actual particle.[38] An overlooked fact is that Anderson also confirms that Dirac’s positive-negative mass symmetry is a natural phenomenon. In his photographs, Anderson observed that subjected to uniform force (F) opposite electrons, each with inertial mass me, experience equal acceleration (a) but curve in the opposite directions.[39] The magnitude of the curvature varies with that of the particle’s inertial mass. From Newton’s second law of motion, F/me = a. When ‘F’ is unform (fixed sign), ‘a’ can gain plus or minus sign only if ‘me’ is ascribed a corresponding sign. In one direction, force (F) equals m+e x a+; in the other, it equals me– x a–. Put simply, a force that accelerates positive electron mass to the left will accelerate negative electron mass to the right. Hence, in agreement with Equation (4), Anderson’s finding proves that positron and negatron have opposite inertial masses.
To complement the Dirac-Anderson finding, the test charge experiments demonstrate that electrostatic field is either positive or negative. Placed alternately in the fields around opposite charges, a test charge oscillates in opposite directions.[40] The usual interpretation is that field lines face radially outwards (out-facing arrows) in positive charge and radially inwards (in-facing arrows) in negative charge.[41] Explicitly, the experiments reveal that electrostatic fields in opposite charges are inherently opposite as illustrated in Figure 2.
Combined, Dirac’s equation, Anderson’s observation and the test charge experiments compel two conclusions. One, an electron is fundamentally different from an ordinary particle. Its physical components – electron mass and electrostatic field – are either positive or negative. In contrast, ordinary mass and ordinary (gravitational) field do not exhibit positive-negative symmetry. Hence, it is rational to conclude that electron mass and electrostatic field are electrically active while ordinary mass and gravitational field are electrically passive.
Two, positron (E+) and negatron (E–) are opposite simply because they are made of intrinsically opposite masses and the fields. The prevailing theory is that positron and negatron have identical positive mass[42] but carry opposite charges.[43] The theory, however, does not define or explain charge[44] in terms of the fundamental quantities of the universe – mass, length and time.[45] The failure has been termed “a problem of great importance” and an hindrance to “development in physics.”[46] Equation (2) and Equation (3) partially solve the problem: if charge is the feature that distinguishes positron and negatron, then charge is the sum of electron mass and electrostatic field. But Equation (1) defines electron (E) in the same parameters, implying that, as physical entities, charge (e) and electron (E) are indistinguishable. Hence, electron does not carry ‘charge’. Rather, electron mass (me) and electrostatic field (ef) constitute a charge (e):
The conclusion resolves positive (e+) and negative (e–) charges, like positive (E+) and negative (E–) electrons, to opposite electron masses and electrostatic fields:
Thus,
Consequently,
Empirically, however, charge (e) and electron (E) behave differently. But physicists know that electricity at rest and in motion behaves differently. At rest, electricity is an electrostatic phenomenon; in motion, it is an electrodynamic phenomenon. Taken together with Equation (8), these facts reveal that charges are electricity at rest; electrons are electricity in motion. Explicitly, the difference between a charge and an electron is behavioural rather than physical. Established scientific facts support this inference.
3. Charge and electron: one physical entity two behavioural identities
Our knowledge of electricity is based on two parallel lines of research: one focusing on ‘charge’ and the other on ‘electron’. The natural relation of the two is blurred. In 1874 Stoney interpreted Faraday’s laws of electrolysis to mean that “positive as well as negative electricity”, like matter, comprises “indivisible particles.”[47] He proposed the name “electron” for the “atom of electricity.”[48] By then it was known that electricity exists in positive and negative types. Thus, in Stoney’s original terminology, electricity comprises discrete positive and negative “electrons”. With time, Stoney’s “electron” was renamed ‘charge’ and his “atoms of electricity” are the modern charges. Later, Millikan proved “very directly”[49] that a quantity of charge consists of individual elementary charges. His oil drop experiment provides hard evidence that a charge, consistent with Stoney’s description, is a particle. Charges behave like infinitesimal, perfectly uniform billiard balls occurring in electrically opposite types. For instance, charges are countable,[50] storable [51] and transferable from one object to another. Regardless, the physical nature of the Stoney-Millikan charge is enigmatic.[52,53,54] Confusion exists because rest mass (hence volume) defines a physical particle but no one has ever ascertained whether charge, a physical particle on other counts, has rest mass.
In 1897 Thomson discovered a definite physical particle that was finally named “electron”. Accurately, he discovered the negatron and demonstrated that it has rest mass. Later, Anderson discovered the positron, proving that electrons, like charges, have positive-negative electric symmetry. Besides this symmetry, however, it appeared like ‘positive and negative charges’ and ‘positive and negative electrons’ have nothing in common. Physicists took the position that a charge and an electron are fundamentally different entities cojoined in such a way that the known particle – the electron – carries[55] the mysterious charge. This position arises from four considerations (Table 1). 1) The atomic ratio of negative to positive charges is 1:1; but the atomic ratio of negative to positive electrons is 1:0 – positrons are deemed absent in the atom.[56] 2) Rest mass defines an electron as a physical particle; but a charge is tacitly considered massless. 3) Opposite electrons annihilate; but opposite charges neutralise. 4) The environmental ratio of negative to positive charges is 1:1, resulting in the conservation of electric charge; but by far more negative than positive electrons are observed. [57,58]
According to CERN, “one of the greatest challenges in physics is to figure out … why we see an asymmetry between matter and antimatter.”[59] Conspicuously, negatrons are deemed present in the atom and positrons absent[60] (Table 1). Further, CERN puts the chances of observing a positron in the environment, rather than a negatron, at one to a billion. This results in the observable numerical asymmetry. By early 1930s, however, positive beta (β+) decay was taken as evidence that positrons do exist in atomic nuclei.[61,62] The interpretation was based on the Curie-Joliot inference that proton is a “complex structure” that breaks up into a “positron” and an electrically neutral particle they termed “neutron.”[63] Clearly, Curie and Joliot deduced that proton (p+) as a whole is no more an electric object than, for example, a sodium ion (Na+). Its electric effects stem from a discrete positron that it carries, and which beta decay frees (along with a neutrino), leaving behind the “neutron”. In that case, there is a positron on every proton. And since for every proton there is a negatron, the atomic ratio of negatrons to positrons is 1:1.
Elsasser, among others, recognised the Curie-Joliot explanation of the source of the positrons as “superior to Dirac’s hole theory.”[64] Essentially, the explanation means that ‘positron-on-proton’ is the negatron’s natural counterpart. This solves an outstanding problem. The proton was initially considered the “positive electron”[65] and – since the positron is deemed absent in the atom – it is still regarded as the negatron’s atomic counterpart. However, proton is 1,837 times heavier than negatron. The mass difference disqualifies it as negatron’s natural counterpart. Prior to the discovery of the actual positive electron, Rutherford faced this difficulty: “It might a priori have been anticipated that the positive electron should be the counterpart of the negative electron and have the same small mass. There is, however, not the slightest evidence of the existence of such a counterpart.”[66] A few years later, “such a counterpart” (positron) with “the same small mass” was found. Still, the positron did not fit as negatron’s natural opposite. Whereas negatron and proton fail to match due to mass asymmetry, negatron and the observable positron fail to match due to numerical asymmetry. Against these difficulties, the Curie-Joliot positron-on-proton emerges as the negatron’s natural match – equal in mass, in magnitude of charge, in natural abundance; but opposite in electric effects (Table 2).
Despite its ability to identify positron-on-proton as negatron’s natural match, the Curie-Joliot version of β+ decay was downplayed and finally forgotten. This is because the distinction between positron-on-proton and the environmental positron was missed. If Curie and Joliot described the environmental positron, then their inference contradicts experiment. First, it would mean that positrons and negatrons have a ratio of 1:1, whereas, empirically, negatrons outnumber positrons. Second, it would mean that opposite electrons coexist in the short intra-atomic distances whereas, empirically, at such short distance a pair of opposite electrons should ‘annihilate’.[67] But Curie and Joliot described positron-on-proton; not the environmental positron. The difference is significant because positron-on-proton and environmental positron behave differently. Notably, positrons-on-protons and atomic negatrons are numerically equal and interact by pair neutralisation rather than by pair annihilation. Thus, positron-on-proton and orbital negatron behave, respectively, like positive and negative charges (Table 3).
From Table 3, positron-on-proton and orbital negatron are charges rather than electrons – they neutralise rather than annihilate; and manifest numerical symmetry rather than asymmetry. Within the atom, electricity is at rest and observable as charges. Ejected from the atom at high speed, it is in motion and observable as electrons. This analysis validates Equation (8): charge is the static (nonrelativistic) electron; electron is the ultrahigh speed (relativistic) charge (Table 4).
Interpretation of charge as static electron explains, effortlessly, why more negatrons than positrons are observed in our environment. Located in the atomic nuclei, the Curie-Joliot positron-on-proton (positive charge) is heavily shielded by the orbital static negatrons (negative charges) and has negligible chances of escaping to the extra-atomic environment where it is detectable as the usual positron. In other words, more energy is required to liberate a positive charge (static positron) from the nucleus than to liberate a negative charge (static negatron) from the orbit. However, whether positive or negative, an ‘atom of electricity’ is ejected from the ‘atom of element’ at tremendous speed, losing the characteristics of a charge and gaining those of an electron. Rutherford (1925) used such logic when he identified Thomson’s negative electron as “an actual disembodied atom of electricity”. In plain terms, negatron is Stoney’s ‘atom of negative electricity’ detached from the ‘atom of element’. Conversely, Anderson’s positron is Stoney’s ‘atom of positive electricity’, or the Curie-Joliot positron-on-proton, detached from the ‘atom of element’. Additional pieces of evidence leave no doubt that Rutherford was correct in associated ‘atomic charge’ with ‘environmental electron’.
First, negatrons originate from the atomic orbits where Stoney’s negative charges are located. Likewise, Anderson[68] and Curie[69] concluded that positrons originate from the atomic nuclei – where Stoney’s positive charges are located (Figure 3). But charge and electron are inseparable[70]; nature has neither chargeless (electrically neutral) electron nor electronless (electron-independent) charge. Hence, at its atomic origin, an ‘atom of electricity’ is the charge; but travelling at high speed outside the atom, it is an electron. Second, the historical methods used to investigate electricity reveal that the sole difference between charges and electrons is the speed at which they are observed. Coulomb, Faraday, Millikan, and other ‘electrostatic students’ observed ‘atoms of electricity’ at near-static speeds – in jars, electrolytes, electroscopes, oil drops, glass rods, etc – and recognized them as charges. In contrast, Thomson, Anderson, Dirac[71] and other ‘electrodynamic students’ observed the same ‘atoms of electricity’ detached from atoms of elements and moving at ultrahigh speed through vacuumed cathode tubes and cosmic rays and recognised them as electrons. Strictly, therefore, electrons – as ultrahigh speed particles – do not exist inside the atoms; they are observable in the extra-atomic environment. Within the atoms, latent positive and negative electrons coexist as pairs of positive and negative charges.
4. Unification of electric charge and gravitational mass
A colliding pair of opposite electrons (highspeed charges) ‘annihilates’;[72,73] but a pair of opposite charges (static electrons) neutralises[74] (Table 4). However, evidence shows that ‘annihilation’ does not literally obliterate the electrons. With a lifespan of more than 6.6x1028 years,[75] the electron has been described as “practically immortal”,[76] “indivisible and unbreakable”,[77] as well as “absolutely stable.”[78] Unlike any other known particle, the electron is irreducible. Put simply, the electron – positive or negative – is the veritable unit of matter that can neither be created nor destroyed. If nature prefers the most stable particle as the foundational block of the material universe, then the electron has no competitor. Plausibly, therefore, ‘annihilation’ mutually plunges opposite electrons into their lowest energy level, where they coexist as a relativistic neutron charge, and their opposite fields annihilate into gamma rays.
Similarly, positive and negative charges (static electrons) mutually ‘fall’ into their lower energy level and convert to an electrically neutral entity. In the process, opposite electrostatic fields annihilate into a spectrum of lower frequency electromagnetic radiations. Thus, ‘electron pair annihilation’ and ‘charge pair neutralisation’ are essentially the same process occurring, in that order, at relativistic and nonrelativistic speeds. A key difference is that neutralised positive and negative charges (static electrons) remain relatively far apart compared with the ‘annihilated’ positive and negative electrons (moving electrons).
Empirically, neutralised positive and negative charges mutually conceal their opposite electric properties such that they become undetectable by a third charge. This is analogous to the mutual cancellation of ‘a peg and a hole’, where nothing disappears in a literal sense. Expanding e+ and e– as in Equation (6) and Equation (7), respectively, sheds fresh light on the charge pair neutralisation process – Equation (9).


Equation (9) reveals that in their independent existence, e+ and e– are electrically active and exhibit electric behaviours. However, coexisting at subatomic distances (neutralised state) e+ and e– cease to exhibit their individual electric behaviours and mutually exhibit the mechanical behaviours that characterise ordinary mass. The pair becomes a neutral charge (2e0); the natural quantum of gravitational mass. Thus, the equation reveals that charge pair neutralisation is the natural process by which positive and negative units of electrically active matter convert to a unit of electrically passive (gravitational) mass (Table 4).
Applied to the simplest (hydrogen) atom, Equation (9) reveals that the observable positive and negative charges in the atomic ‘outer zone’ constitute a single unit of neutral charge (2e0) or a natural quantum of ordinary (gravitational) mass (Figure 6). Since any atom has the same number of positive nuclear and negative orbital charges (static electrons), it can be generalised that the material content of the atomic outer zone is pure neutral electric charges or integral multiples of 2e0.
Figure 4.
A pair of opposite charges constitutes a unit of ordinary mass or the electrically neutral charge (2e0). An integral multiple of such units form the material content (gravitational mass) of the atomic outer zone.
Figure 4.
A pair of opposite charges constitutes a unit of ordinary mass or the electrically neutral charge (2e0). An integral multiple of such units form the material content (gravitational mass) of the atomic outer zone.

The process that reverses charge pair neutralisation can be termed ‘charge pair production’, which is the nonrelativistic equivalence of electron pair production. Charge pair production is familiar and easy to observe but has never been recognised for what it is. It is observable in frictional electrification, for example when glass rod is rubbed with silk. The rubbing literary splits a unit of electrically passive (gravitational) mass (2e0) to positive (e+) and negative (e–) units of the electrically active matter. The processes of charge pair production and neutralisation reveal that: 1) ordinary mass and electric charge do interconvert; 2) contrary to the view that ordinary mass exists in indefinite and unpolarised continuum, it is ultimately quantized and polarized; 3) positive and negative ‘atoms of electricity’ are the natural bricks of which both electrically active and passive matter are made (Figure 7).
Figure 5.
Interconversion of the electrically active matter (electric charge) and the electrically passive (ordinary mass) matter is an interplay of discrete positive, negative and neutral electric charges.
Figure 5.
Interconversion of the electrically active matter (electric charge) and the electrically passive (ordinary mass) matter is an interplay of discrete positive, negative and neutral electric charges.

5. The atom as pure positive and negative charges
Equation (9) establishes that nature combines positive (e+) and negative (e-) charges to construct a unit of gravitational mass (2e0). Based on the equation, the whole atom, which is a gravitational mass particle, comprises pure positive and negative charges (static electrons). That is, the atom’s mass is electrically neutral for the sole reason that half of it is positive and half is negative. This is evident in the atomic outer zone, where positive nuclear and orbital negative charges contribute an equal number of positive and negative elementary masses to for the gravitational mass (Figure 4). Similarly, a number of scientific facts reveals that the nucleons – which occupy the atomic inner zone – are solely made of an equal number of positive and negative charges.
First, the proton carries a positive charge but the neutron is electrically neutral. This fact has natural significance. Blackett established that proton is 1,837 times heavier than the electron,[79] implying that 1,837 electron mass units (1,837me) go into a proton. Similarly, Chadwick determined that the neutron is 1,840 times heavier than the electron, meaning that 1,840 electron mass units (1,840me) go into a neutron. But Equation (5) associates elementary mass (me) with elementary charge (e), such that the number of elementary mass units in a particle equals the number of the elementary charge units. In this light, the proton comprises 1,837 individual charges (1,837e) and the neutron consists of 1,840 individual charges (1,840e). Consistent with Equation (9), the neutron’s electric neutrality is due to its even number of charges, which translate to an even number of elementary masses (920me+ and 920me–). Conversely, proton’s positive charge is due to its odd number of charges, which translate to an odd number of elementary masses (920me+ and 920me–). Simply put, the proton has one unpaired (un-neutralised) positive charge.
Neutron and proton masses point at a universal principle: an electrically neutral particle must have an even number of electron masses; and a particle that carries one elementary charge must have an odd number of the masses. Experiment backs the principle. Rounding off the empirical masses of baryons[80] to the nearest whole electron mass exposes natural patterns that associate each particle’s electric charge status with the evenness or oddness of its constituent number of electron masses (Table 5). The patterns validate Equation (5) as the natural association of elementary charge (e) and elementary mass (me).
Second, proton mass (1,837me) is 3me less than neutron mass (1,840me). Beta decays explain the natural significance of this difference. In beta negative (β-) decay, neutron (N0) disintegrates to proton (P+), negatron (e-) and neutrino (𝜈). Similarly, in beta positive (β+) decay, proton (P+) disintegrates into positron (e+), neutrino (𝜈) and a particle considered a ‘neutron’ (n0). In Pauli’s summary “a neutrino always accompanies the beta electron.”[81] Concurrently, nature chips an electron and a neutrino out of a nucleon. Since mass is strictly conserved, the 3me difference is shared by electron and neutrino. The electron accounts for 1me; therefore, the neutrino accounts for 2me. In this perspective, Pauli’s neutrino matches the neutral electric charge (2e0) – an electrically neutral particle with two units of electron mass (2me0). Pauli was once close to this inference when he suspected that “neutrino might be a combination of a Bose-positron and an electron (negatron).”[82] But the idea that neutrino is massless prevailed.[83] Later studies, however, “have conclusively established that neutrinos”[84] have rest mass. Arising from the evidence presented in this paper, neutrino mass is precisely twice the electron mass (2me0). Moreover, recognition of beta electrons as ultrahigh speed positive (e+) and negative (e–) charges (section 4) provides sound ground to infer that Pauli’s neutrino is the ultrahigh speed (relativistic) neutral charge (Table 6).
Fruitful results emerge when Pauli’s summary is applied to other multiplets, providing extra evidence that the 3me difference and the neutron-proton electric charge states are universal phenomena. It is noted that, invariably, a 3me unit separates a particle and its next neighbour in a multiplet; and charge states alternative as … neutral → positive → neutral → negative → neutral → positive … (Table 7). In harmony with Equation (5) and Equation (9), particles with even-numbers of charges are electrically neutral and the odd-numbered ones are electrically charged. Thus, it is possible to connect known members of each multiplet by filling the gaps between them with a series of 3me units, thereby predicting a range of new particles.
The information in Table 8 opens a way to expand and explore the nucleon multiplet beyond the two known members – the neutron and the proton. Empirically, nucleon decays have four possible emission outcomes. 1) Nothing is emitted besides the neutrino even though the atomic number increases by one (internal adjustment). 2) Spontaneous emission of positive beta (β+) electron (positron) and neutrino. 3) Spontaneous emission of negative beta (β-) electron (negatron) and neutrino. 4) Spontaneous emission of gamma rays (γ) and neutrino. To account for these outcomes, nature imposes four rules (Table 8).
Expanding the nucleon multiplet (Table 8) in accordance with Pauli’s summary and the natural decay rules outlined in Table 8 yields a surprising discovery: besides Chadwick’s neutron, nature has two more stable, electrically neutral nucleons. In addition, an unstable (transient) nucleon with a negative charge is identifiable. In effect, the four rules outlined in Table 9 describe how four different nucleons decay. The implication is that nucleons and the members of the ‘particle zoo’ can repeatedly decay to only positive, negative and neutral ‘atoms’ of electricity. However, the neutral ‘atom’ of electricity decays further into a pair of opposite ‘atoms’ of electricity. In electrostatic conditions, the neutral charge decays into opposite charges. In electrodynamic conditions, the moving neutral charge (neutrino) decays into a pair of opposite electrons via the electron pair production. Hence, an atom can decay, at least in theory, into pure ‘atoms’ of positive and negative electricity.
Rule 1: Chadwick’s neutron (N0) is stable. It decays to proton, static negatron (negative charge) and neutrino: N0 → P+ + e– + 𝜈0. A critical inference is that neutron decay is not the source of the observable negatron. To conserve charge and stabilise the atom, both P+ and e- must be retained in the atom. Hence, neutron decay emits nothing besides the neutrino. However, it raises the atomic number by one.
Rule 2: The proton (P+) is table. In β+ decay it emits a positron, reducing the atomic number by one and converting to a particle presently called ‘neutron’(n0): P+ → n0 + e+ + 𝜈0. But the law of conservation of mass prohibits the conversion of lighter proton to heavier neutron. Hence, the stable, electrically neutral particle resulting from proton decay is a new nucleon, here named the nairotron (n0) (Table 9).
Rule 3: The nairotron (n0) is stable (Table 9). It decays into an unstable nucleon that carries a negative charge, and which is here named transitron (t): n0 → t- + e+ + 𝜈0. In this decay, negative and positive charges emerge concurrently in the nucleus and orbit respectively. Consequently, both are concurrently ejected from nucleus as opposite electrons (highspeed charges) and ‘annihilate’ into gamma rays.
Rule 4: The transitron (t-) is unstable as it introduces negative charge in the nucleus. Hence, decays to a smaller but stable neutral particle, here named the afritron (A), as well as the observable negatron: t- → A0 + e- + 𝜈0. The fact that the transitron accounts for the observable negatron implies that the electrically neutral and stable Afritron (1,828e0) can be found in the atomic nucleon. If the Afritron decays at all, it must follow the same route as that of ordinary neutron – restarting the four-step decay cycle (Table 9).
Table 10.
Empirical beta decay outcomes fit into a clear 'segment' of the nucleon decay spectrum (shaded grey). This identifies three new nucleons – nairotron, transitron and Afritron. The nairotron differs from Chadwick’s neutron because it has smaller mass and has different decay products. The Afriton, other being lighter, is exactly like Chadwick’s neutron.
Table 10.
Empirical beta decay outcomes fit into a clear 'segment' of the nucleon decay spectrum (shaded grey). This identifies three new nucleons – nairotron, transitron and Afritron. The nairotron differs from Chadwick’s neutron because it has smaller mass and has different decay products. The Afriton, other being lighter, is exactly like Chadwick’s neutron.
| Particle’s EMUs & charge status | Decay route | Original particle | Non-neutrino emission | Decay cycle/rule |
| ↑ … | … | … | … | … ↑ |
| Predicted 1843e- | 1843e- → 1840e0 + 1e- + 2e0 | Unstable | ß- | Rule 4 |
| Neutron 1840e0 | 1840e0 → 1837e+ + 1e- + 2e0 | Stable (neutron) | None | Rule 1 |
| Proton 1837e+ | 1837e+ → 1834e0 + 1e+ + 2e0 | Stable (proton) | ß+ | Rule 2 |
| Nairotron 1834e0 | 1834e0 → 1831e- + 1e+ + 2e0 | Stable (Nairotron) | ß+ + ß- (2e0 + γ-rays) | Rule 3 |
| Transitron 1831e- | 1831e- → 1828e0 + 1e- + 2e0 | Unstable (transient) | ß- | Rule 4 |
| Afritron 1828e0 | 1828e0 → 1825e+ + 1e- + 2e0 | Stable | None | Rule 1 |
| Predicted 1825e+ | 1825e+ → 1822e0 + 1e+ + 2e0 | Stable | ß+ | Rule 2 |
| Predicted 1822e0 | 1822e0 → 1819e- + 1e+ + 2e0 | Stable | ß+ + ß- (2e0 + γ- rays) | Rule 3 |
| Predicted 1819e- | 1819e- → 1816e0 + 1e- + 2e0 | Unstable | ß- | Rule 4 |
| Predicted 1816e0 | 1816e0 → 1813e+ + 1e- + 2e0 | Etc | Etc | Etc |
| ↓ … | … | … | … | …↓ |
6. Unification of gravity and electricity
A decisive proof that Equation (9) correctly portrays nature is that it verifiably unifies Newton’s law of gravity and Coulomb’s law of electrostatics to 8G/mpme = K/e2, where G and K are the respective constants, mp the proton mass, me the electron mass, and e the elementary charge. A clear-cut principle underlies this discovery: Newton deals with ‘electrically passive mass and field’; Coulomb with ‘electrically active mass and field’. The fact that both interactions deal with ‘mass and field’ explains the analogy. But Newton’s matter is ‘electrically passive’ while Coulomb’s is ‘electrically active’. This explains the difference. Essentially, therefore, Newton’s mass (M) is a neutral electric charge; and gravitation is the electrostatic attraction between unlike halves of like masses M1 and M2:
Empirically, opposite charges – and opposite magnetic poles – attract. Equation (10) extends this rule to gravitational mass such that ‘opposite halves’ of ‘like masses’ attract (Figure 8). This explains a familiar puzzle of gravity, namely that unequal masses, such as the earth and the moon, attract each other with a force of the same magnitude. The current explanation is that a gravitational mass has an intrinsic active-passive symmetry,[85] where the active component is the source of gravitational field lines and the passive component is the sink.[86] Equation (9) makes it plain that a gravitational mass comprises half positive and half negative elementary masses (Figure 8).
Figure 6.
A gravitational mass (M) with an intrinsic positive-negative mass symmetry explains why unequal masses (M1 and M2) attract with the same magnitude of force.
Figure 6.
A gravitational mass (M) with an intrinsic positive-negative mass symmetry explains why unequal masses (M1 and M2) attract with the same magnitude of force.

Besides the positive-negative intrinsic symmetry, Equation (9), as simplified in Table 4, shows that a gravitational mass has a tangible (inertial mass) and an intangible (gravitational field). This throws new light into Newton’s gravitation: gravitational force is directly proportional to the product of the tangible (inertial) masses (M1M2) and inversely proportional to the product of the intangible gravitational fields, which correspond with r-2. The tangible mass and the intangible field are inseparable, mechanical parts of a gravitational mass. Therefore, two gravitational masses are constantly in mechanical contact; there is no distance between them. Hence, the slightest alteration in one mass instantly affects the other. Newton’s Law of Universal Gravitation reveals, therefore, that gravitational field mechanically connects every inertial mass to every other inertial mass in the universe; and that what seems like ‘instant action at a distance’[87] is really instant action at no distance. Distance (gravitational field) exists between two inertial masses; but there exists no distance (gravitational field) between two gravitational masses. Moreover, a gravitational field that emanates from the centre of an inertial mass and increases in direct proportion to the quantity of the mass, and which extends and thins out equally in a three-dimensional space, must have the geometrical properties that Einstein equated to curved space. Contrary to Einstein’s conclusion, inertial mass does not curve space; inertial mass and the curved space (gravitational field) are components of a gravitational mass (Figure 8). In this light, gravitational field does not fill the space between two inertial masses; it is the space.
Figure 7.
Newton’s gravitational mass has two components: the tangible electrically passive inertial mass and the intangible electrically passive gravitational field. Rather than fill the space around the inertial mass, the field is the space. .
Figure 7.
Newton’s gravitational mass has two components: the tangible electrically passive inertial mass and the intangible electrically passive gravitational field. Rather than fill the space around the inertial mass, the field is the space. .

The relation of electric charge to gravitational mass (Table 4) hints that Newton’s equation of gravity and Coulomb’s equation of electrostatics have an underlying uniformity. Two factors mask this uniformity. One, electric charge in Coulomb’s equation (F = KQ1Q2/r2) is polarised – it is either positive or negative – but it is not quantised. That is, the equation utilises artificial units (coulombs) rather than natural quanta. Two, mass in Newton’s equation (F = GM1M2/r2) is neither polarised nor quantised. That is: first, the equation does not take into account the fact that a gravitational mass has an intrinsic positive-negative mass symmetry; and, second, like Coulomb’s equation, it utilises artificial units (kilograms). Thus, to unify the two equations, both Coulomb’s product of charges (Q1Q2) and Newton’s product of masses (M1M2) must be unified. That is, polarised and quantised.
From Millikan’s experiment, quantity Q of charge comprises whole number multiple of the elementary charge (e). In terms of elementary charges, Q1 equal Q1/e and Q2 equals Q2/e. Thus, e2 is the natural quantum of Coulomb’s product of charges (Q1Q2). Consolidating Coulomb’s variables on one side:
Quantising the variables (dividing by e2) yields a new constant K/e2 or T1:
Equation (10) has already polarised the product of Newton’s masses, such that the product of polarised masses (¼M1M2–) is interactively equivalent to the product of polarised charges (Q1Q2–). But how does nature quantise gravitational mass? Aston’s “whole number rule” states that “masses of the isotopes are whole number multiples of the mass of the hydrogen atom (protium).”[88] Unambiguously, any gravitational mass is a whole number multiple of the mass of the simplest (hydrogen) atom. But hydrogen atom has distinct inner and outer zones (Figure 5): nuclear proton mass (mass = mp) and masses of nuclear and orbital charges (mass = 2me). That is, the mass of hydrogen atom is organised into two quanta – mp and 2me. Equation (9), however, shows that 2me0 is the natural quantum of any electrically passive inertial mass. Thus, mp0, through distinct, is a whole number multiple of 2me0. The implication is that mp and 2me are the same type of inertial mass organised into low- and high-density zones. In the low-density outer zone, pairs of opposite charges (each equal to 2me) are relatively far apart. But within the proton, the pairs of are so tightly compacted that the proton exists as a discrete natural unit of gravitational mass. Thus, nature has two separate quanta of gravitational mass, and the total gravitational mass is the average of the two: proton mass (mp) and mass of the neutral charge (2me). In this perspective, the natural quantum of Newton’s product of polarised masses (¼M1M2–) is:
Consolidating Newton’s variables on one side:
Quantising the variables (dividing by ½mpme) yields a new constant G/mpme or T2:
Calculations based on CODATA values[89] of physical constants show that T1 and T2 are equal. The value of K/e2 is 3.506 x 1047 Nm2/C4 and that of 8G/mpme is 3.506 x 1047Nm2/kg4. Hence:
The term Fr2 in Equation (11) and Equation (12) cancels out, making it evident that gravitational mass and electric charge are fundamentally the same thing:
The numerical and conceptual equality of electrostatic and gravitational interactions as displayed in Equation (143 leaves no doubt that electrostatic and gravitation have a common origin. Consequently, Coulomb’s and Newton’s laws can be unified and stated as a more universal law: two quantities of electric charge separated by distance r experience a force (F) that is directly proportional to their product and inversely proportional to the square of the distance (r-2). Traditionally, the quantities of passive electric charge (gravitational mass) in Newton’s law are neither polarized nor quantized. On the other hand, the quantities of active electric charge in Coulomb’s law are polarized but not quantized. Quantisation and polarisation of both Newton’s masses and Coulomb’s charges expose the underling uniformity of the two interactions.
7. Conclusion
This article has synthesised scattered bits of scientific evidence, collected over centuries, to arrive at a verifiable conclusion that positive and negative ‘atoms of electricity’ – collectively charges and electrons – are the ultimate building blocks of the material universe. The finding opens new vistas into physics.
References
- Malcolm, S. ‘Leucippus, Democritus and the ou mallon principle: an examination of Theophrastus Phys. Op. Fr. 8,’ Phronesis, 47(3): 253–63 (2002).
- Dalton, J. A new system of chemical philosophy (S. Russell (for R. Bickerstaff), London and Manchester), vol. 1, part 1 (1808).
- Griffiths, D. Introduction to elementary particles, second edition, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, pg. 15 (2008).
- Weiner, C. 1932: Moving into the new physics, Physics Today 25, 5, 40 (1972). [CrossRef]
- Reader, J. & and Clark. C. 1932, a watershed year in nuclear physics, Physics Today 66, 3, 44 (2013). [CrossRef]
- Karel, V. A. The particle zoo. In: The multi-universe cosmos. Springer, Boston, MA, (1992). [CrossRef]
- Jagger, J. Atoms: what the universe is made of. In: The Nuclear Lion. Springer, Boston, MA (1991). [CrossRef]
- Oerter, R. The theory of almost everything: The Standard Model, the unsung triumph of modern physics (Kindle ed.). Penguin Group. p. 2 (2006).
- Gaillard, M.K., Grannis, P.D., Sciulli, F.J. The Standard Model of Particle Physics. In: Bederson, B. (eds) More Things in Heaven and Earth. Springer, New York, NY, (1999). [CrossRef]
- Cottingham, W. N. & Greenwood, D. A. An introduction to the Standard Model of Particle Physics, Cambridge University Press, Second Ed. (2012).
- CERN. The Standard Model (2022). https://home.web.cern.ch/science/physics/standard-model.
- Riordan, M. The discovery of quarks, Science, Vol 256, Issue 5061, pp. 1287-1293 (1992). [CrossRef]
- Bian, J. & Wang J. A novel scheme to search for fractional charge particles in low energy accelerator experiments, Journal of Instrumentation, Volume 7, Issue 07 (2012). [CrossRef]
- Smith, P. F. Searches for fractional electric charge in terrestrial materials, Annu. Rev. Nucl. Part. Sci. 1989.39: 73-II 1 (1989).
- Irwin, T. et al. Large bulk matter search for fractional charge particles, Phys. Rev. D 66, 012002 (2002). [CrossRef]
- Halyo, V. et al. Search for free fractional electric charge elementary particles, SLAC-PUB-8283 (1999).
- Sleator, W. W. The Faraday laws of electrolysis, American Journal of Physics 9, 166 (1941). [CrossRef]
- Stoney, G. J. On the "Electron" or “Atom of Electricity". Phil. Mag. 5. 38: 418–420 (2009).
- Franklin, A. Millikan’s oil-drop experiments, The Chemical Educator 2(1):1-14 (1997). [CrossRef]
- Pakulin, V. What is charge. Preprint, (2020). [CrossRef]
- Hestenes, D. & Weingartshofer, A. (Eds.) The electron: new theory and experiment (1991). [CrossRef]
- McGinn, C. electric charge: a case study, basic structures of reality: essays in meta-physics, New York, (2012). [CrossRef]
- Stoney, G. J. XLIX. Of the “electron,” or atom of electricity, Philosophical Magazine Series 5, 38:233, 418-420 (1894). [CrossRef]
- Wilczek, F. Unification of force and substance. Phil. Trans. R. Soc. A 374: 20150257 (2016). [CrossRef]
- Wilczek, F. The enigmatic electron. Nature 498, 31–32 (2013). [CrossRef]
- Franklin, A. & Perovic, S. evidence for a new entity: J.J. Thomson and the electron, Stanford Encyclopaedia of Philosophy, Appendix 7 (2021).
- Britannica, The Editors of Encyclopaedia. "line of force". Encyclopaedia Britannica, 28 Sep. 2016, https://www.britannica.com/science/line-of-force. Accessed 31 January 2022.
- Feynman, R. P. The Feynman Lectures on Physics Vol I. Addison Wesley Longman (1970).
- Wheeler, J. A. Black Holes, and Quantum Foam: A Life in Physics p. 163, London (1998).
- Grieder, P. K.F. in Cosmic Rays at Earth, Researcher's Reference Manual and Data Book, pg. 669-891 (2001).
- Winterberg, F. T. Space Interpretation of Quantum Mechanics, Gauss Press, Reno, Nevada, Zf. Naturforsch 58a, 231 (2003).
- Stephen, B. Ariel, S. the making of twentieth century science, how theories became knowledge, P. 271, Oxford University Press (2015).
- Golden, G. N. Avoiding Negative Probabilities in Quantum Mechanics, Journal of Modern Physics, 4, 1066-1074 (2013).
- Brush, S. G. The Making of Twentieth Century Science: How Theories Became Knowledge, p. 271, Oxford University Press (2015).
- Pollard, D. & Dunning, J. A Consideration of the Possibility of Negative Mass, Il Nuovo Cimento Vol.110 B, N. 7 (1995).
- Bonnor, W. B. Negative Mass in General Relativity, Gen Relat Gravit, 21:1143 (1989). [CrossRef]
- Forward, R. L. Negative matter propulsion, Journal of Propulsion and Power, Vol. 6, No. 1, pp. 28-37 (1990). [CrossRef]
- Bergstrom, L. Goobar, A. Cosmology and Particle Astrophysics, Second Edition, Springer, p.310 (2006).
- Anderson, C. The positive electron, Phys. Rev., 43 6, 491–494 (1933). [CrossRef]
- Purcell, E.M., Morin D. J. Electricity and Magnetism (3rd Ed.) Harvard University, Cambridge University Press, New York pp. 5-7 (2013).
- Li, J., Singh, C. Eur. J. Phys. 39 045711 (2018). [CrossRef]
- Chadwick, J., Blackett P. M. S., Occhialini G. P. S., Some experiments on the production of positive electrons (1934); downloaded from https://royalsocietypublishing.org/ on 10 February 2022.
- Britannica, The Editors of Encyclopaedia. "electron". Encyclopedia Britannica, 19 Dec. 2019, https://www.britannica.com/science/electron. Accessed 11 April 2022.
- Sus, B. Physical meaning of concepts “electrical charge” and “electric field”, Computational Problems of Electrical Engineering vol. 8, no. 1 (2018).
- Butto, Nr. A new theory for the essence and nature of electron charge, Journal of High Energy Physics, Gravitation and Cosmology Vol.7 No.3 (2021). [CrossRef]
- Kreidik, L.G., Shpenkov G.P., Atomic Structure of Matter-Space, Alternative Picture of the World, Vol. 1-3, Bydgoszcz, (1996).
- Wayman, P. A. Stoney’s electron, Europhysics News September/December, p. 159 (1997).
- "George Johnstone Stoney 1826–1911". The Daily Express (1911).
- Millikan, R. A. On the elementary electrical charge and the Avogadro Constant, Phys Rev.2.109 (1913). [CrossRef]
- Britannica, The Editors of Encyclopaedia. "electric charge". Encyclopedia Britannica, 26 Feb. 2021, https://www.britannica.com/science/electric-charge. Accessed 30 August 2021.
- Lüttgens, G., Lüttgens, S., Schubert, W. A. Principles of static electricity, In book: Static Electricity: Understanding, Controlling, Applying (pp.19-39), (2017). (2017). [CrossRef]
- Mahdi, J. N. On the nature of electric charge, Int. J. Phys. Sci. 9(4), pp. 54-60, (2014).
- Etkin, V. A. Modified Coulomb law, World Scientific News 87 163-174, (2017).
- Sus, B. Physical meaning of concepts “electrical charge” and “electric field”, Computational Problems of Electrical Engineering vol. 8, no. 1 (2018).
- Marton, L. & Marton, C. Evolution of the concept of the elementary charge, Advances in Electronics and Electron Physics, Vol. 50, pp. 449-472 (1980). [CrossRef]
- Ojovan, M.I. & Lee, W.E. An introduction to nuclear waste immobilization, Second Edition, Elsevier, Amsterdam, p.12. (2014).
- Simak, C.D. (ed.). “From Atom to Infinity, Readings in Modern Science”, p.282 (1964).
- Grimani, C. Upper limit to the cosmic-ray positron flux generated at the pulsar polar cap, 29th International Cosmic Ray Conference, Pune (2005).
- https://home.cern/science/physics/matter-antimatter-asymmetry-problem (accessed 13 November 2022).
- Scholtz, J.J., Dijkkamp D.A., & Schmitz, R.W. Secondary electron emission properties, Philips Journal of Research, 50 (3–4), 375-389 (1996). [CrossRef]
- Jensen, C. Controversy and census: nuclear beta decay 1911-1934 (Springer Basel, Ag, 2000).
- Brown, L. M. Nuclear structure and beta decay (1932–1933), American Journal of Physics 56, 982 (1988). [CrossRef]
- Saha, M. N. & Kothari, D.S. A suggested explanation of β-Ray activity, Nature: Letters to the editor (1933).
- Elsasser, W. A Possible property of the positive electron. Nature 131, 764 (1933). [CrossRef]
- Compton A. H. The elementary particle of positive electricity, Nature, 106, 828-828; (1921). [CrossRef]
- Rutherford, E. Electricity and matter, The Scientific Monthly, Vol. 20, No. 2 pp. 121-128 (1925).
- Frolov, A. M. & Farrukh, A. C. Annihilation of the electron-positron pairs in polyelectrons, Journal of Physics A, Mathematical and Theoretical 40(39) (2007). [CrossRef]
- Anderson, C. The positive electron, Phys. Rev., 43 (6), 491–494 (1933). [CrossRef]
- Curie, I., Joliot F. β-emission of positive electrons, C. R. Acad. Sci. 198, 254 (1934).
- Thomson, G. The Electron (United States Atomic Energy Commission, Office of Information Services, 1972).
- Dirac, P. A. M. The quantum theory of electron, Proc. R. Soc. London A 117, 610–624 (1928). [CrossRef]
- Sodickson, L. et al. “Single-quantum annihilation of positrons" Physical Review. 124: 1851 (1970). [CrossRef]
- Hubbell, J. H. Electron positron pair production by photons: A historical overview, Radiation Physics and Chemistry, 75 (6): 614–623 (2006). [CrossRef]
- Soddy, F. The Complexity of Chemical Elements, ‘The Scientific Monthly’, Vol. 5, No. 5, pp. 451-462 (1917).
- Agostini, M. et al. Test of electric charge conservation with Borexino, Phys. Rev. Lett. 115, 231802 (2015). [CrossRef]
- Nagy, S. Subatomic particles, nuclear structure and stability, Radiochemistry and Nuclear Chemistry, 2. 357-408 (2007).
- Stacey, K. (media contact), Can the wave function of an electron be divided and trapped? News from Brown, 401-863-3766 (2014).
- Weinberg, S. The decay of the proton, Scientific American, vol. 244, p. 64-75 (1981).
- Blackett. P.M.S. The elementary particles of nature, The British Journal of Radiology, Vol. XXXI, No.361 (1958).
- Parker, S.P. (ed.): McGraw-Hill Encyclopedia of Science and Technology,' Fifth Edition, Vol. 5, McGraw-Hill Book Co., New York (1982).
- Brown M. L. Brown, The idea of the neutrino, Physics Today, 23-28 (1978).
- Creţu, A. Diagnosing disagreements: the authentication of the positron 1931-1934, studies in history and philosophy of science part B: Studies in history and philosophy of modern physics 70, 28-38 (2020). [CrossRef]
- Murayama, H. The origin of neutrino mass, Physics World, 36-37 (2002).
- Mohapatra, R. N. Physics of neutrino mass, SLAC Summer Institute on particle physics (SSI04), (2004).
- Roll, P. G. Krotkove, R. and Dicke, R. H. The Equivalence of Inertial and Passive Gravitational Mass, Annals of Physics, 26, 442-517 (1964). [CrossRef]
- Carlip, S. Kinetic Energy and the Equivalence Principle, Am. J. Phys. 66, 409 (1998). [CrossRef]
- L. J. Wang, Unification of Gravitational and Electromagnetic Forces, J Phys Chem Biophys, (2018).
- Budzikiewicz, H. Grigsby, R.D. Mass spectrometry and isotopes: a century of research and discussion, Mass Spectrometry Reviews. 25 (1): 146–57 (2006). [CrossRef]
- Mohr, P.J. et al. CODATA Recommended Values of the Fundamental Physical Constants, A Rev. Mod. Phys, 84 1527-1605 (2012).
Figure 1.
An electron comprises only two physical components: electron mass and electrostatic field. It lacks any independent entity identifiable as a charge.
Figure 1.
An electron comprises only two physical components: electron mass and electrostatic field. It lacks any independent entity identifiable as a charge.

Figure 2.
Opposite electron masses and electrostatic fields are the physical constituents of opposite electrons.
Figure 2.
Opposite electron masses and electrostatic fields are the physical constituents of opposite electrons.
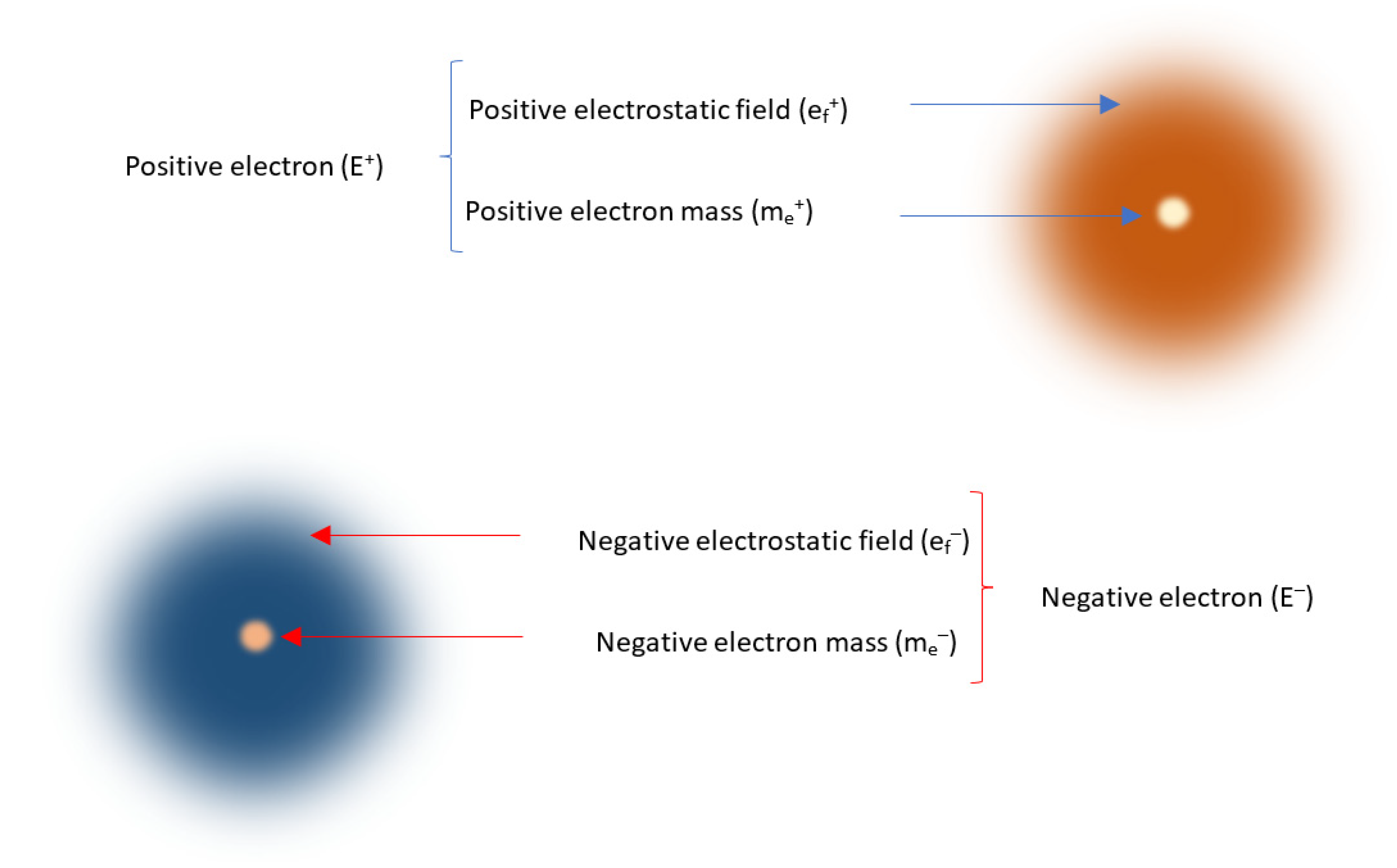
Figure 3.
Atomic locations of opposite charges match the atomic origins of opposite electrons. This suggests that an electron is a charge travelling at high speed outside the atom.
Figure 3.
Atomic locations of opposite charges match the atomic origins of opposite electrons. This suggests that an electron is a charge travelling at high speed outside the atom.

Table 1.
Four considerations depict a charge and an electron as fundamentally different things (in blue colour). 1) The atomic ratio of positive to negative charges is 1:1 but the ratio of negative to positive electrons is 1:0 – positive electrons are considered absent in the atom. 2) An electron has known rest mass but a charge is tacitly considered massless. 3) A pair of opposite charges neutralises but a pair of opposite electrons annihilates. 4) The ratio of positive to negative charges in our environment is 1:1 but negative electrons considerably outnumber positive electrons.
Table 1.
Four considerations depict a charge and an electron as fundamentally different things (in blue colour). 1) The atomic ratio of positive to negative charges is 1:1 but the ratio of negative to positive electrons is 1:0 – positive electrons are considered absent in the atom. 2) An electron has known rest mass but a charge is tacitly considered massless. 3) A pair of opposite charges neutralises but a pair of opposite electrons annihilates. 4) The ratio of positive to negative charges in our environment is 1:1 but negative electrons considerably outnumber positive electrons.
| Entity |
Electric symmetry (a shared feature) |
Presence in the atom | Rest mass | Positive-negative pair interaction | Numerical symmetry |
| Charge | Positive (known) | Present (50% of charges) | Absent? | Neutralisation | Symmetrical (same number of opposite charges observed) |
| Negative (known) | Present (50% of charges) | Absent? | |||
| Electron | Positive (known) | Absent (0% of electrons)? | Present | Annihilation | Asymmetrical (more negative than positive elections observed) |
| Negative (known) | Present (100% of electrons) | Present |
Table 2.
The Curie-Joliot interpretation of β+ decay reveals that a positron-on-proton is the negatron’s natural counterpart. A negatron-proton pair fails to match due to mass asymmetry; a negatron-positron pair due to numerical asymmetry.
Table 2.
The Curie-Joliot interpretation of β+ decay reveals that a positron-on-proton is the negatron’s natural counterpart. A negatron-proton pair fails to match due to mass asymmetry; a negatron-positron pair due to numerical asymmetry.
| Negatron (negative electron) | |||||
| Equal mass | Equal charge | Equal number | Opposite electric effect | ||
|
Natural positive counterpart |
Proton? | X | √ | √ | √ |
| Environmental positron? | √ | √ | X | √ | |
| Positron-on-proton? | √ | √ | √ | √ | |
Table 3.
Positron-on-proton and orbital negatron have characteristics of charges rather than those of electrons.
Table 3.
Positron-on-proton and orbital negatron have characteristics of charges rather than those of electrons.
| Empirical characteristics | ||
| Subatomic pair | Pair interaction | Numerical symmetry |
| Nuclear positive charge and orbital negative charge | Neutralisation (coexistence) | Symmetrical |
| Positron-on-proton and orbital negatron | Neutralisation (coexistence) | Symmetrical |
Table 4.
The sole difference between a charge and an electron is the speed at which they are moving. An ‘atom of electricity’ at near-static and ultrahigh speeds is recognised as a charge and an electron 7respectively.
Table 4.
The sole difference between a charge and an electron is the speed at which they are moving. An ‘atom of electricity’ at near-static and ultrahigh speeds is recognised as a charge and an electron 7respectively.
| Material uniformity of charge and electron | Differences due to behaviours | |||||||
| Entity | Speed | Location | Name | Types | Rest mass | Presence in atom | Positive-negative pair interaction | Natural abundance |
|
‘Atoms of electricity’ |
Near-static | Inside the atom or on material surface | Charges |
Positive | Positive electron mass | Present | Neutralisation | Symmetrical (positive to negative ratio of 1:1) |
| Negative | Negative electron mass | Present | ||||||
| Ultrahigh |
Extra-atomic environment | Electrons |
Positive | Positive electron mass | Absent | Annihilation | Asymmetrical (more negative than positive) | |
| Negative | Negative electron mass | Absent | ||||||
Table 5.
Coexisting at subatomic distances, opposite charges neutralise into a natural unit of electrically neutral matter – which is the quantum of ordinary (gravitational) mass.
Table 5.
Coexisting at subatomic distances, opposite charges neutralise into a natural unit of electrically neutral matter – which is the quantum of ordinary (gravitational) mass.
| Positive charge (e+) | = | Positive electron mass (me+) | + | Positive electrostatic field (ef+) |
| + | + | + | ||
| Negative charge (e–) | = | Negative electron mass (me–) | + | Negative electrostatic field (ef–) |
| ‖ | ‖ | ‖ | ||
| Neutral charge (2e0) or quantum of ordinary mass | = | Quantum of electrically neutral inertial mass (2me0) | + | Neutral electrostatic field (2ef0) or gravitational field |
Table 6.
Rounding off the empirical masses of baryons to the nearest whole electron mass (me) reveals that a particle’s charge status depends on whether it consists of an odd or an even number of electron masses. The charge-mass relation harmonizes with Equation (5) and Equation (9), implying that positive and negative electron masses are the natural bricks of which baryonic masses are made.
Table 6.
Rounding off the empirical masses of baryons to the nearest whole electron mass (me) reveals that a particle’s charge status depends on whether it consists of an odd or an even number of electron masses. The charge-mass relation harmonizes with Equation (5) and Equation (9), implying that positive and negative electron masses are the natural bricks of which baryonic masses are made.
| Multiplet | Electron or elementary mass (me) units in a particle | Number of charges (e) and charge states (superscript) | Electron mass even-odd status | Electric charge status |
| Nucleon | 1837me | 1837e+ | Odd | Charged |
| 1840me | 1840e0 | Even | Neutral | |
| Pion | 264me | 264e0 | Even | Neutral |
| 273me | 273e+ | Odd | Charged | |
| Kaon | 965me | 965e+ | Odd | Charged |
| 968me | 968e0 | Even | Neutral | |
| 974me | 974e0 | Even | Neutral | |
| Eta | 1074me | 1074e0 | Even | Neutral |
| 1077me | 1077e+ | Odd | Charged | |
| Lambda | 2153me | 2153e+ | Odd | Charged |
| 2183me | 2183e– | Odd | Charged | |
| Sigma | 2328me | 2328e0 | Even | Neutral |
| 2343me | 2343e– | Odd | Charged | |
| Xi | 2573me | 2573e– | Odd | Charged |
| 2579me | 2579e+ | Odd | Charged |
Table 7.
The particles recognised as positive, negative and neutral electric charges at nonrelativistic speeds (static state) are the same ones recognised as positive (beta) electron, negative (beta) electron, and beta neutrino at relativistic speeds.
Table 7.
The particles recognised as positive, negative and neutral electric charges at nonrelativistic speeds (static state) are the same ones recognised as positive (beta) electron, negative (beta) electron, and beta neutrino at relativistic speeds.
| Name of particle at non-relativistic (near-static) speed | Symbol and charge status of particle at nonrelativistic speed | Name of particle at relativistic (ultra-high) speed | |
| 1 | Positive charge | e+ | Positron (beta positive electron) |
| 2 | Negative charge | e– | Negatron (beta negative electron) |
| 3 | Neutral charge | 2e0 | Neutrino (beta neutrino) |
Table 8.
A unit of 3me differentiates a proton and a neutron. The principle works in other particle multiplets, revealing linking known particles (bolded) by filling the gaps between them with a series of 3me units. The scheme predicts an array of new particles in terms of their masses and electric charge statuses.
Table 8.
A unit of 3me differentiates a proton and a neutron. The principle works in other particle multiplets, revealing linking known particles (bolded) by filling the gaps between them with a series of 3me units. The scheme predicts an array of new particles in terms of their masses and electric charge statuses.
| Multiplet | Known (bolded) and potential members of multiplets in elementary mass units and charge states |
| Nucleon | ...1831e–…1834e0...1837e+…1840e0...1843e–… |
| Pion | ... 264e0 … 267e– … 270e0 … 273e+... |
| Kaon | ... 965e+ … 968e0 … 971e– … 974e0... |
| Eta | …1071e–... 1074e0 … 1077e+...1080e0… |
| Lambda | ... 2153e+… 2156e0… 2159e–… 2162e0 … 2165e+ … 2168e0… 2171e– … 2174e0 … 2177e+… 2180e0 … 2183e–... |
| Sigma | ... 2328e0 … 2331e+… 2334e0… 2337e–… 2340e0… 2343e+... |
| Xi | ... 2573e- … 2576e0… 2579e+... |
Table 9.
Four natural rules govern beta decays, yielding the four observable outcomes.
| No. | Rule | Emission results | Non-neutrino emission |
| 1 | Nuclear positive and orbital negative charges (static electrons) can appear concurrently and remain in the atom. | No emission besides neutrino. This is ‘internal adjustment’ and increases atomic number by one. To conserve charge or keep the atom stable, the new positive and negative charges (static electrons) are retained in the nucleus and the orbit respectively. | None |
| 2 | Positive charge not allowed in orbits. | Beta positive electron (positron) emission. | β+ |
| 3 | Nuclear negative and orbital positive charges may emerge concurrently but both must be expelled from the atom. | Positive and negative electrons concurrently ejected and ‘annihilate’ into gamma rays. | γ |
| 4 | Unpaired negative charge in nucleus not allowed. | Beta negative electron emitted. | β- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






